Experimental and Computational Approaches to Interfacial Resistance in Solid-State Batteries

1. Introduction

Lithium-ion batteries predominate in today’s rechargeable battery systems because of their high energy densities. They have been used portable electronics devices including cellular phones and notebook PC’s and serving as a key component in this information society for more than 20 years. Moreover, they start to be installed in vehicles and smart grids for realizing a low-carbon society; however, some issues including safety originating from the thermal and electrochemical instability of their organic-solvent electrolytes have not gone out completely. Because inorganic solid electrolytes exhibit higher thermal and electrochemical stability, use of the solid electrolytes is expected to be an efficient solution (Tarascon and Armand, 2001), even if the electrochemical stability is attributed to the kinetic stabilization as suggested in Zhu et al. (2015). However, solid-state lithium batteries had been suffering from low power densities.

Essential materials to improve the power densities are, of course, solid electrolytes with high ionic conductivities. Since ions generally diffuse faster in liquids than in solids, the use of solid electrolytes lowers the power densities. However, high ionic conductivities that are comparable to that in liquid systems have been achieved among sulfide solid electrolytes. Sulfide ions are larger in size and higher in polarizability than oxide counterparts. The large ionic radius leaves wide opening for ionic conduction, and the higher polarizability weakens attraction between lithium and sulfide ions to make the lithium ions mobile (Zheng et al., 2003). Therefore, high ionic conductivities have been often observed in sulfides, as reviewed in Minami et al. (2006) and Takada (2013b), and the highest conductivities in sulfide electrolyte systems have recently reached 10⁻² S cm⁻¹ (Kamaya et al., 2011; Seino et al., 2014).

In addition, sulfide solid electrolytes exhibit high processability. They are relatively soft materials (Sakuda et al., 2013) and show low grain boundary resistance only by compression. Therefore, sintering process is not essential to connect the particles, whereas high temperature sintering is inevitable to connect ionic conduction between particles in oxide solid electrolytes, for instance. Besides the high ionic conductivity, this feature is beneficial for developing solid-state batteries, because high temperature sintering promotes mutual diffusion that forms impurity phases at the interface. However, even such solid electrolytes had not improve the power density to be high enough for practical application by themselves.

As reported in Takada et al. (2008), when a sulfide electrolyte is combined with graphite and LiCoO₂, which are typical anode and cathode materials, respectively, to assemble a lithium-ion-type solid-state battery, high resistance is found in its cathode. Because the resistance is the highest in the battery to be rate-determining in the battery reaction, power density will not be improved without reducing the cathode resistance. Ohta et al. (2006) integrates a novel interface structure between the sulfide electrolyte and LiCoO₂ into the cathode in order to improve the power density to a practical level. In the interface structure, surface of the LiCoO₂ particles is coated with Li₄Ti₅O₁₂, which act as an oxide solid electrolyte on the surface. This surface coating has reduced the cathode resistance by 1/20 and increased the power density to be as high as that of commercial lithium-ion batteries with liquid electrolytes. The interface is designed on the basis of “nanoionics” (Maier, 1995).

Ionic conductors often exhibit anomalous ionic conduction at their surface or interface. It is explained that the anomalous ionic conduction is induced by the changing concentration of mobile ions to form space-charge layers at the interface. Nanoionics has been often reported as enhanced ionic conduction at interfaces, as reviewed in Maier (2014). On the other hand, Takada (2013a) suggests that the space-charge layer appears as a lithium-depleted layer at the cathode interface in solid-state batteries with sulfide electrolytes. Noble potential of the cathode material depletes lithium ions of the sulfide electrolyte at the interface to the cathode material and makes the interface highly resistive. The surface coating, which interposes the oxide electrolyte between the high-voltage cathode and sulfide electrolyte materials, suppresses the lithium depletion to reduce the interfacial resistance.

Although the changes in the electrode properties upon the surface coating are well explainable by the interface model based on nanoionics, origin of the high interfacial resistance and its reduction are still under debate, because changes in the interfacial structure upon the coating, which are predicted by the interface model, have not been visualized yet. Since the space-charge layer lies between solids with only several nanometers in thickness, it has never shown up even on advanced analyses. This study employs computational science using the first-principle calculations in order to get a clear picture of the interfacial phenomena. Results from density functional theory (DFT) calculation for the interfaces to Li_1−xFePO₄ cathode materials are combined with experimental results from the interfaces to Li_1−xCoO₂ and Li_1−xMn₂O₄ in Ohta et al. (2007) and Takada et al. (2012) to reveal the validity of the space-charge layer model.

2. Materials and Methods

2.1. Experiments

The materials presented in this paper have been already reported in Ohta et al. (2007) and Takada et al. (2012). Thin layer of LiNbO₃ was formed on the particle surface of LiCoO₂ and LiMn₂O₄ from an ethanol solution of alkoxides of Li and Nb by a rolling fluidized coating method. The LiCoO₂ and LiMn₂O₄ powders are commercially available (D10 and M811, respectively; Toda Kogyo). Average particle size and Brunauer–Emmett–Teller (BET) surface area of the LiCoO₂ powder are 11.2 μm and 0.26 m² g⁻¹, respectively, while those of the LiMn₂O₄ powder are 5 μm and 0.40 m² g⁻¹, respectively. Alkoxides used to form LiNbO₃ layer are lithium ethoxide and niobium pentaethoxide. The amount of LiNbO₃ coated on the surface varies from 0 (uncoated) to 94 mg m⁻². The maximum amount corresponds to LiNbO₃ layer of 20 nm in thickness, if the surface of active material particles is uniformly covered with the LiNbO₃.

The sulfide solid electrolyte to make the interface to the cathode materials in this study is Li_3.25Ge_0.25P_0.75S₄ (Kanno and Murayama, 2001). It is mixed with the LiCoO₂ and the LiMn₂O₄ at weight ratios of 3:7 and 1:1, respectively, to form the interfaces in the composite electrodes. Solid-state cells for the electrochemical measurements are assembled from the mixtures (12.7 mg for the LiCoO₂ and 15 mg for the LiMn₂O₄) as the working electrodes, In–Li alloy as the counter electrodes and Li_3.25Ge_0.25P_0.75S₄ as the separators. Because electrode potential of the In–Li electrode is 0.62 V vs. Li⁺/Li, cell voltage is presented by adding 0.62 V in this paper as if the electrode properties were investigated in electrochemical cells with lithium metal anodes. The LiCoO₂ cathodes are charged to 4.2 V vs. Li⁺/Li, that is, 3.58 V in the cell voltage at a constant current of 127.4 μA cm⁻², while the LiMn₂O₄ are charged to 4.3 V vs. Li⁺/Li at 20 μA cm⁻², before the electrochemical impedance spectroscopy to evaluate the electrode impedance.

2.2. Computations

The cathode material used in the computations is LiFePO₄. Li₃PO₄ and Li₃PS₄ are selected as oxide and sulfide-based solid electrolytes, respectively, in order to compare cathode/oxide electrolyte and cathode/sulfide electrolyte interfaces. The LiFePO₄/Li₃PO₄ interface is constructed between LiFePO₄ (010) and γ-Li₃PO₄ (100) planes by the computation method reported in Sumita et al. (2015) and Sumita et al. (2016).

On the other hand, because lattice mismatch between LiFePO₄ and Li₃PS₄ is too large to form a coherent interface, Li₃PS₄ is amorphized on the LiFePO₄ (010) plane by first principles molecular dynamics simulation (FP-MD) to form the interface as follows. The amorphous Li₃PS₄ is constructed from 16 Li₃PS₄ units stacked on (010) plane of a 1 × 3 × 2 supercell of LiFePO₄. The interface is stabilized by FP-MF calculation with a constant-temperature, constant-pressure (NPT) ensemble at the temperature of 400 K, and the pressure of 1.0 atom with the valuable cell dimension perpendicular to the interface. The interface structure is equilibrated under the temperature control by canonical sampling through velocity rescaling thermostat (Bussi et al., 2007) for 40 ps.

In this study, cathode interfacial structures during the cell operation are also investigated. Fully charged LiFePO₄, i.e., FePO₄, is stacked onto Li₃PO₄ and Li₃PS₄, respectively, and the interface structures are relaxed by FP-MD simulations with an NPT ensemble at 400 K under 1.0 atom for ca. 200 ps. These interfaces are connected to lithium metal in order to calculate energies relative to its Fermi level.

Computational analyses for these interfaces are according with the procedures in Sumita et al. (2015) and Sumita et al. (2016). Total energies are calculated at the Γ point in the super cell approach within DFT implemented in CP2K at www.cp2k.org. The Goedecker, Teter, and Hutter (GTH) pseudopotentials are selected for PBE functional (Perdew et al., 1996) with the local spin density approximation in this study. Valence pseudowave functions are expanded in Gaussian-type orbitals, and the density is represented in a plane wave auxiliary basis in the hybrid Gaussian (MOLOPT DZVP) and plane-wave (240 Ry for cutoff energy) basis set. The +U strategy is applied to include the electronic correlation within the d orbital of Fe, in which the effective U is set to 4.3 eV as in Wang et al. (2007).

3. Results

3.1. Changes in the Electrode Properties upon the LiNbO₃ Coating in the Experiments

The surface coating reduces the cathode impedance, as demonstrated in Figure 1. Each Nyquist plot consists of an arc followed by a tail in the low frequency region. The impedance at the high frequency limit agrees with the resistance of the solid electrolyte layer calculated from the cross section and the thickness of the electrolyte layer and the ionic conductivity of the solid electrolyte. It is, in general, very difficult to derive intrinsic interfacial resistance from impedance data of composite electrodes; however, it is clear that the surface coating decreases the interfacial resistance. The impedance including the interfacial resistance, which draws an arc in the Nyquist plot, is decreased from 670 to 10 Ω cm² for the Li_1−xCoO₂ cathode and from 8000 to 150 Ω cm² for the Li_1−xMn₂O₄ cathode, that is, by almost two orders of magnitude.

FIGURE 1

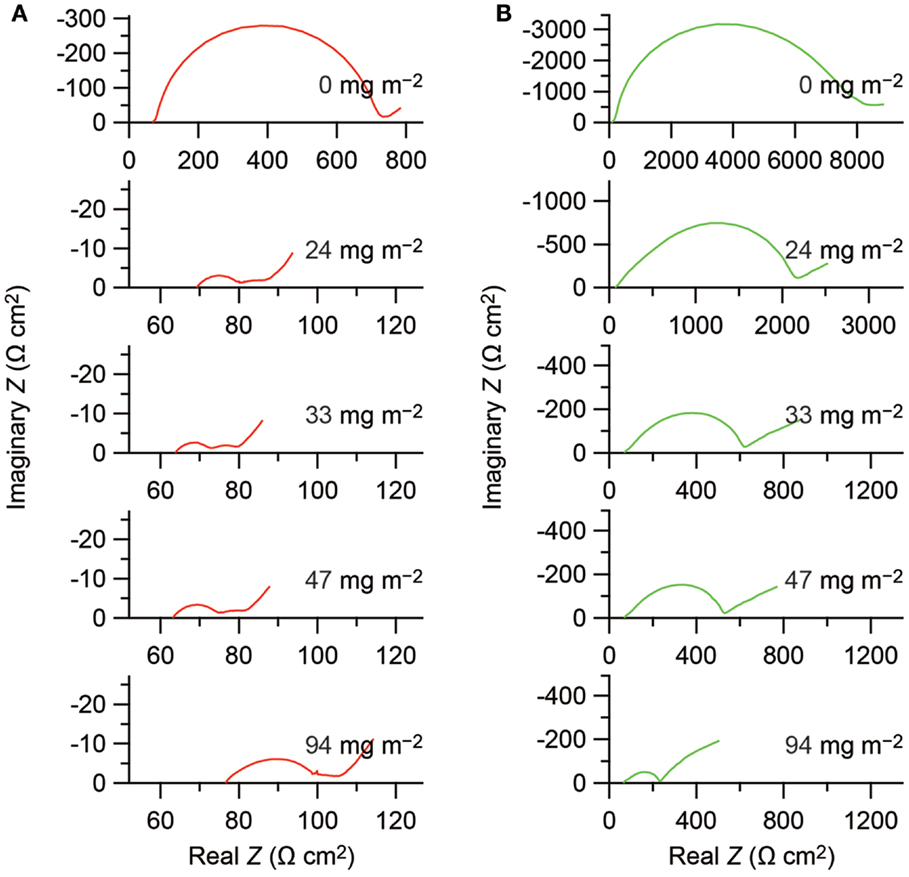
Figure 1. Nyquist plots obtained from the solid-state electrochemical cells with configuration of In–Li_x/Li_1−xCoO₂ (A) and In–Li_x/Li_1−xMn₂O₄ (B). Horizontal and vertical axes indicate real and imaginary parts of the complex impedance based on the projection areas of the cathodes, respectively. The amounts of the LiNbO₃ coating on the active materials are indicated on the basis of the BET surface areas of the active materials in the figures. Impedance date reported in Ohta et al. (2007) and Takada et al. (2012) are replotted in this figure, copyright © 2007 and 2012, with permission from Elsevier.

The surface coating has another effect on the electrode properties. Lithium ions are deintercalated from LiCoO₂ and LiMn₂O₄ in potential plateaus at 4 V vs. Li⁺/Li. However, they exhibit additional potential slopes prior to the 4 V plateaus in the sulfide solid electrolyte during the charging, as shown in the top panels of Figure 2. The surface coating changes the length of the slopes. Before surface coating, both of the LiCoO₂ and LiMn₂O₄ show potential slopes with almost the same length of 0.2 μAh cm⁻². The increasing amount of LiNbO₃ gradually shortens the potential slopes, and the slopes finally disappear at the LiNbO₃ amount of 94 mg m⁻².

FIGURE 2

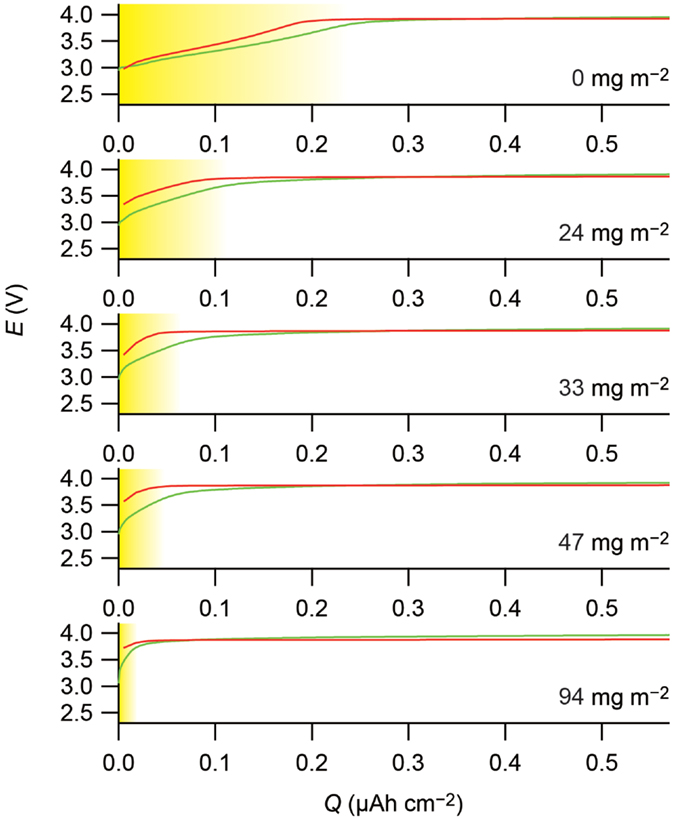
Figure 2. The beginning parts of the charge curves of the cathodes. The curves for the In–Li_x/Li_1−xCoO₂ and In–Li_x/Li_1−xMn₂O₄ are shown in red and green, respectively. The horizontal axes indicate the charge capacities normalized by the BET surface areas of the active materials, and the vertical axes indicate the cathode potential calculated by adding 0.62 V, which is the electrode potential vs. Li⁺/Li of the In–Li_x counter electrodes, to the cell voltage. The amounts of the LiNbO₃ coated on the active materials are indicated on the basis of the BET surface areas of the active materials in the figures. The potential slopes described in the text are shaded in yellow. Charge curves reported in Ohta et al. (2007) and Takada et al. (2012) are replotted in this figure, copyright © 2007 and 2012, with permission from Elsevier.

The capacities in the potential slopes are very small. For example, the capacity of 0.2 μAh cm⁻² based on the BET surface area corresponds only to 0.5 mAh g⁻¹ for the LiCoO₂ and 0.8 mAh g⁻¹ for the LiMn₂O₄. However, the slopes are not artifact. They appear both in LiCoO₂ and LiMn₂O₄ with almost the same capacity based on the BET surface areas of the materials and fade to the same degree with increasing amounts of LiNbO₃.

3.2. Electronic and Interface Structures Obtained from the Computations

Figure 3 plots density of states (DOS) in LiFePO₄, Li₃PO₄, and Li₃PS₄ against energy relative to Fermi level of lithium metal. They are semiconductors with band gap energies of 3.7, 5.9, and 2.4 eV, respectively. The valence band maximum (VBM) of the LiFePO₄, which mainly consists of Fe 3d orbital, is located at −3.5 V, indicating that charge reaction of LiFePO₄ extracts electrons from the 3d orbitals at 3.5 V to give the electromotive force in a Li/Li_1−xFeO₄ cell. The VBM’s in Li₃PO₄, and Li₃PS₄, where contribution of O 2p and S 3p orbitals is predominant, are located at −4.0 and −2.0 V, respectively.

FIGURE 3

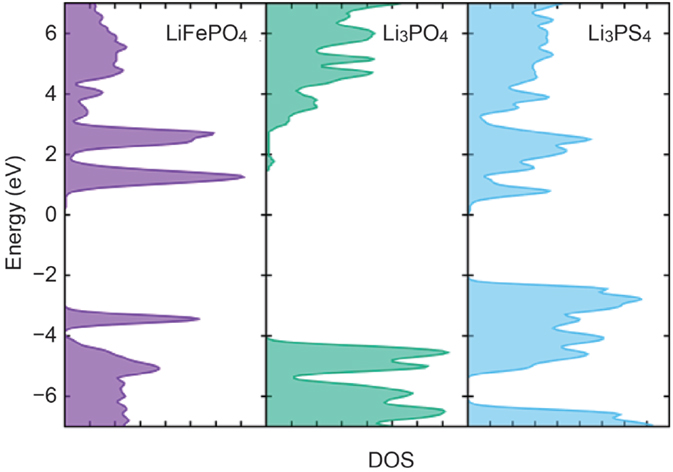
Figure 3. Density of states calculated for LiFePO₄, Li₃PO₄, and Li₃PS₄. Zero in energy is set to the Fermi level of Li metal.

Figures 4B and 5B show the crystallographic structures of the interfaces during the cell operation, which are computed by relaxing FePO₄/Li₃PO₄ and FePO₄/Li₃PS₄ stacks displayed in Figures 4A and 5A, respectively, by the FP-MD. It shows a clear difference between the interfaces. The structure relaxation leads to little change in the FePO₄/Li₃PO₄ interface, while it transfers a significant amount of lithium ions residing in the interface region of Li₃PS₄ to the FePO₄. As a result, FePO₄ has become Li_1−xFePO₄. At the same time, the interface region of the Li₃PS₄ becomes low in the lithium-ion concentration, while that in the bulk region is not changed significantly, as can be seen in Figure 5B.

FIGURE 4

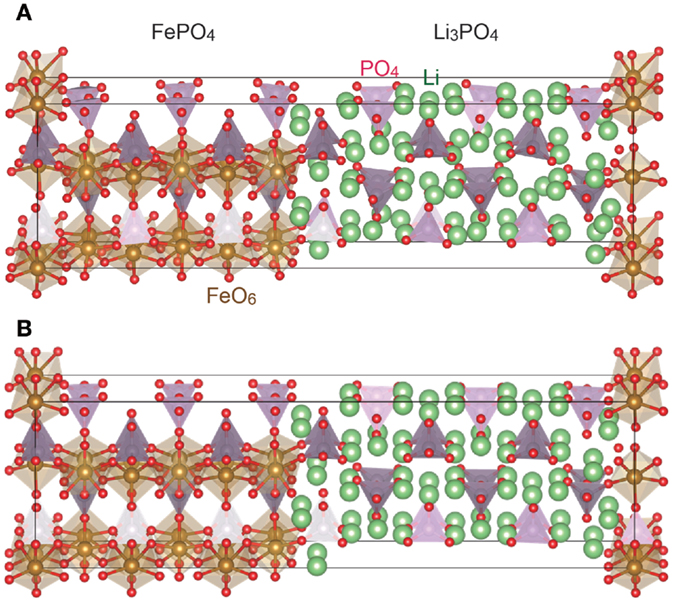
Figure 4. Interface structure between FePO₄ and Li₃PO₄ before (A) and after (B) the FP-MD. The crystal structures are drawn by a computer program, VESTA (Momma and Izumi, 2011).

FIGURE 5

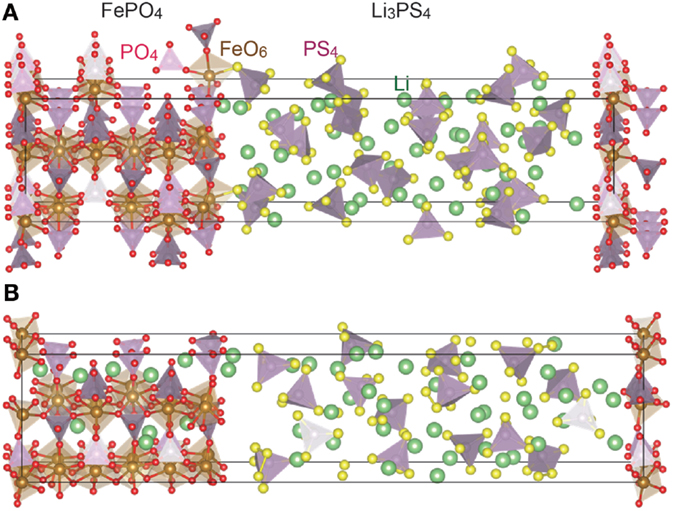
Figure 5. Interface structure between FePO₄ and Li₃PS₄ before (A) and after (B) the FP-MD. The crystal structures are drawn by a computer program, VESTA (Momma and Izumi, 2011).

4. Discussion

4.1. Formation of Lithium-Depleted Layer at Cathode/Sulfide Solid Electrolyte Interface

Origin of the high interface resistance at oxide cathodes/sulfide electrolytes can be found in Figure 5B. The FP-MD, which leads the interface to the equilibrium, transfers lithium ions from Li₃PS₄ to FePO₄ and depletes lithium ions on the Li₃PS₄ side of the interface. This result reveals that the space-charge layer appears as a lithium-depleted layer at the Li_1−xFePO₄/Li₃PS₄ interface, which should make the interface highly resistive owing to the absence of charge-carrying lithium ions.

This computational results demonstrate that the ion concentration on the electrode surface will be a critical factor governing the interfacial resistance. It is needless to mention that the ion concentration is related to the electrode potential through a Nernst equation.

$E=E^0+\frac{\mathit{RT}}{\mathit{zF}}\ln \frac{a_{\text{Ox}}}{a_{\text{Red}}}$ (1)

In the Nernst equation, electrode potential, E is connected to activities of oxidant and reductant, a_Ox and a_Red, respectively, with the standard electrode potential, E⁰; the gas constant, R; the absolute temperature, T; the number of transferred electrons, z; and the Faraday constant, F. Because activities are related to ion concentration through activity coefficient, the concentrations of oxidant and reductant determine the E and vice versa. In solid electrolytes, only lithium ions are mobile to change the concentration; therefore, presence and absence of lithium should be regarded as the reductant and oxidant, respectively. That is, lithium-ion concentration at the interface is governed by the electrode potential, and noble potential of the oxide cathodes will decrease it.

E⁰ in sulfide will be much lower than that in oxides, because lithium ions are much more loosely bonded to the lattice framework in sulfides. Therefore, a_Ox/a_Red, which corresponds to concentration of lithium vacancies, should become very large in order to make the E reach the redox potential of the cathode and start the charge reaction. In other word, the oxidation current in the beginning of charging is spent to remove lithium ions from the sulfide solid electrolyte side of the cathode/sulfide electrolyte interface to increase the a_Ox/a_Red in equation (1) before E reaches the redox potential. After the E becomes equal to the redox potential of the cathode, lithium deintercalation from the cathode material begins.

This classical picture may be rough but seems reasonable. The preferential removal of lithium ions from the sulfide electrolyte side can be seen as potential slopes appearing for the uncoated materials in Figure 2, which are distinguishable from the following potential plateaus originated from lithium deintercalation from the cathode materials. Moreover, because E determines the lithium-ion concentrations on the electrode surface in equation (1), the potential slopes should have the same capacity between the LiCoO₂ and LiMn₂O₄ due to the same electrode potential of 4 V, which is also evidenced by the top panels in Figure 2.

In addition, equation (1) suggests that change in the electrode potential changes lithium-ion concentration exponentially; that is, increasing E results in the drastic decrease of lithium ions. A buffer layer in the first report on the reduced interfacial resistance (Ohta et al., 2006) is Li₄Ti₅O₁₂. Although it decreases the interfacial resistance at Li_1−xCoO₂/Li_3.25Ge_0.25P_0.75S₄ by 1/20, its ionic conductivity is only 10⁻¹³–10⁻¹⁰ S cm⁻¹ (Wilkening et al., 2007; Fehr et al., 2010), while ionic conductivity of the sulfide electrolyte, Li_3.25Ge_0.25P_0.75S₄, is as high as 2.2 × 10⁻³ S cm^–1 (Kanno and Murayama, 2001). A reasonable explanation for the reduced resistance inferred from the Nernst equation is that the high bulk conductivity of Li_3.25Ge_0.25P_0.75S₄ becomes so low at the interface due to the exponential decrease in the carrier concentration that even the Li₄Ti₅O₁₂ with low ionic conductivity reduces the resistance.

The DFT calculation results shown in Figure 3 gives a clear explanation for the preferential removal of lithium ions from the Li₃PS₄ side upon charging. Charge reaction in LiFePO₄ is lithium deintercalation accompanied by the extraction of electrons in 3d orbitals of LiFePO₄ located around −3.5 V. On the other hand, VBM of the Li₃PS₄ is located at −2.0 eV, which is higher than the 3d orbital of LiFePO₄. Therefore, electrons will be extracted not from the LiFePO₄ but from the Li₃PS₄ at the beginning of the charge reaction, and simultaneously lithium ions will be extracted from the Li₃PS₄ to keep charge neutrality.

4.2. Reduction of Interfacial Resistance by Surface Coating

High interfacial resistance at oxide cathodes/sulfide electrolytes is considered to come from lithium-depleted layer formed at the interface, as discussed above. Therefore, reduction of the interfacial resistance by interposing oxide electrolytes observed in the experiment should be attributed to the suppression of lithium depletion; that is, lithium-depleted layer is not formed at oxide cathode/oxide solid electrolyte interfaces.

In fact, the FP-MD to relax the interfacial structure does not change distribution of lithium ions around the FePO₄/Li₃PO₄ interface, as demonstrated in Figure 4. The Li₃PO₄ keeps its original structure at the interface to the FePO₄, and lithium depletion is not recognized there. Moreover, the DOS’s calculated for LiFePO₄ and Li₃PO₄ indicate that lithium ions are not preferentially removed from the solid electrolyte. VBM of the Li₃PO₄ is located above 3d orbital of LiFePO₄ as shown in Figure 3, and thus charging current should be electrons removed from LiFePO₄ even at the beginning. That is, lithium deintercalation from the LiFePO₄ takes place at the interface to Li₃PO₄ from the beginning of charging.

Because lithium ions are not preferentially removed from the oxide electrolyte side of the interface, cathode/oxide electrolyte interfaces do not provide a potential slope to the charging curves. In fact, Figure 2 indicates fading of the potential slopes for the LiCoO₂ and LiMn₂O₄ observed in the Li_3.25Ge_0.25P_0.75S₄ interfaces upon the LiNbO₃ coating. The increasing amount of LiNbO₃ coated on the cathode materials gradually shortens the potential slope, which is attributable to the increasing coverage by the coating layer. It decreases the interface area, where the cathode materials are directly contacted to the sulfide solid electrolyte, to eliminate the potential slope. Simultaneously, it increases the cathode/oxide electrolyte interface area, where lithium-depleted layer is not formed, to decrease the interfacial resistance.

The above discussions have revealed that the high interfacial resistance and the effects of surface coating on the electrode properties are explainable by the space-charge model. On the other hand, Sakuda et al. (2010) has proposed another mechanism for the interfacial resistance and its reduction. It reports that transition metals and anions, as well as lithium ions, diffuse across a Li_1−xCoO₂/Li₂S–P₂S₅ to form an impurity phase. The impurity phase is concluded to be the reason for the high interfacial resistance, and the surface coating suppresses the mutual diffusion and reduces the interfacial resistance. On the other hand, such mutual diffusion is not observed in the present computations. Figure 5B exhibits that the structure relaxation changes the lithium-ion distribution around the interface without changing the flamework structure. However, it is premature to deny the mutual diffusion, because the relaxation time in the FP-MD simulations is only 200 ps.

It should be noted that Li_1−xFePO₄ is used as the cathode material in the computations instead of Li_1−xCoO₂ in the experiments in this study. LiFePO₄ forms a coherent interface to Li₃PO₄, as reported in Sumita et al. (2015). In addition, the surface spin-state of LiCoO₂ is complicated, although the manifold spin-states may not affect the band alignment at the interface significantly (Sumita and Ohno, 2016). That is, Li_1−xFePO₄ is better than Li_1−xCoO₂ to eliminate ambiguities in the computation models, and thus is used in this study. Although computations using Li_1−xCoO₂ is preferable to provide an accurate picture on the interfacial phenomena observed in the experiments, coincidences in the electrode properties between the LiCoO₂ and LiMn₂O₄ in the Li_3.25Ge_0.25P_0.75S₄ and the effects of the surface coating to the interfaces, which are displayed in Figures 1 and 2, and the above discussions strongly suggest that electrode potential of cathode materials dominates the lithium-ion concentration at the interface and the interfacial resistance. Of course, electrode potential of Li_1−xFePO₄ is 3.5 V and lower than 4.0 V for Li_1−xCoO₂ to a certain extent; however, both of them are far enough from the VBM of Li₃PS₄ not to give significant differences. Therefore, the picture given from the Li_1−xFePO₄ will be valid also for the interface to Li_1−xCoO₂. Computations on Li_1−xCoO₂ are in progress, and the results will appear in near future.

However, some differences may be found between the interfaces to Li_1−xFePO₄ and Li_1−xCoO₂. These cathode materials are quite different in the electronic conduction: Li_1−xCoO₂ exhibits metallic conduction, while Li_1−xFePO₄ is poor in electronic conduction and moreover insulating at x = 0. When they come into contact with a sulfide electrolyte, part of lithium ions in the electrolyte move into the cathode materials, as displayed in Figure 5B. By the way, Li_1−xFePO₄ is a two-phase system. Roughly speaking, Li_1−xFePO₄ is a mixture of FePO₄ and LiFePO₄. Therefore, the movement of lithium ions from the electrolyte into the material may form a LiFePO₄ layer at the electrode surface. Consequently, Li_1−xFePO₄ particles become to have a core–shell structure in sulfide electrolytes, where the core is a mixture of FePO₄ and LiFePO₄, while the shell mainly consists of LiFePO₄. Because the LiFePO₄ is electronically insulating, the lithium depletion may be suppressed at the surface of Li_1−xFePO₄, and thus the Li_1−xFePO₄ may work relatively well even without surface coating in sulfide electrolytes. That is, Li_1−xFePO₄ may have a self-origanized core–shell structure for high power, which is similar to that proposed in Xu et al. (2011), where the coating layer is formed only by compositional change in the cathode material.

Author Contributions

KT and TO are responsible for the experimental and computational studies, respectively.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank Dr. Narumi Ohta and Dr. Masato Sumita for their collaboration in the experiments and computations, respectively. This work was partially funded by the Ministry of Economy, Trade and Industry (METI), New Energy and Industrial Technology Development Organization (NEDO), ALCA-SPRING project of Japan Science and Technology Agency, and Ministry of Education, Culture, Sports, Science and Technology (MEXT).

References

Bussi, G., Donadio, D., and Parrinello, M. (2007). Canonical sampling through velocity rescaling. J. Chem. Phys. 126, 014101. doi:10.1063/1.2408420

PubMed Abstract | CrossRef Full Text | Google Scholar

Fehr, K., Holzapfel, M., Laumann, A., and Schmidbauer, E. (2010). DC and AC conductivity of Li_4/3Ti_5/3O₄ spinel. Solid State Ionics. 181, 1111–1118. doi:10.1016/j.ssi.2010.05.026

CrossRef Full Text | Google Scholar

Kamaya, N., Homma, K., Yamakawa, Y., Hirayama, M., Kanno, R., Yonemura, M., et al. (2011). A lithium superionic conductor. Nat. Mater. 10, 682–686. doi:10.1038/nmat3066

PubMed Abstract | CrossRef Full Text | Google Scholar

Kanno, R., and Murayama, M. (2001). Lithium ionic conductor thio-lisicon: the Li₂S–GeS₂–P₂S₅ system. J. Electrochem. Soc. 148, A742–A746. doi:10.1149/1.1379028

CrossRef Full Text | Google Scholar

Maier, J. (1995). Ionic conduction in space charge regions. Prog. Solid State Chem. 23, 171–263. doi:10.1016/0079-6786(95)00004-E

CrossRef Full Text | Google Scholar

Maier, J. (2014). Pushing nanoionics to the limits: charge carrier chemistry in extremely small systems. Chem. Mater. 26, 348–360. doi:10.1021/cm4021657

CrossRef Full Text | Google Scholar

Minami, T., Hayashi, A., and Tatsumisago, M. (2006). Recent progress of glass and glass-ceramics as solid electrolytes for lithium secondary batteries. Solid State Ionics. 177, 2715–2720. doi:10.1016/j.ssi.2006.07.017

CrossRef Full Text | Google Scholar

Momma, K., and Izumi, F. (2011). VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276. doi:10.1107/S0021889811038970

CrossRef Full Text | Google Scholar

Ohta, N., Takada, K., Sakaguchi, I., Zhang, L., Ma, R., Fukuda, K., et al. (2007). LiNbO₃-coated LiCoO₂ as cathode material for all solid-state lithium secondary batteries. Electrochem. commun. 9, 1486–1490. doi:10.1016/j.elecom.2007.02.008

CrossRef Full Text | Google Scholar

Ohta, N., Takada, K., Zhang, L., Ma, R., Osada, M., and Sasaki, T. (2006). Enhancement of the high-rate capability of solid-state lithium batteries by nanoscale interfacial modification. Adv. Mater. 18, 2226–2229. doi:10.1002/adma.200502604

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865

CrossRef Full Text | Google Scholar

Sakuda, A., Hayashi, A., and Tatsumisago, M. (2010). Interfacial observation between LiCoO₂ electrode and Li₂S–P₂S₅ solid electrolytes of all-solid state lithium secondary batteries using transmission electron microscopy. Chem. Mater. 22, 949–956. doi:10.1021/cm901819c

CrossRef Full Text | Google Scholar

Sakuda, A., Hayashi, A., and Tatsumisago, M. (2013). Sulfide solid electrolyte with favorable mechanical property for all-solid state lithium batteries. Sci. Rep. 3, 2261. doi:10.1038/srep02261

CrossRef Full Text | Google Scholar

Seino, Y., Ota, T., Takada, K., Hayashi, A., and Tatsumisago, M. (2014). A sulphide lithium super ion conductor is superior to liquid ion conductors for use in rechargeable batteries. Energy Environ. Sci. 7, 627–631. doi:10.1039/C3EE41655K

CrossRef Full Text | Google Scholar

Sumita, M., and Ohno, T. (2016). Multi-spin-state at Li₃PO₄/LiCoO₂ (104) interface. Phys. Chem. Chem. Phys. 18, 4316–4319. doi:10.1039/C5CP07735D

CrossRef Full Text | Google Scholar

Sumita, M., Tanaka, Y., Ikeda, M., and Ohno, T. (2015). Theoretically designed Li₃PO₄ (100)/LiFePO₄ (010) coherent electrolyte/cathode interface for all solid-state Li ion secondary batteries. J. Phys. Chem. C 119, 14–22. doi:10.1021/jp5060342

CrossRef Full Text | Google Scholar

Sumita, M., Tanaka, Y., Ikeda, M., and Ohno, T. (2016). Theoretical insight into charging process in a Li₃PO₄ (100)/LiFePO₄ (010) coherent interface system. Solid State Ionics. 285, 59–65. doi:10.1016/j.ssi.2015.09.029

CrossRef Full Text | Google Scholar

Takada, K. (2013a). Interfacial nanoarchitectonics for solid-state lithium batteries. Langmuir 29, 7538–7541. doi:10.1021/la3045253

CrossRef Full Text | Google Scholar

Takada, K. (2013b). Progress and prospective of solid-state lithium batteries. Acta Mater. 61, 759–770. doi:10.1016/j.actamat.2012.10.034

CrossRef Full Text | Google Scholar

Takada, K., Ohta, N., Zhang, L., Cu, X., Hang, B. T., Ohnishi, T., et al. (2012). Interfacial phenomena in solid-state lithium battery with sulfide solid electrolyte. Solid State Ionics. 225, 594–597. doi:10.1016/j.ssi.2012.01.009

CrossRef Full Text | Google Scholar

Takada, K., Ohta, N., Zhang, L., Fukuda, K., Sakaguchi, I., Ma, R., et al. (2008). Interfacial modification for high-power solid-state lithium batteries. Solid State Ionics. 179, 1333–1337. doi:10.1016/j.ssi.2008.02.017

CrossRef Full Text | Google Scholar

Tarascon, J.-M., and Armand, M. (2001). Issues and challenges facing rechargeable lithium batteries. Nature 414, 359–367. doi:10.1038/35104644

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, L., Zhou, F., Meng, Y. S., and Ceder, G. (2007). First-principles study of surface properties of LiFePO₄: surface energy, structure, wulff shape, and surface redox potential. Phys. Rev. B 76, 165435. doi:10.1103/PhysRevB.76.165435

CrossRef Full Text | Google Scholar

Wilkening, M., Amade, R., Iwaniak, W., and Heitjans, P. (2007). Ultraslow Li diffusion in spinel-type structured Li₄Ti₅O₁₂ – a comparison of results from solid state nmr and impedance spectroscopy. Phys. Chem. Chem. Phys. 9, 1239–1246. doi:10.1039/B616269J

CrossRef Full Text | Google Scholar

Xu, X., Takada, K., Watanabe, K., Sakaguchi, I., Akatsuka, K., Hang, B. T., et al. (2011). Self-organized core–shell structure for high-power electrode in solid-state lithium batteries. Chem. Mater. 23, 3798–3804. doi:10.1021/cm103665w

CrossRef Full Text | Google Scholar

Zheng, N., Bu, X., and Feng, P. (2003). Synthetic design of crystalline inorganic chalcogenides exhibiting fast-ion conductivity. Nature 426, 428–432. doi:10.1038/nature02159

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, Y., He, X., and Mo, Y. (2015). Origin of outstanding stability in the lithium solid electrolyte materials: insights from thermodynamic analyses based on first-principles calculations. ACS Appl. Mater. Interfaces 7, 23685–23693. doi:10.1021/acsami.5b07517

PubMed Abstract | CrossRef Full Text | Google Scholar