Structure and Ionic Conductivity of Li2S–P2S5 Glass Electrolytes Simulated with First-Principles Molecular Dynamics

Lithium thiophosphate-based materials are attractive as solid electrolytes in all-solid-state lithium batteries because glass or glass-ceramic structures of these materials are associated with very high conductivity. In this work, we modeled lithium thiophosphates with amorphous structures and investigated Li⁺ mobilities by using molecular dynamics calculations based on density functional theory (DFT-MD). The structures of xLi₂S–(100 − x)P₂S₅ (x = 67, 70, 75, and 80) were created by randomly identifying appropriate compositions of Li⁺, ${\text{PS}}_{\text{4}}^{\text{3}-},{\text{P}}_{\text{2}}{\text{S}}_{\text{7}}^{\text{4}-}$, and S²⁻ and then annealing them with DFT-MD calculations. Calculated relative stabilities of the amorphous structures with x = 67, 70, and 75 to crystals with the same compositions were 0.04, 0.12, and 0.16 kJ/g, respectively. The implication is that these amorphous structures are metastable. There was good agreement between calculated and experimental structure factors determined from X-ray scattering. The differences between the structure factors of amorphous structures were small, except for the first sharp diffraction peak, which was affected by the environment between Li and S atoms. Li⁺ diffusion coefficients obtained from DFT-MD calculations at various temperatures for picosecond simulation times were on the order of 10⁻³–10⁻⁵ Ų/ps. Ionic conductivities evaluated by the Nernst–Einstein relationship at 298.15 K were on the order of 10⁻⁵ S/cm. The ionic conductivity of the amorphous structure with x = 75 was the highest among the amorphous structures because there was a balance between the number density and diffusibility of Li⁺. The simulations also suggested that isolated S atoms suppress Li⁺ migration.

Introduction

The possibility of producing all-solid-state lithium-ion batteries (LIBs) has attracted much attention because the replacement of an organic liquid electrolyte with an inorganic solid electrolyte (SE) would simplify battery design, increase energy density, and make batteries safer and more durable. Realization of such batteries is critical for practical applications such as electric vehicles and plug-in hybrid electric vehicles. A major obstacle to the development of all-solid-state LIBs is that the ionic conductivity of SEs at room temperature (RT) is too low to achieve high-rate charging and discharging. In recent years, inorganic ceramics with high ionic conductivity have been widely studied (Knauth, 2009; Fergus, 2010; Takada, 2013; Ren et al., 2015). Sulfide SEs with the same level of conductivity as conventional liquid electrolytes have been discovered. For example, crystalline thiophosphate with thio-LIthium Super Ionic CONductor (thio-LISICON) have high ionic conductivity. The ionic conductivity of a Li₁₀GeP₂S₁₂ crystal, in particular, is 1.2 × 10⁻² S/cm (Kamaya et al., 2011). Argyrodite-type crystals with the stoichiometry Li₆PS₅X (X = Cl, Br, or I) also have high ionic conductivity (>10⁻³ S/cm) (Deiseroth et al., 2008; Rao and Adams, 2011; Boulineau et al., 2012). In addition, the conductivities of some glasses, including 30Li₂S–26B₂S₃–44LiI (Wada et al., 1983), 50Li₂S–17P₂S₅–33LiBH₄ (Yamauchi et al., 2013), and 63Li₂S–36SiS₂–1Li₃PO₄ (Aotani et al., 1994), have been reported to be as high as 1.5–1.7 × 10⁻³ S/cm.

The focus of this study was on the binary Li₂S–P₂S₅ system. An additional advantage of the Li₂S–P₂S₅ system is that no metallic elements, such as Ge and Si, are needed. The electrochemical stability of an electrolyte with no metallic element might be relatively high because metals might easily be reduced or oxidized during electrochemical reactions. Sulfide SEs are classified into three categories based on their structural characteristics: crystalline, amorphous (glass), and partially crystalline (glass-ceramic), all of which are known to be fast ionic conductors. Among the crystalline SEs, metastable Li₇P₃S₁₁ (Yamane et al., 2007; Minami et al., 2010) and nanoporous β-Li₃PS₄ (Liu et al., 2013) have high conductivities, 3 × 10⁻³ and 1.6 × 10⁻⁴ S/cm, respectively. Much research has been conducted since the first report that the glass and glass-ceramic phases are fast ionic conductors (Zhang and Kennedy, 1990). At present, the maximum conductivity occurs at 70–80 mol% Li₂S (i.e., 30–20 mol% P₂S₅), depending on the conditions during preparation (Minami et al., 2006; Mizuno et al., 2006). In general, it is difficult to prepare sulfide glasses with higher Li concentrations because crystallization occurs easily during the cooling process. The glasses are therefore prepared by mechanical milling technique or by twin-roller rapid-quenching technique. Glass ceramics are prepared by heating mechanically milled glass to a moderately high temperature. Crystals are prepared using solid-state reactions or with the same approach used to prepare glass ceramics. Crystallization of glasses usually results in a lowering of conductivities because the conductivities of the crystals that precipitate out are low. However, the ionic conductivity of Li₂S–P₂S₅ glass ceramics is enhanced by the precipitation of metastable phases with high conductivities. These metastable phases are analogous to crystalline Li₇P₃S₁₁ and Li₃PS₄. However, the role of metastable crystalline phases in glass ceramics is still unclear. In order to understand the mechanism responsible for the high conductivities of the binary Li₂S–P₂S₅ system experimentally, several groups have studied the Li⁺ diffusion profiles using ^6/7Li solid-state nuclear magnetic resonance spectroscopy (NMR) measurements (Graf et al., 2013; Hayamizu and Aihara, 2013; Hayamizu et al., 2014; Murakami et al., 2015). NMR is a powerful tool and provides many findings such as the rate of ionic motion. However, because the obtained signals are limited to the space-averaged information, it is difficult to clarify the origin of the Li⁺ diffusion only by the NMR study.

Since computational studies facilitate analysis of the Li diffusion process at the atomic scale, several researches based on the density functional theory (DFT) calculation have recently been reported. Holzwarth and co-workers have performed the DFT calculations on several crystal structures of the Li₂S–P₂S₅ system, including Li₇P₃S₁₁ and γ- and β-Li₃PS₄. They used the nudged elastic band method to estimate the activation energy for Li⁺ migration in the crystal and obtained results in good agreement with experiments (Holzwarth et al., 2011; Lepley and Holzwarth, 2012; Lepley et al., 2013). Holzwarth and co-workers suggested that the process of vacancy-interstitial pair formation contributes to superionic conductivities. Yang and Tse (2015) used DFT-based molecular dynamics (DFT-MD) calculations to investigate the mechanisms of Li⁺ transport in both the nanoporous and the crystalline phases of β-Li₃PS₄. One of the advantages of DFT-MD studies is that Li⁺ diffusivity can be simulated directly without use of a parametric force field. Mori et al. (2013) used the reverse Monte Carlo method with X-ray and neutron diffraction data to model the structures of Li₂S–P₂S₅ glasses as well as Li₇P₃S₁₁ crystals. Mori et al. used bond valence sum (BVS) analysis (Adams and Swenson, 2004, 2005; Hall et al., 2004) to analyze Li⁺ migration pathways. Mori et al. classified the pathways to the Li⁺ stable and metastable regions and found that the size of latter region was an indicator of Li⁺ diffusivity. However, they also stated that the quantitative relationship between the BVS results and the activation energy of ion migration still remained to be ascertained. Because static analysis is limited in terms of quantification, dynamical considerations must be taken into account to understand the high conductivities of glass SEs.

In the present work, we used DFT-MD calculations to investigate both the structure and the ionic conductivity of the binary Li₂S–P₂S₅ glass. The glass structures were modeled in an ab initio fashion, that is, without adjustments to take into account experimental information. To investigate ionic conductivity, we adopted an approach similar to that of the DFT-MD study of Yang and Tse (2015). Section “Computational Methods” briefly describes the simulation frameworks. Section “Results and Discussion” presents the simulated structures of the SEs and then compares the corresponding mass density and experimental diffraction data. The dynamical properties, such as the diffusion coefficients and ionic conductivities, are then presented. The relationship between the compositions of glasses and the dynamical properties are also discussed. Section “Conclusion” consists of a summary and some conclusions.

Computational Methods

In this work, the amorphous phases of lithium sulfide with compositions of xLi₂S–(100 − x)P₂S₅, where x = 67, 70, 75, or 80, were studied. In order to obtain a realistic model of amorphous structures, we used a melt-and-quench MD method, which is the common computational method for disordered materials (Massobrio et al., 2015). In the melt-and-quench technique, the choice of an initial coordinate is categorized into two types: a structure of the known crystal and a fully random coordinate of component atoms. We could not use the former because crystal structures with the same composition of the amorphous structure with x = 67 and 80 are unknown. Whereas the latter is applicable to any compound, a major issue is that the generated structures are far from the reasonable structures. Specifically, covalent bonding between P and S are missing. Indeed, in our preliminary examination, the convergences of the wavefunction optimization, which is the first part of DFT-MD simulations, were slow and sometimes failed. To circumvent this issue, the ionic units, such as Li⁺, tetrahedral ${\text{PS}}_4^{3-}$, di-tetrahedral ${\text{P}}_2{\text{S}}_7^{4-}$, and S²⁻, are located randomly. In order to pack bulky units in a cell efficiently, we used the Amorphous Cell module in the BIOVIA Materials Studio program (by Dassault Systèmes, BIOVIA Corp.). During the model construction, close contacts between atoms were minimized while ensuring realistic distributions (Allen and Tildesley, 1989) using the COMPASS II force field (Sun, 1998). Stoichiometric compositions were maintained for x = 67, 70, and 75, i.e., 4 × Li⁺ and ${\text{P}}_2{\text{S}}_7^{4-}$; 7 × Li⁺, ${\text{PS}}_4^{3-}$, and ${\text{P}}_2{\text{S}}_7^{4-}$; and 3 × Li⁺ and ${\text{PS}}_4^{3-},$ respectively. The amorphous structures with x = 80 were composed of eight Li⁺, two ${\text{PS}}_4^{3-},$ and one S²⁻. For each amorphous structure, ∼130 atoms were placed in a cubic box. The initial volume sizes were defined by setting the volumetric mass density to 2 g/cm³, which corresponds to the experimental density for Li₃PS₄ and Li₇P₃S₁₁ crystals.

Starting from the initial coordinates, the amorphous structures were annealing by the melt-and-quench procedure in a framework of DFT-MD simulations. All the systems were heated to 1000 K and then cooled to 667, 500, 400, and 300 K in a stepwise manner. The structures were kept at each temperature for ca. 2.8 ps before going to the next temperature. The cooling rate was ca. 48 K/ps, which is a typical value of the DFT-MD study (Massobrio et al., 2015). In all case, variable-cell, Car–Parrinello dynamics (Car and Parrinello, 1985; Laasonen et al., 1993; Bernasconi et al., 1995) were performed by using the CP module in the Quantum ESPRESSO program package (Giannozzi et al., 2009). A fictitious electronic mass of 400 a.u. and a time step of 6 a.u. (ca. 0.14 fs) were applied. The electronic and ionic motions were propagated by a standard Verlet algorithm (Verlet, 1967). Cell dynamics were simulated by use of a damped Parrinello–Rahman method (Parrinello and Rahman, 1981). The ionic and cell temperatures were controlled by a Nosé thermostat (Nosé, 1984; Hoover, 1985; Martyna et al., 1992). Periodic boundary conditions were applied, and only the axis length was allowed to change (i.e., the angles were kept constant). DFT calculations were performed using the Perdew–Burke–Ernzerhof exchange-correlation functional for solids (PBEsol) (Perdew et al., 2008) with Vanderbilt-type ultrasoft pseudopotentials (Vanderbilt, 1990). The energy cutoff of the plane wave basis set was set to 30 Ry (408 eV). Only one k-point of 1 × 1 × 1 was sampled.

After equilibration, DFT-MD calculations at each temperature were accumulated for at least 10 ps for a so-called production step. The computational settings of the DFT and MD components were the same as those described in the previous paragraph. In order to reduce the statistical inaccuracy, at least three simulations of this sequence were performed independently for each amorphous structure. Averaged data were used for the analysis. Furthermore, to validate the duration of equilibration (ca. 2.8 ps) and production (ca. 10 ps) steps, additional 30–40 ps of DFT-MD calculations were performed for some amorphous structures at 500 and 300 K.

Results and Discussion

Amorphous Structures

Figure 1 shows geometrical snapshots of DFT-MD simulations in the final production steps at 300 K for xLi₂S–(100 − x)P₂S₅ amorphous structures with x = 67, 70, 75, and 80. In almost all amorphous structures, unit structures, such as tetrahedral ${\text{PS}}_4^{3-},$ and di-tetrahedral ${\text{P}}_2{\text{S}}_7^{4-}$, were maintained and were distributed randomly. It is noteworthy that no decomposition or segregation of the units was observed in almost all trajectories, whereas rearrangement of the units, such as 2P₂S₇ → PS₄ + P₃S₁₀, occurred for only one amorphous structure model with x = 67.

FIGURE 1

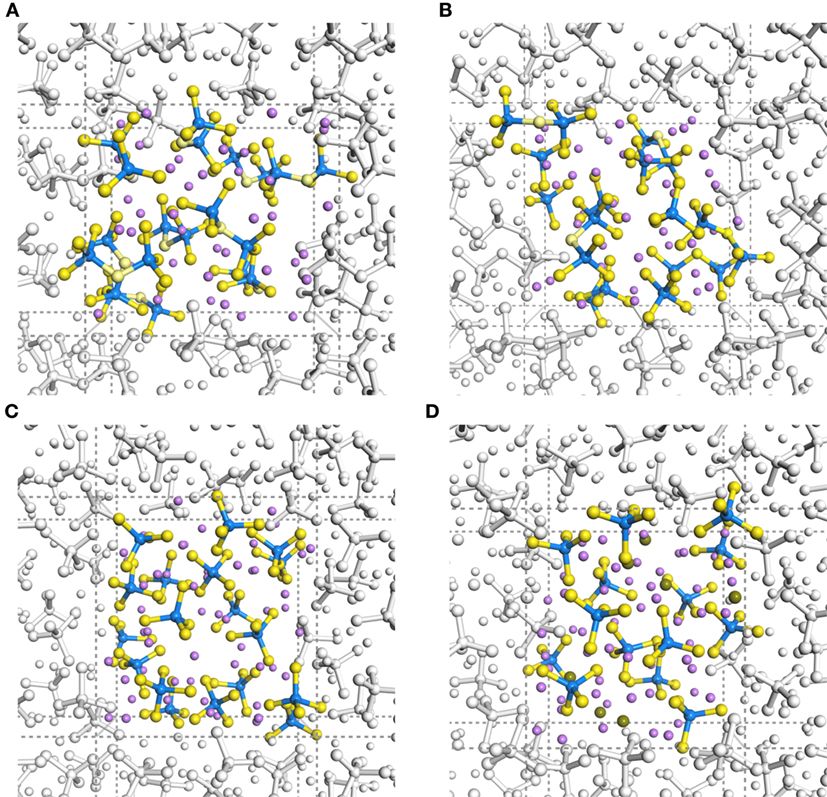
Figure 1. Trajectory snapshots in DFT-MD simulations at 300 K of (A) 67Li₂S–33P₂S₅, (B) 70Li₂S–30P₂S₅, (C) 75Li₂S–25P₂S₅, and (D) 80Li₂S–20P₂S₅ amorphous structures. Purple, blue, and yellow spheres indicate Li, P, and S atoms, respectively. Sticks with standard bond distances represent P–S bonds.

In order to examine the effect of the simulation duration, the energy, the cell volume, and the atomic orientation with respect to the time evolution were investigated. Figure 2A shows the time evolution of the relative stability and the volumetric mass density for amorphous structure with x = 75 at 300 K simulation. The relative stability was defined as the energy difference between the amorphous structure and the crystal with the same composition (γ-Li₃PS₄) and normalized by the molecular weight. The relative stabilities averaged over first 10 ps and total 40 ps were 0.159 and 0.144 kJ/g, respectively. The mass densities averaged over the first and total duration were 1.789 and 1.788 g/cm³, respectively. In both cases, the difference was relatively small. We investigated the pair correlation function (PCF) between Li and S and that between S and S belongs to the other ${\text{PS}}_4^{3-}$ units. To clarify the duration effect, the PCF averaged over each ca. 10 ps are shown in Figure 2B. There were no significant differences in the sampling period for both PCFs. Therefore, the procedure that consists of equilibration (ca. 2.8 ps) and production (10 ps) steps is enough to discuss the amorphous structures.

FIGURE 2

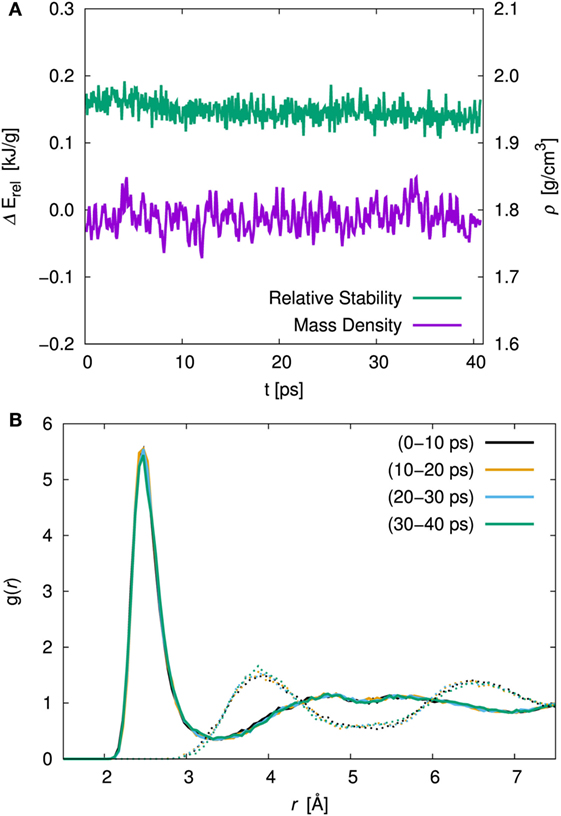
Figure 2. (A) Time evolution of the relative stability, ΔE_rel, and the volumetric mass density, ρ, and (B) pair correlation function (PCF), g(r) of Li–S (solid line) and inter-thiophosphate S–S (dotted line) for the 75Li₂S–25P₂S₅ amorphous structure at 300 K simulation. The averaged PCF were sampled every 10 ps.

Figure 3A shows the volumetric mass densities simulated by the DFT-MD at each temperature. As temperature decreased, the densities increased monotonically. Regardless of composition, the difference of the density between high (1000 K) and low (300 K) temperatures was ca. 0.15 g/cm³, which corresponds to approximately a 1.5% variation of each lattice length. Thus, our calculation simulated a trend of lattice expansion with increasing temperature, which is considered to be an important factor for Li⁺ migration.

FIGURE 3

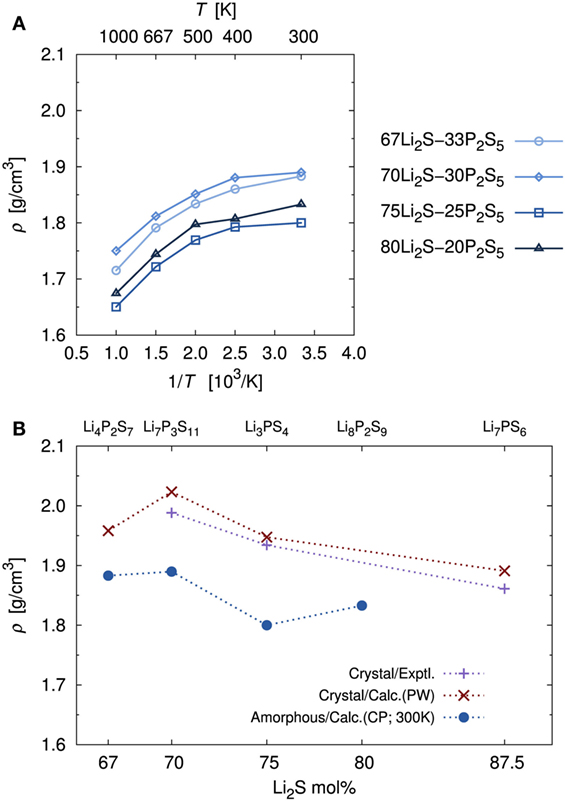
Figure 3. (A) Temperature dependence of mass densities, ρ, of amorphous structures determined by DFT-MD simulations and (B) comparisons with experimental and calculated crystal mass densities. Crystal calculations were performed with the PW module in the Quantum ESPRESSO package using the same functional and pseudopotential as the CP module. The major difference was the number of k-point meshes. Note that because the Li₄P₂S₇ crystal structure is unknown, the known Li₄P₂O₇ crystal structure (P$\overline{1}$) was used as an initial geometry. This approach is the same one used in a previous computational study (Holzwarth et al., 2011). The Li₇PS₆ (corresponding to 87.5Li₂S–12.5P₂S₅) crystal structure, which has been reported, was added to address the accuracy of the calculation.

The calculated density of the amorphous structures decreased in the order x = 70, 67, 80, and 75, which is not the same as the order of the molecular ratios. Experimental densities for amorphous structures have not been measured, to the best of our knowledge. Thus, Figure 3B provides a comparison of the calculated densities of amorphous structures and the experimental densities of the crystals (Yamane et al., 2007; Onodera et al., 2010; Homma et al., 2011). In addition, Figure 3B shows comparisons with the density of crystal obtained by geometrical optimization of the usual DFT calculation. Crystals with x = 80, for which the stoichiometric composition is Li₈P₂S₉, are also unknown, to our knowledge. To assess the accuracy of the calculation, we added the known Li₇PS₆ (corresponding to 87.5Li₂S–12.5P₂S₅) crystal (Kong et al., 2010). For the crystals, the calculated densities were in good agreement with the experimental ones. In general, the densities of the amorphous structure were lower than those of the corresponding crystals. This pattern is common in silica and alumina glasses (Benoit et al., 2000). The pattern with respect to molecular ratios, as mentioned above, is also similar between amorphous and crystalline structures.

To investigate stability of the amorphous structure, we compared the relative stabilities as defined above. The stability for x = 80 was not examined because there is no reference crystal, as mentioned in the previous paragraph. The averaged relative stabilities of amorphous structures with x = 67, 70, and 75 were 0.035, 0.121, and 0.155 kJ/g, respectively. A positive value means that the amorphous structure is less stable than the corresponding crystal. Our analysis thus indicates that the amorphous structures were metastable.

The simulated amorphous structures can be compared directly to experimental results by calculating the static structure factor, S(Q), obtained from X-ray and neutron diffraction studies. Figure 4 shows the X-ray structure factor S_X(Q) for each amorphous structure. The neutron diffraction results S_N(Q) are shown in Supplementary Material. The calculated results were analyzed for trajectories by a DFT-MD simulation at 300 K using the ISAACS program (Le Roux and Petkov, 2010). We determined the experimental data based on the previous work of Ohara et al. (2016). Whereas the calculated results show the fluctuations due to our limited sampling, the agreement between our results and the experimental data is good for large values of Q, and the agreement is still good for small values of Q with respect to the positions of maxima and minima. In both the DFT-MD-simulated and experimental results, the first sharp diffraction peaks (FSDP) were observed at ca. 1.3 1/Å. The appearance of FSDP is a fundamental characteristic of amorphous structures. There was little difference between the structure factors of the amorphous structures, except for the FSDP. Although there was no sharp peak at 1.3 1/Å for the amorphous structure with x = 67, the peak heights of the FSDPs of the amorphous structures with x = 70 and 75 were in good agreement with the experimental ones. This peak is thought to mainly reflect the environment between Li and S, and it was enhanced as the Li concentration increased for x = 67, 70, and 75. However, the amorphous structure with x = 80 resulted in a smaller peak than the other amorphous structures. The implication is that the environment between Li and S is not uniform. The amplitudes of the second peaks (SSDPs) at ca. 2.1 1/Å were smaller than the experimental amplitudes. Further refinement of the spectrum will require a system at least 10 times as large as the system used in the previous study of Mori et al. (2013).

FIGURE 4

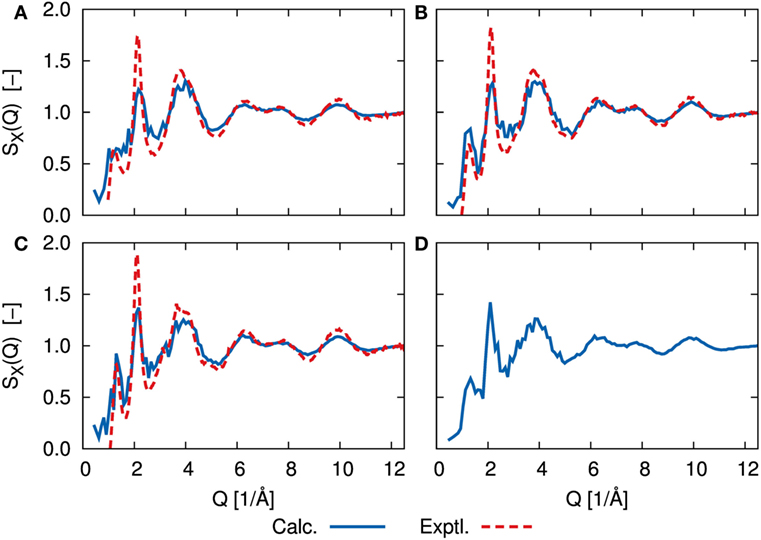
Figure 4. X-ray structure factor, S_X(Q), determined by DFT-MD simulations (solid blue line) and scattering experiments (dashed red line) of (A) 67Li₂S–33P₂S₅, (B) 70Li₂S–30P₂S₅, (C) 75Li₂S–25P₂S₅, and (D) 80Li₂S–20P₂S₅ amorphous structure. Experimental measurements are lacking for 80Li₂S–20P₂S₅. Neutron scattering results, S_N(Q), are shown in Supplementary Material.

Diffusion Properties

As is usual in a MD study, we used the production steps of trajectories to investigate the diffusion profile. The diffusion coefficient was calculated from the slope of the average mean square displacement (MSD) of Li atoms over time. Before evaluating the diffusion coefficient, we examine the effect of the simulation duration as the previous section. Figure 5 shows the MSD as a function of lag-time among short (ca. 10 ps) and long (ca. 50 ps) duration for the amorphous structure with x = 75 and 80 at 500 K. The plots obtained from short duration coincide with those obtained from the long duration. To assess the individual Li mobilities, the root-MSD (RMSD) were evaluated. Figure 6 shows the relative frequency distributions of RMSD after 10 ps for amorphous structures with x = 75 at 1000, 667, 500, 400, and 300 K temperature, respectively. The time evolutions of RMSD for all Li in one model are shown in Supplemental Material. At 300 K, almost all (99.1%) of Li moved within 2.5 Å. It means most of Li were unable to reach the nearest neighbor Li sites in the amorphous structures. At 400 K, 11.9% of Li moved over 2.5 Å from the initial coordinate after 10 ps. A few (1.6%) Li also migrated over 4.5 Å, which corresponds to the distance to the second nearest neighbor site. More Li migrated at higher temperature (9.5, 36.5, and 85.2% of Li migrated over 4.5 Å at 500, 667, and 1000 K, respectively). Certainly our simulation time was much shorter than typical setting in the classical MD method, but the electronic environment around Li, which was obtained by the DFT method accurately, was important to define the flexibility of Li as discussed later. Thus, we used the sampling over 10-ps duration to analyze the diffusion property for each amorphous structure, although the results for 300 K were removed from the consideration. Figure 7 shows the Arrhenius plot of the calculated diffusion coefficients for the amorphous structures with temperatures from 400 to 1000 K. The relationship for each amorphous structure was linear in this region. Whereas the diffusion coefficients for amorphous structures with x = 67, 70, and 75 were similar, the diffusion coefficient for x = 80 was slightly lower than the others. The implication is that the diffusivity of only the amorphous structure with x = 80 was low. It would be confirmed by the comparison of the distribution of RMSD between amorphous structures with x = 75 and 80 (shown in the inset figure in Figure 6). This difference will be discussed later.

FIGURE 5

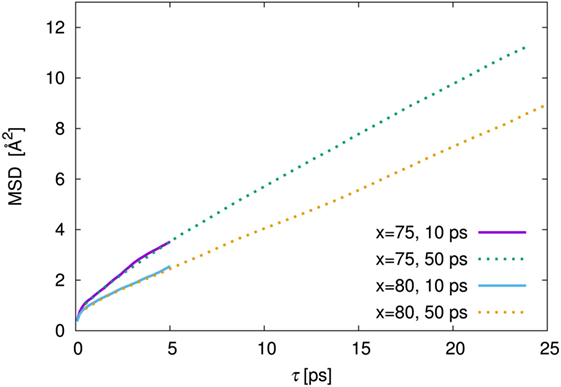
Figure 5. Mean square displacement (MSD) against lag time, τ, among 10 ps (solid line) and 50 ps (dotted line) of production steps for the amorphous structures with 75Li₂S–25P₂S₅ (x = 75) and 80Li₂S–20P₂S₅ (x = 80) amorphous structures at 500 K simulation. The MSD of 10 and 50 ps were derived from the independent trajectories.

FIGURE 6

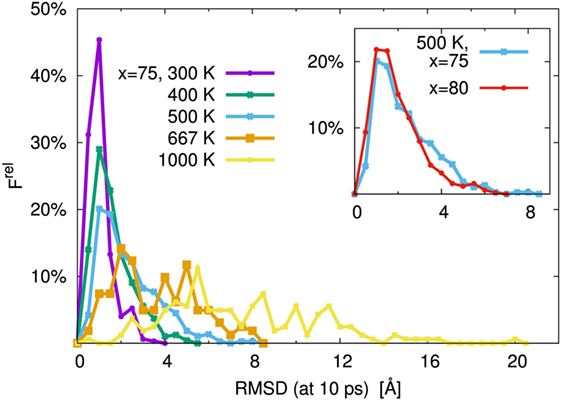
Figure 6. Relative frequency distribution, F^rel, of root mean square displacement (RMSD) after 10 ps for Li. The main figure was the distributions for the 75Li₂S–25P₂S₅ amorphous structure at T = 300, 400, 500, 667, and 1000 K, respectively. The inset figure was comparison of 75Li₂S–25P₂S₅ (x = 75) and 80Li₂S–20P₂S₅ (x = 80) amorphous structures at 500 K distribution. The bin width was 0.5 Å.

FIGURE 7

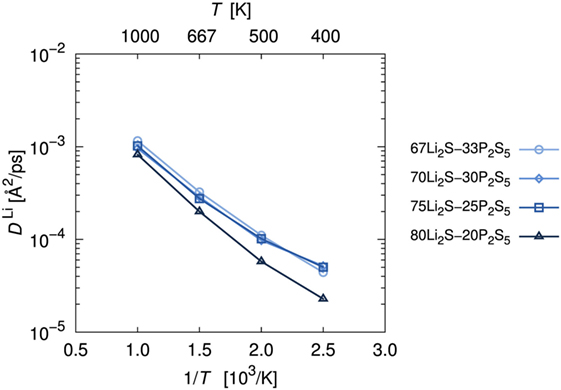
Figure 7. Arrhenius plot of lithium diffusion coefficients, D^Li. Diffusion coefficients were estimated by averaging the mean square displacement of Li atoms at each trajectory.

To estimate the ionic conductivity, σ, we used the Nernst– Einstein relationship:

$\mathrm{\sigma }=\frac{N{\left(\mathit{Ze}\right)}^2}{k_{\text{B}}T}D$

where N, Z, e, k_B, T, and D are the number density of transported species, the charge of the transported species, the elementary charge, the Boltzmann constant, the target temperature, and the diffusion coefficient of the transported species, respectively. The target temperature is set to the RT (298.15 K) to compare the computational results with experimental ones. Because the transported species was the Li⁺ in this study, N is the concentration of Li atoms in each amorphous structure calculated by using the number of Li atoms in a unit cell and the average simulated volume at 300 K, which is close to the target temperature. For Li⁺, Z = 1. D is the diffusion coefficient of Li⁺ at the target temperature. Because the diffusion coefficients obtained from 300 K trajectories were less accurate for small movements in our simulations, we used values of D extrapolated from the diffusion coefficients between 1000 and 400 to 298.15 K.

Table 1 summarizes the estimated σ values as well as the N and D values. The calculated and experimental (Mizuno et al., 2005) σ versus the composition of the amorphous structures are shown in Figure 8. The fact that the highest calculated ionic conductivity of an amorphous structure corresponded to x = 75 is consistent with experimental results. Whereas the calculated diffusion coefficient of the amorphous structure was lower for x = 75 than for x = 70, the ionic conductivity of the amorphous structure was higher for x = 75 than for x = 70. These results explain why the percentage difference was larger for number densities than for diffusion coefficients. The ionic conductivity of the amorphous structure was lower for x = 67 than for x = 70 and 75 because both the number density and the diffusion coefficient were lower for x = 67. However, the number density of the amorphous structure with x = 80 was the highest, but the calculated ionic conductivity was the lowest. The explanation is that the diffusion coefficient was significantly lower for the x = 80 structure than for the other structures. These results suggest that a relatively high number density of conductive species enhances conductivity, but only up to a certain density. In other words, the balance between the number density and diffusion coefficient is important.

TABLE 1

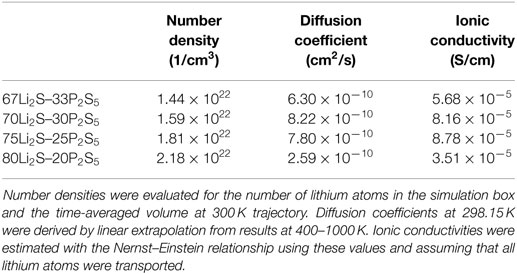
Table 1. Number densities, diffusion coefficients, and ionic conductivities of lithium at the RT for xLi₂S–(100 − x)P₂S₅ amorphous structures.

FIGURE 8

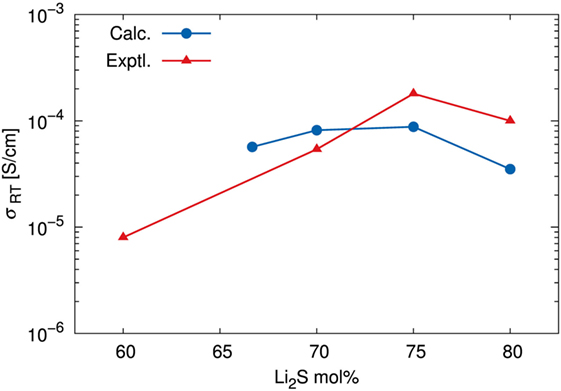
Figure 8. Ionic conductivity σ at room temperature (298.15 K). Calculated results were estimated by using the Nernst–Einstein relationship, an extrapolated diffusion coefficient, and the number density of Li determined by DFT-MD simulations. Experimental data are adapted from Mizuno et al. (2005).

It might seem that the agreement between the calculated and experimental conductivity was only semiquantitative. Indeed, we averaged sampling results among only a few independent models for each amorphous structure. We would have to increase the number of samples and/or cell size to achieve higher accuracy, as was apparent in the discussion of structure factors. It is noteworthy that Mo et al. (2012) argued for the limitation of the DFT-MD study due to the statistical uncertainty associated with fitting a curve to the MSD versus time data. Therefore, it seems reasonable to conclude that our simulations correctly determined the order of magnitude of the ionic conductivity and represented the diffusion properties of amorphous structures as a function of their composition.

Let us now turn to the argument that only the diffusivity of the amorphous structure with x = 80 was low. To reveal the environment around Li⁺, we examined the PCF of Li and S. Figure 9 shows the PCF for the amorphous structure with x = 80 over production steps at 300 K (the results for the other amorphous structures are shown in Supplementary Material). Note that we distinguished the bond type of S atoms, i.e., isolated S atoms for which the formal bond number is zero, and that of S atoms in a PS₄ unit, for which the bond number is one. We denoted the latter as “non-bridged S.” The total PCFs were divided between PCFs involving Li and isolated S and the PCF of Li and non-bridged S. Interestingly, the position of the first peak was slightly different; the statistically stable distances between Li and S atoms of the former and latter were 2.36 and 2.45 Å, respectively. The results mean that isolated S attracts Li atoms more than non-bridged S does.

FIGURE 9

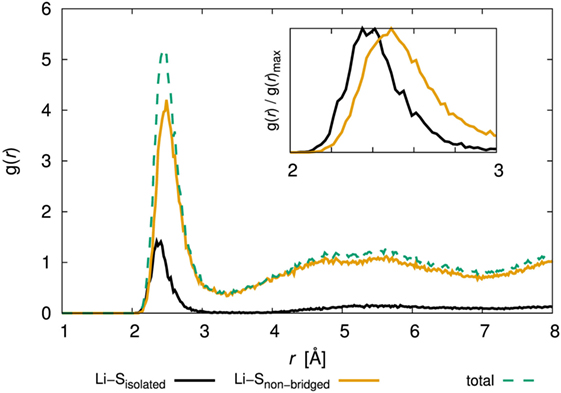
Figure 9. Pair correlation function, g(r), of Li–S for the 80Li₂S–20P₂S₅ amorphous structure determined by DFT-MD simulation. The inset figure shows an enlarged view of 2–3 Å and normalized maximum values. The results for the other amorphous structures are shown in Supplementary Material.

Further evidence relevant to the Li–S attraction comes from the difference of atomic charges. Table 2 summarizes the average atomic populations based on a Bader charge analysis (Bader, 1990; Tang et al., 2009). Because bond numbers of S atom are distinguished in a way similar to the method discussed in the previous paragraph to characterize bond types, we have denoted the S atoms for which the bond number is two, namely, the S atoms in the P₂S₇ unit (i.e., S of –P–S–P–) in our models, as “bridged S.” The atomic charge distributions of Li, 0.88–0.89, were very similar among the amorphous structures (Table 2). The deviations were very small. The atomic charge distributions of P atom were also similar among the amorphous structures and fell within the range of 1.24–1.28, but the deviations were an order of magnitude larger for P than for Li atom. The atomic charge distribution of isolated S was −1.70, those of non-bridged S varied from −0.99 to −0.91, and those of bridged S ranged from −0.61 to −0.59. The deviations were relatively modest. It is clear that the bond type defines the charge distributions of S. In the case of the amorphous structure with x = 80, the isolated S had approximately twice the negative charge of the non-bridged S. In other words, an isolated S with a relatively large negative charge may more strongly attract positive Li⁺ electrostatically. This conclusion is consistent with the above discussion of PCF. The implication with respect to diffusibility is that the attraction of Li to isolated S suppresses the migration of Li⁺, and this suppression accounts for the fact that the amorphous structure with x = 80 has the lowest diffusion coefficient among the amorphous structures.

TABLE 2

Table 2. Average atomic charge distributions for xLi₂S–(100 − x)P₂S₅ amorphous structures determined by Bader analyses.

To briefly summarize these results, the ionic conductivities of amorphous structures based on lithium sulfide depend on both the number density and the diffusibility of Li⁺. A higher number density enhances conductivity. However, when the ratio of S to P atom is above the stoichiometric ratio (S/P > 4), the residual S atoms interfere with the migration of Li⁺. Because isolated S is derived from Li₂S, the conditions under which the amorphous structure is synthesized are quite important. What is needed is an environment in which all the S atoms from Li₂S react. Such an environment is characterized not only by the most appropriate relative amounts of Li₂S and P₂S₅ but also by the process conditions, such as the mechanical milling techniques. Although our modeling involves several assumptions and limitations, including ideal compositions, a single phase of amorphous structures, model size, and sampling steps, the DFT-MD simulations provided important insights that were based on accurate descriptions of the electronic states and atomic interactions.

Conclusion

In this study, we used DFT-MD calculations to investigate the structural and dynamical properties of glass sulfide SEs. We initiated the study by modeling the glass structures in ab initio fashion. The structures of xLi₂S–(100 − x)P₂S₅ (x = 67, 70, 75, and 80) were created by randomly identifying appropriate compositions of Li⁺, ${\text{PS}}_4^{3-},{\text{P}}_2{\text{S}}_7^{4-}$, and S²⁻ and then annealing them with DFT-MD calculations. Because the calculated mass densities as a function of composition corresponded to the mass densities of crystals and because the calculated structure factors were also in good agreement with experimental structures, the model seemed appropriate for simulating the characteristics of sulfide glass.

Second, Li⁺ diffusion coefficients were obtained from the DFT-MD calculations at various temperatures for picosecond simulation times. Ionic conductivities evaluated by the Nernst–Einstein relationship at 298.15 K were in the order of 10⁻⁵ S/cm. The ionic conductivity of the amorphous structure with x = 75 was the highest because there was a balance between the number density and the diffusibility of Li⁺. The simulations also suggested that isolated sulfur suppresses Li⁺ migration.

Our computational methodology is clearly applicable to not only sulfide glasses but also to crystalline phases. In other words, although the size of the model was limited, the study established the efficacy of the method for evaluating the properties of various SEs. Further computational studies may lead to better understanding of the so-called lithium superionic conductors.

Author Contributions

All calculations were performed by TB. Analysis and discussion were performed by TB and YK. Manuscript was written by TB and revised by YK.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Akio Mitsui for helpful discussions about structure factors.

Supplementary Material

The Supplementary Material for this article can be found online at http://journal.frontiersin.org/article/10.3389/fenrg.2016.00022

References

Adams, S., and Swenson, J. (2004). Structure conductivity correlation in reverse Monte Carlo models of single and mixed alkali glasses. Solid State Ionics 175, 665–669. doi: 10.1016/j.ssi.2004.08.038

CrossRef Full Text | Google Scholar

Adams, S., and Swenson, J. (2005). Bond valence analysis of reverse Monte Carlo produced structural models; a way to understand ion conduction in glasses. J. Phys. Condens. Matter 17, S87. doi:10.1088/0953-8984/17/5/010

CrossRef Full Text | Google Scholar

Allen, M. P., and Tildesley, D. J. (1989). Computer Simulation of Liquids. New York: Oxford University Press.

Google Scholar

Aotani, N., Iwamoto, K., Takada, K., and Kondo, S. (1994). Synthesis and electrochemical properties of lithium ion conductive glass, Li₃PO₄-Li₂S-SiS₂. Solid State Ionics 68, 35–39. doi:10.1016/0167-2738(94)90232-1

CrossRef Full Text | Google Scholar

Bader, R. F. W. (1990). Atoms in Molecules: a Quantum Theory. New York: Oxford University Press.

Google Scholar

Benoit, M., Ispas, S., Jund, P., and Jullien, R. (2000). Model of silica glass from combined classical and ab initio molecular-dynamics simulations. Eur. Phys. J. B 13, 631–636. doi:10.1007/s100510050079

CrossRef Full Text | Google Scholar

Bernasconi, M., Chiarotti, G., Focher, P., Scandolo, S., Tosatti, E., and Parrinello, M. (1995). First-principle-constant pressure molecular dynamics. J. Phys. Chem. Solids 56, 501–505. doi:10.1016/0022-3697(94)00228-2

CrossRef Full Text | Google Scholar

Blöchl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50, 17953–17979. doi:10.1103/PhysRevB.50.17953

CrossRef Full Text | Google Scholar

Boulineau, S., Courty, M., Tarascon, J.-M., and Viallet, V. (2012). Mechanochemical synthesis of Li-argyrodite Li₆PS₅X (X = Cl, Br, I) as sulfur-based solid electrolytes for all solid state batteries application. Solid State Ionics 221, 1–5. doi:10.1016/j.ssi.2012.06.008

CrossRef Full Text | Google Scholar

Car, R., and Parrinello, M. (1985). Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 55, 2471–2474. doi:10.1103/PhysRevLett.55.2471

CrossRef Full Text | Google Scholar

Deiseroth, H.-J., Kong, S.-T., Eckert, H., Vannahme, J., Reiner, C., Torsten, Z., et al. (2008). Li₆PS₅X: a class of crystalline Li-rich solids with an unusually high Li⁺ mobility. Angew. Chem. Int. Ed. 47, 755–758. doi:10.1002/anie.200703900

CrossRef Full Text | Google Scholar

Fergus, J. (2010). Ceramic and polymeric solid electrolytes for lithium-ion batteries. J. Power Sources 195, 4554–4569. doi:10.1016/j.jpowsour.2010.01.076

CrossRef Full Text | Google Scholar

Giannozzi, P., Baroni, S., Bonini, N., Calandra, M., Car, R., Cavazzoni, C., et al. (2009). QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502. doi:10.1088/0953-8984/21/39/395502

PubMed Abstract | CrossRef Full Text | Google Scholar

Graf, M., Kresse, B., Privalov, A. F., and Vogel, M. (2013). Combining ⁷Li field-cycling relaxometry and stimulated-echo experiments: a powerful approach to lithium ion dynamics in solid-state electrolytes. Solid State Nucl. Magn. Reson. 5, 25–30. doi:10.1016/j.ssnmr.2013.01.001

CrossRef Full Text | Google Scholar

Hall, A., Adams, S., and Swenson, J. (2004). The nature of conduction pathways in mixed alkali phosphate glasses. Ionics 10, 396–404. doi:10.1007/BF02378000

CrossRef Full Text | Google Scholar

Hayamizu, K., and Aihara, Y. (2013). Lithium ion diffusion in solid electrolyte (Li₂S)₇(P₂S₅)₃ measured by pulsed-gradient spin-echo 7Li NMR spectroscopy. Solid State Ionics 238, 7–14. doi:10.1016/j.ssi.2013.02.014

CrossRef Full Text | Google Scholar

Hayamizu, K., Aihara, Y., and Machida, N. (2014). Anomalous lithium ion migration in the solid electrolyte (Li₂S)₇(P₂S₅)₃; fast ion transfer at short time intervals studied by PGSE NMR spectroscopy. Solid State Ionics 259, 59–64. doi:10.1016/j.ssi.2014.02.016

CrossRef Full Text | Google Scholar

Holzwarth, N., Lepley, N., and Du, Y. A. (2011). Computer modeling of lithium phosphate and thiophosphate electrolyte materials. J. Power Sources 196, 6870–6876. doi:10.1016/j.jpowsour.2010.08.042

CrossRef Full Text | Google Scholar

Homma, K., Yonemura, M., Kobayashi, T., Nagao, M., Hirayama, M., and Kanno, R. (2011). Crystal structure and phase transitions of the lithium ionic conductor Li₃PS₄. Solid State Ionics 182, 53–58. doi:10.1016/j.ssi.2010.10.001

CrossRef Full Text | Google Scholar

Hoover, W. G. (1985). Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A 31, 1695–1697. doi:10.1103/PhysRevA.31.1695

CrossRef Full Text | Google Scholar

Kamaya, N., Homma, K., Yamakawa, Y., Hirayama, M., Kanno, R., Yonemura, M., et al. (2011). A lithium superionic conductor. Nat. Mater. 10, 682–686. doi:10.1038/nmat3066

PubMed Abstract | CrossRef Full Text | Google Scholar

Knauth, P. (2009). Inorganic solid Li ion conductors: an overview. Solid State Ionics 180, 911–916. doi:10.1016/j.ssi.2009.03.022

CrossRef Full Text | Google Scholar

Kong, S. T., Gun, O., Koch, B., Deiseroth, H. J., Eckert, H., and Reiner, C. (2010). Structural characterisation of the Li argyrodites Li₇PS₆ and Li₇PSe₆ and their solid solutions: quantification of site preferences by MAS-NMR spectroscopy. Chem. Eur. J. 16, 5138–5147. doi:10.1002/chem.200903023

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775. doi:10.1103/PhysRevB.59.1758

CrossRef Full Text | Google Scholar

Laasonen, K., Pasquarello, A., Car, R., Lee, C., and Vanderbilt, D. (1993). Car-Parrinello molecular dynamics with Vanderbilt ultrasoft pseudopotentials. Phys. Rev. B 47, 10142–10153. doi:10.1103/PhysRevB.47.10142

CrossRef Full Text | Google Scholar

Le Roux, S. É., and Petkov, V. (2010). ISAACS – interactive structure analysis of amorphous and crystalline systems. J. Appl. Crystallogr. 43, 181–185. doi:10.1107/S0021889809051929

CrossRef Full Text | Google Scholar

Lepley, N. D., and Holzwarth, N. A. W. (2012). Computer modeling of crystalline electrolytes: lithium thiophosphates and phosphates. J. Electrochem. Soc. 159, A538–A547. doi:10.1149/2.jes113225

CrossRef Full Text | Google Scholar

Lepley, N. D., Holzwarth, N. A. W., and Du, Y. A. (2013). Structures, Li⁺ mobilities, and interfacial properties of solid electrolytes Li₃PS₄ and Li₃PO₄ from first principles. Phys. Rev. B 88, 104103. doi:10.1103/PhysRevB.88.104103

CrossRef Full Text | Google Scholar

Liu, Z., Fu, W., Payzant, E. A., Yu, X., Wu, Z., Dudney, N. J., et al. (2013). Anomalous high ionic conductivity of nanoporous β-Li3PS4. J. Am. Chem. Soc. 135, 975–978. doi:10.1021/ja3110895

PubMed Abstract | CrossRef Full Text | Google Scholar

Martyna, G. J., Klein, M. L., and Tuckerman, M. (1992). Nose-Hoover chains: the canonical ensemble via continuous dynamics. J. Chem. Phys. 97, 2635–2643. doi:10.1063/1.463940

CrossRef Full Text | Google Scholar

Massobrio, C., Du, J., Bernasconi, M., and Salmon, P. S. (2015). Molecular Dynamics Simulations of Disordered Materials. Switzerland: Springer International Publishing.

Google Scholar

Minami, K., Hayashi, A., and Tatsumisago, M. (2010). Preparation and characterization of superionic conducting Li₇P₃S₁₁ crystal from glassy liquids. J. Ceram. Soc. Jpn. 118, 305–308. doi:10.2109/jcersj2.118.305

CrossRef Full Text | Google Scholar

Minami, T., Hayashi, A., and Tatsumisago, M. (2006). Recent progress of glass and glass-ceramics as solid electrolytes for lithium secondary batteries. Solid State Ionics 177, 2715–2720. doi:10.1016/j.ssi.2006.07.017

CrossRef Full Text | Google Scholar

Mizuno, F., Hayashi, A., Tadanaga, K., and Tatsumisago, M. (2005). New, highly ion-conductive crystals precipitated from Li₂S-P₂S₅ glasses. Adv. Mater. 17, 918–921. doi:10.1002/adma.200401286

CrossRef Full Text | Google Scholar

Mizuno, F., Hayashi, A., Tadanaga, K., and Tatsumisago, M. (2006). High lithium ion conducting glass-ceramics in the system Li₂S-P₂S₅. Solid State Ionics 177, 2721–2725. doi:10.1016/j.ssi.2006.04.017

CrossRef Full Text | Google Scholar

Mo, Y., Ong, S. P., and Ceder, G. (2012). First principles study of the Li₁₀GeP₂S₁₂ lithium super ionic conductor material. Chem. Mater. 24, 15–17. doi:10.1021/cm203303y

CrossRef Full Text | Google Scholar

Mori, K., Ichida, T., Iwase, K., Otomo, T., Kohara, S., Arai, H., et al. (2013). Visualization of conduction pathways in lithium superionic conductors: Li₂S-P₂S₅ glasses and Li₇P₃S₁₁ glass-ceramic. Chem. Phys. Lett. 584, 113–118. doi:10.1016/j.cplett.2013.08.016

CrossRef Full Text | Google Scholar

Murakami, M., Shimoda, K., Shiotani, S., Mitsui, A., Ohara, K., Onodera, Y., et al. (2015). Dynamical origin of ionic conductivity for Li₇P₃S₁₁ metastable crystal as studied by ^6/7Li and ³¹P solid-state NMR. J. Phys. Chem. C 119, 24248–24254. doi:10.1021/acs.jpcc.5b06308

CrossRef Full Text | Google Scholar

Nosé, S. (1984). A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 81, 511–519. doi:10.1063/1.447334

CrossRef Full Text | Google Scholar

Ohara, K., Mitsui, A., Mori, M., Onodera, Y., Shiotani, S., Koyama, Y., et al. (2016). Strucutral and electronic features of binary Li₂S-P₂S₅ glasses. Sci. Rep. 6, 21302. doi:10.1038/srep21302

CrossRef Full Text | Google Scholar

Onodera, Y., Mori, K., Otomo, T., Hannon, A. C., Kohara, S., Itoh, K., et al. (2010). Crystal structure of Li₇P₃S₁₁ studied by neutron and synchrotron X-ray powder diffraction. J. Phys. Soc. Jpn. 79SA, 87–89. doi:10.1143/JPSJS.79SA.87

CrossRef Full Text | Google Scholar

Parrinello, M., and Rahman, A. (1981). Polymorphic transitions in single crystals: a new molecular dynamics method. J. Appl. Phys. 52, 7182–7190. doi:10.1063/1.328693

CrossRef Full Text | Google Scholar

Perdew, J. P., Ruzsinszky, A., Csonka, G. I., Vydrov, O. A., Scuseria, G. E., Constantin, L. A., et al. (2008). Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100, 136406. doi:10.1103/PhysRevLett.100.136406

CrossRef Full Text | Google Scholar

Rao, R. P., and Adams, S. (2011). Studies of lithium argyrodite solid electrolytes for all-solid-state batteries. Phys. Status Solidi A 208, 1804–1807. doi:10.1002/pssa.201001117

CrossRef Full Text | Google Scholar

Ren, Y., Chen, K., Chen, R., Liu, T., Zhang, Y., and Nan, C.-W. (2015). Oxide electrolytes for lithium batteries. J. Am. Ceram. Soc. 98, 3603–3623. doi:10.1111/jace.13844

CrossRef Full Text | Google Scholar

Sun, H. (1998). COMPASS: an ab initio force-field optimized for condensed-phase applications – overview with details on alkane and benzene compounds. J. Phys. Chem. B 102, 7338–7364. doi:10.1021/jp980939v

CrossRef Full Text | Google Scholar

Takada, K. (2013). Progress and prospective of solid-state lithium batteries. Acta Mater. 61, 759–770. doi:10.1016/j.actamat.2012.10.034

CrossRef Full Text | Google Scholar

Tang, W., Sanville, E., and Henkelman, G. (2009). A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Matter 21, 084204. doi:10.1088/0953-8984/21/8/084204

PubMed Abstract | CrossRef Full Text | Google Scholar

Vanderbilt, D. (1990). Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 41, 7892–7895. doi:10.1103/PhysRevB.41.7892

CrossRef Full Text | Google Scholar

Verlet, L. (1967). Computer “Experiments” on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules. Phys. Rev. 159, 98–103. doi:10.1103/PhysRev.159.98

CrossRef Full Text | Google Scholar

Wada, H., Menetrier, M., Levasseur, A., and Hagenmuller, P. (1983). Preparation and ionic conductivity of new B₂S₃-Li₂S-LiI glasses. Mater. Res. Bull. 18, 189–193. doi:10.1016/0025-5408(83)90080-6

CrossRef Full Text | Google Scholar

Yamane, H., Shibata, M., Shimane, Y., Junke, T., Seino, Y., Adams, S., et al. (2007). Crystal structure of a superionic conductor, Li₇P₃S₁₁. Solid State Ionics 178, 1163–1167. doi:10.1016/j.ssi.2007.05.020

CrossRef Full Text | Google Scholar

Yamauchi, A., Sakuda, A., Hayashi, A., and Tatsumisago, M. (2013). Preparation and ionic conductivities of (100 – x)(0.75Li₂S⋅0.25P₂S₅)⋅xLiBH₄ glass electrolytes. J. Power Sources 244, 707–710. doi:10.1016/j.jpowsour.2012.12.001

CrossRef Full Text | Google Scholar

Yang, J., and Tse, J. S. (2015). First-principles molecular simulations of Li diffusion in solid electrolytes Li₃PS₄. Comput. Mater. Sci. 107, 134–138. doi:10.1016/j.commatsci.2015.05.022

CrossRef Full Text | Google Scholar

Zhang, Z., and Kennedy, J. H. (1990). Synthesis and characterization of the B₂S₃-Li₂S, the P₂S₅-Li₂S and the B₂S₃-P₂S₅-Li₂S glass systems. Solid State Ionics 38, 217–224. doi:10.1016/0167-2738(90)90424-P

CrossRef Full Text | Google Scholar