Interfacial Thermal Transport via One-Dimensional Atomic Junction Model

In modern information technology, as integration density increases rapidly and the dimension of materials reduces to nanoscale, interfacial thermal transport (ITT) has attracted widespread attention of scientists. This review introduces the latest theoretical development in ITT through one-dimensional (1D) atomic junction model to address the thermal transport across an interface. With full consideration of the atomic structures in interfaces, people can apply the 1D atomic junction model to investigate many properties of ITT, such as interfacial (Kapitza) resistance, nonlinear interface, interfacial rectification, and phonon interference, and so on. For the ballistic ITT, both the scattering boundary method (SBM) and the non-equilibrium Green’s function (NEGF) method can be applied, which are exact since atomic details of actual interfaces are considered. For interfacial coupling case, explicit analytical expression of transmission coefficient can be obtained and it is found that the thermal conductance maximizes at certain interfacial coupling (harmonic mean of the spring constants of the two leads) and the transmission coefficient is not a monotonic decreasing function of phonon frequency. With nonlinear interaction—phonon–phonon interaction or electron–phonon interaction at interface, the NEGF method provides an efficient way to study the ITT. It is found that at weak linear interfacial coupling, the nonlinearity can improve the ITT, but it depresses the ITT in the case of strong-linear coupling. In addition, the nonlinear interfacial coupling can induce thermal rectification effect. For interfacial materials case which can be simulated by a two-junction atomic chain, phonons show interference effect, and an optimized thermal coupler can be obtained by tuning its spring constant and atomic mass.

Introduction

In the development of microelectronic devices, accumulation of heat becomes a bottleneck because of a fast-growing power density. To efficiently manipulate thermal transport has been widely recognized as a crucial issue in modern energy science and information technology. Recent years have seen the emergence of significant research on thermal transport in nanostructures, such as thermal diodes, thermal logic gates, thermal memories, thermal transistors, thermal resistors, and thermal rectifiers (Li et al., 2012; Maldovan, 2013; Song et al., 2016; Hu et al., 2017; Juraschek and Spaldin, 2017). As the dimensions of systems shrink into the nanoscale, interfaces dramatically affect thermal transport (Alexeev et al., 2015; Chen et al., 2015, 2016), therefore, it is of great importance to study the interfacial thermal transport (ITT) in nanoscale (Cahill et al., 2014; Gordiz and Henry, 2015).

To study the ITT, there are some widely applied methods. Among them, two extensively used approaches are the acoustic mismatch model, proposed by Little (1959) to study the perfect interface without scattering between two dissimilar solids, and the diffuse mismatch model, developed by Swartz and Pohl (1989) and more applicable to investigate the non-perfect interface with complete diffusive scattering. Both of them need to be improved on accuracy in calculating the interfacial thermal resistance (Zhang et al., 2016), since they do not consider the atomic details in actual interface structures (Reddy et al., 2005; Stevens et al., 2005). Another widely applied method is classical molecular dynamics (MD) (Ong and Pop, 2010; Gordiz and Mehdi Vaez Allaei, 2014; Yang et al., 2015; Zhang et al., 2017), based on Newton’s equations of motion; however, it offers low precision below the Debye temperature and fails to capture the quantum effect, owing to its classical nature. For the sake of high accuracy in interfacial thermal conductance, one good choice is the scattering boundary method (SBM), which was created by Lumpkin et al. (1978) to investigate the Kapitza conductance of a one-dimensional (1D) lattice and has been applied in the study of ballistic thermal transport with analytical expressions in various models (Wang and Wang, 2006; Zhang et al., 2008, 2011; Cuansing and Wang, 2009; Hu et al., 2010). What is more, it was by this approach that Shafranjuk (2014) successfully observed heat to electricity conversion in grapheme stripes with heavy chiral fermions. The other good choice is the non-equilibrium Green’s function (NEGF) method, a powerful method to rigorously treat non-equilibrium and interacting systems, was originated from the investigation of electron transport, and has recently been applied to study phonon transport (Mingo, 2006; Lü and Wang, 2007; Zhang et al., 2007, 2009, 2013a,c) and magnon transport (Zhang et al., 2013b).

In this paper, we will start with a 1D atomic junction model with only linear coupling interactions. Owing to full consideration of the atomic interfacial structures, such model really uncovers the ITT properties for ballistic thermal transport regime, which is briefly introduced in Section “The ballistic thermal transport.” Moreover, two effective computational methods—the SBM and NEGF method—are reviewed in this section, and the Landauer formula is also introduced. In Section 3, we will focus on the findings on transmission coefficient and interfacial thermal conductance for interfacial coupling case, then the nonlinear ITT is discussed in Section 4 by using NEGF method.

Theoretical Approaches

1D Atomic Model

The 1D atomic model consisting of two semi-infinite leads and a center part, in fact, is a general model since it is usually justified in realistic material structure that the junction part is relatively smaller than the two leads (Wang et al., 2006). Not only the model can be applied to study electron transport (Peyrard and Remoissenet, 1982; Ness and Fisher, 2002), but also can be exploited to investigate thermal transport in quantized thermal transport (Wang et al., 2008; Cui et al., 2017), ITT (Hu et al., 2010; Zhang et al., 2011; Chen and Zhang, 2015), nonlinear effect (Hopkins and Serrano, 2009; Zhang et al., 2013a,c), and so on.

For simplicity, we first discuss the general harmonic case where two semi-infinite leads (left, L, and right, R) connected to a center region (C) coupled by harmonic springs with constant strength k₁₂ and k₂₃, as shown in Figure 1. Note that all of the three parts (L, C, R) are harmonic chains whose spring constants and mass are k_α and m_α, α = L,C,R. Furthermore, the two leads are at different equilibrium temperatures T_L and T_R and owing to their semi-infinite nature, the waves scattered back into the bath will get dissipated rather than reflected back to the central part. Let the relative displacement for the nth atom in region α be $x_n^{\mathrm{\alpha }}$, α = L,C,R, and N_α represents the size of region α. Thus, the total Hamiltonian is given by (Zhang et al., 2011)

$H={\displaystyle \sum _{\alpha =L,C,R}}{H}_{\mathrm{\alpha }}+\frac{1}{2}{k}_{12}{\left(x_1^L-x_1^C\right)}^2+\frac{1}{2}{k}_{23}{\left(x_{N_C}^C-x_1^R\right)}^2.$ (1)

Here, $H_{\mathrm{\alpha }}={\sum }_{n=1}^{N_{\mathrm{\alpha }}}\frac{1}{2}{m}_{\mathrm{\alpha }}{\left({\dot{x}}_n^{\mathrm{\alpha }}\right)}^2+{\sum }_{n=1}^{N_{\mathrm{\alpha }}}\frac{1}{2}{k}_{\mathrm{\alpha }}{\left(x_n^{\mathrm{\alpha }}-x_{n+1}^{\mathrm{\alpha }}\right)}^2$ is coupled harmonic oscillators, where N_L and N_R are infinity for the leads. When it comes to the one-junction case, namely, the two semi-infinite leads directly connected by k₁₂, in order to obtain corresponding Hamiltonian, we can set k₂₃ = 0, N_C = 0, and $x_1^C$ changes to $x_1^R$. If we use the mass-normalized displacement, $u^{\mathrm{\alpha }}=\sqrt{m_{\mathrm{\alpha }}}{x}^{\mathrm{\alpha }}$, then the Hamiltonian will be written as (Wang et al., 2006)

$H={\displaystyle \sum _{\alpha =L,C,R}}{H}_{\mathrm{\alpha }}+{\displaystyle \sum _{\beta =L,R}}{\left(U_{}^{\mathrm{\beta }}\right)}^T{V}_{}^{\mathrm{\beta }C}{U}_{}^C,$ (2)

where $H_{\mathrm{\alpha }}=\frac{1}{2}{\left({\dot{U}}_{}^{\mathrm{\alpha }}\right)}^T{\dot{U}}_{}^{\mathrm{\alpha }}+\frac{1}{2}{\left(U_{}^{\mathrm{\alpha }}\right)}^T{K}_{}^{\mathrm{\alpha }}{U}^{\mathrm{\alpha }}$, U^α is a column vector composed of all the displacement variables in the region α, ${\dot{U}}^{\mathrm{\alpha }}$ is the conjugate momentum, K^α denotes the spring constant matrix, and $V_{}^{\mathrm{\beta }C}={\left(V_{}^{C\mathrm{\beta }}\right)}^T$ represents the coupling matrix of the region β to the central part.

FIGURE 1

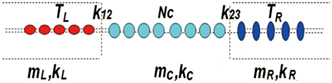
Figure 1. Schematic of the one-dimensional atomic chain model, adapted with permission from the copyright holder (American Physical Society), Zhang et al. (2011).

We can introduce a nonlinear coupling at the interface, e.g., a fourth-order interaction, then the Hamiltonian in Eq. 1 can be revised by adding the term $H_n=\frac{1}{4}{\sum }_{\alpha \beta }{\mathrm{\lambda }}_{\alpha \beta }{\left(x_1^{\mathrm{\alpha }}-x_1^{\mathrm{\beta }}\right)}^4$, where λ_αβ is the fourth-order nonlinear coupling connecting region α and β, and in Eq. 2 we add $H_n=\frac{1}{4}{\sum }_{\mathit{ijkl}}{T}_{\mathit{ijkl}}{U}_i^C{U}_j^C{U}_k^C{U}_l^C$ (Wang et al., 2007; Zhang et al., 2013c).

The Ballistic Thermal Transport

Landauer Formula

When the mean free path of the phonon is longer than the length scale of the medium through which the phonon travels, the phonon transport can be strictly regarded as elastic scattering without energy loss. Such progress is called as a ballistic thermal transport.

As early as 1957, based on the wave scattering mechanism, R. Landauer proposed an intuitive explanation of electron conduction in 1D nanoscale junctions. The argument, however, is not only limited to electrons but can also be applied to phonons. According to the Landauer formula, thermal current across a segment that connects two leads kept in equilibrium at different heat-bath temperatures T_L and T_R can be written as (Wang et al., 2008)

$I=\underset{0}{\stackrel{\infty }{\int }}\frac{d\mathrm{\omega }}{2\pi }\hslash \mathrm{\omega }\mathit{Tr}\left[\mathrm{\omega }\right]\left(f_L-f_R\right),$ (3)

where $f_{L,R}={\left\{\mathit{exp}\left[\hslash \mathrm{\omega }∕\left(k_B{T}_{L,R}\right)\right]-1\right\}}^{-1}$ is known as the Bose–Einstein distribution for phonons, k_B denotes the Boltzman constant and Tr[ω] represents the transmission coefficient for phonons. Note that due to the ballistic transport the transmission coefficient Tr[ω] is independent of temperature whose dependences are in the Bose–Einstein distribution function f_L,R.

Using the definition of thermal conductance as (Wang et al., 2008)

$\mathrm{\sigma }=\underset{T_L\to T,T_R\to T}{\lim }\frac{I}{T_L-T_R},$ (4)

we can develop the junction conductance formula (Zhang et al., 2011)

$\mathrm{\sigma }=\underset{0}{\stackrel{\infty }{\int }}\frac{d\mathrm{\omega }}{2\pi }\hslash \mathrm{\omega }\mathit{Tr}\left[\mathrm{\omega }\right]\frac{\partial f\left(\mathrm{\omega }\right)}{\mathrm{\partial T}}.$ (5)

Scattering Boundary Method

In this section, we will briefly introduce the SBM, which is an efficient way to calculate the interfacial thermal conductance for ballistic thermal transport, following Wang et al. (2006) and Zhang et al. (2011). For convenience, we first consider the condition that two semi-infinite leads are connected directly by the spring k₁₂. We label the atoms by n = −∞, … , − 1, 0, 1, 2, … , +∞, and the atom 0 and 1 are connected by the spring k₁₂. The dynamic equation of motion for each atom in the system is given by (Wang et al., 2006)

$-m_n{\mathrm{\omega }}^2{x}_n+{\sum }_{n\prime }{K}_{n{n}^{\prime }}{x}_{n\prime }=0,$ (6)

where m_n denotes the mass of the nth atom, x_n and $x_{n^{\prime }}$ are the displacement of the nth atom and the n′th atom, respectively, and K_nn′ represents the force constants between the nth atom and the n′th atom. Then the lattice wave solution can take the form as

$x_n^{\mathrm{\alpha }}={\mathrm{\lambda }}_{\mathrm{\alpha }}^n{e}^{-i\mathrm{\omega }t},$ (7)

representing the displacement of the nth atom for each normal mode. Here, ${\mathrm{\lambda }}_{\mathrm{\alpha }}^{}=e^{i{a}_{\mathrm{\alpha }}{q}_{\mathrm{\alpha }}}$, q is the wave number and α denotes lattice constant, that is, the interatomic spacing.

We assume that the incident wave $x_n^L$ transmitted from the left lead to the right lead, then the reflected wave and the transmitted wave can be given, respectively, by $r_{\mathit{LR}}{x}_{-n}^L$ and $t_{\mathit{LR}}{x}_{n-1}^R$, where r_LR and t_LR are the reflection and transmission coefficients which are still unknown. Hence, the boundary conditions have the form as (Zhang et al., 2011)

$\begin{array}{l}\hfill x_n^L={\mathrm{\lambda }}_L^n{e}^{-i\mathrm{\omega }t}+r_{\mathit{LR}}{\mathrm{\lambda }}_L^{-n}{e}^{-i\mathrm{\omega }t},\end{array}$ (8)

$\begin{array}{l}\hfill x_n^R=t_{\mathit{LR}}{\mathrm{\lambda }}_R^{n-1}{e}^{-i\mathrm{\omega }t}.\end{array}$ (9)

Substituting Eq. 7 into Eq. 6, λ_α satisfies the dispersion relation (Zhang et al., 2011)

${\mathrm{\omega }}^2{m}_{\mathrm{\alpha }}=-k_{\mathrm{\alpha }}\left({\mathrm{\lambda }}_{\mathrm{\alpha }}^{-1}-2+{\mathrm{\lambda }}_{\mathrm{\alpha }}^{}\right).$ (10)

Clearly, Eq. 10 is a quadratic equation with two roots. It can be proved that the eigenvalues are inversely proportional to each other, i.e., λ₊λ_– = 1. For 1D atomic chains, there are no evanescent modes, the two roots satisfying |λ| = 1 represent two traveling waves, one is forward and another is backward (Wang et al., 2008). To determine the forward one, one can replace ω with ω + iη, where η→ 0⁺, which can be treated as a small perturbation. Then, for the traveling waves, λ has the modulus in the form of (Velev and Butler, 2004)

$\left|\mathrm{\lambda }\right|=1-\mathrm{\eta }\frac{a}{v}.$ (11)

This means that for the forward moving waves with group velocity v > 0 have |λ| < 1. Hence, we ought to choose the one with |λ| < 1 of the two. In addition, the continuity condition at the interface can be illustrated as (Hu et al., 2010; Zhang et al., 2011)

$\begin{array}{l}\hfill {\mathrm{\omega }}^2{m}_L{x}_0^{}=-k_L{x}_{-1}^{}+\left(k_L+k_{12}\right)x_0^{}-k_{12}{x}_1^{};\end{array}$ (12)

$\begin{array}{l}\hfill {\mathrm{\omega }}^2{m}_R{x}_1^{}=-k_{12}{x}_0^{}+\left(k_{12}+k_R\right)x_0^{}-k_R{x}_2.\end{array}$ (13)

From these equations, we can get the transmission amplitudes r_LR and t_LR. Finally, the analytical expression of the phonon transmission is given by (Hu et al., 2010; Zhang et al., 2011)

$T{r}_1\left[\mathrm{\omega }\right]=1-{\left|r_{\mathit{LR}}\right|}^2=1-{\left|r_{\mathit{RL}}\right|}^2.$ (14)

Here, the reflection coefficient for the phonon wave transmits from region α to region β is expressed as

$r_{\mathrm{\alpha }\beta }=\frac{k_{\mathrm{\alpha }}\left({\mathrm{\lambda }}_{\mathrm{\alpha }}-1∕{\mathrm{\lambda }}_{\mathrm{\alpha }}\right)\left(k_{\mathrm{\beta }}-k_{\mathrm{\alpha }\beta }-k_{\mathrm{\beta }}∕{\mathrm{\lambda }}_{\mathrm{\beta }}\right)}{\left(k_{\mathrm{\alpha }}-k_{\mathrm{\alpha }\beta }-k_{\mathrm{\alpha }}∕{\mathrm{\lambda }}_{\mathrm{\alpha }}\right)\left(k_{\mathrm{\beta }}-k_{\mathrm{\alpha }\beta }-k_{\mathrm{\beta }}∕{\mathrm{\lambda }}_{\mathrm{\beta }}\right)-k_{\mathrm{\alpha }\beta }^2}-1,$ (15)

where ${\mathrm{\lambda }}_{\mathrm{\alpha }}=\frac{-h_{\mathrm{\alpha }}\pm \sqrt{h_{\mathrm{\alpha }}^2-4}}{2}$ and $h_{\mathrm{\alpha }}=\frac{m_{\mathrm{\alpha }}}{k_{\mathrm{\alpha }}}{\left(\mathrm{\omega }+i\mathrm{\eta }\right)}^2-2$. If there are N atoms in the center region labeling by n = 1, 2, … , N_C, what we need is to add two equations similar to the Eqs 12 and 13. Note that we have so far made an assumption that the interactions in junctions reach only the first atoms adjacent to the center in the semi-infinite leads. Then the total transmission, Tr₂[ω], can be obtained as (Hu et al., 2010; Zhang et al., 2011)

$T{r}_2\left[\mathrm{\omega }\right]=\frac{\left(1-{\left|r_{\mathit{LC}}\right|}^2\right)\left(1-{\left|r_{\mathit{CR}}\right|}^2\right)}{{\left|1-r_{\mathit{CR}}{r}_{\mathit{CL}}{\mathrm{\lambda }}_C^{2\left(N_C-1\right)}\right|}^2}.$ (16)

NEGF Method

Another efficient approach to calculating the transmission coefficient is NEGF method, which can be used to an interface with arbitrary linear or nonlinear interaction. As proved by Khomyakov et al. (2005), Harbola and Mukamel (2008) and Zhang et al. (2011), without many-body interaction, namely, for the ballistic thermal transport, the SBM and the NEGF method are equivalent.

For the simplest condition without any nonlinear interaction, we directly define a contour-ordered Green’s function as (Wang et al., 2008)

$G_{}^{\mathrm{\alpha }\beta }\left(\mathrm{\tau },\mathrm{\tau }\prime \right)\equiv -\frac{i}{\hslash }⟨\mathcal{T}{U}^{\mathrm{\alpha }}\left(\mathrm{\tau }\right)U^{\mathrm{\beta }}{\left(\mathrm{\tau }\prime \right)}^T⟩,$ (17)

where τ is the contour variable and 𝒯 is the contour-ordering operator. For ballistic transport, the motion equation of the center-only Green’s function can be given by (Wang et al., 2007)

$\begin{array}{ll}\hfill \left(\frac{{\partial }^2}{\partial {\mathrm{\tau }}^2}+K^C\right)G_0\left(\mathrm{\tau },\mathrm{\tau }\prime \right)& =-I\mathrm{\delta }\left(\mathrm{\tau }-\mathrm{\tau }\prime \right)-\int d\mathrm{\tau }″\sum r\left(\mathrm{\tau },\mathrm{\tau }″\right)G_0\left(\mathrm{\tau }″,\mathrm{\tau }\prime \right),\end{array}$ (18)

Here ${\sum }_{}^r={\sum }_L^r+{\sum }_R^r$, where ${\sum }_{\mathrm{\alpha }}^r=V^{C\mathrm{\alpha }}{g}_{\mathrm{\alpha }}^r{V}^{\mathrm{\alpha }C},\mathrm{\alpha }=L,R,$ represents the retarded self-energy of the corresponding lead as a result of the interaction with the heat bath, and $g_{\mathrm{\alpha }}^r={\left[{\left(\mathrm{\omega }+i\mathrm{\eta }\right)}^{2}I-K^{\mathrm{\alpha }}\right]}^{-1}$ is the surface Green’s function for the semi-infinite leads.

With a nonlinear interaction, the contour-ordered Green’s function can be expressed by scattering matrix operator as (Wang et al., 2006, 2007)

$G_{}^{\mathrm{\alpha }\beta }\left(\mathrm{\tau },\mathrm{\tau }\prime \right)=-\frac{i}{\hslash }⟨T{U}^{\mathrm{\alpha }}\left(\mathrm{\tau }\right)U^{\mathrm{\beta }}{\left(\mathrm{\tau }\prime \right)}^T{e}^{-i\int V_n^{}\left(\mathrm{\tau }″\right)d\mathrm{\tau }″}⟩.$ (19)

Then in frequency domain we can obtain (Haug and Jauho, 1996)

$\begin{array}{l}\hfill G_0^r={\left({\left(\mathrm{\omega }+i\mathrm{\eta }\right)}^{2}I-K^C-{\sum }_{}^r\right)}^{-1},\end{array}$ (20)

$\begin{array}{l}\hfill G_0^{<}=G_0^r{\sum }^{<}{G}_0^a,\end{array}$ (21)

$\begin{array}{l}\hfill G_C^r={\left(G_0^{r-1}-{\sum }_n^r\right)}^{-1},\end{array}$ (22)

$\begin{array}{l}\hfill G_c^{<}=G_c^r\left({\sum }^{<}+{\sum }_n^{<}\right)G_c^a.\end{array}$ (23)

where, ∑_n is the nonlinear self-energy. Note that if there is no nonlinearity, then ∑_n = 0, G = G₀ = G_c. In addition, utilizing the time translational invariance of the system, G^r and G^α are Hermitian conjugate to each other, namely, G^r = (G^α)^† The transmission coefficient can be computed by the so-called Caroli formula (Wang et al., 2008)

$\mathit{Tr}\left[\mathrm{\omega }\right]=\mathit{Tr}\left(G_{}^r{\mathrm{\Gamma }}_L{G}_{}^a{\mathrm{\Gamma }}_R\right),$ (24)

where ${\mathrm{\Gamma }}_{\mathrm{\alpha }}=i\left({\sum }_{\mathrm{\alpha }}^r-{\sum }_{\mathrm{\alpha }}^a\right)$ denotes the interaction between the semi-infinite leads and the central part.

So far the equations are all exact. Since it is obviously impossible to evaluate the nonlinear self-energy ∑_n in interacting systems, several ways of approximation is unavoidable. Due to the relatively weak nonlinear interaction of the actual system, the perturbation treatment above can just be applied to the cases where the temperatures are not too high. The standard approach is to apply a mean-field approximation with which the solution must be computed iteratively.

Thermal Transmission and Interfacial Resistance

One-Junction Case

According to Hu et al. (2010) and Zhang et al. (2011), the ballistic ITT in 1D atomic chains with only linear couplings was investigated via SBM and the analytical expressions of the phonon transmission were obtained. With these analytical expressions, the role of each parameter on the thermal transport in single-junction and two-junction cases can be analyzed.

For one-junction case, the transmission coefficient decreases with the increasing frequency for all the coupling k₁₂, as shown in Figure 2, which matches well with that of the studies on silicon–amorphous polyethylene interfaces by MD (Hu et al., 2009). Furthermore, for the two leads with the same spring constant and mass, supposed that k_L = k_R = k₁₂, the transmission Tr₁[ω] will equal one in the whole frequency domain due to the homogeneous chains, as illustrated in Figure 2A. While for the heterogeneous lead structure case, as shown in Figure 2B, it seems that for a given frequency ω the transmission will reach its maximum at k₁₂ taking the value ranging from k_L to k_R. Figure 3 illustrates that with the increasing coupling k₁₂, the thermal conductivity will initially increase, then reach a certain maximum, and then slightly decrease, and finally tend to a constant. Zhang et al. (2011) found that either the maximum transmission or the maximum conductance occurs when the interface spring equals the harmonic mean of the spring constants on both sides of the interface, that is, at k₁₂ given by (Zhang et al., 2011)

$k_{12}=k_{12m}=\frac{2k_L{k}_R}{k_L+k_R}.$ (25)

Provided that the interfacial coupling is equal to k_12m, if k_L/m_L = k_R/m_R that is, for the curve with m_R = 2 in Figure 4, the transmission coefficient Tr₁[ω] is consistent with the one in the long-wave limit (Zhang et al., 2011):

$T{r}_1\left[0^{+}\right]=\frac{4\sqrt{k_L{m}_L{k}_R{m}_R}}{{\left(\sqrt{k_L{m}_L}+\sqrt{k_R{m}_R}\right)}^2},$ (26)

which is a constant independent of frequency ω and in agreement with the one for the acoustic mismatch model (Little, 1959) $\mathit{Tr}=\frac{4Z_L{Z}_R}{{\left(Z_L+Z_R\right)}^2}$, where $Z_{\mathrm{\alpha }}\left(\mathrm{\omega }=0^{+}\right)=\sqrt{k_{\mathrm{\alpha }}{m}_{\mathrm{\alpha }}}$. While in the range between the point of equal-spectrum where ω_m = k_L/m_L = k_R/m_R and the one of equal-impedance where Z(ω = 0⁺) = k_Lm_L = k_Rm_R, that is, for the curve with $m_R=\frac{1}{6},\frac{1}{3},4$ and 6 in Figure 4, with the increasing frequency, the transmission Tr₁[ω] will increase first then decrease; otherwise, a monotonous decline will occur. In terms of extremely dissimilar materials, the transmission coefficient of the entire frequency domain is large in comparison with the one in long-wave limit. Thus, this may explain the reason why the acoustic mismatch model usually overestimates the interfacial thermal resistance. For weak interfacial coupling, either the cut-off frequency or the interface conductance is linearly dependent on the interfacial coupling; while the transmission coefficient is in proportion to the square of the interfacial coupling.

FIGURE 2

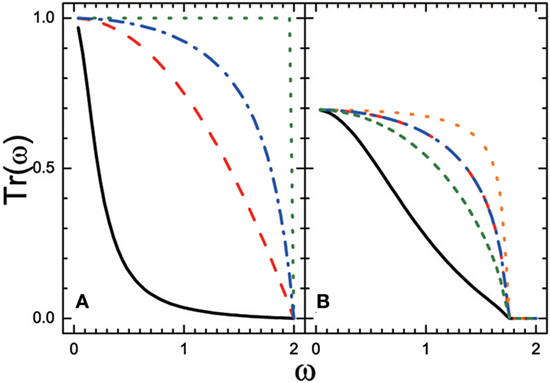
Figure 2. Transmission coefficient Tr[ω] as a function of frequency ω for different interfacial coupling k₁₂ in single-junction model, adapted with permission from the copyright holder (American Physical Society), Zhang et al. (2011). (A) k_L = k_R = 1.0, m_L=m_R = 1.0; dash-dotted, dotted, dashed, and solid lines correspond to k₁₂ = 2.0,1.0,0.5,0.1. (B) k_L = 1.0, m_L = 1.0, k_R = 3.0, and m_R = 4.0; shot-dashed, dash-dotted, dotted, long-dashed, and solid lines correspond to k₁₂ = 8.0,3.0,1.5,1.0,0.5.

FIGURE 3

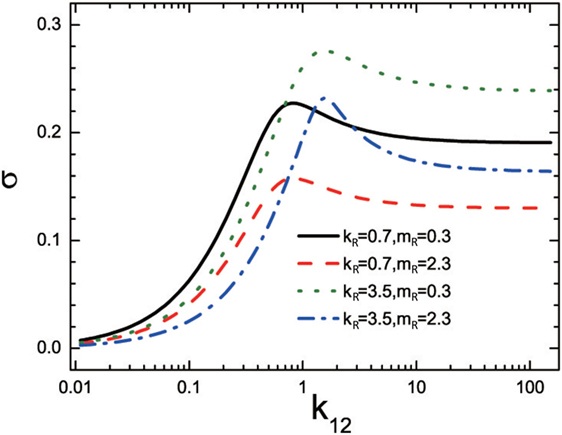
Figure 3. Thermal conductance σ as a function of interfacial coupling k₁₂ in one-junction model, adapted with permission from the copyright holder (American Physical Society), Zhang et al. (2011). Here k_L = 1.0 and m_L = 1.0.

FIGURE 4

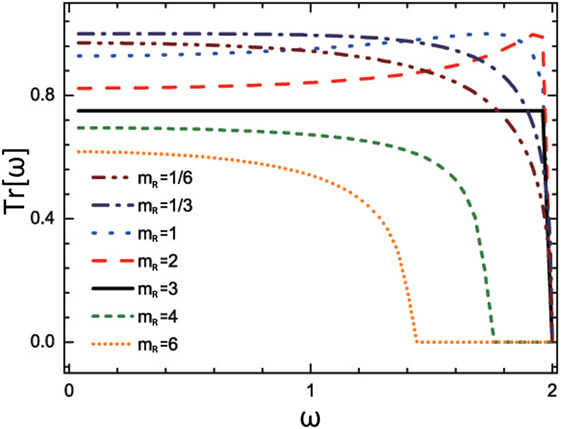
Figure 4. Transmission coefficient Tr[ω] as a function of frequency ω for different mass ratios m_R/k_12m at k_12m, adapted with permission from the copyright holder (American Physical Society), Zhang et al. (2011). Here, k_L = 1.0, k_R = 3.0, k₁₂ = 1.5, and m_L = 1.0.

Saltonstall et al. (2013) reproduced some of Zhang’s results and elaborated on them via NEGF method. Separately taking an impurity mass and variable bonding into consideration, the authors derived solutions to the interfacial phonon transmission and found that for the case of one interface spring, one can make the transmission at maximum by setting the interface spring to k_12m, while in the case of interface mass, the maximum transmission occurs when the mass impurity is equal to the arithmetic average of the mass on both sides of the interface. Note that in many conditions, the maximum transmission for each case is not necessarily the same. For the interface mass case, the maximum transmission is predicted by a frequency-dependent acoustic mismatch model. Whereas, for the interface spring case, the maximum transmission cannot be exactly identical to the transmission predicted by the model mentioned in the above case.

Two-junction Case

Phonon Interference

So far, the most important efforts in phonon engineering have to do with the work on superlattices, for which the phonon interference is directly displayed by measuring the phonon transmission (Narayanamurti et al., 1979; Luckyanova et al., 2012).

For two-junction atomic chains, since the transmission wave is scattered by the second boundary, which results in multiple reflections, the overall transmission can be regarded as the behavior which comprises both the transmission behavior in one-junction model and the oscillatory behavior. Similarly using SBM, Zhang et al. (2011) finally obtained the corresponding phonon transmission coefficient and found that the transmission oscillates with frequency between the envelope lines of minimum $T{r}_{2\mathit{min}}\left[\mathrm{\omega }\right]=\left(1-{\left|r_{\mathit{LC}}\right|}^2\right)\left(1-{\left|r_{\mathit{CR}}\right|}^2\right)∕\left(1+{\left|r_{\mathit{CR}}{r}_{\mathit{CL}}\right|}^2\right)$ and maximum transmission $T{r}_{2\mathit{max}}\left[\mathrm{\omega }\right]=\left(1-{\left|r_{\mathit{LC}}\right|}^2\right)\left(1-{\left|r_{\mathit{CR}}\right|}^2\right)∕\left(1-{\left|r_{\mathit{CR}}{r}_{\mathit{CL}}\right|}^2\right)$, as shown in Figures 5A–C.

FIGURE 5

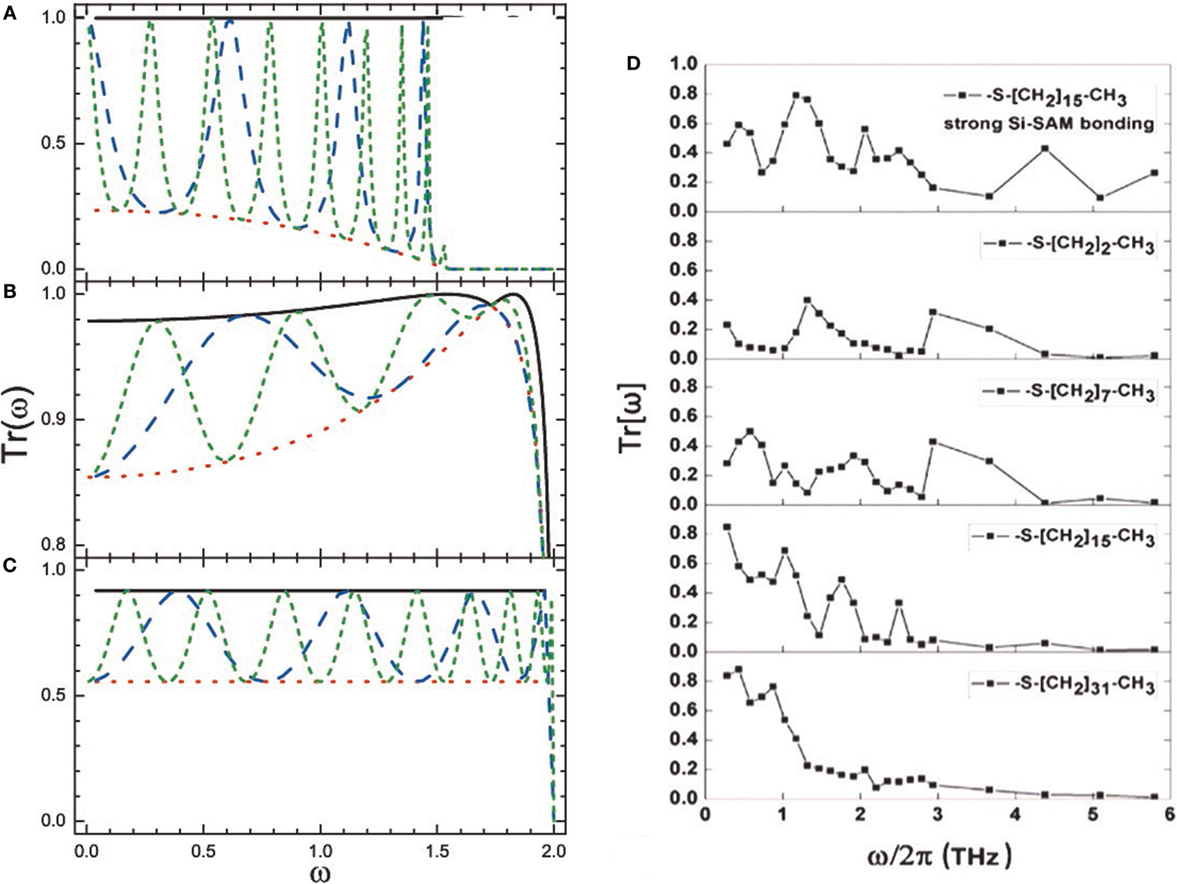
Figure 5. (A–C) Transmission coefficient Tr[ω] as a function of frequency ω of two-junction atomic chains, which is adapted with permission from the copyright holder (American Physical Society), Zhang et al. (2011). (D) Transmission coefficient Tr[ω] as a function of frequency ω of the incident longitudinal acoustic wave packet for various self-assembled monolayer (SAM) thicknesses, adapted with permission from the copyright holder (American Physical Society), Hu et al. (2010).

The transmission oscillatory behavior with frequency was confirmed by Hu et al. (2010), who applied MD simulations and SBM calculations to demonstrate phonon interference at the nanoscale layers connecting two materials, e.g., the self-assembled monolayer (SAM) interfaces, as seen in Figure 5D. As is known to all, interference effects can be exploited to adjust the reflection and transmission of electromagnetic waves at the interface adjoining two media. In addition, both the typical wavelength and the mean free path of phonons for thermal transport are in nanoscopic scale (Ziman, 1960) leading to the difficulty in directly observing the performance of the phonon interference. As a consequence, in the light of Hu et al. (2010), the system has been assumed ideal with nanoscopic coatings and atomistically smooth interfaces, which is similar to the interference effect in optical.

Apart from the direct evidence mentioned before, numerous indications have been observed in SAM structure. Comparing the interfacial conductance for various lengths of atomic chains with each other, some differences indicate that under certain conditions the interfacial conductance increasing with the longer chains, which suggests that for certain thicknesses of the SAM domain, the transmission coefficient of phonons may be decreased due to strong interference effects. Corresponding evidence sketched in Figure 5D shows that with the increasing frequency the oscillatory features diminish as the chain length increases and decreases monotonically, which is in agreement with the investigation of phonon transport through mass-mismatched fcc thin films (Tian et al., 2010). The understanding given by Hu et al. (2010) is as flowing. For longer SAM molecules, with the coherent nature of phonon propagation along the atomic chain diminishing due to the phonon–phonon scattering, the interference effects will be eliminated.

Moreover, Hu et al. (2010) varied the length of atomic chains via much larger factors in the experiment, which makes it possible to find further evidence for phonon interference effect. Comparing the temperature drop at the Si–SAM interface with the one at the SAM–Au interface, the result shows that the apparent conductance of one interface determined by the interfacial bonding on the other one owing to the interference effect.

Since the phonon interference can be understood analytically, these findings are extremely practical and may offer guidelines to make phonon filters tailored by the interfacial interactions and layer thickness, such as the phonon selective frequency filter designed by Zhang et al. (2011).

The Optimized Thermal Coupler

It has been a long-lasting problem that in spite of an impressive promise as a thermal material, nanotubes had disappointing limited performance in practical systems due to the weak adhesion at interface (Marconnet et al., 2013). Kaur et al. (2014) bridged the interface with short, covalently bonded organic molecules between vertically aligned multiwall carbon-nanotube (CNT) arrays and either noble or reactive metal surfaces to increase the adhesion between them. Finally, the significantly increased adhesion led to a dramatic sixfold enhanced thermal interface conductance of the CNT array contact. This means that by coupling two materials directly, optimized ITT cannot be obtained. Therefore, the maximum conductance found by Zhang et al. (2011) is not applicable in this case, and one should select a thermal coupler to bridge the two material interfaces.

For ITT, the phonon scattering owing to the mismatch at the interface leads to the thermal resistance and in turn constrains the thermal conductance, which agrees well with Han et al. (2016) and Wang et al. (2016). Thus, to find optimized thermal couplers is to minimize scattering caused by the interfacial mismatch. Supposing that the coupling strength for the thermal coupler is very weak, owing to the large scattering at interfaces, the thermal conductance will be small. Therefore, one should find optimized thermal coupler with relatively larger coupling strength to the leads.

Chen and Zhang (2015) investigated ITT though a 1D atomic chain where the center region serving as a thermal coupler and focused on k_C and m_C to obtain the optimized coupler. The authors first considered two special cases–two semi-infinite leads with equal cut-off phonon frequencies and with equal acoustic impedance. Then they turned to a general case, where either the cut-off frequencies or acoustic impedances took values at random. For the first case, Chen and Zhang (2015) found that if the cut-off frequency of the coupler is equal to that of the two leads, namely k_C/m_C = k_L/m_L = k_R/m_R, and the acoustic impedance is equal to the geometric average of the two leads, namely $\sqrt{k_C{m}_C}=\sqrt{\sqrt{k_L{m}_L}\sqrt{k_R{m}_R}}$, the conductance will be maximum. Then the authors obtained (Chen and Zhang, 2015)

$k_C=\sqrt{k_L{k}_R}.$ (27)

That is to say, the spring constant in the interface coupler equals the geometric mean of those on both sides of the interface. For the second case, Chen and Zhang (2015) found that the optimized interfacial coupler can be found around the point where all of the three parts of the model have identical acoustic impedance and the spring constant of the interfacial coupler is equal to the harmonic mean of those of the leads, that is (Chen and Zhang, 2015)

$k_C=\frac{2k_L{k}_R}{k_L+k_R}.$ (28)

For the general case, the optimized interfacial couplers may appear near the cross point of the harmonic average of cut-off frequencies and the geometric average of impedances of the two leads. All the findings promise to be applied in high performance ITT.

Nonlinear Interaction

In the studies mentioned above, phonon transports are linearly across the interface. In this section, the nonlinear effect at the interface will be discussed by mainly following the step of Zhang et al. (2013c).

Zhang et al. (2013c) simplified the problem of thermal transport across a solid–solid interface, where two linear leads connected by an interfacial linear coupling k₁₂ and a fourth-order nonlinear interaction λ, as illustrated in Figure 6. Note that the model has excluded the nonlinear phonon or electron transport in both materials; therefore, the thermal resistance only appears at the interface. Introducing the mass-normalized displacement, the center Hamiltonian takes the form (Zhang et al., 2013c):

$H_C=\frac{1}{2}{\left({\dot{U}}_{}^C\right)}^T{\dot{U}}_{}^C+\frac{1}{2}{\left(U_{}^C\right)}^T{K}_{}^C{U}^C+\frac{1}{4}{\displaystyle \sum _{i,j,k,l=1}^2}{T}_{\mathit{ijkl}}{u}_i{u}_j{u}_k{u}_l,$ (29)

where U^C = (u₁,u₂)^T, T_ijkl = (− 1)^i+j+k+lλ and

${\text{K}}^C=\left(\begin{array}{cc}\hfill \frac{k_L+k_{12}}{m_L}\hfill & \hfill \frac{-k_{12}}{\sqrt{m_L{m}_R}}\hfill \\ \hfill \frac{-k_{12}}{\sqrt{m_L{m}_R}}\hfill & \hfill \frac{k_{12}+k_R}{m_L}\hfill \end{array}\right).$ (30)

For the two leads, the Hamiltonian is $H_{\mathrm{\alpha }}=\frac{1}{2}{\left({\dot{U}}_{}^{\mathrm{\alpha }}\right)}^T{\dot{U}}_{}^{\mathrm{\alpha }}+\frac{1}{2}{\left(U_{}^{\mathrm{\alpha }}\right)}^T{K}_{}^{\mathrm{\alpha }}{U}^{\mathrm{\alpha }}$, where α = L, R and the corresponding coupling to the center region is $H_{\mathrm{\alpha }C}={\left(U_{}^{\mathrm{\alpha }}\right)}^T{V}_{}^{\mathrm{\alpha }C}{U}^C$. In the light of Eq. 18 discussed in Section “Non-Equilibrium Green’s Function Method” and taking the nonlinearity into account, the equation of motion for the full Green’s function can be written as (Zhang et al., 2013c):

$\begin{array}{llll}\hfill & \frac{{\partial }^2}{\partial {\mathrm{\tau }}^2}{G}_{\mathit{im}}\left(\mathrm{\tau },\mathrm{\tau }\prime \right)+{\displaystyle \sum _j}{K}_{\mathit{ij}}^C{G}_{\mathit{im}}\left(\mathrm{\tau },\mathrm{\tau }\prime \right)+{\displaystyle \sum _{\mathit{jkl}}}{T}_{\mathit{ijkl}}{G}_{\mathit{jm}}\left(\mathrm{\tau },\mathrm{\tau },\mathrm{\tau },\mathrm{\tau }\prime \right)& \hfill & \\ \hfill & =-\mathrm{\delta }\left(\mathrm{\tau }-\mathrm{\tau }\prime \right){\mathrm{\delta }}_{\mathit{im}}-{\displaystyle \sum _j}\int d\mathrm{\tau }″{\displaystyle \sum _{\mathit{ij}}}\left(\mathrm{\tau },\mathrm{\tau }″\right)G_{\mathit{jm}}\left(\mathrm{\tau }″,\mathrm{\tau }\prime \right).\end{array}$ (31)

Based on the NEGF method, Zhang et al. (2013c) developed the quantum self-consistent mean-field (QSCMF) theory for nonlinear ITT, which is a mean-field-like approximation similar to that applied by Bruus and Flensberg (2004). They introduced an effective dynamic matrix (Zhang et al., 2013c):

${\tilde{K}}_{\mathit{ij}}^C=K_{\mathit{ij}}^C+3\mathrm{i\hslash }{\displaystyle \sum _{\mathit{kl}}}{T}_{\mathit{ijkl}}{G}_{\mathit{kl}}\left(0\right)=K_{\mathit{ij}}^C+3\mathrm{i\hslash }{\displaystyle \sum _{\mathit{kl}}}{T}_{\mathit{ijkl}}⟨u_k{u}_l⟩,$ (32)

and finally found that the nonlinearity λ works as a modulator for the interfacial linear coupling k₁₂, then the effective interfacial coupling takes the form (Zhang et al., 2013c):

$k_{12\mathit{ef}}=k_{12}+3\lambda \left(\frac{⟨u_1^2⟩}{m_L}-2\frac{⟨u_1{u}_2⟩}{\sqrt{m_L{m}_R}}+\frac{⟨u_2^2⟩}{m_R}\right),$ (33)

which is temperature dependent. Clearly, all the scattering only takes place at the interface due to all the other parts are harmonic.

FIGURE 6

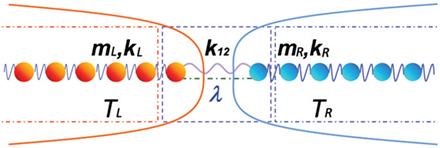
Figure 6. Schematic of the one-dimensional atomic junction model for a solid–solid interface, adapted with permission from the copyright holder (Europhysics Letters), Zhang et al. (2013c).

For the homogeneous lattice with k_L = k_R = k₁₂, Zhang et al. (2013c) found that the nonlinearity at interface suppresses the thermal transport as sketched in Figure 7. If there is no nonlinear interaction, the thermal conductance will initially increase with the average temperature increasing and then tend to a constant since the phonons contributing to thermal transport reach the saturation, as shown in Figure 7A. For non-zero nonlinearity, the thermal conductance will first exhibit similar behavior, owing to more excited phonon modes which participate and enhance thermal transport; however, with the further increase of the average temperature, the conductance will decrease after reaching its maximum since the nonlinear effect increases and, thus, blocks thermal transport. The suppressive behavior of nonlinear effect is illustrated in Figure 7B, where the conductance decreases with increasing nonlinearity.

FIGURE 7

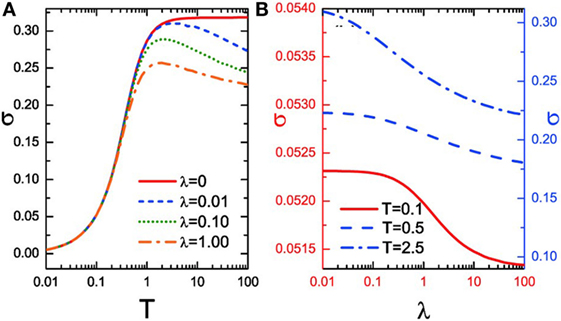
Figure 7. (A) Interfacial thermal conductance σ for homogeneous lattice as a function of the average temperature T = (T_L+ T_R)/2. (B) Interfacial thermal conductance σ for homogeneous lattice as a function of the interfacial nonlinearity λ. Here, k_L = k_R = k₁₂ = 1.0, m_L = m_R = m₁₂ = 1.0. The figure has been adapted with permission from the copyright holder (Europhysics Letters), Zhang et al. (2013c).

While in the weak-interfacial-coupling regime, namely, k₁₂ < k_L = k_R, Zhang et al. (2013c) calculated the interfacial thermal conductance σ and effective interfacial coupling k_12ef for different average temperatures as sketched in Figure 8A. With the increase of nonlinearity, the interfacial conductance will increase first and then decrease owing to the larger interfacial scattering after reaching the maximum value at the point where the effective coupling k_12ef equals one; while the effective coupling k_12ef increases monotonically with nonlinearity increasing and finally larger than k₁₂. This means that in the weak-linear-interface-coupling regime, the nonlinearity can make a larger k_12ef which reduces the mismatch between the leads and the interface, thus enhances the ITT. We can understand such enhancement from an extreme case of k₁₂ = 0, where only a nonlinear channel will definitely enhance phonon transport, since the thermal conductance will be zero if the nonlinear channel is also absent. As we can see in Figure 8B, due to the increasing temperature which allows more phonons to transport, the point where the thermal conductance reaches its maximum is inconsistent with k_12ef = 1. Therefore, for the weak-interfacial-coupling case, the nonlinearity has the ability to improve the ITT, which does not found in strong-linear-coupling case.

FIGURE 8

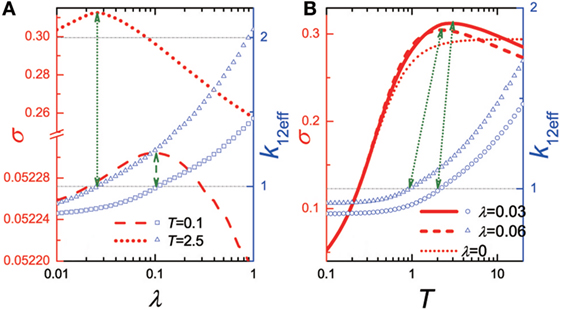
Figure 8. (A) Interfacial thermal conductance σ and effective interfacial coupling k_12ef in the weak-interfacial-coupling regime as a function of the interfacial nonlinearity λ. (B) Interfacial thermal conductance σ and effective interfacial coupling k_12ef in the weak-interfacial-coupling regime as a function of the average temperature T. Here, k_L = k_R = 1.0, k₁₂ = 0.80 and m_L = m_R = 1.0. The figure has been adapted with permission from the copyright holder (Europhysics Letters), Zhang et al. (2013c).

In addition, in spite of two linear leads, thanks to the asymmetric structure and the interfacial nonlinearity λ, thermal rectification can be observed. Let the temperature of the cold and hot bath be T_c and T_h, respectively. Then the rectification can be defined as (Zhang et al., 2010)

$R=\frac{\left(J_{+}-J_{-}\right)}{\text{max}\left\{J_{+},J_{-}\right\}},$ (34)

where J₊ represents the forward direction heat flux for T_L = T_c and T_R = T_h; while J₋ denotes that of the backward direction for T_L = T_h and T_R = T_c. Applying the QSCMF theory, Zhang et al. (2013a) calculated interfacial thermal rectification R as a function of the interfacial nonlinearity λ and the interfacial linear coupling k₁₂ as shown in Figure 9. With the nonlinear interaction λ rising, the interfacial thermal rectification R will increase initially and then decrease because the interfacial scattering plays a leading role to decrease the difference between J₊ and J₋, as illustrated in Figure 9A. Figure 9B shows that owing to the relative role for the channel of phonon transport between k₁₂ and λ, the interfacial rectification shows various behaviors. To be specific, the interfacial rectification will almost be a constant, if k₁₂ > > λ; it will drop dramatically, if k₁₂ ~ λ; otherwise, it will nearly vanish.

FIGURE 9

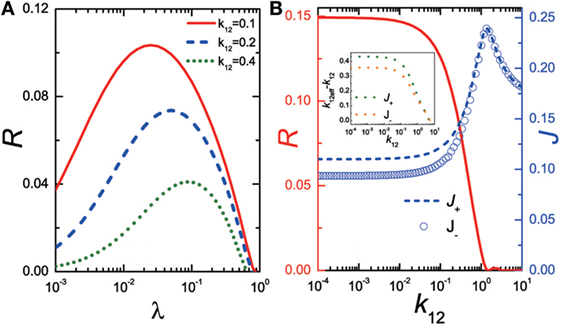
Figure 9. (A) Interfacial thermal rectification R as a function of the interfacial nonlinearity λ. (B) Interfacial thermal rectification R as a function of the interfacial linear coupling k₁₂. The inset in (B) shows the effective coupling from the nonlinearity k_12ef − k₁₂ as a function of the interfacial linear coupling k₁₂. The figure has been adapted with permission from the copyright holder (Europhysics Letters), Zhang et al. (2013c).

According to Zhang et al. (2013a), similarly using the NEGF method, the thermal rectification through metal–insulator interface was studied under the self-consistent Born approximation by a 1D atomic chain model where an electron–phonon interaction (EPI) V_ep connecting an electron lead and a phonon lead and a linear coupling k₁₂ connecting another phonon lead with the right one, as shown in Figure 10. In this study, Zhang et al. (2013a) excluded the phonon contribution in metal by setting k₁₂ = 10⁻⁴ and T_Lp = T_R to avoid divergence without changing the physical properties of the rectification. It is found that the rectification R across the metal–insulator interface can change sign with different average temperatures T and electron–phonon interactions. For a relatively larger EPI, namely V_ep = 0.01, as shown in Figure 11A, with the increasing mean temperature T, the rectification R will first be positive then negative; while for a weak EPI ranging from 10⁻⁴ to 10⁻², as illustrated in Figure 11B, the rectification R will be always negative except at lower temperatures, at which the rectification R can change to a positive one. In terms of the EPI, the Green’s functions of electrons change far more than that of the phonons and the electron Green’s functions G^< and G^> will be more asymmetric with the EPI increasing. At a weak EPI, the backward thermal current J₋is larger than the forward one (Figures 11C1,C3), owing to the locally available density of states (LADOS) of phonons increasing in the backward direction; therefore, the rectification R will be negative (Figure 11B). While for a stronger EPI, it can induce a relatively larger G^< within the energy range from −2 to −1, where larger density of states for the center electrons takes place. In addition, more electrons with energy aloof from the Fermi level make contributions to the thermal current, thus the forward thermal current J₊ is larger than the backward one (Figure 11C2), and the rectification R is found positive (Figure 11A). For the higher temperature, the contribution from energy aloof from the Fermi level will decrease and the main change for the electron LADOS in the forward transport is smaller than that in the backward one. Therefore, the forward thermal current J₊ is small in comparison with the backward one (Figure 11C4) and the rectification can change to a negative one (Figure 11A). In summary, owing to the mismatch of phonon and electron LADOS, the rectification R is negative for high mean temperatures or weak EPI, while it is positive at low average temperatures with larger EPI.

FIGURE 10

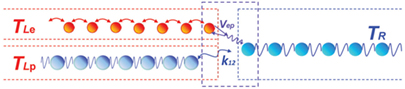
Figure 10. The lattice model of the metal–insulator interface, adapted with permission from the copyright holder (Institute of Physics), Zhang et al. (2013a).

FIGURE 11

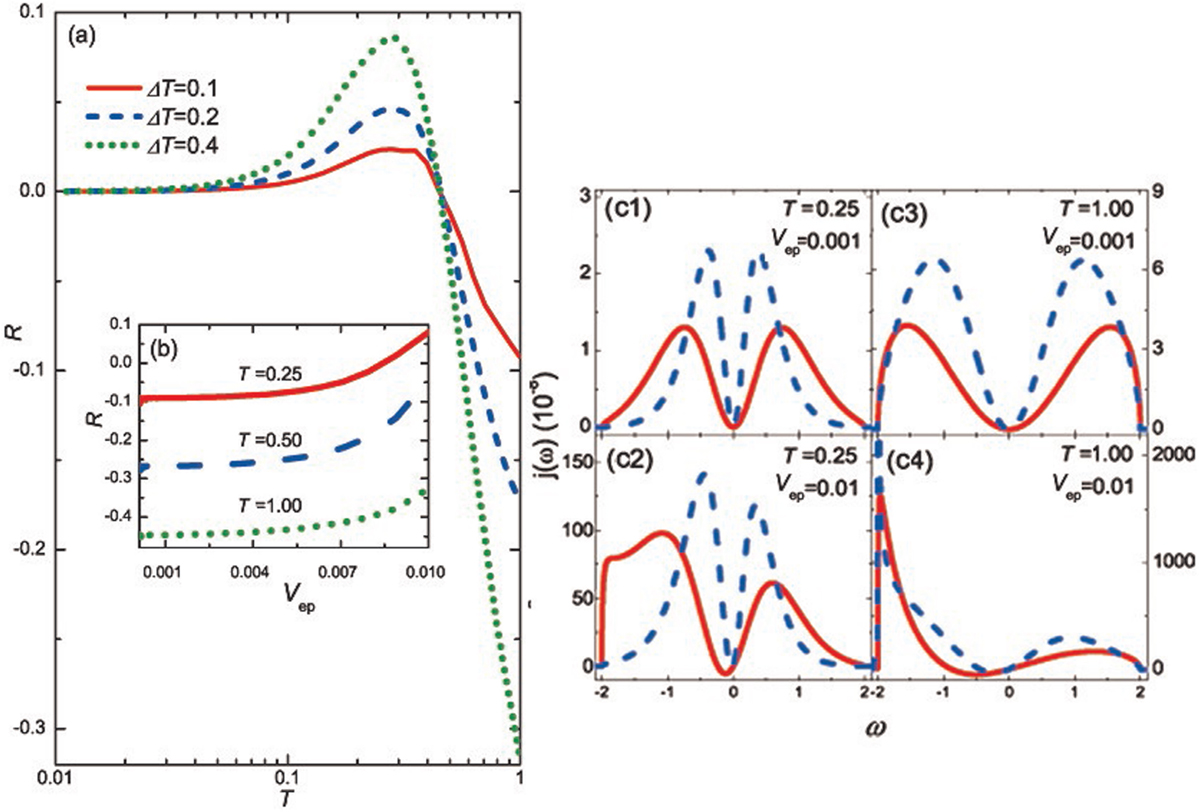
Figure 11. (A) Thermal rectification R through the metal–insulator interface as a function of average temperature T for different temperature differences at electron–phonon interaction V_ep = 0.01 (B) Thermal rectification R as a function of the EPI at different temperatures. (C1–C4) Thermal current density j(ω) in the backward (dashed lines) and forward (solid lines) transport for various EPI and temperatures. The figure has been adapted with permission from the copyright holder (Institute of Physics), Zhang et al. (2013a).

The reverse of rectification is of great importance for the study of one-way thermal transport and adjusting the thermal transport direction; thus, it can have promises to be widely applied in energy science.

Summary and Outlook

This paper reviews the latest theoretical development mainly made by us and our collaborators in ITT through 1D atomic junction model, by introducing the SBM and NEGF method. Such simple model is efficient in exploring various aspects on ITT, including phonon transmission, interfacial thermal conductance, phonon interference, nonlinear interfacial coupling, interfacial thermal rectification, etc. Although many exotic properties have found through the 1D atomic model, such as non-monotonic transmission, optimized coupling and coupler, nonlinearity enhancing interfacial conductance, and nonlinear coupling induced thermal rectification, there are still much work worth doing on the ITT through the 1D atomic model. Here, we only talk about a uniform interfacial coupler, how about a non-uniform chain, and how about disorder or nonlinearity affect the interfacial conductance? Can we apply SBM to a nonlinear atomic chain? Can we generalize all the findings to 2D and 3D interface? All these problems are desirable to be investigated for understanding the actual ITT. Thus, the ITT through 1D atomic model is very important for understanding the microscopic mechanism of thermal transport across the interface. We hope this brief review can shed some light on the study of the ITT and provide helpful guidance on the thermal experiments and applications.

Author Contributions

All named authors have contributions to the writing process, including the initial conception, the drafting and revision of the review.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer JL and handling Editor declared their shared affiliation.

Acknowledgments

We acknowledge support from NSFC (Grant No. 11574154).

References

Alexeev, D., Chen, J., Walther, J. H., Giapis, K. P., Angelikopoulos, P., and Koumoutsakos, P. (2015). Kapitza resistance between few-layer graphene and water: liquid layering effects. Nano Lett. 15, 5744–5749. doi: 10.1021/acs.nanolett.5b03024

PubMed Abstract | CrossRef Full Text | Google Scholar

Bruus, H., and Flensberg, K. (2004). Many-Body Quantum Theory in Condensed Matter Physics: An Introduction. Oxford: Oxford University Press.

Google Scholar

Cahill, D. G., Braun, P. V., Chen, G., Clarke, D. R., Fan, S., Goodson, K. E., et al. (2014). Nanoscale thermal transport. II. 2003–2012. Appl. Phys. Rev. 1, 011305. doi:10.1063/1.4832615

CrossRef Full Text | Google Scholar

Chen, B., and Zhang, L. (2015). Optimized couplers for interfacial thermal transport. J. Phys. Condens.Matter 27, 125401. doi:10.1088/0953-8984/27/12/125401

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, J., Walther, J. H., and Koumoutsakos, P. (2015). Covalently bonded graphene–carbon nanotube hybrid for high-performance thermal interfaces. Adv. Funct. Mater. 25, 7539–7545. doi:10.1002/adfm.201501593

CrossRef Full Text | Google Scholar

Chen, J., Walther, J. H., and Koumoutsakos, P. (2016). Ultrafast cooling by covalently bonded graphene-carbon nanotube hybrid immersed in water. Nanotechnology 27, 465705. doi:10.1088/0957-4484/27/46/465705

PubMed Abstract | CrossRef Full Text | Google Scholar

Cuansing, E., and Wang, J. S. (2009). Quantum transport in honeycomb lattice ribbons with armchair and zigzag edges coupled to semi-infinite linear chain leads. Eur. Phys. J. B 69, 505–513. doi:10.1140/epjb/e2009-00187-2

CrossRef Full Text | Google Scholar

Cui, L., Jeong, W., Hur, S., Matt, M., Klöckner, J. C., Pauly, F., et al. (2017). Quantized thermal transport in single-atom junctions. Science 355, 1192–1195. doi:10.1126/science.aam6622

PubMed Abstract | CrossRef Full Text | Google Scholar

Gordiz, K., and Henry, A. (2015). Examining the effects of stiffness and mass difference on the thermal interface conductance between Lennard-Jones solids. Sci. Rep. 5, 18361. doi:10.1038/srep18361

PubMed Abstract | CrossRef Full Text | Google Scholar

Gordiz, K., and Mehdi Vaez Allaei, S. (2014). Thermal rectification in pristine-hydrogenated carbon nanotube junction: a molecular dynamics study. J. Appl. Phys. 115, 163512. doi:10.1063/1.4873124

CrossRef Full Text | Google Scholar

Han, H., Zhang, Y., Wang, N., Samani, M. K., Ni, Y., Mijbil, Z. Y., et al. (2016). Functionalization mediates heat transport in graphene nanoflakes. Nat. commun 7, 11281. doi:10.1038/ncomms11281

PubMed Abstract | CrossRef Full Text | Google Scholar

Harbola, U., and Mukamel, S. (2008). Superoperator nonequilibrium Green’s function theory of many-body systems; applications to charge transfer and transport in open junctions. Phys. Rep. 465, 191–222. doi:10.1016/j.physrep.2008.05.003

CrossRef Full Text | Google Scholar

Haug, H., and Jauho, A. P. (1996). Quantum Kinetics and Optics of Semiconductors. Berlin: Springer.

Google Scholar

Hopkins, P. E., and Serrano, J. R. (2009). Phonon localization and thermal rectification in asymmetric harmonic chains using a nonequilibrium Green’s function formalism. Phys. Rev. B 80, 201408. doi:10.1103/PhysRevB.80.201408

CrossRef Full Text | Google Scholar

Hu, L., Zhang, L., Hu, M., Wang, J. S., Li, B., and Keblinski, P. (2010). Phonon interference at self-assembled monolayer interfaces: molecular dynamics simulations. Phys. Rev. B 81, 235427. doi:10.1103/PhysRevB.81.235427

CrossRef Full Text | Google Scholar

Hu, M., Keblinski, P., and Schelling, P. K. (2009). Kapitza conductance of silicon–amorphous polyethylene interfaces by molecular dynamics simulations. Phys. Rev. B 79, 104305. doi:10.1103/PhysRevB.79.104305

CrossRef Full Text | Google Scholar

Hu, S., An, M., Yang, N., and Li, B. (2017). A series circuit of thermal rectifiers: an effective way to enhance rectification ratio. Small 13, 1602726. doi:10.1002/smll.201602726

PubMed Abstract | CrossRef Full Text | Google Scholar

Juraschek, D. M., and Spaldin, N. A. (2017). Sounding out optical phonons. Science 357, 873–874. doi:10.1126/Science.aao2446

CrossRef Full Text | Google Scholar

Kaur, S., Raravikar, N., Helms, B. A., Prasher, R., and Ogletree, D. F. (2014). Enhanced thermal transport at covalently functionalized carbon nanotube array interfaces. Nat. Commun. 5, 3082. doi:10.1038/ncomms4082

PubMed Abstract | CrossRef Full Text | Google Scholar

Khomyakov, P. A., Brocks, G., Karpan, V., Zwierzycki, M., and Kelly, P. J. (2005). Conductance calculations for quantum wires and interfaces: mode matching and Green’s functions. Phys. Rev. B 72, 035450. doi:10.1103/PhysRevB.72.035450

CrossRef Full Text | Google Scholar

Li, N., Ren, J., Wang, L., Zhang, G., Hänggi, P., and Li, B. (2012). Colloquium: phononics: manipulating heat flow with electronic analogs and beyond. Rev. Mod. Phys. 84, 1045. doi:10.1103/RevModPhys.84.1045

CrossRef Full Text | Google Scholar

Little, W. A. (1959). The transport of heat between dissimilar solids at low temperatures. Can. J. Phys. 37, 334–349. doi:10.1139/p59-037

CrossRef Full Text | Google Scholar

Lü, J. T., and Wang, J. S. (2007). Coupled electron and phonon transport in one-dimensional atomic junctions. Phys. Rev. B 76, 165418. doi:10.1103/PhysRevB.76.165418

CrossRef Full Text | Google Scholar

Luckyanova, M. N., Garg, J., Esfarjani, K., Jandl, A., Bulsara, M. T., Schmidt, A. J., et al. (2012). Coherent phonon heat conduction in superlattices. Science 338, 936. doi:10.1126/science.1225549

PubMed Abstract | CrossRef Full Text | Google Scholar

Lumpkin, M. E., Saslow, W. M., and Visscher, W. M. (1978). One-dimensional Kapitza conductance: comparison of the phonon mismatch theory with computer experiments. Phys. Rev. B 17, 4295. doi:10.1103/PhysRevB.17.4295

CrossRef Full Text | Google Scholar

Maldovan, M. (2013). Sound and heat revolutions in phononics. Nature 503, 209–217. doi:10.1038/nature12608

PubMed Abstract | CrossRef Full Text | Google Scholar

Marconnet, A. M., Panzer, M. A., and Goodson, K. E. (2013). Thermal conduction phenomena in carbon nanotubes and related nanostructured materials. Rev. Mod. Phys. 85, 1295. doi:10.1103/RevModPhys.85.1295

CrossRef Full Text | Google Scholar

Mingo, N. (2006). Anharmonic phonon flow through molecular-sized junctions. Phys. Rev. B 74, 125402. doi:10.1103/PhysRevB.74.125402

CrossRef Full Text | Google Scholar

Narayanamurti, V., Störmer, H. L., Chin, M. A., Gossard, A. C., and Wiegmann, W. (1979). Selective transmission of high-frequency phonons by a superlattice: the “dielectric” phonon filter. Phy. Rev. Lett. 43, 2012–2016. doi:10.1103/PhysRevLett.43.2012

CrossRef Full Text | Google Scholar

Ness, H., and Fisher, A. J. (2002). Mechanisms for electron transport in atomic-scale one-dimensional wires: soliton and polaron effects. Europhys. Lett. 57, 885. doi:10.1209/epl/i2002-00593-6

CrossRef Full Text | Google Scholar

Ong, Z. Y., and Pop, E. (2010). Molecular dynamics simulation of thermal boundary conductance between carbon nanotubes and SiO₂. Phys. Rev. B 81, 155408. doi:10.1103/PhysRevB.81.155408

CrossRef Full Text | Google Scholar

Peyrard, M., and Remoissenet, M. (1982). Solitonlike excitations in a one-dimensional atomic chain with a nonlinear deformable substrate potential. Phys. Rev. B 26, 2886. doi:10.1103/PhysRevB.26.2886

CrossRef Full Text | Google Scholar

Reddy, P., Castelino, K., and Majumdar, A. (2005). Diffuse mismatch model of thermal boundary conductance using exact phonon dispersion. Appl. Phys. Lett. 87, 211908. doi:10.1063/1.2133890

CrossRef Full Text | Google Scholar

Saltonstall, C. B., Polanco, C. A., Duda, J. C., Ghosh, A. W., Norris, P. M., and Hopkins, P. E. (2013). Effect of interface adhesion and impurity mass on phonon transport at atomic junctions. J. Appl. Phys. 113, 013516. doi:10.1063/1.4773331

CrossRef Full Text | Google Scholar

Shafranjuk, S. E. (2014). Converting heat to electricity by a graphene stripe with heavy chiral fermions. Eur. Phys. J. B 87, 99. doi:10.1140/epjb/e2014-40794-0

CrossRef Full Text | Google Scholar

Song, Q., An, M., Chen, X., Peng, Z., Zang, J., and Yang, N. (2016). Adjustable thermal resistor by reversibly folding a graphene sheet. Nanoscale 8, 14943–14949. doi:10.1039/C6NR01992G

PubMed Abstract | CrossRef Full Text | Google Scholar

Stevens, R. J., Smith, A. N., and Norris, P. M. (2005). Measurement of thermal boundary conductance of a series of metal-dielectric interfaces by the transient thermoreflectance technique. J. Heat Transfer 127, 315–322. doi:10.1115/1.1857944

CrossRef Full Text | Google Scholar

Swartz, E. T., and Pohl, R. O. (1989). Thermal boundary resistance. Rev. Mod. Phys. 61, 605. doi:10.1103/RevModPhys.61.605

CrossRef Full Text | Google Scholar

Tian, Z. T., White, B. E. Jr., and Sun, Y. (2010). Phonon wave-packet interference and phonon tunneling based energy transport across nanostructured thin films. Appl. Phys. Lett. 96, 263113. doi:10.1063/1.3458831

CrossRef Full Text | Google Scholar

Velev, J., and Butler, W. (2004). On the equivalence of different techniques for evaluating the Green function for a semi-infinite system using a localized basis. J. Phys. Condens.Matter 16, R637. doi:10.1088/0953-8984/16/21/r01

CrossRef Full Text | Google Scholar

Wang, J., and Wang, J. S. (2006). Mode-dependent energy transmission across nanotube junctions calculated with a lattice dynamics approach. Phys. Rev. B 74, 054303. doi:10.1103/PhysRevB.74.054303

CrossRef Full Text | Google Scholar

Wang, J. S., Wang, J., and Lü, J. T. (2008). Quantum thermal transport in nanostructures. Eur. Phys. J. B 62, 381–404. doi:10.1140/epjb/e2008-00195-8

CrossRef Full Text | Google Scholar

Wang, J. S., Wang, J., and Zeng, N. (2006). Nonequilibrium Green’s function approach to mesoscopic thermal transport. Phys. Rev. B 74, 033408. doi:10.1103/PhysRevB.74.033408

CrossRef Full Text | Google Scholar

Wang, J. S., Zeng, N., Wang, J., and Gan, C. K. (2007). Nonequilibrium Green’s function method for thermal transport in junctions. Phys. Rev. E 75, 061128. doi:10.1103/PhysRevE.75.061128

CrossRef Full Text | Google Scholar

Wang, Y., Qin, Z., Buehler, M. J., and Xu, Z. (2016). Intercalated water layers promote thermal dissipation at bio–nano interfaces. Nat. Commun. 7, 12854. doi:10.1038/ncomms12854

CrossRef Full Text | Google Scholar

Yang, N., Luo, T., Esfarjani, K., Henry, A., Tian, Z., Shiomi, J., et al. (2015). Thermal interface conductance between aluminum and silicon by molecular dynamics simulations. J. Comput. Theor. Nanosci. 12, 168–174. doi:10.1166/jctn.2015.3710

CrossRef Full Text | Google Scholar

Zhang, J., Hong, Y., Liu, M., Yue, Y., Xiong, Q., and Lorenzini, G. (2017). Molecular dynamics simulation of the interfacial thermal resistance between phosphorene and silicon substrate. Int. J. Heat Mass Transfer 104, 871–877. doi:10.1016/j.ijheatmasstransfer.2016.08.021

CrossRef Full Text | Google Scholar

Zhang, L., Keblinski, P., Wang, J. S., and Li, B. (2011). Interfacial thermal transport in atomic junctions. Phys. Rev. B 83, 064303. doi:10.1103/PhysRevB.83.064303

CrossRef Full Text | Google Scholar

Zhang, L., Lü, J. T., Wang, J. S., and Li, B. (2013a). Thermal transport across metal–insulator interface via electron–phonon interaction. J. Phys. Condens.Matter 25, 445801. doi:10.1088/0953-8984/25/44/445801

CrossRef Full Text | Google Scholar

Zhang, L., Ren, J., Wang, J. S., and Li, B. (2013b). Topological magnon insulator in insulating ferromagnet. Phys. Rev. B 87, 144101. doi:10.1103/PhysRevB.87.144101

CrossRef Full Text | Google Scholar

Zhang, L., Thingna, J., He, D., Wang, J. S., and Li, B. (2013c). Nonlinearity enhanced interfacial thermal conductance and rectification. Europhys. Lett. 103, 64002. doi:10.1209/0295-5075/103/64002

CrossRef Full Text | Google Scholar

Zhang, L., Wang, J. S., and Li, B. (2008). Ballistic magnetothermal transport in a Heisenberg spin chain at low temperatures. Phys. Rev. B 78, 144416. doi:10.1103/PhysRevB.78.144416

CrossRef Full Text | Google Scholar

Zhang, L., Wang, J. S., and Li, B. (2009). Phonon hall effect in four-terminal nano-junctions. New J. Phys. 11, 113038. doi:10.1088/1367-2630/11/11/113038

CrossRef Full Text | Google Scholar

Zhang, L., Wang, J. S., and Li, B. (2010). Ballistic thermal rectification in nanoscale three-terminal junctions. Phys. Rev. B 81, 100301. doi:10.1103/PhysRevB.81.100301

CrossRef Full Text | Google Scholar

Zhang, W., Fisher, T. S., and Mingo, N. (2007). The atomistic Green’s function method: an efficient simulation approach for nanoscale phonon transport. Numer. Heat Transfer, Part B 51, 333–349. doi:10.1080/10407790601144755

CrossRef Full Text | Google Scholar

Zhang, Y., Ma, D., Zang, Y., and Yang, N. (2016). A Modified Theoretical Model to Predict the Thermal Interface Conductance Considering Interface Roughness. arXiv preprint arXiv:1612.05357.

Google Scholar

Ziman, J. M. (1960). Electrons and Phonons: The Theory of Transport Phenomena in Solids. Oxford: Oxford University Press.

Google Scholar