Nonlinear Heat Radiation Induces Thermal Rectifier in Asymmetric Holey Composites

1. Introduction

In analogy to the familiar electric diode in modern electronics, thermal rectifier is a device that can achieve non-reciprocal heat transport. Theoretical models for thermal rectifiers are proposed relying on various mechanisms (Roberts and Walker, 2011), including different temperature-dependent thermal properties between dissimilar materials at a contact (Stevenson et al., 1991; Dames, 2009; Kobayashi et al., 2009), asymmetric design of nanostructure (Wu and Li, 2008; Yang et al., 2009), and quantum thermal systems, such as quantum dots and other quantum heterojunctions (Scheibner et al., 2007; Ruokola et al., 2009; Wu and Segal, 2009; Ren and Zhu, 2013a). Similar concepts are even extended to the spin Seebeck diode and transistor (Ren, 2013; Ren and Zhu, 2013b; Ren et al., 2013), and the multiferroic thermal diode (Chotorlishvili et al., 2015), multiferroic switch and memory (Li et al., 2014). All these device concepts lay the foundation for the emerging field: phononics, where scientists are devoted to control heat flow and thermal information carried by phonons and beyond with electronic analogs (Li et al., 2012; Maldovan, 2013; Ren and Li, 2015).

It has been well established that asymmetric design and nonlinearity are essential to give rise to thermal rectification (Roberts and Walker, 2011; Li et al., 2012). Thus, there have been more theoretical studies of thermal rectification focusing on nonlinear systems (Wehmeyer et al., 2017). Nonlinearity can be provided in different ways to design a thermal rectifier, including one-dimensional nonlinear lattice (Terraneo et al., 2002; Li et al., 2004; Hu and Yang, 2005), nonlinear electron gas dispersion in conductors (Segal, 2008), nonlinear Schrödinger equation (Li and Ren, 2014), nonlinear near-field radiation (Otey et al., 2010; Basu and Francoeur, 2011), and even a vapor generation rectifier (Ding et al., 2017).

Punching holes in an isotropic material can induce a new heat transfer mechanism—radiation or convection (if the hole is filled with fluid or gas) in addition to the thermal conduction of the material. Thus, some interesting thermal work of materials with holes has been studied for thermal buckling analysis (Zhao et al., 2009), thermal rectifier (Hu et al., 2017) and thermal cloaking (Maldovan, 2013). Yet, few researches of materials with holes consider the heat radiation process on the surface of holes as a nonlinear procedure required in thermal rectification.

In this paper, we design a simple model of thermal rectifier, in which required nonlinearity is met by thermal radiation which is proportional to the fourth power of temperature within the framework of Stefan–Boltzmann Law. The rectification design comes from the asymmetry of the structure and the competition between nonlinear thermal radiation and linear thermal conduction.

We discuss how asymmetry and nonlinearity works to achieve thermal rectification in our model, with results of simulation and analytical explanation. In our simulation models, we consider two kinds of heat transfer mechanisms: (i) thermal conduction that is linear as we consider constant thermal conductivity and (ii) thermal radiation that is proportional to the fourth power of temperature. We report the simulation results of our holey diodes that have non-reciprocal heat transfer due to the nonlinearity of the thermal radiation and the asymmetric geometry. We obtain the clear thermal rectification, and find that there is a best average temperature, where the rectification reaches maximum, when the temperature difference is fixed. All the simulation results can be analytically explained by a simple thermal circuit model, which is composed of a central thermal radiation region sandwiched by two conduction regions with different thermal conductances.

2. Results

Since there are already thermal diodes achieved with different temperature-dependent conductivity (Dames, 2009) or emissivity (Roberts and Walker, 2011), in our study we consider the bulk material itself to be homogenous and isotropic. In the homogenous material, the local heat flux density is expressed as $\overrightarrow{J}=-\mathrm{\kappa }\nabla T$, according to Fourier’s Law, where J is the heat flux, κ is the material’s thermal conductivity and on the vacuum interface of the holes, heat transfer follows the Stefan–Boltzmann Law $\overrightarrow{J}=-\mathrm{\epsilon }\mathrm{\sigma }\nabla T^4$, where ε is the emissivity and σ is the Stefan–Boltzmann constant. For simplification, we consider no medium inside the holes so that there is no need to consider the convection and conduction mechanism of the medium. It has been proven that (Li and Ren, 2014) combination of nonlinearity and asymmetry is an effective method to give rise to rectification. It is, therefore, reasonable to infer that holey structures could be able to transfer heat non-reciprocally and the analytical explanation will be demonstrated later.

2.1. Simulation Results for a Feasible Holey Diode Model

To achieve heat rectifier effect, we design a structure with dense periodic organization of circle holes in a pattern, only on a half of the structure itself, as shown in Figure 1A,B. This system is too complicated to be tackled analytically. Therefore, we perform two dimensional finite-element simulations, to investigate the heat transport across the structure. The temperature of the left and the right boundaries of the diode are fixed at T₀ + ΔT and T₀ − ΔT, respectively, where T₀ represents the average temperature of the structure approximately and 2ΔT the temperature difference of two terminals. In the reverse temperature biased scenario (ΔT = −ΔT), the temperatures of the boundaries are exchanged.

FIGURE 1

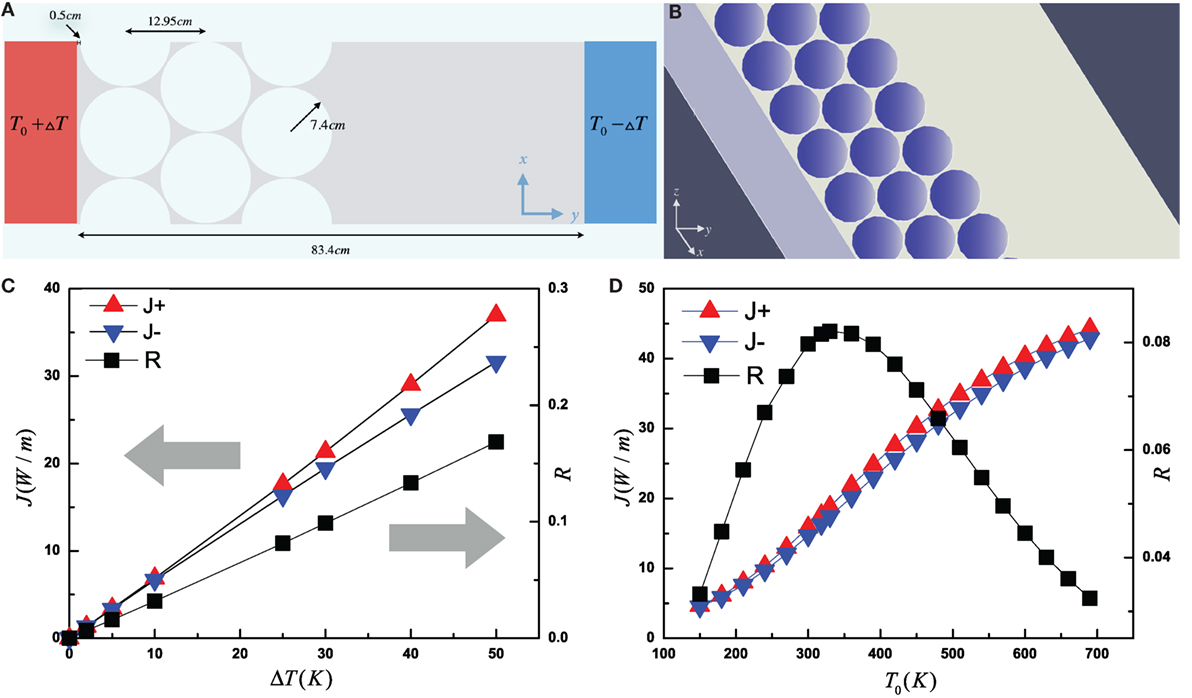
Figure 1. Simulation model of holey concrete structure. (A) Sketch of the thermal diode model with periodic boundary condition in the vertical direction. The width of the structure is 83.4 cm. For the hole patterns, the hole diameter is 7.4 cm, and the horizontal distance between two centers of the adjacent holes is 12.95 cm. The gray area is the body of the concrete structure, and the blue area is the background that we consider as vacuum. The thermal conductivity of the concrete is κ = 1.7 W/(m⋅K) and emissivity is set as ε = 1. (B) Schematic graph depicting the infinite periodic holey thermal diode. We consider the model infinite in x and z axis direction. (C) Heat flux in forward (J₊) and reverse (J₋) temperature biased system and rectification factor R versus ΔT for thermal rectifier model in (A) and (B). T₀ is fixed at 318 K. (D) Heat flux in forward and reverse temperature biased system and rectification factor versus T₀. ΔT is fixed at 25 K.

If the magnitudes of thermal energy transfer in the two directions are different, we can safely say that there is a thermal rectification. Since no energy escapes from the system in the two-dimension and infinite periodic structure we proposed, we can calculate the total heat flux passing through the whole structure by integrating the normal heat flux along the boundary either the left one or the right one. We define J₊ as heat flux flowing from left to right when the value of ΔT is positive in the setting of the boundary temperature, while J₋ with negative ΔT denotes the right-to-left heat flux in the reversed temperature biased scenario. To quantify the magnitude of thermal rectification, we define a rectification factor $R=\frac{J_{+}-J_{-}}{J_{-}}$.

Heat flux in the forward and reverse bias as well as the corresponding rectification factor as a function of ΔT are plotted in Figure 1C. As shown in the plot, the heat transfer in the forward bias is always stronger than in the reverse bias. J₊, J₋, and rectification factor R are shown to increase with the increasing ΔT, in an approximately linear relationship. Moreover, it is shown in Figure 1D that although J₊ and J₋ increase with the average temperature T₀, R does not monotonically increase with T₀, and reaches its maximum at about 330 K in this settings.

The thermal rectification is achieved by satisfying the required asymmetry and nonlinearity. Therefore, if the holes in our proposed model are punched exactly in the center of the structure, rectification would not appear, since the geometry of the structure is totally symmetric. To achieve a strong rectification effect, we design the model in an asymmetric way. The asymmetric setup is constructed by using two materials with different constant thermal conductivity, where material on the left holey side has thermal conductivity κ_L and the right complete side κ_R. Both the results of the simulation and the sketch of the new model are shown in Figure 2. Note the left and right materials can be identical so that κ_L = κ_R is allowed.

FIGURE 2

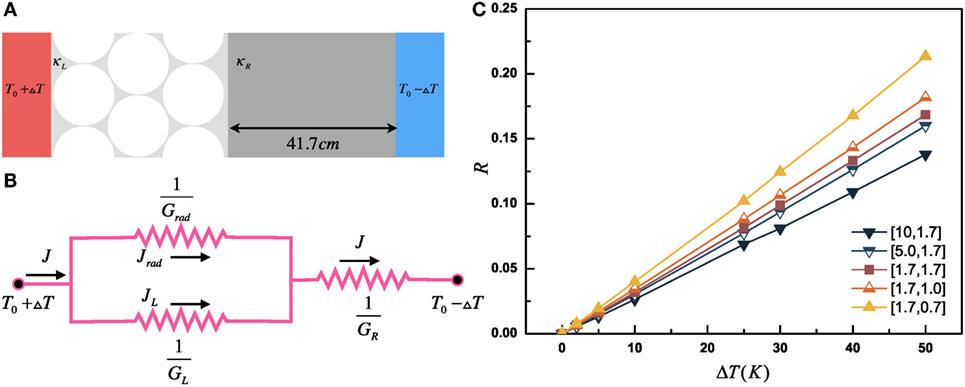
Figure 2. (A) Sketch of the two-material junction model, which have different thermal conductivity in left half (κ_L) and the right half (κ_R). Parameters and geometries are the same as the previous ones. (B) Schematic graph depicting the equivalent thermal circuits of the new model. Note that thermal resistance R = 1/G, where G is the corresponding thermal conductance. (C) Thermal rectification factor R versus ΔT of the model with different combination of thermal conductivity of left and right with [κ_L, κ_R] in the legend. Unit of all thermal conductivity mentioned is W/(m⋅K).

As shown in Figure 2C, we keep one of the κ_L and κ_R in the new model equal to the thermal conductivity of the single material model, 1.7 W/(m⋅K), and compare the new model with the previous one. The simulation results show that if κ_L = 1.7 W/(m⋅K) and κ_R = 1 or 0.7 W/(m⋅K), the rectification factor is improved, since not only the geometry but also the thermal properties are asymmetric in this model. However, if κ_R = 1.7 W/(m⋅K) and κ_L = 10 or 5 W/(m⋅K), even though with stronger asymmetry, the rectification effect becomes weaker.

To understand the phenomenon in a more clear way, we introduce the equivalent thermal circuit of the model in Figure 2B. G_R is the conductance of the right half of the structure, which can be easily calculated by G_R = κ_R/0.417 m, since the right half is totally homogenous. However, the left half is more complicated. G_L is the equivalent conductance of the conduction mechanisms on the left. Moreover, G_rad denotes the equivalent conductance contributed by the radiation of holes on the left. Due to the circle geometry of the holes, G_L can not be easily expressed like G_R. But, It is evident that G_L ∝ κ_L and G_rad has nonlinear positive relationship with temperature. Therefore, when κ_L is larger, so does G_L, the resistance of conduction would be smaller guiding more heat flux flow through it rather than through radiation. Since little flux through radiation means little nonlinearity, although in this case the model has stronger asymmetry, the nonlinearity is weaker leading to the weaker diode effect. In the proposed model, thermal resistance of conduction and radiation mechanisms is in series and in parallel. In the holey side, heat can transfer in two channels, and competition between the channels weaken the required nonlinearity to give rise to rectification. To improve the rectification effects, we construct a more effective model, where thermal resistances of radiation and conduction are only in series, in the next subsection. This case also renders us an analytical explanation.

2.2. Two Infinite Plate Model with Analytical Explanation

As shown in the Figure 3, we analyze the heat transfer between two infinite parallel plates of different conductance in the simplified model. The thermal conductance instead of thermal conductivity are considered here, and can be calculated through G_i = κ_i/w_i, where κ_i is the thermal conductivity and w_i represents the thickness of two infinite plates, with i = 1, 2. In this case, the combined processes of thermal conduction and thermal radiation form an equivalent thermal circuit in series. Since all the heat flux leaving one plate will arrive at the other plate, the heat flux through the three regions (I, II, III) would be the same:

$J=G_1(T_0+\mathrm{\Delta }T-T_1)=\mathrm{\epsilon \sigma }(T_1^4-T_2^4)=G_2(T_2-T_0+\mathrm{\Delta }T).$ (1)

FIGURE 3

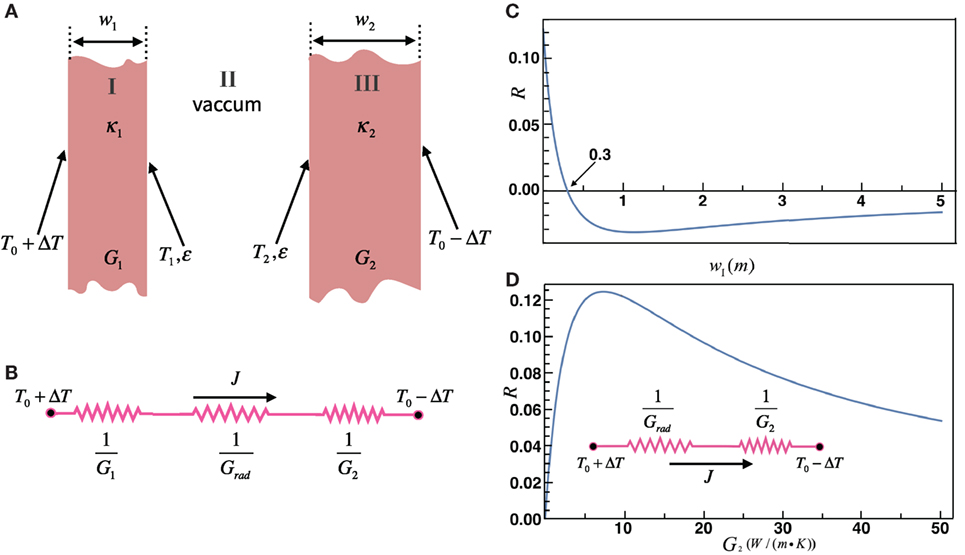
Figure 3. (A) Sketch of the two infinite plate model. This is a one-dimensional model with three separated region. Temperature of two outer surfaces is set T₀ + ΔT and T₀ − ΔT, respectively. w₁ and w₂ denotes the thickness of two infinite plate. ε is the emissivity of the inner surface. T₁ and T₂ are measured as temperature of two inner surface. (B) Schematic graph depicting the equivalent thermal circuits of the plate-vaccum-plate sandwich model. Thermal resistance of conductance of region I and region III, and the equivalent thermal resistance of radiation in region II are in series. (C) w₁ versus rectification factor R. T₀ and ΔT are fixed at 318 and 25 K. (D) G₂ versus rectification factor R in the two-part model. T₀ and ΔT are fixed at 318 and 25 K.

Note the Stefan-Boltzmann constant σ is at −8 order of magnitude in SI units, which makes the nonlinear radiation contribution rather weak. If we consider the situation where ΔT as well as J is small, we can obtain the expressions of J₊ and J₋ up to the second order of thermal bias, as following:

$J_{\pm }\approx \frac{\mathrm{4\epsilon \sigma }{G}_1{G}_2{T}_0^3}{G_1{G}_2+\mathrm{4\epsilon \sigma }{T}_0^3(G_1+G_2)}\mathrm{2\Delta }T\pm \frac{24{(\mathrm{\epsilon \sigma })}^2{G}_1{G}_2(G_1-G_2)}{{[G_1{G}_2/T_0^3+\mathrm{4\epsilon \sigma }(G_1+G_2)]}^2}\frac{{(\mathrm{2\Delta }T)}^2}{T_0}.$ (2)

The first term of equation (2) is a linear contribution that has a clear physical picture: with linear response, region II is approximated as a homogenous material with conductance $G_{rad}=\frac{\partial (\mathrm{\epsilon \sigma }{T}^4)}{\partial T}{|}_{T=T_0}=\mathrm{4\epsilon \sigma }{T}_0^3$, so that the equivalent conductance of the model is composed of thermal resistances of three regions in series: $G_e=\frac{1}{1/G_1+1/G_2+1/(\mathrm{4\epsilon \sigma }{T}_0^3)}$, with the temperature bias 2ΔT. For a temperature difference 2ΔT smaller than T₀, the second order term is small compared with the first term. Therefore, the heat flux J₊ and J₋ is approximately proportional to the temperature difference ΔT, which also explain the nearly linear relationship of J₊ and J₋ versus ΔT shown in the Figure 1C. Equation (2) also shows that the dominant first term of heat flux, although linear respect to thermal bias, has a nonlinear positive relationship with T₀, which well explains the nonlinear positive relationship and gradually saturated dependence on T₀, revealed in Figure 1D.

The second term in the heat flux expression equation (2) is very important to heat rectification. From the expression of heat flux, we can obtain the rectification factor up to the first order of thermal bias:

$R=\frac{J_{+}-J_{-}}{J-}\approx \frac{\mathrm{12\epsilon \sigma }(G_1-G_2)}{G_1{G}_2/T_0^3+\mathrm{4\epsilon \sigma }(G_1+G_2)}\frac{\mathrm{2\Delta }T}{T_0}.$ (3)

Therefore, the rectification coefficient is also linear to the ΔT as showed in Figure 1C and Figure 2C, which will vanish if the system becomes symmetric G₁ = G₂. Through the analytical result, we can understand the nontrivial relationship between R versus T₀, as shown in Figure 1D. Clearly from equation (2), when T₀ increases from low temperature, R increases while when T₀ is already at high temperature, R decreases as T₀ increases. With simple differential method, we can calculate that the denominator of the R reaches its minimum value when $T_0={[\frac{G_1{G}_2}{\mathrm{2\epsilon \sigma }(G_1+G_2)}]}^{1/3}$, where R has a maximum value when changing the average temperature T₀. This behavior coincides with what one observed in Figure 1D.

We also study the dependence of R on the width w₁ in the plate–vacuum–plate sandwich model, to see the effect of competition between linear conduction and nonlinear radiation on the rectification. In Figure 3C, we keep w₂ fixed at 0.3 m, and both κ₁ and κ₂ are equal to 1.7 W/(m⋅K). By changing w₁ only, we can see the importance of asymmetry in giving rise to the rectification that can be reversed. There is an exact vanishing point of R at w₁ = w₂, which means G₁ = G₂ in this case. If we increase w₁ from the initial value 0.3 m, |R| first increases with w₁, since the asymmetry of the system increases. However, while increasing w₁ further, the left conductance G₁ gets smaller, so the temperature difference at two inner surfaces (T₁–T₂) gets smaller. Note that T₁–T₂ determines the flux (so as the total flux) through radiation within the nonlinear framework of Stefan–Boltzmann’s Law, so when w₁ goes even larger, the radiative flux of nonlinear nature goes smaller so that the rectification R falls down. When we decrease w₁ from the initial value 0.3 m, R increases quickly, and reaches a maximum at about 12%. This is reasonable since when w₁ becomes smaller and smaller, approaching to 0, G₁ becomes larger and gets close to infinity. The strongest asymmetry is achieved in this way, so that R can reach its maximum limit in this case when G₁ → ∞.

To further maximize the rectification factor, we may consider a two-segment model with only region II and III where the left plate region I is removed. Temperature at the left boundary is imposed at the border of the vacuum part (region II). In Figure 3D, we show the numerical rectification factor R vs G₂ with fixed T₀ and ΔT in the two-segment model. As we discussed above, the thermal rectification results from the competition between nonlinear radiation and linear conduction. When there is only one mechanism—either radiation or conduction, rectification can not appear since the system is symmetrical even with nonlinearity. Only if G₂ and G_rad are comparable, which means the nonlinear and linear mechanisms are comparable to make the system most asymmetric, rectification effect becomes strongest. In other word, R reaches its maximum around G₂ ≈ G_rad. As shown in the case of Figure 3D, $G_{rad}=\mathrm{4\epsilon \sigma }{T}_0^3=7.3{\text{\hspace{0.17em}W\hspace{0.17em}m}}^{-1}{\text{K}}^{-1}$, and R indeed reaches the maximum when G₂ is about 7, comparable with G_rad.

3. Conclusion and Discussion

We have designed the asymmetric holey composites as a thermal rectifier, which has non-reciprocal heat transfer. The non-reciprocal heat transfer is attributed to the thermal radiation of nonlinear nature and the asymmetric geometric of the system. We have simulated and then confirmed from the theoretical analysis that the thermal rectification is approximately linear to the temperature difference of the system with the average temperature fixed and the maximal thermal rectification can be obtained by tuning the average temperature when the temperature difference is fixed. There have been considerable interests in realizing thermal rectifiers for its ability in thermal management and control for heat energy in the recent years. Most researches focus on achieving thermal rectifiers in nanoscale or even smaller, for its numerous potential applications in micro/nano-electronic cooling, thermal memory and computations. We have designed our thermal rectification model at macro-scale by inducing the nonlinearity with holes in the design, which is a simple model for thermal rectifiers. This means that the setup can be easily built, which might have potential applications in materials of architecture for diverse thermal management problems, e.g., energy-saving buildings, solar cells, and efficient refrigerator.

Furthermore, the rectification strength of the holely diodes can be further improved by constructing with two materials that with different temperature-dependent thermal conductivity of opposite trends [similar to the one in Dames (2009)]. In some way, the crucial nonlinearity induces the effective temperature-dependent conductance. For the nonlinear radiation, the conductance $G_{rad}=\frac{\mathrm{\epsilon \sigma }(T_1^4-T_2^4)}{T1-T2}=\mathrm{\epsilon \sigma }(T_1+T_2)(T_1^2+T_2^2)$, which under asymmetric geometry and bias reversing will effectively change the values. Therefore, a rectification action emerges. Beyond the nonlinear thermal radiation, the nonlinearity can also be introduced by the ballistic transport at quantum regime, since the phonon population is described by the Bose–Einstein distribution $N(\mathrm{\omega })=1/[\text{exp}(\mathrm{\hslash \omega }/k_{B}T)-1]$ that has nonlinear dependence on temperature. Explicitly, the ballistic quantum thermal transport is described by the well-known Landauer-Büttiker formula:

$J={\displaystyle {\int }_0^{\mathrm{\infty }}}d\mathrm{\omega \hslash \omega }\mathcal{T}(\mathrm{\omega })[N_L(\mathrm{\omega })-N_R(\mathrm{\omega })],$ (4)

with $\mathcal{T}(\mathrm{\omega })$ the phononic transmission coefficient, N_L(ω) − N_R(ω) the phonon population difference between two sides. When combining this ballistic transport with diffusive transport described by the linear Fourier’s law and with asymmetric geometry of the system, the rectification emerges due to the nonlinear Bose–Einstein distribution. However, the rectification disappears in the high temperature classical regime since $1/[\text{exp}(\mathrm{\hslash \omega }/k_{B}T)-1]\to k_{B}T/\mathrm{\hslash \omega }$. As such, equation (4) reduces to the one with linear temperature dependence: $J=k_B{\displaystyle {\int }_0^{\mathrm{\infty }}}d\mathrm{\omega }\mathcal{T}(\mathrm{\omega })(T_L-T_R)$. Therefore, it is readily to prove that when combing with the Fourier’s law, even with asymmetric geometry, the system can not have rectification. Both nonlinearity and asymmetry are necessary to construct the thermal rectifier (Li and Ren, 2014).

Author Contributions

GW and WZ carried out the simulation, performed the theoretical analysis, and contributed equally to this work. GW, WZ, HC, and JR, all contributed to discussion and the writing. JR conceived the project.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer, QC, and handling editor declared their shared affiliation.

Funding

This work is supported by the National Natural Science Foundation of China (Grant Nos. 11775159 and 61621001), the National Key Research Program of China (No. 2016YFA0301101), and the National Youth 1000 Talents Program in China.

References

Basu, S., and Francoeur, M. (2011). Near-field radiative transfer based thermal rectification using doped silicon. Appl. Phys. Lett. 98, 184301. doi: 10.1063/1.3567026

CrossRef Full Text | Google Scholar

Chotorlishvili, L., Etesami, S. R., Berakdar, J., Khomeriki, R., and Ren, J. (2015). Electromagnetically controlled multiferroic thermal diode. Phys. Rev. B 92, 134424. doi:10.1103/PhysRevB.92.134424

CrossRef Full Text | Google Scholar

Dames, C. (2009). Solid-state thermal rectification with existing bulk materials. J. Heat Transfer 131, 177–181. doi:10.1115/1.3089552

CrossRef Full Text | Google Scholar

Ding, H., Peng, G., Mo, S., Ma, D., Sharshir, S. W., and Yang, N. (2017). Ultra-fast vapor generation by a graphene nano-ratchet: a theoretical and simulation study. Nanoscale 9, 19066–19072. doi:10.1039/C7NR05304E

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, B., and Yang, L. (2005). Heat conduction in the Frenkel-Kontorova model. Chaos 15, 1073. doi:10.1063/1.1862552

CrossRef Full Text | Google Scholar

Hu, S., An, M., Yang, N., and Li, B. (2017). A series circuit of thermal rectifiers: an effective way to enhance rectification ratio. Small 13, 1602726. doi:10.1002/smll.201602726

PubMed Abstract | CrossRef Full Text | Google Scholar

Kobayashi, W., Teraoka, Y., and Terasaki, I. (2009). An oxide thermal rectifier. Appl. Phys. Lett. 95, 143501. doi:10.1063/1.3253712

CrossRef Full Text | Google Scholar

Li, B., Wang, L., and Casati, G. (2004). Thermal diode: rectification of heat flux. Phys. Rev. Lett. 93, 184301. doi:10.1103/PhysRevLett.93.184301

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, N., and Ren, J. (2014). Non-reciprocal geometric wave diode by engineering asymmetric shapes of nonlinear materials. Sci. Rep. 4, 6228–6228. doi:10.1038/srep06228

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, N., Ren, J., Wang, L., Zhang, G., Hanggi, P., and Li, B. (2012). Phononics: manipulating heat flow with electronic analogs and beyond. Rev. Mod. Phys. 84, 1045–1066. doi:10.1103/RevModPhys.84.1045

CrossRef Full Text | Google Scholar

Li, S., Ding, X., Ren, J., Moya, X., Li, J., Sun, J., et al. (2014). Strain-controlled thermal conductivity in ferroic twinned films. Sci. Rep. 4, 6375. doi:10.1038/srep06375

PubMed Abstract | CrossRef Full Text | Google Scholar

Maldovan, M. (2013). Sound and heat revolutions in phononics. Nature 503, 209–217. doi:10.1038/nature12608

PubMed Abstract | CrossRef Full Text | Google Scholar

Otey, C. R., Lau, W. T., and Fan, S. (2010). Thermal rectification through vacuum. Phys. Rev. Lett. 104, 154301. doi:10.1103/PhysRevLett.104.154301

PubMed Abstract | CrossRef Full Text | Google Scholar

Ren, J. (2013). Predicted rectification and negative differential spin Seebeck effect at magnetic interfaces. Phys. Rev. B 88, 4045–4050. doi:10.1103/PhysRevB.88.220406

CrossRef Full Text | Google Scholar

Ren, J., Fransson, J., and Zhu, J. X. (2013). Nanoscale spin Seebeck rectifier: controlling thermal spin transport across insulating magnetic junctions with localized spin. Phys. Rev. B 89, 106–114. doi:10.1103/PhysRevB.89.214407

CrossRef Full Text | Google Scholar

Ren, J., and Li, B. (2015). Phononics: controlling thermal energy, information carried by phonons and beyond. AIP Adv. 5, 294–303. doi:10.1063/1.4922168

CrossRef Full Text | Google Scholar

Ren, J., and Zhu, J. X. (2013a). Heat diode effect and negative differential thermal conductance across nanoscale metal-dielectric interfaces. Phys. Rev. B Condens. Matter 87, 291–295. doi:10.1103/PhysRevB.87.241412

CrossRef Full Text | Google Scholar

Ren, J., and Zhu, J. X. (2013b). Theory of asymmetric and negative differential magnon tunneling under temperature bias: towards a spin Seebeck diode and transistor. Phys. Rev. B Condens. Matter 88, 3169–3182. doi:10.1103/PhysRevB.88.094427

CrossRef Full Text | Google Scholar

Roberts, N. A., and Walker, D. G. (2011). A review of thermal rectification observations and models in solid materials. Int. J. Ther. Sci. 50, 648–662. doi:10.1016/j.ijthermalsci.2010.12.004

CrossRef Full Text | Google Scholar

Ruokola, T., Ojanen, T., and Jauho, A. P. (2009). Thermal rectification in nonlinear quantum circuits. Phys. Rev. B Condens. Matter 79, 897–899. doi:10.1103/PhysRevB.79.144306

CrossRef Full Text | Google Scholar

Scheibner, R., Koenig, M., Reuter, D., Wieck, A. D., Buhmann, H., and Molenkamp, L. W. (2007). Quantum dot as thermal rectifier. New J. Phys. 10, 807–820. doi:10.1088/1367-2630/10/8/083016

CrossRef Full Text | Google Scholar

Segal, D. (2008). Single mode heat rectifier: controlling energy flow between electronic conductors. Phys. Rev. Lett. 100, 105901. doi:10.1103/PhysRevLett.100.105901

PubMed Abstract | CrossRef Full Text | Google Scholar

Stevenson, P. F., Peterson, G. P., and Fletcher, L. S. (1991). Thermal rectification in similar and dissimilar metal contacts. J. Heat Transfer 113, 30–36. doi:10.1115/1.2910547

CrossRef Full Text | Google Scholar

Terraneo, M., Peyrard, M., and Casati, G. (2002). Controlling the energy flow in nonlinear lattices: a model for a thermal rectifier. Phys. Rev. Lett. 88, 094302. doi:10.1103/PhysRevLett.88.094302

PubMed Abstract | CrossRef Full Text | Google Scholar

Wehmeyer, G., Yabuki, T., Monachon, C., Wu, J., and Dames, C. (2017). Thermal diodes, regulators, and switches: physical mechanisms and potential applications. Appl. Phys. Rev. 4, 041304. doi:10.1063/1.5001072

CrossRef Full Text | Google Scholar

Wu, G., and Li, B. (2008). Thermal rectifier from deformed carbon nanohorns. J. Phys. Condens. Matter 20, 1871–1876. doi:10.1088/0953-8984/20/17/175211

CrossRef Full Text | Google Scholar

Wu, L. A., and Segal, D. (2009). Sufficient conditions for thermal rectification in hybrid quantum structures. Phys. Rev. Lett. 102, 095503. doi:10.1103/PhysRevLett.102.095503

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, N., Zhang, G., and Li, B. (2009). Thermal rectification in asymmetric graphene ribbons. Appl. Phys. Lett. 95, 033107. doi:10.1063/1.3183587

CrossRef Full Text | Google Scholar

Zhao, X., Lee, Y. Y., and Liew, K. M. (2009). Mechanical and thermal buckling analysis of functionally graded plates. Compos. Struct. 90, 161–171. doi:10.1016/j.compstruct.2009.03.005

CrossRef Full Text | Google Scholar