Nanograined GeSe4 as a Thermal Insulation Material

Owing to its amorphous structure, a chalcogenide glass exhibits a thermal conductivity k approaching the theoretical minimum of its composition, called the Einstein’s limit. In this work, this limit is beaten in an amorphous solid consisting of glassy particles joined by nanosized contacts. When amorphous particles are sintered below the glass transition temperature under a high pressure, these particles can be mechanically bonded with a minimized interfacial thermal conductance. This reduces the effective k below the Einstein’s limit while providing superior mechanical strength under a high pressure for thermal insulation applications under harsh environments. The lowest room temperature k for the solid counterpart can be as low as 0.10 W/m·K, which is significantly lower than k≈0.2 W/m·K for the bulk glass.

Thermal insulation materials (TIMs) with solid-like mechanical properties are critical for many harsh-environment applications. However, this cannot be easily satisfied by conventional TIMs that exhibit highly porous structures (e.g., polyurethane foam) and suffer from poor mechanical strength as well as low resistance to moisture penetration. In that respect, the best thermal insulation techniques such as vacuum insulation panels (Alam et al., 2011) and aerogels with 90–99.9% porosity (Akimov, 2003) pose serious durability issues. Instead of pushing the porosity to extremes, alternative approaches have been pursued to effectively reduce k of fully dense materials, particularly by boundary or interface scattering of phonons (Cahill et al., 2014). The largely suppressed lattice contribution k_L is often compared with the theoretical minimum for solids, known as the Einstein’s limit (Einstein, 1911; Cahill and Pohl, 1989). This limit is reached when the phonon mean free path (MFP) decreases to half of the phonon wavelength (~1 Å) and thus invalidates the wave description of lattice vibrations. This limit is effectively approached in amorphous solids where structural disorder reduces the phonon MFP to the order of interatomic distance. Beyond amorphous bulk materials, it has been found that this limit can be beaten within a fully dense material when weak phonon coupling and thus negligible phonon transmission exist across various nanostructured interfaces within thin films (Chiritescu et al., 2007; Duda et al., 2013) or C₆₀/C₇₀ pellets (Olson et al., 1993). Despite some record-low k values for a solid [e.g., cross-plane k~0.05 W/m·K at 300 K for WSe₂ films (Chiritescu et al., 2007)], these materials are unsuitable for practical applications due to their prohibitive manufacturing cost to achieve sufficient thickness for thermal insulation. Along another line of thought, packed nanoparticles (Hu et al., 2007a) or nanospheres (Gao et al., 2013) can be used as bulk TIMs, with largely reduced thermal transport across these nanostructures with nanosized contacts. However, no bonding is formed at the interface between these networked nanostructures to form a rigid bulk material for large-scale applications.

In this work, we investigate the potential of using nanostructured amorphous solids as an effective approach to achieve bulk k values below the Einstein’s limit, along with superior mechanical strength. The selected amorphous (glassy) solids offer multiple advantages for this approach, including k already close to their Einstein’s limit and structural pliancy to accommodate interface defects. By ball milling a bulk glass into nanoparticles and then cold pressing these nanoparticles into a bulk disk, a high density of nanograined interfaces can be created within a bulk glass. When grains are weakly bonded to minimize the inter-grain heat transfer, a high grain-interface thermal resistance R_K would occur and further reduce k below the Einstein’s limit. Meanwhile, the nanostructured solid remains mechanically strong under a high pressure and thus satisfies the durability requirements. This work addresses the long-term challenge of finding TIMs with not only an extremely low k but also superior durability under harsh conditions.

GeSe₄ glass was selected for this application due to (1) its excellent glass-forming ability which precludes the risk of crystal formation, and (2) its high mean atomic weight to reduce the phonon group velocity and thus k (equaling to k_L for electrically nonconductive glasses). The starting bulk GeSe₄ glass was synthesized by conventional melt quenching method (Yang and Lucas, 2009) and was then ball milled into nanopowder with a SPEX 8000 Mixer/Mill for more than 24 h. Particle sizes ranged from 200 nm to 1 µm and the majority size was ~500 nm, as examined by scanning electron microscopy (SEM). No apparent particle size reduction was observed with longer ball milling period. Further reducing the nanoparticle size may require cryogenic ball milling. The amorphous nature of GeSe₄ was confirmed by X-ray diffraction (XRD) before and after ball milling.

Using a home-built hot press setup, the glassy nanoparticles were pressed into a disk that is typically 12.7 cm in diameter and 4–8 mm in thickness. To minimize the covalent bond formation across grain interfaces, pressing was carried out below the glass transition temperature (T_g~160°C for GeSe₄), at which significant atom diffusion would lead to complete fusion of the grains. Here, the hot-press temperature (pressure) was 100°C (80−100 MPa), 150°C (80−100 MPa), and 100°C (~400 MPa) for Samples 1–3, respectively.

The thermal conductivity of the disks was measured under a high vacuum (<1 × 10⁻⁵ torr) based on the one-dimensional and steady-state heat conduction along the axial direction of a disk (Figure 1A, inset) (Lucas et al., 2013). A temperature difference was applied across the sample via a heater on its top, whereas two 1 mil (i.e., 1 milli-inch in diameter) type-K thermocouples were used to read the temperature gradient along the sample. A copper plate was glued between the heater and the sample to uniformly distribute the heat and reduce the radiation loss from the sample top. The sample was also surrounded with an Al-foil radiation shield to minimize the radiation loss from its sidewall. Radiative and lead wire conduction heat losses from the heater (<7% influence for all samples) were calibrated in the self-heating test of a suspended heater (Goldsmid, 1964) and then subtracted in k calculations.

FIGURE 1

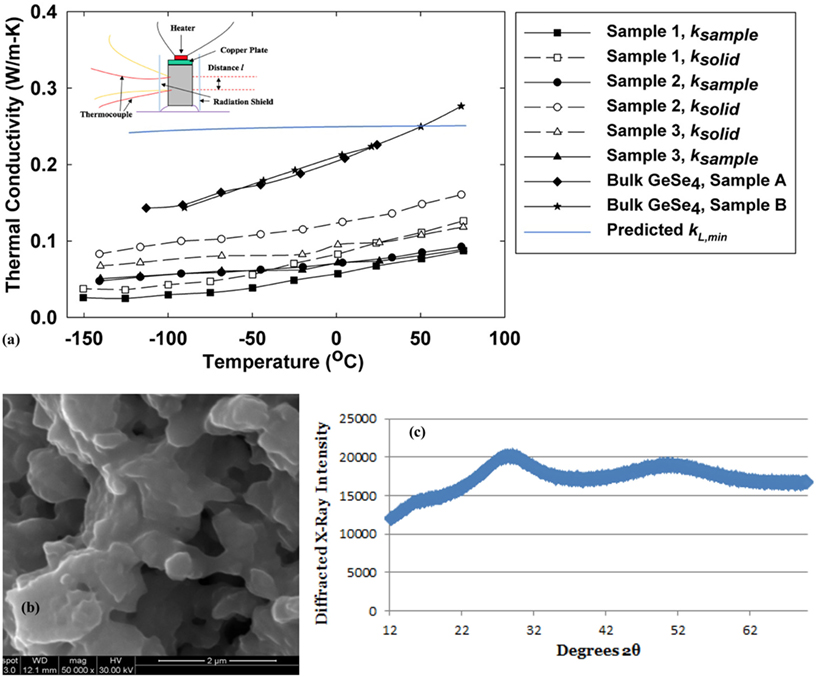
Figure 1. (A) Temperature-dependent k values of GeSe₄ glass and nanograined bulk GeSe₄ glass. The inset is experimental setup. Solid symbols connected by solid lines are the measurement results, whereas empty symbols with dashed lines indicate the nanoporous k_solid for nanograined bulk samples. The symbols used for nanograined bulk samples are square (Sample 1), triangle (Sample 2), and circle (Sample 3); (B) scanning electron microscopy image of Sample 1, with the scale bar as 2 µm; and (C) the X-ray diffraction pattern of representative sample powder.

The data for two bulk GeSe₄ samples are presented in Figure 1A and show <4% divergence below room temperature. The thickness t is 6−7 mm for both samples, whereas the diameter d is 11.77 and 8.83 mm for Samples A (star in Figure 1A) and B (diamond), respectively. Although it was not pointed out for similar Ge-Se-Te glasses (Zhang et al., 2009), attention should be paid to the k enhancement due to radiative heat transfer across the disk that is optically transparent (α_Rt < < 1) to the infrared radiation, in which the absorption coefficient α_R is less than 5 m⁻¹ for the infrared range (Boudebs et al., 2004). Between the top and bottom ends of a disk, Δk due to radiation is roughly 4n^2σT³t/(2/ε − 2 + 1/F₁₂), in which n≈2.4 is the refractive index of GeSe₄ (Boudebs et al., 2004), the Stefan–Boltzmann constant σ = 5.67 × 10⁻⁸ Wm⁻²K⁻⁴, ε≈0.3 is the emissivity of silver epoxy layers on the disk ends, and F₁₂ is the view factor between two circular ends. Assuming d = t = 6 mm, Δk is only 0.02 W/m·K at 300 K. This is also indicated by the excellent k agreement between the two samples with quite different dimensions and thus different Δk.

The Einstein’s limit k_L,min of GeSe₄ is computed using the model proposed by Cahill and Pohl (1989):

$k_{\text{L},\text{min}}={\left(\frac{\pi }{6}\right)}^{1/3}{k}_{\text{B}}{n}^{2/3}{\displaystyle \sum _i{v}_i}{\left(\frac{T}{{\theta }_i}\right)}^2{\displaystyle {\int }_0^{{\theta }_i/T}\frac{x^3{e}^x}{{(e^x-1)}^2}}\text{d}x,$ (1)

in which the cutoff frequency for polarization i is ${\theta }_i=v_i(\hslash /k_{\text{B}}){(6{\pi }^{2}n)}^{1/3}$ (in Kelvin), v_i is the sound velocity, n = 3.38 × 10²⁸ m⁻³ is the number density of atoms in GeSe₄. Only one longitudinal acoustic branch and two transverse acoustic branches are considered here. Using an Olympus Panametrics^® 35 ultrasonic gage, v_i for longitudinal and transverse acoustic phonons are measured as 2,093 and 1,130 m/s, respectively. At room temperature, the estimated k_L,min≈0.25 W/m·K is close to the measured k_L≈0.2 W/m·K. The temperature-dependent k_L,min is further plotted in Figure 1A as the solid line, with weaker temperature dependence than that for real bulk glasses. Similar trend has been observed in one early study (Zhang et al., 2009), which can be partially attributed to increased radiative Δk~T³ at elevated temperatures. Based on the Debye model, Eq. 1 tends to overpredict the k_L contribution by high-frequency modes with slower propagation speed. The Debye frequency can also be higher than the maximum frequency in the real phonon dispersion (Morelli et al., 2002). More discussions can be found elsewhere (Feser et al., 2013).

Figure 1A further compares the temperature-dependent k values of three representative nanograined samples (solid symbols) synthesized as described earlier. Here, the porosity φ was estimated by comparing the measured density ρ of samples with that measured for the bulk GeSe₄ glass (ρ = 4360 kg/m³), which is close to ρ = 4,370 kg/m³ reported in the literature (Guin et al., 2002). The estimated porosity was 23, 33, and 18% for Samples 1–3, respectively. The averaged grain size was determined by SEM to be 500 nm for all samples. Figure 1B shows the SEM image of Sample 1. Despite the porosity variation, no significant difference is found between the three samples with randomized porous structures. Figure 1C further shows the XRD pattern of representative sample powder, where no peak for crystalline phases can be detected. Each measurement took several days, and each sample was remeasured at 300 K in between to assure no structure changes during the heating and cooling processes. Nanograined bulk samples were found to be more resilient under rapid temperature variation, whereas initial GeSe₄ glass easily cracked during fast cooling processes due to thermal shock.

Significant porosity was found in the sintered samples. To eliminate the contribution of porosity on k_L, the thermal conductivities for equivalent fully dense samples k_solid (labeled as empty symbols in Figure 1A) were estimated from the measured k_sample by the Eucken’s formulation, given as k_solid = k_sample/[(1 − φ)/(1 + φ/2)] (Eucken, 1932). At room temperature, the computed k_solid values range from 0.10 to 0.14 W/m·K and are remarkably lower than k_L≈0.2 W/m·K for the bulk glass, indicating weak thermal transport between adjacent nanograins. Starting from Sample 1, increasing the sintering temperature (Sample 2) or pressure (Sample 3) leads to higher k_solid due to increased contact area and/or more covalent bonds formed between adjacent nanograins. Mechanically, all samples have graphite-like strength and can be diced with a diamond wheel saw without damaging their nanoporous structures, which is challenging for highly porous materials such as aerogel.

For porous TIMs, ~10 nm nanopores are normally required to reduce the additional k contribution by the in-pore air conduction, which can be significantly suppressed when the pore sizes are smaller than air molecule MFPs [~68 nm at room temperature (Jennings, 1988)]. With submicrometer pores, thin disks cut from Samples 1 and 3 were remeasured in air with an infrared microscope (Figure 2), following the same measurement principle as thermal interface materials (Hu et al., 2007b). In this setup, the GeSe₄ disk was sandwiched between a heated Cu block and a reference fused quartz disk (k = 1.4 W/m·K) of the same diameter as the heat flow meter. To improve the accuracy of the infrared temperature reading, a micrometer-thick graphite layer was sprayed onto the sample sidewall to make it closer to a blackbody. An infrared camera, with its spatial resolution of 25 µm, was used to measure the lateral temperature slope along both disks (inset of Figure 2). The estimated k values of Samples 1 and 3 were 0.092 and 0.105 W/m·K at 300 K, respectively. These values were higher than those measured in vacuum and can be reduced by decreasing the pore size to the order of 10 nm.

FIGURE 2

Figure 2. Measurement setup for thin-disk samples and the measured temperature profile (~25 μm per pixel) along the cross-plane direction of two disks (inset). Thermal compound and pressure are used to improve the thermal contacts of all interfaces.

With weak radiation influence, the measured k values are mostly attributed to the lattice contribution and are further analyzed using an effective medium formulation recently developed for polycrystals (Hao, 2012). In its simplest form, the effective k_eff is given as

$k_{\text{eff}}=\left(\frac{1-\phi }{1+\phi /2}\right)\left(\frac{k_{\text{G}}}{1+R_{\text{K}}{k}_{\text{G}}/2d}\right),$ (2)

in which k_G is the lattice thermal conductivity of a single grain, d is the grain size, R_K is the grain-interface thermal resistance, and φ is the porosity. Because phonon MFPs already approach the theoretical minimum inside a glassy grain [a few Å only (Zhang et al., 2009)], phonon size effects are not considered and k_G can be approximated as the bulk k_L≈0.20 W/m·K at 300 K. Without grain growth during the low-temperature press, d is mainly around 500 nm as the hot-pressed particle sizes. Equation 2 therefore predicts an effective grain-boundary R_K of 5.3 × 10⁻⁶, 2.4 × 10⁻⁶, and 5.2 × 10⁻⁶ m²·K/W for Samples 1, 2, and 3, respectively. These effective R_K values are orders of magnitude higher than typical R_K values, which range from ~1 × 10⁻⁹ to ~1 × 10⁻⁸ m²·K/W for crystal–crystal interfaces (Chen, 2005; Tai et al., 2013), to ~1 × 10⁻⁷ m²·K/W for crystal–liquid interfaces or nanocarbon-related interfaces (Huxtable et al., 2003; Moisala et al., 2006; Konatham et al., 2012). However, the contrast here can be largely attributed to the limited contact area between adjacent grains with surface roughness, where full contact between adjacent approximately cubic grains is assumed in Eq. 2. Such a limited inter-grain contact area is expected when nanoparticles are hot pressed below the glass transition temperature, i.e., the softening temperature of each nanoparticle. The radius a of the contact spot can be estimated as done in the study by Prasher (2006)

$a={\left(0.375\frac{\pi P}{E^{\ast }}\right)}^{1/3}R,$ (3)

where surface tension of the nanoparticles is neglected and the only force exerted is due to the hot-press pressure P. The averaged nanoparticle radius R = 250 nm is assumed here. Further considering the surface tension can increase the a value (Johnson et al., 1971). Here, 1/E* = 2(1 − v²)/E, where E is the Young’s modulus and v is the Poisson’s ratio. Using E = 14.8 GPa and v = 0.286 for bulk GeSe₄ (Rouxel et al., 2010), a is estimated to be 60 nm at P = 100 MPa. The actual contact area, πa², is only 4.7% of the interface between packed cubes, as assumed in Eq. 2. This ratio is even smaller when the surface roughness of individual nanoparticles is considered. Following this, the actual R_K per unit area between bonded nanoparticles should be less than 2.5 × 10⁻⁷ m²·K/W.

For mechanical properties, nanoindentation test using Keysight NanoIndenter G200 was performed on representative samples. This type of measurements has not been performed on any reported thin films with an ultra-low thermal conductivity (Chiritescu et al., 2007; Duda et al., 2013; Liu et al., 2013). By pushing a probe onto the sample surface, the load and displacement were recorded simultaneously to extract the nanoscale elastic modulus and hardness of the material. For Sample 3 with its porosity φ = 18%, an elastic modulus of 10.2 ± 0.6 GPa was found from the curve based on 1,600 tests. The corresponding hardness was 0.67 ± 0.06 GPa. In contrast, a sample (φ = 22.4%) pressed under identical conditions as Sample 1 exhibited an elastic modulus of 3.9 ± 2.1 GPa and hardness of 0.1 ± 0.08 GPa. This is anticipated as increased hot-press pressure should lead to better mechanical strength under a high pressure. In comparison, commercial TIMs are not considered for loading capabilities (Papadopoulos, 2005). For materials such as aerogel and polyurethane foam, their highly porous structures can be easily compacted or broken even with the pressure applied by a finger.

In conclusion, our studies show that k comparable or lower than that of conventional TIMs can be potentially achieved in nanostructured amorphous solids with disordered and nanosized grain boundaries, in which phonon transport is minimized both within and across nanograins. Compared to expensive thin films (Chiritescu et al., 2007; Duda et al., 2013; Liu et al., 2013), this approach could lead to the mass production of bulk TIMs with unprecedented compression strength. In the future, the material cost can be further reduced using cheaper sulfur-based glasses and thus satisfy various large-scale applications.

Author Contributions

QH and PL conceived the idea and wrote the draft. QH also carried out the data analysis. GC prepared the GeSe₄ glass. DX and ES sintered the nanograined bulk GeSe₄ and measured the thermal properties. PA and SW measured the mechanical properties of representative samples.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank Prof. Pak Kin Wong and Yi Lu for the help on infrared thermal measurements and Dr. Sandip Basu for nanoindentation tests at Agilent Technologies, Inc. This work was supported by National Science Foundation CAREER Award (grant number CBET-1651840).

References

Akimov, Y. K. (2003). Fields of application of aerogels (review). Instrum. Exp. Tech. 46, 287–299. doi: 10.1023/A:1024401803057

CrossRef Full Text | Google Scholar

Alam, M., Singh, H., and Limbachiya, M. C. (2011). Vacuum insulation panels (VIPs) for building construction industry – a review of the contemporary developments and future directions. Appl. Energy 88, 3592–3602. doi:10.1016/j.apenergy.2011.04.040

CrossRef Full Text | Google Scholar

Boudebs, G., Cherukulappurath, S., Guignard, M., Troles, J., Smektala, F., and Sanchez, F. (2004). Linear optical characterization of chalcogenide glasses. Opt. Commun. 230, 331–336. doi:10.1016/j.optcom.2003.11.021

CrossRef Full Text | Google Scholar

Cahill, D. G., Braun, P. V., Chen, G., Clarke, D. R., Fan, S., Goodson, K. E., et al. (2014). Nanoscale thermal transport. II. 2003–2012. Appl. Phys. Rev. 1, 011305. doi:10.1063/1.4832615

CrossRef Full Text | Google Scholar

Cahill, D. G., and Pohl, R. O. (1989). Heat flow and lattice vibrations in glasses. Solid State Commun. 70, 927–930. doi:10.1016/0038-1098(89)90630-3

CrossRef Full Text | Google Scholar

Chen, G. (2005). Nanoscale Energy Transport and Conversion: A Parallel Treatment of Electrons, Molecules, Phonons, and Photons. New York: Oxford University Press.

Google Scholar

Chiritescu, C., Cahill, D. G., Nguyen, N., Johnson, D., Bodapati, A., Keblinski, P., et al. (2007). Ultralow thermal conductivity in disordered, layered WSe₂ crystals. Science 315, 351–353. doi:10.1126/science.1136494

PubMed Abstract | CrossRef Full Text | Google Scholar

Duda, J. C., Hopkins, P. E., Shen, Y., and Gupta, M. C. (2013). Exceptionally low thermal conductivities of films of the fullerene derivative PCBM. Phys. Rev. Lett. 110, 015902. doi:10.1103/PhysRevLett.110.015902

PubMed Abstract | CrossRef Full Text | Google Scholar

Einstein, A. (1911). Elementary observations on thermal molecular motion in solid bodies. Ann. Phys. 35, 679–694.

Google Scholar

Eucken, A. (1932). Thermal conductivity of ceramic refractory materials: calculation from thermal conductivity of constituents. Ceram. Abstr. 11, 353–360.

Google Scholar

Feser, J. P., Chan, E. M., Majumdar, A., Segalman, R. A., and Urban, J. J. (2013). Ultralow thermal conductivity in polycrystalline CdSe thin films with controlled grain size. Nano Lett. 13, 2122–2127. doi:10.1021/nl400531f

CrossRef Full Text | Google Scholar

Gao, T., Jelle, B. P., Sandberg, L. I. C., and Gustavsen, A. (2013). Monodisperse hollow silica nanospheres for nano insulation materials: synthesis, characterization, and life cycle assessment. ACS Appl. Mater. Interfaces 5, 761–767. doi:10.1021/am302303b

CrossRef Full Text | Google Scholar

Goldsmid, H. J. (1964). Thermoelectric Refrigeration. New York: Plenum.

Google Scholar

Guin, J.-P., Rouxel, T., Keryvin, V., Sangleboeuf, J.-C., Serre, I., and Lucas, J. (2002). Indentation creep of Ge–Se chalcogenide glasses below Tg: elastic recovery and non-Newtonian flow. J. Non Cryst. Solids 298, 260–269. doi:10.1016/S0022-3093(01)01053-5

CrossRef Full Text | Google Scholar

Hao, Q. (2012). Effective medium formulation for phonon transport analysis of nanograined polycrystals. J. Appl. Phys. 111, 014307. doi:10.1063/1.3675273

CrossRef Full Text | Google Scholar

Hu, X. J., Prasher, R., and Lofgreen, K. (2007a). Ultralow thermal conductivity of nanoparticle packed bed. Appl. Phys. Lett. 91, 203113. doi:10.1063/1.2814959

CrossRef Full Text | Google Scholar

Hu, X. J., Panzer, M. A., and Goodson, K. E. (2007b). Infrared microscopy thermal characterization of opposing carbon nanotube arrays. J. Heat Transfer 129, 91–93. doi:10.1115/1.2401202

CrossRef Full Text | Google Scholar

Huxtable, S. T., Cahill, D. G., Shenogin, S., Xue, L., Ozisik, R., Barone, P., et al. (2003). Interfacial heat flow in carbon nanotube suspensions. Nat. Mater. 2, 731–734. doi:10.1038/nmat996

PubMed Abstract | CrossRef Full Text | Google Scholar

Jennings, S. G. (1988). The mean free path in air. J. Aerosol Sci. 19, 159–166. doi:10.1016/0021-8502(88)90219-4

CrossRef Full Text | Google Scholar

Johnson, K., Kendall, K., and Roberts, A. (1971). Surface energy and the contact of elastic solids. Proc. Roy. Soc. London A Math. Phys. Eng. Sci. 324, 301–313. doi:10.1098/rspa.1971.0141

CrossRef Full Text | Google Scholar

Konatham, D., Papavassiliou, D. V., and Striolo, A. (2012). Thermal boundary resistance at the graphene–graphene interface estimated by molecular dynamics simulations. Chem. Phys. Lett. 527, 47–50. doi:10.1016/j.cplett.2012.01.007

CrossRef Full Text | Google Scholar

Liu, J., Yoon, B., Kuhlmann, E., Tian, M., Zhu, J., George, S. M., et al. (2013). Ultralow thermal conductivity of atomic/molecular layer-deposited hybrid organic–inorganic zincone thin films. Nano Lett. 13, 5594–5599. doi:10.1021/nl403244s

CrossRef Full Text | Google Scholar

Lucas, P., Conseil, C., Yang, Z., Hao, Q., Cui, S., Boussard-Pledel, C., et al. (2013). Thermoelectric bulk glasses based on the Cu-As-Te-Se system. J. Mater. Chem. A 1, 8917–8925. doi:10.1039/c3ta11117b

CrossRef Full Text | Google Scholar

Moisala, A., Li, Q., Kinloch, I., and Windle, A. (2006). Thermal and electrical conductivity of single- and multi-walled carbon nanotube-epoxy composites. Compos. Sci. Technol. 66, 1285–1288. doi:10.1016/j.compscitech.2005.10.016

CrossRef Full Text | Google Scholar

Morelli, D. T., Heremans, J. P., and Slack, G. A. (2002). Estimation of the isotope effect on the lattice thermal conductivity of group IV and group III-V semiconductors. Phys. Rev. B 66, 195304. doi:10.1103/PhysRevB.66.195304

CrossRef Full Text | Google Scholar

Olson, J. R., Topp, K. A., and Pohl, R. O. (1993). Specific heat and thermal conductivity of solid fullerenes. Science 259, 1145–1148. doi:10.1126/science.259.5098.1145

PubMed Abstract | CrossRef Full Text | Google Scholar

Papadopoulos, A. (2005). State of the art in thermal insulation materials and aims for future developments. Energy Build. 37, 77–86. doi:10.1016/j.enbuild.2004.05.006

CrossRef Full Text | Google Scholar

Prasher, R. (2006). Ultralow thermal conductivity of a packed bed of crystalline nanoparticles: a theoretical study. Phys. Rev. B 74, 165413. doi:10.1103/PhysRevB.74.165413

CrossRef Full Text | Google Scholar

Rouxel, T., Ji, H., Guin, J., Augereau, F., and Rufflé, B. (2010). Indentation deformation mechanism in glass: densification versus shear flow. J. Appl. Phys. 107, 094903. doi:10.1063/1.3407559

CrossRef Full Text | Google Scholar

Tai, K., Lawrence, A., Harmer, M. P., and Dillon, S. J. (2013). Misorientation dependence of Al₂O₃ grain boundary thermal resistance. Appl. Phys. Lett. 102, 034101. doi:10.1063/1.4788688

CrossRef Full Text | Google Scholar

Yang, Z., and Lucas, P. (2009). Tellurium-based far-infrared transmitting glassess. J. Am. Ceram. Soc. 92, 2920–2923. doi:10.1111/j.1551-2916.2009.03323.x

CrossRef Full Text | Google Scholar

Zhang, S. N., He, J., Zhu, T. J., Zhao, X. B., and Tritt, T. M. (2009). Thermal conductivity and specific heat of bulk amorphous chalcogenides Ge20Te80−xSex (x= 0, 1, 2, 8). J. Non Cryst. Solids 355, 79–83. doi:10.1016/j.jnoncrysol.2008.10.014

CrossRef Full Text | Google Scholar