- 1Institut de Ciència i Tecnologia Ambientals, Universitat Autònoma de Barcelona, Bellaterra, Spain
- 2Institució Catalana de Recerca i Estudis Avançats, Barcelona, Spain
- 3Faculty of Integrated Arts and Sciences, Tokushima University, Tokushima, Japan
The term “Jevons Paradox” flags the need to consider the different hierarchical scales at which a system under analysis changes its identity in response to an innovation. Accordingly, an analysis of the implications of the Jevons Paradox must abandon the realm of reductionism and deal with the complexity inherent in the issue of sustainability: when studying evolution and real change how can we define “what has to be sustained” in a system that continuously becomes something else? In an attempt to address this question this paper presents three theoretical concepts foreign to conventional scientific analysis: (i) complex adaptive systems—to address the peculiar characteristics of learning and self-producing systems; (ii) holons and holarchy—to explain the implications of the ambiguity found when observing the relation between functional and structural elements across different scales (steady-state vs. evolution); and (iii) Holling's adaptive cycle—to illustrate the existence of different phases in the evolutionary trajectory of a complex adaptive system interacting with its context in which either external or internal constraints can become limiting. These concepts are used to explain systemic drivers of the Jevons Paradox. Looking at society's thermodynamic foundations, sustainability is based on a dynamic balance of two contrasting principles regulating the evolution of complex adaptive systems: the minimum entropy production and the maximum energy flux. The co-existence of these two principles explains why in different situations innovation has to play a different role in the “sustainable development” of society: (i) when society is not subject to external biophysical constraints improvements in efficiency serve to increase the final consumption of society and expand its diversity of functions and structures; (ii) when the expansion of society is limited by external constraints improvements in efficiency should be used to avoid as much as possible the loss of the existing diversity. It is concluded that sustainability cannot be achieved by technological innovations alone, but requires a continuous process of institutional and behavioral adjustment.
Introduction
The Jevons Paradox states that, in the long term, an increase in efficiency in resource use will generate an increase in resource consumption rather than a decrease. Understanding the nature of the Jevons Paradox is important in relation to the Sustainable Development Goals because it challenges the narratives behind sustainable energy policies striving for improvements in energy efficiency. Indeed, the Jevons Paradox has generated an intense debate in the field of sustainability science among scientists attempting to prove or disprove its validity (Sorrell, 2009; Madureira, 2014).
In the field of economics the Jevons Paradox is framed in terms of “rebound effect” and analyzed through conventional economic narratives (Amado and Sauer, 2012) despite obvious difficulties in its quantification (Sorrell, 2009; Gillingham et al., 2016). The problem with the quantification of the rebound effect lies in the underlying epistemological conundrum: the investigated system becomes something “different” after the “efficiency improvement” has been introduced. Indeed, a change in the identity of a system generating energy services goes hand in hand with a change in definition of the relevant attributes describing the performance of the original process. For example, it makes no sense to use the same set of attributes for comparing the performance of 30 horses with that of a 30-HP tractor. This is a standard predicament faced in the analysis of evolving systems, such as human society. Therefore, those attempting to quantify the rebound effect face a problem generated by the adoption of a simplistic analytical tool and the choice to remain within the comfort zone of reductionist science. Indeed, the very use of the term “rebound effect” reflects the implicit adoption of the ceteris paribus hypothesis—i.e., that the original selection of variables describing what the system is and what it does in relation to the chosen definition of performance remains valid and useful also after the introduced change (innovation) has actually taken place.
In this paper we propose a novel biophysical framework of analysis to deal with phenomena of the Jevons Paradox aimed at escaping the pitfalls of reductionism. It explicitly acknowledges structural and functional change (i.e., emergence of new features) in response to evolution (innovation) and the consequent need to update the quantitative representation on the semantic and formal side across different levels of analysis and scales. As Jevons (1865) stated:
“Now, if the quantity of coal used in a blast-furnace, for instance, be diminished in comparison with the yield, the profits of the trade will increase, new capital will be attracted, the price of pig-iron will fall, but the demand for it increase; and eventually the greater number of furnaces will more than make up for the diminished consumption of each. And if such is not always the result within a single branch, it must be remembered that the progress of any branch of manufacture excite a new activity in most other branches” (Jevons, 1865, p. 141, italics added).
The first phrase in italics refers to the structural change, the second to the functional change taking place at a different (larger) level of analysis. Jevons clearly says that a change in efficiency will result in a change in the identity previously assigned to the observed system and that these changes will take place at different scales. Thus, an improvement in efficiency at a given scale and in relation to a given function can result in the expression of new functions in the system at different levels and scales. This makes it impossible to measure the relative change in performance (before vs. after) with a simple analytical model based on a single-scale representation of the original set of relevant attributes and indicators. When dealing with the analysis of efficiency improvements the ceteris paribus assumption is simply untenable.
Indeed, the nature of the Jevons Paradox can only be understood and represented by introducing new theoretical concepts that capture “genuine change.” Genuine change is necessarily associated with uncertainty and escapes quantification by conventional scientific analysis. As stated by Frank H. Knight:
“We do not perceive the present as it is and in its totality, nor do we infer the future from the present with any high degree of dependability, nor yet do we accurately know the consequences of our own actions” (Knight, 1921/2002, p. 202).
We cannot make models of things that do not yet exist. We can only make extrapolations based on the representation of the present situation into the future. The problem with the latter solution is that extrapolations remain only valid for a limited period (as long as the observed system does not change its identity). Therefore a strategy based on extrapolations cannot capture genuine change. In fact, the validity of extrapolations relies on the assumption that the parameters determining the validity of the model will not change. The Jevons Paradox defies exactly this assumption in that an increase in efficiency causes the system to “become something else,” thus requiring the adoption of different parameters and, in case of extreme changes, even different variables and new functional relations among them (emergence). More than four decades ago, Georgescu-Roegen (1976, p. 21–22) neatly described this problem with regard to econometric extrapolations:
“The fact that econometric models of the most refined and complex kind have generally failed to fit future data—which means that they failed to be predictive—finds a ready, yet self-defeating, excuse: history has changed the parameters. If history is so cunning, why persist in predicting it?”
Acknowledging that the description of the effects of an increase in efficiency does require a change in the parameters used in the quantitative representation, we also have to recognize that understanding the nature and the implications of the Jevons Paradox requires the adoption of new conceptual tools to describe evolutionary changes. In this paper, we seek to solve the problem of how to analyze the Jevons Paradox acknowledging that the innovation introduced causes genuine change of the system under analysis. To this purpose, in the next section, we first introduce three theoretical concepts from outside the realm of reductionist science: complex adaptive systems (Kampis, 1991; Gell-Mann, 1994; Holland, 1995, 2006); holons and holarchies (Koestler, 1967; Allen and Starr, 1982); and Holling's adaptive cycle (Holling, 1986; Holling and Gunderson, 2002). Building on these concepts, we propose a theoretical framework to explore the Jevons Paradox from a biophysical perspective, and establish a bridge between the principles of minimum entropy and maximum power. We conclude with a brief discussion of the possibility of framing the analysis of the Jevons Paradox in relation to the concept of metabolic pattern of societies, using the approach Multi-scale Integrated Analysis of Societal and Ecosystem Metabolism (MuSIASEM).
Three Key Theoretical Concepts
Defying Reductionism: Complex Adaptive Systems
The concept of complex adaptive system is key to our discourse. Complex adaptive systems (CAS) are: (1) open systems operating under thermodynamic non-equilibrium capable of expressing specific structural and functional patterns associated to their identity; (2) hierarchically organized in nested structures observable across multiple spatial-temporal scales; and (3) reproducing themselves using “coded information” about their own identity that is adjusted according to the circumstances through a process of evolution. CAS learn in time how to (re)produce themselves in a more effective way depending on both the experience accumulated and perceived changes in boundary conditions. They are therefore continuously “becoming something else” in time (Prigogine, 1987). The concept of CAS shatters the Cartesian dream of prediction and control embraced by conventional reductionist science.
Reflexive systems, such as human beings and human societies, are a special class of CAS. They can model themselves and in doing so they can express “telos” or purposive behavior in that they strive for specific results. Indeed, reflexive CAS not only act based on what they have learned in the past but also based on a desired “virtual future” (Rosen, 1985). This peculiarity has tremendous implications for a proper framing of the role of “efficiency” in their sustainability. Reflexive CAS must find a subtle balance between efficiency—doing better according to what is already known at present—and adaptability—surviving in face of unknown and unexpected changes in boundary conditions on their path toward a desired virtual future. (Lack of) sustainability of reflexive CAS is therefore not only determined by a shortage of resources (external thermodynamic constraints) but also by an excess of expectations in the system (internal constraints determining what is desirable or unacceptable). This tension is at the core of the Jevons Paradox.
The Meaning of Innovation: Holon and Hierarchy Theory
The concept of holon, first introduced by Koestler (1967), provides insight in the functioning of complex adaptive systems (Giampietro et al., 2006). A holon is at the same time a whole made up of smaller parts (e.g., a human being made up of organs, tissues, etc.) and a part of some greater whole (an individual human being part of a family, a community, etc.). An appropriate combination of holons organized over various hierarchical levels contributes to so-called emergent properties detectable only from higher levels of analysis. Such a hierarchy of holons has also been termed “holarchy” (Koestler, 1967). The concept of holon was developed in hierarchy theory, a branch of complexity theory, to deal with the epistemological implications of multiple scales.
Indeed, the dual nature of holons explains the systemic ambivalence found in the perception of the elements of complex adaptive systems and the ensuing epistemological predicament for the scientific representation of these systems (Allen and Starr, 1982, p. 8–16). Simon (1962) casts this issue in terms of forced handling of mapping an organized structure onto a relational function. At the interface of the focal and the lower hierarchical level, we see structural types (how the components of the “black box” are organized and interacting). On the other hand, at the interface of the focal and the higher hierarchical level we see functional types (how the “black box” interacts with its context). For example, the president of the United States is an organized structure (human being) that expresses an expected function defined by the institutional settings of the country (the role of US president). Bailey (1990) proposes a similar concept for the ambiguity in observing social systems using the couplet of terms incumbent and role. In either case, holons cannot be adequately represented by looking at just one of the two aspects.
The analysis of the two categories of types (structural and functional) making up a holon requires the simultaneous adoption of at least two different scales because the space–time closure of a holon's structure does not coincide with that of its role. To study the structural type we have to adopt a smaller scale (the internal view) in order to see the organized structure inside the black box—how does it work (the what/how question)? To study the functional type we need a larger scale in order to see how the black box relates to its context (the external view)—why is it useful (the what/why question)? This is illustrated in Figure 1.
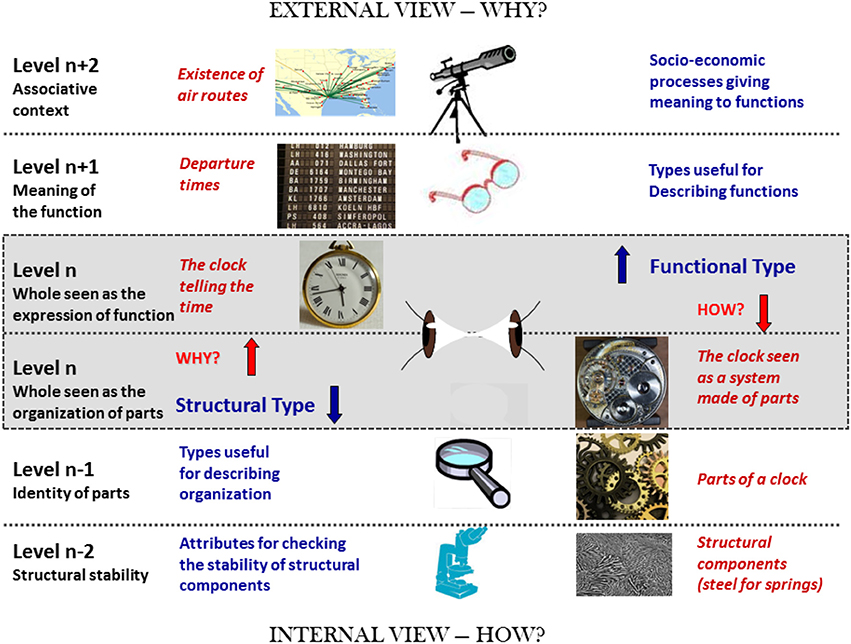
Figure 1. Scale of perception and representation of the functional and structural type associated with a clock.
A second epistemological complication resides in that the identity of a type (description of the representation) never exactly coincides with its special realization(s). We recognize and characterize elements of complex adaptive systems on the basis of expected attributes associated to known typologies, such as a liver, a dog, a policy officer, etc. However, we can only observe special instances of these known typologies, such as the liver of patient X, the dog of my neighbor, the policy officer who fined me. The unique history of any realization makes each instance of a type special. This implies a certain level of variability in the perception of the relevant attributes associated with the type.
Thus, there are two ambiguities inherent in the identity of a holon: (i) a given holon is at the same time a structural and a functional type, and (ii) observations and measurements refer to characteristics of instances of types, not to the attributes of types themselves. In practice, this implies a “many-to-one mapping.” A functional type maps onto different structural types, and an instance of a structural type may map onto different functional types. For example, one same person can be at the same time a policy officer and a father of two children, and many persons can become policy officer or father of two. Another example of this degeneracy in possible mappings over types and instances is illustrated in Figure 2.
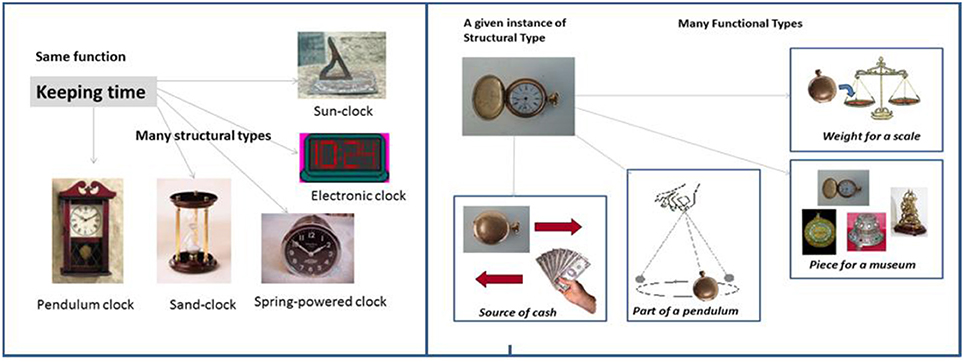
Figure 2. Many-to-one mapping of structural and functional types (adaptation from Giampietro et al., 2006, with permission from Elsevier).
In the quantitative characterization of complex adaptive systems we must always acknowledge that its elements (holons) are (i) instances belonging to two different categories of type that must be coupled in order to determine simultaneously the “what/why” (a functional type) and the “what/how” (a structural type); (ii) generated within a multi-scale organized process capable of reproducing instances of these two types. This second condition can only be fulfilled by expressing coordinated agency across different levels (inside and outside the black box) at different scales. The definition of the “what/why” entails the identification of relevant attributes of functional types (and their behavior). This requires perceptions based on a large-scale view. The definition of the “what/how” entails the identification of relevant attributes of structural types (and their fabrication) and this requires perceptions based on a local-scale view. As a result, no special instance of a holon (an individual realization) can be associated with one specific one-to-one mapping between a functional and structural type. Nor does it have characteristics that are exactly predictable from those of known types. These two aspects permit the complex adaptive system to evolve and improve in time by creating the possibility of emergence of new functional holons in response to changing boundary conditions. Attributes of a structural type irrelevant for a given function may become relevant for a different (new) function. Hence due to special circumstances, instances of a structural type originally associated with one function can become useful (the structural type) for expressing another function. Examples of this type of emergence are illustrated in Figure 3.
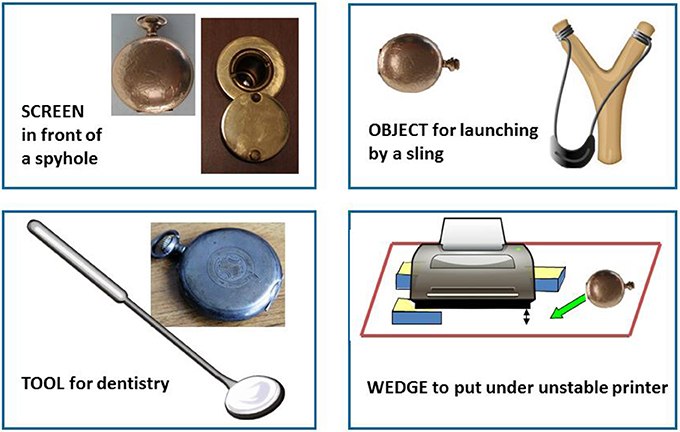
Figure 3. The emergence of new holons as a fortuitous combination of an existing realization of structural type playing a new role needed by the complex adaptive system.
The examples in Figure 3 illustrate that it is not necessary to create a new structural type for a new holon to emerge. The establishment of a new meaningful coupling of a structural and functional type is determined by the need for a new function—perceivable only at the larger scale—by the larger whole to which the holon belongs. A new function can emerge for a given instance of a structural type, even if not originally designed for the new role. The expression of this new function, if stabilized and recorded in time, will introduce a new functional type in the information space of the complex adaptive system and eventually define the criteria of performance for reproducing a better structural type to express the new function. In this process of expanding the diversity of functions in the system, the ability of expressing purposes is essential to accelerate the pace of innovations and improvements of efficiency. For instance, all the innovations illustrated in Figure 3 depend on the need felt by the complex adaptive system to express a new function. When a new functional holon is introduced to achieve new purposes we deal with innovation by emergence. On the other hand, when we innovate structural types to better express a given (existing) function, we deal with innovation by design (e.g., changing the technical coefficients of a local process to improve its performance in relation to a known set of indicators).
Thus, we can state that:
• In innovation by design: (i) the performance associated with the function for which we develop a better design is already known and justified by the existence of both stable boundary conditions (a stable and controlled context) and a given set of objectives associated with the behavior of the system; (ii) the changes refer to the characteristics of a process operating at the local scale. Eventually this change may be amplified at a larger scale by massive reproduction, but the original change takes place at the local scale;
• In innovation by emergence: (i) the function to be expressed is new and determined by either a change in boundary conditions (the system needs an adjustment because the context is no longer behaving as expected by the information recorded in the system) or a change in purpose (the system wants to express a new function currently unavailable); (ii) the changes refer to the characteristics of processes operating at the large scale either in the context determining the boundary conditions or in the higher levels of the system itself where purposes for lower-level holons are defined. Eventually, the effects of these large-scale changes are transmitted to events taking place at the local scale.
Studying Evolutionary Patterns: Holling's Adaptive Cycle
Holling's idea of adaptive cycles (Holling, 1986) is one of the most intriguing narratives proposed for dealing with the perception and representation of the phenomena of evolution and life. It addresses the question as to whether it is possible to define an expected pattern of relations for changes in structural and functional types in the process of evolution. However, because of its metaphorical power, created by the use of semantic definitions without formalizations, the concept of adaptive cycle has also proven to be a difficult tool, notably for quantitative analyses (Giampietro, 2003). A representation of the adaptive cycle, as conceptualized in Holling and Gunderson (2002), also known as “Lazy 8,” is shown in Figure 4.
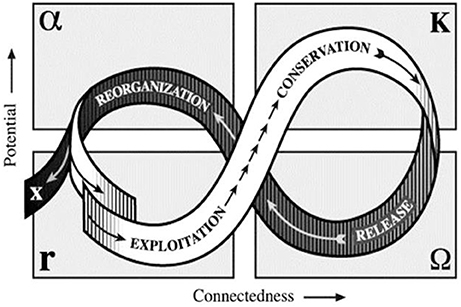
Figure 4. Representation of Holling's adaptive cycle (From Panarchy edited by Gunderson and Holling, 2002. Copyright ©2002 Island Press. Reproduced by permission of Island Press, Washington, DC).
In the original semantic characterization of the adaptive cycle, Holling recognizes four element/steps based on the metaphor of ecosystem successions (and the four seasons). Obviously, being an iterative cycle, there is no step that can be labeled as the initial one (as if the succession were described in simple time). We arbitrarily start the description with the step Holling indicates with the Greek letter α:
(α) Reorganization—this step is associated with the “re-birth of the phoenix from the ashes.” It is the step in which a new cycle starts by proposing a set of realization of types expected to perform successfully in a given context;
(r) Exploitation—this step is associated with an amplification of the winning solutions (the best performing types) adopted in the given cycle. An example from ecology would be the rapid colonization of a recently disturbed area, in which the most effectively performing species occupy as first the available space and resources;
(K) Conservation—this step concerns the preservation and handling of the existing set of structures and functions at the level of the whole complex. An example is the situation of climax in a mature terrestrial ecosystem: the incoming solar energy (the available inflow of resources) is not used to build up additional biomass, but to preserve the already existent diversity of interactions and species; and
(Ω) Release (or creative destruction)—this step is associated with a release of the resources, used so far, which leads to a re-evaluation of the existing profile of space and resource allocation to the universe of existing types. This step creates a window of opportunity for the system to reset the existing cycle. Whenever a combination of internal and external changes makes it possible to get out of the lock-in generated by the combination of external and internal constraints to a new definition of “reorganization” (α) based on a different selection of types (including newly emerged ones) and individual realizations.
The different actions and steps of the cycle refer to a complex of interrelated events taking place simultaneously, but at different time scales. For this reason the analysis of the cycle requires the adoption of the concept of complex time (Giampietro et al., 2006). Indeed, to explain the evolution of a perception or representation of an evolving system we have to deal with at least four relevant “time differentials” within the adaptive cycle:
• dt referring to the pace of action inside the chosen representation—the modeled dynamic behavior of individual realizations—within each one of the phases. For example, representations of the behavior of instances of organisms or ecosystems;
• dτ referring to the pace of movement from an expected phase to another—changes in the parameters of the model. For example, the pace of change of the expected characteristics of types of organisms or types of ecosystems (moving through transitional trajectories);
• dθ referring to the pace of evolution of the identity of the observed system and the definition of its relevant attributes—changes requiring new models. For instance, the evolution of the typologies of organisms or typologies of ecosystems under analysis;
• dT referring to the time duration of the salience of the complex “observer-observed.” The definition of this last time differential requires considering also the observer into the analysis. In fact, the perception/representation of a complex adaptive system can only exist as long as it remains relevant for those perceiving and representing it.
Roles and Types of Innovation in the Evolution of Complex Adaptive Systems
As early as 1911 Schumpeter, working on a theory of innovation in the economic process, proposed the idea of creative destruction (Schumpeter, 1951). Perhaps the most important implications of Schumpeter's idea are that we should (i) bear in mind that the economic process passes through different phases associated to economic cycles, and (ii) expect occasional large-scale collapses of the economic system in response to major changes in boundary conditions or societal expectations that make the existing structural-functional complex obsolete (a situation in which the institutions of the economic system require major re-adjustments). Thus, in order to discuss the role of innovation, such as an increase in efficiency, we must first of all understand what phase the economic process (in which the innovation is to take place) finds itself in: (i) Is the economic system in a phase of expansion (operating under favorable boundary conditions) so that it is possible to continue the strategy that has been successful thus far (doing more of the same)? or (ii) Is the strategy “more of the same” no longer effective under present boundary conditions? Are we in a cyclical crisis that requires moving onto the next phase of the same cycle? or (iii) Are we facing an unavoidable major collapse and re-organization of the system? Do we need to drastically readjust the economic process because the boundary conditions or the expectations of society no longer match those that generated the present institutions regulating the economy?
Accepting that it may be wise—or at least prudent—to contextualize the role of innovation within an analysis of evolutionary cycles, we have to acknowledge that: (1) the term innovation may have different meanings in different contexts; and (2) different types of innovations are needed in different phases of the economic process.
Schumpeter's vision of innovation within the evolutionary pattern of the economic process anticipated biologist Richard Goldschmidt's idea of the hopeful monster (Goldschmidt, 1933), and is perfectly consistent with the punctuated equilibrium theory of Gould and Eldredge (1977) in evolutionary biology. These theories share two main points: (i) Changes take place at different scales—local changes are scaled-up thus affecting patterns of large-scale processes (entrepreneurs introduce new products that change the entire economy; new populations appear through speciation and affect the existing ecosystem); and (2) the pace of evolutionary change is not constant in time: long periods of small and smooth adjustments are interrupted by rapid bursts of profound change (collapse) associated with changing boundary conditions. The occurrence of a large-scale collapse of the organizational network of the complex adaptive system then translates into a top-down push for restructuring activities at the lower local levels.
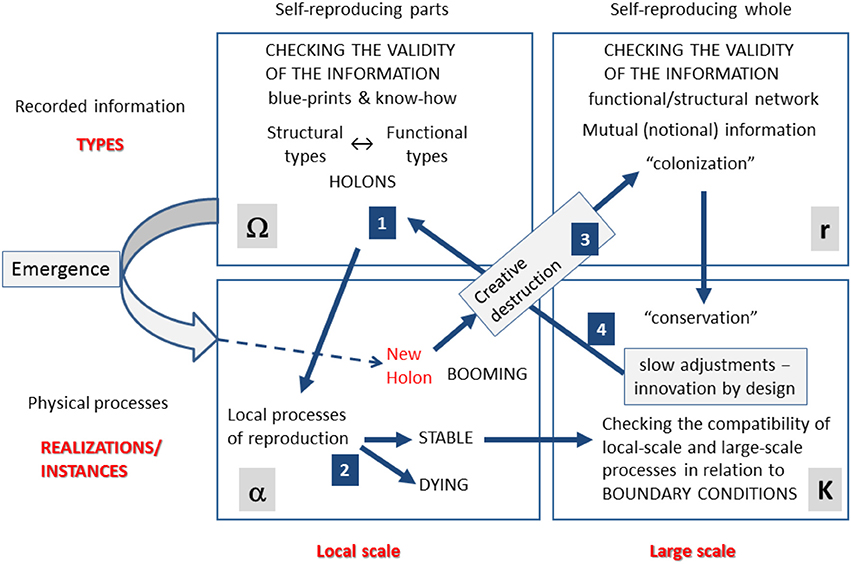
In relation to these questions we can reinterpret Holling's original adaptive cycle by looking at the different roles that innovation plays in its different phases. This re-arranged version of the cycle is illustrated in Figure 5. Note that the four phases of the cycle (α, r, K, Ω) illustrated in Figure 4 have been rotated in Figure 5 to organize the information space along two axes:
(i) Types vs. instances (upper vs. lower row)—notional definitions provided on the basis of direct information (genes used to make organisms) and mutual information (niches and communities) are in the upper row, definition of instances of biophysical processes (organisms and ecosystems) are in the lower row;
(ii) Local-scale perceptions vs. large-scale perceptions (left vs. right column)—patterns expressed at the local scale (niches and organisms) are in the left column, patterns expressed at the large scale (communities and ecosystems) in the right column.
Below we describe three trajectories (cycles) of innovation using the scheme presented in Figure 5.
A system in quasi-steady-state (1 → 2 [stable] → 4 → 1): In a situation of quasi steady-state the information recorded in the system (in the form of blue-prints, know-how and narratives at the local scale and in the form of socio-economic institutions at the large scale) permits the reproduction of the integrated set of economic (or ecological) processes across different scales. The effective coupling of instances of holons makes it possible to reproduce the parts at the local scale (1 → 2) (e.g., representing the economic viability of both entrepreneurs and households). In this case the process of self-reproduction remains more or less faithful to the original set of functional holons; only small innovations by design take place (2 [stable] → 4) aimed at and introducing minor adjustments at the local scale. The network of interactions is compatible with the viability of holons at the local scale and the feasibility of large-scale processes in relation to boundary conditions at the large scale.
A system in transitional state—innovation by creative destruction (1 → 2 [booming] → 3 → 4 → 1): When the emergence of a novelty provides a major comparative advantage, the associated holon is amplified both in terms of recorded information and biophysical activity (arrow 3) through autocatalytic loops (doing “more of the same” provide comparative advantage). The more the information and activity associated with the holon expand, the more the rest of the system is forced to follow along. (This happened in US agriculture when tractors replaced horses). As a result also other holons are forced to innovate to adjust to the new “sheriff in town” by either eliminating the obsolete structural types or re-using them to express new functions. When this event takes place in a situation in which there is room for expansion the whole system will be pushed to grow as much and as fast as possible using the edge given by the new solutions. (In the 1940s abundant oil in the USA provided favorable boundary conditions at the large scale to expand the use of thermal engines in substitution of animal power). In fact, the speed of take-over by innovative holons is a key factor here. If they are able to push and shape the innovation of the others they will set the identity of the new institutional settings emerging at the large scale, biasing them in their favor. In theoretical ecology this phenomenon is called “the survival of the first” (Hopf, 1988). After the industrial revolution (late twentieth century) the combination of abundant, cheap fossil energy (oil), resources, technology and information (a “compact technological package” of western civilization) generated an unprecedented expansion of human activity world-wide. According to theoretical ecology this explosion of economic growth (colonization phase), due to creative destruction of the previous institutional order, sooner or later will move to the next phase of “conservation.” Considering the biophysical roots of the economic process, we may expect that exponential growth will sooner or later face external constraints generated by the instability of boundary conditions. A famous line of economist Kenneth Boulding—“Anyone who believes that exponential growth can go on forever in a finite world is either a madman or an economist”—neatly makes this point. The phase of “conservation” will eventually bring the system back in a quasi-steady state.
A system in senescence ready for a new transition—In the phase of conservation the system increases interactions, regulations and mutual dependency among the various holons within its hierarchical organization. This improves its efficiency in resource use but it also makes the system more subject to the impact of external limits. A very efficient system is fragile and brittle in case of changing boundary conditions and/or societal aspirations (Giampietro and Mayumi, 2008). In such a situation it is difficult to realize significant changes in the internal organization (the various technological systems and institutional settings are fully locked-in) and it becomes increasingly difficult to react to large-scale changes in boundary conditions or changing definitions of “desirability.” In the long period this situation moves the system in a state of senescence in which the holons have less strength (1 → 2 [dying]) and the holarchy to which they belong becomes weaker. This state of senescence allows the occurrence of destructive innovation by emergence (the start of a new cycle of innovation by creative destruction). In this case a local instability triggered by an “emergent” holon capable of eliminating obsolete competitors will be amplified to a scale that can trigger a collapse and then a radical re-setting of the structural and functional organization of the whole socio-economic system.
Building on these premises, different meanings and effects of innovation can be defined:
Innovations in the phase of colonization—In the phase of colonization, the key to success is the ability to identifying gradients of yet unexploited resources for fast exploitation. This is a bottom-up process in which individual holons try to impose their values, perspectives, and preferences on others and the environment. In this phase it is important to have an edge over the competition. Innovation in this phase tends to focus on solving one problem at the time (silver bullet approach to eliminate bottlenecks) by generating better structural types inside the system for an already-defined goal (e.g., achieving better technical coefficients to establish more effective processes). After having individuated, at the local scale, winning criteria the system looks for innovations, obtained by design, for doing more of the same but better. Scaling-up local winning patterns makes it possible for the complex adaptive system to track and use new available resources. The diagonal labeled 3 in Figure 5 (from α to r) describes a bottom-up driver (upward causation).
Innovations in the phase of conservation—In the phase of conservation the system focuses on building better relationships among its components and with its context. This includes identifying the external limits imposed on the expansion of large-scale patterns and transmitting this information to holons operating at lower levels (at the local scale). The identification of external limits is translated in the identification of resources to be conserved as much as possible inside the system by a collaboration of lower-level holons. This phase deals with a mix of upward and downward causation in which it is essential to consider both: (i) values, perspectives and preferences of the holons operating within the system at lower level, and (ii) the identity of ecological processes determining the existence of favorable boundary conditions for the whole system. In this phase it is important to establish cooperative relations at different scales: inside the system among holons and outside the system with other complex adaptive systems. This phenomenon has been called the drive toward “double asymmetry” (Greene, 1969) or equipollence (Iberall et al., 1981). Therefore, innovation tends to focus on improving the definition of functions in terms of regulations and institutions—e.g. more effective behaviors and better controls rather than exploiting more resources. The diagonal labeled 4 in Figure 5 (from k to Ω) describes such a top-down driver (downward causation).
Also in this case innovations are by design. However, the objective is no longer rapidly expanding a local pattern (upward causation) aimed at consuming more resources in order to express more activity (expanding the diversity of functions and structures), but rather integrating the different patterns across scales sharing the stress among levels (integration of downward and upward causation)—from an innovation based on changing technology to an innovation based on changing behavior.
Innovation through catastrophic re-adjustment—Innovation by creative destruction refers to a dramatic re-shuffling of the activities taking place in a complex adaptive system (e.g., socio-economic systems) simultaneously both at the local and large scale. Innovation here means “going for something completely different,” which cannot be known at the moment of the change. This type of innovation cannot be planned. It requires a timely combination of: (a) major change in the identities of the set of holons operating at the local scale; and (b) a radical restructuring of institutional settings operating at the large scale. This event of emergence of a totally different pattern of self-reproduction of human society may take place when the boundary conditions of the system no longer guarantee the reproduction of both the institutions (large scale) and the functional holons (local scale). Put in another way, popular disaffection with the existing living conditions and socio-economic identity may cause a collapse of social fabric leading to an implosion of the system (e.g., a political revolution or collapse of a civilization).
This overview suggests that at present different countries are operating in different evolutionary contexts. Most developed countries have come to realize that their evolution is limited by external constraints and that they ought to move as quickly as possible into the phase of conservation to not get caught into the attractor of “release.” Nevertheless, in many cases cultural lock-in—heritage of the phase of colonization—makes it hard to change the perception of the role of innovation (that of boosting economic growth or doing more of the same). On the other hand, many developing countries, due to their delayed position in the evolutionary cycle, still perceive “innovation” as the required solution to expand the diversity of functions and structures of their economies through further economic growth.
Yin-yang Tension Between Minimum Entropy Production and Maximum Energy Flux
The representation of the energy metabolism of a complex adaptive system comprises a set of energy transformations across different energy forms. As seen before with the holon, the system can be described from an outside or an inside perspective. The outside view describes the interaction of the system (black box) with the context. In the case of the energy metabolism of modern society this concerns the characterization of primary energy sources, such as coal, oil, wind, solar radiation, or biomass (Giampietro et al., 2013). The inside view describes the functioning of the parts inside the system and concerns the characterization of energy carriers, such as electricity and fuels (Giampietro et al., 2013).
This distinction is relevant with regard to the principles of minimum entropy production and maximum energy flux. As explained below these principles were proposed by different authors in relation to the analysis of the evolution of complex adaptive systems. Although the two principles may seem to provide contrasting explanations of the thermodynamic drivers of evolution, there is no incongruity among them. The apparent contradiction simply reflects two different interpretations of the concept of efficiency for the metabolism of complex adaptive systems operating away from thermodynamic equilibrium: the inside and the outside view. Kawamiya's work (Kawamiya, 1983) is helpful in defining these two types of efficiency in physical terms:
1. Efficiency of type 1 (EFT1) refers to energy transformations associated with defined processes taking place within the system (inside the black-box) and measures the ratio between output and input. A major problem with this definition of output/input efficiency lies in that it ignores the time required to generate output. The power level at which the process is operating is not considered relevant.
2. Efficiency of type 2 (EFT2) refers to energy transformations determining the pace of generation of an output (per unit of time) associated with the interaction of the system (black-box) with its environment. The problem with this definition is that it considers only the power level and ignores the amount of energy input required by the process to produce the output. The quantity of input required to operate the process is not considered relevant.
Returning to the two thermodynamic principles, a maximum in EFT1 defines the minimum energy throughput required by the system to realize a particular structure/function in society. The concept of EFT1 has been formalized by Prigogine (Prigogine, 1961; Glansdorff and Prigogine, 1971; Nicolis and Prigogine, 1977) in relation to the analysis of energy-dissipating systems under the term “minimum entropy production principle” (even though it should be considered a phenomenological principle rather than a physical law). It is important to observe that, even if developed within the field of non-equilibrium thermodynamics, the validity of this principle is based on the assumption that the system under analysis is stable and approaching steady-state. This means that the pattern of dissipation associated with the particular choice of variables and equations used in the model must occur sufficiently close to equilibrium to guarantee that the chosen formalization remains reliable in time.
For living systems interacting with a challenging environment, the minimization of the flow of energy throughput (by reducing the input required to obtain the same output) can reduce the option space of behaviors. Such limit in the diversity of behaviors can become a liability when boundary conditions change or for a society willing to improve its living standards by expanding its set of functions. Expanding the ability to produce more in order to consume more—maximizing the energy flux—is a common attractor for socioeconomic systems. This explains why in both economic and biophysical analyses the idea that the maximization of EFT2 drives evolution has always been very popular. The principle of maximum energy flux in economics has been formalized in terms of the maximization of profit and welfare. In ecological theory, the metaphor of maximization of EFT2 has been formalized in terms of the maximization of energy flows within ecosystems. Indeed, Lotka's maximum energy flux principle (Lotka, 1922) has been proposed under a series of different names by other authors: evolution through Malthusian instability (Layzer, 1988); maximum exergy degradation (Morowitz, 1979; Jørgensen, 1992; Schneider and Kay, 1994); maximum power principle (Odum and Pinkerton, 1955; Odum, 1971, 1996).
Thus, the two concepts refer to two different perceptions of change and evolution:
1. At lower hierarchical levels, adopting a quasi-steady-state view of the system, we deal with dissipative components of complex adaptive systems operating under a strict set of constraints within stable boundary conditions (e.g., cells within an organism or firms in a stable socio-economic context). Under these conditions, system performance is well-defined and it is reasonable to assume a steady trend of learning new ways of reducing the required energy and matter input for sustaining a given function. An increase in performance of the given function can therefore be measured using type 1 efficiency. In this situation, the minimum entropy production principle is more relevant for the analysis than the maximum energy flux principle;
2. At the level of the whole complex adaptive system it is reasonable to expect that it will express as many functions as possible in order to enhance its chances of survival and well-being in its interaction with the context. In this situation, when perceiving the performance of the system at a large scale, the resulting systemic uncertainty calls for the development of adaptability. At this level, system performance can only be improved by increasing the option space of behaviors: the larger is the diversity, the better. In this perception, the maximum energy flux principle is more relevant in the analysis than the minimum entropy production.
In conclusion, the principles of minimum entropy production and maximum energy flux are not exclusive of or in contrast with each other. They operate simultaneously on different hierarchical scales as long as the favorable boundary conditions and the definition of goals for the system as a whole are maintained. The final outcome is a better integration of the complex adaptive system with its context in the process of evolution because of the continuous diversification of functions expressed. For example, in household economy we see that by increasing the efficiency of monetary expenditure inside the household (minimum entropy principle) the money saved in daily household routines can be spent into the expression of more/different social interactions (maximum energy flux). The two principles (and the two efficiencies defined by Kawamiya) also explain the rapid take-over of engine horse power on animal horse power. In fact, the use of tractors in agriculture not only makes it possible to easily harness hundreds of horse power at the local scale—achieving a much higher EFT2—but also reduces the consumption of energy input to generate this power—much higher EFT1 (Giampietro et al., 2013). Indeed, whereas hundred horses used once a year for harvesting need to be fed for their entire life time (consuming also when the peak of power demand is over), the 100-horse-power tractor does not consume gasoline when switched off.
The Jevons Paradox in Relation to the Energy Metabolism of Society
The concepts derived from complex system thinking discussed in the previous sections not only provide useful insights in the understanding of the nature of the Jevons Paradox, but also help explain the impasse faced in trying to quantify the rebound effect. According to the Law of Requisite Variety (Ashby, 1956) if one wants to characterize, monitor, and control the behavior of a system, one first of all has to be able to identify the relevant features to be characterized, monitored and controlled for achieving the expected goals. The more the system is complex, the more the characterization will be complex too. Sustainability of complex metabolic systems, such as modern economies, requires policies aimed at the expression of an integrated set of functions guaranteeing, in the long term, the maintenance and reproduction of their structural components across different levels of organization. Considering this goal, it is unlikely that we can develop effective policies by relying on simplistic systems of monitoring and control based on the analysis of a simple relation between an output and an input such as the rebound effect. The use of an input/output ratio as indicator of efficiency calculated at a given scale and without proper contextualization does not provide useful information for policy (Giampietro et al., 2017).
Analyzing the link between innovation, efficiency and sustainability from a complex system perspective, we obtain two clear lessons for quantitative analysis:
1. Move away from a mono-scale, mono-dimensional quantitative analysis of efficiency toward a multi-scale, multidimensional quantitative analysis of performance;
2. Move away from predicative representations (based on deterministic results uncontested in relation to both the definitions and the assumptions used in the models) toward impredicative representations. Impredicativity is a standard predicament faced in the study of autopoietic systems—a class of systems capable of producing themselves (Giampietro, in press). With relational analysis one can generate impredicative (contingent) representations of the expected relations among the characteristics of structural and functional elements operating in the autopoietic process. However, because it is impossible to provide a unique or deterministic representation of causality for these systems (chicken-egg paradox) the resulting representation will necessarily be pluralistic (Giampietro, in press).
The authors have developed a more complex method of analysis based on the rationale of bio-economics proposed by Georgescu-Roegen: Multi-scale Integrated Analysis of Societal and Ecosystem Metabolism (MuSIASEM). MuSIASEM is a semantically open system of accounting based on grammars after Chomsky's ideas (Chomsky, 1998). It has been proposed in conceptual terms (Giampietro and Mayumi, 2000a,b) and tested in quantitative applications (e.g., Giampietro et al., 2012, 2013). Recently, MuSIASEM has been improved by incorporating principles of relational system analysis (Giampietro, in press), and applied to energy efficiency (Giampietro et al., 2017).
The proposed quantitative method of analysis makes it possible to assess the feasibility, viability and desirability of a given metabolic pattern of society by answering the following questions:
• What is the set of functions expressed by society and what organized structures does this require? What are the expected characteristics of structural-functional compartments (holons) generating the metabolic pattern at the local scale?
• How to study the impredicative set of relations over the metabolic characteristics of compartments in charge of expressing these functions over different hierarchical levels?
• What are the external constraints faced by society in relation to its internal consumption? How can changes in technology or behavior be used to deal with the implications of external biophysical limits?
• What are the relative priorities that must be given to the various functions in case resource shortage should require a re-adjustment of the metabolic pattern? In particular, what is the minimum value for the metabolic speed of the elements within the socioeconomic system that must be guaranteed to avoid the collapse of the social fabric?
These questions require the integration of non-equivalent representation of the metabolic process, combining assessments based on both extensive (size) and intensive variables (flow per unit of size), to establish bridges across different hierarchical levels. They cannot be addressed with the simplistic representations typical of reductionism.
Conclusions
Jevons Paradox requires us to consider different hierarchical scales at which the system under analysis changes its identity in response to an innovation. For this reason, if we want to consider several relevant scales simultaneously (steady-state vs. evolutionary view), it is impossible to assess (in quantitative terms) the rebound effect. In fact, an increase in energy efficiency has exactly the effect of changing: (1) what the system is; (2) what it does, and consequently (3) the relevance of the attributes of performance used by the modeler to study a given transformation. The combination of these changes requires a systemic adjustment (update) of the set of proxy variables, parameters and indicators of performance used in the model.
The framing of the Jevons Paradox in terms of complex system thinking flags the limited usefulness of the concept of energy efficiency as an indicator of sustainability. Any assessment of efficiency refers to an output/input ratio. It is by default an intensive variable—an achievement of a task per unit of input of energy carrier. Such indicator ignores not only the overall size of the flow (an essential piece of information to address the issue of external constraints) but also the time dimension (an essential piece of information to check the viability of specific end-uses). Hence it misses the implications of the minimum entropy and the maximum flux principles. As a result, it also completely overlooks the definition of desirability of the end-use in question.
A second problem with indicators based on efficiency lies in the total lack of contextualization of the assessment. By default, complex adaptive systems have an evolutionary drive and this implies that they pass through evolutionary cycles. In order to study and discuss the implications of the Jevons Paradox and the link between innovation, efficiency and sustainability, it is essential to adopt a more sophisticated quantitative analysis of the energetic metabolic pattern of modern society capable of contextualizing the evolutionary phase in which the society is operating.
During a phase of economic expansion (upward causation) the insurgence of the Jevons Paradox is practically inevitable. Whether it is because of an uneven distribution of wealth or a strong aspiration for a higher material standard of living, it is unlikely that an energy surplus generated by an increase in efficiency will not be consumed by a society to fix a problem or improve living conditions.
During phases in which society is limited by external constraints (downward causation)—e.g., in case of a deterioration of the quality of primary sources (peak oil, peak water, peak soil)—we may expect a reduced supply of energy carriers for final end-uses. External limits translate into an increase in the share of energy carriers used for the exploitation of primary sources. In this situation, improvements in efficiency are required to offset the severity of external constraints on society rather than to increase final consumption. Then the implications of the Jevons Paradox will be different: society will have to negotiate new definitions of desirability through cultural and political adjustments (a new acceptable standard of living). In this case, improvements in energy efficiency may be used to generate surpluses to explore alternative sets of behaviors more compatible with new boundary conditions.
In conclusion, the Jevons Paradox entails that sustainability problems cannot be solved by technological innovations alone. They must be solved through institutional and behavioral changes.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors are indebted to Sandra Bukkens for editing the manuscript and the reviewers of the manuscript for their very pertinent comments and suggestions. The first author (MG) gratefully acknowledges funding from the European Union's Horizon 2020 research and innovation programme under grant agreement No 649342 (EUFORIE).This work reflects only the authors' view; the funding agency is not responsible for any use that may be made of the information it contains.
References
Amado, N. B., and Sauer, I. L. (2012). An ecological economic interpretation of the Jevons effect. Ecol. Complex. 9, 2–9. doi: 10.1016/j.ecocom.2011.10.003
Georgescu-Roegen, N. (1976). Energy and Economic Myths: Institutional and Analytical Essays. New York, NY: Pergamon Press.
Giampietro, M. (2003). Multi-Scale Integrated Analysis of Agroecosystems. Boca Raton, FL: CRC Press.
Giampietro, M. (in press). “Anticipation in agriculture,” in Handbook of Anticipation: Theoretical and Applied Aspects of the Use of Future in Decision Making, ed R. Poli (New York, NY: Springer).
Giampietro, M., Allen, T., and Mayumi, K. (2006). The epistemological predicament associated with purposive quantitative analysis. Ecol. Complex. 3, 307–327. doi: 10.1016/j.ecocom.2007.02.005
Giampietro, M., and Mayumi, K. (2000a). Multiple-scale integrated assessment of societal metabolism: Introducing the approach. Popul. Environ. 22, 109–153. doi: 10.1023/A:1026691623300
Giampietro, M., and Mayumi, K. (2000b). Multiple-scales integrated assessments of societal metabolism: Integrating biophysical and economic representations across scales. Popul. Environ. 22, 155–210. doi: 10.1023/A:1026643707370
Giampietro, M., and Mayumi, K. (2008). “The jevons paradox: the evolution of complex adaptive systems and the challenge for scientific analysis,” in The Jevons Paradox and the Myth of Resource Efficiency Improvements, eds J. M. Polimeni, K. Mayumi, M. Giampietro, and B. Alcott (London: Earthscan Research Edition), 79–140.
Giampietro, M., Mayumi, K., and Sorman, A. H. (2012). The Metabolic Pattern of Societies:Where Economists Fall Short. London: Routledge.
Giampietro, M., Mayumi, K., and Sorman, A. H. (2013). Energy Analysis for a Sustainable Future: Multi-Scale Integrated Analysis of Societal and Ecosystem Metabolism. London: Routledge.
Gillingham, K., Rapson, D., and Wagner, G. (2016). The rebound effect and energy efficiency policy. Rev. Environ. Econ. Policy 10, 68–88. doi: 10.1093/reep/rev017
Giampietro, M., Velasco-Fernández, R., and Ripa, M. (2017). Characterizing the Factors Determining “Energy Efficiency” of an Economy Using the Multi-Level end Use Matrix of Energy Carriers. European Futures of Energy Efficiency (EUFORIE), Deliverable 4.2. ICTA, Autonomous University of Barcelona, Bellaterra. Available online at: http://www.utu.fi/en/units/euforie/Research/deliverables/Documents/EUFORIE-D4.2.pdf
Glansdorff, P., and Prigogine, I. (1971). Thermodynamics Theory of Structure, Stability and Fluctuations. New York, NY: John Wiley & Sons.
Goldschmidt, R. (1933). Some aspects of evolution. Science 78, 539–547. doi: 10.1126/science.78.2033.539
Gould, S. J., and Eldredge, N. (1977). Punctuated equilibria: the tempo and mode of evolution reconsidered. Paleobiology 3, 115–151. doi: 10.1017/S0094837300005224
Greene, M. (1969). “Hierarchy: one word, how many concepts?” in Hierarchical Structures, eds L. L. Whyte, A. G. Wilson, and D. Wilson (New York, NY: American Elsevier Publishing Company Inc.), 56–58.
Holland, J. H. (2006). Studying complex adaptive systems. J. Syst. Sci. Complex. 19, 1–8. doi: 10.1007/s11424-006-0001-z
Holling, C. S. (1986). “Resilience of ecosystems; local surprise and global change,” in Sustainable Development of the Biosphere, eds W. C. Clark and R. E. Munn (Cambridge: Cambridge University Press), 292–317.
Holling, C. S., and Gunderson, L. H. (2002). “Resilience and adaptive cycles,” in Panarchy: Understanding Transformations in Human and Natural Systems, eds L. Gunderson and C. S. Holling (Washington, DC: Island Press), 25–62.
Hopf, F. A. (1988). “Entropy and evolution: sorting through confusion,” in Entropy, Information and Evolution, eds D. J. Weber and D. Smith (Cambridge, MA: The MIT Press), 263–74.
Iberall, A. H., Soodak, H., and Arensburg, C. (1981). “Homeokinetic physics of societies - a new discipline: autonomous groups, cultures, politics,” in Perspectives in Biomechanics, Vol. 1, Part 1, eds H. Real, D. Ghista, and G. Rau (New York NY: Harwood Academic Press).
Jevons, W. S. (1865). The Coal Question (Reprint of the Third Edition−1906), New York, NY: Augustus, M. Kelley.
Jørgensen, S. E. (1992). Integration of Ecosystem Theories: A Pattern. Dordrecht: Kluwer Academic Publishers.
Kampis, G. (1991). Self-modifying Systems in Biology and Cognitive Science: A New Framework for Dynamics, Information, and Complexity. Oxford: Pergamon Press.
Kawamiya, N. (1983). Entropii to Kougyoushakai no Sentaku (in Japanese) (Entropy and Future Choices for the Industrial Society). Tokyo: Kaimei.
Layzer, D. (1988). “Growth of order in the universe,” in Entropy, Information, and Evolution, eds B. H. Weber, D. J. Depew, and J. D. Smith (Cambridge, MA: MIT Press), 23–39.
Lotka, A. J. (1922). Contribution to the energetics of evolution. Proc. Natl. Acad. Sci.U.S.A. 8, 147–151.
Madureira, N. L. (2014). “Chapter 3: The rebound effect,” in Key Concepts in Energy. (Cham: Springer International Publishing), 33–52.
Nicolis, G., and Prigogine, I. (1977). Self-Organization in Nonequilibrium Systems. New York, NY: John Wiley & Sons.
Odum, H. T., and Pinkerton, R. C. (1955). Time's speed regulator: the optimum efficiency for maximum power output in physical and biological systems, Am. Sci. 43, 331–343
Prigogine, I. (1961). Introduction to Thermodynamics of Irreversible Processes, 2nd Revised Edn. New York, NY: Interscience Publishers.
Rosen, R. (1985). Anticipatory Systems: Philosophical, Mathematical and Methodological Foundations. New York, NY: Pergamon Press.
Schneider, E. D., and Kay, J. J. (1994). Life as a manifestation of the second law of thermodynamics. Math. Comput. Model. 19, 25–48.
Keywords: Jevons paradox, energy efficiency, innovation, complex adaptive system, holon, rebound effect, MuSIASEM, complexity theory
Citation: Giampietro M and Mayumi K (2018) Unraveling the Complexity of the Jevons Paradox: The Link Between Innovation, Efficiency, and Sustainability. Front. Energy Res. 6:26. doi: 10.3389/fenrg.2018.00026
Received: 10 January 2018; Accepted: 20 March 2018;
Published: 04 April 2018.
Edited by:
Franco Ruzzenenti, University of Groningen, NetherlandsReviewed by:
Grégoire Wallenborn, Université libre de Bruxelles, BelgiumMarco Raugei, Oxford Brookes University, United Kingdom
Copyright © 2018 Giampietro and Mayumi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mario Giampietro, bWFyaW8uZ2lhbXBpZXRyb0B1YWIuY2F0
 Mario Giampietro
Mario Giampietro Kozo Mayumi
Kozo Mayumi