- 1Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Engineering Mechanics and Center for Nano and Micro Mechanics (CNMM), Tsinghua University, Beijing, China
- 2Department of Micro/Nano Electronics, Institute of NanoMicroEnergy, Shanghai Jiao Tong University, Shanghai, China
The knowledge of interfacial phonon transport accounting for detailed phonon spectral properties is desired because of its importance for design of nanoscale energy systems. In this work, we investigate the interfacial phonon transport through Si/Ge multilayer films using an efficient Monte Carlo scheme with spectral transmissivity, which is validated for cross-plane phonon transport through both Si/Ge single-layer and Si/Ge bi-layer thin films by comparing with the discrete-ordinates solution. Different thermal boundary conductances between even the same material pair are declared at different interfaces within the multilayer system. Furthermore, the thermal boundary conductances at different interfaces show different trends with varying total system size, with the variation slope, very different as well. The results are much different from those in the bi-layer thin film or periodic superlattice. These unusual behaviors can be attributed to the combined interfacial local non-equilibrium effect and constraint effect from other interfaces.
Introduction
In the 1950s, semiconductors became to be used as thermoelectric material for energy conversion in refrigeration (Majumdar, 2004). The efficiency of thermoelectric material can be quantitatively determined by its dimensionless figure of merit, ZT = S2σT/k, where S is the Seebeck coefficient, σ is the electrical conductivity, T is the absolute temperature, and k is the thermal conductivity (Jeng et al., 2008). To achieve a highly efficient thermoelectric device, ZT should be larger than 3, whereas for the conventional bulk materials, ZT only lies between 0.6 and 1 around room temperature (Majumdar, 2004). Recently, thermoelectrics play an appealing role toward the global energy crisis due to their direct conversion of heat to electricity in an environmentally friendly way (Wu and Wu, 2016). Therefore, there is a strong desire for the development of highly efficient thermoelectric materials. With the rapid development of nanoengineering in the past decades, people have attained significant increase of thermoelectric efficiency by nanostructuring, such as superlattices and nanocomposites (Majumdar, 2004; Kim et al., 2006; Dresselhaus et al., 2007; Jeng et al., 2008; Joshi et al., 2008; Snyder and Toberer, 2008; Hu and Poulikakos, 2012; Wu and Wu, 2016). When the size of nanostructures is smaller than the phonon mean free path (MFP) but still larger than the electron MFP, the fruitful interfaces contribute to large reduction of the thermal conductivity with negligible destruction of the electrical conductivity. In spite of the substantial improvement of thermoelectric efficiency, a further progress remains challenging due to the elusive understanding of interfacial phonon scattering in micro and nanomaterials.
There exist several approaches in studying phonon transport across interfaces, mainly including molecular dynamics simulation (Schelling et al., 2002; Landry and McGaughey, 2009; Sun and Murthy, 2010; Liang et al., 2014), atomistic Green's function method (Li and Yang, 2012; Tian et al., 2012), phonon Boltzmann equation modeling (Majumdar, 1993; Chen, 1998; Murthy and Mathur, 2002; Jeng et al., 2008; Huang et al., 2009; Péraud and Hadjiconstantinou, 2011; Singh et al., 2011; Hua and Minnich, 2014; Hori et al., 2015; Guo and Wang, 2016; Yang and Minnich, 2017), and experimental measurements (Norris and Hopkins, 2009; Minnich et al., 2011; Hua et al., 2017). The molecular dynamics simulation and atomistic Green's function method are usually suitable for relatively small and simple structures due to their large consumption of computational resources. The experimental measurement is very difficult because of many uncertain factors from interfacial roughness, disorder, dislocations, etc. In contrast, the phonon Boltzmann equation modeling provides a more robust and feasible avenue with a clear physical picture of phonon scattering at the interface. Two categories of numerical schemes are available to solve the phonon Boltzmann equation: (i) the deterministic method [discrete-ordinates method (Majumdar, 1993; Chen, 1998), finite volume method (Murthy and Mathur, 2002), lattice Boltzmann method (Guo and Wang, 2016), etc.], (ii) the stochastic method (Monte Carlo scheme; Jeng et al., 2008; Huang et al., 2009; Péraud and Hadjiconstantinou, 2011; Hua and Minnich, 2014; Hori et al., 2015; Yang and Minnich, 2017). In comparison to the deterministic methods, Monte Carlo scheme is a better choice to simulate phonon transport within complex geometries due to its simple and intuitive boundary and interface treatment.
Hitherto, there are mainly two classical models for phonon transmission coefficient in interfacial modeling based on phonon Boltzmann equation, including the acoustic mismatch model (AMM) (Little, 1959) and the diffuse mismatch model (DMM) (Swartz and Pohl, 1989). The phonon transmission coefficient is the crucial parameter in determining the thermal boundary conductance, which is defined as the heat flux across the interface over the interfacial temperature jump (Swartz and Pohl, 1989). The AMM assumes that the phonon completely specularly transmits or reflects as acoustic waves at the interface. It works well in low temperature situation while much underestimates the thermal boundary conductance at elevated temperature due to stronger Rayleigh scattering (Majumdar, 1989; Swartz and Pohl, 1989). The DMM assumes that the phonon experiences completely diffuse scattering at the interface. Previous studies have shown that the DMM is appreciably valid around room temperature for rough and disordered interface, which are common situations in realistic applications (Swartz and Pohl, 1989; Hopkins, 2013; Kakodkar and Feser, 2017). In recent years, both the experimental measurement and microscopic calculations have uncovered the strong frequency dependence of interfacial phonon transmission coefficient (Schelling et al., 2002; Li and Yang, 2012; Hua et al., 2017). The spectral diffuse mismatch model (SDMM) is a crude approximation yet still the most appropriate theoretical model available for describing the detailed phonon spectral feature (Duda et al., 2010; Monachon et al., 2016). The coherent and incoherent phonon scatterings have been shown to synthetically influence the heat transport in multilayer films (Simkin and Mahan, 2000; Chen et al., 2005; Luckyanova et al., 2012; Ravichandran et al., 2014; Cheaito et al., 2018). Minimum thermal conductivity has been found in superlattice at the crossover from coherent to incoherent phonon transport (Simkin and Mahan, 2000; Chen et al., 2005; Ravichandran et al., 2014). For relatively large layer thickness in the currently considered multilayer system around ordinary temperature, the phase information carried by phonons is usually lost by the diffuse scattering at the rough interface or boundary (Luckyanova et al., 2012; Ravichandran et al., 2014). Therefore, the coherent phonon scattering is negligibly weak and not taken into account in the present work.
Monte Carlo modeling of interfacial phonon transport has been widely considered in previous studies (Jeng et al., 2008; Huang et al., 2009; Péraud and Hadjiconstantinou, 2011; Hua and Minnich, 2014; Hori et al., 2015; Yang and Minnich, 2017), which yet consider either gray transmission coefficient between dissimilar materials or empirical spectral transmission coefficient between grain boundaries within single material. In the present study, we introduce the SDMM into the kinetic-type Monte Carlo scheme (Péraud and Hadjiconstantinou, 2012; Péraud et al., 2014) to study the interfacial phonon transport through Si/Ge multilayer film. The remainder of this article is organized below: the numerical and physical models are given in Section Numerical and Physical Models. The numerical method is validated in Section Validations by modeling cross-plane phonon transport through both single-layer and bi-layer thin films. The results and discussions for interfacial phonon transport through Si/Ge multilayer system are presented in section Results and Discussions. The concluding remarks are finally made in section Conclusions.
Numerical and Physical Models
Phonon Monte Carlo scheme is a statistical approach for solving the phonon Boltzmann equation with the counterpart direct simulation Monte Carlo (DSMC) in rarefied gas flow (Bird, 1978; Hadjiconstantinou, 2000; Wang and Li, 2003, 2004). An efficient Monte Carlo scheme is adopted to model phonon transport across the Si/Ge multilayer film in the present work, namely the kinetic-type Monte Carlo scheme (Péraud and Hadjiconstantinou, 2012; Péraud et al., 2014). This scheme solves the linearized version of the energy-based deviational phonon Boltzmann equation under small temperature difference assumption (Péraud and Hadjiconstantinou, 2011, 2012; Péraud et al., 2014):
where is the deviational energy distribution, with the phonon energy distribution e and equilibrium energy distribution at the referenced equilibrium temperatureTeq, f0 denoting the Planck distribution; vg and τ represent the phonon group velocity and relaxation time at the phonon angular frequency ω and local equilibrium temperature T for the phonon polarization p; denotes the pseudo-equilibrium energy distribution at the local pseudo-equilibrium temperatureTloc.
The kinetic Monte Carlo scheme tracks energy packets one by one, which is much different from the traditional ensemble Monte Carlo scheme tracking all the energy packets. This scheme starts with the initialization of phonon properties (frequency, polarization, group velocity, sign, initial position, and initial time) for all the energy packets used for computation. Each energy packet will be tracked until it encounters with the isothermal boundary or the simulation time approaches to the end, during which advection and scattering occur sequentially. Two kinds of scattering events are considered: the Umklapp scattering and interface scattering. The desired macroscopic statistical information (temperature, heat flux) is finally obtained by averaging over these computational energy packets at a certain time.
The SDMM is applied to treat the interface phonon scattering neglecting inelastic scattering and polarization conversion. The frequency-dependent phonon transmission coefficient from side 1 to side 2 is dependent on the wave number as Duda et al. (2010):
where 1 and 2 denote the labels of two dissimilar materials. The frequency-dependent phonon transmission coefficient from side 2 to side 1 is derived based on the principle of detailed balance as Duda et al. (2010):
The present spectral DMM is slightly different from the typical frequency-dependent DMM model adopted in Singh et al. (2011), which considers the polarization conversion shown to be weak elsewhere (Duda et al., 2010). The transmitted or reflected phonons keep only the frequency and polarization but change other properties following the dispersion of material at the new side. The SDMM assumes that phonons diffusely transmit or reflect when scattering with the interface (Aksamija, 2017). Thus, the direction of group velocity of the transmitted or reflected phonon is specified based on the Lambert's cosine law (Aksamija, 2017). By tracking the energy packets one by one, we can determine which scattering time is the shortest along the trajectory of the present energy packet. If the interface scattering takes place first, then one random number is generated and compared with the interfacial phonon transmission coefficient to determine its transmission or reflection. In comparison to the Monte Carlo scheme as a kind of particle method, the deterministic numerical method (such as discrete-ordinate method) is often inconvenient in treating complex interface due to its non-trivial spatial and angular discretization near the interface.
The one-dimensional cross-plane interfacial phonon transport across a four-layer thin film made of Si and Ge is modeled, as is shown in Figure 1. The thickness of each layer is the same and denoted as L0. The left side and the right side of the whole system are kept in contact with isothermal hot source and cold source, respectively. The dispersion relation and relaxation time expressions of Si and Ge are taken from Hopkins et al. (2011) and Singh et al. (2011), respectively. We do not consider the optical phonons due to their negligible contribution to heat transport at steady state.
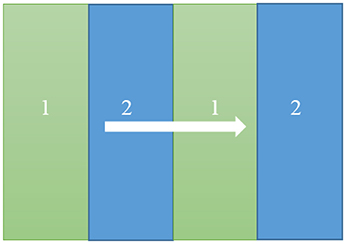
Figure 1. Schematic of cross-plane interfacial phonon transport through a four-layer thin film, 1 and 2 denote two dissimilar materials as 1(Si) and 2(Ge) or 1(Ge) and 2(Si), respectively.
Validations
In this section, the numerical scheme in section Numerical and Physical Models is validated by modeling the cross-plane phonon transport through single-layer thin film made of Si or Ge and cross-plane interfacial phonon transport across Ge/Si bi-layer thin film as shown in Figure 2. The benchmark is not easy and direct mainly due to the following two reasons: (a) multiple uncertain factors (such as interfacial roughness, disorder and dislocations, etc., Hopkins, 2013) in realistic interface system make a direct comparison to experimental results almost impossible; (b) the analytical expression of thermal boundary conductance (known as the Landauer formalism; Chen, 2005) is derived based on the difference of emitted phonon temperature at the interface (Simons, 1974; Chen, 1998), which is difficult to specify in Monte Carlo scheme. Therefore, a DOM scheme incorporating the SDMM is developed and validated through predicting the Landauer's thermal boundary conductance attributed to its capability to calculate the emitted phonon temperature. Then the numerical results of cross-plane temperature distributions and effective thermal conductivity or thermal boundary conductance by the DOM scheme are used as benchmarks for the present Monte Carlo scheme.
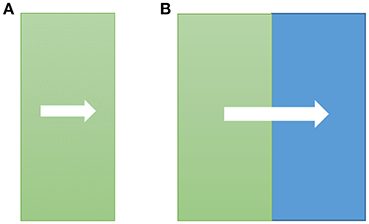
Figure 2. Schematic of cross-plane phonon transport across the single-layer thin film and cross-plane interfacial phonon transport across the bi-layer thin film: (A) the single-layer thin film made of Si and Ge separately; (B) the bi-layer thin film made of Ge/Si.
Cross-plane phonon transport across the single-layer thin film is firstly considered. Initially, the thin film maintains a uniform temperature as 299 K, then the temperatures of the left side (Tl) and right side (Tr) change to 301 and 299 K, respectively. Subsequently, the system evolves till it reaches the steady state. At steady state, the temperature at a spatial unit cell is computed by:
where si denotes the sign of tracked energy packet, being the effective deviational energy of an energy packet, CV the volumetric heat capacity, and V is the volume of unit cell. The effective cross-plane thermal conductivity is calculated by λeff = qaveL/(Tl – Tr), where qave is the average value of heat flux along the system at steady state, and L the thickness of this thin film. To better illustrate the relation between the effective thermal conductivity and film thickness, an average Knudsen number is defined as Péraud and Hadjiconstantinou (2016):
where the average MFP is defined as: with the density of phonon states D. The non-dimensional temperature distributions and effective thermal conductivity for both Si and Ge thin films obtained by the present Monte Carlo scheme are compared with those by the DOM scheme in Figure 3, where a pretty good agreement is achieved.
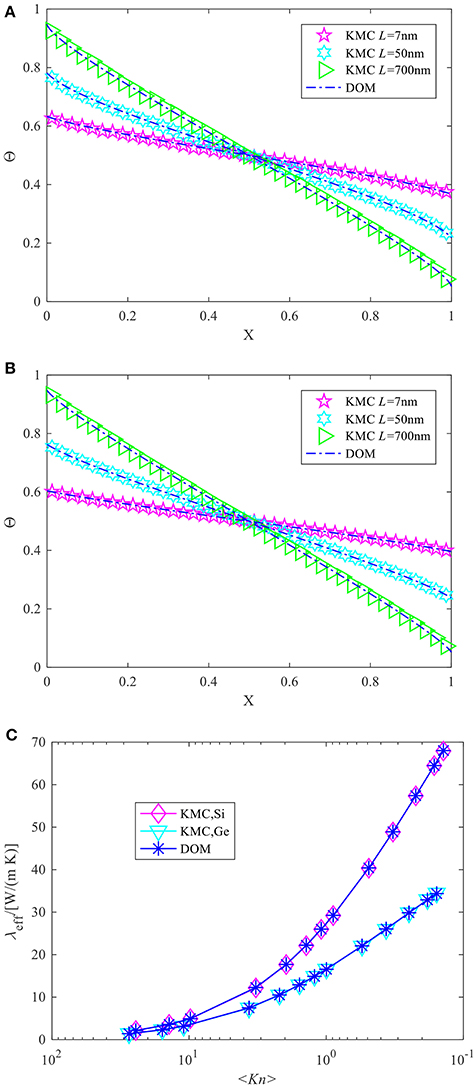
Figure 3. The non-dimensional temperature distributions and the effective thermal conductivity of cross-plane phonon transport through Si and Ge single-layer thin films: (A,B) are non-dimensional temperature distributions for Si and Ge, including three cases with a thickness 7, 50, and 700 nm, respectively. Symbols are the results calculated by Monte Carlo scheme and chain lines are those derived by DOM scheme; (C) is the effective thermal conductivity for Si and Ge thin films at different average Knudsen numbers.
The cross-plane interfacial phonon transport through the Ge/Si bi-layer thin film around room temperature is then considered. The volume ratio of the two materials keeps one for various total film thicknesses. After a period of evolutions to steady state, the temperature distributions and thermal boundary conductances are then calculated. The thermal boundary conductance is computed based on G = qave/ΔT, where ΔT is the equivalent equilibrium temperature jump across the interface. The comparison of the results calculated by Monte Carlo scheme and the DOM scheme is made in Figure 4, which shows a good agreement between each other. When the total thickness of thin film decreases, a stronger non-equilibrium effect at the interface gives rise to a larger temperature jump across the interface.
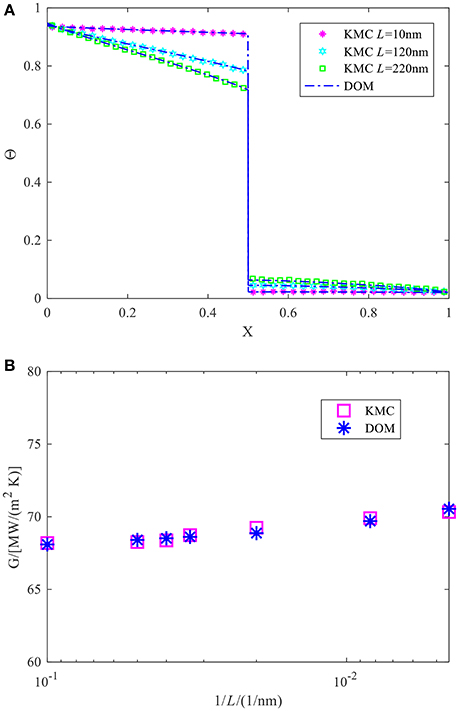
Figure 4. The non-dimensional temperature distributions and thermal boundary conductances in cross-plane interfacial phonon transport across Ge/Si bi-layer thin film: (A) the non-dimensional temperature distributions for three cases with a total thickness 10, 120, and 220 nm, respectively. Symbols are the results from the present Monte Carlo simulation whereas chain lines are that from the DOM scheme; (B) thermal boundary conductances vs. the inverse of total thicknesses.
Results and Discussions
After the present Monte Carlo scheme is validated, it is applied to study the phonon transport through a four-layer thin film as shown in Figure 1. The thickness L0 of each layer is varied from 5 to 70 nm. The multilayer film system is simulated between Tl = 301 K and Tr = 299 K, whereas the initial uniform temperature is 299 K and the referenced temperature is Teq = 300 K. After a sequence of evolutions, the system will reach the steady state. For 1(Si) and 2(Ge) collocation, we take the total evolving time tmax as 20 ns for 5–40 nm cases, 80 ns for 50 and 60 nm cases, and 120 ns for 70 nm case. The time intervals used for counting macroscopic information are 4 ps for the former two total evolving times and 6 ps for the latter one total evolving time. The total numbers of tracked energy packets are 500 million for 5–40 nm cases and 900 million for 50, 60, 70 nm cases. For 1(Ge) and 2(Si) collocation, the total evolving times tmax are set as 12 ns for 5–40 nm cases, and other numerical parameters are the same as those for 1(Si) and 2(Ge) collocation. Because of the fluctuations in kinetic Monte Carlo simulation, we average all the computational results from the last 30 time intervals when evaluating both the temperature and heat flux distributions.
The effective cross-plane thermal conductivity of the four-layer thin films is calculated from the uniform heat flux distribution at steady state and the exerted temperature difference based on Fourier's law: λeff = 4qaveL0/(Tl − Tr), which is given in Figure 5. The effective thermal conductivity decreases almost linearly with decreasing thickness of each layer, which is consistent with the trend shown by Chen (1998) based on a gray interface transmission coefficient in superlattice. This result shows that the linear length dependence of the effective thermal conductivity of multilayer film may be not much influenced by the phonon dispersion in the incoherent phonon transport regime. On the other hand, the thermal rectification has not been obtained when reversing the Si/Ge sequence, which may be due to a small temperature difference within the whole system.
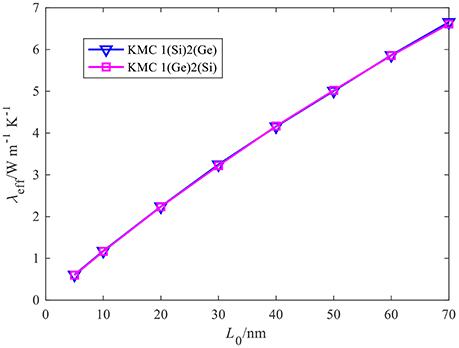
Figure 5. The effective thermal conductivity at different thicknesses for one layer of the multilayer film system. The line with down triangle is for 1(Si) and 2(Ge) collocation whereas the line with square is for 1(Ge) and 2(Si) collocation.
Then the thermal boundary conductances are computed through calculating the average heat flux and the temperature jump at the interfaces. The temperature jump is extracted by fitting the temperature distributions within the four-layer system at steady state, as illustrated in Figure 6. The results of thermal boundary conductance are given in Figure 7. Four indications are, thus, inferred: (i) the thermal boundary conductances of the interfaces that have the same relative position in the two-material collocations are almost identical. For 1(Si) and 2(Ge) collocation, its first, second, and third interfaces have nearly the same thermal boundary conductances as those of the third, second, and first interfaces of 1(Ge) and 2(Si) collocation; (ii) for a fixed thickness of one layer in multilayer film system, the thermal boundary conductances at different interfaces are different, which is similar to the conclusion in a very recent study (Gordiz and Henry, 2017); (iii) for 1(Si) and 2(Ge) system, the thermal boundary conductance of the first interface almost keeps a constant, whereas that of its second and third interfaces decrease as the thickness of each layer increases. For the other collocation, the trend is similar. In comparison, the thermal boundary conductance between material pairs within bi-layer thin film or periodic superlattice increases with increasing thickness of each layer (Balasubramanian and Puri, 2011; Jones et al., 2013). This difference is mainly attributed to different boundary or interface conditions in different interfacial structures, which directly influence the phonon scattering at boundary or interface, which will be elucidated in detail later; (iv) the decreasing slope of thermal boundary conductance at increasing thickness is different. For 1(Si) and 2(Ge) system, the decreasing rate of thermal boundary conductance at the second interface is faster than that at the third interface. For the other collocation, the trend is similar.
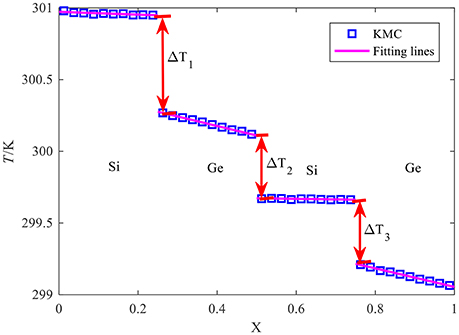
Figure 6. The temperature distribution of four-layer thin film with 1(Si) and 2(Ge) collocation and L0 equal to 70 nm: blue squares are results for the present Monte Carlo simulation and magenta lines are fitting lines for results of Monte Carlo simulation. The non-dimensional position coordinates for the three interface temperature jumps are as 0.25, 0.5, and 0.75, respectively.
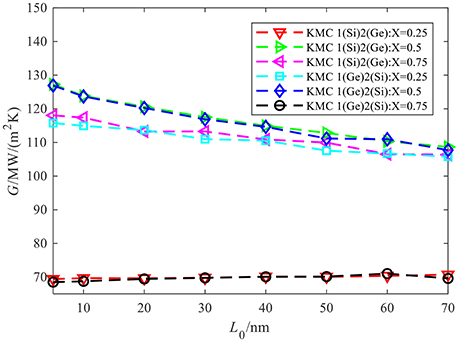
Figure 7. The thermal boundary conductance of three interfaces for different material collocations vs. the thickness of one layer of the multilayer system: the red dash line with the down triangle is the result of non-dimensional position coordinates X at 0.25 for 1(Si) and 2(Ge) collocation; the green dash line with the right triangle is the result of non-dimensional position coordinates X at 0.5 for 1(Si) and 2(Ge) collocation; the magenta dash line with the left triangle is the result of non-dimensional position coordinates X at 0.75 for 1(Si) and 2(Ge) collocation; the blue-green dash line with the square is the result of non-dimensional position coordinates X at 0.25 for 1(Ge) and 2(Si) collocation; the blue dash line with the diamond is the result of non-dimensional position coordinates X at 0.5 for 1(Ge) and 2(Si) collocation; the black dash line with the circle is the result of non-dimensional position coordinates X at 0.75 for 1(Ge) and 2(Si) collocation.
The indication (i) can be naturally understood. We will interpret the other three indications in terms of the material collocation 1(Si) and 2(Ge) as illustrated in Figure 8. For the given materials and interface, the thermal boundary conductance is dependent on the local non-equilibrium effect at the interface. Stronger local non-equilibrium at the interface results in a smaller thermal boundary conductance. Firstly, we provide a paradigm to interpret the size effect on thermal boundary conductance in bi-layer thin film in Figure 4B. An increase of the total thickness of bi-layer thin film is amounted to extend the boundaries with the same materials as the original film layer for each side. The contacted face between the added materials and the original film layer can be treated as two imaginary interfaces, where phonons can completely transmit without any change of properties. This will enhance the phonon–phonon interaction within the film layer and decrease the extent of non-equilibrium therein. Therefore, the local non-equilibrium effect at the interface will be reduced and the thermal boundary conductance will increase correspondingly. The indication (ii) can be explained based on a similar physical picture. The transmissivity of phonons between Si and Ge for both LA and TA polarizations based on SDMM is illustrated in Figure 9, which shows that the probability of phonons transmitting from Si to Ge is much larger than that in the reverse direction. For the first interface, the local non-equilibrium effect will be alleviated the least when adding the Si to Ge film layer at right side; the alleviation is improved at the third interface with the added Ge to Si film layer at the left side; the largest alleviation is achieved at the second interface where the left side and right side are added by Si and Ge, respectively. Therefore, the thermal boundary conductances of the first, third, and second interfaces increase in turn, as seen in Figure 7.
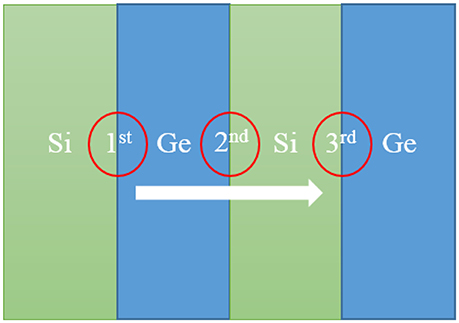
Figure 8. Schematic of the four-layer system with material collocation 1(Si) and 2(Ge): the three interfaces from left to right are denoted as 1st, 2nd, and 3rd interface, respectively.
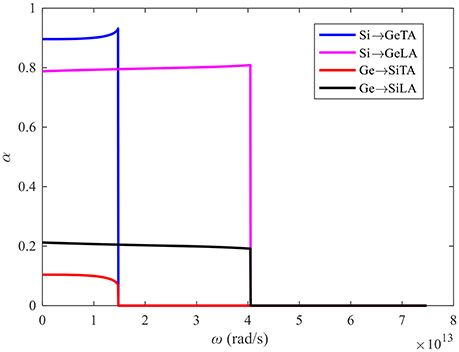
Figure 9. The spectral transmissivity of phonon through the interface from Si to Ge or from Ge to Si for transverse acoustic (TA) polarization and longitudinal (LA) polarization, respectively.
Finally, the indications (iii) and (iv) are explained as below. The thermal boundary conductance, G = qave/ΔT, is determined by both the temperature jump at the interface and average heat flux across system at steady state. In principle, the average heat flux will increase at decreasing system size under the given temperature difference in the present study. In contrast, the change of interface temperature jump is elusive because it is influenced by both the local non-equilibrium effect and the constraint effect from other interfaces. As the system size decreases, stronger local non-equilibrium effect tends to strengthen the interface temperature jump. However, the constraints from other interfaces will weaken the temperature jump, since the total temperature drop across the multilayer system is fixed. In other words, when the temperature jump at a specific interface is enhanced, the jump value at other interfaces will be reduced. Therefore, this kind of constraint effect from other interfaces is proportional to the local non-equilibrium effect therein. As a result, when the system size decreases, the increase of temperature jump at the second interface is the smallest one due to both its least local non-equilibrium effect and largest constraint from the two nearby interfaces. Followed will be the third interface and first interface, respectively, as the local non-equilibrium effect at the former is smaller than that at the latter, whereas nearly the same constraint is seen from the second interface. The quantitative increasing rate of the heat flux and the interface temperature jump and their ratios with decreasing thickness are given in Figure 10. The non-dimensional heat flux and interface temperature jump are defined as Q = qave/qave, 0 and Θ = ΔT/(ΔT)0, where qave, 0 and (ΔT)0 are heat flux and temperature jump for L0 = 5 nm case. For the second and third interfaces, the increasing rate of interface temperature jump is smaller than the increasing rate of heat flux at decreasing L0. Therefore, the thermal boundary conductance will even increase at a smaller system size. For the first interface, both increasing rates are nearly the same, which results in a nearly constant thermal boundary conductance at different system sizes. This provides exactly an explanation of the indication (iii), whereas the indication (iv) can be also deduced from the preceding analysis of the relative magnitude of temperature jump increase at each interface.
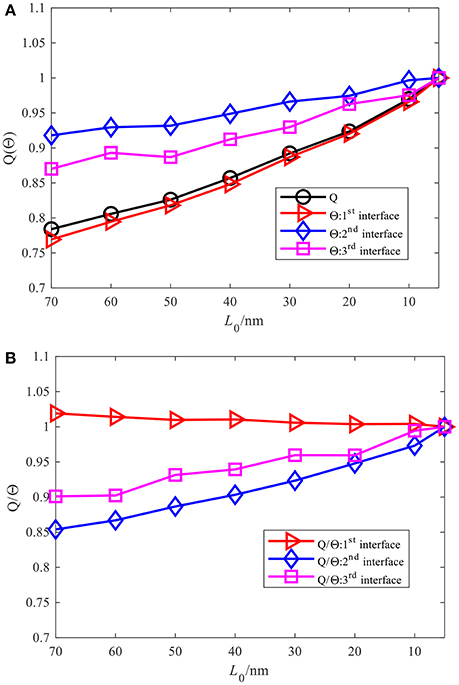
Figure 10. The non-dimensional heat flux and non-dimensional temperature jump at the interfaces and their ratios vs. thickness of one layer: (A) the non-dimensional heat flux and non-dimensional temperature jump of the 1st, 2nd, and 3rd interface vs. thickness of one layer, with Q = qave/qave, 0 and Θ = ΔT/(ΔT)0, where qave, 0 and (ΔT)0 are heat flux and temperature jump for L0 = 5 nm case. (B) The ratios of the non-dimensional heat flux and non-dimensional temperature jump vs. thickness of one layer.
Conclusions
In summary, the interfacial phonon transport through Si/Ge four-layer thin film is studied using an efficient Monte Carlo scheme with spectral transmissivity. The following points are concluded: (1) different thermal boundary conductances between the same material pair are obtained at different interfaces within the multilayer system; (2) the variation trends of the thermal boundary conductance vs. the film thickness are different at different interfaces, with the variation slope different as well. These unusual behaviors are explained by the comprehensive influence of both local non-equilibrium effect and constraint effect from other interfaces. The present work will promote the understanding of mechanism in interfacial phonon transport and the optimization of the design of interface structure.
Author Contributions
MW organized the research. XR did the MC simulations. YG modified the theoretical model. ZH participated discussions on mechanisms. XR and YG wrote the manuscript, and MW and ZH finalized it.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work is financially supported by NSF of China (No. 91634107, 51621062).
References
Aksamija, Z. (2017). Nanophononics: Thermal Generation, Transport, and Conversion at the Nanoscale. Singapore: CRC Press.
Balasubramanian, G., and Puri, I. K. (2011). Heat conduction across a solid-solid interface: understanding nanoscale interfacial effects on thermal resistance. Appl. Phys. Lett. 99:013116. doi: 10.1063/1.3607477
Bird, G. (1978). Monte Carlo simulation of gas flows. Ann. Rev. Fluid Mech. 10, 11–31. doi: 10.1146/annurev.fl.10.010178.000303
Cheaito, R., Polanco, C. A., Addamane, S., Zhang, J., Ghosh, A. W., Balakrishnan, G., et al. (2018). Interplay between total thickness and period thickness in the phonon thermal conductivity of superlattices from the nanoscale to the microscale: coherent versus incoherent phonon transport. Phys. Rev. B. 97:085306. doi: 10.1103/PhysRevB.97.085306
Chen, G. (1998). Thermal conductivity and ballistic-phonon transport in the cross-plane direction of superlattices. Phys. Rev. B. 57:14958. doi: 10.1103/PhysRevB.57.14958
Chen, G. (2005). Nanoscale Energy Transport And Conversion: A Parallel Treatment Of Electrons, Molecules, Phonons, and Photons. New York, NY: Oxford University Press.
Chen, Y., Li, D., Lukes, J. R., Ni, Z., and Chen, M. (2005). Minimum superlattice thermal conductivity from molecular dynamics. Phys. Rev. B. 72:174302. doi: 10.1103/PhysRevB.72.174302
Dresselhaus, M. S., Chen, G., Tang, M. Y., Yang, R. G., Lee, H., Wang, D. Z., et al. (2007). New directions for low-dimensional thermoelectric materials. Adv. Mater. 19, 1043–1053. doi: 10.1002/adma.200600527
Duda, J. C., Hopkins, P. E., Smoyer, J. L., Bauer, M. L., English, T. S., Saltonstall, C. B., et al. (2010). On the assumption of detailed balance in prediction of diffusive transmission probability during interfacial transport. Nanoscale Microscale Thermophys. Eng. 14, 21–33. doi: 10.1080/15567260903530379
Gordiz, K., and Henry, A. (2017). Phonon transport at interfaces between different phases of silicon and germanium. J. Appl. Phys. 121:025102. doi: 10.1063/1.4973573
Guo, Y., and Wang, M. (2016). Lattice Boltzmann modeling of phonon transport. J. Comput. Phys. 315, 1–15. doi: 10.1016/j.jcp.2016.03.041
Hadjiconstantinou, N. G. (2000). Analysis of discretization in the direct simulation Monte Carlo. Phys. Fluids. 12, 2634–2638. doi: 10.1063/1.1289393
Hopkins, P. E. (2013). Thermal transport across solid interfaces with nanoscale imperfections: effects of roughness, disorder, dislocations, and bonding on thermal boundary conductance. ISRN Mech. Eng. 2013:682586. doi: 10.1155/2013/682586
Hopkins, P. E., Reinke, C. M., Su, M. F., Olsson, R. H., Shaner, E. A., Leseman, Z. C., et al. (2011). Reduction in the thermal conductivity of single crystalline silicon by phononic crystal patterning. Nano Lett. 11, 107–112. doi: 10.1021/nl102918q
Hori, T., Shiomi, J., and Dames, C. (2015). Effective phonon mean free path in polycrystalline nanostructures. Appl. Phys. Lett. 106:171901. doi: 10.1063/1.4918703
Hu, M., and Poulikakos, D. (2012). Si/Ge superlattice nanowires with ultralow thermal conductivity. Nano Lett. 12, 5487–5494. doi: 10.1021/nl301971k
Hua, C., Chen, X., Ravichandran, N. K., and Minnich, A. J. (2017). Experimental metrology to obtain thermal phonon transmission coefficients at solid interfaces. Phys. Rev. B. 95:205423. doi: 10.1103/PhysRevB.95.205423
Hua, C., and Minnich, A. J. (2014). Importance of frequency-dependent grain boundary scattering in nanocrystalline silicon and silicon–germanium thermoelectrics. Semicond. Sci. Tech. 29:124004. doi: 10.1088/0268-1242/29/12/124004
Huang, M. J., Tsai, T. C., Liu, L. C., Jeng, M. S., and Yang, C. C. (2009). A fast Monte-Carlo solver for phonon transport in nanostructured semiconductors. Comput. Model. Eng. Sci. 42, 107–130. doi: 10.3970/cmes.2009.042.107
Jeng, M.-S., Yang, R., Song, D., and Chen, G. (2008). Modeling the thermal conductivity and phonon transport in nanoparticle composites using monte carlo simulation. J. Heat Transfer 130:042410. doi: 10.1115/1.2818765
Jones, R. E., Duda, J. C., Zhou, X. W., Kimmer, C. J., and Hopkins, P. E. (2013). Investigation of size and electronic effects on Kapitza conductance with non-equilibrium molecular dynamics. Appl. Phys. Lett. 102:183119. doi: 10.1063/1.4804677
Joshi, G., Lee, H., Lan, Y., Wang, X., Zhu, G., Wang, D., et al. (2008). Enhanced thermoelectric figure-of-merit in nanostructured p-type silicon germanium bulk alloys. Nano Lett. 8, 4670–4674. doi: 10.1021/nl8026795
Kakodkar, R. R., and Feser, J. P. (2017). Probing the validity of the diffuse mismatch model for phonons using atomistic simulations. Phys. Rev. B 95:024102. doi: 10.1103/PhysRevB.95.125434
Kim, W., Zide, J., Gossard, A., Klenov, D., Stemmer, S., Shakouri, A., et al. (2006). Thermal conductivity reduction and thermoelectric figure of merit increase by embedding nanoparticles in crystalline semiconductors. Phys. Rev. Lett. 96:045901. doi: 10.1103/PhysRevLett.96.045901
Landry, E. S., and McGaughey, A. J. H. (2009). Thermal boundary resistance predictions from molecular dynamics simulations and theoretical calculations. Phys. Rev. B 80:165304. doi: 10.1103/PhysRevB.80.165304
Li, X., and Yang, R. (2012). Effect of lattice mismatch on phonon transmission and interface thermal conductance across dissimilar material interfaces. Phys. Rev. B 86:054305. doi: 10.1103/PhysRevB.86.054305
Liang, Z., Sasikumar, K., and Keblinski, P. (2014). Thermal transport across a substrate-thin-film interface: effects of film thickness and surface roughness. Phys. Rev. Lett. 113:065901. doi: 10.1103/PhysRevLett.113.065901
Little, W. (1959). The transport of heat between dissimilar solids at low temperatures. Can. J. Phys. 37, 334–349. doi: 10.1139/p59-037
Luckyanova, M. N., Garg, J., Esfarjani, K., Jandl, A., Bulsara, M. T., Schmidt, A. J., et al. (2012). Coherent phonon heat conduction in superlattices. Science 338, 936–939. doi: 10.1126/science.1225549
Majumdar, A. (1989). Effect of interfacial roughness on phonon radiative heat conduction. ASME. Trans. J. Heat Transfer 113, 797–805. doi: 10.1115/1.2911206
Majumdar, A. (1993). Microscale heat conduction in dielectric thin films. J. Heat Transfer 115, 7–16. doi: 10.1115/1.2910673
Majumdar, A. (2004). Thermoelectricity in semiconductor nanostructures. Science 303, 777–778. doi: 10.1126/science.1093164
Minnich, A. J., Johnson, J., Schmidt, A., Esfarjani, K., Dresselhaus, M., Nelson, K. A., et al. (2011). Thermal conductivity spectroscopy technique to measure phonon mean free paths. Phys. Rev. Lett. 107:095901. doi: 10.1103/PhysRevLett.107.095901
Monachon, C., Weber, L., and Dames, C. (2016). Thermal boundary conductance: a materials science perspective. Ann. Rev. Mater. Res. 46, 433–463. doi: 10.1146/annurev-matsci-070115-031719
Murthy, J. Y., and Mathur, S. R. (2002). Computation of sub-micron thermal transport using an unstructured finite volume method. J. Heat Transfer 124, 1176–1181. doi: 10.1115/1.1518495
Norris, P. M., and Hopkins, P. E. (2009). Examining interfacial diffuse phonon scattering through transient thermoreflectance measurements of thermal boundary conductance. J. Heat Transfer 131:043207. doi: 10.1115/1.3072928
Péraud, J.-P. M., and Hadjiconstantinou, N. G. (2011). Efficient simulation of multidimensional phonon transport using energy-based variance-reduced Monte Carlo formulations. Phys. Rev. B 84:205331. doi: 10.1103/PhysRevB.84.205331
Péraud, J.-P. M., and Hadjiconstantinou, N. G. (2012). An alternative approach to efficient simulation of micro/nanoscale phonon transport. Appl. Phys. Lett. 101:1.4757607. doi: 10.1063/1.4757607
Péraud, J.-P. M., and Hadjiconstantinou, N. G. (2016). Extending the range of validity of Fourier's law into the kinetic transport regime via asymptotic solution of the phonon Boltzmann transport equation. Phys. Rev. B. 93:045424. doi: 10.1103/PhysRevB.93.045424
Péraud, J.-P. M., Landon, C. D., and Hadjiconstantinou, N. G. (2014). Monte Carlo methods for solving the Boltzmann transport equation. Ann. Rev. Heat Transfer 17, 205–265. doi: 10.1615/AnnualRevHeatTransfer.2014007381
Ravichandran, J., Yadav, A. K., Cheaito, R., Rossen, P. B., Soukiassian, A., Suresha, S. J., et al. (2014). Crossover from incoherent to coherent phonon scattering in epitaxial oxide superlattices. Nat. Mater. 13, 168–172. doi: 10.1038/nmat3826
Schelling, P. K., Phillpot, S. R., and Keblinski, P. (2002). Phonon wave-packet dynamics at semiconductor interfaces by molecular-dynamics simulation. Appl. Phys. Lett. 80, 2484–2486. doi: 10.1063/1.1465106
Simkin, M., and Mahan, G. (2000). Minimum thermal conductivity of superlattices. Phys. Rev. Lett. 84, 927–930. doi: 10.1103/PhysRevLett.84.927
Simons, S. (1974). On the thermal contact resistance between insulators. J. Phys. C 7, 4048–4052. doi: 10.1088/0022-3719/7/22/009
Singh, D., Murthy, J. Y., and Fisher, T. S. (2011). Effect of phonon dispersion on thermal conduction across Si/Ge interfaces. J. Heat Transfer 133:122401. doi: 10.1115/1.4004429
Snyder, G. J., and Toberer, E. S. (2008). Complex thermoelectric materials. Nat. Mater. 7, 105–114. doi: 10.1038/nmat2090
Sun, L., and Murthy, J. Y. (2010). Molecular dynamics simulation of phonon scattering at silicon/germanium interfaces. J. Heat Transfer 132:102403. doi: 10.1115/1.4001912
Swartz, E. T., and Pohl, R. O. (1989). Thermal boundary resistance. Rev. Modern Phys. 61, 605–668. doi: 10.1103/RevModPhys.61.605
Tian, Z., Esfarjani, K., and Chen, G. (2012). Enhancing phonon transmission across a Si/Ge interface by atomic roughness: first-principles study with the Green's function method. Phys. Rev. B. 86:235304. doi: 10.1103/PhysRevB.86.235304
Wang, M., and Li, Z. (2003). Nonideal gas flow and heat transfer in micro- and nanochannels using the direct simulation Monte Carlo method. Phys. Rev. E. 68:046704. doi: 10.1103/PhysRevE.68.046704
Wang, M., and Li, Z. (2004). Simulations for gas flows in microgeometries using the direct simulation Monte Carlo method. Int. J. Heat Fluid Flow 25, 975–985. doi: 10.1016/j.ijheatfluidflow.2004.02.024
Wu, C. -W., and Wu, Y.-R. (2016). Optimization of thermoelectric properties for rough nano-ridge GaAs/AlAs superlattice structure. AIP Adv. 6:115201. doi: 10.1063/1.4967202
Keywords: interfacial phonon transport, Monte Carlo method, micro- and nanoscale heat transport, multilayer film, material pair
Citation: Ran X, Guo Y, Hu Z and Wang M (2018) Interfacial Phonon Transport Through Si/Ge Multilayer Film Using Monte Carlo Scheme With Spectral Transmissivity. Front. Energy Res. 6:28. doi: 10.3389/fenrg.2018.00028
Received: 22 January 2018; Accepted: 29 March 2018;
Published: 01 May 2018.
Edited by:
Nuo Yang, Huazhong University of Science and Technology, ChinaReviewed by:
Ming Hu, University of South Carolina, United StatesQing Hao, University of Arizona, United States
Jian Wang, Yangzhou University, China
Copyright © 2018 Ran, Guo, Hu and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Moran Wang, bW9yYWx3YW5nQGdtYWlsLmNvbQ==
 Xin Ran
Xin Ran Yangyu Guo
Yangyu Guo Zhiyu Hu2
Zhiyu Hu2 Moran Wang
Moran Wang