Heat and Mass Transport in Modeling Membrane Distillation Configurations: A Review

Introduction

As the demand for potable water soars across the globe due to increasing population, industrial booming, and extreme drought, there is a need to maximally explore novel desalination technologies to help augmenting the depleting available fresh water. Several membrane-based desalination technologies such as reverse osmosis (RO), forward osmosis (FO), nanofiltration (NF), and electrodialysis (ED), and thermal-based technologies such as multi-stage flash distillation (MSF), multi-effect distillation (MED), and vapor compression distillation (VCD) have been tested at the laboratory and pilot scales (Camacho et al., 2013). ED and RO are the common types of desalination technology that have widely attracted attention by the industry (Camacho et al., 2013; Ruiz-Aguirre et al., 2017). Membrane distillation (MD), a novel desalination process driven by the combination of membrane and thermal mechanisms has only until recently gained attention and only few pilot scale tests have provided insight into the challenges of scaling up the process (El-Bourawi et al., 2006; Khayet, 2011; Bouchrit et al., 2015; Al-Ghamdi, 2017).

Membrane distillation (MD) is a thermal-membrane enhanced separation process driven by a partial-vapor pressure difference due to a temperature gradient across a hydrophobic porous membrane (Ruiz-Aguirre et al., 2017; Sanmartino et al., 2017b). Generally, the heat and mass transport mechanisms in place and frame or column type MD module involve evaporation of liquid at the hot feed side of the membrane, diffusion of vapor through the membrane pores, and condensation of vapor at the permeate side of the membrane. The mechanisms of vapor recovery after diffusion to the permeate side of the membrane vary depending on the type of membrane distillation configurations (Qtaishata et al., 2008). The four main configurations that are commonly employed in the MD process are direct contact membrane distillation (DCMD), air gap membrane distillation (AGMD), sweeping gas membrane distillation (SGMD), and vacuum membrane distillation (VMD) (El-Bourawi et al., 2006; Khayet and Matsuura, 2011e). However, three additional configurations, which have been recently reported in few studies, are liquid or water gap membrane distillation (LGMD/WGMD), thermostatic sweeping gas membrane distillation (TSGMD) and vacuum-assisted air gap membrane distillation (VA-AGMD) (Khayet and Matsuura, 2011e; Khalifa, 2015). All these configurations are based on heat and mass transfer phenomena (Khayet, 2011). Most of the bench-scale work conducted to evaluate MD process has focused on DCMD configuration due to its simplicity in structure design and process operation (Eleiwi et al., 2016; Gustafson et al., 2016); however, for field or commercial applications, the focus has been on AGMD and VMD configurations (Gude et al., 2013; Lee et al., 2015; Cheng et al., 2016; Deshpande et al., 2017; Ruiz-Aguirre et al., 2017).

MD has been the subject of worldwide academic studies by many experimentalists and theoreticians; however, from the commercial standpoint, MD has gained only little acceptance and is yet to be fully implemented in the industry. The various potential areas of application for MD include desalination industry for pure water production from brackish groundwater, sea water, and produced water; food industry for processing milk, and juice concentration; biomedical and pharmaceutical industry for removal of pure water from blood and protein solutions; textile industry for dyes removal; chemical industry for acid concentration, and separation of alcohol and water mixtures; and more generally for the treatment of wastewater (Table 1) (El-Bourawi et al., 2006; Khayet, 2011). The ability of MD to treat hyper-saline solutions, operate at low temperatures using waste heat and renewable energy sources, and operate at low pressure as compared to other pressure-driven technology, has made it attractive to water experts across the globe as the potential future technology for desalination (Khayet, 2011; Manawi et al., 2014a).

TABLE 1

Table 1. Potential areas of application for MD configurations.

Temperature and concentration polarization effects have been identified as major challenges responsible for limiting MD flux decay (Shakaib et al., 2012; Ali et al., 2013; Alsaadi et al., 2014), which is the major metric for evaluating MD at the industrial level. Detailed modeling studies are required to help identify and simulate the magnitude of these effects on the MD process (Martinez-Diez and Vázquez-González, 1999). Additional barriers may include membrane and module design (Hitsov et al., 2015) as well as membrane pore wetting (Khayet, 2011; Shakaib et al., 2012; Ali et al., 2013; Qtaishat and Matsuura, 2015). For MD applications, Camacho et al. (2013) reported that hydrophobic membranes with low thermal conductivity, high porosity, low surface energy, adequate thickness, large pore size, and narrow pore size distribution will be preferred.

The principal objective of MD modeling is to predict permeate flux and its dependency on MD module configuration, membrane characteristic, and MD operating parameters (Khayet et al., 2004b; Camacho et al., 2013; Khalifa, 2015; Gustafson et al., 2016). Several MD mathematical models have been developed and reported, and in many of them the temperature and concentration polarization effects have been taken into consideration (Shakaib et al., 2012; Ali et al., 2013; Alsaadi et al., 2014; Manawi et al., 2014a). One of the major ways to reduce the effects of temperature and concentration polarization in the MD system is by making the temperature at the surface of the membrane in contact with the feed side to be almost equal to the temperature of the bulk feed solution. This can be possible by increasing the feed flow rate so as to establish suitable hydrodynamic conditions favored under turbulent flow regime (Essalhi and Khayet, 2014; Deshpande et al., 2017). The heat transfer concept adopted by MD models is usually based on correlations originally developed for heat transfer through non-porous and rigid heat exchangers (Hayer et al., 2015; Orfi et al., 2016; Swaminathan et al., 2016b). However, the applicability of empirical heat transfer correlations to the MD system must be verified, because there is a difference between the mechanism of heat transfer in MD system, which is coupled with mass transfer, and the mechanism of heat transfer in heat exchangers (El-Bourawi et al., 2006; Chung et al., 2014; Drioli et al., 2015). The mass transfer model commonly applied to MD is the dusty gas model, in which the transmembrane flux takes place via contributions from Knudsen or Molecular diffusion flow (Khayet et al., 2004b; Kim, 2013; Manawi et al., 2014a; Ogden and Trembly, 2017). Combinations between these types of flow have also been applied (Bui et al., 2010; Jensen et al., 2011; Imdakm and Matsuura, 2012). In all MD Models, transport of adsorbed molecules on membrane surfaces has been neglected under assumption that diffusion area of membrane matrix is small compared to membrane pore area (Lawson and Lloyd, 1997; Khayet and Matsuura, 2003; Koo et al., 2013; Prince et al., 2015; Ashoor et al., 2016).

For the successful implementation and full reliability of MD technology applications, building mathematical modeling knowledge for an in-depth understanding of the processes that take place in MD membrane and module is paramount (Hitsov et al., 2015, 2016, 2017b; Wu et al., 2016). If the operating processes are clearly understood and well modeled, MD technology will move from a potential to a real emerging desalination technology that can either be applied as a stand-alone process to treat saline water and wastewater from impaired sources, i.e., brackish groundwater, seawater and wastewater from food and pharmaceutical industries, and produced water, or it can be integrated into other established desalination technologies such as RO and ED processes (Camacho et al., 2013). To bridge existing knowledge gap, there is need for research to be conducted to investigate wide applicability of heat transfer empirical correlations to MD, particularly applied to AGMD, VMD and SGMD, as well as to the most recently proposed TSGMD, WGMD, and VA-AGMD configurations (El-Bourawi et al., 2006; Khayet and Matsuura, 2011e). Most MD modeling studies were achieved based on uniform membrane pore size and pore size distribution assumptions. Past MD review works have established similarities between results using these two assumptions, even though a better result was achieved when considering a uniform mean pore size assumption (Khayet et al., 2004b; Khayet, 2011). In conducting a modeling review for all the MD configurations, the present study exploits the homogeneity of these assumptions as well as the generally assumed uniform membrane pore size. In this study, further insight is provided on the effects of temperature and concentration polarization, heat, and mass transfer mechanisms on the MD configurations. Highlights on strength, research gaps, and possible future outlooks in MD modeling are also included in this review article.

MD Configurations

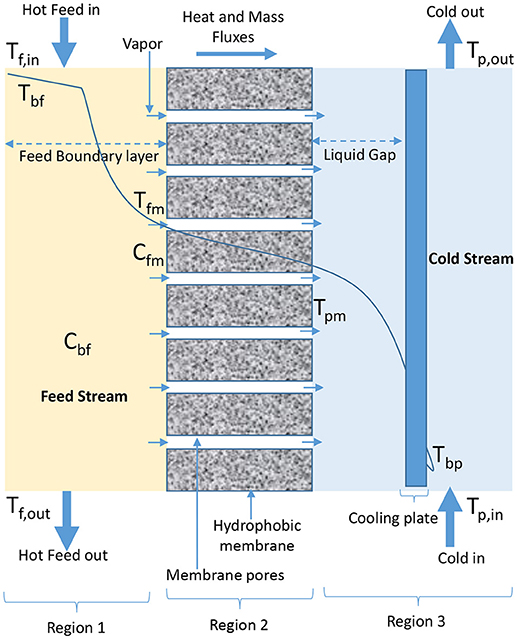
The configurations that have been developed in MD process are DCMD, VMD, AGMD, SGMD, LGMD, TSGMD, and VA-AGMD (Garcia-Payo et al., 2002; Rivier et al., 2002; Ugrozov et al., 2003; Ugrozov and Kataeva, 2004; Khayet and Matsuura, 2011e; Adham et al., 2013; Essalhi and Khayet, 2014; Prince et al., 2015; Ashoor et al., 2016; Deshpande et al., 2017; Liu Z. et al., 2017; Amaya-Vías et al., 2018). The schematic diagrams representing the heat and mass transfer for these configurations using plate and frame module and flat sheet membranes are presented in Figures 1–7. In DCMD process as shown in Figure 1, hot feed water is passed on feed side (Region 1) of a hydrophobic membrane (Region 2) while cold water flows on permeate side (Region 3) to directly condense vapor that passes through the membrane (Gude et al., 2013; Orfi et al., 2016; Swaminathan et al., 2016b; Wu et al., 2016). The transmembrane temperature in DCMD module induces a vapor pressure difference, which is the driving force for volatile molecules from hot water interface to cross the membrane and condense in the cold liquid interface (El-Bourawi et al., 2006; Chung et al., 2014). A typical DCMD is the most widely used in research applications because it is the simplest configuration capable of producing a reasonably high amount of permeate flux (Camacho et al., 2013), without the need of an external condenser (Ashoor et al., 2016). The major challenge associated with the application of DCMD is its low thermal energy efficiency (Manawi et al., 2014a), which is caused by the closeness of evaporator and condenser surfaces (Prince et al., 2015), leading to a high heat transfer coefficient on permeate side of the configuration, responsible for high heat conduction losses (Camacho et al., 2013). Despite its simple configuration, the performance of DCMD is better than VMD in terms of permeate production rate at lower temperatures (Koo et al., 2013). DCMD requires less heat energy when compared to AGMD (Camacho et al., 2013), and is less expensive than SGMD, considering external condenser and air blower cost associated with SGMD configuration (Khayet and Cojocaru, 2013).

FIGURE 1

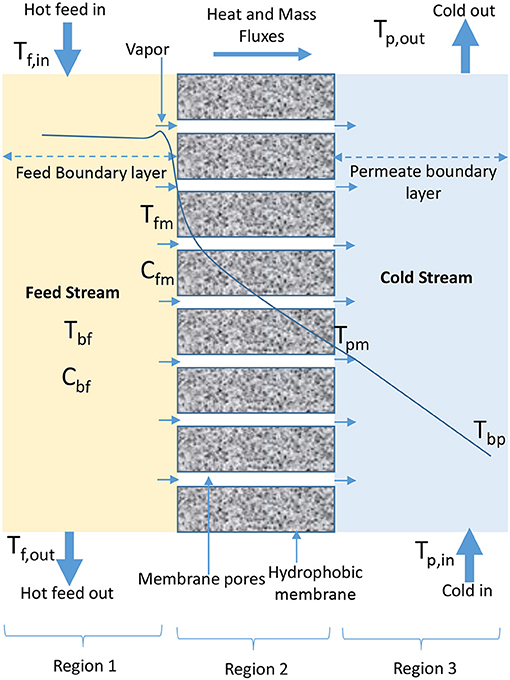
Figure 1. Heat and mass transfer in DCMD configuration (adapted from Khayet and Matsuura, 2011f).

VMD involves the application of vacuum to permeate side of membrane (El-Bourawi et al., 2006; Lee and Kim, 2013; Zhang et al., 2013; Boutikos et al., 2017; Naidu et al., 2017) to continuously remove vapor from vacuum chamber, which is formed due to vapor pressure difference across the membrane (Khayet and Matsuura, 2011b; Criscuoli et al., 2013). In VMD, condensation occurs in the condensation chamber outside MD module and the applied vacuum pressure is less than the saturation pressure of volatile molecules removed from feed side (Figure 2) (El-Bourawi et al., 2006; Ramon et al., 2009; Mericq et al., 2010). In a patented work presented by Prince et al. (2015) it is hypothesized that VMD provides the greatest driving force due to low pressure on permeate side of the membrane. The driving force is responsible for high-pressure difference across the membrane, which causes high permeate flux compared to diffusive vapor flux observed in SGMD and DCMD. A considerable high thermal efficiency is also possible due to negligible heat conduction (Koo et al., 2013). The major drawback of VMD is the complicated setup associated with vacuum and external condensers (Khayet and Matsuura, 2011b; Shao et al., 2014; Ashoor et al., 2016), and the possibility of having the applied vacuum creating high pressure variations on membrane surface, which could lead to wetting or reduction in hydrophobicity of membrane, responsible for reduced permeate quality (Liu J. et al., 2017; Liu Z. et al., 2017).

FIGURE 2

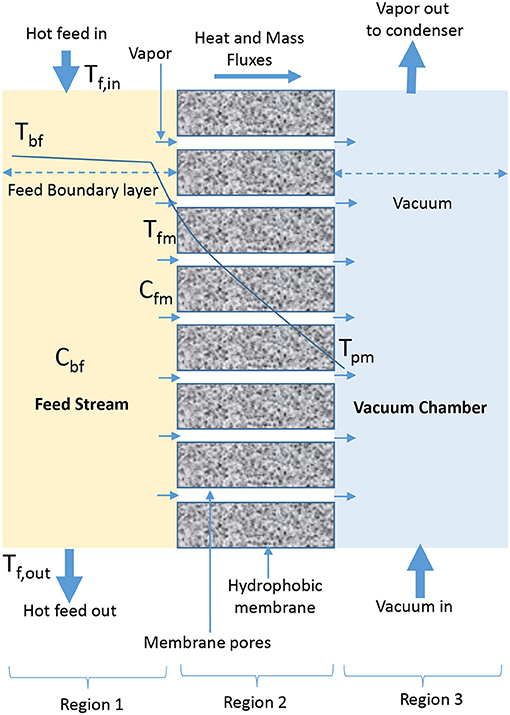
Figure 2. Heat and mass transfer in VMD configuration (adapted from Khayet and Matsuura, 2011b).

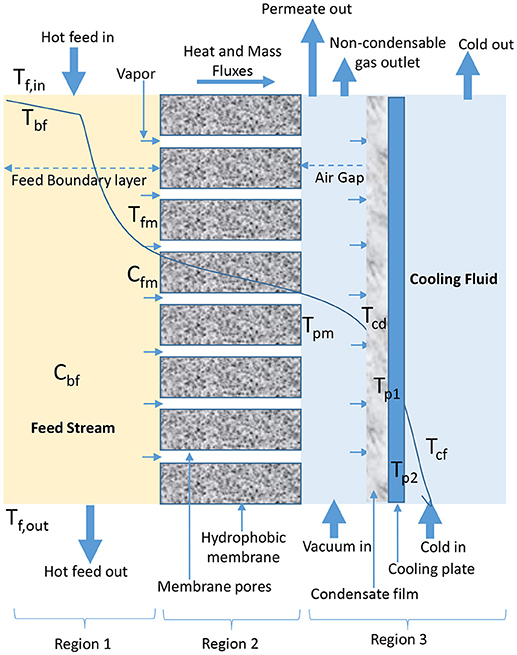
AGMD configuration involves the presence of stagnant air between cold side of membrane and condensation surface (Figure 3). Evaporated volatile molecules pass through both, membrane pores and air gap to condense over a cooling plate surface in permeate side of AGMD module (Khalifa et al., 2015; Ashoor et al., 2016; Alkhudhiri and Hilal, 2017; Janajreh et al., 2017). In AGMD, air gap is typically the controlling factor for mass and heat transfer (Khayet and Cojocaru, 2012a; Alsaadi et al., 2015; Alkhudhiri and Hilal, 2017; Attia et al., 2017), because it helps to reduce heat loss through conduction and improve heat efficiency (Khayet and Cojocaru, 2012a; Liu Z. et al., 2017). Therefore, AGMD is considered the most promising in terms of heat recovery when compared to other basic configurations (Liu Z. et al., 2017). However, according to Cheng et al. (2009) and Liu Z. et al. (2017), air gap and presence of entrapped air transported alongside water vapor which is non-condensable due to air gap pressure above saturation pressure in cold feed stream of AGMD configuration increase mass transfer resistance, which leads to permeate flux decay.

FIGURE 3

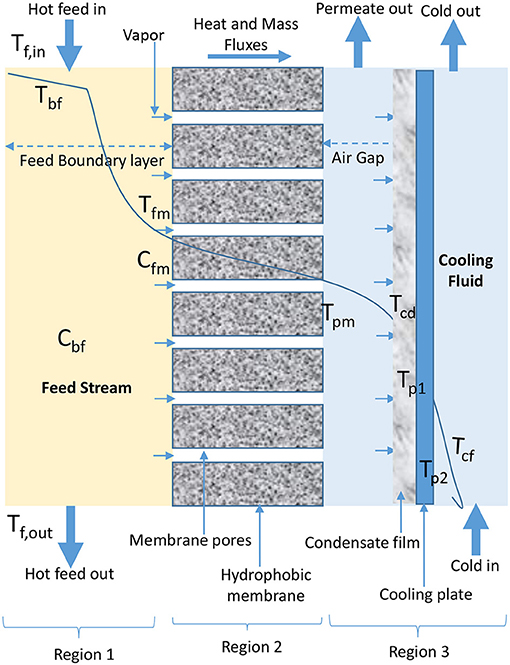
Figure 3. Heat and mass transfer in AGMD configuration (adapted from Khayet and Matsuura, 2011c).

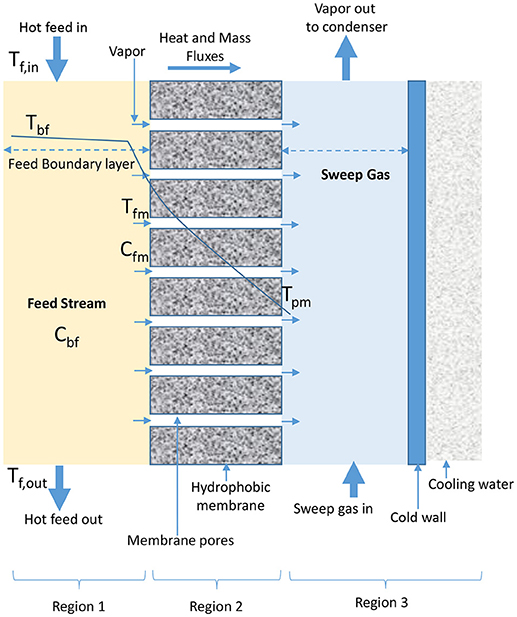
In SGMD, cold inert stream of gas sweeps water vapor from permeate side of membrane into condensation chamber located outside configuration module where condensation takes place (Figure 4) (Shukla et al., 2015; Duyen et al., 2016). SGMD produces higher permeate flux than AGMD due to reduced mass transfer resistance, and higher evaporation efficiency than DCMD due to the presence of low conductive heat loss (Prince et al., 2015; Ashoor et al., 2016). However, the application of SGMD is limited when compared to DCMD, because of high cost associated with the transport of sweeping gas, use of an external condenser, and difficulty in recovering heat associated with its configuration (El-Bourawi et al., 2006; Khayet et al., 2012; Khayet and Cojocaru, 2013; Shirazi et al., 2014).

FIGURE 4

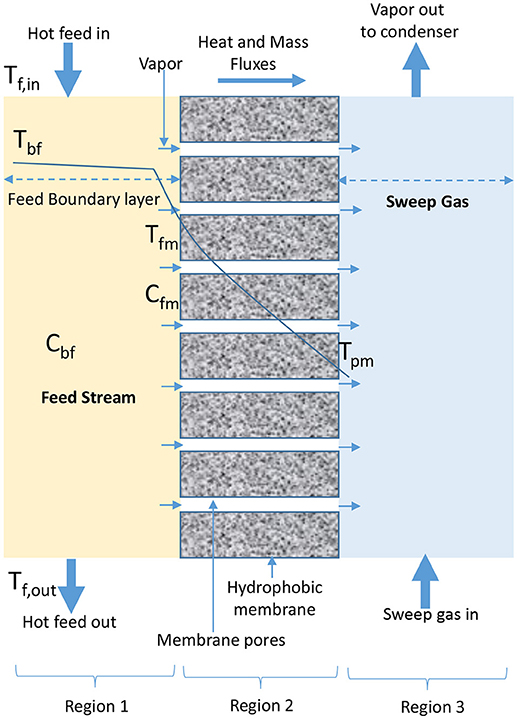
Figure 4. Heat and mass transfer in SGMD configuration (adapted from Khayet and Matsuura, 2011d).

Liquid or water gap membrane distillation (LGMD/WGMD), which emerged from the combinations of DCMD and AGMD configurations, was proposed by Ugrozov et al. (2003). Unlike AGMD where empty air gap exists between membrane and cooling plate, in LGMD as shown in Figure 5, the gap between membrane and condensing surface in permeate side of the module is filled with distilled water, which acts as stagnant cold liquid solution inside membrane module (Ugrozov and Kataeva, 2004; Amaya-Vías et al., 2018). Water vaporizes on feed side of membrane module, diffuses through membrane pores and condenses in the liquid gap between membrane and cooling plate on permeate side of membrane (Essalhi and Khayet, 2014; Amaya-Vías et al., 2018). A comparative study carried out between LGMD and AGMD by Essalhi and Khayet (2014), indicated that specific internal heat loss is lower for LGMD, whereas thermal efficiency is higher for AGMD. For both configurations, feed inlet temperature was observed to increase linearly with thermal efficiency. The overall heat transfer coefficient and the heat transfer on permeate side of the membrane were also found to be greater for LGMD than AGMD. The concentration polarization effect was slightly higher for LGMD due to its higher permeate flux, whereas the temperature polarization effect was found to be slightly higher for AGMD (Essalhi and Khayet, 2014).

FIGURE 5

Figure 5. Heat and mass transfer in LGMD configuration.

Thermostatic sweeping gas membrane distillation (TSGMD) combines the concepts of SGMD and AGMD (Rivier et al., 2002). In TSGMD, the driving force along module length is enhanced by including a cold wall to the system, and this reduces sweeping gas temperature (Rivier et al., 2002; Essalhi and Khayet, 2014). The sweeping gas that is introduced into the cold chamber is placed in contact with permeate and cold wall temperature, causing accumulation of condensable vapors and heat in the gas, which results in changes in temperature, concentration, and flux (Figure 6) (Garcia-Payo et al., 2002). Depending on the operating conditions, particularly feed temperature and feed flow rate, some portions of the vapor condense at cold side of module while bulk of the vapor is swept by sweeping gas out of the module to condense in an external condenser (Rivier et al., 2002). According to Garcia-Payo et al. (2002), TSGMD as an improved SGMD provides much higher permeate fluxes than AGMD while maintaining high temperature polarization coefficient and evaporation efficiency. TSGMD has some advantages over DCMD in terms of better selectivity performance, smaller temperature polarization and higher evaporation efficiency, although at a lower permeate flux (Garcia-Payo et al., 2002).

FIGURE 6

Figure 6. Heat and mass transfer in TSGMD configuration.

Vacuum assisted air gap membrane distillation (VA-AGMD) is a new type of MD configuration that combines AGMD and VMD to reduce air gap pressure that is primarily responsible for the reduction in permeate flux in AGMD configuration (Prince et al., 2015). As shown in Figure 7, in VA-AGMD, vacuum pressure is introduced to the air gap section to bring air gap pressure of cold feed stream below saturation pressure for removal of non-condensable gases (air) (Liu Z. et al., 2017). Studies conducted by Liu Z. et al. (2017), Alsaadi et al. (2015), and Asghari et al. (2015) have shown that permeate flux increases as a result of a decrease in air gap pressure, and this increases the removal rate of entrapped air that diffused with water vapor across hydrophobic membrane. It has been suggested that VA-AGMD is more efficient than basic MD configurations, such as AGMD, VMD, SGMD, and DCMD, in terms of high latent heat and water recovery rates (Prince et al., 2015; Liu Z. et al., 2017). However, the major disadvantage of VA-AGMD compared to DCMD and AGMD configurations may be the cost of providing vacuum pressure to air gap chamber.

FIGURE 7

Figure 7. Heat and mass transfer in VA-AGMD configuration.

Heat and Mass Transport in Modeling MD Configurations

Heat Transfer in MD

The mechanisms of transport in MD incorporates concurrently both heat and mass transfer (Qtaishata et al., 2008). Determination of the governing heat and mass transfer mechanisms is needed in order to be able to generate accurate and reliable predictions of interfacial membrane temperature and permeate flux from MD models (Hwang et al., 2011; Andrjesdóttir et al., 2013). The average temperature inside the membrane is calculated from the predicted interfacial membrane temperature. This average membrane temperature is used to determine vapor pressure at membrane interface, which is needed as input for estimating mass transfer in MD process (Hitsov et al., 2015). Thus, heat and mass transfer are interrelated in MD process. Generally, for all MD configurations, estimation of heat transfer is a prerequisite for prediction of mass transfer. In all MD configurations except VMD, heat is transferred through membrane via conduction in the form of sensible heat and latent heat when vapor molecules diffuse through the pores of hydrophobic membrane. In VMD heat transfer by conduction is negligible (Camacho et al., 2013; Hitsov et al., 2015; Ashoor et al., 2016). It is noteworthy that heat transfer does not only depend on the membrane geometry but also on type of MD configuration (Khayet, 2011).

Heat Transport Mechanisms in MD Configurations

The condition of heat transfer at permeate side of membrane module is the major difference among MD configurations (Zhang et al., 2013). Heat transfer is believed to be the rate-controlling step in MD process (El-Bourawi et al., 2006). It is noteworthy that bulk feed solution is in direct contact with the surface of hydrophobic membrane at the feed side in all MD configurations (Deshpande et al., 2017). There are three regions (feed side, membrane, and permeate side) through which heat is generally transferred in MD process (Qtaishata et al., 2008; Andrjesdóttir et al., 2013; Camacho et al., 2013; Gude et al., 2013; Bouchrit et al., 2015). In the first region, heat is transferred from bulk feed solution by convection through thermal boundary layer to the membrane surface on feed side of MD module (Qtaishata et al., 2008; Chen et al., 2009; Suárez et al., 2010; Bouchrit et al., 2015). The feed heat flux, Q_f, depends on feed heat transfer coefficient, h_f, temperature difference between bulk feed temperature, T_bf, and membrane surface temperature at feed side, T_fm, as illustrated in Equation (1). T_bf is the bulk feed temperature estimated from average temperatures of the solution that enters (T_{f, in}) and leaves (T_{f, out}) feed side of the module and is calculated using Equation (2). The expression in Equation (1) is applicable to all MD configurations.

$\begin{array}{ll}{Q}_f=h_f\left(T_{bf}-T_{fm}\right)& (1)\end{array}$

$\begin{array}{ll}{T}_{bf}=\frac{T_{f,in}-T_{f,out}}{2}& (2)\end{array}$

The second region consists of heat transfer through membrane (polymer) by conduction (sensible heat) and heat transfer due to water vapor transport through gas/air filled pores of the membrane (latent heat) (Khayet, 2011; Khayet and Matsuura, 2011e; Hitsov et al., 2015). These two forms of heat transfer mechanism across the membrane are expressed in Equation (3). Equation (3) is applicable to DCMD, AGMD, LGMD, SGMD, and TSGMD, with the exception of VMD. The presence of low vacuum pressure at permeate side of VMD module makes sensible heat loss by conduction through membrane negligible in the second region of this configuration (Khayet and Matsuura, 2011b; Zhang et al., 2013; Boutikos et al., 2017).

$\begin{array}{ll}{Q}_m=h_m\left(T_{fm}-T_{pm}\right)+J\Delta H_v& (3)\end{array}$

where Q_m, is the membrane heat flux, h_m is the membrane heat transfer coefficient, T_pm is the membrane surface temperature at permeate side, J is the permeate flux, and ΔH_v is the latent heat of vaporization. As expressed in Equation (4), membrane heat transfer coefficient (h_m) is calculated as the ratio of thermal conductivity of membrane (k_m) and membrane thickness (δ_m).

$\begin{array}{ll}{h}_m=\frac{k_m}{{\delta }_m}& (4)\end{array}$

In a complex mixture, thermal conductivity of membrane matrix, which comprised of the mixture of air, polymer, and vapor, may be difficult to estimate (Qtaishata et al., 2008; Andrjesdóttir et al., 2013; Hitsov et al., 2015). Generally, the two models given in Equations (5, 6), have been considered good predictors of thermal conductivity of membranes (Garcia-Payo et al., 2002; Hitsov et al., 2017b).

$\begin{array}{ll}{k}_m=\left(1-\epsilon \right)k_{mm}+\epsilon k_g& (5)\end{array}$

$\begin{array}{ll}{k}_m={\left[\frac{1-\epsilon }{k_{mm}}+\frac{\epsilon }{k_g}\right]}^{-1}& (6)\end{array}$

Where ε is the membrane porosity, and k_mm and k_g are thermal conductivities of membrane material (polymer) and gas in the pores of the membrane, respectively.

The thermal conductivity of gas (air) and water vapor in the pores of the membrane are considered similar and can be calculated as a function of membrane temperature using Equation (7). The average of thermal conductivity of gas in Equation (7) is obtained from gas thermal conductivity expressions reported by Eleiwi et al. (2016) and Bahmanyar et al. (2012). This expression is believed to give a better prediction of gas thermal conductivity.

$\begin{array}{ll}{k}_g=1.36\times 10^{-3}+3.885\text{ x }10^{-5}{T}_m+1.66\times 10^{-3}\sqrt{T_m}& (7)\end{array}$

The thermal conductivity for common hydrophobic membrane materials (polymer) as presented in Table 2, can be estimated at various temperatures using the linear fit expression of Equation (8) reported by Hitsov et al. (2015), based on data presented by Phattaranawika et al. (2003).

$\begin{array}{ll}{k}_{mm}=\alpha *10^{-4}{T}_m+\beta *10^{-2}& (8)\end{array}$

where α and β are constants derived from linear fit expressions for different membrane material and T_m is membrane temperature (K) derived from average membrane surface temperatures as given by Equation (9) (Qtaishata et al., 2008; Hitsov et al., 2015).

$\begin{array}{ll}{T}_m=\frac{T_{fm}+T_{pm}}{2}& (9)\end{array}$

TABLE 2

Table 2. Thermal conductivity of common hydrophobic commercial membrane materials at different membrane temperatures (T_m) [Adapted from Hitsov et al. (2015)].

In the third region, there is convective heat transfer from the membrane surface through thermal boundary layer to bulk permeate side, as described by Equation (10).

$\begin{array}{ll}{Q}_p=h_p\left(T_{bp}-T_{pm}\right)& (10)\end{array}$

However, AGMD has a different heat transfer mechanism in the third region due to the presence of an air gap between the surface of the membrane and the cooling plate at cold side of MD module. The heat transfer mechanism is also different for VMD at the third region due to the presence of vacuum. The temperature at membrane surface on permeate side is higher than the bulk permeate temperature in the AGMD module, due to the effect of temperature polarization in this region (El-Bourawi et al., 2006). Conversely, the temperature at membrane surface on permeate side is lower than bulk permeate temperature in the VMD module, due to application of vacuum in this side of membrane module (El-Bourawi et al., 2006; Khayet, 2011).

The permeate heat flux, Q_p, for all MD configuration, except AGMD and VMD, depends on permeate heat transfer coefficient, h_p, and temperature difference between bulk permeate temperature, T_bp, and interfacial membrane temperature, T_pm at the permeate side. T_bp is estimated from average temperature of cooling water that enters (T_{p, in}) and leaves (T_{p, out}) permeate side of the module using Equation (11) (Qtaishata et al., 2008; Khayet and Matsuura, 2011e).

$\begin{array}{ll}{T}_{bp}=\frac{T_{p,in}-T_{p,out}}{2}& (11)\end{array}$

The overall heat transfer flux around the membrane on feed and permeate sides of the module, under steady state conditions, for all MD configurations except AGMD and VMD in Equation (12) is derived from combining Equations (1, 3, 10).

$\begin{array}{ll}{h}_f\left(T_{bf}-T_{fm}\right)=h_m\left(T_{fm}-T_{pm}\right)+J\Delta H_v=h_p\left(T_{bp}-T_{pm}\right)& (12)\end{array}$

The energy balance expression in Equation (12) can be used to calculate membrane surface temperature on feed and permeate sides in the MD module, which otherwise cannot be measured experimentally. Equations (13, 14) are used to iteratively predict membrane surface temperature on feed and permeate sides, respectively (Qtaishata et al., 2008; Andrjesdóttir et al., 2013; Bouchrit et al., 2015; Hitsov et al., 2017b).

$\begin{array}{ll}{T}_{fm}=\frac{h_m\left(T_{bp}+\left(\frac{h_f}{h_p}\right)T_{bf}\right)+h_f{T}_{bf}-J\Delta H_v}{h_m\left(1+\frac{h_f}{h_p}\right)+h_f}& (13)\end{array}$

$\begin{array}{ll}{T}_{pm}=\frac{h_m\left(T_{bf}+\left(\frac{h_p}{h_f}\right)T_{bp}\right)+h_p{T}_{bp}+J\Delta H_v}{h_m\left(1+\frac{h_p}{h_f}\right)+h_p}& (14)\end{array}$

It is important to first make an initial guess by assuming that T_fm and T_pm are equal to bulk feed and permeate temperatures, which can be determined from Equations (2, 11), respectively. The predicted flux is used to continue the iteration until the difference between two consecutive iterations is <10⁻⁷ (Andrjesdóttir et al., 2013), or until a level of accuracy is achieved for membrane surface temperatures or fluxes (Hitsov et al., 2015). The membrane surface temperature for feed and permeate sides can be easily predicted for an experimental analysis by substituting the observed permeate flux into Equations (13, 14).

The heat transfer mechanisms for VMD in the second region are given in Table 3. The Equation (15) represents the heat transfer that occurs at the second region, which is the membrane surface in VMD configuration, while the overall heat transfer at steady state, and the surface membrane temperature are expressed by Equations (16, 17), respectively. There is no equation developed for VMD to represent the presence of vacuum in the third region (Figure 2). The heat transfer mechanism described in Equation (1) for the first region is also applicable to VMD.

TABLE 3

Table 3. Heat transfer mechanisms for VMD at the membrane.

The heat transfer mechanisms at the third region (cold side) of both AGMD and VA-AGMD are represented by Equations (18–23) (Table 4), as reported in recent studies (Khalifa et al., 2015; Pangarkar and Deshmukh, 2015; Swaminathan et al., 2016a; Attia et al., 2017; Hitsov et al., 2017a). The expressions from Equations (1–9) are also applicable to obtain heat transfer at the first and second regions of both AGMD and VA-AGMD.

TABLE 4

Table 4. Heat transfer mechanisms for AGMD.

In Equations18–23 for AGMD modeling, Q_ag, Q_cd, Q_cp, and Q_cf (W/m²) are heat fluxes through air gap, condensation film, cooling plate, and cooling fluid, respectively. As shown in Figure 3, T_cd, T_p1, T_p2, and T_cf are temperature of condensation film, surface temperature at condensation side of cooling plate, surface temperature at cold side of cooling plate, and temperature at the bulk cooling film, respectively. The heat transfer coefficient (W/m²C) of condensate and cooling fluid are h_cd and h_cf, respectively. The air gap thickness, thickness of cooling plate, and thermal conductivity of cooling plate are ∂ (m), ∂_c (m), and k_c (W/m K), respectively.

Many Nusselt number relationships for laminar and turbulent flows are used to calculate heat transfer coefficient, as have been reported in several studies (Khayet, 2011; Andrjesdóttir et al., 2013). However, based on experimental and predicted results by Andrjesdóttir et al. (2013), Equations (24, 25) may provide best predictions for heat transfer coefficients in the feed and permeate sides for laminar and turbulent flows, respectively.

$\begin{array}{ll}\text{N}{\text{u}}_{\text{f},\text{p}}=1.62{\left(R{e}_{\text{f},\text{p}}P{r}_{\text{f},\text{p}}\left(d_{\text{h}}/L\right)\right)}^{1/3}Re<2300& (24)\end{array}$

$\begin{array}{ll}\text{N}{\text{u}}_{\text{f},\text{p}}=0.023R{e}_{\text{f},\text{p}}^{4/5}P{r}_{\text{f},\text{p}}^{1/3},Re>2300& (25)\end{array}$

The heat transfer coefficients in the feed and permeate boundary layers can be estimated by using Nusselt number relationship obtained from combining Reynolds and Prandtl numbers (Equations 26, 27) (Andrjesdóttir et al., 2013; Bouchrit et al., 2015).

$\begin{array}{ll}R{e}_{f,p}=\frac{\rho v{d}_h}{\mu }& (26)\end{array}$

$\begin{array}{ll}P{r}_{f,p}=\frac{C_p\mu }{k_m}& (27)\end{array}$

Once Equations 24, 25 are substituted into Equations (26, 27) to obtain Nusselt number for feed and permeate streams, the heat transfer coefficients can then be calculated using Equations (28, 29) (Qtaishata et al., 2008; Khayet, 2011; Andrjesdóttir et al., 2013; Bouchrit et al., 2015).

$\begin{array}{ll}{h}_f=\frac{N{u}_f{k}_f}{d_h}& (28)\end{array}$

$\begin{array}{ll}{h}_p=\frac{N{u}_p{k}_p}{d_h}& (29)\end{array}$

where d_h, L, c_p, ν, ρ, μ, Nu_f, and Nu_p are the hydraulic diameter, length of membrane module, specific heat, velocity, density, viscosity, Nusselt number for feed stream, and Nusselt number for permeate stream, respectively.

Temperature Polarization in Modeling MD Configuration

An increase in the temperature of a MD system will cause more heat to flow from the higher to the lower temperature region, leading to high temperature difference (El-Bourawi et al., 2006). A decline in permeate flux results from the resistances imposed on heat transferred from bulk feed and bulk permeate, caused by the formation of thermal boundary layers on the feed and permeate sides of the MD module (Lin et al., 2014; Hitsov et al., 2015; Alkhudhiri and Hilal, 2017; Ruiz-Aguirre et al., 2017). The temperature polarization coefficient (TPC) is generally expressed as the ratio of the difference between membrane surface temperature at feed (T_fm) and permeate (T_pm) sides, and the difference between bulk feed (T_bf) and bulk permeate (T_bp) temperatures as given by Equation (30) (Qtaishata et al., 2008; Khayet, 2011; Shakaib et al., 2012; Alsaadi et al., 2014).

$\begin{array}{ll}TPC=\frac{T_{fm}-T_{pm}}{T_{bf}-T_{bp}}& (30)\end{array}$

As TPC decreases, its effect on the MD process increases (Abu-Zeid et al., 2015; Hitsov et al., 2015). Even though an increase in the feed temperature in the process leads to an increase in the permeate flux, TPC decreases as reported in the experimental work conducted by Bouchrit et al. (2015). The negative impact of temperature polarization on permeate flux in MD process has been a concern for MD researchers (Shakaib et al., 2012; Ali et al., 2013; Alsaadi et al., 2014). MD modeling has been used as a viable tool to predict membrane surface temperature of the feed and permeate sides, which otherwise cannot be determined experimentally (Khayet, 2011; Bouchrit et al., 2015; Hitsov et al., 2015), and further estimate the effect of temperature polarization.

Equation (30) is applicable to all MD configurations except VMD due to the existence of a vacuum on the permeate side of the membrane. Unlike DCMD and other MD configurations, temperature polarization takes place only at the feed side of VMD configuration (Alsaadi et al., 2014). The TPC expression reported by Abu-Zeid et al. (2015) and given by Equation (31) is valid for VMD and is defined as the ratio of surface membrane temperature on feed side to bulk temperature on feed side.

$\begin{array}{ll}TPC\left(VMD\right)=\frac{T_{fm}}{T_{bf}}& (31)\end{array}$

Effects of Temperature Polarization on MD Performance

As heat is transferred from bulk feed through boundary layer to membrane surface on the feed side, temperature polarization causes heat at the surface of the membrane to be lower than temperature in the bulk feed. The temperature polarization effect is very significant at the surface of the membrane when heat is lost by conduction through membrane polymer, and by convection through the gas-filled pores of the membrane (Shakaib et al., 2012). To prevent temperature polarization at membrane interfaces, membranes with high thermal conductivity, small tortuosity, and minimal pore size should be employed in all MD configurations (Khayet, 2011). A reduced temperature at membrane surface on the feed side caused by temperature polarization will bring low water vapor pressure across the membrane, resulting in a reduction of permeate flux (El-Bourawi et al., 2006). The effect of temperature polarization is responsible for the high temperature observed at the membrane surface of permeate side of MD module when compared to bulk permeate temperature (Essalhi and Khayet, 2014). To minimize the effect of temperature polarization in all the MD configurations, it is necessary to ensure good mixing conditions, and this will be possible if optimum flow rate conditions are applied (El-Bourawi et al., 2006; Essalhi and Khayet, 2014; Deshpande et al., 2017). Optimum flow rate should be considered at the start of the process. In all MD configurations, if flow rate adjustment is needed to reduce the effect of temperature polarization, caution must be taken to avoid high pressure drops, which may cause membrane pore wetting and reduction in the quality of permeate flux (El-Bourawi et al., 2006; Deshpande et al., 2017). In a computational fluid dynamics (CFD) study of MD modules conducted by Shakaib et al. (2012), the effect of spacer orientation, inlet velocity, and filament spacing on temperature polarization was investigated. Shakaib et al. (2012) reported that the main advantage of having spacers between module and membrane is that they disrupt concentration and thermal boundary layers, which helps in increasing the permeation rate. The CFD study established that when spacer filaments touch the top or bottom surfaces of the membrane, the temperature polarization is high, which results in low heat transfer rates, but when the filaments are detached from the membrane, the temperature polarization is lower. Improvement of the design of module for all MD configurations has also been established to minimize the effect of temperature polarization (Hitsov et al., 2015).

Mass Transfer in MD

Mass transfer of water vapor molecules through pores of hydrophobic membranes in MD process has been described by various MD models (Hitsov et al., 2015). The existing mass transfer models differ based on the configuration of pores of membrane. The most widely studied and applied model is the Dusty Gas (DG) model (Hitsov et al., 2017b), which employs the average pore size for the prediction of mass transfer of volatile water molecules, and assumes an average temperature across the membrane. The Fick's law model is another model based on the assumption that water vapor molecules diffuse through the pores of the membrane filled with air (Hitsov et al., 2015). The estimation of mass transfer of vapor under the assumption of pore size distribution has been proposed by Khayet (2011) and the Schofield and Dusty Gas models have been proposed for the estimation of mass transfer of vapor under uniform mean pore size assumption (Hitsov et al., 2015, 2017b). Even though, it is believed among MD experts that the membrane does not play a direct role in enhancing the mass transfer phenomena (Khayet and Matsuura, 2011e), the membrane material (polymer), membrane design, and method of membrane fabrication determine the membrane pore formation, which ultimately provides the medium for mass transfer (Khayet and Matsuura, 2011e). Khayet (2011) pointed out the knowledge gap that exist on the effect of membrane characteristics and MD configurations on the permeability of membrane. This gap can be filled by carrying out more investigations on mass transfer in MD configurations. Mass transfer modeling of MD configurations is paramount because the mechanisms of mass transfer can be different even when similar membranes are used. The effect of assuming pore size distribution in mass transfer modeling compared to uniform mean pore is considered insignificant (Phattaranawika et al., 2003; Khayet and Matsuura, 2011e; Hitsov et al., 2015); therefore, in this study, the Dusty Gas Model will be used to discuss mass transfer for all MD configurations.

Mass Transport Mechanisms in MD Configurations

The mass transport of water vapor molecules in MD process is diffusive and viscous in nature as expressed in Equation (32).

$\begin{array}{ll}J=J^v+J^d& (32)\end{array}$

where J, J^v and J^d are total flux, viscous flux, and diffusive flux, respectively. The total flux varies according to MD configuration employed.

The total mass flux in Equation (32) is generally defined according to Darcy's law as expressed in Equation (33). In this equation, it is considered that mass transport of water vapor through hydrophobic porous membrane is directly proportional to partial water vapor pressure across membrane Equation (33) (Drioli et al., 2005; Bouchrit et al., 2015).

$\begin{array}{ll}{\text{J}}^{\text{i}}=B_{\text{m}}^{\text{j}}\Delta P_{\text{v}}=B_{\text{m}}^{\text{j}}\left(P_{\text{fm}}-P_{\text{pm}}\right)& (33)\end{array}$

Where i, and j, B_m (Lm⁻² s ⁻¹ Pa⁻¹), P_fm (Pa) and P_pm (Pa) are the type of flux [diffusive (d) or viscous (v)], mass transfer coefficient, partial vapor pressure at the feed membrane surface, and partial vapor pressure at permeate membrane surface, respectively. It should be noted that, B_m is a function of MD configuration, membrane temperature, and membrane characteristics (Bouchrit et al., 2015).

Surface diffusion, molecular or ordinary diffusion, Knudsen diffusion, Knudsen-molecular diffusion, and viscous or Poiseuille flow are the mass transfer mechanisms employed to theoretically predict mass flux of vapor through a porous membrane in Dusty Gas (DG) Model. However, in MD modeling using DG model, the surface diffusion is negligible (Lawson and Lloyd, 1997; Khayet, 2011; Hitsov et al., 2015). The dominant mass transport mechanism across the pores of membrane is established from the ratio of mean free path (λ) of water vapor molecule (Equations 34, 35) to membrane pore diameter (d_p), known as the Knudsen number (Kn) (Khayet and Matsuura, 2011e; Andrjesdóttir et al., 2013; Attia et al., 2017; Hitsov et al., 2017b).

$\begin{array}{ll}Kn=\frac{\lambda }{d_p}& (34)\end{array}$

$\begin{array}{ll}\lambda =\frac{k_B{T}_m}{\sqrt{2}{P}_m{\sigma }_v^2}\hfill & (35)\end{array}$

where k_B is Boltzmann constant (1.38 × 10⁻²³ JK⁻¹), T_m is mean membrane temperature, P_m is average pressure in the membrane pores, and σ_v is the water vapor collision diameter (0.2641 nm) (El-Bourawi et al., 2006; Andrjesdóttir et al., 2013; Hitsov et al., 2015).

Based on Knudsen number, there are three common ways to determine the governing mass transfer mechanism in MD configurations (Khayet, 2011; Hitsov et al., 2015). Knudsen diffusion governs in the absence of air when water vapor molecules collide with walls of membrane pores, because mean free path for water molecules is greater than membrane pore diameter (λ > d_p or n > 1) (Andrjesdóttir et al., 2013). However, if air exists in the pores of the membrane and membrane pore diameter is larger than mean free path of the molecules of the diffusing water vapor (100 λ < d_p or n < 0.01), there will be collision between water vapor molecules as a result of molecular (ordinary) diffusion dominance (Khayet and Matsuura, 2011e). In the case where Knudsen molecular diffusion prevails in the transition region (λ < d_p < 100 λ or 0.01 < n < 1), collision occurs between water vapor molecules and also between walls of membrane pores and vapor molecules (Bouchrit et al., 2015). It is worth mentioning that, the estimation of mass transfer coefficient depends on the dominant mass transport mechanism (Phattaranawika et al., 2003; Khayet, 2011; Andrjesdóttir et al., 2013; Bouchrit et al., 2015; Hitsov et al., 2015).

The mechanism of mass transfer for DCMD, LGMD, SGMD, and TSGMD is the same, due to direct contact of fluids with membrane at feed and permeate sides of MD module (Essalhi and Khayet, 2014), except for VMD, and AGMD and VA-AGMD, where vacuum and empty air gap exist at permeate side, respectively. The Knudsen, Molecular, and combined mechanisms for DCMD, LGMD, SGMD, and TSGMD, assuming that viscous flow is negligible, are expressed in Equations (36, 37, 38), respectively (Lagana et al., 2000; Ding et al., 2002; Srisurichan et al., 2006; Andrjesdóttir et al., 2013; Bouchrit et al., 2015; Shirazi et al., 2016; Ullah et al., 2018). The mass transfer mechanisms for VMD assumes that molecular diffusion is negligible and is described in Equations (39–41) (Table 5). The mass transfer mechanisms for both AGMD and VA-AGMD, which assume negligible viscous diffusion, are expressed in Equations (42–44) (Table 6). Equations (36–45) for MD configurations are based on the prevailing mass transfer mechanisms and assumed uniform mean membrane pore size.

$\begin{array}{ll}{B}_m^{kd}=\frac{\epsilon d_p}{3\tau {\delta }_m}\sqrt{\frac{8M_w}{\pi R{T}_m}}& (36)\end{array}$

$\begin{array}{ll}{B}_m^{mo}=\frac{\epsilon P_T{D}_{wa}{M}_w}{\tau {\delta }_m{P}_{a}R{T}_m}& (37)\end{array}$

$\begin{array}{ll}{B}_m^T=\frac{1}{\left[\frac{3\tau {\delta }_m}{\epsilon d_p}\sqrt{\frac{\pi R{T}_m}{8M_w}}+\frac{\tau {\delta }_m{P}_{a}R{T}_m}{\epsilon P_T{D}_{wa}{M}_w}\right]}& (38)\end{array}$

TABLE 5

Table 5. Mass transfer mechanisms in VMD.

TABLE 6

Table 6. Mass transfer mechanisms in AGMD and VA-AGMD.

In Equations 39–44, $B_m^{kd}$, $B_m^{mo}$, $B_m^{vi}$, and $B_m^T$ are the MD mass transfer coefficients when Knudsen, molecular, viscous flow, and combined mechanisms, respectively, are dominant. M_w, D_wa, P_T, P_a, τ, ε, ∂, and μ_v are molecular weight of water vapor molecule, water-air diffusion coefficient, average pressure of air inside the membrane, total pressure, tortuosity, hydrophobic membrane porosity, air gap thickness, and vapor viscosity, respectively. The P_TD_wa value for water-air can be estimated from Equation (45) (Khayet and Matsuura, 2011e; Bouchrit et al., 2015).

$\begin{array}{ll}{P}_T{D}_{wa}=1.9x10^{-5}{T}_m^{2.072}& (45)\end{array}$

The partial water vapor pressures at feed and permeate sides can be determined from the estimated membrane surface temperatures using Equation (46) (El-Bourawi et al., 2006; Khayet, 2011), the Antoine equation expressed in Equation (47) (El-Bourawi et al., 2006; Qtaishata et al., 2008; Khayet, 2011; Andrjesdóttir et al., 2013; Bouchrit et al., 2015; Ruiz-Aguirre et al., 2017) and water activity expression in Equation (48) (El-Bourawi et al., 2006; Khayet and Matsuura, 2011e; Andrjesdóttir et al., 2013; Attia et al., 2017).

$\begin{array}{ll}{P}_{im}=P_{im}^0{a}_{iw}\text{ where i}=\text{f or p}& (46)\end{array}$

$\begin{array}{ll}{P}_{im}^0=exp\left(A-\frac{B}{C+T_{im}}\right)& (47)\end{array}$

$\begin{array}{ll}{a}_{iw}=1-{\phi }_i-10{\phi }_i^2& (48)\end{array}$

where P_im is the partial water vapor pressure at membrane surface for feed or permeate side, $P_{im}^0$ is partial pressure of pure water vapor for feed or permeate, and a_iw is water activity for feed or permeate. A, B, and C are average constant values for water, and are given as 23.2, 3878.6, and −43.2, respectively (Khayet, 2011; Andrjesdóttir et al., 2013; Bouchrit et al., 2015; Hitsov et al., 2015). The water activity is considered most of the times equal to one for the permeate side since mole fraction of salt in solution (φ) is very small (Khayet, 2011). Even though activity of water depends on temperature, its effect is considered negligible for salt solutions (Hitsov et al., 2015).

Concentration Polarization in Modeling MD Configurations

To investigate the effects of concentration polarization in MD modeling, it is necessary to understand mass transfer of water vapor molecules, and resistance imposed on membrane by concentration boundary layer that forms close to the surface of membrane on feed side of MD module (El-Bourawi et al., 2006; Qtaishata et al., 2008). As shown in Figures 1–6, concentration boundary layer forms in region close to membrane surface of the feed side, as particles of salts escape with water vapor molecules, making concentration at membrane surface to be higher than at bulk feed. The resistance imposed by concentration boundary layer (concentration polarization) becomes more significant on mass transfer of water vapor molecule as MD separation process progresses with time, leading to decline in transmembrane flux (El-Bourawi et al., 2006; Qtaishata et al., 2008; Chen et al., 2009; Khayet, 2011). Even though, MD process operates at low to moderate flow rates and high heat transfer coefficients, which could help to minimize the impact of concentration polarization (El-Bourawi et al., 2006), there is need to determine favorable optimum conditions to avoid pore wetting, which could result from high flow rate. The significance of the impact of concentration polarization could be deduced from decline in permeate flux as MD process progresses, from physical observation of used membrane, and from characterization of membrane surface (Camacho et al., 2013). However, the effect of concentration polarization on MD, which is best explained through Concentration Polarization Coefficient (CPC), can be better quantified by estimating concentration of salt built at the surface of membrane on feed side in the MD module. Unfortunately, salt concentration at membrane surface has never been determined experimentally (El-Bourawi et al., 2006; Khayet, 2011; Camacho et al., 2013). This can only be estimated theoretically through MD modeling approach. The CPC is generally expressed as ratio of concentration of salt on membrane surface at the feed side (C_fm) to concentration of saline bulk feed (C_fb), as expressed in Equations 49, 50 (El-Bourawi et al., 2006; Khayet, 2011; Andrjesdóttir et al., 2013; Bouchrit et al., 2015; Gustafson et al., 2016). From experimental observations and Equation (50), it can be stated that increase in concentration of particles on membrane surface leads to an increase in CPC (El-Bourawi et al., 2006; Essalhi and Khayet, 2014; Abu-Zeid et al., 2015). This means that high CPC does not favor permeate flux (J).

$\begin{array}{ll}{C}_{fm}=exp\left(\frac{J}{k_{sp}\rho }\right)& (49)\end{array}$

$\begin{array}{ll}CPC=\frac{C_{fm}}{C_{fb}}& (50)\end{array}$

Where k_sp is mass transfer coefficient of salt particles, and can be calculated from Equation (51) by using Sherwood number obtained from Sherwood number correlations reported by Bouchrit et al. (2015), as expressed in Equations (52, 53) for laminar and turbulent flows, respectively. The Sherwood number correlations consist of two dimensionless numbers, namely Reynold's number expressed in Equations (26, 27) and Schmidt number given in Equation (54) (Andrjesdóttir et al., 2013; Bouchrit et al., 2015).

$\begin{array}{ll}Sh=\frac{k_{sp}{d}_h}{D_m}& (51)\end{array}$

$\begin{array}{ll}Sh=0.13R{e}^{0.64}S{c}^{0.38},Re<2100& (52)\end{array}$

$\begin{array}{ll}Sh=0.023R{e}^{0.8}S{c}^{0.33},Re>2100& (53)\end{array}$

$\begin{array}{ll}Sc=\frac{\mu }{\rho D_m}& (54)\end{array}$

Where D_m is the molecular diffusivity of feed solution. The mass transfer of water vapor molecules can be enhanced with the purpose of obtaining high permeate flux, if suitable hydrophobic membrane with proper pore characteristics, and optimal operating conditions are employed in MD process and modeling (Martinez-Diez and Vázquez-González, 1999; Ashoor et al., 2016).

Effect of Concentration Polarization on MD Performance

The most significant effect of concentration polarization on MD process is its contribution to scaling of membrane. Concentration polarization causes blockage of pores in membrane and prevents transmembrane water vapor molecule flow, leading to permeate flux decay (Martinez-Diez and Vázquez-González, 1999; Soni et al., 2009; Liao et al., 2013; Alkhudhiri and Hilal, 2017). As feed concentration increases, there is a decrease of water activity in feed stream, and more salts accumulate on surface of membrane at feed side due to the effect of concentration polarization (Close and Sørensen, 2010; Khayet and Matsuura, 2011e; Essalhi and Khayet, 2014; Alkhudhiri and Hilal, 2017). The concentration polarization effect on mass transfer of vapor molecules is the same for all MD configurations; it is mainly observed on feed side of the membrane, and depends on the design of module (El-Bourawi et al., 2006). An increase in feed concentration leads to an increase in concentration polarization at surface of the membrane on feed side of module, and this increases the risk of scaling of the membrane (Martinez-Diez and Vázquez-González, 1999; Khayet, 2011; Andrjesdóttir et al., 2013; Alsaadi et al., 2014; Bouchrit et al., 2015). When modeling MD configurations, the optimum way to achieve high separation and reduce the effect of concentration polarization is through selection of proper membrane with MD-oriented characteristics, and also through selection of proper operating conditions that favor the transport of volatile components over water (El-Bourawi et al., 2006; Ashoor et al., 2016). According El-Bourawi et al. (2006), by increasing concentration of non-volatile molecules close to surface of membrane causes reduction of transmembrane flux, due to formation of concentration polarization (CP) layers of thickness that behaves as mass transport resistance to vapor molecule across hydrophobic membrane at feed side of MD module. Contrary to most membrane pressure-driven desalination processes, such as reverse osmosis (RO), nanofiltration (NF), and ultrafiltration (UF), where concentration polarization is usually considered a major cause for flux decline, low to moderate flow rates and high heat transfer coefficients can help to reduce CP effects in MD configurations (Martinez-Diez and Vázquez-González, 1999).

Conclusion, Research Gaps, and Future Outlook

In this study, modeling and research gaps on existing configurations for the emerging membrane distillation (MD) desalination technology have been highlighted. There exists many challenges confronting wide industrial application of this novel technology, due to a significant effect of temperature and concentration polarization based on the principles of heat and mass transfer, which are largely responsible for permeate flux decline in MD process. The use of an optimal operating flow rate, among other factors, such as suitable membranes and module design, is recommended as a major approach to reduce the effect of temperature and concentration polarization with the purpose of increasing water recovery and efficiency of MD. There is no doubt that DCMD modeling has been well researched. However, challenges such as lack of suitable membranes and poorly designed modules are associated not only to DCMD, but also to other common MD configurations, such as VMD, AGMD, and SGMD, as well as newly developed configurations, such as LGMD, TSGMD, and VA-AGMD. These challenges limit the deployment of MD at industrial and commercial scale. As mentioned before, design of suitable membranes and modules are currently lacking. Membranes with low tortuosity, high thermal conductivity, large pore size, high porosity, small thickness, and suitable polymer materials are required to reduce the effects of concentration and temperature polarization.

Aside the energy cost associated with MD and the lack of suitable membranes, it is believed that the full industrial application of emerging MD has been slowed down by the lack of appropriate module design. Therefore, more research is needed to provide adequate knowledge of module design for all MD configurations. Module design must allow for effective flow and mixing on feed and permeate sides of MD module to reduce temperature polarization effects. Optimum flow rate is usually recommended to avoid high hydrostatic pressure drop along the length and across the membrane module, which may threaten the integrity of the membrane, cause pore wetting, and eventually reduce permeate quality. However, optimum flow rate may depend on many other factors, which impact can only be determined through modeling and experimentation.

Less or no studies have been conducted to investigate and identify the contributing effect of concentration polarization on membrane scaling, and to determine how MD modeling can help reducing this effect through proper module, membrane, and parameter optimization. It is worth mentioning that the integrity of modeling results on permeate flux obtained from empirical heat and mass transfer models have been questioned among researchers, indicating the need for more research to establish their validity. The effects of stirring rates at the feed and permeate sides of MD modules on transmembrane flux have not been extensively investigated either. Therefore, more MD modeling studies are needed to account for the effects of stirring rate and the interactions among MD operating parameters on permeate flux for existing configurations.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Abu-Zeid, M. A. E., Zhang, Y., Dong, H., Zhang, L., Chen, H-L., and Hou, L. (2015). A comprehensive review of vacuum membrane distillation technique. Desalination 356, 1–14. doi: 10.1016/j.desal.2014.10.033

CrossRef Full Text | Google Scholar

Adham, S., Hussain, A., Matar, J. M., Dores, R., and Jason, A. (2013). Application of membrane distillation for desalting brines from thermal desalination plant. Desalination 314, 101–108. doi: 10.1016/j.desal.2013.01.003

CrossRef Full Text | Google Scholar

AlcheikhHamdon, A. A., Darwish, N. A., and Hilal, N. (2015). The use of factorial design in the analysis of air-gap membrane distillation data. Desalination 367, 90–102. doi: 10.1016/j.desal.2015.03.014

CrossRef Full Text | Google Scholar

Al-Ghamdi, A. A. (2017). Recycling of Reverse Osmosis (RO) reject streams in brackish water desalination plants using fixed bed column softener. Energy Procedia 107, 205–211. doi: 10.1016/j.egypro.2016.12.174

CrossRef Full Text | Google Scholar

Ali, A., Macedonio, F., Drioli, E., Aljlil, S., and Alharbi, O. A. (2013). Experimental and theoretical evaluation of temperature polarization phenomenon in direct contact membrane distillation. Chem. Eng. Res. Design 91, 1966–1977. doi: 10.1016/j.cherd.2013.06.030

CrossRef Full Text | Google Scholar

Alkhudhiri, A., Darwish, N., and Hilal, N. (2012). Membrane distillation: a comprehensive review. Desalination, 287, 2–18. doi: 10.1016/j.desal.2011.08.027

CrossRef Full Text | Google Scholar

Alkhudhiri, A., and Hilal, N. (2017). Air gap membrane distillation: a detailed study of high saline solution. Desalination 403, 179–186. doi: 10.1016/j.desal.2016.07.046

CrossRef Full Text | Google Scholar

Alsaadi, A. S., Francis, L., Amy, G. L., and Ghaffour, N. (2014). Experimental and theoretical analyses of temperature polarization effect in vacuum membrane distillation. J. Mem. Sci. 471, 138–148. doi: 10.1016/j.memsci.2014.08.005

CrossRef Full Text | Google Scholar

Alsaadi, A. S., Francis, L., Maab, H., Amy, G. L., and Ghaffour, N. (2015). Evaluation of air gap membrane distillation process running under sub-atmospheric conditions: experimental and simulation studies. J. Mem. Sci. 489, 73–80. doi: 10.1016/j.memsci.2015.04.008

CrossRef Full Text | Google Scholar

Alsaadi, A. S., Ghaffour, N., Li, J-D., Gray, S., Francis, L., Amy, G. L., et al. (2013). Modeling of air-gap membrane distillation process: A theoretical and experimental study. J. Mem. Sci. 445, 53–65. doi: 10.1016/j.memsci.2013.05.049

CrossRef Full Text | Google Scholar

Amaya-Vías, D., Nebot, E., and López-Ramírez, J. A. (2018). Comparative studies of different membrane distillation configurations and membranes for potential use on board cruise vessels. Desalination 429, 44–51. doi: 10.1016/j.desal.2017.12.008

CrossRef Full Text | Google Scholar

Andrjesdóttir, Ó., Ong, C. L., Nabavi, M., Paredes, S., Khalil, S. G., and Poulikakos, D. A. (2013). An experimentally optimized model for heat and mass transfer in direct contact membrane distillation. Int. Heat J. Mass Trans. 66, 855–867. doi: 10.1016/j.ijheatmasstransfer.2013.07.051

CrossRef Full Text | Google Scholar

Asghari, M., Harandizadeh, A., Dehghani, M., and Harami, H. R. (2015). Persian Gulf desalination using air gap membrane distillation: Numerical simulation and theoretical study. Desalination 374, 92–100. doi: 10.1016/j.desal.2015.07.019

CrossRef Full Text | Google Scholar

Ashoor, B. B., Fath, H., Marquardt, W., and Mhamdi, A. (2012). Dynamic modeling of direct contact membrane distillation processes. Comp. Aid. Chem. Eng. 31, 170–174. doi: 10.1016/B978-0-444-59507-2.50026-3

CrossRef Full Text | Google Scholar

Ashoor, B. B., Mansour, S., Giwa, A., Dufour, V., and Hasan, S. W. (2016). Principles and applications of direct contact membrane distillation (DCMD): a comprehensive review. Desalination 398, 222–246. doi: 10.1016/j.desal.2016.07.043

CrossRef Full Text | Google Scholar

Attia, H., Osman, M. S., Johnson, D. J., Wright, C., and Hilal, N. (2017). Modelling of air gap membrane distillation and its application in heavy metals removal. Desalination 424, 27–36. doi: 10.1016/j.desal.2017.09.027

CrossRef Full Text | Google Scholar

Bahmanyar, A., Asghari, M., and Khoobi, N. (2012). Numerical simulation and theoretical study on simultaneously effects of operating parameters in direct contact membrane distillation. Chem Eng. Process. 61, 42–50. doi: 10.1016/j.cep.2012.06.012

CrossRef Full Text | Google Scholar

Boubakri, A., Hafiane, A., and Bouguecha, S. A. T. (2014). Application of response surface methodology for modeling and optimization of membrane distillation desalination process, of Industrial. J. Eng. Chem. 20, 3163–3169. doi: 10.1016/j.jiec.2013.11.060

CrossRef Full Text | Google Scholar

Bouchrit, R., Boubakri, A., Hafiane, A., and Bouguecha, S. A. (2015). Direct contact membrane distillation: capability to treat hyper-saline solution. Desalination 376, 117–129. doi: 10.1016/j.desal.2015.08.014

CrossRef Full Text | Google Scholar

Boutikos, P., Sh. Mohamed, E., Mathioulakis, E., and Belessiotis, V. (2017). A theoretical approach of a vacuum multi-effect membrane distillation system. Desalination 422, 25–41. doi: 10.1016/j.desal.2017.08.007

CrossRef Full Text | Google Scholar

Bui, V. A. L., Vu, T. T., and Nguyen, M. H. (2010). Modelling the simultaneous heat and mass transfer of direct contact membrane distillation in hollow fibre modules. J. Mem. Sci. 353, 85–93. doi: 10.1016/j.memsci.2010.02.034

CrossRef Full Text | Google Scholar

Camacho, L. M., Dumee, L., Zhang, J., Li, J., Duke, M., Gomez, J., and Gray, S. (2013). Advances in membrane distillation for water desalination and purification applications. Water 5, 94–196. doi: 10.3390/w5010094

CrossRef Full Text | Google Scholar

Chang, H., Wang, G., Chen, Y., Li, C., and Chang, C. (2010). Modeling and optimization of a solar driven membrane distillation desalination system. Renew. Energy 35, 2714–2722. doi: 10.1016/j.renene.2010.04.020

CrossRef Full Text | Google Scholar

Chen, T., Ho, C., and Yeh, H. (2009). Theoretical modeling and experimental analysis of direct contact membrane distillation. J. Mem. Sci. 330, 279–287. doi: 10.1016/j.memsci.2008.12.063

CrossRef Full Text | Google Scholar

Cheng, D., Gong, W., and Li, N. (2016). Response surface modeling and optimization of direct contact membrane distillation for water desalination. Desalination 394, 108–122. doi: 10.1016/j.desal.2016.04.029

CrossRef Full Text | Google Scholar

Cheng, L. H., Wu, P. C., and Chen, J. (2009). Numerical simulation and critical design of AGMD based hollow fiber modules for desalination. Ind. Eng. Chem. Res. 48, 4948–4959. doi: 10.1021/ie800832z

CrossRef Full Text | Google Scholar

Chiam, C., and Sarbatly, R. (2014). Heat transfer in the rectangular cross-flow flat-sheet membrane module for vacuum membrane distillation. Chem. Eng. Process. 79, 23–33. doi: 10.1016/j.cep.2014.03.005

CrossRef Full Text | Google Scholar

Chiam, C., and Sarbatly, R. (2016). Study of the rectangular cross-flow flat-sheet membrane module for desalination by vacuum membrane distillation. Chem. Eng. Process. 102, 169–185. doi: 10.1016/j.cep.2016.01.014

CrossRef Full Text | Google Scholar

Chung, S., Seo, C. D., Lee, H., Choi, J., and Chung, J. (2014). Design strategy for networking membrane module and heat exchanger for direct contact membrane distillation process in seawater desalination. Desalination 349, 126–135. doi: 10.1016/j.desal.2014.07.001

CrossRef Full Text | Google Scholar

Close, E., and Sørensen, E. (2010). Modelling of direct contact membrane distillation for desalination. Comp. Aided Chem. Eng. 28, 649–654. doi: 10.1016/S1570-7946(10)28109-9

CrossRef Full Text | Google Scholar

Criscuoli, A., Carnevale, M. C., and Drioli, E. (2013). Modeling the performance of flat and capillary membrane modules in vacuum membrane distillation. J. Mem. Sci. 447, 369–375. doi: 10.1016/j.memsci.2013.07.044

CrossRef Full Text | Google Scholar

Dehesa-Carrasco, U., Pérez-Rábago, C. A., and Arancibia-Bulnes, C. A. (2013). Experimental evaluation and modeling of internal temperatures in an air gap membrane distillation unit. Desalination 326, 47–54. doi: 10.1016/j.desal.2013.07.014

CrossRef Full Text | Google Scholar

Deshpande, J., Nithyanandam, K., and Pitchumani, R. (2017). Analysis and design of direct contact membrane distillation. J. Mem. Sci. 523, 301–316. doi: 10.1016/j.memsci.2016.10.004

CrossRef Full Text | Google Scholar

Diban, N., Voinea, O. C., Urtiaga, A., and Ortiz, I. (2009). Vacuum membrane distillation of the main pear aroma compound: experimental study and mass transfer modeling. J. Mem. Sci. 326, 64–75. doi: 10.1016/j.memsci.2008.09.024

CrossRef Full Text | Google Scholar

Ding, Z., Ma, R., and Fane, A. G. (2002). A new model for mass transfer in direct contact membrane distillation. Desalination 15l, 217–227. doi: 10.1016/S0011-9164(02)01014-7

CrossRef Full Text | Google Scholar

Drioli, E., Ali, A., and Macedonio, F. (2015). Membrane distillation: recent developments and perspectives. Desalination 356, 56–84. doi: 10.1016/j.desal.2014.10.028

CrossRef Full Text | Google Scholar

Drioli, E., Curcio, E., and di Profio, G. (2005). State of the art and recent progresses in membrane contactors. Chem. Eng. Res. Design 83, 223–233. doi: 10.1205/cherd.04203

CrossRef Full Text | Google Scholar

Duong, H. C., Duke, M., Gray, S., Cooper, P., and Nghiem, L. D. (2016). Membrane scaling and prevention techniques during seawater desalination by air gap membrane distillation. Desalination 397, 92–100. doi: 10.1016/j.desal.2016.06.025

CrossRef Full Text | Google Scholar

Duyen, P. M., Jacob, P., Rattanaoudom, R., and Visvanathan, C. (2016). Feasibility of sweeping gas membrane distillation on concentrating triethylene glycol from waste streams. Chem. Eng. Process. 110, 225–234. doi: 10.1016/j.cep.2016.10.015

CrossRef Full Text | Google Scholar

El-Bourawi, M. S., Ding, Z., Ma, R., and Khayet, M. (2006). A framework for better understanding membrane distillation separation process. J. Mem. Sci. 285, 4–29. doi: 10.1016/j.memsci.2006.08.002

CrossRef Full Text | Google Scholar

Eleiwi, F., Ghaffour, N., Alsaadi, A. S., Francis, L., and Laleg-Kirati, T. M. (2016). Dynamic modeling and experimental validation for direct contact membrane distillation (DCMD) process. Desalination 384, 1–11. doi: 10.1016/j.desal.2016.01.004

CrossRef Full Text | Google Scholar

Eleiwi, F., and Laleg-Kirati, T. M. (2014). Dynamic modeling and optimization in membrane distillation system. IFAC Proceed. 47, 3327–3332. doi: 10.3182/20140824-6-ZA-1003.02475

CrossRef Full Text | Google Scholar

Essalhi, M., and Khayet, M. (2014). Application of a porous composite hydrophobic/hydrophilic membrane in desalination by air gap and liquid gap membrane distillation: a comparative study. Separ. Purif. Technol. 133, 176–186. doi: 10.1016/j.seppur.2014.07.006

CrossRef Full Text | Google Scholar

Garcia-Payo, M. C., Rivier, C. A., Marison, I. W., and von Stockar, U. (2002). Separation of binary mixtures by thermostatic sweeping gas membrane distillation: II. Experimental results with aqueous formic acid solutions. J. Mem. Sci. 198, 197–210. doi: 10.1016/S0376-7388(01)00649-4

CrossRef Full Text | Google Scholar

Geng, H., Wu, H., Li, P., and He, Q. (2014). Study on a new air-gap membrane distillation module for desalination. Desalination 334, 29–38. doi: 10.1016/j.desal.2013.11.037

CrossRef Full Text | Google Scholar

Gude, V. G., Camacho, L. M., Pinappu, S., and Deng, S. (2013). Portable water recovery from AS, U, and F contaminated ground waters by direct contact membrane distillation process. J. Hazard. Mater. 192, 1388–1394. doi: 10.1016/j.jhazmat.2011.06.056

CrossRef Full Text | Google Scholar

Gustafson, R. D., Murphy, J. R., and Achilli, A. (2016). A stepwise model of direct contact membrane distillation for application to large-scale systems: experimental results and model predictions. Desalination 378, 14–27. doi: 10.1016/j.desal.2015.09.022

CrossRef Full Text | Google Scholar

Hayer, H., Bakhtiari, O., and Mohammadi, T. (2015). Simulation of momentum, heat and mass transfer in direct contact membrane distillation: a computational fluid dynamics approach, of Industrial. J. Eng. Chem. 21, 1379–1382, doi: 10.1016/j.jiec.2014.06.009

CrossRef Full Text | Google Scholar

He, Q., Li, P., Geng, H., Zhang, C., Wang, J., and Chang, H. (2014). Modeling and optimization of air gap membrane distillation system for desalination. Desalination 354, 68–75. doi: 10.1016/j.desal.2014.09.022

CrossRef Full Text | Google Scholar

Hitsov, I., De Sitter, K., Dotremont, C., Cauwenberg, P., and Nopens, I. (2017a). Full-scale validated Air Gap Membrane Distillation (AGMD) model without calibration parameters. J. Mem. Sci. 533, 309–320. doi: 10.1016/j.memsci.2017.04.002

CrossRef Full Text | Google Scholar

Hitsov, I., Eykens, L., De Schepper, W., De Sitter, K., Dotremont, C., and Nopens, I. (2017b). Full-scale direct contact membrane distillation (DCMD) model including membrane compaction effects. J. Mem. Sci. 524, 245–256. doi: 10.1016/j.memsci.2016.11.044

CrossRef Full Text | Google Scholar

Hitsov, I., Eykens, L., De Sitter, K., Dotremont, C., Pinoy, L., Van der Bruggen, B., and Nopens, I. (2016). Calibration and analysis of a direct contact membrane distillation model using Monte Carlo filtering. J. Mem. Sci. 515, 63–78. doi: 10.1016/j.memsci.2016.05.041

CrossRef Full Text | Google Scholar

Hitsov, I., Maere, T., De Sitter, K., Dotremont, C., and Nopens, I. (2015). Modelling approaches in membrane distillation: a critical review. Separ. Purif. Technol. 142, 48–64. doi: 10.1016/j.seppur.2014.12.026

CrossRef Full Text | Google Scholar

Ho, C., Chang, H., Yang, T., Wu, K., and Chen, L. (2016). Theoretical and experimental studies of laminar flow hollow fiber direct contact membrane distillation modules. Desalination 378, 108–116. doi: 10.1016/j.desal.2015.10.003

CrossRef Full Text | Google Scholar

Hwang, H. J., He, K., Gray, S., Zhang, J., and Moon, I. S. (2011). Direct contact membrane distillation (DCMD): experimental study on the commercial PTFE membrane and modeling. J. Mem. Sci. 371, 90–98. doi: 10.1016/j.memsci.2011.01.020

CrossRef Full Text | Google Scholar

Imdakm, A., and Matsuura, T. (2012). Simulation of heat and mass transfer in direct contact membranedistillation (md): the effect of membrane pore space description. Procedia Eng. 44:1874. doi: 10.1016/j.proeng.2012.08.984

CrossRef Full Text | Google Scholar

Janajreh, I., Kadi, K. E., Hashaikeh, R., and Ahmed, R. (2017). Numerical investigation of air gap membrane distillation (AGMD): Seeking optimal performance. Desalination 424, 122–130. doi: 10.1016/j.desal.2017.10.001

CrossRef Full Text | Google Scholar

Jensen, M. B., Christensen, K. V., Andrésen, R., Søtoft, L. F., and Norddahl, B. (2011). A model of direct contact membrane distillation for black currant juice. J. Food Eng. 107, 405–414. doi: 10.1016/j.jfoodeng.2011.06.014

CrossRef Full Text | Google Scholar

Jeong, S., Lee, S., Chon, H., and Lee, S. (2014). Structural analysis and modeling of the commercial high performance composite flat sheet membranes for membrane distillation application. Desalination 349, 115–125. doi: 10.1016/j.desal.2014.05.027

CrossRef Full Text | Google Scholar

Karanikola, V., Corral, A., Jiang, F. H., Sáez, A. E., Ela, W. P., and Arnold, R. G. (2015). Sweeping gas membrane distillation: Numerical simulation of mass and heat transfer in a hollow fiber membrane module. J. Mem. Sci. 483, 15–24. doi: 10.1016/j.memsci,0.2015.02.010

CrossRef Full Text | Google Scholar

Khalifa, A., Lawal, D., Antar, M., and Khayet, M. (2015). Experimental and theoretical investigation on water desalination using air gap membrane distillation. Desalination 376, 94–108. doi: 10.1016/j.desal.2015.08.016

CrossRef Full Text | Google Scholar

Khalifa, A. E. (2015). Water and air gap membrane distillation for water desalination – An experimental comparative study. Sep. Purif. Tech. 141, 276–284. doi: 10.1016/j.seppur.2014.12.007

CrossRef Full Text | Google Scholar

Khalifa, A. E., Alawad, S. M., and Antar, M. A. (2017). Parallel and series multistage air gap membrane distillation. Desalination 417, 69–76. doi: 10.1016/j.desal.2017.05.003

CrossRef Full Text | Google Scholar

Khayet, M. (2011). Membranes and theoretical modeling of membrane distillation: a review. Adv. Colloid Interf. Sci. 164, 56–88. doi: 10.1016/j.cis.2010.09.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Khayet, M., and Cojocaru, C. (2012a). Air gap membrane distillation: desalination, modeling and optimization. Desalination 287, 138–145. doi: 10.1016/j.desal.2011.09.017

CrossRef Full Text | Google Scholar

Khayet, M., and Cojocaru, C. (2012b). Artificial neural network modeling and optimization of desalination by air gap membrane distillation. Separ. Purif. Tech. 86, 171–182. doi: 10.1016/j.seppur.2011.11.001

CrossRef Full Text | Google Scholar

Khayet, M., and Cojocaru, C. (2013). Artificial neural network model for desalination by sweeping gas membrane distillation. Desalination 308, 102–110. doi: 10.1016/j.desal.2012.06.023

CrossRef Full Text | Google Scholar

Khayet, M., Cojocaru, C., and Baroudi, A. (2012). Modeling and optimization of sweeping gas membrane distillation. Desalination 287, 159–166. doi: 10.1016/j.desal.2011.04.070

CrossRef Full Text | Google Scholar

Khayet, M., Imdakm, A. O., and Matsuura, T. (2010). Monte Carlo simulation and experimental heat and mass transfer in direct contact membrane distillation. Int. Heat J. Mass Trans. 53, 1249–1259. doi: 10.1016/j.ijheatmasstransfer.2009.12.043

CrossRef Full Text | Google Scholar

Khayet, M., Khulbe, K., and Matsuura, T. (2004a). Characterization of membranes for membrane distillation by atomic force microscopy and estimation of their water vapor transfer coefficients in vacuum membrane distillation process. J. Membr. Sci. 238, 199–211. doi: 10.1016/j.memsci.2004.03.036

CrossRef Full Text | Google Scholar

Khayet, M., and Matsuura, T. (2003). Application of surface modifying macromolecules for the preparation of membranes for membrane distillation. Desalination 158, 51–56. doi: 10.1016/S0011-9164(03)00432-6

CrossRef Full Text | Google Scholar

Khayet, M., and Matsuura, T. (2004). Pervaporation and vacuum membrane distillation processes: modeling and experiments. AlChE J. 50, 1697–1712.

Google Scholar

Khayet, M., and Matsuura, T. (2011a). “Chapter 16—future directions,” in Membrane Distillation, (Oxford, UK: Elsevier), 453–460.

Google Scholar

Khayet, M., and Matsuura, T. (2011f). “Chapter 10 - Direct contact membrane distillation,” in Membrane Distillation (Elsevier), 249–293.

Google Scholar

Khayet, M., and Matsuura, T. (eds.). (2011b). “Chapter 12 - Vacuum Membrane Distillation,” in Membrane Distillation, (Oxford, UK: Elsevier), 323–359.

Google Scholar

Khayet, M., and Matsuura, T. (eds.). (2011c). “Chapter 13 - air gap membrane distillation,” in Membrane Distillation, (Oxford, UK: Elsevier), 61–398.

Google Scholar

Khayet, M., and Matsuura, T. (eds.). (2011d). “Chapter 11 - Sweeping gas membrane distillation,” in Membrane Distillation, (Oxford, UK: Elsevier), 295–322.

Google Scholar

Khayet, M., and Matsuura, T. T. (2011e). “Chapter 1 - Introduction to membrane distillation,” in Membrane Distillation, (Oxford, UK: Elsevier), 1–16.

Google Scholar

Khayet, M., Velazquez, A., and Mengual, J. I. (2004b). Modeling mass transport through a porous partition: effects of pore size distribution. J. Non Equlibr. Thermodyn 29, 279–299. doi: 10.1515/JNETDY.2004.055

CrossRef Full Text | Google Scholar

Kim, A. S. (2013). A two-interface transport model with pore-size distribution for predicting the performance of direct contact membrane distillation (DCMD). J. Mem. Sci. 428, 410–424. doi: 10.1016/j.memsci.2012.10.054

CrossRef Full Text | Google Scholar

Kim, A. S. (2014). Cylindrical cell model for direct contact membrane distillation (DCMD) of densely packed hollow fibers. J. Mem. Sci. 455, 168–186. doi: 10.1016/j.memsci.2013.12.067

CrossRef Full Text | Google Scholar

Kim, K. Y., and Thu, C. S. (2015). Solar-assisted multi-stage vacuum membrane distillation system with heat recovery unit. Desalination 367, 161–171. doi: 10.1016/j.desal.2015.04.003

CrossRef Full Text | Google Scholar

Koo, J., Han, J., Sohn, J., Lee, S., and Hwang, T. M. (2013). Experimental comparison of direct contact membrane distillation (DCMD) with vacuum membrane distillation (VMD). Desalination Water Treat. 51, 6299–6309. doi: 10.1080/19443994.2013.780817

CrossRef Full Text | Google Scholar

Kurdian, A. R., Bahreini, M., Montazeri, G. H., and Sadeghi, S. (2013). Modeling of direct contact membrane distillation process: flux prediction of sodium sulfate and sodium chloride solutions. Desalination 323, 75–82. doi: 10.1016/j.desal.2013.05.002

CrossRef Full Text | Google Scholar

Lagana, F., Barbieri, G., and Drioli, E. (2000). Direct contact membrane distillation: modelling and concentration experiments. J. Membr. Sci. 166, 1–11. doi: 10.1016/S0376-7388(99)00234-3

CrossRef Full Text | Google Scholar

Lawson, K. W., and Lloyd, D. R. (1997). Membrane distillation. J. Membrane Sci. 124, 1–25.

Google Scholar

Lee, J., and Kim, W. (2013). Numerical modeling of the vacuum membrane distillation process. Desalination 331, 46–55. doi: 10.1016/j.desal.2013.10.022

CrossRef Full Text | Google Scholar

Lee, J., and Kim, W. (2014). Numerical study on multi-stage vacuum membrane distillation with economic evaluation. Desalination 339, 54–67. doi: 10.1016/j.desal.2014.02.003

CrossRef Full Text | Google Scholar

Lee, J., Kim, Y., Kim, W., Francis, L., Amy, G., and Ghaffour, N. (2015). Performance modeling of direct contact membrane distillation (DCMD) seawater desalination process using a commercial composite membrane. J. Mem. Sci. 478, 85–95. doi: 10.1016/j.memsci.2014.12.053

CrossRef Full Text | Google Scholar

Li, B., and Sirkar, K. K. (2005). Novel membrane and device for vacuum membrane distillation based desalination process. J. Membrane Sci. 257, 60–75. doi: 10.1016/j.memsci.2004.08.040

CrossRef Full Text | Google Scholar

Lian, B., Wang, Y., Le-Clech, P., Chen, V., and Leslie, G. (2016). A numerical approach to module design for crossflow vacuum membrane distillation systems. J. Mem. Sci. 510, 489–496. doi: 10.1016/j.memsci.2016.03.041

CrossRef Full Text | Google Scholar

Liao, Y., Wang, R., and Fane, A. G. (2013). Engineering superhydrophobic surface on poly (vinylidene fluoride) nanofiber membranes for direct contact membrane distillation. J. Mem. Sci. 440, 77–87. doi: 10.1016/j.memsci.2013.04.006

CrossRef Full Text | Google Scholar

Lin, S., Yip, N. Y., and Elimelech, M. (2014). Direct contact membrane distillation with heat recovery: thermodynamic insights from module scale modeling. J. Mem. Sci. 453, 498–515. doi: 10.1016/j.memsci.2013.11.016

CrossRef Full Text | Google Scholar

Liu, J., Liu, M., Guo, H., Zhang, W., Xu, K., and Li, B. (2017). Mass transfer in hollow fiber vacuum membrane distillation process based on membrane structure. J. Mem. Sci. 532, 115–123. doi: 10.1016/j.memsci.2017.03.018

CrossRef Full Text | Google Scholar

Liu, Z., Gao, Q., Lu, X., Ma, Z., Zhang, H., and Wu, C. (2017). Experimental study of the optimal vacuum pressure in vacuum assisted air gap membrane distillation process. Desalination 414, 63–72. doi: 10.1016/j.desal.2017.03.031

CrossRef Full Text | Google Scholar

Lovineh, S. G., Asghari, M., and Rajaei, B. (2013). Numerical simulation and theoretical study on simultaneous effects of operating parameters in vacuum membrane distillation. Desalination 314, 59–66. doi: 10.1016/j.desal.2013.01.005

CrossRef Full Text | Google Scholar

Manawi, Y. M., Khraisheh, M., Fard, A. K., Benyahia, F., and Adham, S. (2014a). Effect of operational parameters on distillate flux in direct contact membrane distillation (DCMD): comparison between experimental and model predicted performance. Desalination 336, 110–120. doi: 10.1016/j.desal.2014.01.003

CrossRef Full Text | Google Scholar

Manawi, Y. M., Majeda, A., Khraisheh, M. M., Fard, A. K., Benyahia, F., and Adham, S. (2014b). A predictive model for the assessment of the temperature polarization effect in direct contact membrane distillation desalination of high salinity feed. Desalination 341, 38–49. doi: 10.1016/j.desal.2014.02.028

CrossRef Full Text | Google Scholar

Martinez-Diez, L., and Vázquez-González, M. I. (1999). Temperature and concentration polarization in membrane distillation of aqueous salt solutions. J. Mem. Sci. 156, 265–273. doi: 10.1016/S0376-7388(98)00349-4

CrossRef Full Text | Google Scholar

Mericq, J. P., Laborie, S., and Cabassud, C. (2010). Vacuum membrane distillation of seawater reverse osmosis brines. Water Res. 44, 5260–5273. doi: 10.1016/j.watres.2010.06.052

PubMed Abstract | CrossRef Full Text | Google Scholar

Mohammadi, T., and Safavi, M. A. (2009). Application of Taguchi method in optimization of desalination by vacuum membrane distillation. Desalination 249, 83–89. doi: 10.1016/j.desal.2009.01.017

CrossRef Full Text | Google Scholar

Naidu, G., Choi, Y., Jeong, S., Hwang, T. M., and Vigneswaran, S. (2014). Experiments and modeling of a vacuum membrane distillation for high saline water, of Industrial. J. Eng. Chem. 20, 2174–2183. doi: 10.1016/j.jiec.2013.09.048

CrossRef Full Text | Google Scholar

Naidu, G., Shim, W. G., Jeong, S., Choi, Y., Ghaffour, N., and Vigneswaran, S. (2017). Transport phenomena and fouling in vacuum enhanced direct contact membrane distillation: experimental and modelling. Separat. Purif. Technol. 172, 285–295. doi: 10.1016/j.seppur.2016.08.024

CrossRef Full Text | Google Scholar

Ogden, D. D., and Trembly, J. P. (2017). Desalination of hypersaline brines via Joule-heating: Experimental investigations and comparison of results to existing models. Desalination 424, 149–158. doi: 10.1016/j.desal.2017.10.006

CrossRef Full Text | Google Scholar

Orfi, J., Loussif, N., and Davies, P. A. (2016). Heat and mass transfer in membrane distillation used for desalination with slip flow. Desalination 381, 135–142. doi: 10.1016/j.desal.2015.12.009

CrossRef Full Text | Google Scholar

Pangarkar, B. L., and Deshmukh, S. K. (2015). Theoretical and experimental analysis of multi-effect air gap membrane distillation process (ME-AGMD). J. Environ. Chem. Eng. 3, 2127–2135. doi: 10.1016/j.jece.2015.07.017

CrossRef Full Text | Google Scholar

Phattaranawika, V. J., Jiraratananona, R., and Faneb, A. G. (2003). Effect of pore size distribution and air flux on mass transport in direct contact membrane distillation. J. Mem. Sci. 215, 75–85. doi: 10.1016/S0376-7388(02)00603-8

CrossRef Full Text | Google Scholar

Prince, J. A., Singh, G., and Shanmugasundaram, T. S. (2015). Vacuum Air Gap Membrane Distillation System for Desalination. WO. CN 104411384 A., (US 2015O1 14818A11).

Qtaishat, M. R., and Matsuura, T. (2015). “13 - Modelling of pore wetting in membrane distillation compared with pervaporation,” in Woodhead Publishing Series in Energy, In Pervaporation, Vapour Permeation and Membrane Distillation, (Cambridge, UK: Woodhead Publishing), 385–413.

Google Scholar

Qtaishata, M. T., Kruczeka, B., and Khayet, M. (2008). Heat and mass transfer analysis in direct contact membrane distillation. Desalination 219, 272–292. doi: 10.1016/j.desal.2007.05.019

CrossRef Full Text | Google Scholar

Ramezanianpour, M., and Sivakumar, M. (2014). An analytical flux decline model for membrane distillation. Desalination 345, 1–12. doi: 10.1016/j.desal.2014.04.006

CrossRef Full Text | Google Scholar

Ramon, G., Agnon, Y., and Dosoretz, C. (2009). Heat transfer in vacuum membrane distillation: Effect of velocity slip. J. Mem. Sci. 331, 117–125 doi: 10.1016/j.memsci0.2009.01.022

CrossRef Full Text | Google Scholar

Rivier, C. A., Garcia-Payo, M. C., Marison, I. W., and von Stockar, U. (2002). Separation of binary mixtures by thermostatic sweeping gas membrane distillation: theory I and simulations. J Mem. Sci. 201, 1–16. doi: 10.1016/S0376-7388(01)00648-2

CrossRef Full Text | Google Scholar

Ruiz-Aguirre, A., Andrés-Mañas, J. A., Fernández-Sevilla, J. M., and Zaragoza, G. (2017). Modeling and optimization of a commercial permeate gap spiral wound membrane distillation module for seawater desalination. Desalination 419, 160–168. doi: 10.1016/j.desal.2017.06.019

CrossRef Full Text | Google Scholar

Sanmartino, J. A., Khayet, M., and García-Payo, M. C. (2017a). Reuse of discarded membrane distillation membranes in microfiltration technology. J. Mem. Sci. 539, 273–283. doi: 10.1016/j.memsci.2017.06.003

CrossRef Full Text | Google Scholar

Sanmartino, J. A., Khayet, M., García-Payo, M. C., El-Bakouri, H., and Riaza, A. (2017b). Treatment of reverse osmosis brine by DCMD: Chemical pretreatment approach. Desalination 420, 79–90. doi: 10.1016/j.desal.2017.06.030

CrossRef Full Text | Google Scholar

Shakaib, M., Hasani, S. F. M., Ahmed, I., and Yunus, R. M. (2012). A CFD study on the effect of spacer orientation on temperature polarization in membrane distillation modules. Desalination 284, 332–340. doi: 10.1016/j.desal.2011.09.020

CrossRef Full Text | Google Scholar

Shao, F., Hao, C., Ni, L., Zhang, Y., Du, R., Meng, J., et al. (2014). Experimental and theoretical research on N-methyl-2-pyrrolidone concentration by vacuum membrane distillation using polypropylene hollow fiber membrane. J. Mem. Sci. 452, 157–164. doi: 10.1016/j.memsci.2013.09.041

CrossRef Full Text | Google Scholar

Shirazi, M. M. A., Kargari, A., Ismail, A. F., and Matsuura, T. (2016). Computational Fluid Dynamic (CFD) opportunities applied to the membrane distillation process: state-of-the-art and perspectives. Desalination 377, 73–90. doi: 10.1016/j.desal.2015.09.010

CrossRef Full Text | Google Scholar

Shirazi, M. M. A., Kargari, A., Tabatabaei, M., Ismail, A. F., and Matsuura, T. (2014). Concentration of glycerol from dilute glycerol wastewater using sweeping gas membrane distillation. Chem. Eng. Process. 78, 58–66. doi: 10.1016/j.cep.2014.02.002

CrossRef Full Text | Google Scholar

Shukla, S., Benes, N. E., Vankelecom, I., Méricq, J. P., Belleville, M. P., Hengl, N., et al. (2015). Sweep gas membrane distillation in a membrane contactor with metallic hollow-fibers. J. Mem. Sci. 493, 167–178. doi: 10.1016/j.memsci.2015.06.040

CrossRef Full Text | Google Scholar

Soni, V., Abildskov, J., Jonsson, G., and Gani, R. (2009). A general model for membrane-based separation processes. Comp. Chem. Eng. 33, 644–659. doi: 10.1016/j.compchemeng.2008.08.004

CrossRef Full Text | Google Scholar

Soukane, S., Chelouche, S., and Naceur, M. W. (2014). A ballistic transport model for vacuum membrane distillation. J. Mem. Sci. 50, 397–406. doi: 10.1016/j.memsci.2013.08.038

CrossRef Full Text | Google Scholar

Srisurichan, S., Jiraratananon, R., and Fane, A. G. (2006). Mass transfer mechanisms and transport resistances in direct contact membrane distillation process. J. Mem. Sci. 277, 186–194. doi: 10.1016/j.memsci.2005.10.028

CrossRef Full Text | Google Scholar

Suárez, F., Tyler, S. W., and Childress, A. E. (2010). A theoretical study of a direct contact membrane distillation system coupled to a salt-gradient solar pond for terminal lakes reclamation. Water Res. 44, 4601–4615. doi: 10.1016/j.watres.2010.05.050

PubMed Abstract | CrossRef Full Text | Google Scholar

Summers, E. K., and Lienhard, J. H. (2013). Experimental study of thermal performance in air gap membrane distillation systems, including the direct solar heating of membranes. Desalination 330, 100–111. doi: 10.1016/j.desal.2013.09.023

CrossRef Full Text | Google Scholar

Swaminathan, J., Chung, H. W., Warsinger, D. M., AlMarzooqi, F. A., Arafat, H. A., and Lienhard, H. V. (2016a). Energy efficiency of permeate gap and novel conductive gap membrane distillation. J. Mem. Sci. 502, 171–178. doi: 10.1016/j.memsci.2015.12.017

CrossRef Full Text | Google Scholar

Swaminathan, J., Chung, H. W., Warsinger, D. M., and Lienhard, H. V. (2016b). Membrane distillation model based on heat exchanger theory and configuration comparison. Appl. Energy 184, 491–505. doi: 10.1016/j.apenergy.2016.09.090

CrossRef Full Text | Google Scholar

Tang, N., Zhang, H., and Wang, W. (2011). Computational fluid dynamics numerical simulation of vacuum membrane distillation for aqueous NaCl solution. Desalination 274, 120–129. doi: 10.1016/j.desal.2011.01.078

CrossRef Full Text | Google Scholar

Tavakolmoghadam, M., and Safavi, M. (2012). An optimized neural network model of desalination by vacuum membrane distillation using genetic algorithm. Procedia Eng. 42, 106–112. doi: 10.1016/j.proeng.2012.07.400

CrossRef Full Text | Google Scholar

Tian, R., Gao, H., Yang, X. H., Yan, S. Y., and Li, S. (2014). A new enhancement technique on air gap membrane distillation. Desalination 332, 52–59. doi: 10.1016/j.desal.2013.10.016

CrossRef Full Text | Google Scholar

Ugrozov, V. V., Elkina, I. B., Nikulin, V. N., and Kataeva, L. I. (2003). Theoretical and experimental research of liquid-gap membrane distillation process in membrane module. Desalination 157, 325–331. doi: 10.1016/S0011-9164(03)00412-0

CrossRef Full Text | Google Scholar

Ugrozov, V. V., and Kataeva, L. I. (2004). Mathematical modeling of membrane distiller with liquid gap. Desalination 168, 347–353. doi: 10.1016/j.desal.2004.07.018

CrossRef Full Text | Google Scholar

Ullah, R., Khraisheh, M., Esteves, R. J., McLeskey, J. T., AlGhouti, M., Gad-el-Hak, M., et al. (2018). Energy efficiency of direct contact membrane distillation. Desalination 433, 56–67. doi: 10.1016/j.desal.2018.01.025

CrossRef Full Text | Google Scholar

Wang, C. (2011). On the heat transfer correlation for membrane distillation. Energy Conv. Manag. 52, 1968–1973. doi: 10.1016/j.enconman.2010.11.014

CrossRef Full Text | Google Scholar

Woods, J., Pellegrino, J., and Burch, J. (2011). Generalized guidance for considering pore-size distribution in membrane distillation. J. Mem. Sci. 368, 124–133. doi: 10.1016/j.memsci.2010.11.041

CrossRef Full Text | Google Scholar

Wu, C., Li, Z., Zhang, J., Jia, Y., Gao, Q., and Lu, X. (2015). Study on the heat and mass transfer in air-bubbling enhanced vacuum membrane distillation. Desalination 373, 16–26. doi: 10.1016/j.desal.2015.07.001

CrossRef Full Text | Google Scholar

Wu, H. Y., Tay, M., and Field, R. W. (2016). Novel method for the design and assessment of direct contact membrane distillation modules. J. Mem. Sci. 513, 260–269. doi: 10.1016/j.memsci.2016.04.009

CrossRef Full Text | Google Scholar

Xie, Z., Duong, T., Hoang, M., Nguyen, C., and Bolto, B. (2009). Ammonia removal by sweep gas membrane distillation. Water Res. 43, 1693–1699. doi: 10.1016/j.watres.2008.12.052

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, H., Yang, X., Wang, R., and Fane, A. G. (2012). Analysis of heat and mass transfer by CFD for performance enhancement in direct contact membrane distillation. J. Mem. Sci. 406, 38–47. doi: 10.1016/j.memsci.2012.02.035

CrossRef Full Text | Google Scholar

Zhang, J., Gray, S., and Li, J. (2012). Modelling heat and mass transfers in DCMD using compressible membranes. J. Mem. Sci. 387–388, 7–16. doi: 10.1016/j.memsci.2011.08.034

CrossRef Full Text | Google Scholar

Zhang, J., Li, J., Duke, M., Hoang, M., Xie, Z., Groth, A., et al. (2013). Modelling of vacuum membrane distillation. J. Mem. Sci. 434, 1–9. doi: 10.1016/j.memsci.2013.01.048

CrossRef Full Text | Google Scholar

Zhang, Y., Peng, Y., Ji, S., Qi, J., and Wang, S. (2017). Numerical modeling and economic evaluation of two multi-effect vacuum membrane distillation (ME-VMD) processes. Desalination 419, 39–48. doi: 10.1016/j.desal.2017.05.032

CrossRef Full Text | Google Scholar

Zuo, G., Guan, G., and Wang, R. (2014). Numerical modeling and optimization of vacuum membrane distillation module for low-cost water production. Desalination 339, 1–9. doi: 10.1016/j.desal.2014.02.005

CrossRef Full Text | Google Scholar

Nomenclature