Thermogravimetric Characteristics and Non-isothermal Kinetics of Macro-Algae With an Emphasis on the Possible Partial Gasification at Higher Temperatures

Introduction

The last few decades have seen an increase in the use of biofuels and high-value biochemicals derived from biomass. Biomass is a renewable carbonaceous source, an alternative to fossil fuel, and a precursor of biochemicals. Non-food biomasses are widespread in nature and are also cultivated at ~100 billion tons annually (Sheldon, 2014). According to an estimate, biofuels are expected to satisfy around 10% of the global energy demand by 2035, and they have the potential to replace 27% of global transportation fuel by 2050. The main reason for the growing interest in the use of biomass, besides its renewable nature, is its carbon-neutral and less polluting characteristics. The Paris climate agreement requires clean energy transformation in order to reach net zero emissions by 2060, which can only be achieved by scaling-up efficient energy conversion systems to generate bio-energy with carbon capture and storage (BECCS) (Agency, 2017).

Marine macro-algae or seaweeds are efficient photosynthetic organisms. Besides their use in the food, pharmaceutical, and cosmetic industries, they are also well-known for their use in bio-sequestration and bioremediation, thereby mitigating climate change (Maceiras et al., 2011; Oliveira, 2016). There has been increased interest in macro-algae as a renewable and sustainable energy source over the past decade among the scientific and industrial communities because of its high biomass productivity (Baghel et al., 2017). Macro-algae biomass is mainly produced from the harvesting of wild stocks, a recent report of FAO reveals that a volume of around 12 million tons is produced annually (Ferdouse et al., 2018). Its cultivation is normally carried out through ocean farming and thus does not require land or fresh water, allowing these to be used for food crops and aquaculture. Macro-algae is a cheap source of carbon with a varying chemical composition depending on the type and the environmental conditions. It can be crudely classified into four main groups depending on the stored nutrients, pigments and chemical composition, namely red seaweeds (Rhodophyceae), green seaweeds (Chlorophyceae), brown seaweeds (Phaeophyceae), and blue-green seaweeds (Cyanophyceae) (Manivannan et al., 2009).

Seaweeds, like terrestrial forms of biomass, are lignocellulosic in nature with a complicated embedding of cellulose, hemicellulose, lignin, and intracellular substances. However, compared to terrestrial biomass, they may have higher costs attached to their cultivation in conjunction with the presence and effects of heavy metal concentrations in aquatic environments, while the removal of harmful contents (sulfur and nitrogen) from the resulting fuel (Ghadiryanfar et al., 2016) is another problem. Furthermore, some studies have revealed that the transesterification of oil extracted from macro-algae is restricted due to low lipid contents, and they have suggested the conversion of carbohydrates into biofuel but with a higher gas yield (Roesijadi et al., 2010; Hong et al., 2017). Therefore, the most suited conversion technologies, such as anaerobic digestion and hydrous pyrolysis (Ross et al., 2008), are likely to be employed for macro-algal biomass containing high levels of ash and alkali metals. Macro-algae are rich in macro and micronutrients, but also display an uptake of heavy metals from the environment. The heavy metals in macro-algae may indicate the fractions of industrial effluents affecting the aquatic ecosystems, which is also a serious concern. These accumulations depend upon their biochemical composition, specifically the properties of the cell wall (Davis et al., 2003) and the constituents present in the macro-algae cell walls. The cell wall contains the fibers and matrix of polysaccharides (alginates and fucoidan). The alginates in brown algae have a high accumulation of divalent cations, while sulfated polysaccharides exhibit a tendency toward trivalent cations (Saha and Orvig, 2010; Ortiz-Calderon et al., 2017). Figure 1 presents the various major constituents of the seaweed cell wall.

FIGURE 1

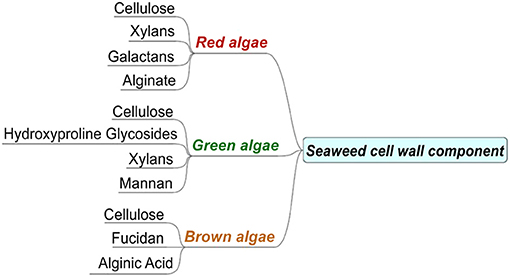
Figure 1. Major chemical constituents of the seaweed cell wall, adapted from Bold and Wynne (1984).

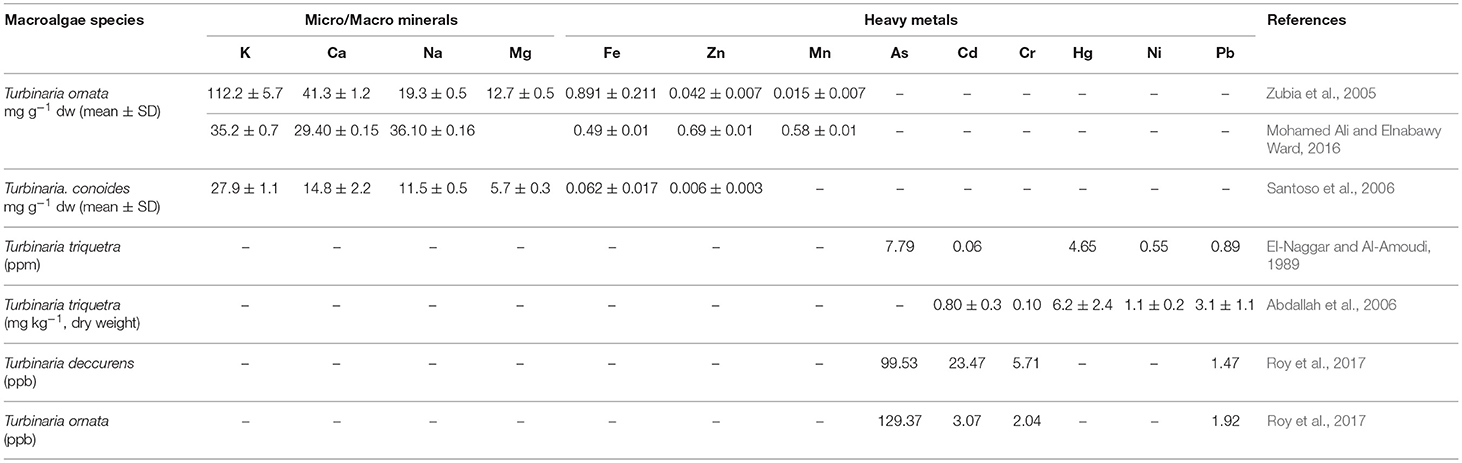
The uptake of heavy metals takes place in macro-algae through bio-sorption or ion exchange processes by the chemical constituents present in the cell wall. The Red Sea, with its diverse ecosystem, has over 500 species of seaweeds, which are spread over 1,900 km covering 438,000 km² of coral reef stretching along its coasts and part of the Indian-Pacific Ocean (Spalding et al., 2001; Siddall et al., 2004; Bruckner et al., 2013). Red Sea seaweeds primarily consist of small green and brown algal filaments found in the northern and central parts, while the southern area of the Red Sea has large brown algal species like Sargassum and Turbinaria spp (Bruckner et al., 2013). Turbinaria ornata (T. ornata) is a well-known brown alga suitable for human consumption due to its antioxidant characteristics (Deepak et al., 2017a). Several studies have discussed its antibacterial, antioxidant, and anticancer properties (Omar et al., 2012; Ponnan et al., 2017; Stranska-Zachariasova et al., 2017; Tenorio-Rodriguez et al., 2017) as well as the biogenic synthesis of crystalline Ag/Au nanoparticles (Rajeshkumar et al., 2013; Kayalvizhi et al., 2014; Deepak et al., 2017b), but to the best of the authors' knowledge, no previous studies are available for its use as a source of biofuel. The mineral and heavy metal uptakes by different Turbinaria species are presented in Table 1.

TABLE 1

Table 1. Macro/micro mineral and heavy metal uptake by Turbinaria macroalgal species.

Chemical looping pyrolysis gasification (CLPG) and chemical looping combustion (CLC) are proven concepts for syngas production and CO₂-capturing, respectively. The use of oxygen carriers such as the oxides of Ni, Mn, Cu, Fe, and Co have previously been investigated in these processes (Adanez et al., 2012; Huang et al., 2017). In the present study, the pyrolysis of T. ornata was realized in a thermogravimetric analyzer (TGA). The unique and novel concept of pyrolysis-gasification with the oxides of heavy metals already embedded in the matrix of polysaccharides of brown macro-algae (T. ornata) has also been considered besides the condensation of polymers at higher temperatures. The understanding of the role of inherent inorganic compounds of T. ornata and the investigation into evolved gases at high temperatures will lead to process optimization, efficient use, and the removal of heavy metals in the form of biochar.

Materials and Methods

Macro-Algae Biomass

T. ornata is a brown alga that has phytochemical constituents like carbohydrates, proteins, flavonoids, alkaloids, and phenols as well as sulfated fucan-polymers like polysaccharide and alginate structures that display tremendous potential for use in various applications. Its ability to bind heavy metals is of particular interest. Its biochar can also be used as a bio-indicator for identifying the type and quantity of heavy metals present in aquatic environments.

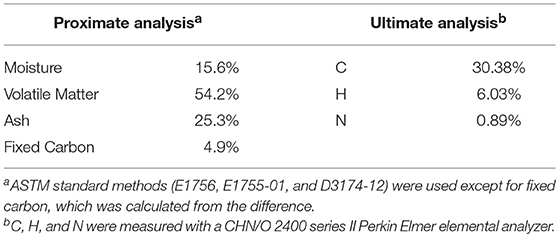
T. ornata was collected from the Red Sea coastal area (N22°48′32″, E38°56′37″). The fresh macro-algae was thoroughly washed to remove adherent dirt and sand with deionized water several times. The cleaned biomass was air-dried for 2 days, then crushed and sieved. A fine powder with a particle size of <0.147 mm (the fraction of the material passed through a 100 mesh sieve) was kept in an air-dried container for further use. Table 2 shows the physicochemical properties of T. ornata.

TABLE 2

Table 2. Physicochemical properties of Turbinaria ornata.

Thermogravimetric Analysis

Pyrolysis is a promising process to convert biomass whereby the distribution of the product depends greatly on the conditions used. It has been reported that slow pyrolysis yields more biochar whereas fast pyrolysis produces more volatiles (Mohan et al., 2006). Extensive development in the pyrolysis process has been made recently and there has been a growing interest in its use because of its simplicity, flexibility, and efficiency. Biochar, a product of pyrolysis, finds in addition to volatiles potential application in the agricultural and environmental sectors. A thermogravimetric analyzer (TGA) is a commonly employed thermo-analytic instrument for the thermal degradation study of biomass. Under well-defined conditions of slow pyrolysis, it provides precise time and temperature-series mass loss data, which are used to estimate the kinetic parameters.

In the present study, the TGA experiments were performed on a Q5000 IR electro-balance analyzer (TA Instruments, USA). Approximately 15 mg of algal biomass sample was used for each run in triplicate to ensure accuracy and precision. The TGA temperature was raised from 50 to 900°C using different heating rates (5, 10, 15, and 30 ^oC·min⁻¹), while a flow of high purity N₂ gas was maintained at 70 ml min⁻¹. Additionally, an isothermal step was introduced before the heating ramp to achieve pyrolysis stabilization. The acquisition, diagnosis, and processing of curves were performed on Platinum™ software.

Kinetic Evaluation and Analysis

The devolatilization of algal biomass through pyrolysis is useful in understanding multi-component and multi-pyrolytic phases for process design, optimization, and scale-up (Ranzi et al., 2017). A global single-step reaction is always used in assessing the kinetic mechanism of pyrolysis. In a simplistic approach, the overall reaction process of T. ornata pyrolysis can be described with the following reaction:

$\begin{array}{ll}Turbinariaornata(s)\to Volatiles(g)+Biochar(s)& (1)\end{array}$

A non-isothermal TGA analysis technique is usually preferred over an isothermal technique for three main reasons. Firstly, the isothermal procedures are simply not possible to realize at higher temperatures because of the large non-isothermal heat-up and cool-down durations. Secondly, the estimation of the kinetic parameters at low heating rates is rather difficult due to weight loss during the heat-up time. Thirdly, there is the existence of the almost non-zero extent of conversions (Vyazovkin and Wight, 1998; Grigiante et al., 2016). For the aforementioned reasons, a non-isothermal technique was selected for this study. The process data recorded by TGA during non-isothermal pyrolysis can be expressed in terms of conversion (α) at any time (t) using the Arrhenius law [43]:

$\begin{array}{ll}\frac{\text{d}\alpha }{\text{d}t}=\beta \frac{\text{d}\alpha }{\text{d}T}=A·exp\left(-\frac{E_a}{RT}\right)·f(\alpha )& (2)\end{array}$

where E_a (J·mol⁻¹) is the apparent activation energy, A (s⁻¹) is the frequency factor, T is the absolute temperature, R is the ideal gas constant (J·mol⁻¹·K⁻¹), β is the heating rate (K·s⁻¹), and f (α) represents the algebraic form of the reaction model. The conversion (α) is defined as the fractional mass loss expressed by the following equation:

$\begin{array}{ll}\alpha =\frac{m_o-m_i}{m_o-m_f}& (3)\end{array}$

where m₀, m_i, and m_f are the intial, instantaneous, and final mass, respectively.

Integrating Equation (1) with respect to conversion and temperature in the ranges α ∈ [0, α] and T ∈ [T_o, T] gives Equation (4):

$\begin{array}{ll}g(\alpha )={\displaystyle \underset{0}{\overset{\alpha }{\int }}}\frac{\text{d}\alpha }{f(\alpha )}=\frac{A}{\beta }{\displaystyle \underset{T_0}{\overset{T}{\int }}}exp\left(-\frac{E_a}{RT}\right)\text{ d}T& (4)\end{array}$

Equation (4) can be used to describe the conversion when the temperature lag between the sample and its environment is very small. E_a is an important kinetic parameter, defined as the energy required to have a reaction, which is usually measured by model-free and model-fitting methods. Each method has its own advantages, and they are complementary and are not in competition. A model-free analysis can be performed without having specified the reaction mechanism, while the model-fitting analysis uses the approach of data-model best fitting to estimate E_a, A, and f(α) (Šesták and Berggren, 1971).

Model-Free Methods

Model-free kinetics methods are mostly isoconversional in nature. They provide an accurate estimation of E_a from isothermal and non-isothermal measurements and are most commonly employed in the pyrolytic kinetics of biomass (Opfermann et al., 2002). These methods have the capability to solve complex processes and are based on the fact that the reaction rate at a particular heating rate (β) is a function of temperature (T) alone at a specific conversion (α), while f(α) remains constant. Model-free methods provide a detailed kinetic analysis without knowledge of the reaction mechanism while indicating multiple processes if E_a varies strongly with α (Vyazovkin et al., 2011). Depending on the mathematical form of the kinetic equation, model-free methods can be differential or integral. The Friedman method (Friedman, 1964) is the most common differential while the Kissinger-Akahira-Sunose (KAS) method (Kissinger, 1957) is a widely used integral method. The Friedman method reveals the dependency of the conversion rate $ln{\left(\frac{d\alpha }{dt}\right)}_{{\alpha }_i}$ over 1/T_αi as a straight line:

$\begin{array}{ll}Friedman:\ln {\left(\frac{\text{d}\alpha }{\text{d}t}\right)}_{{\alpha }_i}=\text{const}-\frac{E_{\alpha }}{R·T_{{\alpha }_i}}& (5)\end{array}$

The apparent activation energy (E_α) at a particular conversion (α) is estimated from the slope of the straight line. Integral methods are relatively less sensitive to data noise as compared to differential isoconversional methods and offer consistent E_α measurements. The KAS method is represented by the following linear Equation (6):

$\begin{array}{ll}KAS:\ln \left(\frac{{\beta }_i}{T_{{\alpha }_i}^2}\right)=\text{const}-\frac{E_{\alpha }}{R·T_{{\alpha }_i}}& (6)\end{array}$

The slope of the linear fit of the $ln\left(\frac{{\beta }_i}{T_{{\alpha }_i}^2}\right)$ vs. 1/T_αi is used to evaluate the apparent E_α.

Model-Fitting Methods

The model-fitting analysis is conventionally used for the pyrolytic assessment of biomass materials on the basis of their devolatilization weight loss measurements using 1st-order decomposition single-step reaction modeling or adding the weight of multiple pseudo-components like cellulose, hemicellulose, lignin, and others (Aboyade et al., 2012). The resulting characteristics from the kinetic analysis by model-fitting yield detailed simulations of biomass pyrolysis experiment data. Also, many studies have reported more precise simulations when using nth-order for specific reaction mechanisms where an optimization of the unknown constant is needed (Osman et al., 2017). Thus, in model-fitting procedures many models were applied to data collected from experiments to achieve the best fit to assess the kinetic parameters.

Combined Kinetics

The simple nth-order reaction has been used extensively to study the pyrolytic kinetics of biomass materials (Xu et al., 2017). The nth-order reaction mechanism for a solid state generally uses an expression like f (α) = (1 − α)ⁿ, which when used in Equation (2) becomes:

$\begin{array}{ll}\frac{\text{d}\alpha }{\text{d}t}=A·\exp \left(-\frac{E_a}{RT}\right)·{\left(1-\alpha \right)}^n& (7)\end{array}$

Another function is the Šesták—Berggren model (Šesták and Berggren, 1971), which was employed for the kinetic fitting of the experimental data. This is because of the high flexibility of the function to investigate the various types of physico-geometrical mechanism of the solid-state reaction (Kissinger, 1957; Opfermann et al., 2002; Vyazovkin et al., 2011; Aboyade et al., 2012), deviating cases with non-integral or fractal reaction geometry (Šimon, 2011; Dussan et al., 2017; Osman et al., 2017), the size distribution of the reactant particles (Orfão et al., 1999), and so on (Zubia et al., 2005). The high flexibility makes it difficult to interpret the physicochemical meanings of the kinetic exponent, but the SB model with the three parameters indicates the highest performance as a fitting function.

$\begin{array}{ll}SB:f\left(\alpha \right)={\alpha }^m.{\left(1-\alpha \right)}^n·{\left[-\ln \left(1-\alpha \right)\right]}^p& (8)\end{array}$

The SB model with three fit parameters (m, n, and p) is considered as one of the highest performing model-fitting methods, where m is accelerating behavior, n represents the order of the reaction and p shows the nuclei growth. By incorporating the SB model, Equation (7) becomes:

$\begin{array}{ll}\frac{\text{d}\alpha }{\text{d}t}=A·exp\left(-\frac{E_a}{RT}\right)·{(1-\alpha )}^n·{\alpha }^m·{\left[-ln(1-\alpha )\right]}^p& (9)\end{array}$

The SB (m, n, p), for specific reaction model functions and other parameters like E_a and A can be optimized by employing a non-linear least square analysis, whereby the residual sum of squares, also known as the sum of squared errors (SSE), is minimized by fitting the data curve of ${\frac{d\alpha }{dt}|}_{\mathit{\text{exp}}}$ from the predicted curve of ${\frac{d\alpha }{dt}|}_{pred}$against time.

$\begin{array}{ll}SSE={\displaystyle \sum }{\left(\frac{\text{d}\alpha }{\text{d}t}{|}_{\mathit{\text{exp}}}-\frac{\text{d}\alpha }{\text{d}t}{|}_{pred}\right)}^2& (10)\end{array}$

A non-linear least square analysis always requires the initial values for SB (m, n, p), E_a and A for optimization. After fitting the data, the goodness of the fit was measured by Fit (%), as in Equation (11).

$\begin{array}{ll}Fit(\%)=\left[1-\frac{\sqrt{SSE}}{{\left(\frac{\text{d}\alpha }{\text{d}t}{|}_{\mathit{\text{exp}}}\right)}_M}\right]\times 100& (11)\end{array}$

where ${\left(\frac{d\alpha }{dt}{|}_{\mathit{\text{exp}}}\right)}_M$ is the peak-maximum conversion rate.

Independent-Parallel Reactions

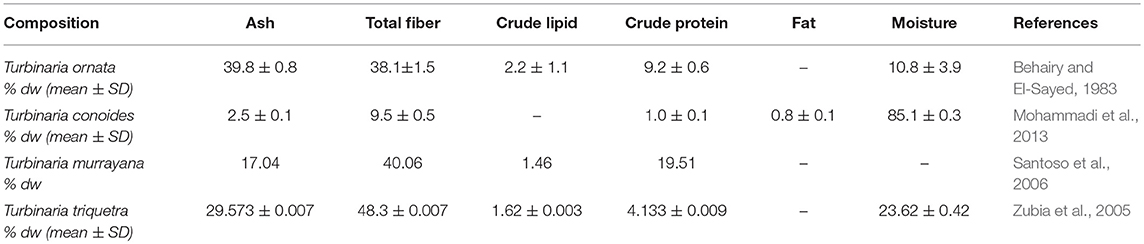
Independent reaction models are mainly employed to identify the roles of the components in the thermal decomposition process. Biomass consists of many components and each component behaves differently. Therefore, these models have a set of discrete multiple reactions and may be extended to continuous distribution, which is largely employed to study the degradation kinetics of lignocellulosic materials. It is commonly accepted that each pseudo-constituent degrades independently at a particular temperature range. The weight loss calculations are performed by taking the sum of the mass fractions from the individual pseudo-components' decomposition rates (Orfão et al., 1999). The polysaccharides of T. ornata are mainly hemicellulose, cellulose, and others. The proximate composition of different Turbinaria species is given in Table 3 below.

TABLE 3

Table 3. Proximate composition of various Turbinaria species.

T. ornata contains many components and each component can be divided into subcomponents. During decomposition, the components which degrade during a similar temperature range may be grouped together and termed as pseudo-component. Lignocellulosic materials are normally classified into three pseudo-components, whereby each pseudo-component is involved in an independent reaction (Orfão et al., 1999). Similarly, the pyrolysis of T. ornata can be presented in terms of three pseudo-independent components, as given in Equation (12).

$\begin{array}{ll}\begin{array}{ll}Pseudo-Hemicellulose\hfill & \stackrel{\frac{\text{d}{\alpha }_1}{\text{d}t}}{\to }\hfill \\ Pseudo-Cellulose\hfill & \stackrel{\frac{\text{d}{\alpha }_2}{\text{d}t}}{\to }\hfill \\ Others\hfill & \stackrel{\frac{\text{d}{\alpha }_3}{\text{d}t}}{\to }\hfill \end{array}\}Volatiles1+Biochar1& (12)\end{array}$

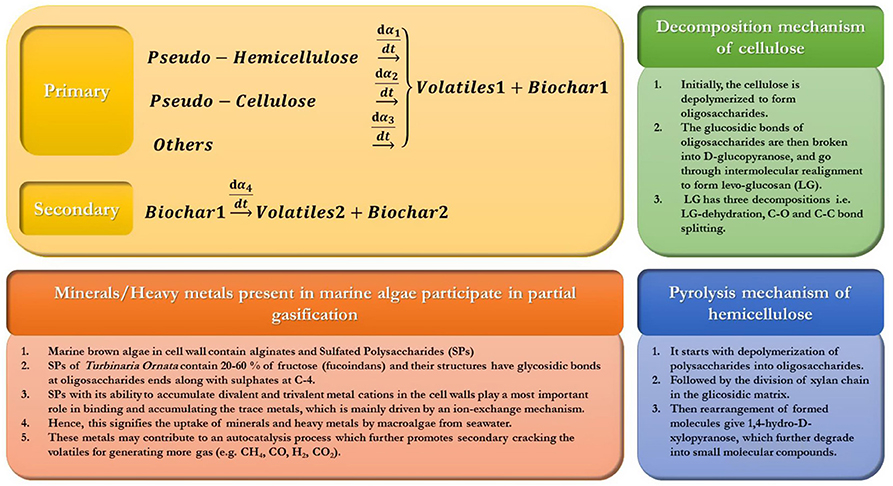
During the main stage of the pyrolysis process, the pseudo-components are subjected to the thermal splitting of chemical bonds for the production of primary Volatiles1, gases (e.g., CH₄, CO₂, and CO), and condensates and yield biochar solids at <500°C, named as Biochar1. Biochar contains minerals and even trace elements which were present in parent biomass. The pyrolytic conversion of three pseudo-components (i.e., pseudo-hemicellulose, pseudo-cellulose, and others) mainly depends on the temperature, particle size, and reactor type. The decomposition of hemicellulose and cellulose usually occurs between 470 to 530 K and 510 to 620 K, respectively, while others like lignin degrade at 550–770 K (Wang et al., 2017). The decomposition of cellulosic materials is mainly induced by depolymerization reactions forming oligosaccharides an then levoglucosan, which is finally decomposed into smaller molecules (Patwardhan et al., 2011). Similarly, the hemicellulose pyrolysis is initiated by the depolymerization of polysaccharides into oligosaccharides and, subsequently, leads to the rearrangement of the molecules, producing 1,4-Anhydro-D-xylopyranose, which further disintegrates into smaller molecular weight components.

At high temperature, secondary decomposition leads to the formation of secondary volatiles (Volatiles2) and biochar (Biochar2). This may include cracking, reforming, condensation, polymerization, oxidation, and gasification (Di Blasi, 2008). During the secondary reactions, Biochar1 forms Volatiles2 and Biochar2, as presented in Equation (13).

$\begin{array}{ll}Biochar1\stackrel{\frac{\text{d}{\alpha }_4}{\text{d}t}}{\to }Volatiles2+Biochar2& (13)\end{array}$

Likewise, the inorganic compounds are also greatly affected during pyrolysis. These inorganic compounds, including heavy metals, may be accumulated in the cell wall and bind ionically and covalently to polysaccharides, which can initiate autocatalytic pyrolysis (Keown et al., 2005). Here, a concept of the partial gasification of T. ornata polluted with heavy metals from the Red Sea is presented in Figure 2.

FIGURE 2

Figure 2. Primary and secondary reactions during pyrolysis of Turbinaria ornata.

These inorganic compounds may include macro/micro minerals (e.g., K, Ca, Na, Mg, Fe, Zn, and Mn) and heavy metals (e.g., Ag, Al, As, Cd, Cr, Co, Hg, Mo, Ni, Pb, and Ti). The pyrolysis process has been previously employed for processing these minerals and heavy metals for valuable products like biochar and bio-oil. For example, alkali and alkaline earth metals (such as K, Ca, and Mg) have notable catalytic effects on the pyrolytic conversion. Vaporization of K has been shown to take place at lower temperatures, while Ca and Mg vaporize at higher temperatures depending on their ionic or covalent bonding with organic molecules (Wei et al., 2012). Liu et al. (2017) reviewed biomass pyrolysis in the presence of inorganic elements including heavy metals and contributed a critical analysis for optimizing the pyrolytic mechanisms with productive resource utilization and a reduction in pyrolysis-based pollutants. Liu et al. (2017) also found that the prior literature has exhibited the enrichment of heavy metals in the solid biochar phase rather than being released into the volatile (gaseous/liquid) phase, and that there is no need to focus on the release of heavy metals in later research. Also, Ni and Cu have been previously used to enhance the quality of pyrolysis products (Richardson et al., 2013; Zhao et al., 2015). Hence, there is an urgent need to investigate the mechanisms for the use of inherited available inorganics and heavy metals to improve the processes and products (Liu et al., 2017). Table 4 presents a few studies on biomass pyrolysis containing salts of heavy metals.

TABLE 4

Table 4. Influence of heavy metals present in biomass during pyrolysis.

The summation of the rate equations in Equation (14) gives the overall degradation rate.

$\begin{array}{ll}\frac{\text{d}\alpha }{\text{d}t}={\displaystyle \sum _{j=1}^4}\frac{{\text{d}\alpha }_j}{\text{d}t}={\displaystyle \sum _{j=1}^4}{x}_j·A_j·exp\left(-\frac{E_{aj}}{RT}\right)·f(\alpha )& (14)\end{array}$

The separation of the pseudo-component peaks was carried out assuming an asymmetric Fraser–Suzuki (FS) distribution with the following function (Perejón et al., 2011):

$\begin{array}{ll}\frac{\text{d}{\alpha }_j}{\text{d}t}=a_{0}exp\left[-ln2{\left\{\frac{ln\left(1+2a_1\frac{T-T_m}{HW}\right)}{a_1}\right\}}^2\right]& (15)\end{array}$

where a₀ is the amplitude, a₁ is the asymmetry, T_m is the peak maximum temperature and HW is the half width of the peak.

Initial values of kinetic parameters were obtained from model-free methods applied to the separated pseudo-components. The optimization of the kinetic parameters was performed by non-linear least square fitting using Equation (10).

Results and Discussions

Thermal Behavior and Reactivity Analysis

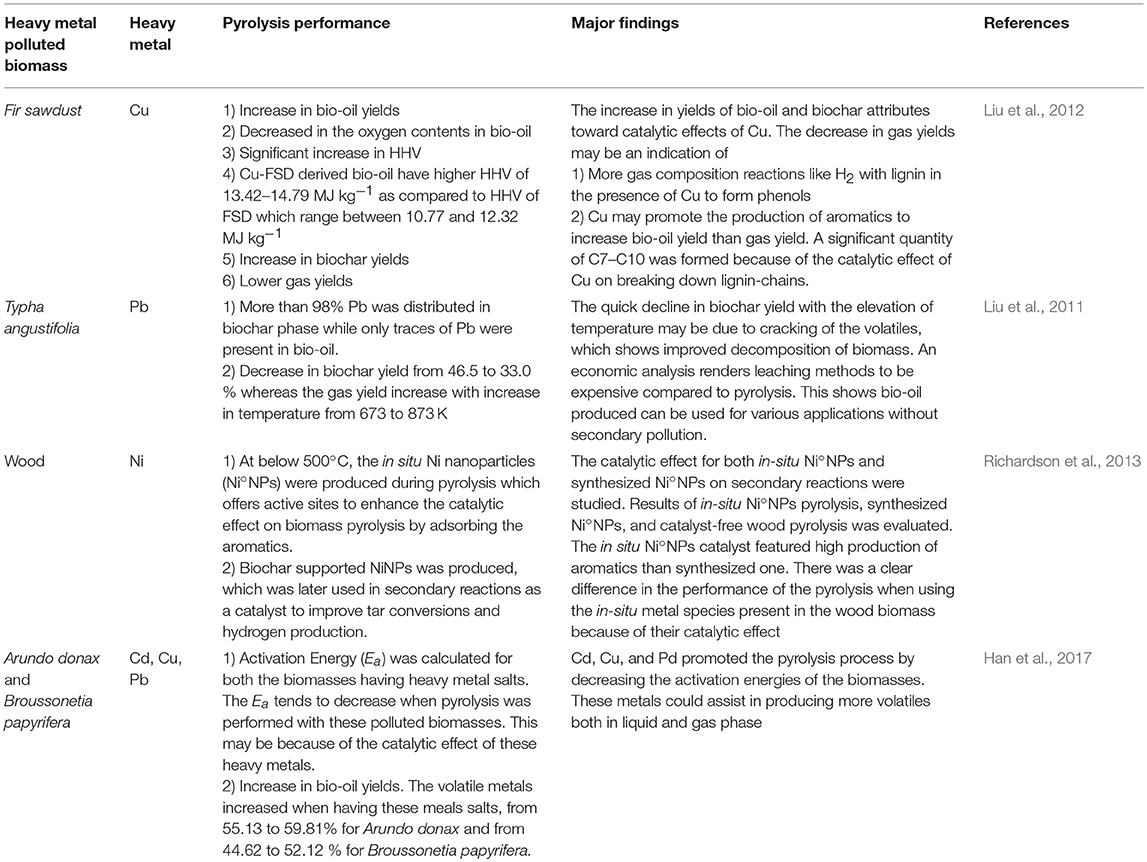
Figure 3 shows the TG and DTG profiling of T. ornata against temperature at different heating rates. T. ornata biomass was pyrolyzed to 850°C at different heating rates. The DTG curves feature two prominent zones, as illustrated in Figure 3B: A primary pyrolysis zone and a secondary reaction zone. In the primary pyrolysis zone, more than 90% of the total amount of mass loss was observed, resulting from reactions such as depolymerization, decarboxylation, and cracking. The maximum mass loss rates increased from 0.043 to 0.290%·s⁻¹ with an incremental increase in the heating rates of 5 to 30°C·min⁻¹. Secondary reaction zones (Zone II), initiated at 875 K, and the remaining mass was decomposed at a slower rate. This slow rate is caused by the trapped volatile matter present in the biochar and delays the decomposition (Richardson et al., 2013). The most common characteristic of all the DTG and TG curves is the increase in the conversion rate and the shifting of the peaks toward the higher temperatures when the heating rates are increased. This increase in conversion rates may be ascribed to the improved transport phenomenon. Meanwhile, the shifting of peaks is rendered to the slowing down of the pyrolysis process owing to the difficulty in the heat transfer from the surrounding to the sample for a shorter time and larger thermal lag (Shuping et al., 2010; Han et al., 2017; Özsin and Pütün, 2017). It can also be perceived from the DTG curves that the peaks in the secondary reaction zone (900–1,100 K) may be caused by the catalytic effect and gasification of the biochar due to the presence of inorganic oxides.

FIGURE 3

Figure 3. (A) Conversion and (B) DTG curves of Turbinaria ornata at 5, 10, 15, and 30°C min⁻¹.

Isoconversional Methods

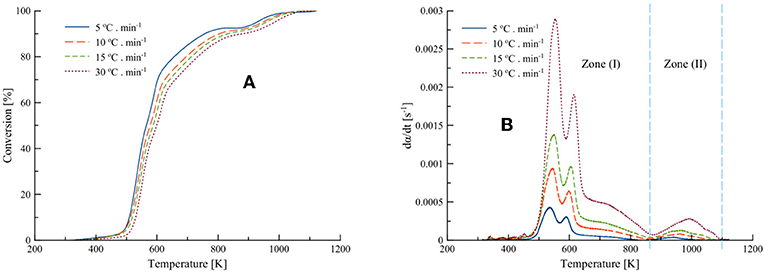
The pyrolytic characteristics were measured using the two isoconversional methods Friedman and KAS. Figure 4 establishes the Arrhenius plot using Equations (5, 6) at different conversions. The data were fitted using linear regression lines for both differential and integral isoconversional methods at the progressive increase of conversion from 10 to 90% with a step size of 5%, as depicted in Figure 4.

FIGURE 4

Figure 4. (A) Friedman and (B) KAS graphs at the different extent of conversions.

The apparent activation energy E_a was measured from the slope of the straight lines from the plots. The quality of the regression models was estimated by the coefficient of determination (R²), which strengthens our confidence in the estimation of E_a from the observed data. The mean apparent activation energy E_α, calculated from the Friedman and KAS isoconversional models, are 164.03 and 146.41 kJ·mol⁻¹, respectively.

Model-Fitting Methods

Model-fitting methods have two stages, namely (a) the estimation of the initial parameters and (b) the application of iterative routines to obtain the optimized values of the kinetic parameters.

Combined Kinetics

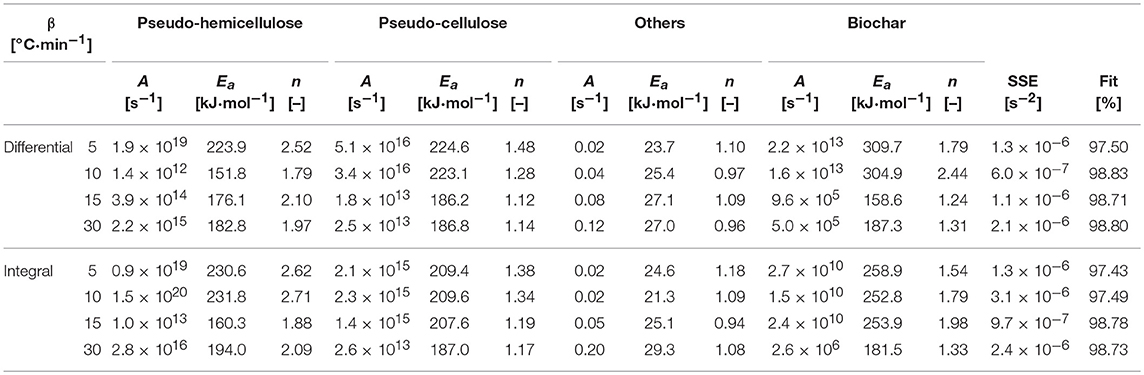
The average activation energies (E_a) obtained from the isoconversional methods (both differential and integral) were used to obtain the order-based and SB model parameters by optimizing Equations (7, 9) using MS Excel Solver. The differential best-fit curves of T. ornata with optimized order-based and SB model parameters at different heating rates (5, 10, 15, and 30°C·min⁻¹) are shown in Figure 5. It is worth noting here that this displays the fitting of the data to order-based and SB models through a single reaction. Moreover, a single heating rate may render inaccuracies; therefore, the mean values calculated at different heating rates are presented in Table 5.

FIGURE 5

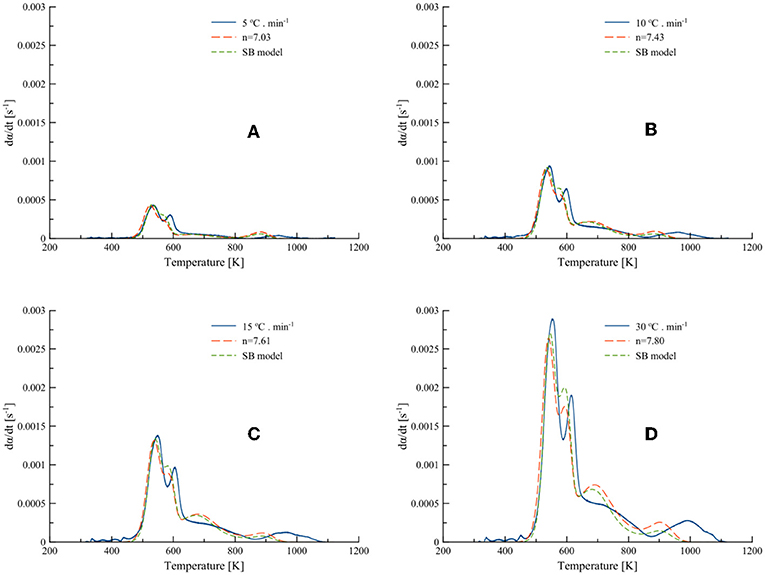
Figure 5. Best-fit DTG curves of Turbinaria ornata with optimized order-based and SB model parameters at (A) 5, (B) 10, (C) 15, and (D) 30°C·min⁻¹.

TABLE 5

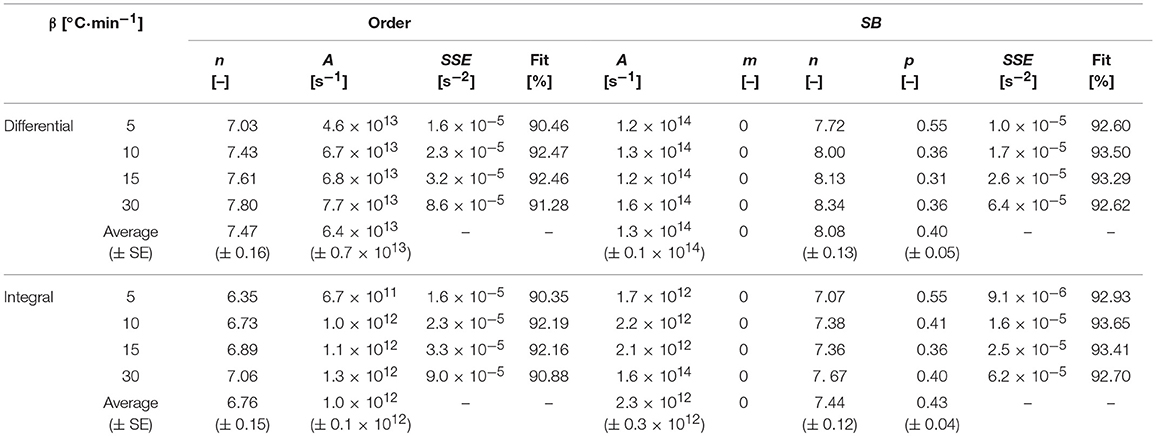
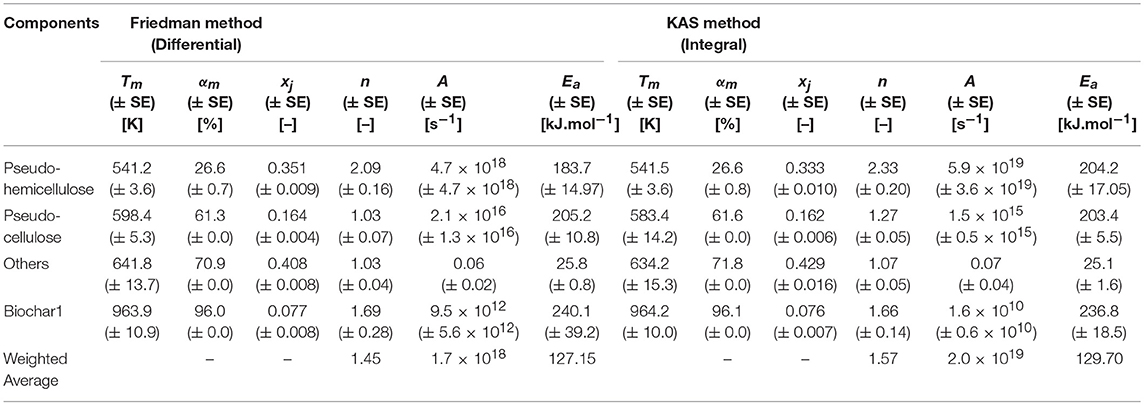
Table 5. Optimized order-based and SB model parameters at different heating rates with isoconversional methods.

The SB model is a powerful tool that allows the measurement of complex degradation mechanisms (Gámiz-González et al., 2017). As is evident from Table 5 and has been previously found as well, one of the SB model parameters is numerically absent (Šesták and Berggren, 1971; Ali et al., 2018). In the present study for all heating rates, parameter m, which corresponds to the deceleration mechanism, was not involved and hence the pyrolysis of macro-algae (T. ornata) was most probably driven by random nucleation and growth (Wang et al., 2006; Li et al., 2010; Ye et al., 2010). Table 5 shows a Fit% higher for the SB model, which indicates that the SB model can better explain thermal degradation than the order-based model. Thus, the parameters obtained from the SB model can better represent the pyrolysis mechanism. The average values of A obtained from the Friedman method were 6.4 × 10¹³ and 1.3 × 10¹⁴, while for the KAS method these were 1.0 × 10¹² and 2.3 × 10¹² for the order-based and SB models, respectively. The values of n for the order-based and SB models were 7.47 and 8.08 for the Friedman method and 6.76 and 7.44 for the KAS method, respectively. The high value of n in the SB model with a higher Fit% (>92) highlights the roles of order-based, diffusion and geometrical contraction in T. ornata pyrolysis. The order-based mechanism can be attributed to the nucleation process in a solid state reaction where the nucleus growth is induced by nuclei collisions with each other (Poletto et al., 2012). The optimum p-values (0.40 and 0.43) signify that the degradation process is partially controlled by the random nucleation mechanism, which randomly promotes the generation of activation centers. It is highly likely that the presence of oxygen carriers (gases and inorganic salts containing heavy metals) could initiate partial gasification (Huang et al., 2013) and catalyze T. ornata pyrolysis. This would increase the weight loss rate and increase the gases produced (like CH₄, H₂, and CO₂) from the pyrolysis of T. ornata and could remove lattice oxygen from the oxygen carriers. Depending upon the amount of inorganics accumulated by the marine algae T. ornata, the catalytic characteristics of heavy metals stimulating pyrolysis and partial gasification could vary.

Independent-Parallel Reactions

From the DTG curves of samples in Figure 3B, it is indicated that the degradation process is taking place in a multiple reaction scheme since the peaks are overlapping in the close temperature range. The thermal decomposition of hemicellulose in T. ornata biomass started at about 473 K, followed by a major mass loss between 550 and 660 K and tailing up to 900 K; then there was a slight shoulder followed by a tail in the temperature range 880–1100 K, which could have induced the partial gasification mechanism using inherited minerals. Most of the mass loss occurs in Zone (I), as shown in Figure 3B, which takes the shape of a shoulder with overlapping peaks, which corresponds to hemicellulose and cellulosic material, followed by the contribution of other components with an interplay of the inherited minerals present in T. ornata collected from the Red Sea. The shoulder and tailing in Zone (II) may correspond to the decomposition of inorganics and could proceed further to a partial gasification process. Hence, it is necessary to apply three parallel-reaction models for the primary reactions in Zone (I) pertaining to the decomposition of pseudo-hemicellulose, pseudo-cellulose and pseudo-others. Overall, the DTG curves at 5, 10, 15, and 30°C·min⁻¹ were decomposed into three primary and one secondary decomposition reactions by employing asymmetric Fraser-Suzuki (FS) distributions, as presented in Figure 6. Recent studies show have shown that the application of the FS function suits the thermal degradation of a solid state reaction into its individual processes (Millán et al., 2017). The mass loss contributions (x_j) of separated peaks obtained from Figure 6 are presented in Table 6.

FIGURE 6

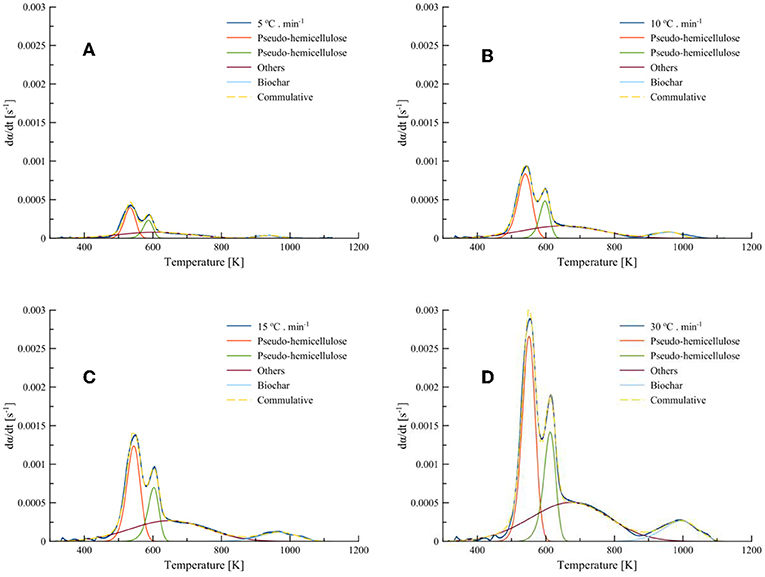
Figure 6. Model-fitting of Turbinaria ornata with three pseudo-components and biochar degradation at (A) 5; (B) 10; (C) 15; and (D) 30°C·min⁻¹.

TABLE 6

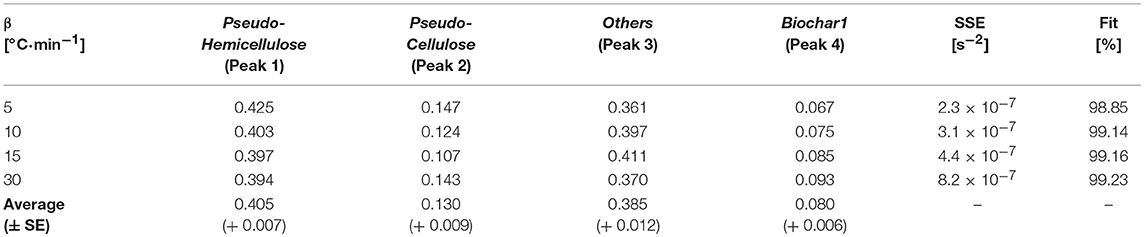
Table 6. Fractional mass loss (x_j) of deconvoluted Turbinaria ornata pseudo-components using FS distribution at different heating rates.

The average relative mass loss contribution (x_j) for pseudo-hemicellulose, pseudo-cellulose, pseudo-others, and biochar at 5, 10, 15, and 30°C·min⁻¹ was 40.5, 13.0, 38.5, and 8.0%, respectively. It can also be seen from Figure 5 that the degradation rates of pseudo-components increase with increasing heating rates. Furthermore, with increasing heating rates the Fit% increases.

The major mass loss comes from the degradation of pseudo-hemicellulose and others, accounting for relative mass loss contributions of 40.5 and 38.5%, respectively. The decomposition continues over wide temperature ranges. The secondary decomposition in Zone (II) contributes to an additional mass loss of 8%, which results in the evolution of more volatiles. Therefore, the remaining mass after secondary decomposition, termed as Biochar2, further decreases. The decompositions of carbohydrates, others, and Biochar1 in the presence of inorganics indicates the cumulative effects of catalysts and gasification. This could encourage flash pyrolysis or rapid heating in order to fully utilize the gasification and catalytic effects of these inorganically rich marine biomasses.

The kinetic parameters of the pseudo-component degradations were estimated using the Friedman and KAS model-free methods on separated deconvoluted peaks. The E_a of the independent-parallel reactions were calculated from the regression plots of Friedman and KAS and the evolution of activation energies with respect to conversion; these are shown in Figure 7.

FIGURE 7

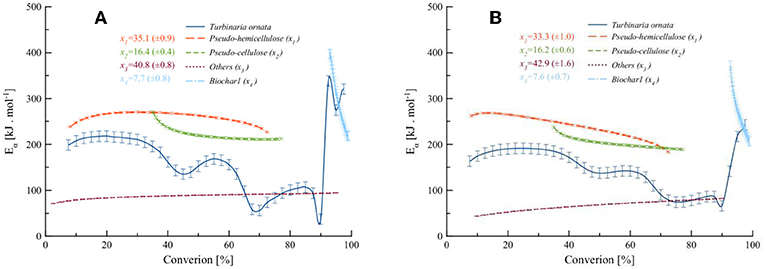
Figure 7. Evolution of activation energies with the conversion from the (A) Friedman method and (B) KAS method.

It is clear from Figure 7 that the primary decompositions overlap and that the interplay of the components causes the overall activation energy decrease until around 90% of the conversion. This aspect has been regarded by some researchers to the condensation of polymers at higher temperature to form char (Chorley, 1892; Basile et al., 2016; Anca-Couce and Scharler, 2017; Ciuta et al., 2018). The secondary conversion of Biochar1 at a higher temperature with a higher activation energy, which drops as the conversion proceeds toward completion. Average activation energies of the pseudo-components and initial parameter values obtained from the Friedman and KAS methods were used to optimize the kinetic parameters via non-linear regression. The SB parameters m and p were absent, hence both order-based and SB models were found to be equivalent. The obtained parameters using differential and integral methods at different heating rates are presented in Table 7.

TABLE 7

Table 7. Optimized kinetic parameters of pseudo-components.

A summary of the key thermal and kinetic parameters is tabulated in Table 8. It is evident that the peak-maximum temperature (T_m) for the decomposition of pseudo-hemicellulose is 541.2 K for the differential Friedman method and 541.5 K for the integral KAS method. The T_m for pseudo-cellulose is 598.4 and 583.4 K using the Friedman and KAS methods, respectively. Pseudo-others decompose with a T_m of 641.8 to 634.2 K according to the Friedman and KAS methods. The decomposition at mild-to-high temperatures may also involve condensation of polymers. Depending on the heating rate, the secondary decomposition of Biochar1 occurs in a temperature range of 870–1,100 K with a T_m of 963.9 and 964.2 K using the Friedman and KAS methods, respectively.

TABLE 8

Table 8. Thermal characteristics of the pseudo-components of Turbinaria ornata pyrolysis.

The average reaction order (n) of the decomposition of pseudo-hemicellulose, pseudo-cellulose, others, and biochar was found to be 2.09, 1.03, 1.03, and 1.69 for the Friedman method and 2.33, 1.27, 1.07, and 1.66 for the KAS method, respectively. Similarly, the average pre-exponential factor (A) of the decomposition of pseudo-hemicellulose, pseudo-cellulose, others, and biochar was found to be 4.7 × 10¹⁸, 2.1 × 10¹⁶, 0.06, and 9.5 × 10¹² s⁻¹, respectively, for the Friedman method and 5.9 × 10¹⁹, 1.5 × 10¹⁵, 0.07, and 1.6 × 10¹⁰ for the KAS method, respectively.

The average E_a of pseudo-hemicellulose obtained from the Friedman and KAS methods was 183.7 and 204.2 kJ.mol⁻¹, respectively. Similarly, the average E_a of pseudo-cellulose using the Friedman and KAS methods was 205.2 and 203.4 kJ.mol⁻¹, respectively. Pseudo-others decomposed with a lower average E_a of 25.8 and 25.1 kJ.mol⁻¹, as estimated from the Friedman and KAS methods, respectively. The average E_a of pseudo-others is very low, which may be due to the formation of polymers owing to the metal oxides from inherited inorganics taken up by T. ornata macro-algae. Jian et al. (2014) found that the E_a of metal oxides was low at higher heating rates, indicating oxygen transport to be a rate limiting step at high temperatures and high heating rates. This may induce a partial gasification phenomenon at this stage. The partial gasification, according to Equation (8), could be due to the inherited metal oxides present in the cell wall of the polysaccharide matrix of T. ornata. The average E_a was calculated for the degradation of Biochar1, which was 240.1 and 236.5 kJ.mol⁻¹ using the Friedman and KAS methods, respectively. It can also be deduced that the variation in the values of A, n, and E_a was the greatest during the secondary decomposition of Biochar1 in Zone (II) among the other pseudo-components. Moreover, the sharp decrease in the E_a of Biochar1 is a mere indication of the spontaneity of the process.

Conclusions

Marine macro-algae contains inorganics, including heavy metals, the amount of which depends on the macro-algae's ability to uptake these as well as the concentration of inorganics dissolved in the marine environment. While this help mitigates the heavy metals, their disposal needs care. Pyrolysis offers not only a means to handle such materials but also the ability to use these to our benefit in the form of valuable products such as volatiles and biochar. The Red Sea is a rich source of many minerals, which are taken up by the organisms living there. The role of these organisms in this process is important and needs to be evaluated using complex models. A four-component independent-reaction model using a simple order-based mechanism for each reaction is sufficient to analyze the pyrolytic kinetics. This shows that three primary reactions proceed simultaneously, producing a solid product which degrades through a secondary decomposition reaction at a higher temperature. Interestingly, the activation energy drops considerably for the secondary reaction, hinting at the partial gasification and the catalytic effects of the minerals inherent in the macro-algae.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling Editor declared a shared affiliation at the time of review, though no other collaboration, with the authors.

References

Abdallah, A. M. A., Abdallah, M. A., Beltagy, A., and Siam, E. (2006). Contents of heavy metals in marine algae from Egyptian Red Sea coast. Toxicol. Environ. Chem. 88, 9–22. doi: 10.1080/02772240500414911

CrossRef Full Text | Google Scholar

Aboyade, A. O., Carrier, M., Meyer, E. L., Knoetze, J. H., and Görgens, J. F. (2012). Model fitting kinetic analysis and characterisation of the devolatilization of coal blends with corn and sugarcane residues. Thermochim. Acta 530, 95–106. doi: 10.1016/j.tca.2011.12.007

CrossRef Full Text | Google Scholar

Adanez, J., Abad, A., Garcia-Labiano, F., Gayan, P., and de Diego, L. F. (2012). Progress in chemical-looping combustion and reforming technologies. Prog. Energy Combust. Sci. 38, 215–282. doi: 10.1016/j.pecs.2011.09.001

CrossRef Full Text | Google Scholar

Agency, I. E. (2017). Energy Technology Perspectives 2017: Catalysing Energy Technology Transformations. OECD/IEA.

Ali, I., Naqvi, S. R., and Bahadar, A. (2018). Kinetic analysis of Botryococcus braunii pyrolysis using model-free and model fitting methods. Fuel 214, 369–380. doi: 10.1016/j.fuel.2017.11.046

CrossRef Full Text | Google Scholar

Anca-Couce, A., and Scharler, R. (2017). Modelling heat of reaction in biomass pyrolysis with detailed reaction schemes. Fuel 206, 572–579. doi: 10.1016/j.fuel.2017.06.011

CrossRef Full Text | Google Scholar

Baghel, R. S., Mantri, V. A., and Reddy, C. R. K (2017). “A new wave of research interest in marine macroalgae for chemicals and fuels: challenges and potentials,” in Fuels, Chemicals and Materials from the Oceans and Aquatic Sources, eds. F. M. Kerton, and N. Yan (John Wiley and Sons, Ltd), 43–63. doi: 10.1002/9781119117193.ch3

CrossRef Full Text | Google Scholar

Basile, L., Tugnoli, A., Stramigioli, C., and Cozzani, V. (2016). Thermal effects during biomass pyrolysis. Thermochim. Acta 636, 63–70. doi: 10.1016/j.tca.2016.05.002

CrossRef Full Text | Google Scholar

Behairy, A. K. A., and El-Sayed, M. M. (1983). Biochemical Composition of Some Marine Brown Algae From Jeddah Coast, Saudi Arabia. IJMS Vol.12(3) [September 1983]. Available online at: http://nopr.niscair.res.in/handle/123456789/38893 (Accessed December 17, 2017).

Bold, H. C., and Wynne, M. J. (1984). Introduction to the Algae, 2nd Edn. Englewood Cliffs, NJ: Prentice-Hall.

Google Scholar

Bruckner, A., Rowlands, G., Riegl, B., Purkis, S., Williams, A., and Renaud, P. (2013). Atlas of Saudi Arabian Red Sea Marine Habitats. Oceanography Faculty Books and Book Chapters. Available online at: http://nsuworks.nova.edu/occ_facbooks/33

Chorley, C. (1892). The destructive distillation of wood. J. Soc. Chem. Industry 11, 872–874. doi: 10.1002/jctb.5000111104

CrossRef Full Text | Google Scholar

Ciuta, S., Tsiamis, D., and Castaldi, M. J. (2018). “Chapter two - fundamentals of gasification and pyrolysis,” in Gasification of Waste Materials, eds S. Ciuta, D. Tsiamis, and M. J. Castaldi (Academic Press), 13–36. doi: 10.1016/B978-0-12-812716-2.00002-9

CrossRef Full Text

Davis, T. A., Volesky, B., and Mucci, A. (2003). A review of the biochemistry of heavy metal biosorption by brown algae. Water Res. 37, 4311–4330. doi: 10.1016/S0043-1354(03)00293-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Deepak, P., Sowmiya, R., Balasubramani, G., and Perumal, P. (2017a). Phytochemical profiling of Turbinaria ornata and its antioxidant and anti-proliferative effects. J. Taibah Univ. Med. Sci. 12, 329–337. doi: 10.1016/j.jtumed.2017.02.002

CrossRef Full Text | Google Scholar

Deepak, P., Sowmiya, R., Ramkumar, R., Balasubramani, G., Aiswarya, D., and Perumal, P. (2017b). Structural characterization and evaluation of mosquito-larvicidal property of silver nanoparticles synthesized from the seaweed, Turbinaria ornata (Turner) J. Agardh 1848. Artif. Cells Nanomed. Biotechnol. 45, 990–998. doi: 10.1080/21691401.2016.1198365

PubMed Abstract | CrossRef Full Text | Google Scholar

Di Blasi, C. (2008). Modeling chemical and physical processes of wood and biomass pyrolysis. Progr. Energy Combust. Sci. 34, 47–90. doi: 10.1016/j.pecs.2006.12.001

CrossRef Full Text | Google Scholar

Dussan, K., Dooley, S., and Monaghan, R. (2017). Integrating compositional features in model compounds for a kinetic mechanism of hemicellulose pyrolysis. Chem. Eng. J. 328, 943–961. doi: 10.1016/j.cej.2017.07.089

CrossRef Full Text | Google Scholar

El-Naggar, M. E. E., and Al-Amoudi, O. A. (1989). Heavy metal levels in several species of marine algae from the Red Sea of Saudia Aabia. J. King Abdulaziz Univ. Sci. J. 1, 5–13. doi: 10.4197/Sci.1-1.1

CrossRef Full Text | Google Scholar

Ferdouse, F., Holdt, S. L., Smith, R., Murúa, P., and Yang, Z. (2018). The Global Status of Seaweed Production, Trade and Utilization. Rome, Italy: Products, Trade and Marketing Branch, Fisheries and Aquaculture Policy and Resources Division, Food and Agriculture Organization of the United Nations Available online at: http://www.fao.org/in-action/globefish/publications/details-publication/en/c/1154074/ (Accessed Jan 26, 2019).

Friedman, H. L. (1964). Kinetics of thermal degradation of char-forming plastics from thermogravimetry. application to a phenolic plastic. J. Polym. Sci. C Polym. Symp. 6, 183–195.

Google Scholar

Gámiz-González, M. A., Correia, D. M., Lanceros-Mendez, S., Sencadas, V., Gómez Ribelles, J. L., and Vidaurre, A. (2017). Kinetic study of thermal degradation of chitosan as a function of deacetylation degree. Carbohydr. Polym. 167, 52–58. doi: 10.1016/j.carbpol.2017.03.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghadiryanfar, M., Rosentrater, K. A., Keyhani, A., and Omid, M. (2016). A review of macroalgae production, with potential applications in biofuels and bioenergy. Renew. Sustain. Energy Rev. 54, 473–481. doi: 10.1016/j.rser.2015.10.022

CrossRef Full Text | Google Scholar

Grigiante, M., Brighenti, M., and Antolini, D. (2016). A generalized activation energy equation for torrefaction of hardwood biomasses based on isoconversional methods. Renew. Energy 99, 1318–1326. doi: 10.1016/j.renene.2016.07.054

CrossRef Full Text | Google Scholar

Han, Z., Guo, Z., Zhang, Y., Xiao, X., Xu, Z., and Sun, Y. (2017). Pyrolysis characteristics of biomass impregnated with cadmium, copper and lead: influence and distribution. Waste Biomass Valor 2017, 1–8. doi: 10.1007/s12649-017-0036-5

CrossRef Full Text | Google Scholar

Hong, Y., Chen, W., Luo, X., Pang, C., Lester, E., and Wu, T. (2017). Microwave-enhanced pyrolysis of macroalgae and microalgae for syngas production. Bioresour. Technol. 237, 47–56. doi: 10.1016/j.biortech.2017.02.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, Z., Deng, Z., He, F., Chen, D., Wei, G., Zhao, K., et al. (2017). Reactivity investigation on chemical looping gasification of biomass char using nickel ferrite oxygen carrier. Int. J. Hydrogen Energy 42, 14458–14470. doi: 10.1016/j.ijhydene.2017.04.246

CrossRef Full Text | Google Scholar

Huang, Z., He, F., Feng, Y., Liu, R., Zhao, K., Zheng, A., et al. (2013). Characteristics of biomass gasification using chemical looping with iron ore as an oxygen carrier. Int. J. Hydrogen Energy 38, 14568–14575. doi: 10.1016/j.ijhydene.2013.09.022

CrossRef Full Text | Google Scholar

Jian, G., Zhou, L., Piekiel, N. W., and Zachariah, M. R. (2014). Low effective activation energies for oxygen release from metal oxides: evidence for mass-transfer limits at high heating rates. ChemPhysChem 15, 1666–1672. doi: 10.1002/cphc.201301148

PubMed Abstract | CrossRef Full Text | Google Scholar

Kayalvizhi, K., Asmathunisha, N., Subramanian, V., and Kathiresan, K. (2014). Purification of silver and gold nanoparticles from two species of brown seaweeds (Padina tetrastromatica and Turbinaria ornata). J. Med. Plants Stud. 2, 32–37.

Google Scholar

Keown, D. M., Favas, G., Hayashi, J., and Li, C. Z. (2005). Volatilisation of alkali and alkaline earth metallic species during the pyrolysis of biomass: differences between sugar cane bagasse and cane trash. Bioresour. Technol. 96, 1570–1577. doi: 10.1016/j.biortech.2004.12.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Kissinger, H. E. (1957). Reaction kinetics in differential thermal analysis. Anal. Chem. 29, 1702–1706 doi: 10.1021/ac60131a045

CrossRef Full Text | Google Scholar

Li, D., Chen, L., Yi, X., Zhang, X., and Ye, N. (2010). Pyrolytic characteristics and kinetics of two brown algae and sodium alginate. Bioresour. Technol. 101, 7131–7136. doi: 10.1016/j.biortech.2010.03.145

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, W. J., Li, W. W., Jiang, H., and Yu, H. Q. (2017). Fates of chemical elements in biomass during its pyrolysis. Chem. Rev. 117, 6367–6398. doi: 10.1021/acs.chemrev.6b00647

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, W. J., Tian, K., Jiang, H., Zhang, X. S., Ding, H. S., and Yu, H. Q. (2012). Selectively improving the bio-oil quality by catalytic fast pyrolysis of heavy-metal-polluted biomass: take copper (Cu) as an example. Environ. Sci. Technol. 46, 7849–7856. doi: 10.1021/es204681y

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, W. J., Zeng, F. X., Jiang, H., Zhang, X. S., and Yu, H. Q. (2011). Techno-economic evaluation of the integrated biosorption–pyrolysis technology for lead (Pb) recovery from aqueous solution. Bioresour. Technol. 102, 6260–6265. doi: 10.1016/j.biortech.2011.02.104

PubMed Abstract | CrossRef Full Text | Google Scholar

Maceiras, R., Rodri'guez, M., Cancela, A., Urréjola, S., and Sánchez, A. (2011). Macroalgae: raw material for biodiesel production. Appl. Energy 88, 3318–3323. doi: 10.1016/j.apenergy.2010.11.027

CrossRef Full Text | Google Scholar

Manivannan, K., Thirumaran, G., Devi, G. K., Anantharaman, P., and Balasubramanian, T. (2009). Proximate composition of different group of seaweeds from Vedalai coastal waters (Gulf of Mannar): southeast coast of India. Middle East J. Sci. Res. 4, 72–77.

Google Scholar

Millán, L. M. R., Vargas, F. E. S., and Nzihou, A. (2017). Kinetic analysis of tropical lignocellulosic agrowaste pyrolysis. Bioenerg. Res. 10, 832–845. doi: 10.1007/s12155-017-9844-5

CrossRef Full Text | Google Scholar

Mohamed Ali, D., and Elnabawy Ward, F. M. (2016). Ecological and biochemical analyses of the brown alga Turbinaria ornata (Turner) J. Agardh from Red Sea coast, Egypt. J. Coastal Life Med. 4, 187–192. doi: 10.12980/jclm.4.2016j6-10

CrossRef Full Text | Google Scholar

Mohammadi, M., Tajik, H., and Hajeb, P. (2013). Nutritional composition of seaweeds from the Northern Persian Gulf. Iran. J. Fish. Sci. 12, 232–240.

Google Scholar

Mohan, D., Pittman Charles, U., and Steele, P. H. (2006). Pyrolysis of wood/biomass for bio-oil: a critical review. Energy Fuels 20, 848–889. doi: 10.1021/ef0502397

CrossRef Full Text | Google Scholar

Oliveira, J. (2016). An Integrated Use of Macroalgae as Bioproducts Source and Biosorbent for Environmental Applications. Porto: Faculdade de Engenharia da Universidade do Porto.

Google Scholar

Omar, H. H., Shiekh, H. M., Gumgumjee, N. M., El-Kazan, M. M., and El-Gendy, A. M. (2012). Antibacterial activity of extracts of marine algae from the Red Sea of Jeddah, Saudi Arabia. Afr. J. Biotechnol. 11, 13576–13585. doi: 10.5897/AJB12.780

CrossRef Full Text | Google Scholar

Opfermann, J. R., Kaisersberger, E., and Flammersheim, H. J. (2002). Model-free analysis of thermoanalytical data-advantages and limitations. Thermochimica Acta 391, 119–127. doi: 10.1016/S0040-6031(02)00169-7

CrossRef Full Text | Google Scholar

Orfão, J. J. M., Antunes, F. J. A., and Figueiredo, J. L. (1999). Pyrolysis kinetics of lignocellulosic materials—three independent reactions model. Fuel 78, 349–358 doi: 10.1016/S0016-2361(98)00156-2

CrossRef Full Text | Google Scholar

Ortiz-Calderon, C., Silva, H. C., and Vásquez, D. B. (2017). “Metal removal by seaweed,” in Biomass Volume Estimation and Valorization for Energy, ed J. S. Tumuluru (InTechOpen), 361–380.

Google Scholar

Osman, A. I., Abdelkader, A., Johnston, C. R., Morgan, K., and Rooney, D. W. (2017). Thermal investigation and kinetic modeling of lignocellulosic biomass combustion for energy production and other applications. Ind. Eng. Chem. Res. 56, 12119–12130. doi: 10.1021/acs.iecr.7b03478

CrossRef Full Text | Google Scholar

Özsin, G., and Pütün, A. E. (2017). Insights into pyrolysis and co-pyrolysis of biomass and polystyrene: thermochemical behaviors, kinetics and evolved gas analysis. Energy Convers. Manage. 149, 675–685. doi: 10.1016/j.enconman.2017.07.059

CrossRef Full Text | Google Scholar

Patwardhan, P. R., Dalluge, D. L., Shanks, B. H., and Brown, R. C. (2011). Distinguishing primary and secondary reactions of cellulose pyrolysis. Bioresour. Technol. 102, 5265–5269. doi: 10.1016/j.biortech.2011.02.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Perejón, A., Sánchez-Jiménez, P. E., Criado, J. M., and Pérez-Maqueda, L. A. (2011). Kinetic analysis of complex solid-state reactions. A new deconvolution procedure. J. Phys. Chem. B 115, 1780–1791. doi: 10.1021/jp110895z

PubMed Abstract | CrossRef Full Text | Google Scholar

Poletto, M., Zattera, A. J., and Santana, R. M. (2012). Thermal decomposition of wood: Kinetics and degradation mechanisms. Bioresour. Technol. 126, 7–12. doi: 10.1016/j.biortech.2012.08.133

PubMed Abstract | CrossRef Full Text | Google Scholar

Ponnan, A., Ramu, K., Marudhamuthu, M., Marimuthu, R., Siva, K., and Kadarkarai, M. (2017). Antibacterial, antioxidant and anticancer properties of Turbinaria conoides (J. Agardh) Kuetz. Clin. Phytosci. 3:5. doi: 10.1186/s40816-017-0042-y

CrossRef Full Text | Google Scholar

Rajeshkumar, S., Malarkodi, C., Gnanajobitha, G., Paulkumar, K., Vanaja, M., Kannan, C., et al. (2013). Seaweed-mediated synthesis of gold nanoparticles using Turbinaria conoides and its characterization. J. Nanostruct. Chem. 3:44. doi: 10.1186/2193-8865-3-44

CrossRef Full Text | Google Scholar

Ranzi, E., Debiagi, P. E. A., and Frassoldati, A. (2017). Mathematical modeling of fast biomass pyrolysis and bio-oil formation. note I: kinetic mechanism of biomass pyrolysis. ACS Sustain. Chem. Eng. 5, 2867–2881. doi: 10.1021/acssuschemeng.6b03096

CrossRef Full Text | Google Scholar

Richardson, Y., Motuzas, J., Julbe, A., Volle, G., and Blin, J. (2013). Catalytic investigation of in situ generated Ni metal nanoparticles for tar conversion during biomass pyrolysis. J. Phys. Chem. C 117, 23812–23831. doi: 10.1021/jp408191p

CrossRef Full Text | Google Scholar

Roesijadi, G., Jones, S., Snowden-Swan, L., and Zhu, Y. (2010). Macroalgae as a Biomass Feedstock: A Preliminary Analysis. U.S. Department of Energy. doi: 10.2172/1006310

CrossRef Full Text | Google Scholar

Ross, A. B., Jones, J. M., Kubacki, M. L., and Bridgeman, T. (2008). Classification of macroalgae as fuel and its thermochemical behaviour. Bioresour. Technol. 99, 6494–6504. doi: 10.1016/j.biortech.2007.11.036

PubMed Abstract | CrossRef Full Text | Google Scholar

Roy, S., P, A., Attia, A. M., and Attia, A. A. A. (2017). Heavy Metals Accumulation of Different Parts of Turbinaria spp. along the Olaikuda Coast, Rameshwaram, Tamilnadu, India. IARJSET 4, 99–102. doi: 10.17148/IARJSET.2017.4319

CrossRef Full Text | Google Scholar

Saha, B., and Orvig, C. (2010). Biosorbents for hexavalent chromium elimination from industrial and municipal effluents. Coordinat. Chem. Rev. 254, 2959–2972. doi: 10.1016/j.ccr.2010.06.005

CrossRef Full Text | Google Scholar

Santoso, J., Gunji, S., Yoshie-Stark, Y., and Suzuki, T. (2006). Mineral contents of indonesian seaweeds and mineral solubility affected by basic cooking. Food Sci. Technol. Res. 12, 59–66. doi: 10.3136/fstr.12.59

CrossRef Full Text | Google Scholar

Šesták, J., and Berggren, G. (1971). Study of the kinetics of the mechanism of solid-state reactions at increasing temperatures. Thermochim. Acta 3, 1–12 doi: 10.1016/0040-6031(71)85051-7

CrossRef Full Text | Google Scholar

Sheldon, R. A. (2014). Green and sustainable manufacture of chemicals from biomass: state of the art. Green Chem. 16, 950–963. doi: 10.1039/C3GC41935E

CrossRef Full Text | Google Scholar

Shuping, Z., Yulong, W., Mingde, Y., Chun, L., and Junmao, T. (2010). Pyrolysis characteristics and kinetics of the marine microalgae Dunaliella tertiolecta using thermogravimetric analyzer. Bioresour. Technol. 101, 359–365. doi: 10.1016/j.biortech.2009.08.020

PubMed Abstract | CrossRef Full Text | Google Scholar

Siddall, M., Smeed, D. A., Hemleben, C., Rohling, E. J., Schmelzer, I., and Peltier, W. R. (2004). Understanding the Red Sea response to sea level. Earth Planet. Sci. Lett. 225, 421–434. doi: 10.1016/j.epsl.2004.06.008

CrossRef Full Text | Google Scholar

Šimon, P. (2011). Fourty years of the Šesták–Berggren equation. Thermochim. Acta 520, 156–157. doi: 10.1016/j.tca.2011.03.030

CrossRef Full Text | Google Scholar

Spalding, M. D., Green, E. P., and Ravilious, C. (2001). World Atlas of Coral Reefs, 1st Edn. Berkeley, CA: University of California Press.

Google Scholar

Stranska-Zachariasova, M., Kurniatanty, I., Gbelcova, H., Jiru, M., Rubert, J., Nindhia, T. G., et al. (2017). Bioprospecting of turbinaria macroalgae as a potential source of health protective compounds. Chem. Biodivers. 14:201600192. doi: 10.1002/cbdv.201600192

PubMed Abstract | CrossRef Full Text | Google Scholar

Tenorio-Rodriguez, P. A., Murillo-Álvarez, J. I., Campa-Cordova, Á. I., and Angulo, C. (2017). Antioxidant screening and phenolic content of ethanol extracts of selected Baja California Peninsula macroalgae. J. Food Sci. Technol. 54, 422–429. doi: 10.1007/s13197-016-2478-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Vyazovkin, S., Burnham, A. K., Criado, J. M., Pérez-Maqueda, L. A., Popescu, C., and Sbirrazzuoli, N. (2011). ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 520, 1–19. doi: 10.1016/j.tca.2011.03.034

CrossRef Full Text | Google Scholar

Vyazovkin, S., and Wight, C. A. (1998). Isothermal and non-isothermal kinetics of thermally stimulated reactions of solids. Int. Rev. Phys. Chem. 17, 407–433. doi: 10.1080/014423598230108

CrossRef Full Text | Google Scholar

Wang, J., Wang, G., Zhang, M., Chen, M., Li, D., Min, F., et al. (2006). A comparative study of thermolysis characteristics and kinetics of seaweeds and fir wood. Process Biochem. 41, 1883–1886. doi: 10.1016/j.procbio.2006.03.018

CrossRef Full Text | Google Scholar

Wang, S., Dai, G., Yang, H., and Luo, Z. (2017). Lignocellulosic biomass pyrolysis mechanism: a state-of-the-art review. Prog. Energy Combust. Sci. 62, 33–86. doi: 10.1016/j.pecs.2017.05.004

CrossRef Full Text | Google Scholar

Wei, X., Zhang, G., Cai, Y., Li, L., and Li, H. (2012). The volatilization of trace elements during oxidative pyrolysis of a coal from an endemic arsenosis area in southwest Guizhou, China. J. Analyt. Appl. Pyrol. 98, 184–193. doi: 10.1016/j.jaap.2012.08.015

CrossRef Full Text | Google Scholar

Xu, T., Xu, F., Hu, Z., Chen, Z., and Xiao, B. (2017). Non-isothermal kinetics of biomass-pyrolysis-derived-tar (BPDT) thermal decomposition via thermogravimetric analysis. Energy Convers. Manage. 138, 452–460. doi: 10.1016/j.enconman.2017.02.013

CrossRef Full Text | Google Scholar

Ye, N., Li, D., Chen, L., Zhang, X., and Xu, D. (2010). Comparative studies of the pyrolytic and kinetic characteristics of maize straw and the seaweed ulva pertusa. PLoS ONE 5:e0012641. doi: 10.1371/journal.pone.0012641

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, H., Guo, L., and Zou, X. (2015). Chemical-looping auto-thermal reforming of biomass using Cu-based oxygen carrier. Appl. Energy 157, 408–415. doi: 10.1016/j.apenergy.2015.04.093

CrossRef Full Text | Google Scholar

Zubia, M., Payri, C. E., Deslandes, E., and Guezennec, J. (2005). Chemical Composition of Attached and Drift Specimens of Sargassum mangarevense and Turbinaria ornata (Phaeophyta: Fucales) from Tahiti, French Polynesia. Bot. Mar. 46, 562–571. doi: 10.1515/BOT.2003.059

CrossRef Full Text | Google Scholar