Study on Calculation Method of Soluble Aerosol Removal Efficiency Under High Humidity Condition

Introduction

Containment is the last shield for protecting the safety of nuclear power plants (NPPs). It is of significance to guarantee its integrity. However, once a long-term loss of core coolant accident (LOCA) occurred, the core molten materials would melt through the pressure vessel. Then, large amounts of coolant would flow into the containment and experience flash evaporation, accompanied by large amounts of non-condensable gas generated by the interaction of a core meltdown and concrete in the pitch. It would cause the pressure inside the containment to rise persistently. Once the containment pressure rises beyond the threshold pressure, rupture of containment would appear and cause leakage of radioactive material into the environment. Filter Containment Venting System (FCVS) is designed to reduce the pressure in the containment through actively venting and reducing the radioactive release through multi-scrubbers. Because of the advantages of a larger specific transfer area and long bubble resident time in liquid pool, bubble column possesses a potential capability for aerosol retention. So far, the bubble column has been used in FCVS, such as the FCVS system composed of wet scrubber and metal fiber designed by Control Components Inc. (CCI) which has been installed in Swiss Nuclear Power Plants (Basu, 2014).

Aerosol as the main component of fission products behaves strong diffusion and migration properties, thus, it is important to prevent aerosol leak into the environment. According to its solubility, aerosol can be divided into soluble aerosol (such as CsI, CsOH, etc) and insoluble aerosol (such as ⁹⁰Sr, SnO₂, etc) (Jokiniemi, 2007; Tamotsu et al., 2007; Miwa et al., 2015). Soluble aerosol has hygroscopic properties. It means soluble aerosol can absorb water when the relative humidity (RH) of the surrounding environment increases. In the process of increasing relative humidity, significant particle growth occurs only once a critical relative humidity is reached (the exact value of which depends on the temperature and the initial size of the dry particle), called the deliquescence point (DRH). At the same time, a droplet of saturated solution is instantaneously formed. However, the dissolved aerosol will lose water when the relative humidity keeps decreasing. Similarly, it will transform into a crystalline particulate once a critical relative humidity is attained which is called the efflorescence point (ERH). Besides, the hysteresis phenomenon (DRH>ERH) also exists (Hämeri et al., 2001; Gysel et al., 2002). The relative humidity of aerosol laden gas will increase significantly when passing through the liquid pool, which will cause the hygroscopic growth of soluble aerosol. For the aerosol removal efficiency evaluation method based on the mass concentration or the count concentration, this hygroscopic growth phenomenon will lead to a significant deviation in the calculation results of aerosol removal efficiency (Peyres and Herranz, 1996).

Similar scenes of accidents also include the suppression pool in the boiling water reactor and the rupture of the steam generator tube in the pressurized water reactor. All of the above accidents involve the process of aerosol laden gas passing through a liquid pool, which will cause the relative humidity of carried gas to increase (Herranz et al., 1997). The research on the hygroscopic properties of soluble aerosol mainly focuses on the atmospheric environment field. In terms of experimental research, Gysel studied the hygroscopic properties of 100 nm sodium chloride (NaCl), ammonium sulfate ((NH4)₂SO₄) and sodium nitrate (NaNO₃) under different humidity conditions through H-TDMA experimental facility (Gysel et al., 2002). The experiment results showed that NaCl and (NH4)₂SO₄ had an obvious deliquescence point and efflorescence point, while NaNO₃ did not show an obvious deliquescence and efflorescence phenomenon. Biskos measured the hygroscopic growth characteristics of 6–60 nm NaCl, and found that the hygroscopic growth factor of NaCl decreased with the decrease of particle size, yet the deliquescence point increased with the decrease of particle size (Biskos et al., 2006). In terms of theoretical research, the hygroscopic growth model of aerosol is mainly based on the Kohler theory (Kohler, 1936), which is based on the spherical hypothesis and takes into account the Kelvin effect of particle size, and proposes a theoretical relationship between particle size and the relative humidity when aerosol particle reaches the hygroscopic equilibrium. Subsequently, Biskos et al. (2006) considered the shape correction factor related to particle size and modified the hygroscopic growth model. In this study, a Scanning Mobility Particle Sizer (SMPS, TSI3082), equipped with a condensation particle counter (CPC) were used to analyze the aerosol size distribution and concentration at the inlet and outlet of a bubble column. It is expected to modify the size distribution and concentration curve of aerosol at the outlet of the bubble column with the help of the hygroscopic growth theory to obtain the actual size-dependency of removal efficiency.

Experimental Setup

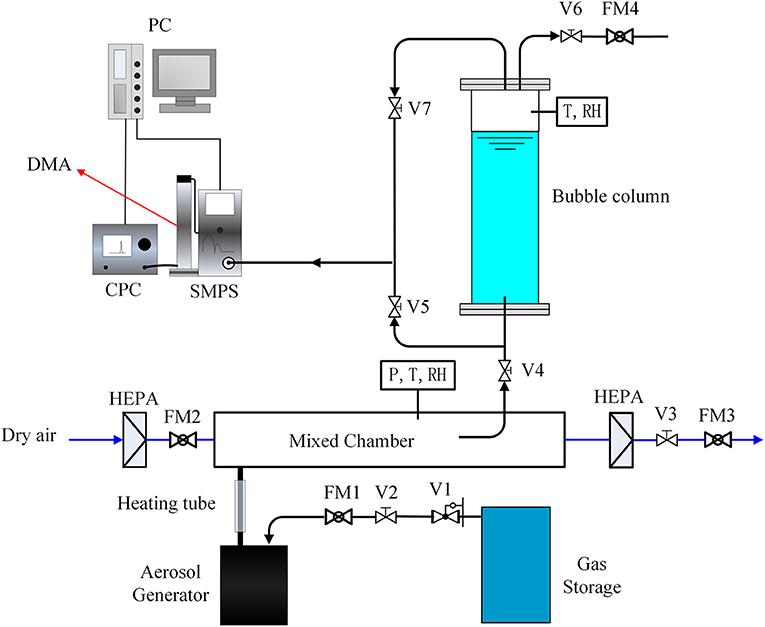
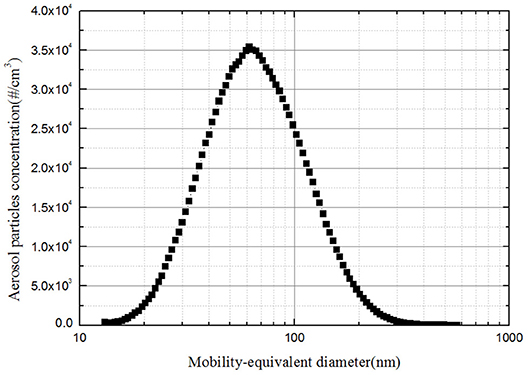
Figure 1 shows the schematic diagram of the aerosol test facility. The experiments were conducted in a rectangular bubble column, which is made of polymethyl methacrylate with a cross section of 150 × 150 mm and a variable height of up to 1.5 m. As model soluble particles, sodium chloride was used because the hygroscopicity of NaCl has been deeply investigated in the previous research. The sodium chloride particles were generated by atomization of 3 wt% salt solutions. The salt aerosol generator(TSI Model 8118A)uses compressed air, supplied to five atomizer jets within the liquid reservoir producing an aerosol mist. The atomized solution droplets were dried in a heating tube and further dried by clean and dry air in the mixed chamber. The geometric mean diameter of the number size distribution is 66 nm with a geometric standard deviation of 1.6, which was satisfied with lognormal distribution (Figure 2). Additionally, it is possible to guarantee the aerosol concentration constant by setting the mass flow controller FM1 and FM2.

FIGURE 1

Figure 1. Schematic of the test facility.

FIGURE 2

Figure 2. Typical size distribution of NaCl generated by the TSI Model 8118A.

Bubbles are generated in a stagnant liquid by two steel nozzles with an inner diameter of 1.4 mm. Deionized water was selected as the retention liquid to prevent formation of secondary aerosol particles when the bubbles burst at the liquid surface. By setting the valves V3 and V4, it allows to adjust the gas flow injected into the column. The mass flow controller FM3 allows to know the bypass flow and thus to determine the flow injected into the column by balance. This gas flow can also be measured with the mass flow controller FM4 (V7 closed).

The characterization of the aerosol size distribution is analyzed upstream and downstream of the bubble column with a TSI Scanning Mobility Particle Sizer (SMPS), which associates a Condensation Particle Counter (CPC) with a Differential Mobility Analyzer (DMA). To determine the aerosol particles concentrate upstream of the bubble column, the value V5 is opened so that the SMPS can pump a suitable flow. Similarly, to determine of the aerosol particles concentrate downstream of the bubble column, the value V6 is closed and the value V7 is opened so that the SMPS can collect the aerosol laden gas flow. For each particle size, the removal efficiency is determined from these concentration measurements upstream and downstream of the bubble column.

The experiment was conducted at the gas flow rate of 4 lpm and liquid height of 80 cm. The gas flow rate was measured by GFM37 mass flow meter with measurement accuracy of 1%. The temperature and RH of outlet aerosol laden gas were determined by measurement of a temperature and humidity sensor which inserted into the top of the bubble column.

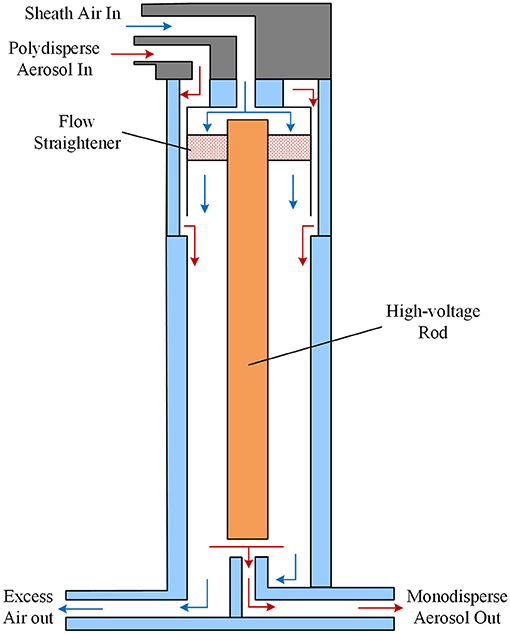
Figure 3 shows the schematic diagram of the long DMA which is the key component of SMPS. It is a cylindrical configuration. A filtered flow loop recirculates the sheath flow. Sheath air enters the Sheath Flow+ port on the top of the DMA and passes to an annular chamber at the top of the DMA. The flow then goes through a Dacron mesh to straighten the flow. The air flows downward axially through the classifier region. The polydisperse aerosol was drawn into the inlet at the top of the DMA. To reduce aerosol loss due to Brownian diffusion, the length of the annular aerosol passage was shortened while maintaining a laminar and steady flow. This thin annular flow is introduced into the classifier region and smoothly merged with the laminar sheath air flow. The aerosol flow rate of 0.3 lpm and sheath air flow rate of 3 lpm were preset. Because aerosol of different sizes has different electric charges, the polydisperse aerosol was classified in the electric field which is provided by the high-voltage rod at the center of the DMA. The size-classified aerosol continues to the external CPC to be counted. Besides, the RH of the sheath air was measured by a humidity transducer installed in circulation loop.

FIGURE 3

Figure 3. Schematic diagram of the long DMA.

Hygroscopic Growth Theory of Soluble Aerosol

Aerosol particles that are soluble in water exhibit hygroscopic properties such that they can absorb moisture from an atmosphere with relative humidity less than 100%. This effect will lead to a growth of the particle size as water vapor condenses into the soluble particle. Maxwell's classical differential equations, which describe particle size and mass changes that result from water vapor diffusion to or form a single spherical droplet, was used to track growth and evaporation of atmospheric condensation nuclei (Hiller, 1991; Pruppacher and Klett, 1997). This approach was also applied to study the effect of hygroscopic growth of soluble aerosol. Previous study shows that the equilibrium time of nanoscale soluble aerosol is very short, usually less than 1 s under RH < 90% (Broday and Georgopoulos, 2001).

The growth factor (GF) is used to indicate the hygroscopic ability of soluble aerosol. It is defined as the ratio between the particle equilibrium diameter d_RH in humid air and the volume equivalent diameter d₀ of the solid particle. Considering that a spherical salt droplet will be formed due to the surface tension of droplet if deliquescence of sodium chloride occurs. Theoretical growth factors can be calculated from the solution concentration c_sol, the solution density ρ_sol and the salt density ρ_s by:

$\begin{array}{ll}g\left(RH\right)=\frac{d_{RH}}{d_0}={\left(\frac{100{\rho }_s}{c_{sol}{\rho }_{sol}}\right)}^{1/3}& (1)\end{array}$

The Kohler theory gives the equilibrium relationship between particle diameter and relative humidity (Kohler, 1936). In the equilibrium state, the RH is equal to the ratio between the vapor pressure over the solution droplet P_d and the saturation vapor pressure of water P_s, which is also called the saturation ratio S_r. The inclusion of the effect of the surface tension and aqueous solution lead to

$\begin{array}{ll}RH[\%]=S_r=\frac{P_d}{P_s}=a_w{S}_{Kelvin}=a_w\exp \left(\frac{4M_w{\sigma }_{sol}}{RT{\rho }_w{d}_m}\right)& (2)\end{array}$

Where a_w denotes the water activity and S_Kelvin is the Kelvin correction factor. M_w is the molecular weight of water, and σ_sol is the surface tension of the solution. R is the ideal gas constant, and T is the temperature at the particle surface. The empirical values of solution of density, surface tension and water activity as a function of concentration and temperature are used for the theoretical calculations (Pitzer, 1991; Gysel et al., 2002).

It is well-known that dry sodium chloride particles are not spherical but instead have a cubic shape (Hämeri et al., 2001). Therefore, the measured mobility diameter of sodium chloride must be shape corrected to get the volume equivalent diameter by adding a shape correction factor to ensure the aerodynamic drag force unchanged. The drag force on non-spherical particles are described with a modified Stokes' law (Willeke and Baron, 2011)

$\begin{array}{ll}{F}_{drag}=\frac{3\pi \eta v\chi a_0}{C_c\left(a_0\right)}& (3)\end{array}$

Where

$\begin{array}{ll}{C}_c\left(d\right)=1+\frac{2\lambda }{d}(1.165+0.483\exp (-\frac{0.997}{2\lambda /d}))& (4)\end{array}$

$\begin{array}{ll}\chi =\{\begin{array}{cc}1.08& 2\lambda /d_0<0.1\\ 1.08\frac{C_c\left(d_0\right)}{C_c\left(1.15d_0\right)}& 0.1<2\lambda /d_0<10\\ 1.24& 2\lambda /d_0>10\end{array}& (5)\end{array}$

Here η is the gas viscosity, v is the velocity, and λ is the dynamic shape factor, which is concerned with the size of the aerosol particles (Decarlo et al., 2004). C_c is the Cunningham slip correction factor, a₀is the dried sodium chloride size, λ is the mean free path of gas molecules.

Therefore, the modified coefficient of hygroscopic growth factor is:

$\begin{array}{ll}{f}_{cube}=\frac{d_o}{d_{ve}}=\frac{1}{\chi }\frac{C_c\left(d_0\right)}{C_c\left(d_{ve}\right)}& (6)\end{array}$

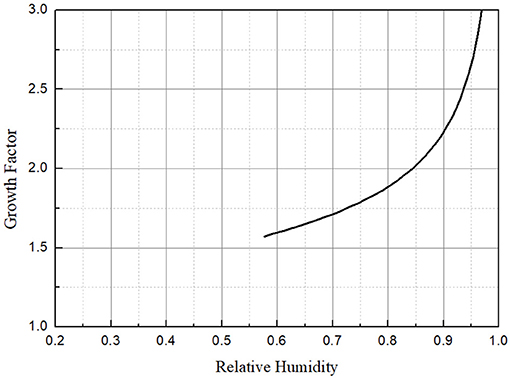
Growth factor of 65 nm NaCl as a function of RH for T = 20°C calculated by Equations (2)–(8) was plotted in Figure 4. It is obvious that the hygroscopic growth factor of NaCl particles is closely related to the relative humidity of the environment. Furthermore, the growth factor of NaCl particles increases faster with the increase of the relative humidity. Besides, growth factor of NaCl particles as a function of particles size for T = 20°C and RH = 72.4% calculated by Equations (2)–(8) was plotted in Figure 5. It can be seen that the hygroscopic growth factor of NaCl particles increases with the increase of aerosol size.

FIGURE 4

Figure 4. Growth factors of d₀ = 65 nm NaCl particles as a function of RH for T = 20°C.

FIGURE 5

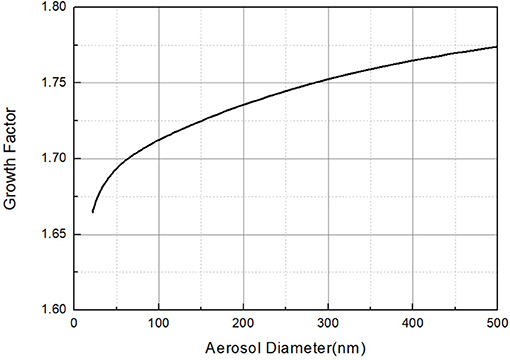
Figure 5. Growth factors of NaCl particles as a function of aerosol diameter for T = 20°C and RH = 72.4%.

Results and Discussion

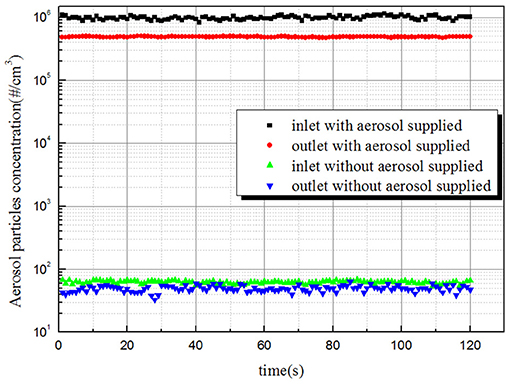
In order to clarify whether entrainment droplets caused by the bubble bursting on the surface of the liquid pool will have noticeable impact on the measurement results, the aerosol concentration at the inlet and outlet of the bubble column were measured with an aerosol generator turned on and turned off, respectively. The gas flow rate was 4 lpm and liquid level was 80 cm. The experimental results are shown in Figure 6. It can be seen that when the aerosol generator was turned on, the aerosol particles number concentration in the inlet and outlet of the bubble column are much higher, almost four orders of magnitude higher than that without the aerosol supplied. This means that the background aerosol fraction produced by the bubble bursting is negligible. In addition, the stability of aerosol concentration at the inlet and outlet also indicated the reliability of the experimental results.

FIGURE 6

Figure 6. Inlet and outlet aerosol concentration with or without aerosol supplied.

The aerosol laden gas enters the bubble column through stainless nozzles, the final gas phase will exist as discrete bubbles in the liquid pool. During the rising period of bubbles, the relative humidity of the gas in the bubbles will increase gradually due to the strong heat and mass transfer between gas and liquid phases. According to our experiment's results, the relative humidity of the gas above the liquid surface exceeded 85%, which is much greater than the deliquescence point of NaCl (76%). Therefore, the NaCl particles will absorb water and grow up which will result in the difference of aerosol size distribution between the inlet and outlet of the bubble column. A 0.3 lpm of the sample gas will enter the DMA and mix with a 3.0 lpm of sheath air, so the sample gas will experience a process of decreasing RH. Meanwhile, the relative humidity of the sheath air will increase, and then become stable after waiting enough time.

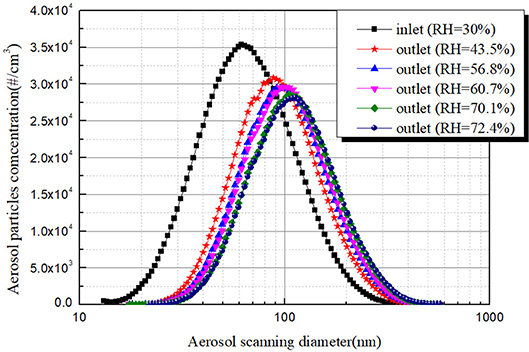
Figure 7 shows the sample measurement results of aerosol particles size distribution and concentration curve at the inlet and outlet of bubble column. The RH of inlet laden gas was 30% which indicated the NaCl particles were dry crystal substance. The relative humidity of outlet gas represented the relative humidity of sheath air in SMPS. The RH of the sheath air exceeded the efflorescence point (42%) which indicated the NaCl particles were metastable salt droplet because the outlet sample gas lies in reducing humidity process. It is obvious that the outlet aerosol size distributions shifted to right compared with the inlet aerosol size distribution. Besides, the larger the relative humidity of sheath air, the more apparent aerosol size distributions shifted to the right. It can be seen that the aerosol number concentration at the outlet is significantly higher than the inlet aerosol number concentration of the same aerosol particle size when the aerosol particle size is greater than 100 nm. This experiment's results indicate that during the process of the aerosol laden gas passing through the bubble column, the hygroscopic growth of soluble aerosol will lead to the increase of the aerosol particles size. So, it is obviously unreasonable to directly calculate the removal efficiency by using the data results in Figure 6.

FIGURE 7

Figure 7. Aerosol size distributions under different relative humidity of sheath air.

To get the removal efficiency of aerosol particles with different sizes, the outlet aerosol size distribution and concentration under same RH with the inlet condition should also be achieved. One approach is adding a diffusion drying tube before the sample gas enters the SMPS to reduce the RH of sample gas below the ERH. The circle line in Figure 8 represents the outlet aerosol size distribution and concentration curve under dried condition. It can be seen that the aerosol size distribution and concentration curve in the inlet and outlet under dried condition have a similar peak particle size. Furthermore, there is no case that the outlet aerosol concentration is higher than the inlet aerosol concentration of the same aerosol particles size, which is reasonable and in agreement with the actual situation.

FIGURE 8

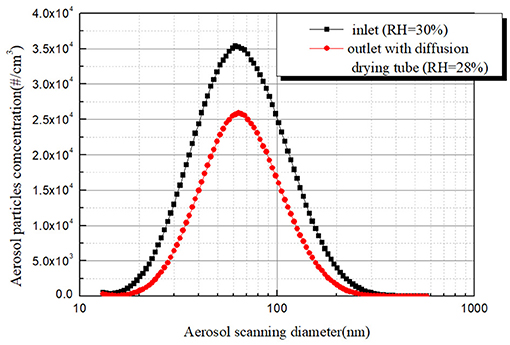
Figure 8. Aerosol size distributions at inlet and outlet of bubble column with diffusion drying tube.

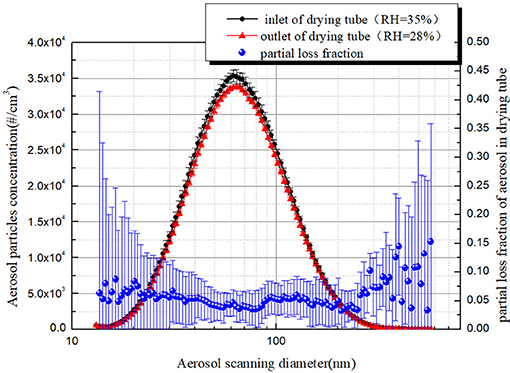
In view of the partial loss of aerosol particles when the aerosol laden gas passes through the diffusion drying tube, it is necessary to verify the performance of the diffusion drying tube. The performance test of the diffusion drying tube was also conducted under a gas flow rate of 4.0 lpm, and the result was shown in Figure 9. It can be seen that the aerosol size distribution and concentration curve at the inlet and outlet of the diffusion drying tube is close. When the aerosol number concentration is greater than 5000 per cubic centimeter, the partial loss fraction of aerosol particles is almost 5%. Therefore, to gain more accurate aerosol removal efficiency, it is necessary to modify the outlet aerosol concentration with a partial loss fraction.

FIGURE 9

Figure 9. Performance test of diffusion drying tube.

According to the hygroscopic growth theory of soluble aerosol, growth factors of aerosol particles with different sizes can be calculated at given temperature and RH. Because the equilibrium time of nanometer aerosol particles is very short under RH < 90%, it's reasonable to consider aerosol particles reach hygroscopic equilibrium in the DMA. Another approach to achieve the aerosol removal efficiency under high humidity condition is obtained by using the hygroscopic growth theory of soluble aerosol to modify the outlet aerosol particles size distribution and concentration curve. The hygroscopic growth theory of soluble aerosol described by equations (2)–(8) is used to modify the aerosol particles size distribution and concentration curve at the outlet under stable humidity environment. And the modified curve is compared with the curve measured by the diffusion drying tube (Figure 10). It can be seen that there is a subtle difference between the modified aerosol size distribution and concentration curve and the aerosol size distribution and concentration curve obtained by adding a diffusion drying tube when the RH of sheath air is 60.7%. It may be caused by the unstable humidity in DMA. While, the modified aerosol size distribution and concentration curve basically coincides with the aerosol size distribution and concentration curve obtained by adding a diffusion drying tube when the RH of sheath air exceeded 70% and maintain constant for more than 2 min, and all particles size was located at the inlet aerosol size distribution range. It shows that the aerosol particle size distribution and concentration curve modified by the aerosol hygroscopic growth theory can accurately represent the actual outlet aerosol situation under dry condition.

FIGURE 10

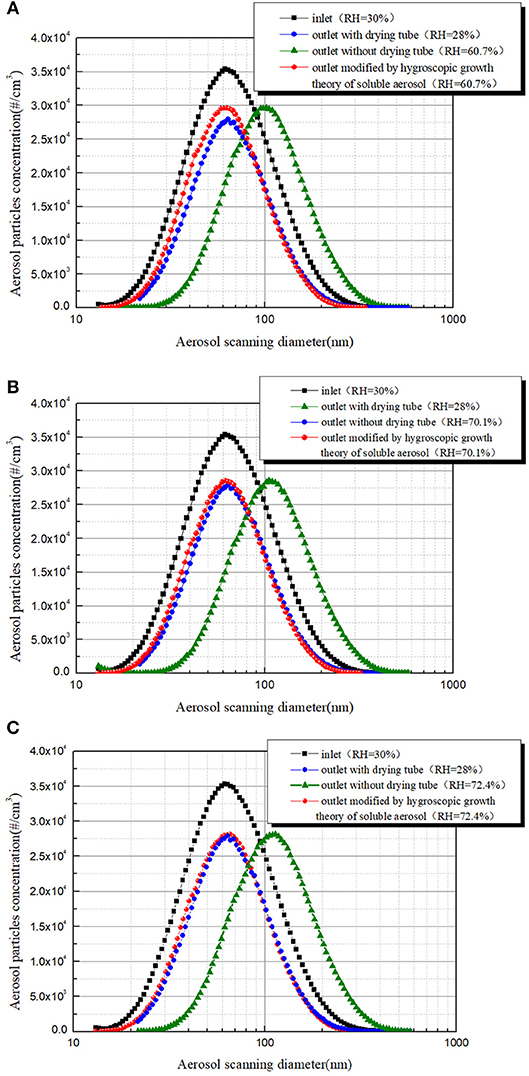
Figure 10. Using aerosol hygroscopic growth theory to modify the outlet aerosol size distribution curve: (A) RH = 60.7%, (B) RH = 70.1% and (C) RH = 72.4%.

In order to further verify the feasibility of using a hygroscopic growth model to calculate soluble aerosol removal efficiency, aerosol removal efficiency calculated by the modified aerosol size distribution and concentration curve was compared with that directly, measured with the diffusion drying tube, and the results were shown in Figure 11. As can be seen, aerosol removal efficiencies obtained by the two methods are in good agreement with the relative error within 25% when the RH maintains constant. The large error at both sides of the curve is mainly because the low aerosol number concentration results in the large uncertainty of measurement results.

FIGURE 11

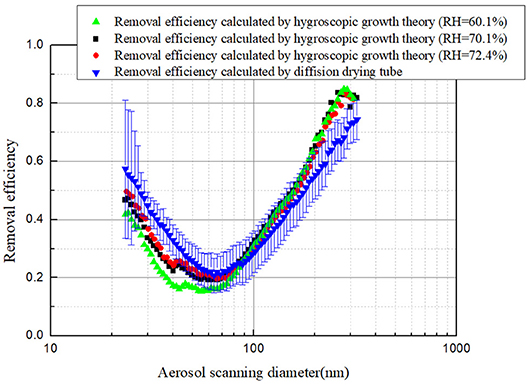
Figure 11. Comparison removal efficiency calculated by diffusion drying tube and hygroscopic growth theory.

Conclusions

Pool scrubbing is a key measure to capture soluble aerosol in case of severe accident at nuclear power plants. Under high humidity conditions such as pool scrubbing, the hygroscopic growth of soluble aerosol will lead to the increase of aerosol size, which further causes a large deviation in calculating the aerosol size-dependency removal efficiency. Kohler theory coupling shape correction factor related to the aerosol particles size can be used to accurately describe the hygroscopic growth of soluble aerosols in the equilibrium state. To account for the aerosol's actual size-dependency removal efficiency, two methods of calculating the removal efficiency were proposed. One method is directly calculating the removal efficiency by adding a diffusion drying tube to reduce the RH of sample gas below the ERH. Another method is modifying the aerosol size distribution and concentration curve by using the hygroscopic growth theory of soluble aerosol. The experiment results obtained by the two methods are in good agreement.

Author Contributions

YL and QM carried out experiments, analyzed the experimental results, and wrote the paper. YZ and HG assisted in experimental work and dealt with the experimental data. ZS and KS gave the guideline of this research and modified the language of the manuscript. YL and YZ developed the hygroscopic growth theory of soluble aerosol. YZ and KS designed the experimental loop and guided the experimental work.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors greatly appreciate the support of the Natural Science Foundation of China (Grant No. 11675045). The author thanks the Key Supported Discipline of Guizhou Province (Qian Xuewei He Zi ZDXK[2016]24), 2011 Collaborative Innovation Center of Guizhou Province (Qian Jiao he xietongchuangxin zi [2016]02). Additionally, the authors are thankful for the support of the Fundamental Science on Nuclear Safety and Simulation Technology Laboratory, Harbin Engineering University, China.

References

Basu, D. J. S. (2014). Status Report on Filtered Containment. Paris. 146, 38–45.

Biskos, G., Paulsen, D., Russell, L. M., Buseck, P. R., and Martin, S. T. (2006). Prompt deliquescence and efflorescence of aerosol nanoparticles. Atmos. Chem. Phy. 6, 4633–4642. doi: 10.5194/acp-6-4633-2006

CrossRef Full Text | Google Scholar

Broday, D. M., and Georgopoulos, P. G. (2001). Growth and deposition of hygroscopic particulate matter in the human lungs. Aerosol Sci. Technol. 34, 144–159. doi: 10.1080/02786820118725

CrossRef Full Text | Google Scholar

Decarlo, P., Slowik, J., Worsnop, D., Davidovits, P., and Jimenez, J. L. (2004). Particle morphology and density characterization by combined mobility and aerodynamic diameter measurements. part 1: theory. Aerosol Sci. Technol. 38, 1185–1205. doi: 10.1080/027868290903907

CrossRef Full Text | Google Scholar

Gysel, M., Weingartner, E., and Baltensperger, U. (2002). Hygroscopicity of aerosol particles at low temperatures. 2. Theoretical and experimental hygroscopic properties of laboratory generated aerosols. Environ.Sci. Technol. 36, 63–68. doi: 10.1021/es010055g

PubMed Abstract | CrossRef Full Text | Google Scholar

Hämeri, K., Laaksonen, A., Väkevä, M, and Suni, T. (2001). Hygroscopic growth of ultrafine sodium chloride particles. J. Geophy. Res. Atmosp. 106, 20749–20758. doi: 10.1029/2000JD000200

CrossRef Full Text | Google Scholar

Herranz, L. E., Polo, J., Escudero, M. J., Espigares, M. M., Lopezjimenez, J., and Peyres, V. (1997). Experimental and analytical study on pool scrubbing under jet injection regime. Nucl. Technol. 120, 95–109.

Google Scholar

Hiller, F. C. (1991). Health implications of Hygroscopi c Particle Growth in theHuman Respiratory Tract. J. Aerosol Med. 4, 1–23.

Google Scholar

Jokiniemi, J. (2007). Effect of selected binary and mixed solutions on steam condensation and aerosol behavior in containment. Aerosol Sci. Technol. 12, 891–902. doi: 10.1080/02786829008959401

CrossRef Full Text | Google Scholar

Kohler, H. (1936). The nucleaus in and the growth of atmospheric droplets. Trans. Faraday Soc. 32, 1152–1161.

Google Scholar

Miwa, S., Yamashita, S., Ishimi, A., Osaka, M., Tanaka, K., Amaya, M., et al. (2015). Research program for the evaluation of fission product and actinide release behaviour, focusing on their chemical forms. Energy Procedia 71, 168–181. doi: 10.1016/j.egypro.2014.11.867

CrossRef Full Text | Google Scholar

Peyres, V., and Herranz, L. E. (1996). Analysis of dominant phenomena during aerosol scrubbing in saturated pools. J. Aerosol Sci. 27, 471–472.

Google Scholar

Pitzer, K. S. (1991). Activity Coefficients in Electrolyte Solutions, 2nd edn. (Boca Raton, FL: CRC Press).

Google Scholar

Pruppacher, H. R., and Klett, J. D. (1997). Microphysics of Clouds and Precipitation, 2nd ed. (Dordrecht: Kluwer Academic Publishers).

Google Scholar

Tamotsu, K., Mitsuko, K., Takehiko, N., Nagase, FN., Fuketa, T., et al. (2007). Effects of fuel oxidation and dissolution on volatile fission product release under severe accident conditions. J. Nuclear Sci. Technol. 44, 1428–1435. doi: 10.1080/18811248.2007.9711390

CrossRef Full Text | Google Scholar

Willeke, K., and Baron, P. A. (2011). Aerosol Measurement: Principles, Techniques, and Applications. NTIS, National Institute for Occupational Safety and Health, Cincinnati, OH.