- 1Nuclear and Radiation Safety Center, Beijing, China
- 2School of Nuclear Science and Technology, Xi'an Jiaotong University, Xi'an, China
Aqueous Homogeneous Solution Reactor concept has been proposed for producing medical isotopes (Medical Isotope Production Reactor-MIPR). However, there are several difficulties in transient calculation of aqueous homogeneous solution reactors. First, there are no assemblies in the core which is different from the traditional reactor core. Second, the operation of aqueous solution reactor at a power of 200 kW will generate radiolytic-gas bubbles. The void volume created by these bubbles in the solution core will introduce a strong negative reactivity feedback. Third, the complex structure of the coolant pipes immersed in fuel solution requires unstructured neutron diffusion calculation methods. Therefore, analytic basis functions expansion nodal method for arbitrary triangular-z node is established to solve the complex structure geometry neutron diffusion equation. Based on this, a software named TABFEN-K has been developed to solve the three-dimensional space-time neutron kinetic equations. Then, TABFEN-K code is used for typical accident analysis of a solution reactor. A simplified geometry model, bubbles generation model, thermal conduction model, and cross section feedback model are given in this paper. A software called TABFEN-MIPR is developed and used for the simulations of the control rod ejection and drop. The same characteristics in the transient process with the results from literatures are obtained.
Introduction
Other than the irradiation of uranium targets in heterogeneous reactors, aqueous homogeneous solution reactors is an alternative way to produce medical isotopes (Ball, 1997). Based on many potential advantages of aqueous homogeneous solution reactors, the Medical Isotope Production Reactor (MIPR) concept has been proposed for producing medical isotopes.
However, many difficulties exist in transient calculation of aqueous homogeneous solution reactors (Briesmeister, 2002). First, there are no assemblies in the core which is very different from the traditional reactor core. Second, the operation of aqueous solution reactor at a power of 200 kW will generate radiolytic-gas bubbles. The void volume created by these bubbles in the solution core will introduce a strong negative reactivity feedback (Dunenfeld and Stitt, 1963). Third, the complex structure of the coolant pipes immersed in fuel solution requires unstructured neutron diffusion calculation methods (Lecorche and Seale, 1973).
Therefore, analytic basis functions expansion nodal method for arbitrary triangular-z node is established to solve the complex structure geometry neutron diffusion equation. The distribution of detailed neutron flux within each node is expanded into the sum of a set of analytic basis functions by accurately formulating the multi-group matrix form neutron diffusion equation and appropriately choosing the expansion order and characteristically directions. To balance between accuracy and efficiency, adjacent nodes are coupled with each other through the zero- and first-order partial current moments defined at the interface. Coordinate conversion technique is used to transform arbitrary triangle into a regular triangle to simplify the derivation of the response matrix between the incoming and outgoing partial currents. A new sweeping scheme is designed for the triangular-z node to solve the nodal diffusion equation iteratively. Then, this analytic basis function expansion nodal method is extended for solving the space-time neutron kinetic equations. The efficient fully implicit difference method is applied to discretize the time variable of the prompt neutron diffusion equation together with the time integration method employed to handle the delayed neutron precursor equations. At each step after the time variable discretization, a fixed source neutron diffusion equation is obtained. Different from the steady-state case, an intranodal neutron flux consists of two components, they are an analytic basis function expanded homogeneous terms and a heterogeneous term which can be approximated into a second-order orthogonal polynomial. Similar to the steady-state, nodal averaged volume flux and surface partial current moments are calculated by introducing the coordinate conversion scheme. Based on this, a code named TABFEN-K has been developed to solve the three-dimensional space-time neutron kinetic equations.
At last, the TABFEN-K code is used for typical accident analysis of a solution reactor. The simplified geometry model, bubbles generation model and the thermal conduction model of solution reactor are given together with the cross section feedback model. A code called TABFEN-MIPR is developed and used for the simulations of the control rod ejection and drop accident. The same characteristics in the transient process with the results from literatures are obtained.
Calculation Model
The simplified geometry model, bubbles generation model, and the thermal conduction model of solution reactor are given together with the cross section feedback model.
Solution of the Diffusion Equation
In a particular homogeneous mesh, the matrix form of the standard multigroup neutron diffusion equation in triangular geometry can be written as (Noh and Cho, 1993, 1994; Nam Zin and Noh, 1995):
where Φ(r) = col{Φ1(r), Φ2(r), …, ΦG(r)} is the neutron flux and ΦG(r) denotes the G-th group neutron flux; the matrix Σ (keff) is a square matrix of order G with its elements as follows:
where is the Kronecker symbol and the other notations are as in conventional manner.
The solution of the diffusion Equation (1) depends on whether the eigenvalues λm and corresponding eigenvectors um of the matrix Σ(keff) are real or complex. For simplicity, we present our derivation here only for the case in which the eigenvalues are real. In fact, the eigenvalues are exactly real for two-group problem. Then, Ψ(r) is introduced as:
Substitute Equation (4) to Equation (1) to reduce Equation (1) to a decoupled form
Equation (5) is a typical Helmholz equation with analytical solution
where el is an arbitrary unit vector. In practice, the number of terms l in Equation (6) mainly depends on the number of the available nodal boundary conditions. Generally speaking, the higher of the terms result in higher accuracy but lower calculation speed, vice versa. For triangular geometry, 3 interfaces' averaged partial current and first-order partial current moment are chosen as the coupling condition to determine the expansion coefficients. Therefore, Equation (6) can be written as:
where , by using Equation (5) and Equation (7), the intranodal flux distribution can be eventually obtained as:
where ugm is the element of the matrix U defined in Equation (3).
Based on this, a code named TABFEN-K has been developed for solving the three-dimensional space-time neutron kinetic equations. The code is verified by 3D-LMW, 3D-LRA benchmarks. Both the relative power and power distribution are in good agreement with the benchmarks (Ban et al., 2012).
Void Bubbles Model
In aqueous homogeneous solution reactors, void bubbles affect the core state by changing the density and volume of fuel solution. The change of fuel solution density was considered by interpolating macroscopic cross-sections in terms of void fraction, while the volume change of fuel solution was considered by modifying the height of fuel solution surface.
In the volume calculation of void bubbles, the total void volume is given by (Souto et al., 2005).
where
: total void volume (m3);
: the reactor power (MW);
G(H2) : hydrogen yield in fuel solution (J−1);
ξ : fraction of H2 molecules per O2 molecule produced by water radiolysis;
NA : Avogadro's constant (mol−1);
Rg : gas constant (J·mol−1·K−1);
Tg: void bubble temperature (K);
rB : void bubble characteristic radius (um);
σ : fuel solution surface tension (Kg·s−1);
τB : the characteristic time for void bubble release from the fuel solution (s).
The distributions of void bubbles in radial and axial direction are different. In radial direction, void distribution is decided by radial power distribution; while in axial direction by the law of axial void movement. In this paper, it assumes that void distribution in axial direction obeys integral power distribution.
Fuel solution volume expansion is caused by generation of void bubbles and thermal expansion and contraction of the fuel solution. The increment of the fuel solution volume can be determined by
where
VVoid : total void volume (cm3);
ΔVHot : solution volume increment caused by thermal expansion and contraction (cm3);
ρCold : density of cold solution (g/l);
ρPower : density of hot solution (g/l);
VCold : volume of cold solution (cm3).
Temperature Model
The solution of the fluidity of liquid fuel, combined with the solution of smaller volume, so that the temperature of the solution of liquid fuel is equal, then according to the quantity of heat production and export, the calculation formula of fuel solution can be written as:
where
cf : specific heat capacity (J/Kg/K);
mf : Solution fuel weight (kg);
p(t) : Power (W);
τt : Characteristics of the time (s);
T(t) : volume of cold solution (K).
Few-Group Constants Fitting
The few-group constants are fitted with the following form
where
fi(x) (i = 1,2,3,4): a polynomial of variable x;
δ(Cr) : a dirac function which equals to 1 or 0 when control rods exist or not;
Bu : burnup (MW·d/tU);
v : void fraction;
p : relative power.
At last, the TABFEN-K code is used for typical accident analysis of a solution reactor. The simplified geometry model, bubbles generation model and the thermal conduction model of solution reactor are given together with the cross section feedback model. A code called TABFEN-MIPR is developed.
Numerical Results
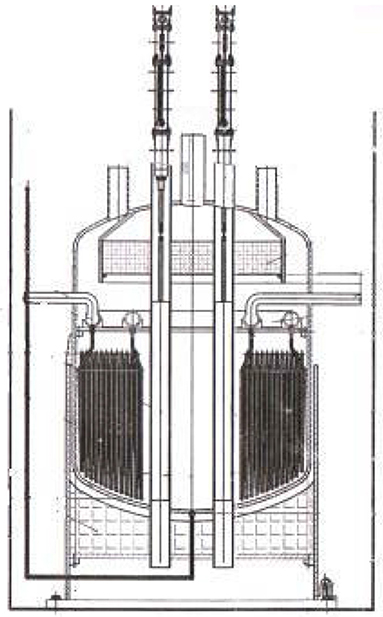
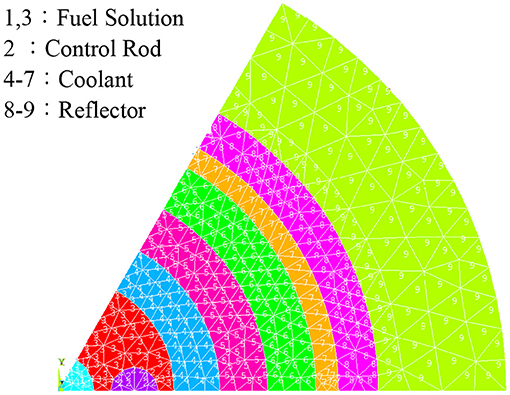
The structure and material of the aqueous homogeneous solution reactor are given in Figures 1, 2 gives the radial mesh of the core used in the calculation, respectively.
The code TABFEN-MIPR is used for the simulations of the control rod ejection and drop accident. The same characteristics in the transient process with the results from literatures are obtained. At the beginning, the power of MIPR is 0.033MW, the temperature of the fuel solution is 344.4164K, the volume of bubble is 376.2742 cm3. The control rods are at 25.68 cm from the bottom of the core.
Rods Ejection Accident
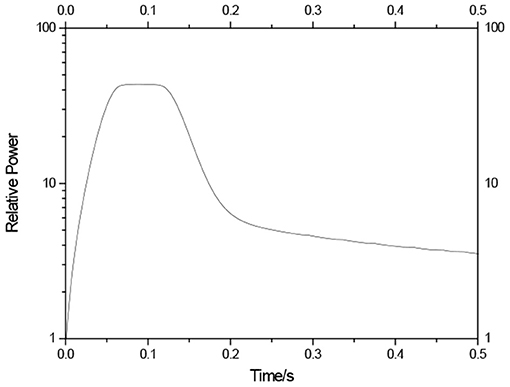
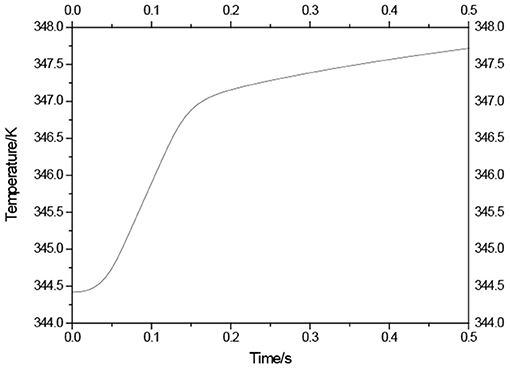
Rods ejection accident belongs to the limit accident, accident control rod in the pop-up core in the process of introducing positive reactivity, which can cause power has arisen sharply, the safety of the pile is affected by the great, usually is the focus of the nuclear safety analysis of the research object. For rods ejection accident, the control rods eject to the top of the core at 32.05 cm, in this case 1,143 pcm reactivity are introduced. Figure 3 gives the solution of ejection rod in the change of the power, Figure 4 gives the corresponding solution temperature and bubble content changes over time. We can find that, after the control rod pop-up, due to the introduction of larger positive reactivity, power rises rapidly in a short time, because of the heat transfer lag, the temperature of the fuel and air bubble content is slowly rising, then began to rapid increase in power; The increment of fuel temperature and bubble content, in turn, has affected the nuclear reaction cross section, the comprehensive result of negative feedback effect to power up to a certain value began to decline, with declining power, and the solution temperature and content of bubble growth began to slow, finally the change of power tend to flat, and finally stability on above the level of the power of the initial time, temperature, and bubble content at this time also started to become stable, and keep on the above the level of the initial time. Because of solution temperature and bubble content, are under the influence of power, has obvious lag in time, Figure 4 also shows that the change of the solution temperature and air bubbles curve shape is consistent, and lagging behind the growth of the power, hence TABFEN-MIPR calculation results conform to play well the transient progress regularity of the accident.
Rod Drop Accident
For rods drop accident, the control rods drop to the core at 20 cm, in this case −1,733 pcm reactivity are introduced. The negative reactivity caused power drops rapidly, but due to the solution of temperature and air bubbles in the feedback, is likely to lead to power fluctuations, may also cause reactor shutdown, therefore must also be analyzed. The results show that, at the beginning of the rod drop, core into larger negative reactivity, core power fells sharply; With declining power, temperature, and decreases in the bubble content and temperature of the solution and the bubble content is introduced to reduce the reactivity of the reactivity makes for control rod falling into negative reactivity decreases, so power after plunging began to slow down. As the accumulation of feedback effects, stable power eventually below the initial power of the power level. And solution temperature and bubble content change lag, which makes them relatively flat. Therefore, TABFEN—MIPR calculation result is reasonable and accords with the transient progress law of rod drop accident.
Conclusions
In this study, TABFEN-K software is used for typical accident analysis of a solution reactor. The simplified geometry model, bubbles generation model and the thermal conduction model of solution reactor are given together with the cross section feedback model. The code TABFEN-MIPR is developed and used for the simulations of the control rod ejection and drop accident. The same characteristics in the transient process with the results from literatures are obtained as well.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
KW developed the code and wrote the manuscript. CX performed the calculation. CL edited the manuscript. YL and JJ analyzed the data. HW gave advice and comments. CX, CL and YL gave the technical support. HW and JJ gave advice for this project.
Funding
The research was supported by National Science and Technology Major Project of China (2019ZX06005001).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Ban, Y., Endo, T., and Yamamoto, A. (2012). A unified approach for numerical calculation of space-dependent kinetic equation[J]. J. Nucl. Sci. Technol. 49, 496–515. doi: 10.1080/00223131.2012.677126
Briesmeister, J. F. (2002). MCNP-A General Monte Carlo N-Particle Transport Code. Version 4C, LA-13709–M.
Dunenfeld, M. S., and Stitt, R. K. (1963). Summary Review of the Kinetics Experiments on Water Boilers. NAA-SR-7087. Atomics International.
Lecorche, P., and Seale, R. L. (1973). Review of the Experiments Performed to Determine the Radiological Consequences of a Criticality Accident. Y-CDC-12. Oak Ridge National Laboratory.
Nam Zin, C., and Noh, J. M. (1995). Analytic function expansion nodal method for hexagonal geometry. Nuclear Sci. Eng. 121, 245–253. doi: 10.13182/NSE95-A28561
Noh, J. M., and Cho, N. Z. (1993). A new diffusion nodal method based on analytic basis function expansion. Transac. Am. Nucl. Soc. 69, 462–463.
Noh, J. M., and Cho, N. Z. (1994). A new approach of analytic basis function expansion to neutron diffusion nodal calculation. Nucl. Sci. Eng. 116, 165–180. doi: 10.13182/NSE94-A19811
Keywords: solution reactor, typical accident, dynamic analysis, control rod, neutron diffusion
Citation: Wang K, Xu C, Li C, Liu Y, Jing J and Wu H (2019) Rod Ejection and Drop Accident Analysis of Aqueous Homogeneous Solution Reactor. Front. Energy Res. 7:138. doi: 10.3389/fenrg.2019.00138
Received: 11 September 2019; Accepted: 14 November 2019;
Published: 28 November 2019.
Edited by:
Jun Wang, University of Wisconsin-Madison, United StatesReviewed by:
Jun Yang, Huazhong University of Science and Technology, ChinaTengfei Zhang, Shanghai Jiao Tong University, China
Claudio Tenreiro, University of Talca, Chile
Copyright © 2019 Wang, Xu, Li, Liu, Jing and Wu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Congxin Li, bGljb25neGluQGNoaW5hbnNjLmNu
 Kunpeng Wang
Kunpeng Wang Chao Xu
Chao Xu Congxin Li1*
Congxin Li1*