Novel Predictive Home Appliance's Management Algorithm in Smart Grids

Introduction

The advancements in modern societies are regarded in the development and deployment of electrical grids. Electricity provides the necessary power to run all modern appliances. In addition to the widespread of renewable energy initiatives to accommodate the global increase in electricity demands, a more efficient and well-managed electricity resources is needed. The continual increase in electricity consumption by residential premises is expected to account for 30–40% of the total electricity usage worldwide (Tchuisseu et al., 2019). Hence, an efficient in-home smart grid control and management solutions deem useful. The notion of automation is strongly associated with electrical energy. The future advancement of electrical grids is challenged by both environmental and economic concerns. To overcome these challenges, the concept of smart grids has emerged. The main objective of smart grids is to provide cost-effective and environmentally friendly electrical power to consumers. Electricity is a secondary source of energy, and it uses other sources, such as coal and wind. Facilitating a reliable and well-grounded smart grid system can be achieved by expediting and optimizing the power requests in a real-time and automated fashion (Erol-Kantarci and Mouftah, 2015). An efficient utilization for using smart grid mostly depends on the wide-spread participation of users (Alam et al., 2013).

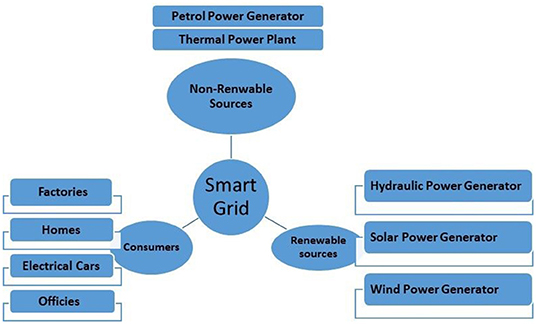
Energy sources are classified into renewable and non-renewable sources. Renewable sources are available in a timely manner from natural resources on regular or irregular bases. Sunlight is an example of renewable source; it is available on a daily basis in most parts of the world. Other examples of renewable sources are wind power, tidal power, solar power, wave power, radiant energy, hydroelectricity, compressed natural gas, biomass, and geothermal power (Ipakchi and Albuyeh, 2009).

Non-renewable sources are not renewable at constant rates. For example, oil takes thousands of years to build naturally and cannot be available at a relevant proportion of consumption. Examples of such sources are natural gas, petroleum, coal, and nuclear power. Electricity can be defined as the set of physical phenomena associated with the flow of electric charge (Ipakchi and Albuyeh, 2009). Traditionally, electricity is generated from non-renewable sources. However, recent literature has placed considerable emphasis on generating electricity from renewable sources as a cheap and environment-friendly alternative. Electrical appliances are common in houses (e.g., oven, washer, dishwasher, TV, and microwaves), and each appliance consumes a specific amount of energy. The increase and spread of these appliances increase the demand for electricity. Such an increase in demands increases the amount of consumed electricity, and hence, its cost.

Smart grids are a modern form of electrical grids that are based on digital technologies to supply electricity to consumers via two-way digital communication between the grid operator and the users. It enables end-users to generate electricity (usually from a renewable source) and to insert part of this generated electricity in the main electricity network. Moreover, it provides the users with the capability to monitor and control their consumption patterns. In typical electricity networks, grid refers to the distribution system, which transmits electricity from the power plants to the end users' locations.

As we mentioned above, smart grids can monitor and control electricity consumption. Each appliance has different operations. In a smart grid system, each appliance is assumed to have the capability to be started, resumed, suspended, and stopped by a special module connected to the home smart meter (Erol-Kantarci and Mouftah, 2010a). Smart grids usually employ a scheduling module to plan these operations to reduce energy consumption during peak hours, reduce cost, increase reliability, and reduce power interruptions periods. The smart grid consists of four main components (Erol-Kantarci and Mouftah, 2010a):

1. Supportive communication systems, which are communication infrastructures used to exchange data between the different elements of the system (e.g., utility and user, and user and appliance). Both wired and wireless networks can be used to implement this sub-system.

2. Advanced metering infrastructure (AMI), which provides accurate real-time readings of power and energy consumption for users.

3. Advanced distribution operations.

4. Advanced asset management.

Smart grids support a two-way flow of energy and information and aim to achieve multiple objectives. The main goals of smart grids are improving energy storage, enabling self-healing grid, making it more environment-friendly, and imposing user-oriented solution with customized management policies. However, smart grids face many challenges, such as regulation, standardization, and security. Figure 1 shows a typical smart grid layout.

FIGURE 1

Figure 1. General smart grid layout.

This work considers supportive communication systems, in particular, the communication between users and home appliances. In such systems, the users communicate with home appliances to start, modify or shut down a particular appliance or service. Wireless Sensor Networks (WSNs) are typically used to support the communication services required by the smart grid (Erol-Kantarci and Mouftah, 2010a). WSNs provide low-cost and low-power solutions. Environment monitoring with consumption and fault detection is a common example of the usage of WSNs in smart grids. However, harsh environmental conditions (e.g., high humidity, vibrations, and dust), security, constrained resource, and system reliability are the main challenges for using WSNs in smart grids. The design and implementation of WSNs are constrained by three types of resources: energy, memory, and processing.

As we mentioned above, in a smart home environment, scheduling is a key operation performed by smart grids to manage energy consumption smartly. It is responsible for deciding which electrical appliance (machine) will start (run) and when it will start. Scheduling mechanisms are divided into two types: non-preemptive scheduling, which assumes that a connection request is served to completion without service interruption, and preemptive scheduling, which aims at achieving higher throughput by allowing service preemption.

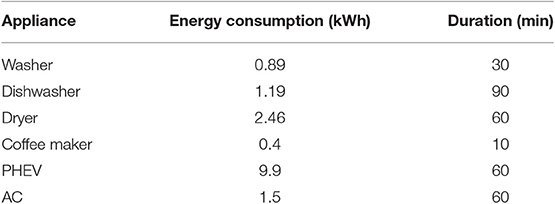
Electrical appliances are major energy consumption appliances (e.g., washer, dishwasher, dryer, coffee maker, plug-in hybrid electric vehicle, and air conditioning), where each appliance consumes a specific amount of electrical energy that can be measured in kilo watt per hour (kWh). Each appliance has many different cycles and an energy consumption level for each cycle. Typical cycles in minutes are 10, 30, 60, 60, 60, and 90 for the coffee maker, washer, dryer, plug-in hybrid electric vehicle, air conditioning, and dishwasher, respectively. Moreover, the energy consumption for each appliance in kWh is 0.4, 0.89, 2.46, 9.9, 1.5, and 1.19, respectively. Table 1 lists some common house appliances and their characteristics (Erol-Kantarci and Mouftah, 2010a,b, 2011).

TABLE 1

Table 1. List of appliances and their properties.

Traditional electricity grids were built to generate and distribute energy services. Urbanization and automation pushed the consumption levels to very high limits. The smart and innovative solution was needed to control this unstoppable growth. Dynamic pricing is one of the possible solutions in which prices are increased at peak hours and reduced at normal hours. This work considers the integration between dynamic pricing and scheduling mechanism to achieve the main goals of the smart grid in terms of controlling and managing energy consumption in the home environment.

This paper is composed of six sections. Section Introduction introduces the general concepts and framework. Section Literature Review presents the literature review. Section System Model presents a detailed comparison and evaluation between the proposed works with other schemes. Section Simulation and Results presents the methodology of the work and its implementation details. Section Conclusions and Future Work summarizes the topic, the experiments, the conclusion of the suggested work, and future work.

Literature Review

In this section, we first discuss various pricing schemes used in smart grids. Then we review and consider many algorithms and techniques used in smart grids among houses, and other schemes used to schedule appliances' operations inside single house.

Many pricing schemes are proposed for use in the smart grid including Real Time Pricing (RTP), Time of Use (TOU), Critical Peak Pricing (CPP), and Day Ahead Pricing (DAP). In smart grids, real time (dynamic) pricing is an effective tool for reducing pressures on the electricity infrastructure, encouraging energy efficiency, and saving consumers money (Mohsenian-Rad and Leon-Garcia, 2010).

An example of pricing schemes usage in some popular techniques is TOU pricing which is used in Appliance Coordination with Feed In (ACORD-FI), Optimization-based Residential Energy Management (OREM), and in-Home Energy Management (iHEM). The RTP is used in Residential Energy Load Consumption (RLC) scheme, and it also uses TOU and CPP pricing in the decision support tool scheme (Erol-Kantarci and Mouftah, 2011).

The RTP is a pricing scheme that changes hourly and is fixed. The RTP reflects the wholesale prices weather conditions, generator failures, and wrong of generation (Mohsenian-Rad and Leon-Garcia, 2010). The pricing changes in intervals of 15 min to an hour. This is described as a critical component of energy efficiency programs, because it enables the user to reduce consumption at peak load hours, which saves billions of dollars and contributes to the efficiency of the grid system. The RTP consists of a meter that is capable of recording usage data in intervals; this communication allows consumers to modify consumption, and market operator to modify generation and distribution.

Rehmani et al. (2018) presented an overview of recent works that aim to integrate renewable energy resources into the environment of smart grids. These studies consider the resources along with the smart grids supporting communication networks.

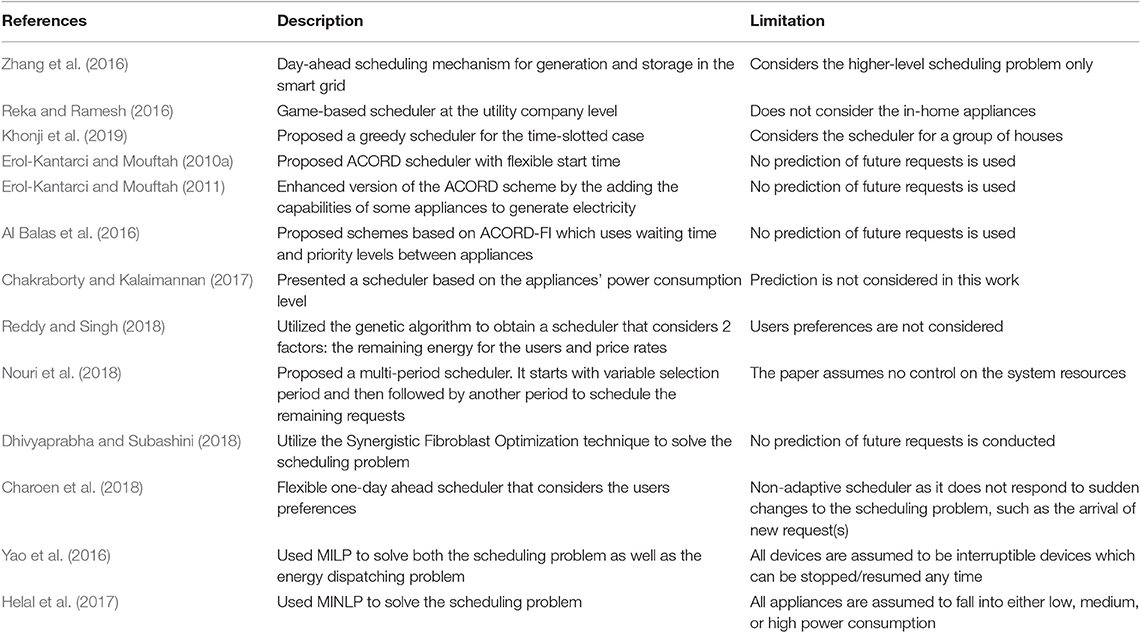
The scheduling problem in smart grids is investigated at different levels of the network. For example, the work by Zhang et al. (2016) proposed a day-ahead scheduling mechanism for generation and storage appliances in the smart grid. A game-based strategy is proposed by Reka and Ramesh (2016) for scheduling at the utility company level among different residential users (homes). The work in Reka and Ramesh (2016) does not consider the in-home appliance level scheduling in their solution. Moreover, the work by Khonji et al. (2019) formulates the scheduling problem in smart grid at the users' level (house) and devise a greedy algorithm for the time-slotted case.

Communication between appliances in the smart grid is a crucial issue and it must be considered carefully as it can greatly affect the performance of the smart grid. The communication issues are beyond the scope of this paper, an optimal communication model is proposed in Zhang et al. (2019). Tchuisseu et al. (2019) proposed a management module for smart grid utilizing two main concepts: communication between appliances to exchange important information, and frequency fluctuations. The main goal in Tchuisseu et al. (2019) is to stabilize the overall system frequency and to avoid frequency fluctuations at peak times.

Erol-Kantarci and Mouftah's work (2010a) proposes the Appliance Coordination (ACORD) scheme for smart grids, which allows flexibility in the start time for home appliances. The main goal of the ACORD scheme is to shift the start time of appliances to off-peak hours when the consumer's desired start time falls between peak hours. The scheme uses the in-home WSN to relay the data between the coordinator and the different appliances in the home. When the consumer presses on the start button of the appliance, it generates the START-REQ packet, which contains the desired duration cycle of the appliance (e.g., a washing cycle of the washer), and the packet is sent to an Energy Management Unit (EMU) by the WSN.

If no hard start time is requested, after communicating with the smart meter to check the TOU rate and peak hour information, the EMU receives the START-REQ packet, which schedules the available start time. In a large house environment, the EMU may be physically far away from the appliances. This means that the EMU is not reachable in one hop by all appliances. Thus, a multi-hoping is required for message delivery. The waiting time or the scheduled start time is sent back to the consumer by the START-REP packet and set to zero, if the consumer requests a hard start time or the desired start time is in off-peak hours, and no other requests are scheduled on that time. The final decision of the consumer, if any, based on the new scheduled time, is sent back to the EMU in notification packets, using decision in reserve time slot for the device. They tested the performance of the scheme using two different load scenarios high and low consumer activity cases. In the high and low activity cases, the inter-arrival times between two requests are assumed to be a negative exponential distribution with means of 6 and 48 h. Used devices included a washer, dryer, dishwasher, and coffee maker. Also, the peak hours are chosen between 7–11 a.m. and 5–9 p.m. in the winter week days. The maximum acceptable delay is 10 h. The performance metrics are the total cost saving in dollars and the number of lost requests in a sensor network. Finally, the results showed the total contribution of devices to the energy bill 46US$ of the consumer requests at the period time 210 days (i.e., ~7 months).

Erol-Kantarci and Mouftah (2011) proposed the ACORD-FI scheme as an improvement of the ACORD scheme (Erol-Kantarci and Mouftah, 2010b). The authors' main assumption is that the device could manage the consumer demands and locally generated energy to reduce the sharing of the appliances in the total energy bill, and provides savings on the energy bill. The scheme uses the in-home WSN to relay the data between the coordinator and the different devices in the home. When the consumer presses on the start button of the device, it generates the START-REQ packet, which contains the desired on duration cycle of the device (e.g., washing cycle of the washer), and the packet is sent to an EMU by the WSN.

Once the EMU receives the START-REQ packet, it schedules the available start time, if no hard start time is requested, after communicating with the smart meter to check the TOU rate and peak hour information. In a large house environment, the EMU may be physically far away from the appliances. This means that the EMU is not reachable in one hop by all devices. Thus, a multi-hoping is required for message delivery.

The waiting time or the scheduled start time is sent back to the consumer by the START-REQ packet and the waiting time is then set to zero, if the consumer requests a hard start time or the desired start time is in off-peak hours, and no other requests are scheduled on that time. The final decision of the consumer, if any, based on the new scheduled time, is sent back to EMU in notification packets, using decision in reserve time slot for the device.

They tested the performance of the scheme using two different load scenarios high and low consumer activity cases. In the high and low activity cases, the inter-arrival times between two requests are assumed to be a negative exponential distribution with means of 6 and 48 h. The devices used include a washer, dryer, dishwasher, and coffee maker, and the peak hours are chosen between 7–11 a.m. and 5–9 p.m. in the winter week days. The maximum acceptable delay is 10 h. The performance metrics used are the total cost saving in dollars and the number of lost requests in a sensor network. The results improved over ACORD by a rate of 37US$ as the total contribution of devices to the energy bill.

Al Balas et al. (2016) introduced an efficient scheme to reduce the total cost of the energy bills. The proposed schemes utilized the ACORD-FI (Erol-Kantarci and Mouftah, 2010b, 2011) scheme to obtain an efficient solution. The scheduling schemes proposed in this work are the Appliances Coordination that uses waiting for a time (ACORD-WT) and Appliances Coordination that uses a priority scheme (ACORD-P) (Erol-Kantarci and Mouftah, 2010b, 2011). The authors compared their scheme with these schemes and the results show that the efficiency of the ACORD-WT scheme is better than the ACORD-FI and the (ACORD-P) schemes, regardless of the number of appliances. Moreover, the preemptive scheduling scheme by giving priority (ACORD-P) is still better than the standard ACORD-FI scheme.

Chakraborty and Kalaimannan (2017) studied the peak hours load re-scheduling of applicable devices based on their power consumption level. The proposed solution is based on the two-dimensional bin packing problem. The authors discussed obtaining an exact solution using optimization solvers. And they also presented an approximation technique that give acceptable solutions much faster.

Reddy and Singh (2018) discussed the load scheduling of commonly used devices daily (called Delayable in the paper) and less usable devices which are used less frequently (Non-Delayable devices). The scheduling is done first for a group of users for the Delayable devices and then, in the second phase, for the Non-Delayable devices. Two main factors are taken into account, namely first the remaining energy for the users having solar PV and then the price rates. The authors formulated an optimization problem based on Genetic Algorithm Optimization (GAO). The authors provided two types of results: Day-ahead and Hour-ahead scheduling, which can help in matching closely load for real-time consumption.

Nouri et al. (2018) proposed a multi-period scheduling scheme to minimize the cost. The authors generated various scenarios to model any uncertainties that could arise with renewable resources, upstream systems, and system loads. The model consists of different periods: firstly, variable selection is performed, which will be used for all scenarios; Then the same process is applied until the final scheduling is achieved. The authors tested and illustrated the method for a couple of case studies.

Dhivyaprabha and Subashini (2018) used Synergistic Fibroblast Optimization (SFO) to solve the multi-objective scheduling problem. The objectives the authors used were: minimize the consumption cost and maximize renewable resources usage. The authors discussed a case study to illustrate the effectiveness of the approach compared to some other strategies, such as First Fit, Best Fit, Firefly Algorithm (FA), Particle Swarm Optimization (PSO), and Invasive Weed Optimization (IWO).

Charoen et al. (2018) used user preferences to optimally schedule the operation of the device in the user premises. They calculated the optimal energy consumption scheduling based on, for example, day-ahead schedules. They considered the implications of allowing users to change their preferences and request new schedules at any time. Besides, they proposed single-user and multi-user adaptive rescheduling algorithms which address any changes in user preferences. The algorithms reschedule deviating energy consumption optimally, thus reducing the total energy cost. Simulation results show that the total energy cost of the community can be reduced by as much as 11.4% in specific scenarios.

Yao et al. (2016) devised an energy management system based on dynamic user responses and the ability of shifting start time of home appliances based on the current pricing tarrif. The authors presented a home energy management system using Mixed Integer Linear Programing (MILP) technique, aiming to solve both load scheduling problem of home appliances and the energy dispatch problem of utility grid under a single optimization framework in real time. The results show that the proposed system minimized the energy cost required to satisfy the scheduled load.

Helal et al. (2017) formulated the power requests scheduling problem as a mixed-integer non-linear programming. The authors took the technical constraints of the grid as well as users' preferences into account, where the users inform a centralized controller with their preferences, which are included in the proposed optimization problem according to the type of the appliance. The simulation results show that the proposed scheduling scheme can significantly reduce the overall system operating costs via demand side management.

The main results of the surveyed literature are presented in Table 2. In this work we propose an adaptive online schedules (preemptive and non-preemptive ones) to the in-home appliances scheduling problem. The proposed schedulers takes into consideration users' preferences, available energy, and any other fluctuations in the system, such as the arrival of new request. Most of the works done in the literature formulates the scheduling problem and constructs the scheduler in advance (e.g., a day ahead) using the available users requests. No or minimal consideration of future requests is done. Moreover, no prediction components are used to predict the near-future trends and construct the scheduler accordingly.

TABLE 2

Table 2. Literature review summary.

System Model

The framework we proposed in this work is designed for the smart grid in the home environment, and considers common electrical appliances used in typical houses, as we outlined above. In the following, we present some notations, assumptions, and definitions to be used in the proposed framework:

– Set of request R(r_i, i = 1, …,N), in which each appliance's request r_i is defined by the following parameters:

– The request's weight is computed for each request, based on several factors, and is used to differentiate and prioritize between competing requests. The objective of the proposed framework is to maximize the sum of served request weights ∑w_i.

– P_time is a parameter that denotes a length of the prediction period used in computing the overload probability from the transition diagram.

– Pw_total is the total power allocated to serve appliances. Power is assigned to appliances based on their manufacturing requirements, as Table 1 indicates.

– P_admit is a parameter (a probability) used in accepting new requests. It is set by the smart grid operator.

– Each appliance may have a maximum of one request at any given time.

– Time is slotted. The algorithm views time as a sequence of slots, each of length Time_slot (e.g., 1 s).

– If a request i does not receive the required service within the acceptable delay interval [a_i, a_i + d_i−1 or d_i], then that request is considered to be inadequately served.

– α_qos is a quality parameter (α_qos > 0) to fix an upper bound on the maximum acceptable processing time experienced by any of the admitted appliances. The derivation of this bound will be introduced later.

– P_overload is the overload probability that is defined as the probability that the object will be in an overload state at time t + t_predict.

In order to derive the quality parameter α_qos, we define the following notation: for any given appliance i, define a_i as the start time for serving this appliance, l_i as the service time length, c_i as the completion time, and d_i as an upper bound on the acceptable total time. In order to simplify the notations, these parameters are measured in time slots. Thus, the total processing time of appliance i is (1 + c_i − l_i) slots, hence, di = [(1 + α_qos)l_i].

Proposed Schemes

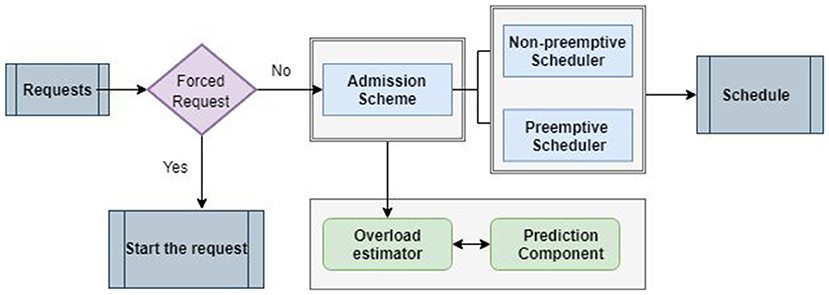
Figure 2 depicts the general architecture of the proposed framework. In this architecture, once the user makes a new request, the system checks to validate whether this is a forced request (i.e., a request that must start immediately) or not; if it is a forced one, it gets started immediately. If it is not a forced request, then the admission scheme is invoked, which, in turn, performs overload estimation. Once the admission scheme is completed, it invokes the scheduling component (in this work, we propose two different scheduling schemes, namely preemptive and non-preemptive schedulers). The scheduler constructs a schedule of which appliances to start and when.

FIGURE 2

Figure 2. General architecture of the proposed framework.

The proposed scheme is distinguished from other schemes by making the following assertions:

– Serving a particular appliance is bounded by a deadline, so any appliance must be served within a specific time frame.

– A request does not need to be either accepted or rejected. A request can also be delayed (for a reasonable amount of time) to be served later, in case of many requests arriving at the same time.

The approach taken in this work devises a management framework that utilizes the following modules (Liu et al., 2017; Hans et al., 2018):

1. A predictive scheme that utilizes a priori knowledge of distributions of appliances to predict the overload probability.

2. A scheduler to determine which appliance will be served next.

Proposed Admission and Planning Scheme

Given the above-mentioned definitions and assumption, in the following, we present the general admission scheme. However, we note that the user may opt to force a appliance to start right away (we will refer to these requests as “forced requests”), without being subjected to the admission and the scheduling procedures. In this case, the appliance request will not be considered among the total requests.

The goal of the quality check is to ensure that the system will not be in an overload situation in case it accepted the incoming request. It basically computes the overload probability given the current requests distribution vector for the interval [t, t + t_predict].

In order to estimate the overload probability that is necessary for the quality test, we devise the following simple probabilistic model. We remark that the probability of having m appliances (from n appliances) operating at time t + T_predict follows the binomial distribution B(m; n, p_active), where p_active is the probability that any appliance remains active. The probability of new appliance becoming active during the time interval t + T_predict is denoted by p_new, and the probability that z appliances will be active during this interval follows the binomial distribution B(z; q, p_new). Therefore, the overload probability is computed using the convolution sum of two binomial distributions, namely B(m; n, pr) and B(z; q, p_new).

We note that the choice of the prediction interval (P_time) is essential to achieve the best performance. Hence, we propose an adaptive planning estimator to adjust the value of the planning interval based on the number of incoming requests. For high demanding situations, the interval is decreased. On the other hand, the planning interval is increased as the request demand decreases. Initially, the interval is set to the average requests rate. Then, the value is adjusted with an exponential moving average using Equation (1):

$\begin{array}{ll}{P}_{\text{time}}=\alpha P_{\text{time}}+(1-\alpha )DT& (1)\end{array}$

where α is a favoring factor, 0 ≤ α ≤ 1, and is used to favor the historical average over the most recent reading, and DT is the most recent reading. For simplicity, we set α to 0.5, in this paper. Figure 3 shows the steps of the general admission scheme.

FIGURE 3

Figure 3. General admission scheme.

Proposed Non-preemptive Scheduling Scheme

The scheduling scheme is the main module in the proposed framework. Calling the scheduling function at time t, with available resources (energy), a set R(t) of all of the outstanding unexpired requests, and P_time. Now, we construct a non-preemptive scheduler that can select a subset R′ ∈ R(t) of requests that can start no later than t + P_time and maximizes the total weights. In order to facilitate the design of the proposed scheduler, we make the following definitions and assumptions:

DR is the set of all request that is seeking to be scheduled. It consists of both undelayed and delayed instances of traffic requests. The delayed request is bounded by P_time units.

• M_DR is the total number of requests in set DR. Mathematically, M_DR is computed using the following formula: $M_{DR}=\sum _{ri\in R}(1+min(d_i,P_{time})).$

• For request r_i, the undelayed component is accounted for by the term “1,” and the delayed version is compensated for by the term “min (d_i, P_time).”

• L[1, 2, …, M_DR] is a non-decreasing order sorted list of the set DR; the instances in L are sorted according to their starting times.

• L[k] is the identity (i.e., the index j) of a request with index k in list L that correspond to instance r_{j, d} of request r_j.

• A subset of the first k entries of L, where L[z]| z = 1, 2, …, k, is of type S^(k)[i, j], if it satisfies the following two conditions:

The proposed scheduler finds the optimal solution using a dynamic program that considers all instances of requests in DR, according to the ordering determined by L. In particular, at the kth phase, k = 0, 1, 2, …, M_DR, for request L[k], the algorithm computes the effect of including and excluding this request by tracking all S^(k)[i, j] quantities.

To construct the scheduler, it is best to view the available power (Pw_total) as a spectrum that is divided into m bands; each band is divided into k channels of equal capacity. Each appliance requires a specific number of channels to be served. For any K requests, where K > m, we define a sub-scheduler that can schedule a maximum of K′ requests at a time, namely SS-K. The SS-K scheduler needs to be called [K/m] times. Each call selects a subset of size 2 to start simultaneously. NP-SK utilizes dynamic programming concepts in its design. Figure 4 depicts the NP-SK algorithm.

FIGURE 4

Figure 4. Non-preemptive scheduling function.

In this algorithm, L[k] is the set of all requests, both new and delayed requests. S^(k)[i, j] is a subset of valid requests in the interval [t, t+P_time]. Thus, each of these requests can be scheduled over m bands such that the latest requests can start over the two bands i, and j, respectively, where i ≤ j. S^(k−1)[i, j] is a subset of the maximum weighted sets of the corresponding types. Request L[k] can be scheduled with set S^(k−1)[i, j] if S^(k−1)[i, j] can be scheduled over 2 channels. Also, in case of L[k] being a delayed instance of request r_j, then no idle or overlap time occurs between its scheduled start time and the finish time of its predecessor on the same channel.

Lemma: The proposed non-preemptive scheduler is a correct one.

Proof:The scheduling algorithm considers the effect of including and excluding all qualified instances in the DR set; hence, it is proven to be correct. In particular, the loop in the scheduler accounts for the two cases of including and excluding L[k] as the new set S^(k)[i, j] takes the maximum weighted set of these two cases.

The scheduler runs for M_DR iterations. The length of each iteration is bounded by the shortest request size (M_l). Therefore, the run time of each iteration is bounded by $O(\frac{1}{2}{(\frac{P_{time}}{M_l})}^2)$). The total run time is $O(\frac{1}{2}{(\frac{P_{time}}{M_l})}^2)$. M_DR).

For the NP-SK algorithm to work, the number of channels must be even. In case of an odd number of channels, the algorithm must schedule one request over one channel, assuming the second channel is occupied by request with infinity request length.

Proposed Preemptive Scheduling Scheme

One way of enhancing the proposed scheduling algorithm is to replace the non-preemptive scheduler with a preemptive one, where the service of any appliance can be preempted several times during the operation period of the appliance. The proposed preemptive scheduler follows a similar approach as the non-preemptive one. However, a key difference between the preemptive scheduler and the non-preemptive one is the set of connections considered by the scheduler, namely the set R(t). In the preemptive scheduler, the set R(t) is defined as the set of all outstanding unexpired service requests plus all requests already in service. The proposed scheduler may select an active appliance and decide to shut it down for a certain amount of time to serve another appliance. Hence, at the arrival of a new request, the scheduling mechanism is invoked, and a new schedule is computed, taking into account all active, delayed, and new requests.

In addition to the notations and variables we defined for the non-preemptive case, we define the following attributes for the preemptive case:

• id_i is the allowable maximum total service interruption delay for request r_i.

• st_i is the allowable maximum start of service time (delay) for request r_i.

Hence, the appliance request is dropped in two cases: first if it cannot be started on, or before, (s_i = a_i+st_i), secondly, if a request cannot be completed before (s_i + l_i + rd_i).

The scheduling (i.e., P-S2) takes as input the timing information of all requests in the set R(T), namely two time instants (i, j), such as i, j ϵ [0, P_time], where the two channels are available for service. The function yields a subset denoted SR, which can be scheduled over two channels (i.e., SR ⊆ R).

The algorithm works iteratively. In each iteration, the algorithm selects a subset S of at most three requests to be scheduled to start over two available channels to start at times i, j. The chosen subset S is required to have the maximum total weight among the candidate subsets. If S can be computed (i.e., exists), then a sub-schedule is constructed to start at two channels at times i and j. The function is terminated if S does not exist, and it will return the computed subset SR. Figure 5 shows the algorithm.

FIGURE 5

Figure 5. Preemptive scheduling function.

Computing the best request(s) to include in each schedule is done exhaustively over the set of all active and inactive requests by packing three requests over two channels.

Let M_l be the length of the shortest request. Hence, at most $\frac{P_{time}}{M_l}$sub-schedules are computed by the scheduler. Each sub-schedule needs $O({n_{DR}}^3)$ to perform a brute force search in the set DR for the set (S) that achieves the maximum weight with two or three requests. Hence, the total running time for the scheduler is $O(\frac{1}{2}{(\frac{P_{time}}{M_l})}^3)$M_DR).

In order to prove the correctness of the preemptive scheduler, assume we have three requests (r₁, r₂, and r₃) to be served interchangeably over two channels only. The start times for these requests are denoted by H₁, H₂, and H₃, respectively. The end times are denoted by E₁, E₂, and E₃, respectively, where E₁ < E₂ < E₃. Assume OT is the total duration where the three requests overlap. The three requests can be scheduled as follows:

1. Serve connections r₁ and r₂ during the interval [H₁, H₃+ $\frac{OT}{2}$].

2. Serve connections r₂ and r₃ during the interval [H₃+ $\frac{OT}{2}$,E₁].

3. Serve connections r₁ and r₃ during the interval [E₁, E₁+ $\frac{OT}{2}$].

Using this sub-schedule, each request is delayed by the maximum of $\frac{OT}{2}$.

Simulation and Results

The performance of the proposed non-preemptive and preemptive scheduler is evaluated using simulation. We conducted and wrote a discrete event simulator as a code in C++. The user requests are modeled as follows: inter-arrival rate in off-peak hours follows a negative exponential probability distribution function with a mean of 12 h, while in the peak hours it is assumed as 1 h. The appliances used are a washer, dryer, dishwasher, and coffee maker, in the winter peak period from 7 to 11 a.m. and from 5 to 9 p.m., and the mid peak hours from 11 to 5 p.m. The simulation runs on the period between 10 and 210 days, and the maximum delay is set to 24 h.

The obtained results are compared against results obtained from state- of the art algorithms in the literature; in particular, we compare the performance of the proposed schemes against Erol-Kantarci and Mouftah's work (2010b, 2011), namely on-off ACCORD-FI Al Balas et al.'s (2016) work, namely modified ACCORD (both preemptive and non-preemptive versions). The performance metric we used to evaluate the performance of the investigated schemes is the total cost (cumulative) of electricity usage during the simulation time (~7 months). The reported results are the average of 10 runs, and to eliminate the transient effects, the results of the first 5 days in the simulation were cropped from the final results. Table 3 lists the main parameters and assumptions we used in the simulation study. Table 4 shows energy consumption and cycle durations of the appliances used in the simulations. Table 5 shows the TOU rates and two price models: one from Ontario/Canada (Erol-Kantarci and Mouftah, 2010a, 2011) and another from Jordan, as presented in Al Balas et al. (2016) research. We refer to these two models as model 1 and model 2, respectively. Moreover, we assume that 10% of the initiated requests by the users are forced requests. Hence, these requests will not be handled by the admission or the scheduling schemes.

TABLE 3

Table 3. Simulation parameters.

TABLE 4

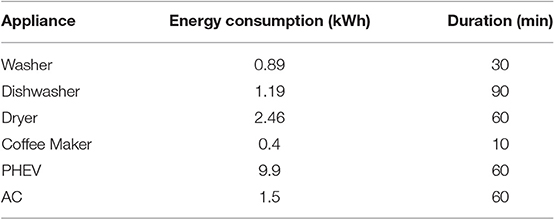
Table 4. Energy consumption and cycle durations (Erol-Kantarci and Mouftah, 2010a, 2011).

TABLE 5

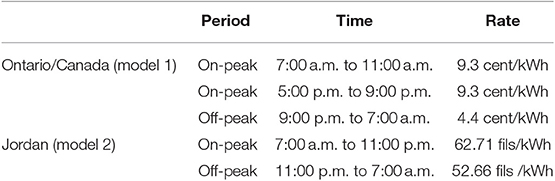
Table 5. TOU rates (Erol-Kantarci and Mouftah, 2010a,b, 2011).

The five schemes are shown in the comparison figure are:

• The proposed non-preemptive scheme.

• The proposed preemptive scheme.

• ACCORD-FI scheme [Erol-Kantarci and Mouftah's work (2010b, 2011)].

• The non-preemptive modified ACORD (Al Balas et al., 2016).

• The preemptive modified ACORD (Al Balas et al., 2016).

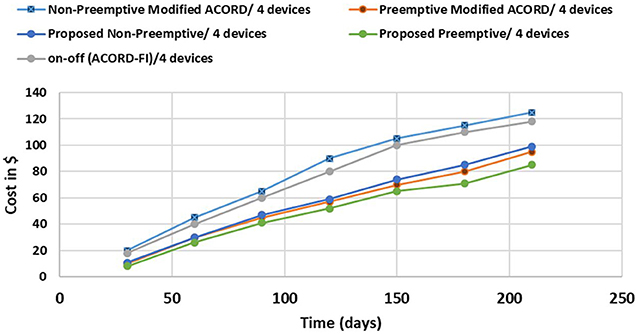
Figures 6, 7 depict the obtained simulation results for price model 1 used in Ontario/Canada, for both 4 and 6 appliances, respectively. Figure 6 compares the total energy cost when using 4 appliances for all 5 schemes. It is apparent that the proposed non-preemptive scheme achieved slightly more total cost than the ACCORD-FI scheme. This is rather expected as service interruption to free the resources to more important request is not permitted in non-preemptive scheduling. For this reason, it is also apparent that the preemptive approaches outperformed the non-preemptive ones. Moreover, the proposed preemptive approach with overload prediction achieved better results than all other approaches. In addition, the overload prediction component enhanced the performance of the proposed schemes, both proposed preemptive and non-preemptive schemes, achieved lower total costs than their respective counterparts. For example, at day 210, the proposed non-preemptive approach managed to achieve a saving of about 25US$ in comparison to the non-preemptive approach of the modified ACORD (Al Balas et al., 2016) proposed.

FIGURE 6

Figure 6. Total energy cost of using 4 appliances with price model 1.

FIGURE 7

Figure 7. Total energy cost of using 6 appliances with price model 1.

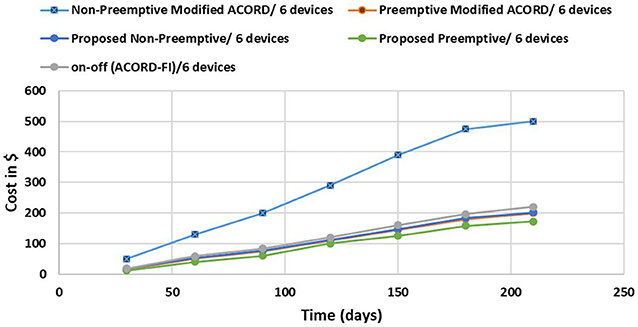
Figure 7 reports a similar behavior with higher saving values when 6 appliances are used. For example, the saving reaches around 300US$ during the same period at 210 days. This can be justified by the addition of the admission phase (overload prediction). However, the other schemes achieved lower saving and relatively comparable performance. Nonetheless, the proposed preemptive approach achieved the best savings.

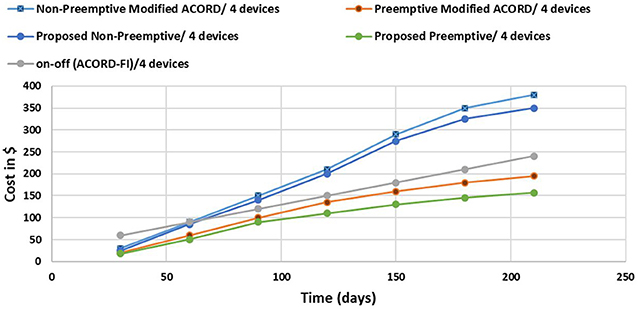
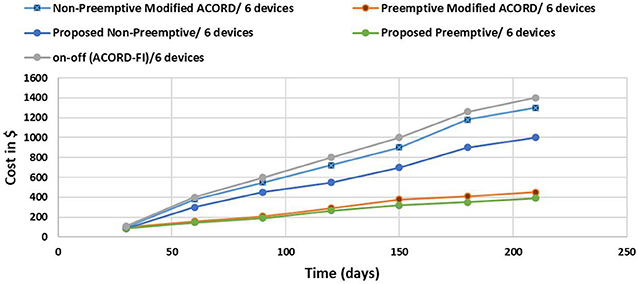
We conducted the same set of experiments for the other pricing model (model 2) adopted in Jordan. Figures 8, 9 depict the results for the pricing model 2. Although the 2 pricing models (1 and 2) exhibit different pricing strategies, the proposed schemes achieved similar behavior, as in the case of model 1, in comparison to the other schemes from the literature. Again, the proposed preemptive approach managed to achieve the highest savings in the energy bill.

FIGURE 8

Figure 8. Total energy cost of using 4 appliances with price model 2.

FIGURE 9

Figure 9. Total energy cost of using 6 appliances with price model 2.

Conclusions and Future Work

Smart grids are an emerging and innovative solution to overcome the limitations of traditional energy grid systems. Smart grids encompass many components, such as smart energy generation from renewable resources, smart metering, and smart management. From the perspective of the user of a typical home, smart grids must provide a smart solution, inside the house, that monitors and controls the energy bill. The main goal of this work was to design and implement novel and efficient appliances scheduling schemes that aim to reduce the total energy cost by deciding which appliances will start and when they will start. In this paper, we proposed two scheduling schemes, namely non-preemptive and preemptive ones. The proposed schemes will invoke a prediction component to predict whether the system will be overloaded or not in the near future. Then, a scheduling component is invoked (in fact, we proposed the two above-mentioned scheduling schemes) to decide which request will be served and when. The scheduling component will try to pack as many requests as possible at the same time. We compared the performance of the proposed schemes with other schemes from the literature under two different pricing models. Simulation results show improvements in terms of consumed energy expressed as total saving in electricity bill cost, with percentages ranging, for example, from 5 to 20% when comparing our proposed preemptive scheme with the modified preemptive scheme (solid green and blue curves in the figures). We note that the admission phase of our approach played an important role in shaping the input and the output of the scheduling schemes.

The performance of the proposed schemes is to be enhanced in the future by considering more sophisticated and realistic prediction models, such as Markovian process and game theory. Moreover, it is necessary to investigate their performance under other pricing models from different regions around the world.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

WM and YK contributed the conception and design of this research and worked on implementing the algorithms and obtaining the simulations results. WM outlined the model and the methodology that will be used to develop the solution. YK worked on the algorithms and details needed to achieve the solution. HM discussed the related work area and provided the required background for the work and discussed the results and compared them to the previous solutions. All authors contributed to the manuscript revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Al Balas, F. A., Mardini, W., Khamayseh, Y., and Bani-Salameh, D. A. (2016). Improved appliance coordination scheme with waiting time in smart grids. Int. J. Adv. Comp. Sci. Appl. 7, 16–30. doi: 10.14569/IJACSA.2016.070403

CrossRef Full Text | Google Scholar

Alam, M. R., St-Hilaire, M., and Kunz, T. (2013). “A survey on cost saving methods for smart grids,” in Proceedings of IEEE SEGE'13 (Oshawa, ON). doi: 10.1109/SEGE.2013.6707914

CrossRef Full Text | Google Scholar

Chakraborty, N., and Kalaimannan, E. (2017). “Selective scheduling: controlling non-preemptive devices in smart grid environment,” in Proceedings of IEEE ISGT'17. (Washington, DC). doi: 10.1109/ISGT.2017.8085962

CrossRef Full Text | Google Scholar

Charoen, P., Javaid, S., Lim, Y., Tan, Y., and Charoenlarpnopparut, C. (2018). Adaptive rescheduling of energy consumption based on user preferences for the future smart grid. in Proceedings of IEEE ISGT Asia (Singapore). doi: 10.1109/ISGT-Asia.2018.8467718

CrossRef Full Text | Google Scholar

Dhivyaprabha, T. T., and Subashini, P. (2018). “Multi-objective optimization for smart energy grids using synergistic fibroblast optimization algorithm,” in Proceedings of REPS-GIE'18 (Casablanca). doi: 10.1109/REPSGIE.2018.8488801

CrossRef Full Text | Google Scholar

Erol-Kantarci, M., and Mouftah, H. T. (2010a). “Using wireless sensor networks for energy-aware homes in smart grids,” in Proceedings of IEEE ISCC'10 (Riccione). doi: 10.1109/BSC.2010.5473004

CrossRef Full Text | Google Scholar

Erol-Kantarci, M., and Mouftah, H. T. (2010b). “TOU-aware energy management and wireless sensor networks for reducing peak load in smart grids,” in Proceedings of IEEE VTC 2010-Fall (Ottawa, ON). doi: 10.1109/VETECF.2010.5594388

CrossRef Full Text | Google Scholar

Erol-Kantarci, M., and Mouftah, H. T. (2011). Wireless sensor networks for cost-efficient residential energy management in the smart grid. IEEE Trans. Smart Grid 2, 314–325. doi: 10.1109/TSG.2011.2114678

CrossRef Full Text | Google Scholar

Erol-Kantarci, M., and Mouftah, H. T. (2015). Energy-efficient information and communication infrastructures in the smart grid: a survey on interactions and open issues. IEEE Commun. Surv. Tutorials 17, 179–197. doi: 10.1109/COMST.2014.2341600

CrossRef Full Text | Google Scholar

Hans, M., Phad, P., Jogi, V., and Udayakumar, P. (2018). “Energy management of smart grid using cloud computing,” in Proceedings of ICICET'18 (Pune). doi: 10.1109/ICICET.2018.8533692

CrossRef Full Text | Google Scholar

Helal, S. A., Najee, R. J., Hanna, M. O., Shaaban, M. F., Osman, A. H., and Hassan, M. S. (2017). “On optimal scheduling for smart homes and their integration in smart grids,” in Proceedings of IEEE CCECE'17 (Windsor, ON). doi: 10.1109/CCECE.2017.7946833

CrossRef Full Text | Google Scholar

Ipakchi, A., and Albuyeh, F. (2009). Grid of the future. IEEE Power Energy Mag. 7, 52–62. doi: 10.1109/MPE.2008.931384

CrossRef Full Text | Google Scholar

Khonji, M., Karapetyan, A., Elbassioni, K., and Chau, S. (2019). Complex-demand scheduling problem with application in smart grid. Theoreti. Comp. Sci. 761, 34–50. doi: 10.1016/j.tcs.2018.08.023

CrossRef Full Text | Google Scholar

Liu, C., Liu, C., Shang, Y., Chen, S., Cheng, B., and Chen, J. (2017). An adaptive prediction approach based on workload pattern discrimination in the cloud. J. Net. Comp. Appl. 80, 35–44. doi: 10.1016/j.jnca.2016.12.017

CrossRef Full Text | Google Scholar

Mohsenian-Rad, A.-H., and Leon-Garcia, A. (2010). Optimal residential load control with price prediction in real-time electricity pricing environments. IEEE Trans. Smart Grid 1, 120–133. doi: 10.1109/TSG.2010.2055903

CrossRef Full Text | Google Scholar

Nouri, A., Soroudi, A., and Keane, A. (2018). “Strategic scheduling in smart grids,” in Proceedings of IEEE EEEIC/I&CPS Europe'18 (Palermo). doi: 10.1109/EEEIC.2018.8494489

CrossRef Full Text | Google Scholar

Reddy, M. S., and Singh, J. G. (2018). “Optimal scheduling of customers' demand based upon power availability and its price in smart grid,” in Proceedings of IEEE UPCON'18 (Gorakhpur). doi: 10.1109/UPCON.2018.8596803

CrossRef Full Text | Google Scholar

Rehmani, M. B., Reisslein, M., Rachedi, A., Erol-Kantarci, M., and Radenkovic, M. (2018). Integrating renewable energy resources into the smart grid: recent developments in information and communication technologies. IEEE Trans. Ind. Info. 14, 2814–2825. doi: 10.1109/TII.2018.2819169

CrossRef Full Text | Google Scholar

Reka, S., and Ramesh, V. (2016). A demand response modeling for residential consumers in smart grid environment using game theory based energy scheduling algorithm. Ain Shams Eng. J. 7, 835–845. doi: 10.1016/j.asej.2015.12.004

CrossRef Full Text | Google Scholar

Tchuisseu, E. B., Gomila Tchawou, D., and Colet, P. (2019). Reduction of power grid fluctuations by communication between smart devices. Int. J. Elect. Power Energy Syst. 108, 145–152. doi: 10.1016/j.ijepes.2019.01.004

CrossRef Full Text | Google Scholar

Yao, L., Shen, J., and Lim, W. H. (2016). “Real-time energy management optimization for smart household,” in Proceedings of IEEE iThings'16, IEEE GreenCom'16, IEEE CPSCom'16, and IEEE SmartData'16 (Chengdu). doi: 10.1109/iThings-GreenCom-CPSCom-SmartData.2016.31

CrossRef Full Text | Google Scholar

Zhang, L., Kerrigan, E. C., and Pal, B. C. (2019). Optimal communication scheduling in the smart grid. IEEE Trans. Ind. Info. 15, 5257–5265. doi: 10.1109/TII.2019.2915051

CrossRef Full Text | Google Scholar

Zhang, Y., Rahbari-Asr, N., Duan, J., and Chow, M. (2016). Day-ahead smart grid cooperative distributed energy scheduling with renewable and storage integration. IEEE Trans. Sustain. Energy 7, 1739–1748. doi: 10.1109/TSTE.2016.2581167

CrossRef Full Text | Google Scholar