Transient Temperature Distribution of Underground Carbon Dioxide Salt Cavern Storage With State Space Model

Yuan, Zhou; Zhou, Yanxi; Wei, Minghui; Liao, Xinwei

doi:10.3389/fenrg.2020.00201

ORIGINAL RESEARCH article

Front. Energy Res., 20 October 2020

Sec. Advanced Clean Fuel Technologies

Volume 8 - 2020 | https://doi.org/10.3389/fenrg.2020.00201

This article is part of the Research Topic Low-Carbon Technologies for the Petroleum Industry View all 19 articles

Transient Temperature Distribution of Underground Carbon Dioxide Salt Cavern Storage With State Space Model

$\nZhou Yuan,&#x;$ Zhou Yuan^1,2^†

Yanxi Zhou¹^†

Minghui Wei¹^*

Xinwei Liao²

¹School of Mechanical and Electrical Engineering, Southwest Petroleum University, Chengdu, China
²State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum, Beijing, China

Underground salt caverns have become one of the potential methods for carbon dioxide (CO₂) storage due to its advantages including high storage capacity and easy construction. The wellbore and salt cavern heat transfer models for the CO₂ injection process was developed and solved by the state space method. This method can not only solve the partial differential equation, but can also be used as the basic model of automatic control. The results indicate that the temperature of annulus and the salt cavern are significantly influenced by the injection rate during the injection process, while the brine temperature in tubing remains almost unchanged. When the injection process stops, the temperature of annulus and the salt cavern are dominated by the formation temperature. The temperature of tubing brine mainly changes after a few hours, causing crystals to separate out from the brine, which can also explain why the tubing is blocked when the gas injection stops.

Introduction

With the advent of industrial development, carbon dioxide (CO₂) has an increasingly high concentration in the atmosphere as a result of the combustion of fossil fuels, such as coal, petroleum, and natural gas, which has caused the rising trend in the Earth's average temperature. There are nearly 1.03 × 10⁹ tons of CO₂ emissions in China every year (Li et al., 2017). How to deal with carbon dioxide emissions has become a global problem. Carbon capture and storage (CCS) is a technique of lower carbon utilization for fossil fuels on a large scale (Li et al., 2015). This technique was developed in the 1970s and has been used in enhanced oil recovery with CO₂ (CO₂-EOR), in enhanced geothermal systems with CO₂ (CO₂-EGS), CO₂ storage with gas recovery (CO₂-EGR), and CO₂ storage with saline water recovery (CO₂-EWR) (Wang et al., 2012; Sun et al., 2013; Boot-Handford et al., 2014; Li et al., 2014; Luo et al., 2014; Middleton et al., 2015; Wei et al., 2020). In recent years, a group of underground salt cavern storages with various advantages have been built in China (Zhang and Goh, 2012). Firstly, man-made salt caverns can be sized by specific demands by water-jet and the capacity of one salt cavern is usually 2–5 × 10⁵ m³ (Bérest, 2019). Furthermore, using a salt cavern as CO₂ storage is different from traditional methods, where CO₂ can be drawn from all the time. Therefore, the salt cavern has extensive application properties for CO₂ storage (Kushnir et al., 2012).

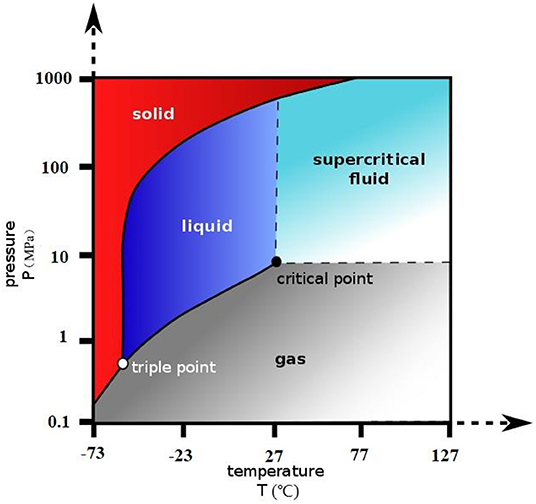
The accurate prediction of wellbore and cavern temperature plays an important role in keeping the storage a safe and smooth process. It has great significance for judging the strength and stability of wellbore and salt caverns. For the underground salt cavern system, while the injection has stopped for a few hours, the crystal in tubing brine may separate out as the temperature changes, which would block the tubing, and affect the CO₂ storage system performance. What is more, when CO₂ approaches a supercritical state (31.1°C, 7.38 MPa) drastic change would occur somewhere along the wellbore and in the salt cavern, which would not be expected during the injection process (Li et al., 2017).

Studies on wellbore temperature distribution have been conducted since the 1950s. Both numerical and analytical approaches have been adopted to estimate the wellbore temperature (Hasan and Kabir, 1996; Wei et al., 2020). The earliest study of wellbore temperature was by Ramey. He drew charts for predicting bottom-hole circulating temperatures (Ramey, 1962; Wei et al., 2020) and proposed a steady-state model for obtaining the hole wellbore temperature distribution, which could not be applied to transient behavior (Hasan and Kabir, 2002; Yang et al., 2017; Wei et al., 2020). Raymond proposed the first numerical model for predicting temperature distributions for both transient and pseudo-steady-state conditions (Raymond, 1969). Hasan proposed the analytic methods for wellbore temperature prediction (Hasan et al., 1997, 1998). For CO₂ injection, the flow and thermal behavior in the wellbore involves some unique characteristics. Many researchers also developed CO₂ two-phase flow models under isothermal conditions (Wang et al., 2011a,b; Guo and Zeng, 2015; Li et al., 2016; Wei et al., 2020). Although using a salt cavern for CO₂ storage is not equal to injecting CO₂ into the wellbore. It needs to consider the heat transfer of annulus, tubing, and the salt cavern (Zhang and Goh, 2015; Wang et al., 2019. There have been few research topics that have focused on this field before (Kyuro and Yuichi, 2011; Goh and Zhang, 2012).

This study develops mathematical models to calculate the wellbore and salt cavern heat transfer models during CO₂ injection and injection-stopped periods, and models were solved by the state space method. This method can not only be used for solving partial differential equations, but also as an automatic control model. The results demonstrated that wellbore and cavern temperatures were significantly influenced by the injection rate during the injection process, and the tubing brine temperature had remained approximately constant. When the injection stopped, the wellbore and cavern temperatures were dominated by the formation temperature. The main variation in the tubing brine temperature occurred a few hours after the injection had stopped which would cause crystals to separate out from the brine. This is the reason why the tubing may be blocked after the injection process is stopped. The model can be used to design CO₂ injection parameters and monitor salt cavern states, and reduce the risk to the underground salt cavern system.

Mathematical Model

Figure 1 shows the phase change of CO₂, when CO₂ approaches the supercritical state (31.1°C, 7.38 MPa), which is likely to occur somewhere along the wellbore and in the salt cavern (Li et al., 2017; Wei et al., 2020).

FIGURE 1

Figure 1. Phase change of carbon dioxide.

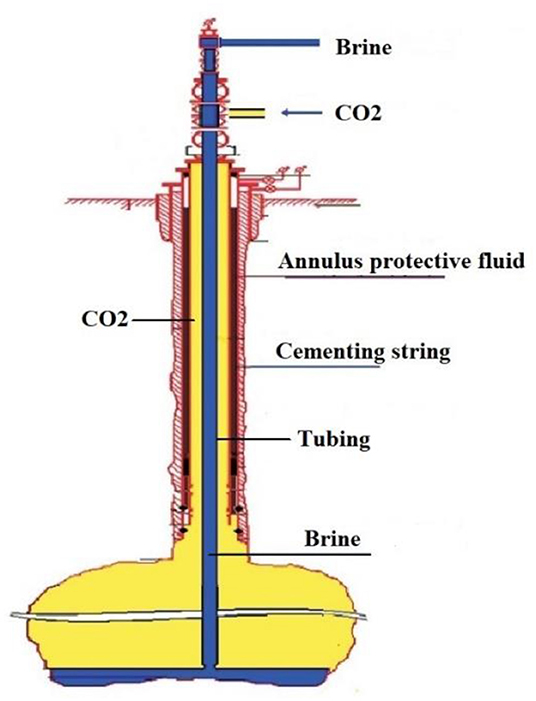
Figure 2 describes the process of injecting CO₂ into the salt cavern storage which can be divided into two parts. The first part: the fluid of CO₂ is injected into the salt cavern storage through annulus. The second part: the fluid of brine in the salt cavern storage flows through the tubing to the ground. Based on the principle of the conservation of energy, the dynamic mathematical model of heat transfer in the process of injecting CO₂ into the salt cavern storage is established (Wei et al., 2020).

FIGURE 2

Figure 2. A schematic of a physical setting for the operation of CO₂ injection.

The Heat Transfer Model of Annulus

According to Figure 2, in the CO₂ heat transfer model of annulus, the energy change is equal to the heat generated by the axial flow of CO₂, the heat transfer between the CO₂ of annulus and the tubing, and that between the well wall and the CO₂ of annulus. Therefore, the heat transfer model is Li et al. (2017) and Wei et al. (2020):

\begin{array}{l} ρ_{a} A_{a} C_{a} \frac{\partial T_{a}}{\partial t} = - M_{a} C_{a} \frac{\partial T_{a}}{\partial z} + 2 π r_{1} λ_{1} [T_{f} - T_{a}] \\ + 2 π r_{2} λ_{2} [T_{w} - T_{a}] & (1) \end{array}

where T_a is the annulus fluid temperature of CO₂, °C. T_w is the tubing temperature, °C. T_f is the well wall temperature, °C. ρ_a is the CO₂ density of annulus, kg/m³. A_a is the area of annulus, m². C_a is the CO₂ specific heat of the annulus fluid, J/kg.°C. M_a is the mass flow of injected CO₂, kg/s. r₁is the radius of annulus, m r₂ is the outer radius of tubing, m. λ₁ is the convective heat transfer coefficient of annulus CO₂ and the well wall, W/m^2.°C. λ₂ is the convective heat transfer coefficient of annulus CO₂ and tubing, W/m^2.°C.

The Heat Transfer Model of Tubing Fluids

The fluid in the tubing is brine, the energy change of it is equal to the heat generated by the axial flow of the brine, and the heat exchange with the tubing brine and the tubing. Therefore, the heat transfer model is:

\begin{array}{l} ρ_{p} A_{p} C_{p} \frac{\partial T_{p}}{\partial t} = ρ_{p} A_{p} C_{p} v_{p} \frac{\partial T_{p}}{\partial z} + 2 π r_{3} λ_{3} [T_{w} - T_{p}] & (2) \end{array}

where T_p is the tubing fluid temperature of brine, °C. ρ_p is the density of the tubing fluid, kg/m³. A_p is the area of the tubing, m². C_p is the specific heat of tubing brine, J/kg.°C. r₃ is the inner radius of tubing, m. v_p is the fluids flow velocity in the tubing, m/s. λ₃ is the convective heat transfer coefficient between the tubing brine and tubing, W/m².°C.

The Heat Transfer Model of Tubing

For the tubing, the energy change is equal to the convection heat transfer between the annulus CO₂ and the tubing, and that between the brine and the tubing. Therefore, the heat transfer model is:

\begin{array}{l} ρ_{w} A_{w} C_{w} \frac{\partial T_{w}}{\partial t} = 2 π r_{2} λ_{2} [T_{a} - T_{w}] + 2 π r_{3} λ_{3} [T_{p} - T_{w}] & (3) \end{array}

where ρ_w is the density of tubing, kg/m³. A_w is the area of tubing, m². C_w is the specific heat of tubing, J/kg°C.

Heat Transfer Model of Salt Cavern Storage

For the CO₂ which is stored in the salt cavern storage, the energy change is equal to the heat transfer between the CO₂ and the salt cavern storage wall, and that between the CO₂ and the brine in the salt cavern storage, and the energy entered from the annulus. Therefore, the heat transfer model is:

\begin{array}{l} m_{c} C_{c} \frac{\partial T_{c}}{\partial t} = A_{f 1} λ_{f 1} [T_{f c} - T_{c}] + A_{c} λ_{b c} [T_{b} - T_{c}] \\ + M_{a} C_{c} [T_{a b} - T_{c}] & (4) \end{array}

where, T_c is a cavern's CO₂ temperature, °C. T_fc is a cavern's formation temperature, °C. T_b is the brine in the salt cavern storage temperature, °C. T_ad is the CO₂ temperature that flows into the cavern from the annulus, °C. m_c is the CO₂ quality in the salt cavern storage, kg. C_c is the CO₂ heat capacity in the salt cavern storage, J/kg.°C. A_f1 is the contact area of the CO₂ and the salt cavern storage wall, m². A_c is the contact area of the brine in the salt cavern storage and the CO₂ in the salt cavern storage, m². λ_f1 is the heat transfer coefficient between the CO₂ and the salt cavern storage wall, W/m^2.°C. λ_bc is the heat transfer coefficient between the CO₂ and the brine in the salt cavern storage, W/m^2.°C. M_a is the mass flow rate of injected gas, kg/s. T_ad is the temperature of the CO₂ which is injected into the salt cavern storage from annulus, °C.

The brine energy change in the salt cavern storage is equal to the heat transfer between brine and the salt cavern wall, and that between the brine and the CO₂. Therefore, the heat transfer model is:

\begin{array}{l} m_{b} C_{b} \frac{\partial T_{b}}{\partial t} = A_{f 2} λ_{f 2} [T_{f} - T_{b}] + A_{c} λ_{c b} [T_{c} - T_{b}] & (5) \end{array}

where, m_b is the quality of brine in the salt cavern storage, kg. C_b is the heat capacity of the brine in the salt cavern storage, J/kg.°C. A_f2 is the contact area of the brine and the salt cavern storage wall, m². A_c is the contact area of the CO₂ in the salt cavern and the brine in the salt cavern, m². λ_f2 is the heat transfer coefficient of the brine and the salt cavern storage wall, W/m^2.°C. λ_cb is the heat transfer coefficient of the brine and CO₂ in the salt cavern storage, W/m^2.°C.

Initial Condition and Boundary Condition and State-Space Method for the Wellbore

In the process of gas injection, mass flow and injection temperature is measured on the ground. The formation temperature is attained using the surface temperature and the formation temperature gradient, the formation temperature gradient is 3°C/100 m, thus T_f = T_f0 + yz, T_f0 is the formation temperature, y is the formation temperature gradient, and z represents depth.

The state space method is a basic model of modern control theory. So it can not only solve the partial differential equation, but can also be used as the basic model of automatic control.

For Equations (1–4), using difference instead of integral, therefore:

\begin{array}{l} \frac{\partial T}{\partial t} = \frac{T (k + 1, 1) - T (k, 1)}{Δ t} \frac{\partial T}{\partial z} = \frac{T (1, j) - T (1, j - 1)}{Δ z} & (6) \end{array}

Equation (1) can be expressed as:

\begin{array}{l} \begin{array}{l} ρ_{a} A_{a} C_{a} \frac{T_{a} (k + 1, j) - T_{a} (k, j)}{Δ t} = - M_{a} C_{a} \frac{T_{a} (k, j) - T_{a} (k, j - 1)}{Δ z} \\ + 2 π r_{2} λ_{2} [T_{w} (k, j) - T_{a} (k, j)] + 2 π r_{3} λ_{3} [T_{f} (k, j) - T_{a} (k, j)] \end{array} & (7) \end{array}

The depth of wellbore is divided into L nodes, each discrete time is represented by k, according to the linear system theory, each grid temperature in the tubing and annulus is an independent state. Set the gas injection temperature as T_a(k, 0), and set $x_{1} = - \frac{M_{a} Δ t}{ρ_{a} A_{a} Δ z}$ , $x_{2} = \frac{2 π r_{2} λ_{2} Δ t}{ρ_{a} A_{a} C_{a}}$ , $x_{2} = \frac{2 π r_{3} λ_{3} Δ t}{ρ_{a} A_{a} C_{a}}$ , and the state space model for the wellbore heat transfer system can be obtained. Equation (1) converts to Wei et al. (2020):

\begin{array}{l} T_{A} (k + 1) = A_{a} T_{A} (k) + B_{a} T_{W} (k) + C_{a} T_{F} (k) + D_{a} U_{d} (k) & (8) \end{array}

where,

\begin{array}{l} T_{A} (k) = {[T_{a} (k, 1), T_{a} (k, 2), T_{a} (k, 3), \dots T_{a} (k, L)]}_{L \times 1}^{T} \\ T_{W} (k) = {[T_{w} (k, 1), T_{w} (k, 2), T_{w} (k, 3), \dots T_{w} (k, L)]}_{L \times 1}^{T} \\ T_{F} (k) = {[T_{f} (k, 1), T_{f} (k, 2), T_{f} (k, 3), \dots T_{f} (k, L)]}_{L \times 1}^{T} \\ U_{d} (k) = {[T_{a} (k, 0), 0, 0, \dots 0]}_{L \times 1}^{T} \end{array}

\begin{array}{l} A_{a} = {[\begin{array}{c} x_{1} + 1 - x_{2} - x_{3} & 0 & 0 & \dots & 0 \\ - x_{1} & x_{1} + 1 - x_{2} - x_{3} & 0 & \dots & 0 \\ 0 & - x_{1} & ⋱ & ⋱ & 0 \\ ⋮ & 0 & ⋱ & x_{1} + 1 - x_{2} - x_{3} & 0 \\ 0 & 0 & 0 & - x_{1} & x_{1} + 1 - x_{2} - x_{3} \end{array}]}_{L \times L} \\ B_{a} = x_{2}, C_{a} = x_{3}, D_{a} = - x_{1} \end{array}

where, T_A is the state vector of the heat transfer state space model for annulus fluid of CO₂, T_W is the state vector of tubing temperature, T_F is the state vector of formation temperature, U_d is the input vector for the state space model, and A_a is the system matrix. In the same way, set $z_{1} = - v_{p} \frac{Δ t}{Δ z}$ , $z_{2} = \frac{2 π r_{1} λ_{1} Δ t}{ρ_{P} A_{P} C_{P}}$ , and the brine temperature from the cavern that entered into the tubing as T_p(k, 0), we can get the state space model of the brine temperature in the tubing (Wei et al., 2020).

\begin{array}{l} T_{P} (k + 1) = A_{P} T_{P} (k) + B_{P} T_{W} (k) + D_{P} U_{P} (k) & (9) \end{array}

where,

\begin{array}{l} T_{P} (k) = {[T_{P} (k, 1), T_{P} (k, 2), T_{P} (k, 3), \dots T_{P} (k, L)]}_{L \times 1}^{T} \\ T_{W} (k) = {[T_{w} (k, 1), T_{w} (k, 2), T_{w} (k, 3), \dots T_{w} (k, L)]}_{L \times 1}^{T} \\ U_{P} (k) = {[T_{p} (k, 0), 0, 0, \dots 0]}_{L \times 1}^{T} \\ A_{p} = \\ {[\begin{array}{c} z_{1} + 1 - z_{2} & 0 & 0 & \dots & 0 \\ - z_{1} & z_{1} + 1 - z_{2} & 0 & \dots & 0 \\ 0 & - z_{1} & ⋱ & ⋱ & 0 \\ ⋮ & 0 & ⋱ & z_{1} + 1 - x_{2} & 0 \\ 0 & 0 & 0 & - z_{1} & z_{1} + 1 - z_{2} \end{array}]}_{L \times L} \\ B_{a} = z_{2}, D_{a} = - z_{1} \end{array}

where, T_P is the state vector of the heat transfer state-space model for the tubing fluid of brine, U_p is the input vector, and A_p is the system matrix.

Salt cavern storage temperature state space model:

Set $y_{1} = \frac{A_{f 1} λ_{f 1} Δ t}{m_{c} C_{c}}$ , $y_{2} = \frac{A_{c} λ_{b c} Δ t}{m_{c} C_{c}}$ , $y_{3} = \frac{M_{a} C_{c} Δ t}{m_{c} C_{c}}$ , $z_{1} = \frac{A_{f 2} λ_{f 2} Δ t}{m_{b} C_{b}}$ , $z_{2} = \frac{A_{c} λ_{c b} Δ t}{m_{b} C_{b}}$ , So (3), (4) can be transformed into the state space model for calculating the temperature of gas and brine in salt cavern storage

\begin{array}{l} [\begin{array}{l} T_{c} (k + 1) \\ T_{b} (k + 1) \end{array}] = \\ [\begin{array}{l} 1 - y_{1} - y_{2} - y_{3} & y_{3} \\ z_{2} & 1 + z_{1} + z_{2} \end{array}] [\begin{array}{l} T_{c} (k) \\ T_{b} (k) \end{array}] + [\begin{array}{l} y_{1} & 1 \\ z_{1} & 0 \end{array}] [\begin{array}{l} T_{f} \\ T_{a d} \end{array}] & (10) \end{array}

The CO₂ gas in the salt cavern storage satisfies the gas equation. Before calculation, the initial density of gas in the salt cavern storage can be calculated according to the initial pressure of the gas in the salt cavern storage and the gas state equation.

\begin{array}{l} ρ_{c} = \frac{P_{c} M}{8.314 Z T_{c}} & (11) \end{array}

where M is the molecular mass of natural gas, and Z is the pressure factor, which can be obtained by:

\begin{array}{l} Z = 0.702 e^{- 2.5 T_{r}} p_{r}^{2} - 5.524 e^{- 2.5 T_{r}} p_{r} \\ + (0.044 T_{r}^{2} - 0.164 T_{r} + 1.15) & (12) \end{array}

\begin{array}{l} p_{r} = \frac{p}{p_{e}}, T_{r} = \frac{T}{T_{e}} & (13) \end{array}

where Pr is the pseudo-reduced pressure, dimensionless; Tr is the pseudo-reduced temperature, dimensionless; Pc is the critical pressure of CO₂ gas, Pa; Tc is the critical temperature of gas, K (Ren et al., 2016).

After every step, the mass of CO₂ gas in the cavern is:m_c(k + 1) = M_aΔt + m_c(k). The density of natural gas in the cavern is:

\begin{array}{l} ρ_{c} (k) = m_{c} (k) / V_{c} & (14) \end{array}

According to Equations (11–14), the pressure of the cavern can be obtained. To ensure that the carbon dioxide in the salt cavern storage will not have a phase change, the allowed pressure of the cavern is generally <7 MPa.

Case Study

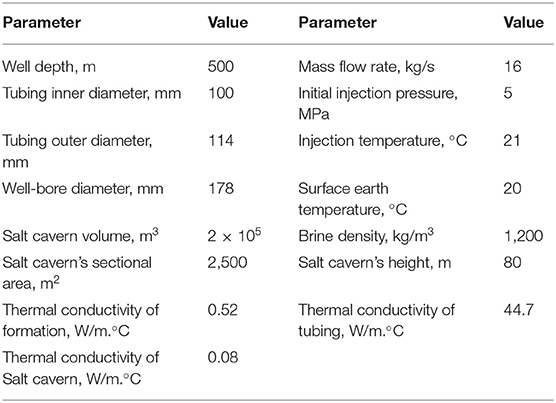
The state space model was used to show the transient temperature distribution of underground CO₂ salt cavern storage, supposing the salt cave's shape is cylindrical and its simulation data were shown in Table 1 (Zhang and Goh, 2012; Bérest, 2019).

TABLE 1

Table 1. Calculation parameters.

The wellbore temperature profiles, as a function of well depth under different injection times, are calculated by the state space method. As shown in Figure 3A, the temperature decreases with injection and reaches a quasi-stable state temperature of 27.5°C at the bottom of annulus. The time needed to reach the quasi steady state is about 20 min. Therefore, special attention should be paid to monitoring in the first 20 min during the injection process. Figure 3B signifies the annulus temperature profiles after injection for 0.1, 1, and 2 h. With the increase of injection time, the annulus temperature decreases, its temperature variation is 1.5°C at the bottom of the annulus. Figure 3C manifests the effect of different gas injection times on the brine temperature distribution in the tubing. The steady state temperature of the tubing brine remains almost unchanged at two injection times. Therefore, the crystal separating out from brine due to the temperature changes would not occur during the injection process.

FIGURE 3

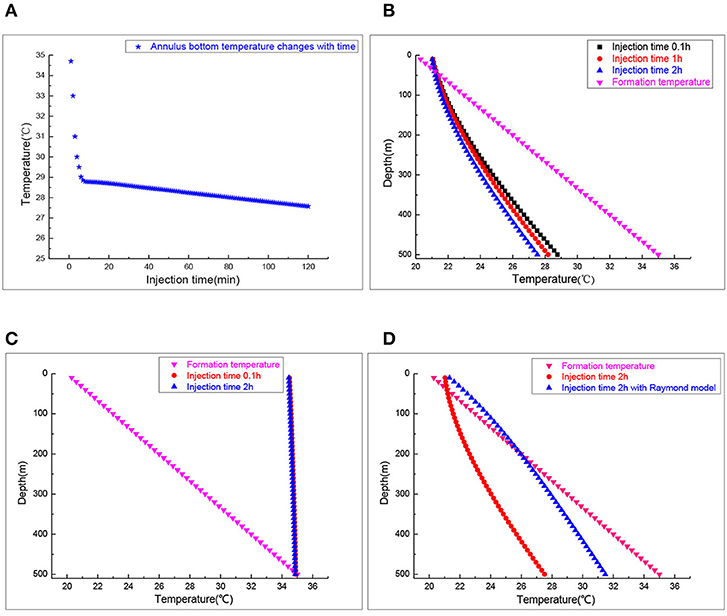
Figure 3. The wellbore temperature profile during the injection process. (A) Annulus bottom temperature. (B) Annulus temperature profiles. (C) Inside tubing brine temperature profiles. (D) Annulus temperature profiles.

The tubing heat transfer effect was neglected in the Raymond model while tubing's influence on temperature distribution of the annulus was considered in the state space model. The material of the tubing used is steel which is used in petroleum and matches the American Petroleum Institute (API) specifications. Figure 3D displays the tubing heat transfer effect on the annulus temperature distribution. More heat would enter the annulus from the formation transferring without considering it. The annulus CO₂ temperature calculated by the Raymond model is about 3–4°C lower than that by the state space model. Therefore, when calculating the annulus CO₂ temperature, the influence of tubing heat transfer could not be ignored.

Figure 4 presents the change of the salt cavern temperature and pressure during the injection process. The pressure prediction is also very important for stable operation of the gas storage. For salt cavern gas storage, the general pressure range is about 5–25 MPa. As shown in Figure 4A, salt cavern pressure increases from 5 to 6.1 MPa in an 80-h injection. It is in the allowable operating pressure range. Figure 4B shows the temperature variation of salt cavern CO₂ and brine in a 60-h injection, and CO₂ temperature decreases to a new quasi-steady state. According to Figure 1, there is no CO₂ phase change during the injection process so it meets the design requirement. We can calculate that the CO₂ mass is 1.9978 × 10⁷ Kg.

FIGURE 4

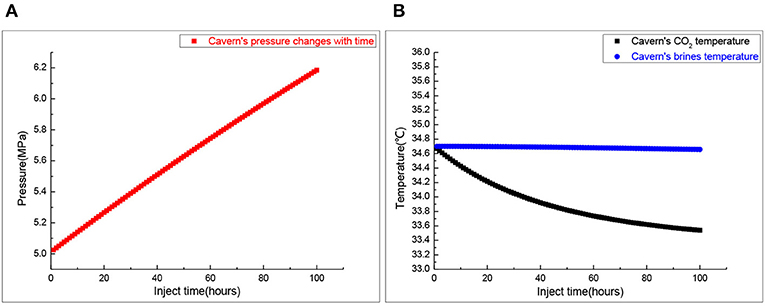
Figure 4. The cavern's pressure and temperature during the injection process. (A) Salt cavern pressure. (B) Salt cavern temperature.

Figure 5 is the effect of the gas injection rate on CO₂ storage system operation state. Figure 5A demonstrates the annulus CO₂ temperature profiles in CO₂ injection rates of 13, 16, and 20 kg/s. Different CO₂ injection rates have little influence on the annulus temperature above 100-m depth. The annulus temperature in the middle and lower part gradually decreased with the increased injection rate. Figure 5B shows the temperature variation of the brine in the tubing. When the CO₂ injection rate changed, the brine temperature changed very little. Figure 5C manifests the CO₂ gas pressure in the salt cavern at different CO₂ injection rates. When the CO₂ injection rates were 13, 16, and 20 kg/s, the CO₂ gas pressure in the salt cavern was 5.9, 6.1, and 6.4 MPa, respectively, after an 100-h CO₂ injection. The CO₂ gas pressure in the salt cavern increased significantly with the increase of the gas injection rate. Figure 5D shows the variation of CO₂ gas temperature in the salt cavern at different injection rates. As the injection rate increased, the CO₂ gas temperature in the salt cavern decreased significantly, and reached new and different quasi-steady states.

FIGURE 5

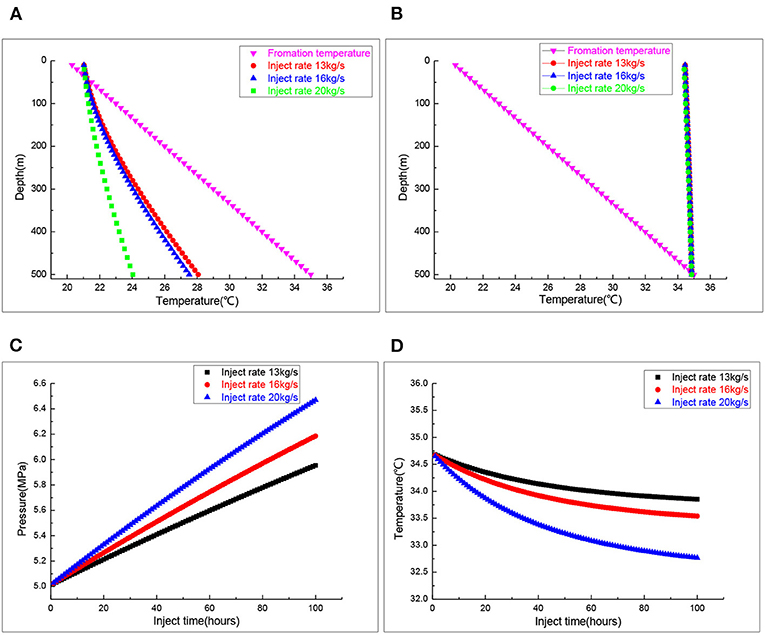
Figure 5. The wellbore and cavern's temperature at different injection rates. (A) Annulus temperature profiles. (B) Inside tubing temperature profiles. (C) Salt cavern pressure. (D) Salt cavern temperature.

Figure 6 is the change of the temperature in the wellbore and salt cavern when the well was shut in. Figure 6A signifies the change of CO₂ gas temperature in the salt cavern storage when the well was shut in. During the injection process, the temperature of injection CO₂ plays a dominant role in the salt cavern's temperature. When CO₂ injection stops, the heat transfer between the formation and salt cavern's CO₂ plays a dominant role in the salt cavern's temperature. The CO₂ gas temperature in the salt cavern storage increases after the well is shut in, but the increasing trend slows and gradually approaches the formation temperature. Figure 6B shows the change of CO₂ gas pressure in salt cavern storage when the well is shut in. When the well was shut in, the CO₂ gas pressure in salt cavern storage changes with the temperature change, but the change is very small. Figure 6C shows the distribution of annulus CO₂ temperature at different time points when the well is shut in. Due to the heat transfer between the formation and the brine in the tubing, the annulus temperature firstly increases and then decreases. At first, the annulus temperature is lower than the formation temperature, then it becomes higher than it, and finally approaches the current formation temperature. Figure 6D shows the brine temperature in the tubing in 1, 5, and 20 h after the well was shut in, and the brine temperature in the tubing gradually approached the formation temperature. The result shows that heat transfer between the wellbore and formation play a dominant role in the brine temperature distribution in the tubing after the well is shut in.

FIGURE 6

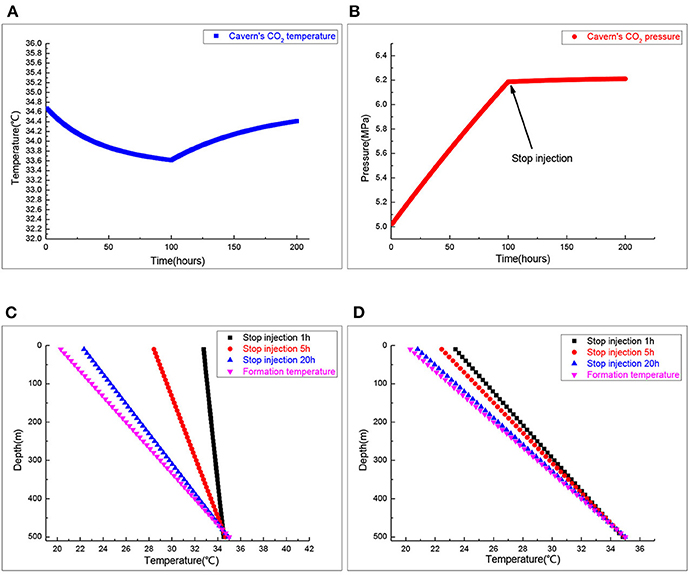
Figure 6. The wellbore and cavern's temperature when injection stops. (A) Salt cavern CO₂ temperature. (B) Salt cavern CO₂ pressure. (C) Annulus CO₂ temperature profiles. (D) Inside tubing brine temperature.

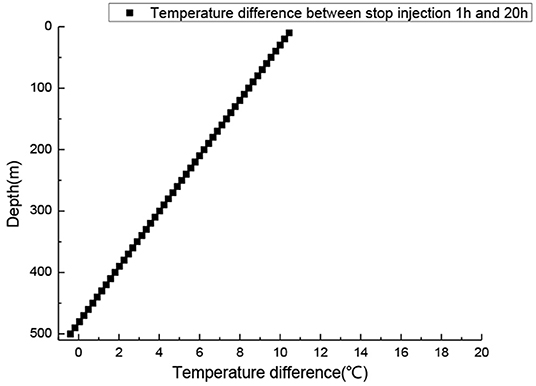
Figure 7 shows the distribution of the temperature variation between the temperature when the well was shut in for 20 h and the temperature just after gas injection was stopped. The change of brine temperature in the tubing mainly occurs when the well was shut in. The change of temperature will cause crystals to separate out from the brine, which can explain the blockage of the tubing when the well was shut in.

FIGURE 7

Figure 7. The wellbore and cavern's temperature with different injection rate.

Conclusion

This thesis proposes a new method (using underground salt cavern storage) for CO₂ storage and a mathematical model for transient temperature distribution during the CO₂ injection process. Furthermore, state space method is used for solving this model, where CO₂ storage's temperature-pressure can be predicted, and parameters of CO₂ storage can be monitored and optimized during the CO₂ injection process.

The operating parameters analysis manifests that flow rates have a significant impact on the temperature of the wellbore and the cavern. In addition, when the injection is stopped, heat transfer is dominated by the formation temperature, resulting in a remarkable increase in annulus temperature. The temperature of tubing brine mainly changes when injection stops, which is very important in preventing blockages in the tubing.

This research may help interpret the mechanism of wellbore and cavern heat transfer during CO₂ injection. This heat transfer model of wellbore and cavern is our primary work. Future work will be focused on the CO₂ releasing process and the phase variation in the process.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

ZY and YZ: stimulation, data curation, and writing manuscript. MW: construction of thesis ideas, establish mathematical model, and provide research fund. XL: manuscript review. All authors contributed to the article and approved the submitted version.

Funding

This research was funded by the State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum, Beijing, grant number PRP/open-1610 and the National Natural Science Foundation of China, grant number 51804267.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer NW declared a shared affiliation, with no collaboration, with with several of the authors YZ and MW to the handling editor.

References

Bérest, P. (2019). Heat transfer in salt caverns. Int. J. Rock Mech. Rock Eng. Min. Sci. 120, 82–95. doi: 10.1016/j.ijrmms.2019.06.009

CrossRef Full Text | Google Scholar

Boot-Handford, M., Abanades, J. C., Anthony, E., Blunt, M., and Brandani, S. (2014). Carbon capture and storage update. Energy Environ. Sci. 7, 130–189. doi: 10.1039/C3EE42350F

CrossRef Full Text | Google Scholar

Goh, A. T., and Zhang, W. (2012). Reliability assessment of stability of underground rock caverns. Int. J. Rock Mech. Mining Sci. 55, 157–163. doi: 10.1016/j.ijrmms.2012.07.012

CrossRef Full Text | Google Scholar

Guo, J., and Zeng, J. (2015). A coupling model for wellbore transient temperature and pressure of fracturing with supercritical carbon dioxide. Shi You XueBao/ActaPet. Sin. 36, 203–209. doi: 10.7623/syxb201502009

CrossRef Full Text

Hasan, A. R., and Kabir, C. S. (1996). A mechanistic model for computing fluid temperature profiles in gas-lift wells. SPE Prod. Facil. 11, 179–185. doi: 10.2118/26098-PA

CrossRef Full Text | Google Scholar

Hasan, A. R., and Kabir, C. S. (2002). Fluid Flow and Heat Transfer in Wellbores. Richardson, TX: SPE.

Google Scholar

Hasan, A. R., Kabir, C. S., and Wang, X. (1997). Development and Application of a Wellbore/Reservoir Simulator for Testing Oil Wells. SPEFE.

Google Scholar

Hasan, A. R., Kabir, C. S., and Wang, X. (1998). Wellbore Two-Phase Flow and Heat Transfer During Transient Testing. SPEJ.

Google Scholar

Kushnir, R., Dayan, A., and Ullmann, A. (2012). Temperature and pressure variations within compressed air energy storage caverns. Int. J. Heat Mass Transfer 55, 5616–5630. doi: 10.1016/j.ijheatmasstransfer.2012.05.055

CrossRef Full Text | Google Scholar

Kyuro, S., and Yuichi, S. (2011). Heat Transfer and Phase Change in Deep CO2 Injector for CO2 Geological Storage. Two Phase Flow, Phase Change and Numerical Modeling. Fukuoka: InTech.

Google Scholar

Li, Q., Wei, Y. N., Liu, G., and Lin, Q. (2014). Combination of CO₂ geological storage with deep saline water recovery in western China: insights from numerical analyses. Appl. Energy 116, 101–110. doi: 10.1016/j.apenergy.2013.11.050

CrossRef Full Text | Google Scholar

Li, X., Li, G., Wang, H., Lu, P., Tian, S., and Song, X. (2017). A unified model for wellbore flow and heat transfer in pure CO₂ injection for geological sequestration, EOR and fracturing operations. Int. J. Greenhouse Gas Control 42, 602–614. doi: 10.1016/j.ijggc.2016.11.030

CrossRef Full Text | Google Scholar

Li, X., Li, G., Wang, H., Lu, P., Tian, S., Yang, R., et al. (2016). “A coupled model for predicting flowing temperature and pressure distribution in drilling ultra-short radius radial wells,” in IADC/SPE Asia Pacific Drilling Technology Conference, (Singapore), 22–24.

Google Scholar

Li, X., X, R., Wei, L., and Jiang, P. (2015). Modeling of wellbore dynamics of a CO2 injector during transient well shut-in and start-up operations. Int. J. Greenhouse Gas Control 42, 602–614. doi: 10.1016/j.ijggc.2015.09.016

CrossRef Full Text | Google Scholar

Luo, F., Xu, R. N., and Jiang, P. X. (2014). Numerical investigation of the doublet enhanced geothermal system with CO2as working fluid (CO2-EGS). Energy 64, 307–322. doi: 10.1016/j.energy.2013.10.048

CrossRef Full Text

Middleton, R. S., Carey, J. W., Currier, R. P., Hyman, J. D., Kang, Q., Karra, S., et al. (2015). Shale gas and non-aqueous fracturing fluids: opportunities and challenges for supercritical CO₂. Appl. Energy 147, 500–509. doi: 10.1016/j.apenergy.2015.03.023

CrossRef Full Text | Google Scholar

Ramey, H. J. (1962). Wellbore heat transmission. J. Pet. Technol. 14, 427–435. doi: 10.2118/96-PA

CrossRef Full Text | Google Scholar

Raymond, L. R. (1969). Temperature distribution in a circulating drilling fluid. J. Pet. Technol. 21, 333–341. doi: 10.2118/2320-PA

CrossRef Full Text | Google Scholar

Ren, W., Li, G., Tian, S., Sheng, M., and Fan, X. (2016). An analytical model for real gas flow in shale nanopores with non-circular cross-section. AIChE J. 62, 2893–2901. doi: 10.1002/aic.15254

CrossRef Full Text | Google Scholar

Sun, H., Yao, J., Gao, S. H., Fan, D. Y., Wang, C. C., and Sun, Z. X. (2013). Numerical study of CO₂ enhanced natural gas recovery and sequestration in shale gas reservoirs. Int. J. Greenh. Gas Control 19, 406–419. doi: 10.1016/j.ijggc.2013.09.011

CrossRef Full Text | Google Scholar

Wang, H., Li, G., and Shen, Z. (2012). A feasibility analysis on shale gas exploitation with supercritical carbon dioxide. Energy Sources Part A 34, 1426–1435. doi: 10.1080/15567036.2010.529570

CrossRef Full Text | Google Scholar

Wang, H., Shen, Z., and Li, G. (2011a). Influences of formation water invasion on the wellbore temperature and pressure in supercritical CO₂ drilling. Pet. Explor. Dev. 38, 362–368. doi: 10.1016/S1876-3804(11)60039-6

CrossRef Full Text | Google Scholar

Wang, H., Shen, Z., and Li, G. (2011b). Wellbore temperature and pressure coupling calculation of drilling with supercritical carbon dioxide. Pet. Explor. Dev. 38, 97–102.

Google Scholar

Wang, Z., Wang, L., and Zhang, W. (2019). A random angular bend algorithm for two- dimensional discrete modeling of granular materials. Materials. 12:2169. doi: 10.3390/ma12132169

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, M., Wu, C., and Zhou, Y. (2020). Study on wellbore temperature and pressure distribution in process of gas hydrate mined by polymer additive CO₂ jet. Adv. Polymer Technol. 2020, 1–7. doi: 10.1155/2020/2914375

CrossRef Full Text | Google Scholar

Yang, M., Zhao, X., and Meng, Y. (2017). Determination of transient temperature distribution inside a well bore considering drill string assembly and casing program. Appl. Thermal Eng. 118, 299–314. doi: 10.1016/j.applthermaleng.2017.02.070

CrossRef Full Text | Google Scholar

Zhang, W., and Goh, A. T. (2012). Reliability assessment on ultimate and serviceability limit states and determination of critical factor of safety for underground rock caverns. Tunnel. Undergr. Space Technol. 32, 221–230. doi: 10.1016/j.tust.2012.07.002

CrossRef Full Text | Google Scholar

Zhang, W. G., and Goh, A. T. C. (2015). Regression models for estimating ultimate and serviceability limit states of underground rock caverns. Eng. Geol. 188, 68–76. doi: 10.1016/j.enggeo.2015.01.021

CrossRef Full Text | Google Scholar

Keywords: salt cavern, CO₂ storage, heat transfer, state space method, injection process

Citation: Yuan Z, Zhou Y, Wei M and Liao X (2020) Transient Temperature Distribution of Underground Carbon Dioxide Salt Cavern Storage With State Space Model. Front. Energy Res. 8:201. doi: 10.3389/fenrg.2020.00201

Received: 27 March 2020; Accepted: 30 July 2020;
Published: 20 October 2020.

Edited by:

Kaiqiang Zhang, Imperial College London, United Kingdom

Reviewed by:

Wengang Zhang, Chongqing University, China
Na Wei, Southwest Petroleum University, China
Jie Chen, Chongqing University, China

Copyright © 2020 Yuan, Zhou, Wei and Liao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Minghui Wei, d21oODgxOTg4JiN4MDAwNDA7MTYzLmNvbQ==

^†These authors have contributed equally to this work

Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.