- 1Fundamental Science on Nuclear Safety and Simulation Technology Laboratory, Harbin Engineering University, Harbin, China
- 2Science and Technology on Reactor System Design Technology Laboratory, Nuclear Power Institute of China, Chengdu, China
Corrugated plate dryer is an important steam-water separation equipment in steam generator of secondary loop of nuclear power plant. Its steam-water separation efficiency has a certain influence on economic index of nuclear power plants. It is meaningful to understand flow characteristics of liquid film on corrugated plate wall. Besides, the fluctuation of the liquid film may cause the occurrence of liquid film rupture, thus the research on the fluctuation of the liquid film on the wall of the corrugated plate is very important. This paper uses Plane laser induced fluorescence (PLIF) method to measure liquid film thickness. Curve of film thickness with time is obtained. Calculation formula of average value of liquid film thickness is given. Based on power spectral density (PSD) method, non-linear characteristics of liquid film thickness are studied. Results show that the relationship between film thickness and Reynolds number conforms to Nusselt theory. Nevertheless, the results show deviation from Nusselt as well as Karapantsios estimation. When Reynolds number is in the range of 600 to 3000 and surface roughness is 0.03, the fluctuation of the power spectrum of the liquid film thickness caused by gravity can be ignored, which provides a reference for study on steam-water separation.
Introduction
The corrugated plate dryer is an important device in the steam generator in the secondary loop of the nuclear power plant (Wang and Tian, 2019a; Wang et al., 2019, 2020a,b). The schematic diagram of its structure and the distribution of the phases inside the corrugated plate are shown in Figure 1. Its main parameters are the plate spacing d of the corrugated plate, the folded edge length L of the corrugated plate, the height H of the corrugated plate, and the folding angle θ. The main function of the corrugated plate dryer is to dry high-temperature and high-pressure steam. Therefore, it is important to understand the characteristics of liquid film flow and rupture in the corrugated plate dryer (Wang and Tian, 2019b; Chen et al., 2020a,b; Wang et al., 2020c). In 1916, Nusselt first proposed the analytical solution of laminar film condensation of pure steam. Some assumptions were made.
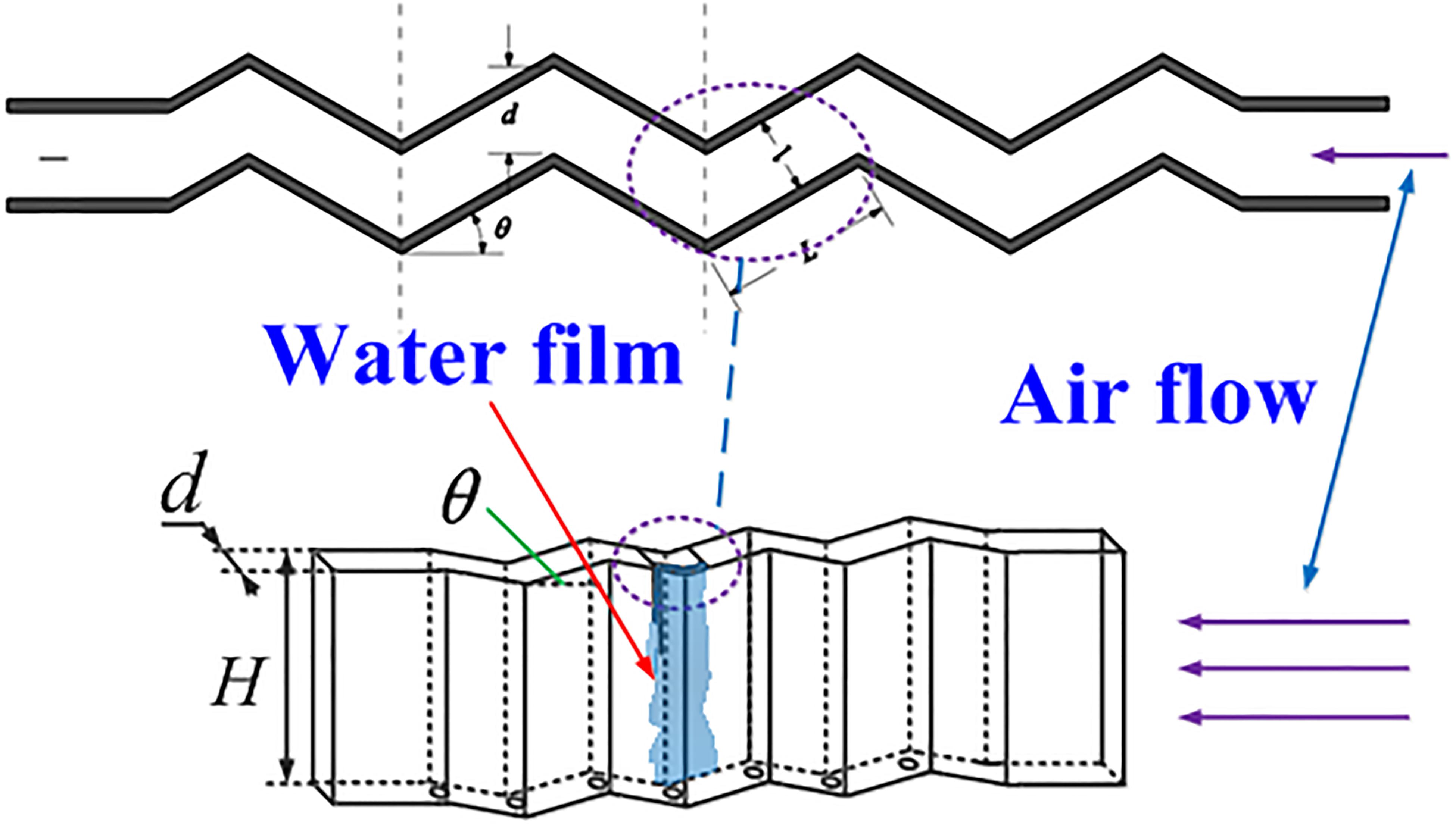
Figure 1. Structure of the corrugated plate dryer and the distribution of different phases in corrugated plate.
(1) The liquid film is a two-dimensional laminar flow.
(2) Each physical property parameter is constant.
(3) The gas-phase medium is stationary, and the surface of the liquid film is smooth. The effect of gas on the liquid film flow is ignored.
The Nusselt’s theoretical equation between liquid film thickness h and Reynolds number is given in Eq. (1).
Where μl is the dynamic viscosity of the fluid, m2s−1.
Wang et al. have studied the flow and rupture characteristics of the liquid film on the wall of the corrugated plate based on probability density method (Wang and Tian, 2019a; Wang et al., 2020b, c). The results show that the source of energy generated by liquid film fluctuations is mainly the superposition of isolated peaks. Chen et al. (2020a,b) analyzed the motion characteristics of droplets in the corrugated plate. In addition, the experimental study of the coronal spray produced when droplets hit the liquid film on the wall of the corrugated plate. Zhang et al. (2015) studied the separation effect of the corrugated plate (Zhuang and Liu, 2020). The phenomenon of liquid film recirculation on the wall of the corrugated plate was observed when the flow velocity of the traverse air flow was large. The liquid film reflux model was established. Zhao et al. (2019) set up the droplet motion model in theory. Although some scholars have done research on the characteristics of liquid film flow in the corrugated plate. The conclusions on liquid film flow fluctuation have not yet been unified. In addition, with the development of measurement level, the measurement method of liquid film thickness has improved. The PLIF method is currently often used to measure the thickness of thin liquid films.
The fluctuation of the liquid film may generate energy, which will cause the occurrence of liquid film rupture. Therefore, the study of the volatility of the liquid film on the wall of the corrugated plate is very important. In this paper, firstly, the thickness of the liquid film flowing steadily on the wall surface of the corrugated plate is measured by the method of PLIF technology. Thus, the curve of liquid film thickness with time is obtained. The calculation equation of the average value of the liquid film thickness is given. In addition, based on the power spectral density (PSD) method, the fluctuation and non-linear characteristics of the liquid film thickness are studied. This research is expected to provide a reference for the study of the flow characteristics of the liquid film on corrugated plate wall and the study of the mechanism of steam-water separation of the corrugated plate dryer. In an actual nuclear power plant, the liquid film flow rate in the corrugated plate is very large. Therefore, the study of the liquid film under a larger Reynolds number can better predict the flow inside the steam generator. Thus study on the fluctuation characteristics of liquid film with a larger Reynolds number is a vital prospect.
Experiment
Experimental System
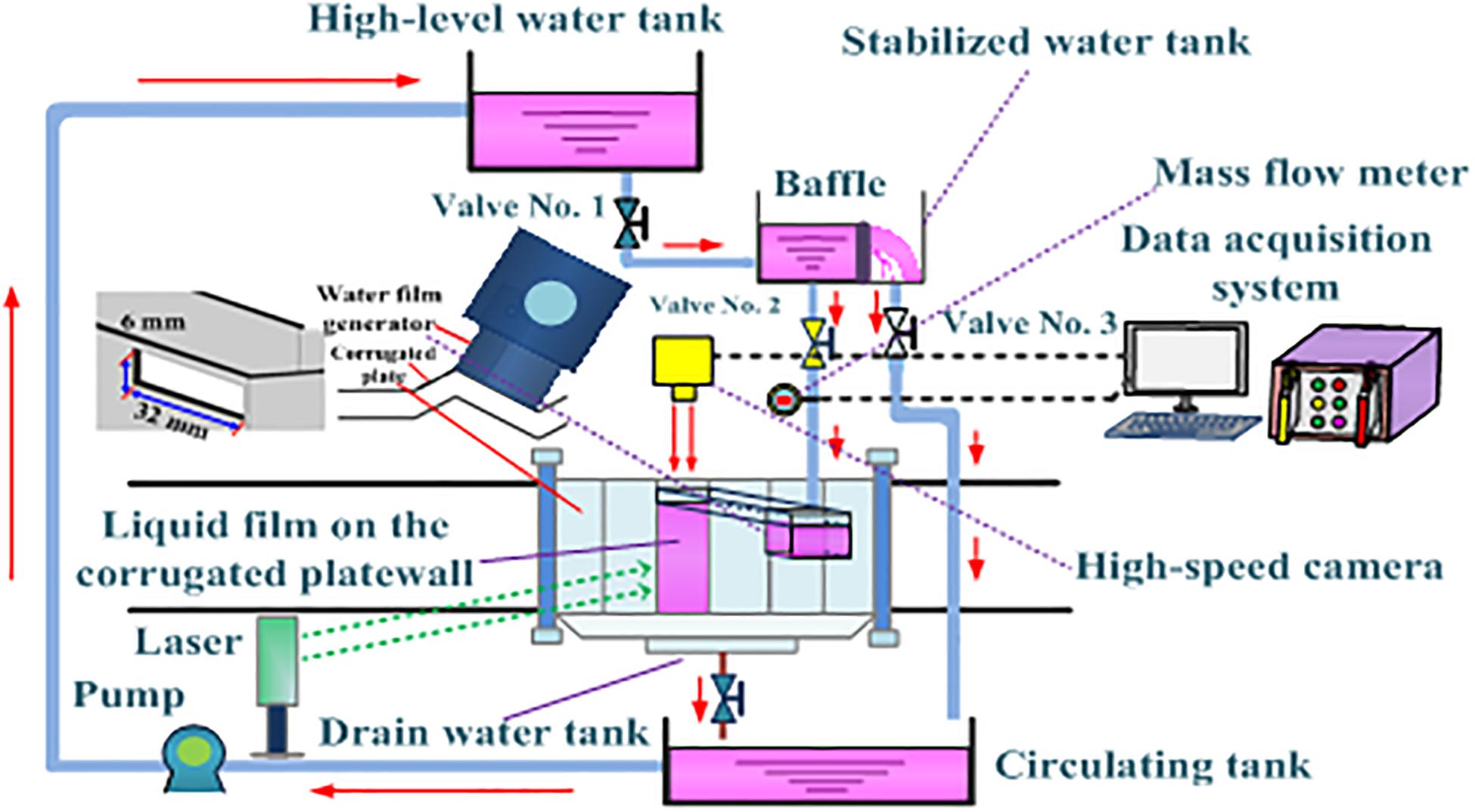
Schematic diagram of the experimental system is shown in Figure 2.
Liquid film containing Rhodamine B fluorescent stain with a maximum absorption wavelength of 555 nm flows from high-level water tank to the stabilized water tank. The liquid level height of the liquid on the left side of the stabilized water tank remains unchanged, and the excess liquid on the right side of the water tank is directly discharged into the circulating water tank, which makes the pressure of the liquid film constant. Liquid film generated by the liquid film generator flows stably and uniformly down the wall. The liquid film flowing through the experiment section flows from the drain water tank at the bottom of the corrugated plate to the water collection tank and enters the circulating water tank. In this study, the narrow slit method is used to generate a thin liquid film, that is, a horizontal narrow slit is set at the top of corrugated plate so that the liquid film flows smoothly to the plate wall. The structure of water film generator is shown in Figure 2. The parameters of the corrugated plate used in this experiment are as follows. d, L, H, and θ are 19.5 mm, 50 mm, 200 mm, and 45°, respectively. Surface roughness of corrugated plate wall is 0.03.
PLIF Method for Water Film Thickness Measurement
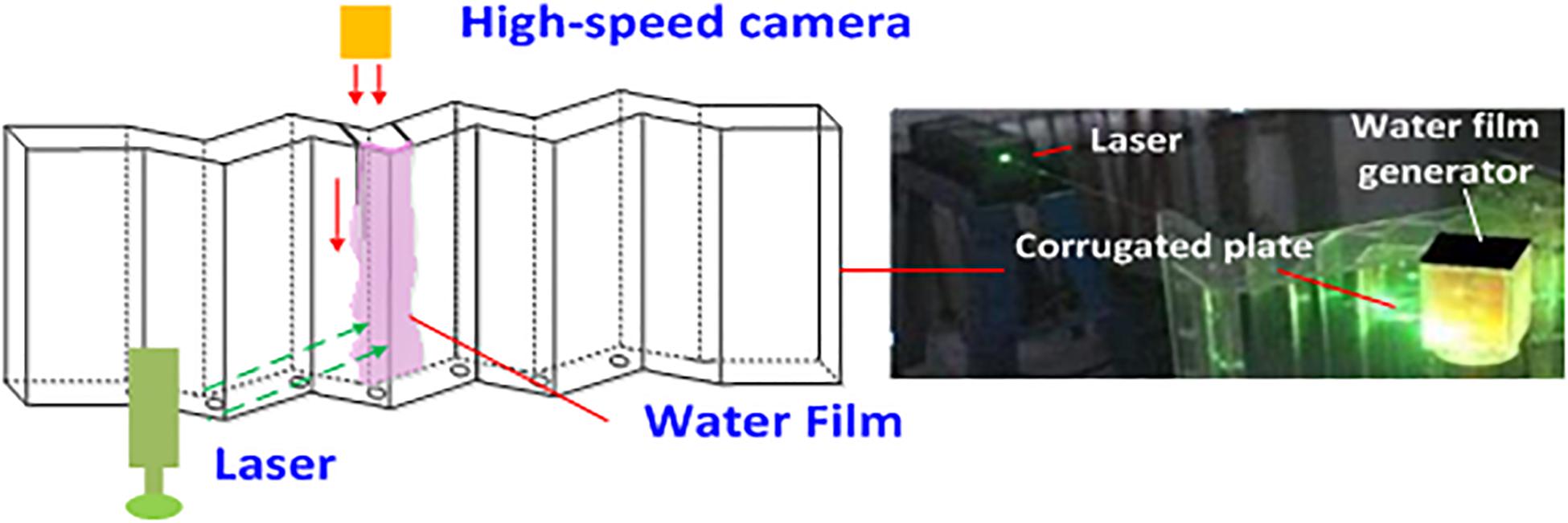
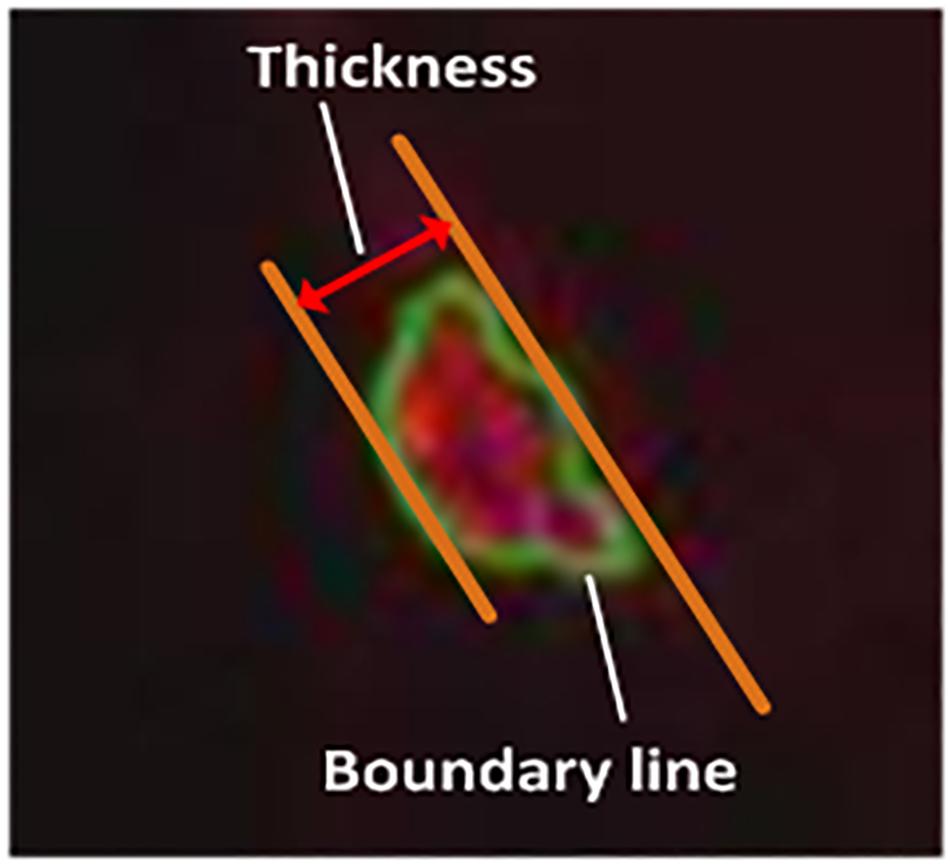
Schematic diagram of capture of liquid film thickness image is shown in Figure 3. The maximum absorption wavelength of rhodamine B is 555 nm (Wang and Tian, 2019a). The wavelength of the solid-state laser in Figure 3 is 532 nm. Initially, the particles of Rhodamine B are in the ground state. When the solid-state laser is irradiated on the wall surface of the corrugated plate in the vertical direction, the rhodamine B particles in the liquid film will be excited. Rhodamine B particles are unstable, they will return from the excited state to the ground state, which causes visible light to be generated. The light can be captured by high-speed camera (as shown in Figure 4). In the experiment, liquid film images were collected 500 times per second. The boundary of the liquid film can be identified by the computer program and the principle of boundary differentiation. The green outline shown in Figure 4 is the recognized boundary line of the liquid film. The distance between the two parallel lines in Figure 4 represents the thickness of the liquid film. The grayscale image of the liquid film image can be obtained through image processing software. In this way, the measurement of liquid film thickness can be converted into a measurement of the number of pixels in the grayscale image (Wang and Tian, 2019a).
According to the digital image processing and scale, the true thickness of the liquid film can be obtained. Instantaneous film thickness is as follows.
Where h is the corrugated plate wall thickness, m is the pixel amount of the corrugated plate wall thickness image and n is instantaneous pixel amount of liquid film thickness image, respectively. Average film thickness is as follows.
Where N is the sample points amount and δi is water film thickness of the point number i.
The measurement error analysis of the PLIF method is given below. The real thickness of the water film is shown in Eq. (3).
Where k is the length of the scale. b is the amount of pixels of the scale. hib(t) is the amount of pixels of the water film thickness number i. According to the transmission of absolute error, the Eq. (5) of water thickness absolute error can be obtained.
hb(t) is average amount of pixels of the water film and theΔ represents the absolute error of each terms in the equations.
In the experiment, the amount of 916 pixels are applied to representing the length of the corrugated plate wall edge. Thus the absolute error of the film thickness measured by the PLIF method in this experiment is 0.075 mm.
Results and Discussion
Liquid Film Thickness
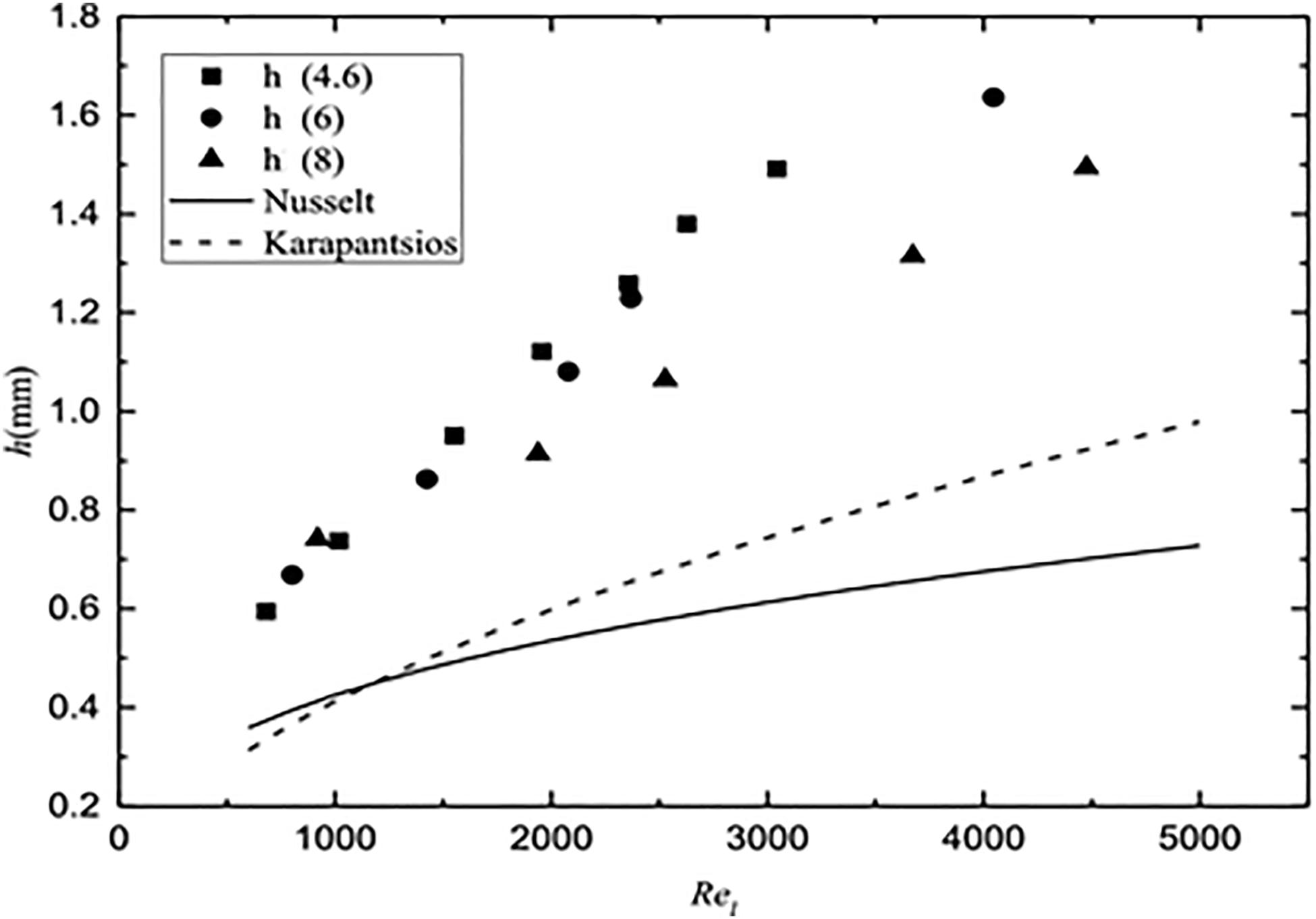
The thickness of the liquid film is measured at three positions on the wall of the corrugated plate, 4.6, 6, and 8 cm from the liquid film inlet. The relationship between the measured liquid film thickness and the liquid film Reynolds number is shown in Figure 5.
Comparing the experimental results with Nusselt’s theoretical formula and the Karapantsios semi-empirical correlation, the following conclusions can be drawn. When the Reynolds number is the same, the thickness of the liquid film experimentally measured in this paper is all greater than the Nusselt theoretical results and the semi-empirical results of Karapantsios (Karapantsios et al., 1995). The deviation between the experimental results and the two is smaller when the Reynolds number is lower, and the deviation gradually increases as the Reynolds number increases. This clearly shows that the Nusselt theoretical model is based on the assumption of low Reynolds number laminar flow. At the same time, the higher the Reynolds number of the liquid film in this experiment, the more obvious the superposition effect between different liquid films. This makes the situation in the experiment not satisfy Nusselt’s assumption. In order to illustrate the reliability of the results of this experiment, the semi-empirical relationship fitted by this article and other scholars is given in Table 1.
According to Figure 5, at the same Reynolds number, there is a slight difference between the average thickness of the liquid film at different measurement locations. In addition, this difference is not large when the Reynolds number is around 1000, and gradually increases as the Reynolds number of the liquid film increases.
Analysis of Fluctuation Characteristics of Liquid Film Thickness
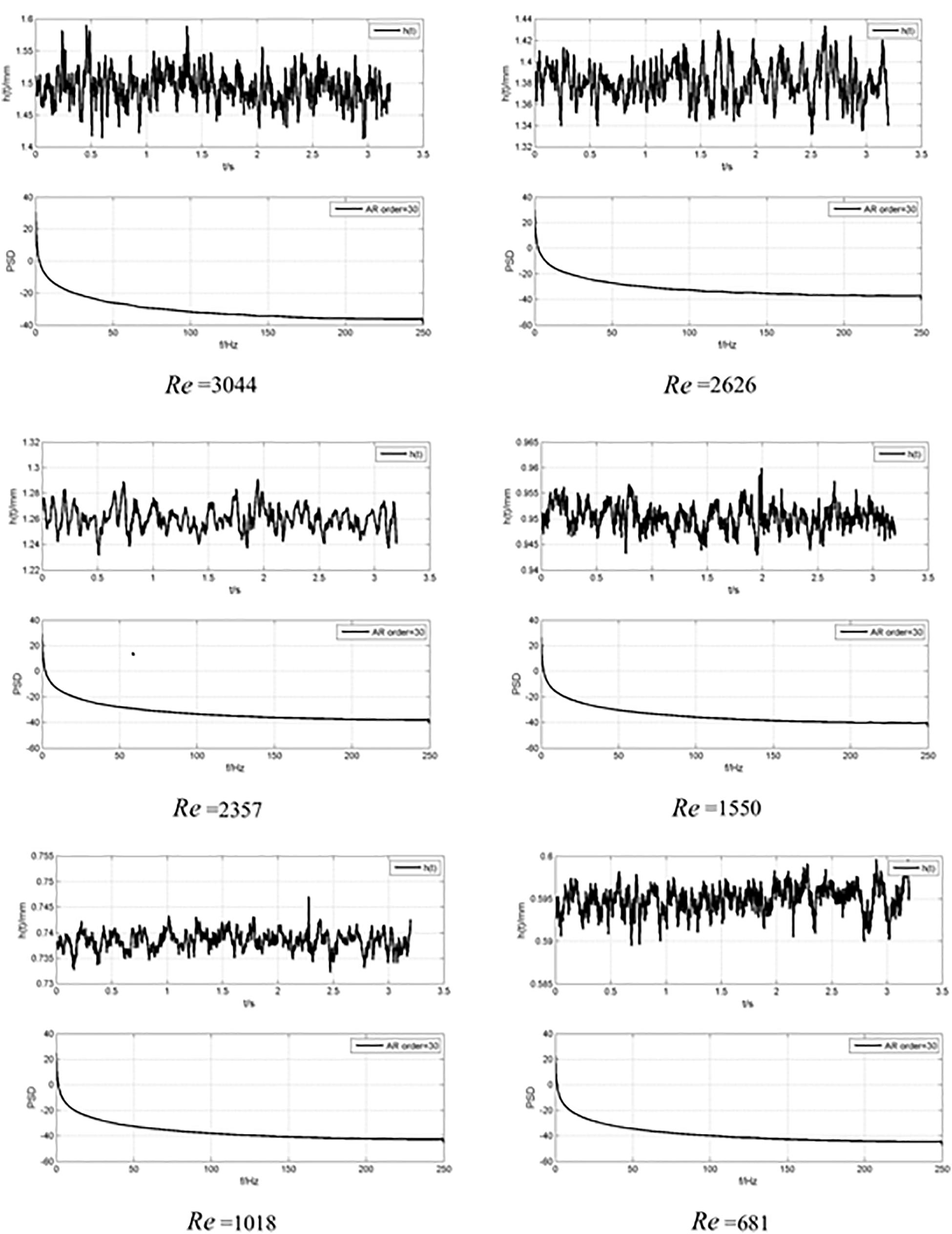
The PSD estimation method is generally used to detect vibration in random signals. For example, in the ultra-precision machining process of the surface, the PSD estimation method is used to analyze the effect of turning, polishing and other machining processes on the surface roughness. In the preparation of optical components, PSD estimation is used to evaluate the parametric performance of the components. Figure 6 shows the curves of the liquid film thickness with time and its PSD distribution when the Reynolds number Re is 681, 1018, 1550, 2357, 2626, and 3044, respectively.
The frequency of data acquisition is 500 Hz. The change of the thickness of the liquid film in each time domain is transformed into the frequency domain by Fourier transform in PSD method, thus the abscissa of the power spectrum distribution diagram obtained is the frequency f, Hz. It can be seen intuitively from Figure 5 that there is only one peak of the PSD curve, and it appears when the frequency is zero. This shows that the liquid film thickness value does not have fluctuation characteristics. The randomness of the liquid film thickness in the time domain is normal.
In general, for liquid film on corrugated plate wall, when Re is in the range of 20–30, the liquid film flow is laminar. The surface of the liquid film is smooth without fluctuations, and the thickness of the liquid film is constant. For 20–30 < Re < 1000–2000, although the liquid film is still laminar flow, its surface is no longer smooth. It has a certain degree of fluctuation, which is caused by the superposition of the surface waves of the liquid film. For 1000–2000 < Re < 3000, the liquid film flow is laminar flow. Fluctuations could result in turbulence locally. The liquid film thickness data obtained in this paper is also consistent with the phenomenon observed during the experiment, that is, there is no dramatic fluctuation on the surface of the liquid film. The flow of the larger Reynolds number has exceeded the scope of the free falling liquid film flow study in this experiment. The frequency corresponding to the peak is the characteristic frequency of the PSD curve. In Figure 6, there is no peak, thus the fluctuation of liquid film thickness has no characteristic frequency. At this time, the dominant factor of the fluctuation of the liquid film flowing down the wall is gravity. When the Reynolds number of the free-falling thin liquid film is in the range of 600 to 3000, and the surface roughness is 0.03, the fluctuation of the power spectrum of the liquid film thickness caused by gravity can be ignored. Study on the fluctuation characteristics of liquid film with a larger Reynolds number is a vital prospect.
Conclusion and Prospects
In this paper, the PLIF method is used to measure liquid film thickness on corrugated plate wall. Relationship between liquid film thickness and time is obtained. In addition, based on PSD method, the non-linear characteristics of the liquid film thickness are studied. The specific conclusions are as follows.
(1) The calculation formula of the average value of the liquid film thickness is given. The correlation between the thickness of the liquid film on the wall surface of the corrugated plate dryer and the Reynolds number conforms to Nusselt’s theory. Besides, the index of the Reynolds number in the fitted correlation is 0.505.
(2) When the Reynolds number of the free-falling thin liquid film is in the range of 600 to 3000, and the surface roughness is 0.03, the fluctuation of the power spectrum of the liquid film thickness caused by gravity can be ignored. Study on the fluctuation characteristics of liquid film with a larger Reynolds number is a vital prospect.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
BW designed this study, mainly performed the experiments, and mainly co-wrote the most of manuscript. BC, GW, RL, BK, JW, CL, and RT contributed to performing the experiment. All authors contributed to writing the manuscript.
Funding
The authors would like to acknowledge financial support provided by the Ph.D. Student Research and Innovation Fund of the Fundamental Research Funds for the Central Universities (3072020GIP1518), the Fundamental Research Funds for the Central Universities, China Scholarship Council, Chinese Universities Scientific Fund, and the National Natural Science Foundation of China (No. 51676052).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Chen, B.-W., Wang, B., Mao, F., Wen, J., and Tian, R. (2020a). Numerical study on characteristics of single droplet impacting on wetted surface. Exper. Comput. Mult. Flow 3, 59–67. doi: 10.1007/s42757-019-0048-44
Chen, B.-W., Wang, B., and Tian, R.-F. (2020b). Experimental study of droplet impacting on inclined wetted wall in corrugated plate separator. Ann. Nuclear Energy 2020:107155. doi: 10.1016/j.anucene.2019.107155
Karapantsios, T. D., Kostoglou, M., and Karabelas, A. J. (1995). Local condensation rates of steam-air mixtures in direct contact with a falling liquid film. Intern. J. Heat Mass Transf. 38, 779–794. doi: 10.1016/0017-9310(94)00213-f
Wang, B., Chen, B.-W., and Tian, R.-F. (2019). Review of research progress on flow and rupture characteristics of liquid film on corrugated plate wall. Ann. Nuclear Energy 132, 741–751. doi: 10.1016/j.anucene.2019.06.060
Wang, B., Chen, B.-W., and Ke, B.-Z. (2020a). Effect of physical property parameters on critical airflow velocity of a corrugated plate dryer. Ann. Nuclear Energy 140:107330. doi: 10.1016/j.anucene.2019.107300
Wang, B., Ke, B.-Z., Chen, B.-W., Li, R., and Tian, R. (2020b). A technical review of research progress on thin liquid film thickness. Exper. Comput. Multi. Flow 2, 199–211. doi: 10.1007/s42757-019-0051-9
Wang, B., Ke, B.-Z., Chen, B.-W., Li, R., and Tian, R. (2020c). Study on the size of secondary droplets generated owing to rupture of liquid film on corrugated plate wall. Intern. J. Heat Mass Transf. 147:118904. doi: 10.1016/j.ijheatmasstransfer.2019.118904
Wang, B., and Tian, R.-F. (2019a). Investigation on flow and breakdown characteristics of water film on vertical corrugated plate wall. Ann. Nuclear Energy 127, 120–129. doi: 10.1016/j.anucene.2018.12.001
Wang, B., and Tian, R.-F. (2019b). Judgement of critical state of water film rupture on corrugated plate wall based on SIFT feature selection algorithm and SVM classification method. Nuclear Eng. Design 347, 132–139. doi: 10.1016/j.nucengdes.2019.03.025
Zhang, H., Liu, Q., Qin, B., and Bo, H. (2015). Simulating particle collision process based on Monte Carlo method. J. Nuclear Sci. Technol. 52, 1393–1401. doi: 10.1080/00223131.2014.1003152
Zhao, F., Liu, Q., and Yu, L. (2019). Ratio analysis of two mechanisms of static droplet evaporation driven by pressure difference. Exper. Comput. Mult. Flow 1, 116–129. doi: 10.1007/s42757-019-0011-4
Keywords: liquid film, corrugated plate, steam generator, flow characteristics, fluctuation
Citation: Wang B, Chen B, Ke B, Wang G, Li R, Wen J, Lu C and Tian R (2020) Analysis of the Flow Characteristics of the Liquid Film on the Wall Surface of the Corrugated Plate Dryer Based on PSD Method: A Short Communication. Front. Energy Res. 8:215. doi: 10.3389/fenrg.2020.00215
Received: 04 June 2020; Accepted: 07 August 2020;
Published: 07 September 2020.
Edited by:
Dalin Zhang, Xi’an Jiaotong University, ChinaReviewed by:
Kangning Zhao, Shanghai University, ChinaMuhammad Saeed, East China University of Technology, China
Khalil Ur. Rahman, Pakistan Nuclear Regulatory Authority, Pakistan
Keyou S. Mao, Oak Ridge National Laboratory (DOE), United States
Copyright © 2020 Wang, Chen, Ke, Wang, Li, Wen, Lu and Tian. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bo Wang, Ym93YW5nQGhyYmV1LmVkdS5jbg==; Ruifeng Tian, cnVpZmVuZ3RpYW5AaHJiZXUuZWR1LmNu
 Bo Wang
Bo Wang Bowen Chen1
Bowen Chen1