Simulation Uncertainty of Near-Surface Wind Caused by Boundary Layer Parameterization Over the Complex Terrain

Introduction

With the continuous decreasing in traditional energy resources, the sustainable development of renewable and clean energy has become an important topic around the world. Wind energy is an important and widely developed renewable and clean energy worldwide, which will present a steady growth in the future of the wind power market. Recently, with the rapid economic growth and the increasing electric consumption in China, the government has faced the pressing concern of the sustainably generate electricity, wind energy is a key component of China’s renewable energy strategy because of the country’s vast wind resources (McElroy et al., 2009; Lam et al., 2013), and government policy support has led to high growth in wind development. According to the “Middle and Long Term Developing Plan for Renewable Energy,” the total number of installed wind turbines will reach 30 GW and will set up six GW-level wind farms in China in the coming 2020 (Duan, 2011), making China be the world’s leader in installed wind capacity (Lam et al., 2013).

Wind resource assessments, wind farm construction, wind power prediction and wind turbine operation mainly depend on the accurate prediction of near-surface wind, especially during power generation periods. However, due to the relatively low accuracy of near-surface wind prediction, a considerable wind power has no choice but to be abandoned (Zhang and Qi, 2020). Physical model, also called as mesoscale meteorological model, which considers the weather and geographical conditions, is the primary method for near-surface wind prediction. It has achieved better forecasting accuracy (Lange and Focken, 2006) and has provided better inputs for statistical models. Recent literatures review by Jung and Broadwater (2014) have shown that the physical models could provide satisfactory results in the ultra-short-term and short-term wind power prediction. As a mature developed mesoscale weather model, the Weather Research and Forecasting (WRF) model is popular applied for assessing wind resources (Wang and Jin, 2013) and predicting near-surface wind (Wang and Jin, 2013; Zhang and Wang, 2014). This potentially allows for significant improvement in wind power utilization. Recent news from the National Center for Atmospheric Research (NCAR) also reported that the wind forecast system they use, which is based on the WRF model, saved millions of dollars for Xcel Energy (Parks et al., 2011). Kruyt et al. (2018) explored and validated the wind power potential in Switzerland using the Consortium for small-scale modeling (COSMO), they found that simulation errors are larger in wind-sheltered stations than in wind-exposed stations; besides, the capacity factors can reach up to 0.42 in view of the modeled wind speeds. Based on wind simulations results during the years 2015 and 2016 using WRF model, Guozden et al. (2020) found that a capacity factor of 54% for wind parks can be obtained for the current distribution of existing and tendered facilities in Argentina.

The accuracy of near-surface wind prediction mainly depends on the two factors, initial conditions and Boundary Layer (BL) schemes (Zhang et al., 2015; Zhang and Pu, 2019; Liu et al., 2020). As a product of atmospheric boundary layers, near-surface wind is transient in nature and influenced by terrain and BL processes etc. (Mahrt, 2009; Belušić and Güttler, 2010; Güttler and Belušić, 2012). Therefore, the physical parameterization of BLs plays a crucial role in the accurate forecasting of near-surface wind and reducing the uncertainties in the prediction of wind power. Previous studies have also indicated that BL parameterizations in numerical models act an inevitable role on near-surface wind prediction and wind power harvesting. For instance, Zhang and Zheng (2004) used five BL schemes to examine the relationship between near-surface wind and near-surface layer temperature; they noted that although the model can provide a reliable simulation for the near-surface temperature and its thermal structure during the day-night alternation periods, simulations of wind speed and its variation achieved poor results. Storm et al. (2009) employed the WRF to forecast low-level jets over western Texas and southern Kansas; their results indicated that the WRF model could capture some of the essential characteristics of the observed low-level jets with a suitable BL scheme. Hu et al. (2010) examined the sensitivity of the performance of the WRF model to the use of three different BL schemes over Texas; they found that the simulations are sensitive to different BL schemes. Wang et al. (2011) employed the WRF model to simulate the near-surface wind over a complex terrain; their results showed that although different BL schemes forecast predominant wind direction and the trend of wind speed accurately, however, systematic biases still exist. Carvalho et al. (2014) assessed the simulation effects of near-surface wind with different BL schemes in the WRF model, and determined the best configurations of BL schemes, which produced wind simulation estimates closest to measured wind data.

Currently, near-surface wind forecasting errors are still significant in Chinese wind farms, approximately in the 25–40% range (Yang et al., 2005; Guo et al., 2011; Wang et al., 2015), thus, accurate wind speed and wind power forecasting are extremely important. However, most researches mainly focus on the performance of different BL schemes in predicting near-surface wind, but the possible reasons for simulation error, especially over the complex terrain, are rarely discussed in literature. In fact, an analysis of the contributing factors to near-surface wind simulation errors, which provides a possible approach to improve and develop the BL schemes, is more important for improving near-surface wind prediction, and thus is essential to wind power prediction and utilization. On this basis, the motivation of this study is to examine and evaluate the performance of different BL schemes in WRF model on the simulation of near-surface wind over the complex terrain. In addition, the characteristics and distributions of near-surface wind and the possible reasons for simulation errors with the best BL scheme will be also explored to provide a suggestion for eliminating the simulation errors.

The next section provides the descriptions of data, model, experiment design and methods. In Simulation Performance on Near Surface Wind and Wind Power, the distribution and its simulating effect of near-surface wind are compared and analyzed for four commonly used BL schemes. The potential reasons for simulation errors with the best BL scheme are discussed in Diurnal Characteristics of Near Surface Wind Simulation. Discussion and Conclusion includes the discussion and summary.

Data, Model, Experiment Design, and Methods

The research region is located in northeastern China, in which there are vast of wind resources need to be developed and utilized (Liu et al., 2013). The near-surface wind data are acquired from a wind farm located in the research region (see Figure 2). The height of the observational tower is 70 m above ground level (AGL), and wind speeds are observed at 30 and 70 m simultaneously. The recording interval is 10 min, and the integrity and reliability of wind data from March 2008 to February 2009 (Beijing Standard Time, BST, hereafter) is 99%. Because wind turbines are generally installed at a height of 70 m, thus the prediction results at 70 m are mainly analyzed in this study.

Figure 1 shows the annual variation of observed wind speed and its standard deviation, and the wind power density from March 2008 to February 2009. Results indicate that the mean wind speed, its standard deviation and wind power density are evidently larger in Spring (seasonal shift period) than that in other season. Moreover, the wind speed, its standard deviation and wind power density peaked in April 2008, indicating that the wind speed, its standard deviation and wind power density are most evident and have great volatility in April 2008, which could be challenging for numerical simulation. To examine the performance of different BL schemes of the WRF model on the simulations of near-surface wind, April 2008 is selected as the simulation period in current study.

FIGURE 1

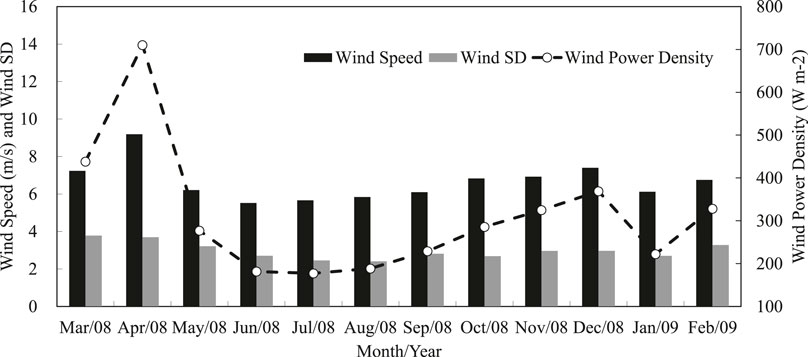
FIGURE 1. The observed mean and standard deviation (SD) of wind speed (unit: m s⁻¹), wind power density (unit: W m⁻²) in each month from March 2008 to February 2009 (The x-axis represents the month of a specific year; the y-axis on the left is the mean and standard deviation of wind speed, the y-axis on the right represents the wind power density).

An advanced research version of the WRF (ARW) model (Skamarock et al., 2008) is employed for numerical simulations. Three-level, two-way nested domains (Figure 2) in Lambert conformal projection are used, with horizontal grid resolutions of 45, 15, and 5 km, respectively. The physical parameterization schemes include the Kain-Fritsch cumulus scheme (Kain, 2004; for the “d01” and “d02” domains only); the Rapid Radiative Transfer Model for GCMs (RRTMG; Iacono et al., 2008) for longwave and Dudhia (1989) for shortwave radiation schemes; the Noah land surface scheme (Chen and Dudhia, 2001); cloud microphysics scheme is the Purdue-Lin scheme (Chen and Sun, 2002). Four popular BL schemes such as YSU (Hong et al., 2006), MYJ (Janjic, 1994), QNSE (Sukoriansky et al., 2005), and MYNN^2.5 (referred to as MYNN, Nakanishi and Niino, 2006) are used in this study. YSU is a nonlocal, first-order closure scheme that represents entrainment at the top of the PBL explicitly; MYJ is a local, 1.5-order closure scheme with an equation for prognosis of turbulent kinematic energy; similar to MYJ, QNSE is also a local, 1.5-order closure scheme but further accounts for wave phenomena within stable boundary layers; MYNN used in this study is also a local, 1.5-order closure scheme, compared to MYJ, expressions of stability and mixing length in this scheme are based on the results of large eddy simulations rather than on observations, while the expressions of mixing length are more applicable to a variety of static stability regimes. Detailed comparison and introduction of the four schemes can be found in Skamarock et al. (2008) and Cohen et al. (2015).

FIGURE 2

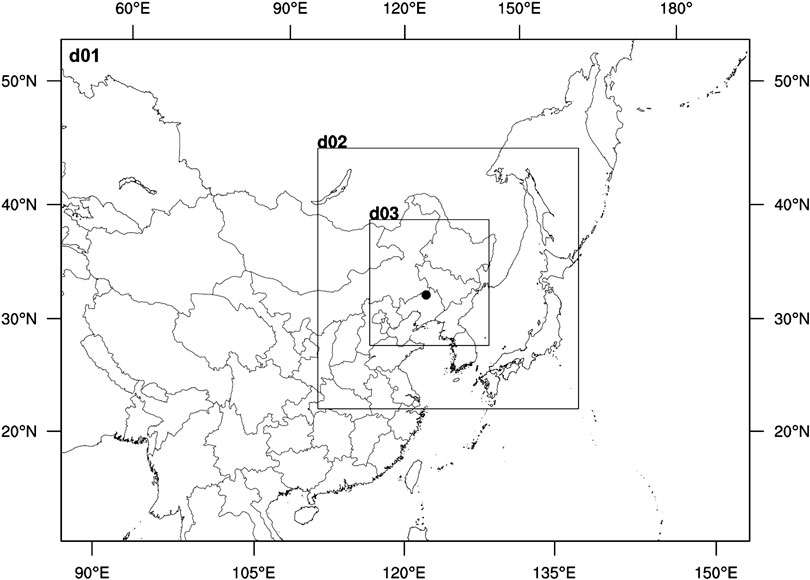
FIGURE 2. Simulation domain in Lambert conformal projection (The black dot represents the location of the wind tower).

The initial and boundary conditions, which are used to drive the WRF model, are FNL data from the National Centers for Environmental Prediction (NCEP) and sea surface temperature data from the National Oceanic and Atmospheric Administration (NOAA), with horizontal resolution of 1° × 1° and 0.5° × 0.5°, respectively. The one month simulation period is divided into 12 sub-periods. The forecast length of each forecast case is 84 h. The data from 12 to 84 h are analyzed because of the spin-up process in the WRF model. Simulation results output every 30 min, and the simulated wind speeds at 70 m are then analyzed and examined. The following statistics are used to validate the simulation results:

Absolute Error (AE):

$AE=\text{abs}\left(P_i-O_i\right)(1)$

Mean Relative Error (MRE):

$MRE=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left|(P_i-O_i)\right|/O_i}(2)$

where the observed and simulated values are represented by $O_i$ and $P_i$, respectively; n is the total number of samples.

Weibull distribution function is a two-parameter function with a single peak, which can be used to describe the overall distribution of different wind speeds in the research region and period, it is calculated as:

$f\left(v\right)=\frac{k}{c}{\left(\frac{v}{c}\right)}^{k-1}\exp \left[-{\left(\frac{v}{c}\right)}^k\right]\begin{array}{ccc}& & \left(k>0,v>0\right)\end{array}(3)$

where k is the shape parameter, which is a dimensionless quantity and determines the basic shape of the distribution curve. c is the scale parameter, v is wind speed. Parameters of k and c can be estimated by mean wind speed and wind speed standard deviation, estimating formulas are as follows:

$\text{Average}\text{of}\text{wind}\text{speed}\text{:}\overline{v}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{v}_i}(4)$

$\text{Standard}\text{deviation}\text{of}\text{wind}\text{speed}\text{:}{\sigma }^2=\frac{1}{n-1}{\displaystyle \sum _{i=1}^n{(v_i-\overline{v})}^2}(5)$

$\text{Parameter}\text{of}k\text{:}k={\left(\frac{\sigma }{\overline{v}}\right)}^{-1.086}\begin{array}{cc}& \left(1\le k\le 10\right)\end{array}(6)$

$\text{Parameter}\text{of}c\text{:}c=\frac{\overline{v}}{\Gamma \left(1+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$k$}\right.\right)}(7)$

$\text{Gamma}\text{function}\text{:}\Gamma \left(1+\frac{1}{k}\right)={\left(0.568+\frac{0.434}{k}\right)}^{\frac{1}{k}}(8)$

The parameter k and c of Weibull distribution can be used to justify if the features of simulated wind speed distribution fit to observation features.

Due to the nonlinear relationship between wind speed and power, the wind power density ($PW$) is calculated as (Manyonge et al., 2012):

$PW=\frac{1}{2}\rho V^3(9)$

where $\rho$ and V are air density and wind speed, respectively.

Despite the factors infect the power curve such as location and topographical conditions of the wind farm and the power control system of the specific turbine, the Ideal Energy Production (IEP) based on the machine power curve of the turbine is defined as (Taylor et al., 2009; El-Naggar et al., 2015):

$IEP=33\times {\displaystyle \sum _{u_c}^{u_f}f\left(u\right)\cdot 720\cdot p\left(u\right)}(10)$

where $u_f$ and $u_c$ is the cut in and cut out speed, respectively; $p\left(u\right)$ is the machine power curve, and $f\left(u\right)$ is the probability density function which is obtained from the wind simulation results; the two constants such as 33 and 720 are the number of wind turbines and the number of hours in April 2008, respectively.

Simulation Performance on Near Surface Wind and Wind Power

Figure 3 and Table 1 compare the Weibull distributions and its parameters between observation and simulation. The results indicate that the parameter k simulated with each BL scheme obeys the Rayleigh distribution, YSU and MYJ schemes better simulate the large near-surface wind range of the observed Weibull distribution at 70 m. However, the frequency is relatively low. The position of the Weibull distribution curve simulated by the QNSE and MYNN schemes are located to the left of the observed curve, which means that the scale parameter k will significantly decreases when simulating strong winds using the QNSE and MYNN schemes. In this case, the time and frequency of the observed stronger wind speed will not be accurately simulated. Results of Table 1 further suggest that, the simulated ideal energy production with YSU, MYJ, MYNN, QNSE schemes decreased gradually because of the gradually decrease of parameter c in Weibull distribution, in addition, the simulated ideal energy production with YSU scheme is the best among all schemes, compared to the observation. The variation tendency between parameter c and wind power density is similar, the observed wind power density is smaller than that with YSU and MYJ scheme and larger than that with MYNN and QNSE scheme. The above analyses imply that, the wind power density and ideal energy production depend mainly on MRE and parameter c. In terms of the absolute error of the scale parameter k, the YSU scheme simulates the wind speed better than the others.

FIGURE 3

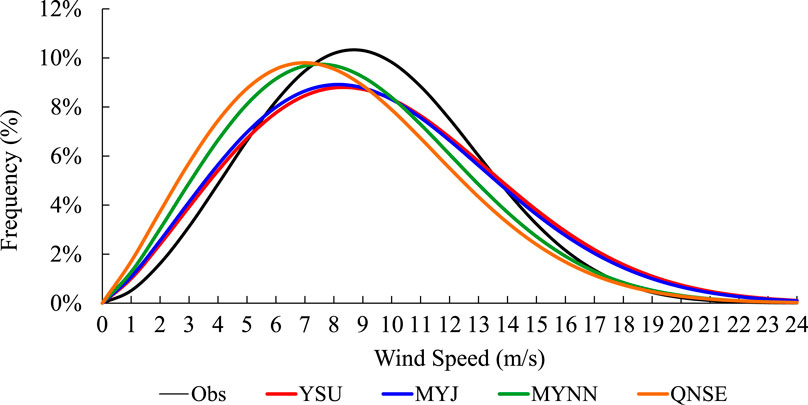
FIGURE 3. The Weibull distribution of observed and simulated wind speed (unit: m s⁻¹) with different BL schemes.

TABLE 1

TABLE 1. The MRE of near-surface wind speed, Weibull parameters, wind power density and ideal energy production in observation and simulations.

Overall results above indicate that YSU and MYJ schemes produce higher prediction accuracy of the parameter c, wind power density and ideal energy production than other schemes, which is significant to wind power utilization. Considering the MRE of near-surface wind speed is best simulated by the YSU scheme, and YSU scheme can also provide the reasonable results for wind power density and ideal energy production. Therefore, the YSU scheme could be regarded as the optimal BL scheme in reproducing near-surface wind and wind power in the research region and the period, and results based on YSU scheme will be further focused to investigate the key reasons associated with the simulation errors of near-surface wind speed in YSU scheme in the next sections.

Diurnal Characteristics of Near Surface Wind Simulation

Since the near-surface wind is the results of atmospheric turbulent movement, its evolution could be strongly related with the near-surface atmospheric stability conditions. To further analyze the reason in the simulation error of near-surface wind with the YSU scheme, the near-surface stability is further compared between the simulation and the observation. The near-surface stability conditions, which can be represented by the wind shear between 30 and 70 m, is defined as (Wharton and Lundquist, 2010):

$\alpha =\frac{\ln \left[\mathrm{u}\left({\mathrm{z}}_2\right)/\mathrm{u}\left({\mathrm{z}}_1\right)\right]}{\ln \left({\mathrm{z}}_2/{\mathrm{z}}_1\right)}(11)$

where $\mathrm{u}\left({\mathrm{z}}_2\right)$ and $\mathrm{u}\left({\mathrm{z}}_1\right)$ are the wind speed at 70 and 30 m, respectively, and $\alpha$ is the wind shear between ${\mathrm{z}}_2$ (70 m) and ${\mathrm{z}}_1$ (30 m). The stability level classifications in the near-surface layer defined by Wharton and Lundquist (2010) show the following relationship, $\alpha \ge$0.3, 0.2$<\alpha \le$0.3, 0.1$<\alpha \le$0.2, 0.0$<\alpha \le$0.1 and $\alpha \le$0.0 represent strong stable, stable, neutral, unstable and strong unstable, respectively.

Figure 4 compares the daily variation of near-surface stability between observation and simulation. Results indicate that, the daily variation of wind shear cannot be correctly reproduced, and the difference of wind shear between observation and simulation is larger during the day-night alternation periods than any other periods. In addition, the YSU scheme improperly simulates the observed strong stable near-surface atmospheric condition of the BL as an unstable near-surface atmospheric condition.

FIGURE 4

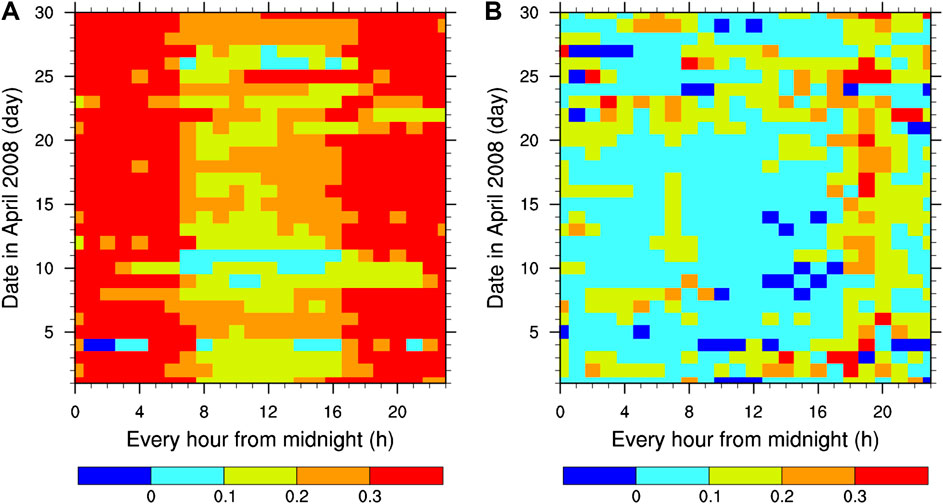
FIGURE 4. The near-surface atmospheric stability of (A) observations and (B) simulations in the YSU scheme.

Because strong unstable conditions rarely appear in the analyzed samples, the unstable and strong unstable conditions are classified in the same class (referred to as unstable). Figure 5 illustrates the percentage of observed and simulated stability in the near-surface layer during research period. Results indicate that strong stable conditions account for the highest proportion and unstable conditions are the least common to observe. However, unstable conditions account for the highest proportion of simulated conditions, while strong stable conditions are the least commonly simulated. This means that the YSU scheme improperly simulates the strong stable and unstable conditions of the actual BL as unstable and strong stable conditions. Therefore, the YSU scheme is unable to correctly describe the near-surface stability. As a result, a large simulation error occurs when simulating the near-surface stability, which may result in a large simulation error of near-surface wind.

FIGURE 5

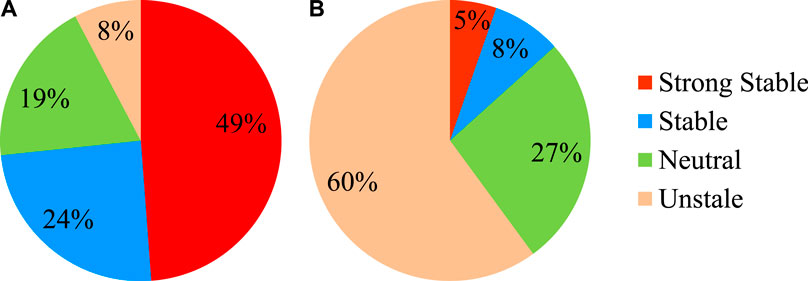
FIGURE 5. The percentage of near-surface atmospheric stability of (A) observations and (B) simulations in the YSU scheme.

To further demonstrate the relationship between the simulation effect of near-surface stability and simulation error of near-surface wind in YSU scheme, composite analysis of the whole month is further used here.

Figure 6 shows the daily variation of simulated and observed wind speed, wind shear and absolute error of simulated near-surface wind. Results indicate that during the day-night alternation periods of 00:00 to 7:30 and 19:30 to 00:00, the simulation error of near-surface wind is larger than any other periods. In addition, during the day-night alternation periods, the simulation error of near-surface wind is obviously correlated with the simulating effect of near-surface stability. It is also clear that a possible reason for the simulation error is that from 00:00 to 7:30 and 19:30 to 00:00, the near-surface stability is strong stable in reality, but is incorrectly simulated as unstable. Therefore, the near-surface stability simulated by the YSU scheme during these two periods is inaccurate and leads to a large simulation error in near-surface wind.

FIGURE 6

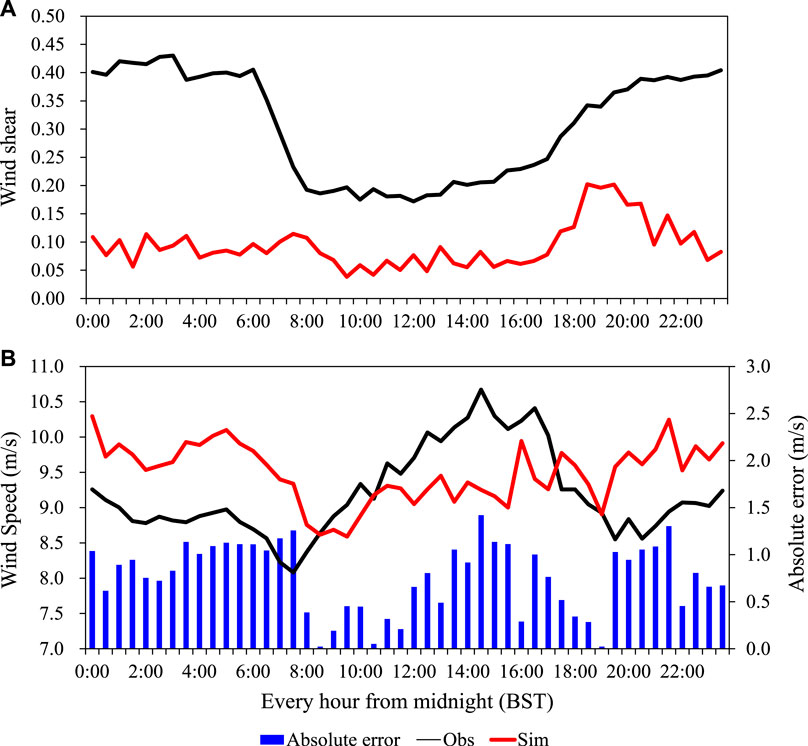
FIGURE 6. Comparisons of the daily variations of (A) near-surface wind shear and (B) near-surface wind speed between observations and simulations in YSU scheme. The blue rectangle denotes the absolute error of simulated near-surface wind speed. In (B), the y-axis on the left is the near-surface wind speed, and the y-axis on the right represents the absolute error of simulated near-surface wind speed.

Discussion and Conclusion

Improvement of near-surface wind and its prediction is an urgent issue for wind turbine operation and efficient energy harvesting. In wind power prediction practice, the WRF has been the prevailing model, and the BL scheme plays a critical role in near-surface wind prediction, which should be carefully studied during WRF modeling.

In this study, a series of numerical experiments and statistical analyses are carried out to assess the performances of different BL parameterization schemes on the simulation of near-surface wind during the April when observed near-surface wind and its variation are distinctly stronger than other periods. Simulation results suggest that the effects of near-surface wind and its variation obtain higher prediction accuracy using the YSU scheme rather than the other BL schemes, such as the MYJ, MYNN, and QNSE schemes, in the study region and period. It is also recognized as a major contribution for reliable wind power prediction.

Further investigations on the simulation results with YSU scheme indicate that, the stability in the near-surface layer has a significant relationship with near-surface wind. The YSU scheme wrongly simulates the observed strong stable near-surface atmosphere as stable and neutral near-surface atmosphere, thus cannot correctly reflect the daily variations in observed stability in the near-surface layer, which may result in large simulation errors of near-surface wind, especially during the day-night alternation periods. These results suggest that improving the parameterization of near-surface stability in YSU scheme is crucial to the improvement of near-surface wind and wind power prediction in the research region and period.

Results of this study reveal that near-surface stability is an important factor that degrades the near-surface wind simulation accuracy in YSU scheme. Previous studies showed that near-surface stability is influenced by the combined effects of land surface and boundary layer processes. Therefore, our future works will focus on the model representation of land-air interactions. Except for the improvement of BL schemes in WRF model, conducting the observation of atmospheric stability in wind farm and investigating their relations with near-surface wind using various statistical methods or machine learning models, could be an important and promising approach to effectively correct or modify model simulation biases. Besides, assimilation of surface observations, which has been proved to be an effective way to improve forecasts of near-surface conditions (Pu et al., 2013; Massey et al., 2014), will also be concentrated in our future works.

Data Availability Statement

The data analyzed in this study is subject to the following licenses/restrictions: These data are provided by local wind farms because part of the research are supported by the fundings. They are not open to public. Requests to access these datasets should be directed to Feimin Zhang, zfm@lzu.edu.cn.

Author Contributions

LC designed the experiment and conducted the analysis; GL processed the data and figures; FZ conducted the numerical simulation and wrote the manuscript; CW reviewed and revised the manuscript.

Funding

This work is supported by the National Science Foundation of China (41675098, 41805032), Natural Science Foundation of Gansu Province of China (20JR5RA309), and the Young Science and Technology Talents Lifting Project supported by Gansu Province of China.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Many thanks to NCEP and NOAA for providing the data to drive the WRF model. We thank Gansu Super Computing Center (GSPCC) and the Supercomputing Center of Cold and Arid Region Environment and Engineering Research Institute of Chinese Academy of Sciences (CAS) for providing attractive computing resources. Two reviewers are greatly appreciated for their constructive comments and suggestions for improving the manuscript.

References

Belušić, D., and Güttler, G. (2010). Can mesoscale models reproduce meandering motions?. Q. J. R. Meteorol. Soc. 136 (648), 553–565. doi:10.1002/qj.606

CrossRef Full Text | Google Scholar

Carvalho, D., Rocha, A., Gómez-Gesteira, M., and Silva Santos, C. (2014). Sensitivity of the WRF model wind simulation and wind energy production estimates to planetary boundary layer parameterizations for onshore and offshore areas in the Iberian Peninsula. Appl. Energy. 135, 234–246. doi:10.1016/j.apenergy.2014.08.082

CrossRef Full Text | Google Scholar

Chen, F., and Dudhia, J. (2001). Coupling an advanced land surface-hydrology model with the Penn state-NCAR MM5 modeling system. Part I: model implementation and sensitivity. Mon. Weather Rev. 129, 569–585. doi:10.1175/1520-0493(2001)129<0569:caalsh>2.0.co;2

CrossRef Full Text | Google Scholar

Chen, S.-H., and Sun, W.-Y. (2002). A one-dimensional time dependent cloud model. J. Meteorol. Soc. Jpn. 80 (1), 99–118. doi:10.2151/jmsj.80.99

CrossRef Full Text | Google Scholar

Cohen, A. E., Cavallo, S. M., Coniglio, M. C., and Brooks, H. E. (2015). A review of planetary boundary layer parameterization schemes and their sensitivity in simulating southeastern U.S. cold season severe weather environments. Weather Forecast. 30 (3), 591–612. doi:10.1175/waf-d-14-00105.1

CrossRef Full Text | Google Scholar

Dudhia, J. (1989). Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 46, 3077–3107. doi:10.1175/1520-0469(1989)046<3077:nsocod>2.0.co;2

CrossRef Full Text | Google Scholar

Duan, L. P. (2011). Analysis of the relationship between international cooperation and scientific publications in energy R&D in China. Appl. Energy, 88, 4229–4238. doi:10.1016/j.apenergy.2011.02.045

CrossRef Full Text | Google Scholar

El-Naggar, M., Adma, M. A., Elmasry, S. S., and Elmonem, A. (2015). “Comparison of wind turbine energy calculation methods,” in 17th international Conference on automatic control and simulation. Spain. Available at: https://www.researchgate.net/publication/332320249_Comparison_of_Wind_Turbine_Energy_Calculation_Methods (Accessed March, 2015).

Google Scholar

Güttler, I., and Belušić, D. (2012). The nature of small-scale non-turbulent variability in a mesoscale model. Atmos. Sci. Lett. 13 (3), 169–173. doi:10.1002/asl.382

CrossRef Full Text | Google Scholar

Guo, Z.-h., Wu, J., Lu, H.-y., and Wang, J.-z. (2011). A case study on a hybrid wind speed forecasting method using BP neural network. Knowl. Base Syst. 24, 1048–1056. doi:10.1016/j.knosys.2011.04.019

CrossRef Full Text | Google Scholar

Guozden, T., Carbajal, J. P., Bianchi, E., and Solarte, A. (2020). Optimized balance between electricity load and wind-solar energy production. Front. Energy Res. 8, 16. doi:10.3389/fenrg.2020.00016

CrossRef Full Text | Google Scholar

Hong, S.-Y., Noh, Y., and Dudhia, J. (2006). A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 134, 2318–2341. doi:10.1175/mwr3199.1

CrossRef Full Text | Google Scholar

Hu, X.-M., Nielsen-Gammon, J. W., and Zhang, F. (2010). Evaluation of three planetary boundary layer schemes in the WRF model. J. Appl. Meteor. Climatol. 49 (9), 1831–1844. doi:10.1175/2010jamc2432.1

CrossRef Full Text | Google Scholar

Iacono, M. J., Delamere, J. S., Mlawer, E. S., Shephard, M. W., Clough, S. A., and Collins, W. D. (2008). Radiative forcing by long-lived greenhouse gases: calculations with the AER radiative transfer models. J. Geophys. Res. 113, D13103. doi:10.1029/2008jd009944

CrossRef Full Text | Google Scholar

Janjic, I. (1994). The step–Mountain Eta coordinate model: further developments of the convection, viscous sublayer, and turbulence closure schemes. Mon. Weather Rev. 122, 927–945. doi:10.1175/1520-0493(1994)122%3C0927:TSMECM%3E2.0.CO;2

CrossRef Full Text | Google Scholar

Jung, J., and Broadwater, R. P. (2014). Current status and future advances for wind speed and power forecasting. Renew. Sustain. Energy Rev. 31, 762–777. doi:10.1016/j.rser.2013.12.054

CrossRef Full Text | Google Scholar

Kain, J. S. (2004). The Kain-Fritsch convective parameterization: an update. J. Appl. Meteorol. 43 (1), 170–181. doi:10.1175/1520-0450(2004)043<0170:tkcpau>2.0.co;2

CrossRef Full Text | Google Scholar

Kruyt, B., Dujardin, J., and Lehning, M. (2018). Improvement of wind power assessment in complex terrain: the case of COSMO-1 in the Swiss Alps. Front. Energy Res. 6, 102. doi:10.3389/fenrg.2018.00102

CrossRef Full Text | Google Scholar

Lam, J. C. K., Woo, C. K., Kahrl, F., and Yu, W. K. (2013). What moves wind energy development in China? Show me the money! Appl. Energy. 105, 423–429. doi:10.1016/j.apenergy.2012.11.067

CrossRef Full Text | Google Scholar

Lange, M., and Focken, U. (2006). Physical approach to short-term wind power prediction. New York, NY: Springer.

Google Scholar

Liu, P., Yang, Y., Gao, J., Wang, Y., and Wang, C. (2020). An approach for assimilating FY4 lightning and cloud top height data using 3DVAR. Front. Earth Sci. 8, 288. doi:10.3389/feart.2020.00288

CrossRef Full Text | Google Scholar

Liu, W., Hu, W., Lund, H., and Chen, Z. (2013). Electric vehicles and large-scale integration of wind power—the case of Inner Mongolia in China. Appl. Energy. 104, 445–456. doi:10.1016/j.apenergy.2012.11.003

CrossRef Full Text | Google Scholar

Mahrt, L. (2009). Variability and maintenance of turbulence in the very stable boundary layer. Boundary-Layer Meteorol. 135 (1), 1–18. doi:10.1007/s10546-008-9336-4

CrossRef Full Text | Google Scholar

Manyonge, A. W., Ochieng, R. W., Onyango, F. N., and Shichika, J. (2012). Mathematical modelling of wind turbine in a wind energy conversion system: power coefficient analysis. Appl. Math. Ences. 6 (91), 4527–4536.

Google Scholar

Massey, J. D., Steenburgh, W. J., Hoch, S. W., and Knievel, J. C. (2014). Sensitivity of near-surface temperature forecasts to soil properties over a sparsely vegetated dryland region. J. Appl. Meteorol. Climatol. 53, 1976–1995. doi:10.1175/jamc-d-13-0362.1

CrossRef Full Text | Google Scholar

McElroy, M. B., Lu, X., Nielsen, C. P., and Wang, Y. X. (2009). Potential for wind-generated electricity in China. Science 325, 1378–1380. doi:10.1126/science.1175706

CrossRef Full Text | Google Scholar

Nakanishi, M., and Niino, H. (2006). An improved Mellor-Yamada level-3 model: its numerical stability and application to a regional prediction of advection fog. Boundary-Layer Meteorol. 119, 397–407. doi:10.1007/s10546-005-9030-8

CrossRef Full Text | Google Scholar

Parks, K., Wan, Y. H., Wiener, G., and Liu, Y. B. (2011). Wind energy forecasting: a collaboration of the national center for atmospheric research (NCAR) and Xcel energy. Contract 303, 275–3000.

Google Scholar

Pu, Z., Zhang, H., and Anderson, J. (2013). Ensemble Kalman filter assimilation of near-surface observations over complex terrain: comparison with 3DVAR for short-range forecasts. Tellus Dyn. Meteorol. Oceanogr. 65, 19620. doi:10.3402/tellusa.v65i0.19620

CrossRef Full Text | Google Scholar

Skamarock, W. C., Klemp, J. B., Dudhia, J., Gill, D. O., Barker, M., and Duda, K. G. (2008). A description of the advanced research WRF Version 3. NCAR Tech. Note, NCAR/TN-475/STR. Univ. Corp. Atmos. Res. 113. doi:10.5065/D68S4MVH

CrossRef Full Text | Google Scholar

Storm, B., Dudhia, J., Basu, S., Swift, A., and Giammanco, I. (2009). Evaluation of the weather research and forecasting model on forecasting low-level jets: implications for wind energy. Wind Energy. 12 (1), 81–90. doi:10.1002/we.288

CrossRef Full Text | Google Scholar

Sukoriansky, S., Galperin, B., and Perov, V. (2005). Application of a new spectral theory of stably stratified turbulence to the atmospheric boundary layer over sea ice. Boundary-Layer Meteorol. 117, 231–257. doi:10.1007/s10546-004-6848-4

CrossRef Full Text | Google Scholar

Taylor, J. W., Mcsharry, P. E., and Buizza, R. (2009). Wind power density forecasting using ensemble predictions and time series models. IEEE Trans. Energy Convers. 24 (3), 775–782. doi:10.1109/tec.2009.2025431

CrossRef Full Text | Google Scholar

Wang, C. H., Jin, S. L., Hu, J., Zhang, F. M., Feng, S. L., and Liu, C. (2011). “Comparing different boundary layer schemes of WRF by simulation the low-level wind over complex terrain,” in The international workshop on environment management and energy economic (EMEE), Dengleng, China, August 8--10, 2011(IEEE) Vol. 8 (Part I), 8–10. doi:10.1109/AIMSEC.2011.6009632

CrossRef Full Text | Google Scholar

Wang, C., and Jin, S. (2013). Error features and their possible causes in simulated low-level winds by WRF at a wind farm. Wind Energy. 17 (9), 1315−1325. doi:10.1002/we.1635

CrossRef Full Text | Google Scholar

Wang, J. Z., Wang, Y., and Jiang, P. (2015). The study and application of a novel hybrid forecasting model-A case study of wind speed forecasting in China. Appl. Energy, 143, 472–488. doi:10.1016/j.apenergy.2015.01.038

CrossRef Full Text | Google Scholar

Wharton, S., and Lundquist, J. (2010). “Assessing atmospheric stability and the impacts on wind characteristics at an onshore wind farm,” in 19th symposium on boundary layers and turbulence, August 3, 2010. Available at: https://webcache.googleusercontent.com/search?q=cache:LVqIBhcd_CAJ:https://ams.confex.com/ams/19Ag19BLT9Urban/techprogram/paper (Accessed August 3, 2020).

Google Scholar

Yang, X., Xiao, Y., and Chen, S. (2005). Wind speed and generated power forecasting in wind farm. Proc. Chin. Soc. Electr. Eng. 25, 1–5. doi:10.3390/su12093778

CrossRef Full Text | Google Scholar

Zhang, D. L., and Zheng, W. Z. (2004). Diurnal cycles of surface winds and temperature as simulated by five boundary layer parameterizations. J. Appl. Meteorol. 4 (3), 157–169. doi:10.1175/1520-0450(2004)043<0157:dcoswa>2.0.co;2

CrossRef Full Text | Google Scholar

Zhang, F. M., and Wang, C. M. (2014). Experiments of surface-layer wind forecast improvement by assimilating conventional data with WRF-3DVAR. Plateau Meteorol. 33 (3), 675–685. doi:10.7522/j.issn.1000-0534.2012.00198

Google Scholar

Zhang, F., Yang, Y., and Wang, C. (2015). The effects of assimilating conventional and ATOVS data on forecasted near-surface wind with WRF-3DVAR. Mon. Weather Rev. 143, 153–164. doi:10.1175/mwr-d-14-00038.1

CrossRef Full Text | Google Scholar

Zhang, F., and Pu, Z. (2019). Sensitivity of numerical simulations of near-surface atmospheric conditions to snow depth and surface Albedo during an ice fog event over Heber valley. J. Appl. Meteorol. Climatol. 58 (4), 797–811. doi:10.1175/jamc-d-18-0064.1

CrossRef Full Text | Google Scholar

Zhang, T., and Qi, X. (2020). Analysis of performance deviation of wind power enterprises in China. Frontiers in Energy Research. 8, 126. doi:10.3389/fenrg.2020.00126

CrossRef Full Text | Google Scholar