A Robust Control Method for Damping and Tracking of Secondary Network Voltage of a PV Based Hybrid AC/DC Microgrid

Future microgrids (MGs) will comprise of an enormous number of little secondary networks (SN) that will convey complex control for grid collaboration as well as tracking of operation. In this paper, a robust blended integral linear-quadratic-Gaussian (ILQG) controller is proposed for damping and tracking control of SN voltage of a PV based hybrid source of AC-DC microgrid against a number of operating conditions. The structure of this mixed controller is made by expanding the SN dynamics with the utilization of an integrator. The term SN signifies a network that can take power from the DC bus connected with the AC main grid and PV based DC grid. The aim of developing a DC bus is to provide the constant DC voltage in the SN load terminal which is made of a parallel combination of several uncertain and unknown loads that may produce the oscillation of its performance. The proposed blended integral linear-quadratic-Gaussian controller provides a large control bandwidth that not only reduces the oscillation but also confirms the improved tracking performance over the number of loads in SN premises. Additionally, several uncertainties are considered within the SN dynamics to check the robustness of the proposed blended controller. The evaluation of this blended controller is studied for the various load dynamics and compared with the linear-quadratic Gaussian (LQG), linear-quadratic-regulator (LQR), and integral controller (IC) in terms of settling time, bandwidth and tracking performances.

1. Introduction

Microgrid (MG) is considered as an alternative way to provide un-interrupted power to the end-user when it is apart from the main AC grid (Malik et al., 2017). In modern electrical network, it is widely used because of its ability to run independently (Bouzid et al., 2015). A typical MG consists of energy storage (ES) elements (e.g., flywheel, battery, etc.), heterogeneously combined with a number of distributed generation (DG) units, point of common-coupling, loads and renewable power sources (RPS) (Xia et al., 2017). The idea of MG has become increasingly popular as it demands low cost in case of power generation from RPS, enhances local reliability, compensates feeder losses, and provides voltage support/voltage sag correction (Badal et al., 2019; Armin et al., 2020; Rizi and Eliasi, 2020). Several types of MG like AC MG, DC MG and hybrid source of AC/DC MG can be found in power system (Sarkar et al., 2018b; Toghani Holari et al., 2020). Among them, the hybrid source of AC/DC MG with energy technologies are brought up new opportunities for the use of renewable energy sources as it can operate in both cases.

The hybrid source of AC-DC MG may compose of a DC source like solar panel/energy storage unit, AC source like wind, diesel generator/main AC grid and controllable AC/DC loads. The combination of these sources are done with a single bus system that offers reliable, stable, and secure energy for the end-user (Jayachandran and Ravi, 2017; Lotfi and Khodaei, 2017; Liang et al., 2019). The DG units and AC/DC loads can be accessed from the DC bus through the use of the power electronic converter. A grid-tried inverter, which converts the DC power into AC power, is mainly used as a bridge between the AC and DC source so as the power can be easily exchanged according to the end-user demand (Llaria et al., 2011; Kim et al., 2012). Besides, the DC source can provide an immediate backup power response dynamically to meet the exceeding power demand. The main role of this type of MG is to generate power using the green energy and supply it to the end-user through the low amount emission of the greenhouse gas that keeps the environment clean and increases the overall efficiency of the transmitting power (Infield and Freris, 2020).

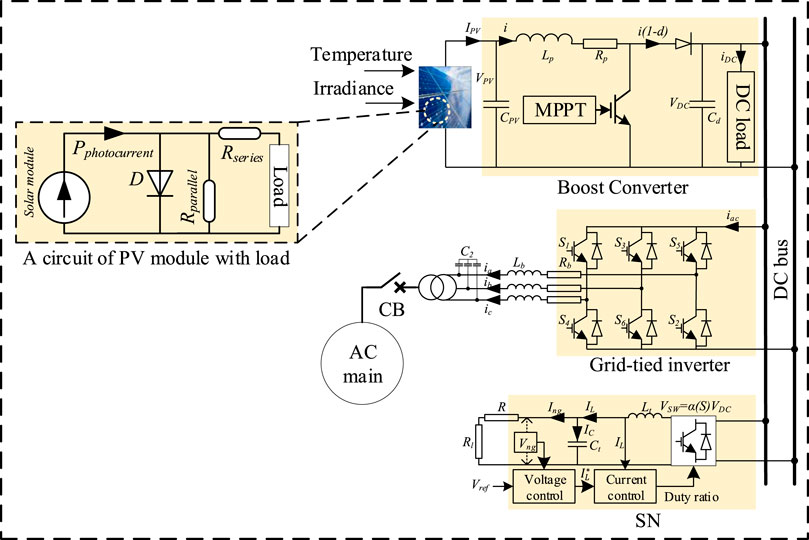
Figure 1 represents a typical hybrid source of AC-DC MG system mostly used in the real-time environment consisting of a secondary network, AC main grid, and PV based power generation unit. The function of the PV unit is to generate DC power and supply it into the secondary networks (SN) premises with the use of an inverter, where the AC main grid provides power when the PV unit can not meet the user demand power due to the environmental conditions. The interaction among the main AC and DC grid makes a way to maintain the constant power source for the SN. This is necessary as the generation of power using a PV panel may vary due to the unpredictable nature of the solar strength. This unpredictable nature produces the oscillation in MG system operation.

FIGURE 1

FIGURE 1. A basic circuit diagram of the proposed hybrid source of AC-DC MG system.

The operation of an hybrid source of MG fundamentally relies on the connection between the principle AC and the DC framework that may fail due to the unknown disturbances (Carpinelli et al., 2017; Salman and Xin, 2020). Accordingly, the performance of the SN may degrade causes the variable nature of sustainable energy sources which act as the prime mover for the operation of SN. The solar strength, irradiance, wind speed, and others are the main key factors to drive the performance of these prime movers. The variation of these factors may create a large number of oscillations that are responsible to reduce the tracking operation of the SN (Bouzid et al., 2015). Additionally, the variation of load dynamics in the SN system can alter the system dynamics that can also create the un-damped resonance during its operation.

A few control methods have been already reported for enhancing the voltage quality of the SN (Sikder et al., 2018a; Sikder et al., 2018b; Armin et al., 2018). Proportional-integral-derivative (PID) controller is developed for tracking the voltage due to its simplicity (Sarkar et al., 2018a). The controller is designed by assuming the constant input DC source. Although this controller can provide improved tracking performance over the constant source, the variation of PV parameters can alter the input DC source that may reason to confirm the lower tracking performance of the PID controller. An LQR is considered to regulate the MG voltage (Das et al., 2016; Levine, 2018). This controller achieves high performance against the RLC network connected in a parallel manner with the MGs. However, the absence of robustness with the adjustment in the plant dynamics restricts the utilization of the LQR. An H$\infty$ optimal control strategy is developed to obtain the improved tracking performance against the variation of the load dynamics (Mongkoltanatas et al., 2013). The design of this H$\infty$ controller carries the utilization of standard minimization of the goal work. The mitigation of the H$\infty$ norm results in conservative controller in terms of robustness.

Model Predictive Controller (MPC) has also been considered with the aim of providing robustness in terms of plant dynamics change (Lou et al., 2017). However, the response speed of the MPCs is limited due to their low-bandwidth. Distributed adaptive control techniques perform independently to control the voltage of the MG using remote sensing methods (Bidram et al., 2014; Kammer and Karimi, 2017). The communication speed with the correspondence load framework constrains the utilization of this control. Three levels of hierarchical control strategy have been considered to relieve from the tracking deviation and optimize the economic dispatch over the entire MG system (Mohamed and Radwan, 2011; Simpson-Porco et al., 2015). When one of the levels of this control fails, it departs from the tracking accuracy level.

To obatin the tracking voltage for the operation of the MG, the structure of a servo controller is introduced (Karimi et al., 2010). The design of this controller follows linear-time-invariant (LTI) theory (Sadabadi et al., 2017). The performance of this controller strays from the ideal result in the case of nonlinear load. A hybrid controller, which combines a proportional-integral (PI) controller and a harmonic resonant controller, has been considered to obtain the zero steady-state error and tracking performance over the various loads (Shen et al., 2010). In high resonant frequencies, this controller performs as a low pass controller and produces a lower gain and phase margin. The lower control margin shortens the application of this controller over the uncertainties.

Motivated by previously mentioned issues, in this research, we propose a robust blended integral linear-quadratic-Gaussian (ILQG) control framework for improving the load voltage profile of a solar-powered MG system consisting of AC and DC sources with a secondary network. The inspiration for planning this strategy is its capacity to follow the reference sign and exhibit the robustness over the plant vulnerability/uncertainty. This research aim is to control and secure the fast robust balancing of the secondary network voltage mismatch for the variation of linear and nonlinear load dynamics and the variation of temperature and irradiance of the PV system.

The contributions of this paper are as per the following:

• Design a robust high-performance controller by expanding the SN plant elements with an integrator which decreases the voltage swaying by increasing the control bandwidth that results in offering high phase and gain margin. The increasing control margin confirms the improved tracking performance for the SN.

• Develop a reliable DC bus using the conventional PI controller that provides a controlled constant DC voltage for the secondary network over the variation of temperature and irradiance.

• Several load dynamics are considered into the SN premises and simulated to measure the tracking capability of the controller.

• Various uncertainties are considered to affirm the robust performance of the ILQG framework.

• Performance comparison between the ILQG, linear-quadratic Gaussian (LQG), and LQR is done over the various load dynamics to ensure the high tracking performance of the proposed controller.

The remainder of this paper is sorted out as follows: Section 2 describes the details design of the solar-powered based hybrid AC-DC MGs with modelling of the secondary network. The modelling of the blended ILQG control structure for the voltage control of an SN is completed in Section 3. Section 4 arrangements with the presentation assessment of the ILQG controller for the voltage control of SN. The paper is finished up in Section 5.

2. System Configuration and Modeling

2.1. Hybrid Microgrid Configuration

The concept of a hybrid source of MG induces for improving the operation of the renewable energy resources having with a main AC grid systems and loads. Figure 1 shows a compact representation of the MGs carrying with a PV source and load which is connected with the corresponding AC and DC networks through a three-phase grid-tried inveter. An SN is connected with the corresponding DC bus through a voltage source inverter (VSI) and filter. The switching voltage from the voltage source inverter is used to drive the loads connected with the secondary networks.

An MG can drive the power in both grids and islanded connected mode. In grid-connected, a three-phase grid-tried inverter is required to provide the stable DC bus voltage. The role of this converter is to exchange power from the primary AC network to the DC bus or vice-versa. The solar PV array acts as an energy source that is associated with the DC bus by a DC/DC boost converter. This converter aims to extract the extreme power from the PV framework and track it using an artificial neural network. When the output from the PV system is greater than the total power consumed at the DC bus, the three-phase converter infuses power to the essential primary AC network while going about as an inverter. On the other hand, if the generation of total power at the DC bus is less than the required power, the converter infuses power to the DC network.

In the case of the secondary network operation, the harmonics may produce during the switching action from the DC to AC voltage. An inductive load is used to attenuate the harmonics and keep up the stability of the exchanging mode voltage. The use of inductive load may demand more current from the DC bus. As a result, an additional capacitor is used to cover the peak demand current without causing the need for an extra converter in input voltage. The combination of an inductor and capacitor acts as a filter for the SN that not only keeps the constant voltage but also increase the injected power to the load.

A voltage control method for the SN carrying with an inverter is also depicted in Figure 1. This method carries two control loop; outer and inner control loop that provides the required duty ratio for the switching performance of the inverter. The inner control loop is considered to produce the duty ratio, whereas the outer control loop uses the controlled duty ratio for tracking the SN voltage. The generation of the duty ratio is done by comparing a triangular carrier signal and a sinusoidal reference signal. The comparison between the two signals produces the required pulses when the peak of the reference signal is lower than the amplitude of the carrier signal. These pulses are considered to perform the switching action of the inverter. The deviation of the switching signal is measured by using the modulation index which provides the desired duty ratio. The proper duty ratio allows the controller to achieve the large bandwidth that provides high tracking performance for the SN over the un-modeled loads and uncertainties.

2.2. Modeling of PV Source

The PV arrays consist of several P-N junction diodes that can produce electricity from the insulation of solar radiation. The simple and mostly used model to represent the solar cell is a single diode circuit model reported in Figure 1 carrying of a PV and a diode with series-parallel resistance. The function of the diode is to identify the nature of the I-V and P-V characteristic curves. In practically, the output of the diode may degrade the perception level of the P-V or I-V curve due to the poor design or manufacturing defects. A shunt diode resistance is connected in parallel with a diode that enables a bypass way to generate the current. The output current from the PV module in Figure 1 is represented as:

$I_{PV}=N_{pc}{I}_{pc}-N_{pc}{I}_{rsc}$

$\times \left[exp\left(\langle \frac{q}{F_{c}k{T}_s}\rangle \langle \frac{V_{P}V}{N_{s}c}+I_{PV}{R}_{series}\rangle \right)\right],$

$I_{pc}=\left(I_{scc}+k_{tc}\langle T_s-T_{ref}\rangle \right)\times \frac{S_{rr}}{1000},$

$I_{rsc}=I_{T_{ref}}\left(\frac{T_s}{T_{\mathit{ref}}}\right)exp\left(\langle \frac{q{E}_{bg}}{k{F}_c}\rangle \times \langle \frac{1}{T_{ref}}-\frac{1}{T_s}\rangle \right).$

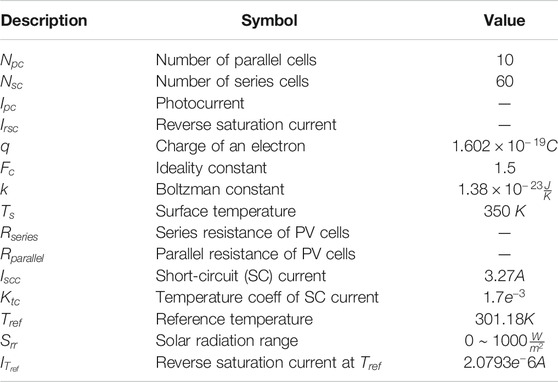
The notations and designed parameters value of the PV system are presented in Table 1. These values are determined by using the criteria of the real PV system so that the studied PV system can meet all the conditions to work in a real-time environment.

TABLE 1

TABLE 1. Model parameter for PV module.

2.3. Control Modeling of Secondary Network

Let I_L be the current passing through the SN inductor as:

$I_L\left(s\right)=\frac{V_L\left(s\right)}{s{L}_t}=\frac{V_{sw}\left(s\right)-V_{ng}\left(s\right)}{s{L}_t},(1)$

where V$sw$(s) is the inverted switching voltage multiplied with the $\alpha \left(s\right)$ duty ratio and the input DC bus voltage V$DC$(s). Now the SN voltage through the capacitor can be obtained by using (Eq. 2).

$\frac{d{V}_{ng}}{dt}=\frac{1}{C_t}{I}_c.(2)$

Where I_c represents the capacitor current. Now the state-space representation of proposed system with disturbance can be written as:

$\frac{d}{dt}\left[\begin{array}{c}{I}_L\\ V_{ng}\end{array}\right]=\left[\begin{array}{cc}0& -\frac{1}{L_t}\\ \frac{1}{C_t}& 0\end{array}\right]\left[\begin{array}{c}{I}_L\\ V_{ng}\end{array}\right]+\left[\begin{array}{c}\frac{1}{L_t}\\ 0\end{array}\right]\left[\begin{array}{c}{V}_{sw}\end{array}\right]+\left[\begin{array}{c}0\\ -\frac{1}{C_t}\end{array}\right]\left[\begin{array}{c}{I}_g\end{array}\right],$

and the system output equation is:

$y=\left[\begin{array}{c}{V}_{ng}\end{array}\right]=\left[\begin{array}{cc}0& 1\end{array}\right]\left[\begin{array}{c}{I}_L\\ V_{ng}\end{array}\right].$

Here, $A=\left[\begin{array}{cc}0& -\frac{1}{L_t}\\ \frac{1}{C_t}& 0\end{array}\right]$ is the system matrix, the input/contribution matrix $B=\left[\begin{array}{c}\frac{1}{C_t}\\ 0\end{array}\right]$, $C=\left[\begin{array}{cc}0& 1\end{array}\right]$ presents the output matrix, and the transition matrix $D=0$ and the term $\left[\begin{array}{c}0\\ -\frac{1}{C_t}\end{array}\right]I_g$ indicates the uncertainty added with the system output from the input. The parameters for SN are chosen in a way that it can act like a real-time mini-grid which takes power from the developed DC bus and supply it to the SN load premises. An LC filter with a value of 2 $mH$ and 15 $\mu F$ is used to remove the noises from the supply voltage. The controller is designed for the voltage control of a secondary network of PV based hybrid AC-DC microgrid plant by eliminating the nonlinear disturbance grid current Ig in the state space representation of the system.

3. Control of Hybrid Microgrid

3.1. Coordination Control for Booster and Bidirectional Converter

A control block diagram is shown in Figure 2A to maintain the steady operation among the main AC and DC grid under variable load demand and supply condition. The development of the MPPT algorithm is needed to identify the maximmum power (MP) from the solar PV module under variable temperature and shading conditions. The variation of these parameter creates the variation of the DC-link voltage used for the control of MP point as shown in Figure 3A. In this paper, the ANN is chosen to determine the reference voltage $v_{PV}^{ref}$ of the solar panel terminal. A feed-forward neural network with a back-propagation algorithm is applied to track the MP of the PV panel. The MPPT algorithm carries on the combination of three layers where the first layer takes input from the solar irradiance G and the temperature T. The function of the hidden or second layer is to receive input from the first one and performs the nonlinear mapping by using the activation function. The final layer sums the weighted inputs from the hidden layer and gives the final output which is set as a reference voltage for the PV unit.

FIGURE 2

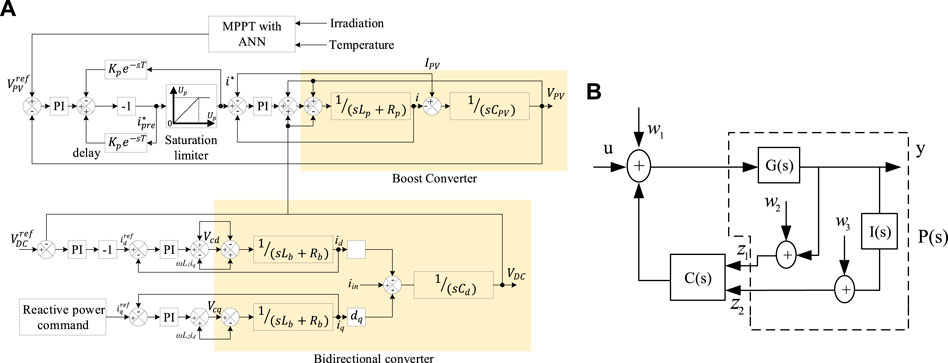
FIGURE 2. Block diagram of (A) DC bus voltage stabilizer using conventional PI regulator and (B) proposed integral linear-quadratic-Gaussian (ILQG) controller.

FIGURE 3

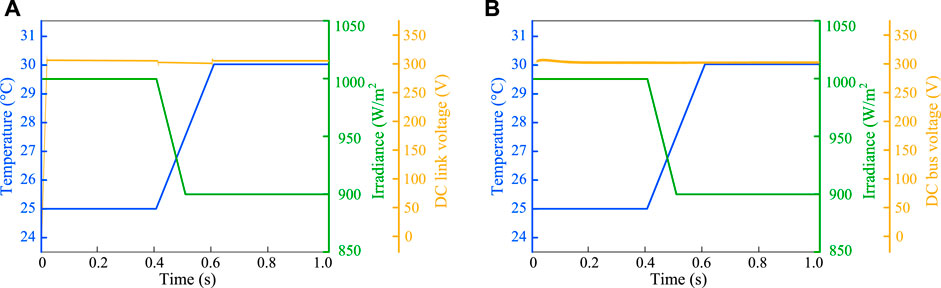
FIGURE 3. (A) DC-link voltage used for the control of MPPT, (B) Stable DC bus voltage over the variation of temperature and irradiance.

A dual-loop control scheme is considered to track the reference voltage $v_{PV}^{ref}$ that confirms to receive the optimum power from the PV module. The saturation limiter and the one-cycle delay assist the proportional-integral (PI) regulator to first track the $v_{PV}^{ref}$. When the capacity of a load or temperature and irradiance of the PV source changes, the PI controller controls power to keep the constant voltage over the entire DC bus as shown in Figure 3B. A controlled voltage source with a grid-tried inverter makes a way to exchange the power among the AC main and DC grid when the surplus or comparable power exists at the DC side. The capacitor $C_d$ absorbs the active power which in turn rises the dc-link voltage $V_{DC}$. Rising of $V_{DC}$ produces the negative $\left(V_{DC}^{ref}-V_{DC}\right)$ and increases the active reference current $i_d^{ref}$ through the PI controller. The higher positive reference $i_d^{ref}$ in the control loop forces the active current $i_d$ to rise in the inner-current control loop. Therefore, the generated extra power at the DC grid is transferred to the main AC grid.

Likewise, during the power shortage at the DC bus, the grid-tried inverter injects power from the main AC grid to the DC grid. The lack of DC bus power produces a positive error of $\left(V_{DC}^{ref}-V_{DC}\right)$, which in turn increases the magnitude of $i_d^{ref}$. Being the negative of both $i_d^{ref}$ and $i_d$, the magnitude of $i_d$ is raised through the inner-current control loop and thus the power is injected from the main AC to DC grid.

3.2. Proposed Voltage Control for Secondary Network

This section explores the design of blended controller for SN voltage control of a hybrid source of MGs. The proposed controller carries the combination of an integral controller (IC) and a LQG controller. The goal of designing this controller is to address the challenges made during the design of LQG and IC, respectively.

3.2.1. Design of Proposed Controller

Consider the following state-space model of the plant:

$\dot{x}\left(t\right)=Ax\left(t\right)+Bu\left(t\right)+D_{1}w\left(t\right),(3)$

$y\left(t\right)=Cx\left(t\right)+D_2\overline{w}\left(t\right),(4)$

where x speaks to the state vector, the term u signifies the contribution for the framework, y is the deliberate output from the ideal plant, and w is a Gaussian repetitive disturbance following up on the framework; A, B, and C represent the system matrix, input matrix, output matrix, and D$1$ and D$2$ are the noise matrices.

The design of an optimal LQG controller starts with a model in the form (Eq. 3)–((Eq. 4). Here, the quantity w(t) describes the process noise and $\overline{w}\left(t\right)$ is the measurement noise. The feedback control in optimal LQG controller is constructed to minimize the following quadratic cost function:

$J=\underset{T\to +\infty }{\text{lim}}\mathbf{E}\left[\frac{1}{T}{{{\displaystyle \int }}^{\text{}}}_0^T\left(x{\left(t\right)}^{T}Qx\left(t\right)+u{\left(t\right)}^{T}Ru\left(t\right)\right)dt\right].(5)$

Here, Q$\ge$0 and R$>$0 are symmetric weighting matrices, $\mathbf{E}[.]$ is the expected value. In (Eq. 5), the term x^TQx and u^TRu compares to a prerequisite to limit the states and the size of control inputs, separately. The selection of the matrices Q and R in the cost function (Eq. 5) depends on the desired performance of the system.

It should be noted that the design of the LQG controller does not directly address the robustness issues against the plant uncertainty. The robustness of the LQG controller is tended to by the reasonable decision of the noise terms in the plant model (Eq. 3)–(Eq. 4) that reflects the desired bandwidth and robustness characteristics. The control objective in this article is to minimize the tracking error among the command signal and the measured output. To make this, an IC is associated with an SN system because of its its phenomenal low-frequency tracking execution. Although the high gain of the IC reduces tracking errors, it shows lower bandwidth that confirms the lack of robustness.

Motivated by the above practical limitations, we have proposed an integral LQG controller for improving the tracking performance of SN. The integral action in proposed controller is presented by adding an additional term in the cost function (Eq. 5). The additional term involves the integral of the output y. The block diagram of the proposed ILQG controller is shown in Figure 2B, where G(s) is the transfer function of the plant, $\frac{1}{s}$ is the transfer function of an IC I(s) and C(s) is the LQG controller. The updated plant P(s) with an IC of the plant can written as

$\dot{x_f}\left(t\right)=A_f{x}_f\left(t\right)+B_{f}u\left(t\right)+B_f{w}_1,(6)$

$z_f\left(t\right)=C_f{x}_f\left(t\right)+v.(7)$

Here, $v={\left[w_2{w}_3\right]}^T$ and the augmented state and output vectors are $x_f={\left[x{{\displaystyle \int }}^{\text{}}ydt\right]}^T$ and $z_f={\left[z_1{z}_2\right]}^T$ . The matrices for the augmented system are defined as $A_f=\left[\begin{array}{cc}A& 0\\ C& 0\end{array}\right]$, $B_f=\left[\begin{array}{c}B\\ 0\end{array}\right]$, and $C_f=\left[\begin{array}{cc}C& 0\\ C& I\end{array}\right]$, where A, B, C are defined in (Eq. 3)–((Eq. 4). A generalized representation of a plant to design the LQG controller of any form such as the ILQG controller is presented in (Eq. 3)–(Eq. 5), whereas the form of (Eq. 6)–(Eq. 7) is the state space representation of the augmented plant by combining nominal plant and IC.

In (Eq. 6)–(Eq. 7), the quantity w$1$ and w$2$ is the Gaussian white noise and sensor noise with the variance of ${\gamma }_1^2$ and ${\gamma }_2^2$. The quantity w$3$ which is assumed to be Gaussian white noise with variance ${\gamma }_3^2$ added to the integral of the sensor output. As mentioned above, the LQG controller does not automatically address the issues such as bandwidth and robustness in the design process, the selection of the parameters ${\gamma }_1^2$, ${\gamma }_2^2$, and ${\gamma }_3^2$ satisfies these requirements. Following criterias are used to select ${\gamma }_1^2$ and ${\gamma }_2^2$:

(1) The increase of ${\gamma }_1$ increases the bandwidth of the closed-loop system.

(2) The decrease of ${\gamma }_2$ increases the bandwidth of the closed-loop system. The increase in bandwidth results in poor robustness.

(3) The amount of the integral action depends on the size of the ${\gamma }_2$ and ${\gamma }_3$. Decreasing ${\gamma }_3$ increases the integral action that results in show robust performance.

(4) The choosing a small value for r defines a control strategy with high gain system that results in provides robust performance over the uncertainties. On the other hand, selecting a large value for q defines the stable system with the least possible changes in the system states.

For the augmented plant outlined in (Eq. 6)–((Eq. 7), the integral LQG controller is designed by defining a quadratic cost function of the form

$J=\underset{T\to +\infty }{\text{lim}}\mathbf{E}\left[\frac{1}{T}{{{\displaystyle \int }}^{\text{}}}_0^T\left(x^{T}Qx+f{\left(y\right)}^T{Q}_{I}f\left(y\right)+u^{T}Ru\right)dt\right],(8)$

where $f\left(y\right)={{{\displaystyle \int }}^{\text{}}}_0^{T}y\left(\tau \right)d\tau$, Q$\ge 0$, $Q_I\ge 0,$ and R$>0$ are weighting matrices associated with the integral state, control input, and system state respectively. The additional term involves the integral of the output y to provide integral action to the controller. The integral LQG controller is represented as:

$\dot{{\widehat{x}}_f}\left(t\right)=A_f{\widehat{x}}_f\left(t\right)+B_{f}u\left(t\right)+K\left(z_f-C_f{\widehat{x}}_f\right),(9)$

$u\left(t\right)=-L{\widehat{x}}_f.(10)$

Here, ${\widehat{x}}_f$ is the enlarged state vector assessed by Kalman channel and K is the related Kalman gain characterized as,

$K=P_K{C}_f^T{R}_K^{-1},(11)$

where P$\ge K$ is the arrangement of the accompanying Riccati condition:

$\dot{P_K}=A_f{P}_K+P_K{A}_f^T-P_K{C}_f^T{R}_K^{-1}{C}_f{P}_K+Q_K.(12)$

Here, the factor Q$\ge K0$ denotes the process noise matrices, while R$>K0$ describes the measurement noise matrices that can be defined as

$Q_K={\gamma }_1^2,\text{and }{R}_K=\left[\begin{array}{cc}{\gamma }_2^2& 0\\ 0& {\gamma }_3^2\end{array}\right],(13)$

where ${\gamma }_1$ is the level of deviation related to the process noise, and w$1$, ${\gamma }_2$ and ${\gamma }_3$ are the level of deviation related to the output sensor noise w$2$ and the augmented integral output sensor noise w$3$. The feedback gain matrix L in (Eq. 10) is given by

$L=R_C^{-1}{B}_f{P}_C,(14)$

where P$\ge C0$ is the arrangement of the accompanying Riccati condition:

$\dot{P_C}=A_f{P}_C+P_C{A}_f^T-P_C{C}_f^T{R}_C^{-1}{C}_f{P}_C+Q_C.(15)$

Here, R_C=r Is the Controller Weighting Matrix and

$Q_C=C_f^T\left[\begin{array}{cc}1& 0\\ 0& q\end{array}\right]C_f.(16)$

The controller design parameters ${\gamma }_1$, ${\gamma }_2$, ${\gamma }_3$, r and q are adjusted for good controller performance. This includes a requirement that the control system has a suitable gain and phase margins and a reasonable controller bandwidth. The controller design parameters for voltage control of the SN are shown in Table 2.

TABLE 2

TABLE 2. Proposed controller parameters.

4. Performance Evaluation

4.1. Formulation of the Simulated System

This section discusses the tracking and damping ability of the proposed controller for the operation of the SN. A framework of the solar-powered MG system consisting of AC and DC sources with a SN is considered and simulated to measure the ability of the proposed controller where the controller is applied to damp and control the load voltage of the SN. The implementation of the proposed controller for the SN carrying with the DC-AC inverter is reported in Figure 1 where the controller controls the action of the DC-AC inverter to obtain the tracking performance over the variation of loads. The studied system is designed with a PV source which is interlinked with the primary AC grid through the DC bus. The variation of the PV parameters like temperature and irradiance confirm the variation of the DC-link voltage used for MPPT control as shown in Figure 3A that may reason to imbalance the DC bus voltage. The DC bus is maintained through the use of grid-tried inverter controlled by the conventional proportion-integral (PI) controller which provides a constant source of input voltage for the SN over the variation of temperature and irradiance as shown in Figure 3B.

The operation of the SN where the controller is applied to the DC-AC inverter may experience with the various load dynamics that may alter the SN dynamics and add the number of uncertainties which confirms the poor tracking performance without the controller. The controller is implemented to secure the fast robust balancing of the SN voltage mismatch and ensure the improved tracking performance by controlling the inverter. This event is simulated for the variation of linear and nonlinear load dynamics on the MATLAB environment and the results are compared with other control strategies. The performance of the controller is assessed with the three major studies for SN; 1) Damping performance of the proposed controller, 2) Robust performance of the proposed controller, and 3) Tracking performance of the proposed controller against various load dynamics. The detailed assessment of these studies is discussed in the following section.

4.2. Damping Performance of the Proposed Controller

The performance of the SN over the various loads may produce a large amount of voltage oscillation as the variation of loads change the system states. The open-loop time and frequency-domain response over the consumer load is reported in Figure 4. From this result, it is confirmed that the system continuously leads the oscillation in its time-domain performance while the frequency response making the damping of its peak resonance upto 150 dB. To ensure the steady-state and transient response, a high gain controller is required to operate with the open-loop system that will lead to a better reduction of oscillation. The integral action having with the proposed controller makes sure the high gain in its performance that enables the controller to provide high damping performance for the closed-loop system. The closed-loop performance using the proposed control framework is delineated in Figure 4. The closed-loop behavior of the system shows that the controller contributes to set the system state quickly by significantly reducing the oscillation. Accordingly, the outcomes from the frequency plot indicating that the peak of the resonance frequency can be set smoothly and practically close to 0 dB line. This performance confirms the high damping capability of the proposed controller.

FIGURE 4

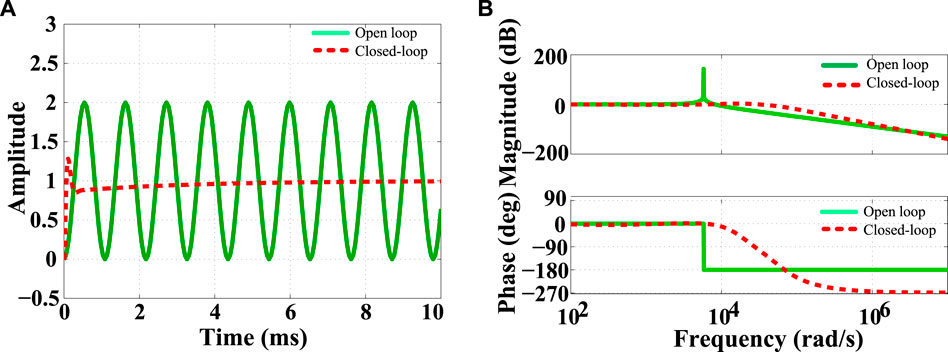
FIGURE 4. Comparison of open-loop and closed-loop for secondary networks (SN): (A) Time-domain response; (B) Frequency-domain response.

4.3. Robust Performance of the Proposed Controller

The robustness of the proposed controller is studied by adding a number of uncertainties with the plant model shown in Figure 5. Here, $G\left(s\right)$ is the SN transfer function, ${\omega }_i\left(s\right)$ or ${\omega }_0\left(s\right)$ and ${\text{Δ}}_i\left(s\right)$ or ${\text{Δ}}_0\left(s\right)$ are the variation of uncertainties. The values of ${\omega }_i\left(s\right)$ or ${\omega }_0\left(s\right)$ and ${\text{Δ}}_i\left(s\right)$ or ${\text{Δ}}_0\left(s\right)$ are chosen such that the variation of the uncertainty is twenty-five percent of the amplitude of the plant command signal. The nominal plant produces new dynamics due to the effect of the various uncertainties that may create undesired performances. The frequency-domain performances of the controller against different uncertainties are presented in Figure 6, where the closed-loop resonance frequency having with uncertainties still near to remain 0 dB that confirms the robustly stable performance of the controller.

FIGURE 5

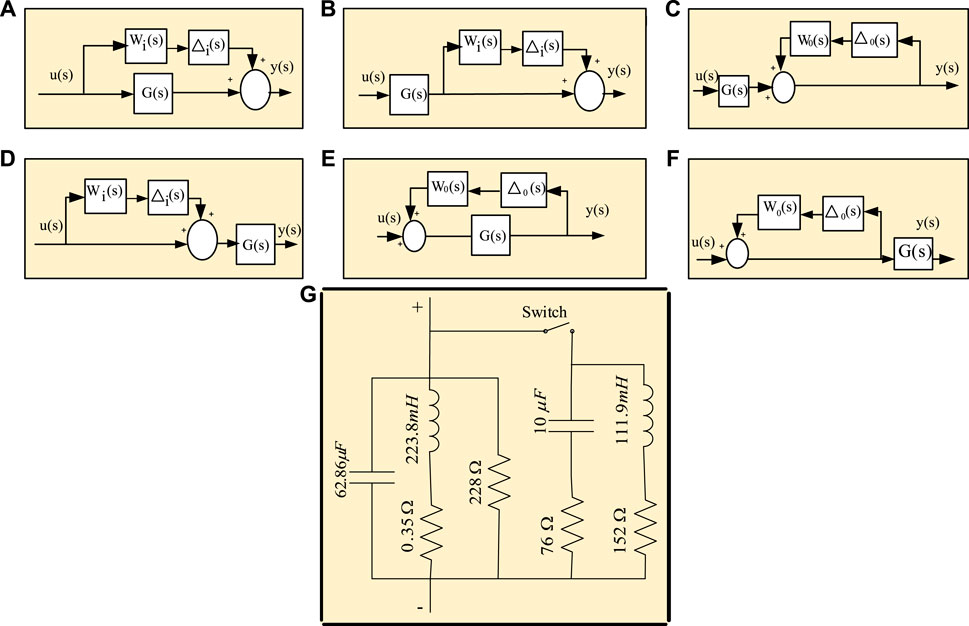
FIGURE 5. (A) Additive uncertainty; (B) Additive output uncertainty; (C) Augmentative output inverse uncertainty, (D) Augmentative input uncertainty; (E) Additive inverse uncertainty, (F) Inverse augmentative input uncertainty; (G) Inclusion of unknown passive load to the SN system.

FIGURE 6

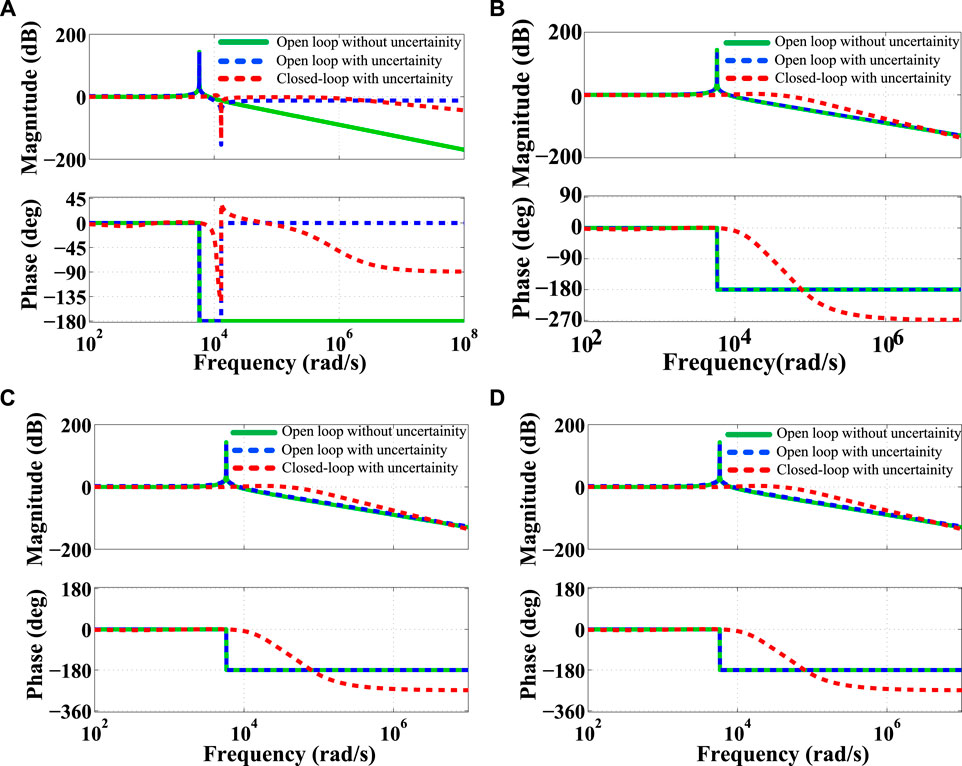
FIGURE 6. Comparison of Bode diagram using open and closed-loop: (A) for Figure 5A; (B) for Figures 5B,C; (C) for Figure 5D; (D) for Figures 5E,F.

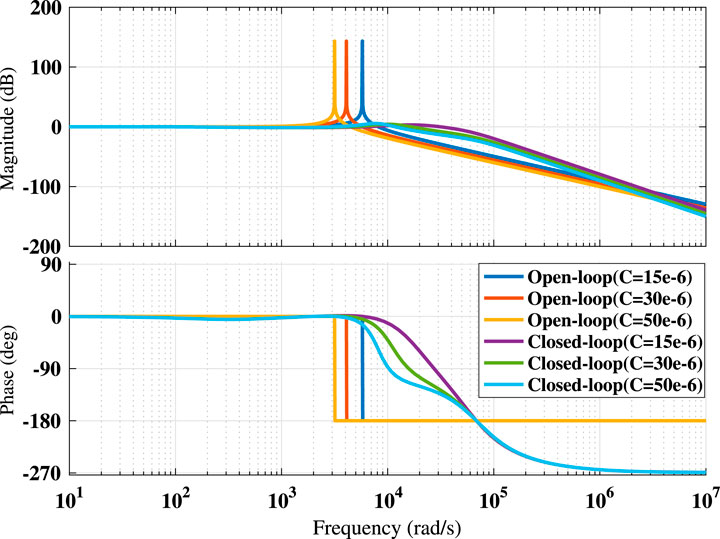
Again, the time-domain performances for the same uncertainties are reported in Figure 7. It is observed that the open-loop behavior of the plant continuously makes more oscillation in the presence of uncertainties, while the closed-loop system takes a certain time to reduce the oscillation and reach its steady-state condition. The quantitative measurements from the frequency- and time-domain performances are given in Table 3. From these measurements, it is seen that the controller achieves high-bandwidth and takes a little time to set the system state that not only confirms the stable performance but also guarantees the robustness of the proposed controller in the presence of uncertainty. The robustness of the proposed controller is further examined by varying the system capacitor value. The variation of this value creates wide-band un-damped resonance frequency that may reason to creat the system instability. To show the effectiveness of the controller, a comparison between the open- and closed-loop performance is illustrated in Figure 8. It shows the closed-loop system can provide the same level of damping under the variation of capacitor value. Finally, it is concluded that the proposed controller guarantees the robustly stable performance for all cases.

FIGURE 7

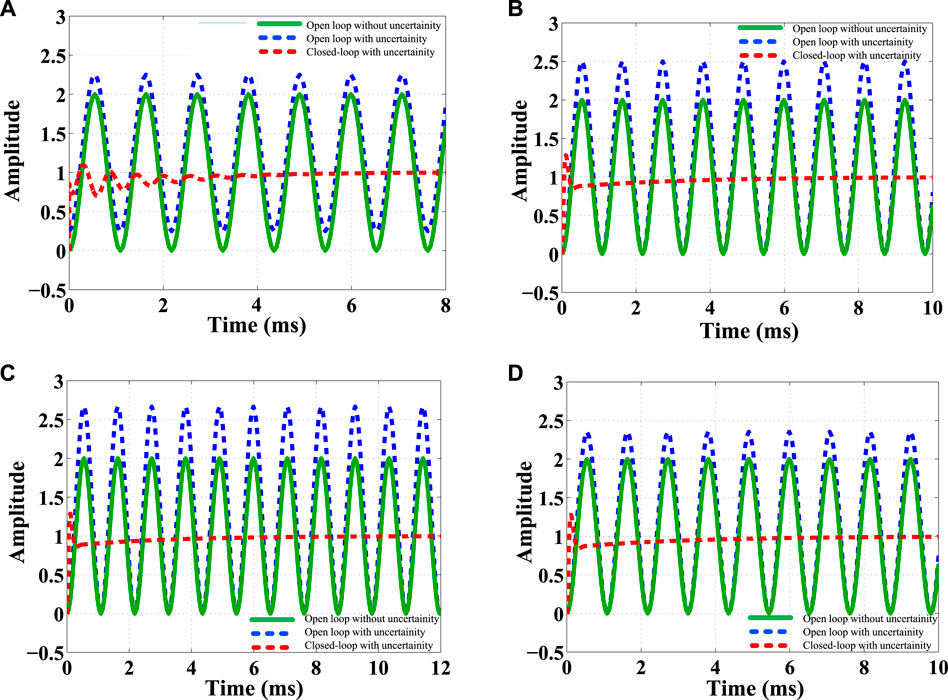
FIGURE 7. Comparison of step responses using open and closed-loop: (A) for Figure 5A; (B) for Figures 5B,C; (C) for Figure 5D; (D) for Figures 5E,F.

TABLE 3

TABLE 3. Closed-loop steady state time and bandwidth with and without uncertainty.

FIGURE 8

FIGURE 8. Comparison of open and closed-loop Bode diagram for various capacitor value.

4.4. Tracking Performance of the Proposed Controller Against Various Load Dynamics

Firstly, a consumer load with a value of $40\text{Ω}$ is simulated to measure the tracking performance of the proposed controller. The response from Figure 9A confirms that the proposed controller is capable to successfully track the reference signal. To prove the high tracking performance of the ILQG controller, the performance is studied by considering the several load dynamics. Figure 5G presents the model of an unknown passive load connected in parallel to the SN premises. The SN is initially operated at a steady-state condition, and the load resistance, capacitance, and inductance are changed after t = 0.3 seconds that creates an unknown environment in the SN system. The performance of the proposed controller against the unknown load dynamics is shown in Figure 9B. It is seen that the SN reaches a new steady-state operating point after five cycles which indicates the effective response of the proposed controller.

FIGURE 9

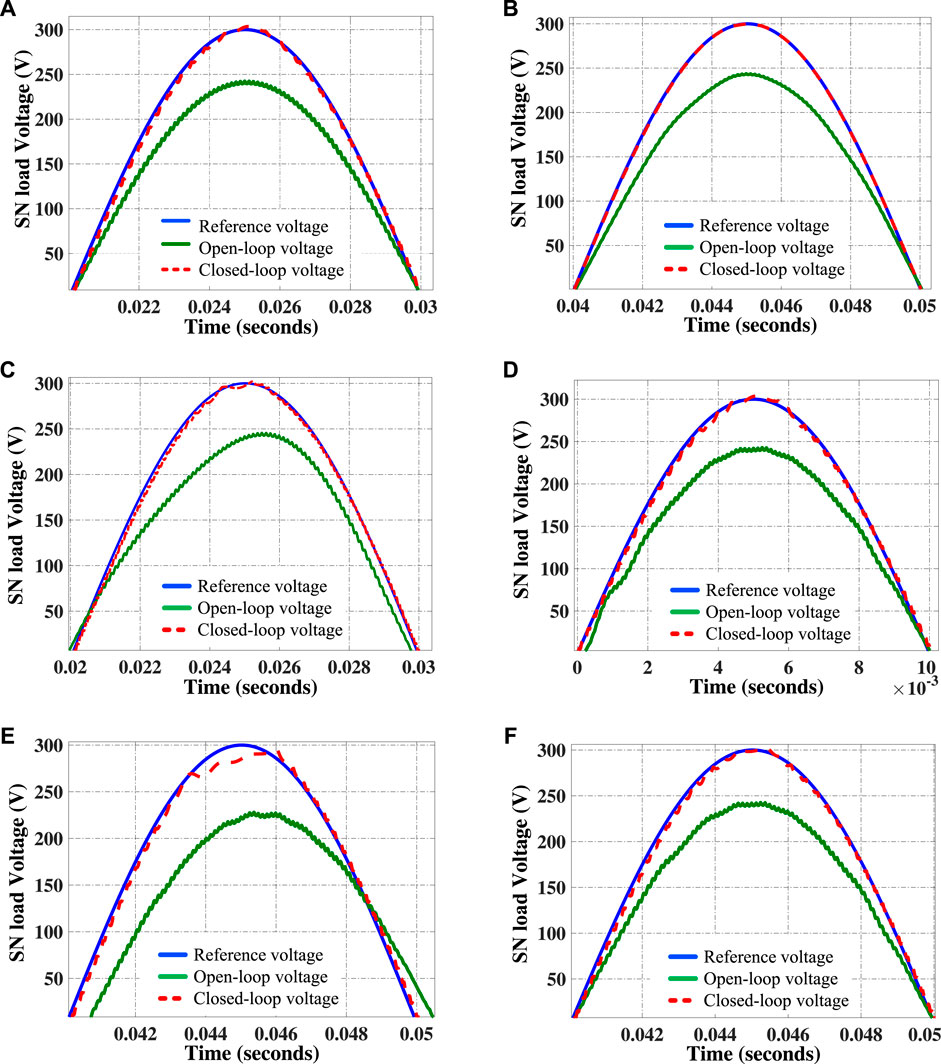
FIGURE 9. Comparison of open-loop, closed-loop and reference SN voltage tracking under (A) Consumer load; (B) Unknown load; and (C) Harmonic load; (D) Nonlinear load; (E) Asynchronous machine load; and (F) Dynamic load.

In electric networks, computers, television, fluorescent lamps, and rectifiers are used as a non-linear load. The effect of these non-linear loads produces harmonics that lead to voltage distortion in the power system. This distortion reduces the long life-sustaining of electrical loads. To produce the third harmonics in the current waveform, resistance with the value of $30\text{Ω}$ is directly connected with a current source of 7A amplitude and 150 Hz frequency. The closed-loop performance having this load is shown in Figure 9C which confirms the reliable performance of the controller.

Further, the performance of the blended ILQG controller is studied by adding a nonlinear load in SN premises. A nonlinear load is composed of a four-pulse diode unit which is feeding with a value of $R=80\text{Ω}$ resistive and $C=5\mu$F capacitive load. Figure 9D shows the assessment of the proposed blended ILQG controller for the nonlinear load which guarantees the extensive tracking performance. During the operation of a hybrid source of AC-DC MG system, it may act as a little conventional power framework where the dynamic burdens can cause significant and predominant impacts on its exhibition. A current source block with active power 50 MW and reactive power 25 MW is considered as a single-phase dynamic load in this paper. Another powerful load to be a specific single-stage asynchronous machine is additionally concentrated in this paper. The performance of the proposed controller is investigated having with the capacitor-start and capacitor-start-run and shown in Figure 9E and Figure 9F. For all the variety of load elements, the proposed blended control technique gives steady, dependable, and improved voltage tracking performance for the SN.

4.5. Comparative Study With Existing Controller

A comparative study between ILQG, LQG, LQR, and IC is discussed in this section. The design of the LQG, LQR and IC is done based on (Skogestad and Postlethwaite, 2007; Das et al., 2016) and (Janert, 2013), respectively. Figure 10A and Figure 10C presents the comparison of closed-loop frequency and time responses, while in Figure 10B presents the loop gains using different controllers. The results from the comparison are presented in Table 4 and Table 5. The comparison shows that the proposed controller achieves a bandwidth of 6.86 $\times {10}^4$ rad/s which is approximately three times larger than the other controllers. Although the LQG controller provides lower settling time as compared to the proposed controller, it has more percentage of overshoot (OS) that confirms the oscillation in its tracking performance. The proposed controller obtains a gain and phase margin of 13.3 $dB$ and ${43.5}^{\circ }$ which confirms the high stability margin as compared to LQG, LQR, and IC. The comparison between the proposed controller, LQG, and LQR controller for consumer, unknown and nonlinear loads voltage tracking is given in Figure 11. The quantitative measurements from Figure 11 is presented in Table 5. From the given analysis, it is seen that the proposed ILQG controller performs better reference voltage tracking as compared to others. Besides, the comparison of advantages between the proposed and others control strategies is reported in Table 6. Considering all the mentioned analysis, it is confirmed that the proposed controller is the capable of showing the reliable, robust, and fast tracking performance as compared to others.

FIGURE 10

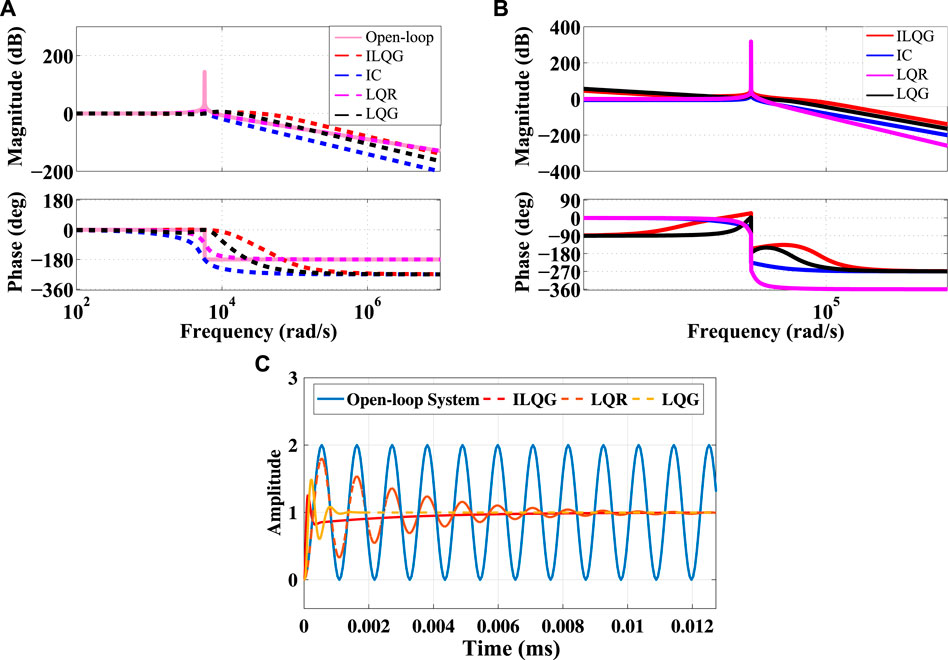
FIGURE 10. Comparative performance between (A) proposed controller, linear-quadratic Gaussian (LQG), LQR and Integral controller (IC) for Closed-loop Bode diagram, (B) proposed controller, LQG, LQR, and IC for Bode diagram of the loop-gain $G\ast C$, (C) ILQG, LQG, LQR controller using time-domain response. Where G and C represents the SN plant and controller.

TABLE 4

TABLE 4. Comparison of bandwidth, gain margin and phase margin using different controllers.

TABLE 5

TABLE 5. Error voltages (RMS value) between desired and actual load voltages comparison with settling time and overshoot.

FIGURE 11

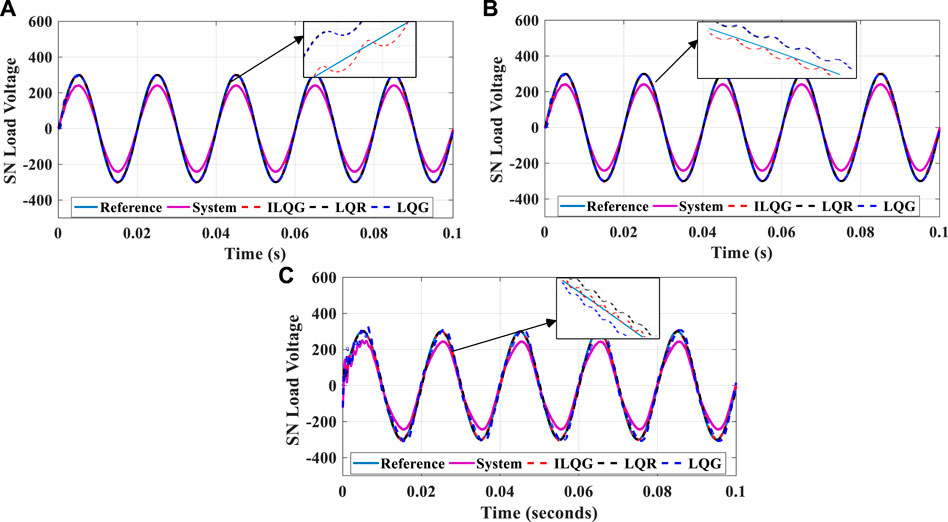
FIGURE 11. Secondary grid voltage tracking using (A) Consumer load; (B) Nonlinear load; and (C) Harmonic load model for subgrid system.

TABLE 6

TABLE 6. Comparisons of merits between the proposed and others controller.

5. Conclusion

In this paper, the design of an ILQG is presented to damp the oscillation and track the secondary network voltage of a hybrid source of AC-DC MGs. The controller carries the combination of an integral and an LQG controller that able to address the low bandwidth and lack of robustness. The design of the controller is done by augmenting the SN output with an integrator. The integral action of the controller confirms the high gain which provides large bandwidth and robust performance against a number of uncertainties. Furthermore, a comparison between the proposed, LQG, LQR, and IC is presented to confirm the high effectiveness of the proposed controller. The comparative analysis is done in terms of stability parameters like bandwidth, phase and gain margin, settling time, percentage of OS, and load voltage tracking. The comparison results depicted in this paper show that the proposed controller has the ability to provide high bandwidth as well as to achieve excellence tracking performance over the variation of load dynamics as compared to others. This work should be extended for an aromatic complex power system network where several renewable sources like Biogas, PV, and wind turbine would be used to generate power.

Data Availiability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author/s.

Author Contributions

DD, SF, and SS developed the microgrid model, designed and evaluated the performance of the controller. SD and MRIS developed the theoretical concept of the model and proposed it for the microgrid. SS wrote the manuscript. SM reviewed and edited the manuscript. All authors read and agreed to submit this manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Armin, M., Rahman, M., Rahman, M. M., Sarker, S. K., Das, S. K., Islam, M. R., et al. (2020). Robust extended H∞ control strategy using linear matrix inequality approach for islanded microgrid. IEEE Access. 8, 135883–135896. doi:10.1109/access.2020.3009188

CrossRef Full Text | Google Scholar

Armin, M., Roy, P. N., Sarkar, S. K., and Das, S. K. (2018). Lmi-based robust pid controller design for voltage control of islanded microgrid. Asian J. Contr. 20, 2014–2025. doi:10.1002/asjc.1710

CrossRef Full Text | Google Scholar

Badal, F. R., Das, P., Sarker, S. K., and Das, S. K. (2019). A survey on control issues in renewable energy integration and microgrid. Protection and Control of Modern Power Systems. 4, 8. doi:10.1186/s41601-019-0122-8

CrossRef Full Text | Google Scholar

Bidram, A., Davoudi, A., Lewis, F. L., and Sam Ge, S. (2014). Distributed adaptive voltage control of inverter-based microgrids. IEEE Trans. Energy Convers. 29, 862–872. doi:10.1109/tec.2014.2359934

CrossRef Full Text | Google Scholar

Bouzid, A. M., Guerrero, J. M., Cheriti, A., Bouhamida, M., Sicard, P., and Benghanem, M. (2015). A survey on control of electric power distributed generation systems for microgrid applications. Renew. Sustain. Energy Rev. 44, 751–766. doi:10.1016/j.rser.2015.01.016

CrossRef Full Text | Google Scholar

Carpinelli, G., Mottola, F., Proto, D., and Varilone, P. (2017). Minimizing unbalances in low-voltage microgrids: optimal scheduling of distributed resources. Appl. Energy. 191, 170–182. doi:10.1016/j.apenergy.2017.01.057

CrossRef Full Text | Google Scholar

Das, D., Gurrala, G., and Shenoy, U. J. (2016). Linear quadratic regulator based bumpless transfer in microgrids. IEEE Trans. Smart Grid. 9, 416–425. doi:10.1109/TSG.2016.2580159

CrossRef Full Text | Google Scholar

Infield, D., and Freris, L. (2020). Renewable energy in power systems. Hoboken, NJ: John Wiley & Sons.

Janert, P. K. (2013). Feedback control for computer systems: introducing control theory to enterprise programmers. Newton, MA: O’Reilly Media, Inc.

Jayachandran, M., and Ravi, G. (2017). Design and optimization of hybrid micro-grid system. Energy Procedia. 117, 95–103. doi:10.1016/j.egypro.2017.05.111

CrossRef Full Text | Google Scholar

Kammer, C., and Karimi, A. (2017). Decentralized and distributed transient control for microgrids. IEEE Trans. Contr. Syst. Technol. 27, 311–322. doi:10.1109/TCST.2017.2768421

CrossRef Full Text | Google Scholar

Karimi, H., Davison, E. J., and Iravani, R. (2010). Multivariable servomechanism controller for autonomous operation of a distributed generation unit: design and performance evaluation. IEEE Trans. Power Syst. 25, 853–865. doi:10.1109/tpwrs.2009.2031441

CrossRef Full Text | Google Scholar

Kim, H.-S., Ryu, M.-H., Baek, J.-W., and Jung, J.-H. (2012). High-efficiency isolated bidirectional ac–dc converter for a dc distribution system. IEEE trans. Power Electronics. 28, 1642–1654. doi:10.1109/TPEL.2012.2213347

CrossRef Full Text | Google Scholar

Levine, W. S. (2018). “Linear quadratic regulator control,” in The control systems handbook. Boca Raton, FL: CRC Press, 403–426.

Liang, B., Kang, L., He, J., Zheng, F., Xia, Y., Zhang, Z., et al. (2019). Coordination control of hybrid ac/dc microgrid. J. Engineering. 2019, 3264–3269. doi:10.1049/joe.2018.8505

CrossRef Full Text | Google Scholar

Llaria, A., Curea, O., Jiménez, J., and Camblong, H. (2011). Survey on microgrids: unplanned islanding and related inverter control techniques. Renew. Energy. 36, 2052–2061. doi:10.1016/j.renene.2011.01.010

CrossRef Full Text | Google Scholar

Lotfi, H., and Khodaei, A. (2017). Hybrid ac/dc microgrid planning. Energy. 118, 37–46. doi:10.1016/j.energy.2016.12.015

CrossRef Full Text | Google Scholar

Lou, G., Gu, W., Xu, Y., Cheng, M., and Liu, W. (2017). Distributed mpc-based secondary voltage control scheme for autonomous droop-controlled microgrids. IEEE Trans. Sustain. Energy. 8, 792–804. doi:10.1109/tste.2016.2620283

CrossRef Full Text | Google Scholar

Malik, S. M., Ai, X., Sun, Y., Zhengqi, C., and Shupeng, Z. (2017). Voltage and frequency control strategies of hybrid ac/dc microgrid: a review. IET Gener., Transm. Distrib. 11, 303–313. doi:10.1049/iet-gtd.2016.0791

CrossRef Full Text | Google Scholar

Mohamed, Y. A.-R. I., and Radwan, A. A. (2011). Hierarchical control system for robust microgrid operation and seamless mode transfer in active distribution systems. IEEE Trans. Smart Grid. 2, 352–362. doi:10.1109/tsg.2011.2136362

CrossRef Full Text | Google Scholar

Mongkoltanatas, J., Riu, D., and LePivert, X. (2013). “H infinity controller design for primary frequency control of energy storage in islanding microGrid,” in Power electronics and applications (EPE), 2013 15th European conference on, Piscataway, NJ, September 2-6, 2013 (IEEE) Vol. 1–11.

Rizi, M. T., and Eliasi, H. (2020). Nonsingular terminal sliding mode controller for voltage and current control of an islanded microgrid. Elec. Power Syst. Res. 185, 106354. doi:10.1016/j.epsr.2020.106354

CrossRef Full Text | Google Scholar

Sadabadi, M. S., Shafiee, Q., and Karimi, A. (2017). Plug-and-play robust voltage control of dc microgrids. IEEE Trans. Smart Grid. 9, 6886–6896. doi:10.1109/TSG.2017.2728319

CrossRef Full Text | Google Scholar

Salman, S., and Xin, A. (2020). Droop control based approach for frequency and voltage in hybrid ac/dc microgrid. J. Electr. Eng. Technol. 1–10.

Sarkar, S. K., Badal, F. R., and Das, S. K. (2018a). A comparative study of high performance robust pid controller for grid voltage control of islanded microgrid. Int. J. Dynam. Control. 6, 1207–1217. doi:10.1007/s40435-017-0364-0

CrossRef Full Text | Google Scholar

Sarkar, S. K., Roni, M. H. K., Datta, D., Das, S. K., and Pota, H. R. (2018b). Improved design of high-performance controller for voltage control of islanded microgrid. IEEE Sys. J. 13, 1786–1795. doi:10.1109/JSYST.2018.2830504

CrossRef Full Text | Google Scholar

Shen, G., Zhu, X., Zhang, J., and Xu, D. (2010). A new feedback method for PR current control of LCL-filter-based grid-connected inverter. IEEE Trans. Ind. Electron. 57, 2033–2041. doi:10.1109/TIE.2010.2040552

CrossRef Full Text | Google Scholar

Sikder, S. H., Rahman, M. M., Sarkar, S. K., and Das, S. K. (2018a). “Fractional order robust pid controller design for voltage control of islanded microgrid,” in 2018 4th International Conference on Electrical Engineering and Information & Communication Technology (iCEEiCT), Piscataway, NJ, September 13-15, 2018 (IEEE), 234–239.

Sikder, S. H., Rahman, M. M., Sarkar, S. K., Das, S. K., Rahman, M. A., and Akter, M. (2018b). “Implementation of nelder-mead optimization in designing fractional order pid controller for controllingvoltageof islanded microgrid,” in 2018 International conference on advancement in electrical and electronic engineering (ICAEEE) Piscataway, NJ, November 22-24, 2018 (IEEE), Vol. 1–4.

Simpson-Porco, J. W., Shafiee, Q., Dörfler, F., Vasquez, J. C., Guerrero, J. M., and Bullo, F. (2015). Secondary frequency and voltage control of islanded microgrids via distributed averaging. IEEE Trans. Ind. Electron. 62, 7025–7038. doi:10.1109/tie.2015.2436879

CrossRef Full Text | Google Scholar

Skogestad, S., and Postlethwaite, I. (2007). Multivariable feedback control: analysis and design. Hoboken, NJ: Wiley, Vol. 2.

Toghani Holari, Y., Taher, S. A., and Mehrasa, M. (2020). Distributed energy storage system‐based nonlinear control strategy for hybrid microgrid power management included wind/PV units in grid‐connected operation. Int Trans Electr Energ Syst. 30, e12237. doi:10.1002/2050-7038.12237

CrossRef Full Text | Google Scholar

Xia, Y., Wei, W., Yu, M., Wang, X., and Peng, Y. (2017). Power management for a hybrid ac/dc microgrid with multiple subgrids. IEEE Trans. Power Electron. 33, 3520–3533. doi:10.1109/TPEL.2017.2705133

CrossRef Full Text | Google Scholar