Uncertainty Analysis on k-ε Turbulence Model in the Prediction of Subcooled Boiling in Vertical Pipes

Computational fluid dynamics (CFD) has become an effective method for researching two-phase flow in reactor systems. However, the uncertainty analysis of Computational fluid dynamics simulation is still immature. The effects of uncertainties from two-phase models and boundary conditions have been analyzed in our previous work. In this work, the uncertainties from a turbulence model on the prediction of subcooled boiling flow were analyzed with the DEBORA benchmark experiments by a deterministic sampling method. Seven parameters in the standard k-ε model, which interrelated momentum, energy, turbulent kinetic energy, and dissipation rate, were studied as uncertainty sources, including C_μ, C_μ,g, C_1ε, C_2ε, σ_k, σ_ε, and Pr_t. Radial parameters were calculated to study the effects of uncertainties from the turbulence model. The contributions of each uncertainty source on void fraction and liquid temperature were also analyzed. It was found that the models can simulate subcooled boiling flow accurately and uncertainty analysis by deterministic sampling can give a reference interval to increase the reliability of results. The C_2ε and C_1ε, parameters in the production term and dissipation term of transport equations, dominate the radial distributions of void fraction and liquid temperature.

Introduction

Subcooled boiling flow has received attention from industrial designers due to its high heat transfer coefficient. However, if the heat flux reaches a critical value a transient vapor film will appear on the heated wall due to the polymerization of bubbles. It may hinder the heat transfer and cause the wall temperature to rise.

In most Computational fluid dynamics (CFD) analysis on subcooled boiling flow, the boundary conditions and models are all treated as deterministic values. However, there might be some uncertainties from boundary condition measuring or the simplification of the model that needs to be considered for the numerical simulation of boiling flow (Bestion et al., 2016). The best estimated code plus uncertainty (BEPU) analysis method, which could obtain a set of output results by sampling a series of inputs of research targets, was suggested for the uncertainty analysis of nuclear safety in Pericas et al. (2017). The statistical parameters of outputs were analyzed to obtain the uncertainty quality. Traditionally, researchers have used random sampling, such as Monte Carlo random sampling and Latin Hypercube sampling, in uncertainty analysis (Chen et al., 2015; Rakhimov et al., 2018). However, this type of analysis requires a large number of samples to be set as inputs, which consumes huge computing resources for CFD applications. Different to random sampling, the deterministic sampling (DS) method, reviewed by Bestion et al. (2016), describes the probability density function of uncertainty sources with deterministic points. These points must have the same statistical moments with uncertainty sources. This method has been used in uncertainty analysis with high computational costs, since the calculating cost can be reduced with a smaller sample size (Zhang et al., 2018a).

In two-phase flow simulations uncertainty analysis is significantly important due to the deficiency in two-phase flow theory and the measuring technique. Compared to the reality or truth value of interest, the errors in simulation results are divided into three parts by ASME V&V 20-2009 standards, which are simulation inputs, numerical methods, and modeling assumptions (McHale et al., 2009). Theoretically, the flow characteristics and heat transfer in two-phase flow are mainly described by the turbulence model and the two-phase model. The uncertainties of modeling assumptions in two-phase flow come from these models. The effects of two-phase model uncertainties and boundary condition uncertainties were analyzed systematically in our previous work by assuming that these errors are independent (Cong et al., 2018; Zhang et al., 2018c). On the other hand, the errors in the numerical solutions of equations can be reduced by grid sensitivity analysis and with a convergence check of the solver. Thus, we focus on the uncertainties from turbulence models in the current work.

The uncertainty brought by turbulence models for single phase flow and heat transfer has already attracted the attention of researchers (Platteeuw et al., 2008; Dunn et al., 2011; Hedberg and Hessling, 2015). Nevertheless, the turbulence model uncertainty in two-phase flow is still indistinct. These uncertainties may influence the distributions of key parameters, including void fraction, liquid temperature, and phase velocity. What is more, the k-ε turbulence model, which was suggested by Zhang et al. (2015) for subcooled boiling flow simulation, was developed for single-phase flow decades ago. The parameters, which interrelated momentum, energy, turbulence kinetic energy, and dissipation rate, were summarized from common single phase experiments. For example, the value of coefficient C_2ε in the dissipation term is usually derived from the experimental values of decay exponent, which was obtained in single-phase experiments (Mohamed and Larue, 1990). Thus, the parameters may need to be modified for two-phase flow in the future. The uncertainty analysis on the k-ε turbulence model in this work assessed the sensitivity of model parameters to the subcooled boiling flow. The results can be used as a reference to modify the turbulence model for two-phase flow simulation in the future.

The uncertainty of two-phase models and boundary conditions have been analyzed in our previous work (Cong et al., 2018; Zhang et al., 2018c), as a series research, the uncertainty effects of the turbulence model on local parameters were studied by the DS method in this paper. The DEBORA subcooled boiling experiment (Garnier et al., 2001) was chosen as the benchmark and four different cases were calculated by Fluent to avoid experimental coincidence.

Mathematical and Physical Models

The Eulerian two-fluid model along with the RPI model has been widely used in subcooled boiling flow simulations. Their equations and the closure auxiliary models of the RPI model can be found in our previous work (Zhang et al., 2018b). The interphase momentum transfer is considered using drag force (Schiller and Naumann, 1935), lift force (Moraga et al., 1999), and turbulence dispersion force (Burns et al., 2004), and the interphase energy transfer is calculated by the Ranz-Marshall model (Ranz and Marshall, 1952).

The standard k-ε model applied in this work is composed of the turbulent kinetic energy (k) transport equation and turbulent dissipation rate (ε) transport equation, which are:

$\frac{\partial }{\partial t}\left(\rho k\right)+\frac{\partial }{\partial x_i}\left(\rho k{u}_i\right)=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\frac{\partial k}{\partial x_j}\right]+G_k+G_b-\rho \epsilon (1)$

and

$\frac{\partial }{\partial t}\left(\rho \epsilon \right)+\frac{\partial }{\partial x_i}\left(\rho \epsilon u_i\right)=\frac{\partial }{\partial x_j}\left[\left(\mu +\frac{{\mu }_t}{{\sigma }_{\epsilon }}\right)\frac{\partial \epsilon }{\partial x_j}\right]+C_{1\epsilon }\frac{\epsilon }{k}(G_k+C_{3\epsilon }{G}_b)-C_{2\epsilon }\rho \frac{{\epsilon }^2}{k}(2)$

where G_k and G_b represent the turbulent kinetic energy generated by mean velocity gradients and buoyancy, respectively:

$G_k=-\rho \overline{u_i^{\text{'}}{u}_j^{\text{'}}}\frac{\partial u_j}{\partial u_i}(3)$

$G_b=-\frac{1}{\rho }{\left(\frac{\partial \rho }{\partial T}\right)}_p{g}_i\frac{{\mu }_t}{{\mathrm{Pr}}_t}\frac{\partial T}{\partial x_i}(4)$

where g_i is the gravitation vector in the i th direction. As shown in Eq. (2), the C_1ε concerns the production term with a default value of 1.44 and the C_2ε influences the calculation of the dissipation term. The parameter σ_k is the Prandtl number of turbulent kinetic energy. It represents the ratio of turbulent viscosity to turbulent kinetic energy diffusion. The turbulent viscosity is used to calculate the turbulent stress term in the momentum equation. Thus, the parameter σ_k interrelates momentum and turbulent kinetic energy in the k-ε model. Similarly, the parameter σ_ε denotes the ratio of turbulent viscosity to turbulent dissipation rate diffusion and the energy Prandtl number Pr_t represents the ratio of turbulent viscosity to the thermal diffusion induced by turbulence.

The μ_t in transport equations is the turbulent viscosity. As mentioned before, it is a crucial step to determine the value of μ_t, since it will be used to calculate the turbulent stress, which is an addition item induced by turbulent fluctuation in the momentum equation. It is different from single-phase flow where the bubbles induce additional turbulence in subcooled boiling flow. This phenomenon can be described by adding a term to the turbulent viscosity (Sato and Sekoguchi, 1975), which is

${\mu }_t=C_{\mu }\rho \frac{k_l^2}{{\epsilon }_l}+C_{\mu ,g}\rho {\alpha }_g{d}_g\left|u_g-u_l\right|(5)$

where C_μ and C_μ,g are the empirical coefficient achieved by experimental results. Besides, the standard wall function is applied for the near-wall region.

The parameters, including C_μ, C_μ,g, C_1ε, C_2ε, σ_k, σ_ε, and Pr_t, interrelated momentum, energy, turbulent kinetic energy, and dissipation rate in the standard k-ε model. The values significantly influence the applicability and accuracy of the k-ε model. These parameters have a set of default values in Fluent (Fluent, 2013), which were obtained from experimental results under special conditions. However, it still has some limitations. For example, the default value of parameter C_μ is obtained by the experiments which have a dynamic equilibrium between the production and the dissipation of pulsation kinetic energy in the boundary layer, while it may be not applicable to the flow that deviates from the dynamic equilibrium (Rodi, 1984). The uncertainties of these parameters can be transmitted to the CFD results. In consideration of the probability density, the functions of these parameters are indistinct for two-phase flow simulations, it is assumed that the parameters are independent and the distributions obey the normal distribution with a 5% relative error band for the ±3σ interval which means that the relative uncertainty of the uncertainty sources is within ±5% at the 99.74% confidence level. The values recommended by Launder and Sharma (1974) and Sato and Sekoguchi (1975) are assumed as the mean value of distributions:

$C_{\mu }=0.09,C_{1\epsilon }=1.44,C_{2\epsilon }=1.92,{\sigma }_k=1.0,{\sigma }_{\epsilon }=1.3,C_{\mu ,g}=0.6(6)$

Deterministic Sampling Method

In our previous work, the effects of two-phase model uncertainties and boundary condition uncertainties were analyzed by the Latin Hypercube sampling (LHS) method, respectively (Cong et al., 2018; Zhang et al., 2018c). However, the large number of samples (1,040 samples for two-phase model uncertainty analysis and 740 samples for boundary condition uncertainty analysis) shows poor efficiency in UQ calculations. It consumes huge computing resources which would be an issue for complex CFD simulations.

Thus, the DS method, which can reduce the number of samples substantially, was applied in this paper to predict the effects of turbulence model uncertainties on the simulation results. Unlike random sampling which characterizes the continuous probability density function of the sources, the DS method tries to represent them with a number of deterministic locations, known as sigma points (Bestion et al., 2016). These sigma points need to share the same statistical moments with the probability density function. The different sample methods could satisfy the different order of statistical moments. In order, the first four moments are mean, variance, skewness, and flatness. If we assume a parameter, q, and the number of samples, N, these statistical moments can be written as:

$mean=\frac{1}{N}{\displaystyle {\sum }_{n=1}^N{q}_n}=\overline{q}(7)$

$\mathrm{var}=\frac{1}{N}{{\displaystyle {\sum }_{n=1}^N\left(q_n-\overline{q}\right)}}^2(8)$

$skewness=\frac{1}{N}{{\displaystyle {\sum }_{n=1}^N\left(q_n-\overline{q}\right)}}^3/{\sigma }^3(9)$

$flatness=\frac{1}{N}{{\displaystyle {\sum }_{n=1}^N\left(q_n-\overline{q}\right)}}^4/{\sigma }^4(10)$

$x^{th}statisticalmoment=\frac{1}{N}{{\displaystyle {\sum }_{n=1}^N\left(q_n-\overline{q}\right)}}^x/{\sigma }^x(11)$

where σ is the standard deviation. With the increase in the order of statistical moments satisfied, higher accuracy can be achieved but more samples are needed in the ensemble. And it is more difficult to calculate the sigma points if higher order statistical moments need to be satisfied. Besides, the different probability density functions of sources can also increase the difficulty of calculating the sigma points.

In the current work, the DS method with fourth order statistical moments, which is abbreviated to DS4, will be used and its results will be compared with the experimental data to provide a confidence interval for parameters. Besides, the contribution of each uncertainty source can be obtained by data analysis. As described in Hedberg and Hessling (2015), with the assumption that uncertainty sources are independent and all obey normal distributions, it will extract two circumjacent points and one central point for the ensemble:

$q_{i1}={\mu }_i-\sqrt{3}{\sigma }_i,q_{i2}={\mu }_i,q_{i3}={\mu }_i+\sqrt{3}{\sigma }_i(12)$

$w_{i1}=\frac{1}{6},w_{i2}=\frac{4}{6},w_{i3}=\frac{1}{6}(13)$

where i represents the i th uncertainty source. In order to merge all the central points, the weights w_i2 need to be reset due to the fact that the sum of all weights should be one. The central point weight will then become:

$w_c={\displaystyle {\sum }_{i=1}^I{w}_{i2}}-(I-1)(14)$

where I is the number of uncertainty sources.

Then the fifteen samples extracted by DS4 are set as inputs in functions or codes, respectively. The outputs will be analyzed to quantify the effects propagated from the input uncertainty sources by statistical parameters, including mean value $\overline{\phi }$, standard deviation $\delta \phi$, and uncertainty bandwidth UB, which are:

$\overline{\phi }={\displaystyle {\sum }_{n=1}^N{w}_n}f\left(S_n\right)(15)$

$\delta \phi =\sqrt{{{\displaystyle {\sum }_{n=1}^N{w}_n\left(f\left(S_n\right)-\overline{\phi }\right)}}^2}(16)$

$UB=3\delta \phi (17)$

The contributions of each uncertainty source can be evaluated by:

$\delta {\phi }_i=\sqrt{w_{2i-1}{\left(f\left(S_{2i-1}\right)-\overline{\phi }\right)}^2+w_{2i}{\left(f\left(S_{2i}\right)-\overline{\phi }\right)}^2-w_{2I+1}{\left(f\left(S_{2I+1}\right)-\overline{\phi }\right)}^2/I}(18)$

$U{B}_i=3\delta {\phi }_i(19)$

$C_i=U{B}_i/{\displaystyle \sum _{i=1}^{I}U{B}_i}(20)$

where S_n represents the n th group of samples, $\delta {\phi }_i$ and $U{B}_i$ are the standard deviation and uncertainty bandwidth of the i th uncertainty source, respectively, and C_i is the contribution of the i th source.

Benchmark Case and Numerical Modeling

The DEBORA experiment (Garnier et al., 2001) was selected as the benchmark case to analyze the uncertainty quality of the turbulence model. The R12 used as the working fluid in the DEBORA experiment has similar relevant non-dimensional numbers with water in high pressure when it works in relatively low pressure, which means the operation and measurement was easier. The fluid was heated in a vertical pipe with 3,500 mm length and 19.2 mm inner diameter. The tube was simplified into a 2D axial symmetry domain and the axisymmetric boundary was enabled in Fluent. Several parameters, such as void fraction, liquid temperature, and bubble diameter, were measured at the end of the heated tube. To avoid contingency, four experimental conditions of the DEBORA experiment were applied in this work, whose results can be extracted from public literature.

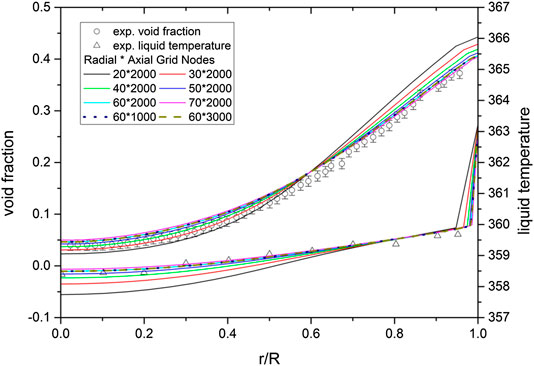
In order to avoid the error introduced by mesh, eight meshes with different radial and axial nodes were used to analyze the grid sensitivity with Case4. The radial distributions of void fraction and liquid temperature were compared and the results are presented in Figure 1. Finally, considering the computational accuracy and expense, the mesh with 60 × 2,000 nodes was employed in this work.

FIGURE 1

FIGURE 1. Grid sensitivity analysis.

Results and Discussion

The samples of turbulence model parameters were set as computational inputs to analyze the uncertainty transition. The uncertainties of radial parameters in the DEBORA benchmark are presented and discussed in Effects of Model Parameters Uncertainty on Subcooled Boiling. For convenience of expression, the radial positions are processed into non-dimensional parameters by r/R, where R is the radius of the heated pipe. Besides, the contribution of uncertainty sources is evaluated in Contribution of Uncertainty Sources with the computational data of DS4.

Effects of Model Parameters Uncertainty on Subcooled Boiling

The distribution of radial parameters with uncertainties, including void fraction, liquid temperature, phase velocity, and bubble diameter, are presented in Figure 2. It is shown that the void fraction and liquid temperature agree well with the benchmark data while the bubble diameter deviates. The reason is that the bubble diameter model applied in this work is simplified to a function of the local subcooling, which do not consider the coalescence and break of bubbles. The results of vapor velocity perform the same trend with experiment data, but some differences exist in the values. This is because, on the one hand, the effect of the bubble diameter deviation on the momentum equation solving, on the other hand, the wall function in this work is developed based on single-phase fluid. It is indicated that a two-phase wall law based on bubble-equivalent surface roughness can improve the phase velocity adjacent to the boiling surface (Končar and Borut, 2010).

FIGURE 2

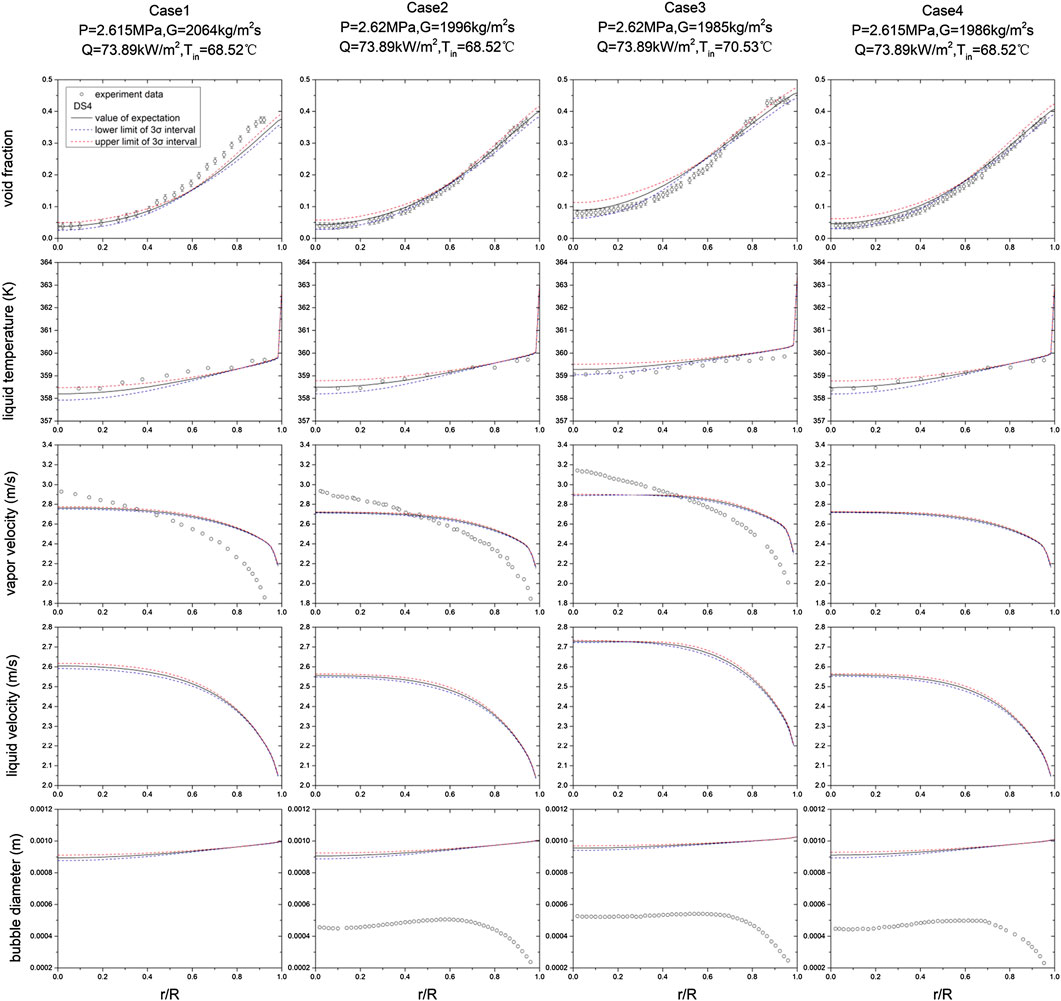
FIGURE 2. Effects of model uncertainties on radial parameters (the experiment data of Case1 are extracted from Končar and Borut (2010) where the liquid velocity and bubble diameter are not given, the experiment data of Case2 and Case3 are extracted from Krepper and Rzehak (2011) where the liquid velocity are not given, the experiment data of Case4 are extracted from Yun et al. (2012) where the vapor velocity and liquid velocity are not given).

According to the results in Figure 2, the void fraction increases along the radial direction gradually, since the bubbles produced at the heated wall are spread from the near-wall region to the pipe center by the phase interaction forces. The uncertainty appears to be larger at the center and around of the pipe which means the void fraction is more sensitive to the turbulence model in these regions. This is different with the void fraction, the maximum value of the liquid temperature uncertainty bandwidth occurs only at the center of the pipe. Then the uncertainty bandwidth drops down along with the radial direction and finally the lower and the upper limit are almost overlapped at the near-wall region. This suggests that there is very little influence of turbulence model uncertainties on the liquid temperature near the wall. The distribution of bubble diameter uncertainty exhibits a similar property to the liquid temperature, due to the strong relationship between bubble diameter and liquid temperature which has been introduced above. Besides, we can find that the effects of turbulence model uncertainty to phase velocity are small, and occurs mainly in the region near r/R=0.6.

Contribution of Uncertainty Sources

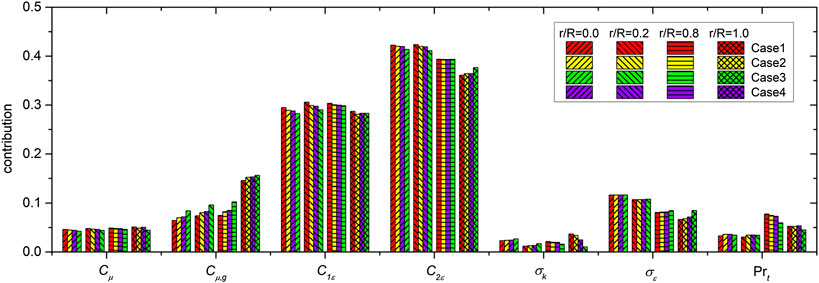
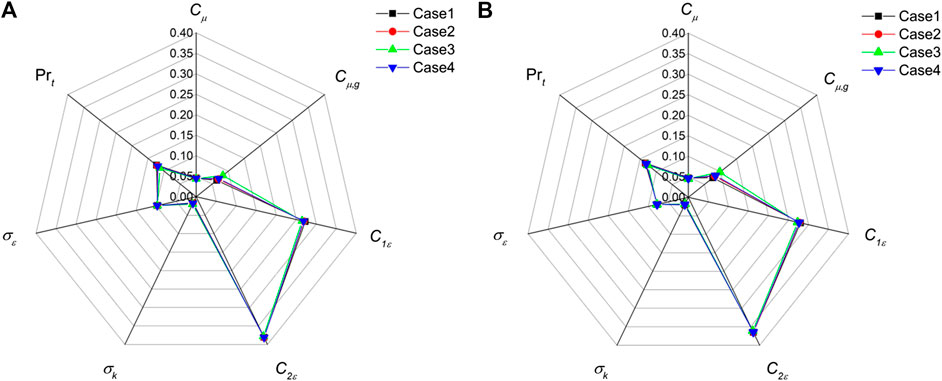
Based on the assumption that the parameters are independent from each other, the contributions of each uncertainty source to the radial void fraction and radial liquid temperature can be calculated by using Eq. (18)(19)(20).

As shown in Figure 2, the turbulence model uncertainties mainly influence the void fraction in partial regions, including the center of the pipe and the region close to the wall. Thus, several radial positions at the pipe exit, except the area around r/R=0.5, are selected to investigate the contribution of each uncertainty source along the radius. The results are given in Figure 3. And considering the same factors, parts of radial positions are selected for the contribution analysis of liquid temperature which is shown in Figure 4. A similar trend of contribution is presented by different cases, which avoid the accident of results. It is worth mentioning that the results of r/R=1 present the sources contribution to the maximum void fraction on the heated wall, which is a key parameter in critical heat flux prediction. It can be seen that the uncertainties of parameters C_2ε and C_1ε have a significant influence on the calculation of wall maximum void fraction. In addition, compared with the pipe center, the source contribution of C_μ,g to void fraction increases in the near-wall area. This means that the parameters C_2ε, C_1ε, and C_μ,g must be treated seriously in critical heat flux prediction. What is more, no matter the amount of void fraction or liquid temperature, the parameters C_2ε and C_1ε are always the most influential parameters in radial positions. This means that, to reasonably simulate subcooled boiling flow, the accurate value or probability density functions of C_2ε and C_1ε in the standard k-ε model need to be investigated further. Compared to the results of void fraction, the Pr_t contributes more in liquid temperature calculation. This is because turbulence will enhance the properties of thermal conduction, while Pr_t is an important parameter for heat conductivity coefficient calculation.

FIGURE 3

FIGURE 3. Uncertainty sources contribution on void fraction.

FIGURE 4

FIGURE 4. Uncertainty sources contribution on liquid temperature.

Conclusions

The uncertainty of two-phase models and boundary conditions has been analyzed using Latin Hypercube sampling in our previous work (Cong et al., 2018; Zhang et al., 2018c). As a series research, the effects of standard k-ε model uncertainties in two-phase flow was analyzed using a more efficient and economical method, deterministic sampling, in this study. The DEBORA experiments were chosen as benchmarks. Seven parameters in the standard k-ε model interrelated momentum, energy, turbulent kinetic energy, and dissipation rate were studied as uncertainty sources. The contribution of each uncertainty source was evaluated. In detail, the following conclusions can be drawn.

(1) Compared with the experiment data, a reasonable result within the confidence interval could be obtained. The results suggested that the models in our work can reasonably simulate the DEBORA experiments and the deterministic sampling can be a powerful tool for uncertainty quantification.

(2) The uncertainty band of radial parameters, including void fraction, liquid temperature, phase velocity, and bubble diameter, were obtained, which produced the sensitive parameter regions of the turbulence model.

(3) The contribution of each uncertainty source on different radial positions was analyzed. The parameters C_2ε and C_1ε always played predominant roles on the radial distributions of void fraction and liquid temperature, which specifies that these two parameters need to be treated carefully in further boiling flow simulations.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

XZ contributed to the CFD simulation work and uncertainty analysis. GX contributed to the guidance of the deterministic sampling method. TC contributed to the guidance of Fluent. MP contributed to the guidance of the theory of numerical heat transfer. ZW contributed to the data processing

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (No. 11705035) and the Natural Science Foundation of Heilongjiang (No. LH2019A009), which are gratefully acknowledged.

References

Bestion, D., de Crécy, A., Camy, R., Barth, A., Bellet, S., Badillo, A., et al. (2016). Review of uncertainty methods for computational fluid dynamics application to nuclear reactor thermal hydraulics. Paris, France: Nuclear Safety NEA/CSNI R .

Google Scholar

Burns, A. D., Frank, T., Hamill, I., and Shi, J.-M. (2004). “The Favre averaged drag model for turbulent dispersion in Eulerian multi-phase flows,” in 5th International conference on multiphase flow (ICMF-5), Yokohama, Japan, May 30–June 4, (Japan Society of Multiphase Flow), 1–17

Google Scholar

Chen, H., Fu, L., Jiong, G., and Lidong, W. (2015). Uncertainty and sensitivity analysis of filling fraction of pebble bed in pebble bed HTR. Nucl. Eng. Des. 292, 123–132. doi:10.1016/j.nucengdes.2015.05.032

CrossRef Full Text | Google Scholar

Cong, T., Lv, X., Zhang, X., and Zhang, R. (2018). Investigation on the effects of model uncertainties on subcooled boiling. Ann. Nucl. Energy 121, 487–500. doi:10.1016/j.anucene.2018.08.001

CrossRef Full Text | Google Scholar

Dunn, M. C., Shotorban, B., and Frendi, A. (2011). Uncertainty quantification of turbulence model coefficients via Latin hypercube sampling method. J. Fluid Eng. 133, 041402. doi:10.1115/1.4003762

CrossRef Full Text | Google Scholar

Fluent, A. (2013). ANSYS fluent theory guide 15.0. Canonsburg, PA: ANSYS Inc. .

Google Scholar

Garnier, J., Manon, E., and Cubizolles, G., (2001). Local measurements on flow boiling of refrigerant 12 in a vertical tube. Multiphas. Sci. Technol. 13, 1–111. doi:10.1615/multscientechn.v13.i1-2.10

CrossRef Full Text | Google Scholar

Hedberg, P., and Hessling, P. (2015). “Use of Deterministic sampling for uncertainty quantification in CFD,” in 16th International topical meeting on nuclear reactor thermal hydraulics-16 (NURETH-16), Chicago, Illinois, American Nuclear Society, 4907–4920

Google Scholar

Končar, B., and Borut, M. (2010). Wall function approach for boiling two-phase flows. Nucl. Eng. Des. 240, 3910–3918. doi:10.1016/j.nucengdes.2010.08.004

CrossRef Full Text | Google Scholar

Krepper, E., and Rzehak, R. (2011). CFD for subcooled flow boiling: simulation of DEBORA experiments. Nucl. Eng. Des. 241, 3851–3866. doi:10.1016/j.nucengdes.2011.07.003

CrossRef Full Text | Google Scholar

Launder, B., and Sharma, B. I. (1974). Application of the energy-dissipation model of turbulence to the calculation of flow near a spinning disc. Int. Commun. Heat Mass Tran. 1, 131–137. doi:10.1016/0735-1933(74)90024-4

CrossRef Full Text | Google Scholar

McHale, M., Friedman, J., and Karian, J. (2009). Standard for verification and validation in computational fluid dynamics and heat transfer. The American Society of Mechanical Engineers, ASME V&V

Google Scholar

Mohamed, M. S., and Larue, J. C. (1990). The decay power law in grid-generated turbulence. J. Fluid Mech. 219, 195–214. doi:10.1017/s0022112090002919

CrossRef Full Text | Google Scholar

Moraga, F. J., Bonetto, F. J., and Lahey, R. T. (1999). Lateral forces on spheres in turbulent uniform shear flow. Int. J. Multiphas. Flow 25, 1321–1372. doi:10.1016/s0301-9322(99)00045-2

CrossRef Full Text | Google Scholar

Pericas, R., Ivanov, K., Reventós, F., and Batet, L. (2017). Comparison of best-estimate plus uncertainty and conservative methodologies for a PWR MSLB analysis using a coupled 3-D neutron-kinetics/thermal-hydraulic code. Nucl. Technol. 198 (2), 193–201. doi:10.1080/00295450.2017.1299493

CrossRef Full Text | Google Scholar

Platteeuw, P., Loeven, G., and Bijl, H. (2008). “Uncertainty quantification applied to the k-epsilon model of turbulence using the probabilistic collocation method,” in 49th Structures, Structural Dynamics, and Materials Conference, Schaumburg,07 April–10 April,American Institute of Aeronautics and Astronautics, 2150. doi:10.2514/6.2008-2150

CrossRef Full Text | Google Scholar

Rakhimov, A. C., Visser, D. C., and Komen, E. M. J. (2018). Uncertainty Quantification method for CFD applied to the turbulent mixing of two water layers. Nucl. Eng. Des. 333, 1–15. doi:10.1016/j.nucengdes.2018.04.004

CrossRef Full Text | Google Scholar

Ranz, W., and Marshall, W. (1952). Evaporation from drops. Chem. Eng. Prog. 48, 141–146

Google Scholar

Rodi, W. (1984). Turbulence models and their application in hydraulics: a state of the art review. The Netherlands: International Association for Hydraulic Research

Google Scholar

Sato, Y., and Sekoguchi, K. (1975). Liquid velocity distribution in two-phase bubble flow. Int. J. Multiphas. Flow 2, 79–95. doi:10.1016/0301-9322(75)90030-0

CrossRef Full Text | Google Scholar

Schiller, L., and Naumann, Z. (1935). A drag coefficient correlation. Zeitschrift des Vereins Deutscher Ingenieure 77, 318–320

Google Scholar

Yun, B.-J., Splawski, A., Lo, S., and Song, C.-H. (2012). Prediction of a subcooled boiling flow with advanced two-phase flow models. Nucl. Eng. Des. 253, 351–359. doi:10.1016/j.nucengdes.2011.08.067

CrossRef Full Text | Google Scholar

Zhang, R., Cong, T., Tian, W., Qiu, S., and Su, G. (2015). Effects of turbulence models on forced convection subcooled boiling in vertical pipe. Ann. Nucl. Energy 80, 293–302. doi:10.1016/j.anucene.2015.01.039

CrossRef Full Text | Google Scholar

Zhang, H., Li, Y., Xiao, J., and Jordan, T. (2018a). Uncertainty analysis of condensation heat transfer benchmark using CFD code GASFLOW-MPI. Nucl. Eng. Des. 340, 308–317. doi:10.1016/j.nucengdes.2018.10.007

CrossRef Full Text | Google Scholar

Zhang, X., Yu, T., Cong, T., and Peng, M. (2018b). Effects of interaction models on upward subcooled boiling flow in annulus. Prog. Nucl. Energy 105, 61–75. doi:10.1016/j.pnucene.2017.12.004

CrossRef Full Text | Google Scholar

Zhang, X., Zhang, R., Lv, X., and Cong, T. (2018c). Investigation on the subcooled boiling in vertical pipe with uncertainties from boundary conditions by using FLUENT. Frontiers in Energy Research 6, 23. doi:10.3389/fenrg.2018.00023

CrossRef Full Text | Google Scholar