Effect of Stress-Sensitive Fracture Conductivity on Transient Pressure Behavior for a Multi-Well Pad With Multistage Fractures in a Naturally Fractured Tight Reservoir

This paper presents a semianalytical solution for evaluating transient pressure behavior of a multi-well pad with multistage fractures in a naturally fractured tight reservoir by considering the stress-sensitive effect imposed by both natural and hydraulic fractures. More specifically, the model pertaining to matrix/natural fractures is considered as a dual-porosity continuum, while its analytical flow model can be obtained by use of a slab-source function in the Laplace domain. The hydraulic fracture model is solved by discretizing each fracture into small segments to describe the flow behavior, while stress sensitivity in both the natural fracture (NF) subsystem and hydraulic fracture (HF) subsystem has been taken into account. To validate the newly developed semianalytical model, its solution has been obtained and compared with those of a commercial numerical simulator. By generating the type curves, there may exhibit eight flow regimes: pure wellbore storage, skin effect transition flow, linear flow regime within HFs, early radial flow, biradial flow, transition flow, pseudo-steady diffusion, and the late-time pseudo-radial flow. Furthermore, late-time flow regimes are found to be significantly distorted by the multi-well pressure interference. The smaller the well-rate ratio is, the more distorted the pressure and pressure derivative curves will be. In addition, well spacing and fracture length are found to dominate the flow behavior when multi-well pressure interference occurs. As the well spacing is decreased, the fracture length is increased, and thus occurrence of multi-well pressure interference is initiated earlier. Permeability moduli of NFs and HFs impose no impact on the multi-well pressure interference; however, it can distort flow regimes, leading to a severe distortion of pressure and pressure derivative curves. Similarly, the effect of HF permeability modulus on the flow in a hydraulic fracture, the minimum fracture conductivity is another key factor affecting the “hump” on the pressure curve. As the crossflow coefficient is increased, flow exchange between matrix and NFs is increased. With an increase in the storage ratio, flow exchange lasts longer and the second “dip” on the pressure curve becomes deeper.

Introduction

With the increasing oil and gas consumption, more attentions have recently been directed to exploit the unconventional resources (Schmoker, 2002; Jia 2017; Yekeen et al., 2018; Gao et al., 2018; Chen et al., 2019). As an important and unconventional clean fossil fuel, tight oil is expected to play an increasingly important role in meeting the energy demand (Song et al., 2015; Yang et al., 2015a; Song and Yang, 2017; Wang M. et al., 2018; Amjed et al., 2019; Jiang et al., 2020a). Owing to the advancement of drilling horizontal wells with multistage hydraulic fractures (HFs), tight oil reservoirs have been exploited commercially though the flow behavior is quite different from those of the conventional reservoirs due to the extremely low permeability (Miller et al., 2008; Meyer and Bazan, 2011; Liu et al., 2018b; Liu et al., 2020a; Liu et al., 2020b, Liu et al., 2020c). To reduce operational costs and mitigate the negative environmental impact, multi-well pad schemes have proven to be more effective for exploiting tight oil/gas reservoirs with and without natural fractures (NFs) (Manchanda and Sharma, 2013; Meng et al., 2017; Xiao et al., 2018; Jiang et al., 2020b; Jiang et al., 2020c); however, multi-well pressure interference under multi-well pad schemes severely distorts the flow patterns. In addition to greatly affecting well production, such a distortion inevitably makes the transient pressure analysis more challenging while the stress-sensitivity effect and contribution of NFs are usually excluded (Liu et al., 2018a). Therefore, it is of fundamental and practical importance to accurately evaluate performance for a multi-well pad with multistage HFs and NFs in a tight formation by taking their stress-sensitive effects into account.

Considering its geological characteristics, fluid flow behavior in a tight formation with both NFs and HFs can be simulated with two main methods: the continuum model and the discrete fracture network (DFN) model. The most classical continuum model is the dual-porosity model proposed by Warren and Root (1963), assuming matrix and NFs as the main storage spaces and flow path. Then, the flow exchange between matrix subsystem and NF subsystem can be quantified (Kazemi 1969; Jalali and Ershaghi, 1987; Hassanzadeh et al., 2009; Wang, L et al., 2018). On the basis of the dual-porosity model, Wu et al. (2004) proposed a triple-porosity model to estimate the flow exchange among matrix, NFs, and HFs, which was subsequently improved with respect to algorithm convergence and computational expenses (Ozkan et al., 2009, 2011; Stalgorova and Mattar, 2012). Due to its simple assumptions and high computational efficiency, the continuum model has been widely used to describe fluid flow in tight oil/shale gas reservoirs.

Using the micro-seismic monitoring and surveillance techniques, it is found that HFs do not occupy the entire formation after being hydraulically fractured. In a DFN model, the HFs are usually described as high permeability channels by means of local grid refinement (Noorishad et al., 1982; Juanes et al., 2002; Rogers et al., 2010). As such, the DFN model is considered to be more rigorously to capture the details of flow behavior in complex fracture network, while it needs to be solved by either numerical difference or dimension reduction. Although the DFN method can be used to accurately describe the fluid flow, its computational expenses are too high (Cipolla et al., 2011).

Combining the advantages of the aforementioned two models, the latest development is to combine the dual-porosity model and the HF model (Zhao et al., 2014; Zhao et al., 2015; Chen et al., 2016; Jia et al., 2016, Jia et al., 2017; Morteza et al., 2018). Such combined models can not only accurately describe fluid flow within the HFs at different angles, but also consider the contribution of the secondary-fracture networks (Ren et al., 2016; Chen et al., 2017b). In practice, either a line-source function or a slab-source function can be used to obtain the semianalytical solution for such complex flow systems under different conditions, though convergence difficulties are encountered and computational expenses are high (Zhang and Yang, 2014; Yang et al., 2015b; Wang et al., 2017; Liu et al., 2018a, Zhang and Yang, 2018). Physically, more practical models together with computational algorithms are desired when the stress-sensitive effect needs to be taken into account (Liu et al., 2015; Chen et al., 2016; Wang et al., 2017). Usually, the stress sensitivities of both NFs and HFs are assumed to be the same while this is found to be not reasonable in reality (Jiang et al., 2019b). In fact, it has been found from laboratory experiments that proppant has a great influence on stress sensitivity of HFs, i.e., the HF permeability modulus is larger than that of NFs (Montgomery and Steanson, 1985; Feng et al., 2017). So far, no attempts have been made to examine the stress sensitivity for NFs and HFs with different contributions in a multi-well pad with consideration of the multi-well pressure interference.

In this paper, a new semianalytical model has been developed and validated to examine the stress-sensitive fracture conductivity on transient pressure response for a multi-well pad in a naturally fractured tight reservoir. More specifically, matrix/NFs is considered as a dual-porosity continuum, which can be solved analytically by use of a slab-source function in the Laplace domain, while HFs can be solved by discretizing each fracture into small segments. Then, the perturbation technique together with superposition principle and the Stehfest algorithm has been employed to solve such a highly nonlinear equation matrix with consideration of different stress-sensitivity for NFs and HFs. In order to validate the semianalytical model, its solution has been compared with that of a commercial simulator. With the assistance of this new approach, not only can flow regimes of multi-well pad with multiple fractures be identified, but also sensitivity analysis has been made to illustrate how key parameters affect the transient pressure responses in such a complex flow system.

Theoretical Formulations

In this study, two hydraulically fractured horizontal wells are considered as a multi-well pad, producing at two different surface flow rate q_sc1 and q_sc2 see (Figure 1). It is worthwhile mentioning that this two-well model can be extended to multiple wells, though computational expenses will be correspondingly increased (Appendix B). For convenience, the tight reservoir including matrix subsystem, NF subsystem, and HF subsystem is assumed to be isotropic, while other main assumptions are listed as follows:

• The reservoir upper and lower boundaries are impermeable and the lateral boundary is infinite.

• Two hydraulic fracturing horizontal wells are parallel to the upper and lower boundaries and penetrate completely, assuming the fractures have finite conductivity.

• Stress-sensitive effects in the NFs and HFs are considered, while their stress sensitivity coefficients are different.

• A pseudo-steady crossflow occurs between the matrix and the NFs, while the HFs are the only pathway for the fluid flow from the NFs to the wellbore.

• Oil flow in the HFs and NFs obeys the Darcy law, and incompressible flow is assumed in the HFs because the fracture volume is negligible compared with that of the NFs (Cinco-Ley and Meng, 1988; Jiang et al., 2019a).

• Single phase and isothermal flow is considered but gravity and capillary effects are neglected.

FIGURE 1

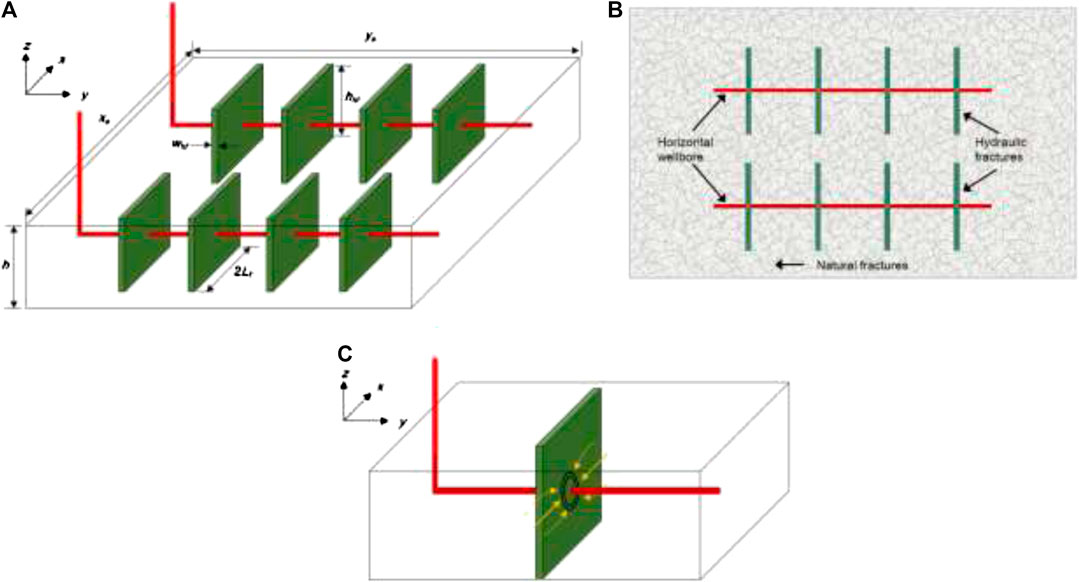
FIGURE 1. (A) 3D view and (B) Top view of multi-well pad with multiple fractures in a tight oil reservoir, and (C) Convergence flow effect around the wellbore in hydraulic fractures (HFs).

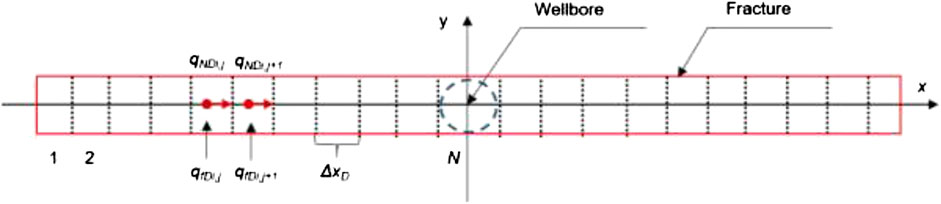
With the aforementioned assumptions, we first discretize the HFs (Figure 2) each of which for Well #1 and Well #2 is respectively divided into 2*N₁ and 2*N₂ segments, assuming the number of HFs for Well #1 and Well #2 is M₁ and M₂, respectively. The superposition principle can then be used to calculate the pressure responses for these sub-fracture segments. Finally, the dual-porosity flow model and HF flow model are dynamically coupled and solved. In this study, the stress-sensitive effects in the NFs and HFs are considered, while their stress-sensitivity coefficients are different.

FIGURE 2

FIGURE 2. Schematic diagram for the discretized fracture model in a multi-well pad scheme.

The NF permeability modulus, γ_nf, is defined as the exponential relationship between NF permeability and its pressure (Chen et al., 2008), i.e.,

$k_{nf}\left(p_{nf}\right)=k_{nfi}\exp \left[-{\gamma }_{nf}\left(p_i-p_{nf}\right)\right](1)$

where k_nf is the NF permeability, p_nf is the NF pressure, p_i is the initial pressure, k_nfi is the initial NF permeability, and γ_nf is the NF permeability modulus.

As for HFs, the HF permeability tends to have a minimum value (i.e., k_hfmin) due to the influence of proppants when the effective stress increases continuously (Weaver et al., 2010). The stress sensitivity of hydraulic fractures can be adjusted by changing the ratio of k_hfmin to k_hfi, which is usually obtained by experiments. The larger the ratio of k_hfmin to k_hfi is, the weaker the impact of effective stress on HF permeability will be. As such, the relationship between HF permeability and its pressure can be described as follow (Zhang et al., 2014),

$k_{hf}\left(p_{hf}\right)=k_{hf\min }+\left(k_{hfi}-k_{hf\min }\right)exp\left[-{\gamma }_{hf}\left(p_i-p_{hf}\right)\right](2)$

where k_hf is the HF permeability, p_i is the initial reservoir pressure, p_hf is the HF pressure, k_hfi is the initial HF permeability, γ_hf is the HF permeability modulus, and k_hfmin is the minimum HF permeability.

Governing Equations

Matrix Subsystem

Since the matrix permeability of a tight oil reservoir is extremely low, the fluid flow in the matrix can be neglected, and the matrix is considered as evenly distributed sources when the oil in the matrix flows into natural fractures (Li et al., 2017). In this way, the governing equation of the matrix subsystem can be described by:

$\frac{\partial \left(\rho {\varphi }_m\right)}{\partial t}+q_{ex}=0(\mathrm{3a})$

$q_{ex}=\frac{\alpha k_m\rho }{\mu }\left(p_m-p_{nf}\right)(\mathrm{3b})$

where ρ is the fluid density, ϕ_m is the matrix porosity, k_m is the matrix permeability, p_m is the matrix pressure, μ is the fluid viscosity, α is the shape factor, t is time, and q_ex is the flow rate between the matrix and NFs.

Because of no flow in the matrix, the initial condition can be described as the following:

$\frac{\partial p_m}{\partial x}=\frac{\partial p_m}{\partial y}=0(\mathrm{4a})$

$p_m\left(x,y,t=0\right)=p_i(\mathrm{4b})$

Natural Fracture Subsystem

Considering the stress sensitivity of NFs, the governing equation of NFs can be expressed as follows:

$\frac{\partial }{\partial x}\left[e^{-{\gamma }_{nf}(p_i-p_{nf})}\frac{\partial p_{nf}}{\partial x}\right]+\frac{\partial }{\partial y}\left[e^{-{\gamma }_{nf}(p_i-p_{nf})}\frac{\partial p_{nf}}{\partial y}\right]+\frac{k_m}{k_{nfi}}\alpha \left(p_m-p_{nf}\right)=\frac{{\varphi }_{nf}\mu c_{tnf}}{k_{nfi}}\frac{\partial p_{nf}}{\partial t}(5)$

where c_tnf is the total NF compressibility.

Then, the initial condition and boundary conditions can be expressed as follow:

$p_{nf}\left(x,y,t=0\right)=p_i(\mathrm{6a})$

${\frac{\partial p_{nf}}{\partial x}|}_{x=0,x_e}=0,0\le y\le y_e\begin{array}{cc}& \end{array}{\frac{\partial p_{nf}}{\partial y}|}_{y=0,y_e}=0,0\le x\le x_e(\mathrm{6b})$

Hydraulic Fracture Subsystem

To date, as for fluid flow in the HFs, both compressible and incompressible flows have been extensively studied. Since the reservoir volume is much larger than the hydraulic fracturing volume in a tight oil reservoir (Cinco-Ley and Samaniego, 1981), fluid compressibility is not considered in this study. Considering the stress sensitivity of HFs, the governing equation of HFs can be written as follows:

$\frac{k_{hfi}}{\mu }\frac{\partial }{\partial x}\left\{\left[\frac{k_{hf\min }}{k_{hfi}}+\left(1-\frac{k_{hf\min }}{k_{hfi}}\right)e^{-{\gamma }_{hf}(p_i-p_{hf})}\right]\right\}+\frac{q_f}{w_{hf}{h}_{hf}}=0(7)$

where w_hf and h_hf are the HF width and height, respectively, µ is fluid viscosity and q_f is the flow rate from reservoir into HFs.

The initial condition and boundary conditions are expressed as follow:

$\frac{k_{hfi}{h}_{hf}{w}_{hf}}{\mu }{\left[\frac{k_{hf\min }}{k_{hfi}}+\left(1-\frac{k_{hf\min }}{k_{hfi}}\right)e^{-{\gamma }_{hf}\left(p_i-p_{hf}\right)}\right]\frac{\partial p_{hf}}{\partial x}|}_{x=x_w}=q_{Ni,1},i=\mathrm{1,2},\dots ,2M(\mathrm{8a})$

${\frac{\partial p_{hf}}{\partial x}|}_{x=x_w+x_{hf}}=0(\mathrm{8b})$

$p_{hf}(x,t=0)=p_i(\mathrm{8c})$

where q_Ni;1 is the flow rate from the N node of the ith HF to the wellbore and M is the number of hydraulic fractures.

Non-Dimensionalization

For the convenience of derivation, analysis, and improving the applicability of the model proposed in this study, dimensionless variables are defined as follows (Chen et al., 2016; Wang et al., 2017; Jiang et al., 2019a; Jiang et al., 2019b):

$t_D=\frac{k_{nfi}t}{\left({\varphi }_m{C}_{tm}+{\varphi }_{nf}{C}_{tnf}\right)\mu x_{hf}^2}(\mathrm{9a})$

$p_{hfD}=\frac{2\pi k_{nfi}h(p_i-p_{hf})}{q_{sc}B\mu }(\mathrm{9b})$

$p_{mD}=\frac{2\pi k_{nfi}h(p_i-p_m)}{q_{sc}B\mu }(\mathrm{9c})$

$p_{nfD}=\frac{2\pi k_{nfi}h(p_i-p_{nf})}{q_{sc}B\mu }(\mathrm{9d})$

$C_{fD}=\frac{k_{hf}{w}_{hf}}{k_{nfi}{x}_{hf}}(9e)$

$q_{fD}=\frac{2q_f{x}_{hf}}{q_{sc}B}(\mathrm{9f})$

$q_{ND}=\frac{q_N{x}_{hf}}{q_{sc}B}(\mathrm{9g})$

$x_D=\frac{x}{x_{hf}}(\mathrm{9h})$

$y_D=\frac{y}{y_{hf}}(\mathrm{9i})$

$\lambda =\alpha \frac{k_m}{k_{nfi}}{x}_{hf}^2(\mathrm{9j})$

$w=\frac{{\varphi }_{nf}{C}_{tnf}}{({\varphi }_m{C}_m+{\varphi }_{nf}{C}_{tnf})}(\mathrm{9k})$

${\gamma }_{nfd}=\frac{q_{sc}B\mu }{2\pi k_{nfi}h}{\gamma }_{nf}(\mathrm{9l})$

${\gamma }_{hfd}=\frac{q_{sc}B\mu }{2\pi k_{nfi}h}{\gamma }_{hf}(\mathrm{9m})$

Matrix Subsystem

According to the aforementioned definitions of dimensionless variables, Eqs 3a–4b can be rewritten as follows:

$\lambda (p_{mD}-p_{nfD})+(1-\omega )\frac{\partial p_{mD}}{\partial t_D}=0(\mathrm{10a})$

$p_{mD}(x_D,y_D,t_D=0)=0(\mathrm{10b})$

$\frac{\partial p_{mD}}{\partial x_D}=\frac{\partial p_{mD}}{\partial y_D}=0(\mathrm{10c})$

Natural Fracture Subsystem

With the aforementioned definitions, Eqs 5–6b can be rewritten as follows:

$e^{-{\gamma }_{nfD}{p}_{nfD}}\left[\frac{{\partial }^2{p}_{nfD}}{\partial x_D^2}+\frac{{\partial }^2{p}_{nfD}}{\partial y_D^2}-{\gamma }_{nfD}{\left(\frac{\partial p_{nfD}}{\partial y_D}\right)}^2\right]=\omega \frac{\partial p_{nfD}}{\partial t_D}-\lambda \left(p_{mD}-p_{nfD}\right)(\mathrm{11a})$

${\frac{\partial p_{nfD}}{\partial x_D}|}_{x_D=0,x_{eD}}=\mathrm{0,0}\le y_D\le y_{eD,}{\frac{\partial p_{nfD}}{\partial y_D}|}_{y_D=0,y_{eD}}=\mathrm{0,0}\le x_D\le x_{eD,}(\mathrm{11b})$

$p_{nfD}(x_D,y_D,t_D=0)=0(\mathrm{11c})$

Hydraulic Fracture Subsystem

Similarly, Eqs 7–8c can be rewritten as follows:

$\frac{\partial }{\partial x_D}\left\{\left[\frac{C_{fD\min }}{C_{fDi}}+\left(1-\frac{C_{fD\min }}{C_{fDi}}\right)e^{-{\gamma }_{hfD}{p}_{hfD}}\right]\frac{\partial p_{hfD}}{\partial x_D}\right\}-\frac{\pi q_{fD}}{C_{fDi}}=0(\mathrm{12a})$

${\left({\delta }_s\frac{\partial p_{hfD}}{\partial x_D}\right)|}_{x_D=x_{wD}}=-\frac{\pi q_{NDi,1}}{C_{fDi}},N=\mathrm{1,2},\dots ,N(\mathrm{12b})$

${\frac{\partial p_{hfD}}{\partial x_D}|}_{x_D=x_{wD}+x_{fD}}=0(\mathrm{12c})$

$p_{hfD}(x_D,y_D,t_D=0)=0(\mathrm{12d})$

${\delta }_s=\frac{C_{fD\min }}{C_{fDi}}+\left(1-\frac{C_{fD\min }}{C_{fDi}}\right)e^{-{\gamma }_{hfD}{p}_{hfD}}(12e)$

Solutions for a Multi-Well Pad

Matrix/Natural Fractures.

After considering the NF stress sensitivity, it is difficult to obtain analytical solutions for the mathematical models of matrix and NFs. In this paper, we use the perturbation theory (Pedrosa, 1986) to obtain semianalytical solutions of matrix and NFs, i.e., p_nfD can be rephrased as follows:

$p_{nfD}=-\frac{1}{{\gamma }_{nfD}}\ln \left(1-{\gamma }_{nfD}{\eta }_{nfD}\right)(\mathrm{13a})$

According to perturbation theory, η_nfD can be rewritten as follow:

${\eta }_{nfD}={\eta }_{nfD0}+{\gamma }_{nfD}{\eta }_{nfD1}+{\gamma }_{nfD}^2{\eta }_{nfD2}^2+\dots (\mathrm{13b})$

$\frac{1}{1-{\gamma }_{nfD}{\eta }_{nfD}}=1+{\gamma }_{nfD}{\eta }_{nfD}+{\lambda }_{nfD}^2{\eta }_{nfD}^2+\dots (\mathrm{13c})$

Numerous studies have found that the zero-order approximate solution completely meets the solution requirements (Jiang et al., 2019b). Therefore, Eqs 5–b can be rewritten as follows:

$\lambda \left(p_{mD}-{\eta }_{nfD0}\right)+\left(1-\omega \right)\frac{\partial p_{mD}}{\partial t_D}=0(\mathrm{14a})$

$\frac{{\partial }^2{\eta }_{nfDo}}{\partial x_D^2}+\frac{{\partial }^2{\eta }_{nfDo}}{\partial y_D^2}=\omega \frac{\partial {\eta }_{nfD0}}{\partial t_D}+\left(1-\omega \right)\frac{\partial p_{mD}}{\partial t_D}(\mathrm{14b})$

${\frac{\partial {\eta }_{nfD0}}{\partial x_D}|}_{x_D=0,x_{eD}}=0,0\le y_D\le y_{eD},{\frac{\partial {\eta }_{nfD0}}{\partial y_D}|}_{y_D=0,y_{eD}}=0,0\le x_D\le x_{eD}(\mathrm{14c})$

And the initial condition can be rewritten as follows:

${\eta }_{fD0}\left(x_D,y_D,t_D=0\right)=0(\mathrm{14d})$

Then, the equation can be solved in the Laplace domain. In this paper, a slab-source function is derived and presented in Appendix A, while the solution for multi-well pad schemes can be expressed as the follow:

${\overline{\eta }}_{nfD0}\left(x_D,y_D,s_D,u_D\right)=\frac{\pi x_{fD}}{x_{eD}{y}_{fD}}{\overline{q}}_f\left(s_D\right)\left[\begin{array}{l}{\overline{s}}_p\left(y_D,y_{wD},y_{fD},u_D\right)+\\ 2{\displaystyle \sum _{n=1}^{\infty }{F}_n\left(x_{fD}/x_{eD}\right)cos\frac{n\pi x_{wD}}{x_{eD}}\cos }\frac{n\pi x_D}{x_{eD}}{\overline{s}}_{p\left(n\right)}\left(y_D,y_{wD},y_{fD},{\alpha }_{nD},u_D\right)\end{array}\right](\mathrm{15a})$

$f\left(s_D\right)=\frac{\omega (1-\omega )s_D+\lambda }{(1-\omega )s_D+\lambda }(\mathrm{15b})$

$u_D=s_D\times f\left(s_D\right)(\mathrm{15c})$

Hydraulic Fractures

Considering the HF stress sensitivity, the corresponding flow equation becomes highly nonlinear and is solved by discretizing each fractures into small segments. According to the dimensionless definitions, Eqs 12e–13a can be rewritten as follows:

${\delta }_S=\frac{C_{fD\min }}{C_{fD}}\exp \left({\gamma }_{nfD}{p}_{hfD}\right)+\left(1-\frac{C_{fD\min }}{C_{fD}}\right)exp\left[-\left({\gamma }_{hfD}-{\gamma }_{nfD}\right)p_{hfD}\right](\mathrm{16a})$

$p_{hfD}=-\frac{1}{{\gamma }_{nfD}}\ln \left(1-{\gamma }_{nfD}{\eta }_{hfD}\right)(\mathrm{16b})$

Therefore, the governing equation for segments can be rewritten:

$\frac{{\partial }^2{\eta }_{hfD}}{\partial x_D^2}-\frac{\pi q_{fDi,j}^{\ast }}{C_{fDi}}=0,x_{Di,j}\le x_D\le x_{Di,j+1}(\mathrm{17a})$

with the boundary condition and initial condition:

${\left(\frac{\partial {\eta }_{hfD}}{\partial x_D}\right)|}_{x_D=x_{Di,j}}=-\frac{\pi q_{NDi,j}^{\ast }}{C_{fDi}}(\mathrm{17b})$

${\left(\frac{\partial {\eta }_{hfD}}{\partial x_D}\right)|}_{x_D=x_{Di,j+1}}=-\frac{\pi q_{NDi,j+1}^{\ast }}{C_{fDi}}(\mathrm{17c})$

${\eta }_{hfD}\left(x_D,t_D=0\right)=0(\mathrm{17d})$

where

$q_{fDi,j}^{\ast }=\frac{q_{fDi,j}}{{\delta }_{Si,j}}(17e)$

By integrating with the boundary condition, we can obtain

$\begin{array}{l}{\overline{p}}_{FDi}\left(x_{Di}\right)-{\overline{p}}_{wD}=\frac{2\pi }{C_{FDj}}\left[\frac{\Delta x_D}{8}{q}_{fDi,j}^{\ast }+{\displaystyle \sum _{j=1}^{i-1}{q}_{fDi,j}^{\ast }\left(\frac{\Delta x_D}{2}+x_{Di}-j\Delta x_D\right)}-x_{Di}{\displaystyle \sum _{j=1}^{S_m}{q}_{fDi,j}^{\ast }}\right]\\ \begin{array}{cccc}\begin{array}{ccc}\begin{array}{cccc}& & & \end{array}& & \end{array}& & & \end{array}i=\mathrm{1,2},\dots ,2N\end{array}(\mathrm{18a})$

where

$\Delta x_D=\frac{L_{FD}}{N},x_{Di}=\left(i-\frac{1}{2}\right)\Delta x_D(\mathrm{18b})$

Coupling Matrix/Natural Fractures and Hydraulic Fractures

The solution of transient flow responses is obtained by coupling the Matrix/NFs and HFs dynamically. According to the previous model description, HFs are discretized into 2N₁ × M₁ + 2N₂ × M₂ segments, each of which has three variables: q_fDi,j, q_NDi,j, and p_hfDi,j. In addition, two unknown variables are the flowing bottomhole pressure p_wD1 and p_wD2. A closed [2(2N₁ × M₁ + 2N₂ × M₂) + 2]-order matrix from the pressure-continuity condition can be obtained.

Since pressure in NFs and HFs is the same (2N₁ × M₁ + 2N₂ × M₂) equations can then be obtained,

$p_{hfDi,j}=p_{nfDi,j}(19)$

Because it is assumed that fluid in HFs incompressible, inflow and outflow should be conserved according to the conservation of mass, (2N₁ × M₁ + 2N₂ × M₂) equations can be obtained,

${\overline{q}}_{NDi,j}-{\overline{q}}_{NDi,j+1}-\frac{1}{2}\Delta x_{hfD}{\overline{q}}_{fDi,j}=0(20)$

Either Well #1 or Well #2 is produced at a constant rate, and ratio of the oil production for these two wells is denoted by ε. Then, two equations can be obtained,

${\displaystyle \sum _{i=1}^N{\overline{q}}_{WD1}=\frac{\epsilon }{2s_D}}(\mathrm{21a})$

${\displaystyle \sum _{i=1}^N{\overline{q}}_{WD2}=\frac{1-\epsilon }{2s_D}}(\mathrm{21b})$

Therefore, a closed [2(2N₁ × M₁ + 2N₂ × M₂) + 2]-order matrix is obtained,

$\text{A}\overrightarrow{\text{X}}=\overrightarrow{\text{B}}(22)$

In addition, skin effect and wellbore storage can be introduced into transient-solution directly in the Laplace domain (Cao et al., 2018),

${\overline{\eta }}_{wD}=\frac{s{\overline{\eta }}_{wDN}+S}{s+C_D{s}^2\left(s{\overline{\eta }}_{wDN}+S\right)}(23)$

Coupling Solutions

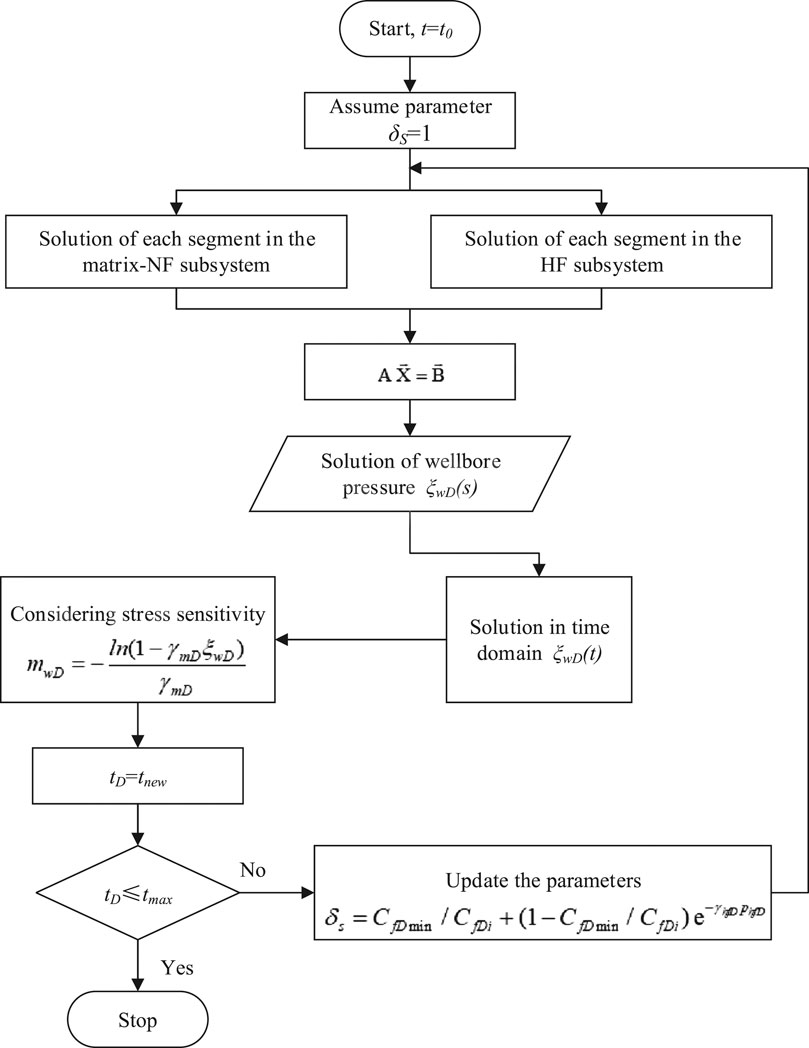
An iterative method proposed by Van Everdingen and Hurst (1949) is applied here to solve the nonlinear matrix, while the detailed flowchart is shown as Figure 3. First, the transient-pressure solution (Eq. 24a) can be obtained with iterations in the Laplace domain, and then stable solution (Eq. 24b) obtained in the real-time domain by using the Stehfest inversion algorithm (Stehfest, 1970). It is worthwhile mentioning that the new semianalytical model can be used to obtain the transient-production solution at a fixed pressure, which can be transformed through Eq. 24c in the Laplace domain.

${\overline{m}}_D=-\frac{1}{{\gamma }_{mD}}\ln \left(1-{\gamma }_{mD}{\overline{\eta }}_{wD}\right)(\mathrm{24a})$

${\overline{m}}_D=-\frac{1}{{\gamma }_{mD}}\ln \left[1-\frac{{\gamma }_{mD}\ln 2}{t_D}{\displaystyle \sum _{i=1}^N{\text{V}}_i\frac{s_i{\overline{\eta }}_{wDN}+S}{s_i+C_D{s}_i^2\left(s_i{\overline{\eta }}_{wDN}+S\right)}}\right](\mathrm{24b})$

where

${\text{V}}_i={\left(-1\right)}^{\frac{N}{2}+i}{\displaystyle \sum _{k=\frac{i+1}{2}}^{\min \left(i,\frac{N}{2}\right)}\frac{k^{\frac{N}{2}}\left(2k+1\right)!}{\left(k+1\right)!k!\left(\frac{N}{2}-k+1\right)!\left(i-k+1\right)!\left(2k-i+1\right)!}}(\mathrm{24c})$

${\overline{q}}_{WD}=\frac{1}{s^2{\overline{m}}_{WD}}(\mathrm{24d})$

FIGURE 3

FIGURE 3. Flowchart for evaluating the performance of a multi-well pad with multiple fractures.

Model Validation

In this section, we used a commercial reservoir simulator (CMG, version 2015) to simulate the performance of a multi-well pad with multiple fractures. In order to simulate the performance of an infinite reservoir, we intentionally enlarged the reservoir scale. The whole grid system is 300 $\times$ 400 $\times$ 5, and the dimension of each grid is 20 m $\times$ 20 m $\times$ 2 m. A “double Klinkenberg permeability, logarithmic spacing and local refined grid (DK-LS-LRG) method” (Cipolla et al., 2010) is used to characterize the HFs. The top view of the multi-well pad with multiple fractures is shown in Figure 4, and the physical properties used for model validation are tabulated in Table 1. As can be seen in Figure 5, there is a good agreement between the numerical simulation and the results obtained from the newly developed model in this study, confirming that our approach is reliable.

FIGURE 4

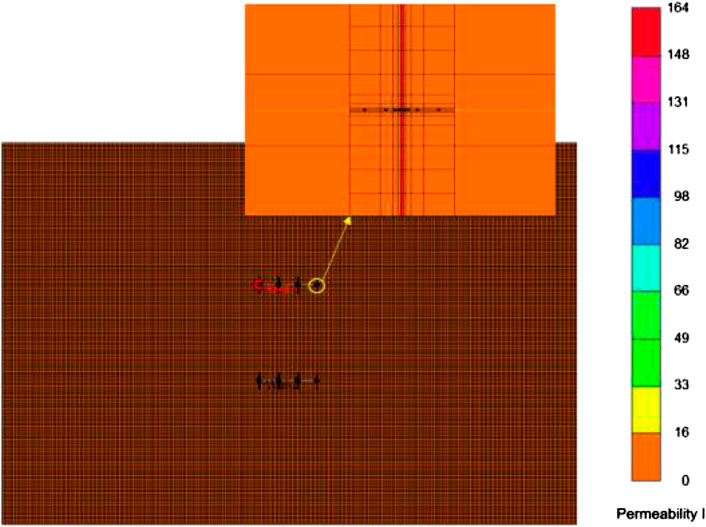
FIGURE 4. Top view of commercial reservoir simulator simulator for the multi-well pad with multiple fractures.

TABLE 1

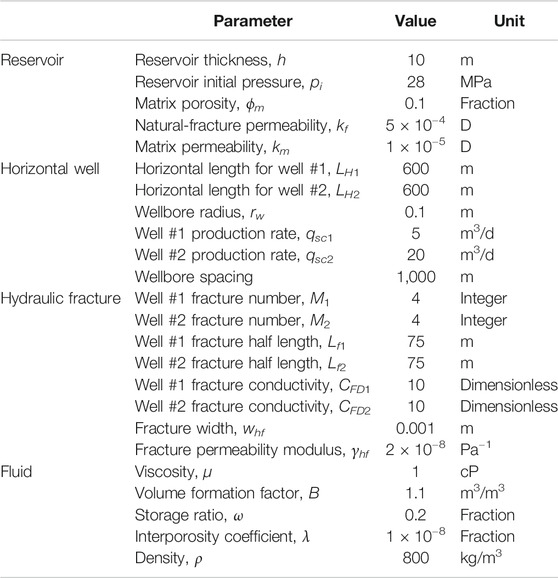
TABLE 1. Physical properties of a multi-well pad with multiple fractures used in the commercial reservoir simulator.

FIGURE 5

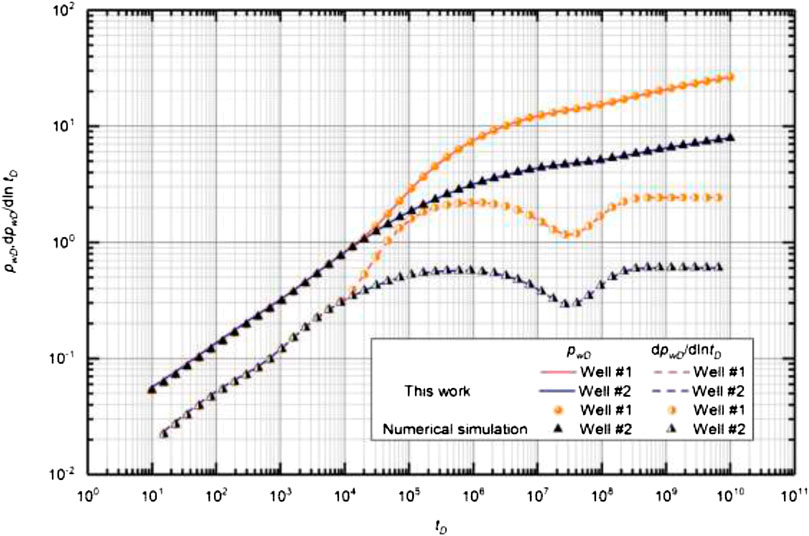
FIGURE 5. Comparison between the results obtained from this work and numerical simulation from commercial reservoir simulator.

Results and Discussion

In this section, type curves of a multi-well pad with multiple fractures are obtained, and the flow regimes are identified. In addition, sensitivity analysis is conducted to examine the effects of some main parameters, including ratio of well rate, hydraulic fracture spacing, hydraulic fracture length, well spacing, permeability modulus of NFs and HFs, minimum fracture conductivity, storage ratio, and crossflow coefficient.

Identification of Flow Regime

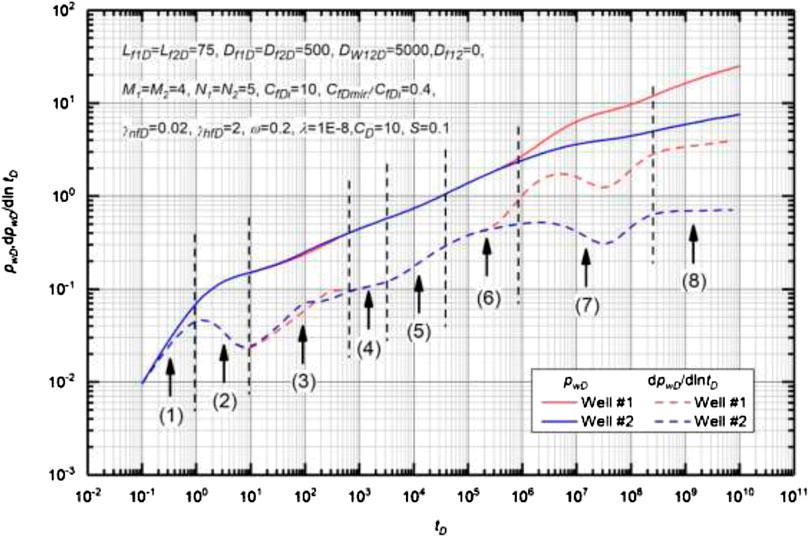
Dimensionless pressure (DP) and the dimensionless pressure derivative (DPD) of a multi-well pad with multiple fractures (MWPMF) are shown in Figure 6. The following dimensionless parameters are used to generate the type curves: L_f1D = L_f2D = 75, D_f1 = D_f2 = 500, M₁ = M₂ = 4, N₁ = N₂ = 5, C_fDi = 10, C_fDmin/C_fDi = 0.4, γ_nfD = 0.02, γ_hfD = 2, ω = 0.2, λ = 1 × 10⁻⁸, C_D = 10, and S = 0.1. After considering the multi-well pressure interference and stress sensitivity, there are eight flow regimes, which can be detailed as follows:

(1) The pure wellbore storage period regime: It can be identified by a slope of unity on the log-log plots, when DP curve and DPD curve align with each other. This period is mainly dominated by wellbore storage effect (Liu et al., 2018a).

(2) The skin effect transition flow regime: The most obvious feature of this stage is a “hump” in the pressure derivative curve. This period is mainly dominated by fluid properties (Cao et al., 2018).

(3) The linear flow regime within HFs: Usually, this period is characterized by a slope of 1/2 on the pressure derivative curve; however, the new model is affected by dynamic conductivity, and the slope of the pressure derivative curve is larger than 1/2. Moreover, the variation rate of the conductivity of two wells is different, which results in that the DP curve and DPD curve of two wells do not overlap at this stage (Yao et al., 2013).

(4) The early radial flow regime: It is characterized by a slope of 0 on the pressure derivative curve. This period is mainly dominated by hydraulic fracture spacing. This regime will occur only when the hydraulic fracture spacing is appropriate (Chen et al., 2016.

(5) The biradial flow regime: It is characterized by a slope of 1/3 on the pressure derivative curve. This period is mainly dominated by wellbore length (Zerzar et al., 2004).

(6) The transition flow regime: This is the transition regime between the biradial flow and pseudo-steady diffusion flow (Cinco-Ley and Meng, 1988).

(7) The pseudo-steady diffusion regime: The most obvious feature of this regime is a “dip” in the pressure derivative curve. In this period, mass transfer occurs between matrix and NFs (Wang et al., 2017).

(8) The late-time pseudo-radial flow regime: Under the influence of matrix stress sensitivity, the DPD curve does not show a horizontal line, and its value is greater than 0.5. Because of the existence of multi-well pressure interference, the smaller the oil rate is, the greater the distorted value will be (Liu et al., 2018a).

FIGURE 6

FIGURE 6. Flow regimes of a multi-well pad with multiple fractures identified by the type curve.

Sensitivity Analysis

Effect of Well-Rate Ratio

Figure 7 demonstrates the effect of well-rate ratio on type curves of MWPMF. The basic data used to generate the type curves are L_f1D = L_f2D = 75, D_f1 = D_f2 = 500, M₁ = M₂ = 4, N₁ = N₂ = 5, C_fDi = 10, C_fDmin/C_fDi = 0.4, γ_nfD = 0.02, γ_hfD = 2, ω = 0.2, λ = 1 × 10⁻⁸, C_D = 10, and S = 0.1. Comparison of different type curves illustrates that a smaller ε leads to a larger value of DPD and DPPD after the occurrence of multi-well pressure interference. In addition, it can be concluded that the well-rate ratio ε does not affect the onset time of multi-well pressure interference (Liu et al., 2018a). This is mainly because the onset time of multi-well pressure interference depends on the velocity of pressure wave propagation, which is only related to reservoir properties and well parameters, mainly including matrix, fracture permeability, fracture half-length, wellbore length, and well spacing, but has nothing to do with the well-rate ratio.

FIGURE 7

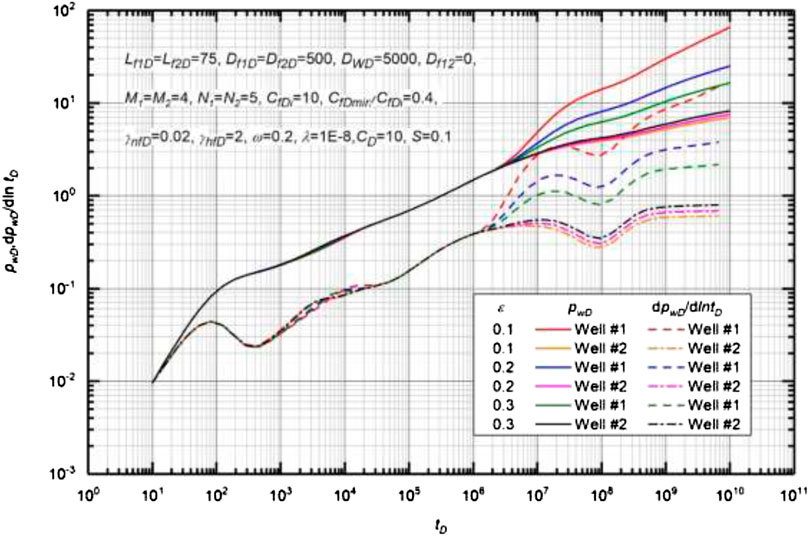
FIGURE 7. Effect of well rate ratio on the transient pressure for multi-well pad with multiple fractures (MWPMF).

Effect of Hydraulic Fractures Permeability Modulus

Figure 8 illustrates the effect of HF permeability modulus on type curves of MWPMF. Basic data used to generate the type curves are L_f1D = L_f2D = 75, D_f1D = D_f2D = 500, M₁ = M₂ = 4, N₁ = N₂ = 5, C_fDi = 10, C_fDmin/C_fDi = 0.4, γ_nfD = 0.02, ω = 0.2, λ = 1 × 10⁻⁸, ε = 0.2, C_D = 10, and S = 0.1. As illustrated in Figure 8, the HF permeability modulus is found to be one of the key factors affecting the “hump,” which only affects the flow in a hydraulic fracture. The slope of the hump becomes larger as the HF permeability modulus is increased (Yao et al., 2013). Certainly, the greater the HF permeability modulus is, the easier it approaches C_fDmin, and it is easier to move to the next regime (i.e., early radial flow regime). For an extreme case γ_hfD = 0, the early radial flow regime will be masked by the linear flow regime within HFs. This is because C_fD maintains a constant value and the linear flow lasts longer, and then it is more difficult for the early radial flow to occur.

FIGURE 8

FIGURE 8. Effect of HF permeability modulus on the transient pressure for MWPMF.

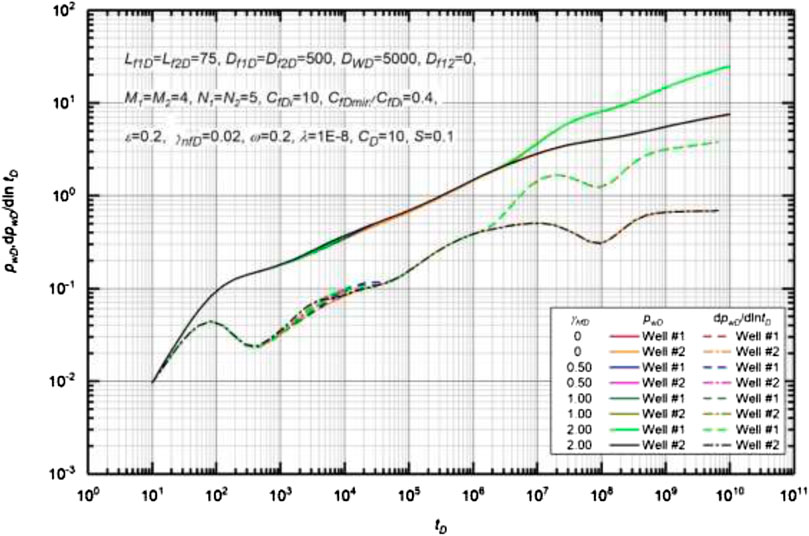
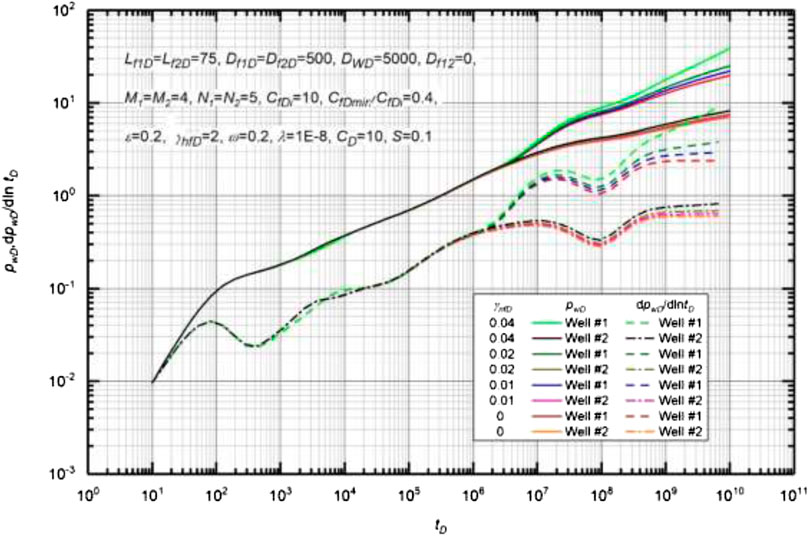
Effect of Natural Fracture Permeability Modulus

Figure 9 displays the effect of NF permeability modulus on type curves of MWPMF. Basic data used to generate the type curves are L_f1D = L_f2D = 75, D_f1D = D_f2D = 500, M₁ = M₂ = 4, N₁ = N₂ = 5, C_fDi = 10, C_fDmin/C_fDi = 0.4, γ_hfD = 2, ω = 0.2, λ = 1 × 10⁻⁸, ε = 0.2, C_D = 10, and S = 0.1. As can be seen in Fig. 9, a larger NF permeability modulus leads to a larger value of DPD and DPPD after the occurrence of multi-well pressure interference (Liu et al., 2018a; Xiao et al., 2018). Besides, the NF permeability modulus can distort flow regimes, and the distortion of pressure curves become severer as the γ_nfD is increased. For the case of γ_nfD = 0, the DPPD value in the late-time pseudo-radial flow regime is equal to 0.5. In the early regime of flow, the flow regime is independent of the NF permeability modulus before the multi-well pressure interference occurs.

FIGURE 9

FIGURE 9. Effect of the natural fracture permeability modulus on the transient pressure for MWPMF.

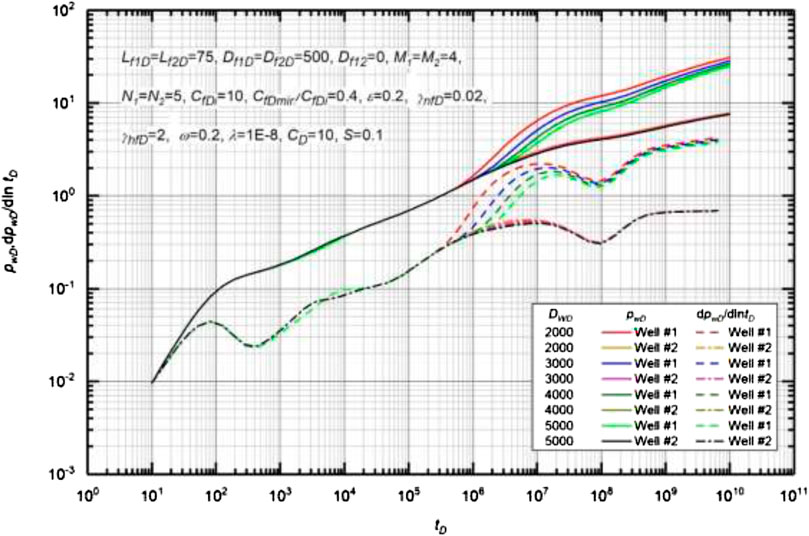
Effect of Hydraulic Fracture Spacings

Figure 10 presents the effect of HF spacing on type curves of MWPMF. Basic data used to generate the type curves are L_f1D = L_f2D = 75, M₁ = M₂ = 4, N₁ = N₂ = 5, C_fDi = 10, C_fDmin/C_fDi = 0.4, γ_nfD = 0.02, γ_hfD = 2, ω = 0.2, λ = 1 × 10⁻⁸, ε = 0.2, C_D = 10, and S = 0.1. Comparison of different type curves illustrates that the HF spacing affects the occurrence time and duration of the biradial flow regime, but has no effect on the distortion of the convection pattern. DPD and DPPD curves only shift from left to right or vice versa (the curve slope remains unchanged) (Liu et al., 2018a). A smaller D_fD leads to the earlier appearance of the biradial flow regime. After the disappearance of this flow regime, the pressure drop and pressure derivative curves overlap again under different well spacings.

FIGURE 10

FIGURE 10. Effect of HF spacing on the transient pressure for MWPMF.

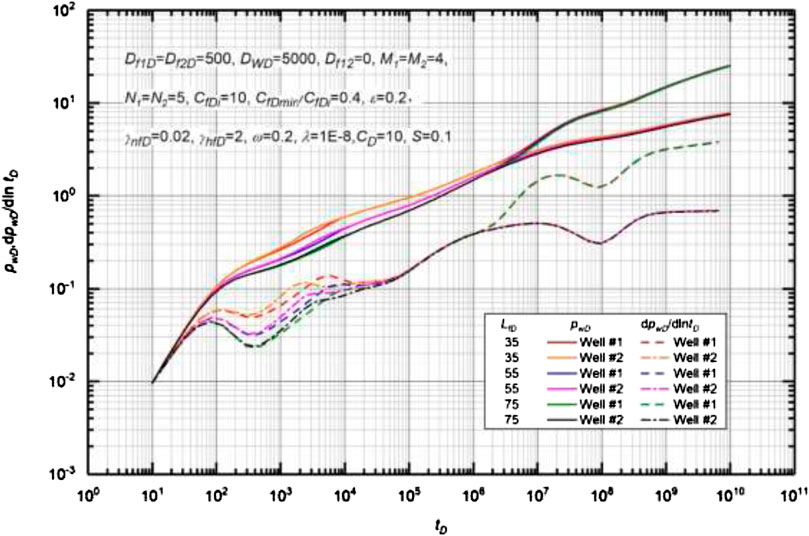
Effect of Hydraulic Fracture Length

Figure 11 plots the effect of HF length on type curves of MWPMF. Basic data used to generate the type curves are D_f1D = D_f2D = 500, M₁ = M₂ = 4, N₁ = N₂ = 5, C_fDi = 10, C_fDmin/C_fDi = 0.4, γ_nfD = 0.02, γ_hfD = 2, ω = 0.2, λ = 1 × 10⁻⁸, ε = 0.2, C_D = 10, and S = 0.1. It is shown that HF length only affects the early flow regimes, including the skin effect transition flow regime, the linear flow regime within HFs, and the early radial flow regime. As the HF length is decreased, pressure drop and pressure derivative curves are shifted upwards (Chen et al., 2016; 2Chen et al., 2017a; Cao et al., 2018). With the decrease of HF length, the duration of linear flow regime within HFs becomes short. Similar to the effect of HF spacing, after the completion of the early radial flow regime, the pressure drop and pressure derivative curves overlap again under different HF lengths.

FIGURE 11

FIGURE 11. Effect of HF length on the transient pressure for MWPMF.

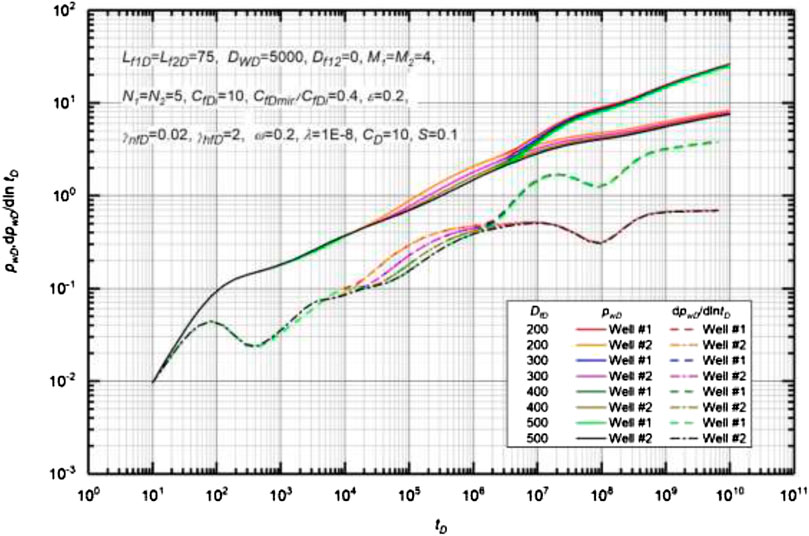
Effect of Well Spacing

Figure 12 depicts the effect of well spacing on type curves of MWPMF. Basic data used to generate the type curves are L_f1D = L_f2D = 75, D_f1D = D_f2D = 500, M₁ = M₂ = 4, N₁ = N₂ = 5, C_fDi = 10, C_fDmin/C_fDi = 0.4, γ_nfD = 0.02, γ_hfD = 2, ω = 0.2, λ = 1 × 10⁻⁸, ε = 0.2, C_D = 10, and S = 0.1. By observing whether the pressure derivative curves overlap, we can judge when the multi-well pressure interference occurs. As shown in Figure 12, well spacing affects flow regimes after multi-well pressure interference starts. Comparison of different type curves illustrates that a smaller D_wD leads to the earlier occurrence of multi-well pressure interference (Liu et al., 2018a; Xiao et al., 2018). It is worthwhile mentioning that well spacing also does not distort the shape of pressure drop and pressure derivative curves, and the curve is only shifted from left to right or vice versa (i.e., the curve slope remains unchanged).

FIGURE 12

FIGURE 12. Effect of well spacing on the transient pressure for MWPMF.

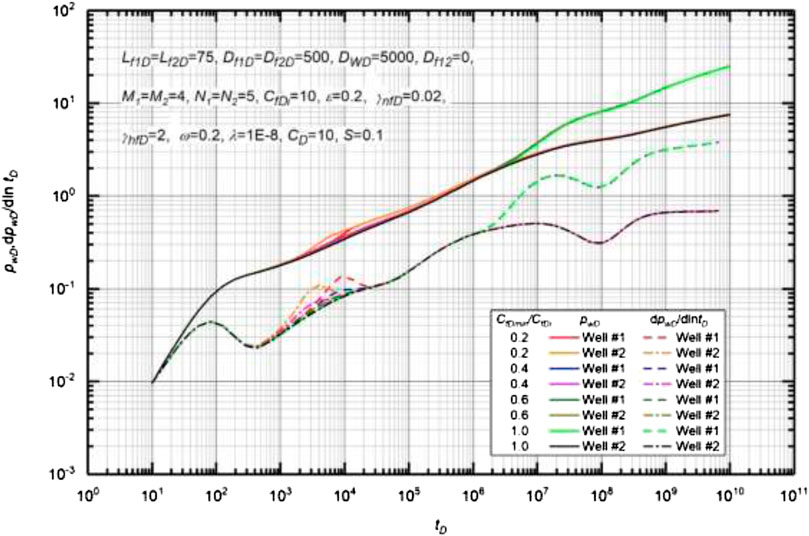
Effect of Minimum Fracture Conductivity

Figure 13 illustrates the effect of minimum fracture conductivity on type curves of MWPMF. Basic data used to generate the type curves are L_f1D = L_f2D = 75, D_f1D = D_f2D = 500, M₁ = M₂ = 4, N₁ = N₂ = 5, C_fDi = 10, γ_nfD = 0.02, γ_hfD = 2, ω = 0.2, λ = 1 × 10⁻⁸, ε = 0.2, C_D = 10, and S = 0.1. The higher the value of C_fDmin/C_fDi is, the stronger the effect of proppant in HFs will be, and the higher the fracture conductivity can be maintained when the effective pressure is increased. Similar to the effect of HF permeability modulus on the flow in a hydraulic fracture, C_fDmin/C_fDi is another key factor affecting the “hump,” whose slope becomes smaller as the minimum fracture conductivity is decreased. As can be seen in Figure 13, when the value of C_fDmin/C_fDi reaches 0.6, the hump basically disappears. This is because a higher C_fDmin/C_fDi means that the hydraulic fracture loses a small part of conductivity, and it is difficult to distinguish the difference among type curves.

FIGURE 13

FIGURE 13. Effect of minimum fracture conductivity on the transient pressure for MWPMF.

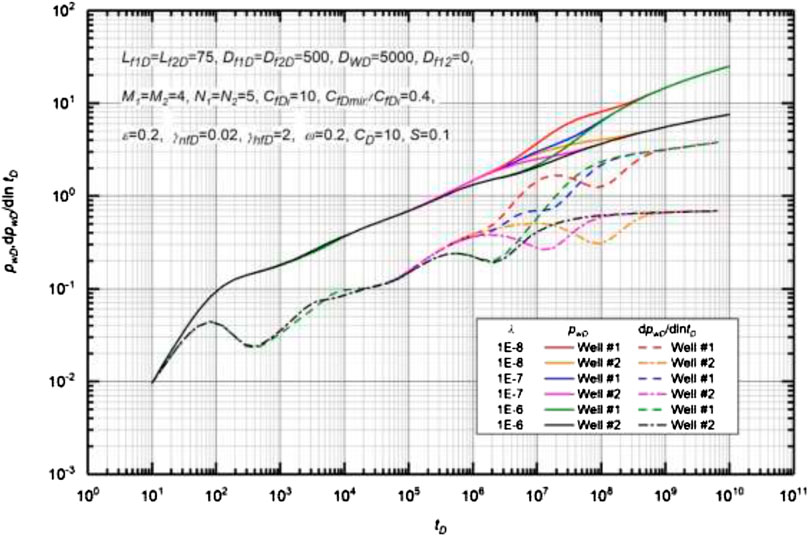
Effect of Crossflow Coefficient

Figure 14 reveals the effect of crossflow coefficient on type curves of MWPMF. Basic data used to generate the type curves are L_f1D = L_f2D = 75, D_f1D = D_f2D = 500, M₁ = M₂ = 4, N₁ = N₂ = 5, C_fDi = 10, C_fDmin/C_fDi = 0.4, γ_nfD = 0.02, γ_hfD = 2, ω = 0.2, λ = 1 × 10⁻⁸, ε = 0.2, C_D = 10, and S = 0.1. As described by Eq. 14a, with a larger λ, the magnitude of the difference between the NF permeability and the matrix permeability becomes smaller. This means that the ability of NFs to maintain production is weakened. Comparison of different type curves illustrates that the larger the λ is, the flow transfers from the matrix to the NFs easier and the “dip” comes earlier. Especially for an oil well with low production, it is more unlikely to have crossflow at a smaller λ (Liu et al., 2015; Li et al., 2017).

FIGURE 14

FIGURE 14. Effect of crossflow coefficient on the transient pressure for MWPMF.

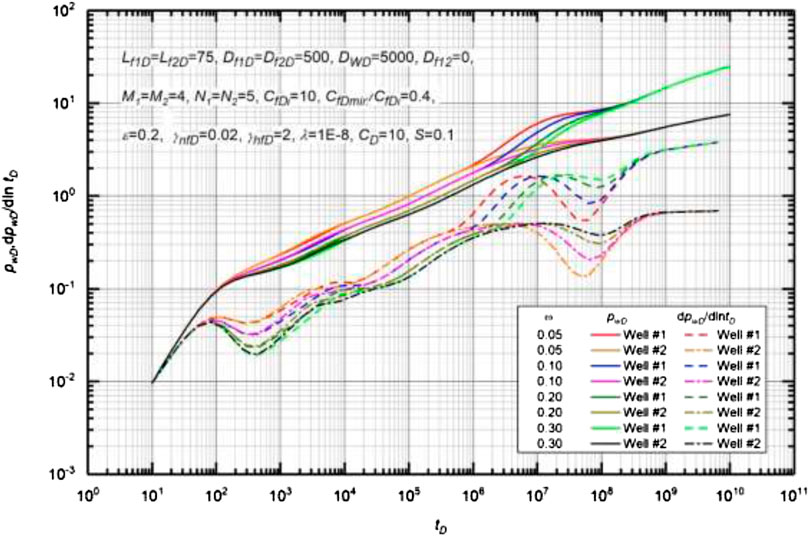
Effect of Storage Ratio

Figure 15 shows the effect of storage ratio on type curves of MWPMF. Basic data used to generate the type curves are L_f1D = L_f2D = 75, D_f1D = D_f2D = 500, M₁ = M₂ = 4, N₁ = N₂ = 5, C_fDi = 10, C_fDmin/C_fDi = 0.4, γ_nfD = 0.02, γ_hfD = 2, λ = 1 × 10⁻⁸, ε = 0.2, C_D = 10, and S = 0.1. As shown in Figure 15, storage ratio ω mainly determinates the duration and the depth of the second “dip” on the pressure derivative curve, while it also has a significant effect on the occurrence of multi-well pressure interference (Li et al., 2017; Jiang et al., 2019a). Comparison of different type curves illustrates that a smaller ω results in the earlier occurrence of the multi-well pressure interference with an increase in the duration of flow exchange. The slope of the second dip becomes larger with a decrease in the storage ratio.

FIGURE 15

FIGURE 15. Effect of storage ratio on the transient pressure for MWPMF.

Conclusions

In this paper, a new semianalytical model has been developed and validated to describe the flow behavior of a multi-well pad with multistage fractures in a naturally fractured reservoir, while various stress-sensitive effects in the NFs and HFs are examined. The main conclusions are summarized as follows:

(1) Type curves of a multi-well pad with multiple fractures are identified, and there may exhibit eight flow regimes: pure wellbore storage, skin effect transition flow, linear flow regime within HFs, early radial flow, biradial flow, transition flow, pseudo-steady diffusion, and the late-time pseudo-radial flow. In addition, changing the location of two wells in a multi-well pad may mask some flow regimes.

(2) Under the multi-well pad schemes, multi-well pressure interference is inevitable and will significantly distort the late-time flow regimes. It is found that the smaller the well-rate ratio is, the more distorted the curve will be. As the well spacing is decreased, the fracture length is increased, and thus the multi-well pressure interference occurs earlier.

(3) Stress-sensitive effects in the NFs indicate the permeability damage which occurs at intermediate times, resulting in an increasing pressure drop. Stress-sensitive effects in the HFs and minimum fracture conductivity only affect the flow regime in hydraulic fractures. The sensitivity analysis shows that the “hump” becomes stronger as the minimum fracture conductivity is decreased.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary materials, further inquiries can be directed to the corresponding author/s.

Author Contributions

ZM: Conceptualization, Methodology, Formal analysis, Writing ‐ original draft; HL: Methodology, Validation; XT: Revision; GL: Resources, Supervision; LW: Validation, Formal analysis; DY: Conceptualization, Supervision, Funding acquisition, Resources, Writing ‐ review & editing.

Funding

The authors are grateful to the State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation at the Southwest Petroleum University for their support of this work. The authors acknowledge a Natural Science Foundation of China (Grant No.: 51704246 and Grant No.: 51404282) for financial support. Also, the authors acknowledge a Discovery Grant and a Collaborative and Research Development (CRD) Grant awarded to D. Yang from the Natural Sciences and Engineering Research Council (NSERC) of Canada.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Glossary

B = volume formation factor, m³/m³
C_FD1 = dimensionless Well #1 fracture conductivity, fraction
C_FD2 = dimensionless Well #2 fracture conductivity, fraction
C_tnf = total compressibility, MPa⁻¹
h = reservoir thickness, m
h_hf = hydraulic fracture height, m
k_hf = hydraulic fracture permeability, D
k_nf = natural fracture permeability, D
k_nfi = initial natural fracture permeability, D
k_m = matrix permeability, D
k_hfmin = minimum hydraulic fracture permeability, D
L_H1 = horizontal length for Well #1, m
L_H2 = horizontal length for Well #2, m
L_f1 = Well #1 fracture half length, m
L_f2 = Well #2 fracture half length, m
M₁ = Well #1 fracture number, integer
M₂ = Well #2 fracture number, integer
N₁ = Well #1 discrete-fracture segments number, integer
N₂ = Well #2 discrete-fracture segments number, integer
p_nf = natural fracture pressure, MPa
p_hf = hydraulic fracture pressure, MPa
p_m = matrix pressure, MPa
p_i = reservoir initial pressure, MPa
q_Ni;1 = parameter defined in Eq. 8a
q_sc1 = Well #1 production rate, m³/d
q_sc2 = Well #2 production rate, m³/d
q_f = flow-rate strength from reservoir into HFs, m³/d
q_n = flow-rate strength within HFs, m³/d
r_w = wellbore radius, m
s = Laplace transformation variable
t = time, hour
w_hf = HF width, m
x_hf = reference length, m
x_e = reservoir length along x direction, m
y_e = reservoir length along y direction, m
α = shape factor, m⁻²
ω = storage ratio, fraction
λ = interporosity coefficient, fraction
γ_nf = NF permeability modulus, MPa⁻¹
γ_hf = HF permeability modulus, MPa⁻¹
ε = well-rate ratio, fraction
ρ = fluid density, kg/m³
µ = viscosity, cp
ϕ_m = matrix porosity, fraction

Subscripts

D = dimensionless
hf = hydraulic fracture
nf = natural fracture
m = matrix
i = initial condition

Superscript

- = Laplace transform

Appendix A: Derivation of Slab-Source Solution

A slab-source function can be obtained for the intersection of a slab-source in the x-direction and the y-direction (Zhang et al., 2014; Jiang et al., 2019a). Then, the instantaneous source function for a multi-well pad with stress-sensitive effect in both NFs and HFs can be expressed as follows,

$S\left(x,y,x_w,y_w,x_f,y_f,t\right)=VII\left(x,x_w,x_f,t\right)VII\left(y,y_w,y_f,t\right)(\mathrm{A1})$

Taking the Laplace transform, Eq. A1 can be written as follow,

$\overline{S}\left(x,y,x_w,y_w,x_f,y_f,s\right)={\left[\frac{h\left(s_0\right)}{g^{\prime }\left(s_0\right)}\right]}_{\left(1\right)}{\overline{S}}_p\left(y,y_w,y_f,s\right)+{\displaystyle \sum _{n=1}^{\infty }{\left[\frac{h\left(s_n\right)}{g^{\prime }\left(s_n\right)}\right]}_{\left(1\right)}{\overline{S}}_{p\left(n\right)}\left(y,y_w,y_f,{\alpha }_n,s\right)}(\mathrm{A2})$

where

${\overline{S}}_p\left(y,y_w,y_f,s\right)=\frac{2\sinh \left(y_f\sqrt{s/\chi }\right)}{\sqrt{s/\chi }}\frac{\cosh \left[\left(y_e-y\right)\sqrt{s/\chi }\right]cosh\left(y_w\sqrt{s/\chi }\right)}{\chi \sqrt{s/\chi }\sinh \left(y_e\sqrt{s/\chi }\right)}(\mathrm{A3})$

${\overline{S}}_{p\left(n\right)}\left(y,y_w,y_f,{\alpha }_n,s\right)=\frac{2\sinh \left(y_f\sqrt{s/\chi +{\alpha }_n}\right)}{s+{\alpha }_n\chi }\frac{\cosh \left[\left(y_e-y\right)\sqrt{s/\chi +{\alpha }_n}\right]cosh\left(y_w\sqrt{s/\chi +{\alpha }_n}\right)}{\sinh \left(y_e\sqrt{s/\chi +{\alpha }_n}\right)}(\mathrm{A4})$

${\alpha }_n={\left(n\pi /x_e\right)}^2(\mathrm{A5})$

where Eq. A2 can be rewritten as follow,

$\overline{S}\left(x,y,x_w,y_w,x_f,y_f,s\right)=\frac{2x_f}{x_e}\left[{\overline{S}}_p\left(y,y_w,y_f,s\right)+2{\displaystyle \sum _{n=1}^{\infty }{F}_n\left(x_f/x_e\right)}cos\frac{n\pi x_w}{x_e}cos\frac{n\pi x}{x_e}{\overline{S}}_{p\left(n\right)}\left(y,y_w,y_f,{\alpha }_n,s\right)\right](\mathrm{A6})$

$F_n\left(x_f/x_e\right)=\frac{\sin \left[\left(n\pi \right)\left(x_f/x_e\right)\right]}{\left(n\pi \right)\left(x_f/x_e\right)}(\mathrm{A7})$

Since the slab source is assumed, the source-shape-dependent rate in terms of withdrawal rate is

$\widehat{q}=\frac{q}{2y_{f}h}(\mathrm{A8})$

The pressure-rate-source function in the Laplace domain can be obtained through Eqs A6 and A8,

$\begin{array}{c}\Delta {\overline{p}}_{hf}\left(x,y,s\right)=\frac{1}{2\varphi C_t{y}_{f}h}\overline{q}\left(s\right)\overline{S}\left(x,y,x_w,y_w,x_f,y_f,s\right)\\ \begin{array}{ccc}& & \end{array}=\frac{\overline{q}\left(s\right)x_f}{\varphi C_t{x}_e{y}_{f}h}\left[{\overline{S}}_p\left(y,y_w,y_f,s\right)+2{\displaystyle \sum _{n=1}^{\infty }{F}_n\left(x_f/x_e\right)}cos\frac{n\pi x_w}{x_e}cos\frac{n\pi x}{x_e}{\overline{S}}_{p\left(n\right)}\left(y,y_w,y_f,{\alpha }_n,s\right)\right]\end{array}(\mathrm{A9})$

According to the aforementioned definitions of dimensionless variables, Eqs A2–A7 can be rewritten as follows,

${\overline{p}}_{hfD}\left(x_D,y_D,s_D\right)=\frac{\pi x_{fD}}{x_{eD}{y}_{fD}}{\overline{q}}_{fD}\left[\begin{array}{l}{\overline{S}}_p\left(y_D,y_{wD},y_{fD},s_D\right)+\\ 2{\displaystyle \sum _{n=1}^{\infty }{F}_n\left(x_{fD}/x_{eD}\right)}cos\frac{n\pi x_{wD}}{x_{eD}}cos\frac{n\pi x_D}{x_{eD}}{\overline{S}}_{p\left(n\right)}\left(y_D,y_{wD},y_{fD},{\alpha }_{nD},s_D\right)\end{array}\right](\mathrm{A10})$

where

${\overline{S}}_p\left(y_D,y_{wD},y_{fD},s_D\right)=\frac{2\sinh \left(y_{fD}\sqrt{s_D}\right)cosh\left[\left(y_{eD}-y_D\right)\right]cosh\left(y_{wD}\sqrt{s_D}\right)}{s_D\sinh \left(y_{eD}\sqrt{s_D}\right)}(\mathrm{A11})$

${\overline{S}}_{p\left(n\right)}\left(y_D,y_{wD},y_{fD},{\alpha }_{nD},s_D\right)=\frac{2\sinh \left(y_{fD}\sqrt{s_D+{\alpha }_{nD}}\right)cosh\left[\left(y_{eD}-y_D\right)\right]cosh\left(y_{wD}\sqrt{s_D+{\alpha }_{nD}}\right)}{\left(s_D+{\alpha }_{nD}\right)\sinh \left(y_{eD}\sqrt{s_D+{\alpha }_{nD}}\right)}(\mathrm{A12})$

$s_D=\frac{s}{\chi }{L}_r^2(\mathrm{A13})$

${\alpha }_{nD}={\left(n\pi /x_{eD}\right)}^2(\mathrm{A14})$

$F_n\left(x_{fD}/x_{eD}\right)=\frac{\sin \left[\left(n\pi \right)\left(x_{fD}/x_{eD}\right)\right]}{\left(n\pi \right)\left(x_{fD}/x_{eD}\right)}(\mathrm{A15})$

Then, the solution for multi-well pad schemes can be expressed as the follow:

${\overline{\eta }}_{nfD0}\left(x_D,y_D,s_D,u_D\right)=\frac{\pi x_{fD}}{x_{eD}{y}_{fD}}{\overline{q}}_f\left(s_D\right)\left[\begin{array}{l}{\overline{s}}_p\left(y_D,y_{wD},y_{fD},u_D\right)+\\ 2{\displaystyle \sum _{n=1}^{\infty }{F}_n\left(x_{fD}/x_{eD}\right)cos\frac{n\pi x_{wD}}{x_{eD}}\cos }\frac{n\pi x_D}{x_{eD}}{\overline{s}}_{p\left(n\right)}\left(y_D,y_{wD},y_{fD},{\alpha }_{nD},u_D\right)\end{array}\right](\mathrm{15a})$

$f\left(s_D\right)=\frac{\omega (1-\omega )s_D+\lambda }{(1-\omega )s_D+\lambda }(\mathrm{15b})$

$u_D=s_D\times f\left(s_D\right)(\mathrm{15c})$

Appendix B: Extension to Multiple Wells

A closed [2(2N₁ × M₁ + 2N₂ × M₂) + 2]-order matrix from the pressure-continuity condition can be obtained as,

$\text{A}\overrightarrow{\text{X}}=\overrightarrow{\text{B}}(22)$

where matrix A is a coefficient matrix of dimension [2(2N₁ × M₁ + 2N₂ × M₂)+2], $\overrightarrow{\text{X}}$ is the unknown vector, and $\overrightarrow{\text{B}}$ is the known vector. The matrix and vectors are further expanded as the submatrix,

$A=\left[\begin{array}{l}{{\displaystyle A}}_{\mathrm{1,1}}\mathrm{.}{{\displaystyle A}}_{1,mn}\mathrm{.}{{\displaystyle A}}_{\mathrm{1,2}mn}{{\displaystyle A}}_{\mathrm{1,2}mn+1}{{\displaystyle A}}_{\mathrm{1,2}mn+2}\\ \mathrm{.}\\ {{\displaystyle A}}_{v,1}\mathrm{.}{{\displaystyle A}}_{v,mn}\mathrm{.}{{\displaystyle A}}_{v,2mn}{{\displaystyle A}}_{v,2mn+1}{{\displaystyle A}}_{v,2mn+2}\\ \mathrm{.}\\ {{\displaystyle A}}_{2mn+\mathrm{1,1}}\mathrm{.}{{\displaystyle A}}_{2mn+1,mn}\mathrm{.}{{\displaystyle A}}_{2mn+\mathrm{1,2}mn}{{\displaystyle A}}_{2mn+\mathrm{1,2}mn+1}{{\displaystyle A}}_{2mn+\mathrm{1,2}mn+2}\\ {{\displaystyle A}}_{2mn+\mathrm{2,1}}\mathrm{.}{{\displaystyle A}}_{2mn+2,mn}\mathrm{.}{{\displaystyle A}}_{2mn+\mathrm{2,2}mn}{{\displaystyle A}}_{2mn+\mathrm{2,2}mn+1}{{\displaystyle A}}_{2mn+\mathrm{2,2}mn+2}\end{array}\right](\mathrm{B1})$

where mn means 2N₁ × M₁ + 2N₂ × M₂, and

${{\displaystyle A}}_{v,w}=\{\begin{array}{l}{{\displaystyle \left(-1,\cdot \cdot \cdot -1,\cdot \cdot \cdot -1\right)}}^{\text{T}}v\le 2M_1{N}_1,w=2mn+1\\ {{\displaystyle \left(0,\cdot \cdot \cdot 0,\cdot \cdot \cdot 0\right)}}^{\text{T}}2M_1{N}_1<v\le 2M_1{N}_1+2M_2{N}_2,w=2mn+1\\ {{\displaystyle \left(-1,\cdot \cdot \cdot -1,\cdot \cdot \cdot -1\right)}}^{\text{T}}2M_1{N}_1<v\le 2M_1{N}_1+2M_2{N}_2,w=2mn+2\\ {{\displaystyle \left(0,\cdot \cdot \cdot 0,\cdot \cdot \cdot 0\right)}}^{\text{T}}v\le 2M_1{N}_1,w=2mn+2\\ 1v=2mn+1,w=N_1,N_1+\mathrm{1,2}{N}_1,2N_1+1\cdot \cdot \cdot M_1{N}_1,M_1{N}_1+1\\ 1v=2mn+2,w-2M_1{N}_1=N_2,N_2+\mathrm{1,2}{N}_2,2N_2+1\cdot \cdot \cdot M_2{N}_2,M_2{N}_2+1\end{array}(\mathrm{B2})$

The submatrix A_v,w can be further written in Eq. B2 if v and w do not meet the previously discussed conditions:

$A_{v,w}=\left[\begin{array}{l}{{\displaystyle a}}_{\mathrm{1,1}}\mathrm{.}{{\displaystyle a}}_{1,j}\mathrm{.}{{\displaystyle a}}_{\mathrm{1,2}mn}\\ \mathrm{.}\\ {{\displaystyle a}}_{i,1}\mathrm{.}{{\displaystyle a}}_{i,j}\mathrm{.}{{\displaystyle a}}_{i,2mn}\\ \mathrm{.}\\ {{\displaystyle a}}_{2mn,1}\mathrm{.}{{\displaystyle a}}_{2mn,j}\mathrm{.}{{\displaystyle a}}_{2mn,2mn}\end{array}\right](\mathrm{B3})$

The element of a_{i, j} in submatrix A_v,w is given as

${{\displaystyle a}}_{i,j}=\{\begin{array}{l}\frac{\pi \Delta x_D}{4C_{fD}{\delta }_{v,j}}j=iv\le mn,w\le mn\\ \frac{2\pi \Delta x_D}{C_{fD}{\delta }_{v,j}}j<i\left(k-1\right)N_1+1\le v\left(w\right)\le k{N}_1,\left(k=\mathrm{1,3,5}\cdot \cdot \cdot mn-1\right)\\ 0j>i\left(k-1\right)N_1+1\le v\left(w\right)\le k{N}_1,\left(k=\mathrm{1,3,5}\cdot \cdot \cdot mn-1\right)\\ \frac{2\pi \Delta x_D}{C_{fD}{\delta }_{v,j}}j>i\left(k-1\right)N_1+1\le v\left(w\right)\le k{N}_1,\left(k=\mathrm{2,4,6}\cdot \cdot \cdot mn\right)\\ 0j<i\left(k-1\right)N_1+1\le v\left(w\right)\le k{N}_1,\left(k=\mathrm{2,4,6}\cdot \cdot \cdot mn\right)\\ 0\left|i-j\right|>N_1\end{array}(\mathrm{B4})$

${{\displaystyle a}}_{i,j}={{\displaystyle S}}_{v,i}^{w-mn,j}mn\text{<}v\le 2mn,w\le mn(\mathrm{B5})$

where ${{\displaystyle S}}_{v,i}^{w-mn,j}$ can be calculated by Eq. 15a,

${{\displaystyle a}}_{i,j}=\{\begin{array}{l}-1j=i\\ 1j=i+1mn<v\le 2mn,w\le 2mn\\ \text{0 }j\ne i,j\ne i+1\end{array}(\mathrm{B6})$

${{\displaystyle a}}_{i,j}=\{\begin{array}{l}\Delta {\text{x}}_{\text{D}}\text{/}2j=imn<v\le 2mn,mn<w\le 2mn\\ \text{0 }j\ne i,j\ne i+1\end{array}(\mathrm{B7})$

The vectors of $\overrightarrow{\text{X}}$ and $\overrightarrow{\text{B}}$ can be expressed as

$\overrightarrow{\text{X}}=\left({\overline{q}}_{NDv,1},{\overline{q}}_{NDv,2},\cdot \cdot \cdot {\overline{q}}_{NDv,mn},{\overline{q}}_{fDv,1},{\overline{q}}_{fDv,2},\cdot \cdot \cdot {\overline{q}}_{fDv,mn},{\overline{p}}_{wD1},{\overline{p}}_{wD2}\right)(\mathrm{B8})$

$\overrightarrow{\text{B}}=\left(\underset{2mn}{\underbrace{\text{0},\text{0},\text{0}\cdot \cdot \cdot \text{0}}},\frac{\epsilon }{2s_D},\frac{1-\epsilon }{2s_D}\right)(\mathrm{B9})$

The aforementioned equations show the coupled solution for the nonlinear systems of multi-well pad with two wells. It is worthwhile mentioning that one of the advantages of the newly developed model is that it can be extended to multiple wells.

Here, three horizontal wells are used as an example to demonstrate such an extension. A closed [2(2N₁ × M₁ + 2N₂ × M₂ + 2N₃ × M₃) + 3]-order matrix from the pressure-continuity condition can then be obtained,

$\text{A}\overrightarrow{\text{X}}=\overrightarrow{\text{B}}$

where matrix A is a coefficient matrix of dimension [2(2N₁ × M₁ + 2N₂ × M₂ + 2N₃ × M₃) + 3], $\overrightarrow{\text{X}}$ is the unknown vector, and $\overrightarrow{\text{B}}$ is the known vector. The matrix and vectors are further expanded as the submatrix,

$A=\left[\begin{array}{l}{{\displaystyle A}}_{\mathrm{1,1}}\mathrm{.}{{\displaystyle A}}_{1,xy}\mathrm{.}{{\displaystyle A}}_{\mathrm{1,2}xy}{{\displaystyle A}}_{\mathrm{1,2}xy+1}{{\displaystyle A}}_{\mathrm{1,2}xy+2}{{\displaystyle A}}_{\mathrm{1,2}xy+3}\\ \mathrm{.}\\ {{\displaystyle A}}_{v,1}\mathrm{.}{{\displaystyle A}}_{v,xy}\mathrm{.}{{\displaystyle A}}_{v,2xy}{{\displaystyle A}}_{v,2xy+1}{{\displaystyle A}}_{v,2xy+2}{{\displaystyle A}}_{v,2xy+3}\\ \mathrm{.}\\ {{\displaystyle A}}_{2xy+\mathrm{1,1}}\mathrm{.}{{\displaystyle A}}_{2xy+1,xy}\mathrm{.}{{\displaystyle A}}_{2xy+\mathrm{1,2}xy}{{\displaystyle A}}_{2xy+\mathrm{1,2}xy+1}{{\displaystyle A}}_{2xy+\mathrm{1,2}xy+2}{{\displaystyle A}}_{2xy+\mathrm{1,2}xy+3}\\ {{\displaystyle A}}_{2xy+\mathrm{2,1}}\mathrm{.}{{\displaystyle A}}_{2xy+2,xy}\mathrm{.}{{\displaystyle A}}_{2xy+\mathrm{2,2}xy}{{\displaystyle A}}_{2xy+\mathrm{2,2}xy+1}{{\displaystyle A}}_{2xy+\mathrm{2,2}xy+2}{{\displaystyle A}}_{2xy+\mathrm{2,2}xy+3}\\ {{\displaystyle A}}_{2xy+\mathrm{3,1}}\mathrm{.}{{\displaystyle A}}_{2xy+3,xy}\mathrm{.}{{\displaystyle A}}_{2xy+\mathrm{3,2}xy}{{\displaystyle A}}_{2xy+\mathrm{3,2}xy+1}{{\displaystyle A}}_{2xy+\mathrm{3,2}xy+2}{{\displaystyle A}}_{2xy+\mathrm{3,2}xy+3}\end{array}\right](\mathrm{B10})$

where xy means 2N₁ × M₁ + 2N₂ × M₂ + 2N₃ × M₃, and

${{\displaystyle A}}_{v,w}=\{\begin{array}{l}{{\displaystyle \left(-1,\cdot \cdot \cdot -1,\cdot \cdot \cdot -1\right)}}^{\text{T}}v\le 2M_1{N}_1,w=2xy+1\\ {{\displaystyle \left(0,\cdot \cdot \cdot 0,\cdot \cdot \cdot 0\right)}}^{\text{T}}2M_1{N}_1<v\le xy,w=2xy+1\\ {{\displaystyle \left(-1,\cdot \cdot \cdot -1,\cdot \cdot \cdot -1\right)}}^{\text{T}}2M_1{N}_1<v\le 2M_1{N}_1+2M_2{N}_2,w=2xy+2\\ {{\displaystyle \left(0,\cdot \cdot \cdot 0,\cdot \cdot \cdot 0\right)}}^{\text{T}}v\le 2M_1{N}_1,w=2xy+2\\ {{\displaystyle \left(0,\cdot \cdot \cdot 0,\cdot \cdot \cdot 0\right)}}^{\text{T}}v>2M_1{N}_1+2M_2{N}_2,w=2xy+2\\ {{\displaystyle \left(-1,\cdot \cdot \cdot -1,\cdot \cdot \cdot -1\right)}}^{\text{T}}2M_1{N}_1+2M_2{N}_2\text{<}v\le xy,w=2xy+3\\ {{\displaystyle \left(0,\cdot \cdot \cdot 0,\cdot \cdot \cdot 0\right)}}^{\text{T}}v\le 2M_1{N}_1+2M_2{N}_2,w=2xy+3\\ 1v=2mn+1,w=N_1,N_1+\mathrm{1,2}{N}_1,2N_1+1\cdot \cdot \cdot M_1{N}_1,M_1{N}_1+1\\ 1v=2mn+2,w-2M_1{N}_1=N_2,N_2+\mathrm{1,2}{N}_2,2N_2+1\cdot \cdot \cdot M_2{N}_2,M_2{N}_2+1\\ 1v=2mn+3,w-2M_1{N}_1-2M_2{N}_2=N_3,N_3+\mathrm{1,2}{N}_3,2N_3+1\cdot \cdot \cdot M_3{N}_3,M_3{N}_3+1\end{array}(\mathrm{B11})$

The submatrix A_v,w can be further written in Eq. B2 if v and w do not meet the previously discussed conditions:

$A_{v,w}=\left[\begin{array}{l}{{\displaystyle a}}_{\mathrm{1,1}}\mathrm{.}{{\displaystyle a}}_{1,j}\mathrm{.}{{\displaystyle a}}_{\mathrm{1,2}xy}\\ \mathrm{.}\\ {{\displaystyle a}}_{i,1}\mathrm{.}{{\displaystyle a}}_{i,j}\mathrm{.}{{\displaystyle a}}_{i,2xy}\\ \mathrm{.}\\ {{\displaystyle a}}_{2xy,1}\mathrm{.}{{\displaystyle a}}_{2xy,j}\mathrm{.}{{\displaystyle a}}_{2xy,2xy}\end{array}\right](\mathrm{B12})$

The element of a_{i, j} in submatrix A_v,w is given as

${{\displaystyle a}}_{i,j}=\{\begin{array}{l}\frac{\pi \Delta x_D}{4C_{fD}{\delta }_{v,j}}j=iv\le xy,w\le xy\\ \frac{2\pi \Delta x_D}{C_{fD}{\delta }_{v,j}}j<i\left(k-1\right)N_1+1\le v\left(w\right)\le k{N}_1,\left(k=\mathrm{1,3,5}\cdot \cdot \cdot xy-1\right)\\ 0j>i\left(k-1\right)N_1+1\le v\left(w\right)\le k{N}_1,\left(k=\mathrm{1,3,5}\cdot \cdot \cdot xy-1\right)\\ \frac{2\pi \Delta x_D}{C_{fD}{\delta }_{v,j}}j>i\left(k-1\right)N_1+1\le v\left(w\right)\le k{N}_1,\left(k=\mathrm{2,4,6}\cdot \cdot \cdot xy\right)\\ 0j<i\left(k-1\right)N_1+1\le v\left(w\right)\le k{N}_1,\left(k=\mathrm{2,4,6}\cdot \cdot \cdot xy\right)\\ 0\left|i-j\right|>N_1\end{array}(\mathrm{B13})$

${{\displaystyle a}}_{i,j}={{\displaystyle S}}_{v,i}^{w-xy,j}\text{ xy<}v\le 2\text{xy},w\le xy(\mathrm{B14})$

where ${{\displaystyle S}}_{v,i}^{w-xy,j}$ can be calculated by Eq. 15a,

${{\displaystyle a}}_{i,j}=\{\begin{array}{l}-1j=i\\ 1j=i+1\text{ xy}<v\le 2xy,w\le 2xy\\ \text{0 }j\ne i,j\ne i+1\end{array}(\mathrm{B15})$

${{\displaystyle a}}_{i,j}=\{\begin{array}{l}\Delta {\text{x}}_{\text{D}}\text{/}2j=i\text{ xy}<v\le 2xy,xy<w\le 2xy\\ \text{0 }j\ne i,j\ne i+1\end{array}(\mathrm{B16})$

The vectors of $\overrightarrow{\text{X}}$ and $\overrightarrow{\text{B}}$ can be expressed as

$\overrightarrow{\text{X}}=\left({\overline{q}}_{NDv,1},{\overline{q}}_{NDv,2},\cdot \cdot \cdot {\overline{q}}_{NDv,xy},{\overline{q}}_{fDv,1},{\overline{q}}_{fDv,2},\cdot \cdot \cdot {\overline{q}}_{fDv,xy},{\overline{q}}_{wD1},{\overline{p}}_{wD2},{\overline{p}}_{wD3}\right)(\mathrm{B17})$

$\overrightarrow{\text{B}}=\left(\underset{2xy}{\underbrace{\text{0},\text{0},\text{0}\cdot \cdot \cdot \text{0}}},\frac{{\epsilon }_1}{2s_D},\frac{{\epsilon }_2}{2s_D},\frac{1-{\epsilon }_1-{\epsilon }_2}{2s_D}\right)(\mathrm{B18})$

References

Amjed, H., Mohamed, M., Abdulaziz, A., Mustafa, B., Salaheldin, E., Mohammed, B., et al. (2019). Gas condensate treatment: a critical review of materials, methods, field applications, and new solutions. J. Petrol. Sci. Eng. 177, 602–613. doi:10.1016/j.petrol.2019.02.089

CrossRef Full Text | Google Scholar

Cao, L., Lu, L., Li, X., Wang, H., He, W., Xu, B., et al. (2018). Transient model analysis of gas flow behavior for a multi-fractured horizontal well incorporating stress-sensitive permeability. J. Pet. Explor. Prod. Technol. 9 (2), 855–867. doi:10.1007/s13202-018-0555-z

CrossRef Full Text | Google Scholar

Chen, S., Li, H., and Zhang, Q. (2008). A New technique for production prediction in stress-sensitive reservoirs. J. Can. Petrol. Technol. 47 (3), 49–54. doi:10.2118/08-03-49

CrossRef Full Text | Google Scholar

Chen, Z., Liao, X., Zhao, X., Lv, S., and Zhu, L. (2016). A semianalytical approach for obtaining type curves of multiple-fractured horizontal wells with secondary-fracture networks. SPE J. 21 (2), 538–549. doi:10.2118/178913-pa

CrossRef Full Text | Google Scholar

Chen, Z., Liao, X., Zhao, X., Lyu, S., and Zhu, L. (2017a). A comprehensive productivity equation for multiple fractured vertical wells with non-linear effects under steady-state flow. J. Petrol. Sci. Eng. 149, 9–24. doi:10.1016/j.petrol.2016.09.050

CrossRef Full Text | Google Scholar

Chen, Z., Liao, X., Zhao, X., Dou, X., Zhu, L., and Sanbo, L. (2017b). A finite-conductivity horizontal-well model for pressure-transient analysis in multiple-fractured horizontal wells. SPE J. 22 (4), 1112–1122. doi:10.2118/177230-pa

CrossRef Full Text | Google Scholar

Chen, Y., Ma, G., Jin, Y., Wang, H., and Wang, Y. (2019). Productivity evaluation of unconventional reservoir development with three-dimensional fracture networks. Fuel 244, 304–313. doi:10.1016/j.fuel.2019.01.188

CrossRef Full Text | Google Scholar

Cinco-Ley, H., and Meng, H. (1988). “Pressure transient analysis of wells with finite conductivity vertical fractures in double porosity reservoirs,” in SPE annual technical conference and exhibition, Houston, TX, October 2–5, 1988, Paper SPE-18172-MS.

Google Scholar

Cinco-Ley, H., and Samaniego, -V., F. (1981). Transient pressure analysis for fractured wells. J. Petrol. Technol. 33 (9), 1749–1766. doi:10.2118/7490-pa

CrossRef Full Text | Google Scholar

Cipolla, C. L., Lolon, E. P., and Erdle, J. C. (2010). Modeling well performance in shale-gas reservoirs. SPE Reservoir Eval. Eng. 13 (4), 638–653. doi:10.2118/125530-pa

CrossRef Full Text | Google Scholar

Cipolla, C. L., Fitzpatrick, T., Williams, M. J., and Ganguly, U. K. (2011). “Seismic-to-simulation for unconventional reservoir development,” in SPE reservoir characterization and simulation conference and exhibition, Abu Dhabi, UAE, October 9–11, 2011, Paper SPE-146876-MS.

Google Scholar

Feng, Q., Xia, T., Wang, S., and Singh, H. (2017). Pressure transient behavior of horizontal well with time-dependent fracture conductivity in tight oil reservoirs. Geofluids 2017, 5279792. doi:10.1155/2017/5279792

CrossRef Full Text | Google Scholar

Gao, G., Zhang, W.-W., Ma, G.-F., Chen, G., Li, T., Hu, L.-Z., et al. (2018). Mineral composition and organic geochemistry of the lower cretaceous Xiagou formation source rock from the Qingxi Sag, Jiuquan Basin, Northwest China. Petrol. Sci. 15, 51–67. doi:10.1007/s12182-017-0213-y

CrossRef Full Text | Google Scholar

Chen, H., Pooladi-Darvish, M., and Atabay, S. (2009). Shape factor in the drawdown solution for well testing of dual-porosity systems. Adv. Water Resour. 32 (11), 1652–1663. doi:10.1016/j.advwatres.2009.08.006

CrossRef Full Text | Google Scholar

Jalali, Y., and Ershaghi, I. (1987). “Pressure transient analysis of heterogeneous naturally fractured reservoirs,” in SPE California regional meeting, Ventura, CA, April 8–10, 1987, Paper SPE-16341-MS.

Google Scholar

Jia, P., Cheng, L., Huang, S., and Wu, Y. (2016). A semi-analytical model for the flow behavior of naturally fractured formations with multi-scale fracture networks. J. Hydrol. 537, 208–220. doi:10.1016/j.jhydrol.2016.03.022

CrossRef Full Text | Google Scholar

Jia, P., Cheng, L., Huang, S., Xu, Z., Xue, Y., Cao, R., et al. (2017). A comprehensive model combining Laplace-transform finite-difference and boundary-element method for the flow behavior of a two-zone system with discrete fracture network. J. Hydrol. 551, 453–469. doi:10.1016/j.jhydrol.2017.06.022

CrossRef Full Text | Google Scholar

Jia, C. (2017). Breakthrough and significance of unconventional oil and gas to classical petroleum geology theory. Petrol. Explor. Dev. 44 (1), 1–10. doi:10.1016/s1876-3804(17)30002-2

CrossRef Full Text | Google Scholar

Jiang, L., Liu, T., and Yang, D. (2019a). Effect of stress-sensitive fracture conductivity on transient pressure behavior for a horizontal well with multistage fractures. SPE J. 24 (3), 1342–1363. doi:10.2118/194509-pa

CrossRef Full Text | Google Scholar

Jiang, L., Liu, T., and Yang, D. (2019b). A semianalytical model for predicting transient pressure behavior of a hydraulically fractured horizontal well in a naturally fractured reservoir with non-darcy flow and stress-sensitive permeability effects. SPE J. 24 (3), 1322–1341. doi:10.2118/194501-pa

CrossRef Full Text | Google Scholar

Jiang, L., Liu, J., Liu, T., and Yang, D. (2020a). A semianalytical model for transient pressure analysis of a horizontal well with non-uniform fracture geometry and shape-dependent conductivity in tight formations. J. Petrol. Sci. Eng. 195, 107860.

Jiang, L., Liu, J., Liu, T., and Yang, D. (2020b). Semi-analytical modeling of transient pressure behaviour for a fractured vertical well with hydraulic/natural fracture networks by considering stress-sensitive effect. J. Nat. Gas Sci. Eng. 82, 103477.

Jiang, L., Liu, J., Liu, T., and Yang, D. (2020c). Semi-analytical modeling of transient rate behaviour of a horizontal well with multistage fractures in tight formations considering stress-sensitivity effect. J. Nat. Gas Sci. Eng. 82, 103461.

Juanes, R., Samper, J., and Molinero, J. (2002). A general and efficient formulation of fractures and boundary conditions in the finite element method. Int. J. Numer. Methods Eng. 54, 1751–1774. doi:10.1002/nme.491

CrossRef Full Text | Google Scholar

Kazemi, H. (1969). Pressure transient analysis of naturally fractured reservoirs with uniform fracture distribution. SPE J. 9 (4), 451–462. doi:10.2118/2156-a

CrossRef Full Text | Google Scholar

Li, X., Cao, L., Luo, C., Zhang, B., Zhang, J., and Tan, X. (2017). Characteristics of transient production rate performance of horizontal well in fractured tight gas reservoirs with stress-sensitivity effect. J. Petrol. Sci. Eng. 158, 92–106. doi:10.1016/j.petrol.2017.08.041

CrossRef Full Text | Google Scholar

Liu, M., Xiao, C., Wang, Y., Li, Z., Zhang, Y., Chen, S., et al. (2015). Sensitivity analysis of geometry for multi-stage fractured horizontal wells with consideration of finite-conductivity fractures in shale gas reservoirs. J. Nat. Gas Sci. Eng. 22, 182–195. doi:10.1016/j.jngse.2014.11.027

CrossRef Full Text | Google Scholar

Liu, G., Meng, Z., Cui, Y., Wang, L., Liang, C., and Yang, S. (2018a). A semi-analytical methodology for multiwell productivity index of well-industry-production-scheme in tight oil reservoirs. Energies 11 (5), 1054. doi:10.3390/en11051054

CrossRef Full Text | Google Scholar

Liu, G., Bai, Y., Gu, D., Lu, Y., and Yang, D. (2018b). Determination of static and dynamic characteristics of microscopic pore-throat structure in a tight oil-bearing sandstone formation. AAPG (Am. Assoc. Pet. Geol.) Bull. 102(9), 1867–1892. doi:10.1306/0108181613217061

CrossRef Full Text | Google Scholar

Liu, G., Meng, Z., Luo, D., Wang, J., Gu, D., and Yang, D. (2020a). Experimental evaluation of interlayer interference during commingled production in a tight sandstone gas reservoir with multi-pressure systems. Fuel 262, 116557. doi:10.1016/j.fuel.2019.116557

CrossRef Full Text | Google Scholar

Liu, G., Yin, H., Lan, Y., Fei, S., and Yang, D. (2020b). Experimental determination of dynamic pore-throat structure characteristics in a tight gas sandstone formation with consideration of effective stress. Mar. Petrol. Geol. 113, 104170. doi:10.1016/j.marpetgeo.2019.104170

CrossRef Full Text | Google Scholar

Liu, J., Jiang, L., Liu, T., and Yang, D. (2020c). Modeling tracer flowback behaviour for a fractured vertical well in a tight formation by coupling fluid flow and geomechanical dynamics. J. Nat. Gas Sci. Eng. 84, 103656.

Manchanda, R., and Sharma, M. M. (2013). “Time-delayed fracturing: a new strategy in multi-stage, multi-well pad fracturing,” in the SPE annual technical conference and exhibition, New Orleans, LA, September 30-October 2, 2013, Paper SPE-166489-MS.

Google Scholar

Meng, Z., Yang, S., Wang, L., Zou, J., Jiang, Y., Liang, C., et al. (2017). CO₂ storage capacity for multi-well pads scheme in depleted shale gas reservoirs. Energies 10 (11), 1724. doi:10.3390/en10111724

CrossRef Full Text | Google Scholar

Meyer, B. R., and Bazan, L. W. (2011). “A discrete fracture network model for hydraulically induced fractures-theory, parametric and case studies,” in SPE hydraulic fracturing technology conference, Woodlands, TX, January 24–26, 2011, Paper SPE-140514-MS.

Google Scholar

Miller, B. A., Paneitz, J. M., Yakeley, S., and Evans, K. A. (2008). “Unlocking tight oil: selective multistage fracturing in the Bakken shale,” in SPE annual technical conference and exhibition, Denver, CA, September 21–24, 2008, Paper SPE-116105-MS.

Google Scholar

Montgomery, C. T., and Steanson, R. E. (1985). Proppant selection: the key to successful fracture stimulation. J. Petrol. Technol. 37 (12), 2163–2172. doi:10.2118/12616-pa

CrossRef Full Text | Google Scholar

Morteza, D., Hassan, H., and Chen, Z. (2018). Semi-analytical solution for pressure transient analysis of a hydraulically fractured vertical well in a bounded dual-porosity reservoir. J. Hydrol. 565, 289–301. doi:10.1016/j.jhydrol.2018.08.020

CrossRef Full Text | Google Scholar

Noorishad, J., Ayatollahi, M. S., and Witherspoon, P. A. (1982). A finite-element method for coupled stress and fluid flow analysis in fractured rock masses. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 19, 185–193. doi:10.1016/0148-9062(82)90888-9

CrossRef Full Text | Google Scholar

Ozkan, E., Brown, M., Raghavan, R., and Kazemi, H. (2009). “Comparison of fractured horizontal-well performance in conventional and unconventional reservoirs,” in SPE Western regional meeting, San Jose, CA, March 24–26, 2009, Paper SPE-121290-MS.

Google Scholar

Ozkan, E., Brown, M. L., Raghavan, R., and Kazemi, H. (2011). Comparison of fractured-horizontal-well performance in tight sand and shale reservoirs. SPE Reservoir Eval. Eng. 14 (2), 248–259. doi:10.2118/121290-pa

CrossRef Full Text | Google Scholar

Pedrosa, O. A. (1986). “Pressure transient response in stress-sensitive formations,” in SPE California regional meeting, Oakland, CA, April 2–4, 1986, Paper SPE-15115-MS.

Google Scholar

Ren, Z., Wu, X., W., Liu, D., Rui, R., Wei, G., Chen, Z., et al. (2016). Semi-analytical model of the transient pressure behavior of complex fracture networks in tight oil reservoirs. J. Nat. Gas Sci. Eng. 35, 497–508. doi:10.1016/j.jngse.2016.09.006

CrossRef Full Text | Google Scholar

Rogers, S., Elmo, D., Dunphy, R., and Bearinger, D. (2010). “Understanding hydraulic fracture geometry and interactions in the horn river basin through DFN and numerical modeling,” in SPE Canadian unconventional resources and international Petroleum conference, Calgary, AB, October 19–21, 2010, Paper SPE-137488-MS.

Google Scholar

Schmoker, J. W. (2002). Resource-assessment perspectives for unconventional gas systems. AAPG (Am. Assoc. Pet. Geol.) Bull. 86 (11), 1993–1999. doi:10.1306/61EEDDDC-173E-11D7-8645000102C1865D

CrossRef Full Text | Google Scholar

Song, C., and Yang, D. (2017). Experimental and numerical evaluation of CO₂ huff-n-puff processes in Bakken formation. Fuel 190 (4), 145–162. doi:10.1016/j.fuel.2016.11.041

CrossRef Full Text | Google Scholar

Song, Y., Li, Z., Jiang, L., and Hong, F. (2015). The concept and the accumulation characteristics of unconventional hydrocarbon resources. Petrol. Sci. 12 (4), 563–572. doi:10.1007/s12182-015-0060-7

CrossRef Full Text | Google Scholar

Stalgorova, E., and Mattar, L. (2012). “Analytical model for history matching and forecasting production in multifrac composite systems,” in SPE Canadian unconventional resources conference, Calgary, AB, October 30-November 1, 2012, SPE 162516-MS.

Google Scholar

Stehfest, H. (1970). Algorithm 368: numerical inversion of laplace transforms [D5]. Commun. ACM. 13 (1), 47–49. doi:10.1145/361953.361969

CrossRef Full Text | Google Scholar

Van Everdingen, A. F., and Hurst, W. (1949). The application of the laplace transformation to flow problems in reservoirs. J. Petrol. Technol. 1 (12), 305–324. doi:10.2118/949305-g

CrossRef Full Text | Google Scholar

Wang, H., Guo, J., and Zhang, L. (2017). A semi-analytical model for multilateral horizontal wells in low-permeability naturally fractured reservoirs. J. Petrol. Sci. Eng. 149, 564–578. doi:10.1016/j.petrol.2016.11.002

CrossRef Full Text | Google Scholar

Wang, L., Yang, S., Meng, Z., Chen, Y., Qian, K., Han, W., et al. (2018). Time-dependent shape factors for fractured reservoir simulation: effect of stress sensitivity in matrix system. J. Petrol. Sci. Eng. 163, 556–569. doi:10.1016/j.petrol.2018.01.020

CrossRef Full Text | Google Scholar

Wang, M., Chen, S., and Lin, M. (2018). Enhancing recovery and sensitivity studies in an unconventional tight gas condensate reservoir. Petrol. Sci. 15, 305318. doi:10.1007/s12182-018-0220-7

CrossRef Full Text | Google Scholar

Warren, J. E., and Root, P. J. The behavior of naturally fractured reservoirs. SPE J. (1963). 3(3), 235–255. doi:10.2118/426-pa. CrossRef Full Text

Google Scholar

Weaver, J. D., Rickman, R. D., and Luo, H. (2010). Fracture-conductivity loss caused by geochemical interactions between man-made proppants and formations. SPE J. 15 (1), 116–124. doi:10.2118/118174-pa

CrossRef Full Text | Google Scholar

Wu, Y., Liu, H., and Bodvarsson, G. S. (2004). A triple-continuum approach for modeling flow and transport processes in fractured rock. J. Contam. Hydrol. 73, 145–179. doi:10.1016/j.jconhyd.2004.01.002

CrossRef Full Text | Google Scholar

Xiao, C., Dai, Y., Tian, L., Lin, H., Zhang, Y., Yang, Y., et al. (2018). A semianalytical methodology for pressure-transient analysis of multiwell-pad-production scheme in shale gas reservoirs, Part 1: new insights into flow regimes and multiwell interference. SPE J. 23 (3), 0885–0905. doi:10.2118/187958-pa

CrossRef Full Text | Google Scholar

Yang, D., Song, C., Zhang, J., Zhang, G., Ji, Y., and Gao, J. (2015a). Performance evaluation of injectivity for water-alternating-CO₂ processes in tight oil formations. Fuel 139 (1), 292–300. doi:10.1016/j.fuel.2014.08.033

CrossRef Full Text | Google Scholar

Yang, D., Zhang, F., Styles, J. A., and Gao, J. (2015b). Performance evaluation of a horizontal well with multiple fractures by use of a slab-source function. SPE J. 20 (3), 652–662. doi:10.2118/173184-pa

CrossRef Full Text | Google Scholar

Yao, S., Zeng, F., and Liu, H. (2013). “A semi-analytical model for hydraulically fractured wells with stress-sensitive conductivities,” in SPE unconventional resources conference, Calgary, AB, November 57, 2013, Paper SPE-167230-MS.

Google Scholar

Yekeen, N., Padmanabhan, E., and Idris, A. K. (2018). A review of recent advances in foam-based fracturing fluid application in unconventional reservoirs. J. Ind. Eng. Chem. 66, 45–71. doi:10.1016/j.jiec.2018.05.039

CrossRef Full Text | Google Scholar

Zerzar, A., Tiab, D., and Bettam, Y. (2004). “Interpretation of multiple hydraulically fractured horizontal wells,” in SPE Abu Dhabi international conference and exhibition, Abu Dhabi, UAE, October 10–13, 2004, Paper SPE-88707-MS.

Google Scholar

Zhang, F., and Yang, D. (2014). Determination of fracture conductivity in tight formations with non-Darcy flow behavior. SPE J. 19 (1), 34–44. doi:10.2118/162548-pa

CrossRef Full Text | Google Scholar

Zhang, F., and Yang, D. (2018). Effects of non-Darcy flow and penetrating ratio on performance of horizontal wells with multiple fractures in a tight formation. J. Energy Resour. Technol. 140 (3), 032903. doi:10.1115/1.4037903

CrossRef Full Text | Google Scholar

Zhang, Z., He, S., Liu, G., Guo, X., and Mo, S. (2014). Pressure buildup behavior of vertically fractured wells with stress-sensitive conductivity. J. Petrol. Sci. Eng. 122, 48–55. doi:10.1016/j.petrol.2014.05.006

CrossRef Full Text | Google Scholar

Zhao, Y., Zhang, L., Luo, J., and Zhang, B. (2014). Performance of fractured horizontal well with stimulated reservoir volume in unconventional gas reservoir. J. Hydrol. 512, 447–456. doi:10.1016/j.jhydrol.2014.03.026

CrossRef Full Text | Google Scholar

Zhao, L., Zhang, L., Liu, Y., Hu, S., and Liu, Q. (2015). Transient pressure analysis of fractured well in bi-zonal gas reservoirs. J. Hydrol. 524, 8999. doi:10.1016/j.jhydrol.2015.02.006

CrossRef Full Text | Google Scholar