Enhanced Dynamic Behaviour of Grid Connected Wind Farms in Load Participation and Frequency Regulation

The control of grid frequency in power systems due to the penetration of wind turbines is vital to maintaining the stability of power grids, based on recent grid requirements. In this paper, the dynamic behaviour of a wind farm connected to an existing grid is presented. The existing grid is made up of steam turbines, while the wind farm is based on squirrel cage induction generators. An energy capacitor system is used to stabilize the wind farm during periods of wind speed change. Loads with various capacities were connected to the grid to test the robustness of the controllers of the energy capacitor system employed. Furthermore, the effect of varying the time constant of the in-built DC-DC chopper of the energy capacitor system was investigated, considering load participation in the grid. One of the targets of this paper is the stabilization of the grid frequency of the network, despite the load capacity and the nature of the wind speed in the wind farm. The system performance was evaluated using Power System Computer Design and Electromagnetic Transient Including DC (PSCAD/EMTDC). The same conditions of operation were used to investigate the various scenarios considered in this study, to ensure an effective comparison. The natural wind speed employed was the same for all the considered scenarios. The presented results show that small load capacity with a high value low pass filter time constant, provided better response for the grid frequency and the entire variables of the power network.

Introduction

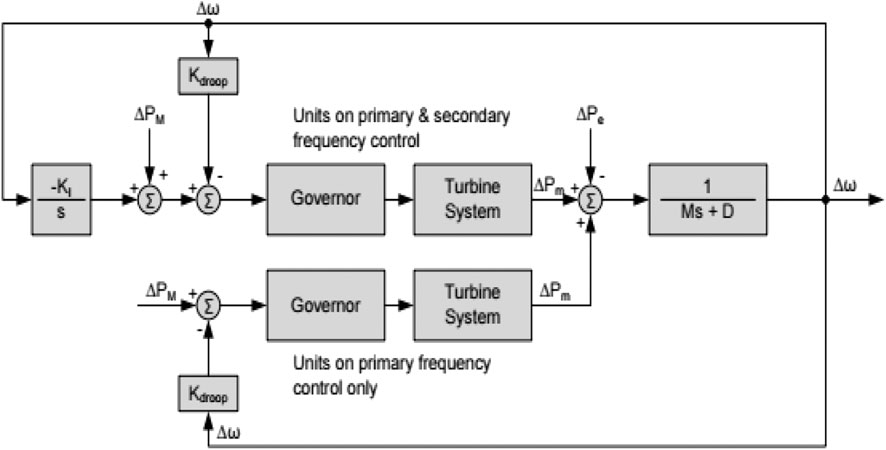
Frequency control in power grids require three mechanisms, at different time scales, which are traditional, and are usually implemented on the generation side of the turbine system (Wood and Wollenberg, 1996; Bergen and Vittal, 2000; Machowski et al., 2008). The primary frequency control employs a governor to maintain a set point, and to regulate the input of the mechanical power to the generator. This control is usually operated based on a low tens of seconds’ timescale. This control strategy is known as the droop control and it is mainly decentralized. In the primary control, the nominal frequency is not usually restored; however, the primary control can rebalance power and stabilize the frequency of the system. On the other hand, the automatic generation control, also known as the secondary frequency control, has a timescale of operation of up to a minute and maintains the set points of the governors based on a centralized control. This helps in adjusting the frequency of the system to its nominal value.

With the rapid penetration of wind energy into existing grids, the challenges for the smooth operation of power networks, because of grid disturbance, cannot be avoided. New methods are required to tackle this issue as the intricacies and control strategies for power grids are becoming more complex by the day (Okedu, 2013). Based on the stochastic nature of wind energy, wind power penetration into traditional power networks results in constant frequency distortions. In the literature, it has been proposed that users of grid connected loads should adapt their power consumption to the real generation cost at the time of usage. By doing this, loads that are adaptive to frequency would allow the uncertain fluctuating energy more easily, due to its penetration.

It has been proposed that appliances like “refrigerators, water or space heaters, ventilation systems, air conditioners, and plug-in electric vehicles,” which are known to be grid friendly could be of help in managing the energy imbalance of the power network (Lu and Hammerstrom, 2006; Trudnowski et al., 2006; Short et al., 2007; Brooks et al., 2010; Donnelly et al., 2010; Callaway and Hiskens, 2011; Molina-Garcia et al., 2011), The results of many studies, as reported in the literature, have shown tremendous and consistent improvements in dynamic grid performance and a reduced need to rely on spinning reserves. In some countries, the merits of using a grid-friendly connected load approach as a substantial total capacity of the load has reached 18% of their peak demand, in comparison to the current 13% required operating reserve, during peak demand (Hammerstrom et al., 2007; Short et al., 2007; U.K. Market Transformation Programme 2008; Kiani and Annaswamy, 2012; Zhao et al., 2014). The viability of this study approach can be verified in references (Andersson et al., 2005; Report of the Enquiry Committee, 2012; Luo et al., 2018), where it has been validated by measuring the correlation between the frequency and voltage of transmission lines at various places in the network, connected to the end users. This proved that it is sufficient for local frequency measurements of loads to partake in primary frequency control and at the same time be involved in the electromechanical oscillations damping in inter-area modes of large, interconnected power systems.

It should be noted that, while there are many reports that tend to offer solutions to load frequency adaptive control in the literature, not much has really been said regarding the analytical study of the behavior of grid connected loads and the dynamic equilibrium balance of the power system performance, in multi-machine systems. Although some key issues regarding the dynamic behavior of the grid connected system in load participation, with frequency regulation when considering the penetration of wind energy have been recognized (Trudnowski et al., 2006; Messikh et al., 2008; Jagathessan, 2015) they have not been addressed.

Recently, since frequency security is now the focus of the grid operation, it is imperative to reflect and strike a balance between the active power and frequency of the system, within specified limits, to ensure continuous operation of the power system. Otherwise, the protection devices that are frequency related would trigger, which may lead to fatal consequences in the power network. Modern power grids keep moving toward a complex large artificial system (Saiteja and Krishnarayalu, 2015; Wilches-Bernal and Chow, 2015). The interactions of the power components are more sophisticated in such a way that, a small grid disturbance may trigger a chain reaction, resulting in power blackouts due to cascading failures (Kumar and Kothari, 2005; Singh, 2014). The outages of the power system elements and the unforeseen spreading of the cascading failure of the system could cause a great mismatch of power. If this situation is not properly handled, it will lead to frequency insecurity. A further consequence would be a massive loss of load and generation or the collapse of the entire power system.

In light of the above, it would be correct to infer that the dynamics of the grid frequency and other variables of the power network play an important role in the process of power system cascading failures. The genetic algorithm (Molina and Mercado, 2011; Gu et al., 2013; Adhikari and Li, 2014; Ngamroo and Karaipoom, 2014; Serban and Marinescu, 2014) and the implemented adaptive notch filter (Ghazanfari et al., 2012; Sebastián and Peña Alzola, 2012; Suvire et al., 2012; Inthamoussou et al., 2013; Islam et al., 2013; Hussain et al., 2014) are some of the solutions that have already been reported. The Flywheel Energy Storage (FES) (Cardenas et al., 2004; Cimuca, et al., 2006; Jerbi et al., 2009; Cimuca et al., 2010), Superconducting Magnetic Energy Storage (SMES) and an Energy Capacitor System could be employed as short-term energy storage systems, to reduce fluctuations in wind energy. On the other hand, for a long-term energy storage system, the Battery Energy Storage System (BESS) could be used. However, because a fast response is required to effectively compensate and control the uncertain wind energy fluctuations, the BESS scheme may not be a good solution due to its slow charging and discharging process in a wind farm (Chang, et al., 2015; Zhang, et al., 2017). When considering high performance efficiencies and quick responses, the earlier schemes can be used to smooth out the fluctuating wind generator’s power (Causebrook, et al., 2007; Wang et al., 2011; Toshiba Documents Corporation, 1997), however, their initial and maintenance costs are major challenges (Yang et al., 2010).

As the need to propose a solution to grid frequency dynamics in grid connected power networks is on the rise, the FES has recently been used as a common control scheme to improve power quality and frequency control. Some of the reasons for this is that this control topology offers a short response time, is low cost, and has improved system reliability compared to other control schemes. FES has been employed to compensate for fluctuations of wind power to improve wind energy penetration into existing power networks, where it was concluded that a large FES can regulate the grid frequency of a power network. However, due to its components like the generator, inertia mass, bearings, and other ancillary devices, the cost of this system is quite high. A small sized FES can, however, store small fractions of energy which could be used to control variations in wind energy. A cheap small sized braking resistor was employed to improve the performance of wind farms that are connected to the grid (Causebrook et al., 2007; Yang et al., 2010; Okedu et al., 2011; Okedu et al., 2012), since it could enhance the wind generator output and mitigate dynamic effect of the speed of the wind turbine. A topology enacting the effect of this scheme, together with an ECS flexible ac transmission system was presented (Okedu, 2017), in a mixed generation system, while the DFIG flywheel-based system (Okedu, 2018a) was used for frequency control of the power network.

Researchers (Changgang et al., 2020) carried out a study on the drop of grid frequency as a result of massive generation loss, causing a threat to the power system’s frequency stability. In this study, a scheme based on precise load control was employed on a line-by-line basis for power grids that have no controllable loads. A proportional integral differential controller method, using a dynamic matrix control study, was reported (Wang and Tan, 2013), to solve load frequency control problems. In this paper, a detailed mathematical model of the controlled plant was not required, because a simple controller was used to achieve the step response of the system. However, the receding horizon dynamic matrix control requires a difficult computation burden for the perfect operation in a traditional distributed control system. A reduced generalized predictive control, into proportional integral differential control, was proposed (Hong et al., 2014), to improve the performance of grid frequency. However, the tuning of the controller parameters was not considered in the study. The integration of the interconnected power system requires an improvement of the automatic emergency control and harmonization with the load-frequency control, based on the recent grid codes. An investigation of the frequency and active power control, was carried out in a detailed simulation model that consist of under frequency load scheme (Vsevolod et al., 2017). The simulation results for different disturbances were presented in the study.

The need for power smoothing approaches considering intermittent wind power output, is imperative in a grid-connected multi-machine network. SMES and super-capacitors could also be used to reduce frequency fluctuations and power leveling in a grid connected system like the ECS. Both schemes could help in power flow smoothing under different wind conditions. The SMES technology is based on storing energy in the form of a magnetic field (Nielsen and Molinas, 2010; Okedu, 2018b). A direct current penetrates from a large superconducting coil and creates a magnetic field, thus, preserving energy (Vitale, 2017). The super-capacitors strategy is based on the charging and discharging modes of the super-capacitors. The charging and discharging modes are the key factors for the wind power ramp and frequency fluctuation control, in a grid connected wind farm, utilizing this kind of technology (Aranizadeh et al., 2016).

Although the above studies carried out investigations of load frequency in a power grid, most did not consider the integration of wind farms and the participation of different loads in the grid, considering the tuning of the excitation parameters of an energy storage device, used in stabilizing the grid during disturbances.

The salient part of this paper is the enhancement of the grid frequency performance of a multi-machine grid connected system considering the energy capacitor system control strategy. A model system made of traditional steam synchronous based generators that are grid tied to a wind farm is considered in this study. The energy capacitor system controller was used to stabilize the wind farm composed of squirrel cage induction generators. In the course of the operation of the wind farm, the control strategy is carried out based on the dynamics resulting from constant changes in wind power. Simulations were run using the Power System Computer Aided Design and Electromagnetic Transient Including DC (PSCAD/EMTDC) environment (PSCAD/EMTDC Manual, 1994). This study considered natural wind speed data obtained from Hokkaido Island, Japan, used for the wind turbines in the wind farm. Three grid-connected loads with different capacities were considered in the participation of the grid dynamics. The simulations were carried out for different scenarios where the loads were gradually increased at a time, under the same operating conditions for an effective comparative study. The time constant parameter of the DC-DC chopper circuitry of the low pass filter embedded in the energy capacitor system was varied for the different load capacities. The presented simulation results show the enhanced performance of the power network variables, using the control scheme employed in the wind farm.

Model System of the Study

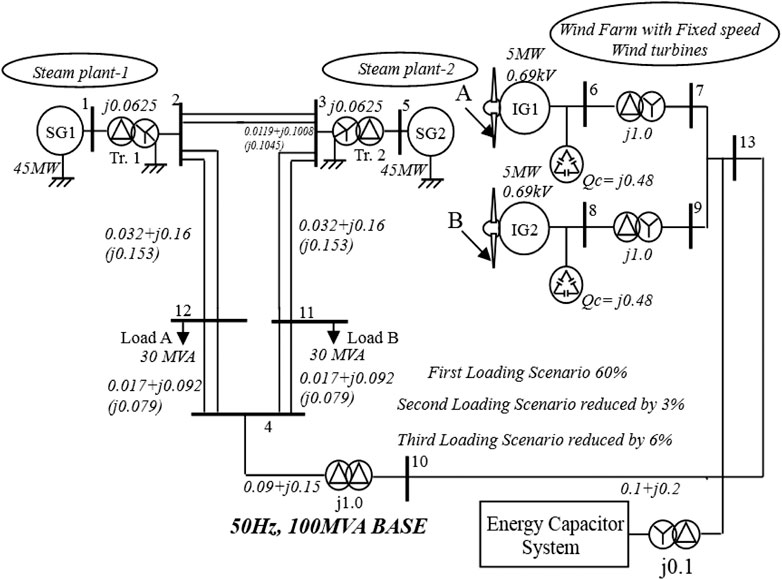
Figure 1 shows the considered model system used in this study, with the parameters of the lines, transformers, and loads given. The existing grid network is made up of steam synchronous generators. The wind farm in the model system is made up of only fixed speed wind turbines and is connected to the existing grid network, consisting of two steam driven turbine plants. The capacities of the two wind turbines are 5 MW each and those of the steam turbines are 45 MW each.

FIGURE 1

FIGURE 1. Model system of study.

For simulation purposes, only the aggregated wind turbines and steam turbines were used to study the dynamic behaviour of the system. Load A and load B have a 30 MW capacity and they are connected, as shown in the model system, to bus bars 11 and 12, respectively. The capacities of the loads were varied for different power factors of the grid operation for three scenarios to investigate their dynamic behavior. In the first scenario, the load capacity was 60% of the entire load rating, with a further reduction by 3% and 6% for the second and third scenarios, respectively. The energy capacitor system was connected to the terminal of the fixed speed wind farm to provide a smooth output during dynamics. The energy capacitor system has an built-in low pass filter system with gain and time constants. The same natural wind speed was used for the various scenarios of load capacities.

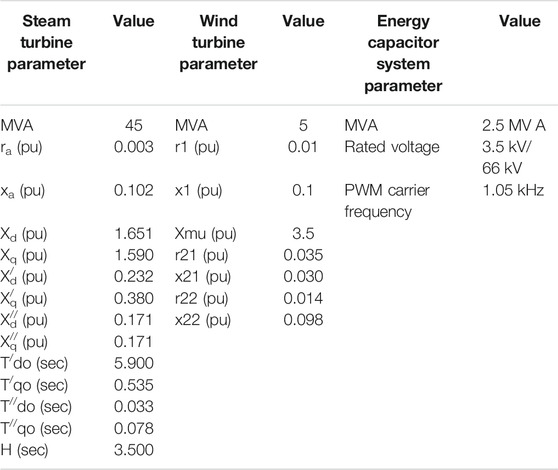
The grid was operated under the same condition, for effective comparison of the dynamic performance of the various load scenarios, based on the control strategy of the energy capacitor system. The parameters of the wind turbines and those of the steam synchronous generator plants in the model system are given in Table 1 (Okedu, 2017). The parameters of the energy capacitor system are also given in the same table. The Pulse Width Modulation (PWM) carrier frequency for the energy capacitor system is 1.05 kHz.

TABLE 1

TABLE 1. Turbine and energy capacitor parameters.

The Mathematical Dynamics of the Model System

The power system main part of the model system in Figure 1 is shown in Figure 2. From Figure 2, the generator inertia constant is $H$, the damping constant of the loads is $D$, while the change in the electrical power is $\Delta P_e$.

FIGURE 2

FIGURE 2. Dynamic representation of the model system.

The change in the turbine valve opening $\Delta y$ is based on the deviation of the frequency $\Delta \omega$, while that of the mechanical power $\Delta P_m$ is adjusted by the turbine itself. The characteristics of the electrical and mechanical parts of the steam turbine synchronous generator can be expressed with the differential equations given as (Omine et al., 2008a; Omine et al., 2008b):

$2H\frac{d\Delta \omega }{dt}=P_{mech}-P_e(1)$

$\frac{d\delta }{ dt}= \Delta \omega (2)$

$\frac{d{e}_q^{\prime }}{dt}= \frac{1}{T_{d0}^{\prime }}\left[e_{fd}-\left(x_d-x_d^{\prime }\right)i_d-e_q^{\prime }\right](3)$

$\frac{d{e}_d^{\prime }}{dt}= \frac{1}{T_{q0}^{\prime }}\left[e_d^{\prime }-\left(x_q-x_q^{\prime }\right)i_q\right](4)$

From Eqs 1–4, $H$ is the inertia constant, $P_{mech}$ is the mechanical input into the generator, $P_e$ is the generator output, $\delta$ is the angular phase difference, $\Delta \omega$ is the angular speed deviation, $e_d^{\prime }, e_q^{\prime }$ are the transient voltage for the direct and quadrature axis of the synchronous steam plant generator, $e_{fd}$ is the converted excitation voltage to the $q-axis$, $x_d, x_q$ are the reactance of the $d$ and $q$ axes, $x_d^{\prime }, x_q^{\prime }$ are the transient reactance of the $d$ and $q$ axes, $i_d, i_q$ are the terminal currents of the generator for the $d-q$ axes, while $T_{d0}^{\prime },T_{q0}^{\prime }$ are the transient time constants for the open circuit, respectively. The values of the parameters for the elements are given in Table 1.

It should be noted that the wind generator in Figure 1 is modeled as a fluctuating source because its output power is fluctuated by the stochastic nature of wind.

Considering that the loads are equipped with motors, the power frequency would be sensitive and is described as

$\Delta P_e\left(\Delta \omega \right)=D\Delta \omega (5)$

From Eq. 5, D is the damping constant. The presented model in Figure 2 has a speed governor with transfer function expressed as

$G_{gov}\left(s\right)=-\frac{1}{R\left(1+s{T}_G\right)}(6)$

Equation 6 is expressed in such a way that the change in the valve opening is

$\Delta y\left(s\right)=G_{gov}\left(s\right)\Delta \omega \left(s\right)(7)$

The transfer function of the turbine is

$G_{turbine}\left(s\right)= \frac{\left(1+s{F}_{HP}{T}_{RH}\right)}{\left(1+s{T}_{CH}\right)\left(1+s{T}_{RH}\right)}(8)$

From the above equations,

$\Delta P_m\left(s\right)= G_{turbine}\left(s\right)\Delta y\left(s\right) (9)$

Therefore, the transfer function represented by $G_1$ is:

$G_1\left(s\right)=-\frac{1/\left(2Hs+D\right)}{1-1/\left(2Hs+D\right)G_{turbine}\left(s\right)G_{gov}\left(s\right)} (10)$

Effect of Wind Energy on Grid Frequency Control

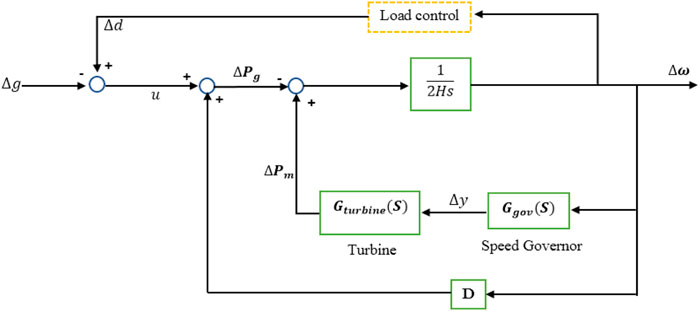
Power generation and supply in a grid changes from time to time. This imbalance is referred to as the frequency control of the network. Basically, the causes of the change in the grid imbalance are variations that are due to connected loads, power failures, or fault lines. This study is based on the variations that are due to connected load capacity. In a classical frequency control scheme shown in Figure 3, there is normally a primary frequency control scheme that adjusts the prime mover of the machine power flow, based on filtering activation with a time constant (Kundur, 1994; Andersson, 2008). This mechanism is a primary frequency control of the grid. However, to adjust the frequency variable during disturbances, a secondary control is required in addition to the earlier primary control. From the typical frequency control scheme shown in Figure 3, the first part is made up of the frequency controllers that allow the turbine to take or give out their kinetic energy, to mitigate frequency changes. This part of the system is referred to as the inertia response, because it dampens the inertia during frequency changes. The other part of Figure 3 is based on frequency stabilization with respect to its original value, using the primary or governor control scheme along with its secondary mechanism (UCTE, 2004).

FIGURE 3

FIGURE 3. Frequency control scheme in power networks.

With the integration of wind energy in Figure 3, the response of the inertia, due to changes in frequency, is expressed as (Omine et al., 2008b):

$P_g-P_l=\frac{d\left(\left(1/2\right)J_{system}\cdot {\omega }_{el}^2\right)}{dt}(11)$

Where, P_g is the generated power, P_l is the power demand, ${\omega }_{el}$ is the electrical angular frequency and J_system is the inertia of the system. The derivative of the kinetic energy stored in the turbines is given in Eq. 11. This is proportional to the power rating of the turbines and leads to the expression of the inertia constant given as (Anderson and Fouad, 2002):

$H_{gen}=\frac{\left(J_{gen}/P^2\right)\cdot {\omega }_{el,0}^2}{2.S_{gen}}(12)$

Where S_gen is the apparent power of the generator, ${\omega }_{el,0}$ is the system frequency and p the number of pole pairs. The range for the inertia constant is normally 2–9 s for large turbines (Stevenson and Grainger, 1994), for this work the inertia constant used is 3.5 sec as shown in Table 1. Clubbing Eqs 1, 2 give:

${\overline{P}}_g-{\overline{P}}_t=2\cdot {\displaystyle \sum \frac{H_{gen}{S}_{gen}}{S_{base}}}\cdot {\overline{\omega }}_{el}\cdot \frac{d{\overline{\omega }}_{el}}{dt}2\cdot H_{system}\cdot {\overline{\omega }}_{el}\cdot \frac{d{\overline{\omega }}_{el}}{dt}(13)$

Where, H_system is the initial constant of the system. Assuming, ${\overline{\omega }}_{el}\approx 1$, the initial rate of frequency change of the system may be expressed as:

$\frac{d{\overline{\omega }}_{el}}{dt}=\frac{{\overline{P}}_g-{\overline{P}}_t}{2.H_{system}}(14)$

In light of the equations above, the frequency rate of change depends on the magnitude of the imbalance power and the inertia. Moreover, the inertia of the system depends on the number of turbines in operation in the grid and the self-inertia of the various turbines. Based on the rotational speed and frequency coupling of synchronous generators, they can partake in the inertia response, unlike wind generators. This is due to the fact that wind generators decouple electrically (the generator motion from the grid frequency) and consequently lack the ability to partake in the inertia control.

As a result, integrating wind energy into the traditional grid would mean a lower system inertia that may cause a high rate of frequency change. However, if virtual inertia control is considered for wind generators, the difference in the power imbalance, due to the change in frequency, can be reduced. This study employs the fixed speed squirrel cage induction wind turbine based on the induction generator in the considered model system of Figure 1.

The Control Strategy of the Wind Farm and Energy Capacitor System

The control structure for the energy capacitor system is shown in Figure 4. From the control structure in Figure 4, the direct axis grid current is used to control the DC-link voltage of the energy capacitor system, while the quadrature axis grid current is used to control its reactive power dissipation to the grid during operation. The values of the Proportional Integrators (PI) are obtained by a trial-and-error method.

FIGURE 4

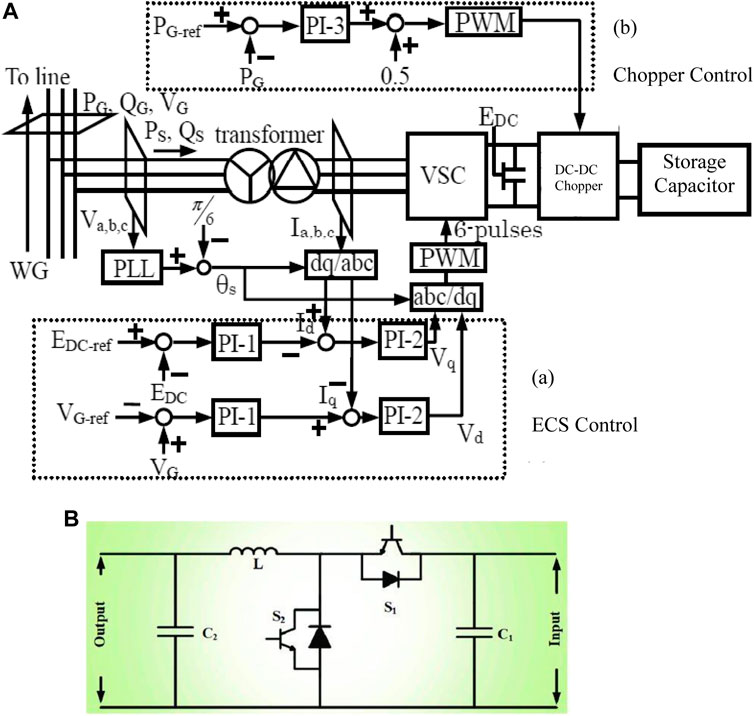
FIGURE 4. Control strategies of the energy capacitor system and chopper circuitry. (A) Energy capacitor system. (B) Structure of the dc-dc converter.

The Phase Lock Loop (PLL) helps in synchronizing the grid voltage at the grid side inverter of the energy capacitor system to that of the operational values of the grid. The obtained PLL angle is used in the conversion of dq to abc components based on the six pulses generated for the switching of the energy capacitor system. These pulses were obtained after a comparator compares a PWM signals with a triangular saw tooth carrier frequency of 1.05 kHz, for the energy capacitor system. Also, the Low Pass Filter (LPF) and DC-DC chopper circuitry are shown in the same figure. The wind turbine real power and the reference maximum power point tracking obtained from the wind turbine characteristics are used to obtain the switching signal for the DC-DC chopper circuitry. The low pass filter time and gain constants were manipulated to control the behaviour of the wind generator during operation. In this study, the model system load capacity and the time constant were varied, to investigate the dynamic behaviour of the grid.

Evaluation of the System Performance

System Evaluation with Constant Load and Different ECS Filter Time Constants

The simulations of this study were carried out in PSCAD/EMTDC environment using the considered model system of Figure 1. The first part of the evaluation of the system performance was carried out using real wind speed data obtained from Hokkaido Island in Japan, shown in Figure 5A. This wind speed was used for the aggregated wind turbine in the grid connected wind farm of the model system. The simulations were run for 600 s to demonstrate the robustness of the controllers the system employed in the stability of the grid during dynamics. In this scenario, different low pass filter time constants of the ECS unit were used to investigate its effect on the dynamics of the grid network, considering the light fixed load in the model system. Figure 5B shows the responses of no ECS grid frequency control and those of the different time constants for the ECS low pass filter circuitry. When no control was implemented, the grid frequency dipped as much as 48 Hz, thus in this case, the wind farm must be shut down based on the stipulated grid codes that do not allow a frequency dip below 49.5 or 49 Hz in some cases. Furthermore, a scheme considering the series dynamic braking resistor connected to the stator of the wind generator and controlled based on the grid frequency was also investigated. The grid frequency response of the series resistor could not match the grid requirement. However, with the use of the low pass filter, having a high time constant of 240 s for the ECS, the grid frequency was effectively stabilized based on the stipulated grid codes, as compared to scenarios of using lower time constants for the ECS low pass filter circuitry, as shown in Figure 5. Figure 5C shows that the output power can be reduced or increased during low and high wind speeds by smoothening, compared to no smoothening. The control system of the ECS selects the line power as a reference and follows it by absorbing or discharging active power from or to the capacitor system. The LPF is used to estimate the reference line power, thus, enhancing the system performance by smoothening the power fluctuations and keeping the terminal voltage within the required level.

FIGURE 5

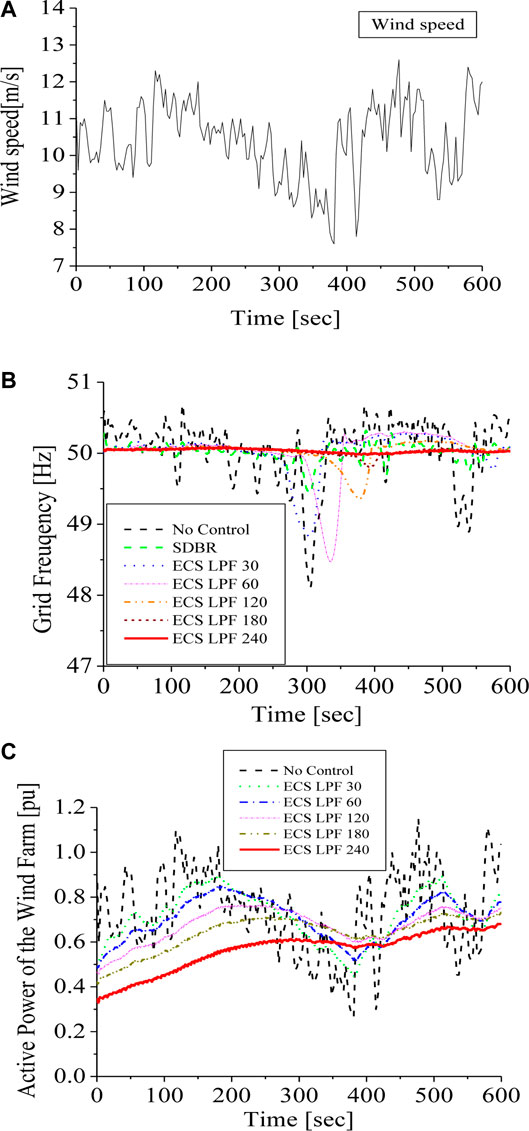
FIGURE 5. Dynamics of the system with constant load. (A) Wind speed. (B) Grid frequency. (C) Active power.

System Evaluation with Varying Load and Different ECS Filter Time Constants

The same natural wind speed data shown in Figure 5A, was used in this section, to effectively judge the performance of the system. Three scenarios of load participation were carried out. In the first scenario, the connected load capacity is 60% of the total load. The load capacity was then reduced by 3% and then by 6% for the second and third scenarios, respectively. The time constant variable for the low pass filter was also varied for 60, 120, and 240 s, respectively, to show the dual effects of the load capacity and the time constant of the energy capacitor system on the behavior of the grid connected wind farm and the entire grid. The wind farm was connected as per the three scenarios at a time to the existing grid network of steam turbines under the same operating condition of wind speed, for an effective comparative study of the responses of the variables of the network. Some of the simulation results for the grid variables of the system are discussed.

Figure 6A shows the behavior of the grid frequency dynamics for scenario 1 with different load capacities and an energy capacitor low pass filter time constant of 60 s. The respective power factor of operation of these loads are also shown. With a load capacity of 60% and a power factor of 0.8, a dip was observed with increased settling time for the grid frequency variable during dynamics. The grid frequency distortions were a lot for this case because of the huge effect of the wind speed change and the high capacity of the grid connected load, thus, the controller was not able to restore the performance of the grid variable as per the grid codes or requirements stipulating a minimum of a 49 Hz frequency dip.

FIGURE 6

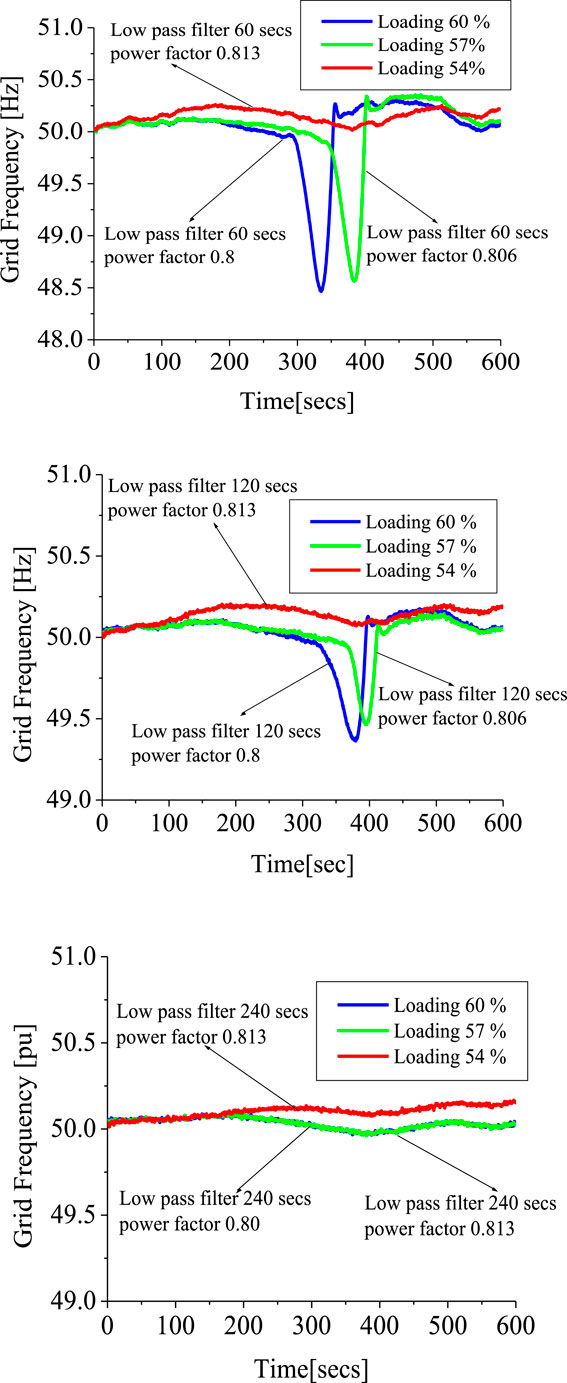
FIGURE 6. Dynamics of the system with varying loads. (A) Dynamics for low pass filter 60 s. (B) Dynamics for low pass filter 120 s. (C) Dynamics for low pass filter 240 s.

The performance of the grid frequency, considering a reduction of load capacity by 3% using the same energy capacitor time constant, is almost the same as that of a 60% load capacity. With a further reduction of the load capacity by 6%, the grid frequency was further enhanced, considering the same energy capacitor time constant. Figure 6B for scenario 2 shows similar responses to scenario 1 in Figure 6A, however, the performance of the grid frequency was better due to the increase of the time constant of the energy capacitor system from 60 to 120 s, with a frequency dip slightly lower than 49.5 Hz.

A further increase of the energy capacitor system time constant to 240 s for scenario 3, shows a far better behavior of the grid frequency dynamics, despite the load capacity of the power system (Figure 6C). In this case, the response of the load capacity at 60 and 57% are exactly the same and the difference between these responses and that of the 54% load is slightly less than a 2% deviation. Based on the responses of Figures 6A–C, it could be concluded that it is better to operate the energy capacitor system with high value of time constant parameter for optimal performance of the grid frequency dynamics, despite the load capacity connected to the entire network.

The active power responses for the wind farm, considering all scenarios, are shown in Figure 7A. The responses of the wind farm active power are different for different load capacities; however, the responses are the same for the same energy capacitor timing constant. Thus, the load capacity of the grid plays a major role in the response of the wind farm active power, compared to the energy capacitor time constant. The responses of the energy capacitor reactive power are given in Figure 7B. Figure 7B shows that more reactive power is dissipated with a higher load capacity, despite the energy capacitor time constant. Thus, the load capacity of the grid is directly related to the dissipation of reactive power by the energy capacitor system. More load capacity requires more reactive power to stabilize the system.

FIGURE 7

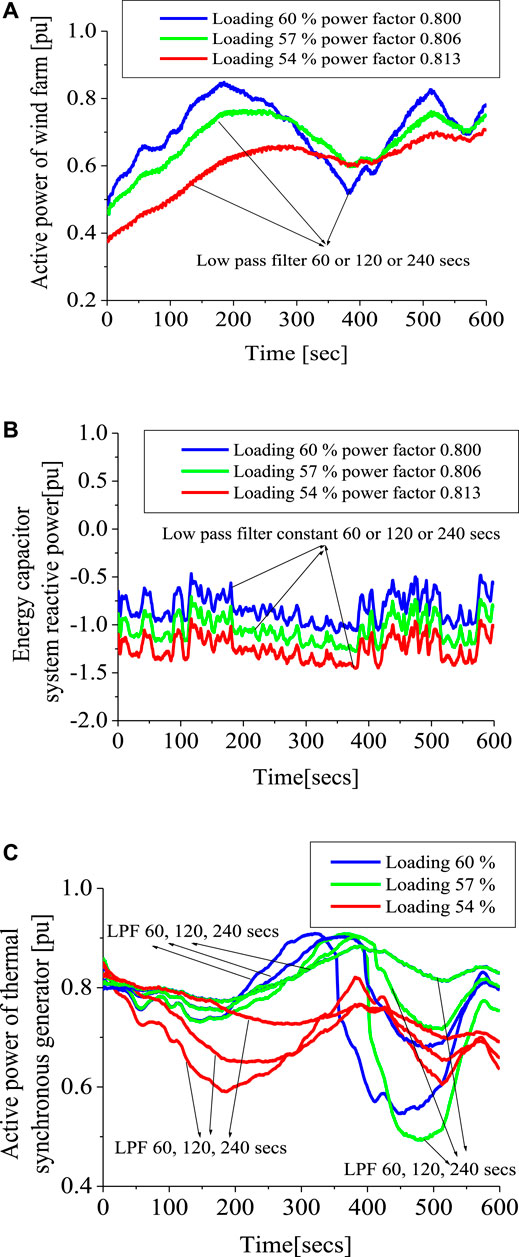
FIGURE 7. Dynamics of the variables of the grid. (A) Active power of the wind farm for all scenarios. (B) Reactive power of ECS for all scenarios. (C) Active power of the thermal steam turbine for all scenarios.

Figure 7C shows that the active power of the grid connected existing steam synchronous generator turbines depend on both the load capacity of the grid and the energy capacitor timing constant parameter. A higher load capacity of 60% with a higher time constant of the energy capacitor system, shows a better grid frequency dynamic behavior. On the other hand, when the load capacity of the grid was reduced by 6% and the time constant was of a high value of 240 s, an improved performance of the active power of the synchronous generator was achieved during dynamics.

Figure 8 shows the dynamics of the wind farm. In Figure 8A, the terminal voltage of the wind farm was kept constant for all conditions despite the varying wind speed. Thus, showing the robustness of the controller of the energy capacitor system employed in the study. The results for the terminal voltage of the wind farm shows that with more grid connected loads, the wind farm voltage would drop further compared to scenarios with low grid connected loads. In Figure 8B, the reactive power of the wind farm is the same for all scenarios. This is because the reactive power does not partake in the stabilization of the grid frequency; rather the active power of the wind farm has a relationship with the grid frequency. The rotor speed of the wind turbine in the farm is shown in Figure 8C. The rotor speed was the same for all conditions of the low pass filter time constant and the varying conditions of the wind speed from 0 to 300 s. After 300 s, there was a drop in the wind speed close to 7 m/s. This led to a drop in the rotor speed of the wind turbine when the grid-connected load was of higher capacity. The rotor speed of the wind turbine was not affected for low grid-connected load capacities, despite the various values of the low pass filter used in the dc chopper circuitry of the energy capacitor system.

FIGURE 8

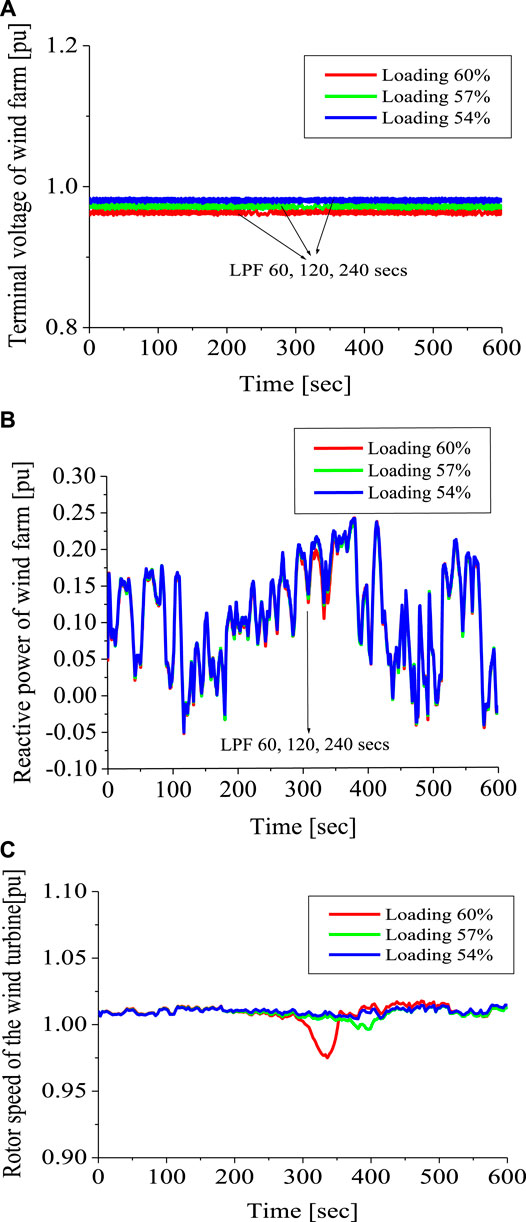
FIGURE 8. Dynamics of the variables of the wind farm. (A) Terminal voltage of the wind farm. (B) Reactive power of the wind farm. (C) Rotor speed of wind turbine.

Figure 9 shows the dynamics of the energy capacitor system. In Figure 9A, the dc chopper current was much lower for higher grid-connected loads during operation. This is due to fact that a large current and voltage drop would occur as the capacity of the load increases, leading to more stress on the energy capacitor system beyond its operating limits. In Figure 9B, the DC-link voltage of the energy capacitor drops with a lower capacity of grid-connected loads. The higher load capacity in the grid provided a slight increase in the responses of the DC-link during dynamic conditions of operation. The grid current for phase A of the energy capacitor system is shown in Figure 9C. There was a drop in the grid current, just like the dc chopper current with an increase in grid-connected loads, when compared to the scenario with a lower load capacity of the grid.

FIGURE 9

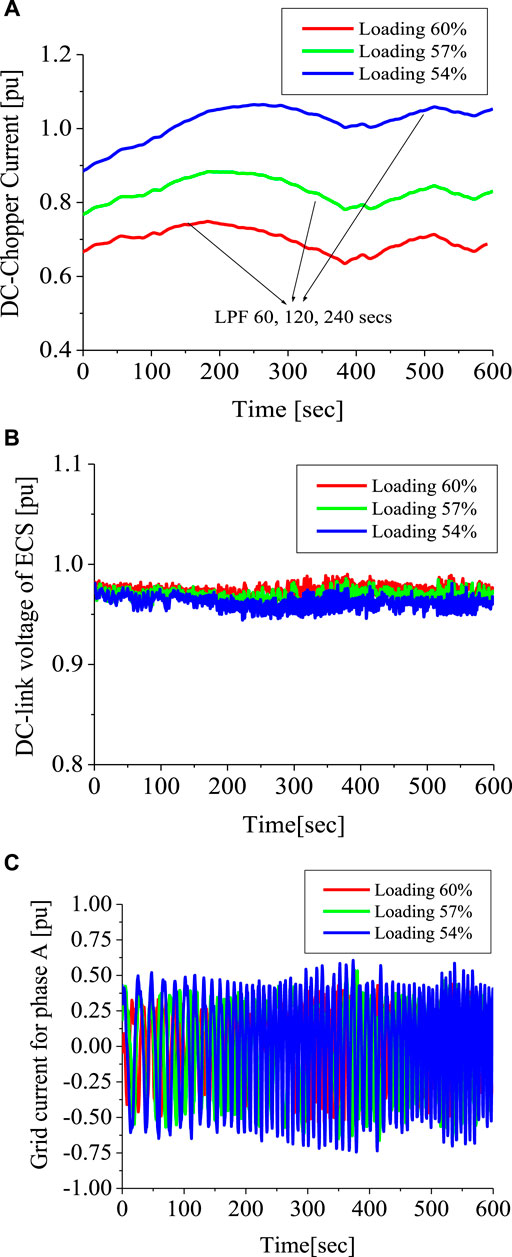
FIGURE 9. Dynamics of the energy capacitor system. (A) DC chopper current of energy capacitor system. (B) DC-link voltage of energy capacitor system. (C) Grid current of energy capacitor system.

Conclusion

It is paramount to reduce the fluctuations in power grids, due to the penetration of huge amounts of wind energy in modern power systems. Failure to achieve this objective would lead to the continuous shut down of grid connected wind farms in a multi-machine power system. In this paper, an energy capacitor system was used to provide smoothing and stability for a wind farm connected to a steam turbine power plant in an existing grid. The dynamic behavior of the grid connected wind farm was investigated considering different scenarios of grid connected load capacities and the time constant of the energy capacitor system. One of the targets of this work was the improved performance of the grid frequency of the network, despite the load capacity and the nature of wind speed in the wind farm. The presented results of the variables of the power grid, reflect that power grids should not be operated too close to their stability limit of high load capacity. Also, high values of an energy capacitor time constant provided better performance of the grid system variables during dynamic analysis. As part of future work to validate the control strategy employed in this study, a real time test bench composed of dSPACE/AD5435 based control scheme using MATLAB/Simulink and a real time workshop is preferred. Gate signals will be supplied to the frequency converter from the DSP (Digital Signal Processor) system. It has been investigated that the Danfoss inverter is suitable for this work as the interfacing card. Also, an optimization technique could be used to define the PI parameters in future work.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

KO did initiated the concept, design of model, simulation results and writing of the paper. HB did the literature review of the work.

Funding

German University of Technology (GUtech) in Oman, seed fund.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Adhikari, S., and Li, F. (2014). Coordinated V-f and P-Q control of solar photovoltaic generators with MPPT and battery storage in microgrids. IEEE Trans. Smart Grid. 5, 1270–1281. doi:10.1109/tsg.2014.2301157

CrossRef Full Text | Google Scholar

Andersson, G. (2008). Dynamics and control of electric power systems. ZurichETH Zurich: CH. EEH—Power Systems Laboratory.

Google Scholar

Andersson, G., Donalek, P., Farmer, R., Hatziargyriou, N., Kamwa, I., Kundur, P., et al. (2005). Causes of the 2003 major grid blackouts in North America and Europe, and recommended means to improve system dynamic performance. IEEE Trans. Power Syst. 20, 1922–1928. doi:10.1109/tpwrs.2005.857942

CrossRef Full Text | Google Scholar

Anderson, P., and Fouad, A. (2002). Power system control and stability. Piscataway, NJ: Wiley—IEEE Press.

CrossRef Full Text | Google Scholar

Aranizadeh, A., Vahidi, B., and Rahiminejad, A. (2016). Wind turbine power output smoothing in microgrid using ultra-capacitor with continuous wind speed forecasting and online supervisory control. J. Renew. Sustain. Energy. 8, 033301. doi:10.1063/1.4950958

CrossRef Full Text | Google Scholar

Bergen, A. R., and Vittal, V. (2000). Power systems analysis. 2nd Edn. Upper Saddle River, NJ: Prentice Hall, Inc.

Google Scholar

Brooks, A., Reicher, D., Spirakis, C., and Weihl, B. (2010). Demand dispatch. IEEE Power Energy Mag. 8 (3), 20–29. doi:10.1109/mpe.2010.936349

CrossRef Full Text | Google Scholar

Callaway, D. S., and Hiskens, I. A. (2011). Achieving controllability of electric loads. Proc. IEEE. 99 (1), 184–199. doi:10.1109/jproc.2010.2081652

CrossRef Full Text | Google Scholar

Cardenas, R., Pena, R., Asher, G. M., Clare, J., and Blasco-Gimenez, R. (2004). Control strategies for power smoothing using a flywheel driven by a sensorless vector-controlled induction machine operating in a wide speed range. IEEE Trans. Ind. Electron. 51, 603–614. doi:10.1109/tie.2004.825345

CrossRef Full Text | Google Scholar

Causebrook, A., Atkinson, D. J., and Jack, A. G. (2007). Fault ride-through of large wind farms using series dynamic braking resistors (March 2007). IEEE Trans. Power Syst. 22 (3), 966–975. doi:10.1109/tpwrs.2007.901658

CrossRef Full Text | Google Scholar

Chang, X., Li, Y., Zhang, W., Wang, N., and Xue, W. (2015). Active disturbance rejection control for a flywheel energy storage system. IEEE Trans. Ind. Electron. 62, 991–1001. doi:10.1109/tie.2014.2336607

CrossRef Full Text | Google Scholar

Changgang, L., Yue, W., Yanli, S., Hengxu, Z., Yutian, L., Yilu, L., et al. (2020). Continuous under-frequency load shedding scheme for power system adaptive frequency control. IEEE Trans. Power Syst. 35 (2), 950–961. doi:10.1109/TPWRS.2019.2943150

CrossRef Full Text | Google Scholar

Cimuca, G., Breban, S., Radulescu, M. M., Saudemont, C., and Robyns, B. (2010). Design and control strategies of an induction-machine-based flywheel energy storage system associated to a variable-speed wind generator. IEEE Trans. Energy Convers. 25, 526–534. doi:10.1109/tec.2010.2045925

CrossRef Full Text | Google Scholar

Cimuca, G. O., Saudemont, C., Robyns, B., and Radulescu, M. M. (2006). Control and performance evaluation of a flywheel energy-storage system associated to a variable-speed wind generator. IEEE Trans. Ind. Electron. 53, 1074–1085. doi:10.1109/tie.2006.878326

CrossRef Full Text | Google Scholar

Donnelly, M., Harvey, D., Munson, R., and Trudnowski, D. (2010). “Frequency and stability control using decentralized intelligent loads: benefits and pitfalls,” in Proc.of IEEE Power and Energy Society General Meeting, Minneapolis, MN, United States, July 25, 2010 (IEEE), 1–6.

Google Scholar

Ghazanfari, A., Hamzeh, M., Mokhtari, H., and Karimi, H. (2012). Active power management of multihybrid fuel cell/supercapacitor power conversion system in a medium voltage microgrid. IEEE Trans. Smart Grid. 3, 1903–1910. doi:10.1109/tsg.2012.2194169

CrossRef Full Text | Google Scholar

Gu, W., Liu, W., Wu, Z., Zhao, B., and Chen, W. (2013). Cooperative control to enhance the frequency stability of Islanded Microgrids with DFIG-SMES. Energies. 6, 3951–3971. doi:10.3390/en6083951

CrossRef Full Text | Google Scholar

Hammerstrom, D. J., Brous, J., Chassin, D. P., Horst, G. R., Kajfasz, R., Michie, P., et al. (2007). Pacific northwest GridWise testbed demonstration projects, part II: grid friendly appliance project. Pacific Northwest Nat. Lab., Tech. Rep. 2007, 17079. doi:10.2172/926122

CrossRef Full Text | Google Scholar

Hong, Z., Yuchun, H., and Wen, T. (2014). “Partially decentralized load frequency control of multi-area power systems in deregulated environments,” in Proceedings of the 11th world congress on intelligent control and automation date of conference, Shenyang, China, June 29–July 4, 2014.

Google Scholar

Hussain, E. K., Benchebra, D., Atallah, K., Ooi, H. S., Burke, H., and Goodwin, A. (2014). “A flywheel energy storage system for an isolated micro-grid,” in Proceedings of the renewable power generation conference, Naples, Italy, September 24–25, 2014, 1–6.

Google Scholar

Inthamoussou, F. A., Pegueroles-Queralt, J., and Bianchi, F. D. (2013). Control of a supercapacitor energy storage system for microgrid applications. IEEE Trans. Energy Convers. 28, 690–697. doi:10.1109/tec.2013.2260752

CrossRef Full Text | Google Scholar

Islam, F., Al-Durra, A., and Muyeen, S. M. (2013). Smoothing of wind farm output by prediction and supervisory-control-unit-based FESS. IEEE Trans. Sustain. Energy. 4, 925–933. doi:10.1109/tste.2013.2256944

CrossRef Full Text | Google Scholar

Jagathessan, K. (2015). Artificial intelligence in performance analysis of load frequency control in thermal wind hydropower system. Int. J. Adv. Comput. Sci. Appl. 6 (7), 203–212. doi:10.14569/IJACSA.2015.060727

CrossRef Full Text | Google Scholar

Jerbi, L., Krichen, L., and Ouali, A. (2009). A fuzzy logic supervisor for active and reactive power control of a variable speed wind energy conversion system associated to a flywheel storage system. Elec. Power Syst. Res. 79, 919–925. doi:10.1016/j.epsr.2008.12.006

CrossRef Full Text | Google Scholar

Kiani, A., and Annaswamy, A. (2012). “A hierarchical transactive control architecture for renewables integration in smart grids,” in Proc. of IEEE conference on decision and control (CDC), Maui, HI, December 2012, 4985–4990.

Google Scholar

Kumar, I., and Kothari, D. P. (2005). Recent philosophies of automatic generation control strategies in power systems. IEEE Trans. Power Syst. 20 (1), 346–357. doi:10.1109/TPWRS.2004.840438

CrossRef Full Text | Google Scholar

Kundur, P. (1994). Power system stability and control. New York, NY: McGraw-Hill.

Google Scholar

Lu, N., and Hammerstrom, D. (2006). “Design considerations for frequency responsive grid friendly appliances,” in Proc. of IEEE Transmission and Distribution Conf. Expo., Dallas, TX, 647–652.

Google Scholar

Luo, C., Yang, J., and Sun, Y. (2018). Risk assessment of power system considering frequency dynamics and cascading process. Energies. 11 (422), 1–16. doi:10.3390/en11020422

CrossRef Full Text | Google Scholar

Machowski, J., Bialek, J., and Bumby, J. (2008). Power system dynamics: stability and control. 2nd Edn. Hoboken, NJ: John Wiley & Sons, Inc.

Google Scholar

Messikh, T., Mekhilef, S., and Rahim, N. A. (2008). Adaptive notch filter for harmonic current mitigation. Wor. Acad. Sci. Engineer. and Tech. 22, 907–913. doi:10.5281/zenodo.1085828

Google Scholar

Molina, M. G., and Mercado, P. E. (2011). Power flow stabilization and control of microgrid with wind generation by superconducting magnetic energy storage. IEEE Trans. Power Electron. 26, 910–922. doi:10.1109/tpel.2010.2097609

CrossRef Full Text | Google Scholar

Molina-Garcia, A., Bouffard, F., and Kirschen, D. S. (2011). Decentralized demand-side contribution to primary frequency control. IEEE Trans. Power Syst. 26 (1), 411–419. doi:10.1109/tpwrs.2010.2048223

CrossRef Full Text | Google Scholar

Ngamroo, I., and Karaipoom, T. (2014). Improving low-voltage ride-through performance and alleviating power fluctuation of DFIG wind turbine in DC microgrid by optimal SMES with fault current limiting function. IEEE Trans. Appl. Supercond. 24, 1–5. doi:10.1109/TASC.2014.2333031

CrossRef Full Text | Google Scholar

Nielsen, K. E., and Molinas, M. (2010). “Superconducting magnetic energy storage (SMES) in power systems with renewable energy sources,” in Proceedings of the 2010 IEEE international symposium on industrial electronics, Bari, Italy, July 4–7, 2010, 2487–2492.

Google Scholar

Okedu, K. E. (2018a). A variable speed wind turbine flywheel based coordinated control system for enhancing grid frequency dynamics. Int. J. of Smart Grid. 2, 123–134.

Google Scholar

Okedu, K. E. (2018b). Improving the dynamic performance of grid connected wind farm using new SMES switching technique. J. Renew. Sustain. Energy. 10, 043311–043314. doi:10.1063/1.5040244

CrossRef Full Text | Google Scholar

Okedu, K. E., Muyeen, S. M., Takahashi, R., and Tamura, J. (2011). “Improvement of fault ride through capability of wind farm using DFIG considering SDBR”, 14th European conference of power electronics EPE, Birmingham, United Kingdom, August 7, 2011, 1–10.

Google Scholar

Okedu, K. E., Muyeen, S. M., Takahashi, R., and Tamura, J. (2012). Wind farms fault ride through using DFIG with new protection scheme. IEEE Trans. Sustain. Ener. 3 (2), 242–254. doi:10.1109/tste.2011.2175756

CrossRef Full Text | Google Scholar

Okedu, K. E. (2013). Hybrid control strategy for variable speed wind turbine power converters. Int. J. Renew. Energy Resour. 3 (2), 283–288.

Google Scholar

Okedu, K. E. (2017). Effect of ECS low‐pass filter timing on grid frequency dynamics of a power network considering wind energy penetration. IET Renew. Power Gener. 11 (9), 1194–1199. doi:10.1049/iet-rpg.2016.0855

CrossRef Full Text | Google Scholar

Omine, E., Senjyu, T., Muhando, E. B., Sekine, H., Funabashi, T., and Saber, A. Y. (2008a). “Torsional torque suppression of decentralized generators using H-infinity observer,” in Proc. IEEE international conference on sustainable energy technologies, Singapore, November 24–27, 2008, 1007–1012.

Google Scholar

Omine, E., Senjyu, T., Muhando, E. B., Yona, A., Sekine, H., Funabashi, T., and Saber, A. Y. (2008b). “Coordinated control of Battery energy storage system and diesel generator for isolated power system stabilization,” in Proc. IEEE 2nd international power and energy conference, Johor Bahru, Malaysia, December 1–3, 2008, 925–930.

Google Scholar

PSCAD/EMTDC Manual (1994). PSCAD/EMTDC Manual. Canada: Manitoba HVDC research center.

Google Scholar

Report of the Enquiry Committee (2012). Report of the enquiry committee on grid disturbance in northern region on 30 July 2012 and in northern, eastern & north-eastern region on 31 July 2012. Available at: http://www.powermin.nic.333in\/pdf\/GRID_ENQ_REP_16_8_12.pdf (Accessed January 25, 2018).

Google Scholar

Saiteja, K., and Krishnarayalu, M. S. (2015). Load frequency control of two-area smart grid. Ijca. 117, 1–9. doi:10.5120/20619-3323

CrossRef Full Text | Google Scholar

Sebastián, R., and Peña Alzola, R. (2012). Flywheel energy storage systems: review and simulation for an isolated wind power system. Renew. Sustain. Energy Rev. 16, 6803–6813. doi:10.1016/j.rser.2012.08.008

CrossRef Full Text | Google Scholar

Serban, I., and Marinescu, C. (2014). Control strategy of three-phase Battery energy storage systems for frequency support in microgrids and with uninterrupted supply of local loads. IEEE Trans. Power Electron. 29, 5010–5020. doi:10.1109/tpel.2013.2283298

CrossRef Full Text | Google Scholar

Short, J., Infield, D., and Freris, F. (2007). Stabilization of grid frequency through dynamic demand control. IEEE Trans. Power Syst. 22 (3), 1284–1293. doi:10.1109/tpwrs.2007.901489

CrossRef Full Text | Google Scholar

Singh, K. P. (2014). Load frequency control of multi-source power system with redox flow batteries: an analysis. Int. J. Comput. Appl. 88 (8), 46–52. doi:10.5120/15376-4053

CrossRef Full Text | Google Scholar

Stevenson, W., and Grainger, J. (1994). Power system analysis. New York, NY: McGraw-Hill.

Google Scholar

Suvire, G. O., Molina, M. G., and Mercado, P. E. (2012). Improving the integration of wind power generation into AC microgrids using flywheel energy storage. IEEE Trans. Smart Grid. 3, 1945–1954. doi:10.1109/tsg.2012.2208769

CrossRef Full Text | Google Scholar

Toshiba Documents Corporation, (1997). Toshiba World’s first successful commercial operation of double-fed adjustable-speed flywheel generating system. Available at: https://www.toshiba.co.jp/tech/review/1997/high97/power/p3/index.htm (Accessed January 21, 2015).

Google Scholar

Trudnowski, D., Donnelly, M., and Lightner, E. (2006). “Power-system frequency and stability control using decentralized intelligent loads,” in Proc. of IEEE transmission and distribution conf. expo., Dallas, TX, August 15–18 2006, 1453–1459.

Google Scholar

UCTE (2004). Operation handbook—appendix 1: load-frequency control and performance. Available at: www.pse-operator.pl.

Google Scholar

U.K. Market Transformation Programme (2008). Dynamic demand control of domestic appliances. U. K. Market Transformation Programme. Tech. Rep., 23–70.

Google Scholar

Vitale, G. (2017). “Frequency stability improvement in weak grids by storage systems,” in Smart energy grid design for Island countries. Suva, Fiji: Springer, 223–258.

CrossRef Full Text | Google Scholar

Vsevolod, P., Anton, S., Oleg, L., Vitaly, Z., and Mykyta, V. (2017). “Frequency stability simulation considering under frequency load shedding relays, special protection automatics and AGC software models,” in 2017 IEEE Manchester Power Tech, Manchester, UK, June 2017, 18–22.

Google Scholar

Wang, L., Yu, J., and Chen, Y. T. (2011). Dynamic stability improvement of an integrated offshore wind and marine-current farm using a flywheel energy-storage system. IET Renew. Power Gener. 5, 387–396. doi:10.1049/iet-rpg.2010.0194

CrossRef Full Text | Google Scholar

Wang, Y., and Tan, W. (2013). “Load frequency control for power systems via DMC,” in 25th Chinese Control and Decision Conference (CCDC), Guiyang, China, May 25–27, 2013.

CrossRef Full Text | Google Scholar

Wilches-Bernal, F., and Chow, J. H. (2015). “A fundamental study of applying wind turbines for power system frequency control,” in CFES annual conference, Troy, NY, February 26, 2015.

Google Scholar

Wood, A. J., and Wollenberg, B. F. (1996). Power generation, operation, and control. 2nd Edn. Hoboken, NJ: John Wiley & Sons, Inc.

Google Scholar

Yang, Y., Fletcher, E., and O’Reilly, J. (2010). A series dynamic resistor-based converter protection schemes for doubly fed induction generator during various fault conditions. IEEE Trans. Energy Convers. 25 (2), 422–432. doi:10.1109/TEC.2009.2037970

CrossRef Full Text | Google Scholar

Zhang, Y., Liu, X., and Qu, B. (2017). Distributed model predictive load frequency control of multi-area power system with DFIGs. IEEE/CAA J. Autom. Sinica. 4 (1), 125–135. doi:10.1109/jas.2017.7510346

CrossRef Full Text | Google Scholar

Zhao, C., Topcu, U., Li, N., and Low, S. (2014). Design and stability of load-side primary frequency control in power systems. IEEE Trans. Automat. Contr. 59 (5), 1177–1189. doi:10.1109/tac.2014.2298140

CrossRef Full Text | Google Scholar