Generating Hexahedral Mesh for Wire-wrapped Fuel Assembly With RBF Mesh Deformation Method

Fuel assemblies with wire spacer are widely used in Generation IV liquid nuclear reactors. With the rapid development of computational power, the Computational Fluid Dynamic (CFD) method is becoming an effective tool to investigate the detailed three-dimensional thermal hydraulic characteristics in wire-wrapped fuel assemblies. Due to the complexity of geometry, most of the published researches are performed with large number tetrahedron or polyhedral cells. The simulation is quite time-consuming and is generally limited to assemblies with small number of fuel pins. In this paper, a hexahedron meshing strategy is developed based on the Radial Basis Function (RBF) theory in present paper. This strategy would be beneficial for the modeling for the wire-wrapped fuel assemblies in real nuclear reactor core with large number of fuel pins. To validate this strategy, two experiments are simulated and detailed flow parameter distributions within the bundle, including the pressure distribution and the temperature distribution, have been compared. Good agreements have been achieved between the simulation results and the experimental results.

Introduction

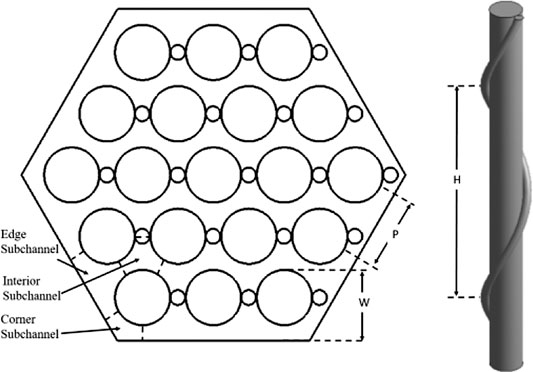
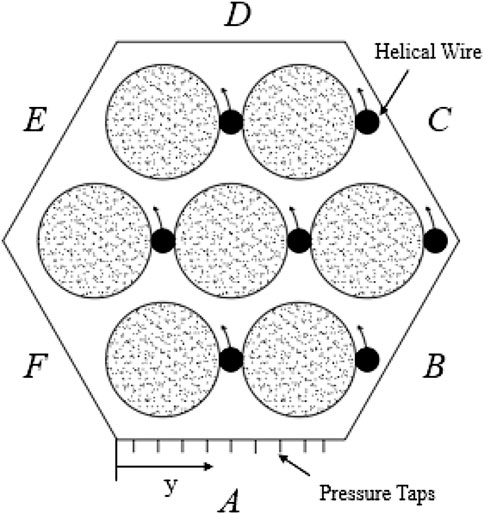
Wire-wrapped fuel assembly is a type of fuel assembly adopting helically wound wires as spacer grids to maintain the gap between adjacent fuel rods. Compared to the fuel assembly with grid-type spacers, wire-wrapped fuel assembly could generally achieve a lower pressure drop with a compact fuel rod packing (Todreas and Kazimi, 2011). Wire-wrapped fuel assembly are widely used in the Generation IV nuclear reactors, including the Sodium-cooled Fast Reactors (SFR) (Chen et al., 2018), the Lead-cooled Fast Reactors (LFR) (Pacio et al., 2018) and the Super Critical Water Cooled Reactors (SCWRs) (Shan et al., 2014). In the wire-wrapped fuel assembly, fuel rods are generally arranged in a hexagonal array, and the coolant flows in gaps around fuel rods, which are termed as the sub-channels. The geometry of a typical wire-wrapped fuel assembly is determined with four parameters, the diameter of fuel rod D, the pitch distance p, the wall distance W, and the lead pitch H, as shown in Figure 1. Alternate configurations with multiple wires (Liu et al., 2017) and non-hexagonal duct (Zhao et al., 2020) are not considered in present paper.

FIGURE 1

FIGURE 1. A typical wire-wrapped fuel assembly configuration.

As one of key components of the nuclear reactor, the modeling for the fuel assembly is of great value for the design and safety analysis (Wang et al., 2021). Traditionally, the analysis is performed based on the use of correlations called mixing laws (Todreas and Wilson, 1968; Nishimura et al., 2000), which could provide the thermal-hydraulic characteristics of the main flow. Such analysis is useful for the global design of the nuclear core and the primary coolant loop. However, the traditional analysis relies on a large number of experiments, the analysis is quite costly. And furthermore, the analysis could provide very limited information about the detailed flow field for the design optimization. With the increased computational power during the past 2 decades, more and more people are performing analysis for wire-wrapped fuel assemblies with the Computational Fluid Dynamic (CFD) method. Kim and Ahmad (Ahmad and Kim, 2005), Pointer et al. (Pointer et al., 2009), Natesan et al. (Natesan et al., 2010), Gajapathy et al. (Gajapathy et al., 2015)and Chai (Chai et al., 2020) successfully analyzed the thermal-hydraulic characteristics within wire-wrapped assemblies based on the Reynolds Averaged Navier-Stokes (RANS) approach. And various factors of the numerical approach have been investigated, including the turbulence model (Shams et al., 2018), cell aspect ratio (Smith et al., 2008) and wire wrap contact representation (Merzari et al., 2012). These results are encouraging as they provided an insight to the internal flow field within the wire-wrapped fuel assembly. However, it should be noted that most of these researches are limited to assemblies with small number of fuel rod pins due to the heavy computational cost. So far, only few people have successfully performed the simulation for the full length fuel assembly with larger number of fuel rod pins (Cadiou and Saxena, 2015; Chen et al., 2018).

Due to the geometry complexity of the wire-wrapped fuel assembly, it is hard to mesh the wire-wrapped assembly with high mesh quality (Rolfo et al., 2012). Most of present simulations were performed with meshes consisting of tetrahedron or polyhedron cells. For these cells, the axial height is limited, tens of millions cells are required even for the fuel assembly with 19 pins (Chai et al., 2020). To reduce the computational cost, several different mesh strategies have been proposed. In 2015, Cadiou (Cadiou and Saxena, 2015) developed a dedicated meshing tool based on the technique of multi-block grid with the mesh generator from the National Eronautics and Space Administration (NASA). The fluid region of the sub-assembly is divided into a set of two-Dimensional (2D) slices in axial direction and surface meshes are generated on each slice region separately. After the 2D slice meshing, the initial rod bundle is rebuilt by assembling all the axial slices. With this meshing tool, they performed a CFD simulation for 217-pin fuel assembly with 15 million cells. Liu (Liu et al., 2017) and Jeong (Jeong et al., 2017) proposed a similar strategy based on the hybrid mesh technique independently. In their work, the fluid region of the sub-assembly is divided into regular regions around fuel pins and irregular regions connecting the former regions in radial direction. Hexahedron meshes and pentahedral meshes are generated for regular regions and irregular regions separately. And then different regions are combined to rebuilt the assembly through the mesh interface technique. For both of methods mentioned above, non-conformal nodes exist on the interface between different slices or regions as they are meshed independently. In 2018, Chen (Chen et al., 2018) developed a marking and separating meshing method for wire-wrapped fuel assembly based on the domain extension method. The helical surface of the wire is approximated through fine hexahedral cells. Besides these traditional methods, Smith (Smith et al., 2008) and Rolfo (Rolfo et al., 2012) adopted a special technique called the node-matched body-fitted conformal mesh technique. The hexahedral mesh is first generated for the fuel assembly without the helical wire and then the mesh is deformed to account for the position of the wire wrap. Unfortunately, no details have been reported about the deformation process.

In present paper, we provide the mesh deformation details for the mesh strategy described by Smith (Smith et al., 2008) based on the Radial Based Function (RBF) theory (Buhmann, 2009). To validate the mesh strategy, two experiments were simulated and detail flow parameters from the flow fields within the assembly were compared between the CFD simulation and the experimental measurements, including the detailed pressure distribution and the detailed temperature distribution. The mesh strategy is briefly described in Mesh Strategy, and the validations are presented in Validation and Discussion, including a hydraulic simulation for a 7-pin wire-wrapped fuel assembly and a heat transfer simulation for a 19-pin wire-wrapped fuel assembly. And finally, a short conclusion is drawn for present work in Conclusion.

Mesh Strategy

As stated in the introduction, present mesh strategy contains two steps: firstly, generating a hexahedral mesh for the bare rod fuel assembly, which holds the same geometry parameters with those of the desired wire-wrapped fuel assembly; secondly, deforming the mesh from the first for the helical wires. The first step could be easily performed with common mesh tools that support the hexahedral mesh, such as the ANSYS ICEM (ANSYS, 2012), ANSYS Meshing (ANSYS, 2013) and the Automatic Net-generation for Structure Analysis (ANSA) (ANSA, 2012). The main task for present mesh strategy is performing the mesh deformation.

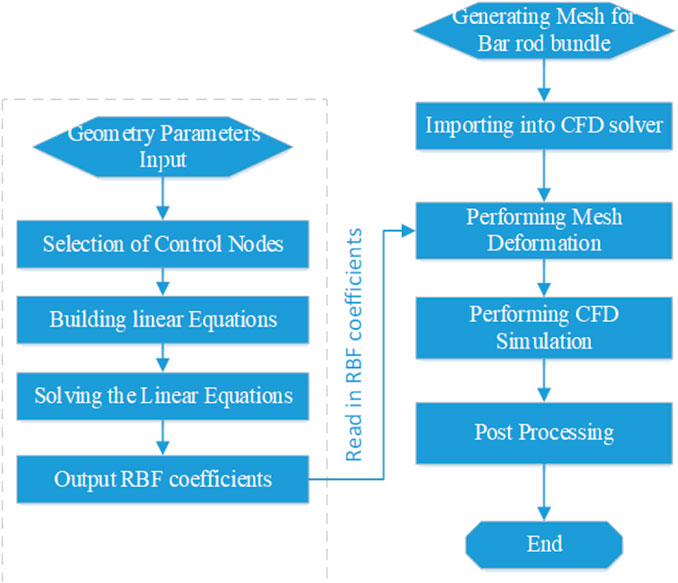
The mesh deformation method adopted here is based on the RBF theory, and it is one of the most popular schemes for large mesh deformation in recent years (Kedward et al., 2017). The mesh deformation process contains three steps: firstly, selecting an appropriate type of the radial function; secondly, selecting some control nodes from the original mesh and the deformed mesh; thirdly, solving some linear equations for the RBF coefficient and calculating the deformation for the original mesh. The whole process for the proposed mesh strategy in present paper is shown in Figure 2.

FIGURE 2

FIGURE 2. The proposed mesh strategy.

In the following section, a general introduction to the RBF mesh deformation is given first, and then the selection of control nodes is discussed in detail for wire-wrapped fuel assembly.

RBF Mesh Deformation

Supposing the coordinate of the original mesh node is $\overrightarrow{x}$, the coordinate of the deformed mesh node is $\overrightarrow{y}$, the displacement between the two nodes is $d\overrightarrow{r}$.

$d\overrightarrow{r}=\overrightarrow{y}-\overrightarrow{x},(1)$

According to the RBF theory, the displacement could also be determined by nodes from the original mesh.

$d\overrightarrow{r}={\displaystyle \sum _{i=1}^N{\overrightarrow{\alpha }}_i\phi \left(\Vert \overrightarrow{x}-{\overrightarrow{x}}_i\Vert \right)},(2)$

where ${\overrightarrow{x}}_i$ is the node from the original mesh, $\phi$ is the radial function, the ${\overrightarrow{\alpha }}_i$ is the RBF coefficients, N is the number of nodes from original mesh model, $\Vert \overrightarrow{x}-{\overrightarrow{x}}_i\Vert$ is the Descartes distance between two nodes.

Assuming the displacements for N nodes from the deformed mesh are known, 3N linear equations could be built with Eq. 2.

$\left[\begin{array}{cccc}{\phi }_{11}& {\phi }_{12}& \cdots & {\phi }_{1N}\\ {\phi }_{21}& {\phi }_{22}& \cdots & {\phi }_{2N}\\ ⋮& ⋮& \ddots & ⋮\\ {\phi }_{N1}& {\phi }_{N2}& \cdots & {\phi }_{NN}\end{array}\right]\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ ⋮\\ {\alpha }_N\end{array}\begin{array}{c}{\beta }_1\\ {\beta }_2\\ ⋮\\ {\beta }_N\end{array}\begin{array}{c}{\gamma }_1\\ {\gamma }_2\\ ⋮\\ {\gamma }_N\end{array}\right]=\left[\begin{array}{c}d{r}_{1x}\\ d{r}_{2x}\\ ⋮\\ d{r}_{3x}\end{array}\begin{array}{c}d{r}_{1y}\\ d{r}_{2y}\\ ⋮\\ d{r}_{3y}\end{array}\begin{array}{c}d{r}_{1z}\\ d{r}_{2z}\\ ⋮\\ d{r}_{3z}\end{array}\right],(3)$

where ${\alpha }_i$, ${\beta }_i$, and ${\gamma }_i$ are the RBF coefficient for displacement in x, y and z direction respectively.

Solving the equations to obtain these weighting function coefficient, the displacement could be obtained for any node in the original mesh with Eq. 2. The quality of the deformed mesh is greatly influenced by the form of the radial function. With some pre-testing, it is found that the deformation is more likely to succeed with the Wendland’s C² function. This function is presented as following:

$\phi \left(\eta \right)=\{\begin{array}{cc}0& \eta >1\\ {\left(1-\eta \right)}^4\left(4\eta +1\right)& \eta \le 1\end{array},(4)$

where $\eta =\Vert \overrightarrow{x}-{\overrightarrow{x}}_i\Vert /R$, R is the support radius. More description about the RBF theory could be found in the work of Buhmann (Buhmann, 2009).

Selection of Control Nodes

As many researchers have stated that, in the wire-wrapped fuel assembly, the wire is in line contacts with fuel pins and it is hard to generate a proper mesh model for such a geometry. To simplify the geometry, the wire is blended to the central fuel pin with a small displacement. And a fillet is generally introduced at the contact region between the wire surface and fuel pin surface. Such a simplification has been tested by Gajapathy (Gajapathy et al., 2007), Hamman and Berry (Hamman and Berry, 2010), the simplification would not change the turbulent flow and heat transfer characteristics of the wire-wrapped rod bundles significantly.

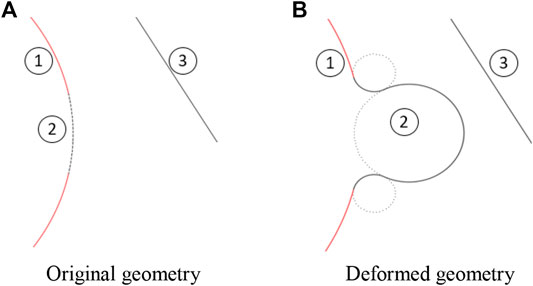
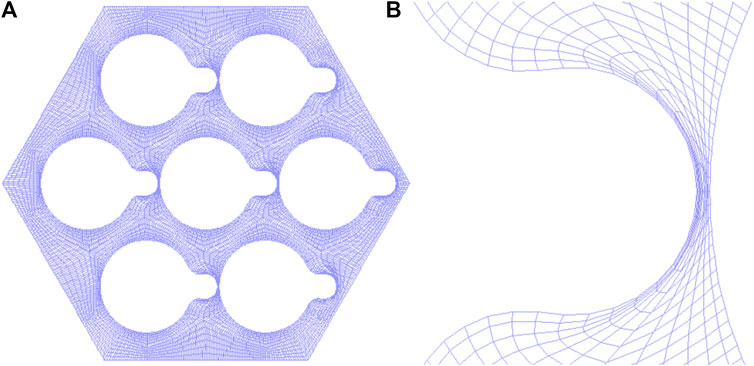
Instead of performing the mesh deformation for the whole fluid domain in one time, the domain is divided into a set of 2D slices in axial direction and the deformation is performed on each 2D zone. According to the geometry shape and deformation, geometries in the 2D zone could be categorize into three types: type 1, non-deformed lines for the duct wall; type 2, deformed circular arcs for the fuel pins; type 3, non-deformed circular arcs for the fuel pins, as shown in Figure 3. For geometry 1 and geometry 3, equations for them could be built with primary geometry theory. Control nodes were taken evenly, and the displacements were assumed to 0.

FIGURE 3

FIGURE 3. Original geometry and deformed geometry. (A) Original geometry. (B) Deformed geometry.

For geometry 2, part of the deformed circular arc will be converted into arcs for the wire and the rest will be converted into arcs of the fillet circles, as shown in Figure 4.

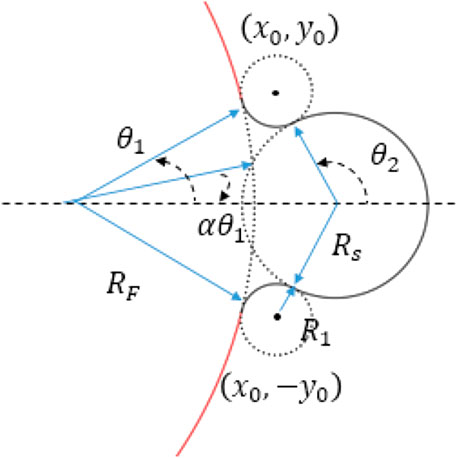
Assuming the radii for the fuel pin, the wire and fillet circle are R_F, R_s and R₁ respectively. And the distance between the center of the wire and the fuel pin is D. Coordinates for the center of the fillet circles is (x₀, y₀) and (x₀, −y₀).

As the fillet circle is in tangency contact with the fuel pin circle and the wire circle, the following equations could be obtained.

$x_0^2+y_0^2={\left(R_F+R_1\right)}^2,(5)$

${\left[x_0-D\right]}^2+{\left[y_0\right]}^2={\left(R_s+R_1\right)}^2,(6)$

By solving these equations, the coordinates for the center of the fillet circles are determined.

$x_0=\frac{{\left(R_F+R_1\right)}^2+D^2-{\left(R_s+R_1\right)}^2}{2D},(7)$

FIGURE 4

FIGURE 4. Parameters for the deformed geometry.

$y_0^2={\left(R_F+R_1\right)}^2-{\left[\frac{{\left(R_F+R_1\right)}^2+D^2-{\left(R_s+R_1\right)}^2}{2D}\right]}^2,(8)$

Taking the center of the fuel pin circle as the reference original node, the angle coordinate of the contact nodes between the fillet circle and the fuel pin circle, and between the fillet circle and the wire circle is obtained,

${\theta }_1=\arctan \left(\frac{y_0}{x_0}\right),(9)$

${\theta }_2=\arctan \left(\frac{y_0}{x_0-\text{D}}\right)+\pi ,(10)$

Supposing node on the fuel pin circle is evenly mapped to the fillet circle and the wire circle, node arc between 0 and $\alpha {\theta }_1$ will be mapped to wire arc, arc between $\alpha {\theta }_1$ and ${\theta }_1$ will be mapped to the fillet arc. $\alpha$ is positive number less than 1, and is calculated as following,

$\alpha =\frac{R_s{\theta }_2}{R_1\left({\theta }_2-{\theta }_1\right)+R_s{\theta }_2},(11)$

The corresponding relationship between the control nodes on the original mesh and on the deformed mesh is summarized as Table 1.

TABLE 1

TABLE 1. Corresponding relationship between the original mesh and the deformed mesh.

Validation and Discussion

To validate the mesh strategy, two experiments with detailed flow parameter measurements were simulated, including the Fernandez’s pressure measurements with 7-pin wire-wrapped fuel assembly and the Karlsruhe Liquid Metal Laboratory (KALLA) experiment with 19-pin wire-wrapped fuel assembly. In these experiments, the test sections contain several lead pitches. To reduce the computational cost, boundary layer meshes were not pursued during the simulation. And three turbulence models were adopted for both experiments, and they are the Realizable k-ε model (RKE), the SST k-w model (SST-KW) and the Reynolds Stress Model (RSM).

Flow Analysis

Description of the Model

The experiment adopted here should be conducted by Fernandez and Carajilescov in 1979, aiming at providing local experimental data for code validation (Fernandez y Fernandez and Carajilescov, 2000). The experiment was performed in an open loop with air as the working fluid. The test section consists of seven wire-wrapped rods. To reduce flow perturbations due to the instrumentations, the fuel rod takes a large diameter of 50 mm the pitch to diameter ratio P/D and wire lead to diameter ratio L/D are 1.20 and 15 respectively. The full length of the test section is 2,300 mm. While the measuring level is located at L/D = 40 from the entrance section.

Pressure taps are uniformly distributed on the hexagonal duct, and each side of the housing holds nine pressure taps. For fuel rods, a static pressure take is installed on a portion of the rods and this section can rotate independently of the remaining parts. Therefore, flow parameters around the rod surface could be measured continuously in azimuth direction. Figure 5 shows the cross section and the pressure taps arrangement. More experimental details could be found in (Fernandez y Fernandez and Carajilescov, 2000).

FIGURE 5

FIGURE 5. Cross section for the 7-pin wire-wrapped fuel assembly.

With the mesh deformation strategy in Mesh Strategy, a hexahedron mesh was generated for the test section. The original hexahedron mesh for the bare rod assembly was generated with the meshing tool, Ansys Meshing. The axial height for grid is 5 mm, and 12 cells are placed between two fuel pins, as shown in Figure 6. The mesh model used for simulation consists of two million cells with a minimum orthogonality of 0.11.

FIGURE 6

FIGURE 6. Meshing model for 7-pin wire-wrapped fuel assembly.

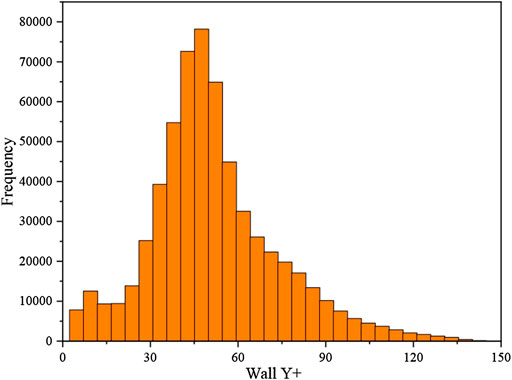
To check the mesh quality, the wall y + values for all the cells near the rod and the wire are obtained and are shown in the histogram of Figure 7. The largest wall y+ is 142, and majority of wall y + cells are below 100. For the k-ε turbulence was adopted here, the enhanced wall function was used for the near wall treatment.

FIGURE 7

FIGURE 7. Number of cells with wall y + values.

Pressure Distribution

Figures 8A–C show the pressure distribution on the duct wall, the central rod and the periphery rod obtained by CFD prediction and experimental measurement. The results was obtained at an inlet Reynolds number of 33,000. The dimensionless process for pressure is presented as following:

$p^{\ast }=\frac{p-\overline{p}}{\left(\rho {\overline{u}}^2/2\right)},(12)$

where p is the local pressure, $\overline{p}$ is the averaged pressure at the measuring level, $\overline{u}$ is the averaged velocity at the measuring level, $\rho$ is the density of air.

FIGURE 8

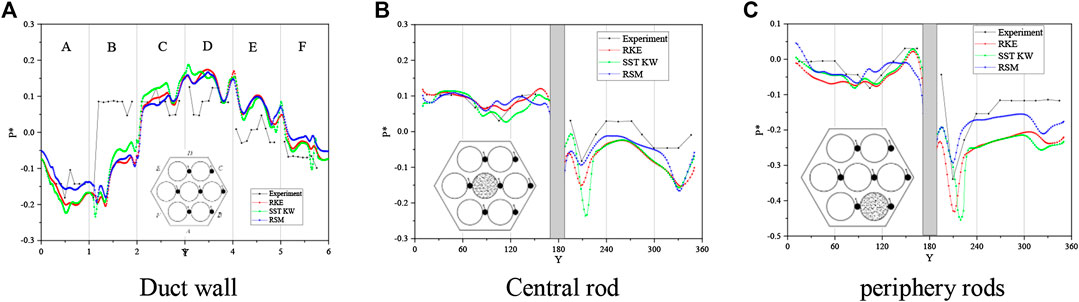
FIGURE 8. Comparison of the pressure Distribution. (A) Duct wall. (B) Central rod. (C) periphery rods.

For the duct wall, pressure shows an approximately sine distribution, the lowest pressure appears roughly on the side A, while the highest pressure appears on the side D. In the peripheral sub-channels (including edge channels and corner channels), the wire always moves in a counter clockwise direction, which forces the air to flow in the same direction. For the side B, C, and D, the wire forces the air to flow against the duct wall, thus causing the rising pressure. On the side A, E, and F, the wire no longer pushes the air, and the pressure for the air gradually drops in circumferential direction due to the friction caused by the duct surface and the rod surface. Furthermore, due to the wake effect behind the wire and the flow diversion caused by the rods, there are small fluctuations in the local pressure near the duct wall. The pressures distribution around the central rod and the periphery rod show a decreasing trend in the circumferential direction. And due to similar influence caused by the surrounding geometries, the pressures hold some local fluctuations. The biggest influence comes from the wire round neighbor rods. The pressures show distinct fluctuations at azimuth angle of 180.

For the duct wall pressure distribution, the CFD prediction agrees well with the experimental measurement, and both the global distribution and local fluctuations are correctly predicted. In the CFD prediction, pressures at vertexes of corner sub-channels show a significant jump. This is because the flow near the vertexes is almost stagnant, and the dynamic pressure head is converted into a static pressure head, so the pressure is higher than the surrounding region. The pressure jump on the side B predicted by the simulation shows a larger amplitude than the experimental measurement, and the transition position predicted by the simulation shows a delay in circumferential direction. The delay of the transition position for the pressure jump may be caused by the simplification of the wire. As the wire is blended to the rod, the gap between the wire and the duct wall is little larger in the simulation than that in the experiment, which results in a larger circumferential cross flow near the duct wall. The cross-flow results in the delay of the transition position and a smaller pressure jump amplitude. The delay of the transition position could also be observed in the side C.

For the pressure distribution on the surface of rods, the simulation also gives a good prediction, but it is obvious that the prediction in the range of 0–180° is better than in the range of 180–360°. In the range of 0–180°, the flow is mainly forced flow driven by the winding wire, while in the range of 180–360°, the flow is mainly wake flow behind the wire. The turbulence models adopted here are more applicable prediction for the forced flow. For the range of 180–360°, the performance of the RSM model is little better than the others. Different to the general agreement that SST k-W model is more applicable for the wire-wrapped fuel assembly, the SST k-W model does not give a better prediction than other turbulence model. It may be caused by the inadequate mesh treatment near the boundary layer.

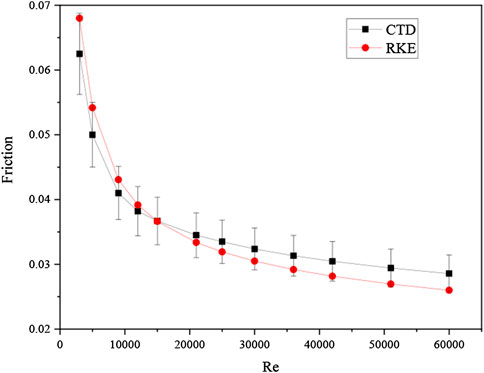
The experiments report does not give the pressure drop under different mass flow rates. To test the mesh strategy against different Reynolds number, we changed the inlet velocity in the simulation, and compared the simulation results against the Cheng-Todreas Detailed (CTD) pressure drop correlation (Chen et al., 2014). Figure 9 shows the comparison results. These results are obtained with the realizable k-ε model. The friction factor obtain with the CFD simulation agrees well with the formulation, and the relative deviation is within 10% over the Reynolds number range from 3,000 to 60,000. As the Reynolds number increase, the prediction deviation of the two methods gradually changes from positive to negative, and the pressure drop predicted by the CFD model is greater than that predicted by the CTD correlation at the low Reynolds number, while the CFD prediction result is lower than the CTD correlation prediction at the high Reynolds number. The different may be caused by the simplification of the geometry. During the mesh generation process, the wire is blended to the fuel pin. This may result in a larger gap and more mass flow rate in the edge sub-channel. As is known, the edge sub-channel is trend to hold a lower friction factor. Therefore, the total pressure drop was under predicted. According to Zohuri (Zohuri and Fathi, 2015), the uncertainty for present friction formulation is ±12%. Therefore, the pressure drop predicted with the present model is acceptable.

FIGURE 9

FIGURE 9. Comparison of the friction factor.

Heat Transfer Analysis

Description of the Model

The experiment adopted here was conducted by J. Pacio in 2016 at Karlsruhe Institute of Technology (KIT), Germany (Pacio et al., 2016), aiming at studying the thermal-hydraulics of the fuel assemblies envisaged for the Multi-purpose hybrid Research Reactor for High-tech Application (MYRRHA) reactor. The experiment was performed on the Thermal-Hydraulics and ADS Design (THEADES) loop with liquid Lead-Bismuth Eutectic (LBE) as the working fluid. The test section consists of 19 wire-wrapped heating rods that simulate the nuclear fuel rods. The geometry of the test section is similar to that of fuel assembly in the MYRRHA reactor, the diameter D, pitch to diameter ratio P/D and wire lead to diameter ratio H/D are 8.2 mm, 1.28 and 40 respectively. The full length for the rods is about 1,694 mm, while the length for the heat section is 870 mm.

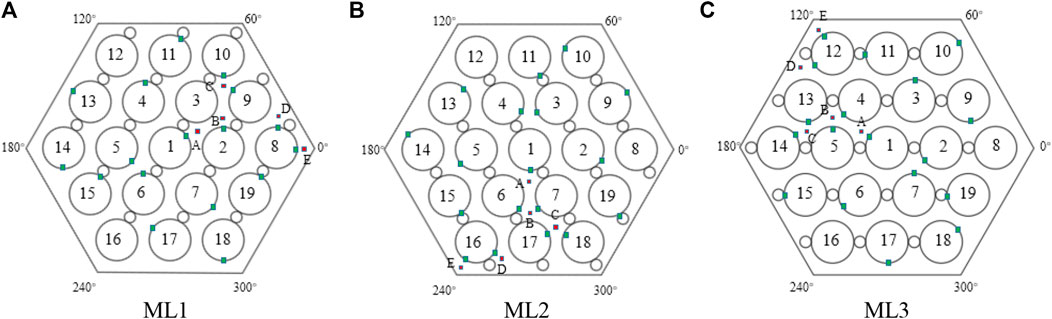
Thermos-couples were installed at three measuring level and temperatures in the center of sub-channels and on the surface of heat rods were measured. The measuring levels are named as ML1, ML2 and ML3, locating at 54.6 mm (L/H = 1/6), 601.3 mm (L/H = 11/6), 820 mm (L/H = 15/6) from the heating section entrance. Figure 10 shows the cross section and the thermal couple arrangements. The red points represent thermos-couples for temperatures in the center of sub-channels, and the green points represent thermos-couples for temperatures on the surface of heating rods. More experimental details could be found (Pacio et al., 2016).

FIGURE 10

FIGURE 10. The cross section for the measuring levels. (A) ML1. (B) ML2. (C) ML3.

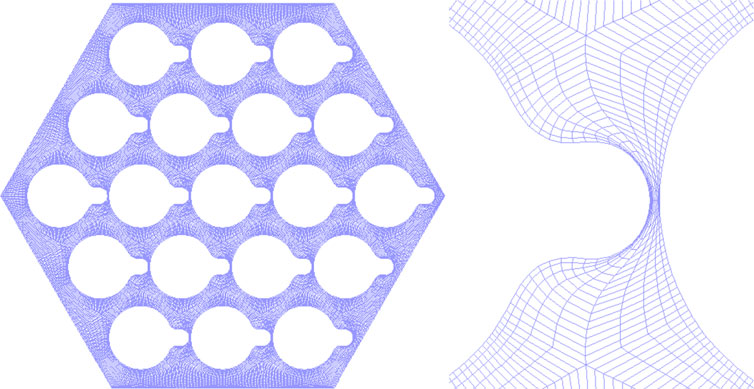
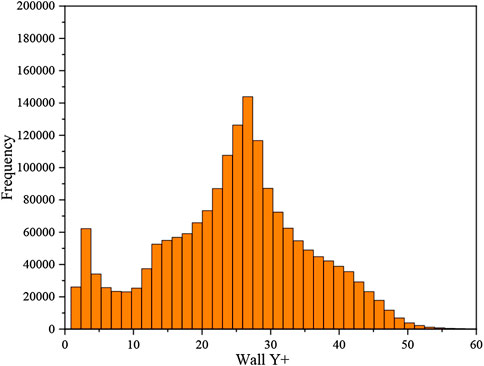
Different to the original geometry, the fillets in the corner sub-channels are ignored. To reduce the computational cost and improve the boundary layer mesh, the bias option has been activated for the node distribution with a bias factor of 3.0.10 layer cells were placed between fuel pins and the axial height for the cell is 0.004 m. The mesh model used for simulation consists of 13 Million cells with a minimum orthogonality of 0.1. Figure 11 shows the mesh for 19-pin wire-wrapped fuel assembly. The largest wall y + for present mesh model is 60, and about 7% cells fall in the viscous layer, as shown in Figure 12.

FIGURE 11

FIGURE 11. Meshing model for 19-pin wire-wrapped fuel assembly.

FIGURE 12

FIGURE 12. Number of cells with wall y + values.

The reference case reported by Pacio (Pacio et al., 2017) was taken for simulation, that is, the mass flow rate and temperature at the inlet of the assembly 15.97 kg/s and 473.15 K, respectively.

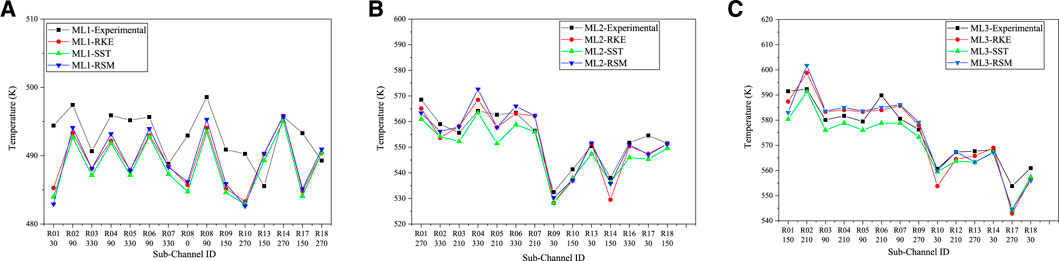
Temperature Distribution

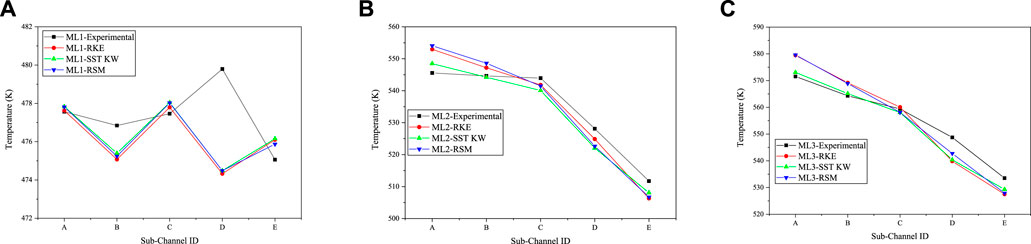
Figures 13A–C show the temperature distribution at the center of sub-channels on the three measuring levels obtained through the simulation and the experiment. From Figures 10B, it could be found that the fluid temperature of the central sub-channels is higher than that of the peripheral sub-channels. This is because the porosity of the central sub-channels is lower than that of the peripheral sub-channels, and the small porosity results in a higher volumetric power density and a smaller coolant flow rate in the central sub-channels. The temperature distribution on ML1 roughly conforms to this law. The temperatures rise at the node C and D should be influenced by the underdeveloped flow. The measuring level ML1 is quite closer to the entrance of the test section and the flow velocity has not been yet fully developed. The flow rate of the central channel is higher than that when it is fully developed, while the flow rate of the peripheral channel is relatively lower than that when it is fully developed.

FIGURE 13

FIGURE 13. Comparison of the temperature at the center of sub-channels. (A) ML1. (B) ML2. (C) ML3.

The temperature at the center of sub-channel predicted by CFD agrees well with the experimental measurement, and the predictions on ML2 and ML3 show better agreement than that on ML1. For the measuring level ML1, the simulation accurately predicted the temperature distribution, except for the node D. From node A to C, the CFD model gives a lower temperature than the experimental measurement. This is caused by the underdeveloped flow at the entrance region of the heat section. The CFD model omits the inlet section before the heating section and assumes a uniform velocity distribution at the inlet of the heat section. Compared to the experiment, more fluid flows in the central sub-channels. For the measuring level ML2 and ML3, the three turbulence models all overestimated the temperature of the central sub-channel and underestimated the temperature of the peripheral sub-channel. Pacio (Pacio et al., 2017) and Fricano (Fricano and Baglietto, 2014) have mentioned such a problem in their report, and they attributed this problem to the distortion of the turbulent heat transfer model. Besides that reason, it may also be influenced by the simplification of the wire. As has been stated in Description of the Model, the simplification results in a larger flow area for peripheral sub-channels, and more fluid flow in peripheral sub-channels. In the SST K-W model, a rough wall was specified for the duct wall, which suppressed the axial flow in peripheral sub-channels. So, the predicted center channel temperature is slightly better than the other two models.

Figures 14A–C show the temperature distribution on the surface of the rods obtained through the experiment and the simulation. The wall temperature also shows a decreasing distribution in radial direction. The temperature on the inner rod is higher than that on the outer rod. This distribution is particularly obvious on the ML3 section. However, it should also be noted that the wall temperature fluctuates greatly. This is because the wall temperature is greatly affected by the local flow field. And the flow velocity in the assembly is highly non-unformed due to the helical wire. The temperature distribution predicted by the CFD model agrees well with the experiments.

FIGURE 14

FIGURE 14. Comparison of the temperature on the rod surfaces. (A) ML1. (B) ML2. (C) ML3.

Figures 15A and 5B show the cumulative frequency distribution histogram of the relative deviation between the simulation and the experiments for the temperature at the center of sub-channels and the temperature on the surface of rods. And the relative deviation is calculated as following:

${\text{Error}}_{\text{Relative}}=\left|\frac{T_{CFD}-T_{\text{Measurement}}}{T_{\text{Measurement}}-T_{\text{inlet}}}\right|\times 100\%,(13)$

where T_CFD is the temperature predicted through CFD, T_Measurement is the experimental value, T_inlet is the inlet fluid temperature.

FIGURE 15

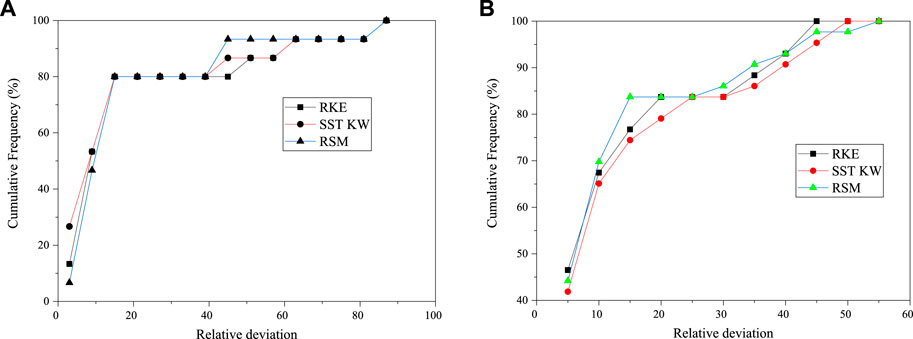
FIGURE 15. Cumulative frequency distribution histogram. (A) Deviation for sub-channel temperature. (B) Deviation for rod surface temperature.

For the temperature at the center of sub-channels, the largest deviation is about 80%. And the deviation comes from the prediction for node D on ML1. For about 80% nodes, the relative deviation falls in 20%. For the temperature on the surface of rods, the largest deviation is about 55%. And large deviations come from the prediction for the Rod-1 on ML1. If the predictions for ML1 are left out, the deviation is greatly reduced, as shown in Figures 16A and 6B. The largest deviation for the sub-channel temperature and wall temperature are greatly reduced and fall to 15%. While the SST K-W model shows a better performance for the prediction of the temperature at the center of sub-channels, this turbulence shows a little bit poorer performance for the temperature on the rod surface. Therefore, three turbulence models show similar performance.

FIGURE 16

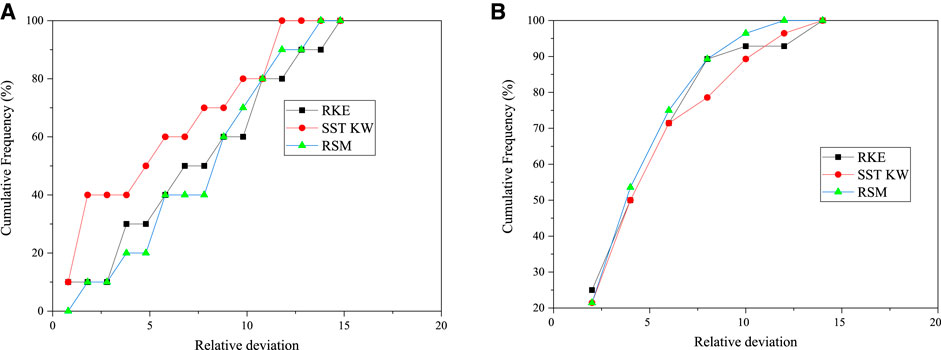
FIGURE 16. Cumulative frequency distribution histogram (without ML1). (A) Deviation for sub-channel temperature. (B) Deviation for rod surface temperature.

Conclusion

Based on the RBF mesh deformation method, a hexahedral mesh strategy is proposed for the wire-wrapped fuel assembly CFD simulation, which could be generated from the deformation of a bare rod fuel assembly mesh model. Compared to the common mesh generation strategy, the cell amount could be greatly reduced. In addition, there is no non-conformal nodes or coarse boundary surface in the mesh model, and so the high order discretization schemes could be used for the numerical investigation, such as the LES or the q-DNS simulation.

The mesh generation strategy was validated with two experiments and detailed flow field parameters were compared between the simulations and the experiments. And good agreements have been achieved. More specifically, for the 7-pin fuel assembly, the maximum relative deviation for pressure drop between the CFD prediction and the experimental formulation prediction is estimated to be 10% over the Reynolds number range from 3,000 to 60,000. For the 19-pin fuel assembly, the maximum relative deviation for temperature distribution between the CFD prediction and the experimental measurement is within 15%. The large deviation between the simulation and the experimental measurement may be caused by the uniform velocity distribution assumption at the inlet during the simulation.

In the future work, the high fidelity thermal hydraulic analysis of the wire-wrapped fuel assembly with large number of fuel pins will be performed with this advance mesh generation technology.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

DZ and WT: Conceptualization, Methodology, Software. XW and MW: Data curation, Writing-Original draft preparation. SW: Visualization, Investigation. GS and SQ: Supervision. YuL: Software, Validation. YaL and LZ: Writing-Reviewing and Editing.

Funding

The authors gratefully acknowledge the supports from Natural Science Foundation of China (Grant No. 11705139, No. 12075185), K. C. Wong Education Foundation and the Innovative Scientific Program of CNNC.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ahmad, A., and Kim, K.-Y. (2005). “Three-dimensional analysis of flow and heat transfer in a wire-wrapped fuel assembly,” in Proc. of ICAPP. Seoul, South Korea. May 15–19, 2005. (Seoul, South Korea: ICAPP). 5071.

Google Scholar

ANSA (2012). ANSA version 13.2.4. user’s guide BETA CAE Systems S.A. Available at: https://www.beta-cae.com/news/20121206_announcement_ansa_v13.2.4.pdf.

Google Scholar

Ansys, I. (2012). ANSYS ICEM CFD user manual. Available at: https://silo.tips/download/ansys-icem-cfd-users-manual.

Google Scholar

Ansys, I. (2013). ANSYS meshing user’s guide. Available at: https://www.academia.edu/27974461/ANSYS_Meshing_Users_Guide.

Google Scholar

Buhmann, M. (2009). Radial Basis functions - theory and implementations, cambridge monographs on applied and computational mathematics. New York, NY: Cambridge.

Google Scholar

Cadiou, T., and Saxena, A. (2015). Thermal–hydraulic numerical simulation of fuel sub-assembly using a dedicated meshing tool. Nucl. Eng. Des. 295, 162–172. doi:10.1016/j.nucengdes.2015.10.001

CrossRef Full Text | Google Scholar

Chai, X., Liu, X., Xiong, J., and Cheng, X. (2020). Numerical investigation of thermal-hydraulic behaviors in a LBE-cooled 19-pin wire-wrapped rod bundle. Prog. Nucl. Energy 119, 103044. doi:10.1016/j.pnucene.2019.103044

CrossRef Full Text | Google Scholar

Chen, J., Zhang, D., Song, P., Wang, S., Wang, X., Liang, Y., et al. (2018). CFD investigation on thermal-hydraulic behaviors of a wire-wrapped fuel subassembly for sodium-cooled fast reactor. Ann. Nucl. Energy 113, 256–269. doi:10.1016/j.anucene.2017.11.023

CrossRef Full Text | Google Scholar

Chen, S., Todreas, N., and Nguyen, N. (2014). Evaluation of existing correlations for the prediction of pressure drop in wire-wrapped hexagonal array pin bundles. Nucl. Eng. Des. 267, 109–131. doi:10.1016/j.nucengdes.2013.12.003

CrossRef Full Text | Google Scholar

Fernandez y Fernandez, E., and Carajilescov, P. (2000). Static pressure and wall shear stress distributions in air flow in a seven wire-wrapped rod bundle. J. Braz. Soc. Mech. Sci. 22, 291–302. doi:10.1590/S0100-73862000000200012

CrossRef Full Text | Google Scholar

Fricano, J., and Baglietto, E. (2014). A quantitative CFD benchmark for sodium fast reactor fuel assembly modeling. Ann. Nucl. Energy 64, 32–42. doi:10.1016/j.anucene.2013.09.019

CrossRef Full Text | Google Scholar

Gajapathy, R., Velusamy, K., Selvaraj, P., and Chellapandi, P. (2015). CFD investigation of effect of helical wire-wrap parameters on the thermal hydraulic performance of 217 fuel pin bundle. Ann. Nucl. Energy 77, 498–513. doi:10.1016/j.anucene.2014.10.038

CrossRef Full Text | Google Scholar

Gajapathy, R., Velusamy, K., Selvaraj, P., Chellapandi, P., and Chetal, S. C. (2007). CFD investigation of helical wire-wrapped 7-pin fuel bundle and the challenges in modeling full scale 217 pin bundle. Nucl. Eng. Des. 237, 2332–2342. doi:10.1016/j.nucengdes.2007.05.003

CrossRef Full Text | Google Scholar

Hamman, K. D., and Berry, R. A. (2010). A CFD simulation process for fast reactor fuel assemblies. Nucl. Eng. Des. 240, 2304–2312. doi:10.1016/j.nucengdes.2009.11.007

CrossRef Full Text | Google Scholar

Jeong, J.-H., Song, M.-S., and Lee, K.-L. (2017). Thermal-hydraulic effect of wire spacer in a wire-wrapped fuel bundles for SFR. Nucl. Eng. Des. 320, 28–43. doi:10.1016/j.nucengdes.2017.05.019

CrossRef Full Text | Google Scholar

Kedward, L., Allen, C., and Rendall, T. (2017). Efficient and exact mesh deformation using multiscale RBF interpolation. J. Comput. Phys. 345, 732–751. doi:10.1016/j.jcp.2017.05.042

CrossRef Full Text | Google Scholar

Liu, L., Wang, S., and Bai, B. (2017). Thermal-hydraulic comparisons of 19-pin rod bundles with four circular and trapezoid shaped wire wraps. Nucl. Eng. Des. 318, 213–230. doi:10.1016/j.nucengdes.2017.04.017

CrossRef Full Text | Google Scholar

Merzari, E., Pointer, W., Smith, J., Tentner, A., and Fischer, P. (2012). Numerical simulation of the flow in wire-wrapped pin bundles: effect of pin-wire contact modeling. Nucl. Eng. Des. 253, 374–386. doi:10.1016/j.nucengdes.2011.09.030

CrossRef Full Text | Google Scholar

Natesan, K., Sundararajan, T., Narasimhan, A., and Velusamy, K. (2010). Turbulent flow simulation in a wire-wrap rod bundle of an LMFBR. Nucl. Eng. Des. 240, 1063–1072. doi:10.1016/j.nucengdes.2009.12.025

CrossRef Full Text | Google Scholar

Nishimura, M., Kamide, H., Hayashi, K., and Momoi, K. (2000). Transient experiments on fast reactor core thermal-hydraulics and its numerical analysis: inter-subassembly heat transfer and inter-wrapper flow under natural circulation conditions. Nucl. Eng. Des. 200, 157–175. doi:10.1016/S0029-5493(99)00324-6

CrossRef Full Text | Google Scholar

Pacio, J., Daubner, M., Fellmoser, F., Litfin, K., and Wetzel, T. (2016). Experimental study of heavy-liquid metal (LBE) flow and heat transfer along a hexagonal 19-rod bundle with wire spacers. Nucl. Eng. Des. 301, 111–127. doi:10.1016/j.nucengdes.2016.03.003

CrossRef Full Text | Google Scholar

Pacio, J., Daubner, M., Fellmoser, F., Litfin, K., and Wetzel, T. (2018). Heat transfer experiment in a partially (internally) blocked 19-rod bundle with wire spacers cooled by LBE. Nucl. Eng. Des. 330, 225–240. doi:10.1016/j.nucengdes.2018.01.034

CrossRef Full Text | Google Scholar

Pacio, J., Wetzel, T., Doolaard, H., Roelofs, F., and Van Tichelen, K. (2017). Thermal-hydraulic study of the LBE-cooled fuel assembly in the MYRRHA reactor: experiments and simulations. Nucl. Eng. Des. 312, 327–337. doi:10.1016/j.nucengdes.2016.08.023

CrossRef Full Text | Google Scholar

Pointer, W., Fischer, P., Smith, J., and Siegel, A. (2009). “Simulations of turbulent diffusion in wire-wrapped sodium fast reactor fuel assemblies,” in International conference on fast reactors and related fuel cycles: challenges and opportunities. Kyoto, Japan. November 2009. (Chicago, IL: Argonne National Laboratory).

Google Scholar

Rolfo, S., Péniguel, C., Guillaud, M., and Laurence, D. (2012). Thermal-hydraulic study of a wire spacer fuel assembly. Nucl. Eng. Des. 243, 251–262. doi:10.1016/j.nucengdes.2011.11.021

CrossRef Full Text | Google Scholar

Shams, A., Roelofs, F., and Baglietto, E. (2018). High fidelity numerical simulations of an infinite wire-wrapped fuel assembly. Nucl. Eng. Des. 335, 441–459. doi:10.1016/j.nucengdes.2018.06.012

CrossRef Full Text | Google Scholar

Shan, J., Wang, H., Liu, W., Song, L., Chen, X., and Jiang, Y. (2014). Subchannel analysis of wire wrapped SCWR assembly. Sci. Tech. Nuclear Installations 2014, 301052. doi:10.1155/2014/301052

CrossRef Full Text | Google Scholar

Smith, J. G., Babin, B. R., Pointer, W., and Fischer, P. F. (2008). Effects of mesh density and flow conditioning in simulating 7-pin wire wrapped fuel pins. ANL/NE/CP-61283.

CrossRef Full Text | Google Scholar

Todreas, N. E., and Wilson, L. (1968). Coolant mixing in sodium cooled fast reactor fuel bundles. Available at: https://www.osti.gov/servlets/purl/4520997.

CrossRef Full Text | Google Scholar

Todreas, N., and Kazimi, M. (2011). Nuclear systems volume I: thermal hydraulic fundamentals. 2nd Edn. Boca Raton, FL: CRC Press.

Google Scholar

Wang, M., Wang, Y., Tian, W., Qui, S., and Su, G. H. (2021). Recent progress of CFD applications in PWR thermal hydraulics study and future directions. Ann. Nucl. Energy 150, 107836. doi:10.1016/j.anucene.2020.107836

CrossRef Full Text | Google Scholar

Zhao, Y., Huang, M., Huang, J., Ouyang, X., and Hou, R. (2020). CFD investigation for a 7-pin wire-wrapped fuel assembly with different shapes of fuel duct wall. Ann. Nucl. Energy 141, 107272. doi:10.1016/j.anucene.2019.107272

CrossRef Full Text | Google Scholar

Zohuri, B., and Fathi, N. (2015). Thermal-hydraulic analysis of nuclear reactors. Cham, Switzerland: Springer.

CrossRef Full Text | Google Scholar