Thermodynamic Analysis of a Conceptual Fixed-Bed Solar Thermochemical Cavity Receiver–Reactor Array for Water Splitting Via Ceria Redox Cycling

We propose a novel solar thermochemical receiver–reactor array concept for hydrogen production via ceria redox cycling. The receiver–reactor array can improve the solar-to-fuel efficiency by realizing the heat recuperation, reduction, and oxidation processes synchronously. A linear matrix model and a lumped parameter model are developed to predict thermal performance of the new solar thermochemical system. The system thermal performance is characterized by heat recovery effectiveness of solid-phase and solar-to-fuel efficiency. Investigated parameters include reduction temperature, oxygen partial pressure, number of receiver–reactors, concentration ratio, and gas-phase heat recovery effectiveness. For baseline conditions, the solid-phase heat recovery effectiveness and the solar-to-fuel efficiency are found to be 81% and 27%, respectively. For perfect gas-phase heat recovery and a solar concentration ratio of 5,000, the solar-to-fuel efficiency exceeds 40%.

Introduction

Solar fuels offer great promise to a sustainable future and can be produced via several pathways such as photo-, electro-, and thermochemical processes, as well as their various combinations (Steinfeld, 2005). Compared to the other processes, the solar thermochemical approach utilizes the entire solar spectrum, allowing for higher theoretical solar-to-fuel efficiency (Steinfeld, 2005; Siegel et al., 2013; Muhich et al., 2016; Bader and Lipiński, 2017). In particular, the two-step non-stoichiometric based redox cycles have been an attractive research area over the past decade (Chueh and Haile, 2010; Furler et al., 2012a; Marxer et al., 2017; Steinfeld, 2019; Qian et al., 2021). Synthesis gas (syngas, a mixture of H₂ and CO) can be produced in two steps. In the first, endothermic step, a metal oxide is non-stoichiometrically reduced, driven by concentrated solar irradiation. In the second, exothermic step, the reduced metal oxide is oxidized with the H₂O and/or CO₂ and H₂ and/or CO are produced, respectively.

A key figure of merit to assess the commercial viability of the solar thermochemical pathway for fuel production is the solar-to-fuel efficiency (defined in Eq. 26). A threshold efficiency value of 20% has been suggested to compete with low-risk approaches such as electrolysis (Siegel et al., 2013). Although solar thermochemical water splitting has a high theoretical solar-to-fuel conversion efficiency of 75% (Steinfeld, 2005), to date the experimental record of this technology is only 5.25% for splitting of CO₂ into CO and O₂ (Marxer et al., 2017).¹ Improvement of the solar-to-fuel efficiency critically relies on the development of both superior redox materials and novel reactor designs (Lapp et al., 2012; Miller et al., 2014; Hathaway et al., 2016; Muhich et al., 2018; Li et al., 2021). A wide variety of non-stoichiometric redox materials have been investigated, including pure and doped ceria, as well as perovskites (Chueh et al., 2010; Hao et al., 2014; Qian et al., 2021). Among these candidates, undoped ceria offers a great promise for efficient fuel production due to its fast kinetics, robust cyclability, and high selectivity, and is thus selected as the model material in this study (Abanades et al., 2010; Chueh et al., 2010; Furler et al., 2012b; Marxer et al., 2017).

Many reactor designs were proposed and tested with the ultimate goal of improving the solar-to-fuel efficiency (Chueh et al., 2010; Diver et al., 2010; Lapp et al., 2013; Dähler et al., 2018; Wang et al., 2020; Wang et al., 2021). They can be categorized into designs with solid and/or gas heat recuperation (Ermanoski et al., 2013; Lapp and Lipiński, 2014; Hathaway et al., 2016) and designs without heat recuperation (Welte et al., 2016; Marxer et al., 2017). The majority of the reactor systems demonstrated so far are based on the fixed-bed type due to the design simplicity and convenient operation (Chueh et al., 2010; Furler et al., 2012b; Hathaway et al., 2016; Marxer et al., 2017; Haeussler et al., 2020; Sun-to-liquid, 2020). However, a key challenge associated with designing an efficient fixed-bed reactor system is to recover the solid sensible heat under temperature-swing cycling due to the immobility of the redox material. This is particularly relevant when using undoped ceria because its efficiency is critically limited by the energy penalty to heat the solid phase (Hathaway et al., 2016; Muhich et al., 2018; Li et al., 2021). A multi-chamber fixed-bed reactor concept was developed by Yuan et al. that allows for solid heat recuperation by using liquid metal as the heat transfer fluid. This concept promises a thermal-to-chemical efficiency of 20% and a heat recovery effectiveness of 80%, but at the expense of complicated design and operation (Yuan et al., 2015). A more generic design concept incorporating counterflow solid heat exchange was proposed by Falter et al., though the design poses technical challenges to practical operation of moving the high-temperature redox materials (Falter et al., 2015). Besides, a new receiver–reactor system with integrated thermocline heat recovery was proposed but lacks theoretical or experimental investigations (Steinfeld et al., 2019). To our best knowledge, realizing efficient solid-phase heat recovery in the fixed-bed reactor system with a simple design and operating strategy is absent in the literature.

In our previous work, we proposed a modified solar beam-down system for realizing solid-phase heat recovery for the fixed-bed reactor configuration, where the analysis of the optical system was presented in detail (Li et al., 2020b). In the present work, we introduce the design of the array of receiver–reactors, coupled to the beam-down system, together with the operating strategy for realizing solid-phase heat recovery. The main merits of this work are: (i) the heat recovery is realized without the need of moving redox materials; (ii) the heat of the solid phase is recovered by the direct gas–solid heat exchange in series; and (iii) hydrogen is produced continuously. The model receiver–reactor system comprising recuperation, reduction, and oxidation zones is introduced in “Problem Statement” section. Model assumptions, as well as mathematical models, are described in sections “Methodology and Assumptions” and “Mathematical Model”. Section “Results and Discussion” presents the assessment of the heat recovery effectiveness from the solid phase and the sensitivity analysis of the total solar-to-fuel efficiency depending on key parameters, including reduction temperature, relative oxygen partial pressure, receiver–reactor numbers, concentration ratio, and gas-phase heat recovery effectiveness.

Problem Statement

Thermochemical water splitting (WS) process based on two-step ceria redox cycles is considered in this study:

$\text{solar, endothermic step: }\frac{1}{\Delta \delta }{\text{CeO}}_{2-{\delta }_{\text{ox}}}\to \frac{1}{\Delta \delta }{\text{CeO}}_{2-{\delta }_{\text{red}}}+\frac{1}{2}{\text{O}}_2(\mathrm{R1})$

$\text{non}-\text{solar, exothermic step: }\frac{1}{\Delta \delta }{\text{CeO}}_{2-{\delta }_{\text{red}}}+{\text{H}}_2\text{O}\to \frac{1}{\Delta \delta }{\text{CeO}}_{2-{\delta }_{\text{ox}}}+{\text{H}}_2(\mathrm{R2})$

where $\Delta \delta ={\delta }_{\text{red}}-{\delta }_{\text{ox}}$ is the change in non-stoichiometry.

Figure 1 depicts the schematic of the proposed beam-down thermochemical system featuring a heliostat field, a tower, a rotating hyperboloidal tower reflector (TR), and a stationary cavity receiver–reactor (CRR) array coupled with compound parabolic concentrators (CPCs) (Li et al., 2020b). The rotating TR directs the concentrated solar irradiation alternately to each CRR through the aperture of the CPCs. Since the focus of this paper is on the reactor system, the radiative input from the optical system is modeled here in a simplified manner assuming step-wise irradiation.

FIGURE 1

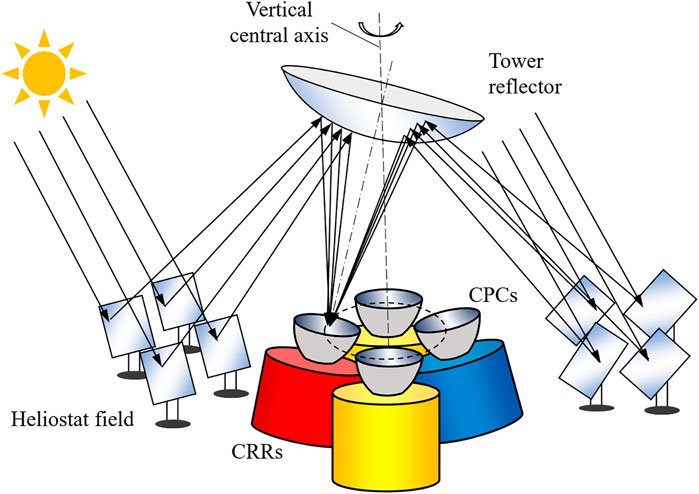
FIGURE 1. Schematic of the proposed solar thermochemical system consisting of a heliostat field, a beam-down reflector, and a cavity receiver–reactor array. This figure is adapted from (Li et al., 2020b).

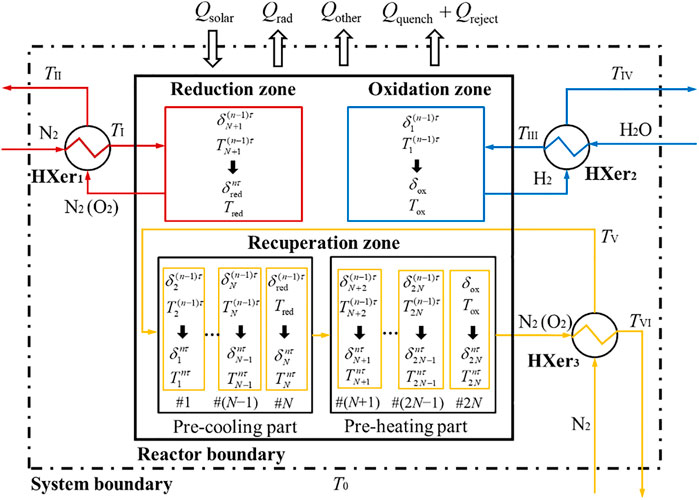
Figure 2 shows an example of an 8-CRR array that is arranged in a circular layout and fixed on a pedestal (not shown). The system is divided into three zones: reduction (red), oxidation (blue), recuperation (including pre-heating and pre-cooling subzones, yellow) zones. The same amount of the monolithic reticulated porous ceria (RPC) is contained in each CRR.² The reduction reaction is realized in the CRR irradiated by the concentrated sunlight (red). The oxidation reaction is realized in the CRR on the opposite side (blue). All other CRRs (yellow) are separated by the central axis into two groups, and heat is exchanged between the two groups. To reduce the emission loss, the aperture of the receiver–reactor is opened only when being irradiated by the concentrated sunlight, and is kept closed otherwise. The CRRs are connected to the neighboring ones and to the gas-phase heat exchangers via pipes. Therefore, the inert gas and water flow through each receiver–reactor to sweep the RPC alternately.

FIGURE 2

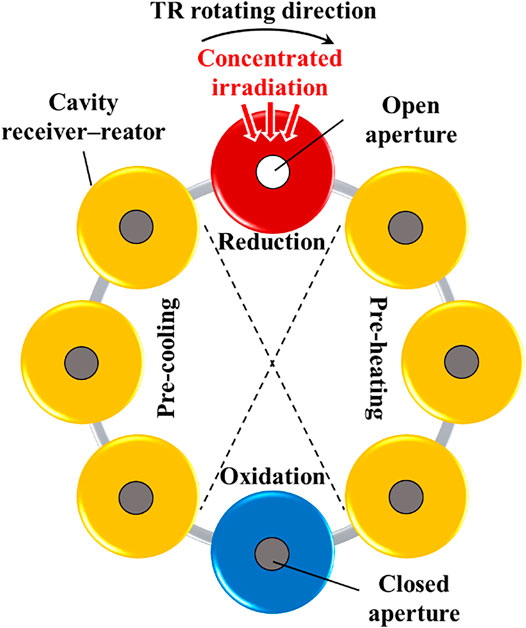
FIGURE 2. Schematic of an example array of 8 receiver–reactors. The gas-phase heat exchangers and the related connecting devices are not shown in the figure. This figure is adapted from (Li et al., 2020b).

As the rotating TR directs the concentrated sunlight to the stationary CRR array in a clockwise manner, the CRR array can be viewed as “rotating” counter-clockwise relative to the position of concentrated solar irradiation. The operating procedure for one cycle duration τ is shown in Figure 3. States 1 and 2 represent the beginning of the nth cycle, and the time instant after “rotating” the CRR array counter-clockwise in one phase, respectively. The transition from State 1 to 2 is assumed instantaneous and thus both states are treated to occur at the same time instant (n−1)τ. States 3 and 4 represent the initial and final states of the thermochemical process of the nth cycle, respectively. For ensuring the synchronization of reduction, oxidation, and recuperation processes, the duration of States 3 and 4, τ, is determined by the duration of the reduction step, and the other two processes are proceeding simultaneously for the same duration τ by adjusting the flow rates of water and sweep gas. After a complete cycle, the system returns to State 1.

FIGURE 3

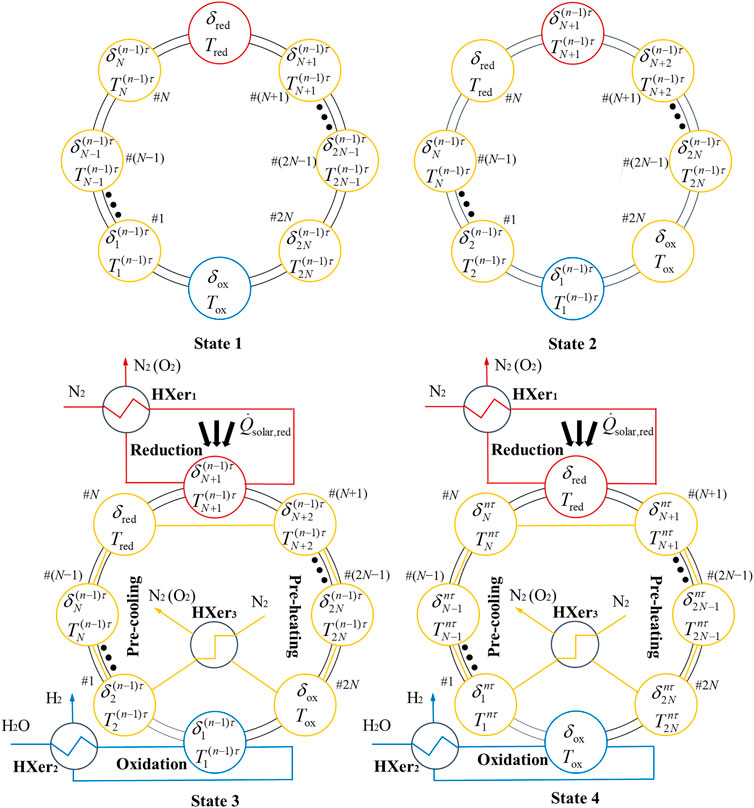
FIGURE 3. Operating procedure (4 states) for the nth redox cycle. N₂ (O₂) represents N₂ mixed with O₂. State 1: initial state of the nth cycle; State 2: “rotated” counter-clockwise in one phase; State 3: begin of reaction or the (n−1)τ time instant; State 4: final state of the nth cycle or the nτ time instant. The red, blue, and yellow arrows indicate mass flows in reduction, oxidation, and recuperation zones, respectively. The black thick arrows indicate the flow of energy. The CRRs and the HXer₃ are connected in series by pipes, which are not shown in this figure.

Reduction Zone

As shown in Figure 3, we assume that the CRR array rotates counter-clockwise by one phase during a change from State 1 to State 2.³ Therefore, the CRR in #(N+1) position of the recuperation zone moves into the reduction zone, where it will be irradiated by concentrated solar irradiation. Then, pure N₂ is used to sweep RPC of the CRR in the reduction zone and to keep rejecting released O₂ from porous media surfaces during the change from State 3 to State 4. The thermal energy of the product gas, the mixture of N₂ and O₂, is recovered to heat the inlet flow of N₂ by using an indirect gas-phase heat exchanger (HXer₁). A reduction period finishes when the thermodynamic state $\left(T_{\text{red}},p_{{\text{O}}_2,\text{red}}\right)$ is reached. The settings of $T_{\text{red}}$ and ${\text{p}}_{{\text{O}}_2,\text{red}}$ values are discussed in “Results and Discussion” section. Because the solar-to-fuel efficiency is affected by the feeding strategy of N₂, the following simplified approach of controlling the N₂ flow rate per kilogram of ceria $r_{{\text{N}}_2}$ is used: (i) set an initial value of $r_{{\mathrm{N}}_2}$ = 10^–3 kg s⁻¹ kg⁻¹); (ii) continuously adjust $r_{{\mathrm{N}}_2}$ to approximate the default final relative oxygen partial pressure. The N₂ feeding strategy is illustrated in detail in “Mathematical Model” section.

Recuperation Zone

The recuperation zone is composed of one gas-phase heat exchanger (HXer₃) and 2N CRRs (yellow) with one half undergoing pre-cooling (from #1 to #N) and another half undergoing pre-heating (from #(N+1) to #2N) as labeled in Figure 3.

N₂ is used as the sweep gas for oxygen scavenger and heat transfer fluid (HTF). A pure cold N₂ flow first goes into an indirect gas-phase heat exchanger (HXer₃) where it is heated by the heat of product gases, namely, a mixture of N₂ and O_2. The mixture gas then flows continuously through the pre-cooling part from #1 to #N to cool the RPC material in each CRR. The sweep gas reaches the peak temperature when leaving #N, and then goes through the pre-heating part from #(N+1) to #2N to heat the RPC material. The state of ceria in each CRR is updated from $\left(T_i^{(n-1)\tau }\text{,}{\delta }_i^{(n-1)\tau }\right)$ to $\left(T_i^{n\tau }\text{,}{\delta }_i^{n\tau }\right)$ during the change from States 3 to 4, where the subscript i represents the ith CCR position (#i) in the recuperation zone. The superscript nτ indicates a time instant.⁴ Note that reduction may occur along with heat recovery processes in the recuperation zone. A detailed systematic study is presented in section “Mathematical Model”.

Oxidation Zone

According to Figure 3, the CRR in #1 position of the recuperation zone containing the reduced ceria $\left({\text{CeO}}_{2-{\delta }_{\text{red}}}\right)$ moves into the oxidation zone during the change from State 1 to State 2, where it will undergo the oxidation reaction. Then, ${\text{CeO}}_{2-{\delta }_{\text{red}}}$ is oxidized at constant oxidation temperature T_ox by water steam during the change from State 3 to State 4, while H₂ is generated. Note that ceria needs to be cooled before undergoing the oxidation process. Because the oxidation step is exothermic, the redundant heat generated during oxidation needs to be removed to keep the temperature constant. The heat may be further utilized in a distributed system such as a Rankine cycle power generation system, which is not discussed in this work.

Methodology and Assumptions

The methodology of modeling transient radiative fixed-bed reduction and cavity cascade heat recuperation is presented next. A lumped parameter model (LPM) and a linear matrix model (LMM) are, respectively, presented to describe the reducing and recuperating processes of the novel receiver–reactor redox system. For the LPM, the reduction is treated as a transient process and the numerical method is applied to solve the non-linear governing equation. For the LMM, mass and heat transfer between recuperation CRRs are expressed by a set of linear equations which is solved by matrix iteration. The main assumptions and settings are as follows:

(1) Thermodynamic quasi-equilibrium is assumed for ceria reduction and oxidation.

(2) Temperature difference between the RPC and sweep gases is neglected.

(3) Lumped parameters of the RPC and gases, including temperature, relative oxygen partial pressure, non-stoichiometry, N₂ flow rate, are concluded for each CRR.

(4) The relative oxygen partial pressure $p_{{\text{O}}_2}$ of the initial pure N₂ flow is set to $p_{{\text{O}}_2,0}$ = 1 × 10^–5 as a conservative estimate based on the existing industrial technologies (Häring, 2008).

(5) The effectiveness of gas-phase heat exchanger is set to 95% according to the literature (Blank and Wu, 1994; El-Ehwany et al., 2010).

(6) The maximum operating temperature is set to 2,000 K, as ceria will undergo a phase change at temperatures $\ge$2,100 K (Chueh and Haile, 1923; Bader et al., 2013).

(7) The oxidation reaction is undergone constantly at 1,000 K.

(8) For the LMM, the temperature of RPC (or sweep gases) in the recuperation zone varies linearly over time, namely, ${\overline{T}}_{\tau }=\frac{1}{\tau }{\displaystyle {\int }_{\left(n-1\right)\tau }^{n\tau }T\mathrm{dt}\approx \left(T^{\left(n-1\right)}+T^{\left(n\right)}\right)/2}$, and the O₂ generating rate is assumed as constant.

Mathematical Model

Figure 4 shows the schematic of the system model for the reaction process in the nth cycle from the (n−1)τ to nτ time instant. It corresponds to the process from State 3 to 4 in Figure 3. The red and blue blocks represent CRRs in the reduction and oxidation zones. In the recuperation zone, the CRRs are represented in a row of yellow rectangular boxes separated into the pre-cooling and pre-heating parts. All CRRs are enclosed by a frame in the solid line as the reactor boundary. For each CRR, the initial and final thermodynamic states of ceria in the nth cycle are given correspondingly. Thick solid arrows are used to show the direction of reactions. The flows of mass and energy are represented by thin solid arrows and thick hollowed arrows, respectively. The outermost dash frame denotes the boundary of the whole system. A steady thermodynamic state of temperature, T₀ = 298 K and gauge pressure, p₀ = 1.013 × 10⁵ Pa is assumed for the surroundings.

FIGURE 4

FIGURE 4. Schematic of system model of State 3 to State 4 for the nth reaction cycle.

Energy conservation of the system undergoing one cycle (shown in Figure 4) is:

$Q_{\text{solar}}=Q_{\text{rad}}+Q_{\text{other}}+Q_{\text{gas}}+Q_{\text{quench}}+Q_{\text{reject}}+Q_{\text{fuel}}(1)$

where Q_solar represents the total solar energy input during one cycle, including energy consumed by the reduction reaction Q_solar,red, and energy for the recovery of heat losses Q_{solar, recovery}. They can be expressed as:

$Q_{\text{solar,}\text{red}}={\displaystyle {\int }_{(n-1)\tau }^{n\tau }{\dot{Q}}_{\text{solar,}\text{red}}\text{d}t}(2)$

$Q_{\text{rad}}={\displaystyle {\int }_{(n-1)\tau }^{n\tau }\frac{\sigma T^4}{C\times \text{DNI}}{\dot{Q}}_{\text{solar,red}}\text{d}t}(3)$

$Q_{\text{solar},\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{y}}=Q_{\text{other}}=F\left(Q_{\text{solar,red}}-Q_{\mathrm{r}\mathrm{a}\mathrm{d}}\right)(4)$

where ${\dot{Q}}_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{r},\mathrm{r}\mathrm{e}\mathrm{d}}$ is the incident solar power into the reduction cavity, Q_rad and Q_other denote the radiative and other heat losses, respectively, σ is the Stefan–Boltzmann constant, σ = 5.67×10^–8 W m⁻² K⁻⁴, C and DNI represent the concentration ratio and direct normal irradiation assumed equal to 3,000 and 1,000 W m⁻², respectively, and F is the heat loss fraction of the entire system assumed to be equal to 0.2.

$Q_{\mathrm{g}\mathrm{a}\mathrm{s}}=Q_{\mathrm{g}\mathrm{a}\mathrm{s},\mathrm{H}\mathrm{X}}+Q_{\mathrm{g}\mathrm{a}\mathrm{s},\mathrm{r}\mathrm{e}\mathrm{d}}+Q_{\mathrm{g}\mathrm{a}\mathrm{s},\mathrm{o}\mathrm{x}}(5)$

$Q_{\text{quench}}=m_{\mathrm{R}\mathrm{P}\mathrm{C}}{\mathrm{c}}_v\left(T_1^{(n-1)}-T_{\mathrm{o}\mathrm{x}}\right)(6)$

$Q_{\text{ox}}=n_{{\text{H}}_2}\left[{\overline{h}}_{{\mathrm{H}}_2\mathrm{O}}\left(T_{\text{ox}}\right)-{\overline{h}}_{{\mathrm{H}}_2}\left(T_{\text{ox}}\right)-\frac{\text{Δ}{\overline{h}}_{{\text{O}}_2}\left({\delta }_1^{(n-1)}\text{,}{\delta }_{\text{ox}}\right)}{2}\right](7)$

$\begin{array}{l}{Q}_{\text{reject}}=Q_{\text{ox}}+n_{{\text{H}}_2\text{O}}\left[{\overline{h}}_{{\text{H}}_2\text{O}}\left(T_{\infty }\right)-{\overline{h}}_{{\text{H}}_2\text{O}}\left(T_{\text{ox}}\right)\right]-\left(n_{{\text{H}}_2\text{O}}-n_{{\text{H}}_2}\right)\frac{\text{Δ}{\overline{h}}_{{\text{O}}_2}\left({\delta }_{\text{ox}}\text{,}{\delta }_{\text{0}}\right)}{2}\\ +\epsilon \left\{\left(n_{{\text{H}}_2\text{O}}-n_{{\text{H}}_2}\right)\left[{\overline{h}}_{{\text{H}}_2\text{O}}\left(T_{\text{ox}}\right)-{\overline{h}}_{{\text{H}}_2\text{O}}\left(T_{\infty }\right)\right]+n_{{\text{H}}_2}\left[{\overline{h}}_{{\text{H}}_2}\left(T_{\text{ox}}\right)-{\overline{h}}_{{\text{H}}_2}\left(T_{\infty }\right)\right]\right\}\end{array}(8)$

$Q_{\mathrm{f}\mathrm{u}\mathrm{e}\mathrm{l}}=n_{{\mathrm{H}}_2}\left[{\overline{h}}_{{\mathrm{H}}_2}\left(T_{\infty }\right)-{\overline{h}}_{{\mathrm{H}}_2\mathrm{O}}\left(T_{\infty }\right)\right](9)$

$Q_{\text{gas,HX}}={\dot{m}}_{{\text{N}}_2\text{,HX}}\tau c_{{p\text{,N}}_2}\left(1-\epsilon \right)\left(\frac{T_{\text{ox}}+T_{2N}^{\left(n\right)}}{2}-T_{\infty }\right)(10)$

$Q_{\text{gas,red}}={\displaystyle {\int }_{(n-1)\tau }^{n\tau }\left[{\dot{m}}_{{\text{N}}_2\text{,red}}{c}_{{p\text{,N}}_2}\left(1-\epsilon \right)\left(T-T_{\infty }\right)+\frac{m_{\text{RPC}}{M}_{{\text{O}}_2}{c}_{{p\text{,O}}_2}}{2M_{\text{RPC}}}\frac{\text{d}\delta }{\text{d}t}\left(T_{\infty }-T\right)\right]\text{d}t}(11)$

$Q_{\text{gas,ox}}=\left(1-\epsilon \right)\left\{n_{{\text{H}}_2}\left[{\overline{h}}_{{\text{H}}_2}\left(T_{\text{ox}}\right)-{\overline{h}}_{{\text{H}}_2}\left(T_{\infty }\right)\right]+\left(n_{{\text{H}}_2\text{O}}-n_{{\text{H}}_2}\right)\left[{\overline{h}}_{{\text{H}}_2\text{O}}\left(T_{\text{ox}}\right)-{\overline{h}}_{{\text{H}}_2\text{O}}\left(T_{\infty }\right)\right]\right\}(12)$

where Q_gas is the gas-phase heat recovery loss equal to the sum of the heat losses during heat exchanging, reducing, and oxidizing processes, Q_gas,HX, Q_gas,red, and Q_gas,ox, respectively, which are calculated using Eqs. 10–12. Q_quench in Eq. 6 is the quenching heat loss for rapidly cooling ceria from $T_1^{(n-1)}$ to T_ox before oxidation. Using Eq. 7 to calculate the heat released during oxidation. $n_{{\text{H}}_2\text{O}}$ and $n_{{\text{H}}_2}$ are the total amounts of H₂O supplied and H₂ produced in one redox cycle, respectively. Q_ox can be partially used for re-heating inlet water steam up to T_ox. The redundant heat of Q_ox is assumed to be rejected completely as calculated by Eq. 8. ε is the heat recovery effectiveness of gas-phase heat exchanger. Q_fuel in Eq. 9 is the thermal energy stored in the product of H₂. The reference temperature is T_ref = 1500 K and the reference pressure is p_ref = 1.013 × 10⁵ Pa. Physical properties of the sweeping gases and non-stoichiometric CeO₂ including the specific heat at constant pressure (c_p) and constant volume (c_v) refer to T_ref and p_ref.

Reduction Reaction

The governing equations of the LPM for simulating the non-linear solar reduction process are:

$\begin{array}{l}{m}_{\text{RPC}}{c}_v\text{d}T+\frac{m_{\text{RPC}}}{2M_{\text{RPC}}}\text{d}\delta \text{Δ}{\overline{h}}_{{\text{O}}_2}\\ =\left(1-\frac{\sigma T^4}{C\times \text{DNI}}\right){\dot{Q}}_{\text{solar,red}}\text{d}t+{\dot{m}}_{{\text{N}}_2\text{,red}}{c}_{{p\text{,N}}_2}\left(1-\epsilon \right)\left(T_{\infty }-T\right)\text{d}t+\frac{m_{\mathrm{R}\mathrm{P}\mathrm{C}}{M}_{{\mathrm{O}}_2}{c}_{p,{\mathrm{O}}_2}}{2M_{\mathrm{R}\mathrm{P}\mathrm{C}}}\text{d}\delta \left(T_{\infty }-T\right)\end{array}(13)$

The implicit Euler time integration scheme is applied. Thus,

$\begin{array}{l}{T}^{\left(m\right)}=T^{(m-1)}+\left(1-\frac{\sigma T^{(m)4}}{C\times \text{DNI}}\right)\frac{{\dot{Q}}_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{r},\text{red}}\Delta \tau }{m_{\mathrm{R}\mathrm{P}\mathrm{C}}{c}_v}\\ -\frac{{\delta }^{\left(m\right)}-{\delta }^{(m-1)}}{2M_{\text{RPC}}{c}_v}\text{Δ}{\overline{h}}_{{\text{O}}_2}\left({\delta }^{(m-1)}\text{,}{\delta }^{\left(m\right)}\right)+\left[\frac{{\dot{m}}_{{\text{N}}_2\text{,red}}{c}_{{p\text{,N}}_2}\left(1-\epsilon \right)\text{Δ}\tau }{m_{\text{RPC}}{c}_v}+\frac{M_{{\text{O}}_2}{c}_{{p\text{,O}}_2}}{2M_{\text{RPC}}{c}_v}\left({\delta }^{\left(m\right)}-{\delta }^{(m-1)}\right)\right]\left(T_{\infty }-T^{\left(m\right)}\right)\end{array}(14)$

$\Delta G_{\text{red}}=\Delta H_{\mathrm{r}\mathrm{e}\mathrm{d}}^{\circ }\left({\delta }^{\left(m\right)}\right)-T_{\mathrm{r}\mathrm{e}\mathrm{d}}\Delta S_{\mathrm{r}\mathrm{e}\mathrm{d}}^{\circ }\left({\delta }^{\left(m\right)}\right)+R{T}_{\mathrm{r}\mathrm{e}\mathrm{d}}\ln \left(\frac{p_{{\mathrm{O}}_2}^{\left(m\right)}}{p_{\mathrm{ref}}}\right)=0(15)$

$p_{{\text{O}}_2}^{\left(m\right)}=\frac{r_{{\text{O}}_2}}{r_{{\text{N}}_2}+r_{{\text{O}}_2}}+p_{{\mathrm{O}}_2,0}=\frac{\frac{m_{\text{RPC}}\left({\delta }^{\left(m\right)}-{\delta }^{\left(m-1\right)}\right)}{2M_{\text{RPC}}\text{Δ}\tau }}{\frac{{\dot{m}}_{{\text{N}}_2\text{,red}}}{M_{{\text{N}}_2}}+\frac{m_{\text{RPC}}\left({\delta }^{\left(m\right)}-{\delta }^{\left(m-1\right)}\right)}{2M_{\text{RPC}}\text{Δ}\tau }}+p_{{\mathrm{O}}_2,0}(16)$

δ at the end of each time step is obtained by solving Eq. 15 using experimental data of non-stoichiometric cerium dioxide at thermodynamic equilibrium (Panlener et al., 1975). $\Delta H_{\mathrm{r}\mathrm{e}\mathrm{d}}^{\circ }$ and $\Delta S_{\mathrm{r}\mathrm{e}\mathrm{d}}^{\circ }$ are the standard reaction enthalpy and entropy of ceria reduction per mole of the released O₂, respectively. A species balance relates the pressure of oxygen at the outlet of the reactor, $p_{{\mathrm{O}}_2}$, to the rate at which oxygen is generated, $r_{{\text{O}}_2}$, by Eq. 16. ${\dot{m}}_{{\mathrm{N}}_2,\mathrm{r}\mathrm{e}\mathrm{d}}$ is continuously adjusted throughout the reducing process to approximate a constant $p_{{\mathrm{O}}_2}$. A relaxation factor χ is used to smoothen the iteration of ${\dot{m}}_{N_2,\mathrm{r}\mathrm{e}\mathrm{d}}$ due to its high sensitivity to the results, namely ${\dot{m}}_{{\text{N}}_2\text{,red}}=\chi {\dot{m}}_{{\text{N}}_2\text{,red}}^{\left(m\right)}+(1-\chi ){\dot{m}}_{{\text{N}}_2\text{,red}}^{(m-1)}$. Figure 5 shows the computational accuracy and time as functions of the time step Δτ. The relative error σ_eff is defined as ${\sigma }_{\mathrm{e}\mathrm{f}\mathrm{f}}=\left|{\eta }_{\mathrm{t}\mathrm{h}}-{\eta }_{\mathrm{t}\mathrm{h},\mathrm{r}\mathrm{e}\mathrm{f}}\right|/{\eta }_{\mathrm{t}\mathrm{h},\mathrm{r}\mathrm{e}\mathrm{f}}$, where η_th,ref is calculated for a reference Δτ = 0.01 s. Based on Figure 5, Δτ is set to 0.1 s to ensure relatively higher accuracy.

FIGURE 5

FIGURE 5. Relative error σ_eff and CPU time as functions of time step duration Δτ.

Heat Recuperation

For modeling the recuperating process, the LMM is established. The energy-balance equation for CRRs in the recuperation zone from State 3 to State 4 in a redox cycle is as follows:

$\begin{array}{l}{m}_{\text{RPC}}{c}_v\left(T_i^{\left(n\right)}-T_{i+1}^{(n-1)}\right)+\frac{m_{\text{RPC}}}{M_{\text{RPC}}}\frac{{\delta }_i^{\left(n\right)}-{\delta }_{i+1}^{(n-1)}}{2}\text{Δ}{\overline{h}}_{{\text{O}}_2}\left({\delta }_{i+1}^{(n-1)}\text{,}{\delta }_i^{\left(n\right)}\right)\\ ={\dot{m}}_{{\text{N}}_2\text{,HX}}{c}_{{p\text{,N}}_2}\tau \left[\left(1+\frac{M_{{\text{O}}_2}{c}_{{p\text{,O}}_2}}{M_{{\text{N}}_2}{c}_{{p\text{,N}}_2}}\frac{p_{{\text{O}}_2\text{,}i-1}^{\left(n\right)}}{p_{{\text{N}}_2\text{,}i-1}^{\left(n\right)}}\right)\left(\frac{T_{i-1}^{\left(n\right)}+T_i^{(n-1)}}{2}-T_{\infty }\right)-\left(1+\frac{M_{{\text{O}}_2}{c}_{{p\text{,O}}_2}}{M_{{\text{N}}_2}{c}_{{p\text{,N}}_2}}\frac{p_{{\text{O}}_2\text{,}i}^{\left(n\right)}}{p_{{\text{N}}_2\text{,}i}^{\left(n\right)}}\right)\left(\frac{T_i^{\left(n\right)}+T_{i+1}^{(n-1)}}{2}-T_{\infty }\right)\right]\\ \left(1<i\le 2N\right)\end{array}(17)$

where the subscript i represents the CRR position of the recuperation zone and the superscript n represents the nth redox cycle. As shown in Figure 3, $X_i^{\left(n\right)}$ and $X_{i+1}^{(n-1)}$ (X: T, δ) correspond to thermodynamic parameter values of RPC in #i CRR position at State 4 and State 3 of the nth redox cycle, respectively. For #N and #2N positions, $X_{i+1}^{(n-1)}$ corresponds to T_red, δ_red, and T_ox, δ_ox, respectively.

The LHS of Eq. 17 represents the change in internal energy of RPC material corresponding to #i position, and the RHS is the net amount of thermal energy input (or output) by N₂ from State 3 to State 4. For #1 position of the recuperation zone, the heat loss of gas-phase heat recovery should be considered, and the modified equation is:

$\begin{array}{l}{m}_{\text{RPC}}{c}_v\left(T_1^{\left(n\right)}-T_2^{\left(n-1\right)}\right)+\frac{m_{\text{RPC}}}{M_{\text{RPC}}}\frac{{\delta }_1^{\left(n\right)}-{\delta }_2^{\left(n-1\right)}}{2}\text{Δ}{\overline{h}}_{{\text{O}}_2}\left({\delta }_2^{\left(n-1\right)}\text{,}{\delta }_1^{\left(n\right)}\right)=\\ {\dot{m}}_{{\text{N}}_2\text{,HX}}{c}_{{p\text{,N}}_2}\tau \left[\epsilon \left(\frac{T_{2N}^{\left(n\right)}+T_{\mathrm{ox}}}{2}-T_{\infty }\right)-\left(1+\frac{M_{{\text{O}}_2}{c}_{{p\text{,O}}_2}}{M_{{\text{N}}_2}{c}_{{p\text{,N}}_2}}\frac{p_{{\text{O}}_2\text{,}1}^{\left(n\right)}}{p_{{\text{N}}_2\text{,}1}^{\left(n\right)}}\right)\left(\frac{T_1^{\left(n\right)}+T_2^{\left(n-1\right)}}{2}-T_{\infty }\right)\right]\end{array}(18)$

where ε is gas-phase heat recovery effectiveness, $p_{{\mathrm{O}}_2,i}^{\left(n\right)}$ is determined by the mass flow rate of N₂ and O₂, ${\dot{m}}_{{\mathrm{N}}_2}$and ${\dot{m}}_{{\mathrm{O}}_2,i}^{\left(n\right)}$ respectively, ${\dot{m}}_{{\mathrm{N}}_2}$and ${\dot{m}}_{{\mathrm{O}}_2,i}^{\left(n\right)}$ can be calculated as:

${\dot{m}}_{{\text{O}}_2\text{,}i}^{\left(n\right)}=\frac{\left[{\delta }_1^{\left(n\right)}-{\delta }_{i+1}^{\left(n-1\right)}+{\displaystyle \sum _{j=2}^{i\text{>}1}\left({\delta }_j^{\left(n\right)}-{\delta }_j^{\left(n-1\right)}\right)}\right]m_{\text{RPC}}{M}_{{\text{O}}_2}}{2M_{\text{RPC}}\tau }(19)$

$p_{{\mathrm{O}}_2,i}^{\left(n\right)}=\frac{\frac{{\dot{m}}_{{\text{O}}_2\text{,}i}^{\left(n\right)}}{M_{{\text{O}}_2}}}{\frac{{\dot{m}}_{{\text{N}}_2\text{,HX}}}{M_{{\text{N}}_2}}+\frac{{\dot{m}}_{O_2,i}^{\left(n\right)}}{M_{{\text{O}}_2}}}+p_{{\mathrm{O}}_2,0}=\frac{{\delta }_1^{\left(n\right)}-{\delta }_{i+1}^{\left(n-1\right)}+{\displaystyle \sum _{j=2}^{i\text{>}1}\left({\delta }_j^{\left(n\right)}-{\delta }_j^{\left(n-1\right)}\right)}}{2\beta {\gamma }_{{\text{N}}_2}^{\text{RPC}}+{\delta }_1^{\left(n\right)}-{\delta }_{i+1}^{\left(n-1\right)}+{\displaystyle \sum _{j=2}^{i\text{>}1}\left({\delta }_j^{\left(n\right)}-{\delta }_j^{\left(n-1\right)}\right)}}+p_{{\mathrm{O}}_2,0}(20)$

where $\beta =\frac{{\dot{m}}_{{\text{N}}_2\text{,HX}}{c}_{{p\text{,N}}_2}\tau }{m_{\text{RPC}}{c}_v}$ and ${\gamma }_{{\text{N}}_2}^{\text{RPC}}=\frac{M_{\text{RPC}}{c}_v}{M_{{\text{N}}_2}{c}_{{p\text{,N}}_2}}$.

A non-dimensional parameter β, defined as the ratio of the speed of thermal front, $v_{\mathrm{T}\mathrm{F}}={\dot{m}}_{{\mathrm{N}}_2,\mathrm{H}\mathrm{X}}{\mathrm{c}}_{p,{\mathrm{N}}_2}$, to the effective rotating speed of CRR-disk, $v_{\text{rotating}}=m_{\text{RPC}}{c}_v/\tau$, is used. Three special cases, β = 0, 1 and ∞, are discussed under simplified conditions: perfect gas-phase heat recovery and no chemical reaction.

Figure 6 shows the steady-state temperature distributions of the CRR array, containing a reduction CRR, an oxidation CRR, and six recuperation CRRs, at the end of a cycle when reaching a steady running condition. For 0 < β < 1, the solid-phase heat recovery in the recuperation zone is insufficient, and the heat recovery efficiency can be improved by increasing β. The highest heat recovery efficiency, η_recovery = (T₄ − T_ox)/(T_red − T_ox), is found at β = 1, where the final temperature distributions of the pre-heating and pre-cooling CRRs are identical (Figure 6B). Further increase of β leads to a detrimental effect on solid-phase heat recovery. Because the temperature of CRR in #3 drops below 1675 K when β > 1, the CRR in #4 will be cooled. Finally, the temperatures of all CRRs in the recuperation zone approach the same value of 1450 K when β = ∞. In this study, β is set to 1.

FIGURE 6

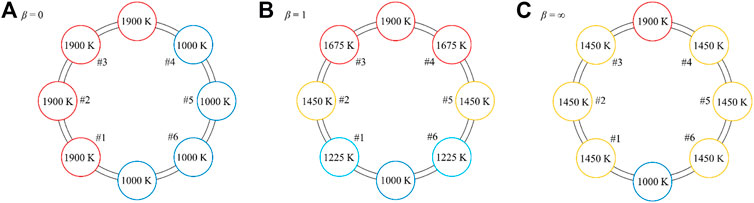
FIGURE 6. Steady-state temperature distributions in the CRR array at the end of a cycle for (A)β = 0, (B)β = 1, and (C)β = ∞.

Besides, as given in Eq. 21, δ in each recuperation CRR is determined by $p_{{\text{O}}_2}$, T, and other constraints. During the change from State 1 to State 2, the recuperation CRR containing CeO_2−δ with ${\delta }_{i+1}^{(n-1)}$ is shifted counter-clockwise from #(i+1) to #i position as shown in Figure 3. Then, the CRR’s thermodynamic state moves from $\left(p_{{\mathrm{O}}_2,i+1}^{\left(n-1\right)},T_{i+1}^{\left(n-1\right)}\right)$ to a new state, $\left(p_{{\mathrm{O}}_2,i}^{\left(n\right)},T_i^{\left(n\right)}\right)$ during the change from State 3 to State 4. For the pre-heating CRRs, namely (N+1) ≤ i ≤ 2N, ${\delta }_i^{\left(n\right)}$ is solely determined by $\left(p_{{\mathrm{O}}_2,i}^{\left(n\right)},T_i^{\left(n\right)}\right)$. For the pre-cooling CRRs, namely 1 ≤ i ≤ N, two possibilities should be discussed. The first possible condition is that δ determined by the new thermodynamic state $\left(p_{{\mathrm{O}}_2,i}^{\left(n\right)},T_i^{\left(n\right)}\right)$, is larger than the previous non-stoichiometry ${\delta }_{i+1}^{(n-1)}$. According to the assumption of thermodynamic quasi-equilibrium, a further reduction can occur and ${\delta }_i^{\left(n\right)}$ is obtained by solving $f\left(p_{{\text{O}}_2\text{,}i}^{\left(n\right)}\text{,}{T}_i^{\left(n\right)}\text{,}{\delta }_i^{\left(n\right)}\right)=0$ which is similar to Eq. 15. The second possible condition is δ < ${\delta }_{i+1}^{(n-1)}$, and a re-oxidation should occur. However, this is inhabited due to the absence of O₂ in pure N₂ flows ($p_{{\text{O}}_2\text{,0}}$ = 1 × 10^–5). Because less O₂ can be regained by the ceria, the reaction extent is too small. It is found that the decrement of Δδ is orders of magnitude smaller than δ_red. Therefore, ${\delta }_i^{\left(n\right)}$ is assumed to be equal to ${\delta }_{i+1}^{(n-1)}$ in the second condition.

${\delta }_i^{\left(n\right)}=\{\begin{array}{cc}\max \left[{\delta }_{i+1}^{(n-1)}\text{,}f\left(p_{{\text{O}}_2\text{,}i}^{\left(n\right)}\text{,}{T}_i^{\left(n\right)}\right)\right],& 1\le i\le N\\ f\left(p_{{\text{O}}_2\text{,}i}^{\left(n\right)}\text{,}{T}_i^{\left(n\right)}\right),& N+1\le i\le 2N\end{array}(21)$

Equations 13 and 14 can be written in a matrix form as:

$\mathbf{A}\cdot {\mathbf{T}}^{\left(n\right)}=\mathbf{B}\cdot {\mathbf{T}}_{\text{shift}}^{(n-1)}+{\mathbf{V}}_{\text{trans}}-{\mathbf{V}}_{\text{chem}}(22)$

where

$\mathbf{{\rm A}}=\left[\begin{array}{cccc}2+\beta \left(1+{\xi }_1^{\left(n\right)}\right)& 0& \cdots & -\epsilon \beta \\ -\beta \left(1+{\xi }_1^{\left(n\right)}\right)& 2+\beta \left(1+{\xi }_2^{\left(n\right)}\right)& \cdots & 0\\ & ⋮& & \\ 0& \cdots & -\beta \left(1+{\xi }_{2N-1}^{\left(n\right)}\right)& 2+\beta \left(1+{\xi }_{2N}^{\left(n\right)}\right)\end{array}\right]$

,

$\mathbf{B}=\left[\begin{array}{cccc}\epsilon \beta & 2-\beta \left(1+{\xi }_1^{\left(n\right)}\right)& \cdots & 0\\ 0& \beta \left(1+{\xi }_1^{\left(n\right)}\right)& 2-\beta \left(1+{\xi }_2^{\left(n\right)}\right)& \cdots \\ & ⋮& & \\ 2-\beta \left(1+{\xi }_{2N}^{\left(n\right)}\right)& \cdots & 0& \beta \left(1+{\xi }_{2N-1}^{\left(n\right)}\right)\end{array}\right],$

${\mathbf{V}}_{\text{trans}}=\left[\begin{array}{c}2\beta \left(1+{\xi }_1^{\left(n\right)}-\epsilon \right)T_{\infty }\\ 2\beta \left({\xi }_2^{\left(n\right)}-{\xi }_1^{\left(n\right)}\right)T_{\infty }\\ ⋮\\ 2\beta \left({\xi }_{2N}^{\left(n\right)}-{\xi }_{2N-1}^{\left(n\right)}\right)T_{\infty }\end{array}\right],{\mathbf{V}}_{\text{chem}}=\left[\begin{array}{c}\frac{{\delta }_1^{\left(n\right)}-{\delta }_2^{\left(n-1\right)}}{M_{\text{RPC}}{c}_v}\Delta {\overline{h}}_{{\text{O}}_2}\left({\delta }_2^{\left(n-1\right)},{\delta }_1^{\left(n\right)}\right)\\ \frac{{\delta }_2^{\left(n\right)}-{\delta }_3^{\left(n-1\right)}}{M_{\text{RPC}}{c}_v}\Delta {\overline{h}}_{{\text{O}}_2}\left({\delta }_3^{\left(n-1\right)},{\delta }_2^{\left(n\right)}\right)\\ ⋮\\ \frac{{\delta }_{2N}^{\left(n\right)}-{\delta }_{ox}}{M_{\text{RPC}}{c}_v}\Delta {\overline{h}}_{{\text{O}}_2}\left({\delta }_{\text{ox}},{\delta }_{2N}^{\left(n\right)}\right)\end{array}\right]$

${\mathbf{T}}^{\left(n\right)}=\left[\begin{array}{c}{T}_1^{\left(n\right)}\\ T_2^{\left(n\right)}\\ ⋮\\ T_{2N}^{\left(n\right)}\end{array}\right],{\mathbf{T}}_{\text{shift}}^{\left(n-1\right)}=\left[\begin{array}{c}{T}_{\text{ox}}\\ T_2^{\left(n-1\right)}\\ ⋮\\ T_{2N}^{\left(n-1\right)}\end{array}\right],{\xi }_i^{\left(n\right)}={\gamma }_{{\mathrm{N}}_2}^{{\mathrm{O}}_2}\frac{p_{{\mathrm{O}}_2,i}^{\left(n\right)}}{p_{{\mathrm{N}}_2,i}^{\left(n\right)}},\text{ and }{\gamma }_{{\mathrm{N}}_2}^{{\mathrm{O}}_2}=\frac{M_{{\mathrm{O}}_2}{c}_{p,{\mathrm{O}}_2}}{M_{{\mathrm{N}}_2}{c}_{p,{\mathrm{N}}_2}}$

Vectors ${\mathbf{T}}^{\left(n\right)}$ and ${\mathbf{T}}_{\text{shift}}^{\left(n-1\right)}$ contain the temperatures of 2N recuperation CRRs with respect to State 4 and State 3 in the nth cycle. V_trans and V_chem are vectors containing the themes related to the item of heat losses via gas-phase transport and the item of chemical enthalpy in the nth cycle. Finally, steady operation can be achieved as the iteration approaches a convergence solution, namely, $\underset{n\to \infty }{\lim }{\mathbf{T}}^{\left(n\right)}=\mathbf{T}$. The convergence criterion is:

$\sqrt{\frac{1}{2N}{\displaystyle \sum _1^{2N}{\left(\frac{T_i^{\left(n\right)}-T_i^{(n-1)}}{T_i^{(n-1)}}\right)}^2}}<{10}^{-6}(23)$

Oxidation Reaction

The process of oxidation involves two synchronous reactions: ceria re-oxidation and water splitting (WS). Similar to the reduction modeling, the lumped transient method is applied with the assumption of quasi thermodynamical equilibrium for each time step, namely ΔG_ox = 0. The expression is given by :

$\Delta G_{\text{ox}}=\left[\Delta H_{\text{WS}}^{\circ }-T_{\text{ox}}\Delta S_{\text{WS}}^{\circ }\right]-\frac{\Delta H_{\mathrm{r}\mathrm{e}\mathrm{d}}^{\circ }\left({\delta }^{\left(m\right)}\right)-T_{\text{ox}}\Delta S_{\mathrm{r}\mathrm{e}\mathrm{d}}^{\circ }\left({\delta }^{\left(m\right)}\right)}{2}+R{T}_{\text{ox}}\ln \left(\frac{r_{{\text{H}}_2}^{\left(m\right)}}{r_{{\text{H}}_2\text{O}}^{\left(m\right)}-r_{{\text{H}}_2}^{\left(m\right)}}\right)=0(24)$

where $\Delta H_{\text{WS}}^{\circ }$ and $\Delta S_{\text{WS}}^{\circ }$ are the standard reaction enthalpy and entropy for water splitting per mole of the released H₂. $r_{{\text{H}}_2\text{O}}$ and $r_{{\text{H}}_2}$ are the flow rate of water at inlet and the generation rate of H₂, respectively. Here, the $r_{{\text{H}}_2\text{O}}$ is set equal to $\frac{n_{{\text{H}}_2\text{O}}}{\tau }$. To re-oxidize ceria as much as possible, $n_{{\text{H}}_2\text{O}}$ is set to the maximum value calculated by Eq. 25, in which case the generated chemical heat is completely utilized for heating water. In addition, the connection of $r_{{\text{H}}_2}$ and $\delta$ is given by Eq. 26.

$n_{{\text{H}}_2\text{O}}={\displaystyle \frac{m_{\text{RPC}}\left({\delta }_{\text{red}}-{\delta }_0\right)}{M_{\text{RPC}}\left(1-\epsilon \right)\left[{\overline{h}}_{{\text{H}}_2\text{O}}\left(T_{\infty }\right)-{\overline{h}}_{{\text{H}}_2\text{O}}\left(T_{\text{ox}}\right)\right]}\left\{\epsilon \left[{\overline{h}}_{{\text{H}}_2}\left(T_{\infty }\right)-{\overline{h}}_{{\text{H}}_2\text{O}}\left(T_{\infty }\right)\right]+\left(1-\epsilon \right)\left[{\overline{h}}_{{\text{H}}_2}\left(T_{\text{ox}}\right)-{\overline{h}}_{{\text{H}}_2\text{O}}\left(T_{\text{ox}}\right)\right]-\frac{\text{Δ}{\overline{h}}_{{\text{O}}_2}\left({\delta }_1^{(n-1)}\text{,}{\delta }_0\right)}{2}\right\}}(25)$

$\delta ={\delta }_{\text{red}}-\frac{M_{\text{RPC}}}{m_{\text{RPC}}}{\displaystyle {\int }_0^t{r}_{{\text{H}}_2}\text{d}t}(26)$

In the present work, we propose an effective recuperation system to enhance the solid-phase heat exchange. System performance is characterized by the heat recovery effectiveness ε_solid defined as the ratio of the recovered thermal energy Q_rec,solid to the thermal enthalpy change of RPC during the redox cycle, and solar-to-fuel efficiency of the overall system defined as the total amount of thermal energy output of hydrogen divided by the concentrated solar energy input:

$Q_{\text{rec,solid}}=m_{\text{RPC}}{c}_v\left(T_{N+1}-T_{\text{ox}}\right)(27)$

${\epsilon }_{\mathrm{solid}}=\frac{Q_{\mathrm{r}\mathrm{e}\mathrm{c},\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{i}\mathrm{d}}}{m_{\mathrm{RPC}}{c}_v\left(T_{\mathrm{r}\mathrm{e}\mathrm{d}}-T_{\mathrm{ox}}\right)}(28)$

${\eta }_{\text{th}}=\frac{Q_{\text{fuel}}}{Q_{\text{solar}}}(29)$

Results and Discussion

In this section, we first present the verification of the described mathematical model and its assumptions. Then, we present the performance of the proposed receiver–reactor array. Finally, we show the results of a sensitivity study of the thermal-to-chemical efficiency as functions of the concentration ratio C, the number of CRRs in the pre-cooling or pre-heating part, N, the gas-phase heat recovery effectiveness ε, the reduction temperature, T_red, and the relative oxygen partial pressure, $p_{{\text{O}}_2}$. The baseline model parameters used in this study are listed in Table 1.

TABLE 1

TABLE 1. Baseline model parameters.

Model Verification

The present model is verified by comparing its selected predictions with the numerical and experimental results obtained by Venstrom et al. (2015) for the reduction reaction of a fixed-bed of ceria. Firstly, we compare the O₂ production rate, $r_{{\text{O}}_2}$. The same operating conditions are applied: (1) the ceria is heated from 1,013 to 1,748 K at a rate of 100 K min⁻¹ and then it kept isothermal for 4 min; (2) N₂ sweep gas flow is constant at 900 mL min⁻¹ g_ceria⁻¹; (3) the mass of ceria is 1.0245 g; and (4) the initial δ is assumed to be equal to 10^–5. Figure 7 shows the O₂ production rates during the reduction reaction of fixed-bed ceria predicted by the two models. A good agreement has been found, indicating that the present model provides adequate accuracy to model the transient thermal reduction reaction of fix-bed ceria. Secondly, experiments were conducted by Venstrom et al. (2015) to test a horizontal reactor under isothermal conditions in an infrared (IR) imaging furnace. The reactor comprised a packed-bed of porous ceria particles. The N₂ sweep gas flows were controlled with the high accuracy mass flow controllers. $r{\text{o}}_2$ was measured in real-time using a Raman laser gas analyzer. The experimental data of $r{\text{o}}_2$ are taken to compare with the results predicted from the present model, which is shown in Figure 8. The two sets of data correspond to N₂ sweep gas flows of 150 and 300 mL min⁻¹ g⁻¹ at a constant reduction temperature T_red = 1773 K. The shaded region in the plots indicates the range of rates predicted by the model due to the uncertainty in the initial δ (0.021 ± 0.002). Figure 8 shows a satisfactory agreement of $r_{{\text{O}}_2}$ predicted by the present model and measured by Venstrom et al. (2015).

FIGURE 7

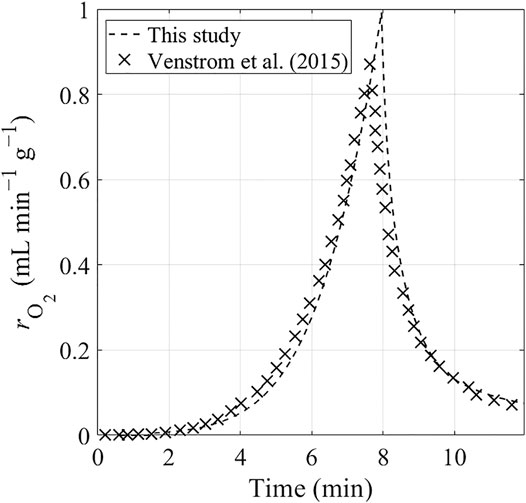
FIGURE 7. Transient O₂ production rate from reduction reaction of fixed-bed ceria predicted by two numerical models: the model developed by Venstrom et al. (2015) (represented by the crosses) and the present model (represented by the dashed curves). The reduction reaction is operated under an increasing temperature and a constant N₂ flow.

FIGURE 8

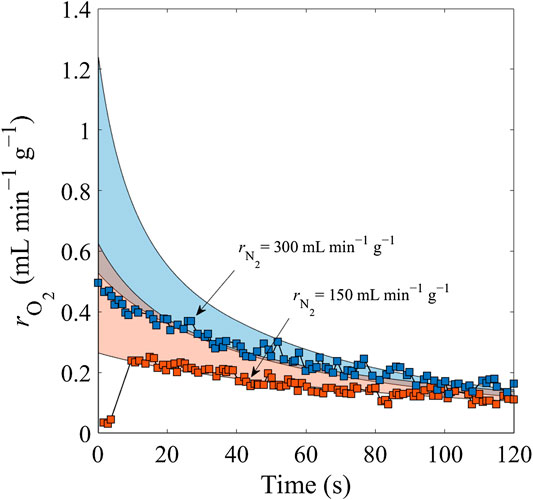
FIGURE 8. Comparison of predicted (color areas) and measured (squares) data for N₂ sweep gas flows of 150 mL min⁻¹ g⁻¹ (orange) and 300 mL min⁻¹ g⁻¹ (blue) at a constant reduction temperature T_red = 1,773 K.

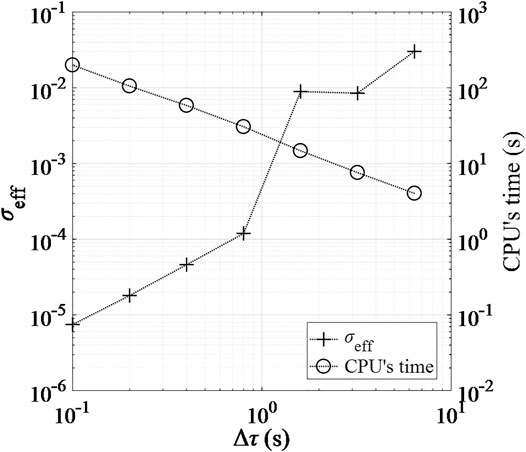
In addition, according to the second law of thermodynamics, Gibbs’s criterion should be followed at any time for chemical processes to spontaneously take place at specified thermodynamical conditions (Li et al., 2018a; Li et al., 2018b). In this study, we made an important assumption that for the recuperation step, the transient change of δ for each pre-heating cavity is linear during a cycle. Chemical reactions are assumed at equilibrium states at the beginning and the end of each cycle, namely ΔG = 0. As shown in the inset of Figure 9A, it takes N cycles to complete the pre-heating process for the cavity to move from #2N to #(N+1) position. The maximum δ at each temperature to reach thermodynamic equilibrium, δ_eq, is calculated and plotted in Figure 9 (the dashed curve in the inserted figure). The curve of δ_eq separates the full area into two regions: the gray region, ΔG < 0, and the white region, ΔG > 0. To meet the Gibbs’ criterion, δ should always be below δ_eq, namely in the gray region. Figure 9A shows that the values of δ under the assumption of linear change of δ in the recuperation process, δ_present, exceed the values of δ under the equilibrium condition, δ_eq, except for the initial and final states of cycles.

FIGURE 9

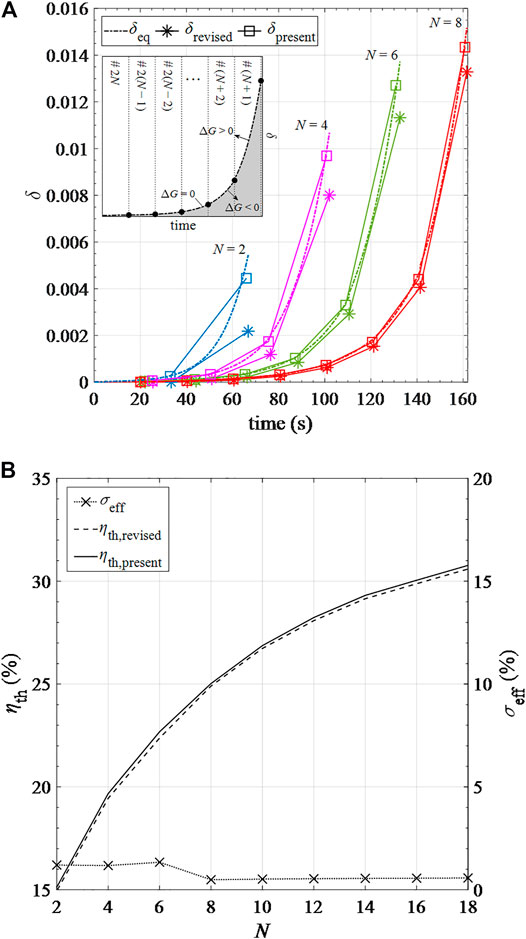
FIGURE 9. Results of (A)δ over time based on the present model (δ_present), the revised model (δ_revised) and the equilibrium assumption (δ_eq) in different pre-heating cavity numbers; (B) solar-to-fuel efficiencies based on the present (η_present) and revised (η_revised) models and their relative errors σ_eff in different pre-heating cavity numbers.

To examine the effect of the assumption of linear change of δ in the recuperation process, we introduce a correction factor α varying from 0 to 1. Instead of setting δ to δ_eq for the initial and final points of each cycle (marked with squares), δ is reduced to δ_revised = αδ_eq (marked with asterisks). α is adjusted by the trial-and-error method for different cavity positions to ensure δ_revised is always below δ_eq, namely $\Delta G\le 0$. Figure 9B shows results of solar-to-fuel efficiencies using this correction for different numbers of pre-heating cavities. It is found that η_th,_present is larger than η_th,_revised due to the overestimation caused by neglecting the limit of the second law. However, the difference between the two efficiencies, Δη_th, is less than 0.3%. The relative error σ_eff is ∼1% for N ≤ 6, and further decreases to ∼0.5% for N > 6. The linear assumption greatly increases the computational efficiency of the model with satisfactory accuracy. Hence, it is used to make the following predictions of the system performance.

Recuperation Unit

We first present the results of thermodynamic parameters, including temperature, relative oxygen partial pressure, and the non-stoichiometric number of ceria in CRRs in the recuperation unit when a steady state is reached.

The temperature distribution of CRRs in the recuperation unit is depicted in Figure 10. The recuperation unit consists of a cascade of 20 CRR positions, and the indexing numbers i of the CRRs in the pre-cooling and pre-heating parts correspond to #1–10 and #11–20, respectively. For 1 ≤ i ≤ 10, the temperature of the CRR in #i position drops from $T_i^{(n-1)}$ (State 1) to $T_i^{\left(n\right)}$ (State 4) after a complete cycle. The sensible heat in CRRs of the pre-cooling zone is captured and transported to the CRRs in the pre-heating part via the N₂ sweep flow. Therefore, for 11 ≤ i ≤ 20, the CRR temperature increase is synchronized. Figure 10 also shows that the temperature peaks in the middle for i = 10 and decreases toward both sides. After 20 cycles, the target CRR, initially located in position #20, passes through all CRR positions and eventually arrives at position #1. The process can be separated into two stages. For the first 10 cycles, the temperature of the target CRR climbs up gradually. A peak value of 1,730 K can be reached at position #11 of the pre-heating part. For the next 10 cycles, the target CRR is cooled down step by step from the reduction temperature, $T_{\text{red}}$ = 1900 K. The minimum value, 1038 K, is obtained as the CRR moves to position #1. The small temperature difference between T₁ and T_ox reduces the quenched heat loss, Q_quench, prior to the water-splitting process. Therefore, a high solid-phase heat recovery efficiency of 81% can be reached, as calculated by Eq. 25.

FIGURE 10

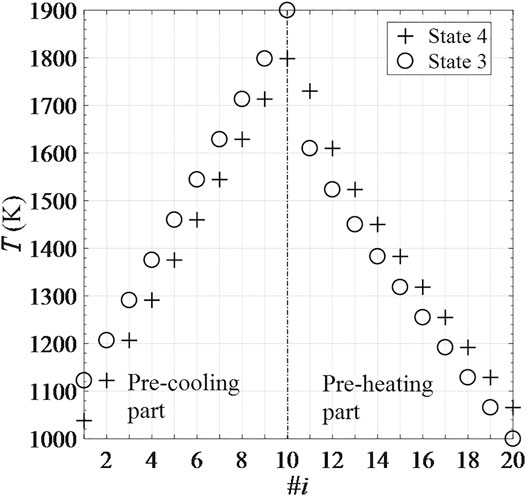
FIGURE 10. Temperature distribution of 20 recuperation CRRs corresponding to State 3 and State 4 of one cycle under steady conditions.

Figure 11 shows the thermodynamic parameters δ and $p_{{\text{O}}_2}$ as a function of recuperation CRR position at the end of a cycle. Pre-reduction may occur in the CRRs of the pre-heating part (11 ≤ i ≤ 20). δ can increase rapidly and reach a peak value of 0.015 when i approaches 11. Because of pre-reduction, O₂ is generated and gradually accumulated in the sweep gas. $p_{{\text{O}}_2}$ of the gas flow increases from 2.4 × 10^–3 to 3.4 × 10^–3 when i varies from 11 to 20. The pre-reducing effect enables storing 10% of the sensible heat in the form of chemical energy by increasing ${\overline{h}}_{{\text{O}}_2}\left(\delta \right)$ during pre-heating. Figure 11 shows that δ can increase by 6% as compared to ${\delta }_{\text{red}}$, and finally reach 0.036.

FIGURE 11

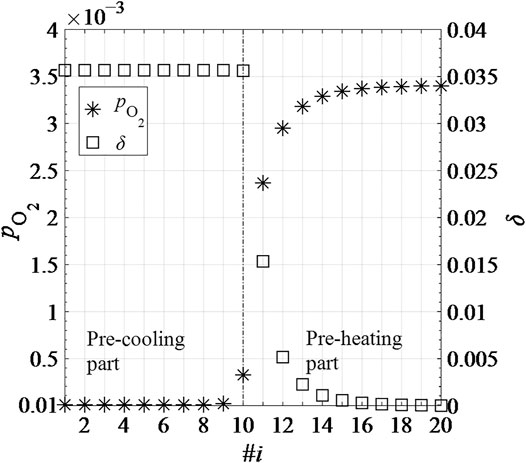
FIGURE 11. Thermodynamic parameters δ and $p_{{\text{O}}_2}$as a function of recuperation CRR position (#i) at the end of a cycle under steady conditions.

Sensitivity Analysis

Here we present the results of sensitivity study relative to change of a single key parameter, including number of CRRs in the pre-cooling or pre-heating part, N, reduction temperature T_red, relative oxygen partial pressure at the end of reduction $p_{{\text{O}}_2}$, and mass of RPC per cavity $m_{\text{RPC}}$, on the receiver–reactor array performance characterized by solid-phase heat recovery effectiveness ε_solid, solar-to-fuel efficiency η_th, hydrogen production rate $r_{{\mathrm{H}}_2}$, gas-phase heat recovery loss fraction F_gas, and reaction duration τ. Then, the results of sensitivity study of the effects of changing parameters, including concentration ratio, C, gas-phase heat recovery effectiveness, ε, N, T_red, and $p_{{\text{O}}_2}$, respectively, on the system performance are presented. C directly affects the cavity radiative heat loss, Q_rad. Increasing C decreases Q_rad for the same T_red. N and ε are key factors influencing the heat recovery efficiency during gas-solid- and gas-gas-phase heat exchange. T_red and $p_{{\text{O}}_2}$ are the driving forces for reduction and affect the cavity heat loss and the heat recovery efficiency during gas-phase heat exchange.

According to Figure 12, ε_solid and ${\eta }_{\text{th}}$ vary from 63% and 15% to 83% and 30%, respectively, by increasing N from 2 to 16. This is because that a large N leads to a small temperature difference between the reduction CRR and the CRR in #(N+1) position, namely (T_red −T_N+1), which improves the solid-phase heat recovery and thus the total solar-to-fuel efficiency. The improvement magnitude is relatively larger when N is increased from 2 to 4 that ε_solid and ${\eta }_{\text{th}}$ are increased by 17% and 33%, respectively. ε_solid and ${\eta }_{\text{th}}$ increase with N at diminishing rates, as limited by other factors such as T_red, $p_{{\text{O}}_2}$, ε, and C. On the other hand, a large N also leads to a large required CRR disk diameter, and thereby a large tilt angle of the tower reflector axis, decreasing the system optical efficiency (Li et al., 2020b). Here, N is set to 10 in the baseline receiver–reactor system.

FIGURE 12

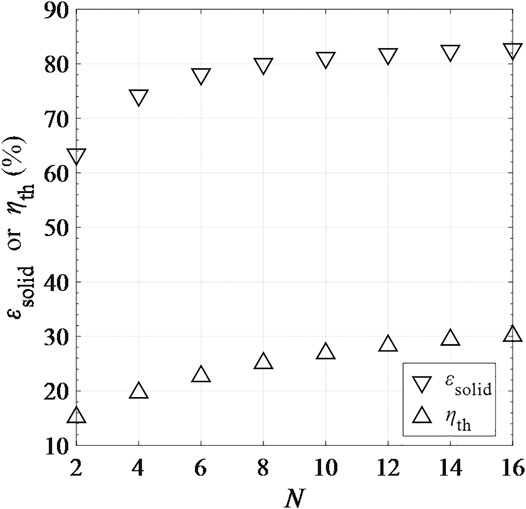
FIGURE 12. Solid-phase heat recovery effectiveness ε_solid and total solar-to-fuel efficiency η_th as functions of number of CRRs in one side of the recuperation zone (the pre-cooling or pre-heating part), N.

Figure 13 shows the increase of hydrogen production rate per kilogram of ceria, $r_{{\text{H}}_2}$, and total solar-to-fuel efficiency, ${\eta }_{\text{th}}$, with reduction temperature, T_red, which is attributed to the robust reduction capacity of non-stoichiometric ceria at high temperatures. The rate and efficiency increases are slower when T_red further increases due to the rapidly increasing emission losses. For example, increasing T_red from 1,600 to 1700 K yields the increment of $r_{{\mathrm{H}}_2}$ and ${\eta }_{\text{th}}$, 2.3 × 10^–3 mol kg⁻¹ s⁻¹ and 5.7%, respectively, whereas increasing T_red from 1,900 to 2,000 K yields the increment of $r_{{\mathrm{H}}_2}$ and ${\eta }_{\text{th}}$ of only 0.2 × 10^–3 mol kg⁻¹ s⁻¹ and 0.6%, respectively. The improvement in the total thermal performance is insignificant for T_red > 1,900 K.

FIGURE 13

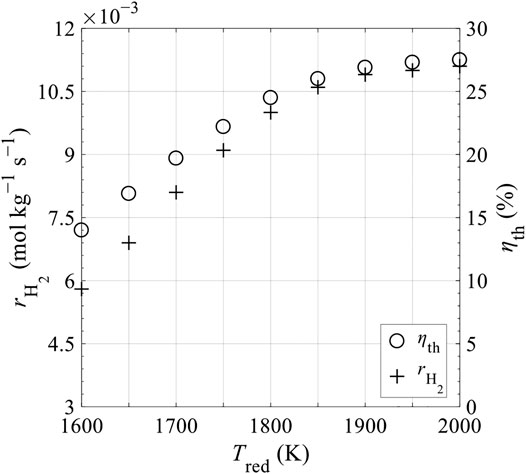
FIGURE 13. Hydrogen production rate per kilogram of ceria, $r_{{\mathrm{H}}_2}$, and total solar-to-fuel efficiency, η_th, as a function of reduction temperature T_red.

The relative oxygen partial pressure, $p_{{\text{O}}_2}$, also affects the thermal performance of the receiver−reactor system. As previously mentioned, ceria reduction is favored at atmosphere of low $p_{{\text{O}}_2}$, which can be created by a certain flow of pure N₂ to keep removing O₂ generated in the ceria. The benefit gained by reducing $p_{{\mathrm{O}}_2}$ should be weighed against the penalty of thermal losses associated with imperfect gas-phase heat recovery. Figure 14 shows solar-to-fuel efficiency, η_th, and gas-phase heat recovery loss fraction, F_gas, as a function of $p_{{\mathrm{O}}_2}$. A peak η_th of 27% is found at relatively high $p_{{\mathrm{O}}_2}$ (0.01–0.1). As $p_{{\mathrm{O}}_2}$ decreases, the gas-phase heat recovery loss gradually becomes the major factor of system heat losses, and η_th declines sharply. F_gas rapidly increases from 0.14 to 0.65 when $p_{{\mathrm{O}}_2}$drops from 0.08 to 10^–4. η_th is only 2% at $p_{{\mathrm{O}}_2}$= 10^–4.

FIGURE 14

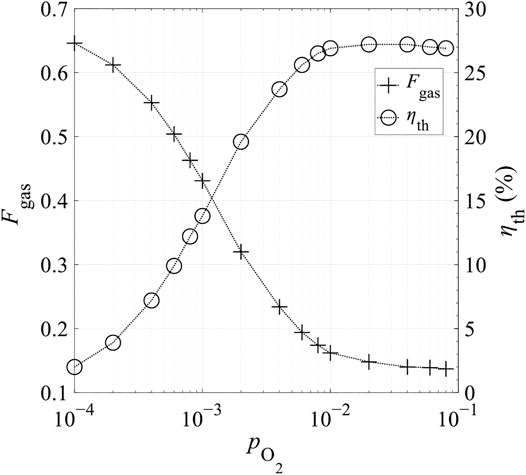
FIGURE 14. Heat loss fraction corresponding to gas-phase heat recovery, F_gas, and total thermal efficiency η_th as a function of relative oxygen partial pressure at the end of reduction, $p_{{\mathrm{O}}_2}$.

Figure 15 shows the effects of the mass of RPC, m_RPC, on reaction duration per cycle, τ, shifting frequency of reactor disk f = 1/τ, and thermal efficiency η_th. τ is proportional to m_RPC, indicating that for higher m_RPC, longer time is needed to finalize the reaction, and the required f is lower. Based on Figure 15, m_RPC has little impact on η_th. Figures 16, 17 show the effects of C and N on η_th for selected values of T_red and assuming ε = 1. η_th is calculated based on selected T_red varying from 1600 to 2000 K in 50 K increments for a fixed $p_{{\mathrm{O}}_2}$ of 5 × 10^–5. As shown in Figure 16, optimal T_red for maximized η_th increases with the increase of C. Peak values of η_th are found at T_red of between 1,600 and 2,000 K for C$\le$ 3,000. For instance, for C = 1,000, 2,000, and 3,000, the maximum η_th of 22%, 33%, and 38%, respectively, are obtained at T_red = 1700 K, 1900 K, and 2,000 K. Further increasing C leads to higher optimal T_red and the corresponding η_th. η_th increases at a diminishing rate with C. Moreover, aiming at high C can lower optical efficiency of the optical sub-system (Li et al., 2016; Li et al., 2020a; Li et al., 2020b). Figure 17 shows that η_th increases monotonically with increasing T_red for given N. The maximum η_th of 29%, 33%, 35%, 37%, and 38% are obtained at maximum T_red = 2,000 K, corresponding to N = 2, 4, 6, 8 and 10, respectively. Increasing N leads to higher η_th under the fixed T_red and $p_{{\mathrm{O}}_2}$, but η_th increases at a diminishing rate with N. For instance, η_th grows 4.6% and 1.1%, when increasing N from 2 to 4, and 8 to 10 at T_red = 1,900 K, respectively. In addition, as mentioned in Section 5.2, increasing N leads to a larger tilt angle of the tower reflector axis and reduces the optical efficiency of the system (Li et al., 2020b).

FIGURE 15

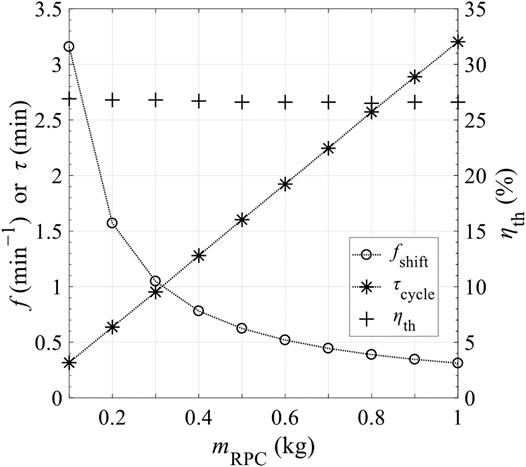
FIGURE 15. Shifting frequency of secondary mirror, f, or reaction duration, τ, and total solar-to-fuel efficiency, η_th, as a function of mass of ceria in CRR, m_RPC.

FIGURE 16

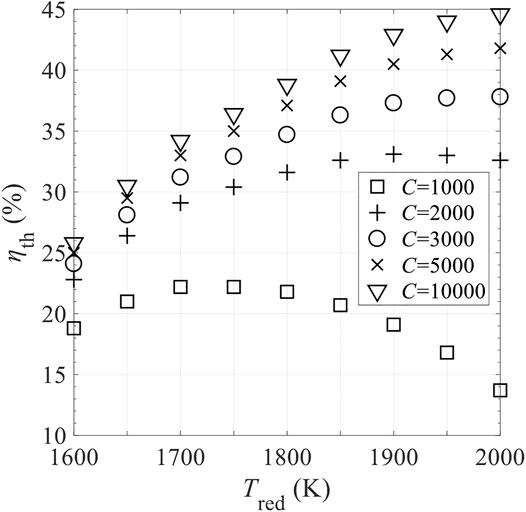
FIGURE 16. Effect of concentration ratio C on total solar-to-fuel efficiency η_th in different levels of reduction temperature, T_red, with perfect gas-phase heat recovery and relative oxygen partial pressure $p_{{\mathrm{O}}_2}$ of 5 × 10^–5.

FIGURE 17

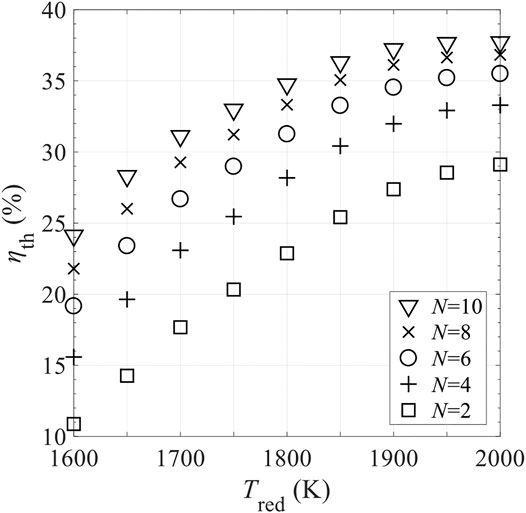
FIGURE 17. Effect of number of CRRs in the pre-cooling and pre-heating zones, N, on total solar-to-fuel efficiency η_th in different levels of reduction temperature, T_red, with perfect gas-phase heat recovery and relative oxygen partial pressure $p_{{\mathrm{O}}_2}$ of 5 × 10^–5.

Figure 18 shows the effects of ε on total solar-to-fuel efficiency, η_th, for selected $p_{{\mathrm{O}}_2}$ varying from 5 × 10^–5 to 0.1. The dashed line shows the limit of η_th for perfect gas-phase heat exchange, namely ε = 1. Without the gas-phase heat recovery loss, η_th increases logarithmically with $p_{{\mathrm{O}}_2}$, namely ${\eta }_{\text{th}}=f\left(\ln p_{{\mathrm{O}}_2}\right)$. A peak value of η_th of 37% is obtained at the lowest simulated $p_{{\mathrm{O}}_2}$ of 5 × 10^–5. For ε < 1, the gas-phase heat recovery loss reduces η_th. It is found that the overall thermal performance of the receiver–reactor system is sensitive to ε, and ε may become a dominant factor of η_th, especially at low $p_{{\mathrm{O}}_2}$ levels. For instance, η_th approaches the limit of 33% for ε = 1, but is only 5% for ε = 0.8 when $p_{{\mathrm{O}}_2}$ = 10^–3. Except for ε = 1, η_th rapidly decreases for all cases of $p_{{\mathrm{O}}_2}$< 10^–3. As an example of ε = 0.95, η_th drops from 24% down to 2% when decreasing $p_{O_2}$ from 5 × 10^–3 to 10^–4. This is because the gas-phase heat recovery loss is positively correlated to ${\dot{m}}_{{\mathrm{N}}_2}$ and thus varies inversely to $p_{{\mathrm{O}}_2}$ (as shown in Eq. 16). Therefore, reducing $p_{{\mathrm{O}}_2}$ at a low level may not lead to improved efficiency because the increased gas-phase heat recovery loss outweighs the thermodynamic benefits gained from the increase in reduction extent. The optimal values of $p_{{\mathrm{O}}_2}$ are found at a relatively large $p_{{\mathrm{O}}_2}$ level of ∼0.01, in which the heat recovery loss becomes a minor impact factor. Correspondingly, η_th approaches its maximum with the optimal $p_{{\mathrm{O}}_2}$. For instance, a peak value over 27% is obtained at $p_{{\mathrm{O}}_2}$= 0.05 for ε = 0.95.

FIGURE 18

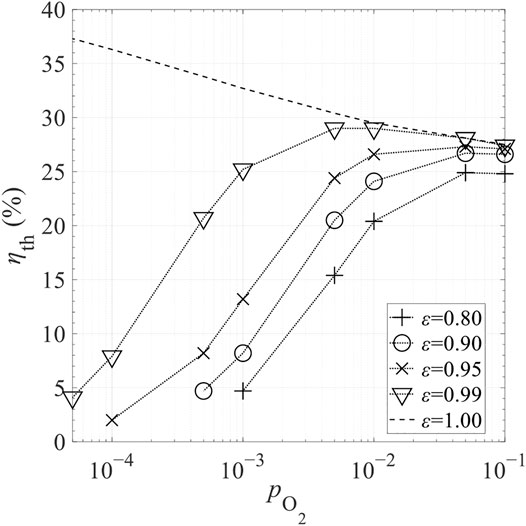
FIGURE 18. Effect of gas-phase heat transfer effectiveness, ε, on total solar-to-fuel efficiency η_th in different levels of relative oxygen partial pressure, $p_{O_2}$, with a concentration ratio C of 3,000 at T_red = 1,900 K. The top dashed line shows the limit of η_th for perfect gas-phase heat exchange.

Figure 19 shows the contour map of η_th for selected ε varying from 0.81 to 0.99 and C from 1,000 to 4,000 at T_red = 1900 K and $p_{{\mathrm{O}}_2}$= 0.01. For the sake of comparison, normalized variables ε^∗ and C^∗ are defined as

${\epsilon }^{\ast }=\frac{\epsilon -{\epsilon }_{\min }}{{\epsilon }_{\max }-{\epsilon }_{\min }};C^{\ast }=\frac{C-C_{\min }}{C_{\max }-C_{\min }}(27)$

where ε_min, ε_max and C_min, C_max are set to 0.8, 1 and 1,000, 4,000, respectively. The colored contour lines present the different levels of η_th. The gradient of η_th is given by $\nabla {\eta }_{\mathrm{t}\mathrm{h}}=\left(\frac{\partial {\eta }_{\mathrm{t}\mathrm{h}}}{\partial {\epsilon }^{\ast }}\right)\overrightarrow{i}+\left(\frac{\partial {\eta }_{\mathrm{t}\mathrm{h}}}{\partial C^{\ast }}\right)\overrightarrow{j}$. As shown in Figure 19, η_th increases when increasing C^∗ or ε^∗. The maximum and minimum values of η_th are 31% and 10%, which are found at (0.95, 1) and (0.05, 0), respectively. The magnitude of the gradient of η_th, $\left|\nabla {\eta }_{\mathrm{t}\mathrm{h}}\right|$, decreases when increasing C^∗ or decreasing ε^∗. ${\left|\nabla {\eta }_{\text{th}}\right|}_{\max }$ and ${\left|\nabla {\eta }_{\text{th}}\right|}_{\min }$, are 0.68 and 0.07, obtained at (0.95, 0) and (0.05, 1). For the region of low C^∗, $\left(\frac{\partial {\eta }_{\text{th}}}{\partial C^{\ast }}\right)$ is much larger than $\left(\frac{\partial {\eta }_{\text{th}}}{\partial {\epsilon }^{\ast }}\right)$. $\nabla {\eta }_{\mathrm{t}\mathrm{h}}$ tends to point upwards. For instance, $\left(\frac{\partial {\eta }_{\text{th}}}{\partial C^{\ast }}\right)$ equals 0.5 at ε^∗ = 0.05, C^∗ = 0, which is fourteen times higher than $\left(\frac{\partial {\eta }_{\text{th}}}{\partial {\epsilon }^{\ast }}\right)$. Hence, C^∗ is the critical parameter for η_th for low C^∗.

FIGURE 19

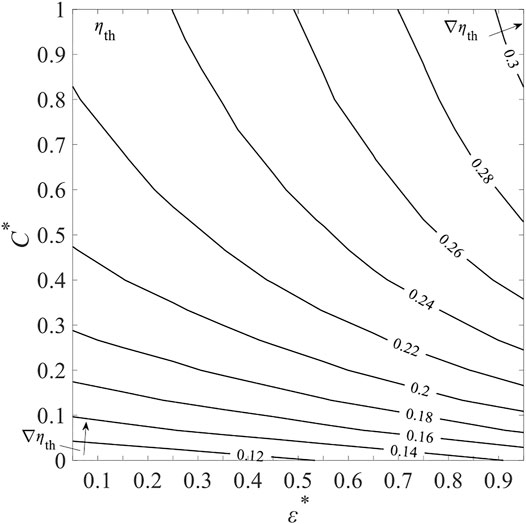
FIGURE 19. Total solar-to-fuel efficiency, η_th, as a function of non-dimensional gas-phase heat transfer effectiveness, ε*, and concentration ratio C* at fixed T_red = 1900 K and $p_{{\mathrm{O}}_2}$= 0.01.

As C^∗ increases, $\left(\frac{\partial {\eta }_{\text{th}}}{\partial {\epsilon }^{\ast }}\right)/\left(\frac{\partial {\eta }_{\text{th}}}{\partial C^{\ast }}\right)$ will gradually increase. It approaches 2.4 and 2.3 at ε^∗ = 0.05 and 0.95, when C^∗ = 1. Since η_th is more sensitive to the change of ε^∗ rather than C^∗ for high C^∗, ε^∗ is more important than C^∗ for η_th under these conditions.

Figure 20 shows the contour map of η_th for selected T_red varying from 1,600 to 2,000 K and $p_{{\mathrm{O}}_2}$ from 10^–4 to 0.096 when ε = 0.95 and C = 3,000. Non-dimensional reduction temperature and relative oxygen partial pressure, θ^∗ and P^∗, are defined as

${\theta }^{\ast }=\frac{T_{\text{red}}-T_{\min }}{T_{\max }-T_{\min }};P^{\ast }=\frac{\ln \left(\raisebox{1ex}{$p_{{\mathrm{O}}_2}$}\!\left/ \!\raisebox{-1ex}{$p_{{\mathrm{O}}_2,\min }$}\right.\right)}{\ln \left(\raisebox{1ex}{$p_{{\mathrm{O}}_2,\max }$}\!\left/ \!\raisebox{-1ex}{$p_{{\mathrm{O}}_2,\min }$}\right.\right)}(28)$

where $p_{{\mathrm{O}}_2,\min }$, $p_{{\mathrm{O}}_2,\max }$ and T_min, T_max are set to 10^–5, 0.1 and 1,000, 2,000 K, respectively. As shown in Figure 20, η_th is low for low P^∗. The values are less than 4% for P^∗ = 0.25. For the range 0.25 ≤ P^∗ ≤ 0.55, increasing $p_{{\mathrm{O}}_2}$ improves η_th. For instance, when increasing P^∗ from 0.25 to 0.55 for θ^∗ = 1, η_th is gradually improved from 2% to 16%. The average growth rate of η_th is 0.29 for the increase from 2% to 6%, which is then improved to 0.67 for the increase from 6% to 16%. By contrast, η_th is much less sensitive to the change of θ^∗ for low P^∗. The differences of η_th are <2% when varying θ^∗ over the range of 0.6–1 for P^∗ = 0.25. As P^∗ increases over 0.55, the increasing magnitude of η_th along the y-axis slows down. Meanwhile, the influence of θ^∗ on η_th is enhanced. θ^∗ becomes the major factor for η_th when further increasing P^∗ to high values. For the range of high P^∗ and low θ^∗, increasing θ^∗ may lead to a rapid increase of η_th. It is shown that η_th is doubled as θ^∗ increases from 0.6 to 0.8 for P^∗ = 1, while the change in η_th is insignificant for P^∗ between 0.92 and 1 and θ^∗ = 0.6. In addition, the gradient of η_th points downwards in the region of high P^∗ and θ^∗ toward a point corresponding to the optimal solution with the maximum of η_th = 29% at θ^∗ = 1 and P^∗ = 0.85.

FIGURE 20

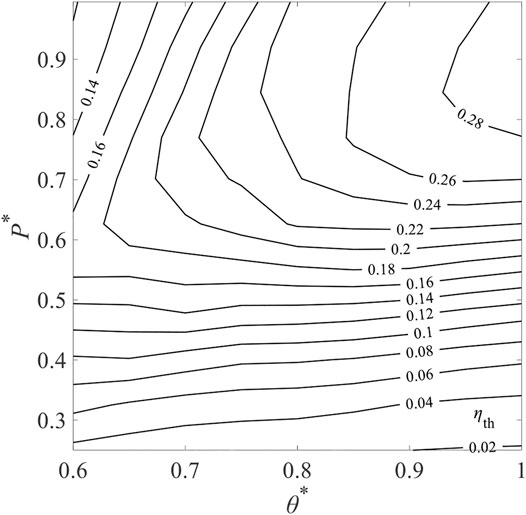
FIGURE 20. Contours of total solar-to-fuel efficiency, η_th in different levels of non-dimensional reduction temperature, θ^∗, and relative oxygen partial pressure P^∗ for ε = 0.95 and C = 3,000.

Conclusion

In this study, a conceptual fixed-bed solar thermochemical cavity receiver–reactor array has been proposed and numerically studied for water-splitting via ceria-based redox cycling. Heat recuperation was modeled by a linear matrix model while reduction and oxidation were modeled by a lumped parameter model. Thermal performance characterized by solid-phase heat recovery effectiveness and total solar-to-fuel efficiency was studied for selected parameters of the proposed system such as the reduction temperature, relative oxygen partial pressure, number of receiver–reactor, concentration ratio, and gas-phase heat recovery effectiveness.

Under the assumptions made in this study, the solid-phase heat recovery effectiveness and the total solar-to-fuel efficiency were found to be 80% and 27%, respectively, for the baseline system. Along with the pre-heating process, pre-reduction occurs simultaneously, resulting in ceria non-stoichiometry of 0.015. which was attributed to the dual function of N₂ as HTF and oxygen scavenger during recuperation. A solar-to-fuel efficiency of 27% was found with a reduction temperature at 1,900 K and relative oxygen partial pressure of 0.01. The concentration ratio and gas-phase heat recovery effectiveness for the baseline case were assumed to be 3,000 and 0.95, respectively. A higher thermal efficiency can be achieved by increasing the total number of receiver–reactors.

Sensitivity analysis demonstrated that the solar-to-fuel efficiency is highly sensitive to the concentration ratio and the gas-phase heat recovery effectiveness at high reduction temperature and low relative oxygen partial pressure conditions. Increasing the concentration ratio and gas-phase heat recovery effectiveness simultaneously improves the system performance. The total solar-to-fuel efficiency was found to be 42% with a concentration ratio of 5,000 and perfect gas-phase heat recovery. In addition, for the baseline values of the concentration ratio and the gas-phase heat recovery effectiveness, the overall solar-to-fuel efficiency can be effectively increased by increasing relative oxygen partial pressure at low temperature or by increasing temperature at high relative oxygen partial pressure.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

SY concept, analysis, writing. LL concept, writing. BW writing. SL writing, JW funding, supervision, writing PL writing WL funding, supervision, concept, writing.

Funding

This work was supported by the National Natural Science Foundation of China (No. 51736006), the Scientific Research Foundation of Graduate School of Southeast University (No. YBPY 1855), the China Scholarship Council (SY, Grant No. (2017)3109), the Australian Renewable Energy Agency (Grant No. 2014/RND005), and the Australian Research Council (Grant No. FT140101213).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Abbreviations

0D, zero dimensional; CPC, compound parabolic concentrator; CRR, cavity receiver–reactor; DNI, direct normal irradiance; HTF, heat transfer fluid; HXer, heat-exchanger; LMM, linear matrix model; LPM, lumped parameter method; RPC, reticulated porous ceria; TR, tower reflector.

Footnotes

¹A higher solar-to-fuel efficiency of 7.5% was reported by (Haeussler et al., 2020) where the realistic parasitic energy consumption is not accounted for.

²RPC and Al₂O₃-made containers have been successfully demonstrated in a series of solar thermochemical water/CO₂ splitting systems. Assessment of potential materials issues is beyond the scope of this study.

³One phase difference represents the angle difference between two adjacent cavities: $\Delta \theta =\frac{2\pi }{2N+2}$.

⁴τ is omitted in the following text and equations for brevity.

References

Abanades, S., Legal, A., Cordier, A., Peraudeau, G., Flamant, G., and Julbe, A. (2010). Investigation of Reactive Cerium-Based Oxides for H₂ Production by Thermochemical Two-step Water-Splitting. J. Mater. Sci. 45 (15), 4163–4173. doi:10.1007/s10853-010-4506-4

CrossRef Full Text | Google Scholar

Bader, R., and Lipiński, W. (2017). “Solar thermal processing,” in Advances in Concentrating Solar Thermal Research and Technology, Woodhead Publishing Series in Energy. Editors M. J. Blanco, and L. R. Santigosa, (Berlin: Springer) 403–459.

CrossRef Full Text | Google Scholar

Bader, R., Venstrom, L. J., Davidson, J. H., and Lipiński, W. (2013). Thermodynamic Analysis of Isothermal Redox Cycling of Ceria for Solar Fuel Production. Energy Fuels 27 (9), 5533–5544. doi:10.1021/ef400132d

CrossRef Full Text | Google Scholar

Blank, D. A., and Wu, C. (1994). Power Potential of a Terrestrial Solar-Radiant Stirling Heat Engine. Int. J. Ambient Energ. 15 (3), 131–139. doi:10.1080/01430750.1994.9675645

CrossRef Full Text | Google Scholar

Chueh, W. C., and Haile, S. M. (2010). A Thermochemical Study of Ceria: Exploiting an Old Material for New Modes of Energy Conversion and CO₂ mitigationMathematical, Physical and Engineering Sciences 368. Philos. Trans. A. Math. Phys. Eng. Sci. 368, 3269–3294. doi:10.1098/rsta.2010.0114

PubMed Abstract | CrossRef Full Text | Google Scholar

Chueh, W. C., Falter, C., Abbott, M., Scipio, D., Furler, P., Haile, S. M., et al. (2010). High-Flux Solar-Driven Thermochemical Dissociation of CO₂ and H₂0 Using Nonstoichiometric Ceria. Science 330 (6012), 1797–1801. doi:10.1126/science.1197834

PubMed Abstract | CrossRef Full Text | Google Scholar

Dähler, F., Wild, M., Schäppi, R., Haueter, P., Cooper, T., Good, P., et al. (2018). Optical Design and Experimental Characterization of a Solar Concentrating Dish System for Fuel Production via Thermochemical Redox Cycles. Solar Energy 170, 568–575. doi:10.1016/j.solener.2018.05.085

CrossRef Full Text | Google Scholar

Diver, R. B., Miler, J. E., Siegel, N. P., and Moss, T. A. (2010). “Testing of a CR5 Solar Thermochemical Heat Engine Prototype,” in Proceedings of the ASME 2010 4th International Conference on Energy Sustainabilty Volume 2, 97–104.

Google Scholar

El-Ehwany, A. A., Hennes, G. M., Eid, E. I., and El-Kenany, E. A. (2010). Development of the Performance of an Alpha-type Heat Engine by Using Elbow-bend Transposed-Fluids Heat Exchanger as a Heater and a Cooler. Energ. Convers. Manage. 52 (2), 1010–1019. doi:10.1016/j.enconman.2010.08.029

CrossRef Full Text | Google Scholar

Ermanoski, I., Siegel, N. P., and Stechel, E. B. (2013). A New Reactor Concept for Efficient Solar-Thermochemical Fuel Production. J. Sol. Energy Eng. 135 (3), 031002. doi:10.1115/1.4023356

CrossRef Full Text | Google Scholar

Falter, C. P., Sizmann, A., and Pitz-Paal, R. (2015). Modular Reactor Model for the Solar Thermochemical Production of Syngas Incorporating Counter-flow Solid Heat Exchange. Sol. Energy 122, 1296–1308. doi:10.1016/j.solener.2015.10.042

CrossRef Full Text | Google Scholar

Furler, P., Scheffe, J., Gorbar, M., Moes, L., Vogt, U., and Steinfeld, A. (2012a). Solar Thermochemical CO₂ Splitting Utilizing a Reticulated Porous Ceria Redox System. Energy Fuels 26 (11), 7051–7059. doi:10.1021/ef3013757

CrossRef Full Text | Google Scholar

Furler, P., Scheffe, J. R., and Steinfeld, A. (2012b). Syngas Production by Simultaneous Splitting of H₂O and CO₂ via Ceria Redox Reactions in a High-Temperature Solar Reactor. Energy Environ. Sci. 5 (3), 6098–6103. doi:10.1039/c1ee02620h

CrossRef Full Text | Google Scholar

Haeussler, A., Abanades, S., Julbe, A., Jouannaux, J., and Cartoixa, B. (2020). Solar Thermochemical Fuel Production from H₂O and CO₂ Splitting via Two-step Redox Cycling of Reticulated Porous Ceria Structures Integrated in a Monolithic Cavity-type Reactor. Energy 201, 117649. doi:10.1016/j.energy.2020.117649

CrossRef Full Text | Google Scholar

Hao, Y., Yang, C.-K., and Haile, S. M. (2014). Ceria-Zirconia Solid Solutions (Ce_1-xZr_xO_2−δ, X ≤ _0.2) for Solar Thermochemical Water Splitting: A Thermodynamic Study. Chem. Mater. 26, 6073–6082. doi:10.1021/cm503131p

CrossRef Full Text | Google Scholar

Häring, H. W. (2008). The Air Gases Nitrogen, Oxygen and Argon, Industrial Gases Processing. Hoboken: John Wiley & Sons, 9–109.

Hathaway, B. J., Bala Chandran, R., Gladen, A. C., Chase, T. R., and Davidson, J. H. (2016). Demonstration of a Solar Reactor for Carbon Dioxide Splitting via the Isothermal Ceria Redox Cycle and Practical Implications. Energy Fuels 30, 6654–6661. doi:10.1021/acs.energyfuels.6b01265

CrossRef Full Text | Google Scholar

Lapp, J., Davidson, J. H., and Lipiński, W. (2013). Heat Transfer Analysis of a Solid-Solid Heat Recuperation System for Solar-Driven Nonstoichiometric Redox Cycles. J. Sol. Energy Eng. 135 (3), 031004. doi:10.1115/es2012-91078

CrossRef Full Text | Google Scholar

Lapp, J., Davidson, J. H., and Lipiński, W. (2012). Efficiency of Two-step Solar Thermochemical Non-stoichiometric Redox Cycles with Heat Recovery. Energy 37, 591–600. doi:10.1016/j.energy.2011.10.045

CrossRef Full Text | Google Scholar

Lapp, J., and Lipiński, W. (2014). Transient Three-Dimensional Heat Transfer Model of a Solar Thermochemical Reactor for H₂O and CO₂ Splitting via Nonstoichiometric Ceria Redox Cycling. J. Sol. Energy Eng. 136 (3), 031006. doi:10.1115/1.4026465

CrossRef Full Text | Google Scholar

Li, L., Coventry, J., Bader, R., Pye, J., and Lipiński, W. (2016). Optics of Solar Central Receiver Systems: a Review. Opt. Express 24 (14), A985–A1007. doi:10.1364/oe.24.00a985

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, L., Wang, B., Pye, J., and Lipiński, W. (2020a). Temperature-based Optical Design, Optimization and Economics of Solar Polar-Field Central Receiver Systems with an Optional Compound Parabolic Concentrator. Sol. Energy 206, 1018–1032. doi:10.1016/j.solener.2020.05.088

CrossRef Full Text | Google Scholar

Li, L., Yang, S., Wang, B., Pye, J., and Lipiński, W. (2020b). Optical Analysis of a Solar Thermochemical System with a Rotating tower Reflector and a Receiver-Reactor Array. Opt. Express 28, 19429–19445. doi:10.1364/oe.389924

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, S., Wheeler, V. M., Kreider, P. B., Bader, R., and Lipiński, W. (2018a). Thermodynamic Analyses of Fuel Production via Solar-Driven Non-stoichiometric Metal Oxide Redox Cycling. Part 2. Impact of Solid-Gas Flow Configurations and Active Material Composition on System-Level Efficiency. Energy Fuels 32 (10), 10848–10863. doi:10.1021/acs.energyfuels.8b02082

CrossRef Full Text | Google Scholar

Li, S., Wheeler, V. M., Kreider, P. B., and Lipiński, W. (2018b). Thermodynamic Analyses of Fuel Production via Solar-Driven Non-stoichiometric Metal Oxide Redox Cycling. Part 1. Revisiting Flow and Equilibrium Assumptions. Energy Fuels 32 (10), 10838–10847. doi:10.1021/acs.energyfuels.8b02081

CrossRef Full Text | Google Scholar

Li, S., Wheeler, V. M., Kumar, A., Venkataraman, M. B., Muhich, C. L., Hao, Y., et al. (2021). Thermodynamic Guiding Principles for Designing Non-stoichiometric Redox Materials for Solar Thermochemical Fuel Production: Ceria, Perovskites, and beyond. Energy Technol. 14, 2000925. doi:10.1002/ente.202000925

CrossRef Full Text | Google Scholar

Marxer, D., Furler, P., Takacs, M., and Steinfeld, A. (2017). Solar Thermochemical Splitting of CO₂ into Separate Streams of CO and O₂ with High Selectivity, Stability, Conversion, and Efficiency. Energ. Environ. Sci. 10, 1142–1149. doi:10.1039/c6ee03776c

CrossRef Full Text | Google Scholar

Miller, J. E., McDaniel, A. H., and Allendorf, M. D. (2014). Considerations in the Design of Materials for Solar-Driven Fuel Production Using Metal-Oxide Thermochemical Cycles. Adv. Energ. Mater. 4, 1300469. doi:10.1002/aenm.201300469

CrossRef Full Text | Google Scholar

Muhich, C. L., Blaser, S., Hoes, M. C., and Steinfeld, A. (2018). Comparing the Solar-To-Fuel Energy Conversion Efficiency of Ceria and Perovskite Based Thermochemical Redox Cycles for Splitting H₂O and CO₂. Int. J. Hydrogen Energ. 43, 18814–18831. doi:10.1016/j.ijhydene.2018.08.137

CrossRef Full Text | Google Scholar

Muhich, C. L., Ehrhart, B. D., Al-Shankiti, I., Ward, B. J., Musgrave, C. B., and Weimer, A. W. (2016). A Review and Perspective of Efficient Hydrogen Generation via Solar thermal Water Splitting. Wires Energ. Environ. 5 (3), 261–287. doi:10.1002/wene.174

CrossRef Full Text | Google Scholar

Panlener, R. J., Blumenthal, R. N., and Garnier, J. E. (1975). A Thermodynamic Study of Nonstoichiometric Cerium Dioxide. J. Phys. Chem. Sol. 36 (11), 1213–1222. doi:10.1016/0022-3697(75)90192-4

CrossRef Full Text | Google Scholar

Qian, X., He, J., Mastronardo, E., Baldassarri, B., Yuan, W., Wolverton, C., et al. (2021). Outstanding Properties and Performance of CaTi_0.5Mn_0.5O_3-δ for Solar-Driven Thermochemical Hydrogen Production. Matter 4 (2), 688–708. doi:10.1016/j.matt.2020.11.016

CrossRef Full Text | Google Scholar

Siegel, N. P., Miller, J. E., Ermanoski, I., Diver, R. B., and Stechel, E. B. (2013). Factors Affecting the Efficiency of Solar Driven Metal Oxide Thermochemical Cycles. Ind. Eng. Chem. Res. 52 (9), 3276–3286. doi:10.1021/ie400193q

CrossRef Full Text | Google Scholar

Steinfeld, A. (2019). Concentrated Solar Energy - the Path for Efficient thermal Conversion to Power and Fuels. Sci. Bull. 64 (8), 485–486. doi:10.1016/j.scib.2019.04.012

CrossRef Full Text | Google Scholar

Steinfeld, A., Furler, P., Haselbacher, A., and Geissbühler, L. (2019). A Thermochemical Reactor System for a Temperature Swing Cyclic Process with Integrated Heat Recovery and a Method for Operating the Same. Google Patents.

Google Scholar

Steinfeld, A. (2005). Solar Thermochemical Production of Hydrogen-A Review. Solar Energy 78 (5), 603–615. doi:10.1016/j.solener.2003.12.012

CrossRef Full Text | Google Scholar

Sun-to-liquid (2020). Available at: https://www.sun-to-liquid.eu/(Accessed September 10, 2020).

Venstrom, L. J., De Smith, R. M., Bala Chandran, R., Boman, D. B., Krenzke, P. T., and Davidson, J. H. (2015). Applicability of an Equilibrium Model to Predict the Conversion of CO₂ to CO via the Reduction and Oxidation of a Fixed Bed of Cerium Dioxide. Energy Fuels 29, 8168–8177. doi:10.1021/acs.energyfuels.5b01865

CrossRef Full Text | Google Scholar

Wang, B., Li, L., Pottas, J. J., Bader, R., Kreider, P. B., Wheeler, V. M., et al. (2020). Thermal Model of a Solar Thermochemical Reactor for Metal Oxide Reduction. J. Sol. Energy Eng. 142 (5), 051002. https://doi.org/10.1115/1.4046229

CrossRef Full Text | Google Scholar

Wang, B., Li, L., Schäfer, F., Pottas, J. J., Kumar, A., Wheeler, V. M., et al. (2021). Thermal Reduction of Iron-Manganese Oxide Particles in a High-Temperature Packed-Bed Solar Thermochemical Reactor. Chem. Eng. J. 412 (C), 128255. doi:10.1016/j.cej.2020.128255

CrossRef Full Text | Google Scholar

Welte, M., Barhoumi, R., Zbinden, A., Scheffe, J. R., and Steinfeld, A. (2016). Experimental Demonstration of the Thermochemical Reduction of Ceria in a Solar Aerosol Reactor. Ind. Eng. Chem. Res. 55, 10618–10625. doi:10.1021/acs.iecr.6b02853

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, C., Jarrett, C., Chueh, W., Kawajiri, Y., and Henry, A. (2015). A New Solar Fuels Reactor Concept Based on a Liquid Metal Heat Transfer Fluid: Reactor Design and Efficiency Estimation. Sol. Energy 122, 547–561. doi:10.1016/j.solener.2015.08.019

CrossRef Full Text | Google Scholar

Nomenclature

C concentration ratio

c_p specific heat at constant pressure, kJ kg⁻¹ K⁻¹

c_v specific heat at constant volume, kJ kg⁻¹ K⁻¹

F heat loss fraction

f shifting frequency, min⁻¹

$\overline{\mathit{h}}$ molar specific enthalpy, kJ mol⁻¹

$\Delta {\overline{h}}_{{\mathrm{O}}_2}$ change in molar enthalpy of the non-stoichiometric ceria per $n_{{\text{O}}_2}$, kJ mol⁻¹

ΔT temperature difference T_red −T_ox, K

M molar mass, kg mol⁻¹

m mass, kg

$\dot{\mathit{m}}$ mass flow rate, kg s⁻¹

n amount of substance, mol

N cavity number in the pre-cooling (or pre-heating) part of recuperation zone

p pressure, Pa

${\mathit{p}}_{{\mathbf{O}}_2}$ relative oxygen partial pressure

P^∗ non-dimensional oxygen partial pressure defined in Eq. 28

Q heat, kJ

$\dot{\mathit{Q}}$ power, kW

${\mathit{r}}_{{\text{O}}_2}$ rates of oxygen production, mL min⁻¹ g_ceria⁻¹

T temperature, K

r gas flow rate per unit mass of ceria, kg s⁻¹ kg_ceria⁻¹

Greek symbols

α correction factor

ε heat recovery effectiveness

β non-dimensional number defined in Eq. 20

γ non-dimensional number defined in Eq. 20

δ non-stoichiometry

ε^∗ non-dimensional heat recovery effectiveness defined in Eq. 27

η_th solar-to-fuel efficiency

θ^∗ non-dimensional reduction temperature defined in Eq. 28

ξ non-dimensional number defined in Eq. 22

τ reaction duration per cycle, min

Δτ time step, s

χ relaxation factor

Δδ change in non-stoichiometry

Subscripts

H high

HX heat exchange

L low

chem chemical item

gas gas-phase transport heat loss

fuel fuel

input input

other other heat loss

ox oxidation

quench quenching heat loss

rad radiative heat loss

recovery recovery of conductive heat loss

red reduction

ref reference

reject rejecting heat loss

shift shifted from the previous phase

solar solar energy

solid solid-phase

trans transport item

∞ ambient