AI-Based Damping of Electromechanical Oscillations by Using Grid-Connected Converter

The proliferation of grid-connected converter interfaced energy sources in Smart Grids, enhance sustainability and efficiency as well as minimizing power losses and costs. However, concerns arise regarding the stability and reliability of future smart grids due to this wide integration of power electronic devices, which are recognized to affect the dynamic response of the system, especially during disturbances. For instance, apart from the lower damping of existing electromechanical modes, new low-frequency oscillations begin to appear. Yet, the ability of grid-connected converters to provide grid support functionalities can alleviate the aforementioned challenges. Relevant studies show that these functionalities can be enhanced even further, if information regarding the oscillation characteristics are available. Traditional methods for extracting modal information are very well suited for monitoring purposes, however, they pose certain limitations when considered for control applications. Therefore, this paper proposes a multi-band intelligent power oscillation damper (MiPOD) that exploits 1) the inherent characteristics of grid-connected converters to damp multiple power oscillations and 2) the modeling capabilities of Artificial Intelligence (AI) for predicting the frequency of electromechanical oscillations in the system, as operating conditions change. Essentially, the MiPOD integrates the AI model in the control loop of the converter to attenuate multiple modes of oscillation. The proposed controller is validated for different disturbances and randomly generated operating points in the two area system. Specifically, in this case the AI model is a Random Forest ensemble regressor that is developed for tracking two electromechanical modes. As it is shown, the MiPOD can improve the overall performance of the system under various contingency scenarios with only 6% of the corresponding total nominal capacity of synchronous generators. In addition, the monitoring and damping abilities of the MiPOD are demonstrated for a vast range of operating points just by tuning two parameters; the predicted oscillation frequencies of the local and inter-area mode.

1 Introduction

The modernization of power systems into Smart Grids (SG) aims to integrate information and communications technologies with the electricity network, thus forming a cyber-physical system (Aleem et al., 2020). In contrast to the conventional operation scheme, SG reinforce the integration of grid-connected converter (GCC), which are usually based on (but not limited to) Renewable Energy Systems (RES) and Energy Storage Systems (ESS) (Kempener et al., 2013). This paradigm shift i.e., from a centralized to a decentralized structure can increase the sustainability and efficiency of power systems while reducing costs and power losses (Howell et al., 2017; Aleem et al., 2020). Although GCC possess financial and environmental benefits, they can also affect the stability of a system. For instance, the RES generation variability caused by the changing weather conditions creates power imbalances, which give rise to frequency fluctuations (Bessa et al., 2014). A popular solution is the coupling of RES with Battery ESS, which mitigates generation variability by injecting or absorbing power accordingly (Beaudin et al., 2010). However, these resources depend on GCCs to convert DC to AC (Masters, 2013), therefore, it is expected that given the current trends power electronics will eventually dominate future SG.

GCC is the main technology to interface RES and ESS with the grid due to its high level of flexibility and efficiency (Lai and Kim, 2016). The hardware of GCCs usually consists of an IGBT-based power module, an output filter to mitigate switching harmonics, and a microprocessor-based controller for implementing control algorithms. To achieve a fast and robust operation of GCCs, the cascaded control structure is often employed (Rocabert et al., 2012). For grid-following GCCs, the main control loops include a current controller, a phase-locked loop (PLL), and a power controller. Whereas, grid-forming GCC, especially those based on virtual synchronous machine concept, usually replaces the PLL by a power balance based synchronization controller which has been proven to be more grid friendly (Rodríguez et al., 2018).

Besides the generation variability of GCC based RES, the increasing penetration of power electronics is associated with certain challenges that have a deeper impact on the reliability of power systems. For instance, unlike conventional synchronous generator power plants such as coal and hydro, power electronic devices do not have mechanical parts and/or rotating masses. Therefore, the inertia of such systems is much lower (if not zero). This implies that the overall inertia weakens as more and more electronic devices connect with the system, altering its dynamic behavior (Kroposki et al., 2017) by responding much faster to contingencies (Fang et al., 2019). Reasonably, concerns arise regarding the rotor angle stability¹ of the system.

Recent studies suggest that higher penetration of power electronics is linked with 1) the appearance of additional low frequency electromechanical oscillations and 2) the reduced damping of the existing ones (ENTSO-E, 2019). Even though, these type of oscillations exist in power systems since the first interconnection of multiple generation units, the size and complexity of today’s power systems makes them more frequent. Sustained or power swings with increasing amplitudes can lead to instability, therefore, damping such oscillations is imperative to ensure a stable and reliable operation. For instance, during 2003 low frequency oscillations that led to widespread blackouts were recorded in Italy (Berizzi, 2004), United States (Andersson et al., 2005) and China (Prasertwong et al., 2010). More recently, in 2017 a particular sequence of events excited an under-damped mode giving rise to a low frequency oscillation between southern Italy and Germany (ENTSO-E, 2018), which through proper coordination and fast response by system operators was quickly put under control.

Traditionally, the power system stabilizer (PSS) is used for improving the damping of low frequency electromechanical oscillations, which typically lie within the range of $0.1-1.0\text{Hz}$ (inter-area modes) and $1.0-2.0\text{Hz}$ (local area modes). The general structure of a PSS is based upon the following main blocks: low-pass filter, washout filter, gain and lead-lag phase compensator(s) (IEEE, 2016). Other types of PSS include the dual input type PSS2C, which exploits combinations of electric power and speed signals to integrate the accelerating power for improving the sensitivity to mechanical power variations and the multi-band type PSS4C used for attacking oscillations at different frequencies (IEEE, 2016). Even though PSS is a cost-efficient approach in attenuating electromechanical low frequency oscillations, the sporadic tuning of their parameters hinder their performance due to the inability to adapt in the ever-changing operating conditions. Depending on the PSS type and tuning strategy the number of tunable parameters may vary. For instance, a typical PSS consists by 6 (i.e., the gain and five time constants), yet, by strategically selecting certain time constants to be fixed, the parameters to be optimized can be halved [Shin et al. (2010); Farah et al. (2012); Hu et al. (2018)]. Regardless, the high number of parameters makes the task of online tuning highly complex and difficult. Furthermore, as the number of fossil fueled synchronous generation plants will slowly decrease (Fang et al., 2019) it is safe to say that the number of PSS devices installed in the system will follow the same trend.

Fortunately, the fast response of power electronics can aid in ensuring stability of the system by means of a proper control algorithm. It has been shown that PSS-like control laws can be implemented in grid-tied power converter to damp sub-synchronous resonance (Wang et al., 2015; Varma and Salehi, 2017). For instance, in (Varma and Salehi, 2017), a damping controller based on grid frequency measurements is proposed for photovoltaic (PV) solar farms. In this work, the PV power plant is utilized as a STATCOM² whose output power corresponds to the variation in the frequency measured at the point of common coupling (PCC). However, the main drawback of PSS-based control methods is that they rely on frequency measurements, which in reality are noisy. Recently, a new control concept called grid-forming power converter appears as an ideal candidate to enhance power grid stability (ENTSO-E, 2019; Tarrasó et al., 2019). By emulating the dynamics of a synchronous generator, grid-forming converters can provide, in addition to grid supporting services, the ability of online tuning for complying with system operator’s requirements as the conditions change. Though the damping provided by grid-forming power converter is considerable, it mainly comes from the virtual inertia that is usually constrained by system requirements. In an attempt to adjust damping gain without altering virtual inertia, a selective power oscillation damper for virtual synchronous machine is presented in (Rodriguez Cortes et al., 2014). In this study, the damping ratio is set individually for each modes by means of using band-pass filters. This approach has been proved to be very effective provided that the information on the oscillation frequency is available. However, in practice, due to the dynamic nature of power systems, obtaining such information is not trivial.

The advancement of computer science and computational power permits AI to be used for deriving models that can provide information, which otherwise would be either difficult or impossible to obtain. The cyber-physical structure of SG facilitates the faster exchange of information through state of the art communication networks, thus paving the way for the applications of AI in power systems. Considering as well the vast deployment of Phasor Measurement Units (PMU) with a sampling rate around 20 ms (De La Ree et al., 2010), monitoring such system dynamics becomes more efficient. Naturally, the high resolution measuring of system variables leads to a rapid growth in the amount of available data. These data have been shown to contain invaluable information, which can be exploited by artificial intelligence (AI) and machine learning techniques to provide fast and accurate estimations about the stability status of the system. For instance, an ensemble of Support Vector Machines is developed in (Zhou et al., 2017) for predicting transient stability after a severe disturbance. Moreover, (Liu et al., 2018) adopts a bagging ensemble called Random Forests (RF) to detect instability in the Danish power system considering forecasting errors of RES generation. Similarly, (Sulla et al., 2014) trains a Neural Network to classify operating points into over or under damped based on a fixed damping ratio.

Driven from the above, in this paper a multi-band intelligent power oscillation damper (MiPOD) is developed to provide additional damping for two low frequency electromechanical oscillation modes. As opposed to the various studies presented above, the MiPOD is trained to track the frequency characteristics of the two modes (i.e., mode frequency) using the RF ensemble when the active and reactive power of the loads in the system are randomly modified. The proposed controller is evaluated under several contingency scenarios and operating points using the two area system (Kundur et al., 1994). The contributions of the present work is to:

• Demonstrate that AI can be used to provide information to controllers that previously were unable to obtain.

• Show that non-synchronous distributed power plants can support the system by providing PSS-like damping.

• Prove that by tuning only two parameters of the MiPOD the overall stability of the system can be enhanced for a wider range of operating points.

• Develop a variation of the iPOD controller presented in Baltas et al. (2020) to attenuate multiple oscillatory modes rather than just one. Special care has been put on decoupling the two frequency bands to ensure damping efficiency.

The rest of the paper is structured as follows. In Section 2, a review of the participation of GCC in power oscillation damping is presented. In Section 3 the structure of the MiPOD is explained in detail including the AI predictor. In Section 4 the characteristics of the case study are discussed. Finally, in Sections 5, 6 the results and conclusions are presented respectively.

2 Grid-Connected Converter in Mechanical Oscillation Damping

During this last decade, the installation of large-scale GCC based plants, such as wind and PV power plants, has been steadily increasing (Aleem et al., 2020). As a result, research efforts focus on the attenuation of mechanical oscillations in the system. Even though small scale GCC based plants cannot influence too much power oscillations, large-scale GCC based systems can provide substantial support to the grid for a wider range of contingencies.

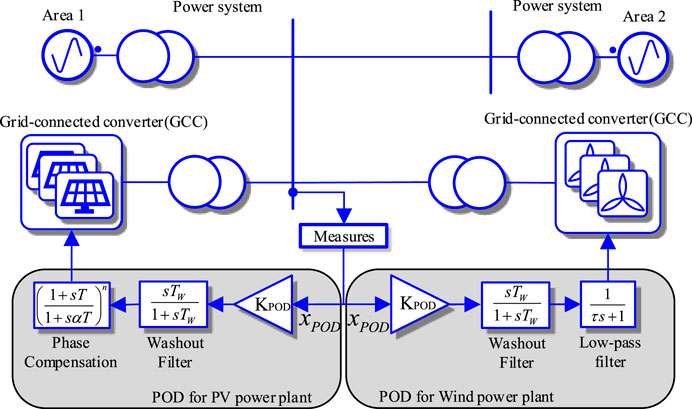
Generally, frequency deviations in the system typically come together with power oscillations in large power systems. In (Varma and Akbari, 2020), a power oscillation damping technique is presented based on reactive power modulation considering the large-scale PV plant as a STATCOM device. The authors highlight the effects of reactive power oscillation damping in conjunction with the fast frequency regulation controller. The control signal for oscillation damping is based on frequency measurements of the system. Regardless, the voltage deviation required to attenuate the oscillation is determined by a washout filter and a phase compensator.

Similarly, in (Knüppel et al., 2013) power oscillation damping is provided by a type 4 wind power plant. The wind power plant consists of 150 individual wind turbines, which are scattered over a wide geographical area to minimize generation variability. The paper proposes the modulation of both active and reactive power for attenuating system oscillations. The efficiency of active power modulation w.r.t. oscillation damping is related to the distance between the wind turbine and the PCC. Furthermore, it is noted that the active power modulation in wind power plants is feasible only when oscillations at the mechanical resonance frequency of the wind turbine are not excited. Regarding reactive power modulation, the location and the operation condition of the plant highly affects the sensitivity of the system.

The general structure for the POD controller, which is based on the PSS implementation for synchronous generators, is depicted in Figure 1. The controller is based on grid frequency measurements and with the main blocks being the gain, the washout filter and phase compensation filters, the plant can generate the desired amount of compensation power. References Varma and Akbari (2020) and Zhou et al. (2017) use the washout filter in addition to the phase compensation device to provide the reactive power modulation. In contrast, in (Knüppel et al., 2013), a simple low-pass filter is used to compensate on the phase displacement.

FIGURE 1

FIGURE 1. Conventional POD controller for grid-connected converter.

Although the above implementations appear in many papers due to its similarity with the PSS, this structure is depending largely on the phase compensation block and on the frequency measurement of the system. In addition, the reactive power modulation may give rise to voltage stability issues, as generally large-scale distributed power plants are located geographically far away from load centers, meaning that they are normally connected to weak transmission systems.

An alternative approach for GCC to provide power oscillation damping is presented in this paper based on active power modulation, which relies on AI to determine the frequency of the inter-area and local modes in the system as operating conditions vary.

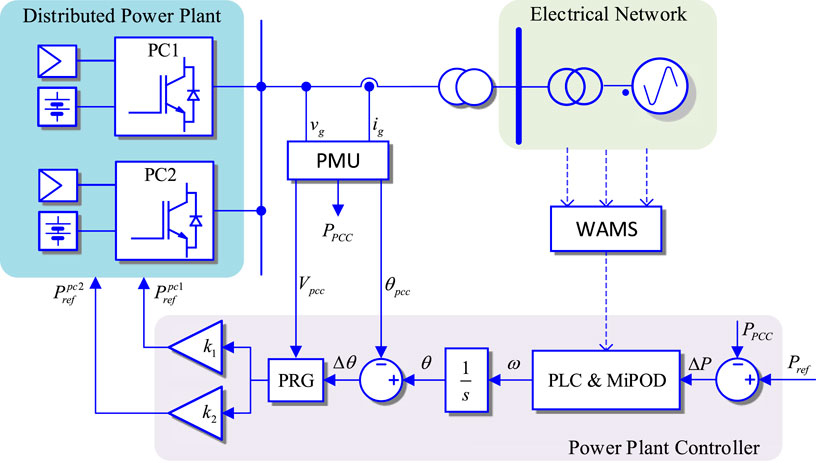
3 Proposed MiPOD for SPC-Based Grid-Forming Power Converter

Figure 2 shows the overall control structure of the MiPOD for grid-forming power converters based on synchronous power controller (SPC). The distributed power plant consists of two central power converters connected to an under-damped electrical network. The power plant is controlled by the power plant controller using 1) measurements at the PCC and 2) phasor measurements from a WAMS. The SPC is mainly responsible for the grid-forming capabilities of the power plant controller. In addition, to enable the GCC to behave as synchronous machine both the power loop controller (PLC) and the MiPOD are used. Specifically, the transfer function for the PLC is given as:

$G_{PLC}\left(s\right)=\frac{1}{Hs+D}(1)$

where H is the inertia and D is the damping of the emulated synchronous machine. The MiPOD, which will be discussed in the following, is implemented in parallel with the PLC.

FIGURE 2

FIGURE 2. Overall Structure of the proposed MiPOD for SPC-based grid forming power converter.

It is noted that the output of the PLC is an angular frequency, which is equivalent to the rotor frequency of a synchronous machine. However, for the SPC to emulate the angle of the induced voltage, the angular frequency (ω) has to be integrated as:

$\theta \left(s\right)=\omega \frac{1}{s}.(2)$

The power reference generator block (PRG) generates the power reference $\left(P_{ref}\right)$ by using the internal angle θ, the measured grid angle ${\theta }_{pcc}$ and voltage magnitude $V_{pcc}$. It is worth mentioning that these feedback signals $\left({\theta }_{pcc},V_{pcc},P_{pcc}\right)$ are measured at the PCC by using a PMU. This reference dictates the amount of active power that needs to be produced by the GCC. The PRG is designed considering the following well-known equation:

$P_{ref}^{pc}=\frac{V_{ref}}{R^2+X^2}\left[R\left(V_{ref}-V_{pcc}\text{cos}\left(\theta -{\theta }_{pcc}\right)\right)+X{V}_{pcc}\text{sin}\left(\theta -{\theta }_{pcc}\right)\right](3)$

where R and X are the virtual resistance and impedance, $V_{pcc}$ is the RMS value of grid voltage, and $V_{ref}$ is the rated grid voltage. For a transmission system where the resistance is much lower than inductance, the term R can be omitted. Therefore, Eq. 3 can be rewritten as:

$P_{ref}^{pc}=\frac{V_{ref}{V}_{pcc}}{X}\sin \left(\theta -{\theta }_{pcc}\right)(4)$

The reference power is divided among the two power converters in the plant by using weighting factors as:

$P_{ref}^{pc,j}=k_j{P}_{ref}^{pc},j\in \left\{\mathrm{1,2}\right\}(5)$

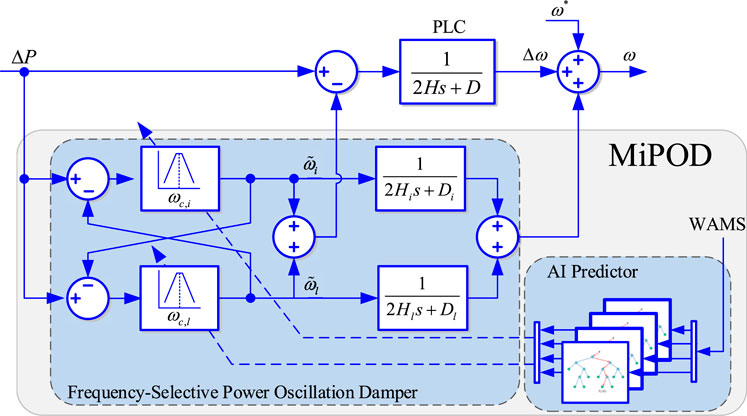
3.1 Multi-Band Power Oscillation Damper

The block diagram of the multi-band power oscillation damper is illustrated in Figure 3. It consists of a frequency-selective power oscillation damper and an AI predictor. The frequency-selective power oscillation damper has two band-pass filters and two blocks implementing the swing equation. The band-pass filter is defined as:

$G_{bpf,m}\left(s\right)=\frac{2{\zeta }_m{\omega }_{c,m}s}{s^2+2{\zeta }_m{\omega }_{c,m}s+{\omega }_{c,m}^2}(6)$

where m can be either l for local mode or i for inter-area mode, ${\zeta }_i$ is the damping ratio and ${\omega }_c$ is the center frequency of the filter. The emulated swing equation for each frequency is given by:

$G_{d,m}\left(s\right)=\frac{1}{2H_{m}s+D_m}.(7)$

FIGURE 3

FIGURE 3. Control block diagram of the MiPOD.

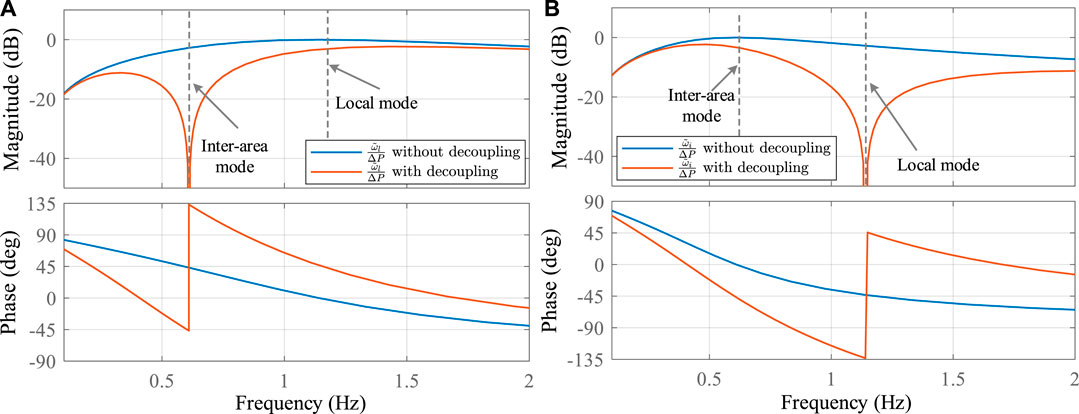
The advantage of the MiPOD is that it allows controlling the participation of the power plant to damp mechanical oscillations by adjusting the virtual inertia. The decoupling network is used to enhance the filtering response of the band-pass filter. To investigate further the dynamics of the decoupling network, Eqs. 6, 7 can be rearranged as follows:

$G_{input,l}\left(s\right)=\left(1-G_{bpf,i}\right)G_{bpf,l}(8)$

$G_{input,i}\left(s\right)=\left(1-G_{bpf,l}\right)G_{bpf,i}(9)$

The frequency response of the above transfer functions is plotted in Figure 4. Observing the figure it can be seen that the magnitude gains of the two modes are quite similar, when the decoupling network is not used. This indicates that the two loops are highly coupled, which can affect the responses of the dampers. In addition, the tuning of each damper cannot be done separately introducing additional difficulties. On the other hand, with the decoupling network the input signals for the local and inter-area dampers are well decoupled. For instance, feeding back the output of $G_{bpf,i}$ to the input of $G_{bpf,l}$ a band-stop filter is formed for the local mode damper at ${\omega }_{c,i}$. Thereby, both dampers act only at the tuned frequency. Moreover, parameter selection for each damper can be carried out separately.

FIGURE 4

FIGURE 4. Frequency response of decoupling network in Eqs. 8, 9.

3.2 AI-Based Oscillation Frequency Predictor

Predictions regarding the frequency of the targeted oscillations is vital for the MiPOD to provide the necessary damping to attenuate them. Obtaining such information online is especially difficult. For instance, modal analysis can calculate the eigenvalues of the system by linearizing the system models around an equilibrium (steady state) point. Although it is very accurate, this approach is time consuming and unsuitable for online applications, because linearized models need to be updated according to the changing operating conditions for the results to reflect reality (Kontis et al., 2018). Measurement based methods, such as Prony and Fast Fourier Transform to name a few, extract the modal characteristics of the system through signal processing techniques, which are fast enough for online applications. However, to minimize the effect of noise, these approaches typically employ high order models that generate artificial modes, which are difficult to identify and discard (Kontis et al., 2018). In addition, the performance of such methods in a power electronics dominated SG have not yet been fully studied (Kontis et al., 2018).

Apart from the aforementioned issues, traditional signal processing techniques require a probing signal (either artificial or natural disturbance) and a time window wide enough to capture the slow electromechanical oscillations [TP462 (2012)]. However, providing optimal damping capabilities depends not only on the accuracy of the mode frequency estimation but also its speed. As shown in Figure 5, measurement-based methods need to observe several seconds of the feedback signals for an accurate prediction, yet such delay will constrain the damping provided by the MiPOD.

FIGURE 5

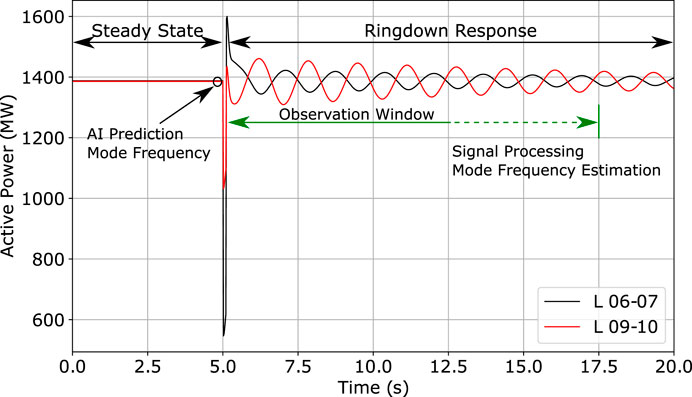
FIGURE 5. Comparison between the proposed AI-based mode estimation approach and the traditional signal processing techniques. A properly trained AI model can provide fast and accurate estimations of the mode frequency faster than signal processing.

The modeling capabilities of AI are becoming more and more appealing as the means to exploit the information and communication network of WAMS (Gopakumar et al., 2014; Senesoulin et al., 2019). AI can overcome the issues of the conventional methods with reasonable computational power and fast processing speeds. Specifically, machine learning is able to derive functions that relate system variables to other system variables or some stability indices: a task commonly known as Supervised Learning where input-output pairs are used to develop a model, as depicted in Figure 6. Concretely, this paper adopts AI to develop a model that will use WAMS information to predict the oscillatory frequency of two modes (instead of one as in Baltas et al. (2020)) from steady state data as depicted in Figure 5.

FIGURE 6

FIGURE 6. Conceptual representation of Supervised Learning.

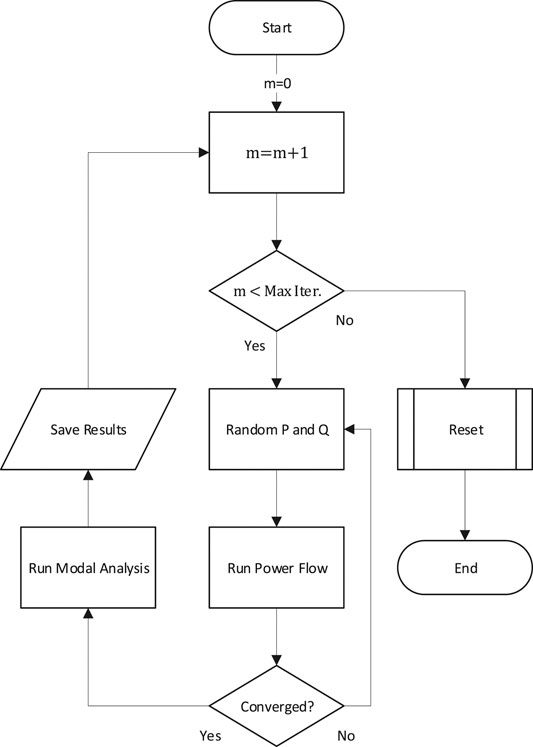
To develop the said model it is necessary to create a database that will contain sufficient amount of system conditions along with their corresponding mode frequencies. The database has to contain input-output pairs that will be used for 1) training and 2) testing the performance. In this case, these inputs or examples are system variables, whereas the outputs or labels are the two mode frequencies for each example. The system conditions are varied using random coefficients that scale upwards or downwards each of the load’s active and reactive power for emulating the demand variations. The process followed to generate the data is graphically illustrated in the flowchart presented in Figure 7. Finally, the database consists of approximately $\mathrm{23,000}$ examples and labels. Each example represents a unique sequence of values that correspond to 22 uncorrelated system variables.

FIGURE 7

FIGURE 7. Database generation flowchart.

3.2.1 Random Forests

Among the wide variety of machine learning algorithm this paper adopts a special case of an ensemble, called Random Forests (RF), to predict the targeted mode frequencies. An ensemble aims to improve the overall performance of several individual machine learning models that (usually) have weak performance by combining them (Duda et al., 2001). Similarly, RF combine Q decision trees placed in parallel using a randomized procedure for training the individual $Q_r$ decision tree (Breiman, 2001; Louppe, 2014), where $r\in \left\{1,\dots ,Q\right\}$. Decision trees are simple and easy to understand (see Figure 8), robust to input types and scales and in addition do not make any assumptions regarding the underlying distribution of the data (i.e., non-parametric). However, they tend to overfit the training samples leading to a high generalization error (Theodoridis and Koutroumbas, 2008).

FIGURE 8

FIGURE 8. Sample decision tree within random forests.

The crucial step toward the development of a decision tree is, at each non-terminal node, the selection of the split criterion. In a regression task, such as in this paper, the split criterion is determined so that the drop of impurity from the parent to the child nodes is maximum (Theodoridis and Koutroumbas, 2008), as in Eq. 10, where $t_{Left}$ and $t_{Right}$ are the left and right ancestor nodes, respectively and $N_{t_{Left}}/N_t$ and $N_{t_{Right}}/N_t$ are the portion of samples that belong to each of the these two nodes. The $I\left(t\right)$ is the mean squared error between true value $y^{\left(p\right)}$ and predicted value ${\widehat{y}}_t$ for patterns in subset $S_t$ averaged over all training patterns $N_t$ at the parent node t, as in Eq. 11. The predicted ${\widehat{y}}_t$ value is calculated according to Eq. 12.

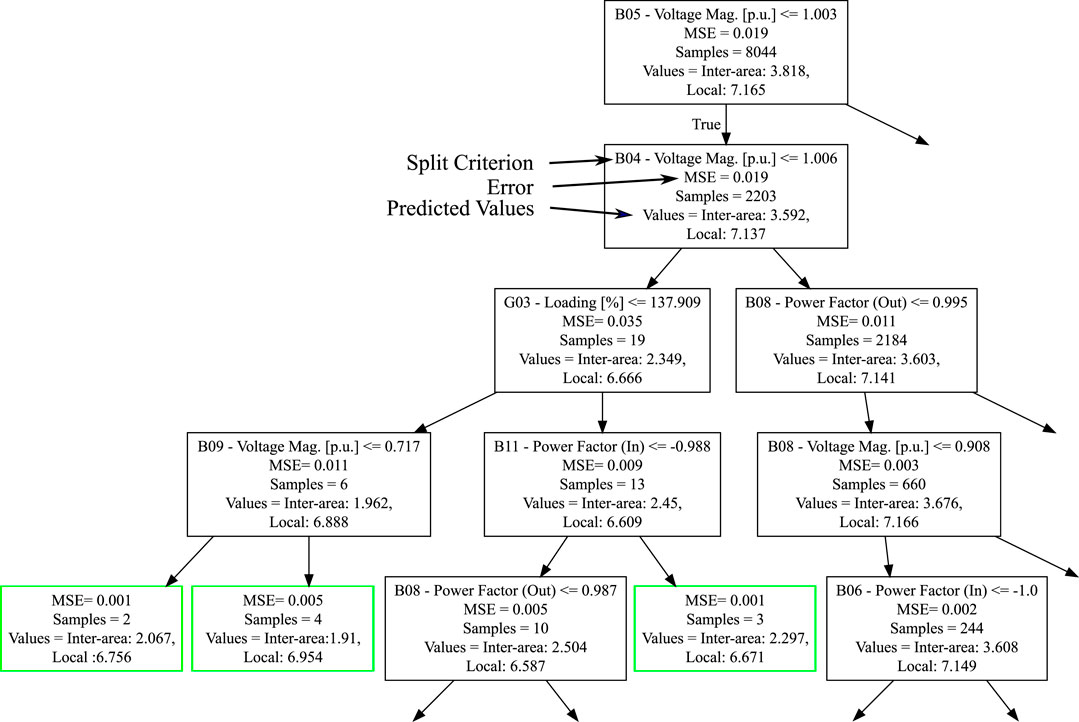
A fraction of one from the 1,000 decision trees of the MiPOD’s RF mode frequency predictor is depicted in Figure 8. Each node is represented by a rectangle that encapsulates all the information characterizing that node. The split criterion lies at the top followed by the MSE and the number of samples allocated at that node. At the bottom, the predicted inter-area and local mode frequency values are shown. Note that the decision path from the top toward the terminal nodes (indicated by the green outline) is straightforward and clearly interpretable. RF build on top of the decision trees’ simple yet intuitive structure to develop individual predictors that collectively yield much higher performance (Breiman, 2001).

$\text{Δ}I\left(t\right)=I\left(t\right)-\frac{N_{t_{Left}}{N}_t}{I}\left(t_{Left}\right)-\frac{N_{t_{Right}}}{N_t}I\left(t_{Right}\right),(10)$

$I\left(t\right)=\frac{1}{N_t}{\displaystyle \sum }_{i\in S_t}{\left(y^{\left(i\right)}-{\widehat{y}}_t\right)}^2,(11)$

${\widehat{y}}_t=\frac{1}{N_t}{\displaystyle {\sum }_{p\in S_t}\left(y^{\left(p\right)}\right)}(12)$

3.2.2 Comparison Between Univariate and Multivariate Random Forest Structure

The development of the frequency predictor for two modes can be designed as a univariate or multivariate multiple regression. In the former case two prediction models are developed to predict the frequency of a specific mode as shown in Figure 9, while in the latter a single prediction model is developed to predict both frequencies at the same time as in Figure 10. Regardless, the univariate/multivariate RF is trained for predicting the frequency of two modes (inter-area and local) while its performance is evaluated through a 5-fold cross validation scheme. Generally, the k-fold cross validation technique is used for obtaining a better approximation of the true error (Shalev-Shwartz and Ben-David, 2017). To do so, k subsets of equal size are created from the original training dataset and a prediction model is trained using a unique combination of k-1 folds and tested with the remainder. The k-fold prediction is simply the average prediction over all models. To quantify the performance of the developed models two metrics are used: the R2 score Eq. 13 and the Mean Absolute Error (MAE) Eq. 14 where n is the number of samples, $\overline{y}$ is the mean true value and $y,\widehat{y}$ are the true and predicted values. The MAE measures the average error between true and predicted values whereas the R2 score shows the fitness of the model for the given task with 0 being the worse possible score and 1 being the best.

$R^2\left(y,\widehat{y}\right)=1-\frac{{\displaystyle {\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}}{{\displaystyle {\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2}}(13)$

$\text{MAE}\left(y,\widehat{y}\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left|y_i-{\widehat{y}}_i\right|}(14)$

FIGURE 9

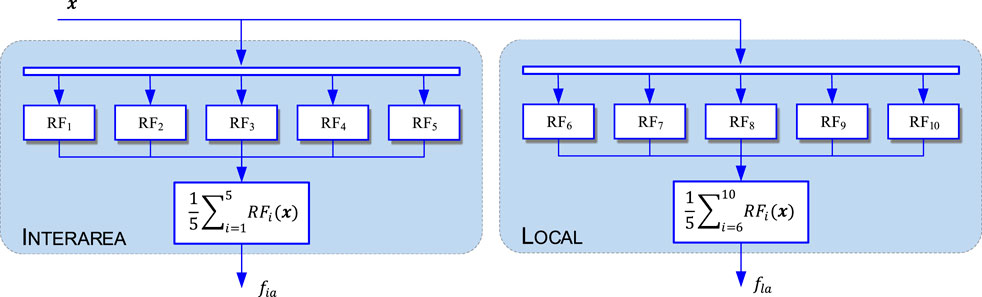
FIGURE 9. Univariate structure of 5-fold cross validated Inter-area and Local mode frequency prediction.

FIGURE 10

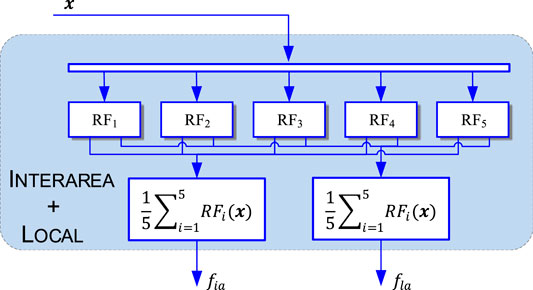
FIGURE 10. Multivariate structure of 5-fold cross validated Inter-area and Local mode frequency prediction.

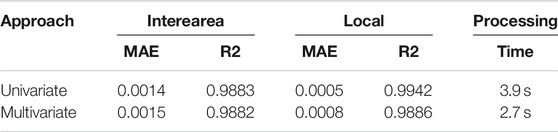
A comparison of the performance and processing time between the two schemes is presented in Table 1. Based on these results, a trade-off is revealed between prediction accuracy and processing speed. Particularly, the accuracy of prediction for both frequencies using separate models is higher although the processing speed is slower. In contrast the time required for obtaining a prediction with the multivariate model is faster, while the accuracy is slightly reduced. Given that the two types of prediction models have similar performance, the decisive factor is the processing speed. Therefore, based on the results of Table 1, the multivariate regression approach is adopted. Note, however, that if parallel computing is employed the gap in processing speed might be lower.

TABLE 1

TABLE 1. Performance of RF on test set.

3.3 Performance Analysis of Multivariate Random Forest

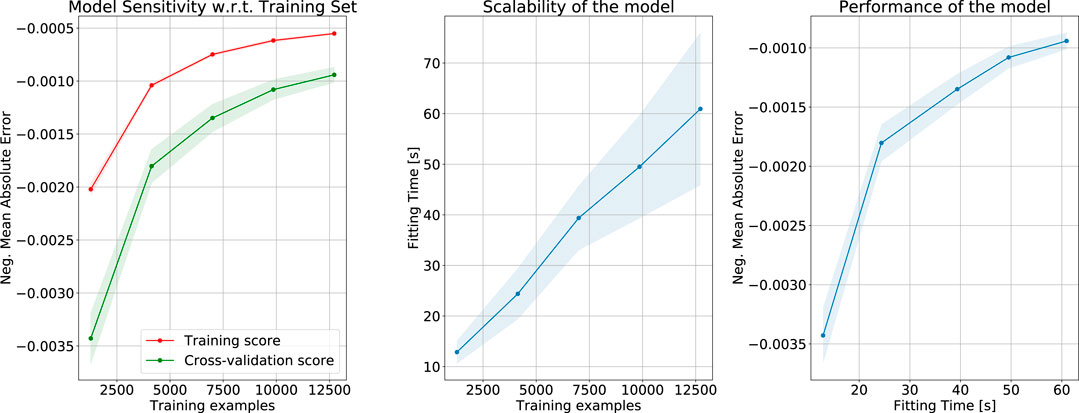
Analyzing the learning curves of the multivariate model with the lowest error, i.e., ${\text{RF}}_{\text{Best}}$, a few comments are necessary. For instance, the gap between cross validated error and training error deceases when the training size increases as it is seen in Figure 11. Assuming this trend remains the same adding around 5,000 samples will reduce the error further. However, adding even more will not contribute much to improving the performance but instead the fitting time could be doubled. Moreover, an attribute of RF worth mentioning is the inherent ability of input variable ranking according to their contribution in the decision process. Specifically, this impurity based measure relies on the calculation of the average drop of impurity, $\text{Δ}I\left(t\right)$, of each feature over all decisions trees of the ensemble Raschka and Mirjalili (2019). Such an attribute is particularly important for removing unnecessary features thus reducing the dimentionality and complexity of the task and improving speed as well as performance at the same time. For instance, in this case Figure 12 reveals the most important features w.r.t. their participation in the decision making. Specifically, if a hard threshold around 0.025 is applied then the installation of measurement units can be limited to only 6 buses instead of 14.

FIGURE 11

FIGURE 11. Learning Curves of the best multivariate Random Forest.

FIGURE 12

FIGURE 12. Random Forest’s feature importance.

4 Validation Setup

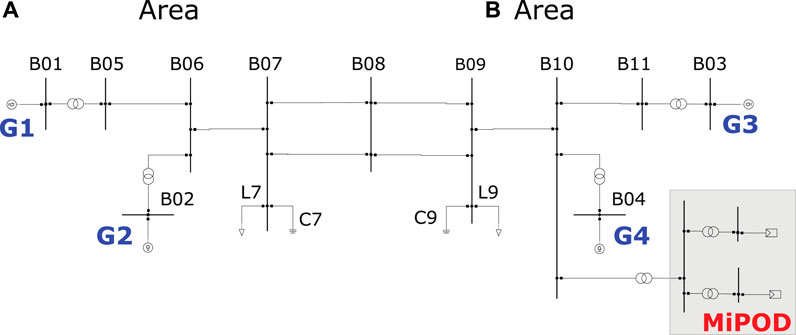
The performance of the proposed MiPOD is demonstrated on a two area system (Kundur et al., 1994), as depicted in Figure 13. This is a well-known system that allows studying electromechanical oscillations, particularly between two interconnected areas. The system is implemented on DIgSILENT Powerfactory 2019, and in addition, the simulation platform’s Python API is used in the development of a script for automating and streamlining the process of the experimental study. For the purpose of this study, two non-synchronous generation units representing the distributed power plants are connected to the B10 through virtual synchronous power converters. The rated apparent power for each plant is 100 MVA, around 2.8% of the total apparent power for the four synchronous generators (G1–G4).

FIGURE 13

FIGURE 13. Modified two area system.

Generally, there are three electromechanical modes of oscillation in the two area system: an inter-area mode at 0.55 Hz, a local mode between G1 and G2 (in area A) at 1.05 Hz, and a local mode between G3 and G4 (in area B) at 1.1 Hz. The developed MiPOD aims to protect the system from low frequency oscillations by damping the inter-area mode and local mode in area B. After connection of the distributed power plant the frequency of the inter-area mode increased to 0.61 Hz, while the local mode increased up to 1.14 Hz.

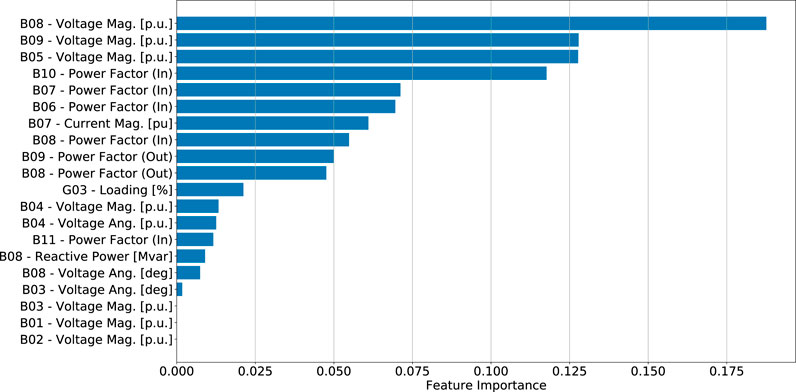
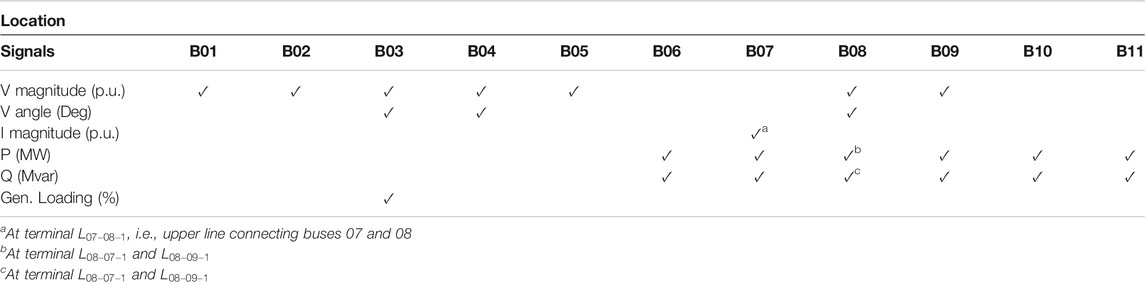
Furthermore, it is assumed that a wide area monitoring system equipped with phasor measurement units and phasor data concentrators, provides full observability of the system by recording, storing and transmitting the required signals to the MiPOD installed in the DPP. A complete list of the feedback signals for the MiPOD is presented in Table 2. The selection of these signals was achieved by using the recursive feature elimination (REF) algorithm [Guyon et al. (2002)]. From Table 2 it can be observed that the REF algorithm identify that important variables from generator buses is voltage magnitude while at load buses are the active and reactive power. Note, also, that the latter two were used to calculate the power factor, which had a higher importance factor in Figure 12.

TABLE 2

TABLE 2. List of feedback signals.

5 Results

Electromechanical oscillations exist naturally in the system due to the interaction between generation units and power exchange among them (Grigsby, 2007). An imperative factor that affects the inter-area mode damping and frequency is the system operating conditions majorly dictated by the loading characteristics (Kundur et al., 1994).

In reality, demand changes constantly and thus the damping and frequency of the oscillatory modes in the system also change. To emulate this behavior and demonstrate the ability of the MiPOD to adapt and damp electromechanical oscillations as system conditions change, the active and reactive power of loads L7 and L9 are varied randomly using scaling factors drawn from a Gaussian distribution with a mean of 1 and a standard deviation of 0.1.

5.1 Modal Analysis for Random Operating Points

Based on the load variation discussed above, approximately 100 random operating points were generated. The inter-area and local mode characteristics are calculated through modal analysis for three study cases: Base case, SPC only, and MiPOD. The probability density function (PDF) of each case is obtained using a Gaussian Kernel density estimation over all randomly created points for their resulted damping ratio as in Eq. 15 and amplitude ratio as in Eq. 16, where α and β are the real and imaginary components of an eigenvalue.

$\zeta =-\frac{\alpha }{\sqrt{{\alpha }^2+{\beta }^2}}(15)$

$\frac{A_1}{A_2}=e^{\frac{\left|2\pi \alpha \right|}{\beta }}(16)$

The estimated PDFs of each ratio are depicted in Figure 14, where the shaded area under the curves represent the probability, which is equal to 1. By observing the areas under the curves, it can be concluded that the overall small signal stability of the system is improved most in the cases using the MiPOD. Specifically, the area defined by the PDF and the grey vertical line is the largest for the MiPOD case, meaning that the probability of an inter-area and local mode damping ratio being more than $5\text{\%}$ is the highest. Similarly, the probability of having the amplitude ratio $A_1/A_2$ more than 2 is higher when the MiPOD is connected, as revealed by the area under the curve defined by the PDFs and the grey vertical line at point 2.0 of the x-axis.

FIGURE 14

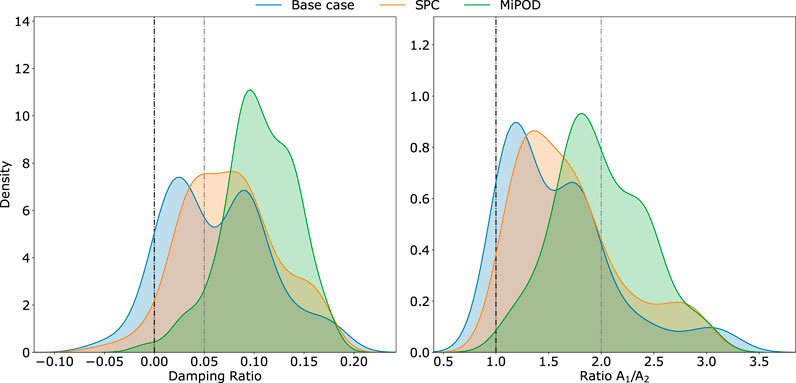
FIGURE 14. Comparison of the probability density functions for the damping and A₁/A₂ ratio for the local and inter-area mode combined per study case.

Apart from the high probability for cases with positive damping ratio, there is a small chance the operating conditions might lead to a negative damping ratio even when the MiPOD is in operation. This may be due to a combination of two things: the system is extremely loaded (thus the damping of the oscillatory modes is very low) and the finite capacity of the DPP imposes a constraint to the available damping that it can provide.

5.2 System Response After a Contingency for Random Operating Points

Following the same rationale, the effectiveness of the MiPOD is demonstrated by analyzing the response of the system under different contingency scenarios for randomly generated operating points. All contingency events occur after 2 s from the beginning of the simulation, which runs with a 10 ms resolution for a total duration of 20 s. The same events and conditions are repeated three times to obtain the system response 1) without the distributed power plant i.e., the Base case, 2) with the distributed plant using SPC and 3) with the distributed plant using MiPOD.

5.2.1 Symmetrical Short Circuit

Due to the particular design of this system a contingency can jeopardize the angular stability and synchronization of the two areas. To test this hypothesis, a three phase short circuit is designed to occur at B07 for 100 ms. The event has been simulated for approximately 30 random operating points. The active power and frequency at the center of the system (i.e., B08) for two random points are plotted in Figure 15. From these trajectories, the positive impact of the MiPOD in the oscillatory response of the system is obvious. In both cases, the system settles at the equilibrium point faster with narrower power oscillations. In reality, the initial frequency overshoot, which is unavoidable considering the severity of the fault and operating conditions, might have caused the activation of power curtailments or breaker tripping. Nevertheless, this initial overshoot is slightly smaller in the case of using MiPOD.

FIGURE 15

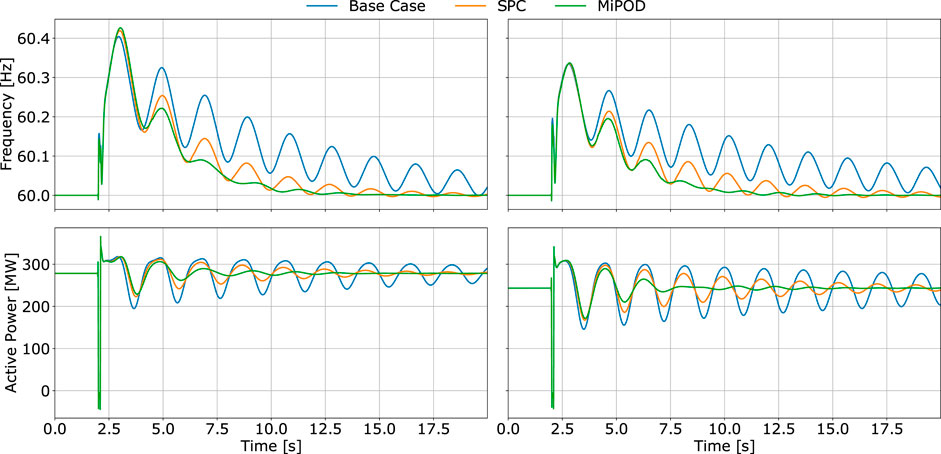
FIGURE 15. Frequency and active power flow at B08 after a symmetrical fault at B07 for 2 random operating points.

5.2.2 Step Change of Load Active and Reactive Power

Load variations are common in actual power systems especially in large interconnected systems. These variations can either be modeled as ramp or step changes. Regardless, both types of load variation affect the power balance, which can excite the electromechanical modes of the system. However, sudden load variations (such as step changes) have greater impact on the system stability. Concretely, a $5\text{\%}$ reactive power increase of load 9 is simulated for 30 random operating points. The results for two selected operating points are illustrated in Figure 16. In this case, the advantage of MiPOD is demonstrated predominantly in the active power flow of the tie line where system settles at the new equilibrium with smaller power fluctuations. Furthermore, the new equilibrium point in terms of frequency is closer to fundamental frequency compared to the base case.

FIGURE 16

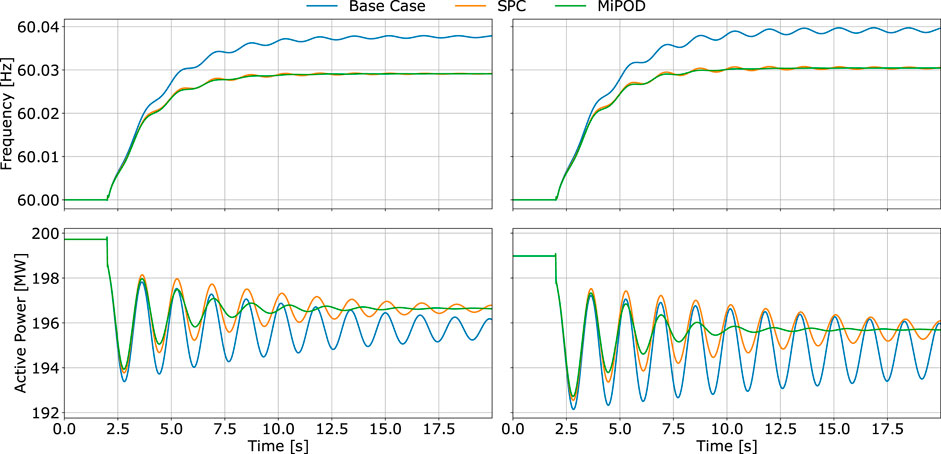
FIGURE 16. System frequency and active power flow at B08 after a sudden 5% increase of reactive power demand by L9 for 2 random operating points.

Similarly, to verify this behavior a second set of simulations (for another 30 random operating points) is conducted but now for a $5\text{\%}$ active power increase at load 9. The results are presented in Figure 17. As expected, the MiPOD adapts to the random operating points providing additional damping to the inter-area mode. Both active power flow and frequency converges promptly to steady state at a higher decaying rate.

FIGURE 17

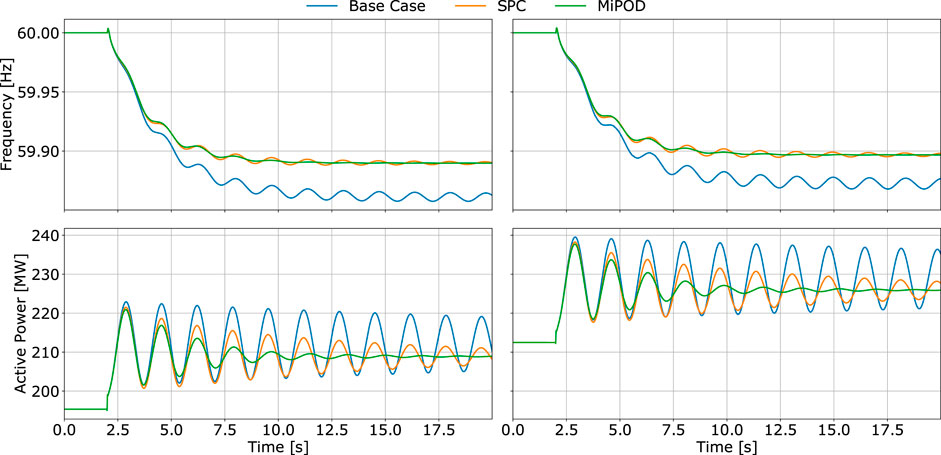
FIGURE 17. System frequency and active power flow at B08 after a sudden 5% increase of active power demand by L9 for 2 random operating points.

5.2.3 Synchronous Generation Event

Generally, the contingencies that have been discussed so far were not able to excite the local mode between G3 and G4. In an attempt to do so, a synchronous machine event is designed to force the two aforementioned generators to oscillate against each other. Specifically at time $t=2s$ the input mechanical torque of G3 is increased by 0.1 per unit while the input mechanical torque of G4 is decreased equally. The results are shown in Figure 18. The local mode component in the system oscillation is revealed only in the first couple of swings in the recorded frequency at Bus 8. After this narrow window the inter-area mode dominates the signal, which converges to steady state faster when the MiPOD is installed. Notably, in the base case the system is unstable as indicated by the increasing amplitude of the active power oscillations. Even with the SPC the system is oscillating very close to the stability boundary. However, with the MiPOD the system behaves significantly better in terms of stability.

FIGURE 18

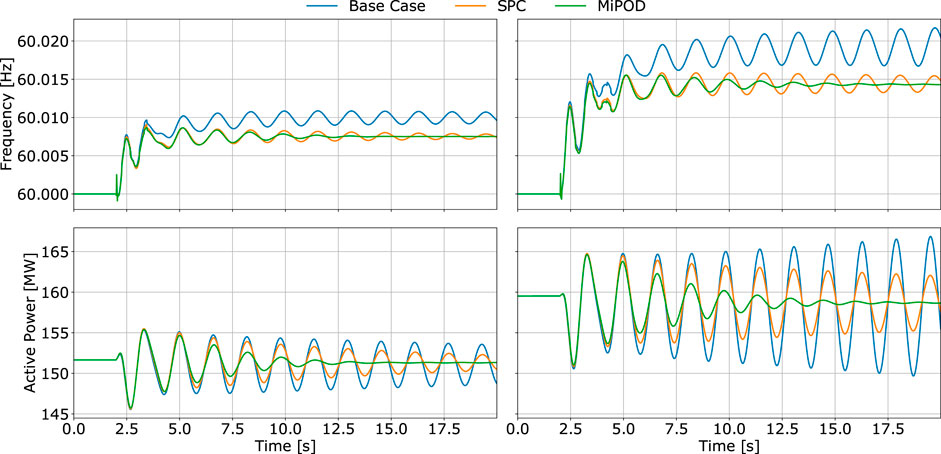
FIGURE 18. System frequency and active power flow at B08 after a sudden change in the mechanical torque of G3 and G4 for 2 random operating points.

5.2.4 Variation of Network Topology

The final contingency is a three phase short circuit at Bus 7 with the transmission line connecting buses 8 and 9 out of service. The remaining lines in the tie line are heavily loaded, which forces the damping and frequencies of the oscillatory modes to alter significantly. This final event not only evaluates the performance of the MiPOD in the most severe (although less probable) occasions but also the ability of the AI predictor to generalize and provide accurate information regarding the characteristics of each mode. The trajectories of the system variables are drawn in Figure 19. As by the severity of the event, large power swings exist in the tie line and frequency fluctuations. Nevertheless, the MiPOD’s superior performance is evident in both figures as opposed to the SPC and base case.

FIGURE 19

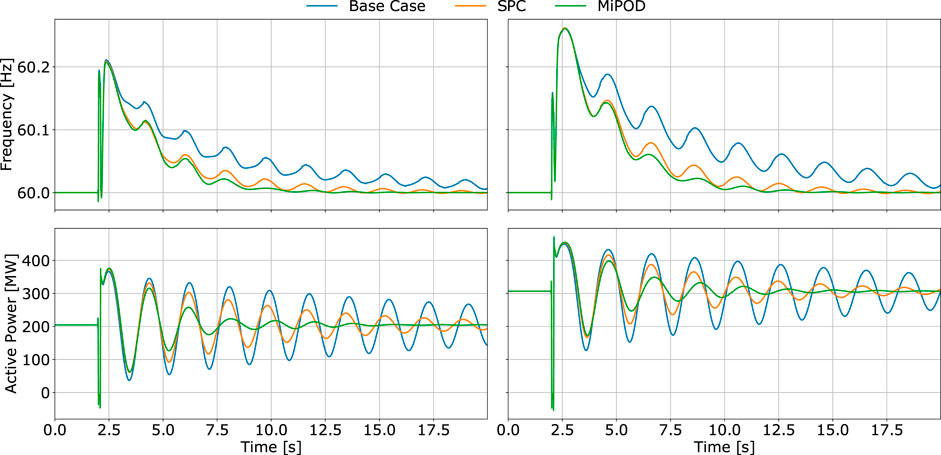
FIGURE 19. System frequency and active power flow at B08 after a symmetrical fault at B07 for 2 random operating points while the lower line connecting B08 and B09 is out of service.

6 Conclusion

Power electronics facilitate the connection of distributed power plants with grid thus contributing to the de-carbonization of power systems. However, wider integration of power electronics can risk the stability and reliability of the system in many aspects. Yet, the versatility and fast response characterizing them can be used to counter attack particular issues and finally improve the overall performance.

The validation of the proposed controller demonstrates the improvement of the damping by accounting for two oscillatory modes over the typical case of using only grid-forming power converters, i.e., SPC. According to the results the following conclusions can be made.

• With the introduction of the MiPOD it is possible to concentrate the available damping capacity of the GCC based power plat to attenuate two critical modes, like the inter-area and local mode of the two area system. After analyzing the damping and $A_1/A_2$ ratios for a large number of random operating points the MiPOD appears to enhance the overall stability of the system much more than the SPC.

• In addition, the dynamic responses of the system under symmetrical faults, variations in mechanical torque, load and topology changes show that the proposed controller can increase the damping of these modes by accurately predicting the frequency of two modes (local and inter-area) as operating conditions vary.

• Most importantly, the distributed power plant has only 6% of the total nominal capacity of the synchronous generators in the system yet it can ensure the stability improvement.

• The RF model developed in this paper assumes the existence of a WAMS, which facilitates for measurements to be received from different locations of the system. As mentioned a hard threshold scheme can be designed to limit the number of buses that need to be monitored in case full observability is not a realistic option.

As opposed to the conventional PSS devices, the number of parameters that need to be tuned for tracking and damping the electromechanical modes are lower e.g., 1 parameter per oscillation band. The lower number of adjustable parameters is achieved by integrating the AI model in the control loop, which provides accurate predictions of the modes frequency.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

Conceptualization, GB and NL; methodology, NL; software, LM; validation, AT, LM and GB; formal analysis, GB, LM; investigation, NL and FB; resources, NL; data curation, GB; writing–original draft preparation, GB; writing–review and editing, AT and FB; visualization, LM, NL and AT; supervision, PR; project administration, PR; funding acquisition, PR.

Funding

This work was supported by the European Commission under project INTERFACE - H2020-LC-SC3-2018-ES-SCC-824330 and by the Spanish Ministry of Science under project ENE2017-88889-C2-1-R.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Nomenclature

General Abbreviations

AI Artificial intelligence

DPP Distributed power plants

ESS Energy storage systems

GCC Grid connected converter

MiPOD Multi-band intelligent power oscillation damper

PCC Point of common coupling

PLC Power loop controller

PMU Phasor measurement units

PSS Power system stabilizer

PV photovoltaic

RES Renewable energy systems

RF Random forests

SG Smart grids

SPC Synchronous power controller

WAMS Wide area measurement system

Controller Symbols

ω Angular frequency of the SPC

${\omega }_c$ Filter center frequency

θ Internal angle of the SPC

${\theta }_{PCC}$ Grid angle

${\zeta }_i$ Damping ratio

D Damping

H Inertia constant

i Inter-area mode

l Local mode

$P_{ref}$ Active power reference

R Virtual resistance

$V_{PCC}$ Grid voltage gagnitude

$V_{ref}$ Voltage referece

X Virtual impedance

Random Forest Symbols

$\text{Δ}I\left(t\right)$ Drop of impurity at node t

${\widehat{y}}_t$ Predicted value at node t

$I\left(t\right)$ Mean Squared Error at node t

$N_t$ Total number of patterns in t

$N_{tLeft}$ Total number of patterns in $t_{Left}$

$N_{tRight}$ Total number of patterns in $t_{Right}$

Q Total Decision Trees in the Ensemble

r Index of Decision tree in the Ensemble

$S_t$ Set of patterns at node t

t Node of Decision Tree i

$t_{Left}$ Left ancestor node

$t_{Right}$ Right ancestor node

$y^{\left(p\right)}$ True value for pattern $p\in S_t$

Footnotes

¹The ability of a system to remain in synchronism after a disturbance (Kundur et al., 1994)

²Static Synchronous Compensator

References

Aleem, S. A., Hussain, S. M. S., and Ustun, T. S. (2020). A review of strategies to increase pv penetration level in smart grids. Energies 13, 636. doi:10.3390/en13030636

CrossRef Full Text | Google Scholar

Andersson, G., Donalek, P., Farmer, R., Hatziargyriou, N., Kamwa, I., Kundur, P., et al. (2005). Causes of the 2003 major grid blackouts in North America and Europe, and recommended means to improve system dynamic performance. IEEE Trans. Power Syst. 20, 1922–1928. doi:10.1109/tpwrs.2005.857942

CrossRef Full Text | Google Scholar

Baltas, G. N., Lai, N. B., Marin, L., Tarraso, A., and Rodriguez, P. (2020). Grid-forming power converters tuned through artificial intelligence to damp subsynchronous interactions in electrical grids. IEEE Access 8, 93369–93379. doi:10.1109/access.2020.2995298

CrossRef Full Text | Google Scholar

Beaudin, M., Zareipour, H., Anthony, S., and Rosehart, W. (2010). Energy storage for mitigating the variability of renewable electricity sources: an updated review. Energ. Sustain. Develop. 14, 302–314. doi:10.1016/j.esd.2010.09.007

CrossRef Full Text | Google Scholar

Berizzi, A. (2004). “The Italian 2003 blackout,” in IEEE power engineering society general meeting, Denver, CO, 6–10 June, 2004, Vol. 2, 1673–1679.

Google Scholar

Bessa, R., Moreira, C., Silva, B., and Matos, M. (2014). Handling renewable energy variability and uncertainty in power systems operation. WIREs Energ. Environ. 3, 156–178. doi:10.1002/wene.76

CrossRef Full Text | Google Scholar

Breiman, L. (2001). Random forests. Machine Learn. 45, 5–32. doi:10.1023/A:1010933404324

CrossRef Full Text | Google Scholar

De La Ree, J., Centeno, V., Thorp, J. S., and Phadke, A. G. (2010). Synchronized phasor measurement applications in power systems. IEEE Trans. Smart Grid 1, 20. doi:10.1109/TSG.2010.2044815

CrossRef Full Text | Google Scholar

Duda, R. O., Hart, P. E., and Stork, D. G. (2001). Pattern classification. 2nd Edn. New York, NY: Wiley.

ENTSO-E (2019). High penetration of power electronic interfaced power sources and the potential contribution of grid forming converters. European Network of Transmission System Operators for Electricity, Tech. Rep.

Google Scholar

ENTSO-E (2018). Oscillation event 03.12.2017—system protection and dynamics WG. Tech. Rep. Brussels, Belgium: European Network of Transmission System Operators for Electricity.

Google Scholar

Fang, J., Li, H., Tang, Y., and Blaabjerg, F. (2019). On the inertia of future more-electronics power systems. IEEE J. Emerg. Sel. Top. Power Electron. 7, 2130–2146. doi:10.1109/jestpe.2018.2877766

CrossRef Full Text | Google Scholar

Farah, A., Guesmi, T., Hadj Abdallah, H., and Ouali, A. (2012). “Optimal design of multimachine power system stabilizers using evolutionary algorithms,” in 2012 First international conference on renewable energies and vehicular technology, Hammamet, Tunisia, 26–28 March, 2012, 497–501. doi:10.1109/REVET.2012.6195319

CrossRef Full Text | Google Scholar

Gopakumar, P., Reddy, M. J. B., and Mohanta, D. K. (2014). Stability control of smart power grids with artificial intelligence and wide-area synchrophasor measurements. Electric Power Components Syst. 42, 1095–1106. doi:10.1080/15325008.2014.913745

CrossRef Full Text | Google Scholar

Grigsby, L. L. (2007). Power system stability and cotrol. Cleveland, OH: CRC Press.

Guyon, I., Weston, J., Barnhill, S., and Vapnik, V. (2002). Gene selection for cancer classification using support vector machines. Machine Learn. 46, 389–422. doi:10.1023/a:1012487302797

CrossRef Full Text | Google Scholar

Howell, S., Rezgui, Y., Hippolyte, J.-L., Jayan, B., and Li, H. (2017). Towards the next generation of smart grids: semantic and holonic multi-agent management of distributed energy resources. Renew. Sustain. Energ. Rev. 77, 193–214. doi:10.1016/j.rser.2017.03.107

CrossRef Full Text | Google Scholar

Hu, W., Liang, J., Jin, Y., and Wu, F. (2018). Model of power system stabilizer adapting to multi-operating conditions of local power grid and parameter tuning. Sustainability 10, 2089. doi:10.3390/su10062089

CrossRef Full Text | Google Scholar

IEEE (2016). “IEEE recommended practice for excitation system models for power system stability studies,” IEEE Std 421.5–2016. (Revision of IEEE Std 421.5-2005) (New York, NY: IEEE), 1–207.

Google Scholar

Kempener, R., Komor, P., and Hoke, A. (2013). Smart grids and renewables: a guide for effective deployment. IRENA—International Renewable Energy Agency, Tech. Rep.

Google Scholar

Knüppel, T., Nielsen, J. N., Jensen, K. H., Dixon, A., and Østergaard, J. (2013). Power oscillation damping capabilities of wind power plant with full converter wind turbines considering its distributed and modular characteristics. IET Renew. Power Generation 7, 431–442. doi:10.1049/iet-rpg.2012.0030

CrossRef Full Text | Google Scholar

Kontis, E. O., Papadopoulos, T. A., Barzegkar-Ntovom, G. A., Chrysochos, A. I., and Papagiannis, G. K. (2018). Modal analysis of active distribution networks using system identification techniques. Int. J. Electr. Power Energ. Syst. 100, 365–378. doi:10.1016/j.ijepes.2018.02.038

CrossRef Full Text | Google Scholar

Kroposki, B., Johnson, B., Zhang, Y., Gevorgian, V., Denholm, P., Hodge, B., et al. (2017). Achieving a 100% renewable grid: operating electric power systems with extremely high levels of variable renewable energy. IEEE Power Energ. Mag. 15, 61–73. doi:10.1109/mpe.2016.2637122

CrossRef Full Text | Google Scholar

Kundur, P., Balu, N. J., and Lauby, M. G. (1994). “Power system stability and control,” in The epri power system engineering (New York: McGraw-Hill Education).

Google Scholar

Lai, N. B., and Kim, K. H. (2016). An improved current control strategy for a grid-connected inverter under distorted grid conditions. Energies 9, 190. doi:10.3390/en9030190

CrossRef Full Text | Google Scholar

Liu, C., Tang, F., and Leth Bak, C. (2018). An accurate online dynamic security assessment scheme based on random forest. Energies 11, 1914. doi:10.3390/en11071914

CrossRef Full Text | Google Scholar

Louppe, G. (2014). Understanding random forests: from theory to practice. arXiv preprint arXiv:1407.7502 [Dataset].

Google Scholar

Masters, G. M. (2013). Renewable and efficient electric power systems. 2nd Edn. Hoboken, NJ: Wiley Press—IEEE.

Prasertwong, K., Mithulananthan, N., and Thakur, D. (2010). Understanding low-frequency oscillation in power systems. Int. J. Electr. Eng. Edu. 47, 248–262. doi:10.7227/IJEEE.47.3.2

CrossRef Full Text | Google Scholar

Raschka, S., and Mirjalili, V. (2019). Python machine learning: machine learning and deep learning with Python,” Scikit-learn, and TensorFlow 2. Birmingham, United Kingdom: Packt Publishing Ltd.

Google Scholar

Rocabert, J., Luna, A., Blaabjerg, F., and Rodríguez, P. (2012). Control of power converters in ac microgrids. IEEE Trans. Power Electron. 27, 4734–4749. doi:10.1109/TPEL.2012.2199334

CrossRef Full Text | Google Scholar

Rodriguez Cortes, P., Candela Garcia, J. I., Rocabert Delgador, J., and Teodorescu, R. (2014). Virtual controller of electromechanical characteristics for static power converters. Abengoa Solar New Technologies SA, US20140067138A1 [Dataset].

Rodríguez, P., Citro, C., Candela, J. I., Rocabert, J., and Luna, A. (2018). Flexible grid connection and islanding of spc-based pv power converters. IEEE Trans. Ind. Applicat. 54, 2690–2702. doi:10.1109/tia.2018.2800683

CrossRef Full Text | Google Scholar

Senesoulin, F., Hongesombut, K., and Dechanupaprittha, S. (2019). “Deep neural network estimation of inter-area oscillation mode based on synchrophasor data,” in 2019 IEEE PES GTD grand international conference and exposition asia (GTD Asia), Thailand, March 19–23, 2019, 1–6.

Google Scholar

Shalev-Shwartz, S., and Ben-David, S. (2017). Understanding machine learning: from theory to algorithms. New York, NY: Cambridge University Press.

Shin, H., Nam, S., Lee, J., Baek, S., Choy, Y., and Kim, T. (2010). A practical power system stabilizer tuning method and its verification in field test. J. Electr. Eng. Tech. 5, 400–406. doi:10.5370/jeet.2010.5.3.400

CrossRef Full Text | Google Scholar

Sulla, F., Måsbäck, E., and Samuelsson, O. (2014). “Linking damping of electromechanical oscillations to system operating conditions using neural networks,” in IEEE PES innovative smart grid technologies, Europe, October 12–15, 2014, 1–6.

Google Scholar

Tarrasó, A., Verdugo, C., Lai, N. B., Ignacio Candela, J., and Rodriguez, P. (2019). “Synchronous power controller for distributed generation units,” in 2019 IEEE energy conversion congress and exposition (ECCE), Baltimore, MD, October 5, 2019, 4660–4664.

Google Scholar

Theodoridis, S., and Koutroumbas, K. (2008). Pattern recognition. 4th Edn. Orlando, FL: Academic Press.

TP462 (2012). IEEE Task Force Report. Identification of electromechanical modes in power systems.

Google Scholar

Varma, R. K., and Akbari, M. (2020). Simultaneous fast frequency control and power oscillation damping by utilizing pv solar system as pv-statcom. IEEE Trans. Sustain. Energ. 11, 415–425. doi:10.1109/tste.2019.2892943

CrossRef Full Text | Google Scholar

Varma, R. K., and Salehi, R. (2017). Ssr mitigation with a new control of PV solar farm as STATCOM (PV-STATCOM). IEEE Trans. Sustain. Energ. 8, 1473–1483. doi:10.1109/tste.2017.2691279

CrossRef Full Text | Google Scholar

Wang, Y., Meng, J., Zhang, X., and Xu, L. (2015). Control of pmsg-based wind turbines for system inertial response and power oscillation damping. IEEE Trans. Sustain. Energ. 6, 565–574. doi:10.1109/tste.2015.2394363

CrossRef Full Text | Google Scholar

Zhou, L., Yu, X., Li, B., Zheng, C., Liu, J., Liu, Q., et al. (2017). Damping inter-area oscillations with large-scale pv plant by modified multiple-model adaptive control strategy. IEEE Trans. Sustain. Energ. 8, 1629–1636. doi:10.1109/tste.2017.2697905

CrossRef Full Text | Google Scholar