- 1School of Mechanical Engineering, College of Engineering, University of Tehran, Tehran, Iran
- 2Department of Energy and Petroleum Engineering, Faculty of Science and Technology, University of Stavanger, Stavanger, Norway
Utilizing nanofluids in heat exchangers can lead to improved thermal performance. Nanofluids with suspended carbon nanotubes are specifically desirable in thermal systems because of their unique capabilities. In this study, convective heat transfer and required pumping power are studied simultaneously for a helical coiled heat exchanger with laminar water flow while incorporating 0.1 and 0.3 percent volume fraction of the hybrid nanofluid MWCNT + Fe3O4/water. Two different geometries of bare and ribbed tubes are used for the heat exchanger part. The ribs are chosen to be orthogonal, i.e., 90° with respect to the inclined ones. Three different Reynolds numbers are selected for investigation, all in laminar flow regime based on the non-dimensional M number defined in coiled tubes. Computational fluid dynamics is used to study thermal and fluid behavior of the problem. The convective heat transfer coefficient can serve as a criterion to measure the effectiveness of utilizing nanofluids in heat exchangers by taking the pressure drop and pumping power of the system into consideration. Finally, the artificial neural network curve fitting tool of MATLAB is used to make a good fit in the data range of the problem. It is shown that for most cases of the study, the pumping power ratio is less than 1 that can be considered appropriate from energy consumption viewpoint.
Introduction
The present trend of gradual decrease in the size of electronic devices and equipment demands improvements in heat transfer and cooling methods Ramezanizadeh et al. (2018). The techniques used for improving heat transfer rate in thermal systems are mainly categorized as passive and active ones. In active approaches, an external medium such as a fan or a pump is used for heat transfer enhancement which leads to an increment in the overall cost of the system. The passive approaches do not require additional components or moving parts, which leads to a further simplicity and cost-effectiveness and their less energy consumption has gained popularity in recent years Ahmadi et al. (2020). Among the passive approaches, employing nanofluids has attracted more attention (Hassanpour et al., 2018; Fallahnezhad and Nazif 2019; Ghalandari et al., 2020). Nanofluids are synthesized by dispersing solid particles of nanometer dimension in a base fluid, which can be pure or mixture of some fluids Sheremet et al. (2016). Nanofluids improve thermal conductivity of the working fluid owing to the presence of highly conductive solid particles (Komeilibirjandi et al., 2019; Maleki et al., 2020a).
Different types of nanofluids have been employed in heat exchangers with the goal of enhancing heat transfer rate and also to reduce their size (Hajatzadeh Pordanjani et al., 2019; Aghayari et al., 2020). It has been shown that implementing nanofluids can also considerably enhance heat transfer rate of thermal systems (Eshgarf et al., 2020; Irandoost Shahrestani et al., 2020). There are different studies which investigated a variety of techniques including machine learning to predict thermal properties of fluids and to improve and optimize various thermal systems (Abdelmalek et al., 2020; Maleki et al., 2020b; Safdari Shadloo 2020; Zheng et al., 2020). Banu et al. (2019) studied the performance of a micro pin-fin heat exchanger by applying three fluids including water, CuO/water, and Al2O3/water nanofluids at different Reynolds numbers. They observed that using CuO nanoparticles in water was more effective in improving heat transfer coefficient compared with Al2O3 particles. Moreover, it was found that at higher Reynolds numbers, the differences in heat transfer coefficients of heat exchangers become more significant. Qi et al. (2019) experimentally evaluated the performance of double tube heat exchanger by using TiO2/water nanofluid. Different nanofluid concentrations of 0.1, 0.3, and 0.5 wt% were considered in their research. They observed that the highest enhancement in heat transfer rate was in case of using the nanofluid with 0.5 wt% concentration which yielded approximately 14.8% higher heat transfer rate compared to the case of pure water. Helically coiled heat exchangers can intensify heat transfer coefficient due to the formation of secondary flow inside the tube Fsadni et al. (2017). Due to centrifugal and torsion effects, the behavior of flow in helical heat exchangers is considerably different from flow in straight tubes Che et al. (2020). Naik and Vinod (2018) carried out a study on the impact of using various nanostructures on the performance of a shell and helical coil heat exchanger. In their research, aqueous carboxymethyl cellulose solution was used as the base fluid and CuO, Al2O3 and Fe2O3 nanoparticles were dispersed in it. They concluded that higher concentrations would result in better thermal performance, for all the tested nanofluids; moreover, using CuO caused the highest increase in the heat transfer rate. In a study by Shiravi et al. (2020), entropy generation and heat transfer coefficient of carbon black nanofluid inside a helical heat exchanger were investigated experimentally. The flow regime was turbulent and effect of Reynolds number and concentration of the nanofluid on friction factor as well as convective heat transfer coefficient were evaluated. It was shown that at 0.21 percent mass of nanofluid where Nusselt number is maximum, entropy generation is minimized. Thanks to the relatively higher thermal conductivity of carbonic material, they are attractive candidates for heat transfer intensification purposes. Various structures of carbonic material such as graphene, graphite, and carbon nanotubes (CNTs) have already been studied in recent years. Many studies have demonstrated considerable potential of carbonic materials for thermal performance enhancement. For instance, according to a study performed by Fares et al. (2020), using 0.2% graphene/water nanofluid in a shell and tube heat exchanger can improve heat transfer coefficient by up to 29% compared to pure water. Sarafraz et al. (2016) investigated the performance of a counter-current double pipe heat exchanger by using CNT/water nanofluid. According to their study, using nanofluid with 0.3 wt% concentration improved the overall heat transfer rate of the investigated heat exchanger by up to 46.5% in comparison with the case of pure water.
Based on the literature review, using CNT-based nanofluids can significantly enhance heat transfer rate of a heat exchanger. The use of CNT-based nanofluids in helically coiled heat exchangers with bare and orthogonal ribbed tubes has limitedly been investigated while taking into consideration both thermal (convective heat transfer) and flow (pumping power) features. This paper aims at addressing this gap and it can be considered as a criterion for effectiveness evaluation of hybrid nanofluids for helical heat exchangers with or without rib turbulators. In this study, computational fluid dynamics is employed to numerically evaluate heat transfer rate and pumping power ratio in a helical coiled heat exchanger by using MWCNT + Fe3O4/water hybrid nanofluids in three volume fractions of 0 (pure water), 0.1% and 0.3%. In addition to the concentration of the hybrid nanofluid, Reynolds number is another operating factor with a key role, and is chosen to be 2,000, 2,500 and 3,000. To preserve the accuracy of the model, the thermophysical properties of the operating fluid are temperature-dependent. Moreover, effect of adding orthogonal ribs on the tube side of the heat exchanger was also investigated. Utilization of MATLAB curve fitting feature can be considered as an appropriate tool for evaluation of effectiveness of nanofluids in heat exchangers at different working conditions while considering both thermal and hydraulic parameters of convective heat transfer coefficient and pumping power.
Methodology
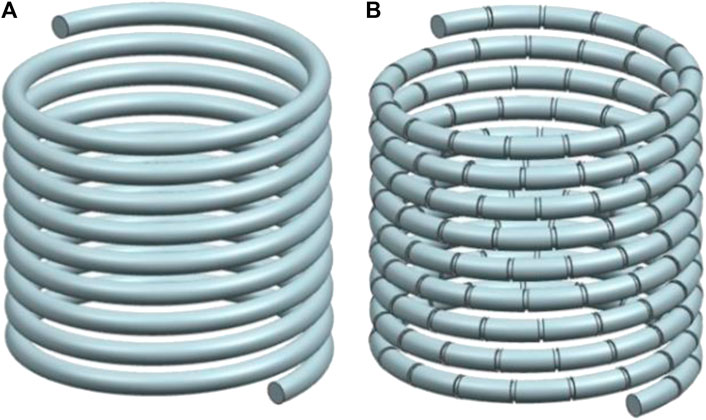
Siemens NX 10.0 is used to produce the geometrical model of the helical coiled heat exchanger. Two geometries of bare tubes and tubes with orthogonal ribs are generated. Details of the studied geometry are presented in Table 1. The pitch of the ribs is 50 mm and it has a rectangular cross section with 4 mm length (streamwise) and 2 mm width (normal to the tube surface). The heat exchanger has a total of 163 rib turbulators. The schematics of the geometries are illustrated in Figure 1.
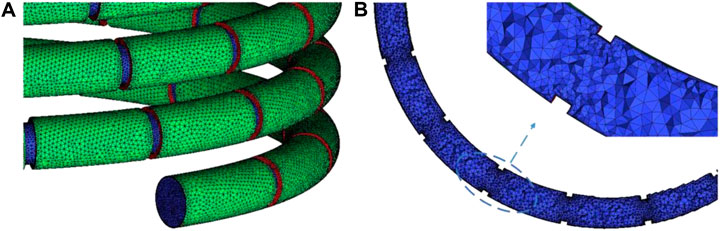
The mesh is generated by ANSYS ICEM CFD 16.0. The schematic of mesh elements for the case of tube with rib turbulators can be seen in Figure 2. Computational fluid dynamics has long been used to model heat transfer and fluid flow of different systems under various operating conditions (Hasanpour et al., 2018; Maleki et al., 2020c). ANSYS CFX 16.0 is utilized to solve the governing equations. For the criteria of convergence, X-momentum, Y-momentum, Z-momentum, energy, and continuity equations are defined to have RMS residuals less than 10–5. To assure the convergence of the solution, mass flow average of temperature and velocity at the outlet of the domain and mass flow average of total pressure at the inlet as well as area average of temperature on the surface of the tubes are all monitored during the solution process. Total energy model for heat transfer, including the viscous work term, is considered in the simulations. The process is steady-state and has a laminar flow regime.
Continuity equation is defined as:
Momentum equations in (x, y, z) directions are:
and the energy equation is:
the thermophysical properties of the operating fluid is considered as temperature-dependent variables, as can be seen in Table 2 Sundar et al. (2014).
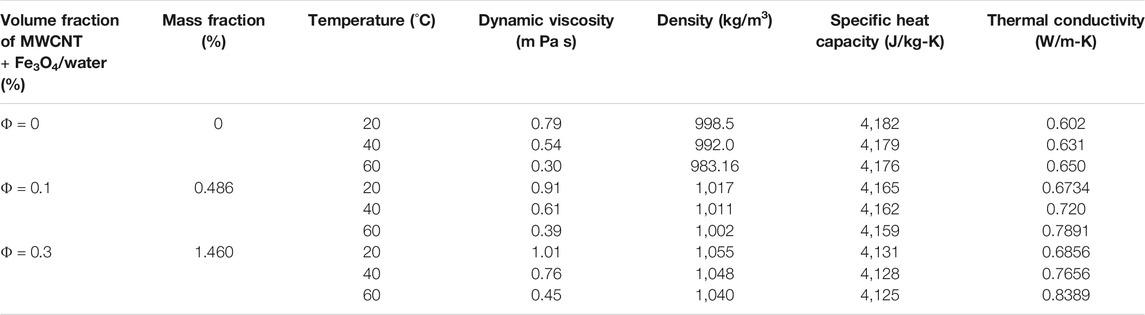
TABLE 2. Thermophysical properties of different working fluids Sundar et al. (2014).
Reynolds number is defined as:
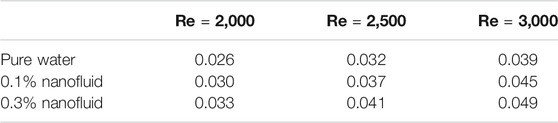
where density and viscosity are considered at inlet of the tubes. Mass flow rate of the working fluid at different Reynolds numbers and volume fractions are given in Table 3. It is worth noting that the variation of mass flow rate at constant Reynolds number is due to change in thermophysical properties of the working fluid at different volume fractions.
Mujawar and Rao (1978) defined a dimensionless number that can serve as a criteria of transition between laminar and turbulent regimes in coiled tubes. The effect of curvature of the tubes is taken into consideration and for Newtonian fluids it is defined as:
in which a is the radius of the tube and R is the radius of the coil. Based on their findings, the flow can be considered as laminar if M is below 2,100. Convective heat transfer coefficient is defined by the following equation Shiravi et al. (2020):
where q is the heat flux of the surface which is equal to 5000 W/m2 K and Tw is the wall average temperature and finally the average temperature Tm is defined as:
The constant heat flux can be considered as outer medium’s boundary condition for the heat exchanger and it is assumed that it is applied on the inner surface of the tube and thus conjugate heat transfer is not solved. The flow approaches the heat exchanger with constant temperature. Zero back pressure is considered at the outlet of the heat exchanger. Although nanofluids can enhance thermal performance of the system, this is at the expense of higher pressure drop and consequently higher energy consumption to run the system. To evaluate the pressure drop of the heat exchanger, the required pumping power is evaluated by:
where
Results and Discussion
To validate the numerical method used in this study, the outcomes of the model are compared with the results of Pawar and Sunnapwar (2014). For this purpose, the outlet temperature of the fluid is considered as the comparison criteria. As can be seen in Figure 3, a good agreement exists between the two set of results. The maximum error corresponds to the dimensionless M number of 2,190 and is equal to 4.9 percent.
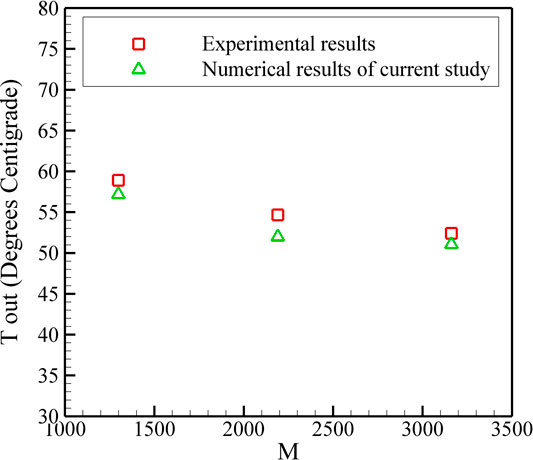
FIGURE 3. Comparison of the results from current numerical study with the experimental investigation of Reference Pawar and Sunnapwar (2014).
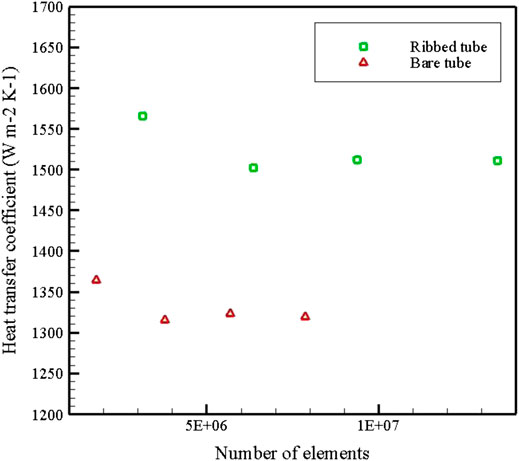
To examine grid independency of the model, four different mesh settings are considered for each of the cases of the heat exchanger with and without rib turbulators. Number of elements for heat exchanger with and without rib turbulators as well as the average heat transfer coefficient (h) for pure water at Reynolds number of 2,000 can be seen in Figure 4. Based on the results, changes in h are negligible for Grid 2, Grid 3, and Grid 4. Therefore, the second one is selected for further simulations.
Figure 5 depicts convective heat transfer coefficient at different Reynolds numbers of 2000, 2,500, and 3,000. Based on dimensionless M number, the flow regime is laminar. Three different hybrid nanoparticle volume fractions of 0, 0.1 and 0.3 percent are considered. In all volume fractions, as the Reynolds number increases, an increment in convective heat transfer rate is observed. Furthermore, in all Reynolds numbers and volume fractions, heat transfer rate of the ribbed tube is higher than the bare tube. The highest increase is 14.2 percent for pure water at Reynolds number of 2,000. To investigate the heat transfer augmentation due to the utilization of the hybrid nanofluid of MWCNT + Fe3O4/Water, convective heat transfer at three different Reynolds numbers of 2,000, 2,500, and 3,000 is illustrated in Figure 6. Clearly, increase in the nanoparticle volume fraction leads to an increase in the heat transfer rate. This enhancement is more significant when volume fraction of the hybrid nanoparticle is at the highest level, i.e., 0.3%.
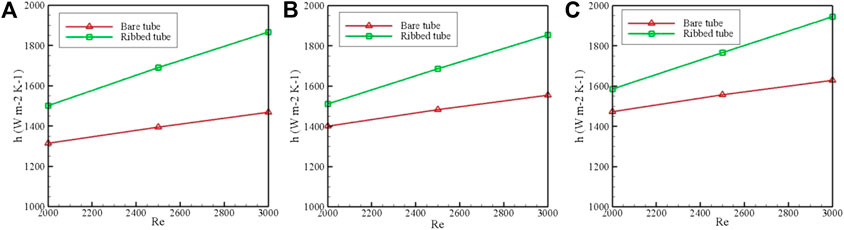
FIGURE 5. Convective heat transfer coefficient at different Reynolds numbers for volume fractions equal to (A) 0 (pure water), (B) 0.1 and (C) 0.3%.
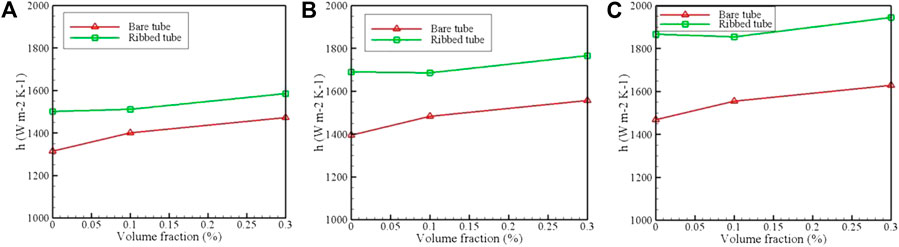
FIGURE 6. Convective heat transfer coefficient at different volume fractions for Reynolds numbers of (A) 2,000, (B) 2,500 and (C) 3,000.
Ratio of convective heat transfer rate of the hybrid nanofluid (h) to that of the pure water (h0) is a useful parameter to measure nanoparticles effectiveness. This ratio is illustrated in Figures 7, 8 for different cases. Figure 7A reveals that for the ribbed tube case at constant volume fraction of 0.1%, the ratio h/h0 roughly equals 1 at three different Reynolds numbers. Therefore, utilization of nanofluid is not beneficial from the heat transfer point of view. This is because the heat transfer rate is more considerably affected by the presence of the ribs and the turbulence in the flow induced by them. As such, nanoparticles barely have any effect in the ribbed tubes. It is worth noting that the ratio remains constant as the Reynolds number increases. However, for bare tube the ratio of h/h0 is about 1.06 leading to 6% growth in heat transfer rate. This ratio is rather constant for all the three Reynolds numbers of 2,000, 2,500, and 3,000. From Figure 7B, it is apparent that 3 percent volume fraction of nanoparticles has a positive heat transfer impact. At all Reynolds numbers, the increment is about 5 and 11 percent for ribbed and bare tubes, respectively. Even in the case of 0.3 percent volume fraction, the ratio of h/h0 is higher for bare tube than for the ribbed one. This can be attributed to the fact that ribs dominate the flow and heat transfer patterns at their presence, while the presence of nanoparticles is less consequential. Figure 8 shows h/h0 at different volume fractions for Reynolds numbers of 2,000, 2,500, and 3,000. Interestingly, h/h0 is always higher for bare tube compared to the ribbed one since the dominant parameter in ribbed tubes is the effect of local turbulence in the flow. In fact, the flow is exposed to attachment and reattachment between successive ribs resulting in local turbulence which ultimately leads to less thermal resistance and larger local heat transfer rates.
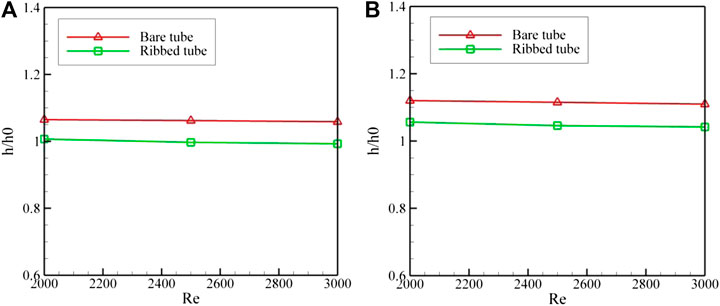
FIGURE 7. Convective heat transfer coefficient ratio at different Reynolds numbers for volume fractions of (A) 0.1% and (B) 0.3%.
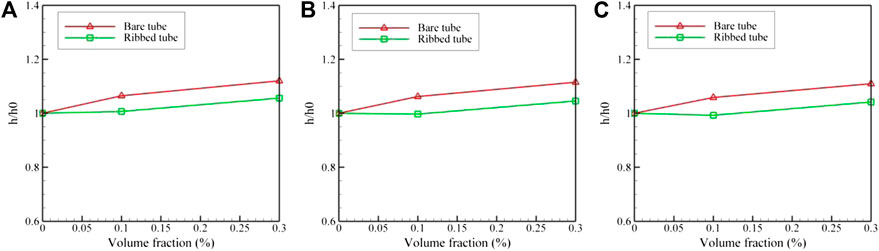
FIGURE 8. Convective heat transfer coefficient ratio at different volume fractions for Reynolds numbers of (A) 2000, (B) 2,500 and (C) 3,000.
One important factor to be investigated in any thermal system consisting a flow, and especially in heat exchangers, is the amount of pressure drop. Higher pressure drop can lead to more energy consumption as the pumping power required to deliver the desired amount of mass flow rate would increase. The ratio of pumping power of the nanofluid at different Reynolds numbers and volume fractions (W) to that of pure water (W0) is depicted in Figures 9, 10. These graphs provide the designer a very good insight to the corresponding pressure drop and consequently pumping power attributed to each case. This would assist the designer to effectively determine the appropriate nanofluid volume fraction. The pumping power for laminar fluid flow inside a tube with constant heat flux is defined as follows Mansour et al. (2007):
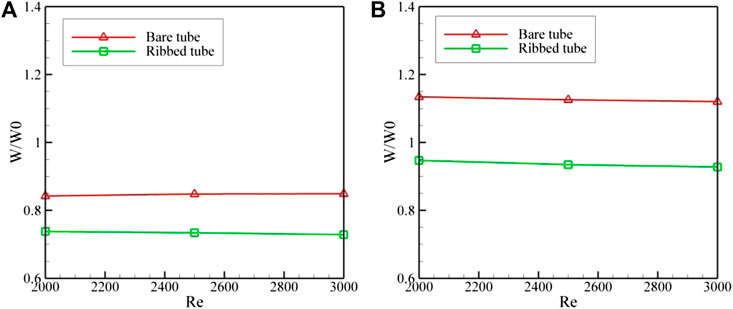
FIGURE 9. Pumping power ratio at different Reynolds numbers for volume fractions of (A) 0.1% and (B) 0.3%.
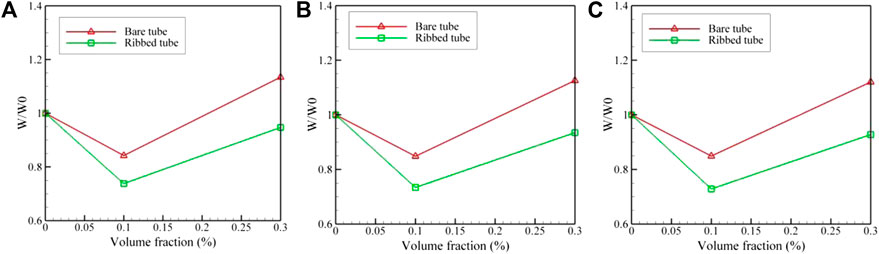
FIGURE 10. Pumping power ratio at different volume fractions for Reynolds numbers of (A) 2000, (B) 2,500 and (C) 3,000.
The ratio of pumping power is dependent on thermo-physical properties of the fluid. When this ratio is less than 1, the heat transfer augmentation is coupled with less energy consumption of the system. From Figure 9 it can be seen that except for 0.3 percent volume fraction of the nanofluid for bare tube, in all other cases the pumping power ratio is less than 1, which is desirable. Figure 10 shows that increasing the nanofluid volume fraction from 0.1 to 0.3 percent leads to an increase of the pumping power ratio. However, this ratio is still below 1 for the heat exchanger with ribbed tubes at different Reynolds numbers.
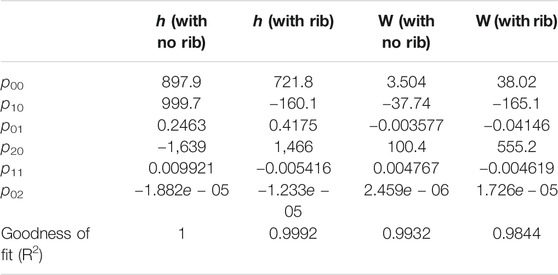
To provide a good fit within the data range, curve fitting tool of MATLAB is used. Therefore, a machine learning method is implemented by using different inputs and outputs while taking goodness of the curve fitting into consideration, Figures 11, 12. The following form of polynomial is considered for the curve fitting. It is of degree 2 for inputs of the problem, i.e., Reynolds number and volume fraction:
in which x is the volume fraction (φ) in percent and y is the Reynolds number and finally f is the output of the problem, i.e., the convective heat transfer coefficient (h) in W m−2 K−1 and pumping power of the heat exchanger (W) in mW. The relevant coefficients are provided in Table 4. Notably, that the curve fitting equation is valid in data range of the problem, i.e., Re number between 2,000 and 3,000 and volume fraction of the nanofluid between 0 and 0.3 percent.
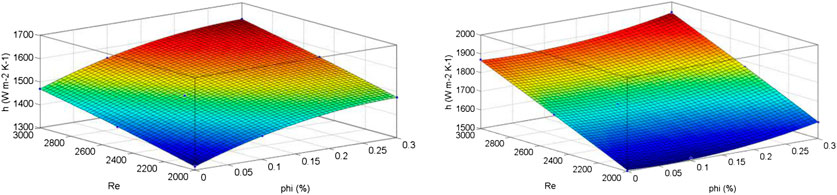
FIGURE 11. Curve fitting of convective heat transfer coefficient vs. Re and phi for heat exchangers without rib turbulators (left) and with rib turbulators (right).
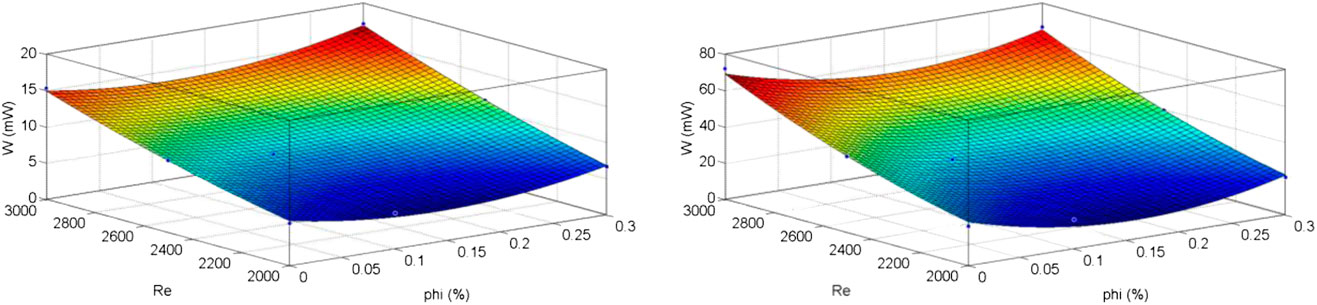
FIGURE 12. Curve fitting of pumping power vs. Re and phi for heat exchangers without rib turbulators (left) and with rib turbulators (right).
Conclusion
Helical coiled heat exchangers with bare and 90-degree inclined ribbed tubes at different Reynold numbers of 2,000, 2,500, and 3,000 and MWCNT + Fe3O4/water hybrid nanofluid with volume fractions of 0 (pure water), 0.1, and 0.3% were investigated in this study. Based on the dimensionless M number, the flow regime is laminar. Computational fluid dynamics (CFD) was used to investigate the forced convective heat transfer coefficient, heat transfer ratio and the pumping power ratio. Results of this study can serve as a criterion to determine the hybrid nanofluid effectiveness while keeping an eye on the pumping power of the heat exchanger for both cases of bare and ribbed tubes. The results revealed that for the heat exchanger with ribbed tubes at 0.3 percent volume fraction of nanoparticles the ratio of convective heat transfer to that of the pure water equals to about 1 which means that the nanofluid is not increasing performance of the system. It was also shown that except for heat exchangers with bare tube at 0.3 percent volume fraction of nanoparticles, all other cases lead to pumping power ratios of less than 1 that can be considered as favorable from energy consumption point of view.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Nomenclature
a Radius of tube, m
cp Specific heat at constant pressure, J/kg K
D, d Inner and outer diameter, m
h Convective heat transfer coefficient, W/m2 K
k Thermal conductivity, W/m K
M Dimensionless number, Ref (Fsadni et al., 2017)
n Number of turns
P Pressure, Pa
q Heat flux, W/m2
R Radius of coil, m
Re Reynolds number
T Temperature, K
u, v, w Velocity at different directions, m/s
W Pumping power, W
x, y, z Coordinate directions, m
Greek Symbols
Φ Particle volume fraction, %
μ Viscosity, Pa s
ρ Density, kg/m3
ΔP Pressure drop, Pa
Subscripts
0 Related to pure water
i Inner
in Inlet
out Outlet
o Outer
Acronyms
CFD Computational fluid dynamics
CNT carbon nanotubes
MWCNT Multi-walled carbon nanotube
References
Abdelmalek, Z., Alamian, R., Safdari Shadloo, M., Maleki, A., and Karimipour, A. (2020). Numerical study on the performance of a homogeneous charge compression ignition engine fueled with different blends of biodiesel. J. Therm. Anal. Calorim. doi:10.1007/s10973-020-09513-1
Aghayari, R., Maddah, H., Pourkiaei, S. M., Ahmadi, M. H., Chen, L., and Ghazvini, M. (2020). Theoretical and experimental studies of heat transfer in a double-pipe heat exchanger equipped with twisted tape and nanofluid. Eur. Phys. J. Plus. 135 (2), 1–26. doi:10.1140/EPJP/S13360-020-00252-8
Ahmadi, S., Irandoost Shahrestani, M., Sayadian, Sh., Maerefat, M., and Haghighi Poshtiri, A. (2020). Performance analysis of an integrated cooling system consisted of earth-to-air heat exchanger (EAHE) and water spray channel. J. Therm. Anal. Calorim. 143 (1), 473–483. doi:10.1007/s10973-020-09268-9
Banu, P. S. A., Krishnan, A., Shafee, S. M., and Raj, A. G. S. (2019). Numerical investigation of micro-pin-fin heat exchanger using nanofluids. Mater. Today: Proceedings 22, 1020–1025. doi:10.1016/j.matpr.2019.11.269
Che, S., Breitenmoser, D., Infimovskiy, Y. Y., Manera, A., and Petrov, V. (2020). CFD simulation of two-phase flows in helical coils. Front. Energy Res. 8 (65). doi:10.3389/fenrg.2020.00065
Eshgarf, H., Kalbasi, R., Maleki, A., Shadloo, M. S., and karimipour, A. (2020). A review on the properties, preparation, models and stability of hybrid nanofluids to optimize energy consumption. J. Therm. Anal. Calorim. 2020, 1–25. doi:10.1007/s10973-020-09998-w
Fallahnezhad, N., and Nazif, H. R. (2019). Heat convection and hydrodynamic analysis of laminar developing nanofluid channel flow with variable properties under constant magnetic field and heat flux. Eur. Phys. J. Plus. 134 (8), 1–16. doi:10.1140/EPJP/I2019-12787-6
Fares, M., Al-Mayyahi, M., and Al-Saad, M. (2020). Heat transfer analysis of a shell and tube heat exchanger operated with graphene nanofluids. Case Stud. Therm. Eng. 18, 100584. doi:10.1016/j.csite.2020.100584
Fsadni, A. M., Whitty, J. P. M., Adeniyi, A. A., Simo, J., and Brooks, H. L. (2017). A review on the application of nanofluids in coiled tube heat exchangers. J Micro Nanomanuf. 2, 443–465. doi:10.1007/978-3-319-67132-1_15
Ghalandari, M., Maleki, A., Haghighi, A., Safdari Shadloo, M., Alhuyi Nazari, M., and Tlili, I. (2020). Applications of nanofluids containing carbon nanotubes in solar energy systems: a review. J. Mol. Liq. 313, 113476. doi:10.1016/j.molliq.2020.113476
Hajatzadeh Pordanjani, A., Aghakhani, S., Afrand, M., Mahmoudi, B., Mahian, O., and Wongwises, S. (2019). An updated review on application of nanofluids in heat exchangers for saving energy. Energy Convers. Manag. 198, 111886. doi:10.1016/j.enconman.2019.111886
Hasanpour, B., Irandoost, M. S., Hassani, M., and Kouhikamali, R. (2018). Numerical investigation of saturated upward flow boiling of water in a vertical tube using VOF model: effect of different boundary conditions. Heat Mass Tran. 54 (7), 1925. doi:10.1007/s00231-018-2289-3
Hassanpour, A., Ranjbar, A. A., and Sheikholeslami, M. (2018). Numerical study for forced MHD convection heat transfer of a nanofluid in a square cavity with a cylinder of constant heat flux. Eur. Phys. J. Plus. 133 (2), 1–15. doi:10.1140/EPJP/I2018-11893-3
Irandoost Shahrestani, M., Maleki, A., Safdari Shadloo, M., and Tlili, I. (2020). Numerical investigation of forced convective heat transfer and performance evaluation criterion of Al2O3/water nanofluid flow inside an axisymmetric microchannel. Symmetry 12 (1), 120. doi:10.3390/sym12010120.
Komeilibirjandi, A., Raffiee, A. H., Maleki, A., Alhuyi Nazari, M., and Safdari Shadloo, M. (2019). Thermal conductivity prediction of nanofluids containing CuO nanoparticles by using correlation and artificial neural network. J. Therm. Anal. Calorim. 139, 2679. doi:10.1007/s10973-019-08838-w
Maleki, A., Elahi, M., Assad, M. E. H., Alhuyi Nazari, M., Safdari Shadloo, M., and Nabipour, N. (2020a). Thermal conductivity modeling of nanofluids with ZnO particles by using approaches based on artificial neural network and MARS. J. Therm. Anal. Calorim. 2020, 1–12. doi:10.1007/s10973-020-09373-9
Maleki, A., Haghighi, A., Irandoost Shahrestani, M., and Abdelmalek, Z. (2020b). Applying different types of artificial neural network for modeling thermal conductivity of nanofluids containing silica particles. J. Therm. Anal. Calorim. 2020, 1–16. doi:10.1007/s10973-020-09541-x
Maleki, A., Ngo, P. T. T., and Shahrestani, M. I. (2020c). Energy and exergy analysis of a PV module cooled by an active cooling approach. J. Therm. Anal. Calorim. 141, 2475. doi:10.1007/s10973-020-09916-0
Mansour, R. B., Galanis, N., and Nguyen, C. T. (2007). Effect of uncertainties in physical properties on forced convection heat transfer with nanofluids. Appl. Therm. Eng. 27 (1), 240–249. doi:10.1016/j.applthermaleng.2006.04.011
Mujawar, B. A., and Roa, M. R. (1978). Flow of non-Newtonian fluids through helical coils. Ind. Eng. Chem. Process Des. Dev. 17 (1), 22–27. doi:10.1021/i260065a005
Naik, B. A. K., and Vinod, A. V. (2018). Heat transfer enhancement using non-Newtonian nanofluids in a shell and helical coil heat exchanger. Exp. Therm. Fluid Sci. 90, 132–142. doi:10.1016/j.expthermflusci.2017.09.013
Pawar, S. S., and Sunnapwar, V. K. (2014). Experimental and CFD investigation of convective heat transfer in helically coiled tube heat exchanger. Chem. Eng. Res. Des. 92 (11), 2294–2312. doi:10.1016/j.cherd.2014.01.016
Qi, C., Luo, T., Liu, M., Fan, F., and Yan, Y. (2019). Experimental study on the flow and heat transfer characteristics of nanofluids in double-tube heat exchangers based on thermal efficiency assessment. Energy Convers. Manag. 197, 111877. doi:10.1016/j.enconman.2019.111877
Ramezanizadeh, M., Alhuyi Nazari, M., Ahmadi, M. H., and Açıkkalp, E. (2018). Application of nanofluids in thermosyphons: a review. J. Mol. Liq. 272, 395. doi:10.1016/j.molliq.2018.09.101
Safdari Shadloo, M. (2020). Application of support vector machines for accurate prediction of convection heat transfer coefficient of nanofluids through circular pipes. Int. J. Numer. Methods Heat Fluid Flow. Available at: https://www.emerald.com/insight/content/doi/10.1108/HFF-09-2020-0555/full/html.
Sarafraz, M. M., Hormozi, F., and Nikkhah, V. (2016). Thermal performance of a counter-current double pipe heat exchanger working with COOH-CNT/water nanofluids. Exp. Therm. Fluid Sci. 78, 41–49. doi:10.1016/j.expthermflusci.2016.05.014
Sheremet, M. A., Pop, I., and Shenoy, A. (2016). Natural convection in a wavy open porous cavity filled with a nanofluid: tiwari and das’ nanofluid model. Eur. Phys. J. Plus. 131 (3), 1–12. doi:10.1140/EPJP/I2016-16062-2
Shiravi, A. H., Shafiee, M., Firoozzadeh, M., Bostani, H., and Bozorgmehrian, M. (2020). Experimental study on convective heat transfer and entropy generation of carbon black nanofluid turbulent flow in a helical coiled heat exchanger. J. Therm. Anal. Calorim. doi:10.1007/s10973-020-09729-1
Sundar, L. S., Singh, M. K., and Sousa, A. C. M. (2014). Enhanced heat transfer and friction factor of MWCNT-Fe3O4/water hybrid nanofluids. Int. Commun. Heat Mass Tran. 52, 73–83. doi:10.1016/j.icheatmasstransfer.2014.01.012
Keywords: CFD, helical heat exchanger, hybrid nanofluid, convective heat transfer coefficient, orthogonal rib turbulator
Citation: Irandoost Shahrestani M, Houshfar E, Ashjaee M and Allahvirdizadeh P (2021) Convective Heat Transfer and Pumping Power Analysis of MWCNT + Fe3O4/Water Hybrid Nanofluid in a Helical Coiled Heat Exchanger with Orthogonal Rib Turbulators. Front. Energy Res. 9:630805. doi: 10.3389/fenrg.2021.630805
Received: 18 November 2020; Accepted: 08 January 2021;
Published: 23 February 2021.
Edited by:
Weiping Zhang, Zhejiang University, ChinaReviewed by:
Bin Xu, Clemson University, United StatesArash Karimipour, Islamic Azad University of Najafabad, Iran
Copyright © 2021 Irandoost Shahrestani, Houshfar, Ashjaee and Allahvirdizadeh. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ehsan Houshfar, aG91c2hmYXJAdXQuYWMuaXI=; Payam Allahvirdizadeh, cGF5YW0uYWxsYWh2aXJkaXphZGVoQHVpcy5ubw==
 Misagh Irandoost Shahrestani
Misagh Irandoost Shahrestani Ehsan Houshfar
Ehsan Houshfar Mehdi Ashjaee1
Mehdi Ashjaee1 Payam Allahvirdizadeh
Payam Allahvirdizadeh