- 1Key Laboratory of Smart Grid of Ministry of Education, Tianjin University, Tianjin, China
- 2State Grid Jiangsu Electric Power Co., Ltd. Marketing Service Center, Nanjing, China
Increasing penetration of distributed generation (DG) has brought more uncertainty to the operation of active distribution networks (ADNs). With the reformation of the power system, increasingly more flexible loads access to distribution network through load aggregators (LAs), which becomes an effective way to solve these issues. Since LAs and ADNs are separate entities with different interests, the traditional centralized and deterministic optimization methods fail to meet the actual operational requirements of ADNs. Based on the linear power flow model, a robust optimal dispatching model of ADNs considering the influence of renewable DG’s uncertain output on voltage security constraints is established. Then, an independent optimal scheduling model for LAs is modeled based on the analysis of the composition and characteristics of flexible load in LAs. LAs and ADNs, as two different stakeholders, use a distributed modeling method to establish different economic optimization goals. The optimization problem is solved by decoupling the coupling exchanging power between LAs and ADNs into virtual controllable loads and virtual DGs. Finally, with the case study of a modified IEEE 33-bus system, the correctness and effectiveness of the proposed method are verified. The effects of the robust level and demand response incentive on the results are also analyzed.
Introduction
With continuously increasing penetration of renewable energy, the uncertainty and intermittency of clean energy challenge the operation of distribution network (Ehsan and Yang, 2019). With the marketization of electric power industry on the demand side and the development of new information and communication technology in recent years, flexible resources in demand side have attracted extensive attention due to its economy and flexibility (Asensio et al., 2018a; Asensio et al., 2018b), which provides a solution for the economic and stable operation of ADNs in the accommodation of renewable energy. Different from the traditional inelastic load, the flexible load, such as smart home appliances, electric vehicles, and energy storage, can respond to the dispatching requirements of the power grid by adjusting its power or transferring its power consumption time (Zhang G. et al., 2019). With Demand Response (DR) technology, the flexible load can improve the economy and stability performance of the distribution system (Parizy et al., 2019; Delavari and Kamwa, 2018) and provide auxiliary services like frequency regulation (Wang et al., 2017), voltage regulation (Zhong et al., 2019), and reserve capacity (Tomasson and Soder, 2020).
Since the low electricity consumption level and DR efficiency of an individual user (Adrian et al., 2018), the flexible load can participate in the DR program through the load aggregators (LAs) (Herre et al., 2020), which promotes the massive participation of flexible loads in the demand side and in guiding the users to consume electricity properly and economically (Wang et al., 2020).
There are many studies on the role of flexible load in the operation of ADNs. In Jiang et al. (2018), the working mode of integrated smart buildings with heating, ventilation, and air-conditioning (HVAC) systems is proposed according to the heat storage characteristics of thermostatically controlled loads. The power loss and voltage fluctuation of the ADN can be decreased by utilizing the flexibility of the smart buildings. A multi-objective scheduling model for ADN based on source-network-load coordination scheduling is proposed in the article(Yong et al., 2018). The operating cost, renewable energy utilization rate and users’ satisfaction are considered as the optimization objectives. In the study by Kong et al. (2020), interruptible loads (ILs) are applied to increase the power supply capability and renewable energy utilization rate of the ADN, considering the uncertainty of distributed generation (DG). The above studies greatly exploit and utilize the capacity of demand side resources and improve the operational status of the ADN. However, most of the present works adopt centralized optimization methods, which are hard to adapt to the widely spread and scattered regional distribution system due to their heavy computational burden and poor expansibility with the increasing access of the flexible load. And in the centralized optimization, the benefits of different subjects are hard to be reconciled. To reflect the different interests of diverse subjects and the decentralized and autonomous characteristics of ADNs, the distributed optimization methods are applied into the optimal scheduling of ADNs.
In the studies of distributed optimization, the article by Meyer-Huebner et al. (2019) proposes a distributed optimal power flow algorithm of the ADN with multiple distributed resources but ignores the different interests of diverse stakeholders. In the study by Du et al. (2018), as a new distributed demand side resource, the source-load dual characteristic of Microgrid (MG) is discussed, and cooperative game theory is applied to realize the benefit assignment between the MG and the ADN. The article by Yu and Hong (2017) proposes a novel incentive-based demand response model from the view of a grid operator to enable system-level dispatch of demand response resources by adjusting the electricity price. Those literatures take the dynamic game process between two stakeholders into consideration. However, some private information, such as cost functions and network topologies, needs to be exchanged in the bargain process, which makes it hard to guarantee the privacy of data. In the study by Wang Z. et al. (2016), the distributed optimal scheduling of the ADN is realized with merely the knowledge of each MG’s expected exchange power in case of securing privacy of each MG. However, the effect of economic incentives to DR participants has not been taken into fully consideration. In the study by Wang D. et al. (2016), the marginal cost of proper constraints is utilized to form an updated price, with which the electricity cost can be reduced and the frequent transitions between battery charging/discharging states can be avoided. However, the method is essentially “source changing with load” mode and lack of interaction, which results in a low DR efficiency.
At the same time, the risk brought by renewable energy’s uncertain output cannot be ignored. At present, stochastic programming and robust optimization are two main methods to deal with the uncertainty of DGs’ output. In the study by Zhang Y. et al. (2019), the ellipsoid set is applied to describe the uncertainty of photovoltaic (PV) and wind turbine (WT), and the terminals of the ellipsoid are introduced into the stochastic optimization as extreme scenarios. The uncertainty of WT is considered by Cobos et al. (2018), and a robust scheduling model is established, which introduces variable cost depending on the uncertain WT output into the objective function. In the study by Liu et al. (2018), a two-stage robust optimization model of the min-max-min structure is established to obtain the scheduling scheme with the lowest operating cost under the worst scenario. However, stochastic programming and robust optimization methods still have their limitations. A large amount of calculation is inevitable in stochastic optimization, and the optimization effect heavily depends on scenarios selection. The traditional robust optimization mostly adopts the Soyster framework, which is also known as the completely robust optimization, whose feasible solutions are too conservative (Wang et al., 2018). Besides, the mentioned studies mainly focus on the power unbalance problem caused by the uncertain output of renewable DG, without considering whether the power flow security constraints of the system can be satisfied under the uncertainty.
To this end, two main questions arise:
(1) The traditional centralized optimization model failed to give full consideration of the benefits and autonomous characteristics of the LA inside the ADN. Therefore, a research question is raised on how to make use of the LA’s DR ability while giving consideration to the different benefits and autonomous characteristics of both the ADN and the LA.
(2) How to reduce the conservativeness of traditional robust optimization and make the effective optimal scheduling plan for the ADN while considering the influence of uncertain parameters on the power flow constraints?
This article tries to answer these questions and presents an effective, robust, and distributed optimal scheduling for ADNs connected with multiple LAs by coordinating the controllable devices in power supply and demand sides, while addressing the uncertain DG output. The contributions of this article are summarized as follows:
(1) This study proposes a distributed optimal scheduling model with DR incentive. In this model, the ADN and LAs are modeled as several stakeholders with different benefits and solve their own optimal scheduling problem autonomously and independently.
(2) A robust optimization method is applied to deal with the uncertainty brought by renewable DG in the power flow constraints of the ADN. Via the robust optimization, the schedules with different robust levels can be obtained to make a trade-off between the voltage violation rate and power supplying cost by adjusting the robust coefficient, which can make the result less conservative.
(3) Analytical target cascading (ATC) theory is applied to solve the distributed optimization problem without the knowledge of private data inside the LA and the ADN. The impact of DR incentive on LAs and ADNs is also analyzed. The ADN can further improve DR efficiency by adjusting DR incentive to an appropriate value.
The remainder of this article is organized as follows. In Optimal Scheduling Models of Active Distribution Network and Load Aggregator, the dispatching model of the ADN and the LA and the interaction model between them are established. The Bertsimas robust optimization and ATC theory are applied to solve the proposed problem in Solution Process. In Case Study, case studies are conducted to demonstrate the correctness and effectiveness of the model. Concluding remarks are presented in Conclusion.
Optimal Scheduling Models of Active Distribution Network and Load Aggregator
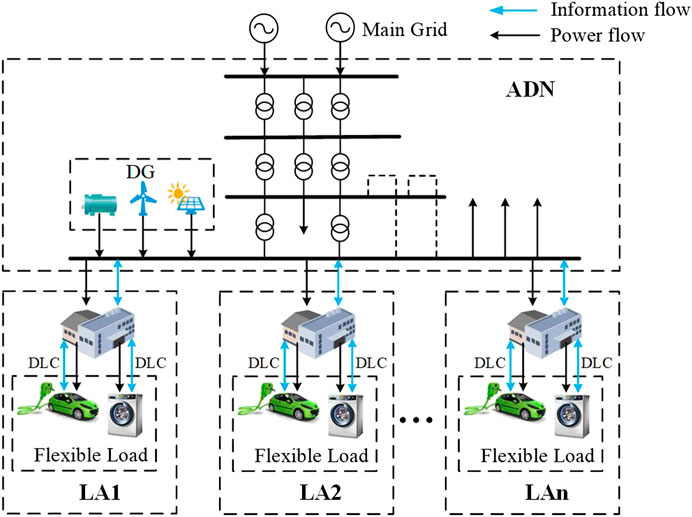
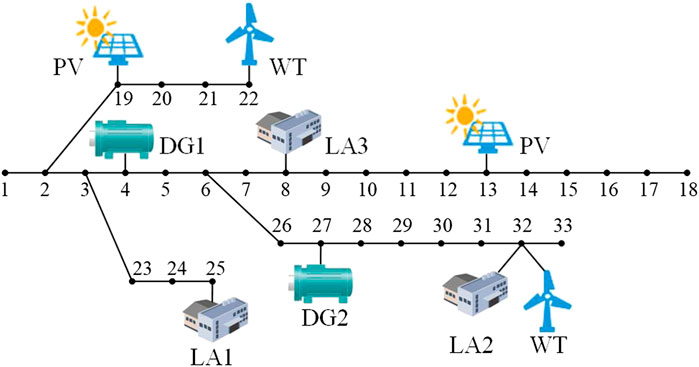
The structure of ADNs connected with LAs is shown in Figure 1. To improve the DR capacity, the LA directly combines the flexible loads (shiftable load and interruptible load) of different users in the region, the power consumption of which is adjusted based on the DR incentive to meet the scheduling requirements of the ADN. Through direct load control (DLC) technology, the LA properly arranges the power consumption plan of each flexible load and coordinates the power exchanged with the distribution network, so as to minimize the total operation cost of itself. With the goal to minimize the total cost while meeting the total power demand, the ADN controls the operational state and output power of controllable units based on the power demand of LAs and other power demand and the renewable DGs’ output in the distribution network.
Normally, LAs and ADNs are with their own scheduling functions and taken as different stakeholders. There is a strong coupling relationship between the LA and the ADN, because the power interaction between them makes their economic dispatching affect each other. The detailed dynamic economic dispatching models of the ADN and the LA are given below.
Optimal Scheduling Model for Active Distribution Network
Objective Function of the Active Distribution Network Optimal Dispatching
The requirement of ADNs’ optimal dispatching is to reduce its power supply cost while meeting its load. The ADN needs to decide its electricity procurement schedule and the operation state of its controllable unit. The ADN’s comprehensive cost
Constraints of the Active Distribution Network Optimal Dispatching
(1) Constraints of controllable DG
The constraints of power output Eq. 6, ramp rate Eq. 7, and running time Eq. 8 are considered:
(2) Constraints of renewable DG
The cubic set is adopted to define the uncertain output of PV and WT (Ding et al., 2017).
(3) Power flow constraints
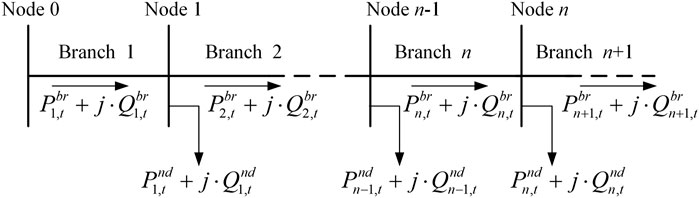
A distribution network is normally configured to be a radial/tree-like topology, which means that each network node has only one parent node. Figure 2 shows a line diagram of a radial power network. The power flows corresponding to Figure 2 can be described by DistFlow branch equations. However, the traditional DistFlow model is nonlinear, which makes the problem difficult to solve. To make relevant problems computationally tractable and meanwhile guarantee an acceptable calculation result, the linearized DistFlow model is adopted here (Song et al., 2019).
According to the definition of robust optimal scheduling, the voltage security must be ensured as the prediction errors of renewable DG change, which is expressed as follows:
Except for the voltage safety constraint, the branch current constraint is also considered in some studies. However, the current carrying capacity of the branch line is usually two to three times larger than its rated current. Besides, the voltage drop will increase as the branch current increase. Therefore, the branch current constraint will also be satisfied if the voltage security constraint is satisfied.
For node i, its total active and reactive load can be calculated as follows:
Since the network losses are much smaller than line flow terms
(4) DR constraint
When the TOU price of the main grid is higher than the selling price inside the ADN, the higher cost will be caused by the higher power purchasing price from the main grid. Therefore, the ADN hopes to reduce its cost by compensating and encouraging LAs to reduce their power consumption in the above period or to transfer their power consumption time to other periods. In this article, the ADN releases DR incentive in the corresponding period to encourage LAs to participate in the DR program. After LAs reduce their power consumption in the DR period set by the ADN, they will get DR compensation according to their reduction. The DR mechanism is shown in Eq. 14
There is a product form of the binary variable and continuous variable in Eq. 14. We apply the Big-M method to transfer Eq. 14 into a linear constraint Eq. 15 where M is a large enough constant.
Thus, in the optimal scheduling model for ADNs, the decision variables are
Optimal Scheduling Model for Load Aggregator
Objective Function of Load Aggregator’s Optimal Dispatching
Based on the electricity selling price and the DR incentive of the ADN, the LA adjusts its power consumption plan of the flexible load to minimize its comprehensive cost Eq. 16, which includes electricity purchasing cost, DLC cost and the profit from participating in the DR program. The subentry cost can be calculated as Eqs. 17–19
Constraints of Load Aggregator’s Optimal Dispatching
(1) Constraints of interruptible load
In order to meet the basic demand of users, the shedding power of the interruptible load cannot be larger than the maximum shedding power.
(2) Constraints of shiftable load
Constraint Eq. 22 represents the power range of the shiftable load. Constraint Eq. 23 indicates that the total energy consumption of the shiftable load remains unchanged after load shifting. In order to remove the absolute value function in Eq. 18, an auxiliary variable
When
(3) DR constraint
The Big-M method is applied to linearize constraint Eq. 26, which is the same as the linearization of Eq. 14.
(4) Power balance constraint in LA
Thus, in the optimal scheduling model for LAs, the decision variables are
Solution Process
Robust Counterpart for Power Flow Constraints
If node n is the leaf node of ADN,
We denote
The last equation in Eq. 10, which represents the relationship between the line transmission power and the node voltage magnitude, can be further expanded into:
According to the graph theory, we can obtain
The uncertain variables and controllable variables are separated in Eq. 31.
Soyster intially gained the solutions under the worst situation of uncertain parameters through linear robust optimization (Wang et al., 2018). The traditional robust optimization methods adopt the Soyster robust framework (Peng et al., 2014; Liang et al., 2019), which is too conservative in most situations. To reduce the conservativeness, this article adopts the Bertsimas robust optimization framework in which the result with different robust levels can be obtained by adjusting the robust coefficient. According to the principle of the Bertsimas robust optimization and Eq. 31, the voltage security constraints Eq. 11 have to be satisfied despite of the uncertainty of renewable DG’s output. As a result, the robust counterpart of voltage security constraints of node i is expressed as follows:
Distributed Optimization Based on Analytical Target Cascading Method
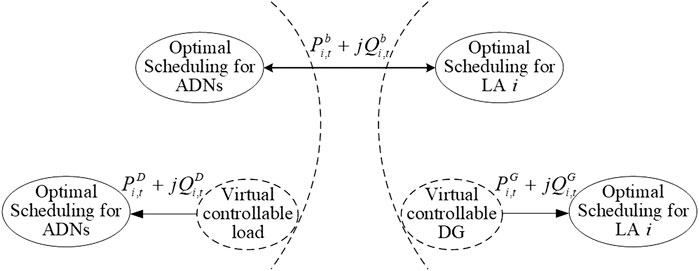
Since the ADNs and LAs are physically connected to each other, the power interaction
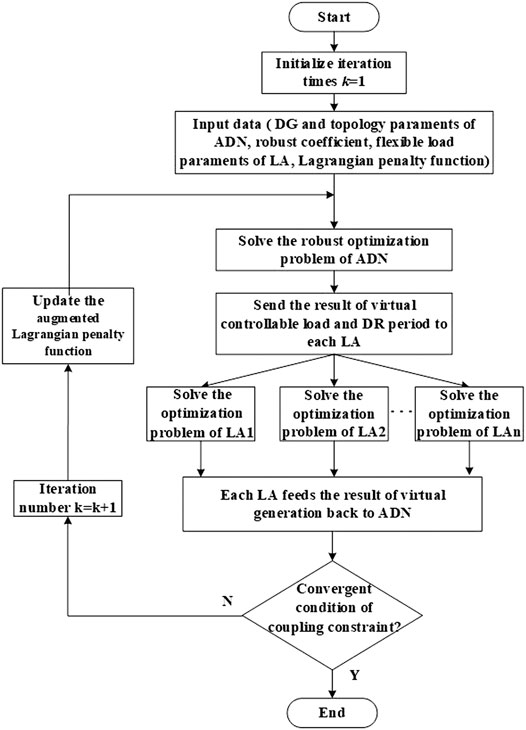
ATC is a parallel processing algorithm to solve the coordination problem with distributed hierarchy and performs well in convergence and stability despite the system scale. ATC can realize the parallel coordinated solution of different stakeholders and can ensure the security of private data inside each stakeholder. In the iterative process of ATC, the upper system (which is the ADN in this article) solves its scheduling problem and sends target information to the lower system (which is the LA in this article). The lower system calculates the response information according to the target information and feeds it back to the upper system. The upper system updates its scheduling problem based on the feedback results. The optimization is processed alternately in these two hierarchies, until the setting convergent condition is met. Since the ADNs and LAs only need to interact with expected exchange power with each other in the framework of ATC, the private data, like the topology parameter of the ADN and the cost functions of LAs, will not be exposed.
When the ADN solves its own optimal scheduling problem, the virtual controllable load term
Similarly, if the ADN is connected with
Therefore, in the scheduling model based on ATC, the optimal scheduling of the LA consists of Eqs. 36, 21–27, and the optimal scheduling of the ADN consists of Eqs. 37, 6–13, 15. Each system solves its own optimal scheduling problem independently and exchanges boundary variables
Based on the principle of ATC, we can obtain the parallel solving process which is shown in Figure 4. The setting convergence condition of the coupling constraint is expressed as:
Considering that LA will not participate in the DR program when there is no DR incentive
Case Study
Case Introduction
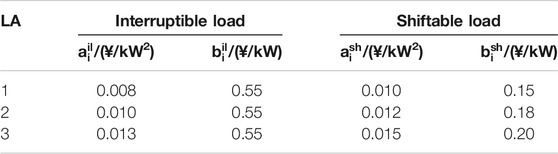
This section focuses on simulation in the case of grid-tied LA. The IEEE 33-bus distribution system connected with three LAs is used as the simulation system, shown in Figure 5. The normalized daily load and forecast output of PV and WT can be found in the article by Yong et al. (2018). The ADN is a 12.66 kV system. The upper and lower limit of voltage magnitude are set to 1.05 and 0.95 pu, respectively. The total load of the ADN is 3.715 MW + j·2300 MVar. The installed capacity of PV and WT are both 300 kW. The maximum prediction error is 30% of its predicted value. The robust coefficient Γ is set to 1.2. The DR incentive is 0.4 ¥/kWh. The interruptible load and shiftable load are both 20% of the total load in LA. The trading price between the ADN and the LA is 0.55 ¥/kWh. The parameters of controllable DG and flexible load are shown in Tables 1 and 2. The TOU price of the main grid is given in the article (Liang et al., 2019). The problem is solved by adopting commercial software CPLEX 12.9.0 through YALMIP in MATLAB on a 1.8 GHz, 16 GB machine, whose convergent gap value is set to 10−4. The convergence accuracy of ATC is set to 10−4.
Result Analysis
Optimal Scheduling Result
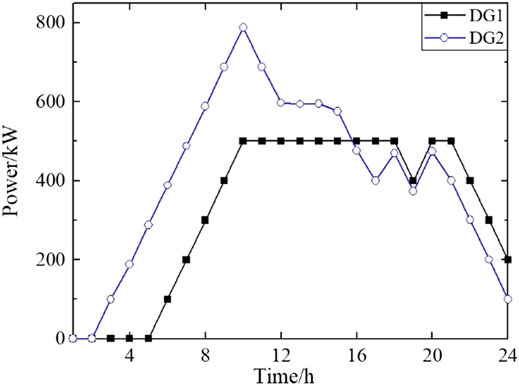
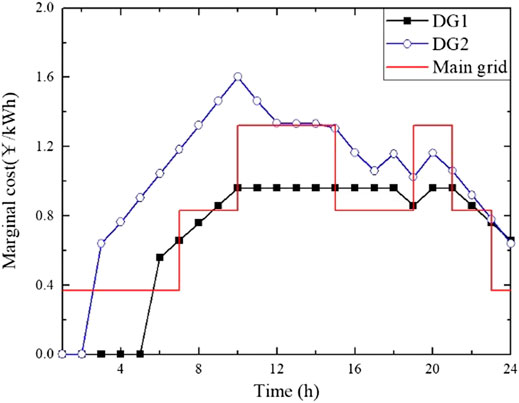
Figure 6 shows the output of controllable DG. DG1 is off during 1–7 h and t = 24 h, as the TOU price in the main grid during these periods are lower than the unit cost of DG1. Due to the ramping rate constraints, DG1 gradually increases its output since t = 6 h until it reaches its maximum value before the peak period. Compared to DG1, DG2 starts increasing its output at t = 2 h due to its higher capacity. DG1 and DG2 both maintain high output during 10–21 h and gradually decrease their output since t = 21 h, with the end of the peak period. Seen from the DGs’ marginal price in Figure 7, the marginal cost of controllable DGs is higher than the TOU price in some period. This is because the controllable DGs have to generate more power to protect the ADN from voltage violation caused by the fluctuating output of renewable DG. With the increasing output of DG, the voltage drop on the distribution line will be decreased due to the less power transmitted through the distribution line.
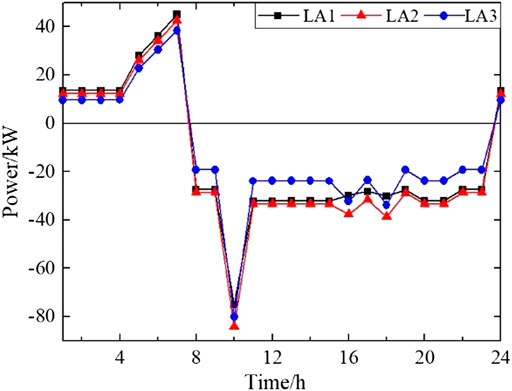
According to the result,
Performance of ATC
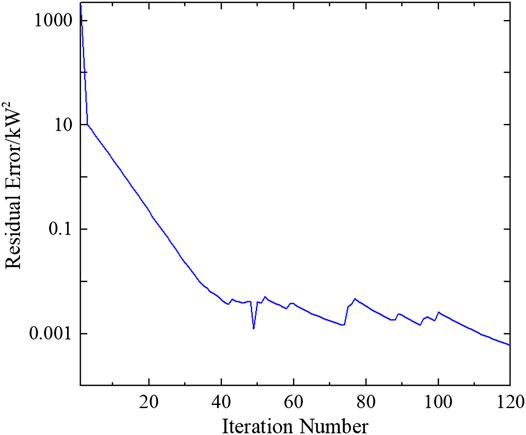
Figure 9 illustrates the convergence performance of the ATC algorithm for the ADN-LA power exchange. The applied distributed optimization scheduling method is stably convergent after 112 times iteration, which means it does not require many computing resources. By applying the ATC algorithm, the optimization times of the LA and the ADN and the communication burden between them can be reduced. Besides, the LA and the ADN only need to send their expected purchasing power to each other in the iteration process. The privacy data inside the LA, such as the cost function of the LA, is unknown to the ADN. As a result, the privacy and security of users’ data can be guaranteed.
To further demonstrate the effectiveness of the proposed method, three scheduling models are used to calculate the operating costs of the ADN and each LA. The three scheduling models are as follows:
(1) Centralized DLC model: assuming that the ADN can directly control the flexible load of users and that the ADN and LAs are regarded as the same stakeholder, the total cost of the ADN and LAs is taken as the objective function, and the centralized optimization method is applied to solve the problem.
(2) The “Source changing with load” model (Wang D. et al., 2016): LAs solve their optimal scheduling problem based on the electricity price and DR incentive of the ADN. Then the ADN makes its scheduling plan according to the result of LAs’ optimal scheduling problem.
(3) The distributed optimization method based on ATC in this article.
The results of different scheduling models are compared in Table 3. The total cost of the centralized DLC method is the lowest among Table 3, but the cost of each LA is higher than that of other methods, which means the total cost is decreased at the expense of each LA. Besides, the ADN needs to collect the relevant parameters of the flexible load under the centralized DLC model, which makes it difficult to guarantee the privacy of users. The benefits of each LA can be ensured under the “source changing with load” model. However, the cost of the ADN and total cost of this model are the highest due to the lack of enough interaction between the ADNs and LAs. Under the distributed optimization model based on ATC where the optimal scheduling problems of the ADNs and LAs are decoupled and solved independently, the economic benefits of LAs and the ADNs can be reconciled, and the privacy and security of users’ electric power data can be guaranteed. Although it takes more time to gain the results through distributed optimization due to its iterative process, the distributed method based on ATC is still fast enough to be applied in the day-ahead optimal scheduling and is more applicable than the centralized optimization for its advantage in guarantying the security of the private data inside each subject.
Robustness and Economy Analysis
To further study the influence of robust level on the optimization results, uncertainty analysis is presented in this article. We denote the violation rate to quantitatively measure the influence of uncertain parameters on voltage security. The violation rate is calculated as Eq. 42 through the Monte Carlo simulation where all uncertain parameters are assumed to follow uniform distribution.
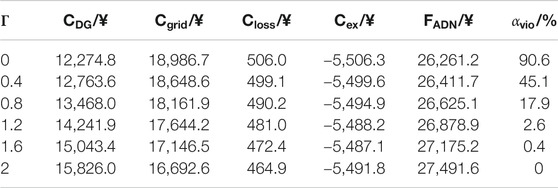
When Γ takes different values, different solutions with different levels of robustness can be obtained (compared in Table 4). For the ADN, different levels of robustness make it possible to make trade-offs between the economy and voltage level.
It can be seen from Table 4 that the cost of the ADN increases with the increasing Γ. The rise in cost was mainly due to the increasing cost of controllable DG. Controllable DG needs to increase its output and reduce the transmission power through distribution network lines, which indicates the role of controllable DG in voltage supporting under uncertain environment. When Γ is less than 1.2, the violation rate goes on declining rapidly, while the cost of the ADN rises with the increasing Γ. This result demonstrates that the ADN has to cost more to improve its power quality under an uncertain environment. However, declining speed of the violation rate is close to 0 when Γ is larger than 1.2, which means the ADN has to cost much more to reach a higher robust level when the current robust level is relatively high.
The robust optimization model proposed in this article is equivalent to the deterministic optimization model when Γ is equal to 0. The cost of the ADN is the least in Table 4 when no uncertainties are considered. However, it does not mean that the solution obtained by deterministic optimization is better than that by robust optimization. The voltage violation rate of deterministic optimization exceeds 90%, which results in the poor power quality caused by insufficient voltage support. The robust optimization model is equivalent to the completely robust optimization model when Γ is equal to 2 in which all uncertainty is considered. While short time voltage violation is allowed in the practical operation of distribution network, the result of completely robust optimization model is too conservative for considering every possible situation, resulting in its highest cost. However, the completely robust optimization model is applicable in the system with high reliability and quality requirements. Therefore, the ADN can select the appropriate robust level according to the practical operation requirements for power supplying.
Effect of DR Incentive
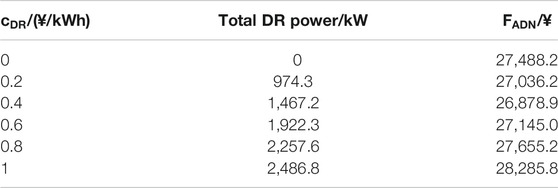
Table 5 shows the effect of DR under different DR incentive. With the increase of DR incentive, the total DR power is also increasing, which means that LAs are more willing to participate in the DR program with higher incentive. LAs can help the ADN reduce power supply cost by peak shifting and valley filling. When the
Conclusion
In this article, a distributed and robust optimal scheduling model of the ADN with LAs is proposed. The global optimal scheduling of the whole distribution system is realized by the autonomous energy management of the ADN and the LA. In the meanwhile, the influence of renewable DG’s uncertain output on the voltage security constraints is also considered in the optimal scheduling model of the ADN.
Numerical simulations on a modified IEEE 33-bus system have verified the effectiveness of the proposed method. The simulation results show that the proposed distributed optimization framework of ADN with LA performs well in convergence and reconciling the interest of the LA and the ADN compared to the traditional centralized DLC model and “source changing with load” model. Besides, the economy and the voltage violation rate of scheduling plans with different robust levels are compared quantitatively. The proposed robust optimization method allows the ADN to make a trade-off between the economy and voltage level, by choosing the schedules with different robust levels. Finally, the costs of the ADN under different DR incentive are also compared. The ADN can further reduce its operation cost by making appropriate DR incentive according to the response of LAs.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
JW contributed toward supervision, conceptualization, and writing—review and editing. QX contributed toward methodology, software, data curation, and writing—original draft. HS and KF contributed toward writing—review and editing.
Funding
This work was supported by the Science and Technology Project from State Grid Jiangsu Electric Power Co., Ltd. (J2020115).
Conflict of Interest
Author HS and KF were employed by State Grid Jiangsu Electric Power Co., Ltd. Marketing Service Center. The authors declare that this study received funding from Science and Technology Project of State Grid Jiangsu Electric Power Co., Ltd. (J2020115). The funder had the following involvement: reviewing and editing. All authors declare no other competing interests.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor declared a past co-authorship with the authors JW and KF.
Acknowledgments
The authors would like to thank the Science and Technology Project from State Grid Jiangsu Electric Power Co., Ltd. (J2020115).
References
Adrian, C. F. C., Alexis, G., Andrea, M., and Georges, K. (2018). Stochastic operation of home energy management systems including battery cycling. Appl. Energy 225, 1205–1218. doi:10.1016/j.apenergy.2018.04.130
Asensio, M., Pilar, M. D. Q., Munoz-Delgado, G., and Contreras, J. (2018a). Joint distribution network and renewable energy expansion planning considering demand response and energy storage part I: stochastic programming model. IEEE Trans. Smart Grid 9, 655–666. doi:10.1109/TSG.2016.2560339
Asensio, M., Pilar, M. D. Q., Munoz-Delgado, G., and Contreras, J. (2018b). Joint distribution network and renewable energy expansion planning considering demand response and energy storage part II: numerical Results. IEEE Trans. Smart Grid 9, 667–675. doi:10.1109/TSG.2016.2560341
Cobos, N. G., Arroyo, J. M., Alguacil, N., and Wang, J. (2018). Robust energy and reserve scheduling considering bulk energy storage units and wind uncertainty. IEEE Trans. Power Syst. 33, 5206–5216. doi:10.1109/TPWRS.2018.2792140
Delavari, A., and Kamwa, I. (2018). Sparse and resilient hierarchical direct load control for primary frequency response improvement and inter-area oscillations damping. IEEE Trans. Power Syst. 33, 5309–5318. doi:10.1109/TPWRS.2018.2795462
Ding, T., Li, C., Yang, Y., Jiang, J., Bie, Z., and Blaabjerg, F. (2017). A two-stage robust optimization for centralized-optimal dispatch of photovoltaic inverters in active distribution networks. IEEE Trans. Sustain. Energy 8, 744–754. doi:10.1109/TSTE.2016.2605926
Du, Y., Wang, Z., Liu, G., Chen, X., Yuan, H., Wei, Y., et al. (2018). A cooperative game approach for coordinating multi-microgrid operation within distribution systems. Appl. Energy 222, 383–395. doi:10.1016/j.apenergy.2018.03.086
Ehsan, A., and Yang, Q. (2019). State-of-the-art techniques for modelling of uncertainties in active distribution network planning: a review. Appl. Energy 239, 1509–1523. doi:10.1016/j.apenergy.2019.01.211
Fu, Y. Y., and Chiang, H. D. (2018). Toward optimal multi-period network reconfiguration for increasing the hosting capacity of distribution networks. IEEE Trans. Power Deliv. 33, 2294–2304. doi:10.1109/TPWRD.2018.2801332
Guo, K., Gao, C., Lin, G., Lu, S., and Feng, X. (2020). Optimization strategy of incentive based demand response for electricity retailer in spot market environment. Autom. Electr. Power Syst. 44, 28–35. [in Chinese, with English summary]. doi:10.7500/AEPS20190726002
Herre, L., Mathieu, J. L., and Soder, L. (2020). Impact of market timing on the profit of a risk-averse load aggregator. IEEE Trans. Power Syst. 35, 3970–3980. doi:10.1109/TPWRS.2020.2971866
Jiang, T., Li, Z., Jin, X., Chen, H., Li, X., and Mu, Y. (2018). Flexible operation of active distribution network using integrated smart buildings with heating, ventilation and air-conditioning systems. Appl. Energy 226, 181–196. doi:10.1016/j.apenergy.2018.05.091
Kong, X., Yong, C., Wang, C., Li, P., Yu, L., and Chen, Y. (2020). Multi-objective power supply capacity evaluation method for active distribution network in power market environment. Int. J. Electr. Power Energy Syst. 115, 1–11. doi:10.1016/j.ijepes.2019.105467
Liang, J., Lin, S., Liu, M., Song, Y., Fan, G., He, S., et al. (2019). Distributed robust optimal dispatch in active distribution networks. Power Syst. Technol. 43, 1336–1344. [in Chinese, with English summary]. doi:10.13335/j.1000-3673.pst.2018.1375
Liu, Y., Guo, L., and Wang, C. (2018). A robust operation-based scheduling optimization for smart distribution networks with multi-microgrids. Appl. Energy 228, 130–140. doi:10.1016/j.apenergy.2018.04.087
Meyer-Huebner, N., Suriyah, M., and Leibfried, T. (2019). Distributed optimal power flow in hybrid ac-dc grids. IEEE Trans. Power Syst. 34, 2937–2946. doi:10.1109/TPWRS.2019.2892240
Parizy, E. S., Bahrami, H. R., and Choi, S. (2019). A low complexity and secure demand response technique for peak load reduction. IEEE Trans. Smart Grid 10, 3259–3268. doi:10.1109/TSG.2018.2822729
Peng, C., Xie, P., Zhan, J., and Sun, H. (2014). Robust economic dispatch of microgrid using improved bacterial foraging algorithm. Power Syst. Technol. 38, 2392–2398. [in Chinese, with English summary]. doi:10.13335/j.1000-3673.pst.2014.09.012
Song, Y., Zheng, Y., Liu, T., Lei, S., and Hill, D. J. (2019). A new formulation of distribution network reconfiguration for reducing the voltage volatility induced by distributed generation. IEEE Trans. Power Syst. 35, 496–507. doi:10.1109/TPWRS.2020.3012367
Tomasson, E., and Soder, L. (2020). Coordinated optimal strategic demand reserve procurement in multi-area power systems. Appl. Energy 270, 1–12. doi:10.1016/j.apenergy.2020.114984
Wang, D., Guan, X., Wu, J., Li, P., Zan, P., and Xu, H. (2016). Integrated energy exchange scheduling for multimicrogrid system with electric vehicles. IEEE Trans. Smart Grid 7, 1762–1774. doi:10.1109/TSG.2015.2438852
Wang, F., Xiang, B., Li, K., Ge, X., and Dehghanian, P. (2020). Smart households’ aggregated capacity forecasting for load aggregators under incentive-based demand response programs. IEEE Trans. Ind. Appl. 56, 1086–1097. doi:10.1109/TIA.2020.2966426
Wang, J., Li, P., Fang, K., and Zhou, Y. (2018). Robust optimization for household load scheduling with uncertain parameters. Appl. Sci. Basel 8, 1–16. doi:10.3390/app8040575
Wang, J., Zhang, H., and Zhou, Y. (2017). Intelligent under frequency and under voltage load shedding method based on the active participation of smart appliances. IEEE Trans. Smart Grid 8, 353–361. doi:10.1109/TSG.2016.2582902
Wang, Z., Chen, B., Wang, J., and Kim, J. (2016). Decentralized energy management system for networked microgrids in grid-connected and islanded modes. IEEE Trans. Smart Grid 7, 1097–1105. doi:10.1109/TSG.2015.2427371
Yong, C., Kong, X., Chen, Y., Cui, K., Cui, K., and Wang, X. (2018). Multiobjective scheduling of an active distribution network based on coordinated optimization of source network load. Appl. Sci. Basel 8, 1–23. doi:10.3390/app8101888
Yu, M., and Hong, S. H. (2017). Incentive-based demand response considering hierarchical electricity market: a Stackelberg game approach. Appl. Energy 203, 267–279. doi:10.1016/j.apenergy.2017.06.010
Zhang, G., Jiang, C., and Wang, X. (2019). Comprehensive review on structure and operation of virtual power plant in electrical system. IET Gener. Transm. Distrib. 13, 145–156. doi:10.1049/iet-gtd.2018.5880
Zhang, Y., Ai, X., Fang, J., Wen, J., and He, H. (2019). Data-adaptive robust optimization method for the economic dispatch of active distribution networks. IEEE Trans. Smart Grid 10, 3791–3800. doi:10.1109/TSG.2018.2834952
Keywords: distributed generation, active distribution network, load aggregator, robust optimization, distributed optimization, demand response
Citation: Wang J, Xu Q, Su H and Fang K (2021) A Distributed and Robust Optimal Scheduling Model for an Active Distribution Network With Load Aggregators. Front. Energy Res. 9:646869. doi: 10.3389/fenrg.2021.646869
Received: 28 December 2020; Accepted: 16 February 2021;
Published: 26 April 2021.
Edited by:
Yue Zhou, Cardiff University, United KingdomReviewed by:
Yan Li, Pennsylvania State University (PSU), United StatesWei Zhou, Dalian, University of Technology, China
Copyright © 2021 Wang, Xu, Su and Fang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jidong Wang, amlkb25nd2FuZ0B0anUuZWR1LmNu
 Jidong Wang1*
Jidong Wang1* Qiuming Xu
Qiuming Xu