- 1College of Economics and Management, Shandong University of Science and Technology, Qingdao, China
- 2Business School, University of Shanghai for Science and Technology, Shanghai, China
- 3Library, Shandong University of Science and Technology, Qingdao, China
As the world faces great challenges from climate change, carbon reduction has become China’s basic national policy. However, as the main model for carbon reduction in China, the non-cooperative carbon reduction model (NCCRM) is a simple regulation mode, which is not beneficial for optimization of electricity generation capacity structure and cannot effectively motivate carbon reduction at the provincial level. Therefore, we propose an interprovincial cooperative carbon reduction model (CCRM) from the perspective of electricity generation, which provides a mechanism integrating two fundamental principles of efficiency and fairness. The CCRM consists of two parts: (1) an optimal model of carbon reduction with the object of minimizing the carbon emission of the cooperation union to determine the optimal annual electricity generation for each participating province and (2) a model that distributes the economic benefits of the cooperation among the provinces in the cooperation based on the Shapley value method. We applied the CCRM to the case of an interprovincial union of Shanghai, Sichuan, Shanxi, and Gansu in China. The results, based on the data from 2014 to 2017, show that cooperation can significantly reduce the carbon emission of the union by 425.78 × 108 kg, 11.06%; meanwhile, Shanghai, Sichuan, Shanxi, and Gansu can, respectively, get 2.79 × 108, 11.11 × 108, 4.07 × 108, and 3.19 × 108 CNY of extra benefits from carbon reduction. To test the impact of different parameter values on the results of the CCRM, a sensitivity analysis was conducted. Some policy recommendations are proposed to promote the implementation of the CCRM.
Introduction
The world is facing great challenges from climate change and environmental pollution. On November 30, 2015, at the United Nations Conference on Climate Change, President Xi Jinping promised to the world that “China pledges to peak CO2 emissions by around 2030,” “and by 2030, reduce CO2 per unit of GDP by 60–65% over the 2005 level” (Zeng et al., 2018). China is under great pressure of carbon reduction, which has forced China to develop a carbon reduction strategy. Carbon reduction has become China’s basic national policy, and guidelines for China’s carbon reducing policies have been issued in the 12th and 13th Five-Year Plan (FYP).
The special energy structure of China determines that optimizing the electricity generation structure is not only effective to carbon reduction but also critical to pollution abatement and energy security. Firstly, electricity power is one of the main forms of energy consumption. Secondly, the structure of electricity generation capacity in China is dominated by coal-fired power generation. Therefore, this paper attempts to resolve the problem of carbon reduction from the perspective of electricity generation so as to get a multi-win effect.
In China, the distributions of economic development and renewable energy resources in different provinces present significant differences. In general, the provinces which abound in renewable energy resources are less developed in economy. This situation means that the provinces with abundant renewable energy resources have great potential of carbon reduction. However, the current model of carbon reduction in China cannot exploit this potential. The current model of carbon reduction is as follows: the central government establishes the carbon reduction goals for the whole country and each province, and at the end of the performance period, which is the Five-Year Plan period, the central government examines the carbon reduction performance of each province. For example, the overall goal for CO2 emission per unit of GDP set by the Twelfth FYP is a 17% reduction over the 2010 level for the whole country. By province, for example, for Shanghai, Jiangsu, it is 19%; for Beijing, Hebei, 18%; for Sichuan, Fujian, 17.5%; for Shanxi, Jilin, 17%; for Guizhou, Gansu, 16%; for Hainan, Xinjiang, 11%; and for Qinghai, Tibet, 10%. If the carbon reduction goal is not achieved, the leaders of the province will lose promotion opportunities or even their jobs. The current non-cooperative carbon reduction model (NCCRM), under which the carbon reduction performance of each province is examined respectively, may result in huge waste of carbon reduction capability and potential. For example, these years, capacity of renewable energy power generation has made great development in north China, northwest China, and northeast China, but most provinces in these regions cannot consume the renewable energy power electricity entirely for the mismatch between economic development and renewable resources under the NCCRM; as a result, serious wind and solar curtailment has taken place in these regions.
To make full use of the capacity of renewable energy and exploit the potential of renewable energy resources so as to promote carbon reduction more effectively and efficiently, this paper proposes an interprovincial cooperative carbon reduction model (CCRM) for China from the perspective of electricity generation. Under the CCRM, the central government examines the performance of carbon reduction of the union as a whole instead of each province. The carbon reducing union in this model is composed of a few provinces. Considering the differences in structure of electricity generation capacity among provinces in a union, and based on meeting the electricity consumption for socioeconomic development of each province in the union, the carbon reducing union reallocates the quota of electricity generation to each member to minimize the carbon emission of the union from electricity generation so as to maximize the benefits of the union from carbon reducing. The benefits from cooperative carbon reduction are then allocated fairly and reasonably to each province according to the Shapley value method. Under the CCRM, renewable energy capacity will be utilized more efficiently and benefits from carbon reduction will be improved significantly.
The remainder of this paper is organized as follows: the related literatures are reviewed in Section 2. Section 3 constructs the interprovincial CCRM, which consists of two parts: (1) an optimization model that calculates the optimal quantities of electricity generation for each participating province and (2) a model that allocates the cooperation benefits based on the Shapley value method. Then, Section 4 presents the case study on a cooperative union composed of four provinces in China: Shanghai, Sichuan, Shanxi, and Gansu. To test the impact of parameter values on the calculation results of the CCRM, a sensitivity analysis was conducted in Section 5. The final section provides conclusions, policy recommendations, and directions for further study.
Literature Review
With the widespread acceptation that climate change is one of the most important global environmental issues, a great number of researchers have been attracted to solve this problem from the perspective of carbon reduction management and policy. Among them, the relationship between carbon emission or carbon-emission reduction and economic development, as well as the relationship between electricity production and carbon emission, is a widely concerned issue.
At first, the relationship between carbon emission or carbon-emission reduction and economic development is a fundamental concern by researchers and governments. Chen et al. (2007) studied the impact of China’s carbon mitigation strategies and corresponding impacts on the social welfare, GDP, investment, and consumption at the national level by applying three MARKAL family models. Zhang et al. (2016) compared the impact of carbon reduction policy on the development of transport sector through carbon tax scenario analyses. Iftikhar et al. (2018) analyzed energy and CO2 emission efficiency of major economies in terms of economic and distributive efficiency. Zou et al. (2020) through the establishment of a spatial Durbin model discussed the relationship between economic growth and CO2 emissions. Wu et al. (2021) by establishing the Cobb–Douglas production function and Kaya function studied carbon emissions and economic growth in China at the national level and regional level. These studies have shown that economic development is an important factor of carbon emissions; in turn, carbon reduction policies affect the development of the economy.
Secondly, given the strong relationship between electricity production and carbon emission, a great deal of researches on carbon reduction is carried out from the perspective of electricity generation. On the one hand, to identify critical industries and sectors for reduction efforts, many researchers carried out inventory analysis on carbon emission, verifying that the energy industry and energy-intensive industries, such as electric power industry and the iron and steel industry, are the main contributors to carbon emission (Munksgaard and Pedersen, 2001; Satterthwaite, 2008; Xi et al., 2011; Guo et al., 2012, 2018; Wang et al., 2013; Liu et al., 2015; Wu et al., 2016, 2020). On the other hand, to formulate effective carbon mitigation policy, a number of carbon reduction studies related to electricity generation have been conducted at multiple levels. At the industry level, Cui et al. (2018) explored the comprehensive policy implications of carbon reduction for the power industry in China from both macro and micro perspectives. Li et al. (2018) used the dynamic computable general equilibrium model to quantitatively analyze the impact of carbon-emission trading on the power industry. At the regional level, Xie et al. (2019) established a risk measurement model considering carbon-capture technology and carbon-emission reduction targets to study the power system management in the Xinjiang Autonomous Region. Chang et al. (2017) took Shanghai as an example to study the path of clean production of power enterprises under emission restriction. Li et al. (2020) used provincial data to study the carbon-emission reduction potential of China’s coal-fired power plants. At the national level, Liu et al. (2014) answered the question of whether China can realize its carbon reduction target from the perspective of China’s thermal power development. At the global level, Cabal et al. (2017) analyzed the application of nuclear fusion technology, which contributes to carbon reduction, in global power systems. These studies show that carbon-emission reduction is closely related to electricity production, and the perspective of electricity generation is a crucial one for carbon-emission reduction research.
Furthermore, both for the world and China, the most important problem for policymakers is to initiate programs that not only will mitigate the global buildup of GHG but also will facilitate cooperation and be perceived as fair (Rose and Tietenberg, 1993). That is to say, an effective policy should embody the two fundamental principles: efficiency and fairness, which are reflected in the UNFCCC principle of “common but differentiated responsibilities.” Based on the fairness principle, nations for the world and provinces for China have the equal entitlements of carbon emission. Following the principal of fairness, several organizations (e.g., the Intergovernmental Panel on Climate Change (IPCC), United Nations Development Program, and Organization for Economic Cooperation and Development) and scholars proposed global carbon-emission burden allocation programs (Intergovernmental Panel on Climate Change (IPCC), 2007; United Nations Development Programme (UNDP), 2007; Organisation for Economic Cooperation and Development (OECD), 2008; Ding et al., 2010), and many researchers put forward a number of provincial allocation proposals on carbon-emission reduction target for China (Yu et al., 2014; Zhang et al., 2014; Hao et al., 2015; Miao et al., 2016; Dong et al., 2018; Wang et al., 2018; Pan et al., 2020; Wen and Wang, 2020). Based on the efficiency principle, a few policy instruments or management programs are explored and designed, such as tradable carbon emission permits (Chang and Wang, 2010; Zhou et al., 2013; Zhao et al., 2018; Tan et al., 2019; Zheng et al., 2020; Foramitti et al., 2021), carbon tax (Mori, 2012; Ouchida and Goto, 2014; Zhao et al., 2018), policies to promote household carbon reduction (Bore et al., 2018), and policies facilitating inter-firm collaborations on carbon reduction (Dong et al., 2014; Zhang and Wang, 2014). Although tradable carbon emission permits have gotten successful implementation effects in different countries and regions, China’s carbon-emission trading systems are still at the stage of pilot experiments; Raufer and Li (2009) argued that the market-based emission trading schemes may not be suitable for China.
Considering the close relationship between carbon reduction and economic development, the crucial role of electricity generation in carbon reduction, and the importance of effective policy on carbon reduction practice, all these researches are necessary and significant. However, previous studies paid little attention on the macro cooperative carbon reduction mechanism from the perspective of power generation. Although very few studies on carbon reduction embodied the cooperation concept (Qin et al., 2020), research on cooperative carbon reduction from the macro management perspective is in its infancy and needs more efforts. In reality, different provinces in China differ greatly in resource endowments (including renewable energy-resource endowments), industrial structures, and economic development levels; effective policy instruments promoting interprovincial cooperation on carbon reduction have great potentials of economic performance. Furthermore, a cooperative carbon reduction mechanism which embodies efficiency and fairness principles is crucial to global optimization of electricity generation capacity structure and potential release of carbon reduction.
This study extends the current literature in the following aspects: (1) This paper constructs an interprovincial CCRM from the perspective of electricity utilization, which can minimize the carbon emission of the cooperation union and improve the carbon-reducing benefits of each member. Differing from the market-based mechanism, this paper attempts to construct an interprovincial CCRM based on the administration coordination mechanism. (2) The CCRM embodies well the principles of efficiency and fairness. An optimization model that calculates the optimal quantities of electricity generation for each participating province to meet the joint carbon reduction goal is constructed based on the optimization theory, which embodies the principle of efficiency, and a model that distributes the economic benefits of carbon reduction among the members is constructed based on the Shapley value method, which embodies the principle of fairness.
Materials and Methods
The mechanism of the interprovincial cooperative carbon reduction includes two aspects: (1) The mechanism of optimizing the benefits of the whole union. If the cooperation union cannot generate additional benefits, cooperation makes no sense. Through optimization of the electricity generation of each participating province, the interprovincial CCRM minimizes the carbon emission of the whole union to maximize the cooperative carbon reduction benefits. (2) Rational allocation mechanism of cooperation benefits. Each participating province has the motivation to get as much benefits from the cooperation as possible, so how to allocate cooperative benefits among the provinces scientifically and reasonably is the key to the interprovincial cooperative carbon reduction. Applying the Shapley value method, which distributes cooperative benefits according to the contribution of each member, the interprovincial CCRM fairly allocates the cooperative carbon reduction benefits. As a result, CCRM consists of an optimal model of carbon reduction to determine the optimal annual electricity generation for each province in the cooperation union and a model to allocate the benefits of cooperation to each province in the union.
Table 1 summarizes the variables and parameters and their definitions that will be used in the CCRM.
The Optimal Model of Carbon Reduction
This paper defines the amount of CO2 emitted by producing a unit of electricity power by an electricity-generation method as the carbon intensity of this electricity-generation method, and the average amount of CO2 emitted by producing a unit of electricity power in a province as the integrated carbon intensity of electricity generation in this province. Therefore, the annual CO2 emission by electricity generation in a province is not only determined by the annual electricity generation but also determined by the integrated carbon intensity. So we built the function of annual CO2 emission by electricity generation in a province as follows:
Here E_i is the annual electricity generation in province i, and b_i is the integrated carbon intensity of electricity production in province i. b_i is determined by the capacity structure of electricity production in province i and the carbon intensity of each electricity-generation method, which can be described as:
Here k = 1 denotes the method of thermal power generation, k = 2 denotes the method of hydroelectric generation, k = 3 denotes the method of solar power generation, k = 4 denotes the method of wind power generation, and k = 5 denotes method of nuclear power generation. aik is the capacity proportion of electricity generation method k in province i and satisfies the following two constraints:
Consequently, the function of the quantity of CO2 emitted by electricity generation in the whole union can be built as follows:
Each province has its own electricity generation capacity range. When all electricity generation facilities in the province work at their full capacity, the maximum quantity of electricity generation in this province can be achieved. The annual electricity generation upper limit is represented as ξui∗Mi. On the other hand, the electricity generation facilities will always produce at least some electricity power. This electricity generation lower limit is represented as . Therefore, the annual electricity generation range for a province is as follows:
The sum of annual CO2 emission by electricity generation of all the provinces in the union should be less than or equal to the target set by the central government. Therefore, we obtain the constraints:
To meet the demands of socioeconomic development, the total annual electricity generation in the union should not be less than the sum of the annual quota of the electricity generation of all the provinces in the union:
Based on the above analysis, we establish the optimal cooperative carbon-reducing model for the whole union, which aimed to minimize the carbon emission by optimizing the amount of electricity generation of each province in the union. For any province i and any electricity generation method k, i ∈ I = {1, 2, …, n}, k ∈ K = {1, 2, 3, 4, 5}, and the optimal cooperative carbon-reducing model in a given union can be written as follows:
s.t.
Cooperative Carbon-Reducing Benefit Allocation Model
In the optimal model, the cooperative carbon-reducing union meets the national carbon-reducing target through cooperative efforts and minimizes the carbon emission by electricity generation, which will create carbon-reducing benefit by selling the available emission right. Each province tries to get more benefits from the cooperation. The allocation of these benefits greatly affects implementation of CCRM. The Shapley value method distributes cooperative benefits according to scientific calculation of the contribution of each member in a cooperation union. Since the Shapley value method has been proved to be highly effective in distributing cooperative benefits (Lozano et al., 2013; Wu et al., 2017; Zeng et al., 2018), this paper apply this method to allocate interprovincial cooperative carbon reduction benefits.
Set N = {1,2,⋯,n} as the collection of the n provinces in mainland China. For any subset of N, S (any combination of m provinces), if there exists a real-valued function μ(S) that satisfies μ(ϕ) = 0, μ(Si⋃Sj)≥μ(Si)+μ(Sj), where Si⋂Sj = ϕ, then [N,μ] is the cooperation strategy for the n provinces, μ is the characteristic function for the strategy, and μ(S) is the benefit for cooperation union S. The Shapley value, denoted by f = (f1,f2,⋯fn), represents the allocation strategy for interprovincial cooperative game benefit that can be a weighted distribution based on the characteristic function μ, which is referred to as
where |S| is the number of elements (cooperating provinces) in subset S, H(|S|) is the weighed factor, and μ(S\{i}) is the cooperation benefit that does not include province i. In this way, the cooperation benefit is allocated to each participant according to each participant’s contribution. The participant who contributes most is rewarded most. Each participant gains economic benefit from the cooperation. As a result, the economic benefit could serve as an incentive to encourage cooperation among participating provinces.
Results and Discussion
Based on the complementarity in economic development, energy-resource endowments, and capacity structure of power generation, this paper selects Shanghai, Sichuan, Shanxi, and Gansu as case study samples for cooperative carbon-reducing model.
Shanghai is one of the most advanced provincial regions in economic development, and its pillar industries include information industry, financial industry, commercial circulation industry, automobile industry, and so on. However, Shanghai is scarce in natural resources, and its power generation capacity is dominated by thermal power generation.
Sichuan is a major economic province, and its pillar industries mainly include metallurgic industry, chemical engineering industry, and hydropower industry. Sichuan is rich in natural resources especially in hydroelectric resource, and its main power generation capacity is hydroelectric generation.
Shanxi is an economically less-developed province, and its pillar industries are mainly heavy industries such as coal industry and metallurgic industry. As one of the most important coal bases in China, Shanxi provides a large proportion of thermal power to the whole country.
Gansu is an economic backward province, and its pillar industry includes petrochemical industry, electricity industry, and so on. Gansu is rich in energy resources and has a variety of energy resources. As a result, Gansu has a diversified capacity structure of power generation.
The four provinces are highly complementary in energy-resource endowments, capacity structure of power generation, and industrial structures, which provide great space and potential for cooperative carbon reduction. Here we denote Shanghai as SH, Sichuan as SC, Shanxi as SX, and Gansu as GS. To demonstrate CCRM, we take the four provinces as a cooperative carbon union for the case study.
SH–SC–SX–GS Optimal Model of Carbon Reduction
To determine the capacity structure of electricity production in SH, SC, SX, and GS in 2017, we first obtained the data of installed capacity of all kinds of electricity-generation method in these provinces from China electricity power statistical yearbook 2018.
Then, we calculated the annual available time for each kind of electricity-generation method in each province (Table 2) according to the following rules and assumptions:
(1) For each kind of electricity-generation method, for each year from 2014 to 2017, for each province of Chinese mainland, based on data from China electricity power statistical yearbook 2015 to 2018, calculate the actual annual mean utilization time of all the electricity-generation facilities of this method;
(2) For thermal power generation, calculate the four maximums of the actual annual mean utilization time from the 31 provinces and then find the maximum from the four values. The maximum is assumed as the annual available time of thermal power generation for all provinces;
(3) For wind power generation in each province, choose the maximum from the four actual annual mean utilization time as the annual available time for this province;
(4) For hydroelectric generation and solar power generation, take the same rule for wind power generation.
Finally, according to the data of installed capacity and annual available time of each kind of electricity-generation method, we get the capacity level and capacity proportion of each method in the sample provinces, shown in Table 3.
According to data from the National Energy Administration, we obtained the standard coal consumption rate of power supply in 2017 in China so that we calculated the carbon intensity of thermal power generation method as 770.44 gCO2/kwh. We denote the carbon intensity of hydroelectric generation, solar power generation, and wind power generation as 0.
With these data, we calculated the integrated carbon intensity of electricity production in the four provinces and then constructed the function of annual CO2 emission by electricity generation in SH, SC, SX, and GS, as Table 4 shows.
According to the carbon-reducing target set by the central government and the data of GDP and electricity generation, we calculated the annual quotas of the maximum CO2 emission by generation and quantity of electricity generation for SH, SC, SX, and GS.
To determine the lower limit and upper limit of the electricity generation of the four provinces (Table 5), we make assumptions about the value of ξli and ξui:
(1) The upper limit of the electricity generation of each province is the maximum capacity of electricity generation, so the value of ξui is assumed as 1.
(2) Each province will always generate some electric power by itself to meet the needs of science and economy, so the value of ξui is assumed as 0.3.
Based on the above analysis, we established the optimal carbon-reducing model for SH–SC–SX–GS cooperative carbon-reducing union as follows:
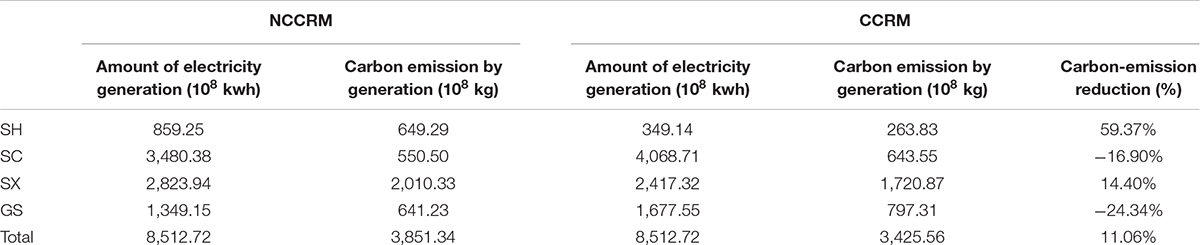
We applied Lingo 16.0 to solve the model and obtained the optimal amount of electricity generation and carbon emission by generation for each province in the union in 2017. On this basis, this paper applied CNY 49.70/tCO2, the carbon-emission trading price of Beijing pilot in China’s average annual carbon trading network in 2017, and calculated the cooperative carbon-reducing benefit. The amount of electricity generation and the carbon-reducing benefits in these provinces under NCCRM and CCRM are shown in Table 6.
Contrasting the carbon emission by generation under two models, we found that the carbon emission of the whole union would decrease greatly by 425.78 × 108 kg, 11.06%, while the total amount of electricity generation was the same. Furthermore, SC and GS, the two provinces with high proportion of renewable energy generation capacity, reached their upper limit of electricity generation, which meant that the renewable energy generation capacity could be fully utilized and almost no renewable energy curtailment would take place in the two provinces. However, SC and GS would emit more CO2 from the optimal model. So if there is no further allocation of the benefits, SC and GS would not take part in the cooperation and the union cannot be formed.
SH–SC–SX–GS Cooperative Carbon-Reducing Benefit Allocation Model
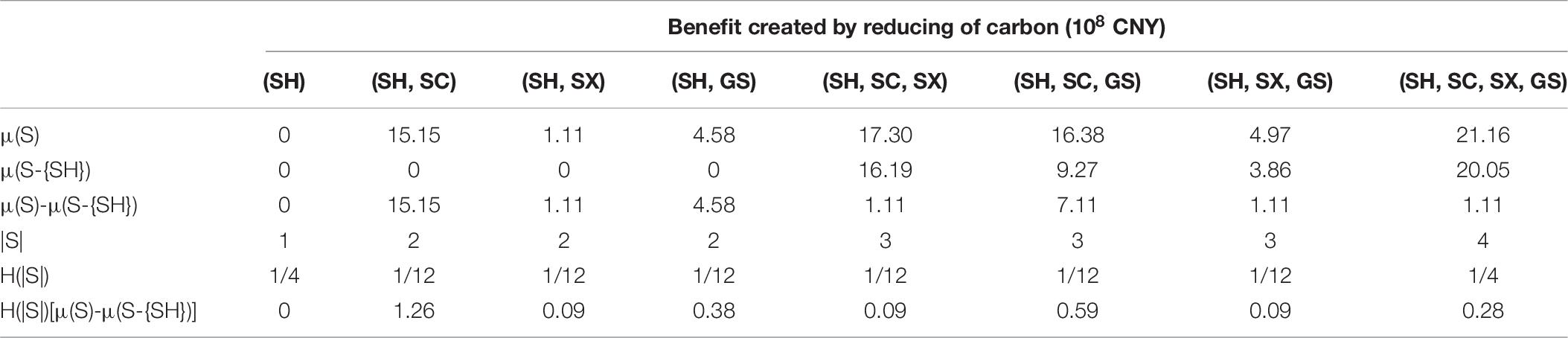
Because the cooperative carbon-reducing union consists of four provinces, there are 12 possible combinations for the cooperation. To obtain Shanghai’s reward from the carbon-reducing cooperation, we firstly calculated the values of μ(S) for all the combinations that involved Shanghai (Table 7) and then calculated the corresponding cooperation benefits if Shanghai does not participate (μ(S\{SH}). In the final step, based on the benefit allocation strategy in Equations (15), (16), we obtained Shanghai’s reward from the cooperation benefits:
That is, Shanghai would get CNY 2.79 × 108 by participating in the CCRM. In the same way, we obtained the benefit allocation for Sichuan, Shanxi, and Gansu: CNY 11.11 × 108, CNY 4.07 × 108, and CNY 3.19 × 108, respectively.
Table 8 summarizes the main results of allocation of benefits among the four provinces in 2014 based on their carbon-reducing cooperation. At first, it is clear that both the union and each participant province would get extra benefits from cooperative carbon reduction under the CCRM. The union would get 2.12 billion CNY cooperation benefits in total, and in the end, SH, SC, SX, and GS would get 0.28, 1.11, 0.41, and 0.32 billion CNY cooperation benefits, respectively, based on the Shapley value method under the CCRM. Secondly, Table 8 shows the money transferred among the four provinces in 2017 according to the actual carbon-reducing benefit before allocation and the Shapley value. SH would need to pay CNY 16.37 × 108, and SX would need to pay CNY 10.31 × 108 to SC and GS, respectively; meanwhile, SC and GS would get CNY 15.73 × 108 and CNY 10.95 × 108 from SH and SX, respectively.
From a perspective of implementation, the differences in capacity structure of electricity generation among the four provinces allow this cooperation. SC and GS have a much higher proportion of renewable energy generation capacity than SH and SX, which makes it possible for the interprovincial union to reduce the carbon emission greatly from electricity generation while SC and GS generate more electricity power and SH and SX generate less than that under the NCCRM. Given the extra benefits from carbon trading, the four provinces are willing to take part in cooperative carbon-reducing union.
In fact, the essence of the cooperative carbon reduction is that the conventional thermal power generation transfers the market to the renewable energy generation through administration coordination, so as to get carbon-reducing benefits. Since the extra benefits of carbon reduction come from the joint efforts of the conventional thermal power generation and the renewable energy generation, these benefits should be allocated to both kinds of power generation plant; that is, these benefits should be used to support the phasing out of backward production capacity in conventional thermal power generation and the running and development of renewable energy generation. Through reasonable allocation of benefits at provincial level and plant level, the CCRM provides an incentive way for the government to optimize the capacity structure of electricity generation, which, in turn, will promote carbon reduction fundamentally in the long run.
Besides carbon reduction, the CCRM can bring additional good effects. Under the CCRM, the provinces with high proportion of renewable energy generation capacity would generate more electricity power, and vice versa. Thus, the CCRM can help to solve the current serious solar and wind energy curtailment in the three north regions and hydro-energy curtailment in the southwest region in China. In addition, the implementation of the CCRM will help the province with high proportion of thermal power generation capacity to alleviate air pollution, such as SX. According to the report published by the Ministry of Ecology and Environment of China, SX accounted for five of 20 rated among the dirtiest cities in China. Less thermal power generation and optimized power generation structure will improve the air quality in SX.
Sensitivity Analysis
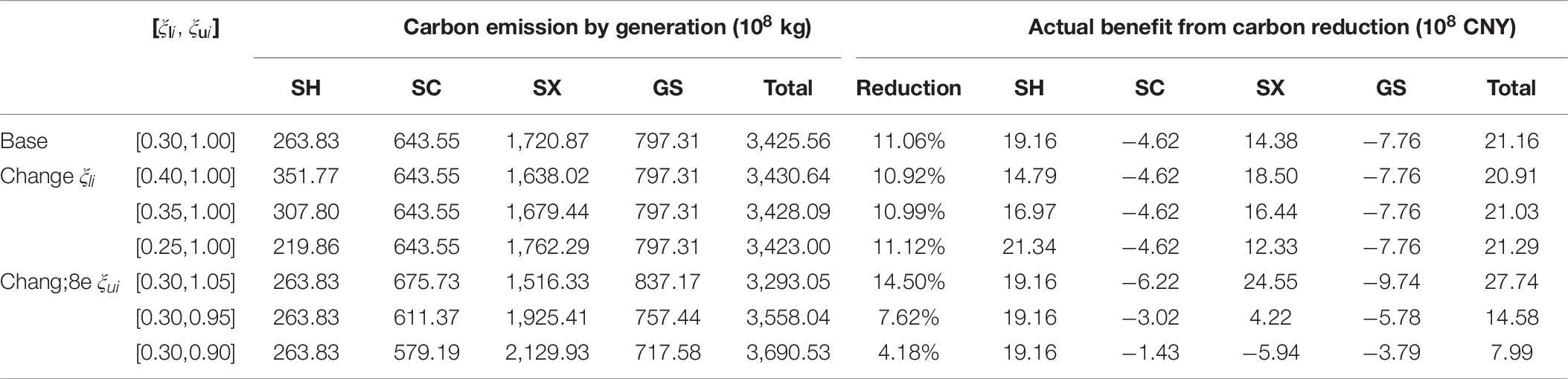
The parameters ξli and ξui in formulas (20)–(23) were set as 0.30 and 1 according to China’s situation. ξli and ξui denote the lower and upper bound coefficients of electricity production for province i. To study the impact of different values of these parameters on the CCRM calculation results, a sensitivity analysis was carried out for the SH–SC–SX–GS union in 2017. Table 9 presents the different calculation results (carbon emission by generation and actual benefit from carbon reduction under the CCRM) in each sample province and the whole union.
ξli, being the lower bound coefficient of electricity production for province i, determines the potential for province i to transfer electricity generation quota out to other provinces. The smaller ξli is, the more potential province i has to transfer electricity generation quota out to other provinces; more electricity might be generated by low-carbon energy, and greater cooperation carbon reduction benefit could then be generated. Therefore, when ξli was reduced from 0.30 to 0.25, the total CO2 emission by generation decreased slightly from 342.556 to 342.300 million tons, the total carbon reduction increased from 11.06% a bit to 11.12% with contrast to the NCCRM, and the total benefit from carbon reduction increased from 2.116 to 2.129 billion CNY. By comparison, when ξli increased from 0.30 to 0.35 and 0.4, which meant less electricity generation could transfer SH out, the total CO2 emission by generation improved slightly from 342.556 to 342.809 and 343.064 million tons, the total carbon reduction decreased from 11.06% to 10.99% and 10.92%, and the total benefit from carbon reduction also went down from 2.116 to 2.103 and 2.091 billion CNY. Generally speaking, the CCRM is not sensitive to changes in ξli.
ξui, as a parameter to calculate the upper limit of electricity generation in province i, decides the potential for province i to accept electricity generation quota from other provinces. The bigger ξui is, the more potential province i has to accept electricity generation quota from other provinces, the provinces with low integrated carbon intensity of electricity production could generate more electricity, and greater cooperation benefit would be generated. As a result, when ξui rose from 1 to 1.05, the total CO2 emission by generation decreased from 342.556 to 329.305 million tons, the total carbon reduction increased from 11.06% to 14.50%, and the total benefit from carbon reduction increased from 2.116 to 2.774 billion CNY. By contrast, when ξui decreased from 1 to 0.95 and 0.9, which represented tightening the constraint in formulas (20)–(23) of the optimization model and less electricity generation quota transferring, the total CO2 emission by generation improved moderately from 342.556 to 355.804 and 369.053 million tons, the total carbon reduction decreased from 11.06% to 7.62% and 4.18% correspondingly, and the total benefit from carbon reduction also went down temperately from 2.116 to 1.458 and 0.799 billion CNY. To sum up, for SH–SC–SX–GS union, the calculation results of CCRM are moderately sensitive to changes in λui.
Conclusions and Policy Recommendations
Optimizing the electricity generation structure through improving the proportion of renewable energy can get a multi-win effect of carbon reduction, pollution abatement, and improving energy security. In view of the widespread interprovincial differences in China’s renewable energy-resource endowment, this paper proposed an interprovincial CCRM, a mechanism embodying both principles of efficiency and fairness, so as to improve the current carbon reduction mode. We applied the CCRM to the case study of Shanghai–Sichuan–Shanxi–Gansu union. Results showed that the total carbon emission of the whole union would decrease greatly and every participated province would get substantial extra benefits from cooperative carbon reduction. Furthermore, the implementation of CCRM provides not only an incentive way for the regional government to achieve the carbon reduction goal and an effective solution to solve the current serious renewable energy curtailment in China in the short time, but also a feasible path to realize long-term carbon reduction strategy for the central government.
As the differences in renewable energy-resource endowment and the consequent differences in cost of renewable energy power are not only universal between provinces in China but also universal between different scales of administrative regions such as different counties, different cities, and even different countries, the CCRM proposed in this paper can be widely applied to cooperative carbon reduction in these situations. As a result, the CCRM provides a cooperative carbon reduction mechanism integrating two fundamental principles of efficiency and fairness for both China and other countries.
To promote the implementation of interprovincial cooperative carbon reduction in China, it is necessary to propose the following policy recommendations:
Firstly, the central government should allow and encourage cooperative carbon reduction among provinces. Although the central government and the local governments have realized that the current carbon reduction policy and management system cannot exploit the carbon reduction potential in some provinces, they have not realize the importance of the CCRM as they pay more attention to the fairness of carbon reduction responsibility among different provinces. The CCRM can not only help the provinces get carbon reduction benefits as much as possible by optimizing the electricity generation structure in the short term but also facilitate the implementation of long-term carbon reduction strategies in China by optimizing the capacity structure of electricity generation in each province. Therefore, the central government should develop policies and measures to promote the implementation of the CCRM.
Secondly, to effectively apply the CCRM, there should be an authority or a department of the central government to be responsible for the administration issues of cooperative carbon reduction such as determining the members of the cooperation union, coordinating the allocation of cooperation benefits, evaluating the performance of the union, and so on. These administrative issues require organizational support.
Thirdly, both the provinces with high proportion of thermal power generation capacity, such as Shanxi and Shanghai, and the provinces with high proportion of renewable energy generation capacity, such as Sichuan and Gansu, should be proactive in finding cooperation partners. The CCRM is a win–win mode for both kinds of province as both of them will get extra carbon reduction benefits. For provinces with high proportion of thermal power generation capacity, the extra benefits from cooperative carbon reduction should be mainly used to support the phasing out of backward thermal power generation capacity so as to optimize the capacity structure of electricity generation and be helpful to long-term carbon reduction. For the provinces with high proportion of renewable energy generation capacity, these benefits should be mainly used to support the development of renewable energy so as to exploit their resource advantages; in addition, it is because there exist large funding gaps in renewable energy subsidies in China.
Fourthly, this paper applied the contribution-based Shapley value method to allocate the cooperation benefits, which provides a reference for determining the practical benefit distribution principles or compensation standards. In addition, this paper is based on complementarity in economic development, energy-resource endowments, and capacity structure of power generation to select the research samples, which ensures enough cooperation space potentials and provides rules and principals for determining the members of the cooperation union. In practical application, the situation may be more complicated, and more factors should be taken into account, such as technology of electricity-generation facilities for benefit distribution, the electric grid structure for determining the union members, and so on.
Finally, it is worth noting that this paper only considered the benefits from carbon-emission permit trading under CCRM. In fact, interprovincial cooperative carbon reduction can create much more benefits from reducing air pollution and the subsequent health benefits by generation with low-carbon and cleaner energy. If these benefits are calculated in the CCRM, the results will be much more incentive. Future research could extend this analysis to include these benefits.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
LZe performed conceptualization, methodology, drafting, and writing. WD performed the review and editing. LZh performed the conceptualization and supervision. ZS performed review. All authors contributed to the article and approved the submitted version.
Funding
This research was sponsored by the National Natural Science Foundation of China (Grant Nos. 71804097, 71704140), China Postdoctoral Science Foundation (Grant No. 2016M601604), Chinese Ministry of Education Humanities and Social Sciences Foundation for Young Scholars (Grant No. 17YJCZH012), and Shandong Province Social Science Planning Research Projects (Grant No. 19CGLJ22).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
CCRM, cooperative carbon reducing model; CNY, China Yuan; CO2, carbon dioxide; FYP, five-year plan; GS, Gansu; KWh, kilowatt-hour; MCCRB, model of collective cooperation and reallocation of benefits; MCRS, minimum-cost-remaining savings; NCCRM, non-cooperative carbon reducing model; SC, Sichuan; SH, Shanghai; SX, Shanxi.
References
Bore, S., Marta, B., Carlo, A., Andersson, C., Herrmann, A., Amelung, D., et al. (2018). Household preferences to reduce their greenhouse gas footprint: a comparative study from four european cities. Sustainability 10:4044. doi: 10.3390/su10114044
Cabal, H., Lechon, Y., Bustreo, C., Gracceva, F., Biberacher, M., Ward, D., et al. (2017). Fusion power in a future low carbon global electricity system. Energy Strategy Rev. 15, 1–8. doi: 10.1016/j.esr.2016.11.002
Chang, Y. C., and Wang, N. (2010). Environmental regulations and emissions trading in China. Energy Policy 38, 3356–3364. doi: 10.1016/j.enpol.2010.02.006
Chang, Z., Wu, H. X., Pan, K. X., Zhu, H., and Chen, J. (2017). Clean production pathways for regional power-generation system under emission constraints: a case study of Shanghai. China. J. Clean. Prod. 143, 989–1000. doi: 10.1016/j.jclepro.2016.12.021
Chen, W., Wu, Z., He, J., Gao, P., and Xu, S. (2007). Carbon emission control strategies for China: a comparative study with partial and general equilibrium versions of the China MARKAL model. Energy 32, 59–72. doi: 10.1016/j.energy.2006.01.018
Cui, H., Zhao, T., and Wu, R. R. (2018). CO2 emissions from China’s power industry: policy implications from both macro and micro perspectives. J. Clean. Prod. 200, 746–755. doi: 10.1016/j.jclepro.2018.07.330
Ding, Z. L., Duan, X. N., Ge, Q. S., and Zhang, Z. Q. (2010). On the major proposals for carbon emission reduction and some related issues. Sci. China Earth Sci. 53, 159–172. doi: 10.1007/s11430-010-0012-4
Dong, F., Long, R. Y., Yu, B. L., Wang, Y., Dai, Y., Yang, Q., et al. (2018). How can China allocate CO 2 reduction targets at the provincial level considering both equity and efficiency? Evidence from its Copenhagen Accord pledge. Resour. Conserv. Recycl. 130, 31–43. doi: 10.1016/j.resconrec.2017.11.011
Dong, H., Ohnishi, S., Fujita, T., Geng, Y., Fujii, M., and Dong, L. (2014). Achieving carbon emission reduction through industrial & urban symbiosis: a case of Kawasaki. Energy 64, 277–286. doi: 10.1016/j.energy.2013.11.005
Foramitti, J., Ivan, S., and van den Bergh, J. C. J. M. (2021). Emission tax vs. permit trading under bounded rationality and dynamic markets. Energy Policy 148(Pt B):112009. doi: 10.1016/j.enpol.2020.112009
Guo, J., Zhang, Z., and Meng, L. (2012). China’s provincial CO2 emissions embodied in international and interprovincial trade. Energy Policy 42, 486–497. doi: 10.1016/j.enpol.2011.12.015
Guo, P., Qi, X., Zhou, X., and Wei, L. (2018). Total-factor energy efficiency of coal consumption: an empirical analysis of China’s energy intensive industries. J. Clean. Prod. 172, 2618–2624. doi: 10.1016/j.jclepro.2017.11.149
Hao, Y., Liao, H., and Wei, Y. M. (2015). Is China’s carbon reduction target allocation reasonable? An analysis based on carbon intensity convergence. Appl. Energy 142, 229–239. doi: 10.1016/j.apenergy.2014.12.056
Iftikhar, Y., Wang, Z., Zhang, B., and Wang, B. (2018). Energy and CO2 emissions efficiency of major economies: a network DEA approach. Energy 147, 197–207. doi: 10.1016/j.energy.2018.01.012
Intergovernmental Panel on Climate Change (IPCC) (2007). Climate Change 2007: The Physical Science Basis. New York, NY: Cambridge university press.
Li, J. J., Zhang, Y. L., Tian, Y. J., Cheng, W., Yang, J., Xu, D., et al. (2020). Reduction of carbon emissions from China’s coal-fired power industry: insights from the province-level data. J. Clean. Prod. 242:118518. doi: 10.1016/j.jclepro.2019.118518
Li, W., Zhang, Y. W., and Lu, C. (2018). The impact on electric power industry under the implementation of national carbon trading market in China: a dynamic CGE analysis. J. Clean. Prod. 200, 511–523. doi: 10.1016/j.jclepro.2018.07.325
Liu, H., Liu, W., Fan, X., and Liu, Z. (2015). Carbon emissions embodied in value added chains in China. J. Clean. Prod. 103, 362–370. doi: 10.1016/j.jclepro.2014.09.077
Liu, L., Zong, H., Zhao, E., Chen, C., and Wang, J. (2014). Can China realize its carbon emission reduction goal in 2020: from the perspective of thermal power development. Appl. Energy 124, 199–212. doi: 10.1016/j.apenergy.2014.03.001
Lozano, S., Moreno, P., Adenso-Díaz, B., and Algaba, E. (2013). Cooperative game theory approach to allocating benefits of horizontal cooperation. Eur. J. Oper. Res. 229, 444–452. doi: 10.1016/j.ejor.2013.02.034
Miao, Z., Geng, Y., and Sheng, J. (2016). Efficient allocation of CO2 emissions in China: a zero sum gains data envelopment model. J. Clean. Prod. 112, 4144–4150. doi: 10.1016/j.jclepro.2015.07.035
Mori, K. (2012). Modeling the impact of a carbon tax: a trial analysis for Washington State. Energy Policy 48, 627–639. doi: 10.1016/j.enpol.2012.05.067
Munksgaard, J., and Pedersen, K. A. (2001). CO2 accounts for open economies: producer or consumer responsibility? Energy Policy 29, 327–334. doi: 10.1016/s0301-4215(00)00120-8
Organisation for Economic Cooperation and Development (OECD) (2008). Environmental Outlook to 2030. Paris: OECD Publishing.
Ouchida, Y., and Goto, D. (2014). Do emission subsidies reduce emission? In the context of environmental R&D organization. Econ. Model. 36, 511–516. doi: 10.1016/j.econmod.2013.10.009
Pan, X. X., Liu, H., Huan, J. J., Sui, Y., and Homg, H. (2020). Allocation model of carbon emission permits for the electric power industry with a combination subjective and objective weighting approach. Energies 13:706. doi: 10.3390/en13030706
Qin, Q., Liu, Y., and Huang, J. P. (2020). A. cooperative game analysis for the allocation of carbon emissions reduction responsibility in China’s power industry. Energy Econo. 92:104960. doi: 10.1016/j.eneco.2020.104960
Raufer, R., and Li, S. (2009). Emissions trading in China: a conceptual ‘leapfrog’ approach? Energy 34, 904–912. doi: 10.1016/j.energy.2009.03.011x
Rose, A., and Tietenberg, T. (1993). An international system of tradable CO2 entitlements: implications for economic development. J. Environ. Dev. 2, 1–36. doi: 10.1177/107049659300200102
Satterthwaite, D. (2008). Cities’ contribution to global warming: notes on the allocation of greenhouse gas emissions. Environ. Urban. 20, 539–549. doi: 10.1177/0956247808096127
Tan, M., Chen, Y., Su, Y. X., Li, X. H., and Li, H. (2019). Integrated optimization model for industrial self-generation and load scheduling with tradable carbon emission permits. J. Clean. Prod. 210, 1289–1300. doi: 10.1016/j.jclepro.2018.11.005
United Nations Development Programme (UNDP) (2007). Human Development Report 2007/2008—Fighting Climate Change: Human Solidarity in a Divided World. New York, NY: Palgrave Macmillan.
Wang, K., Zhang, X., Wei, Y. M., and Yu, S. (2013). Regional allocation of CO2 emissions allowance over provinces in China by 2020. Energy Policy 54, 214–229. doi: 10.1016/j.enpol.2012.11.030
Wang, X. C., Tang, X., Zhang, B. S., McLellan, B. C., and Lv, Y. (2018). Provincial carbon emissions reduction allocation plan in China based on consumption perspective. Sustainability 10:1342. doi: 10.3390/su10051342
Wen, W., and Wang, Q. (2020). Re-examining the realization of provincial carbon dioxide emission intensity reduction targets in China from a consumption-based accounting. J. Clean. Prod. 244:118488. doi: 10.1016/j.jclepro.2019.118488
Wu, D., Geng, Y., and Pan, H. Y. (2021). Whether natural gas consumption bring double dividends of economic growth and carbon dioxide emissions reduction in China? Renew. Sustain. Energy Rev. 137:110635. doi: 10.1016/j.rser.2020.110635
Wu, F., Huang, N. Y., Zhang, F., Niu, L., and Zhang, Y. (2020). Analysis of the carbon emission reduction potential of China’s key industries under the IPCC 2°C and 1.5°C limits. Technol. Forecast. Soc. Chang. 159:120198. doi: 10.1016/j.techfore.2020.120198
Wu, Q., Ren, H., Gao, W., Ren, J., and Lao, C. (2017). Profit allocation analysis among the distributed energy network participants based on Game-theory. Energy 118, 783–794. doi: 10.1016/j.energy.2016.10.117
Wu, R., Geng, Y., Dong, H., Fujita, T., and Tian, X. (2016). Changes of CO2 emissions embodied in China–Japan trade: drivers and implications. J. Clean. Prod. 112, 4151–4158. doi: 10.1016/j.jclepro.2015.07.017
Xi, F., Geng, Y., Chen, X., Zhang, Y., Wang, Z., Xue, B., et al. (2011). Contributing to local policy making on GHG emission reduction through inventorying and attribution: a case study of Shenyang. China. Energy Policy 39, 5999–6010. doi: 10.1016/j.enpol.2011.06.063
Xie, Y. L., Fu, Z. H., Xia, D. H., Lu, W., Huang, G., and Wang, H. (2019). Integrated planning for regional electric power system management with risk measure and carbon emission constraints: a case study of the Xinjiang Uygur autonomous region. China. Energies 12:601. doi: 10.3390/en12040601
Yu, S., Wei, Y. M., and Wang, K. (2014). Provincial allocation of carbon emission reduction targets in China: an approach based on improved fuzzy cluster and Shapley value decomposition. Energy Policy 66, 630–644. doi: 10.1016/j.enpol.2013.11.025
Zeng, L., Zhao, L., Wang, Q., Wang, B., Ma, Y., Cui, W., et al. (2018). Modeling interprovincial cooperative energy saving in China: An electricity utilization perspective. Energies 11:241. doi: 10.3390/en11010241
Zhang, B., and Wang, Z. (2014). Inter-firm collaborations on carbon emission reduction within industrial chains in China: practices, drivers and effects on firms’ performances. Energy Economics 42, 115–131. doi: 10.1016/j.eneco.2013.12.006
Zhang, H., Chen, W., and Huang, W. (2016). TIMES modelling of transport sector in China and USA: comparisons from a decarbonization perspective. Appl. Energy 162, 1505–1514. doi: 10.1016/j.apenergy.2015.08.124
Zhang, Y. J., Wang, A. D., and Da, Y. B. (2014). Regional allocation of carbon emission quotas in China: evidence from the Shapley value method. Energy Policy 74, 454–464. doi: 10.1016/j.enpol.2014.08.006
Zhao, X. L., Yao, J., Sun, C. Y., and Pan, W. (2018). Impacts of carbon tax and tradable permits on wind power investment in China. Renew. Energy 135, 1386–1399. doi: 10.1016/j.renene.2018.09.068
Zheng, J. J., Yang, M. M., Ma, G., Xu, Q., and He, Y. (2020). Multi-agents-based modeling and simulation for carbon permits trading in China: a regional development perspective. Int. J. Environ. Res. Public Health 17:301. doi: 10.3390/ijerph17010301
Zhou, P., Zhang, L., Zhou, D. Q., and Xia, W. J. (2013). Modeling economic performance of interprovincial CO2 emission reduction quota trading in China. Appl. Energy 112, 1518–1528. doi: 10.1016/j.apenergy.2013.04.013
Keywords: optimal model, carbon reduction, Shapley value, game, interprovincial cooperation
Citation: Zeng L, Du W, Zhao L and Sun Z (2021) Modeling Interprovincial Cooperative Carbon Reduction in China: An Electricity Generation Perspective. Front. Energy Res. 9:649097. doi: 10.3389/fenrg.2021.649097
Received: 03 January 2021; Accepted: 11 March 2021;
Published: 27 April 2021.
Edited by:
Xu Tang, China University of Petroleum, ChinaReviewed by:
Di Wang, China University of Mining and Technology, ChinaXiangyun Gao, China University of Geosciences, China
Copyright © 2021 Zeng, Du, Zhao and Sun. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lijun Zeng, emVuZ2xpanVuNTE4QDEyNi5jb20=; Laijun Zhao, bGp6aGFvQHVzc3QuZWR1LmNu
 Lijun Zeng
Lijun Zeng Wenjing Du
Wenjing Du Laijun Zhao
Laijun Zhao Zhimei Sun
Zhimei Sun