Modeling Lithium Transport and Electrodeposition in Ionic-Liquid Based Electrolytes

1. Introduction

Improved lithium transport in separators can enhance the energy efficiency and power density of batteries. The use of ionic-liquid-based electrolytes in lithium-ion batteries has been shown to improve both current tolerance and cycle life (Lu et al., 2014; Piper et al., 2015). Numerous electrolytes based on ionic liquids have been characterized experimentally. Ionic-liquid-based electrolytes pose a challenge for modeling because they contain more than two ions, whose pairwise interactions strongly impact the electrolyte's overall performance. Although ionic-liquid solvents generally support solutions with higher ionic conductivity than conventional solvents, they tend to induce higher Haven ratios (Frömling et al., 2008).

The characterization of mass and charge transport in ionic liquids is impeded by the lack of satisfactory theoretical models. Conventional Nernst–Planck theory (dilute-solution theory) is based on an assumption that ions sit in a background of a neutral solvent species that is present in great excess, and therefore cannot be applied to fully ionic electrolytic solutions. For typical liquid electrolytes, characterization generally involves a series of measurements of individual transport properties (e.g., Hittorf transference number, Fickian lithium-salt diffusivity) whose very definitions are based on the notion that a neutral solvent is present. Even if this ambiguity is ignored, transport properties cannot be measured independently in concentrated solutions, because the thermodynamic properties and transport characteristics of different species are coupled. Moreover, as shown experimentally by Popovic et al. (2015), electrolytes at moderate-to-high salt concentrations contain multiple mobile species that are present with long lifetimes—including free ions, ion pairs, and higher-level structures—all of which contribute to ionic conductivity. Accurate characterization requires a group of orthogonal experiments and data analysis using coupled transport equations in a consistent way (Ma et al., 1995; Valoen and Reimers, 2005; Nyman et al., 2008; Hou and Monroe, 2020). A multispecies concentrated-solution theory for ionic-liquid-based lithium electrolytes would help to link experimental characterization with continuum modeling. The foundational work of Pollard and Newman provides a useful starting point: they developed a model of molten-salt electrolytes based in concentrated-solution theory, applicable to domains where local electroneutrality holds (Pollard and Newman, 1979). We aim to extend that approach here.

In addition to their favorable bulk properties, ionic liquids have been suggested to provide a more stable electrolyte/electrode interface with regard to dendrite formation. Atomic force microscopy has been used to measure the force field near the ionic-liquid/electrode interface, showing a layered structure with enhanced mechanical strength (Gebbie et al., 2017; Hoffmann et al., 2018). Understanding how ionic liquids behave in close proximity to charged solid surfaces is crucial for electrolyte design.

Molecular dynamics has been widely deployed to study electrolyte structure near interfaces, especially ion arrangements in Stern layers (Borodin et al., 2017). Selectivity for ion adsorption at electrode surfaces is highly variable: for example, anions can be chosen that either adsorb or desorb at a positively charged electrode (Vatamanu and Borodin, 2017). In space-charge regions near interfaces, extremely high or low cation-to-anion ratios may occur. Steric effects, rather than solubility considerations, determine the maximum ion concentrations in space-charge domains (McEldrew et al., 2018). Small variations of ion size have been observed to disrupt double-layer structure substantially (Bresme et al., 2012).

Continuum models have also successfully elucidated equilibrium structures of space-charge domains outside the Stern layer (i.e., diffuse double layers) near ionic-liquid/solid interfaces. These approaches tend to incorporate ion/ion interactions by specifying appropriate functionalities for the ions' electrochemical potentials (Kornyshev, 2007; Bazant et al., 2011; Hoffmann et al., 2018; de Souza et al., 2020). Short-range interactions and ion-size effects have been shown to rationalize the formation of layered structures near solid surfaces. Charge screening in the diffuse double layer can be accompanied by a significant pressure field near the interface (Monroe, 2020), and it remains unclear for fully ionic electrolytes how lithium cations would redistribute in response to this compressive force.

It should be emphasized that the practical use of fully ionic electrolytes in lithium-anode batteries is often accompanied by the formation of resistive solid-electrolyte interphase (SEI) layers (Xu, 2014). SEIs have been studied in detail for several fully ionic lithium-electrolyte systems (Xiong et al., 2014; Karimi et al., 2021). Highly resistive SEI layers can strongly impact both apparent reaction kinetics and interfacial capacitance. It is of great interest how fully ionic electrolytes respond as the SEI evolves, since SEI formation and growth during cycling is a significant mode of performance degradation.

A dynamical model of ionic-liquid-based electrolytes that considers mechanical effects is needed to study lithium transport in the diffuse double layer. Goyal and Monroe (2017) extended Newman's concentrated-solution theory by taking into account mechanics and electrodynamics. This paper deploys that framework to model a three-ion electrolyte system. As a case study we explore the baseline system comprising a binary solution of lithium tetrafluoroborate salt (LiBF₄) in the ionic-liquid solvent 3-butyl-1-methyl imidaziolium tetrafluoroborate (bmimBF₄), which combine together to form the three-ion lithium electrolyte Li_xbmim_1−xBF₄. In later parts of the study we also explore the effects of changing both the anion and the ionic-liquid cation.

First we simulate the equilibrated diffuse double layer, to illustrate how pressure and ion partial molar volumes can affect property distributions near the interface. Then, we investigate how conductivity and transference number vary locally in the electrolyte in response to a steady current. Finally, we analyze how interfacial kinetics can affect lithium transport near the electrode surface. We also discuss how ionic-liquid-based electrolytes could be tuned to facilitate plating and stripping of lithium metal. We will emphasize how bulk ion transport is affected by changes in interfacial properties as practical systems age.

2. Model

For the baseline case, we consider an isothermal ternary ionic liquid system composed of Li⁺ cations, bmim⁺ cations, and BF₄⁻ anions, respectively indexed by subscripts k ∈ {Li, +, −}. Species molarities c_k sum up to the total concentration c_T. The mass density ρ = ∑ M_kc_k relates to species molarities through their molar masses M_k. The number-average velocity of species k, ${\overrightarrow{v}}_k$, relates to its molar flux through ${\overrightarrow{N}}_k=c_k{\overrightarrow{v}}_k$. The mass-average velocity of the fluid, $\overrightarrow{v}$, is defined through the relation $\rho \overrightarrow{v}=\sum M_k{\overrightarrow{N}}_k$. Introduction of Faraday's constant F and the equivalent species charges z_k allow definitions of the local excess charge density ρ_e = F ∑ z_kc_k and current density $\overrightarrow{i}=F\sum z_k{\overrightarrow{N}}_k$.

Excess charge density produces an external electric field $\overrightarrow{E}$ governed by Poisson's equation,

$\begin{array}{ll}\overrightarrow{\nabla }·\left(ϵ\overrightarrow{E}\right)={\rho }_{\text{e}},& (1)\end{array}$

in which ϵ is the local dielectric permittivity, assumed to be constant. Each species follows a continuity equation, so that for all k ∈ {Li, +, −}

$\begin{array}{ll}\frac{\partial c_k}{\partial t}=-\overrightarrow{\nabla }·{\overrightarrow{N}}_k.& (2)\end{array}$

A momentum balance relates the mass-average velocity to the hydrodynamic external pressure p, viscous stress $\overrightarrow{\overrightarrow{\tau }}$, and electrostatic body forces ${\rho }_{\mathrm{\text{e}}}\overrightarrow{E}$,

$\begin{array}{ll}\rho \frac{\partial \overrightarrow{v}}{\partial t}=-\rho \overrightarrow{v}·\overrightarrow{\nabla }\overrightarrow{v}-\overrightarrow{\nabla }p-\overrightarrow{\nabla }·\overrightarrow{\overrightarrow{\tau }}+{\rho }_{\text{e}}\overrightarrow{E},& (3)\end{array}$

in which both gravity and the diffusion stress discussed by Goyal and Monroe (2017) have been neglected.

Hirschfelder et al. (1964) derived thermodynamic driving forces ${\overrightarrow{d}}_k$, which can be used to underpin Onsager–Stefan–Maxwell (OSM) equations that account for the energy dissipation through drag coefficients that resist relative species motion. In an isothermal system the OSM equations can be written as (Newman and Thomas-Alyea, 2004).

$\begin{array}{ll}{\overrightarrow{d}}_k=-c_k\left(\overrightarrow{\nabla }{\mu }_k-\frac{M_k}{\rho }\overrightarrow{\nabla }p\right)={\displaystyle \sum _{j\ne k}}\frac{RT{c}_k{c}_j}{c_{\text{T}{{D}}_{kj}}}\left({\overrightarrow{v}}_k-{\overrightarrow{v}}_j\right),& (4)\end{array}$

where R is the gas constant, T is the absolute temperature, and ${D}$_kj is the Stefan–Maxwell diffusivity of species k through species j. Onsager reciprocity guarantees that ${D}$_kj = ${D}$_jk. Because the Gibbs–Duhem relation requires that $\sum _k{\overrightarrow{d}}_k=\overrightarrow{0}$, only two independent OSM equations suffice to model a ternary diffusion system. Inspection of the dissipation function for a liquid electrolyte suggests that the viscous stress is given by

$\begin{array}{ll}\overrightarrow{\overrightarrow{\tau }}=-\eta \left[\overrightarrow{\nabla }\overrightarrow{v}+{\left(\overrightarrow{\nabla }\overrightarrow{v}\right)}^{\text{T}}-\frac{2}{3}\overrightarrow{\overrightarrow{I}}\overrightarrow{\nabla }·\overrightarrow{v}\right],& (5)\end{array}$

in which effects due to bulk viscosity have been discarded. We further take the electrolyte to be a Newtonian fluid, with constant viscosity η.

For species k, composition variation, pressure gradients, and the electric field can all contribute to the electrochemical-potential gradient, through

$\begin{array}{ll}\overrightarrow{\nabla }{\mu }_k=RT\overrightarrow{\nabla }ln\frac{c_k}{c_{\text{T}}}+{\overline{V}}_k\overrightarrow{\nabla }p-F{z}_k\overrightarrow{E}.& (6)\end{array}$

More complex electrochemical-potential functionalities can be used to account for additional details about ion behavior, such as solvation energetics. Several electrochemical-potential functions have been proposed to model short-range ion/ion interactions (Bazant et al., 2011; Hoffmann et al., 2018; de Souza et al., 2020). Here we restrict our discussion to ideal mixtures, as specified by the ln (c_k/c_T) term in Equation (6).

A thermodynamic analysis of the equation of state for volume also shows that the set of molar species concentrations {c_k} is constrained by the set of species partial molar volumes $\left\{{\overline{V}}_k\right\}$, through

$\begin{array}{ll}\sum c_k{\overline{V}}_k=1.& (7)\end{array}$

Assuming a constant composition-independent bulk modulus K, each partial molar volume takes the form

$\begin{array}{ll}{\overline{V}}_k\left(p\right)={\overline{V}}_k^{\theta }exp\left[-\left(p-p^{\theta }\right)/K\right],& (8)\end{array}$

where ${\overline{V}}_k^{\theta }$ is the partial molar volume at reference pressure p^θ. Experimental values of ${\overline{V}}_k^{\theta }$ are expected to reflect information about not only central species k, but also secondary and tertiary structures involving k, such as its solvation shell or coordination environment.

It is useful to express composition through ion k's particle fraction y_k = c_k/c_T, which is convenient because y₋ = 1 − y₊ − y_Li. Each species molarity c_k can be written as a function of {y₊, y_Li, p} through

$\begin{array}{ll}{c}_k=\frac{y_k}{{\displaystyle \sum _j}{y}_j{\overline{V}}_j\left(p\right)},& (9)\end{array}$

which derives from Equations (7) and (8). Thus, all thermodynamic properties of each species are uniquely determined by the pressure (p), external electric field ($\overrightarrow{E}$), and the particle fractions of lithium and bmim cations (y_Li and y₊). The system of Equations (1)–(9) is closed by stating constitutive laws for the electrical properties ϵ and z_k, the thermodynamic properties M_k, ${\overline{V}}_k$, and K, and the transport properties ${D}$_kj and η.

Following Monroe and Delcourt's process (Monroe and Delacourt, 2013), the OSM transport laws from Equation (4) can be transformed into flux-explicit forms that include a generalized form of Ohm's law,

$\begin{array}{ll}\frac{\overrightarrow{i}-{\rho }_{\text{e}}{\overrightarrow{v}}_{-}}{{\kappa }^{-}}=\frac{{\overrightarrow{d}}_{\text{Li}}}{F{z}_{\text{Li}}{c}_{\text{Li}}}+\frac{1-t_{\text{Li}}^{-}}{F}\left(\frac{{\overrightarrow{d}}_{+}}{z_{+}{c}_{+}}-\frac{{\overrightarrow{d}}_{\text{Li}}}{z_{\text{Li}}{c}_{\text{Li}}}\right),& (10)\end{array}$

as well as flux-explicit transport laws for bmim cations,

$\begin{array}{ll}{\overrightarrow{N}}_{+}-c_{+}{\overrightarrow{v}}_{-}=\frac{1-t_{\text{Li}}^{-}}{F{z}_{+}}\left(\overrightarrow{i}-{\rho }_{\text{e}}{\overrightarrow{v}}_{-}\right)+\frac{z_{\text{Li}}{{D}}_{\times }^{-}{c}_{\text{T}}}{RT}\left(\frac{{\overrightarrow{d}}_{+}}{z_{+}{c}_{+}}-\frac{{\overrightarrow{d}}_{\text{Li}}}{z_{\text{Li}}{c}_{\text{Li}}}\right),& (11)\end{array}$

and lithium ions,

$\begin{array}{ll}{\overrightarrow{N}}_{\text{Li}}-c_{\text{Li}}{\overrightarrow{v}}_{-}=\frac{t_{\text{Li}}^{-}}{F{z}_{\text{Li}}}\left(\overrightarrow{i}-{\rho }_{\text{e}}{\overrightarrow{v}}_{-}\right)-\frac{z_{+}{{D}}_{\times }^{-}{c}_{\text{T}}}{RT}\left(\frac{{\overrightarrow{d}}_{+}}{z_{+}{c}_{+}}-\frac{{\overrightarrow{d}}_{\text{Li}}}{z_{\text{Li}}{c}_{\text{Li}}}\right).& (12)\end{array}$

These transport equations have been written in forms that use ${\overrightarrow{v}}_{-}$ as a reference velocity for convection. Three transport properties—conductivity κ⁻, lithium transference number relative to the hexafluorophosphate velocity $t_{+}^{-}$ and cross diffusivity for cation exchange ${{D}}_{\times }^{-}$—link the thermodynamic driving forces to species fluxes and the ionic current density. In all cases the superscript − is included to emphasize that the values of these properties depend on the choice of reference velocity.

The three macroscopic transport properties that appear in Equations (10)–(12) map bijectively into the three Stefan–Maxwell diffusivities ${D}$₊₋, ${D}$_Li+ and ${D}$_Li−:

$\begin{array}{ll}{\kappa }^{-}=\frac{F^2{c}_{\text{T}}}{RT}\frac{\frac{{\left(z_{+}{y}_{+}+z_{\text{Li}}{y}_{\text{Li}}\right)}^2}{\left(1-y_{+}-y_{\text{Li}}\right){{D}}_{\text{Li}+}}+\frac{z_{+}^2{y}_{+}}{{{D}}_{\text{Li}-}}+\frac{z_{\text{Li}}^2{y}_{\text{Li}}}{{{D}}_{+-}}}{\frac{1-y_{+}-y_{\text{Li}}}{{{D}}_{+-}{{D}}_{\text{Li}-}}+\frac{y_{+}}{{{D}}_{+-}{{D}}_{\text{Li}+}}+\frac{y_{\text{Li}}}{{{D}}_{\text{Li}+}{{D}}_{\text{Li}-}}},& (13)\end{array}$

$\begin{array}{ll}{t}_{\text{Li}}^{-}=\frac{\frac{z_{\text{Li}}^2{y}_{\text{Li}}}{{{D}}_{+-}}+\frac{z_{\text{Li}}{y}_{\text{Li}}\left(z_{+}{y}_{+}+z_{\text{Li}}{y}_{\text{Li}}\right)}{\left(1-y_{+}-y_{\text{Li}}\right){{D}}_{\text{Li}+}}}{\frac{{\left(z_{+}{y}_{+}+z_{\text{Li}}{y}_{\text{Li}}\right)}^2}{\left(1-y_{+}-y_{\text{Li}}\right){{D}}_{\text{Li}+}}+\frac{z_{+}^2{y}_{+}}{{{D}}_{\text{Li}-}}+\frac{z_{\text{Li}}^2{y}_{\text{Li}}}{{{D}}_{+-}}},& (14)\end{array}$

$\begin{array}{ll}{{D}}_{\times }^{-}=\frac{z_{+}{z}_{\text{Li}}{y}_{+}{y}_{\text{Li}}}{\frac{{\left(z_{+}{y}_{+}+z_{\text{Li}}{y}_{\text{Li}}\right)}^2}{{{D}}_{\text{Li}+}}+\left(\frac{z_{+}^2{y}_{+}}{{{D}}_{\text{Li}-}}+\frac{z_{\text{Li}}^2{y}_{\text{Li}}}{{{D}}_{+-}}\right)\left(1-y_{+}-y_{\text{Li}}\right)}.& (15)\end{array}$

Note that the first-order pressure dependence of these properties is determined entirely by the total molarity $c_{\mathrm{\text{T}}}=1/\sum y_k{\overline{V}}_k\left(p\right)$.

The ions' molar masses (M₊ = 139.2 g/mol, M₋ = 86.8 g/mol, and M_Li = 6.9 g/mol) are well known. Partial molar volumes at ambient pressure have also been reported by Slattery et al. (2007) for bmim⁺ and ${\text{BF}}_4^{-}$ (${\overline{V}}_{+}^{\theta }=118.034$ mL/mol and ${\overline{V}}_{-}^{\theta }=43.962$ mL/mol). For lithium cations, the partial molar volume is assumed to be the same as the molar volume of lithium in its pure metal state, ${\overline{V}}_{\mathrm{\text{Li}}}^{\theta }=13.109$ mL/mol. The bulk modulus of the electrolyte is taken to be that of pure liquid bmimBF₄, K = 2.8831 GPa (Sunkara et al., 2015); and the relative permittivity ϵ is 11.7 at 303 K and 0.1 MPa (Wakai et al., 2005). At 303 K, the ionic conductivity of pure bmimBF₄ is κ₀ = 0.295 S/m (Yu et al., 2009), which can be used to estimate the Stefan-Maxwell diffusivity ${{D}}_{+-}=5.5017\times 10^{-12}$ m²/s according to the relation ${\kappa }_0=F^2{z}_{+}^2{c}_{\mathrm{\text{T}}}{{D}}_{+-}/\left(RT\right)$ obtained by assuming y_Li = 0 in Equation (13). ${D}$_Li+ and ${D}$_Li− have not been reported systematically, so we assume ${D}$_Li− = ${D}$₊₋ = ${D}$_Li+ for simplicity, unless stated otherwise.

The present analysis focuses on transport phenomena within diffuse-double-layer and bulk-electrolyte domains. Regions between the electrode surfaces and the outer Helmholtz planes—including the SEI, Stern layer, etc.—are treated phenomenologically, in terms of the interfacial characteristic frequency f_int, a property whose value can be deduced from the interfacial impedance.

3. Results

3.1. Equilibrium Double Layers Near Blocking Electrodes

We first investigate the double layer structure in a Li_0.5bmim_0.5BF₄ system between two planar blocking electrodes biased by a 20 mV voltage difference. A one-dimensional system of thickness L = 4 nm is simulated. Although this electrode spacing is unrealistically small, it helps to make the distributions of properties within the interfacial double layers more readily visible in plots. Generally the structures of double layers computed with this model do not change when electrodes are moved further apart.

As Figure 1A shows, ionic liquids between blocking electrodes form an electrolytic capacitor, in which two double layers form near the electrode surfaces and the electric field is screened from the bulk liquid. Figure 1B shows that the fractions of both types of cation rise (fall) near the negative (positive) electrode. The external field imposes forces on the excess charge in the double layers, and a positive gauge pressure around 3.5 MPa builds up near both electrodes, as shown in Figure 1C.

FIGURE 1

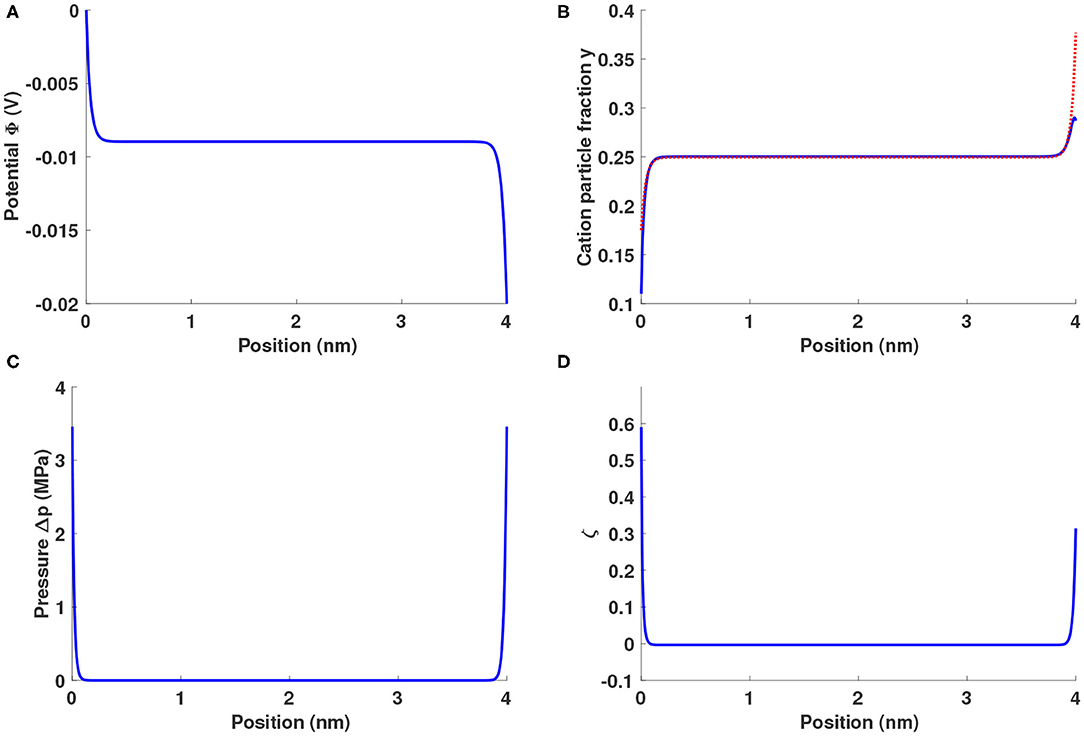
Figure 1. Distributions of (A) potential Φ, (B) cation particle fractions (blue solid line: y₊, red dotted line: y_Li), (C) gauge pressure Δp = p − p_bulk, and (D) lithium excess factor ζ for a Li_0.5bmim_0.5BF₄ system sandwiched between two planar blocking electrodes under a potential bias of 20 mV.

At equilibrium, Poisson's Equation (1) and the momentum balance, Equation (3), combine to give a relationship between the electric field and the pressure,

$\begin{array}{ll}\Delta p=p-p_{\text{bulk}}=\frac{1}{2}ϵ\left(E^2-E_{\text{bulk}}^2\right)=\frac{1}{2}ϵE^2,& (16)\end{array}$

derived using the observation that E_bulk ≈ 0.

When electrodes are blocking, the field is equal at the negative and positive electrodes' surfaces. Equation 16 requires the peak pressure to be identical at both edges of the electrolyte, as seen in Figure 1C. It is worth noting that the pressure distribution is not symmetric—its curvature differs at the electrolyte's boundaries. Due to the disparity in ion sizes, the positive and negative outer Helmholtz planes achieve different total ion concentrations, as shown in Figure 1B, causing the screening lengths at the positive and negative boundaries to differ. This effect leads to the pressure-distribution asymmetry in Figure 1C, as well as the difference between interfacial potential drops in Figure 1A.

Since Li⁺ has both a smaller size and a lower mass than bmim⁺, the substitution of Li⁺ for bmim⁺ alters the energetics associated with double-layer formation. The lithium-ion fraction is apparently enhanced in both double layers, a chemomechanical effect illustrated in Figure 1D through the distribution of the lithium excess factor $\zeta =\frac{y_{\mathrm{\text{Li}}}/{ȳ}_{\mathrm{\text{Li}}}}{y_{+}/{ȳ}_{+}}-1$, where ȳ_Li and ȳ₊ are the global-average particle fractions of Li⁺ and bmim⁺. A positive (negative) ζ means that the ratio of lithium ions to bmim cations is higher (lower) that its average value. Even at the relatively low potential bias of 20 mV, there are about 60% more Li⁺ ions than bmim⁺ ions near the positive electrode and about 30% more near the negative electrode.

In the absence of current, Equations (4) and (6) together give equilibrium conditions for the distributions of bmim⁺ and Li⁺,

$\begin{array}{ll}RT\overrightarrow{\nabla }ln{y}_{+}+\left({\overline{V}}_{+}-\frac{M_{+}}{\rho }\right)\overrightarrow{\nabla }p=F{z}_{+}\overrightarrow{E},& (17)\end{array}$

$\begin{array}{ll}RT\overrightarrow{\nabla }ln{y}_{\text{Li}}+\left({\overline{V}}_{\text{Li}}-\frac{M_{\text{Li}}}{\rho }\right)\overrightarrow{\nabla }p=F{z}_{\text{Li}}\overrightarrow{E}.& (18)\end{array}$

Subtracting Equation (17) from (18) produces a relationship between the gradients of lithium excess factor and pressure,

$\begin{array}{ll}\overrightarrow{\nabla }\zeta =\overrightarrow{\nabla }\left(ln\frac{y_{\text{Li}}}{y_{+}}\right)=-\left({\overline{V}}_{\text{Li}}-{\overline{V}}_{+}-\frac{M_{\text{Li}}-M_{+}}{\rho }\right)\frac{\overrightarrow{\nabla }p}{RT}.& (19)\end{array}$

In all cases studied here, the local mass density ρ satisfies

$\begin{array}{ll}\rho >\frac{M_{\text{Li}}-M_{+}}{{\overline{V}}_{\text{Li}}-{\overline{V}}_{+}}\simeq \frac{M_{\text{Li}}-M_{+}}{{\overline{V}}_{\text{Li}}^{\theta }-{\overline{V}}_{+}^{\theta }},& (20)\end{array}$

so double-layer regions will have a higher lithium fraction than the global average.

It is straightforward to simulate the equilibrium states of different mixtures of lithium salts Li⁺Y⁻ and ionic liquids X⁺Y⁻ that differ from the baseline case shown in Figure 1. In these simulations we continue to fix the potential bias at 20 mV. The ionic-liquid cations are selected from C_nmim⁺ with n = 2, 3, 4, 5, 6, and 8 (note that bmim⁺ corresponds to n = 4), and the anions are varied between BF₄⁻ and Tf₂N⁻ [i.e., bis(trifluoromethane)sulfonimide, a.k.a. TFSI], for which partial molar volumes are available from the extensive report by Slattery et al. (2007). The partial molar volume of Tf₂N⁻ is 139.71 mLmol⁻¹, around three times that of BF₄⁻ and similar to bmim⁺. The global-average particle fraction of Li⁺ was varied from 0.05 to 0.25, corresponding to a molarity range of approximately 0.6–5 M for the lithium salt.

Figure 2A shows that given a particular choice of X⁺ and Y⁻, a higher lithium fraction produces a higher surface pressure. Smaller partial molar volumes for X⁺ and Y⁻ also produce higher surface pressure given a fixed lithium fraction. This behavior owes to the fact that smaller ion sizes and larger lithium fractions give higher ion concentrations according to Equation (9), thereby producing thinner double layers. At a given potential bias, a thinner double layer implies a larger electric field, and a consequent higher surface pressure according to Equation (16).

FIGURE 2

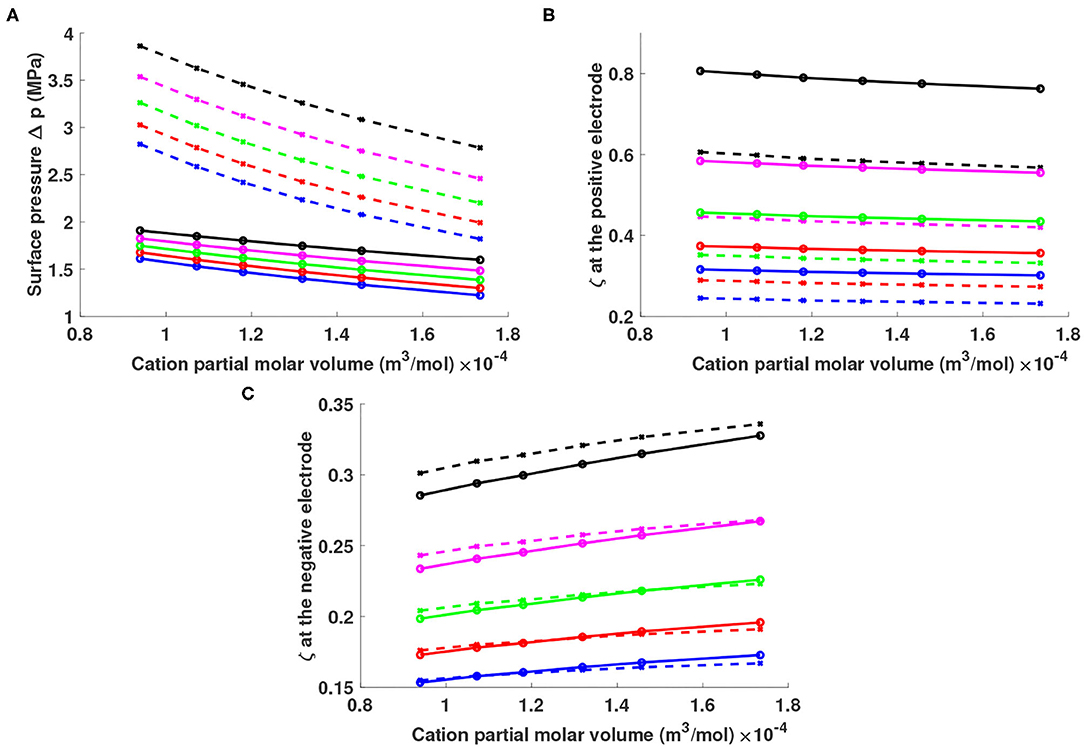
Figure 2. (A) Surface pressure Δp and lithium excess factor ζ at the (B) positive and (C) negative electrode for different mixtures of lithium salts Li⁺Y⁻ in ionic liquids X⁺Y⁻. The horizontal axis shows the partial molar volume of cations X⁺, with points on the curves indicating the indicative values for C_nmim⁺ structures (n = 2, 3, 4, 5, 6, and 8 as volume increases). Solutions were simulated with lithium particle fractions of 0.05 (blue), 0.1 (red), 0.15 (green), 0.2 (magenta), and 0.25 (black). Solid curves represent solutions containing Tf₂N⁻ anions; dashed curves represent solutions containing ${\text{BF}}_4^{-}$.

Figures 2B,C show the lithium excess factor ζ at the surfaces of the positive and negative electrodes, respectively. The lithium excess is positive at both interfaces, ranging from 25 to 80% at the positive electrode and 15–35% at the negative. For a given X⁺, a higher lithium fraction produces a higher lithium excess factor ζ near both electrodes. A larger anion can enhance ζ near the positive electrode up to 20%, whereas anion size has negligible effect on ζ near the negative electrode due to the low anion fraction there. In systems with the same lithium fraction and same choice of anion, a larger ionic-liquid cation produces a higher lithium excess near the negative electrode but a lower ζ near the positive. Changing cation size (from C₂mim⁺ to C₈mim⁺) can change ζ by 5%, but the effect goes in opposed directions at the positive and negative electrode.

3.2. Lithium Transport Between Reactive Electrodes

Interfacial impedance correlates the electric field at the boundary (i.e., the outer Helmholtz plane) with the faradaic current density. This property gives a phenomenological description of all processes happening between the electrode and the outer Helmholtz plane. In an earlier paper (Li and Monroe, 2019), the authors modeled faradaic interfaces with the relationship

$\begin{array}{ll}{E}_{\text{surf}}=R_{\text{int}}{C}_{\text{int}}i/ϵ=\frac{i}{2\pi f_{\text{int}}ϵ},& (21)\end{array}$

in which i is the applied current density, and R_int and C_int are the effective kinetic resistance and interfacial capacitance, respectively. The combined effects of resistance and capacitance are summarized by the single characteristic frequency f_int = 1/(2πR_intC_int), which can be measured with electrochemical impedance spectroscopy and controls how interfaces respond to a potential bias. Interfaces with small f_int values behave more like electrolytic capacitors; large f_int interfaces behave like resistors. Salminen et al. (2006) performed an interfacial impedance measurement from 0.1 to 65535 Hz for Li|bmimBF₄ +1 or 2 mol/kg LiBF₄|Li sandwich cells, providing a complete semicircle on the Nyquist plot. The interfacial frequency is given by the peak frequency of the interfacial semicircle (Li and Monroe, 2019), so a practical interfacial frequency f_int is expected to lie between 1 Hz and 10 kHz in a three-ion lithium electrolyte. In this range, the interface will be somewhat capacitive due to the likely formation of a highly resistive SEI, leading to the distinguishable presence of a double layer in which the potential drop is steep. It is also worth noting that Stern-layer phenomena merely change the relationship between the electric field at the outer Helmholtz plane and the faradaic current, and are therefore encapsulated by f_int.

Figure 3 summarizes simulations of a 10-μm-thick Li_0.5bmim_0.5BF₄ slab sandwiched between two reactive electrodes with f_int = 1 kHz ($2\pi R_{\mathrm{\text{int}}}{C}_{\mathrm{\text{int}}}=10^{-3}$s), subjected to a potential bias of 20 mV. Charge transfer at the electrode/electrolyte interface is assumed to owe only to Faradaic reactions involving Li⁺. The cation/cation diffusivity ${D}$_Li+ controls the drag interactions between lithium ions and ionic-liquid cations, and is studied across values of ${D}$₊₋/${D}$_Li+ = −0.5, 0, and 1, all of which are thermodynamically consistent (Monroe and Delacourt, 2013). When ${D}$₊₋/${D}$_Li+ = 0, cations place no drag on each other; Li⁺ and bmim⁺ flow independently. The flow of bmim⁺ slows the flow of Li⁺ when ${D}$_Li+ > 0, and speeds lithium flux when ${D}$_Li+ < 0.

FIGURE 3

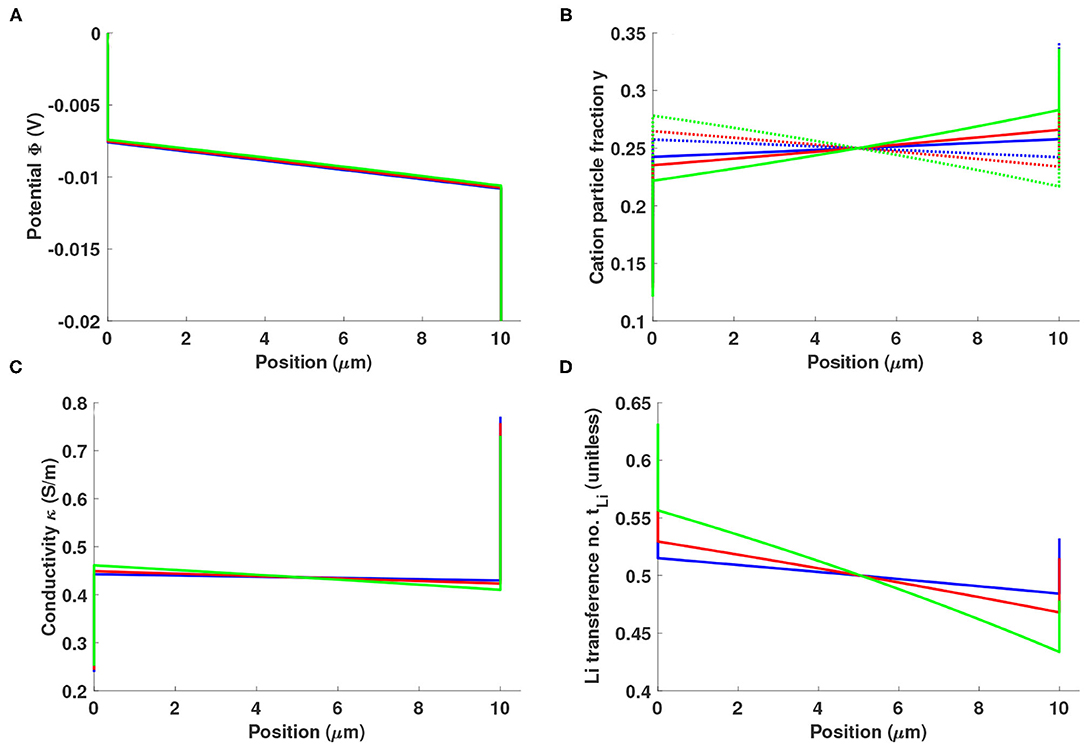
Figure 3. Distributions of (A) potential Φ, (B) cation particle fraction (solid line: y₊, dotted line: y_Li), (C) local ionic conductivity κ, and (D) local lithium transference number in a 10 μm-thick layer of Li_0.5bmim_0.5BF₄ sandwiched between two reactive electrodes with f_int = 1 kHz, under a potential bias of 20 mV. The Stefan-Maxwell diffusivity of Li⁺ through bmim⁺, ${D}$_Li+, is varied across values of ${D}$₊₋/${D}$_Li+ = −0.5 (blue), 0 (red), and 1 (green).

As shown in Figure 3A, the double layer does not entirely screen the interfacial electric field near a reactive electrode. Some unscreened field is associated with Ohmic conduction across the cell. For the f_int value chosen, the potential drop across the double layers is fairly large in comparison to the drop across the bulk. Figure 3B shows that the concentrations of both cations (Li⁺ and bmim⁺) are polarized with opposite slopes in the bulk. The negative concentration gradient of the reactive species, Li⁺, coincides with the direction of the ionic current, while that of bmim⁺ is opposed; anions distribute relatively uniformly, maintaining bulk electroneutrality. As the ratio ${D}$₊₋/${D}$_Li+ gets more positive, the trends remain similar and the magnitude of the polarization effect grows larger.

The local values of conductivity and transference number that result from ion polarization can be calculated from Equations (13) to (14). Figure 3C shows that the electrolyte's conductivity very near the cathode can be significantly larger than the bulk, while that near the anode is smaller. The local conductivity depends strongly on composition—especially on Li⁺ fraction—whereas the transference number is primarily determined by the lithium excess factor. Figure 3D shows that lithium transference decreases across the bulk due to the opposed polarizations of the Li⁺ and bmim⁺ particle-fraction distributions. In the double layer, the lithium transference number is enhanced due to the pressure effect discussed earlier.

Faradaic currents induce bulk cation polarization and reduce the lithium concentration near the negative electrode, which could encourage side reactions. Three phenomena specific to double layers may mitigate the adverse consequences of bulk polarization at the cathode: conductivity is enhanced, Li⁺ concentration is increased by double-layer polarization, and lithium transference is enhanced by the pressure effect. At the anode surface—somewhat counterintuitively—the lithium concentration can be substantially depleted if double-layer polarization is too strong. In a purely ionic electrolyte, the pressure effect that accompanies charge screening enhances both lithium concentration and transference number at both electrodes, potentially improving interfacial kinetics for any reactions involving lithium.

Figure 4 shows how an electrolyte slab with baseline properties responds to a potential bias of 20 mV when the character of the electrode/electrolyte interfaces changes. Three f_int values are studied: 20 kHz, 1 kHz, and 0 Hz. A small interfacial frequency corresponds to a situation with sluggish interfacial kinetics and a very capacitive interface. In this case, most of the potential drop occurs in the double layers, as shown in Figure 4A. Smaller bulk potential drop is associated with less bulk polarization and smaller currents (cf. Figure 4B) and more significant surface pressure (Figure 4C). Local conductivity and local lithium transference number are both substantially affected by the interfacial frequency, as can be seen from the plots on Figures 4D,E. In the case of constant potential bias, interfacial kinetics impacts the cell response in a coupled way, changing both bulk polarization and double-layer structure.

FIGURE 4

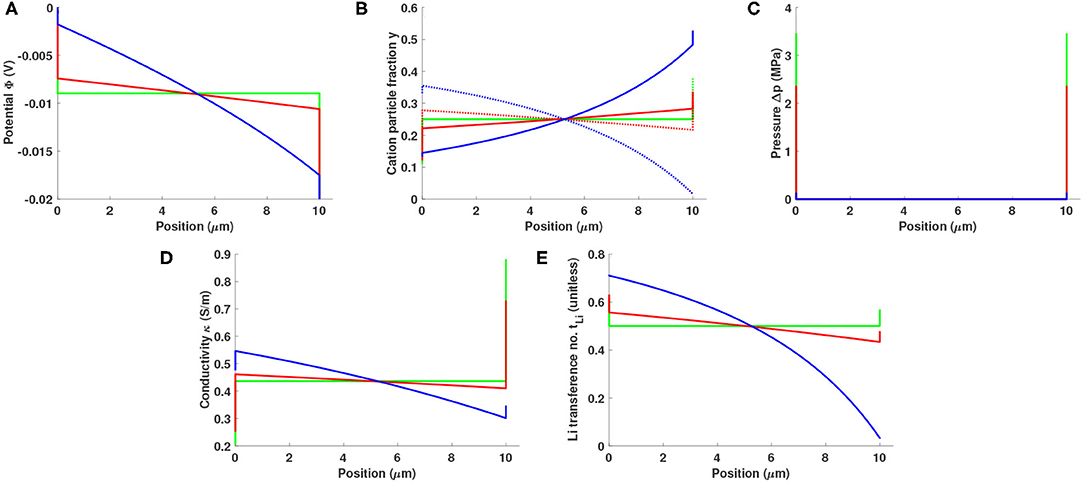
Figure 4. Distributions of (A) potential Φ, (B) cation particle fraction (solid line: y₊, dotted line: y_Li), (C) pressure p, (D) local conductivity κ, and (E) local lithium transference number in a 10 μm Li_0.5bmim_0.5BF₄ slab sandwiched between two reactive electrodes under a potential bias of 20 mV. Interfacial frequencies are 20 kHz (blue), 1 kHz (red), and 0 Hz (green).

Figure 5 shows simulations of four 10-μm-thick systems (Li_0.5C₄mim_0.5BF₄, Li_0.5C₈mim_0.5BF₄, Li_0.5C₄mim_0.5Tf₂N, and Li_0.5C₈mim_0.5Tf₂N) with different interfacial frequencies in the 6.3 Hz to 1 kHz range. A practical current density of 0.1 mA/cm² was used for the simulations. These data illustrate how transport near the electrodes is expected to vary in response to a change in interfacial kinetics. Practically, battery degradation is usually associated with increasing interfacial resistance due to SEI growth, morphology change, passivation, etc., which would correspond in these simulations to a lower interfacial frequency f_int. Thus, as practical systems age, their responses would be expected to move from high f_int to low f_int along the curves in Figure 5.

FIGURE 5

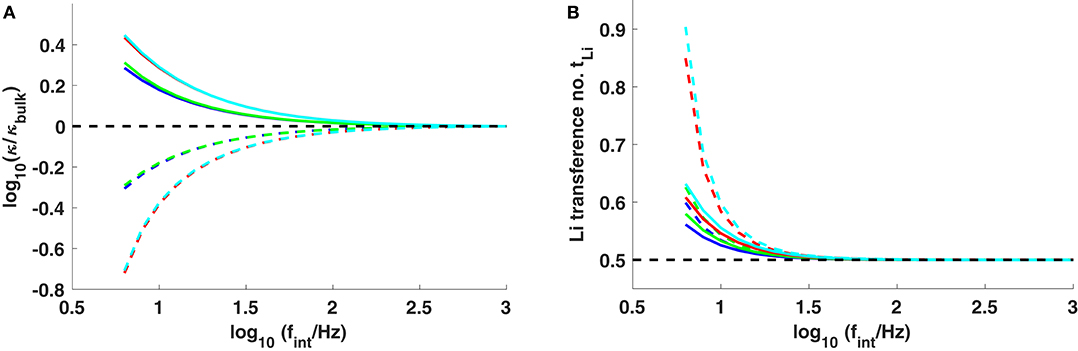
Figure 5. (A) Conductivity and (B) lithium transference number at the surfaces of the positive (dashed lines) and negative (solid lines) electrodes, plotted vs. interfacial frequency f_int. The systems studied are Li_0.5C₄mim_0.5BF₄ (blue), Li_0.5C₈mim_0.5BF₄ (green), Li_0.5C₄mim_0.5Tf₂N (red), and Li_0.5C₈mim_0.5Tf₂N (cyan). The black dashed lines show κ = κ_bulk in (A) and t_Li = 0.5 in (B).

The surface pressure induced by applied current can be found by combining Equations (16) and (21). After assuming E_bulk ≪ E_surf, one finds that

$\begin{array}{ll}\Delta p\propto E_{\text{surf}}^2\propto i^2/f_{\text{int}}^2.& (22)\end{array}$

For the same applied current, a smaller f_int produces a higher surface pressure, and should therefore raise the lithium fraction near the electrodes more. In the high interfacial frequency limit f_int → ∞, the properties at the electrode surface match their properties in the bulk; double-layer effects become insignificant. Conversely, the effects at low interfacial frequencies arise primarily from double-layer polarization. It is worth noting that the concentrations of both cations (Li⁺ and C_nmim⁺) can be dramatically reduced at the positive electrode as a consequence of space charging as f_int → 0. Figure 5A compares the local conductivity near the interface as interfacial frequency varies. As interfaces get more capacitive (smaller f_int), higher double-layer polarization can enhance the conductivity adjacent to the cathode by nearly half an order of magnitude, accompanied by a raised lithium transference number in the range 0.6–0.9. The lithium depletion in the double layer near the anode reduces the conductivity by a factor of ~ 5, but the pressure effect in the double layer still significantly enhances the lithium fraction and the lithium transference number there, as can be seen from Figure 5B. Thus, the use of ionic liquids could improve lithium transport—especially via the surface transference-number enhancement—at both anode and cathode surfaces in systems where interfacial kinetics slows down over time (as it might due to interfacial degradation). Comparing cells run at the same current density, the interfacial performance exhibited by ionic liquids with larger cations and anions is always expected to be better than ionic liquids with smaller ions, as shown in Figure 5.

4. Conclusion

Concentrated-solution theory was exploited to develop a transport model for a three-ion, ionic-liquid-solvated lithium electrolyte, i.e., a mixture of a lithium salt and ionic liquid that share an anion, such as the ternary Li_xbmim_1−xBF₄ system. The theory included three pairwise ion/ion diffusional drag interactions, as well as allowing for electrical non-neutrality and accounting for mechanical effects due to space charge. Simulations explored the steady-state response of this ternary ionic system to a constant potential bias or a constant applied current. The double-layer structure near the electrode surfaces was investigated in detail.

A significant surface pressure (~3.5 MPa for a 20 mV potential bias) can build up in the double layer as a consequence of the Lorentz force that acts on excess charge there. This surface pressure was observed to change the relative amounts of Li⁺ and bmim⁺ near interfaces significantly due to the disparities in their molar masses and sizes, greatly enhancing the surface Li⁺ concentration. In a Li_0.5bmim_0.5BF₄ system under a 20 mV potential bias, 60% more Li⁺ than bmim⁺ was present near the positive electrode, and 30% more was present near the negative electrode. A comparison of various electrolyte formulations showed that the use of large anions can enhance surface lithium concentrations even more. Large cations have more of an effect at the cathode than at the anode. The use of ionic-liquid solvents could greatly facilitate lithium plating and stripping processes via this pressure effect.

Local conductivity and lithium transference number were also studied in a Li_0.5bmim_0.5BF₄ system. The interaction between Li⁺ and bmim⁺ was found to affect bulk cation polarization significantly. The response of electrolytes to currents is determined by the interfacial impedance. If an interface becomes more capacitive as the cell ages, as might be expected if electrode passivation increases over time, currents will induce a stronger double-layer polarization and a more significant pressure effect. Consequently, the local conductivity and lithium transference number near the negative electrode will increase to assist plating processes, while the pressure effect can raise the lithium transference number on the stripping side to compensate for conductivity reduction there. In a comparison of different purely ionic lithium electrolytes at constant currents, a combination of larger ionic-liquid cations and anions was always found to produce higher local lithium transference numbers at both interfaces.

Data Availability Statement

The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.

Author Contributions

GL and CWM designed the research. GL implemented simulations and drafted the manuscript. CWM revised the manuscript and supervised. Both authors contributed to the article and approved the submitted version.

Funding

This work was supported by the EPSRC Faraday Institution within the SOLBAT challenge, grant no. EP/S003053/1.FIRG007, the ISCF Materials Research Hub for Energy Conversion, Capture, and Storage (M-RHEX), grant no. EP/R023581/1, and the UK Engineering and Physical Sciences Research Council (EPSRC), grant no. EP/P003532/1.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Bazant, M. Z., Storey, B. D., and Kornyshev, A. A. (2011). Double layer in ionic liquids: overscreening versus crowding. Phys. Rev. Lett. 106:046102. doi: 10.1103/PhysRevLett.106.046102

PubMed Abstract | CrossRef Full Text | Google Scholar

Borodin, O., Ren, X., Vatamanu, J., von Wald Cresce, A., Knap, J., and Xu, K. (2017). Modeling insight into battery electrolyte electrochemical stability and interfacial structure. Acc. Chem. Res. 50, 2886–2894. doi: 10.1021/acs.accounts.7b00486

PubMed Abstract | CrossRef Full Text | Google Scholar

Bresme, F., Chacón, E., Tarazona, P., and Wynveen, A. (2012). The structure of ionic aqueous solutions at interfaces: an intrinsic structure analysis. J. Chem. Phys. 137:114706. doi: 10.1063/1.4753986

PubMed Abstract | CrossRef Full Text | Google Scholar

de Souza, J. P., Goodwin, Z. A. H., McEldrew, M., Kornyshev, A. A., and Bazant, M. Z. (2020). Interfacial layering in the electric double layer of ionic liquids. Phys. Rev. Lett. 125:116001. doi: 10.1103/PhysRevLett.125.116001

PubMed Abstract | CrossRef Full Text | Google Scholar

Frömling, T., Kunze, M., Schönhoff, M., Sundermeyer, J., and Roling, B. (2008). Enhanced lithium transference numbers in ionic liquid electrolytes. J. Phys. Chem. B 112, 12985–12990. doi: 10.1021/jp804097j

PubMed Abstract | CrossRef Full Text | Google Scholar

Gebbie, M. A., Smith, A. M., Dobbs, H. A., Lee, A. A., Warr, G. G., Banquy, X., et al. (2017). Long range electrostatic forces in ionic liquids. Chem. Commun. 53, 1214–1224. doi: 10.1039/C6CC08820A

PubMed Abstract | CrossRef Full Text | Google Scholar

Goyal, P., and Monroe, C. W. (2017). New foundations of Newman's theory for solid electrolytes: thermodynamics and transient balances. J. Electrochem. Soc. 164, E3647–E3660. doi: 10.1149/2.0611711jes

CrossRef Full Text | Google Scholar

Hirschfelder, J. O., Bird, R. B., and Curtiss, C. F. (1964). Molecular Theory of Gases and Liquids. New York, NY: Wiley.

Google Scholar

Hoffmann, V., Pulletikurthi, G., Carstens, T., Lahiri, A., Borodin, A., Schammer, M., et al. (2018). Influence of a silver salt on the nanostructure of a Au(111)/ionic liquid interface: an atomic force microscopy study and theoretical concepts. Phys. Chem. Chem. Phys. 20, 4760–4771. doi: 10.1039/C7CP08243F

PubMed Abstract | CrossRef Full Text | Google Scholar

Hou, T., and Monroe, C. W. (2020). Composition-dependent thermodynamic and mass-transport characterization of lithium hexafluorophosphate in propylene carbonate. Electrochim. Acta 332:135085. doi: 10.1016/j.electacta.2019.135085

CrossRef Full Text | Google Scholar

Karimi, N., Zarrabeitia, M., Mariani, A., Gatti, D., Varzi, A., and Passerini, S. (2021). Nonfluorinated ionic liquid electrolytes for lithium metal batteries: ionic conduction, electrochemistry, and interphase formation. Adv. Energy Mater. 11:2003521. doi: 10.1002/aenm.202003521

CrossRef Full Text | Google Scholar

Kornyshev, A. A. (2007). Double-layer in ionic liquids: paradigm change? J. Phys. Chem. B 111, 5545–5557. doi: 10.1021/jp067857o

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, G., and Monroe, C. W. (2019). Dendrite nucleation in lithium-conductive ceramics. Phys. Chem. Chem. Phys. 21, 20354–20359. doi: 10.1039/C9CP03884A

CrossRef Full Text | Google Scholar

Lu, Y., Korf, K., Kambe, Y., Tu, Z., and Archer, L. A. (2014). Ionic-liquid-nanoparticle hybrid electrolytes: applications in lithium metal batteries. Angew. Chem. Int. Edn. 53, 488–492. doi: 10.1002/anie.201307137

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, Y., Doyle, M., Fuller, T. F., Doeff, M. M., Jonghe, L. C. D., and Newman, J. (1995). The measurement of a complete set of transport properties for a concentrated solid polymer electrolyte solution. J. Electrochem. Soc. 142, 1859–1868. doi: 10.1149/1.2044206

CrossRef Full Text | Google Scholar

McEldrew, M., Goodwin, Z. A. H., Kornyshev, A. A., and Bazant, M. Z. (2018). Theory of the double layer in water-in-salt electrolytes. J. Phys. Chem. Lett. 9, 5840–5846. doi: 10.1021/acs.jpclett.8b02543

PubMed Abstract | CrossRef Full Text | Google Scholar

Monroe, C. W. (2020). Mechanics of the ideal double-layer capacitor. J. Electrochem. Soc. 167:013550. doi: 10.1149/1945-7111/ab6b04

CrossRef Full Text | Google Scholar

Monroe, C. W., and Delacourt, C. (2013). Continuum transport laws for locally non-neutral concentrated electrolytes. Electrochim. Acta 114, 649–657. doi: 10.1016/j.electacta.2013.10.006

CrossRef Full Text | Google Scholar

Newman, J., and Thomas-Alyea, K. E. (2004). Electrochemical Systems, 3rd Edn. New York, NY: John Wiley & Sons.

Google Scholar

Nyman, A., Behm, M., and Lindbergh, G. (2008). Electrochemical characterisation and modelling of the mass transport phenomena in LiPF₆-EC-EMC electrolyte. Electrochim. Acta 53, 6356–6365. doi: 10.1016/j.electacta.2008.04.023

CrossRef Full Text | Google Scholar

Piper, D., Evans, T., Leung, K., Watkins, T., Olson, J., Kim, S., et al. (2015). Stable silicon-ionic liquid interface for next-generation lithium-ion batteries. Nat. Commun. 6:6230. doi: 10.1038/ncomms7230

PubMed Abstract | CrossRef Full Text | Google Scholar

Pollard, R., and Newman, J. (1979). Transport equations for a mixture of two binary molten salts in a porous electrode. J. Electrochem. Soc. 126, 1713–1717. doi: 10.1149/1.2128782

CrossRef Full Text | Google Scholar

Popovic, J., Pfaffenhuber, C., Melchior, J., and Maier, J. (2015). Determination of individual contributions to the ionic conduction in liquid electrolytes: case study of LiTf/PEGDME-150. Electrochem. Commun. 60, 195–198. doi: 10.1016/j.elecom.2015.09.009

CrossRef Full Text | Google Scholar

Salminen, J. P., Prausnitz, J., and Newman, J. (2006). Studies of ionic liquids in lithium-ion battery test systems. ECS Trans. 1, 107–118. doi: 10.1149/1.2209363

CrossRef Full Text | Google Scholar

Slattery, J., Daguenet, C., Dyson, P., Schubert, T., and Krossing, I. (2007). How to predict the physical properties of ionic liquids: a volume-based approach. Angew. Chem. Int. Edn. 46, 5384–5388. doi: 10.1002/anie.200700941

PubMed Abstract | CrossRef Full Text | Google Scholar

Sunkara, G. R., Tadavarthi, M. M., Tadekoru, V. K., Tadikonda, S. K., and Bezawada, S. R. (2015). Density, refractive index, and speed of sound of the binary mixture of 1-butyl-3-methylimidazolium tetrafluoroborate + N-vinyl-2-pyrrolidinone from T = (298.15 to 323.15) K at atmospheric pressure. J. Chem. Eng. Data 60, 886–894. doi: 10.1021/je500936y

CrossRef Full Text | Google Scholar

Valoen, L. O., and Reimers, J. N. (2005). Transport properties of LiPF₆-based Li-ion battery electrolytes. J. Electrochem. Soc. 152:A882. doi: 10.1149/1.1872737

CrossRef Full Text | Google Scholar

Vatamanu, J., and Borodin, O. (2017). Ramifications of water-in-salt interfacial structure at charged electrodes for electrolyte electrochemical stability. J. Phys. Chem. Lett. 8, 4362–4367. doi: 10.1021/acs.jpclett.7b01879

PubMed Abstract | CrossRef Full Text | Google Scholar

Wakai, C., Oleinikova, A., Ott, M., and Weingärtner, H. (2005). How polar are ionic liquids? Determination of the static dielectric constant of an imidazolium-based ionic liquid by microwave dielectric spectroscopy. J. Phys. Chem. B 109, 17028–17030. doi: 10.1021/jp053946+

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiong, S., Xie, K., Blomberg, E., Jacobsson, P., and Matic, A. (2014). Analysis of the solid electrolyte interphase formed with an ionic liquid electrolyte for lithium-sulfur batteries. J. Power Sour. 252, 150–155. doi: 10.1016/j.jpowsour.2013.11.119

CrossRef Full Text | Google Scholar

Xu, K. (2014). Electrolytes and interphases in Li-ion batteries and beyond. Chem. Rev. 114, 11503–11618. doi: 10.1021/cr500003w

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, Y.-H., Soriano, A. N., and Li, M.-H. (2009). Heat capacity and electrical conductivity of aqueous mixtures of [Bmim][BF₄] and [Bmim][PF₆]. J. Taiwan Inst. Chem. Eng. 40, 205–212. doi: 10.1016/j.jtice.2008.09.006

CrossRef Full Text | Google Scholar