Experimental and Modeling Investigation of CO3=/OH– Equilibrium Effects on Molten Carbonate Fuel Cell Performance in Carbon Capture Applications

Introduction

Molten Carbonate Fuel Cells (MCFCs) are electrochemical devices developed for electricity generation. For this reason, much of the past MCFC research was focused on new materials for increased cell performance (Accardo et al., 2017; Frattini et al., 2017; Accardo et al., 2017; Frattini et al., 2017; Baizeng et al., 1998; Kim et al., 2006; Özkan et al., 2015), resistance to pollutants and corrosion (Hernandez et al., 2014; Nguyen et al., 2013; Kim et al., 2018), the effects of operating conditions (Di Giulio et al., 2013; Rexed et al., 2014; Devianto et al., 2016), and the development of electrochemical models to aid theoretical studies and the design of cells, stacks and plants (Audasso et al., 2016; Liu and Weng, 2010; Ma et al., 2009; Meléndez-Ceballos et al., 2015; Szczęśniak et al., 2020; Lee et al., 2010). More recently, a new application of MCFCs for the conversion of industrial waste to produce electricity as thermo-electrochemical has also been developed (Kandhasamy et al., 2020; Kandhasamy et al., 2017).

However, in the last decades the use of MCFCs in CO₂ recovery for sequestration has gained more and more academic and commercial interest (Duan et al., 2015; Carapellucci et al., 2019; Mahmoudi et al., 2019; Audasso et al., 2018; Campanari et al., 2014; Wee, 2014; Barelli et al., 2016; Rexed et al., 2015; Duan et al., 2015). Compared to conventional amine-based technologies, in addition to the capture of CO₂ from flue gases, MCFCs also allow the simultaneous production of additional electricity, H₂ (if cells are fed with CH₄) and heat (Rosen et al., 2020). This provides a substantial efficiency advantage, as has been well documented by many simulations (Consonni et al., 2021; Campanari, 2002). MCFC operations depend on two parallel reactions: (1) carbonate ion formation from CO₂ and O₂ at the cathode and (2) the reduction of the resulting carbonate ion by H₂ at the anode that releases water and CO₂. This reaction chain (Eq. 1 - 3) transfers CO₂ from the cathode to the anode side, enabling the capture of CO₂ from power generation and industrial flue gases. Driven by the strong thermodynamic driving force of the net reaction, this process can readily capture up to 90% of CO₂ from power generation emissions by enriching the 4-10 vol. % CO₂ in the cathode feed to around 70 vol. % CO₂ (on dry basis) in the anode gas (Rosen et al., 2020). Simultaneously, MCFCs also allow the production of electricity and H₂ by exploiting possible internal reforming reactions. For these reasons, MCFCs are promising for CO₂ Capture and Storage (CCS) (Rosen et al., 2020).

$\frac{1}{2}{\text{O}}_2+{\text{CO}}_2+2e^{-}\to {\text{CO}}_3^{2-}\left(\text{cathode reaction}\right) (1)$

${\text{CO}}_3^{2-}+{\text{H}}_2\to {\text{CO}}_2+{\text{H}}_2\text{O}+2{\text{e}}^{-}\left(\text{anode reaction}\right)(2)$

$\frac{1}{2}{\text{O}}_2+ {\text{H}}_2+{\text{CO}}_{2,\text{cat}}\to {\text{CO}}_{2,\text{an}}+{\text{H}}_2\text{O} \left(\text{overall reaction}\right) (3)$

The deployment of MCFCs for CCS requires the assessment of their performance with dilute CO₂ cathode feeds that are rather different from the ones usually encountered when MCFCs are used for electricity generation. In this line of inquiry, an experimental campaign (Rosen et al., 2020) was conducted with low CO₂/H₂O ratios feed ratios (≤ 1) to simulate natural gas combined cycle plant flue gas exhaust and high CO₂ utilization factors (up to 95%). The results suggested that at these demanding conditions an analogous secondary anion reaction path (Eq. 4 -6) involving hydroxide ions can meaningfully contribute to the electrochemical process due to the depletion of CO₂ in the cathode, making MCFCs working as hydroxide molten carbonate fuel cells (Han et al., 2021; Han et al., 2021). Experimental data also showed that the branching ratio between the two anion paths is determined by the reacting cathode gas composition (Rosen et al., 2020) and that, to favor the carbonate path, it is necessary to enhance CO₂ diffusion (Rosen et al., 2020; Audasso et al., 2020b). We have defined this simultaneous migration of carbonate and hydroxide ions as a “dual-anion” mechanism (Audasso et al., 2020a).

$\frac{1}{2}{\text{O}}_2+{\text{H}}_2\text{O}+2{\text{e}}^{-}\to 2{\text{OH}}^{-}\left(\text{cathode reaction}\right)(4)$

$2{\text{OH}}^{-}+{\text{H}}_2\to 2{\text{H}}_2\text{O}+2{\text{e}}^{-}\left(\text{anode reaction}\right)(5)$

$\frac{1}{2}{\text{O}}_2+{\text{H}}_2+{\text{H}}_2{\text{O}}_{\text{cat}}\to 2{\text{H}}_2{\text{O}}_{\text{an}}\left(\text{overall reaction}\right)(6)$

This newly observed phenomenon has two different effects on cell operations: (i) it improves cell electrochemical performance because of the resulting higher concentration of activated oxidant species, but (ii) it decreases CO₂ capture efficiency because part of the current, and with it part of the fuel, will be used to drive water across the cell instead of CO₂. To first order, this will increase the amount of fuel and potentially the number of fuel cells required for the capture of a given amount of CO₂.

Considering these new findings and based on previous studies (Audasso et al., 2016; Arato et al., 2016), we developed the first semi-empirical dual-anion model to evaluate MCFC performance under these working conditions (Audasso et al., 2020a; Audasso et al., 2020b) using the circuit represented in Figure 1.

FIGURE 1

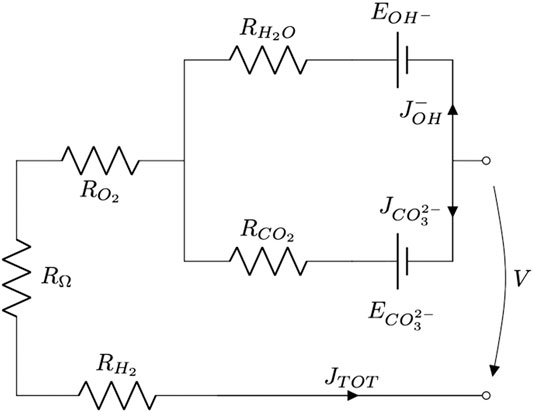
FIGURE 1. Schematic representation of the MCFC working with the dual-anion mechanism (carbonate-hydroxide).

The above circuit can be divided into three parts: a common branch and two parallel branches. The two parallel branches have different driving forces for each ionic path (${\text{E}}_{{\text{CO}}_3^{2-}}$ and ${\text{E}}_{{\text{OH}}^{-}}$ [V]) with corresponding independent current densities generated by the migration of the two anions (${\text{J}}_{{\text{CO}}_3^{2-}}$ and ${\text{J}}_{{\text{OH}}^{-}}$ [A cm^-2]) and cathodic resistances of the reactant gases forming the related anions (${\text{R}}_{{\text{CO}}_2}$ and ${\text{R}}_{{\text{H}}_2\text{O}}$ [Ω cm²]). The common branch has the total current density (J_TOT [A cm^-2]) flowing through the cell, and the anodic H₂ and cathodic O₂ resistances (${\text{R}}_{{\text{H}}_2}$ and ${\text{R}}_{{\text{O}}_2}$ [Ω cm²]), and the overall cell ohmic resistance (${\text{R}}_{\text{Ω}}$ [Ω cm²]). Our previous analysis of experimental data showed negligible effects of having common anodic and ohmic resistances for the paths in the dual-anion mechanism. Finally, in the circuit of Figure 1, V [V] is the measured cell potential. This circuit represents the traditional parallel circuit and follows Kirchoff’s Laws for current flow and common voltage at nodes.

To characterize the branching ratio between the two paths, we defined the transference number of the m-th anion (${\text{t}}_{\text{m}}$) as the ratio between the current due to the m-th ion migration (${\text{J}}_{\text{m}}$) over the total current density flowing through the cell (${\text{J}}_{\text{TOT}}$) as in Eq. 7:

${\text{t}}_{\text{m}}=\frac{{\text{J}}_{\text{m}}}{{\text{J}}_{\text{TOT}}}(7)$

In the present work, on the basis of our Raman evidence, we developed an improved model that is able to accurately model the transference number over a wider range of conditions than our previous models. The starting point of the new model is the carbonate / hydroxide equilibrium determined by Raman spectroscopy. We will show that while the previous model was effective at simulating the then-available experimental data, it performed poorly at the extremes of carbon capture conditions. Furthermore, the previous model did not account for the effect of temperature. These issues will be addressed here with the addition of the equilibrium reaction, improving the agreement between experimental and calculated cell performance data, especially at the extreme operating conditions.

Experimental evidence of carbonate / hydroxide equilibrium

Melt composition

In previous studies (Audasso et al., 2020a; Audasso et al., 2020b; Rosen et al., 2020) we had not directly observed the presence of ${\text{OH}}^{-}$ ions in the electrolyte melt. We developed the dual-anion model construct based on global mass balances that indicated the cathode-anode migration of not only CO₂, but also that of H₂O. The data strongly implied that at low cathode CO₂/H₂O ratios OH^- anions must be present in the molten salt electrolyte phase. To obtain direct evidence, we now used Raman spectroscopy to probe the CO₃^2-/OH^- equilibrium in the molten salt phase as a function of the CO₂ / H₂O ratio in the gas phase. In our experiments, we exposed a molten carbonate eutectic mixture to water vapor (10 mol %) and different concentrations of CO₂, ranging from 0 to 15 mol % with N₂ as the balance in the gas phase keeping a total flow rate of 24 sccm. Each condition was maintained for several hours to reach equilibrium as indicated by the spectral evolution of the molten phase.

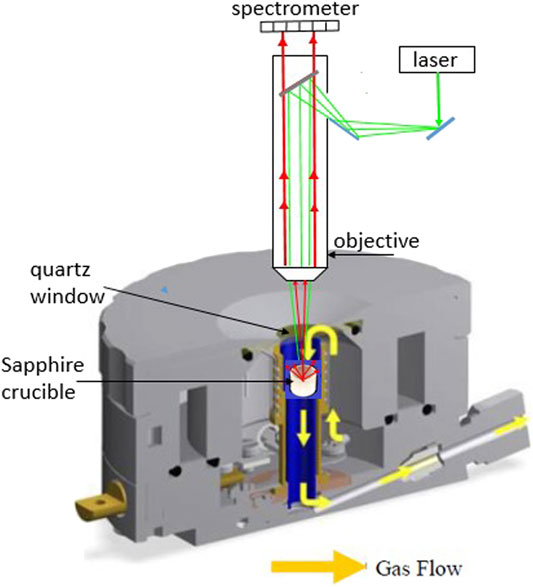
The spectra were collected using a Horiba Jobin-Yvon LabRAM Aramis confocal micro-Raman spectrometer with a 532 nm diode pumped solid state laser and an 1800 grooves mm^-1 grating. The confocal microscope was coupled to a 460-mm focal length spectrograph configured in a 180° backscattered arrangement. We used a free-space Olympus BXFM microscope, a Peltier-cooled 1024 × 256, back-illuminated deep-depletion CCD, with a Mitutoyo M Plan APO, SL20x (NA 0.42) objective having a working distance of 20 mm. A 15-second integration time with 3 scans was averaged per spectrum in a collection range of 100-4000 cm^-1. The data were analyzed using the Grams AI software package. Band fitting was performed using the Gaussian-Lorentz function on the carbonate and hydroxyl peaks in the 900-1200 and 3400-3800 cm^-1 region, respectively.

We used a Linkam CCR1000 high temperature catalyst cell reactor (see schematization in Figure 2). The eutectic was loaded into a sapphire crucible and was placed on a ceramic cloth inside of the sample holder. The sample holder was then loaded into the cell. The cell lid was fitted with a quartz window. The composition of the eutectic electrolyte was 52/48 mol % of Li₂CO₃/Na₂CO₃. All spectra were taken at 923 K, and to reach this temperature the cell was heated with a heating rate of 10 K min^-1. We used the ratio of peak areas to compensate for changes in absolute signal intensities that could occur due to changes in focusing distance over the course of an experiment.

FIGURE 2

FIGURE 2. Schematic of the in-situ Raman experimentation setup using the Linkam cell.

In Figure 3 a representative Raman spectrum obtained in our experiments is presented. The major peak at 1064 cm^-1 corresponds to the symmetric stretching vibration of the ${\text{CO}}_3^{2-}$ ion. It is typically the more intense of the other carbonate peaks at 1409 and 698 cm^-1 (Mizuhata et al., 2009; Zakir’yanova et al., 2018). Additionally, a hydroxide related peak at about 3600 cm^-1 was observed at all the studied conditions (Zakiriyanova et al., 1999). This suggests that even under normal molten carbonate fuel cell operations hydroxide must be present at a very small amount in the molten electrolyte due to the water content of either the anode or cathode.

FIGURE 3

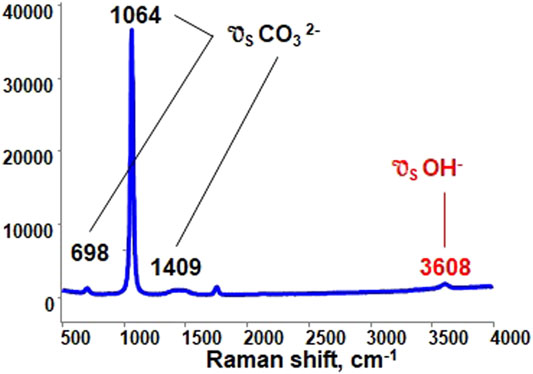
FIGURE 3. Raman spectra of lithium/sodium carbonate eutectic under 10% v/v water vapor, balanced with N₂ at 923 K.

The analysis of the peak areas is the first step to generating experimental estimates of the hydroxide/carbonate equilibrium constant:

$2{\text{OH}}_{\mathrm{}}^{\mathrm{}{-}_{\left(melt\right)}}+{\text{CO}}_{2_{\left(gas\right)}}\mathrm{\leftrightarrows }{\text{H}}_2{\text{O}}_{\mathrm{}\left(gas\right)}+{\text{CO}}_3^{2{-}_{\left(melt\right)}}(8)$

The equilibrium constant, $K_{\text{eq}}$, for the reversible reaction (8) can be expressed as:

${\text{K}}_{\text{eq}}=\frac{\left[{\text{H}}_2\text{O}\right]\left[{\text{CO}}_3^{2-}\right]}{\left[{\text{CO}}_2\right]{\left[{\text{OH}}^{-}\right]}^2}(9)$

Since the water concentration was kept constant in our experiments, the slope of a plot of $\left[{\text{CO}}_3^{2-}\right]/{\left[{\text{OH}}^{-}\right]}^2$ vs. [CO₂] would be also constant and equal to $K_{\text{eq}}/\left[{\text{H}}_2\text{O}\right]$. Determining the Raman response factors for the carbonate and hydroxide ions at these elevated temperatures proved difficult and have not yet been accomplished. Consequently, we could not convert the carbonate and hydroxide Raman peak intensities into concentrations. Nonetheless, the spectral analysis affords the demonstration of the expected equilibrium correlation. This is demonstrated below in Figure 4 showing the expected linear correlation of $\left[{\text{CO}}_3^{2-}\right]/{\left[{\text{OH}}^{-}\right]}^2$ and [CO₂]. This equilibrium conversion between hydroxide and carbonate is also evident in experimental observations on molten hydroxide fuel cells in which CO₂ is poisonous to the cell because it converts hydroxide into carbonate (Hemmes and Cassir, 2011; Frangini and Masi, 2016; Xing et al., 2017). Furthermore, a recent molecular dynamics study (Young et al., 2020) reported that at a gas phase H₂O/CO₂ molar ratio of 10, a 40/60 Li/K molten carbonate eutectic comprises ∼5/95 ${\text{OH}}^{-}$/${\text{CO}}_3^{2-}$ at 923 K.

FIGURE 4

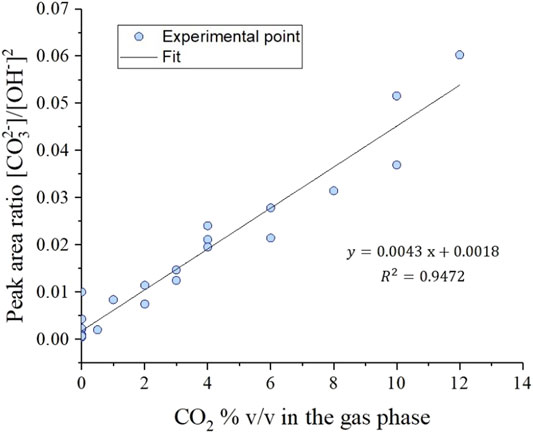
FIGURE 4. Raman ${\left[\mathrm{C}{\mathrm{O}}_3^{2-}]/[\mathrm{O}{\mathrm{H}}^{-}\right]}^2$ peak area ratios vs. CO₂ % v/v at constant 10 mol % steam concentration in the gas phase.

This experimental observation directly proves that the MCFC electrolyte composition is not 100% carbonate under carbon capture conditions. Instead, the electrolyte melt also contains hydroxide ions in accordance with the carbonate/hydroxide equilibrium. To satisfy this equilibrium, hydroxide forms in MCFCs by reducing water introduced in the cathode feed. That hydroxide in turn participates in carrying current in the MCFC and oxidizing H₂ to two H₂O molecules at the anode resulting in a net water transport across the cell. All else being equal, the split between the competing carbonate and hydroxide electrochemical paths is governed by the [${\text{CO}}_3^{2-}$]/[${\text{OH}}^{-}$] ratio and thus ultimately by the equilibrium expressed in Eq. 9.

Internal resistance alteration

The presence of ${\text{OH}}^{-}$ should influence the ohmic resistance (${\text{R}}_{\text{Ω}}$) of the cell as it alters the electrolyte composition and thus its conductivity. Since the melt equilibrium is determined by the gas phase as shown by the Raman results presented above, this means that the inlet gas composition should have an effect on the ohmic resistances, ${\text{R}}_{\text{Ω}}$. This dependence has not been adequately studied in the literature and usually the MCFC ohmic resistance is considered as a function solely of the operating temperature (Yoshiba et al., 2000; Morita et al., 2002). It is important to emphasize that the ohmic resistance is usually considered as the sum of the different contributions due to all of the components that constitute the cell (electrodes, electrolyte, current collectors, etc). In our analysis the focus was on the electrolyte contribution as it is the only one that was assumed influenced by the gas phase. Thus, at constant operating temperature the ohmic resistance can be considered as a constant value due to the overall cell components and a varying contribution due to the electrolyte.

For the development of the dual-anion model, different experimental campaigns were conducted to gain a proper understanding of the mechanisms and dependences involved in the dual-anion mechanism (Rosen et al., 2020). In these campaigns, data were collected in different operating conditions of anode and cathode total flow rates and compositions, operating temperature, fuel (H₂) and oxidant (CO₂ and H₂O) utilization factors. Our data analysis indicates that the measured ${\text{R}}_{\text{Ω}}$ values vary not only with the operating temperature, but also with changes in the gas flow and composition, as expected by changes in electrolyte composition observed by Raman spectroscopy.

As hydroxides have a higher conductivity compared to the corresponding carbonate (Janz and Tomkins, 1983; Mondal et al., 2020) (e.g., Li₂CO₃ vs. LiOH), the ohmic resistance is expected to decrease with increasing hydroxide concentration in the electrolyte melt. Thus, as the carbonate/hydroxide equilibrium shifts, ${\text{R}}_{\text{Ω}}$ should decrease with decreasing CO₂/H₂O ratios in the cathode gas. This dependence of ${\text{R}}_{\text{Ω}}$ on the melt composition may result in measurable effects particularly in the area of the cell where CO₂ in the gas is depleted.

In Figure 5 the various ${\text{R}}_{\text{Ω}}$ values from the wide variety of experiments are plotted against the two main variables related to the hydroxide content in the melt: (A) the cathode CO₂ average concentration between the inlet and the outlet of the cell, and (B) the utilization factor of CO₂. In the experiments in which the ${\text{R}}_{\text{Ω}}$ values were measured the average H₂O concentration was not changed significantly (<±4%), and thus it induced no noticeable changes. 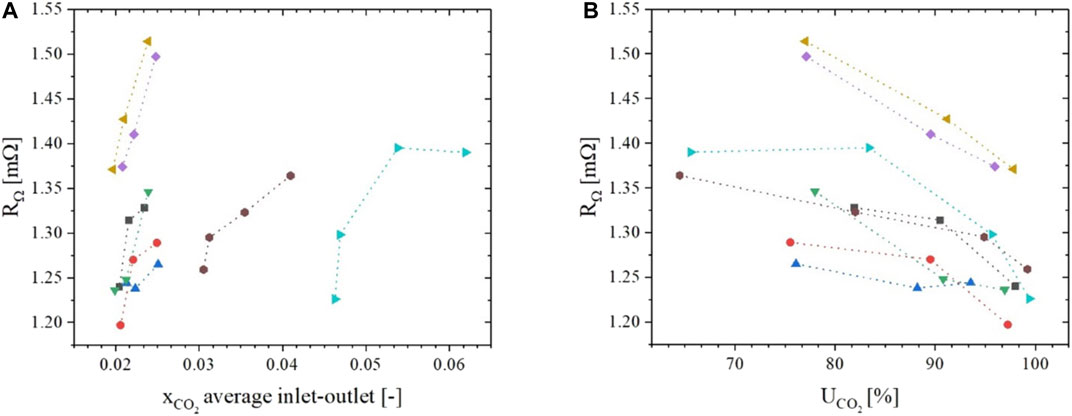Figure 5A shows the resistance dependence on the average cell concentration of CO₂. As expected, the data show that with increasing CO₂ in the cathode gas in a given series, the ohmic resistance increases. The increasing ohmic resistance is in accordance with the above-discussed conductivity change at reduced OH^- concentrations as the OH^- formation is disfavored at higher gas phase CO₂/H₂O ratios. Figure 5B depicts the dependence on the CO₂ utilization factor (${\text{U}}_{{\text{CO}}_2}$). In all sequences of Figure 5B, ohmic resistance decreases with increasing CO₂ utilization as CO₂ concentration goes down at constant H₂O concentration resulting in increasing H₂O/CO₂ ratios and thus increasing OH^- concentrations.

FIGURE 5

FIGURE 5. ${\mathrm{R}}_{\Omega }$ dependence on the inlet-outlet average ${\mathrm{x}}_{\mathrm{C}{\mathrm{O}}_2}$ molar fraction (A) and the utilization factor of CO₂(B). Each series in the graphs represents a set of experimental data with a single variable changed at a time.

Although changing cathode CO₂/H₂O ratios can cause detectable changes in ohmic resistance, the variation in our tests was less than 10%. Hence, our earlier sensitivity analysis (Bove et al., 2020) concluded that it has a negligible impact on the measured voltage (∼1 mV) at typical current densities of 100 mA cm^-2. For this reason, although detectable and interesting from a theoretical point of view, we decided to neglect this aspect in our model. It is possible, though, that at more extreme operating conditions this approach may need to be revised.

Apparent CO₂ utilization

One of the most effective ways we found to understand the extent of the dual-anion mechanism is to analyze the CO₂ utilization factor (${\text{U}}_{{\text{CO}}_2}$). Three different utilization factors can be distinguished: measured, apparent, and simulated. The measured utilization factor, ${\text{U}}_{{\text{CO}}_2,\text{measured}}$, is the CO₂ utilization experimentally obtained from material balances and is the ratio between the CO₂ consumed in the cathodic reactions and the CO₂ in the cathode feed (Eq. 10). The ${\text{U}}_{{\text{CO}}_2,\text{measured}}$, should be properly predicted by the simulated utilization factor, ${\text{U}}_{{\text{CO}}_2,\text{ simulated}},$ which is computed by solving the circuit of Figure 1 using Kirchoff’s Law (Eq. 11). The apparent utilization factor, ${\text{U}}_{{\text{CO}}_2,\text{ apparent}}$ (Eq. 12), on the other hand, is the CO₂ utilization that would be obtained if all the current was due to the migration only of carbonate ions. If the MCFC does not contain water at the cathode inlet or is operated at very low, but not zero, current density, the MCFC will have only carbonate ion migration, and all three utilizations are equal. On the contrary, if some of the current is carried by hydroxide ions, the apparent utilization will be always higher than the measured as the hydroxide ion is now carrying some of the current. Indeed, the apparent utilization can be higher than 100%, which is a clear demonstration of the dual-anion nature of the fuel cell operation. An exception to these comments is operation near an open circuit, where the current due to hydroxide anions can be negative (Rosen et al., 2020).

$U_{{\text{CO}}_2,\text{measured}}=\frac{F_{{\text{CO}}_2,\text{cat}-\text{in}}-F_{{\text{CO}}_2,\text{cat}-\text{out}}}{F_{{\text{CO}}_2,\text{cat}-\text{in}}}\cdot 100(10)$

$U_{{\text{CO}}_2,\text{simulated}}=\frac{\frac{J_{{\text{CO}}_3^{2-}} \text{⋅}{A}_{\text{cell}} }{2F}}{F_{{\text{CO}}_2,\text{cat}-\text{in}}}\cdot 100(11)$

$U_{{\text{CO}}_2,\text{apparent}}=\left(\frac{\left(\frac{J_{\text{TOT}} \text{⋅}{A}_{\text{cell}}}{2F}\right)}{F_{{\text{CO}}_2,\text{cat}-\text{in}}}\right)\cdot 100(12)$

During the analysis of the experimental data (Rosen et al., 2020), we observed that, at otherwise similar conditions, the discrepancy between the apparent and measured CO₂ utilizations increases as the CO₂/H₂O ratio decreases. This is summarized in graphs A and B of Figure 6. This observation suggested, and the above-presented Raman spectroscopy confirmed, that this increasing gap is indeed due to the formation and migration of ${\text{OH}}^{-}$ ions across the cell resulting in a net transport of H₂O from the cathode to the anode side.

FIGURE 6

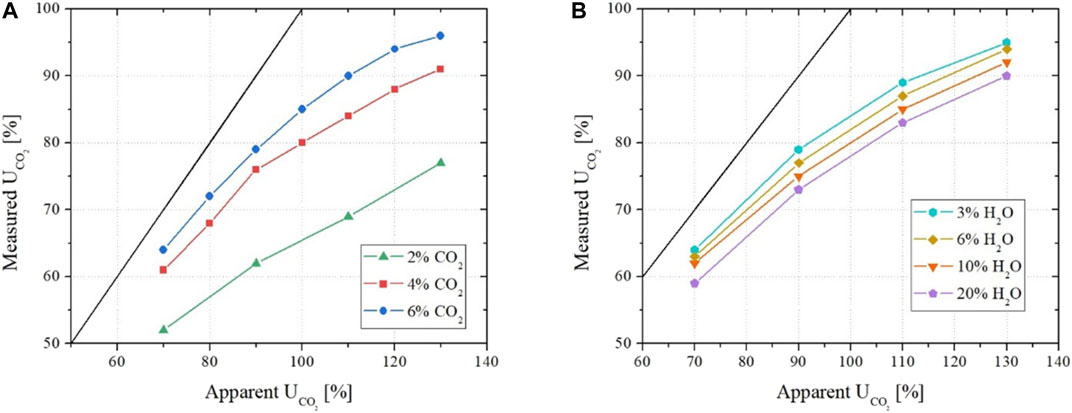
FIGURE 6. Apparent versus measured utilization factor of CO₂ as a function of different inlet concentrations of CO₂(A) and H₂O (B).

The data shown in graphs A and B of Figure 6 were collected at a constant operating temperature of 923 K. To improve the understanding of the phenomenon and thus properly expand the model range of operability, we repeated similar analyses at different operating temperatures. The graph in Figure 7 presents the results for five temperature sets of four experimental conditions. The conditions for those four data sets are presented in Table 1, while information on the single cell apparatus used in the experiments can be found in (Rosen et al., 2020).

FIGURE 7

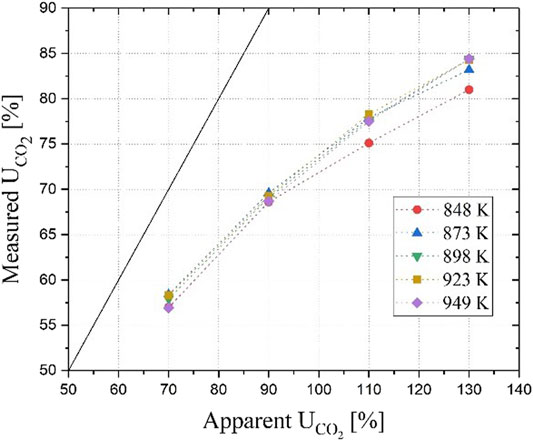
FIGURE 7. Apparent versus measured utilization factor of CO₂ as a function of different operating temperatures. Test conditions for the individual data points are listed in Table 1.

TABLE 1

TABLE 1. Data used in the analysis of the temperature effects on the dual-anion mechanism.

The graph shows that at different operating temperatures the measured utilization factors nearly overlap indicating that temperature has a negligible effect on the ratio of ionic conduction between the carbonate and the hydroxide paths. This is consistent with our previous results (Audasso et al., 2020b) showing that the contribution of one path over the other is mainly dependent on the cathode-side diffusion process and only slightly affected by the temperature in the studied range. Because of the dominance of transport effects, the operating temperature does not have significant influence on the carbonate/hydroxide equilibrium constant in the temperature operability range of MCFCs. These results also justify the simplification of the activation resistance in our earlier-published model because it is either constant (fitting its value with the diffusion polarization) or negligible (assuming a small value due to the high operating temperatures) (Audasso et al., 2020a).

Performance modeling

Temperature dependent dual-anion model

For the first-presented MCFC dual-anion model (Audasso et al., 2020a; Audasso et al., 2020b), we did not include the effects of the operating temperature on the polarization resistances because we initially focused on identifying the electrochemical phenomena involved and their controlling factors. Consequently, the initial experimental data were primarily collected at a constant operating temperature of 923 K and thus the temperature effect on the relative contributions of the competing reaction paths could not be addressed. This limited the model to a single temperature. We now extended the model applicability by allowing for the variation of the operating temperature. This is essential if the model is to be applied in industrial applications that could run at different temperatures at which the contribution of the competing reaction channels may vary. Also, these applications use larger cells (area of about 1 m² (Hishinuma & Kunikata, 1997)) with significant temperature gradients.

Following a previously presented derivation from the Butler-Volmer’s equation (Audasso et al., 2020a), the polarization resistances of the reactants can be rewritten to address the temperature dependence as follows:

$R_{{\text{CO}}_2}=-\frac{P_{{\text{CO}}_2,1} T}{J_{{\text{CO}}_3^{2-}}}\ln \left(1-\frac{J_{{\text{CO}}_3^{2-}}}{P_{{\text{CO}}_2,2} e^{\frac{P_{{\text{CO}}_2,3}}{T}} p y_{{\text{CO}}_2,\text{average}}}\right)(13)$

$R_{{\text{H}}_2\text{O}}=-\frac{P_{{\text{H}}_2\text{O},1} T}{J_{{\text{OH}}^{-}}}\ln \left(1-\frac{J_{{\text{OH}}^{-}}}{P_{{\text{H}}_2\text{O},2} e^{\frac{P_{{\text{H}}_2\text{O},3}}{T}} p y_{{\text{H}}_2\text{O},\text{average}}}\right)(14)$

$R_{{\text{H}}_2}=-\frac{P_{{\text{H}}_2,1}T}{J_{\text{TOT}}}\ln \left(1-\frac{J_{\text{TOT}}}{P_{{\text{H}}_2,2} e^{\frac{P_{{\text{H}}_2,3}}{T}} p\ln \left(1+y_{{\text{H}}_2}\right)}\right)(15)$

$R_{{\text{O}}_2}=P_{{\text{O}}_2,1}T e^{\frac{P_{{\text{O}}_2,2}}{T}} p^{0.5}\frac{y_{{\text{CO}}_2,\text{average}}}{y_{{\text{O}}_2,\text{average}}^{0.5}}(16)$

Note that unlike in our previous work (Audasso et al., 2020a; Audasso et al., 2020b), here we have assumed a non-linear dependence for the H₂. This was done to better handle higher fuel utilizations where a significant portion of the H₂ may be consumed inducing increased diffusion resistance on the anode side.

The ohmic resistance is usually described in the literature with an exponential function of the operating temperature such as the one expressed in Eq. 17 (Bosio et al., 2014; Morita et al., 1998):

$R_{\Omega }=P_{\Omega ,1} e^{\frac{P_{\Omega ,2}}{T}}(17)$

To fit the parameters of the ohmic resistance, experimental data were collected using two different cells at different operating temperatures. The results are shown in Figure 8.

FIGURE 8

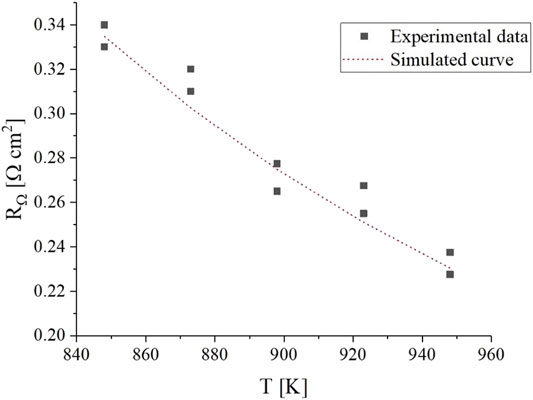
FIGURE 8. Experimental ${\text{R}}_{\Omega }$ as function of the operating temperature. The curve represents fitting to Eq. 17.

The effect of temperature on ohmic resistance is considerably higher than what is caused by electrolyte composition changes induced by changes in gas compositions. Between the highest and lowest analyzed temperatures, the value of resistance spans from 0.23 to 0.34 Ω cm² which corresponds to a ∼11 mV difference at typical current densities of 100 mA cm^-2. This is ten times higher than the effect of gas composition, and we deem it non-negligible.

The final set of kinetic parameters used in the model is presented in Table 2.

TABLE 2

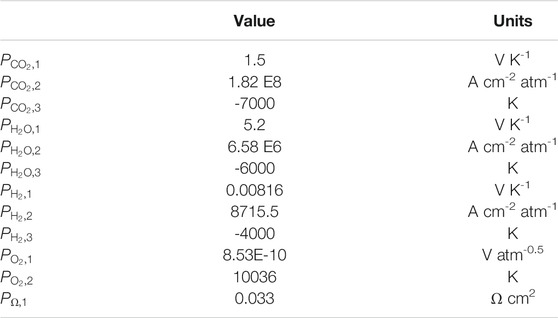
TABLE 2. Kinetic parameters used for the non-isothermal dual-anion model without the equilibrium correction. These parameters are to be used with the resistance formulas of Equations 13 through 17.

Using this temperature-dependent model, the experimental data at different operating temperatures were simulated. In Table 3, some of the main results of the simulations are presented and can be compared to the data in Figure 7. In the first three columns, the measured voltage, the simulated voltage, and the % error (in absolute value) are presented. For most entries the model replicates the experimental results with less than 2% error. Only a few data points collected with apparent CO₂ utilizations higher than 110% have significant errors with a maximum of 13% at 848 K. This outcome agrees with the simulation results presented in the our previous works (Audasso et al., 2020a; Audasso et al., 2020b) that also had the highest errors in correspondence with the data collected with high utilization factors. We attributed this to the lower experimental accuracy and reproducibility of these points. Since these data were acquired at CO₂-starved conditions, they are characterized by having a pronounced influence of the hydroxide path. In the last three columns, the experimentally measured and the simulated utilization factors are presented with the corresponding percentage errors. As shown in Table 3, the simulated utilization factors agree with the measured data both in terms of values and trend. Again, the worst results are the ones for high (>100%) CO₂ apparent utilization in combination with a low temperature (848 K); however, MCFCs are typically not used at these low temperatures.

TABLE 3

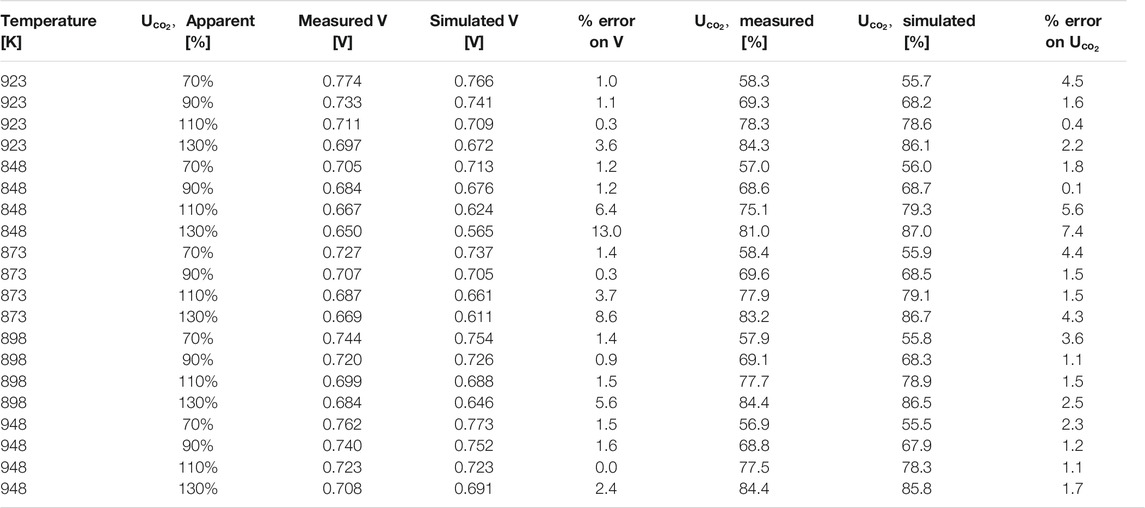
TABLE 3. Results of the temperature dependent model fitting for the data at different operating temperatures and apparent CO₂ utilization.

Using this newly developed temperature-dependent model with the parameters presented in Table 2, all experimental conditions (including the isothermal runs presented in (Rosen et al., 2020; Audasso et al., 2020b)) were simulated. This formulation was also implemented in the SIMFC code, an in-house 2D model based on local mass, energy, and momentum balances. The two graphs of Figure 9 show the results of the simulated vs. measured voltages for the complete experimental data set using the new, temperature-dependent model. In the graph on the top, the different colors represent different ${\text{U}}_{{\text{CO}}_2,\text{ measured}}$ values and the same applies to the experimentally measured ${\text{t}}_{{\text{CO}}_3^{2-}}$ results on the bottom. While now allowing for operation temperature changes, the average error for all the data is low, ∼7.3%, similar to the error found with the earlier-published single-temperature model (Audasso et al., 2020b).

FIGURE 9

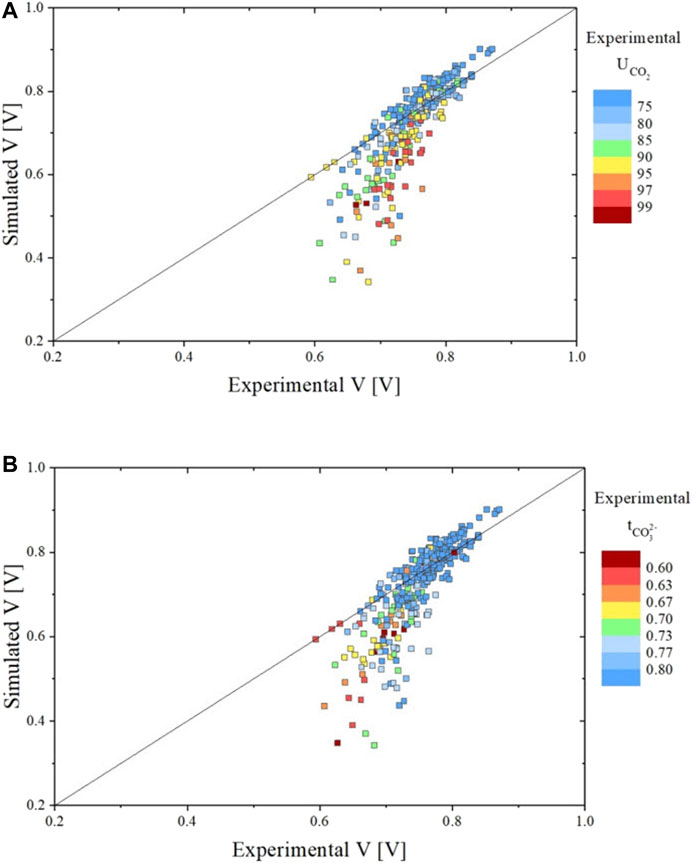
FIGURE 9. Parity plots showing the comparison between experimental and simulated data for all data sets in terms of voltage evaluated using the temperature dependent dual-anion model with H₂ resistance non-linear form. Graph A shows the voltage result colored in function of the ${\text{U}}_{{\text{CO}}_2,\text{measured}}$, Graph B of the experimentally measured ${\text{t}}_{{\text{CO}}_3^{2-}}$.

As observed with our previous model (Audasso et al., 2020b), the simulation results significantly deviate from the experimental values at very high CO₂ utilizations associated with low transference numbers. Model predictions thus worsen when the contribution of the hydroxide path becomes high. We performed additional refinements to mitigate this deviation (see below).

Dual-anion model further corrected by carbonate / hydroxide equilibrium

As discussed above and shown in Figure 9, model accuracy worsens when simulating cell potentials at high (>90%) CO₂ utilizations that correlate with low (<0.7) carbonate transference values. We postulate that this may be because the cathode gas concentrations we use in the resistance equations do not properly represent the local gas composition that determines the carbonate-hydroxide equilibrium (Eq. 8).

To account for the differences between the bulk and local gas concentrations, the polarization resistance equations for CO₂ and H₂O can be expressed in the following form:

$R_i=-\frac{P_{i,1} T}{J_m}\ln \left(1-\frac{J_m}{P_{i,2} e^{\frac{P_{i,3}}{T}} p_i }\right)(18)$

where “i” indicates the i-th component and “m” the followed anionic path.

In this form, the ratio in the logarithmic part is an expression of the ratio between the bulk and the local gas concentrations, the latter corresponding to the gas composition in the cathode pores at the gas-liquid interphase. Thus, as explained in (Audasso et al., 2020a), ${\text{P}}_{\text{i},2}{\text{ e}}^{\frac{{\text{P}}_{\text{i},3}}{\text{T}}}$ groups the mass transfer resistance through the cell that involves transport of the gas from the bulk cathode stream to the gas-liquid interphase in the cathode pores, dissolution of the reactants into the melt, diffusion of reactant in the melt, etc. The pre-logarithmic ${\text{P}}_{\text{i,}1}\text{ T}/{\text{J}}_{\text{m}}$ is actually ${\text{α}}_{\text{i}}^{\text{'}}\text{RT}/{\text{α}}_{\text{e}}^{\text{'}}{\text{nFJ}}_{\text{m}}$, where ${\text{P}}_{\text{i},1}$ groups the following expression of constant: ${\text{α}}_{\text{i}}^{\text{'}}\text{R}/{\text{α}}_{\text{e}}^{\text{'}}{\text{z}}_{\text{e}}\text{F}$. This should have a value of about $4{\text{.}3\mathrm{x}10}^{-5}{\text{ J K}}^{-1}{\text{ s}}^{-1}{\text{ A}}^{-1}$ without taking into account the correction for the ratio between ${\text{α}}_{\text{i}}^{\text{'}}$ and ${\text{α}}_{\text{e}}^{\text{'}}$ that should be around unity (Bosio et al., 2003). However, the final value of ${\text{P}}_{\text{i},1}$ is usually chosen higher than the calculated one (Beale, 2004). This is the same in our model for the ${\text{P}}_{\text{i},1}$ of CO₂, H₂O, and also H₂. Although P_H2,1 is still close to the expected value, it greatly differs for both CO₂ and H₂O. In the development of the earlier models (Audasso et al., 2020a; Audasso et al., 2020b), we implicitly included a correction for the equilibrium, consequently altering the resistance values. However, since it is not properly specified and not necessarily constant over the entire cell plane, it may have resulted in overestimating some resistances, particularly in the sections of the cell where the contribution of the hydroxide path reaches its extremes. Therefore, to properly express the polarization resistances of CO₂ and H₂O, we must consider a more rigorous way to treat the carbonate/hydroxide equilibrium effects.

We begin by assuming that the polarization resistances of both CO₂ and H₂O can be modeled as the product between the pure electrochemical resistance and a function of the concentration of the related anion in the melt that increases or decreases the apparent resistance value according to the melt composition. We assume this function as the one presented in Eq. 19.

$R_i=f\left({\text{C}}_m\right)\times R_{i,\text{electrochemical}}(19)$

As a first attempt, we propose to express these modifying functions as linear functions of the ratio between the two anion concentrations, taking into account of their stoichiometry in the equilibrium reaction. These ratios can be then correlated to the bulk cathode gas concentration as follows:

$f\left({\text{CO}}_3^{2-}\right)=A_{{\text{CO}}_3^{2-}}\left(\frac{C_{{\text{CO}}_3^{2-}}}{C_{{\text{OH}}^{-}}^2}\right)=A_{{\text{CO}}_3^{2-}}\left(\frac{C_{{\text{H}}_2\text{O}}}{C_{{\text{CO}}_2}}\right)\frac{1}{K_{\text{eq}}}(20)$

$f\left({\text{OH}}^{-}\right)=A_{{\text{OH}}^{-}}\left(\frac{C_{{\text{OH}}^{-}}^2}{C_{{\text{CO}}_3^{2-}}}\right)=A_{{\text{OH}}^{-}}\left(\frac{C_{{\text{CO}}_2}}{C_{{\text{H}}_2\text{O}}}\right)K_{\text{eq}}(21)$

where C_m represents the concentration of the m-th reactant species, K_eq is the carbonate-hydroxide equilibrium constant, and A_m represents a constant that can be used to relate the expression to the polarization resistances. To simplify these functions and make them more manageable, we made several additional simplifying assumptions. For example, since the MCFC operating temperature range is limited, $K_{\text{eq}}$, can be assumed to be a constant value at all applied temperatures. Therefore, we can group it together with $A_{{\text{CO}}_3^{2-}}$ and $A_{{\text{OH}}^{-}}$ reducing the number of model parameters. As in our previous models (Audasso et al., 2016; Audasso et al., 2017), the dissolved gas concentrations are expressed as their molar fraction in the melt that can be correlated with their concentration in the gas phase using the Henry’s constants. As the values of the Henry’s constants for the reactants are unknown and not easily determined, and since their value can be assumed constant in the studied temperature range, they were lumped together with other constants in the parameter $P_{\text{i},2}$ in the resistance equation. In a similar way, here we can group them with $A_{{\text{CO}}_3^{2-}}$ and $A_{{\text{OH}}^{-}}$.

With these additional assumptions we obtain the two formulas (Eqs. 22 and 23) that require the fitting to experimental data of only one parameter each.

$f\left({\text{CO}}_3^{2-}\right)=A_{{\text{CO}}_3^{2-}}^{\prime }\left(\frac{y_{{\text{H}}_2\text{O}}}{y_{{\text{CO}}_2}}\right)(22)$

$f\left({\text{OH}}^{-}\right)=A_{{\text{OH}}^{-}}^{\prime }\left(\frac{y_{{\text{CO}}_2}}{y_{{\text{H}}_2\text{O}}}\right)(23)$

Where A′_m is a modified A_m that takes into account the substitution from the use of concentration to molar fractions. Substituting Eqs. 22 and 23 in Eq. 19, we can obtain the polarization resistances of CO₂ and H₂O. Since both A′_m and $P_{\text{m},1}$ are constants we condensed them into the single parameter $P_{\text{m},1}=P_{\text{m,}1}{A}^{\prime }{ }_{\text{m}}$.

$R_{\text{conc},{\text{CO}}_2}=-\left(\frac{y_{{\text{H}}_2\text{O},\text{average}}}{y_{{\text{CO}}_2,\text{average}}}\right)\frac{P_{{\text{CO}}_2,1} T}{J_{{\text{CO}}_3^{2-}}}\ln \left(1-\frac{J_{{\text{CO}}_3^{2-}}}{P_{{\text{CO}}_2,2} e^{\frac{P_{{\text{CO}}_2,3}}{T}} p y_{{\text{CO}}_2,\text{average}}}\right)(24)$

$R_{\text{conc},{\text{H}}_2\text{O}}=-\left(\frac{y_{{\text{CO}}_2,\text{average}}}{y_{{\text{H}}_2\text{O},\text{average}}}\right)\frac{P_{{\text{H}}_2\text{O},1} T}{J_{{\text{OH}}^{-}}}\ln \left(1-\frac{J_{{\text{OH}}^{-}}}{P_{{\text{H}}_2\text{O},2} e^{\frac{P_{{\text{H}}_2\text{O},3}}{T}} p y_{{\text{H}}_2\text{O},\text{average}}}\right)(25)$

For the above-described model equations the fitted kinetic parameters are presented in Table 4. Using these new parameters, the experimental data were refitted to test if an improvement could be achieved after its implementation in the SIMFC code. The comparisons of the measured and simulated voltages are presented in Figure 10. Clearly, the new model improved model predictions, particularly at high CO₂ utilizations, and the average voltage error is now reduced to ∼4% as compared to the ∼7% with the model without the equilibrium correction.

TABLE 4

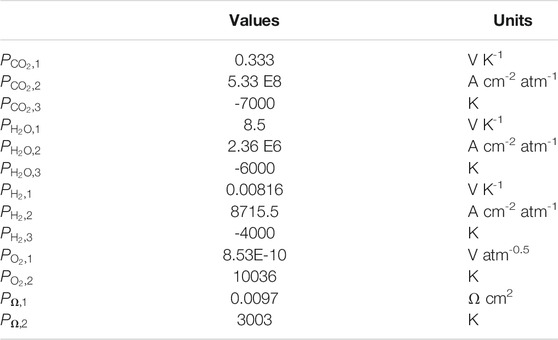
TABLE 4. Kinetic parameters used for the dual-anion model corrected by carbonate / hydroxide equilibrium. These parameters are to be used with the resistance formulas of Equations 15, 16, 17, 24, and 25.

FIGURE 10

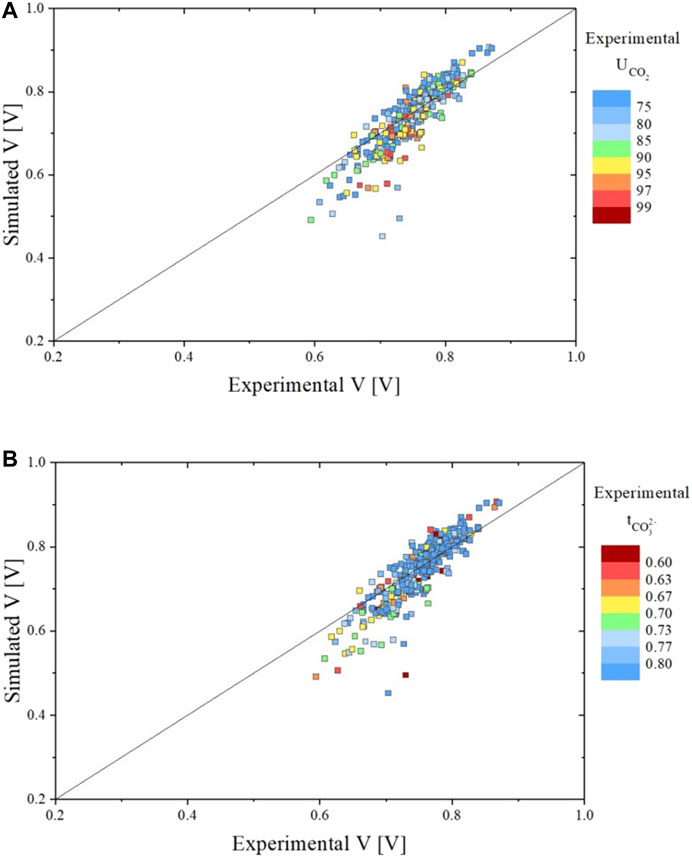
FIGURE 10. Parity plots showing the comparison between experimental and simulated data for all data sets in terms of voltage evaluated using the dual-anion model corrected by carbonate / hydroxide equilibrium. Graph A shows the voltage result colored in function of the $U_{{\text{CO}}_2,\text{measured}}$, graph B of the experimentally measured $t_{{\text{CO}}_3^{2-}}$.

Finally, in Figure 11, the simulation of the utilization factor of CO₂ (A) and the carbonate ions transference number (B) are presented for all the experimental data. For these simulations, the average percentage errors were respectively of about 4.5% for the utilization factor and of about 4.6% for the transference number. Both values were comparable to the one obtained in our previous works.

FIGURE 11

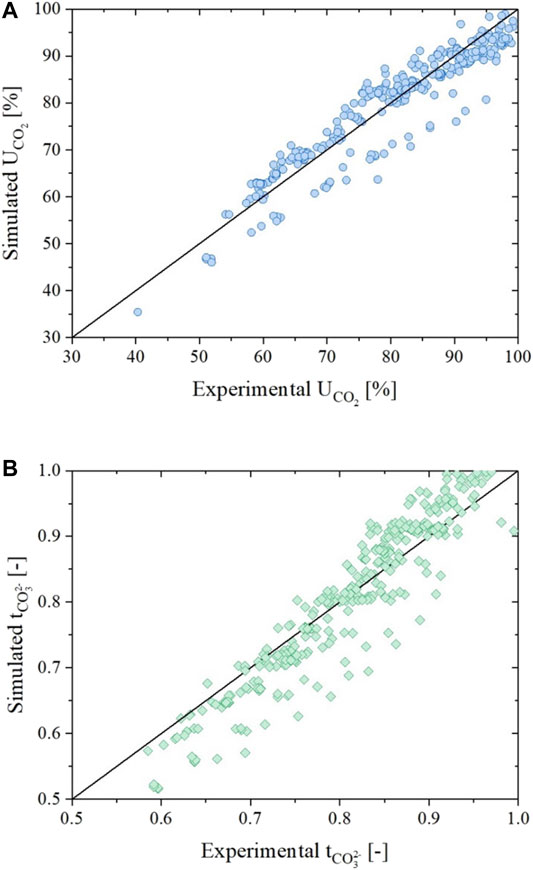
FIGURE 11. Parity plots showing the comparison between experimental and simulated data for all data sets in terms of utilization of CO₂(A) and carbonate ions transference number (B) evaluated using the dual-anion model corrected by carbonate / hydroxide equilibrium.

Conclusions

In a series of previous papers (Audasso et al., 2020a; Audasso et al., 2020b; Rosen et al., 2020), we described a newly discovered dual-anion mechanism that better fits the physical processes observed in MCFC operations, particularly in carbon capture applications where the cathode CO₂/H₂O ratios are low. This extended the model applicability into this low CO₂/H₂O cathode gas ratio. This new mechanism postulated the significant presence of water-derived hydroxide ions in the electrolyte and their participation in carrying charges across the fuel cell.

In the present contribution, through Raman spectroscopy, we were able to directly observe the presence of ${\text{OH}}^{-}$ in the melt even at high (>10% v/v) concentrations of CO₂. We found that the ratio of carbonate/(hydroxide)² peak areas linearly correlate with the gas phase CO₂ concentration at constant steam partial pressure, as can be expected from the corresponding equilibrium expression. The shifting carbonate/hydroxide ratio in the electrolyte as a function of cathode gas composition confirms that the cell ohmic resistance could vary as the conductivity of the electrolyte changes with its anion composition. This effect is particularly noticeable in carbon capture operations characterized by extremely low outlet CO₂/H₂O ratios and has been demonstrated experimentally (Rosen et al., 2020).

The temperature dependence of the polarization resistance was also rendered explicit in the current model and its applicability demonstrated with positive results. Analysis of the data showed that temperature does not have significant effect on the split between the two competing ionic pathways. As with the previous formulation, it showed to have an issue in dealing with conditions at which the hydroxide path becomes high. This model deficiency was hypothesized to derive from an implicit dependence of the polarization resistance on the carbonate/hydroxide equilibrium that could have led to overestimating the hydroxide path resistance. Thus, to improve predictions, the model was reformulated to include an explicit dependence of CO₂ and H₂O resistances on the carbonate-hydroxide equilibrium.

The final temperature-dependent, dual-anion model, and including the carbonate/hydroxide equilibrium was tested on the combined set of our experimental data. It showed satisfactory results with a reduction of the average voltage simulation error from 7.3% with the previous formulation to 4% with the current model, including the high CO₂ utilization conditions. In our experience this new model can be applied to satisfactorily simulate MCFCs integrated in complex systems for energy production and carbon capture applications.

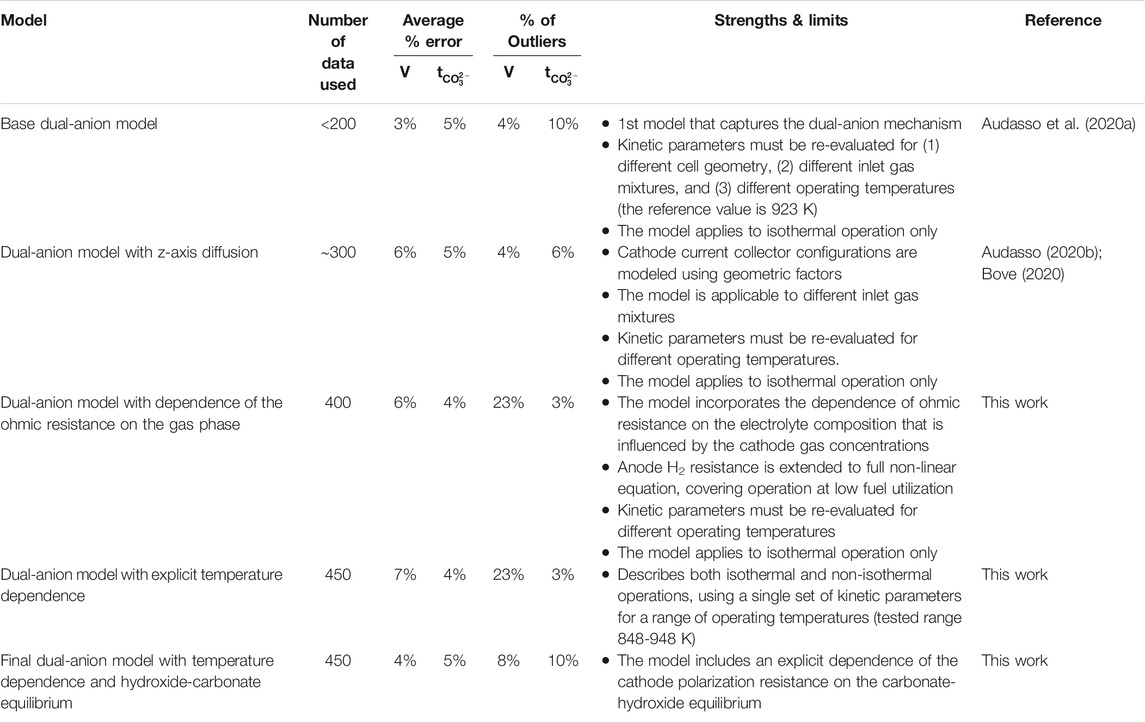
As a final conclusion to the series of papers on the dual-anion model (Audasso et al., 2020a; Audasso et al., 2020b), we show in Table 5 the progression of our model development and the impact each modification had on fitting the experimental data. In the table, the progress through the five modeling stages is presented. The table includes the number of experimental data used for fitting the parameters for each model, the average simulation error for voltage and carbonate ion transference number, the percentage of outliers (data with a simulated error of >10% from experiment), the strengths and limits of each model, and the publication references.

TABLE 5

TABLE 5. The progression of our dual-anion MCFC models.

It should be noted that as the complexity of the model increased, it did so because the range of conditions being covered by the model increased. The final model satisfactorily represents the cell operation over a very wide range of conditions, covering high and low fuel utilizations, high and low inlet CO₂ concentrations, high and low CO₂ apparent utilization, and current densities up to at least 150 mA cm^-2. Less obviously apparent in the data set coverage is that the model also includes terms to account for changes in the cell geometry, so that the electrochemical terms do not need to be refitted when the gas diffusion is changed in the cathode.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

Experimental: TB, HE, PK, GK, and JR. Data analysis: EA, GK, and BB. Software: EA, BB, and DB. Writing: EA, BB, TB, JR, and GK.

Conflict of Interest

DB, EA, and BB have no conflicts to report. TB, HE, PK, GK, and JR are employees of ExxonMobil Research and Engineering which is pursuing the commercial development of this technology.

References

Accardo, G., Frattini, D., Moreno, A., Yoon, S. P., Han, J. H., and Nam, S. W. (2017). Influence of Nano Zirconia on NiAl Anodes for Molten Carbonate Fuel Cell: Characterization, Cell Tests and post-analysis. J. Power Sourc. 338, 74–81. doi:10.1016/J.JPOWSOUR.2016.11.029

CrossRef Full Text | Google Scholar

Accardo, G., Frattini, D., Yoon, S. P., Ham, H. C., and Nam, S. W. (2017). Performance and Properties of Anodes Reinforced with Metal Oxide Nanoparticles for Molten Carbonate Fuel Cells. J. Power Sourc. 370, 52–60. doi:10.1016/J.JPOWSOUR.2017.10.015

CrossRef Full Text | Google Scholar

Arato, E., Audasso, E., Barelli, L., Bosio, B., and Discepoli, G. (2016). Kinetic Modelling of Molten Carbonate Fuel Cells: Effects of Cathode Water and Electrode Materials. J. Power Sourc. 336, 18–27. doi:10.1016/j.jpowsour.2016.08.123

CrossRef Full Text | Google Scholar

Audasso, E., Bosio, B., Bove, D., Arato, E., Barckholtz, T., Kiss, G., et al. (2020a). New, Dual-Anion Mechanism for Molten Carbonate Fuel Cells Working as Carbon Capture Devices. J. Electrochem. Soc. 167. doi:10.1149/1945-7111/ab8979

CrossRef Full Text | Google Scholar

Audasso, E., Bosio, B., Bove, D., Arato, E., Barckholtz, T., Kiss, G., et al. (2020b). The Effects of Gas Diffusion in Molten Carbonate Fuel Cells Working as Carbon Capture Devices. J. Electrochem. Soc. 167, 114515. doi:10.1149/1945-7111/aba8b6

CrossRef Full Text | Google Scholar

Audasso, E., Bosio, B., and Nam, S. (2016). Extension of an Effective MCFC Kinetic Model to a Wider Range of Operating Conditions. Int. J. Hydrogen Energ. 41, 5571–5581. doi:10.1016/j.ijhydene.2015.10.152

CrossRef Full Text | Google Scholar

Audasso, E., Campbell, P., Della Pietra, M., Ferrari, M. C., Bosio, B., and Arato, E. (2018). Molten Carbonate Fuel Cells in Integrated Systems for the Exploitation of Poor Fuels and the Segregation of CO₂. Bulg. Chem. Commun. 50, 99–107. https://www.scopus.com/inward/record.uri?eid=2-s2.0-85060040347&partnerID=40&md5=e6e1c26b442c8fb37c590209ac35e786

Google Scholar

Audasso, E., Nam, S., Arato, E., and Bosio, B. (2017). Preliminary Model and Validation of Molten Carbonate Fuel Cell Kinetics under sulphur Poisoning. J. Power Sourc. 352, 216–225. doi:10.1016/j.jpowsour.2017.03.091

CrossRef Full Text | Google Scholar

Baizeng, F., Xinyu, L., Xindong, W., and Shuzhen, D. (1998). Surface Modification of a MCFC Anode by Electrodeposition of Niobium. J. Electroanal. Chem. 441, 1–3. doi:10.1016/S0022-0728(97)00203-9

CrossRef Full Text | Google Scholar

Barelli, L., Bidini, G., Campanari, S., Discepoli, G., and Spinelli, M. (2016). Performance Assessment of Natural Gas and Biogas Fueled Molten Carbonate Fuel Cells in Carbon Capture Configuration. J. Power Sourc. 320, 332–342. doi:10.1016/j.jpowsour.2016.04.071

CrossRef Full Text | Google Scholar

Beale, S. B. (2004). Calculation Procedure for Mass Transfer in Fuel Cells. J. Power Sourc. 128, 185–192. doi:10.1016/j.jpowsour.2003.09.053

CrossRef Full Text | Google Scholar

Bosio, B., Arato, E., and Costa, P. (2003). Concentration Polarisation in Heterogeneous Electrochemical Reactions: a Consistent Kinetic Evaluation and its Application to Molten Carbonate Fuel Cells. J. Power Sourc. 115, 189–193. doi:10.1016/S0378-7753(02)00729-2

CrossRef Full Text | Google Scholar

Bosio, B., Di Giulio, N., Nam, S. W., and Moreno, A. (2014). An Effective Semi-empiric Model for MCFC Kinetics: Theoretical Development and Experimental Parameters Identification. Int. J. Hydrogen Energ. 39, 12273–12284. doi:10.1016/J.IJHYDENE.2014.04.119

CrossRef Full Text | Google Scholar

Bove, D., Audasso, E., Barckholtz, T., Kiss, G., Rosen, J., and Bosio, B. (2020). Process Analysis of Molten Carbonate Fuel Cells in Carbon Capture Applications. Int. J. Hydrogen Energ. 46. doi:10.1016/j.ijhydene.2020.08.020

CrossRef Full Text | Google Scholar

Campanari, S. (2002). Carbon Dioxide Separation from High Temperature Fuel Cell Power Plants. J. Power SourcesII. 112, 273–289. doi:10.1016/S0378-7753(02)00395-6

CrossRef Full Text | Google Scholar

Campanari, S., Chiesa, P., Manzolini, G., and Bedogni, S. (2014). Economic Analysis of CO₂ Capture from Natural Gas Combined Cycles Using Molten Carbonate Fuel Cells. Appl. Energ. 130, 562–573. doi:10.1016/J.APENERGY.2014.04.011

CrossRef Full Text | Google Scholar

Carapellucci, R., Di Battista, D., and Cipollone, R. (2019). The Retrofitting of a Coal-Fired Subcritical Steam Power Plant for Carbon Dioxide Capture: A Comparison between MCFC-Based Active Systems and Conventional MEA. Energy Convers. Manag. 194, 124–139. doi:10.1016/J.ENCONMAN.2019.04.077

CrossRef Full Text | Google Scholar

Consonni, S., Mastropasqua, L., Spinelli, M., Barckholtz, T. A., and Campanari, S. (2021). Low-carbon Hydrogen via Integration of Steam Methane Reforming with Molten Carbonate Fuel Cells at Low Fuel Utilization. Adv. Appl. Energ. 2, 100010. doi:10.1016/j.adapen.2021.100010

CrossRef Full Text | Google Scholar

Devianto, H., Sasongko, D., Sempurna, F. I., Nurdin, I., and Widiatmoko, P. (2016). Effect of Gas Composition Produced by Gasification, on the Performance and Durability of Molten Carbonate Fuel Cell (MCFC). J. Nat. Gas Sci. Eng. 35, 896–905. doi:10.1016/J.JNGSE.2016.08.075

CrossRef Full Text | Google Scholar

Di Giulio, N., Audasso, E., Bosio, B., Han, J., Nam, S. W., McPhail, S., et al. (2013). “The SO₂ Poisoning Influence on the Kinetics of MCFC,” in EFC 2013 - Proc. 5th Eur. Fuel Cell Piero Lunghi Conf. http://www.scopus.com/inward/record.url?eid=2-s2.0-84926303770&partnerID=MN8TOARS

Google Scholar

Duan, L., Sun, S., Yue, L., Qu, W., and Yang, Y. (2015). Study on a New IGCC (Integrated Gasification Combined Cycle) System with CO₂ Capture by Integrating MCFC (Molten Carbonate Fuel Cell). Energy 87, 490–503. doi:10.1016/J.ENERGY.2015.05.011

CrossRef Full Text | Google Scholar

Duan, L., Yue, L., Qu, W., and Yang, Y. (2015). Study on CO₂ Capture from Molten Carbonate Fuel Cell Hybrid System Integrated with Oxygen Ion Transfer Membrane. Energy 93, 20–30. doi:10.1016/j.energy.2015.07.137

CrossRef Full Text | Google Scholar

Frangini, S., and Masi, A. (2016). Molten Carbonates for Advanced and Sustainable Energy Applications: Part I. Revisiting Molten Carbonate Properties from a Sustainable Viewpoint. Int. J. Hydrogen Energ. 41, 18739–18746. doi:10.1016/J.IJHYDENE.2015.12.073

CrossRef Full Text | Google Scholar

Frattini, D., Accardo, G., Moreno, A., Yoon, S. P., Han, J. H., and Nam, S. W. (2017). A Novel Nickel-Aluminum alloy with Titanium for Improved Anode Performance and Properties in Molten Carbonate Fuel Cells. J. Power Sourc. 352, 90–98. doi:10.1016/J.JPOWSOUR.2017.03.112

CrossRef Full Text | Google Scholar

Frattini, D., Accardo, G., Moreno, A., Yoon, S. P., Han, J. H., and Nam, S. W. (2017). Strengthening Mechanism and Electrochemical Characterization of ZrO₂ Nanoparticles in Nickel–Aluminum alloy for Molten Carbonate Fuel Cells. J. Ind. Eng. Chem. 56, 285–291. doi:10.1016/J.JIEC.2017.07.021

CrossRef Full Text | Google Scholar

Han, Y., Zhang, H., and Hu, Z. (2021). A New Combined System Consisting of a Molten Hydroxide Direct Carbon Fuel Cell and an Alkali Metal thermal Electric Converter: Energy and Exergy Analyses. Appl. Therm. Eng. 185, 116417. doi:10.1016/j.applthermaleng.2020.116417

CrossRef Full Text | Google Scholar

Han, Y., Zhang, H., Hu, Z., and Hou, S. (2021). An Efficient Hybrid System Using a Graphene-Based Cathode Vacuum Thermionic Energy Converter to Harvest the Waste Heat from a Molten Hydroxide Direct Carbon Fuel Cell. Energy 223, 120095. doi:10.1016/j.energy.2021.120095

CrossRef Full Text | Google Scholar

Hemmes, K., and Cassir, M. (2011). A Theoretical Study of the Carbon/Carbonate/Hydroxide (Electro-) Chemical System in a Direct Carbon Fuel Cell. J. Fuel Cel Sci. Technol. 8 (051005), 1–5. doi:10.1115/1.4003750

CrossRef Full Text | Google Scholar

Hernandez, J. M., Lim, D.-H., Nguyen, H. V. P., Yoon, S.-P., Han, J., Nam, S. W., et al. (2014). Decomposition of Hydrogen Sulfide (H₂S) on Ni(100) and Ni₃Al(100) Surfaces from First-Principles. Int. J. Hydrogen Energ. 39, 12251–12258. doi:10.1016/J.IJHYDENE.2014.03.064

CrossRef Full Text | Google Scholar

Hishinuma, Y., and Kunikata, M. (1997). Molten Carbonate Fuel Cell Power Generation Systems. Energ. Convers. Manag. 38, 1237–1247. doi:10.1016/S0196-8904(96)00153-7

CrossRef Full Text | Google Scholar

Janz, G. J., and Tomkins, R. P. T. (1983). Molten Salts: Volume 5, Part 2. Additional Single and Multi‐Component Salt Systems. Electrical Conductance, Density, Viscosity and Surface Tension Data. J. Phys. Chem. Ref. Data 12, 591. doi:10.1063/1.555693

CrossRef Full Text | Google Scholar

Kandhasamy, S., Calandrino, L., Burheim, O. S., Solheim, A., Kjelstrup, S., and Haarberg, G. M. (2017). Influence of Electrode Gas Flow Rate and Solid Oxide Ratio in Electrolyte on the Seebeck Coefficient of Molten Carbonate Thermocell. J. Electrochem. Soc. 164, H5271–H5276. doi:10.1149/2.0391708jes

CrossRef Full Text | Google Scholar

Kandhasamy, S., Haarberg, G. M., Kjelstrup, S., and Solheim, A. (2020). Gas Electrodes with Nickel Based Current Collectors for Molten Carbonate Electrolyte Thermo-Electrochemical Cells. J. Energ. Chem. 41, 34–42. doi:10.1016/j.jechem.2019.05.001

CrossRef Full Text | Google Scholar

Kim, M. H., Hong, M. Z., Kim, Y.-S., Park, E., Lee, H., Ha, H.-W., et al. (2006). Cobalt and Cerium Coated Ni Powder as a New Candidate Cathode Material for MCFC. Electrochim. Acta 51, 6145–6151. doi:10.1016/j.electacta.2006.01.073

CrossRef Full Text | Google Scholar

Kim, M., Youn, J., Lim, J., Eom, K., Cho, E., and Kwon, H. (2018). Corrosion-resistant Coating for Cathode Current Collector and Wet-Seal Area of Molten Carbonate Fuel Cells. Int. J. Hydrogen Energ. 43, 11363–11371. doi:10.1016/j.ijhydene.2018.02.196

CrossRef Full Text | Google Scholar

Lee, S.-Y., Kim, D.-H., Lim, H.-C., and Chung, G.-Y. (2010). Mathematical Modeling of a Molten Carbonate Fuel Cell (MCFC) Stack. Int. J. Hydrogen Energ. 35, 13096–13103. doi:10.1016/j.ijhydene.2010.04.070

CrossRef Full Text | Google Scholar

Liu, A., and Weng, Y. (2010). Modeling of Molten Carbonate Fuel Cell Based on the Volume–Resistance Characteristics and Experimental Analysis. J. Power Sourc. 195, 1872–1879. doi:10.1016/J.JPOWSOUR.2009.10.040

CrossRef Full Text | Google Scholar

Ma, Z., Venkataraman, R., and Farooque, M., (2009). Fuel Cells – Molten Carbonate Fuel Cells. Modeling, Encycl. Electrochem. Power Sourc. 6. 519–532. doi:10.1016/B978-044452745-5.00272-0

CrossRef Full Text | Google Scholar

Mahmoudi, S. M. S., Ghavimi, A. R., and Yari, M. (2019). Two Objective Optimization for a New Molten Carbonate Fuel Cell Based Power Producing System. Appl. Therm. Eng. 155, 313–330. doi:10.1016/J.APPLTHERMALENG.2019.03.153

CrossRef Full Text | Google Scholar

Meléndez-Ceballos, A., Albin, V., Lair, V., Ringuedé, A., and Cassir, M. (2015). A Kinetic Approach on the Effect of Cs Addition on Oxygen Reduction for MCFC Application. Electrochim. Acta 184, 295–300. doi:10.1016/J.ELECTACTA.2015.10.057

CrossRef Full Text | Google Scholar

Mizuhata, M., Ohta, T., and Deki, S. (2009). Polarized Raman Spectra of Molten Carbonates Influenced by the Surface Acidity of the Coexisting Inorganic Powder. Electrochemistry 77, 721–724. doi:10.5796/electrochemistry.77.721

CrossRef Full Text | Google Scholar

Mondal, A., Young, J. M., Barckholtz, T. A., Kiss, G., Koziol, L., and Panagiotopoulos, A. Z. (2020). Transport and Interfacial Properties of Mixed Molten Carbonate/Hydroxide Electrolytes by Molecular Dynamics Simulations. J. Phys. Chem. C. 124, 23532–23540. doi:10.1021/acs.jpcc.0c07295

CrossRef Full Text | Google Scholar

Morita, H., Komoda, M., Mugikura, Y., Izaki, Y., Watanabe, T., Masuda, Y., et al. (2002). Performance Analysis of Molten Carbonate Fuel Cell Using a Li/Na Electrolyte. J. Power Sourc. 112, 509–518. doi:10.1016/S0378-7753(02)00468-8

CrossRef Full Text | Google Scholar

Morita, H., Mugikura, Y., Izaki, Y., Watanabe, T., and Abe, T. (1998). Model of Cathode Reaction Resistance in Molten Carbonate Fuel Cells. J. Electrochem. Soc. 145, 1511–1517. doi:10.1149/1.1838512

CrossRef Full Text | Google Scholar

Nguyen, H. V. P., Song, S. A., Seo, D., Han, J., Yoon, S. P., Ham, H. C., et al. (2013). Hydrogen Sulfide-Resilient Anodes for Molten Carbonate Fuel Cells. J. Power Sourc. 230, 282–289. doi:10.1016/J.JPOWSOUR.2012.12.077

CrossRef Full Text | Google Scholar

Özkan, G., Özkan, G., and İyidir, U. C. (2015). Synthesıs and Characterızatıon of Molten Carbonate Fuel Cell Anode Materıals, Energy Sources, Part A Recover. Util. Environ. Eff. 37, 2487–2495. doi:10.1080/15567036.2011.627415

CrossRef Full Text | Google Scholar

Rexed, I., della Pietra, M., McPhail, S., Lindbergh, G., and Lagergren, C. (2015). Molten Carbonate Fuel Cells for CO₂ Separation and Segregation by Retrofitting Existing Plants – an Analysis of Feasible Operating Windows and First Experimental Findings. Int. J. Greenh. Gas Control. 35, 120–130. doi:10.1016/j.ijggc.2015.01.012

CrossRef Full Text | Google Scholar

Rexed, I., Lagergren, C., and Lindbergh, G. (2014). Effect of Sulfur Contaminants on MCFC Performance. Int. J. Hydrogen Energ. 39, 12242–12250. doi:10.1016/J.IJHYDENE.2014.03.068

CrossRef Full Text | Google Scholar

Rosen, J., Geary, T., Hilmi, A., Blanco Gutierrez, R., Yuh, C. Y., Pereira, C. S., et al. (2020). Molten Carbonate Fuel Cell Performance for CO₂ Capture from Natural Gas Combined Cycle Flue Gas. J. Electrochem. Soc. 167, 064505. doi:10.1149/1945-7111/ab7a9f

CrossRef Full Text | Google Scholar

Szczęśniak, A., Milewski, J., Szabłowski, Ł., Bujalski, W., and Dybiński, O. (2020). Dynamic Model of a Molten Carbonate Fuel Cell 1 kW Stack. Energy 200, 117442. doi:10.1016/j.energy.2020.117442

CrossRef Full Text | Google Scholar

Wee, J.-H. (2014). Carbon Dioxide Emission Reduction Using Molten Carbonate Fuel Cell Systems. Renew. Sustain. Energ. Rev. 32, 178–191. doi:10.1016/J.RSER.2014.01.034

CrossRef Full Text | Google Scholar

Xing, L., Hao, J., Li, X., Zhang, Y., Hu, Z., and Gao, Y. (2017). Polarization Modeling and Performance Optimization of a Molten Sodium Hydroxide Direct Carbon Fuel Cell (MHDCFC). J. Power Sourc. 363, 428–441. doi:10.1016/J.JPOWSOUR.2017.07.113

CrossRef Full Text | Google Scholar

Yoshiba, F., Abe, T., and Watanabe, T. (2000). Numerical Analysis of Molten Carbonate Fuel Cell Stack Performance: Diagnosis of Internal Conditions Using Cell Voltage Profiles. J. Power Sourc. 87, 21–27. doi:10.1016/S0378-7753(99)00352-3

CrossRef Full Text | Google Scholar

Young, J. M., Mondal, A., Barckholtz, T. A., Kiss, G., Koziol, L., and Panagiotopoulos, A. Z. (2020). Predicting Chemical Reaction Equilibria in Molten Carbonate Fuel Cells via Molecular Simulations. AIChE J. N/a 67 (2), e16988. doi:10.1002/aic.16988

CrossRef Full Text | Google Scholar

Zakiriyanova, I. D., Khokhlov, V. A., and Kochedykov, V. A. (1999). Raman Spectra and Microdynamics of the Hydroxide-Ion in Molten NaOH and NaClNaOH Mixtures. J. Mol. Liq. 83, 153–162. doi:10.1016/S0167-7322(99)00082-3

CrossRef Full Text | Google Scholar

Zakir’yanova, I. D., V Nikolaeva, E., Bove, A. L., and Antonov, B. D. (2018). Electrical Conductivity and Raman Spectra of Disperse Systems α-Al₂O₃–Li₂CO₃–Na₂CO₃–K₂CO₃–NaCl Melt. Russ. Metall. 2018, 181–185. doi:10.1134/S0036029518020246

CrossRef Full Text | Google Scholar

Glossary

Latin

A constant in the ohmic resistance equations [Ω cm²]

A_Cell cell area [m²]

A_m constant in the equilibrium function to improve the model [-]

B constant in the ohmic resistance equations [K]

C constant in the ohmic resistance equations [Ω cm²]

C_m concentration of the m-th reactant in the carbonate-hydroxide equilibrium in the melt [mol m^-3]

D constant in the ohmic resistance equations [-]

E constant in the ohmic resistance equations [-]

E_m equilibrium potential of the path driven by the m-th ion [V]

F Faraday’s constant [96485 s A mol^-1]

$F_{{\text{CO}}_2}$ CO₂ molar flow [mol s^-1]

I_m current of the path driven by the m-th ion [A]

I_TOT total cell current [A]

J_m current density of the path driven by the m-th ion [A cm^-2]

J_TOT total cell current density [A cm^-2]

K_eq carbonate-hydroxide equilibrium constant [mol m^-3]

n number of electrons involved in the electrochemical reactions [-]

p pressure [atm]

P_i kinetic parameters [variable]

R gas constant [8.314 J mol^-1 K^-1]

R_i specific area concentration resistance of the i-th reactant [Ω cm²]

R_Ω cell ohmic specific area resistance [Ω cm²]

$R_{\Omega }^0$ cell ohmic specific area resistance if only carbonate anions were present in the melt [Ω cm²]

r_i generation of the i-th component [mol m^-3 s^-1]

T operating temperature [K]

t_m transference number of the m-th anion [-]

${\text{U}}_{{\text{co}}_2}$ utilization factor of CO₂ [-]

V cell measurable voltage [V]

y_i molar fraction of the i-th reactant [-]

${\text{y}}_{\text{i,}\text{average}}$ Average molar fraction of the i-th reactant between the bulk and the reaction sites. [-]

Greeks

${\alpha }_{\text{e}}^{\text{'}}$ reaction rate orders related to the electron in the direct reaction [-]

${\alpha }_{\text{j}}^{\text{'}}$ reaction rate orders related to the i-th reactant in the direct reaction [-]