Performance Indicators for Benchmarking Solar Thermochemical Fuel Processes and Reactors

Introduction

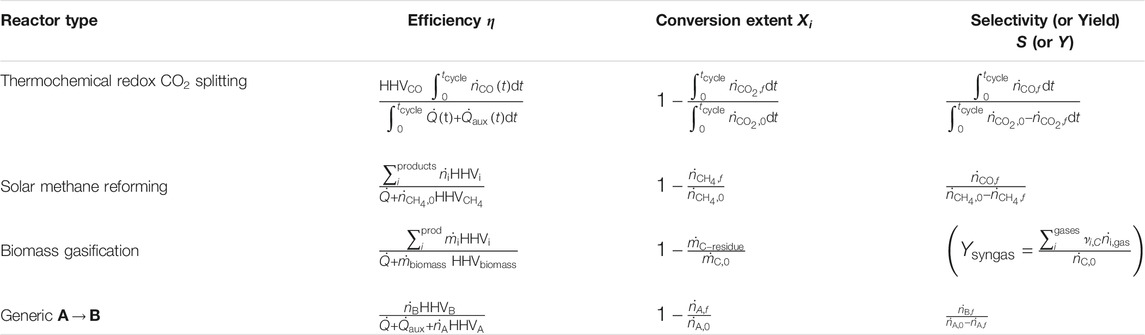
Concentrated solar power plants have been established for large-scale renewable power generation in areas with high direct normal irradiance (DNI). These plants convert the entire spectrum of DNI into high-temperature heat, which in turn is used by a heat engine to generate electricity. Alternatively, heat can be used to drive endothermic chemical processes (Romero and Steinfeld, 2012; Yadav and Banerjee 2016; Rodat et al., 2020), converting solar energy into chemical energy, with the chemical products acting as energy carriers. A promising application in this area is the production of solar fuels. In particular, syngas–a mixture of H₂ and CO−can be produced via a number of routes as illustrated in Figure 1, and further processed to drop-in transportation fuels such as gasoline and kerosene via established gas-to-liquid technologies (Steinfeld 2012; Agrafiotis et al., 2015). Examples of thermochemical processes for solar fuels production include the gasification of biomass, coal, and other carbonaceous feedstock (Nzihou et al., 2012; Piatkowski et al., 2011, Loutzenhiser and Muroyama 2017, Abanades et al., 2021), reforming of hydrocarbons (Agrafiotis et al., 2014; Sheu et al., 2015), and thermochemical redox cycles for splitting H₂O and CO₂ (Romero and Steinfeld, 2012; Lu et al., 2019; Boretti 2021). The study of these solar driven chemical processes is a growing field of research (Kodama 2003; Steinfeld 2014; Mao et al., 2020) with an increasing rate of publications in recent years (Safari and Dincer 2020).

FIGURE 1

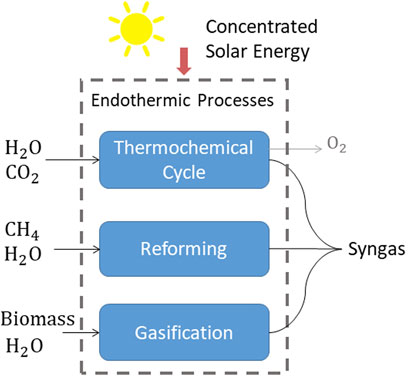
FIGURE 1. Main process routes for the solar thermochemical production of syngas−a mixture of H₂ and CO that can be further processed to drop-in transportation fuels.

The solar reactor for effecting these processes is the key component and its performance can be the deciding factor in assessing its technical and economic feasibility. Thus, when reporting on the R&D of such reactors it is beneficial to follow standard conventions and procedures to facilitate benchmarking progress.

A generic solar thermochemical reactor can be defined as a system with both an energy and mass flow input (see Figure 2), with a thermochemical transformation consuming energy in the form of heat and converting chemical species. It is convenient in chemical engineering to define dimensionless parameters to describe the energy and mass balances which are independent of scale and process, and can be used as performance indicators to benchmark the system. These are the energy efficiency for the energy balance, and the conversion extent, selectivity and yield for the mass balance. In addition, we are interested in the stability of the process, i.e., its performance over time. All of these aspects will affect the investment capital and operating cost of any scaled up fuel production process. In an opinion article in Advanced Science Views, Ozin highlighted the importance of reporting all of these performance indicators to assess the feasibility of renewable fuel production technologies (Ozin 2018), and notes that seldom are all four: conversion, selectivity, efficiency and stability, reported on. When they are reported on, the definitions of these parameters often vary, in particular for the efficiency, but also for standard chemical process parameters such as selectivity and yield. This article aims to tackle these issues by providing clear protocols and definitions of the dimensionless parameters that can be used as performance indicators for reporting on solar fuel reactors. To do this we propose a standardized efficiency definition, and outline the already standardized chemical process parameters of conversion extent, selectivity and yield. Examples for applying them to the solar thermochemical processes shown in Figure 1 are provided.

FIGURE 2

FIGURE 2. Generic thermochemical reactor with a feedstock ${\mathit{n}}_{\mathbf{feed}}$ (moles or molar flow rates), a product stream ${\mathit{n}}_{\mathbf{prod}}$, a heat input $\mathit{Q}$, a waste heat output ${\mathit{Q}}_{\mathbf{waste}}$, and some auxiliary work associated with operating the reactor ${\mathit{W}}_{\mathbf{aux}}$. The heat input is supplied by concentrated solar energy.

Energy Efficiency

Consider a generic thermochemical reactor as illustrated in Figure 2, which has a feedstock input, a product output, energy inputs in the form of heat and auxiliary work, and waste heat output. To illustrate the definitions, we consider a batch process (or an integral over time of a continuous process) and define efficiencies in terms of the number of moles and quantities of heat and work supplied. For a continuous process molar flow rates, and heat and work flow rates can also be used. We can draw a boundary around the reactor illustrated in Figure 2 and treat it as our system. The heat input Q is assumed to be provided by concentrated solar energy, either by direct solar irradiation or by using an indirect method of heat transfer from a solar receiver via heat transfer media. The waste heat can include radiation, conduction, and convection losses, and unrecovered sensible and latent heat in the reaction products and materials of construction. The auxiliary work W_aux is the additional work that is required for the operation of the reactor, for example pumping work to overcome pressure drops or to operate at vacuum/high pressures or the energy required to separate undesired products or the inert gas that is consumed during the process.

We set two criteria for the energy efficiency definition, namely: i) it should reflect the fraction of the supplied energy which is available in the produced fuel, and ii) it should always take a value between zero and one to emphasize the conservation of energy, $\eta \in \left(\mathrm{0,1}\right).$ A generic energy efficiency can thus be defined as,

$\eta =1-\frac{Q_{\text{waste}}}{E_{\text{total}}}(1)$

where $E_{\text{total}}=Q+W_{\text{aux}},$ is the total energy supplied to the system and $Q_{\text{waste}}$ is the heat that leaves the system to the surroundings unused. Evidently,$\eta$ should always have a value between 0 and 1 using Eq. 1, unless some component of the supplied energy is overlooked. However, efficiency is rarely defined explicitly as in Eq. 1 because $Q_{\text{waste}}$ is not usually a term that can be directly measured.

Before considering other efficiency definitions, it is important to first discuss the auxiliary work, as there is some variance in the treatment of this term in the literature. The auxiliary work W_aux is not necessarily an energy consumption taking place within the reactor itself, however it is work that must be done in order for the reactor to operate, such as pumping or recycling sweep gas. It should therefore be included in the energy demand, $E_{\text{total}}$. However, in solar thermochemical fuel processes, the total energy is most often given as a purely thermal energy (see Table 1). Thus, W_aux is substituted by an equivalent thermal energy input Q_aux, calculated using a heat-to-work efficiency,

$Q_{\text{aux}}=\frac{W_{\text{aux}}}{{\eta }_{\text{heat}-\text{to}-\text{work}}}.(2)$

The total energy then includes the heat supplied to the reactor and the heat demand to perform the auxiliary work, E_total = Q + Q_aux, which in principal includes a power cycle within the system boundaries.

TABLE 1

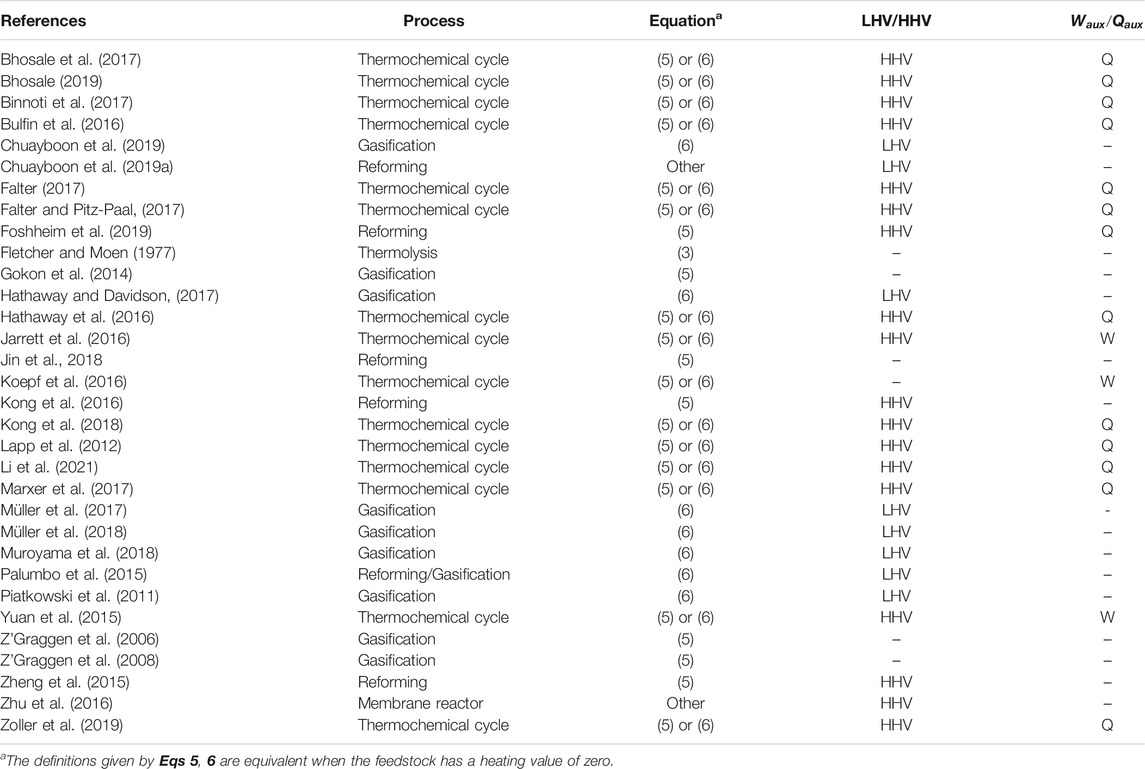
TABLE 1. Efficiency definitions in the literature, with the process type, the type of efficiency equation used, whether they use LHV or HHV, and if they include auxiliary work directly or convert it to heat.

A range of values for the heat-to-work efficiency can be found in the literature, and here we are suggesting a value of ${\eta }_{\text{heat}-\text{to}-\text{work}}$ = 0.4 (Marxer et al., 2017). This conversion is academic in nature, while in practice grid electricity is typically used for auxiliary work or bottled gases in the case of sweep gas requirements. Even for a scaled up industrial plant it may be more economical and flexible to rely on grid electricity if it is available. Indeed, some studies have chosen to include the work directly in the total energy demand, as can be seen in Table 1. However, since the majority of researchers apply this conversion of work to an equivalent heat demand, we include it in the efficiency definitions described here.

We can now look at some common efficiency definitions seen in the literature and discuss the pros and cons of each. We first consider a definition based around the second law of thermodynamics,

$\eta =\frac{{{\displaystyle \sum }}_{\mathit{i}}^{\mathrm{prod}}{\mathrm{n}}_{\mathrm{i}}{\mathit{G}}_{\mathrm{i}}-{{\displaystyle \sum }}_{\mathit{i}}^{\mathrm{feed}}{\mathrm{n}}_{\mathrm{i}}{\mathit{G}}_{\mathrm{i}}}{E_{\text{total}}},(3)$

where ${\displaystyle \sum }_i^{\text{prod}}{\text{n}}_{\text{i}}{G}_{\text{i}}$ is the total Gibbs free energy of the products, and ${\displaystyle \sum }_i^{\text{feed}}{\text{n}}_{\text{i}}{G}_{\text{i}}$ is the total Gibbs free energy of the feedstock. Thus, the numerator represents the change in Gibbs free energy of the process, which is equivalent to the theoretical maximum work that can potentially be performed by the reverse process. This definition was often used in the pioneering research of Fletcher on solar-driven processes (Noring and Fletcher 1982). Fletcher also derived a theoretical upper bound for this efficiency, given by:

${\eta }_{\text{max}}=\left(1-\frac{\sigma T_{\text{H}}^4}{IC}\right)\left(1-\frac{T_{\text{L}}}{T_{\text{H}}}\right),(4)$

where $I$ is the DNI, $C$ is the solar concentration ratio, $T_{\text{H}}$ and $T_{\text{L}}$ are the temperatures of the upper and lower thermal reservoirs of an equivalent heat engine, and σ is the Stefan-Boltzmann constant (Fletcher and Moen 1977). This upper bound results from multiplying of the maximum solar absorption efficiency of a perfectly-insulated blackbody cavity-receiver (taking into account only radiation losses), and the Carnot efficiency for the maximum conversion of heat to work. One issue with the efficiency according to Eq. 3 is that it relates to the fuel’s potential to perform work, but the energy available in a fuel is usually quantified in terms of its heating value, which leads to an alternative efficiency definition, given by:

$\eta =\frac{{{\displaystyle \sum }}_i^{\text{prod}}{n}_i{\text{HHV}}_{\text{i}}-{{\displaystyle \sum }}_i^{\text{feed}}{n}_i{\text{HHV}}_{\text{i}}}{E_{\text{total}}}(5)$

where HHV denotes the higher heating value and the numerator denotes the change in the heating value between the products and the feedstock. Note that lower heating value (LHV) can also be used, as discussed later. The numerator in this case is equivalent to the enthalpy change of the reaction. This efficiency definition has a direct relation to the fuel properties and has been applied in publications on both natural gas reforming and biomass gasification (Jin et al., 2018; Z’Graggen and Steinfeld 2008).

One issue with Eq. 5 is that it can take negative values for some processes. Take for example solar biomass gasification in a hybrid reactor that can switch between solar thermal operation and auto-thermal operation by supplying some oxygen when off Sun (Muroyama et al. (2018), Boujjat et al., 2020). When such a hybrid system is in auto-thermal operation, the heating value of the feedstock would be decreased by the process and the efficiency according to Eq. 5 would be negative. Another interesting example is solar fast pyrolysis of biomass (Zeng, et al., 2017; Bashir et al., 2017), in which the biomass is thermally decomposed in the absence of an oxidizing agent such as steam or oxygen. Depending on the feedstock, this process can become net exothermic (Di Blasi et al., 2017), but a heat source is still required for the rapid heating of the feedstock and starting the decomposition. In this case the efficiency according to Eq. 5 would become negative even during solar operation.

To avoid the possibility of negative efficiencies we can consider the heating value of the feedstock as an energy input to the system, and include it in the denominator, $E_{\text{total}}$. For H₂O and CO₂ splitting cycles, the corresponding heating values are zero. But this is not the case for example for the gasification of biomass or for the reforming of hydrocarbons (Piatkowski et al., 2011; Muroyama et al., 2018; Müller et al., 2017). The efficiency is then defined as,

$\eta =\frac{{{\displaystyle \sum }}_i^{\text{prod}}{n}_i{\text{HHV}}_{\text{i}}}{E_{\text{total}}},(6)$

where the total energy now includes the solar heat supplied to the reactor, the equivalent heat for auxiliary work, and the heating value in the feedstock, E_total = Q + Q_aux + ${\displaystyle \sum }_i^{\text{feed}}{n}_{\text{i}}{\text{HHV}}_{\text{i}}$. Eq. 6 is equivalent to Eq. 5 if the feedstock itself has no heating value (e.g., H₂O or CO₂). This definition is equivalent to Eq. 1, in that it tracks the fraction of waste heat released in the process as the difference between the denominator and numerator. The heat losses can be radiation, convection, and conduction losses, losses in sensible heat from the products, and waste heat from the generation of W_aux (see Eq. 2). Thus, Eq. 6 can be generally applied to any solar thermochemical fuel production process described in Figure 1, will always take a value between 0 and 1, and reflects the fraction of the energy supplied which is available in the fuel.

An interesting point to note is that Eqs 5, 6 are heat-to-heat efficiencies and can have a larger value than the heat-to-work efficiency given by Eqs 3, 4. They are bounded by only the first bracketed term of Eq. 4, which is the maximum absorption efficiency. Thus, while the second law of thermodynamics places a limit on the efficiency according to Eq. 3, only the first law of thermodynamics places a limit on the efficiency according to Eqs 5, 6. This fact is very frequently overlooked, where many studies use a heat-to-heat efficiency definition and state Eq. 3 as an upper bound.

Another point worth noting is that some cases have a number of options for what is included as part of the products in the numerator of the efficiency definition given in Eq. 6. This can require some additional thought, and as a general rule we suggest only the products that are considered to be the produced fuel should be included, while the heating value of unusable byproducts or unreacted feed that cannot be recycled should be neglected. Take for example the thermal cracking of methane for the production of hydrogen (Maag et al., 2009; Rodat et al., 2011),

${\text{CH}}_4\to \text{C}\left(\text{s}\right)+2{\text{H}}_2,(7)$

which forms gaseous hydrogen and solid phase carbon as a byproduct. If only the produced hydrogen is intended to be used as a fuel, and the carbon is sequestered, then the heating value of the carbon byproduct should not be included in the numerator. Similarly, if there is unconverted methane which cannot be recycled or used in the final fuel it should also be omitted from the numerator giving an efficiency,

$\eta =\frac{n_{{\text{H}}_2}{\text{HHV}}_{{\text{H}}_2}}{Q+Q\text{aux }+n_{{\text{CH}}_4}{\text{HHV}}_{{\text{CH}}_4}}.(8)$

The heating value of the byproduct and the heating value of the unconverted feedstock would then be considered part of the waste heat in the efficiency according to Eq. 1, which effectively closes the energy balance.

When choosing the efficiency, we should also consider the prevalence of each definition in the literature, as past work does set some precedent. A selection of publications with explicitly defined efficiencies are shown in Table 1. We distinguish the equations quite generally by whether the use change in Gibbs free energy as in Eq. 3, the change in heating value or enthalpy as in Eq. 5, or include the heating value of the feed in the denominator as in Eq. 6.

From Table 1, it can be seen that both Eqs 5, 6 are frequently applied in gasification and reforming processes. Eq. 6 is the most general formulae, in that it can be applied to a reactor or an entire process chain, as well as solar and non-solar processes. Consider for example a conventional oil refinery where some of the feed is combusted to provide the heat required for the plant. In this case we cannot apply Eq. 3 or Eq. 5 as they will both give a negative efficiency, but Eq. 6 would be suitable. Similarly, if we consider a complete solar fuel production process consisting of the endothermic solar gasification of biomass followed by exothermic Fischer-Tropsch synthesis and subsequent refining of the hydrocarbons, the end product can have less heating value than the original biomass. Again we cannot apply Eq. 3 or Eq. 5 to this complete process as they would give negative values. Therefore, as the most general formula which is already commonly applied, Eq. 6 is the recommended efficiency definition for future studies.

It is often the case that authors want to gauge the solar energy demand per unit of fuel produced, as the solar concentrating infrastructure can make up for a significant part of the capital investment. For gasification and reforming processes, the efficiency defined by Eq. 6 does not provide this directly. To provide this information one can further define dimensionless energy factors (Jarret et al., 2016, Li et al., 2021),

$F_i=\frac{Q_{\text{i}}}{{{\displaystyle \sum }}_i^{\text{prod}}{n}_i{\text{HHV}}_{\text{i}}} ,(9)$

which gives a specific energy demand relative to the fuel’s heating value. The efficiency is then related to the energy factors by $\eta =\frac{1}{{{\displaystyle \sum }}_i{F}_i}.$ The solar energy factor would then be $F_{\text{solar}}=\frac{Q_{\text{solar}}}{{{\displaystyle \sum }}_i^{\text{products}}{n}_i{\text{HHV}}_{\text{i}}}$. Similarly one can give a more detailed breakdown of the energy demands by giving factors for subsystems such as the auxiliary work $F_{\text{aux}=}\frac{W_{\text{aux}}}{{{\displaystyle \sum }}_i^{\text{prod}}{n}_i{\text{HHV}}_{\text{i}}}$, or the heating value of the feedstock $F_{\text{feed}}=\frac{{{\displaystyle \sum }}_i^{\text{feed}}{n}_i{\text{HHV}}_{\text{i}}}{{{\displaystyle \sum }}_i^{\text{prod}}{n}_i{\text{HHV}}_{\text{i}}}$. In this way, a more complete breakdown of the energy balance can be reported together with the efficiency.

Note that other efficiency definitions are found in the literature, some of which are difficult to interpret and should be avoided. For example, subtracting the auxiliary work term from the numerator rather than including it in the denominator (Zhu et al., 2016),

$\eta =\frac{{{\displaystyle \sum }}_i^{\text{feed}}{n}_{\text{i}}{\text{HHV}}_{\text{i}}-W_{\text{aux}}}{Q+ {{\displaystyle \sum }}_i^{\text{prod}}{n}_i{\text{HHV}}_{\text{i}}},(10)$

as this leads to an equation which can easily have negative values. Another variation encountered is the inclusion of the conversion extent of the feedstock $X_{\text{feed}}$ in the denominator of the efficiency definition (Chuayboon et al., 2019)

$\eta =\frac{ {{\displaystyle \sum }}_i^{\text{prod}}{n}_i{\text{HHV}}_{\text{i}}}{X_{\text{feed}}{n}_{\text{feed}}{\text{HHV}}_{\text{feed}}+Q+Q_{\text{aux}}}.(11)$

which mixes up the benchmarks for mass balance with that of the energy balance.

Higher heating value (HHV) vs. lower heating value (LHV)−Some sources use LHV instead of HHV (Table 1). If there is hydrogen or hydrocarbons in the products this will lead to lower efficiency values. The use of HHV is recommended because it offers a strict upper-bound for the useful thermal energy that can be extracted from the fuel in all applications.

Conversion Extent, Selectivity, and Yield

These performance indicators are based on the mass balance and are used to keep track of the chemical reactions taking place, and they are, along with energy efficiency, the most important metrics for assessing the performance of chemical reactors. The conversion extent monitors how much of the feedstock supplied undergoes a chemical change within the reactor, while the selectivity gauges the extent of unwanted side reactions. The yield is the product of conversion and selectivity, and it gives the amount of the desired product formed relative to the stoichiometric maximum product formation, and thus provides information about the purity of the fuel produced. This means that reporting conversion extent and selectivity (or yield) gives the information needed to benchmark the system, while only reporting one of them leaves ambiguity about the other two. Together, these mass balance metrics have very useful implications for reactor design, including relating the reactor free volume and flow rates to production rates, which in turn can be used to rule out processes as unfeasible for large scale industrial production (Lange 2016). For example, a process can exhibit total (100%) selectivity for the conversion of CO₂ to CO, but if its conversion extent is low, it will lead to a fuel of little practical application because of the high dilution in unreacted CO₂. Although these metrics can be considered the nuts and bolts of chemical engineering research, they are often omitted in solar reactor studies.

We first define these indicators for a generic chemical reactor and then give examples for the solar fuel production processes discussed. We follow the definitions formulated in the seminal chemical reactor engineering text book by Levenspiel (2001). The conversion extent is generally formulated in terms of a limiting reactant. The limiting reactant is the reactant fed to the reactor which can be completely consumed according to the chemical reaction stoichiometry and input flow rates. For a trivial chemical process, such as

$\text{A}\to \text{B},(12)$

with only one feedstock, species A is the limiting reactant and B is the desired product. A chemical reactor for this processes is illustrated in Figure 3.

FIGURE 3

FIGURE 3. A continuous-flow thermochemical reactor with an input molar feed rate of ${\dot{\mathit{n}}}_{\mathbf{A},0}$, and a product stream with outflows ${\dot{\mathit{n}}}_{\mathbf{A},\mathit{f}}$ , ${\dot{\mathit{n}}}_{\mathbf{B},\mathit{f}}$ and.${\dot{\mathit{n}}}_{\mathbf{other}}\mathrm{.}$

The conversion extent for this process can be defined as the relative change in the number of moles of the limiting reactant,

$X_{\text{A}}=1-\frac{{\dot{n}}_{\text{A},f}}{{\dot{n}}_{\text{A},0}}.(13)$

where the subscript 0 indicates an input flow rate and the subscript f indicates the final flow rate at the exit of the reactor. For a batch reactor we can use the same formulae but with the number of initial and final moles, instead of molar flow rates. The importance of the conversion extent as a performance indicator is highlighted in classical text’s where the performance equation of a chemical reactor gives the relation between the free volume, species flow rates and the conversion extent (Levenspiel 2001). For example, if we can only achieve a low conversion extent of say 10%, and we assume perfect selectivity, then we must have a feedstock flow rate which is 10 times higher than the desired production rate, and a large volume reactor to accommodate the flow, which has obvious implications for the cost and practical feasibility of a process.

As well as the desired reaction there can also be undesired reactions, for example,

$\text{A}+\text{B}\to \text{C},(14)$

where A is the reactant, B is the desired product, and C is an undesired product. The selectivity of the reactor towards species B is defined as the production rate of the desired product B relative to consumption rate of the feedstock A,

$S_{\text{B}}=\frac{{\dot{n}}_{\text{B},f}}{{\dot{n}}_{\text{A},0}-{\dot{n}}_{\text{A},f}}.(15)$

If there are no side reactions we would have ${\dot{n}}_{\text{B},f}={\dot{n}}_{\text{A},0}-{\dot{n}}_{\text{A},f}$, resulting in a selectivity of 1. The yield is the amount of desired product formed relative to the maximum amount of desired product that can be formed, i.e., it is the product of conversion extent and selectivity,

$Y_{\text{B}}=X_{\text{A}}{S}_{\text{B}}= \frac{{\dot{n}}_{\text{B},f}}{{\dot{n}}_{\text{A},0}}.(16)$

Note then that reporting conversion extent, selectivity, and feed rates can offer a complete description of the chemical transformation in the reactor. However, if the system does not have an ideal selectivity of $S=1$, it is also recommended to report the yield too.

Another point worth noting is that the selectivity and yield need to be adjusted by the relative stoichiometry of the product to the limiting reactant. For example, for the reaction $A\to 2B$, the selectivity would be given by $S_{\text{B}}=\frac{1}{2}\frac{{\dot{n}}_{\text{B},f}}{{\dot{n}}_{\text{A},0}-{\dot{n}}_{\text{A},f}}$, where the factor of one half accounts for the 2 moles of B formed for every 1 mole of A reacted.

When reporting on the mass balance for reactor demonstrations it is recommend to report.

a) The feedstock molar flow rates (or mass flow rates for biomass).

b) The conversion extent of the feedstock in terms of the limiting reactant.

c) The selectivity towards the desired product, and the yield.

In trivial cases where the selectivity can be assumed to have a value of 1, then the conversion extent and yield will be equal. In such cases this should be clearly stated in the results.

Stability

The reactor’s performance stability can be reported using the same mass and energy balance performance indicators described above, by giving their values as a function of time (or cycle # for cyclic processes). In other words, the efficiency η given by Eq. 6, conversion extent $X_i$ given by Eq. 13, the selectivity $S_i$ given by Eq. 15, and the yield given by Eq. 16, should all be monitored over time to gauge the stability of the performance. Other stability issues such as degradation or complete failure of components are much more difficult to report in a consistent way, as there are no scalable measurements of such faults that can be broadly applied. We therefore restrict our recommendations to recording the performance indicators over time.

Examples of the Performance Indicators

Here we outline the performance indicators for some example processes that have been investigated in the literature, namely: solar reforming, thermochemical redox cycles and solar biomass gasification.

Solar methane reforming−Methane can be converted to syngas by reacting it with steam at high temperatures via the endothermic reforming reaction,

${\text{CH}}_4+{\text{H}}_2\text{O}\to \text{CO}+3{\text{H}}_2,(17)$

The heat for this reaction can be supplied by concentrated solar energy (Agrafiotis et al., 2014). This can be performed with a continuous flow reactor as illustrated in Figure 4. The process can also have numerous side reactions such as the reverse water-gas shift,

$\text{CO}+{\text{H}}_2\text{O}\to {\text{CO}}_2+{\text{H}}_2.(18)$

FIGURE 4

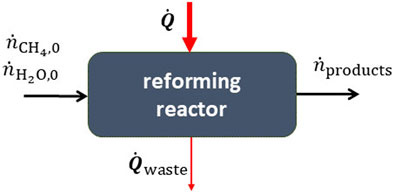
FIGURE 4. A thermochemical reactor for the steam reforming of methane. The heat input is supplied by concentrated solar energy.

For this process we consider the syngas components $\text{CO}$ and ${\text{H}}_2$ to be the produced fuel and the unreacted methane to be lost, so that the efficiency is given as (Eq. 6);

$\eta =\frac{{\dot{n}}_{{\text{H}}_2}{\text{HHV}}_{{\text{H}}_2}+{\dot{n}}_{\text{CO}}{\text{HHV}}_{\text{CO}}}{{\dot{n}}_{{\text{CH}}_4,0}{\text{HHV}}_{{\text{CH}}_4}+\dot{Q}}.(19)$

where the sum in the numerator is over the species flow rates in the products times their HHVs. To avoid coking, steam is used in excess with ${\dot{n}}_{{\text{H}}_2\text{O}}>{\dot{n}}_{{\text{CH}}_4}$ and methane as the limiting reactant, with conversion extent given by,

$X_{{\text{CH}}_4}=1-\frac{{\dot{n}}_{{\text{CH}}_4,f}}{{\dot{n}}_{{\text{CH}}_4,0}}.(20)$

The presence of side reactions means that we should also consider the selectivity towards the syngas products $\text{CO}$ and ${\text{H}}_2$, given by:

${\text{S}}_{\text{CO}}=\frac{{\dot{n}}_{\text{CO},f}}{{\dot{n}}_{{\text{CH}}_4,0}-{\dot{n}}_{{\text{CH}}_4,f}}{\text{ and S}}_{{\text{H}}_2}=\frac{{\dot{n}}_{{\text{H}}_2,f}}{3({\dot{n}}_{{\text{CH}}_4,0}-{\dot{n}}_{{\text{CH}}_4,f})}.(21)$

Solid phase carbon is an unwanted product which can form due to the Boudouard reaction or methane cracking. If present, this can be quantified using the carbon yield (Bulfin et al., 2021),

${\text{Y}}_{\text{C}}=\frac{{\dot{n}}_{\text{C}}}{{\dot{n}}_{{\text{CH}}_4,0}},(22)$

but ideally it should be zero. Note the formulae given can be re-arranged to be in terms of feed rate, and mole fractions in the product stream, as required by the type of measurements taken in the experiment. However, it should be checked that definitions used are equivalent to the standard versions given here.

Thermochemical redox cycles−Two-step metal oxide redox cycles can be used to split H₂O and CO₂, producing H₂ and CO (Romero and Steinfeld, 2012; Bulfin et al., 2017). A metal oxide first undergoes reduction at high temperature and low oxygen partial pressures,

$M{O}_{\text{ox}}\to M{O}_{\text{red}}+\frac{\text{δ}}{2}{\text{O}}_2(23)$

and is then reacted at lower temperature with H₂O or CO₂ to form H₂ and CO,

$M{O}_{\text{red}}+{\text{CO}}_2\to M{O}_{\text{ox}}+\text{CO}(24)$

$M{O}_{\text{red}}+{\text{H}}_2\text{O}\to M{O}_{\text{ox}}+{\text{H}}_2(25)$

Both redox reactions can be performed in the same fixed-bed reactor but at different times in a cyclic sequential mode (Hathaway et al., 2016; Haeussler et al., 2020; Marxer et al., 2017). Alternatively, it could be operated continuously using a particle transport reactor (Ermanoski et al., 2013; Singh et al., 2017; Welte et al.,2016). The process is illustrated in Figure 5, where it is important to note that reduction and oxidation are either taking place at different times or in separate reaction chambers.

FIGURE 5

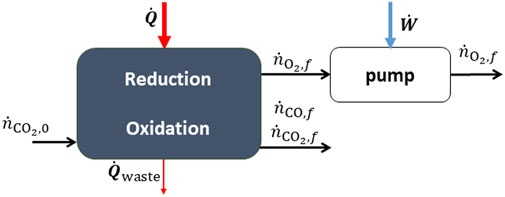
FIGURE 5. A thermochemical reactor for the redox splitting of CO₂. The heat input is supplied by concentrated solar energy.

In the fixed bed case, the system parameters; temperature, pressure, input power, conversion extent, auxiliary work etc., are varying in time. Therefore, integrals are taken over an entire cycle to obtain the desired performance parameters. For CO₂-splitting, we define the efficiency as,

$\eta =\frac{{\text{HHV}}_{\text{CO}} {{\displaystyle \int }}_0^{t_{\text{cycle}}}{\dot{n}}_{\text{CO}}\left(t\right)\text{ d}t}{{{\displaystyle \int }}_0^{t_{\text{cycle}}}\dot{Q}\left(\text{t}\right)+{\dot{Q}}_{\text{aux}}\left(t\right)\text{ d}t}.(26)$

Auxiliary work may include vacuum pumping during reduction and the production of inert sweep gas. This definition is the same for water splitting, where CO is replaced by H_2. In this case the conversion extent is given by:

$X_{{\text{CO}}_2}=1-\frac{{{\displaystyle \int }}_0^{t_{\text{cycle}}}{\dot{n}}_{{\text{CO}}_2,f}\text{ d}t}{{{\displaystyle \int }}_0^{t_{\text{cycle}}}{\dot{n}}_{{\text{CO}}_2,0}\text{ d}t}.(27)$

The selectivity towards $\text{CO}$ is given by:

${\text{S}}_{\text{CO}}=\frac{{{\displaystyle \int }}_0^{t_{\text{cycle}}}{\dot{n}}_{\text{CO},f}\text{ d}t}{{{\displaystyle \int }}_0^{t_{\text{cycle}}}{\dot{n}}_{{\text{CO}}_2,0}-{\dot{n}}_{{\text{CO}}_2,f}\text{ d}t}.(28)$

The yield is given by $Y_{\text{CO}}=X_{{\text{CO}}_2}{S}_{\text{CO}}$.

The literature on thermochemical redox cycles is perhaps the most problematic in terms of reporting standards due to the more complex nature of the cyclic process. There are a few articles in the literature which address all the performance indicators described here, with the work of Marxer et al. a notable example (Marxer et al., 2017). However, many studies omit the conversion extent, selectivity and yield as defined here, and instead only report the moles of H₂ or CO produced per gram of the cycled redox material as the yield (Agrafiotis et al., 2005; Hathaway et al., 2016; Haeussler et al., 2020). Reporting the mass balance using the performance indicators defined here together with the efficiency will offer a more complete picture of the performance. As additional information the moles of fuel per mole of redox material can also be reported, but to avoid confusion this parameter should not be referred to as the yield.

An interesting example that emphasizes the importance of reporting both energy and mass balance performance indicators is that of isothermal redox cycles. In this case both redox steps are conducted at the same temperature by performing a pressure swing. Studies have focused on the energy efficiency (Ermanoski et al., 2014) and experimental demonstrations of the process (Muhich et al., 2013; Hathaway et al., 2016; Hoskins et al., 2019). The conversion extent in the demonstrations are typically not reported, but at the operating conditions considered it is known to be thermodynamically limited to low values on the order of $X\approx 0.01$ (Ermanoski et al., 2014; Bulfin et al., 2016). The feedstock flow rate of H₂O or CO₂ required for a given output is inversely proportional to the conversion extent, with such low values resulting in considerable practical limitations for scaling-up the process. Low conversion extents lead to large feedstock flow rates, which in turn lead to larger reactors with increased capital cost and impractical design constraints. For this reason, classical chemical reactor engineering texts put a large emphasis on the conversion extent as a performance indicator (Levenspiel 2001).

Solar biomass gasification−Biomass, coal, or carbonaceous materials can be reacted with steam at high temperatures to produce syngas, as illustrated in Figure 6 (Piatkowski et al., 2011). Since biomass does not have a simple chemical composition, the mass balance is more complex than the previous examples. Proximate and ultimate analysis are required to determine the chemical breakdown of the biomass (Müller et al., 2018; Muroyama et al., 2018).

FIGURE 6

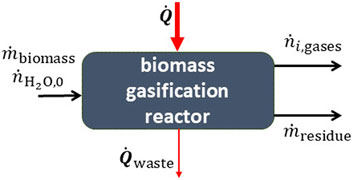
FIGURE 6. A reactor for the gasification of biomass. The high-temperature heat input is supplied by concentrated solar energy.

Biomass gasification is a combination of many independent reactions with the net reaction summarized by the formula,

${\text{C}}_{\text{n}}{\text{H}}_{\text{m}}{\text{O}}_{\text{k}}+{\text{yH}}_2\text{O}\to x_1\text{CO}+x_2{\text{CO}}_2+x_3{\text{H}}_2+x_4{\text{CH}}_4+\text{other gases}+\text{residue},(29)$

where ${\text{C}}_{\text{n}}{\text{H}}_{\text{m}}{\text{O}}_{\text{k}}$ represents biomass. The biomass generally contains sulphur and nitrogen impurities on the order of 1% by mass. The efficiency can be expressed as;

$\eta =\frac{{{\displaystyle \sum }}_i^{\text{prod}}{\dot{m}}_i{\text{HHV}}_i}{\dot{Q} + {\dot{m}}_{\text{biomass}}{\text{ HHV}}_{\text{biomass}}}.(30)$

where we only sum the heating value of the gasified products, as the residue is an ash like byproduct and not a fuel. Note that the HHV are per unit mass and not per mole as in other formulae, which is due to the fact that the feed does not have a well-defined stoichiometric chemical formula. In this case an upgrade factor is also often reported, defined by the relative change in the heating value between the products and feedstock,

$U=\frac{{{\displaystyle \sum }}_i^{\text{prod}}{\dot{m}}_{\text{i}}{\text{HHV}}_{\text{i}}}{{\dot{m}}_{\text{biomass}}{\text{ HHV}}_{\text{biomass}}} .(31)$

The value of U depends on the type of feedstock and the syngas yield. This value can offer non-redundant information on the energy balance when reported together with the efficiency. For carbonaceous materials, the conversion extent is usually defined in terms of the carbon conversion extent (Müller et al., 2018),

$X_{\text{C}}=1-\frac{{\dot{m}}_{\text{C}-\text{residue}}}{{\dot{m}}_{\text{C},0}},(32)$

where ${\dot{m}}_{\text{C},0}$ is the mass flow rate of carbon in the biomass feed (determined by ultimate analysis), and ${\dot{m}}_{\text{C}-\text{residue}}$ is the mass of carbon in the residue (the unreacted carbon), which can be made up of tar and ash. The carbon to syngas yield can be expressed using molar flow rates of carbon containing species in the gas stream,

$Y_{\text{syngas}}=\frac{{{\displaystyle \sum }}_i^{\text{gases}}{\nu }_{i,C}{\dot{n}}_{\text{i},\text{gas}}}{{\dot{n}}_{\text{C},0}}=\frac{{\dot{n}}_{\text{CO}}+{\dot{n}}_{{\text{CO}}_2}+{\dot{n}}_{{\text{CH}}_4}+2{\dot{n}}_{{\text{C}}_2{\text{H}}_6}+\dots }{{\dot{n}}_{\text{C},0}}.(33)$

where ${\nu }_{i,C}$ is the stoicheometric number of carbon in the gas species. Often this sum is only performed for CO, CO₂, and CH₄, which differentiates it from the conversion extent defined above. Given the large number of reactions present there are a number of different selectivity’s which may be of interest. For downstream gas-to-liquid processes, CO may be favored over CO₂ and CH₄, in which case the selectivity towards CO can be defined as,

$S_{\text{CO}}=\frac{{\dot{n}}_{\text{CO}}}{{{\displaystyle \sum }}_i^{\text{gases}}{\nu }_{i,C}{\dot{n}}_{\text{i},\text{gas}}}=\frac{{\dot{n}}_{\text{CO}}}{{\dot{n}}_{\text{CO}}+{\dot{n}}_{{\text{CO}}_2}+{\dot{n}}_{{\text{CH}}_4}}.(34)$

Summary of Reporting Protocols

The dimensioned parameters required to described the reactor system are:

1) The reactor volume and free volume.

2) Mass loading of cycled redox material or catalyst.

3) The operating conditions of the reactor (e.g., temperature, pressure, etc.).

4) The molar/mass flow rates of feedstock into the reactor.

5) The total heat supply to the reactor, Q (e.g., solar heat, etc.).

6) Auxiliary work demands, W_aux, (e.g., pumping work, inert gas production, etc.).

This information should enable the study to be reproduced or modelled by other researchers. The energy and mass balance performance indicators outlined in the previous sections allows for the system to be benchmarked. These are:

1) The energy efficiency: $\eta =\frac{{{\displaystyle \sum }}_i^{\text{prod}}{n}_i{\text{HHV}}_{\text{i}}}{Q + Q_{\text{aux }}+{{\displaystyle \sum }}_i^{\text{feed}}{n}_i{\text{HHV}}_{\text{i}}}$. For solar-upgrading processes such as gasification and reforming, report additionally the upgrade factor: $U=\frac{{{\displaystyle \sum }}_i^{\text{prod}}{n}_i{\text{HHV}}_{\text{i}}}{{{\displaystyle \sum }}_i^{\text{feed}}{n}_i{\text{HHV}}_{\text{i}}}$.

2) The conversion extent: $X_{\text{A}}=1-\frac{{\dot{n}}_{\text{A},f}}{{\dot{n}}_{\text{A},0}}$.

3) The selectivity towards the desired product: $S_{\text{B}}=\frac{{\dot{n}}_{\text{B},f}}{{\dot{n}}_{\text{A},0}-{\dot{n}}_{\text{A},f}}$, or the yield of the desired product: $Y_{\text{B}}=\frac{{\dot{n}}_{\text{B},f}}{{\dot{n}}_{\text{A},0}}$ , for the case that the selectivity is not reported.

4) Performance stability, i.e., report the above indicators over time.

The example definitions given for these performance indicators are summarized in Table 2.

TABLE 2

TABLE 2. The performance indicatoars for the example solar fuel processes discussed in this work.

Conversion extent, product selectivity, and energy efficiency, combined with mass flow rates offer a complete description of the reactor performance, while the performance over time can be used to gauge stability. For cyclic processes, the benchmarks should use integrals of the performance indicators over an entire cycle as outlined here. Similarly, for continuous processes, the benchmarks should use steady-state or integrals over time of the heat and mass flow rates when calculating the performance indicators.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

BB wrote the manuscript and assisted in the planning of the study. MM performed a review of the solar fuel production literature and assisted in writing the article. AS assisted in the planning of the study and in the writing of the article.

Funding

This research work was funded by the European Union’s Horizon 2020 Research Infrastructure Programme (Project SFERA-III–Grant Nr. 823802) and by the Swiss Federal Office of Energy (Project SOLIFUEL-Grant Nr. SI/501213-01).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank Martin Roeb, Valéry Vuillerme, Silvane Rodat, Ricardo Sanchez and other members of the SFERA III consortium who offered feedback on the formulation of standardized reporting protocols for solar fuel processes and reactors.

References

Abanades, S., Rodat, S., and Boujjat, H. (2021). Solar Thermochemical Green Fuels Production: A Review of Biomass Pyro-Gasification, Solar Reactor Concepts and Modelling Methods. Energies 14 (5), 1494. doi:10.3390/en14051494

CrossRef Full Text | Google Scholar

Agrafiotis, C., Roeb, M., Konstandopoulos, A. G., Nalbandian, L., Zaspalis, V. T., Sattler, C., et al. (2005). Solar Water Splitting for Hydrogen Production with Monolithic Reactors. Solar Energy 79 (4), 409–421. doi:10.1016/j.solener.2005.02.026

CrossRef Full Text | Google Scholar

Agrafiotis, C., Roeb, M., and Sattler, C. (2015). A Review on Solar thermal Syngas Production via Redox Pair-Based Water/carbon Dioxide Splitting Thermochemical Cycles. Renew. Sust. Energ. Rev. 42, 254–285. doi:10.1016/j.rser.2014.09.039

CrossRef Full Text | Google Scholar

Agrafiotis, C., von Storch, H., Roeb, M., and Sattler, C. (2014). Solar thermal Reforming of Methane Feedstocks for Hydrogen and Syngas Production-A Review. Renew. Sust. Energ. Rev. 29, 656–682. doi:10.1016/j.rser.2013.08.050

CrossRef Full Text | Google Scholar

Bashir, M., Yu, X., Hassan, M., and Makkawi, Y. (2017). Modeling and Performance Analysis of Biomass Fast Pyrolysis in a Solar-thermal Reactor. ACS Sust. Chem. Eng. 5 (5), 3795–3807. doi:10.1021/acssuschemeng.6b02806

CrossRef Full Text | Google Scholar

Bhosale, R., Kumar, A., AlMomani, F., and Gupta, R. B. (2017). Solar Thermochemical ZnO/ZnSO4 Water Splitting Cycle for Hydrogen Production. Int. J. Hydrogen Energ. 42 (37), 23474–23483. doi:10.1016/j.ijhydene.2017.02.190

CrossRef Full Text | Google Scholar

Bhosale, R. R. (2019). Thermochemical H2 Production via Solar Driven Hybrid SrO/SrSO4 Water Splitting Cycle. Int. J. Hydrogen Energ. 44 (1), 118–127. doi:10.1016/j.ijhydene.2018.02.053

CrossRef Full Text | Google Scholar

Binotti, M., Di Marcoberardino, G., Biassoni, M., and Manzolini, G. (2017). Solar Hydrogen Production With Cerium Oxides Thermochemical Cycle”. In AIP Conference Proceedings (AIP Publishing LLC), 100002.

Boretti, A. (2021). Technology Readiness Level of Solar Thermochemical Splitting Cycles. ACS Energ. Lett. 6 (4), 1170–1174. doi:10.1021/acsenergylett.1c00181

CrossRef Full Text | Google Scholar

Boujjat, H., Yuki Junior, G. M., Rodat, S., and Abanades, S. (2020). Dynamic Simulation and Control of Solar Biomass Gasification for Hydrogen-Rich Syngas Production during Allothermal and Hybrid Solar/autothermal Operation. Int. J. Hydrogen Energ. 45 (48), 25827–25837. doi:10.1016/j.ijhydene.2020.01.072

CrossRef Full Text | Google Scholar

Bulfin, B., Ackermann, S., Furler, P., and Steinfeld, A. (2021). Thermodynamic Comparison of Solar Methane Reforming via Catalytic and Redox Cycle Routes. Solar Energy 215, 169–178.

CrossRef Full Text | Google Scholar

Bulfin, B., Lange, M., de Oliveira, L., Roeb, M., and Sattler, C. (2016). Solar Thermochemical Hydrogen Production Using Ceria Zirconia Solid Solutions: Efficiency Analysis. Int. J. Hydrogen Energ. 41 (42), 19320–19328. doi:10.1016/j.ijhydene.2016.05.211

CrossRef Full Text | Google Scholar

Bulfin, B., Vieten, J., Agrafiotis, C., Roeb, M., and Sattler, C. (2017). Applications and Limitations of Two Step Metal Oxide Thermochemical Redox Cycles; a Review. J. Mater. Chem. A. 5 (36), 18951–18966. doi:10.1039/c7ta05025a

CrossRef Full Text | Google Scholar

Chuayboon, S., Abanades, S., Rodat, S., and Boujjat, H. (2019). “Experimental Assessment of Biomass Feedstock Gasification in a High-Temperature Continuous Solar Gasifier,” in AIP Conference Proceedings (AIP Publishing LLC, Casablanca, Morocco, October 2–5, 2018), 180006. doi:10.1016/j.solener.2020.11.076

CrossRef Full Text | Google Scholar

Chuayboon, S., Abanades, S., and Rodat, S. (2019a). Syngas Production via Solar-Driven Chemical Looping Methane Reforming from Redox Cycling of Ceria Porous Foam in a Volumetric Solar Reactor. Chem. Eng. J. 356, 756–770. doi:10.1016/j.cej.2018.09.072

CrossRef Full Text | Google Scholar

Di Blasi, C., Branca, C., and Galgano, A. (2017). On the Experimental Evidence of Exothermicity in Wood and Biomass Pyrolysis. Energy Technol. 5 (1), 19–29.

Ermanoski, I., Miller, J. E., and Allendorf, M. D. (2014). Efficiency Maximization in Solar-Thermochemical Fuel Production: Challenging the Concept of Isothermal Water Splitting. Phys. Chem. Chem. Phys. 16 (18), 8418–8427. doi:10.1039/c4cp00978a

PubMed Abstract | CrossRef Full Text | Google Scholar

Ermanoski, I., Siegel, N. P., and Stechel, E. B. (2013). A New Reactor Concept for Efficient Solar-Thermochemical Fuel Production. J. Solar Energ. Eng. 135 (3), 031002. doi:10.1115/1.4023356

CrossRef Full Text | Google Scholar

Falter, Christoph. (2017). Efficiency Potential of Solar Thermochemical Reactor Concepts with Ecological and Economical Performance Analysis of Solar Fuel Production. Aachen, Germany: Diss. RWTH Aachen. doi:10.18154/RWTH-2017-06526

CrossRef Full Text

Falter, C. P., and Pitz-Paal, R. (2017). A Generic Solar-Thermochemical Reactor Model with Internal Heat Diffusion for Counter-flow Solid Heat Exchange. Solar Energy 144, 569–579. doi:10.1016/j.solener.2017.01.063

CrossRef Full Text | Google Scholar

Fletcher, E. A., and Moen, R. L. (1977). Hydrogen- and Oxygen from Water. Science 197 (4308), 1050–1056. doi:10.1126/science.197.4308.1050

PubMed Abstract | CrossRef Full Text | Google Scholar

Fosheim, J. R., Hathaway, B. J., and Davidson, J. H. (2019). High Efficiency Solar Chemical-Looping Methane Reforming with Ceria in a Fixed-Bed Reactor. Energy 169, 597–612. doi:10.1016/j.energy.2018.12.037

CrossRef Full Text | Google Scholar

Gokon, N., Izawa, T., Abe, T., and Kodama, T. (2014). Steam Gasification of Coal Cokes in an Internally Circulating Fluidized Bed of thermal Storage Material for Solar Thermochemical Processes. Int. J. Hydrogen Energ. 39 (21), 11082–11093. doi:10.1016/j.ijhydene.2014.05.124

CrossRef Full Text | Google Scholar

Haeussler, A., Abanades, S., Julbe, A., Jouannaux, J., and Cartoixa, B. (2020). Solar Thermochemical Fuel Production from H2O and CO2 Splitting via Two-step Redox Cycling of Reticulated Porous Ceria Structures Integrated in a Monolithic Cavity-type Reactor. Energy 201, 117649. doi:10.1016/j.energy.2020.117649

CrossRef Full Text | Google Scholar

Hathaway, B. J., Bala Chandran, R., Gladen, A. C., Chase, T. R., and Davidson, J. H. (2016). Demonstration of a Solar Reactor for Carbon Dioxide Splitting via the Isothermal Ceria Redox Cycle and Practical Implications. Energy Fuels 30 (8), 6654–6661. doi:10.1021/acs.energyfuels.6b01265

CrossRef Full Text | Google Scholar

Hathaway, B. J., and Davidson, J. H. (2017). Demonstration of a Prototype Molten Salt Solar Gasification Reactor. Solar Energy 142, 224–230. doi:10.1016/j.solener.2016.12.032

CrossRef Full Text | Google Scholar

Hoskins, A. L., Millican, S. L., Czernik, C. E., Alshankiti, I., Netter, J. C., Wendelin, T. J., et al. (2019). Continuous On-Sun Solar Thermochemical Hydrogen Production via an Isothermal Redox Cycle. Appl. Energ. 249, 368–376. doi:10.1016/j.apenergy.2019.04.169

CrossRef Full Text | Google Scholar

Jarrett, C., Chueh, W., Yuan, C., Kawajiri, Y., Sandhage, K. H., and Henry, A. (2016). Critical Limitations on the Efficiency of Two-Step Thermochemical Cycles. J. Sol. Energy 123, 57–73.

Jin, J., Wei, X., Liu, M., Yu, Y., Li, W., Kong, H., et al. (2018). A Solar Methane Reforming Reactor Design with Enhanced Efficiency. Appl. Energ. 226, 797–807. doi:10.1016/j.apenergy.2018.04.098

CrossRef Full Text | Google Scholar

Kodama, T. (2003). High-temperature Solar Chemistry for Converting Solar Heat to Chemical Fuels. Prog. Energ. combustion Sci. 29 (6), 567–597. doi:10.1016/s0360-1285(03)00059-5

CrossRef Full Text | Google Scholar

Koepf, E., Villasmil, W., and Meier, A. (2016). Pilot-scale Solar Reactor Operation and Characterization for Fuel Production via the Zn/ZnO Thermochemical Cycle. Appl. Energ. 165, 1004–1023. doi:10.1016/j.apenergy.2015.12.106

CrossRef Full Text | Google Scholar

Kong, H., Hao, Y., and Jin, H. (2018). Isothermal versus Two-Temperature Solar Thermochemical Fuel Synthesis: A Comparative Study. Appl. Energ. 228, 301–308. doi:10.1016/j.apenergy.2018.05.099

CrossRef Full Text | Google Scholar

Kong, H., Hao, Y., and Wang, H. (2016). A Solar Thermochemical Fuel Production System Integrated with Fossil Fuel Heat Recuperation. Appl. Therm. Eng. 108, 958–966. doi:10.1016/j.applthermaleng.2016.03.170

CrossRef Full Text | Google Scholar

Lange, J.-P. (2016). Catalysis for Biorefineries - Performance Criteria for Industrial Operation. Catal. Sci. Technol. 6 (13), 4759–4767. doi:10.1039/c6cy00431h

CrossRef Full Text | Google Scholar

Lapp, J., Davidson, J. H., and Lipiński, W. (2012). Efficiency of Two-step Solar Thermochemical Non-stoichiometric Redox Cycles with Heat Recovery. Energy 37 (1), 591–600. doi:10.1016/j.energy.2011.10.045

CrossRef Full Text | Google Scholar

Levenspiel, O. (2001). Chemical Reaction Engineering. 3rd edition. New York, NY: John Willey and Sons.

Li, S., Wheeler, V. M., Kumar, A., Venkataraman, M. B., Muhich, C. L., Hao, Y., et al. (2021). Thermodynamic Guiding Principles for Designing Nonstoichiometric Redox Materials for Solar Thermochemical Fuel Production: Ceria, Perovskites, and beyond. Energ. Tech., 2000925. doi:10.1002/ente.202000925

CrossRef Full Text | Google Scholar

Loutzenhiser, P. G., and Muroyama, A. P. (2017). A Review of the State-Of-The-Art in Solar-Driven Gasification Processes with Carbonaceous Materials. Solar Energy 156, 93–100. doi:10.1016/j.solener.2017.05.008

CrossRef Full Text | Google Scholar

Lu, Y., Zhu, L., Agrafiotis, C., Vieten, J., Roeb, M., and Sattler, C. (2019). Solar Fuels Production: Two-step Thermochemical Cycles with Cerium-Based Oxides. Prog. Energ. Combustion Sci. 75, 100785. doi:10.1016/j.pecs.2019.100785

CrossRef Full Text | Google Scholar

Maag, G., Zanganeh, G., and Steinfeld, A. (2009). Solar thermal Cracking of Methane in a Particle-Flow Reactor for the Co-production of Hydrogen and Carbon. Int. J. Hydrogen Energ. 34 (18), 7676–7685. doi:10.1016/j.ijhydene.2009.07.037

CrossRef Full Text | Google Scholar

Mao, Y., Gao, Y., Dong, W., Wu, H., Song, Z., Zhao, X., et al. (2020). Hydrogen Production via a Two-step Water Splitting Thermochemical Cycle Based on Metal Oxide - A Review. Appl. Energ. 267, 114860. doi:10.1016/j.apenergy.2020.114860

CrossRef Full Text | Google Scholar

Marxer, D., Furler, P., Takacs, M., and Steinfeld, A. (2017). Solar Thermochemical Splitting of CO2 into Separate Streams of CO and O2 with High Selectivity, Stability, Conversion, and Efficiency. Energy Environ. Sci. 10 (5), 1142–1149. doi:10.1039/c6ee03776c

CrossRef Full Text | Google Scholar

Muhich, C. L., Evanko, B. W., Weston, K. C., Lichty, P., Liang, X., Martinek, J., et al. (2013). Efficient Generation of H2 by Splitting Water with an Isothermal Redox Cycle. Science 341 (6145), 540–542. doi:10.1126/science.1239454

PubMed Abstract | CrossRef Full Text | Google Scholar

Müller, F., Patel, H., Blumenthal, D., Poživil, P., Das, P., Wieckert, C., et al. (2018). Co-production of Syngas and Potassium-Based Fertilizer by Solar-Driven Thermochemical Conversion of Crop Residues. Fuel Process. Tech. 171, 89–99. doi:10.1016/j.fuproc.2017.08.006

CrossRef Full Text | Google Scholar

Müller, F., Poživil, P., Van Eyk, P. J., Villarrazo, A., Haueter, P., Wieckert, C., et al. (2017). A Pressurized High-Flux Solar Reactor for the Efficient Thermochemical Gasification of Carbonaceous Feedstock. Fuel 193, 432–443. doi:10.1016/j.fuel.2016.12.036

CrossRef Full Text | Google Scholar

Muroyama, A. P., Guscetti, I., Schieber, G. L., Haussener, S., and Loutzenhiser, P. G. (2018). Design and Demonstration of a Prototype 1.5 kWth Hybrid Solar/autothermal Steam Gasifier. Fuel 211, 331–340. doi:10.1016/j.fuel.2017.09.059

CrossRef Full Text | Google Scholar

Noring, J. E., and Fletcher, E. A. (1982). High Temperature Solar Thermochemical Processing-Hydrogen and Sulfur from Hydrogen Sulfide. Energy 7 (8), 651–666. doi:10.1016/0360-5442(82)90002-0

CrossRef Full Text | Google Scholar

Nzihou, A., Flamant, G., and Stanmore, B. (2012). Synthetic Fuels from Biomass Using Concentrated Solar Energy - A Review. Energy 42 (1), 121–131. doi:10.1016/j.energy.2012.03.077

CrossRef Full Text | Google Scholar

Ozin, G. (2018). Drop-In Solar Fuels from Carbon Dioxide and Water: Performance Indicators. Available at: https://www.advancedsciencenews.com/drop-in-solar-fuels-from-carbon-dioxide-and-water-performance-indicators.

Google Scholar

Palumbo, A. W., Sorli, J. C., and Weimer, A. W. (2015). High Temperature Thermochemical Processing of Biomass and Methane for High Conversion and Selectivity to H2-Enriched Syngas. Appl. Energ. 157, 13–24. doi:10.1016/j.apenergy.2015.07.072

CrossRef Full Text | Google Scholar

Piatkowski, N., Wieckert, C., Weimer, A. W., and Steinfeld, A. (2011). Solar-Driven Gasification of Carbonaceous Feedstock—A Review . Energy Environ. Sci. 4 (1), 73–82.

CrossRef Full Text | Google Scholar

Rodat, S., Abanades, S., Boujjat, H., and Chuayboon, S. (2020). On the Path toward Day and Night Continuous Solar High Temperature Thermochemical Processes: A Review. Renew. Sust. Energ. Rev. 132, 110061. doi:10.1016/j.rser.2020.110061

CrossRef Full Text | Google Scholar

Rodat, S., Abanades, S., and Flamant, G. (2011). Co-production of Hydrogen and Carbon Black from Solar thermal Methane Splitting in a Tubular Reactor Prototype. Solar energy 85 (4), 645–652. doi:10.1016/j.solener.2010.02.016

CrossRef Full Text | Google Scholar

Romero, M., and Steinfeld, A. (2012). Concentrating Solar Thermal Power and Thermochemical Fuels. Energ. Environ. Sci. 5, 9234–9245. doi:10.1039/c2ee21275g

CrossRef Full Text | Google Scholar

Safari, F., and Dincer, I. (2020). A Review and Comparative Evaluation of Thermochemical Water Splitting Cycles for Hydrogen Production. Energ. Convers. Manag. 205, 112182. doi:10.1016/j.enconman.2019.112182

CrossRef Full Text | Google Scholar

Sheu, E. J., Mokheimer, E. M. A., and Ghoniem, A. F. (2015). A Review of Solar Methane Reforming Systems. Int. J. Hydrogen Energ. 40 (38), 12929–12955. doi:10.1016/j.ijhydene.2015.08.005

CrossRef Full Text | Google Scholar

Singh, A., Lapp, J., Grobbel, J., Brendelberger, S., Reinhold, J. P., Olivera, L., et al. (2017). Design of a Pilot Scale Directly Irradiated, High Temperature, and Low Pressure Moving Particle Cavity Chamber for Metal Oxide Reduction. Solar Energy 157, 365–376. doi:10.1016/j.solener.2017.08.040

CrossRef Full Text | Google Scholar

Steinfeld, A.. (2014) Solar Thermochemical Production of Hydrogen. in Handbook of Hydrogen Energy. Boca Raton, FL: CRC Press, Chapter 12, 421–443.

CrossRef Full Text | Google Scholar

Steinfeld, A. (2012). Thermochemical Production of Syngas Using Concentrated Solar Energy. Annu. Rev. Heat Transfer 15. doi:10.1615/annualrevheattransfer.2012004537

CrossRef Full Text | Google Scholar

Welte, M., Barhoumi, R., Zbinden, A., Scheffe, J. R., and Steinfeld, A. (2016). Experimental Demonstration of the Thermochemical Reduction of Ceria in a Solar Aerosol Reactor. Ind. Eng. Chem. Res. 55 (40), 10618–10625. doi:10.1021/acs.iecr.6b02853

PubMed Abstract | CrossRef Full Text | Google Scholar

Yadav, D., and Banerjee, R. (2016). A Review of Solar Thermochemical Processes. Renew. Sust. Energ. Rev. 54, 497–532. doi:10.1016/j.rser.2015.10.026

CrossRef Full Text | Google Scholar

Yuan, C., Jarrett, C., Chueh, W., Kawajiri, Y., and Henry, A. (2015). A New Solar Fuels Reactor Concept Based on a Liquid Metal Heat Transfer Fluid: Reactor Design and Efficiency Estimation. Solar Energy 122, 547–561. doi:10.1016/j.solener.2015.08.019

CrossRef Full Text | Google Scholar

Z’Graggen, A., Haueter, P., Maag, G., Vidal, A., Romero, M., and Steinfeld, A. (2006). “Hydrogen Production by Steam-Gasification of Petroleum Coke Using Concentrated Solar Power: Reactor Experimentation with Slurry Feeding”. In International Solar Energy Conference, Denver, CO, July 8–13, 2006 (ASME). 23–27. doi:10.1115/ISEC2006-99029

CrossRef Full Text | Google Scholar

Z'Graggen, A., and Steinfeld, A. (2008). Hydrogen Production by Steam-Gasification of Carbonaceous Materials Using Concentrated Solar Energy–V. Reactor Modeling, Optimization, and Scale-Up. Int. J. Hydrogen Energ. 33 (20), 5484–5492.

Google Scholar

Zeng, K., Gauthier, D., Soria, J., Mazza, G., and Flamant, G. (2017). Solar Pyrolysis of Carbonaceous Feedstocks: A Review. Solar Energy 156, 73–92. doi:10.1016/j.solener.2017.05.033

CrossRef Full Text | Google Scholar

Zheng, R., Diver, R., Caldwell, D., Fritz, B., Cameron, R., Humble, P., et al. (2015). Integrated Solar Thermochemical Reaction System for Steam Methane Reforming. Energ. Proced. 69, 1192–1200. doi:10.1016/j.egypro.2015.03.204

CrossRef Full Text | Google Scholar

Zhu, L., Lu, Y., and Shen, S. (2016). Solar Fuel Production at High Temperatures Using Ceria as a Dense Membrane. Energy 104, 53–63. doi:10.1016/j.energy.2016.03.108

CrossRef Full Text | Google Scholar

Zoller, S., Koepf, E., Roos, P., and Steinfeld, A. (2019). Heat Transfer Model of a 50 kW Solar Receiver–Reactor for Thermochemical Redox Cycling Using Cerium Dioxide. J. Solar Energ. Eng. 141 (2). doi:10.1115/1.4042059

CrossRef Full Text | Google Scholar

Nomenclature

$\eta$ Energy efficiency

$E_{total}$ Total energy demand

$Q$ Quantity of heat

$\dot{Q}$ Heat flow rate

$W$ Quantity of work

$\dot{W}$ Work flow rate

$n_i$ Number of moles of species i

${\dot{n}}_i$ Molar flow rate of species i

$G_i$ Gibbs free energy of species i

${\mathrm{HHV}}_i$ Higher heating value of species i

$X_i$ Conversion extent of reactant i

$S_i$ Selectivity towards product i

$Y_i$ Yield of product i

${\dot{n}}_{i,0}$ Input flow rate of species i

${\dot{n}}_{i,f}$ Output flow rate of species i

$F_i$ Energy factor of component i

$U$ Upgrade factor of the heating value