- 1Department of Chemical Engineering, Columbia University, New York, NY, United States
- 2State Key Laboratory of Information Photonics and Optical Communications, Beijing University of Posts and Telecommunications, Beijing, China
- 3Columbia Center for Computational Electrochemistry, Columbia University, New York, NY, United States
- 4Columbia Electrochemical Energy Center, Columbia University, New York, NY, United States
Materials for solid-state batteries often exhibit complex chemical compositions, defects, and disorder, making both experimental characterization and direct modeling with first principles methods challenging. Machine learning (ML) has proven versatile for accelerating or circumventing first-principles calculations, thereby facilitating the modeling of materials properties that are otherwise hard to access. ML potentials trained on accurate first principles data enable computationally efficient linear-scaling atomistic simulations with an accuracy close to the reference method. ML-based property-prediction and inverse design techniques are powerful for the computational search for new materials. Here, we give an overview of recent methodological advancements of ML techniques for atomic-scale modeling and materials design. We review applications to materials for solid-state batteries, including electrodes, solid electrolytes, coatings, and the complex interfaces involved.
Introduction
Li-ion batteries (LIBs) (Whittingham, 1976; Mizushima et al., 1980; Li et al., 2017b, Li et al., 2018a) have enabled a revolution in portable electronics, but the global transition to a clean energy economy based on renewable sources will require the development of a new generation of batteries that addresses the needs of grid-level storage and transportation. To this end, computational materials discovery has become an important companion to conventional experimentation. Especially first-principles atomistic simulations have contributed significantly to our understanding of fundamental properties and phenomena in LIBs, such as Li migration mechanisms and crystal structure preferences (Saiful Islam and Fisher, 2014; Urban et al., 2016). First-principles predictions have already led to the discovery of novel battery materials (Kirklin et al., 2013; Er et al., 2015; Jain et al., 2016). However, first-principles methods, such as electronic density-functional theory (DFT) (Hohenberg and Kohn, 1964; Kohn and Sham, 1965; Burke, 2012), are computationally demanding, and simulations are currently limited to small, typically crystalline structure models with less than 1,000 atoms and less than nanosecond time scales. It is therefore challenging to investigate non-ideal atomic structures with first-principles, such as the defected or amorphous phases and interphases that are formed at the electrode|electrolyte interfaces in LIBs (Yu and Manthiram, 2018).
Solid-state batteries (SSBs), in which the conventional liquid electrolyte is replaced by a solid ion conductor, are strong contenders for the next generation of more energy dense and safer LIBs (Gao et al., 2018; Banerjee et al., 2020). The development and commercialization of SSBs is currently hindered by a lack of understanding of stability issues at the solid-solid interfaces that can lead to mechanical failure, chemical or electrochemical decomposition, or the growth of Li dendrites (Riphaus et al., 2019; Xiao et al., 2019). As schematically shown in Figure 1, macroscopic (electrode- order interface-scale) properties are often governed by phenomena on the atomic scale. First-principles atomistic simulations would therefore, in principle, be an ideal characterization tool, but the complex structure and composition of the involved materials and interfaces makes the direct first-principles modeling extremely challenging.
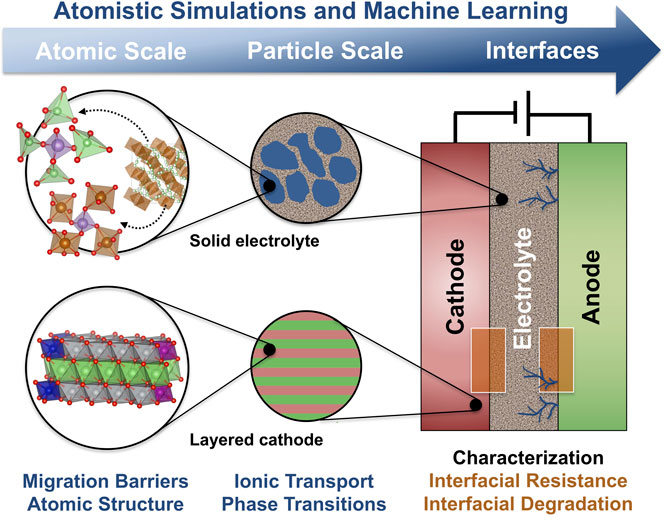
FIGURE 1. The properties of solid-state batteries, such as stability and rate capability, are often dependent on atomic-scale phenomena, such as phase changes or structural motifs at interfaces and grain boundaries. Machine learning techniques can increase the length and time scale that atomistic simulations can access.
During the last decades, machine learning (ML) and artificial intelligence (AI) methods have been developed that can substantially accelerate first-principles modeling. Here, we review common ML/AI strategies for atomic-scale materials simulations and their applications to the discovery and understanding of materials for SSBs. In the following Machine Learning for Materials Modeling, we briefly introduce the most common ML/AI techniques and methods that have previously been applied to research questions related to LIBs. In Applications of ML/AI for the Atomistic Modeling of Solid-State Batteries we review concrete applications of these strategies to materials and interfaces of relevance to SSBs. We also cover select applications to conventional LIBs that are related either by materials or demonstrate techniques that, we believe, could also be applied to research questions related to SSBs. Discussion and Perspective provides a discussion of the current limitations of ML for SSB modeling and potential future directions.
Machine Learning for Materials Modeling
ML is the field of research that deals with algorithms that can improve themselves by extracting knowledge, i.e., learning, from data (Jordan and Mitchell, 2015). ML is an area of AI, which in most textbook definitions includes all artificial implementations of intelligent problem solving and does not necessarily involve learning. In recent years, ML has seen a renaissance because of increasing tool and data availability and owing to the success of deep learning (Goodfellow et al., 2016). Nowadays, standard Python libraries such as scikit-learn (Pedregosa et al., 2011), PyTorch (Paszke et al., 2017), and TensorFlow (Abadi et al., 2015) facilitate the efficient implementation of ML techniques. In materials science, automation has made it feasible to generate large first-principles data sets in a high-throughput fashion (Morgan et al., 2004; Jain et al., 2011; Curtarolo et al., 2013), and there is an increasing number of publicly accessible databases with data from automated first-principles calculations (Curtarolo et al., 2012; Jain et al., 2013; Saal et al., 2013; Talirz et al., 2020). The field of ML for materials modeling is rapidly evolving, and a compilation of tools and data sources that is regularly updated can be found online at https://github.com/atomisticnet/tools-and-data.
As described in the introduction section, quantum-mechanics based electronic structure methods, such as DFT, can provide quantitative predictions of materials properties but at high computational cost. Some properties of batteries are determined by complex structures and compositions (such as interfaces in batteries) and phenomena that occur on long time scales (e.g., Li diffusion at room temperature) that are not directly accessible with DFT calculations. In the last 2 decades, ML and AI techniques have been developed that address these limitations to some extent. Most ML/AI approaches for atomic-scale materials modeling belong to one of the following three categories (Figure 2):
(1) ML potentials for accelerated sampling with first principles accuracy,
(2) Property ML models that are trained to predict the outcome of first-principles calculations for a given atomic structure, and
(3) Inverse design ML/AI approaches that predict an atomic structure for a given set of materials properties.
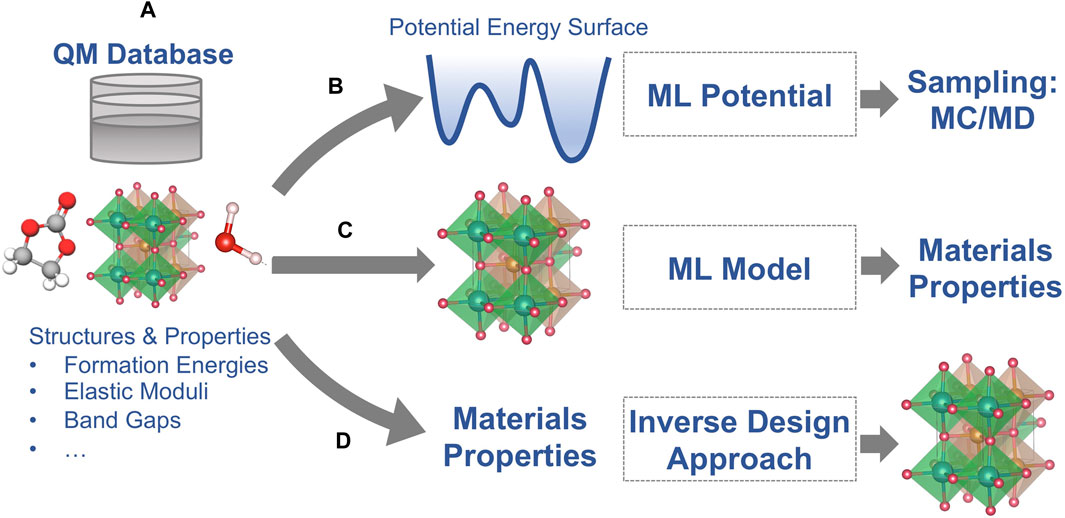
FIGURE 2. Schematic of the three most common applications of machine learning (ML) for materials modeling (A) Reference data from quantum-mechanical (QM) calculations; (B) ML potentials for the regression of potential energy surfaces; (C) ML models for the prediction of materials properties as predicted by the QM reference method; and (D) Inverse design approaches for predicting structure models for a given set of materials properties.
We distinguish between these three classes of models because of differences in their implementation. ML potentials and property ML models are both built on conventional ML techniques that learn from data. ML potentials belong to the general class of regression models, whereas property models can be implemented as either regression or classification models. Each ML model takes as input a set of features that describe, e.g., the atomic structure and composition, and the choice of features for ML potentials differs from those used for property models as is discussed below in greater detail. Inverse design problems are traditionally solved with global optimization algorithms belonging to the more general class of AI methods. In recent years, generative ML models have been developed that can, in some cases, solve inverse design problems more directly than conventional AI algorithms, and we review here applications of both types.
In the following, we briefly discuss the three classes of ML/AI methods on a level of detail that should equip the reader to navigate the Applications of ML/AI for the Atomistic Modeling of Solid-State Batteries of the present review.
ML Potentials
ML regression models trained on the potential energy from DFT or other first-principles methods (Figure 2B) can be used as computationally efficient drop-in replacements for DFT with an accuracy close to that of the reference method. This general approach has a long history, and already in 1995, Blank et al. used artificial neural networks (ANNs) for the representation of potential energy surfaces (PES) for CO adsorption on Ni(111) surfaces (Blank et al., 1995).
ML models trained to directly predict the potential energy of an atomic structure for given Cartesian atomic coordinates 1) do not automatically exhibit the symmetries of the potential energy with respect to rotation and translation of the entire structure and the exchange of equivalent atoms. Additionally, the models 2) are limited to one specific number of atoms and a specific composition. In 2006, Lorentz et al. proposed a transformation of the Cartesian coordinates to symmetry-adapted coordinates to address limitation 1) (Lorenz et al., 2006), an approach that was further generalized by Behler et al. (2007). To overcome limitation 2), Behler and Parrinello (BP) expressed the total potential energy
In the BP approach, ANNs are trained to predict the atomic energies for a given local atomic environment, and
Building on the idea of the BP ANN potential method, various other MLP methods have since been proposed that differ in the representation of the local atomic environment and the choice of model. Currently most widely adopted are the Gaussian Approximation Potential (GAP) by Bartók et al. (2010), Bartók et al. (2013), the spectral neighbor analysis potential (SNAP) by Thompson et al. (2014), and the moment-tensor potential (MTP) by Shapeev, (2016). Zuo et al. recently compared different MLP methods for an example application, concluding that the computational cost of the GAP model is dependent on the size of the data set and was two orders of magnitude more expensive for the benchmark case than the ANN, MTP, and SNAP models (Zuo et al., 2020). On the other hand, in terms of the accuracy, the GAP and MTP models exhibited the lowest root mean square error (RMSE) compared to the reference method.
Several approaches for the representation (or featurization) of local atomic environments have been proposed in the literature and are used in MLP implementations, and recent reviews can be found in references (Himanen et al., 2020; Parsaeifard et al., 2021). Here, we limit the discussion to the presently most popular choices. Behler and Parrinello introduced so called symmetry functions (SFs) that sample the bond lengths and bond angles in the local atomic environment (Behler, 2011). Different chemical species can be distinguished by using individual sets of SFs for each chemical bond and bond angle (Artrith et al., 2011). Artrith, Urban, and Ceder (AUC) showed that, more generally, the radial and angular distribution functions of the local atomic environment can be expanded in orthogonal basis sets (such as Chebyshev polynomials) to obtain a systematically refinable descriptor (Artrith et al., 2017). The AUC descriptor also introduced an alternative way to distinguish between chemical species by introducing species-dependent weights. Reducing the local atomic environment to bonds and angles (2- and 3-body interactions) is an approximation, and descriptors can also be obtained from the direct expansion of the local atomic structure. However, depending on the choice of basis set, the expansion coefficients are not necessarily invariant with respect to translation and rotation. Popular representations based on direct expansion in tailored basis functions or with an additional postprocessing step are bispectrum based descriptors (Bartók et al., 2010; Thompson et al., 2014), the smooth overlap of atomic positions (SOAP) (Bartók et al., 2013), and the invariant polynomial representation of the MTP (Shapeev, 2016).
Owing to improving software availability, the adoption of ANN potentials and other MLPs for materials simulations has been gaining momentum in the past few years, as is also evidenced by the rapidly increasing number of publications that mention ANN potentials (Figure 3). Further details of the different MLP methods can be found in perspectives and reviews (Behler, 2016; Mueller et al., 2020; Noé et al., 2020; Behler, 2021; Shao et al., 2021; Unke et al., 2021).
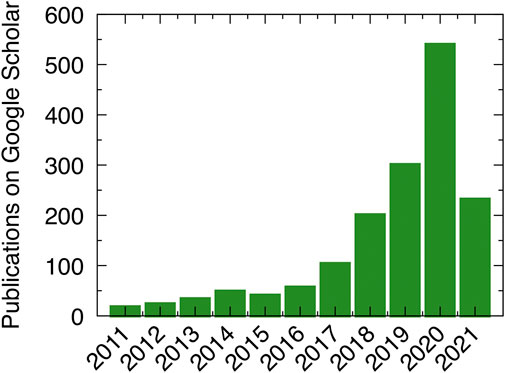
FIGURE 3. Number of publications per year on Google Scholar that include the phrase “neural network potential,” starting from 2011 to May 2021.
A number of publicly available frameworks for the construction and application of MLPs have been released over the last years, including GAP (Bartók et al., 2010), SNAP (Thompson et al., 2015), ænet (Artrith and Urban, 2016), AMP (Khorshidi and Peterson, 2016), ANI-1 (Smith et al., 2017), N2P2 (Singraber et al., 2019), and MLIP (Novikov et al., 2021).
Property Predictions
Instead of training ML models on the potential energy (and its gradients) only, other results from first-principles calculations can be chosen as targets. Property prediction ML models (Figure 2C) are trained to predict directly one or more outcomes of first-principles calculations from existing databases, without involving a physics-based model altogether. First-principles methods are thus replaced by machine learning models that are orders of magnitude faster. This approach has shown the potential to be useful for extending essentially any property databases to new systems, facilitating prediction of new data, rapid exploration of large chemical spaces and the discovery, design and development of new materials.
The underlying ML models for property prediction are often either based on ANNs with different architectures (Eslamloueyan et al., 2011; Jalem et al., 2015; Wu et al., 2017; Allam et al., 2018; Ye et al., 2018; Joshi et al., 2019), Gaussian process regression (GPR) (Jalem et al., 2018), kernel ridge regression (KRR) (Wu et al., 2017; Joshi et al., 2019), support vector machines (SVM) (Gharagheizi et al., 2013; Hosseinzadeh et al., 2016; Joshi et al., 2019), partial least squares (PLS) (Jalem et al., 2014; Wang et al., 2017; Nakayama et al., 2019), decision-tree based models such as random forests (Attarian Shandiz and Gauvin, 2016; Wu et al., 2017; Li et al., 2018b) or gradient-boosted trees (Nakayama et al., 2019) or a linear combination of these.
The features that enter the ML models are typically tabulated elemental properties (e.g., atomic number, mass, radius, number of valence electrons, electronegativity) and/or compound quantities that can be obtained from straightforward DFT calculations (e.g., cohesive energies, lattice parameters). In addition, some models also featurize the atomic structure, and various approaches have been proposed in the literature (Weininger, 1988; Rupp et al., 2012; Hansen et al., 2015; Huang and von Lilienfeld, 2016; Collins et al., 2018; Huo and Rupp, 2018; Ziletti et al., 2018). Popular choices are the Coulomb matrix descriptor (Brown and Martin, 1996; Brown and Martin, 1997; Pilania et al., 2013; Faber et al., 2015; Huan et al., 2015; Isayev et al., 2017; Seko et al., 2017) for molecules and descriptors based on Fourier transforms (Leicester et al., 1988; von Lilienfeld et al., 2015), radial distribution functions (Schütt et al., 2014) or structural fragments/motifs (Brown and Martin, 1996; Pilania et al., 2013; Faber et al., 2015; Huan et al., 2015; Isayev et al., 2017; Seko et al., 2017) for periodic structures. Graph-based representations are also commonly used for molecules (Mahé et al., 2005; Rogers and Hahn, 2010; Faber et al., 2017; Collins et al., 2018) and periodic structures (Xie and Grossman, 2018; Chen et al., 2019).
A number of frameworks specifically designed for the construction of ML models for materials properties have been released over the last years, including magpie (Ward et al., 2016), matminer (Ward et al., 2018), MegNet (Chen et al., 2019), AFLOW ML (Gossett et al., 2018), catlearn (Hansen et al., 2019), and SISSO (Ouyang et al., 2020). An updated list can be found at https://github.com/atomisticnet/tools-and-data.
Inverse Design
The ML models of the previous two sections replicate the conventional direction of atomistic modeling: properties are predicted for a given atomic structure. For the design of new functional materials, the ability to predict an atomic structure for a given set of desired molecular or materials properties would be useful. This is often referred to as inverse design, as the process starts from the functionality and ends in the structures, aiming to find the target material with the desired properties.
Inverse design has been a prototypical application of AI techniques for the last 3 decades (Venkatasubramanian, 2019). For example, evolutionary (or genetic) algorithms are a type of global optimization algorithms that can be used for the search of an atomic structure with specific properties by defining a suitable fitness function and evolution operations, e.g., crossover and mutation (Goldberg, 1989). By using ab initio (free) energies as the fitness function, first-principles structure prediction can be performed (Glass et al., 2006; Sun and Zhao, 2017). Particle swarm optimization (PSO) is another global optimization method that is often used for inverse design (Kennedy et al., 2001). Here, an ensemble (swarm) of trial structures (particles) is optimized by guiding the variation of each particle by their own best-known state in the search space and by the best-known state among the entire swarm (Wang et al., 2010). PSO is commonly used for first-principles structure search (Gao et al., 2019; Tian et al., 2020). Another class of methods that is commonly applied to inverse design tasks is Bayesian Optimization (Mockus, 1989), for which applications to materials discovery have been demonstrated (Zuo et al., 2021).
More recently, generative ML methods have been developed that can address the inverse design problem without explicit sampling. Generative models can explore the chemical configuration space by learning the underlying rules of the data distribution (Sanchez-Lengeling and Aspuru-Guzik, 2018; Schwalbe-Koda and Gómez-Bombarelli, 2020). One class of generative ML methods that begin to be used more frequently are variational autoencoders (VAEs), a type of ANN (Kingma and Welling, 2014). VAEs can encode atomic structures in a latent (reduced dimensional) representation, and the decoding network can be exploited for generating structures. Applications for atomic-scale simulations are still scarce (Court et al., 2020) but can be expected to increase over the next years. Another commonly used generative ML approach are generative adversarial networks (Goodfellow et al., 2014) which can generate structures with intended chemical and physical characteristics by using two competing ANNs. This method has been applied, for example, to generate periodic microstructures of a Li-ion battery cathode and a solid oxide fuel cell anode (Gayon-Lombardo et al., 2020).
Overview of Relevant ML Techniques
Some ML techniques, such as ANNs, have already been introduced in the previous sections. Here we summarize briefly the underlying concepts of other ML techniques that have been applied to research questions related to batteries and are mentioned in Applications of ML/AI for the Atomistic Modeling of Solid-State Batteries.
Linear regression (LR) is one of the simplest regression methods. LR algorithms compute the model output as a linear combination of the input features. During training, the squared distances between the predicted and the true target values are minimized (method of least squares). Ridge regression (RR) extends the objective function of the least-squares linear regression model by a regularization term to prevent overfitting during training (Hoerl and Kennard, 1970). This results in simpler and less complex LR models that typically generalize better to unseen data. The strength of the regularization is determined by a hyperparameter.
LR and RR are limited to model problems with linear correlations, i.e., only linear dependencies between input and output can be captured. Kernel ridge regression (KRR) generalizes linear RR towards nonlinear relationships between data (Hastie et al., 2009; Vovk, 2013). Input data are mapped into a higher-dimensional feature space, transforming the original, nonlinear regression task into a linear task in feature space. Since the choice of an appropriate mapping function can be challenging, so-called kernels are applied instead. A kernel function can be interpreted as a similarity measure between inputs. Instead of mapping the data and solving a nonlinear regression task in high dimensional feature space, a non-linear kernel function can be applied to the data in input space before performing linear regression (kernel trick). Some commonly used kernels are the polynomial kernel, the Gaussian kernel, and the Laplacian kernel. The type and the parameters of the chosen kernel are hyperparameter that need to be optimized separately within a model selection procedure. The fitting of a KRR model becomes computationally more demanding with the size of the dataset, which limits applications to intermediately sized data sets (thousands of data points).
The support vector machine (SVM) is also a kernel-based classification method that, like KRR, solves a linear classification problem in a higher-dimensional feature space (Cortes and Vapnik, 1995; Suykens and Vandewalle, 1999). The objective is to find a hyperplane in feature space that distinctly classifies the data points. Among all possible hyperplanes, the plane that has maximum distance between data points of both classes is chosen. Support vectors are the data points that define the hyperplane by maximizing the margin of the classifier.
k-Nearest Neighbor (kNN) is another well-known and simple nonlinear ML algorithm that can be used to solve both classification and regression problems (Dudani, 1976). The kNN method assumes that similar data points are in close proximity in feature space. For classification tasks, new data points are classified into the category that is most predominant among its k nearest neighbors. For regression tasks, the weighted mean label value among the k nearest neighbors is computed. The number of the nearest neighbors k and the measurement of distances are hyperparameters that have to be chosen beforehand. A limitation of the method is the requirement for a reasonable distance metric.
Bayesian Optimization (BO) is an optimization method used to construct a probabilistic model for a target property or a target function (Mockus, 1989; Snoek et al., 2012), typically employing Gaussian Processes (GPs) (Rasmussen, 2004). GPs are stochastic processes that describe probability distributions over functions, and assign a probability to each of these functions. The mean of this probability distribution represents the most probable characterization of the data. A key benefit of GP regression (GPR) models is that in addition to the prediction, they also describe the uncertainty of each prediction. A drawback is that GPs need to take into account the whole training data each time a prediction is made, so that the computational cost of predictions scales cubically with the number of training samples.
Random forest (RF) is a flexible and simple ML algorithm that can be used for both classification and regression tasks (Tin Kam Ho, 1998; Svetnik et al., 2003). The RF builds an ensemble of decision trees on various subsets of the given dataset. It takes the prediction from each decision tree and computes their average to predict the final output. Choosing a great number of decision trees leads to higher accuracy and prevents overfitting. The ensemble-based architecture allows RFs to handle large datasets efficiently and to deliver predictions with high accuracy.
Gradient boost regression (GBR) is another ensemble ML method for regression and classification problems (Friedman, 2001; Nakayama et al., 2019). The GBR algorithm starts by fitting an initial model (e.g., decision tree or linear regression model) to the data. Then a second model is built that focuses on accurately predicting the cases where the first model performs poorly. The combination of these two models is expected to be better than either model alone. This process of boosting can be repeated many times. Each successive model attempts to correct for the shortcomings of the combined boosted ensemble of all previous models.
Applications of ML/AI for the Atomistic Modeling of Solid-State Batteries
In the following, we review applications of ML and AI techniques to materials with relevance for SSBs. The section is organized by the battery components, i.e., Electrodes (Cathode/Anode) reviews applications to electrode materials, applications to solid electrolyte materials are reviewed in Electrolyte, and Interfaces and Coatings contains applications to coatings and interfaces.
Electrodes (Cathode/Anode)
Cathodes
The candidate cathode materials for SSBs should possess the following properties: 1) high energy density enabled by high voltage and capacity 2) mechanical stability that is resistant to volume shrinkage. Several ML models have been trained for the modeling of materials that match these requirements to search for novel cathode materials, and the examples are summarized in Table 1.
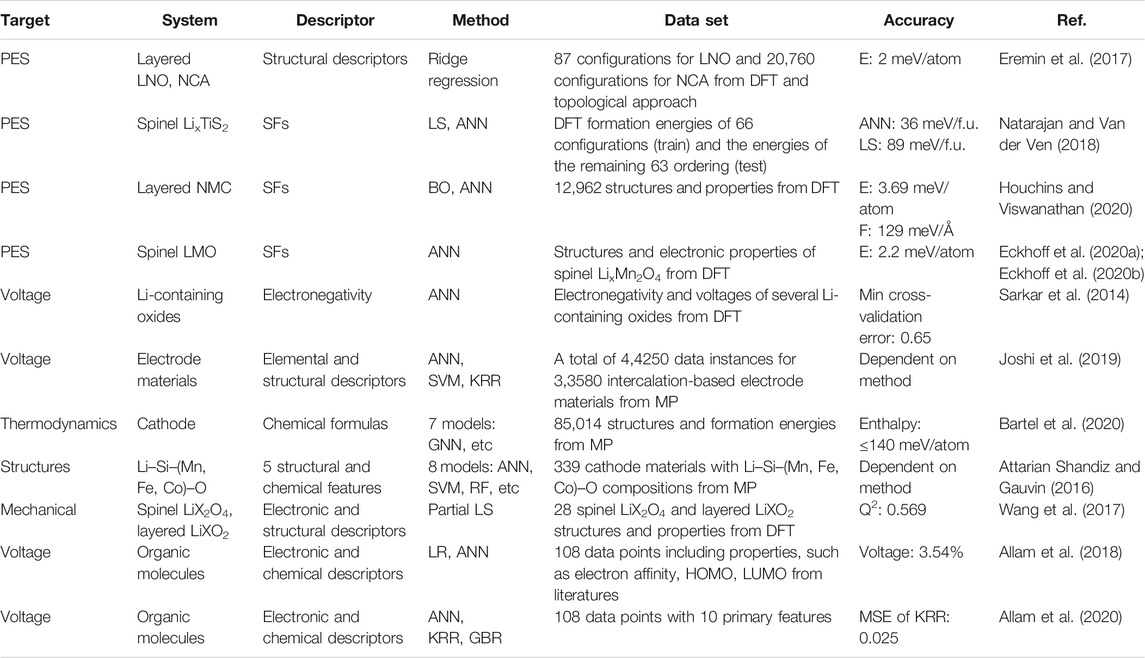
To map the structure-property relationship, Eremin et al. combined topological analysis, DFT modeling, operando neutron diffraction, and ridge regression in the configurational space of LiNiO2 (LNO) and LiNi0.8Co0.15Al0.05O2 (NCA) cathode materials (Eremin et al., 2017). They demonstrated that the topology of Li layers and relative disposition of Li ions and dopants have the most significant effect on the energy balance. Similarly, Natarajan et al. integrated ANNs with symmetry-adapted cluster functions to predict the formation energies of Li-vacancy orderings on the different sites of spinel LiTiS2 (Natarajan and Van der Ven, 2018). The results show that the ANN can reproduce the DFT-calculated convex hull (Figure 4B) with only the information about pair cluster correlations as the input feature. Furthermore, Houchins and Viswanathan developed an accurate ANN potential for the LiNixMnyCo(1−x−y)O2 (NMC) cathode materials using a training set based on DFT calculations (Houchins and Viswanathan, 2020). The generated ML potential exhibits a good approximation for most thermodynamic properties, including the Gibbs free energy and entropy, and predicts voltage profiles that are in good agreement with the experimental curves.
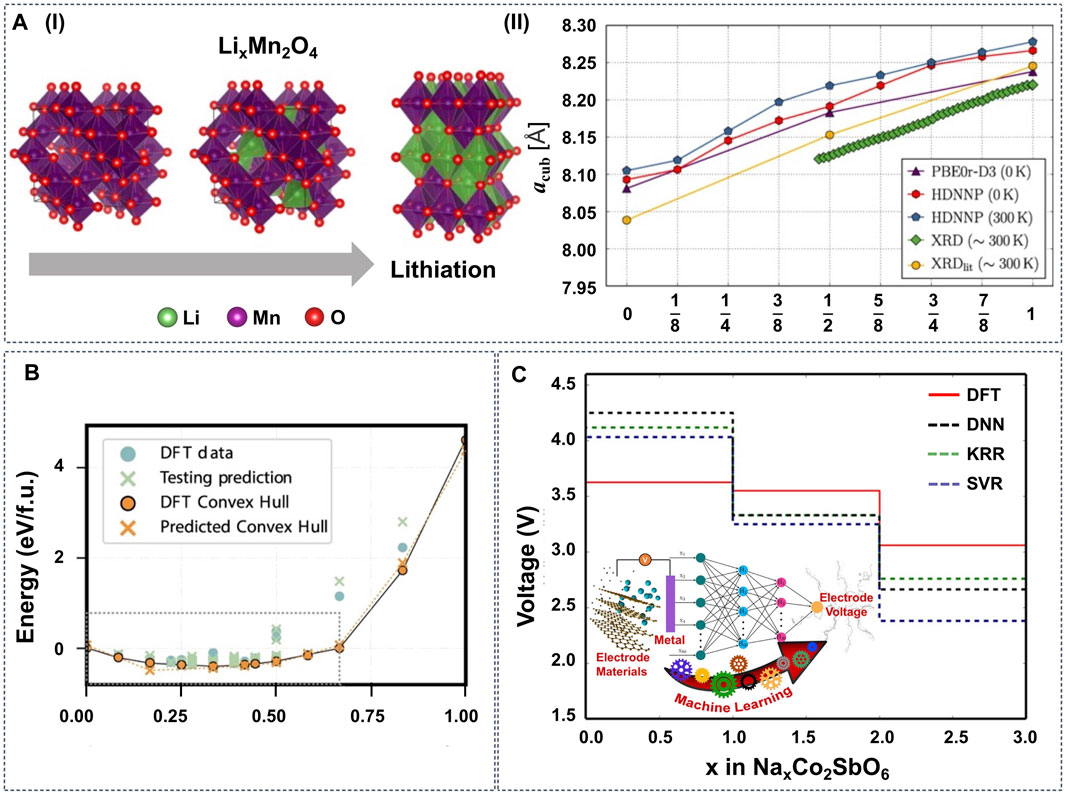
FIGURE 4. (A-I) LixMn2O4 spinel structure with different x (x = 0, 1, 2). The green, red, and purple balls represent Li, O and Mn atoms, respectively. (A-II) Cubic lattice parameter acub as a function of Li content determined by DFT on the PBE0r-D3 level of theory (0 K), high-dimensional neural network potentials (HDNNP) (0 and 300 K) and XRD measurements. Reproduced with permission from (Eckhoff et al., 2020b). Copyright 2020 American Physical Society. (B) Formation energies predicted by an ANN potential for lithium-vacancy orderings on the tetrahedral and octahedral sites of spinel TiS2, with the local features around each site generated from only pair correlations. Reproduced with permission from (Natarajan and Van der Ven, 2018). Copyright 2018 Nature. (C) Voltage profile diagram obtained from different ML models and DFT for NaxCo2SbO6. Reproduced with permission from (Joshi et al., 2019). Copyright 2019 American Chemical Society.
Properly trained ML potentials can predict more than the thermodynamic properties. Eckhoff et al. constructed an ANN potential for LixMn2O4 with Jahn-Teller distortions that can predict a series of properties, including volume change, Li diffusion barrier, phonon frequencies (Figure 4A) (Eckhoff et al., 2020b), oxidation, and spin states (Eckhoff et al., 2020a). Similarly, Vegge and coworkers utilized simple local structural descriptors with LASSO and learning on-the-fly (LOFT) to estimate Li diffusion kinetic barriers efficiently (Bölle et al., 2021; Chang et al., 2021).
Instead of training ML potentials to approximate the PES, ML prediction models can be trained to target specific properties (Property Predictions). Sarkar et al. firstly trained an ANN using electronegativity as the descriptor to predict the voltages of several cathode materials (Sarkar et al., 2014). Although the ANN model did not reach first-principles accuracy due to the limited size of the dataset, it still paved the way to screen Li-containing compounds for cathode materials. Lately, based on data from the Materials Project (MP) database (Jain et al., 2013), Joshi et al. used DNN, SVM, and KRR to train ML models to predict the voltage of electrode materials based on metal-ions (Figure 4C). By using these ML models, the prediction for the voltage of any cathode material can be performed within a minute, and new cathode materials were also screened for Na-ion and K-ion batteries. Similarly, Bartel et al. tested seven ML models for the formation energy prediction of Li transition metal oxides, using the chemical formula as the model input (Bartel et al., 2020). The results show that these ML models can predict formation energies with high accuracy. However, the models fail to predict the stability correctly, i.e., the decomposition enthalpy, and the authors conclude that structural information is indispensable to distinguish stable from unstable compounds within an arbitrary chemical space.
To classify Li-containing crystal structures and predict candidate materials, Attarian Shandiz et al. compared eight ML models, i.e., linear, quadratic and shrinkage discriminant analysis, ANN, SVM, kNN, RF and extremely randomized trees, trained on 339 cathode materials with Li–Si–(Mn, Fe, Co)–O compositions from MP (Attarian Shandiz and Gauvin, 2016). They found that the unit cell volume was the most important feature. The random forests and extremely randomized trees exhibited the best performance for the classification of three major crystal systems (monoclinic, orthorhombic, and triclinic) for Li–Si–(Mn, Fe, Co)–O cathode materials. Related to this, Wang et al. used partial least square (PLS) analysis for predicting volume changes in 28 oxide cathodes with spinel structure LiX2O4 and layered-structure LiXO2. 34 descriptors relevant to the basic physical and chemical properties for element X are adopted to develop the quantitative structure-property relationship. The variable importance in projection shows that the four important factors of volume change are the effective ionic radius of X4+, the bond valence parameter, the average bond length of the X-O polyhedron and the volume of the X-O polyhedron (Wang et al., 2017).
In order to design organic molecular electrodes, Allam et al. trained an ANN based on 108 data points with the quasi-Newton method to predict redox potentials of target molecules (Allam et al., 2018). In contrast to the voltage models for inorganic cathodes, the molecular model by Allam et al. used as features the electron affinity, the energies of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), the HOMO–LUMO gap, the number of aromatic rings, and the number of oxygen, carbon, boron, hydrogen, and lithium atoms. From the individual contribution analysis of the input variables, the electron affinity was shown to have the highest contribution to the redox potential. The ANN demonstrated a capability for accurately estimating the redox potentials with a residual error of R2 = 0.9618. Recently, the same data set with the 10 primary features were further trained by using three different ML models based on ANN, KRR, and GBR (Allam et al., 2020). A series of feature optimization strategies were employed to analyze the role of the various molecular descriptors and accurately predict the redox potential for the organic materials, including composite feature generation, LASSO feature selection, relative contribution analysis, and recursive feature elimination.
Anodes
Solid state electrolytes (SSEs) have the potential to stabilize Li metal anodes by preventing dendrite growth, which would result in significantly increased capacities compared to Li-ion batteries. Nevertheless, the formation of dendrites across the interfaces between SSEs and the Li anode during cycling remains a challenge for present SSB systems. Literature involving interfaces is mainly summarized in Interfaces and Coatings. Here, we review publications of anode material simulations only, which are summarized in Table 2.
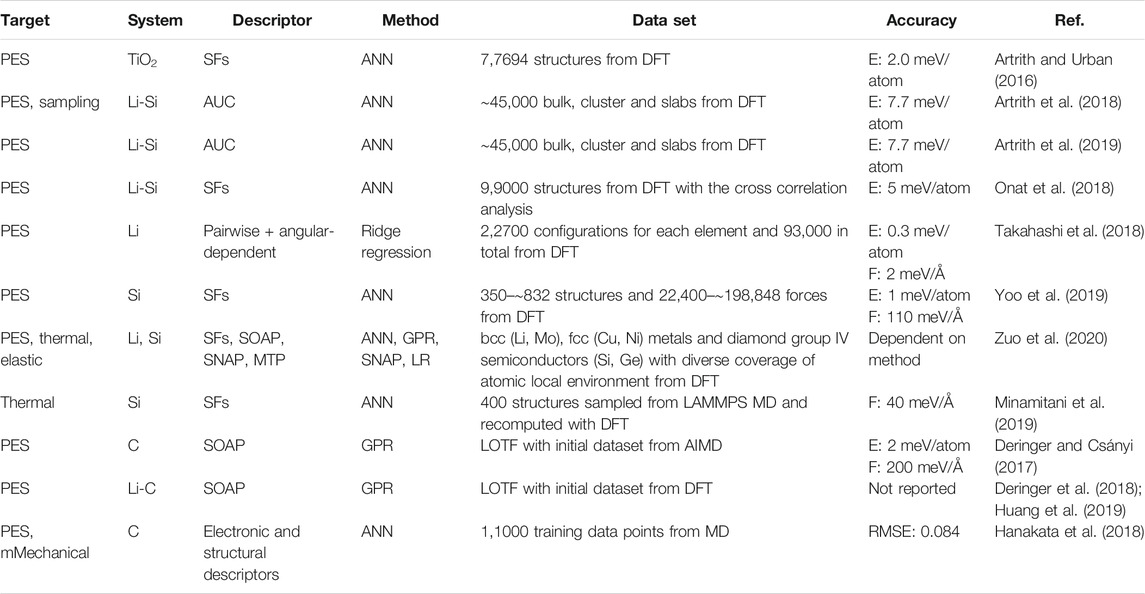
Lithium titanium oxide spinels are used as anode material in conventional and solid-state LIBs and are also a common electrode coating material in SSBs. Artrith et al. implemented atomistic ANN potentials to study the crystal structures of TiO2 (Artrith and Urban, 2016). This approach was further developed to investigate properties of amorphous Si anodes. Combining ANN potentials and a genetic algorithm (GA), the authors were able to sample the low-energy atomic configurations in the entire amorphous LixSi phase space (Figure 5A,B) (Artrith et al., 2018). Based on the determined stable configurations, the average voltages were computed, which are in agreement with experimental measurements. The same authors used ANN potentials further to simulate the delithiation of entire LiSi nanoparticles containing ∼12,000 atoms, as well as to investigate the associated Li diffusion and Si segregation properties (Figure 5C) (Artrith et al., 2019). These simulations clarify the diffusion mechanism of Li in nanostructured amorphous Li-Si alloys, providing a guideline for the design of Si-based anodes with improved rate capability. In related work, Onat et al. developed a methodology based on a collection of ANNs that represents the atomic interactions in complex environments of amorphous Li-Si alloys, calculated the Li diffusivity and compared with experimental references (Onat et al., 2018).
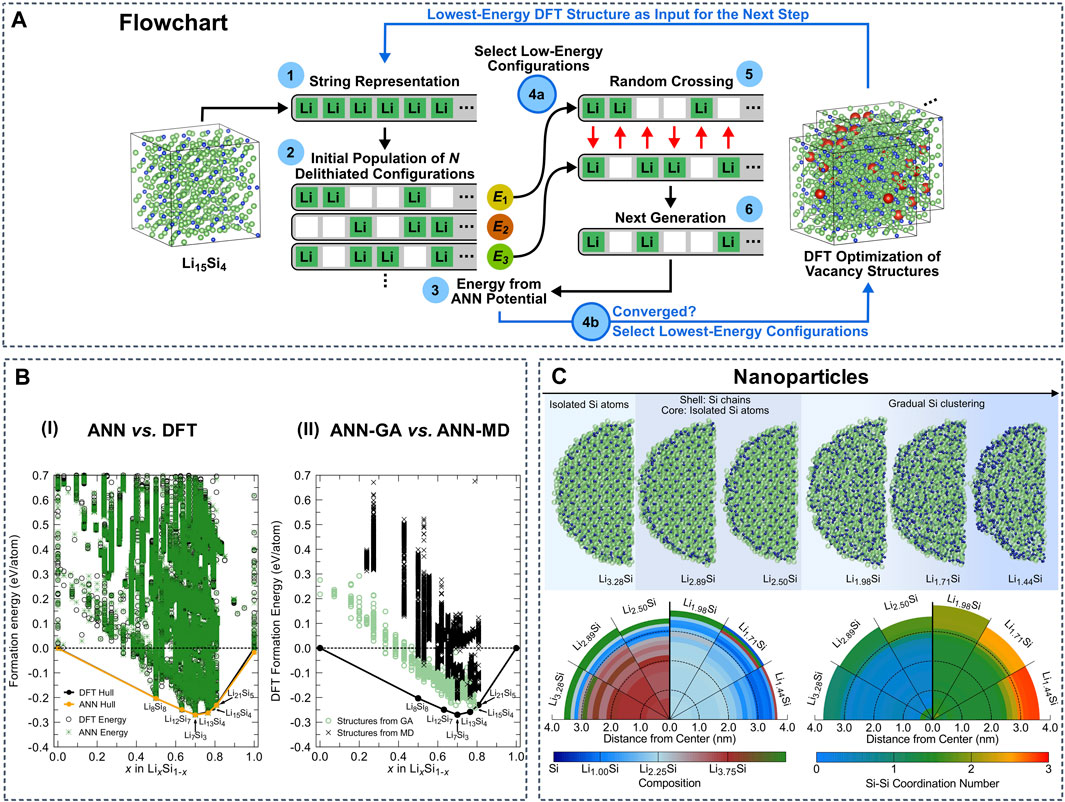
FIGURE 5. (A) Schematic of genetic algorithm (GA) sampling using a specialized ANN potential. Reproduced with permission from (Artrith et al., 2018). Copyright 2018 American Institute of Physics (B-I) Phase diagram based on the formation energies of ∼45,000 LixSi structures including bulk, surface slab, and cluster structures. The energies predicted by the general ANN potential are shown as green stars and the DFT reference energies are black circles. (B-II) DFT formation energies of those structures sampled by the GA with the specialized ANN potential (green circles) and those generated during MD melt-quench simulations with the general ANN potential (black crosses). Reproduced with permission from (Artrith et al., 2018). Copyright 2018 American Institute of Physics (C) Si atoms segregate into clusters and chains during the delithiation of LiSi nanoparticles with 12,000 atoms. Reproduced with permission from (Artrith et al., 2019). Copyright 2019 arXiv.
ML potentials have been constructed to predict the PES of various elemental crystals with potential relevance as conversion anodes. Takahashi et al. constructed accurate ML interatomic potentials with ridge regression for 31 elemental metals, including Li metal (Takahashi et al., 2018), which was further developed to predict grain boundary properties (Nishiyama et al., 2020). Yoo et al. investigated Si crystals, slab models, and nanoclusters with atomic energy mapping inferred by ANN potentials (Yoo et al., 2019). Zuo et al. compared the performance and cost of four different ML interatomic potentials, including an ANN potential with SF descriptor, a GPR potential with SOAP descriptor, SNAP and MTP. The models were trained on a dataset including bcc (Li, Mo) and fcc (Cu, Ni) metals and diamond group IV semiconductors (Si, Ge). All the ML potentials demonstrated reasonable accuracy in predicting energies, forces, as well as elastic and thermal properties (Zuo et al., 2020). Minamitani et al. investigated the thermal conductivity of crystalline Si with ANN potentials, which significantly reduced the expensive DFT calculations for phonon calculations (Minamitani et al., 2019).
At present, the anode material in most commercial LIBs is carbon/graphite, which is also a candidate for SSBs with the advantage of enhanced safety and long-term cycle life. Deringer et al. developed a GPR model for liquid and amorphous elemental carbon, which can accurately describe the PES and therefore thermodynamic properties, e.g., the amorphization behavior (Deringer and Csányi, 2017). With the inclusion of alkali metal (Li, Na, K) into the training set over a range of densities and degrees of disorder, this model was further developed to study battery performance (Deringer et al., 2018; Huang et al., 2019). Hanakata et al. employed a feedforward ANN and convolutional ANN to predict the mechanic properties of graphene kirigami, such as stress and strain as a function of cutting patterns. The results demonstrate that ML could not only be used to effectively search for optimal designs but can also yield a better understanding of how kirigami cuts change the mechanical properties of graphene sheets (Hanakata et al., 2018).
Electrolyte
An ideal SSE should satisfy the following requirements: 1) fast ionic conductivity 2) compatibility with high energy density electrodes, such as NMC, NCA cathodes, and Li anode 3) high mechanical robustness. Among these criteria, the Li conductivity is the most fundamental requirement for SSEs. However, it is extremely computationally expensive to simulate Li migration using first-principles methods, such as ab-initio molecular dynamics (AIMD) simulations.
To reduce the computing time for obtaining diffusion properties and to accelerate the discovery of SSEs, ML techniques have been implemented mainly in three categories: 1) using ML potentials to construct the PES for Li diffusion calculations with molecular dynamics, 2) training ML models to predict the conduction properties directly without simulation based on structural features, and 3) training ML models to predict the candidate materials based on the knowledge of existing superionic conductors. The examples of each category are summarized in Table 3.
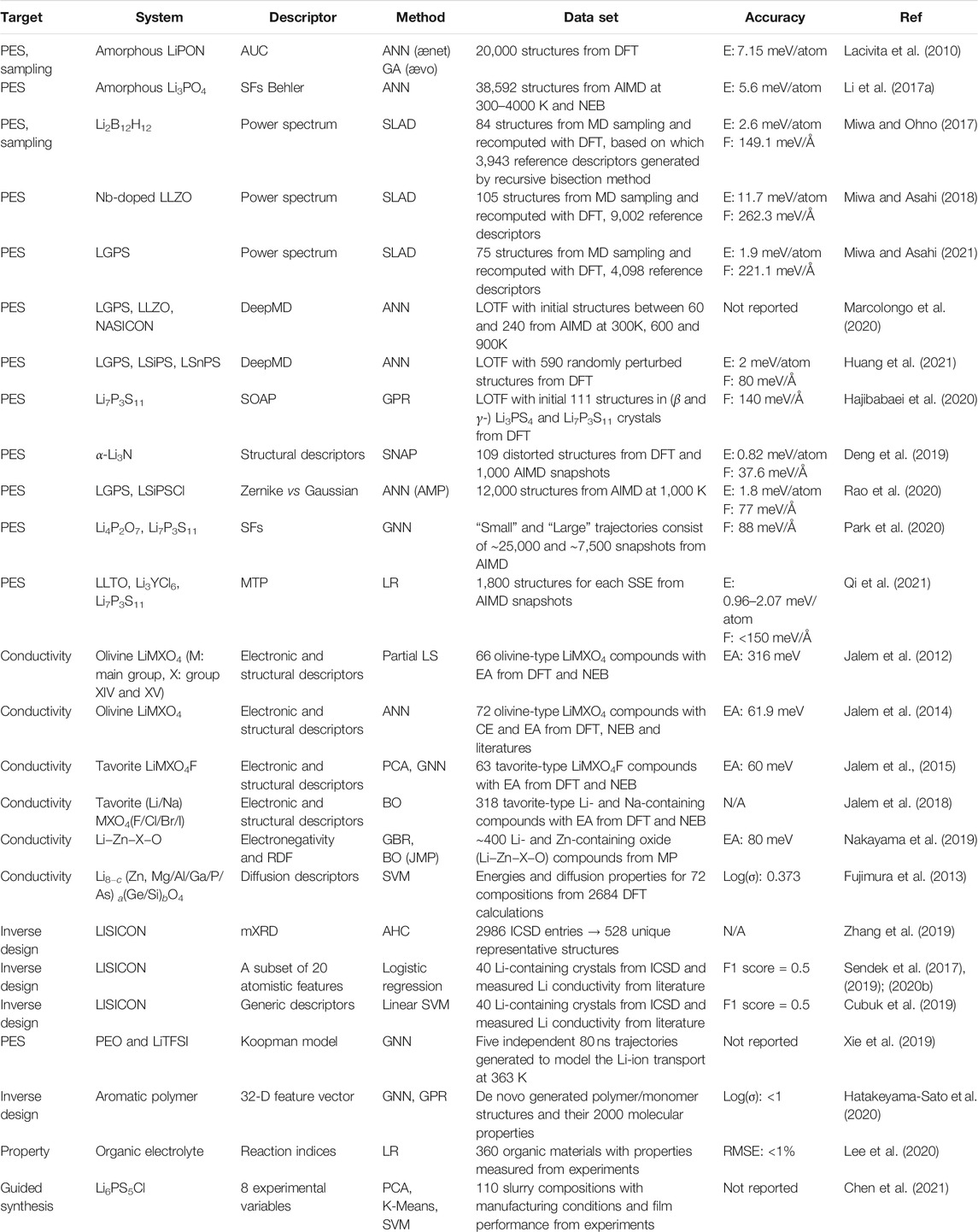
Approximating the PES of Li migration with ML potentials is very promising for the quantitative predictions of conductivity in SSEs. Generally, ML potentials are trained for a certain type of SSEs and require a high-quality dataset that includes all local environments. The constructed ML potential can then accelerate the sampling of structures with first-principles accuracy. Lacivita et al. used a combination of a ML potential and a GA to determine the N defects in crystalline Li3PO4 (Lacivita et al., 2018). The approach served as a computationally optimized method for PES sampling and was based on a specially trained ANN for fast screening.
One specific research question that ML potential simulations can tackle is to investigate Li diffusion properties with long-time MD simulations in complex SSE systems (Figure 6). Li et al. employed ANN potentials to study the Li diffusion in amorphous Li3PO4 (Figure 6A) (Li et al., 2017a). The authors demonstrated that including Li diffusion transient structures sampled by nudged elastic band (NEB) calculations in the training dataset is necessary to reduce the error of predicted barrier energies from 73 to 48 meV. With the aid of ANN potentials, the authors were able to run MD simulations in an amorphous supercell containing more than 1,000 atoms.
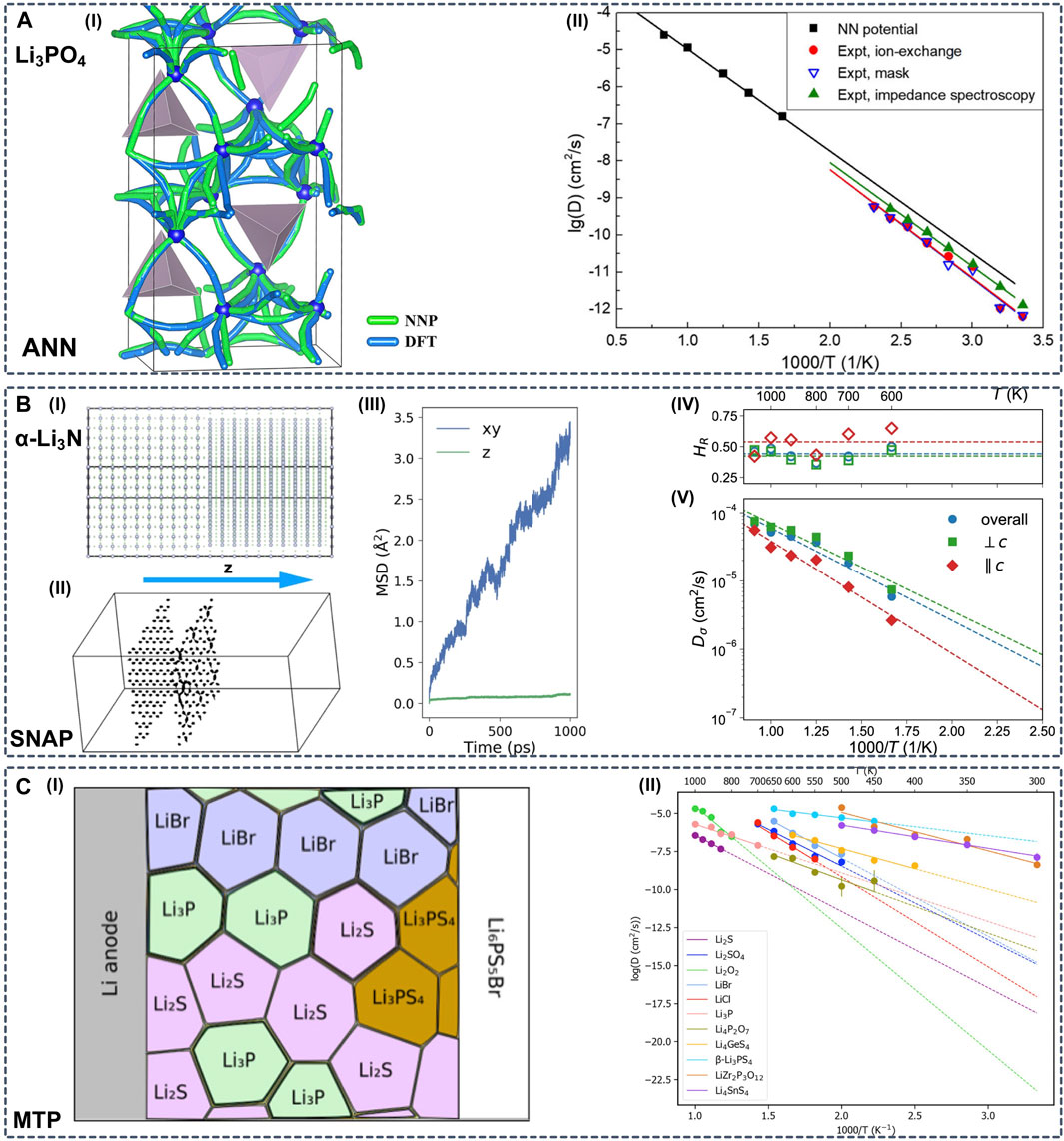
FIGURE 6. (A-I) All diffusion paths of Li atoms in the amorphous Li12P4O16 model, predicted by DFT and ANN potential calculations with the nudged elastic band (NEB) method (A-II) Arrhenius plot of the Li diffusivity in amorphous Li3PO4. The simulation results were obtained from large-scale MD simulations of 1,006 atoms using ANN potentials. The experimental results were measured with different methods. Reproduced with permission from (Li et al., 2017a). Copyright 2017 American Institute of Physics (B-I) Constructed simulation box of α-Li3N with twist Σ7 [0001] grain boundaries (GBs) (B-II) Trajectories for selected Li ions in the box with twist GBs in 0.5 ns. Li ions on the left lie in the bulk region, and the ones on the right are close to one of the GBs (B-III) Mean squared displacement (MSD) by component vs. time for Li ions located at the twist GBs only (bulk Li ions are excluded). The z direction is perpendicular to the GBs. Diffusivity is computed within the 2D GB plane (B-IV) Haven ratio and (B-V) Arrhenius plot for Li charge diffusivity in bulk α-Li3N obtained from eSNAP MD simulations. Reproduced with permission from (Deng et al., 2019). Copyright 2019 Nature (C-I) Arrhenius plot of diffusivities of possible interphase components obtained from LOFT-MD (C-II) Schematic diagram of phase equilibria at the interface between the Li anode and solid electrolyte Li6PS5Br. Reproduced with permission from (Wang et al., 2020a). Copyright 2020 American Institute of Physics.
To construct an accurate ML potential, a high-quality dataset is a prerequisite. To facilitate the sampling of the training structures, Miwa et al. developed an automatic ML potential construction scheme, SLAD, which is similar to Bayesian optimization (BO) with the variance as an acquisition function without the assumption of any stochastic processes (Miwa and Ohno, 2017). This approach was successfully applied to several SSEs, including Li2B12H12 (Miwa and Ohno, 2017), Li7La3Zr2O12 (LLZO) (Miwa and Asahi, 2018), and Li10GeP2S12 (LGPS) (Miwa and Asahi, 2021). The MLP was trained on a small dataset from low-temperature phases, yet exhibits an impressive ability to predict the structures and properties at higher temperatures. With this approach, the authors demonstrated that the promotion of Li diffusion in β-Li2B12H12 is achieved by lattice expansion and orientational disordering of B12H12 complexes, and predicted Li conductivities and activation barriers in Nb-doped LLZO (Miwa and Asahi, 2018) and LGPS that are in reasonable agreement with experimental measurements (Miwa and Asahi, 2021).
Another technique to facilitate the construction of reference datasets is on the fly training, also referred to as learning on the fly (LOTF) (Wang et al., 2020b). Marcolongo et al. constructed ANN potential combining DeePMD and a LOTF approach to investigate the ionic conductivities of LGPS, LLZO, and NASICON (Marcolongo et al., 2020). The authors established an iterative procedure consisting of three steps: exploration, labeling, and training, and they evaluated the diffusion coefficient with MD simulations in the microcanonical (NVE) statistical ensemble. Similarly, Huang et al. applied a deep ANN potential dubbed DeePMD to study three LGPS-type superionic conductors, LGPS, LSiPS, LSnPS (Huang et al., 2021). The same protocol was conducted and the convergence was set to a predetermined number of loops or only a small percentage of candidates are found in the last exploration iteration. With the constructed ML potential, the authors were able to extend the MD simulation to a wide temperature range (300–1000 K) and to systems with large size (∼1,000 atoms), which provides insights into the impact of doping on diffusion properties in LGPS-type materials. Hajibabaei et al. combined LOFT and a sparse Gaussian Process (SGPR) model to construct a universal potential for Li7P3S11, which reproduced the experimental melting and glass-crystallization temperatures and predicted an unchartered phase with much lower ionic conductivity (Hajibabaei et al., 2020).
Various ML models have been trained to determine the PES in SSEs to estimate the ionic conductivities. Deng et al. developed an electrostatic Spectral Neighbor Analysis Potential (eSNAP) and performed a long-time (1 ns) large-scale (5,040 atoms) simulation of Li diffusion in the superionic conductor α-Li3N (Figure 6B), providing insights into the concerted ionic motion and grain boundary diffusion (Deng et al., 2019). Rao et al. trained an ANN potential for four and five element systems, which predicted nearly identical Li diffusivities in LGPS with ANN-MD compared to DFT-MD reference values (Rao et al., 2020). With ANN-MD, the authors investigated the effect of Cl dopants and provided a design strategy for LPGS-type electrolytes. Park et al. developed a GNNFF, to predict atomic forces from automatically extracted features of the local atomic environment that are rotationally-covariant to the coordinate space (Park et al., 2020). The PES of Li7P3S11 was evaluated, yet overall the GNNFF slightly underestimate the force magnitudes compared to DFT. To identify the most rapid Li diffusion pathways through the interphase, Wang et al. examined the Li ionic conductivities for possible Li-containing products at the interfaces of electrolyte/electrode by using LOTF-MD based on MTPs (Figure 6C) (Wang et al., 2020a).
The importance of an accurate dataset was emphasized by Qi et al., who trained MTPs based on energies and forces computed with van der Waals optB88 functional for three types of SSEs, Li0.33La0.56TiO3 (LLTO), Li3YCl6 and Li7P3S11 (Qi et al., 2021). A comparison between MTPs trained on reference data from two different DFT functionals revealed the significance of accurate reference calculations. The choice of DFT functional can lead to substantial errors in lattice parameters, therefore raising the bias in predicted ionic conductivities. In addition, most AIMD simulations in the literatures were performed at high temperatures in the NVT ensemble, and the authors argue that this would not only lead to further errors in the lattice parameters, but may also not capture transitions in quasi-linear Arrhenius regimes at lower temperatures. A carefully trained ML interatomic potential can help to address the statistical errors and size effects.
The second category includes property-prediction ML models (Property Predictions) that are trained to directly predict the diffusion properties and are used for screening of a large number of databases. To predict activation energies and accelerate the search for potential SSEs, Jalem et al. compared two ML methods to augment DFT calculations, the PLS regression (Jalem et al., 2012) and an ANN model (Jalem et al., 2014). The dataset to train the ML models was composed of structure parameters and activation energies of 66 olivine-type LiMXO4 (M: main group elements, X: group XIV, and group XV) from DFT NEB calculations. The PLS method yielded an RMSE of around 316 meV, and it failed near the extreme ends of the attribute dataset. In comparison, the more flexible ANN framework with multi-output node architecture (activation energy and cohesive energy), improves the accuracy significantly and reduces the RMSE to 61.9 meV for the predicted activation energy values. To expand the application of the ML model, the authors included a dataset of tavorite LiMXO4F structures, and used a different graph-based ANN model (Jalem et al., 2015). The important features were identified using principal component analysis (PCA).
Based on the above series of studies, Jalem et al. determined the competing effects among Li pathway bottleneck size, polyanion covalency, and local lattice distortion that control the migration barriers. The tavorite-type compound space, (Li/Na)MXO4(F/Cl/Br/I), including 318 compounds, was further screened with BO, which was twice more efficient than random search (i.e., for EA < 0.3 eV) (Jalem et al., 2018). The scheme requires ∼30% of the total DFT-based evaluations to recover the optimal compound ∼90% of the time. Another advantage of additive BO is that the contribution from each group of descriptors can be interpreted. The results illustrated that the radial distribution functions (RDFs) as structure-derived descriptors and electronegativity as the composition-derived descriptor are the key descriptors to control the Li migration barrier in tavorite-type ionic conductors. The selected features and the BO accelerated approach based on GBR were further extended by Nakayama et al. to screen ∼400 Li- and Zn-containing oxide (Li−Zn−X−O) compounds (Nakayama et al., 2019).
Using SVM regression, Fujimura et al. trained an ML model with diffusion related properties, such as transition temperatures, formation energies and diffusion coefficients. The authors predicted the ionic conductivities at 373 K for 72 compositions with general formula Li8−cAaBbO4, where Am+ = Zn, Mg, Al, Ga, P or As, and Bn+ = Ge or Si, and c = ma + nb (Fujimura et al., 2013). By iteratively performing systematic sets of first-principles calculations and focused experiments, it was shown how the materials design process can be greatly accelerated, suggesting potentially superior candidate lithium superionic conductors.
The connection between structural framework and ionic conductivities is also a clue for the inverse design of SSEs. Based on the understanding of the relationship between anion framework and ionic conductivities in existing superionic conductors (Figure 7A) (Wang et al., 2015; He et al., 2017; He et al., 2019), Zhang et al. selected the modified X-ray diffraction (mXRD) pattern (Figure 7B) as the descriptor to perform unsupervized learning to screen all known Li-containing compounds from the inorganic crystal structure database (ICSD) (Hellenbrandt, 2004) (Figure 7C) (Zhang et al., 2019). The trained unsupervized learning models successfully cluster Li-containing compounds into groups of Li conductors with high conductivity and other groups of materials with poor ionic conduction. The learning model not only clustered the current superionic conductors, such as LLZO and LGPS, but also proposed 16 potential candidates for SSEs with room-temperature conductivities higher than 10–4 S cm−1, which were further validated with AIMD simulations.
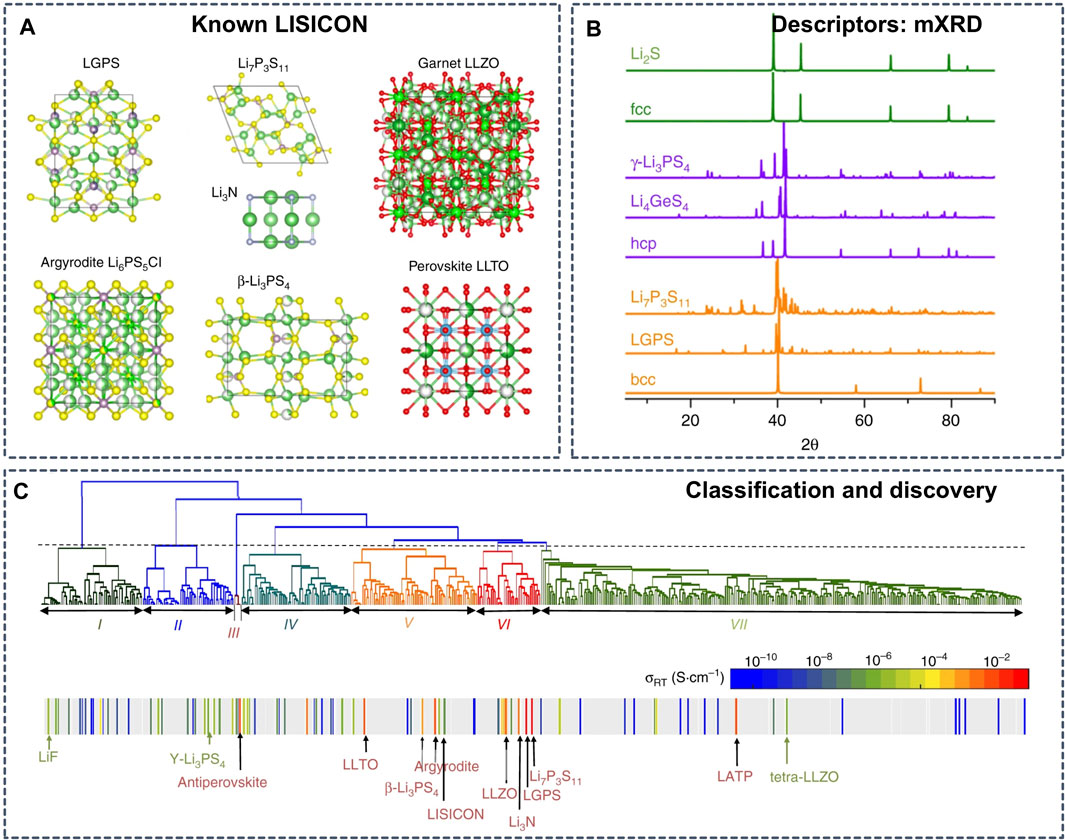
FIGURE 7. (A) Crystal structures of known Li superionic conductors (B) mXRD patterns of selected materials in comparison to those of ideal fcc (face centered cubic), hcp (hexagonal close packed), bcc (body centered cubic) lattices (C) Mapping the bottom-up tree diagram (dendrogram) generated using the agglomerative hierarchical clustering method to the conductivity reveals the grouping of known solid-state Li-ion conductors. The color bar shows the scale of the room temperature conductivity σRT. The gray color indicates that the conductivity has not been measured for the corresponding compound. Reproduced with permission from (Zhang et al., 2019). Copyright 2019 Nature.
With a subset of 20 physics-based atomistic features as descriptors, Sendek et al. developed a data-driven ionic conductivity classification model using logistic regression for identifying the candidate ionic conductors (Sendek et al., 2017). The regression model was trained on 40 crystal structures from the ICSD and on experimentally measured ionic conductivity from literature, which also included poor conductors as negative examples. The ML-based model exhibits an F1 score of 0.50, which is 3.5 times better than random search, allowing for a screening on 12,831 Li-containing crystalline solids from the MP database. Following the recommendations of the ML model, the authors investigated 21 candidate SSEs with AIMD simulations (Figure 8B) (Sendek et al., 2019) and experiments (Figure 8C) (Sendek et al., 2020a). The crystalline lithium−boron−sulfur (Li−B−S) system appears to be more conductive and twice as stable as LGPS, and is at the same time less expensive. Another advantage of the Li-B-S materials is that typically when electrolyte materials degrade over time, they transform into poorly conductive materials. However, degradation of Li-B-S yields another good ionic conductor, which could potentially extend battery lifetime.
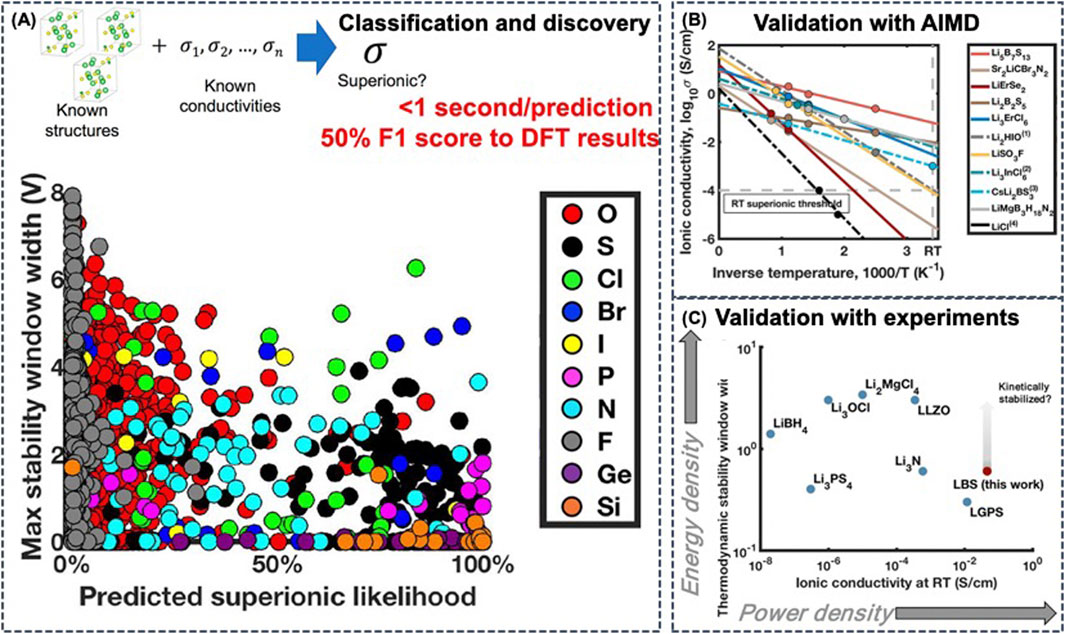
FIGURE 8. (A) Property spectrum of solid Li-ion conductor candidates by anion family. The predicted metrics of electrochemical stability against predicted likelihood of superionic conduction for stable Li-containing crystalline solid materials from the Materials Project database were plotted. These materials have the general composition Li–(X)–Y, where (X) is any combination of elements and Y is an anion from the following group: F, O, S, Cl, Br, I, N, P, F, Si, or Ge. Reproduced with permission from (Sendek et al., 2019). Copyright 2019 American Chemical Society. Copyright 2020 American Chemical Society (B) Computationally observed ionic conductivity in candidate materials and extrapolation to room temperature (RT). Reproduced with permission from (Sendek et al., 2019). Copyright 2019 American Chemical Society (C) The thermodynamic electrochemical stability window widths computed with PBE DFT and the experimentally reported ionic conductivities (on a log–log scale) of several known solid Li-ion conductors, including the predicted values for the best Li–B–S electrolyte compositions. Reproduced with permission from (Sendek et al., 2020b). Copyright 2020 American Chemical Society.
In addition to fast ionic conductivity, electrochemical stability is also crucial for SSEs. Based on these two requirements, the inclusion of Cl-, Br-, and I-based solid ion conductors and doped sulfides were shown to be more promising due to their better electrochemical stability and enhanced ionic conductivity (Figure 8A) (Sendek et al., 2020b).
While the screening of known materials for target properties is certainly impressive, there is still a long way from screening the entire chemical space, including those materials that haven’t been synthesized and characterized. The main bottleneck here is to acquire sufficient labeled data. Cubuk et al. provide an alternative solution, that is to use transfer learning with physics-guided generic descriptors, which allowed for a screening of an impressive 20 billion ternary and quaternary Li-containing compounds (Cubuk et al., 2019). This is achieved by initially training a linear support vector machine model on 40 data points with 30 elemental descriptors, on which a new ML model was trained using the generic descriptors.
Apart from inorganic electrolytes, ML screening has also been applied to polymer electrolytes. To this end, Xie et al. developed graph dynamical networks for unsupervised learning. A linear Koopman model from MD data was constructed for amorphous poly (ethylene oxide) (PEO)/Li bis-trifluoromethane sulfonimide (LiTFSI) polymer electrolyte (Xie et al., 2019). In related work, Hatakeyama-Sato et al. employed GNNs to create a 32-dimensional feature vector by training on de novo polymer and monomeric compound database with 2000 molecular descriptors (e.g., number of nitrogen atoms and polarizability, etc.). The learned feature vector together with other system information was then used as the input for a GPR model for learning the relationship between the composition and the experimentally measured conductivity for 3,000 data points (Hatakeyama-Sato et al., 2020). By screening chemical space, the authors were able to identify highly conducting glass-type polymer complexes (around 10−3 S/cm).
The stability and compatibility between chemical components are crucial for a SSB system. Lee et al. proposed a LR model to predict the general reactivity and chemical compatibility among organic materials, which was used to map the chemical stability among 90 electrolyte solvents and the representative redox mediators, providing a guideline for the design of stable interfaces in SSBs (Lee et al., 2020).
Interfaces and Coatings
The interfacial resistance between electrodes and electrolytes is another crucial challenge for SSBs. Despite previous experimental characterizations, the degradation mechanisms at the electrode|electrolyte interfaces still remain unclear. Therefore, a direct modeling of the solid-solid interface region is desirable.
Gao et al. constructed an AI scheme for the accelerated sampling of the heterogeneous interface structures by applying particle swarm optimization (see Machine Learning for Materials Modeling) (Gao et al., 2020). The energetically favorable interfacial structures between the typical cathode LiCoO2 (LCO) and Li-P-S electrolytes (LPS) are investigated to explore the Li-ion transport mechanism at the interface. The results show that both cation (Co and P) mixing and anion (O and S) mixing are likely to occur in the interfacial region, and the migration of Li ions toward the anode results in the formation of a Li+-depleted layer, which is considered as the origin of the high interfacial resistance. The same methodology was also implemented to explore the Li1.3Al0.3Ti1.7(PO4)3 (LATP)/LCO and LATP/Li interfaces (Tian et al., 2020). The exchange of cation pairs, Li and O vacancies at the interface are constructed to investigate the ion and electron transfer in different conditions.
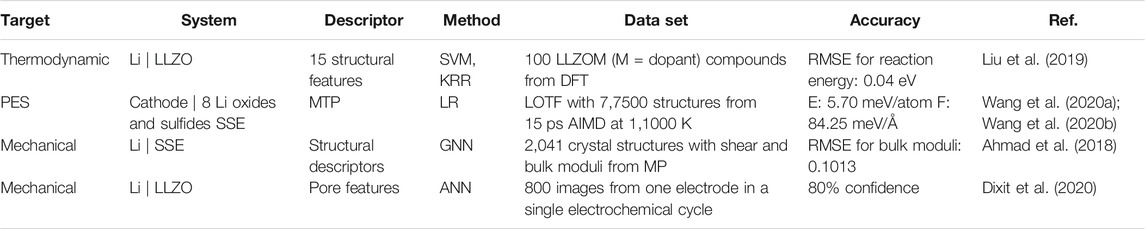
The thermodynamic stability is a descriptor to determine the interfacial stability (Table 4). Liu et al. constructed a KRR model with 100 data to map 15 structural descriptors (the M–O bond strength governs the interface stability) to the formation energy for Li|LLZOM (M = dopant) interfaces. The ML model yielded an RMSE of 0.04 eV for the formation energy and predicted 18 unexplored LLZOM systems, which were validated by DFT calculations (Liu et al., 2019).
Alternatively, Wang et al. examine the possible Li-containing product phases in local thermodynamic equilibrium at the interfaces of 32 representative electrolyte/cathode pairs and 24 electrolyte/anode pairs by combining ab initio phase diagrams with Monte Carlo sampling (Wang et al., 2020a). To predict the possible coating materials with superionic conductivities, the authors performed LOTF-MD based on MTPs. Compared to conventional AIMD, they achieved an impressive computational speedup of 107 with LOTF-MD (Figure 9). Based on the accurate ML potentials and MD simulations, Li3Sc2(PO4)3 and Li3B7O12 were identified as promising cathode coating materials by screening the Li-containing crystalline compositions for thermodynamic stability, electrochemical stability, interface stability and Li conductivity (Wang et al., 2020b).
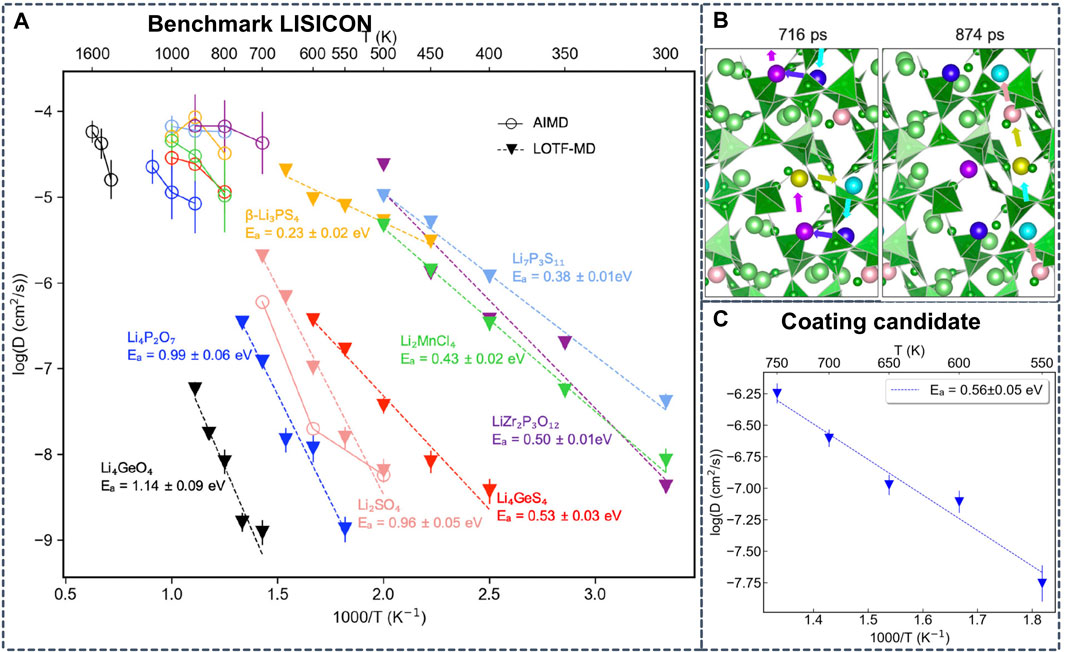
FIGURE 9. (A) Arrhenius plot with diffusivities obtained from AIMD simulations at high temperatures and from learning on-the-fly (LOTF)-MD simulations at intermediate temperatures (B) Snapshots from MD simulations that exemplify diffusion via collective motion of Li+ in Li3B7O12 identified by LOTF-MD at 700 K (C) Calculated Arrhenius plot of Li3B7O12 from LOFT-MD diffusivities. Reproduced with permission from (Wang et al., 2020b). Copyright 2020 American Chemical Society.
In addition to the thermodynamic stability, the mechanical properties are also an important factor for stabilizing interfaces and suppressing dendrite growth in SSBs. Ahmad et al. constructed a GNN model to predict the mechanical properties of the interface of the Li anode and SSEs (Figure 10) (Ahmad et al., 2018). Trained on a dataset of 2041 crystal structures from the MP database containing elastic properties, the GNN model yielded an RMSE of 0.1268 and 0.1013 log (GPa) for the shear and bulk moduli, respectively. Based on the mechanical properties predicted from the GNN model as inputs and derived stability parameters, the authors performed a computational screening of 12,950 Li-containing solids and predicted twenty interfaces between Li metal and four solid electrolytes to be resistant to dendrite growth.
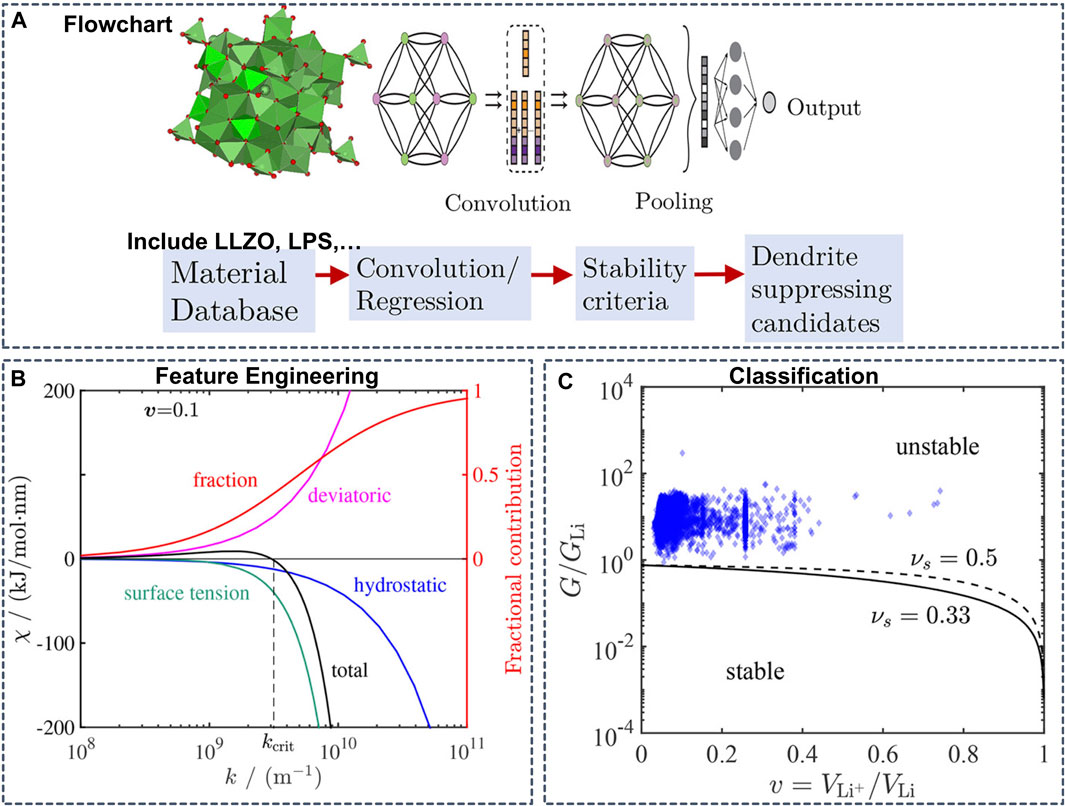
FIGURE 10. (A) Flowchart of a graph convolutional neural network (B) Contribution of hydrostatic stress, deviatoric stress, and surface tension to the stability parameter as a function of surface roughness wavenumber. The red line shows the fraction of surface tension contribution to the stability parameter obtained by dividing the absolute value of its contribution by the sum of absolute values of all components (C) Isotropic stability diagram showing the stability parameters of 2041 solid electrolytes considered in the screening. GLi is the shear modulus of Li (=3.4 GPa). The critical G/GLi line separating the stable and unstable regions depends weakly on the Poisson’s ratio, so the lines corresponding to νs = 0.33 and 0.5 are good indicators for assessment of stability. Reproduced with permission from (Ahmad et al., 2018). Copyright 2018 American Chemical Society.
The Li dendrite formation can be characterized from experimental measurements. However, the interpretation of experimental observations can be challenging due to the lack of understanding. To assist the interpretation of in-situ Li metal morphological transformations during galvanostatic cycling in Li|LLZO|Li cells, Dixit et al. trained a convolution ANN and observed non-uniform Li electrode kinetics at both electrodes during cycling (Figure 11). The hot spots in Li metal are correlated with microstructural anisotropy in LLZO (Dixit et al., 2020). Advanced visualization combined with electrochemistry represents an important strategy to resolve non-equilibrium effects that limit rate capabilities of SSBs.
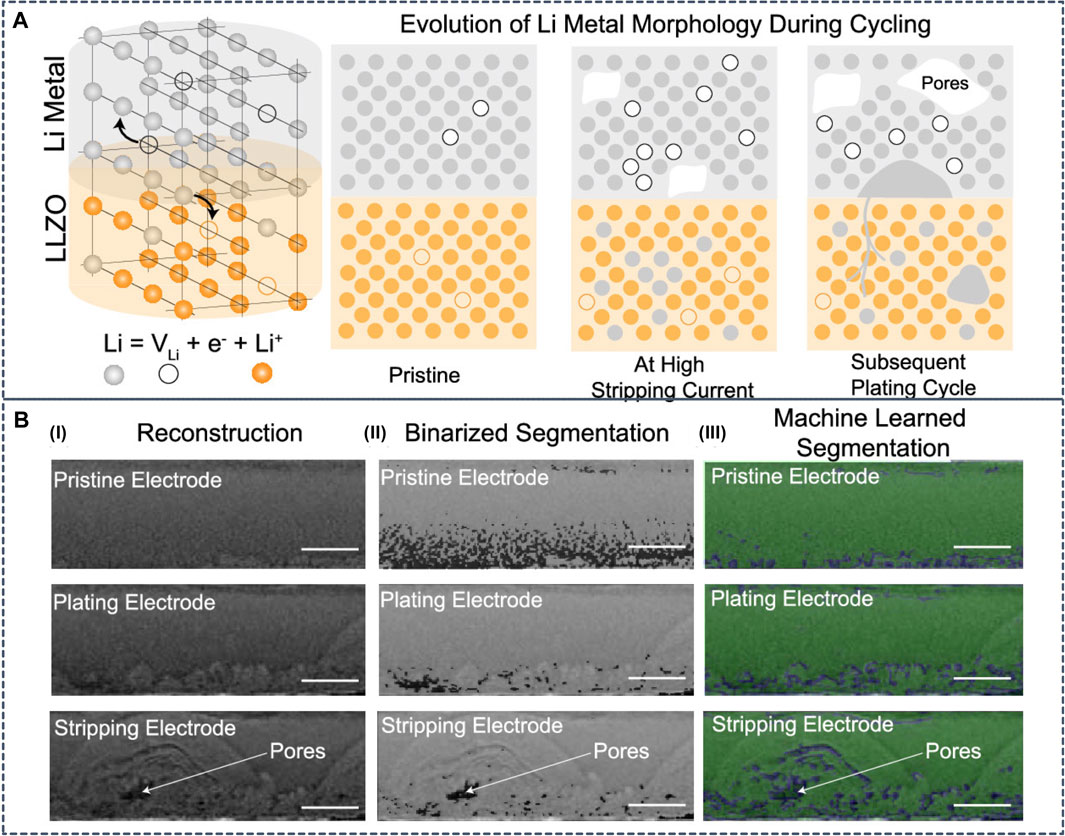
FIGURE 11. (A) Schematic diagram of the interfacial transport challenges in lithium metal solid-state batteries. Lithium metal undergoes oxidation and migrates as Li+ to the solid electrolyte leaving an electron and a vacancy in the lithium metal. During stripping at high current densities, the vacancies formed due to Li+ migration accumulate faster than can be replenished by self-diffusion of Li metal. This results in formation of voids at the anode|SE interface. On subsequent cycling, the void acts as focusing regions for nonplanar Li deposition (B-I) Sample reconstruction slices of the lithium metal electrode imaged for pristine, plating, and stripping steps. Semicircular morphologies are observed in the plating as well as stripping electrode, and pore formation in the stripping electrode is observed (B-II) Segmentation from the conventional binarization process overlaid with raw reconstruction images. Darker regions in these images are identified pores/void phase while the lighter domains are lithium metal (B-III) Segmentation results from convolutional neural networks overlaid with raw reconstruction images. The green phase is the identified lithium metal while the blue phase is the identified pore/void phases. Reproduced with permission from (Dixit et al., 2020). Copyright 2020 American Chemical Society.
Discussion and Perspective
ML-augmented first-principles atomistic modeling provides a new characterization tool for investigating complex systems such as SSBs. Although many of the reviewed ML techniques have only emerged over the last decade, they have already led to a multitude of promising applications to SSB research. As reviewed in the previous section, to date, most applications of ML to research questions related to SSBs have been based on either ML potentials or property-prediction models, most likely because mature software packages for these applications are available (see Machine Learning for Materials Modeling). We anticipate that applications for inverse design of SSB materials will become more commonplace as generative ML models become more robust and more widespread used.
One limitation of current ML potential methods is their lack of universality. So far, ML potentials need to be constructed for a specific domain and cannot replace electronic structure calculations for general applications, i.e., as universal force fields, which makes the modeling of complex processes in batteries (such as degradation) challenging. A promising direction for overcoming this limitation is the incorporation of a physical underpinning into the model, and important progress has recently been made towards combining ML and quantum theory (Schütt et al., 2019; Bogojeski et al., 2020).
Another obstacle that affects the entire field of ML for applied research is reproducibility. While ML techniques have been gaining popularity, the materials science and chemistry communities have not yet established rigorous quality measures for the publication of ML-based research. We believe that the key to robust and impactful ML work lies in the sharing of models and data as well as in systematic and transparent model validation (Artrith et al., 2021).
Finally, perhaps the most important limitation of ML models is the availability of reliable data. The battery applications reviewed in the present article mostly employed ML models trained on data from simulations, but such computational data is also subject to approximations and might not always provide an appropriate description. It is therefore important that 1) progress in the development of more accurate first-principles methods continues and 2) data from experimental measurements is also used for ML model construction.
Although not within the scope of the present review, we note that ML models trained on macroscopic experimental reference data have already found application for ML-guided synthesis of SSB components. Generating synthetic data from calculations is often more straightforward than devising set-ups for automated experimentation, but in some cases sufficient data from experiments are available. For example, Chen et al. implemented an ML workflow to guide the synthesis of SSEs films (Figure 12) through an ML model trained on 110 slurry SSE compositions with manufacturing conditions and film performance from experiments (Chen et al., 2021). The resulting cell featured high ionic conductivity, good uniformity and long cyclability. And Cunha et al. used AI tools to capture the impact of processing on the final electrode electrochemical performance (Cunha et al., 2020).
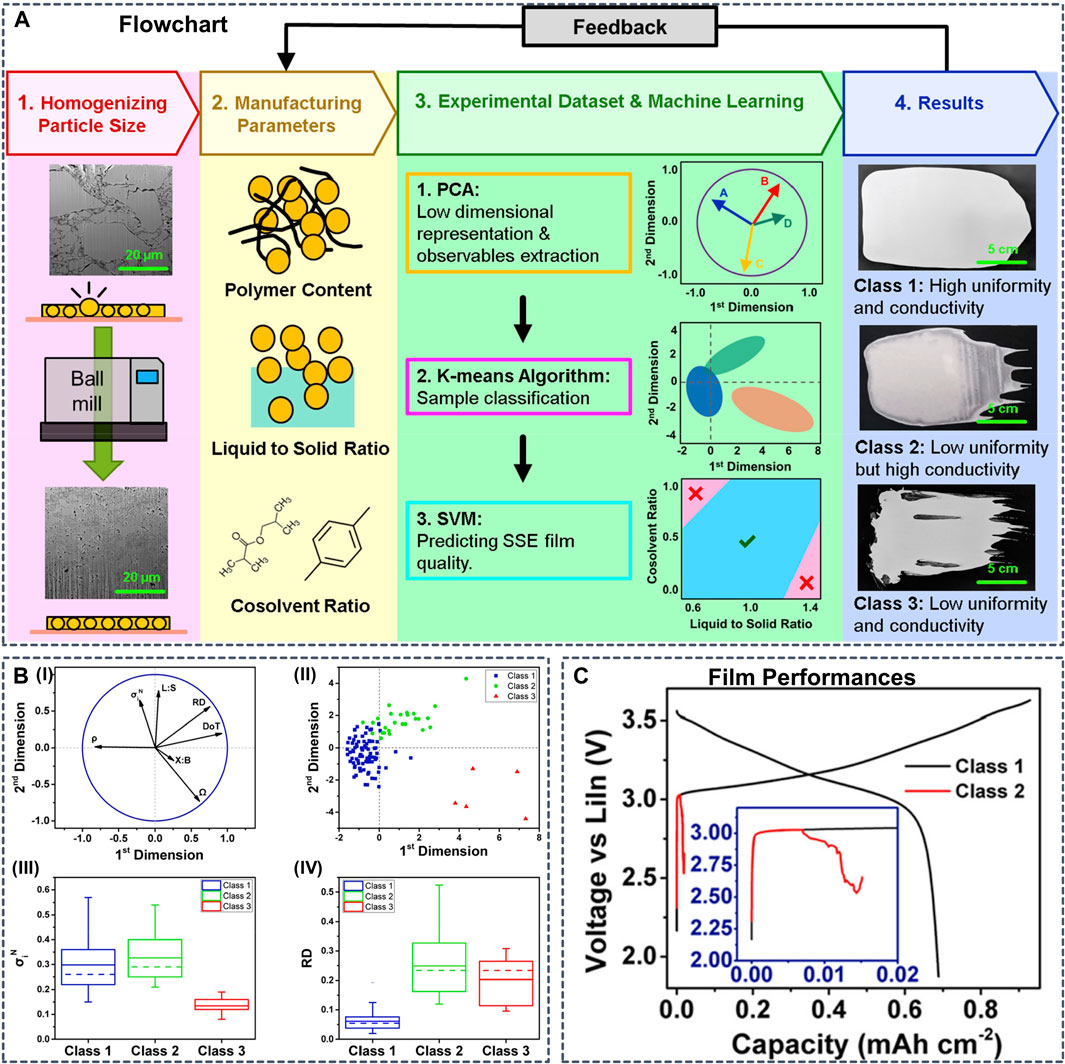
FIGURE 12. (A) Schematic presenting the methodology developed in this work. First, ball-milling is used to reduce the particle size of the LPSCl electrolyte. Then, 110 slurries consisting of different polymer contents, liquid-to-solid ratios, and cosolvent ratios are fabricated to obtain the data set. This data set is fed into the machine learning workflow to categorize samples with different properties, as shown in the fourth step (B) Data analysis results coming from the implementation of the PCA and the K-means algorithm which show the linear dependence between initial variables and the grouping of the samples in terms of performance, respectively (B-I) Projection of the initial variables (symbolized by black arrows) onto the 2D plan formed by the first two principal components resulting from the PCA implementation, with the purpose to visualize and analyze the correlation between each pair of variables. For the PCA implementation, P% is not taken into account because of a low number of different modalities. It is considered as a qualitative variable and did not appear in the initial PCA features for better results. However, P% is used for the rest of the analysis (B-II) All samples are grouped into three clusters with the K-means algorithm, here represented within the two first principal components. Those clusters are explicitly defined as classes in the rest of the study. Box charts for the comparison of distribution of (B-III) normalized conductivity and (B-IV) relative thickness deviation for all three classes. Abbreviations: L:S, liquid-to-solid ratio; X:B, cosolvent ratio; ρ, density; Ω, ohmic resistance; σiN, normalized conductivity; DoT, deviation of thickness; RD, relative thickness deviation (C) First cycle voltage profiles of NCM811 || LPSCl || LiIn cells prepared using SSE films from class 1 and class 2. Because of lower uniformity, the cell using the class 2 film shorts during the first cycle. Reproduced with permission from (Chen et al., 2021). Copyright 2021 American Chemical Society.
With increasing availability of lab automation for high-throughput or combinatorial synthesis and characterization, we expect that such ML models trained on experimental data or a combination of computed and measured data will become more common in the future and will have the potential to significantly accelerate the development of SSBs.
Another emerging application of ML that is tangentially related to SSB research is the text-mining of scientific publications (Kononova et al., 2021). Olivetti and coworkers demonstrated that text-mining can be used for extracting synthesis prescriptions from the literature and that this approach can be applied to the prediction of synthesis conditions for solid electrolytes (Mahbub et al., 2020; Olivetti et al., 2020).
Summary
In this review, we surveyed the current state of machine learning accelerated atomistic modeling of solid-state battery materials with a focus on applications of machine-learning potentials, property prediction models, and inverse design. Despite the emergent nature of this research area, many encouraging examples have already appeared in the literature, demonstrating that machine learning can facilitate the modeling of complex phases and interfaces that are challenging for conventional first-principles methods. An especially active field of research has been the machine learning aided discovery of solid electrolytes, which has benefited from long-time scale molecular dynamics simulations enabled by machine-learning interatomic potentials. Additionally, remarkably successful ML models for the prediction of lithium conductivities without simulation have been proposed. The progress of machine-learning methods for materials discovery in general has benefited tremendously from improving data and software availability, and we anticipate this trend to continue in the near future.
Author Contributions
NA decided the structure and contents of the article. HG performed the literature review with the help of QW and AS. HG, AU, and NA wrote the initial version of the article with contributions from QW and AS. All authors contributed to the discussion and revised the article.
Funding
QW acknowledges financial support from the China Scholarship Council (CSC, No. 201906470009).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors acknowledge support by the Columbia Center for Computational Electrochemistry (CCCE).
Abbreviations
AHC, agglomerative hierarchical clustering; AIMD, ab initio molecular dynamics; ANN, artificial neural network; AUC, Artrith, Urban, and Ceder; BO, Bayesian optimization; CE, cohesive energy; EA, activation energy; GBR, gradient boosting regression; GNN, graph neural network; GPR, Gaussian process regression; kNN, k-nearest neighbors; KRR, kernel ridge regression; LOTF, learning on-the-fly; LR, linear regression; LS, least-squares; MSE, mean square error; MTP, moment tensor potential; MP, Materials Project; NEB, nudged elastic band; PCA, principal component analysis; PES, potential energy surface; PSO, particle swarm optimization; RMSE, root mean square error; RF, random forest; SFs, symmetry functions; SLDA, self-learning and adaptive database; SNAP, spectral neighbor analysis potential; SOAP, smooth overlap of atomic positions; SSE, solid-state electrolyte; SVM, support vector machine; VAEs, variational autoencoders.
References
Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., et al. (2015). TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. Available at: https://www.tensorflow.org/.
Ahmad, Z., Xie, T., Maheshwari, C., Grossman, J. C., and Viswanathan, V. (2018). Machine Learning Enabled Computational Screening of Inorganic Solid Electrolytes for Suppression of Dendrite Formation in Lithium Metal Anodes. ACS Cent. Sci. 4, 996–1006. doi:10.1021/acscentsci.8b00229
Allam, O., Cho, B. W., Kim, K. C., and Jang, S. S. (2018). Application of DFT-Based Machine Learning for Developing Molecular Electrode Materials in Li-Ion Batteries. RSC Adv. 8, 39414–39420. doi:10.1039/C8RA07112H
Allam, O., Kuramshin, R., Stoichev, Z., Cho, B. W., Lee, S. W., and Jang, S. S. (2020). Molecular Structure-Redox Potential Relationship for Organic Electrode Materials: Density Functional Theory-Machine Learning Approach. Mater. Today Energ. 17, 100482. doi:10.1016/j.mtener.2020.100482
Artrith, N., Butler, K. T., Coudert, F.-X., Han, S., Isayev, O., Jain, A., et al. (2021). Best Practices in Machine Learning for Chemistry. Nat. Chem. ASAP. doi:10.1038/s41557-021-00716-z
Artrith, N., Morawietz, T., and Behler, J. (2011). High-dimensional Neural-Network Potentials for Multicomponent Systems: Applications to Zinc Oxide. Phys. Rev. B 83, 153101. doi:10.1103/PhysRevB.83.153101
Artrith, N., and Urban, A. (2016). An Implementation of Artificial Neural-Network Potentials for Atomistic Materials Simulations: Performance for TiO2. Comput. Mater. Sci. 114, 135–150. doi:10.1016/j.commatsci.2015.11.047
Artrith, N., Urban, A., and Ceder, G. (2018). Constructing First-Principles Phase Diagrams of Amorphous LixSi Using Machine-Learning-Assisted Sampling with an Evolutionary Algorithm. J. Chem. Phys. 148, 241711. doi:10.1063/1.5017661
Artrith, N., Urban, A., and Ceder, G. (2017). Efficient and Accurate Machine-Learning Interpolation of Atomic Energies in Compositions with Many Species. Phys. Rev. B 96, 014112. doi:10.1103/PhysRevB.96.014112
Artrith, N., Urban, A., Wang, Y., and Ceder, G. (2019). Atomic-Scale Factors that Control the Rate Capability of Nanostructured Amorphous Si for High-Energy-Density Batteries. arXiv:1901.09272 [cond-mat, physics:physics]. Available at: http://arxiv.org/abs/1901.09272 (Accessed June 3, 2020).
Attarian Shandiz, M., and Gauvin, R. (2016). Application of Machine Learning Methods for the Prediction of Crystal System of Cathode Materials in Lithium-Ion Batteries. Comput. Mater. Sci. 117, 270–278. doi:10.1016/j.commatsci.2016.02.021
Banerjee, A., Wang, X., Fang, C., Wu, E. A., and Meng, Y. S. (2020). Interfaces and Interphases in All-Solid-State Batteries with Inorganic Solid Electrolytes. Chem. Rev. 120, 6878–6933. doi:10.1021/acs.chemrev.0c00101
Bartel, C. J., Trewartha, A., Wang, Q., Dunn, A., Jain, A., and Ceder, G. (2020). A Critical Examination of Compound Stability Predictions from Machine-Learned Formation Energies. Npj Comput. Mater. 6, 97. doi:10.1038/s41524-020-00362-y
Bartók, A. P., Kondor, R., and Csányi, G. (2013). On Representing Chemical Environments. Phys. Rev. B 87, 184115. doi:10.1103/PhysRevB.87.184115
Bartók, A. P., Payne, M. C., Kondor, R., and Csányi, G. (2010). Gaussian Approximation Potentials: The Accuracy of Quantum Mechanics, without the Electrons. Phys. Rev. Lett. 104, 136403. doi:10.1103/PhysRevLett.104.136403
Behler, J. (2011). Atom-centered Symmetry Functions for Constructing High-Dimensional Neural Network Potentials. J. Chem. Phys. 134, 074106. doi:10.1063/1.3553717
Behler, J. (2021). Four Generations of High-Dimensional Neural Network Potentials. Chem. Rev., 0c00868. doi:10.1021/acs.chemrev.0c00868
Behler, J., Lorenz, S., and Reuter, K. (2007). Representing Molecule-Surface Interactions with Symmetry-Adapted Neural Networks. J. Chem. Phys. 127, 014705. doi:10.1063/1.2746232
Behler, J., and Parrinello, M. (2007). Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces. Phys. Rev. Lett. 98, 146401. doi:10.1103/PhysRevLett.98.146401
Behler, J. (2016). Perspective: Machine Learning Potentials for Atomistic Simulations. J. Chem. Phys. 145, 170901. doi:10.1063/1.4966192
Blank, T. B., Brown, S. D., Calhoun, A. W., and Doren, D. J. (1995). Neural Network Models of Potential Energy Surfaces. J. Chem. Phys. 103, 4129–4137. doi:10.1063/1.469597
Bogojeski, M., Vogt-Maranto, L., Tuckerman, M. E., Müller, K.-R., and Burke, K. (2020). Quantum Chemical Accuracy from Density Functional Approximations via Machine Learning. Nat. Commun. 11, 5223. doi:10.1038/s41467-020-19093-1
Bölle, F. T., Bhowmik, A., Vegge, T., Lastra, J. M. G., and Castelli, I. E. (2021). Automatic Diffusion Path Exploration for Multivalent Battery Cathodes Using Geometrical Descriptors. arXiv:2104.06113 [cond-mat]. Available at: http://arxiv.org/abs/2104.06113 (Accessed April 19, 2021).
Brown, R. D., and Martin, Y. C. (1997). The Information Content of 2D and 3D Structural Descriptors Relevant to Ligand-Receptor Binding. J. Chem. Inf. Comput. Sci. 37, 1–9. doi:10.1021/ci960373c
Brown, R. D., and Martin, Y. C. (1996). Use of Structure−Activity Data to Compare Structure-Based Clustering Methods and Descriptors for Use in Compound Selection. J. Chem. Inf. Comput. Sci. 36, 572–584. doi:10.1021/ci9501047
Burke, K. (2012). Perspective on Density Functional Theory. J. Chem. Phys. 136, 150901. doi:10.1063/1.4704546
Chang, J. H., Jørgensen, P. B., Loftager, S., Bhowmik, A., Lastra, J. M. G., and Vegge, T. (2021). On-the-Fly Assessment of Diffusion Barriers of Disordered Transition Metal Oxyfluorides Using Local Descriptors. Electrochimica Acta, 138551. doi:10.1016/j.electacta.2021.138551
Chen, C., Ye, W., Zuo, Y., Zheng, C., and Ong, S. P. (2019). Graph Networks as a Universal Machine Learning Framework for Molecules and Crystals. Chem. Mater. 31, 3564–3572. doi:10.1021/acs.chemmater.9b01294
Chen, Y.-T., Duquesnoy, M., Tan, D. H. S., Doux, J.-M., Yang, H., Deysher, G., et al. (2021). Fabrication of High-Quality Thin Solid-State Electrolyte Films Assisted by Machine Learning. ACS Energ. Lett., 1639–1648. doi:10.1021/acsenergylett.1c00332
Collins, C. R., Gordon, G. J., von Lilienfeld, O. A., and Yaron, D. J. (2018). Constant Size Descriptors for Accurate Machine Learning Models of Molecular Properties. J. Chem. Phys. 148, 241718. doi:10.1063/1.5020441
Cortes, C., and Vapnik, V. (1995). Support-vector Networks. Mach Learn. 20, 273–297. doi:10.1007/BF00994018
Court, C. J., Yildirim, B., Jain, A., and Cole, J. M. (2020). 3-D Inorganic Crystal Structure Generation and Property Prediction via Representation Learning. J. Chem. Inf. Model. 60, 4518–4535. doi:10.1021/acs.jcim.0c00464
Cubuk, E. D., Sendek, A. D., and Reed, E. J. (2019). Screening Billions of Candidates for Solid Lithium-Ion Conductors: A Transfer Learning Approach for Small Data. J. Chem. Phys. 150, 214701. doi:10.1063/1.5093220
Cunha, R. P., Lombardo, T., Primo, E. N., and Franco, A. A. (2020). Artificial Intelligence Investigation of NMC Cathode Manufacturing Parameters Interdependencies. Batteries & Supercaps 3, 60–67. doi:10.1002/batt.201900135
Curtarolo, S., Hart, G. L. W., Nardelli, M. B., Mingo, N., Sanvito, S., and Levy, O. (2013). The High-Throughput Highway to Computational Materials Design. Nat. Mater 12, 191–201. doi:10.1038/nmat3568
Curtarolo, S., Setyawan, W., Wang, S., Xue, J., Yang, K., Taylor, R. H., et al. (2012). AFLOWLIB.ORG: A Distributed Materials Properties Repository from High-Throughput Ab Initio Calculations. Comput. Mater. Sci. 58, 227–235. doi:10.1016/j.commatsci.2012.02.002
Deng, Z., Chen, C., Li, X.-G., and Ong, S. P. (2019). An Electrostatic Spectral Neighbor Analysis Potential for Lithium Nitride. Npj Comput. Mater. 5, 1–8. doi:10.1038/s41524-019-0212-1
Deringer, V. L., and Csányi, G. (2017). Machine Learning Based Interatomic Potential for Amorphous Carbon. Phys. Rev. B 95, 094203. doi:10.1103/PhysRevB.95.094203
Deringer, V. L., Merlet, C., Hu, Y., Lee, T. H., Kattirtzi, J. A., Pecher, O., et al. (2018). Towards an Atomistic Understanding of Disordered Carbon Electrode Materials. Chem. Commun. 54, 5988–5991. doi:10.1039/C8CC01388H
Dixit, M. B., Verma, A., Zaman, W., Zhong, X., Kenesei, P., Park, J. S., et al. (2020). Synchrotron Imaging of Pore Formation in Li Metal Solid-State Batteries Aided by Machine Learning. ACS Appl. Energ. Mater. 3, 9534–9542. doi:10.1021/acsaem.0c02053
Dudani, S. A. (1976). The Distance-Weighted K-Nearest-Neighbor Rule. IEEE Trans. Syst. Man. Cybern. SMC-6, 325–327. doi:10.1109/TSMC.1976.5408784
Eckhoff, M., Lausch, K. N., Blöchl, P. E., and Behler, J. (2020a). Predicting Oxidation and Spin States by High-Dimensional Neural Networks: Applications to Lithium Manganese Oxide Spinels. J. Chem. Phys. 153, 164107. doi:10.1063/5.0021452
Eckhoff, M., Schönewald, F., Risch, M., Volkert, C. A., Blöchl, P. E., and Behler, J. (2020b). Closing the Gap between Theory and Experiment for Lithium Manganese Oxide Spinels Using a High-Dimensional Neural Network Potential. Phys. Rev. B 102, 174102. doi:10.1103/PhysRevB.102.174102
Er, S., Suh, C., Marshak, M. P. M., and Aspuru-Guzik, A. (2015). Computational Design of Molecules for an All-Quinone Redox Flow Battery. Chem. Sci. 6, 885–893. doi:10.1039/C4SC03030C
Eremin, R. A., Zolotarev, P. N., Ivanshina, O. Y., and Bobrikov, I. A. (2017). Li(Ni,Co,Al)O2 Cathode Delithiation: A Combination of Topological Analysis, Density Functional Theory, Neutron Diffraction, and Machine Learning Techniques. J. Phys. Chem. C 121, 28293–28305. doi:10.1021/acs.jpcc.7b09760
Eslamloueyan, R., Khademi, M. H., and Mazinani, S. (2011). Using a Multilayer Perceptron Network for Thermal Conductivity Prediction of Aqueous Electrolyte Solutions. Ind. Eng. Chem. Res. 50, 4050–4056. doi:10.1021/ie101513z
Faber, F. A., Hutchison, L., Huang, B., Gilmer, J., Schoenholz, S. S., Dahl, G. E., et al. (2017). Prediction Errors of Molecular Machine Learning Models Lower Than Hybrid DFT Error. J. Chem. Theor. Comput. 13, 5255–5264. doi:10.1021/acs.jctc.7b00577
Faber, F., Lindmaa, A., von Lilienfeld, O. A., and Armiento, R. (2015). Crystal Structure Representations for Machine Learning Models of Formation Energies. Int. J. Quan. Chem. 115, 1094–1101. doi:10.1002/qua.24917
Friedman, J. H. (2001). Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 29, 1189–1232. Available at: doi:10.1214/aos/1013203451 https://www.jstor.org/stable/2699986 (Accessed May 10, 2021).
Fujimura, K., Seko, A., Koyama, Y., Kuwabara, A., Kishida, I., Shitara, K., et al. (2013). Accelerated Materials Design of Lithium Superionic Conductors Based on First-Principles Calculations and Machine Learning Algorithms. Adv. Energ. Mater. 3, 980–985. doi:10.1002/aenm.201300060
Gao, B., Jalem, R., Ma, Y., and Tateyama, Y. (2020). Li+ Transport Mechanism at the Heterogeneous Cathode/Solid Electrolyte Interface in an All-Solid-State Battery via the First-Principles Structure Prediction Scheme. Chem. Mater. 32, 85–96. doi:10.1021/acs.chemmater.9b02311
Gao, H., Cai, J., Xu, G.-L., Li, L., Ren, Y., Meng, X., et al. (2019). Surface Modification for Suppressing Interfacial Parasitic Reactions of a Nickel-Rich Lithium-Ion Cathode. Chem. Mater. 31, 2723–2730. doi:10.1021/acs.chemmater.8b04200
Gao, Z., Sun, H., Fu, L., Ye, F., Zhang, Y., Luo, W., et al. (2018). Promises, Challenges, and Recent Progress of Inorganic Solid-State Electrolytes for All-Solid-State Lithium Batteries. Adv. Mater. 30, 1705702. doi:10.1002/adma.201705702
Gayon-Lombardo, A., Mosser, L., Brandon, N. P., and Cooper, S. J. (2020). Pores for Thought: Generative Adversarial Networks for Stochastic Reconstruction of 3d Multi-phase Electrode Microstructures with Periodic Boundaries. Npj Comput. Mater. 6, 1–11. doi:10.1038/s41524-020-0340-7
Gharagheizi, F., Sattari, M., Ilani-Kashkouli, P., Mohammadi, A. H., Ramjugernath, D., and Richon, D. (2013). A “Non-linear” Quantitative Structure-Property Relationship for the Prediction of Electrical Conductivity of Ionic Liquids. Chem. Eng. Sci. 101, 478–485. doi:10.1016/j.ces.2013.07.007
Glass, C. W., Oganov, A. R., and Hansen, N. (2006). USPEX-evolutionary crystal Structure Prediction. Computer Phys. Commun. 175, 713–720. doi:10.1016/j.cpc.2006.07.020
Goldberg, D. E. (1989). Genetic Algorithms in Search, Optimization, and Machine Learning. Reading, Mass: Addison-Wesley Pub. Co.
Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep Learning. Cambridge, Massachusetts: The MIT Press.
Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., et al. (2014). Generative Adversarial Nets. in, 2672–2680.
Gossett, E., Toher, C., Oses, C., Isayev, O., Legrain, F., Rose, F., et al. (2018). AFLOW-ML: A RESTful API for Machine-Learning Predictions of Materials Properties. Comput. Mater. Sci. 152, 134–145. doi:10.1016/j.commatsci.2018.03.075
Hajibabaei, A., Myung, C. W., and Kim, K. S. (2020). Towards Universal Sparse Gaussian Process Potentials: Application to Lithium Diffusivity in Superionic Conducting Solid Electrolytes, 6.
Hanakata, P. Z., Cubuk, E. D., Campbell, D. K., and Park, H. S. (2018). Accelerated Search and Design of Stretchable Graphene Kirigami Using Machine Learning. Phys. Rev. Lett. 121, 255304. doi:10.1103/PhysRevLett.121.255304
Hansen, K., Biegler, F., Ramakrishnan, R., Pronobis, W., von Lilienfeld, O. A., Müller, K.-R., et al. (2015). Machine Learning Predictions of Molecular Properties: Accurate Many-Body Potentials and Nonlocality in Chemical Space. J. Phys. Chem. Lett. 6, 2326–2331. doi:10.1021/acs.jpclett.5b00831
Hansen, M. H., Torres, J. A. G., Jennings, P. C., Wang, Z., Boes, J. R., Mamun, O. G., et al. (2019). An Atomistic Machine Learning Package for Surface Science and Catalysis. arXiv:1904.00904 [physics]. Available at: http://arxiv.org/abs/1904.00904 (Accessed April 9, 2021).
Hastie, T., Tibshirani, R., and Friedman, J. H. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer Series in Statistics. 2nd ed. New York, NY: Springer. doi:10.1007/978-0-387-84858-7
Hatakeyama-Sato, K., Tezuka, T., Umeki, M., and Oyaizu, K. (2020). AI-assisted Exploration of Superionic Glass-type Li+ Conductors with Aromatic Structures. J. Am. Chem. Soc. 142, 3301–3305. doi:10.1021/jacs.9b11442
He, X., Bai, Q., Liu, Y., Nolan, A. M., Ling, C., and Mo, Y. (2019). Crystal Structural Framework of Lithium Super‐Ionic Conductors. Adv. Energ. Mater. 9, 1902078. doi:10.1002/aenm.201902078
He, X., Zhu, Y., and Mo, Y. (2017). Origin of Fast Ion Diffusion in Super-ionic Conductors. Nat. Commun. 8. doi:10.1038/ncomms15893
Hellenbrandt, M. (2004). The Inorganic Crystal Structure Database (ICSD)-Present and Future. Crystallogr. Rev. 10, 17–22. doi:10.1080/08893110410001664882
Himanen, L., Jäger, M. O. J., Morooka, E. V., Federici Canova, F., Ranawat, Y. S., Gao, D. Z., et al. (2020). DScribe: Library of Descriptors for Machine Learning in Materials Science. Computer Phys. Commun. 247, 106949. doi:10.1016/j.cpc.2019.106949
Hoerl, A. E., and Kennard, R. W. (1970). Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 12, 55–67. doi:10.1080/00401706.1970.10488634
Hohenberg, P., and Kohn, W. (1964). Inhomogeneous Electron Gas. Phys. Rev. 136, B864–B871. doi:10.1103/PhysRev.136.B864
Hosseinzadeh, M., Hemmati-Sarapardeh, A., Ameli, F., Naderi, F., and Dastgahi, M. (2016). A Computational Intelligence Scheme for Estimating Electrical Conductivity of Ternary Mixtures Containing Ionic Liquids. J. Mol. Liquids 221, 624–632. doi:10.1016/j.molliq.2016.05.059
Houchins, G., and Viswanathan, V. (2020). An Accurate Machine-Learning Calculator for Optimization of Li-Ion Battery Cathodes. J. Chem. Phys. 153, 054124. doi:10.1063/5.0015872
Huan, T. D., Mannodi-Kanakkithodi, A., and Ramprasad, R. (2015). Accelerated Materials Property Predictions and Design Using Motif-Based Fingerprints. Phys. Rev. B 92, 014106. doi:10.1103/PhysRevB.92.014106
Huang, B., and von Lilienfeld, O. A. (2016). Communication: Understanding Molecular Representations in Machine Learning: The Role of Uniqueness and Target Similarity. J. Chem. Phys. 145, 161102. doi:10.1063/1.4964627
Huang, J.-X., Csányi, G., Zhao, J.-B., Cheng, J., and Deringer, V. L. (2019). First-Principles Study of Alkali-Metal Intercalation in Disordered Carbon Anode Materials. J. Mater. Chem. A. 7, 19070–19080. doi:10.1039/C9TA05453G
Huang, J., Zhang, L., Wang, H., Zhao, J., Cheng, J., and E, W. (2021). Deep Potential Generation Scheme and Simulation Protocol for the Li10GeP2S12-type Superionic Conductors. arXiv:2006.03320 [cond-mat, physics:physics]. Available at: http://arxiv.org/abs/2006.03320 (Accessed February 11, 2021).doi:10.5194/amt-2020-201-ac2
Huo, H., and Rupp, M. (2018). Unified Representation of Molecules and Crystals for Machine Learning. arXiv:1704.06439 [cond-mat, physics:physics]. Available at: http://arxiv.org/abs/1704.06439 (Accessed April 9, 2021).
Isayev, O., Oses, C., Toher, C., Gossett, E., Curtarolo, S., and Tropsha, A. (2017). Universal Fragment Descriptors for Predicting Properties of Inorganic Crystals. Nat. Commun. 8, 15679. doi:10.1038/ncomms15679
Jain, A., Hautier, G., Moore, C. J., Ping Ong, S., Fischer, C. C., Mueller, T., et al. (2011). A High-Throughput Infrastructure for Density Functional Theory Calculations. Comput. Mater. Sci. 50, 2295–2310. doi:10.1016/j.commatsci.2011.02.023
Jain, A., Ong, S. P., Hautier, G., Chen, W., Richards, W. D., Dacek, S., et al. (2013). Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation. APL Mater. 1, 011002. doi:10.1063/1.4812323
Jain, A., Shin, Y., and Persson, K. A. (2016). Computational Predictions of Energy Materials Using Density Functional Theory. Nat. Rev. Mater. 1, 1–13. doi:10.1038/natrevmats.2015.4
Jalem, R., Aoyama, T., Nakayama, M., and Nogami, M. (2012). Multivariate Method-AssistedAb InitioStudy of Olivine-type LiMXO4(Main Group M2+-X5+and M3+-X4+) Compositions as Potential Solid Electrolytes. Chem. Mater. 24, 1357–1364. doi:10.1021/cm3000427
Jalem, R., Kanamori, K., Takeuchi, I., Nakayama, M., Yamasaki, H., and Saito, T. (2018). Bayesian-Driven First-Principles Calculations for Accelerating Exploration of Fast Ion Conductors for Rechargeable Battery Application. Sci. Rep. 8, 5845. doi:10.1038/s41598-018-23852-y
Jalem, R., Kimura, M., Nakayama, M., and Kasuga, T. (2015). Informatics-Aided Density Functional Theory Study on the Li Ion Transport of Tavorite-type LiMTO4F (M3+-T5+, M2+-T6+). J. Chem. Inf. Model. 55, 1158–1168. doi:10.1021/ci500752n
Jalem, R., Nakayama, M., and Kasuga, T. (2014). An Efficient Rule-Based Screening Approach for Discovering Fast Lithium Ion Conductors Using Density Functional Theory and Artificial Neural Networks. J. Mater. Chem. A. 2, 720–734. doi:10.1039/C3TA13235H
Jordan, M. I., and Mitchell, T. M. (2015). Machine Learning: Trends, Perspectives, and Prospects. Science 349, 255–260. doi:10.1126/science.aaa8415
Joshi, R. P., Eickholt, J., Li, L., Fornari, M., Barone, V., and Peralta, J. E. (2019). Machine Learning the Voltage of Electrode Materials in Metal-Ion Batteries. ACS Appl. Mater. Inter. 11, 18494–18503. doi:10.1021/acsami.9b04933
Kennedy, J. F., Eberhart, R. C., and Shi, Y. (2001). Swarm Intelligence. San Francisco: Morgan Kaufmann Publishers.
Khorshidi, A., and Peterson, A. A. (2016). Amp: A Modular Approach to Machine Learning in Atomistic Simulations. Computer Phys. Commun. 207, 310–324. doi:10.1016/j.cpc.2016.05.010
Kingma, D. P., and Welling, M. (2014). Auto-Encoding Variational Bayes. arXiv:1312.6114 [cs, stat]. Available at: http://arxiv.org/abs/1312.6114 (Accessed April 10, 2021).
Kirklin, S., Meredig, B., and Wolverton, C. (2013). High-Throughput Computational Screening of New Li-Ion Battery Anode Materials. Adv. Energ. Mater. 3, 252–262. doi:10.1002/aenm.201200593
Kohn, W., and Sham, L. J. (1965). Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 140, A1133–A1138. doi:10.1103/PhysRev.140.A1133
Kononova, O., He, T., Huo, H., Trewartha, A., Olivetti, E. A., and Ceder, G. (2021). Opportunities and Challenges of Text Mining in Materials Research. iScience 24, 102155. doi:10.1016/j.isci.2021.102155
Lacivita, V., Artrith, N., and Ceder, G. (2018). Structural and Compositional Factors that Control the Li-Ion Conductivity in LiPON Electrolytes. Chem. Mater. 30, 7077–7090. doi:10.1021/acs.chemmater.8b02812
Lee, B., Yoo, J., and Kang, K. (2020). Predicting the Chemical Reactivity of Organic Materials Using a Machine-Learning Approach. Chem. Sci. 11, 7813–7822. doi:10.1039/D0SC01328E
Leicester, S. E., Finney, J. L., and Bywater, R. P. (1988). Description of Molecular Surface Shape Using Fourier Descriptors. J. Mol. Graphics 6, 104–108. doi:10.1016/0263-7855(88)85008-2
Li, M., Lu, J., Chen, Z., and Amine, K. (2018a). 30 Years of Lithium-Ion Batteries. Adv. Mater. 30, 1800561. doi:10.1002/adma.201800561
Li, W., Ando, Y., Minamitani, E., and Watanabe, S. (2017a). Study of Li Atom Diffusion in Amorphous Li3PO4 with Neural Network Potential. J. Chem. Phys. 147, 214106. doi:10.1063/1.4997242
Li, W., Song, B., and Manthiram, A. (2017b). High-voltage Positive Electrode Materials for Lithium-Ion Batteries. Chem. Soc. Rev. 46, 3006–3059. doi:10.1039/C6CS00875E
Li, Y., Zou, C., Berecibar, M., Nanini-Maury, E., Chan, J. C.-W., van den Bossche, P., et al. (2018b). Random Forest Regression for Online Capacity Estimation of Lithium-Ion Batteries. Appl. Energ. 232, 197–210. doi:10.1016/j.apenergy.2018.09.182
Liu, B., Yang, J., Yang, H., Ye, C., Mao, Y., Wang, J., et al. (2019). Rationalizing the Interphase Stability of Li|doped-Li7La3Zr2O12via Automated Reaction Screening and Machine Learning. J. Mater. Chem. A. 7, 19961–19969. doi:10.1039/C9TA06748E
Lorenz, S., Scheffler, M., and Gross, A. (2006). Descriptions of Surface Chemical Reactions Using a Neural Network Representation of the Potential-Energy Surface. Phys. Rev. B 73, 115431. doi:10.1103/PhysRevB.73.115431
Mahbub, R., Huang, K., Jensen, Z., Hood, Z. D., Rupp, J. L. M., and Olivetti, E. A. (2020). Text Mining for Processing Conditions of Solid-State Battery Electrolytes. Electrochemistry Commun. 121, 106860. doi:10.1016/j.elecom.2020.106860
Mahé, P., Ueda, N., Akutsu, T., Perret, J.-L., and Vert, J.-P. (2005). Graph Kernels for Molecular Structure−Activity Relationship Analysis with Support Vector Machines. J. Chem. Inf. Model. 45, 939–951. doi:10.1021/ci050039t
Marcolongo, A., Binninger, T., Zipoli, F., and Laino, T. (2020). Simulating Diffusion Properties of Solid‐State Electrolytes via a Neural Network Potential: Performance and Training Scheme. ChemSystemsChem 2, e1900031. doi:10.1002/syst.201900031
Minamitani, E., Ogura, M., and Watanabe, S. (2019). Simulating Lattice Thermal Conductivity in Semiconducting Materials Using High-Dimensional Neural Network Potential. Appl. Phys. Express 12, 095001. doi:10.7567/1882-0786/ab36bc
Miwa, K., and Asahi, R. (2021). Molecular Dynamics Simulations of Lithium Superionic Conductor Li10GeP2S12 Using a Machine Learning Potential. Solid State Ionics 361, 115567. doi:10.1016/j.ssi.2021.115567
Miwa, K., and Asahi, R. (2018). Molecular Dynamics Simulations with Machine Learning Potential for Nb-Doped Lithium Garnet-type Oxide Li7−xLa3(Zr2−xNbx)O12. Phys. Rev. Mater. 2. doi:10.1103/PhysRevMaterials.2.105404
Miwa, K., and Ohno, H. (2017). Interatomic Potential Construction with Self-Learning and Adaptive Database. Phys. Rev. Mater. 1, 053801. doi:10.1103/PhysRevMaterials.1.053801
Mizushima, K., Jones, P. C., Wiseman, P. J., and Goodenough, J. B. (1980). LixCoO2 0. Mater. Res. Bull. 15, 783–789. doi:10.1016/0025-5408(80)90012-4
Mockus, J. (1989). Bayesian Approach to Global Optimization: Theory and Applications. doi:10.1007/978-94-009-0909-0
Morgan, D., Ceder, G., and Curtarolo, S. (2004). High-throughput and Data Mining with Ab Initio Methods. Meas. Sci. Technol. 16, 296–301. doi:10.1088/0957-0233/16/1/039
Mueller, T., Hernandez, A., and Wang, C. (2020). Machine Learning for Interatomic Potential Models. J. Chem. Phys. 152, 050902. doi:10.1063/1.5126336
Nakayama, M., Kanamori, K., Nakano, K., Jalem, R., Takeuchi, I., and Yamasaki, H. (2019). Data‐Driven Materials Exploration for Li‐Ion Conductive Ceramics by Exhaustive and Informatics‐Aided Computations. Chem. Rec. 19, 771–778. doi:10.1002/tcr.201800129
Natarajan, A. R., and Van der Ven, A. (2018). Machine-Learning the Configurational Energy of Multicomponent Crystalline Solids. Npj Comput. Mater. 4, 1–7. doi:10.1038/s41524-018-0110-y
Nishiyama, T., Seko, A., and Tanaka, I. (2020). Application of Machine Learning Potentials to Predict Grain Boundary Properties in Fcc Elemental Metals. arXiv:2007.15944 [cond-mat, physics:physics]. Available at: http://arxiv.org/abs/2007.15944 (Accessed November 9, 2020).
Noé, F., Tkatchenko, A., Müller, K.-R., and Clementi, C. (2020). Machine Learning for Molecular Simulation. Annu. Rev. Phys. Chem. 71, 361–390. doi:10.1146/annurev-physchem-042018-052331
Novikov, I. S., Gubaev, K., Podryabinkin, E. V., and Shapeev, A. V. (2021). The MLIP Package: Moment Tensor Potentials with MPI and Active Learning. Mach. Learn. Sci. Technol. 2, 025002. doi:10.1088/2632-2153/abc9fe
Olivetti, E. A., Cole, J. M., Kim, E., Kononova, O., Ceder, G., Han, T. Y.-J., et al. (2020). Data-Driven Materials Research Enabled by Natural Language Processing and Information Extraction. Appl. Phys. Rev. 7, 041317. doi:10.1063/5.0021106
Onat, B., Cubuk, E. D., Malone, B. D., and Kaxiras, E. (2018). Implanted Neural Network Potentials: Application to Li-Si Alloys. Phys. Rev. B 97, 094106. doi:10.1103/PhysRevB.97.094106
Ouyang, B., Artrith, N., Lun, Z., Jadidi, Z., Kitchaev, D. A., Ji, H., et al. (2020). Effect of Fluorination on Lithium Transport and Short‐Range Order in Disordered‐Rocksalt‐Type Lithium‐Ion Battery Cathodes. Adv. Energ. Mater. 10, 1903240. doi:10.1002/aenm.201903240
Park, C. W., Kornbluth, M., Vandermause, J., Wolverton, C., Kozinsky, B., and Mailoa, J. P. (2020). Accurate and Scalable Multi-Element Graph Neural Network Force Field and Molecular Dynamics with Direct Force Architecture. arXiv:2007.14444 [physics]. Available at: http://arxiv.org/abs/2007.14444 (Accessed November 23, 2020).
Parsaeifard, B., Sankar De, D., Christensen, A. S., Faber, F. A., Kocer, E., De, S., et al. (2021). An Assessment of the Structural Resolution of Various Fingerprints Commonly Used in Machine Learning. Mach. Learn. Sci. Technol. 2, 015018. doi:10.1088/2632-2153/abb212
Paszke, A., Gross, S., Chintala, S., Chanan, G., Yang, E., DeVito, Z., et al. (2017). “Automatic Differentiation in PyTorch,” in 31st Conference on Neural Information Processing Systems NIPS-W.
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2011). Scikit-learn: Machine Learning in Python. J. Machine Learn. Res. 12, 2825–2830. Available at: http://jmlr.org/papers/v12/pedregosa11a.html (Accessed April 13, 2021).
Pilania, G., Wang, C., Jiang, X., Rajasekaran, S., and Ramprasad, R. (2013). Accelerating Materials Property Predictions Using Machine Learning. Sci. Rep. 3, 2810. doi:10.1038/srep02810
Qi, J., Banerjee, S., Zuo, Y., Chen, C., Zhu, Z., Likhit, H. C. M., et al. (2021). Bridging the Gap between Simulated and Experimental Ionic Conductivities in Lithium Superionic Conductors. arXiv:2102.08413 [cond-mat]. Available at: http://arxiv.org/abs/2102.08413 (Accessed February 24, 2021).
Rao, K. K., Yao, Y., and Grabow, L. C. (2020). Accelerated Modeling of Lithium Diffusion in Solid State Electrolytes Using Artificial Neural Networks. Adv. Theor. Simul. 3, 2000097. doi:10.1002/adts.202000097
Rasmussen, C. E. (2004). “Gaussian Processes in Machine Learning,” in Advanced Lectures on Machine Learning: ML Summer Schools 2003, Lectures Lecture Notes in Computer Science. Editors O. Bousquet, U. von Luxburg, and G. Rätsch (Berlin, Heidelberg: Springer), 63–71. doi:10.1007/978-3-540-28650-9_4
Riphaus, N., Stiaszny, B., Beyer, H., Indris, S., Gasteiger, H. A., and Sedlmaier, S. J. (2019). Editors' Choice-Understanding Chemical Stability Issues between Different Solid Electrolytes in All-Solid-State Batteries. J. Electrochem. Soc. 166, A975–A983. doi:10.1149/2.0351906jes
Rogers, D., and Hahn, M. (2010). Extended-Connectivity Fingerprints. J. Chem. Inf. Model. 50, 742–754. doi:10.1021/ci100050t
Rupp, M., Tkatchenko, A., Müller, K.-R., and von Lilienfeld, O. A. (2012). Fast and Accurate Modeling of Molecular Atomization Energies with Machine Learning. Phys. Rev. Lett. 108, 058301. doi:10.1103/PhysRevLett.108.058301
Saal, J. E., Kirklin, S., Aykol, M., Meredig, B., and Wolverton, C. (2013). Materials Design and Discovery with High-Throughput Density Functional Theory: The Open Quantum Materials Database (OQMD). JOM 65, 1501–1509. doi:10.1007/s11837-013-0755-4
Saiful Islam, M., and Fisher, C. A. J. (2014). Lithium and Sodium Battery Cathode Materials: Computational Insights into Voltage, Diffusion and Nanostructural Properties. Chem. Soc. Rev. 43, 185–204. doi:10.1039/C3CS60199D
Sanchez-Lengeling, B., and Aspuru-Guzik, A. (2018). Inverse Molecular Design Using Machine Learning: Generative Models for Matter Engineering. Science 361, 360–365. doi:10.1126/science.aat2663
Sarkar, T., Sharma, A., Das, A. K., Deodhare, D., and Bharadwaj, M. D. (2014). A Neural Network Based Approach to Predict High Voltage Li-Ion Battery Cathode Materials. in 2014 2nd International Conference on Devices, Circuits and Systems (ICDCS), 1–3. doi:10.1109/ICDCSyst.2014.6926140
Schütt, K. T., Gastegger, M., Tkatchenko, A., Müller, K.-R., and Maurer, R. J. (2019). Unifying Machine Learning and Quantum Chemistry with a Deep Neural Network for Molecular Wavefunctions. Nat. Commun. 10, 5024. doi:10.1038/s41467-019-12875-2
Schütt, K. T., Glawe, H., Brockherde, F., Sanna, A., Müller, K. R., and Gross, E. K. U. (2014). How to Represent crystal Structures for Machine Learning: Towards Fast Prediction of Electronic Properties. Phys. Rev. B 89, 205118. doi:10.1103/PhysRevB.89.205118
Schwalbe-Koda, D., and Gómez-Bombarelli, R. (2020). “Generative Models for Automatic Chemical Design,” in Machine Learning Meets Quantum Physics Lecture Notes in Physics. Editors K. T. Schütt, S. Chmiela, O. A. von Lilienfeld, A. Tkatchenko, K. Tsuda, and K.-R. Müller (Cham: Springer International Publishing), 445–467. doi:10.1007/978-3-030-40245-7_21
Seko, A., Hayashi, H., Nakayama, K., Takahashi, A., and Tanaka, I. (2017). Representation of Compounds for Machine-Learning Prediction of Physical Properties. Phys. Rev. B 95, 144110. doi:10.1103/PhysRevB.95.144110
Sendek, A. D., Antoniuk, E. R., Cubuk, E. D., Ransom, B., Francisco, B. E., Buettner-Garrett, J., et al. (2020a). Combining Superionic Conduction and Favorable Decomposition Products in the Crystalline Lithium-Boron-Sulfur System: A New Mechanism for Stabilizing Solid Li-Ion Electrolytes. ACS Appl. Mater. Inter. 12, 37957–37966. doi:10.1021/acsami.9b19091
Sendek, A. D., Cheon, G., Pasta, M., and Reed, E. J. (2020b). Quantifying the Search for Solid Li-Ion Electrolyte Materials by Anion: A Data-Driven Perspective. J. Phys. Chem. C 124, 8067–8079. doi:10.1021/acs.jpcc.9b10650
Sendek, A. D., Cubuk, E. D., Antoniuk, E. R., Cheon, G., Cui, Y., and Reed, E. J. (2019). Machine Learning-Assisted Discovery of Solid Li-Ion Conducting Materials. Chem. Mater. 31, 342–352. doi:10.1021/acs.chemmater.8b03272
Sendek, A. D., Yang, Q., Cubuk, E. D., Duerloo, K.-A. N., Cui, Y., and Reed, E. J. (2017). Holistic Computational Structure Screening of More Than 12 000 Candidates for Solid Lithium-Ion Conductor Materials. Energy Environ. Sci. 10, 306–320. doi:10.1039/C6EE02697D
Shao, Y., Knijff, L., Dietrich, F. M., Hermansson, K., and Zhang, C. (2021). Modelling Bulk Electrolytes and Electrolyte Interfaces with Atomistic Machine Learning. Batteries & Supercaps 4, 585–595. doi:10.1002/batt.202000262
Shapeev, A. V. (2016). Moment Tensor Potentials: A Class of Systematically Improvable Interatomic Potentials. Multiscale Model. Simul. 14, 1153–1173. doi:10.1137/15M1054183
Singraber, A., Behler, J., and Dellago, C. (2019). Library-Based LAMMPS Implementation of High-Dimensional Neural Network Potentials. J. Chem. Theor. Comput. 15, 1827–1840. doi:10.1021/acs.jctc.8b00770
Smith, J. S., Isayev, O., and Roitberg, A. E. (2017). ANI-1: an Extensible Neural Network Potential with DFT Accuracy at Force Field Computational Cost. Chem. Sci. 8, 3192–3203. doi:10.1039/C6SC05720A
Snoek, J., Larochelle, H., and Adams, R. P. (2012). Practical Bayesian Optimization of Machine Learning Algorithms. arXiv:1206.2944 [cs, stat]. Available at: http://arxiv.org/abs/1206.2944 (Accessed May 10, 2021).
Sun, H., and Zhao, K. (2017). Electronic Structure and Comparative Properties of LiNixMnyCozO2 Cathode Materials. J. Phys. Chem. C 121, 6002–6010. doi:10.1021/acs.jpcc.7b00810
Suykens, J. A. K., and Vandewalle, J. (1999). Least Squares Support Vector Machine Classifiers. Neural Process. Lett. 9, 293–300. doi:10.1023/A:1018628609742
Svetnik, V., Liaw, A., Tong, C., Culberson, J. C., Sheridan, R. P., and Feuston, B. P. (2003). Random Forest: A Classification and Regression Tool for Compound Classification and QSAR Modeling. J. Chem. Inf. Comput. Sci. 43, 1947–1958. doi:10.1021/ci034160g
Takahashi, A., Seko, A., and Tanaka, I. (2018). Linearized Machine-Learning Interatomic Potentials for Non-magnetic Elemental Metals: Limitation of Pairwise Descriptors and Trend of Predictive Power. J. Chem. Phys. 148, 234106. doi:10.1063/1.5027283
Talirz, L., Kumbhar, S., Passaro, E., Yakutovich, A. V., Granata, V., Gargiulo, F., et al. (2020). Materials Cloud, a Platform for Open Computational Science. Sci. Data 7, 299. doi:10.1038/s41597-020-00637-5
Thompson, A. P., Swiler, L. P., Trott, C. R., Foiles, S. M., and Tucker, G. J. (2015). Spectral Neighbor Analysis Method for Automated Generation of Quantum-Accurate Interatomic Potentials. J. Comput. Phys. 285, 316–330. doi:10.1016/j.jcp.2014.12.018
Thompson, T., Wolfenstine, J., Allen, J. L., Johannes, M., Huq, A., David, I. N., et al. (2014). Tetragonal vs. Cubic Phase Stability in Al - Free Ta Doped Li7La3Zr2O12 (LLZO). J. Mater. Chem. A. 2, 13431–13436. doi:10.1039/C4TA02099E
Tian, H.-K., Jalem, R., Gao, B., Yamamoto, Y., Muto, S., Sakakura, M., et al. (2020). Electron and Ion Transfer across Interfaces of the NASICON-type LATP Solid Electrolyte with Electrodes in All-Solid-State Batteries: A Density Functional Theory Study via an Explicit Interface Model. ACS Appl. Mater. Inter. 12, 54752–54762. doi:10.1021/acsami.0c16463
Tin Kam Ho (1998). The Random Subspace Method for Constructing Decision Forests. IEEE Trans. Pattern Anal. Machine Intell. 20, 832–844. doi:10.1109/34.709601
Unke, O. T., Chmiela, S., Sauceda, H. E., Gastegger, M., Poltavsky, I., Schütt, K. T., et al. (2021). Machine Learning Force Fields. Chem. Rev., 0c01111. doi:10.1021/acs.chemrev.0c01111
Urban, A., Seo, D.-H., and Ceder, G. (2016). Computational Understanding of Li-Ion Batteries. Npj Comput. Mater. 2, 1–13. doi:10.1038/npjcompumats.2016.2
Venkatasubramanian, V. (2019). The Promise of Artificial Intelligence in Chemical Engineering: Is it Here, Finally? Aiche J. 65, 466–478. doi:10.1002/aic.16489
von Lilienfeld, O. A., Ramakrishnan, R., Rupp, M., and Knoll, A. (2015). Fourier Series of Atomic Radial Distribution Functions: A Molecular Fingerprint for Machine Learning Models of Quantum Chemical Properties. Int. J. Quan. Chem. 115, 1084–1093. doi:10.1002/qua.24912
Vovk, V. (2013). “Kernel Ridge Regression,” in Empirical Inference: Festschrift In Honor Of Vladimir N. Vapnik. Editors B. Schölkopf, Z. Luo, and V. Vovk (Berlin, Heidelberg: Springer), 105–116. doi:10.1007/978-3-642-41136-6_11
Wang, C., Aoyagi, K., Aykol, M., and Mueller, T. (2020a). Ionic Conduction through Reaction Products at the Electrolyte-Electrode Interface in All-Solid-State Li+ Batteries. ACS Appl. Mater. Inter. 12, 55510–55519. doi:10.1021/acsami.0c17285
Wang, C., Aoyagi, K., Wisesa, P., and Mueller, T. (2020b). Lithium Ion Conduction in Cathode Coating Materials from On-The-Fly Machine Learning. Chem. Mater. 32, 3741–3752. doi:10.1021/acs.chemmater.9b04663
Wang, X., Xiao, R., Li, H., and Chen, L. (2017). Quantitative Structure-Property Relationship Study of Cathode Volume Changes in Lithium Ion Batteries Using Ab-Initio and Partial Least Squares Analysis. J. Materiomics 3, 178–183. doi:10.1016/j.jmat.2017.02.002
Wang, Y., Lv, J., Zhu, L., and Ma, Y. (2010). Crystal Structure Prediction via Particle-Swarm Optimization. Phys. Rev. B 82, 094116. doi:10.1103/PhysRevB.82.094116
Wang, Y., Richards, W. D., Ong, S. P., Miara, L. J., Kim, J. C., Mo, Y., et al. (2015). Design Principles for Solid-State Lithium Superionic Conductors. Nat. Mater 14, 1026–1031. doi:10.1038/nmat4369
Ward, L., Agrawal, A., Choudhary, A., and Wolverton, C. (2016). A General-Purpose Machine Learning Framework for Predicting Properties of Inorganic Materials. Npj Comput. Mater. 2, 16028. doi:10.1038/npjcompumats.2016.28
Ward, L., Dunn, A., Faghaninia, A., Zimmermann, N. E. R., Bajaj, S., Wang, Q., et al. (2018). Matminer: An Open Source Toolkit for Materials Data Mining. Comput. Mater. Sci. 152, 60–69. doi:10.1016/j.commatsci.2018.05.018
Weininger, D. (1988). SMILES, a Chemical Language and Information System. 1. Introduction to Methodology and Encoding Rules. J. Chem. Inf. Model. 28, 31–36. doi:10.1021/ci00057a005
Whittingham, M. S. (1976). Electrical Energy Storage and Intercalation Chemistry. Science 192, 1126–1127. doi:10.1126/science.192.4244.1126
Wu, H., Lorenson, A., Anderson, B., Witteman, L., Wu, H., Meredig, B., et al. (2017). Robust FCC Solute Diffusion Predictions from Ab-Initio Machine Learning Methods. Comput. Mater. Sci. 134, 160–165. doi:10.1016/j.commatsci.2017.03.052
Xiao, Y., Wang, Y., Bo, S.-H., Kim, J. C., Miara, L. J., and Ceder, G. (2019). Understanding Interface Stability in Solid-State Batteries. Nat. Rev. Mater. 5, 105–126. doi:10.1038/s41578-019-0157-5
Xie, T., France-Lanord, A., Wang, Y., Shao-Horn, Y., and Grossman, J. C. (2019). Graph Dynamical Networks for Unsupervised Learning of Atomic Scale Dynamics in Materials. Nat. Commun. 10, 2667. doi:10.1038/s41467-019-10663-6
Xie, T., and Grossman, J. C. (2018). Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys. Rev. Lett. 120, 145301. doi:10.1103/PhysRevLett.120.145301
Ye, W., Chen, C., Wang, Z., Chu, I.-H., and Ong, S. P. (2018). Deep Neural Networks for Accurate Predictions of Crystal Stability. Nat. Commun. 9, 3800. doi:10.1038/s41467-018-06322-x
Yoo, D., Lee, K., Jeong, W., Lee, D., Watanabe, S., and Han, S. (2019). Atomic Energy Mapping of Neural Network Potential. Phys. Rev. Mater. 3, 093802. doi:10.1103/PhysRevMaterials.3.093802
Yu, X., and Manthiram, A. (2018). Electrode-electrolyte Interfaces in Lithium-Based Batteries. Energ. Environ. Sci. 11, 527–543. doi:10.1039/C7EE02555F
Zhang, Y., He, X., Chen, Z., Bai, Q., Nolan, A. M., Roberts, C. A., et al. (2019). Unsupervised Discovery of Solid-State Lithium Ion Conductors. Nat. Commun. 10, 5260. doi:10.1038/s41467-019-13214-1
Ziletti, A., Kumar, D., Scheffler, M., and Ghiringhelli, L. M. (2018). Insightful Classification of crystal Structures Using Deep Learning. Nat. Commun. 9, 2775. doi:10.1038/s41467-018-05169-6
Zuo, Y., Chen, C., Li, X., Deng, Z., Chen, Y., Behler, J., et al. (2020). Performance and Cost Assessment of Machine Learning Interatomic Potentials. J. Phys. Chem. A. 124, 731–745. doi:10.1021/acs.jpca.9b08723
Zuo, Y., Qin, M., Chen, C., Ye, W., Li, X., Luo, J., et al. (2021). Accelerating Materials Discovery with Bayesian Optimization and Graph Deep Learning. arXiv:2104.10242 [cond-mat]. Available at: http://arxiv.org/abs/2104.10242 (Accessed May 3, 2021).
Keywords: solid-state batteries, interfaces, atomistic simulations, first-principles calculations, machine learning, neural network potentials
Citation: Guo H, Wang Q, Stuke A, Urban A and Artrith N (2021) Accelerated Atomistic Modeling of Solid-State Battery Materials With Machine Learning. Front. Energy Res. 9:695902. doi: 10.3389/fenrg.2021.695902
Received: 15 April 2021; Accepted: 18 May 2021;
Published: 04 June 2021.
Edited by:
Chi Chen, University of California, San Diego, United StatesReviewed by:
Xingyu Guo, University of California, San Diego, United StatesWeike Ye, University of California, San Diego, United States
Copyright © 2021 Guo, Wang, Stuke, Urban and Artrith. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Haoyue Guo, aGcyNTY4QGNvbHVtYmlhLmVkdQ==; Nongnuch Artrith, bmFydHJpdGhAYXRvbWlzdGljLm5ldA==
 Haoyue Guo1*
Haoyue Guo1* Annika Stuke
Annika Stuke Nongnuch Artrith
Nongnuch Artrith