Accurate Solar Cell Modeling via Genetic Neural Network-Based Meta-Heuristic Algorithms

Accurate solar cell modeling is essential for reliable performance evaluation and prediction, real-time control, and maximum power harvest of photovoltaic (PV) systems. Nevertheless, such a model cannot always achieve satisfactory performance based on conventional optimization strategies caused by its high-nonlinear characteristics. Moreover, inadequate measured output current-voltage (I-V) data make it difficult for conventional meta-heuristic algorithms to obtain a high-quality optimum for solar cell modeling without a reliable fitness function. To address these problems, a novel genetic neural network (GNN)-based parameter estimation strategy for solar cells is proposed. Based on measured I-V data, the GNN firstly accomplishes the training of the neural network via a genetic algorithm. Then it can predict more virtual I-V data, thus a reliable fitness function can be constructed using extended I-V data. Therefore, meta-heuristic algorithms can implement an efficient search based on the reliable fitness function. Finally, two different cell models, e.g., a single diode model (SDM) and double diode model (DDM) are employed to validate the feasibility of the GNN. Case studies verify that GNN-based meta-heuristic algorithms can efficiently improve modeling reliability and convergence rate compared against meta-heuristic algorithms using only original measured I-V data.

Introduction

In recent years, due to rapid fossil fuel depletion (Peng et al., 2020), booming global energy demand (Shangguan et al., 2020a), and a series of severe eco-environmental problems (Yang et al., 2015), concepts of sustainable development and an environmentally friendly society are receiving increasingly widespread attention (Shangguan et al., 2020b). Hence, environmental protection (Sun et al., 2019) and energy structure transition (Sun and Yang, 2020) are becoming global development strategies via the application of renewable energies, e.g., solar (Zhang et al., 2019a; Murty and Kumar, 2020) and wind (Liu et al., 2020). Note that solar energy is one of the most efficient alternatives among various available candidates due to its remarkable superiorities of photovoltaic (PV) systems (Gao et al., 2021; Liu et al., 2021), e.g., wide distribution, abundance, and lack of pollution (He et al., 2020; Huang et al., 2020).

In order to carry out precise performance analysis (Jordehi, 2016), optimal design (Zhang et al., 2019b), and power generation efficiency enhancement (Song et al., 2021; Yang et al., 2021) of PV systems, many solar cell modeling approaches have been devised to investigate their dynamic physical behaviors and output characteristics under various operation conditions (Jordehi, 2016). Generally speaking, two PV cell models have the most widely used applications, i.e., the single diode model (SDM) (Rodriguez et al., 2017) and double diode model (DDM) (Abbassi et al., 2018; Qais et al., 2019a). In particular, precise and reliable estimation of their unknown parameters is the first and foremost step for PV cell mathematical modeling. However, the parameters cannot sustain constant and are tested under standard test conditions (STC) (Xiong et al., 2018). In addition, the value of these parameters also changes with degradation and faults over time.

Over the decades, numerous methods developed to solve such obstacles can be generally categorized into three types, i.e., analytical methods (Wolf and Benda, 2013; Torabi et al., 2017), deterministic approaches, and meta-heuristic algorithms. Analytical methods utilize the data sheet information provided by manufacturers to undertake mathematical calculations, which have the merits of easy implementation but lack stable accuracy as they mainly depend on a group of selected points on a current-voltage (I-V) curve. Meanwhile, deterministic techniques, including Lambert W-functions (Gao et al., 2016) and iterative curve fitting (Villalva et al., 2009) can obtain more accurate results but easily fall into local optimum when solving high multi-modality problems. Thus, limitations of the two aforementioned methods prevent them from maintaining a stable and satisfactory performance on PV cell parameter extraction. Nevertheless, meta-heuristic algorithms can powerfully compensate for the shortcomings, they display high applicability (Nesmachnow, 2014), strong reliability (Roeva and Fidanova, 2018), and a high computation rate (Pillai and Rajasekar, 2018; Figueroa et al., 2020), etc.

Up to now, numerous meta-heuristic algorithms have been utilized for the parameter estimation of PV cells (Yu et al., 2018; Guchhait and Banerjee, 2020; Yang et al., 2020), e.g., genetic algorithm (GA) (Jervase et al., 2001), differential evolution (DE) (Ishaque and Salam, 2011), particle swarm optimization (PSO) (Ye et al., 2009), artificial bee colony (ABC) (Oliva et al., 2014), water cycle algorithm (WCA) (Kler et al., 2017), bacterial foraging algorithm (BFA) (Awadallah, 2016), and imperialist competitive algorithm (ICA) (Fathy and Rezk, 2017), together with many hybrids (Chin et al., 2015; Allam et al., 2016; Nayak et al., 2019).

Besides, as all modeling heavily depends on volume and accuracy of measured data from a data sheet, it is of great significance to undertake reasonable optimization on data samples rather than only focusing on algorithm improvement. Note that the measuring I-V data offered by the manufacturer are always insufficient, which might result in the loss of sample information that can finally decrease simulation accuracy. Hence, it is critical to adopt effective data processing methods to enrich data samples before parameter estimation. In the past few decades, the artificial neural network (ANN) (Mittal et al., 2018) has shown its great effectiveness in data analysis and prediction. To obtain optimal parameters of the ANN, various methods are employed to train networks, such as the Newton-Raphson method (Soloway and Haley, 1996) and gradient descent method (Noriega and Wang, 1998). However, these methods essentially belong to gradient-based optimization, which easily result in a low-quality optimum or a complex computation (Song et al., 2007) as their performance highly depends on neural network structure, complexity of cost function, and so on. Compared with gradient-based optimization, evolutionary algorithms, e.g., genetic algorithms (GAs) which have a superior global searching ability and high application flexibility are more appropriate to train an ANN. Therefore, this paper develops novel genetic neural network (GNN)-based meta-heuristic algorithms for solar cell accurate modeling, which have the following contributions:

The GNN is utilized to generate more virtual I-V data based on inadequate measured I-V data, such that it can provide a more reliable fitness function with adequate I-V data to meta-heuristic algorithms;

GNN-based meta-heuristic algorithms can implement an efficient search for PV cell parameter estimation, which can acquire a higher-quality optimum than conventional meta-heuristic algorithms with only inadequate measured I-V data;

Practical performance is effectively verified via an SDM and DDM, respectively. Experiment results illustrate that the proposed optimization strategy displays higher optimization accuracy and convergence stability on PV cell modeling.

The rest of this paper is organized as follows: PV cell modeling and objective function are presented in Photovoltaic Cell Modeling and Problem Formulation. The proposed GNN-based meta-heuristic algorithms are elaborated on in Methodologies. Case studies and detailed experimental results are shown in Case Studies. Lastly, conclusions are provided in Conclusion.

Photovoltaic Cell Modeling and Problem Formulation

In general, the most commonly utilized equivalent circuit models are SDMs and DDMs. Their mathematical models and corresponding objective functions are introduced in this section.

Mathematical Modeling

The first step for studying the characteristics of PV cells, or to develop a more accurate prediction of PV systems operation is appropriate PV cell modeling (Guchhait and Banerjee, 2020). Then, PV cell parameters can be reliably extracted to depict the output characteristics more accurately for better performance analysis. The most commonly applied equivalent circuit models are SDM and DDM (Ram et al., 2018).

Single Diode Model

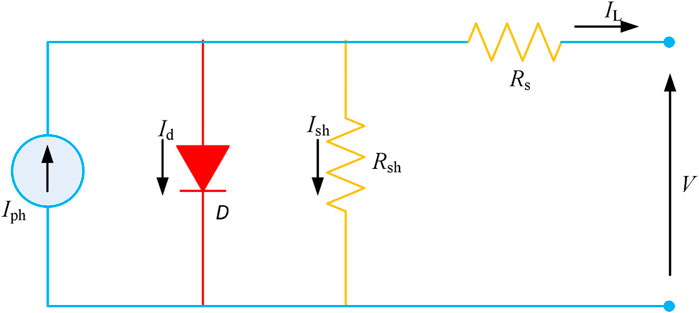
The structure of an SDM is shown in Figure 1, which contains an ideal constant current source I_ph, a series resistance R_s, a shunt resistance R_sh, and a diode D (Ye et al., 2009; Murty and Kumar, 2020). An SDM is characterized by high simplicity and decent accuracy (Humada et al., 2016).

FIGURE 1

FIGURE 1. Equivalent circuit of SDM.

The output current of an SDM defined as I_L can be described by (Nayak et al., 2019; Guchhait and Banerjee, 2020)

$I_{\text{L}}=I_{\text{ph}}-I_{\text{d}}-I_{\text{sh}}(1)$

where I_sh denotes shunt resistance current R_ph; and I_d represents diode current which is able to be further calculated by Jordehi (2016)

$I_{\text{d}}=I_{\text{sd}}\left[\mathbf{exp}\left(V_{\text{L}}+I_{\text{L}}{R}_{\text{s}}/a{V}_{\text{t}}\right)-1\right](2)$

where$I_{\text{sd}}$ represents the diode’s reverse saturation current; $V_{\text{L}}$ denotes the output voltage;$a$ means the diode’s ideality factor; while $V_{\text{t}}$ means junction thermal voltage, as follows Ishaque et al. (2011):

$V_{\text{t}}=\frac{KT}{q}(3)$

where T denotes the temperature of the PV cell; and K$=1.38\times {10}^{-23}\text{ J}/\text{K}$ means the Boltzmann constant; and $q=1.6\times {10}^{-19}\text{ C}$ represents electron charge.

Combining Eqs. 1–3, the output I-V relationship of the SDM is described by

$I_{\text{L}}=I_{\text{ph}}-I_{\text{sd}}\left[\mathbf{exp}\left(\frac{V_{\text{L}}+I_{\text{L}}{R}_{\text{s}}}{a{V}_{\text{t}}}\right)-1\right]-\frac{V_{\text{L}}+I_{\text{L}}{R}_{\text{s}}}{R_{\text{sh}}} (4)$

Hence, five parameters need to be identified for the SDM, e.g., $I_{\text{ph}}$, $I_{\text{sd}}$, $R_{\text{s}}$, $R_{\text{sh}}$, and $a$.

Double Diode Model

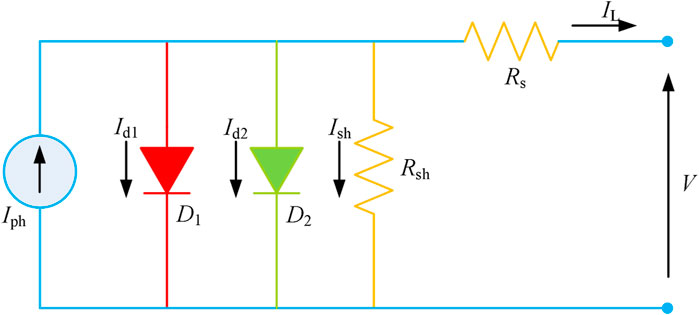
As demonstrated in Figure 2, the only difference between an SDM and DDM is that a DDM has one more diode in parallel, upon which recombination losses in the depletion layer are considered in the DDM (Zhang et al., 2019b). Under such a circumstance, the DDM displays higher accuracy than the SDM, while the increase of unknown parameters also brings an extra computation burden (Ishaque et al., 2011).

FIGURE 2

FIGURE 2. Equivalent circuit of DDM.

Note that the output current of the DDM is described by

$I_{\text{L}}=I_{\text{ph}}-I_{\text{d}1}-I_{\text{d}2}-I_{\text{sh}}(5)$

where currents$I_{\text{d}1}$ and$I_{\text{d}2}$ flowing through diodes $D_1$and$D_2$are written as

$I_{\text{d}1}=I_{\text{sd}1}\left[\mathbf{exp}\left(\frac{V_{\text{L}}+I_{\text{L}}{R}_{\text{s}}}{a_1{V}_{\text{t}}}\right)-1\right](6)$

$I_{\text{d}2}=I_{\text{sd}2}\left[\mathbf{exp}\left(\frac{V_{\text{L}}+I_{\text{L}}{R}_{\text{s}}}{a_2{V}_{\text{t}}}\right)-1\right](7)$

Hence, the output I-V relationship of the DDM can be calculated by

$I_{\text{L}}=I_{\text{ph}}-I_{\text{sd}1}\left[\mathbf{exp}\left(\frac{q\left(V_{\text{L}}+I_{\text{L}}{R}_{\text{s}}\right)}{a_1{V}_{\text{t}}}\right)-1\right]-I_{\text{sd}2}\left[\mathbf{exp}\left(\frac{q\left(V_{\text{L}}+I_{\text{L}}{R}_{\text{s}}\right)}{a_2{V}_{\text{t}}}\right)-1\right]-\frac{V_{\text{L}}+I_{\text{L}}{R}_{\text{s}}}{R_{\text{sh}}}(8)$

Note that the variables in Eq. 8 are demonstrated in the nomenclature.

Thus, seven parameters need to be identified for the DDM, e.g., $I_{\text{ph}}$, $I_{\text{sd}1}$, $I_{\text{sd}2}$, $R_{\text{s}}$, $R_{\text{sh}}$, $a_1$, and $a_2$

Objective Function

Root mean square error (RMSE) is chosen as the objective function as follows Khanna et al. (2015)

$\mathbf{RMSE}\left(x\right)=\sqrt{\frac{1}{N}{\displaystyle \sum }_{k=1}^N{\left(f(V_{\text{L}},I_{\text{L}},x)\right)}^2}(9)$

where$\mathit{ }x$ denotes the solution vector and $N$ means the amount of experimental data.

Error function $f(V_{\text{L}},I_{\text{L}},x)$ for the SDM can be calculated by Qais et al. (2019b)

$\{\begin{array}{c}{f}_{\text{SDM}}\left(V_{\text{L}},I_{\text{L}},x\right)=I_{\text{ph}}-I_{\text{sd}}\left[\mathbf{exp}\left(\frac{V_{\text{L}}+I_{\text{L}}{R}_{\text{s}}}{a{V}_{\text{t}}}\right)-1\right]-\frac{V_{\text{L}}+I_{\text{L}}{R}_{\text{s}}}{R_{\text{sh}}}-I_{\text{L}}\\ x=\{I_{\text{ph}}, I_0, R_{\text{s}}, R_{\text{sh}},a\}\end{array}(10)$

For the DDM, it gives

$\{\begin{array}{c}{f}_{\text{DDM}}\left(V_{\text{L}},I_{\text{L}},x\right)=I_{\text{ph}}-I_{\text{sd}1}\left[\mathbf{exp}\left(\frac{q\left(V_{\text{L}}+I_{\text{L}}{R}_{\text{s}}\right)}{a_1{V}_{\text{t}}}\right)-1\right]\\ -I_{\text{sd}2}\left[\mathbf{exp}\left(\frac{q\left(V_{\text{L}}+I_{\text{L}}{R}_{\text{s}}\right)}{a_2{V}_{\text{t}}}\right)-1\right]-\frac{V_{\text{L}}+I_{\text{L}}{R}_{\text{s}}}{R_{\text{sh}}}-I_{\text{L}}\\ x=\{I_{\text{ph}}, I_{01}, I_{02}, R_{\text{s}}, R_{\text{sh}}, a_1, a_2\}\end{array}(11)$

Methodologies

In this section, the developed GNN and its combination with meta-heuristic algorithms are illustrated.

Genetic Neural Network

The detailed network structure of the GNN is elaborated in this section.

Principle of Artificial Neural Network

ANNs have achieved widespread attention and applications due to their high accuracy and shorter computational time in predictions (Zhou et al., 2020). Particularly, the jth neuron is connected with k inputs ($x_1$, $x_2$, $x_3$,…, $x_k$) and one bias input $b_j$, while its output $y_i$ can be calculated by Chang (2011)

$y_i=F({\displaystyle \sum }_{i=1}^k{w}_{ij}{x}_i-b_j)(12)$

where $w_{ij}$ denotes the ith weight of the jth neuron; $x_i$ means the neuron input layer; $b_j$ denotes the bias of the jth neuron; $k$ represents the number of inputs; and F(.) represents the transfer function, which can be defined by

$F\left(z\right)=\frac{1}{1+e^{-z}}(13)$

where z denotes the function variable, which can be described by$z={\displaystyle \sum }_{i=1}^k{w}_{ij}{x}_i-b_j$ corresponding to Eq. 12.

Weights and biases among each layer can be expressed as

$W^l={\left[\begin{array}{ccc}{\omega }_{11}^l& \cdots & {\omega }_{1n}^l\\ ⋮& \ddots & ⋮\\ {\omega }_{1m}^l& \cdots & {\omega }_{mn}^l\end{array}\right]}_{m\times n}(14)$

$B^l=\left[b_{11}^l\cdots b_{1n}^l\right](15)$

where $W^l$ and $B^l$ denote weights and biases between neurons in layer l and layer (l+1); while m and n represent the number of neurons in layer l and layer (l+1), respectively.

To generate more virtual I-V data of the PV cell, an ANN should accomplish a training process on the basis of training data. In general, it attempts to minimize cost function via optimizing network parameters (i.e., weights and biases) as follows:

$\mathbf{min} f_{\text{train}}\left(W,B\right)={\displaystyle \sum }_{h\in H}{\left(I_{\text{L}}^h-{\widehat{I}}_{\text{L}}^h\right)}^2(16)$

$\mathbf{s}.\mathbf{t}.\{\begin{array}{c}{W}_{\text{lb}}\le W\le W_{\text{ub}}\\ B_{\text{lb}}\le B\le B_{\text{ub}}\end{array}(17)$

where W denotes weight vector; B represents bias vector; $I_{\text{L}}^h$ is the measured output current of the PV cell of the hth training sample; ${\widehat{I}}_{\text{L}}^h$ is the output current of the PV cell generated by the ANN for the hth training sample; $W_{\text{lb}}$ and $W_{\text{ub}}$ denote the lower and upper bounds of weights, respectively; and $B_{\text{lb}}$ and $B_{\text{ub}}$ mean the lower and upper bounds of bias, respectively.

Artificial Neural Network Training by Genetic Algorithms

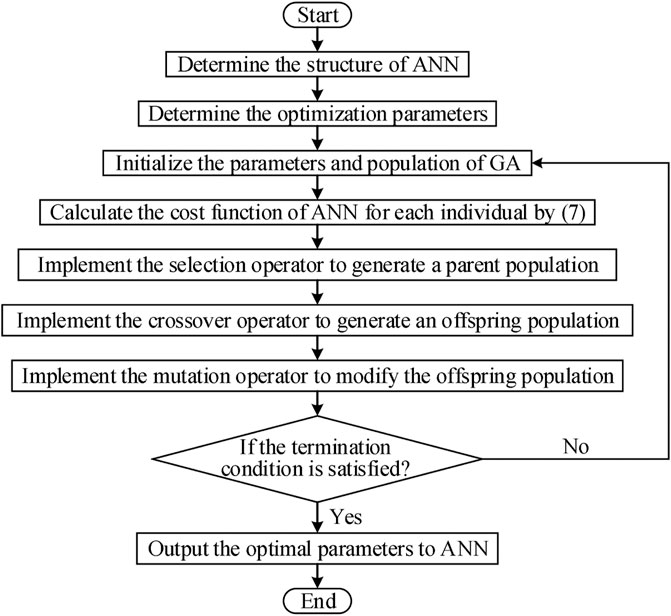
GA mainly contains three critical operators, i.e., selection, crossover, and mutation (Khani et al., 2019). To find optimal parameters for an ANN, a GA can be directly used to handle the training model in Eqs. 16, 17, in which detailed steps are given in Figure 3.

FIGURE 3

FIGURE 3. Detailed steps of ANN training by a GA.

Genetic Neural Network-Based Meta-Heuristic Algorithms

The detailed optimization structure of GNN-based meta-heuristic algorithms for PV cell parameter extraction is illustrated in this section.

Genetic Neural Network-Based Modified Fitness Function

Based on the trained GNN, more virtual I-V data of the PV cell can be generated to modify fitness function for meta-heuristic algorithms. Since all optimization variables show lower and upper bounds during optimization, RMSE can be regarded as the fitness function by taking prediction data into account, as follows:

$\mathbf{RMSE}\left(x\right)=\sqrt{\frac{1}{N+N_{\text{p}}}{\displaystyle \sum }_{k=1}^{N+N_{\text{p}}}{\left(f(V_{\text{L}},I_{\text{L}},x)\right)}^2}(18)$

where $N_{\text{p}}$ denotes the amount of prediction data.

General Execution Procedure

Overall operation framework of GNN-based meta-heuristic algorithms for solar cell modeling mainly consists of three parts, as illustrated in Figure 4. The main differences between various algorithms are individual roles and searching mechanisms of exploration and exploitation. Firstly, measured output I-V data of various PV cells are utilized for GNN training. Secondly, more virtual I-V data are generated by the GNN, thus a more reliable fitness function can be established to guide algorithm searching. Finally, meta-heuristic algorithms implement exploration and exploitation at different stages to find optimal PV cell parameters.

FIGURE 4

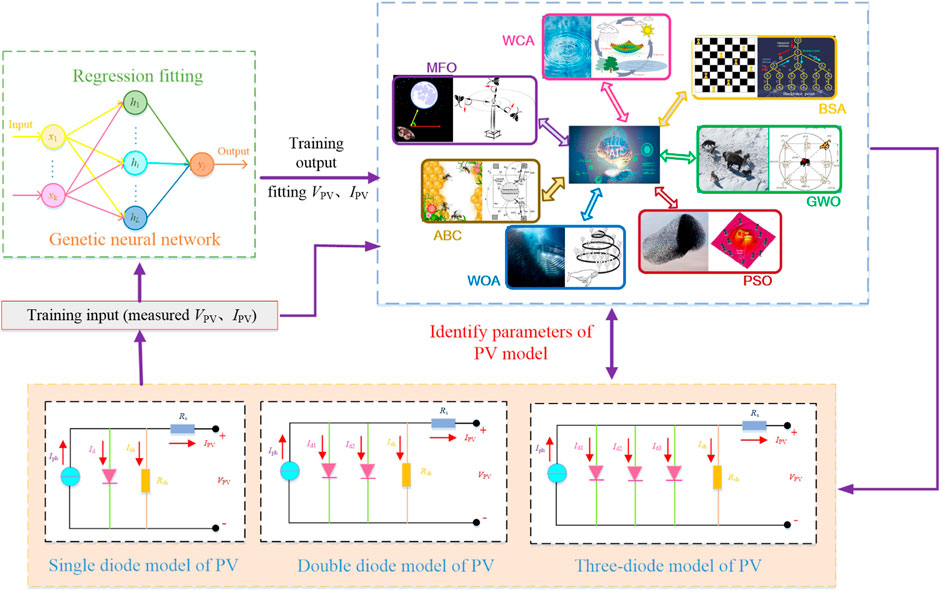
FIGURE 4. Framework of GNN-based data-driven optimization procedure for PV cell parameter estimation.

Parameter Setting of the Genetic Neural Network

Main structure of the GNN is designed to be a five-layer network, including one input layer, three hidden layers with 11 neurons (i.e., five neurons in the first hidden layer and three neurons in each of the other two layers), and one output layer with one neuron for one output. Figure 5 shows the convergence of the GA for the cost function of the GNN under different training datasets and framework design of the GNN, which indicates that cost function obtained by the GA is very small. In the case of a 50% training dataset, weights and biases of the GNN are as follows:

$W^1=\left[\begin{array}{ccccc}0.6537& -7.1844& -1.7803& -0.2099& 1.6838\end{array}\right](19)$

$B^1=\left[\begin{array}{ccccc}0.4259& 3.2080& 3.149841& -2.0999& -3.8189\end{array}\right](20)$

$W^2=\left[\begin{array}{ccccc}-2.9396& -4.1996& -3.09572& 5.0775& 1.1991\\ 1.8545& -5.9097& -5.2801& -0.5460& 8.8733\\ 5.9810& 8.4175& -4.7475& 2.5929& -5.722\end{array}\right](21)$

$B^2=\left[\begin{array}{ccc}2.0807& 5.8701& -2.8972\end{array}\right](22)$

FIGURE 5

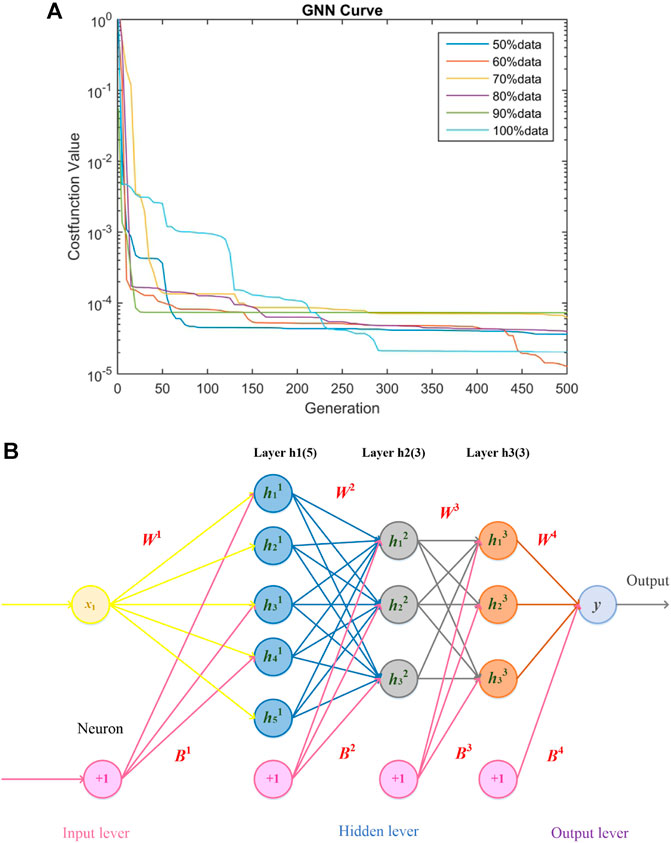
FIGURE 5. Parameter setting of the GNN. (A) Convergence of cost function of the GNN under different training datasets; (B) framework design of the GNN.

Case Studies

Seven meta-heuristic algorithms are adopted to achieve the accurate modeling of three PV cell models. In particular, 26 sets of measured I-V data are collected from a 57 mm diameter R.T.C. France solar cell under the environmental condition (G = 1000 W/m² and T = 33°C) (T = 33°C is the cell temperature). Due to the benchmark, I-V datasets used for case studies are only determined under conditions of G = 1000 W/m² and T = 33°C, thus there is only one single fitted I-V curve. To validate the practical applicability of meta-heuristic algorithms based on inadequate data, six datasets are randomly chosen from 26 pairs of measured data that are 50, 60, 70, 80, 90, and 100% of measured data. To provide a reliable fitness function to the meta-heuristic algorithms, the total number of each dataset and prediction data are set at 50, e.g., 37 pieces of prediction data for a 50% dataset. In addition, each meta-heuristic algorithm is evaluated under two circumstances, that is, without data prediction (i.e., with only selected measured data) and with data prediction.

Note that the maximum iteration number and population size of all meta-heuristic algorithms under each PV model are designed to be the same. Particularly, their maximum iteration number is designed to be identical, i.e., 300, and all methods are independently operated in 80 runs. Besides, population size of each algorithm is designed to be 30 and 50 for the SDM and DDM, respectively.

Results of the Single Diode Model

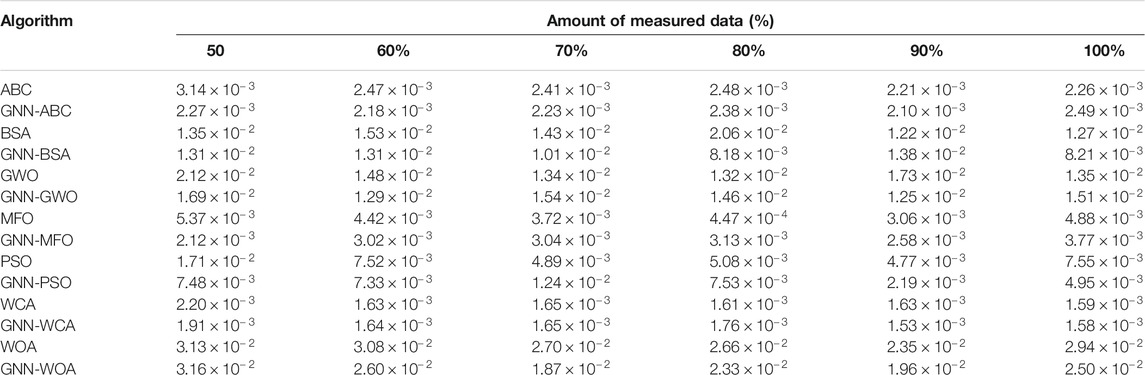
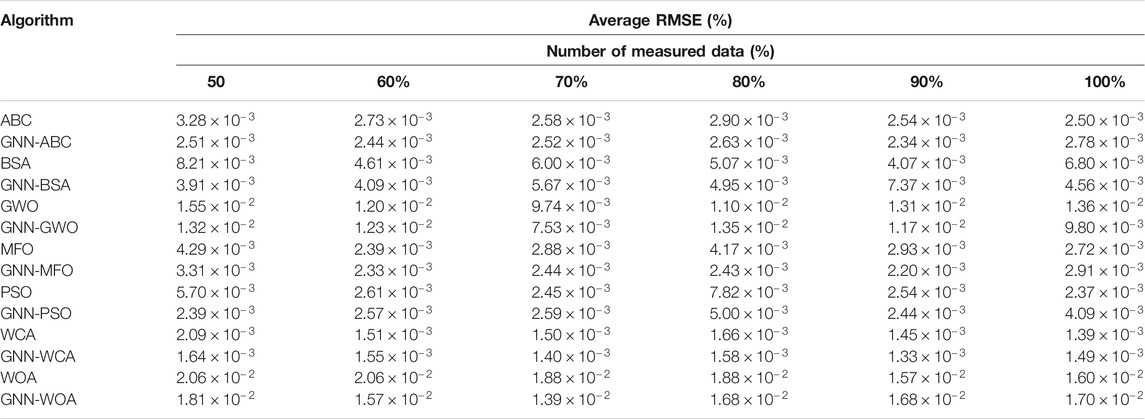
Table 1 shows the simulation results of the average RMSE acquired via seven methods under various measured datasets, which demonstrates that the average RMSE obtained by each GNN-based meta-heuristic algorithm is significantly smaller than that with only measured data, especially under 50% inadequate measured data. For instance, the average RMSE obtained by GNN-PSO is 56.25% smaller than original PSO without data prediction under 50% measured data, which validates that GNN-based I-V data prediction can effectively improve optimization accuracy and stability.

TABLE 1

TABLE 1. Statistical results of average RMSE for SDM.

Besides, Figure 6 shows the convergence of seven approaches without the GNN and with GNN under various datasets. It can be seen that WOA is prone to a low-quality optimum and GWO easily falls into a local optimum at the initial stage under 100% data without the GNN, while GNN-based training can help both of them achieve a more stable convergence and a higher quality optimum. Besides, most algorithms can hardly achieve stable and efficient convergence due to inadequate data. In contrast, an increase of training data helps them to gradually find high-quality solutions in a more stable way.

FIGURE 6

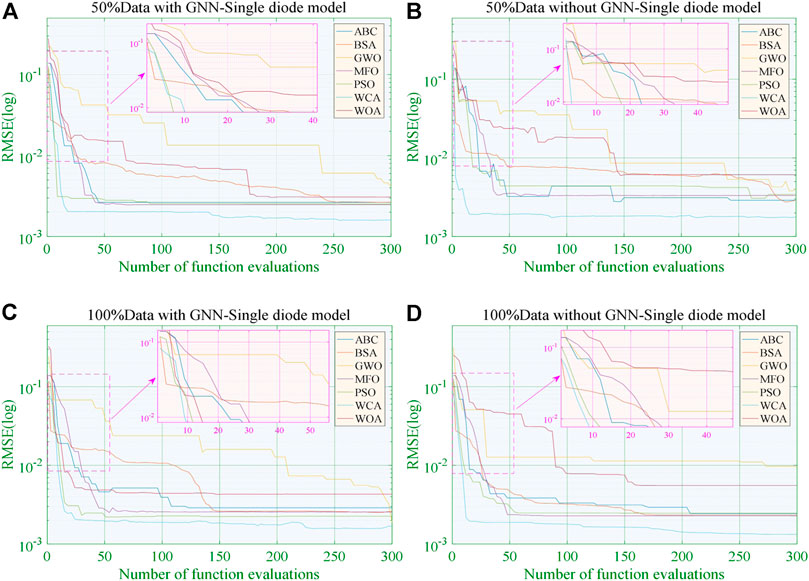
FIGURE 6. Convergence of various algorithms for the SDM. (A) With the GNN under 50% data; (B) without the GNN under 50% data; (A) with the GNN under 100% data; (B) without the GNN under 100% data.

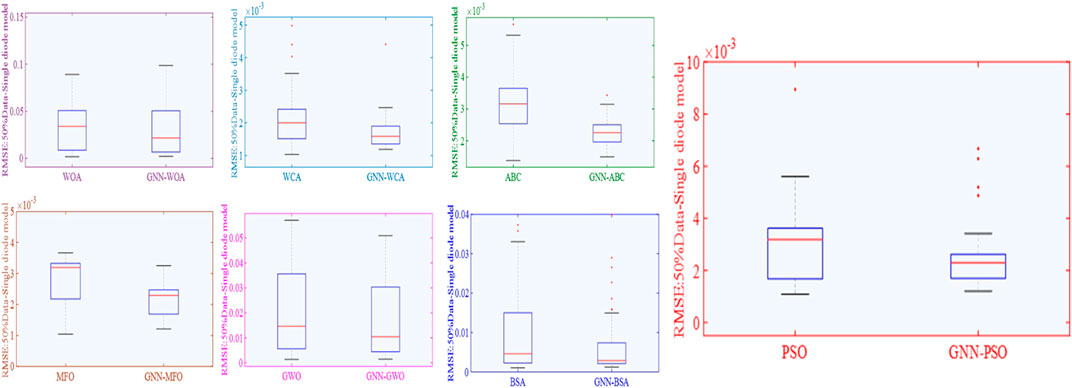
Moreover, boxplots of RMSE for the SDM under 50% data are depicted in Figure 7, which explicitly shows the resulting distribution of the seven different algorithms in 80 runs. Figure 6 clearly indicates that the distribution range and upper/lower bounds of GNN-based meta-heuristic algorithms are smaller than that without a GNN. It can effectively verify that the increase of data based on the GNN can simultaneously enhance convergence stability and searching ability. Besides, outliers of average RMSE of some algorithms can also be efficiently reduced by GNN-based data prediction, such as WCA and ABC. It indicates that each algorithm can find the global optimum more easily via GNN-based experimental data prediction, upon which optimal values of these unknown parameters can be determined in a more accurate and stable way.

FIGURE 7

FIGURE 7. Boxplot of RMSE under different data for the SDM under 50% data.

Figure 8 depicts the I-V and P-V curves acquired via the best algorithm (i.e., the algorithm that can obtain minimum RMSE) under 50% training data and 100% training data, respectively. It can be observed that the output curves acquired by data prediction-based GNN-WCA are extremely consistent with actual data, which proves its strong performance for PV modeling.

FIGURE 8

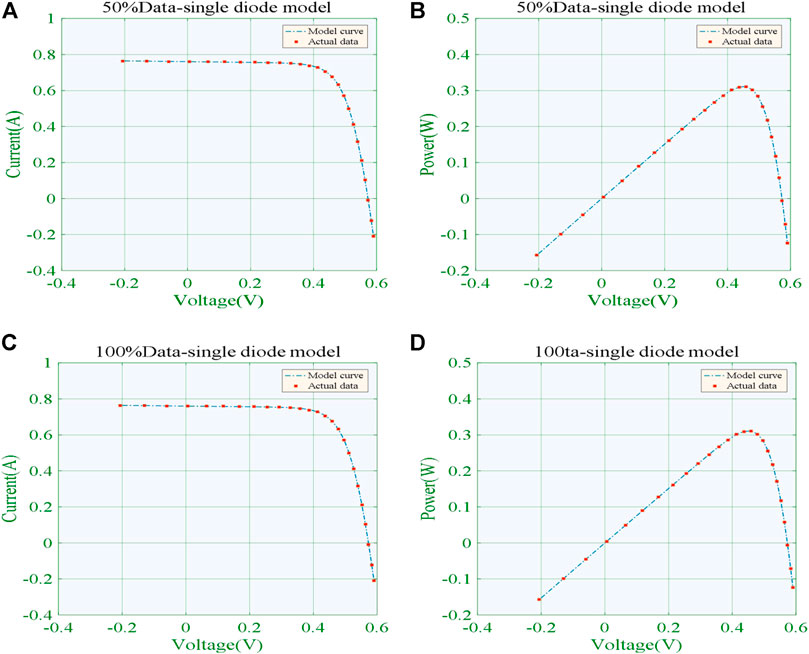
FIGURE 8. Output curves obtained by the best algorithm (GNN-WCA) for the SDM. (A)I-V curve under 50% training data; (B)P-V curve under 50% training data; (C)I-V curve under 100% training data; (D)P-V curve under 100% training data.

Results of the Double Diode Model

For the DDM, the average RMSE achieved via seven different algorithms with different measured datasets in 80 runs is illustrated in Table 2, which indicates that increased prediction data generated by the GNN can effectively improve calculation accuracy and stability. For example, average RMSE obtained by GNN-BSA is 52.37% lower than the BSA without GNN-based data prediction under 50% measured data. This illustrates that a GNN-based meta-algorithm can simultaneously realize high estimation precision and strong stability, thus it can output desirable results when both accuracy and reliability are considered in the DDM.

TABLE 2

TABLE 2. Statistical results of average RMSE for the DDM.

Moreover, Figure 9 shows the convergence of all algorithms under different training data without a GNN and with a GNN, which illustrates that convergence speed of GWO is low and the ABC is prone to a local optimum under 50% training data without a GNN. In contrast, the GNN can effectively increase its optimum searching efficiency and quality with a higher convergence stability. Besides, a large amount of extending data samples can effectively improve the searching efficiency of global optimum.

FIGURE 9

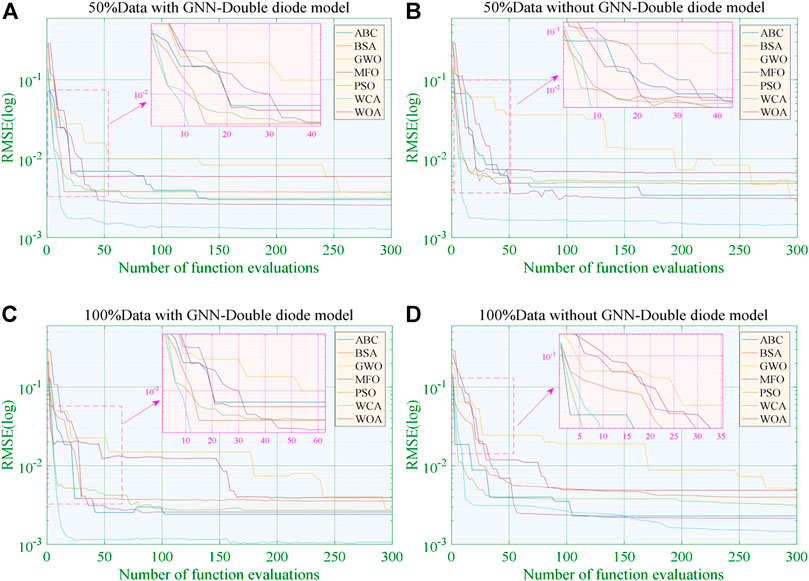
FIGURE 9. Convergence of various algorithms for the DDM. (A) With the GNN under 50% data; (B) without the GNN under 50% data; (A) with the GNN under 100% data; (B) without the GNN under 100% data.

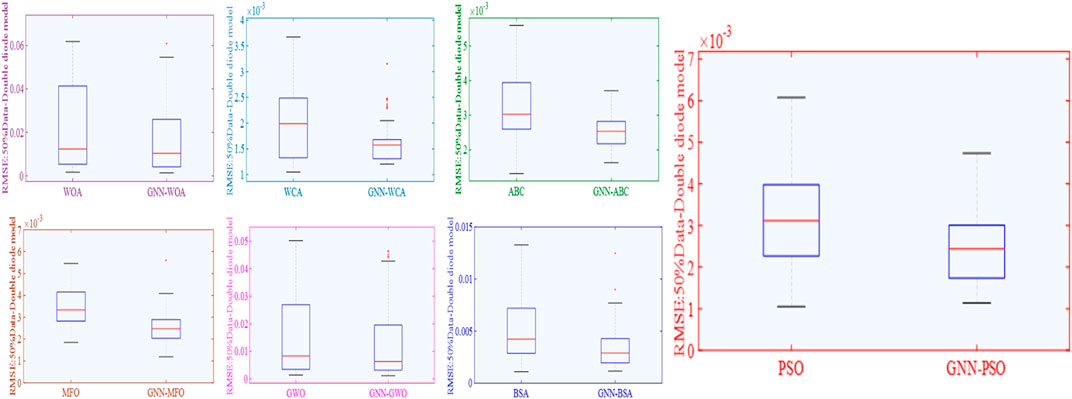
Boxplots of different algorithms under 50% data are depicted in Figure 10, upon which one can easily find that all GNN-based meta-heuristic algorithms have a smaller distribution range and upper/lower bounds in comparison to that without the GNN. Obviously, each algorithm can search for the highest quality solution more easily when experimental data are expanded by GNN-based data prediction, upon which optimal values of these unknown parameters can be determined in a more accurate and stable way. This indicates that the increase of data is able to effectively improve optimization quality and stabilize global searching ability in PV cell parameter estimation.

FIGURE 10

FIGURE 10. Boxplot of RMSE under different data for the DDM under 50% data.

Figure 11 depicts the output curves of the best data prediction-based meta-heuristic algorithm (GNN-WCA) and actual data under 50% and 100% training data, respectively. Apparently, the WCA shows the high fitting accuracy with actual data under both different training datasets.

FIGURE 11

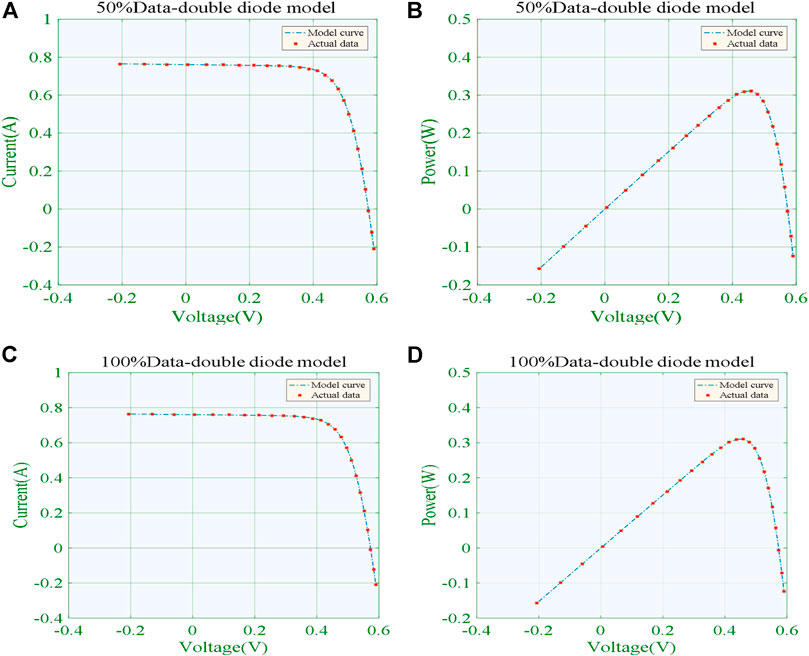
FIGURE 11. Output curves obtained by the best algorithm (GNN-WCA) for the DDM. (A)I-V curve under 50% training data; (B)P-V curve under 50% training data; (C)I-V curve under 100% training data; (D)P-V curve under 100% training data.

Statistical Results and Analysis

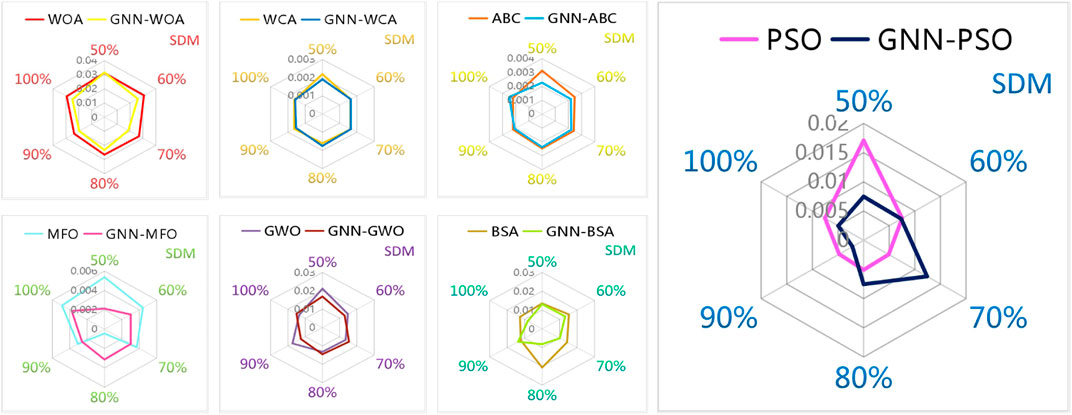
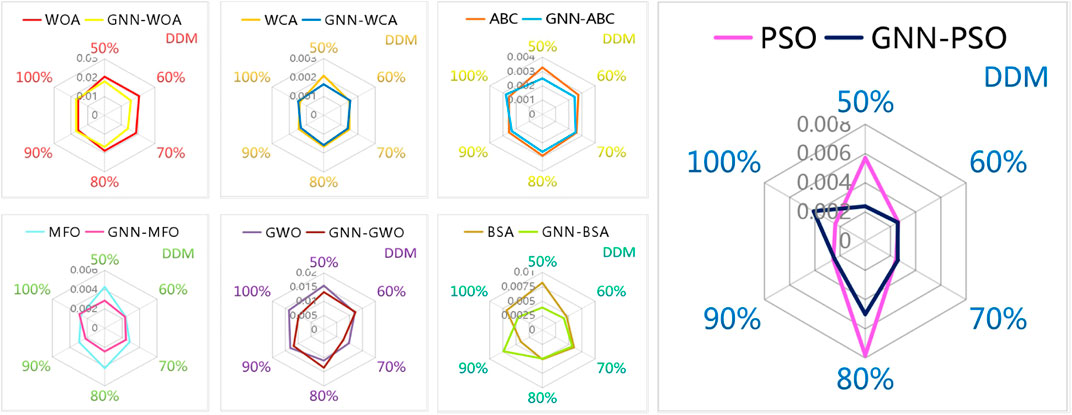
Radars of average RMSE achieved via each meta-heuristic algorithm with six groups of data at different scales are provided in Figures 12, 13, which show that average RMSE acquired via all algorithms with GNN-based data prediction are smaller compared with that obtained without data prediction at different scales of data, especially under 50% data. In particular, the ranking basis of various methods is based on a comprehensive and systematic comparison of their performance in PV cell parameter extraction, e.g., extraction accuracy, convergence speed, and convergence stability. This effectively verifies the outstanding reliability of GNN-based meta-heuristic algorithms for accurate PV cell modeling.

FIGURE 12

FIGURE 12. Radars of average RMSE achieved by different algorithms for the SDM.

FIGURE 13

FIGURE 13. Radar of average RMSE achieved by different algorithms for the DDM.

Conclusion

This paper develops a novel hybrid of a GNN and advanced meta-heuristic algorithms for accurate modeling of different solar cells, and its main contributions are as follows:

• A GNN is applied to generate more virtual I-V data based on inadequate measured data, in which a GA is adopted to find optimal network parameters of an ANN, which can improve the accuracy of generated virtual I-V data. As a result, the GNN can significantly enrich the dataset, and provide a more reliable fitness function to the meta-heuristic algorithms for PV cell modeling;

• Two widely used PV cell models, i.e., the SDM and DDM, are adopted to verify the practical performance of the proposed strategy. For instance, the average RMSE obtained by the ABC, BSA, GWO, MFO, PSO, WCA, and WOA based on GNN prediction for the SDM is 72.29, 97.04, 79.72, 39.48, 43.74, 86.82, 100.96% to that of without GNN data prediction under 50% measured data, respectively;

• Case studies show that GNN-based meta-heuristic algorithms can comprehensively enhance optimization precision and convergence stability compared with original meta-heuristic algorithms utilizing untrained measured I-V data.

Future studies should focus on the improvement and optimization of the structure of the proposed GNN, e.g., data training process and relevant network parameters tuning can be further simplified to reduce the optimization burden. Besides, as all the experiments were carried out in a simulation environment which is different from real operation conditions, experiments combined with hardware platforms under practical working scenarios are imperative for future engineering applications.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

LW: Conceptualization, Writing-Original Draft, Formal analysis; ZC: Project administration, Supervision, Writing-Review and Editing; YG: Visualization, Validation; WH: Data Curation, Visualization; XC: Formal analysis, Software; PW: Investigation, Validation; CH: Writing-Reviewing and Editing, Methodology; JL: Software, Data Curation.

Conflict of Interest

Authors ZC, YG, WH, CH were employed by company Xuchang KETOP Testing Research Institute Co. Ltd. Author JL was employed by company XJ Group Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors gratefully acknowledge the support of the Key Technologies R and D Program of Henan Province (192102210306, 202102210335, 212102210254, 212102210026) and the Henan Province Science and Technology Enterprise Cultivation (Science and Technology Little Giant) Special Fund Project (KPJJ-201701).

References

Abbassi, R., Abbassi, A., Jemli, M., and Chebbi, S. (2018). Identification of Unknown Parameters of Solar Cell Models: A Comprehensive Overview of Available Approaches. Renew. Sustainable Energ. Rev. 90, 453–474. doi:10.1016/j.rser.2018.03.011

CrossRef Full Text | Google Scholar

Allam, D., Yousri, D. A., and Eteiba, M. B. (2016). Parameters Extraction of the Three Diode Model for the Multi-Crystalline Solar Cell/module Using Moth-Flame Optimization Algorithm. Energ. Convers. Management. 123, 535–548. doi:10.1016/j.enconman.2016.06.052

CrossRef Full Text | Google Scholar

Awadallah, M. A. (2016). Variations of the Bacterial Foraging Algorithm for the Extraction of PV Module Parameters from Nameplate Data. Energ. Convers. Management. 113, 312–320. doi:10.1016/j.enconman.2016.01.071

CrossRef Full Text | Google Scholar

Chang, K. Y. (2011). The Optimal Design for PEMFC Modeling Based on Taguchi Method and Genetic Algorithm Neural Networks. Int. J. Hydrogen Energ. 36 (21), 13683–13694. doi:10.1016/j.ijhydene.2011.07.094

CrossRef Full Text | Google Scholar

Chin, V. J., Salam, Z., and Ishaque, K. (2015). Cell Modelling and Model Parameters Estimation Techniques for Photovoltaic Simulator Application: A Review. Appl. Energ. 154, 500–519. doi:10.1016/j.apenergy.2015.05.035

CrossRef Full Text | Google Scholar

Fathy, A., and Rezk, H. (2017). Parameter Estimation of Photovoltaic System Using Imperialist Competitive Algorithm. Renew. Energ. 111, 307–320. doi:10.1016/j.renene.2017.04.014

CrossRef Full Text | Google Scholar

Figueroa, O. R., Castellanos, M. Q., Montes, E. M., and Schütze, O. (2020). Metaheuristics to Solve Grouping Problems: A Review and a Case Study. Swarm Evol. Comput. 53, 100643. doi:10.1016/j.swevo.2019.100643

CrossRef Full Text | Google Scholar

Gao, S. C., Wang, K. Y., Tao, S. C., Jin, T., Dai, H. W., and Cheng, J. J. (2021). A State-Of-The-Art Differential Evolution Algorithm for Parameter Estimation of Solar Photovoltaic Models. Energ. Convers. Management 230, 113784. doi:10.1016/j.enconman.2020.113784

CrossRef Full Text | Google Scholar

Gao, X., Cui, Y., Hu, J., Xu, G., and Yu, Y. (2016). Lambert W-Function Based Exact Representation for Double Diode Model of Solar Cells: Comparison on Fitness and Parameter Extraction. Energ. Convers. Management. 127, 443–460. doi:10.1016/j.enconman.2016.09.005

CrossRef Full Text | Google Scholar

Guchhait, P. K., and Banerjee, A. (2020). Stability Enhancement of Wind Energy Integrated Hybrid System with the Help of Static Synchronous Compensator and Symbiosis Organisms Search Algorithm. Prot. Control. Mod. Power Syst. 5 (2), 138–150. doi:10.1186/s41601-020-00158-8

CrossRef Full Text | Google Scholar

He, X., Chu, L., Qiu, R. C., Ai, Q., Ling, Z., and Zhang, J. (2020). Invisible Units Detection and Estimation Based on Random Matrix Theory. IEEE Trans. Power Syst. 35 (3), 1846–1855. doi:10.1109/tpwrs.2019.2935739

CrossRef Full Text | Google Scholar

Huang, Z., Fang, B. L., and Deng, J. (2020). Multi-objective Optimization Strategy for Distribution Network Considering V2G Enabled Electric Vehicles in Building Integrated Energy System. Prot. Control. Mod. Power Syst. 5 (5), 48–55. doi:10.1186/s41601-020-0154-0

CrossRef Full Text | Google Scholar

Humada, A. M., Hojabri, M., Mekhilef, S., and Hamada, H. M. (2016). Solar Cell Parameters Extraction Based on Single and Double-Diode Models: A Review. Renew. Sustainable Energ. Rev. 56, 494–509. doi:10.1016/j.rser.2015.11.051

CrossRef Full Text | Google Scholar

Ishaque, K., and Salam, Z. (2011). An Improved Modeling Method to Determine the Model Parameters of Photovoltaic (PV) Modules Using Differential Evolution (DE). Solar Energy 85 (9), 2349–2359. doi:10.1016/j.solener.2011.06.025

CrossRef Full Text | Google Scholar

Ishaque, K., Salam, Z., Taheri, H., and Shamsudin, A. (2011). A Critical Evaluation of EA Computational Methods for Photovoltaic Cell Parameter Extraction Based on Two Diode Model. Solar Energy. 85 (9), 1768–1779. doi:10.1016/j.solener.2011.04.015

CrossRef Full Text | Google Scholar

Jervase, J. A., Bourdoucen, H., and Al-lawati, A. M. (2001). Solar Cell Parameter Extraction Using Genetic Algorithms. Meas. Sci. Technology 12, 1922–1925. doi:10.1088/0957-0233/12/11/322

CrossRef Full Text | Google Scholar

Jordehi, A. R. (2016). Parameter Estimation of Solar Photovoltaic (PV) Cells: a Review. Renew. Sustainable Energ. Rev. 61, 354–371. doi:10.1016/j.rser.2016.03.049

CrossRef Full Text | Google Scholar

Khani, M. S., Baneshi, M., and Eslami, M. (2019). Bi-objective Optimization of Photovoltaic-thermal (PV/T) Solar Collectors According to Various Weather Conditions Using Genetic Algorithm: A Numerical Modeling. Energy. 185, 116223. doi:10.1016/j.energy.2019.116223

CrossRef Full Text | Google Scholar

Khanna, V., Das, B. K., Bisht, D., Vandana, , and Singh, P. K. (2015). A Three Diode Model for Industrial Solar Cells and Estimation of Solar Cell Parameters Using PSO Algorithm. Renew. Energ. 78, 105–113. doi:10.1016/j.renene.2014.12.072

CrossRef Full Text | Google Scholar

Kler, D., Sharma, P., Banerjee, A., Rana, K. P. S., and Kumar, V. (2017). PV Cell and Module Efficient Parameters Estimation Using Evaporation Rate Based Water Cycle Algorithm. Swarm Evol. Comput. 35, 93–110. doi:10.1016/j.swevo.2017.02.005

CrossRef Full Text | Google Scholar

Liu, J., Yao, W., Wen, J. Y., Fang, J. K., Jiang, L., He, H. B., et al. (2020). Impact of Power Grid Strength and PLL Parameters on Stability of Grid-Connected DFIG Wind Farm. IEEE Trans. Sustainable Energ. 11 (1), 545–557. doi:10.1109/tste.2019.2897596

CrossRef Full Text | Google Scholar

Liu, K. L., Hu, X. S., Zhou, H. Y., Tong, L., Widanalage, D., and Marco, J. (2021). Feature Analyses and Modelling of Lithium-Ion Batteries Manufacturing Based on Random forest Classification. IEEE/ASME Trans. Mechatronics, 1. doi:10.1109/TMECH.2020.3049046

CrossRef Full Text | Google Scholar

Mittal, M., Bora, B., Saxena, S., and Gaur, A. M. (2018). Performance Prediction of PV Module Using Electrical Equivalent Model and Artificial Neural Network. Solar Energy. 176, 104–117. doi:10.1016/j.solener.2018.10.018

CrossRef Full Text | Google Scholar

Murty, V. V. S. N., and Kumar, A. (2020). Multi-objective Energy Management in Microgrids with Hybrid Energy Sources and Battery Energy Storage Systems. Prot. Control. Mod. Power Syst. 5 (1), 1–20. doi:10.1186/s41601-019-0147-z

CrossRef Full Text | Google Scholar

Nayak, B., Mohapatra, A., and Mohanty, K. B. (2019). Parameter Estimation of Single Diode PV Module Based on GWO Algorithm. Renew. Energ. Focus 30, 1–12. doi:10.1016/j.ref.2019.04.003

CrossRef Full Text | Google Scholar

Nesmachnow, S. (2014). An Overview of Metaheuristics: Accurate and Efficient Methods for Optimization. Int. J. Metaheuristics 3 (4), 320–347. doi:10.1504/ijmheur.2014.068914

CrossRef Full Text | Google Scholar

Noriega, J. R., and Wang, H. (1998). A Direct Adaptive Neural-Network Control for Unknown Nonlinear Systems and its Application. IEEE Trans. Neural Networks 9 (1), 27–34. doi:10.1109/72.655026

CrossRef Full Text | Google Scholar

Oliva, D., Cuevas, E., and Pajares, G. (2014). Parameter Identification of Solar Cells Using Artificial Bee colony Optimization. Eenergy 72, 93–102. doi:10.1016/j.energy.2014.05.011

CrossRef Full Text | Google Scholar

Peng, X. T., Yao, W., Yan, C., Wen, J. Y., and Cheng, S. J. (2020). Two-stage Variable Proportion Coefficient Based Frequency Support of Grid-Connected DFIG-WTs. IEEE Trans. Power Syst. 35 (2), 962–974. doi:10.1109/tpwrs.2019.2943520

CrossRef Full Text | Google Scholar

Pillai, D. S., and Rajasekar, N. (2018). Metaheuristic Algorithms for PV Parameter Identification: A Comprehensive Review with an Application to Threshold Setting for Fault Detection in PV Systems. Renew. Sustainable Energ. Rev. 82 (3), 3503–3525. doi:10.1016/j.rser.2017.10.107

CrossRef Full Text | Google Scholar

Qais, M. H., Hasanien, H. M., Alghuwainem, S., and Nouh, A. S. (2019a). Coyote Optimization Algorithm for Parameters Extraction of Three-Diode Photovoltaic Models of Photovoltaic Modules. Energy 187, 116001. doi:10.1016/j.energy.2019.116001

CrossRef Full Text | Google Scholar

Qais, M. H., Hasanien, H. M., and Alghuwainem, S. (2019b). Identification of Electrical Parameters for Three-Diode Photovoltaic Model Using Analytical and sunflower Optimization Algorithm. Appl. Energ. 250, 109–117. doi:10.1016/j.apenergy.2019.05.013

CrossRef Full Text | Google Scholar

Ram, J. P., Manghani, H., Pillai, D. S., Babu, T. S., Miyatake, M., and Rajasekara, N. (2018). Analysis on Solar PV Emulators: A Review. Renew. Sustainable Energ. Rev. 81, 149–160. doi:10.1016/j.rser.2017.07.039

CrossRef Full Text | Google Scholar

Rodriguez, J. D. B., Petrone, G., Paja, A. R., and Spagnuolo, G. (2017). A Genetic Algorithm for Identifying the Single Diode Model Parameters of a Photovoltaic Panel. Mathematics Comput. Simulation. 134, 38–54. doi:10.1016/j.matcom.2015.10.008

CrossRef Full Text | Google Scholar

Roeva, O., and Fidanova, S. (2018). Comparison of Different Metaheuristic Algorithms Based on Intercriteria Analysis. J. Comput. Appl. Mathematics. 340, 615–628. doi:10.1016/j.cam.2017.07.028

CrossRef Full Text | Google Scholar

Shangguan, X. C., He, Y., Zhang, C. K., Jiang, L., Spencer, J., and Wu, M. (2020a). Robust Load Frequency Control for Power System Considering Transmission Delay and Sampling Period. IEEE Trans. Ind. Inform. 17, 1. doi:10.1109/TII.2020.3026336

CrossRef Full Text | Google Scholar

Shangguan, X. C., He, Y., Zhang, C. K., Jin, L., Yao, W., Jiang, L., et al. (2020b). Control Performance Standards Oriented Event-Triggered Load Frequency Control for Power Systems under Limited Communication Bandwidth. IEEE Trans. Control. Syst. Technology., 1. doi:10.1109/TCST.2021.3070861

CrossRef Full Text | Google Scholar

Soloway, D., and Haley, P. J. (1996). Neural Generalized Predictive Control. Proc. 1996 IEEE Int. Symp. Intell. Control. 277-282. doi:10.1109/ISIC.1996.556214

CrossRef Full Text | Google Scholar

Song, D. R., Chang, Q., Zheng, S. Y., Yang, S., Yang, J., and Joo, Y. H. (2021). Adaptive Model Predictive Control for Yaw System of Variable-Speed Wind Turbines. J. Mod. Power Syst. Clean Energ. 9 (1), 219–224. doi:10.35833/mpce.2019.000467

CrossRef Full Text | Google Scholar

Song, Y., Chen, Z. Q., and Yuan, Z. Z. (2007). New Chaotic PSO-Based Neural Network Predictive Control for Nonlinear Process. IEEE Trans. Neural Networks. 18 (2), 595–601. doi:10.1109/tnn.2006.890809

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, K., Yao, W., Fang, J. K., Ai, X. M., Wen, J. Y., and Cheng, S. J. (2019). Impedance Modeling and Stability Analysis of Grid-Connected DFIG-Based Wind Farm with a VSC-HVDC. IEEE J. Emerging Selected Top. Power Electronics. 8, 1375-1390. doi:10.1109/JESTPE.2019.2901747

CrossRef Full Text | Google Scholar

Sun, L. M., and Yang, B. (2020). Nonlinear Robust Fractional-Order Control of Battery/SMES Hybrid Energy Storage Systems. Power Syst. Prot. Control. 48 (22), 76–83.

Google Scholar

Torabi, K. E., Eddine, I. A., Obbadi, A., Errami, A., Rmaily, R., Sahnoun, S., et al. (2017). Parameters Estimation of the Single and Double Diode Photovoltaic Models Using a Gauss-Seidel Algorithm and Analytical Method: A Comparative Study. Energ. Convers. Management 148, 1041–1054. doi:10.1016/j.enconman.2017.06.064

CrossRef Full Text | Google Scholar

Villalva, M. G., Gazoli, J. R., and Filho, E. R. (2009). Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Trans. Power Electronics. 24, 1198–1208. doi:10.1109/tpel.2009.2013862

CrossRef Full Text | Google Scholar

Wolf, P., and Benda, V. (2013). Identification of PV Solar Cells and Modules Parameters by Combining Statistical and Analytical Methods. Solar Energy. 93, 151–157. doi:10.1016/j.solener.2013.03.018

CrossRef Full Text | Google Scholar

Xiong, G. J., Zhang, J., Shi, D. Y., and He, Y. (2018). Parameter Extraction of Solar Photovoltaic Models Using an Improved Whale Optimization Algorithm. Energ. Convers. Management. 174, 388–405. doi:10.1016/j.enconman.2018.08.053

CrossRef Full Text | Google Scholar

Yang, B., Jiang, L., Yao, W., and Wu, Q. H. (2015). Perturbation Estimation Based Coordinated Adaptive Passive Control for Multimachine Power Systems. Control. Eng. Pract. 44, 172–192. doi:10.1016/j.conengprac.2015.07.012

CrossRef Full Text | Google Scholar

Yang, B., Wang, J. B., Zhang, X. S., Yu, T., Yao, W., Shu, H. C., et al. (2020). Comprehensive Overview of Meta-Heuristic Algorithm Applications on PV Cell Parameter Identification. Energ. Convers. Management. 208, 112595. doi:10.1016/j.enconman.2020.112595

CrossRef Full Text | Google Scholar

Yang, J., Fang, L. Q., Song, D. R., Su, M., Yang, X. B., Huang, L. X., et al. (2021). Review of Control Strategy of Large Horizontal-axis Wind Turbines Yaw System. Wind Energy, 24 (2), 97–115. doi:10.1002/we.2564

CrossRef Full Text | Google Scholar

Ye, M. Y., Wang, X. D., and Xu, Y. S. (2009). Parameter Extraction of Solar Cells Using Particle Swarm Optimization. J. Appl. Phys. 105 (9), 094502. doi:10.1063/1.3122082

CrossRef Full Text | Google Scholar

Yu, K. J., Liang, J. J., Qu, B. Y., Cheng, Z. P., and Wang, H. S. (2018). Multiple Learning Backtracking Search Algorithm for Estimating Parameters of Photovoltaic Models. Appl. Energ. 226, 408–422. doi:10.1016/j.apenergy.2018.06.010

CrossRef Full Text | Google Scholar

Zhang, H. X., Lu, Z. X., Hu, W., Wang, Y. T., Dong, L., and Zhang, J. T. (2019). Coordinated Optimal Operation of Hydro-Wind-Solar Integrated Systems. Appl. Energ. 242, 883–896. doi:10.1016/j.apenergy.2019.03.064

CrossRef Full Text | Google Scholar

Zhang, X. S., Li, S. N., He, T. Y., Yang, B., Yu, T., Li, H. F., et al. (2019). Memetic Reinforcement Learning Based Maximum Power point Tracking Design for PV Systems under Partial Shading Condition. Energy. 174, 1079–1090. doi:10.1016/j.energy.2019.03.053

CrossRef Full Text | Google Scholar

Zhou, Y. H., Romijnders, R., Romijnders, C., Campen, J., Maetzler, W., Hortobágyi, T., et al. (2020). The Detection of Age Groups by Dynamic Gait Outcomes Using Machine Learning Approaches. Scientific Rep. 10, 4426. doi:10.1038/s41598-020-61423-2

CrossRef Full Text | Google Scholar

Abbreviations

$I_{ph}$, photocurrent, A; $I_d$,$I_{d1}$,$I_{d2}$, diode’s currents, A; $I_{sd}$,$I_{sd1}$,$I_{sd2}$,$I_{sd3}$, diode’s reverse saturation currents, A; $R_s$, series resistor, Ω; $R_{sh}$, shunt resistor, Ω; $a$,$a_1$,$a_2$,$a_3$, diode’s ideality factors. ABC, artificial bee colony; ANN, artificial neural network; BFA, bacterial foraging algorithm; BSA, backtracking search algorithm; DDM, double diode model; DE, differential evolution; GA, genetic algorithm; GNN, genetic neural network; GWO, gray wolf optimization; I-V, current-voltage; MFO, month flame optimizer; PSO, particle swarm optimization; P-V, power-voltage; SDM, single diode model; STC, standard test condition; SSA, salp swarm algorithm.