Optimal Array Reconfiguration of a PV Power Plant for Frequency Regulation of Power Systems

This paper establishes a novel optimal array reconfiguration (OAR) of a PV power plant for secondary frequency control of automatic generation control (AGC). Compared with the existing studies, the proposed OAR can further take the AGC signal responding into account except the maximum power output, in which the battery energy storage system is used to balance the power deviation between the AGC signals and the PV power outputs. Based on these two conflicted objects, the OAR is formulated as a bi-objective optimization. To address this problem, the efficient non-dominated sorting genetic algorithm II (NSGA-II) is designed to rapidly obtain an optimal Pareto front due to its high optimization efficiency. The decision-making method called VIKOR is employed to determine the best compromise solution from the obtained Pareto front. To verify the effectiveness of the proposed bi-objective optimization of OAR, three case studies with fixed, step-increasing, and step-decreasing AGC signals are carried out on a 10 × 10 total-cross-tied PV arrays under partial shading conditions.

Introduction

Recently, renewable energies are becoming increasingly welcomed and are gradually replacing most fossil fuels due to their inexhaustibility and eco-friendly nature. One of the most promising of these energies is solar energy (Sahu, 2015) since it can result in zero noise, less maintenance, and ready availability of source with abundant availability. However, the solar photovoltaic (PV) array faces some major challenges on dynamic environmental conditions, including insolation (Yousri et al., 2020a), temperature gradient and partial shading, etc. Among the parameters listed above, partial shading leads to a significant reduction in the PV array’s energy output due to mismatch loss and power loss. The main reason for partial shading is cloud coverage, building shadows, and dropping dust (Koad et al., 2017).

Various PV array topologies like series-parallel (SP), total-cross-tied (TCT), and bridge linked (BL) have been designed to reduce the mismatch and power loss to address this issue (Fathy, 2020). It is verified that the power generated in TCT topology is the highest among the above topologies under partial shading conditions (PSC) (Winston et al., 2020). Three basic techniques for the reconfiguration process of the PV array, including physical relocation (Venkateswari and Rajasekar, 2020), electrical array reconfiguration (EAR) (Dhanalakshmi and Rajasekar, 2018), and electrical rewiring (Rao et al., 2014), were proposed based on the TCT topology. These techniques aimed to mitigate the mismatch loss via shade dispersion over the whole array.

In addition, the reconfiguration can be roughly divided into static (fixed) reconfiguration and dynamic reconfiguration according to whether the electrical interconnection changes after the array rearrangement. In the static reconfiguration group, the physical positions of all the modules are fixed under all shading conditions, which means that the electrical interconnection remains unchanged after array rearrangement, also known as one-time rearrangement (Potnuru et al, 2015). Various static reconfiguration utilized electrical rewiring techniques to improve the power output under PSC, including fixed electrical reconfiguration (Satpathy and Sharma, 2019), column index method (Pillai and Ram, 2018), unique connection method (Pareek and Dahiya, 2016), and Sudoku (Horoufiany and Ghandehari, 2018). Compared with the other three reconfigurations, Su Do Ku is found as one of the most effective ways to relocate PV modules (Rani et al., 2013), which was also proposed to reduce line losses (Potnuru et al., 2015) and to mitigate the mutual shadow (MSH) (Horoufiany and Ghandehari, 2018). In addition to electrical rewiring, many physical relocation techniques, such as Magic-square (MS) puzzle reconfiguration (Yadav et al., 2017), fixed electrical connection (PRM-FEC) (Sahu and Nayak, 2016), odd-even configuration (OEC) (Nasiruddin et al., 2019), were proposed to relocate modules without changing the electrical connection. It has been proved that physical migration based on MS reconstruction can avoid complex MPPT algorithms and provide superior performance (Horoufiany and Ghandehari, 2018; Rakesh and Madhavaram, 2016; Samikannu et al, 2016). On the other hand, OEC performed well compared with the other two technologies under the diagonal processing shadowing scenario (Yadav and Kumar, 2020). Unlike static reconfiguration, dynamic reconfiguration changes the electrical interconnection through a switching arrangement once the shade varies, which does not require massive labor and complex applications (Babu et al., 2018). Based on EAR technology, quite a few meta-heuristic algorithms have become novel techniques in recent years, including particle swarm optimization (PSO) (Babu et al., 2018), grasshopper optimization algorithm (GOA) (Fathy, 2018), multi-objective grey wolf algorithm (MOGWO) (Yousri et al., 2020d), standard genetic algorithm (SDGA) (Rajan et al., 2017), Marine predators algorithm (MPA) (Yousri et al., 2020b), artificial ecosystem-based optimization (AEO) (Yousri et al., 2020c), flow regime algorithm (FRA) (Babu et al., 2020), social mimic optimization algorithm (SMO) (Babu et al., 2020), Rao optimization (Babu et al., 2020).

Nevertheless, the existing studies of PV array reconfiguration did not consider the power response for automatic generation control (AGC) (Xi et al., 2018), while the battery energy storage system (BESS) (Jin et al., 2017) was not taken for the power fluctuation balance. Consequently, this paper establishes a novel optimal array reconfiguration (OAR) of a PV power plant with a BESS for AGC, which not only attempts to maximize the power output, but also aims to minimize the power deviation between the power outputs and the AGC signals. To solve OAR, the meta-heuristic based multi-objective optimization algorithms are suitable to find a high-quality Pareto front due to their flexible application and strong global searching ability. Hence, this work adopts the efficient non-dominated sorting genetic algorithm II (NSGA-II) for OAR, while a decision-making method called VIKOR is employed to determine the best compromise solution from the obtained Pareto front.

The remaining sections are organized as follows: The mathematical model of OAR is given in Mathematical Model of Optimal Array Reconfiguration Section. The solving process of NSGA-II and VIKOR for OAR is provided in Design of NSGA-II and VIKOR for Optimal Array Reconfiguration Section. Case Studies Section shows the simulation results. At last, the conclusion is given in Conclusion Section.

Mathematical Model of Optimal Array Reconfiguration

Model of PV Array

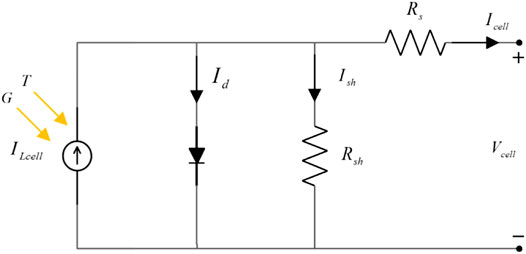
The PV array can be formed by multiple PV modules in series and parallel, usually consisting of numerous series-parallel PV cells. For simplicity, the PV cells can be seen as a current generator. Figure 1 shows the single-diode model (Rajasekar et al., 2013), which is a frequently used model, like the double diode model and triple diode model. Applying Kirchhoff’s current law (KCL), the output current of a PV cell can be calculated by (Krishna and Moger, 2019):

$I_{\text{cell}}=I_{\text{Lcell}}-I_{\text{d}}-I_{\text{sh}}(1)$

where $I_{\text{cell}}$ is the output current of the PV cell; $I_{\text{Lcell}}$ is the light generated current of the PV cell; $I_{\text{d}}$ is the diode current; and $I_{\text{sh}}$ is the current of the shunt resistance.

FIGURE 1

FIGURE 1. Equivalent circuit of a single-diode based PV cell.

Further the PV cell’s output current can be expressed as Eq. 2 by expanding $I_{\text{d}}$ and $I_{\text{sh}}$ in Eq. 1:

$I_{\text{cell}}=I_{\text{Lcell}}-I_{\text{o}}\left[exp\left(q\frac{V_{\text{cell}}+I_{\text{cell}}{R}_{\text{s}}}{b\sigma T_{\text{c}}}-1\right)\right]-\frac{V_{\text{cell}}+I_{\text{cell}}{R}_{\text{s}}}{R_{\text{sh}}}(2)$

where $I_o$, $q$, $V_{cell}$, $T_c$, $\sigma$, $b$, $R_s$, and $R_{sh}$ are the diode’s saturation current, electron charge, PV cell’s output voltage, operating temperature, ideality factor, Boltzmann’s constant, PV cell’s series and shunt resistance, respectively.

For a $n_{\text{s}}$ series connected PV cells constructed PV module, its output current can be given as:

$I_{\text{m}}=I_{\text{L}}-I_{\text{o}}\left[\exp \left(q\frac{V_{\text{m}}+I_{\text{m}}{R}_{\text{S}}}{n_{\text{s}}b\sigma T_{\text{c}}}-1\right)\right]-\frac{V_{\text{m}}+I_{\text{m}}{R}_{\text{S}}}{R_{\text{SH}}}(3)$

where $I_{\text{m}}$ is the output current of the PV module; q is the electron charge; $V_{\text{m}}$ is output voltage of the PV module; $R_{\text{S}}$ and $R_{\text{SH}}$ are the series and shunt resistance of the PV module, respectively; and $I_{\text{L}}$ is the light generated current of the PV module, which can be acquired as

$I_{\text{L}}=\frac{G}{G_0}\left[I_{\text{Lstc}}+K_{\text{sc}}\left(T_{\text{c}}-T_0\right)\right](4)$

where the actual and standard irradiation values are represented by G and G₀, respectively; $I_{\text{Lstc}}$ is the light generated current of the PV module under the standard test condition; $K_{\text{sc}}$ is the short-circuit current coefficient factor; and $T_0$ is the standard values of the operating temperature.

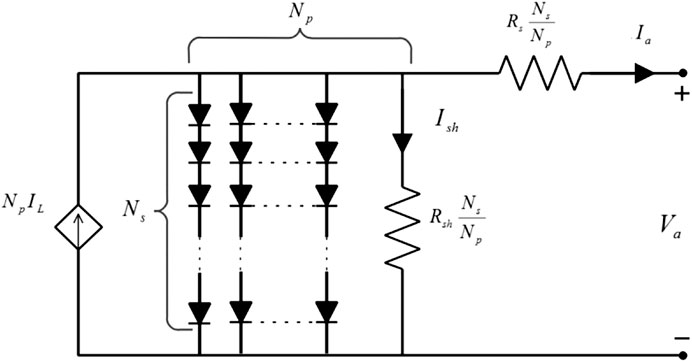
Applying Eq. 3, the output current equations for a PV array consisting of N_s × N_p modules, as shown in Figure 2, can then be rewritten in Eq. 5 as (Krishna and Moger, 2019):

$I_{\text{a}}=N_{\text{p}}{I}_{\text{L}}-N_{\text{p}}{I}_{\text{o}}\left[exp\left(q\frac{V_{\text{a}}+\frac{N_{\text{s}}}{N_{\text{p}}}{I}_{\text{a}}{R}_{\text{S}}}{N_{\text{s}}{n}_{\text{s}}b\sigma T_{\text{c}}}-1\right)\right]-\frac{V_{\text{a}}+\frac{N_{\text{s}}}{N_{\text{p}}}{I}_{\text{a}}{R}_{\text{S}}}{\frac{N_{\text{s}}}{N_{\text{p}}}{R}_{\text{SH}}}(5)$

where $I_{\text{a}}$ and $V_{\text{a}}$ denote output current and output voltage of the PV array, respectively.

FIGURE 2

FIGURE 2. Equivalent circuit of a PV array with N_s × N_p modules.

Total-Cross-Tied Connected Arrays in a PV Power Plant

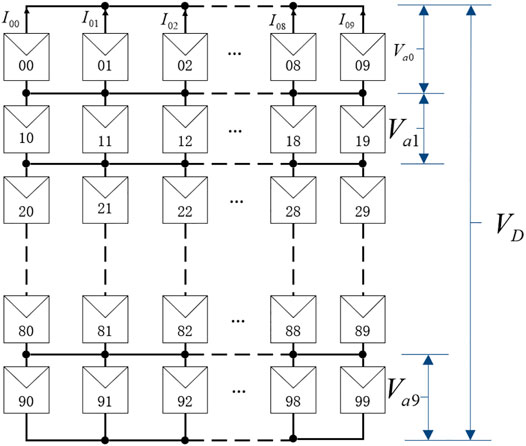
Among conventional PV array topologies, TCT topology has been proved that the power generated is highest under PSC. It’s clearly seen from Figure 3 that the TCT interconnection scheme shows a 10 × 10 PV array’s electrical connection where all the rows are connected in series connection, giving rise to 10 such series strings in parallel at each row.

FIGURE 3

FIGURE 3. 10 × 10 TCT connected arrays in a PV power plant.

Calculating the total output voltage and current of TCT connected PV arrays is of utmost importance. According to the circuit characteristics of TCT topology, the current of each column via PV array, which is in series connection, are equal. And the voltage of each row is also identical as each row via PV array is parallel. Applying Kirchhoff's voltage law (KVL) and KCL, we can get the overall PV power plant output voltage and current calculated as (Babu et al., 2018):

$V_{\text{D}}={\displaystyle \sum }_{p=0}^9{V}_{\text{a}p}(6)$

$I_{\text{D}}={\displaystyle \sum }_{q=0}^9\left(I_{pq}-I_{\left(p+1\right)q}\right)=0,p=\mathrm{0,1,2},\dots ,8(7)$

where $V_{\text{D}}$ is the overall output voltage, $V_{\text{a}p}$ is the maximum voltage at the pth row, I_D is the overall output current, $I_{pq}$ denotes the output current of the array at the pth row and the qth column.

Objective Function

In this work, two conflicted objectives are simultaneously considered, which aims to improve the generation benefit for the PV power plant while helping to balance the power disturbance for the power systems (Xi et al., 2018). The first objective is the maximization of power output for the PV power plant. It can be converted into a minimization of power deviation f₁ between the rated power output and the average power output. The second objective f₂ is the minimization of power deviation between the AGC signals and the power outputs, while the peak-valley difference of the power outputs is also taken into account. As a result, these two objectives can be calculated as follows:

$\{\begin{array}{c}\min f_1=P_{\text{pv}}^{\text{rate}}-\frac{1}{T}{\displaystyle \sum }_{t\in T}{P}_{\text{pv}}\left(t\right)\\ \min f_2=\frac{1}{T}{\displaystyle \sum }_{t\in T}\left|P_{\text{agc}}\left(t\right)-\left[P_{\text{pv}}\left(t\right)-P_{\text{bess}}\left(t\right)\right]\right|+\underset{t\in T}{\max }\left[P_{\text{pv}}\left(t\right)-P_{\text{bess}}\left(t\right)\right]-\underset{t\in T}{\min }\left[P_{\text{pv}}\left(t\right)-P_{\text{bess}}\left(t\right)\right]\end{array}(8)$

where $P_{\text{pv}}^{\text{rate}}$ is the rated power output of the PV power plant; T is the time cycle of AGC ancillary services; $P_{\text{pv}}\left(t\right)$ is the power output of the PV power plant at the tth control time period; $P_{\text{bess}}\left(t\right)$ is the charging power of BESS at the tth control time period; and $P_{\text{agc}}\left(t\right)$ is the AGC signal at the tth control time period.

Note that many existing studies of PV array reconfiguration only focused on the maximum power output. In contrast, the presented objective functions in Eq. 8 not only aims to maximize the power output of PV power plant, but also aims to response the AGC signal as close as possible. Hence, it can guarantee an economic and safe operation simultaneously.

Constraints

Firstly, OAR should satisfy the constraints of electrical switching states since each PV array can only exchange its row with another array from the same column, which can be described as follows (Zhang et al., 2021):

$\{\begin{array}{c}{s}_{pq}\in \left\{\mathrm{0,1},\cdots ,9\right\}, p=\mathrm{0,1,2},\dots ,9;q=\mathrm{0,1,2},\dots ,9 \\ {\cup }_{p=0}^9{s}_{pq}=\left\{\mathrm{0,1},\cdots ,9\right\}, q=\mathrm{0,1,2},\dots ,9 \end{array}(9)$

where $s_{pq}$ denotes the electrical switching state of the array at the pth row and the qth column.

Secondly, the BESS should satisfy the power and energy capability constraints, as follows (Jin et al., 2017):

$P_{\text{bess}}^{\text{min}}\le P_{\text{bess}}\left(t\right)\le P_{\text{bess}}^{\text{max}}, t\in T(10)$

$SO{C}_{\text{bess}}^{\text{min}}\le SO{C}_{\text{bess}}\left(t\right)\le SO{C}_{\text{bess}}^{\text{max}}, t\in T(11)$

$SO{C}_{\text{bess}}\left(t\right)=\{\begin{array}{ll}SO{C}_{\text{bess}}\left(t-1\right)+P_{\text{bess}}\left(t\right)\cdot \Delta t\cdot {\eta }_{\text{ch}}/E_{\text{bess}},\hfill & \text{if} P_{\text{bess}}\left(t\right)\ge 0\hfill \\ SO{C}_{\text{bess}}\left(t-1\right)+P_{\text{bess}}\left(t\right)\cdot \Delta t/\left({\eta }_{\text{dis}}\cdot E_{\text{bess}}\right),\hfill & \text{otherwise}\hfill \end{array}(12)$

where $P_{\text{bess}}^{\text{min}}$ and $P_{\text{bess}}^{\text{max}}$ are the minimum and maximum charging power of BESS, respectively; $SO{C}_{\text{bess}}^{\text{min}}$ and $SO{C}_{\text{bess}}^{\text{max}}$ are the minimum and maximum state of charge (SOC) of BESS, respectively; ${\eta }_{\text{ch}}$ is the charging efficiency; ${\eta }_{\text{dis}}$ is the discharging efficiency; $\Delta t$ is the control interval; and $E_{\text{bess}}$ is the rated energy capability of BESS.

Design of NSGA-II and VIKOR for Optimal Array Reconfiguration

Design of NSGA-II

NSGA-II is suitable for OAR due to its high application flexibility and optimization efficiency. Since NSGA-II is a classical multi-objective optimization algorithm, the specific optimization operations (Deb et al., 2002) are not presented in this work. Here, we will focus on the design combination between NSGA-II and OAR.

Constraints Handling

To satisfy the electrical switching constraints in Eq. 9, all the PV arrays at each column can be assigned with different numbers from 0 to 9. In this work, these numbers will be re-assigned according to the sequence of the current solutions value. For the qth column, the numbers of all the PV arrays can be updated as follows:

$s_{pq}=Rank\left(x_{pq},{\mathit{x}}_q\right)(13)$

where $x_{pq}$ denotes the solution value for the array at the pth row and the qth column, which can be limited within a range; ${\mathit{x}}_q$ denotes the solution vector of the arrays at the qth column; and $Rank\left(x_{pq},{\mathit{x}}_q\right)$ denotes the order of $x_{pq}$ among all the solutions ${\mathit{x}}_q$, which is set to be ascending order.

On the other hand, the solution for the charging power of BESS can be initialized and limited within its lower and upper bounds, as follows:

$x_{\text{bess}}=P_{\text{bess}}^{\text{min}}+r\cdot \left(P_{\text{bess}}^{\text{max}}-P_{\text{bess}}^{\text{min}}\right)(14)$

where r is an uniform random number from 0 to 1.

Fitness Functions

Since the constraints in Eqs 9, 10 can be satisfied during the optimization, the fitness functions can be designed by considering the rest constraints in Eqs 11, 12. Based on the penalty function method, the fitness functions of NSGA-II can be designed as follows:

$\{\begin{array}{c}{F}_1=f_1+{\displaystyle \sum }_{t\in T}M\left(t\right)\\ F_2=f_2+{\displaystyle \sum }_{t\in T}M\left(t\right)\end{array}(15)$

$M\left(t\right)=\{\begin{array}{ll}\chi \cdot \left[SO{C}_{\text{bess}}\left(t\right)-SO{C}_{\text{bess}}^{\text{min}}\right]\cdot \left[SO{C}_{\text{bess}}\left(t\right)-SO{C}_{\text{bess}}^{\text{max}}\right],\hfill & if violated\hfill \\ 0,\hfill & otherwise\hfill \end{array}(16)$

where $M\left(t\right)$ is the penalty component for the constraints in Eq. 11 at the tth control time period; and $\chi$ is the penalty factor, which is used to avoid an infeasible solution and commonly set to be a large positive value.

Design of Vikor

As an ideal solution based decision making method, VIKOR (Lin et al., 2021) can objectively select the best compromise solution according to the distribution of the obtained Pareto front without human intervention. For the OAR with two objective functions, the calculation process of VIKOR can be given as follows (Lin et al., 2021):

Step 1: Determine the positive and negative ideal solutions based on the obtained Pareto front, as

$\{\begin{array}{c}{\mathit{y}}^{+}=\left\{y_1^{+},y_2^{+}\right\}\\ {\mathit{y}}^{-}=\left\{y_1^{-},y_2^{-}\right\}\end{array}(17)$

$\{\begin{array}{c}{y}_j^{+}=\underset{i=\mathrm{1,2},\dots ,n}{\min }{y}_j^i,j=\mathrm{1,2};\\ y_j^{-}=\underset{i=\mathrm{1,2},\dots ,n}{\max }{y}_j^i,j=\mathrm{1,2};\end{array}(18)$

where ${\mathit{y}}^{+}$ and ${\mathit{y}}^{-}$ are the positive and negative ideal solutions, respectively; and $y_j^i$ is the value of the jth objective function corresponding to the ith Pareto solution.

Step 2: Calculate the group utility and the regret of each alternative Pareto solution, as

$G{U}_i={\displaystyle \sum }_{j=\mathrm{1,2}}{\omega }_j\frac{y_j^{+}-y_j^i}{y_j^{+}-y_j^{-}},i=\mathrm{1,2},\dots ,n(19)$

$I{R}_i=\underset{j=\mathrm{1,2}}{\max }\left({\omega }_j\frac{y_j^{+}-y_j^i}{y_j^{+}-y_j^{-}}\right), i=\mathrm{1,2},\dots ,n(20)$

where ${\omega }_j$ is the weight coefficient of the jth objective function; $G{U}_i$ and $I{R}_i$ are the group utility and the regret of the ith Pareto solution, respectively.

Step 3: Calculate the comprehensive evaluation value for each alternative Pareto solution, as

$Q_i=\theta \cdot \frac{G{U}_i-G{U}^{+}}{G{U}^{-}-G{U}^{+}}+\left(1-\theta \right)\cdot \frac{I{R}_i-I{R}^{+}}{I{R}^{-}-I{R}^{+}}, i=\mathrm{1,2},\dots ,n(21)$

$\{\begin{array}{c}G{U}^{+}=\underset{i=\mathrm{1,2},\dots ,n}{\min }G{U}_i\\ G{U}^{-}=\underset{i=\mathrm{1,2},\dots ,n}{\max }G{U}_i\end{array}(22)$

$\{\begin{array}{c}I{R}^{+}=\underset{i=\mathrm{1,2},\dots ,n}{\min }I{R}_i\\ I{R}^{-}=\underset{i=\mathrm{1,2},\dots ,n}{\max }I{R}_i\end{array}(23)$

where $Q_i$ is the comprehensive evaluation value of the ith Pareto solution; $G{U}^{+}$ and $G{U}^{-}$ are minimum and maximum group utilities, respectively; $I{R}^{+}$ and $I{R}^{-}$ are minimum and maximum regrets, respectively; and $\theta$ denotes the weight coefficient of the group utility.

Step 4: Determine the best compromise solution based on the comprehensive evaluation values, as

${\mathit{x}}_{\text{best}}=\arg \underset{i=\mathrm{1,2},\dots ,n}{\min }{Q}_i\left({\mathit{x}}_i^{\ast }\right)(24)$

where ${\mathit{x}}_i^{\ast }$ denotes the ith Pareto solution and ${\mathit{x}}_{\text{best}}$ denotes the best compromise solution.

Execution Procedure

Taken together, the specific execution procedure of NSGA-II and VIKOR for OAR can be given in Table 1, where k denotes the kth iteration of NSGA-II and k_max is the maximum iteration number.

TABLE 1

TABLE 1. The specific execution procedure of NSGA-II and VIKOR for OMAR.

Case Studies

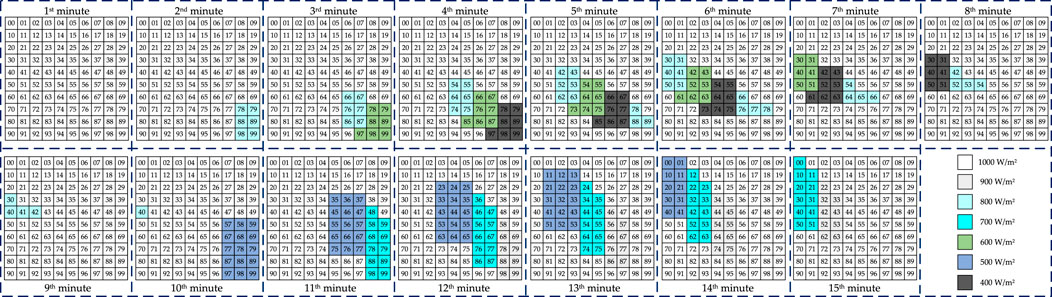
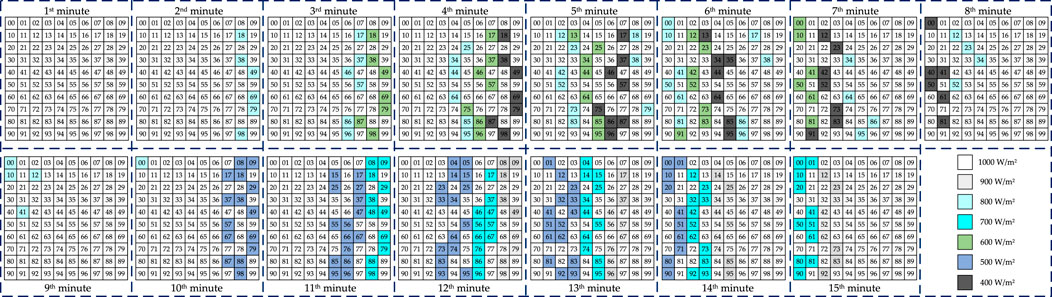
In this work, a 30-MW PV power plant (Zhang et al., 2021) with 30 identical sub-systems is introduced to evaluate the performance of the proposed method, in which each sub-system is formed by the 10 × 10 TCT PV arrays. The specific parameters of the testing system can be found in Zhang et al. (2021). The operating temperature for all the PV arrays is set to be 25°C, while the irradiation distribution for each sub-system at different minutes are given in Figure 4. Figure 5 provides the output features of each sub-systems at the 1st and 5th minutes. It is obvious that PSC at the 5th minute can directly lead to multiple peaks of P-V curves instead of a single peak at the 1st minute. Besides, the main parameters of the BESS is given in Table 2.

FIGURE 4

FIGURE 4. The irradiation distribution for each sub-system of the PV power plant.

FIGURE 5

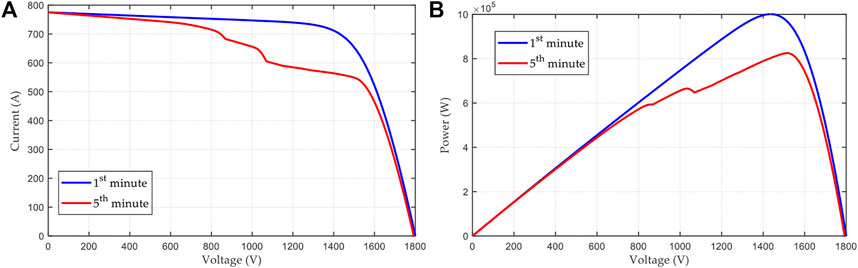
FIGURE 5. Output feature of each sub-system at the 1st and 5th minutes. (A)I–V curve and (B)P–V curve.

TABLE 2

TABLE 2. Main parameters of BESS.

In NSGA-II, a larger population size or maximum iteration number will result in a high-quality Pareto front with a higher probability. However, it also easily leads to a long computation time. Hence, these two parameters can set to be as large as possible if the computation time of NSGA-II can satisfy the real-time optimization of OAR. In this work, they are set to be 200 and 100 respectively via trial-and-error based on this setting rule. Moreover, the penalty factor is set be 10⁸. To guarantee a fair preference for each objective function, all weight coefficients of VIKOR are set to be 0.5. All the simulations are carried out in the platform of Matlab R2020a.

Study on a Constant Automatic Generation Control Signal

In this study, a constant AGC signal $P_{\text{agc}}\left(t\right)=27\text{MW}$ is adopted to test the performance of the proposed method. Figure 6 shows the optimal Pareto front by NSGA-II and the best compromise solution by VIKOR. It is apparent that the obtained Pareto front can distribute equably within a quite large range, while VIKOR can effectively achieve an impersonal decision without any preference on each objective function. Figure 7 gives the irradiation distribution based on the compromise solution. It shows that the PSC of some arrays can be shared by other arrays.

FIGURE 6

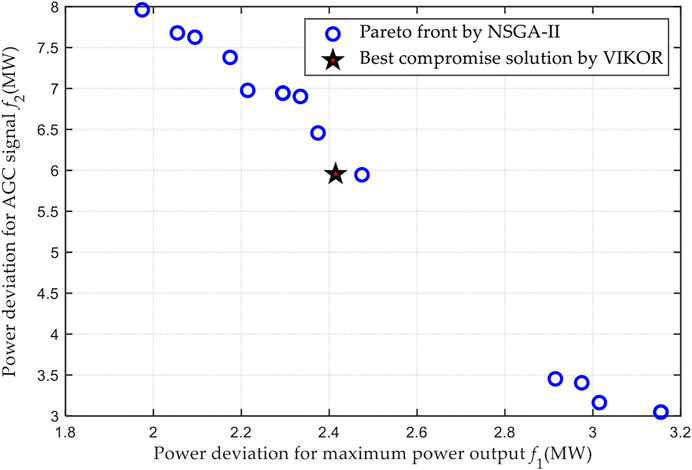
FIGURE 6. Optimal Pareto front by NSGA-II and best compromise solution by VIKOR on a constant AGC signal.

FIGURE 7

FIGURE 7. The irradiation distribution for each sub-system based on the compromise solution.

Based on the reconfiguration scheme, Figure 7 gives the comparison of theoretical output between the compromise solution and the initial distribution at the 5th minute. It can be found from Table 3 that the proposed method can significantly increase the theoretical maximum power point, which is about 116.22% of that with the initial distribution in Figure 4.

TABLE 3

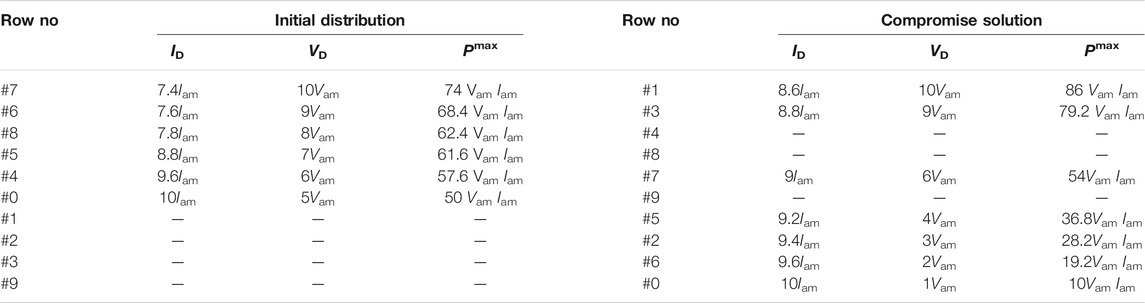
TABLE 3. Comparison of theoretical output between the compromise solution and the initial distribution at the 5th minute

Figure 8 shows the optimal power outputs of the proposed method and that without optimization on a constant AGC signal, where the power outputs of the proposed method is the results corresponding to the best compromise solution. Firstly, it can be seen from Figure 8A that the power outputs obtained by the proposed method can approximate the AGC signal closer than that without optimization. At the same time, the charging power of BESS obtained by the proposed method can effectively adapt to the power output of the PV power plant. Furthermore, it is clearly that the power output of the PV power plant obtained by the proposed method is much higher than that without optimization, as illustrated in Figure 8B.

FIGURE 8

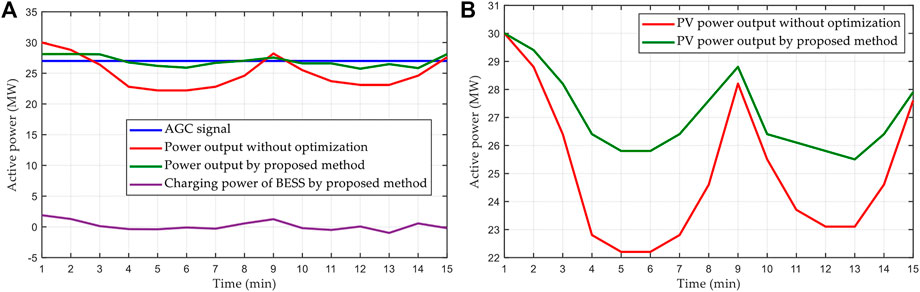
FIGURE 8. Optimal power outputs of the proposed method and that without optimization on a constant AGC signal. (A) Total power output and (B) PV power output.

Figure 9 provides the result comparison between proposed method and that without optimization on a constant AGC signal. Post hoc analysis reveals that the power deviations of the two objective functions obtained by the proposed method are much smaller than that without optimization. Particularly, both of these two power deviations can be reduced 51.27 and 44.03% compared with that without optimization.

FIGURE 9

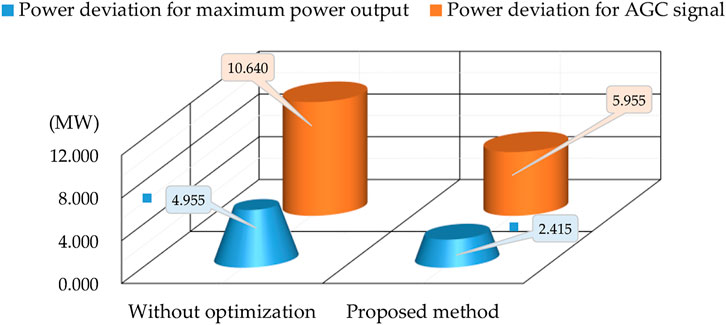
FIGURE 9. Result comparison between proposed method and that without optimization on a constant AGC signal.

Study on the Varying Automatic Generation Control Signals

In this study, the varying AGC signals are design to evaluate the performance of the proposed method, where the AGC signals can be represented as follows:

$P_{\text{agc}}\left(t\right)=\{\begin{array}{l}28, 0\le t<5\hfill \\ 20, 5\le t<10\hfill \\ 26, 10\le t<15\hfill \end{array}(25)$

Figure 10 shows the optimal Pareto front by NSGA-II and the best compromise solution by VIKOR for the varying AGC signals. Similarly, the Pareto front obtained by NSGA-II can effectively cover the large ranges for both of two objective functions. Besides, VIKOR can select an impersonal compromise solution from the Pareto front.

FIGURE 10

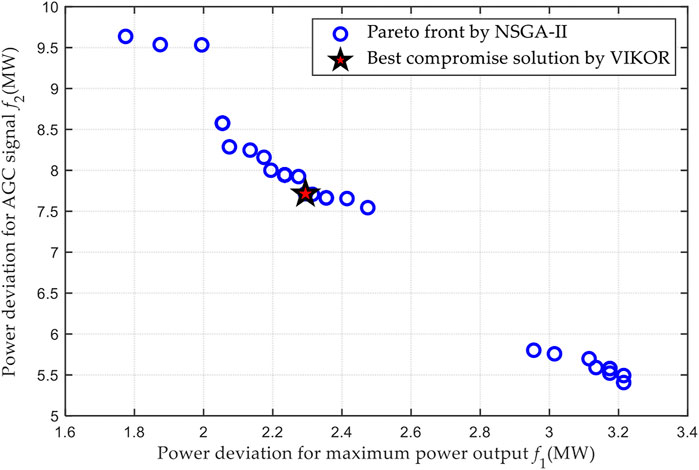
FIGURE 10. Optimal Pareto front by NSGA-II and best compromise solution by VIKOR on the varying AGC signals.

Figure 11 gives the optimal power outputs of the proposed method and that without optimization on the varying AGC signals. Compared with the power output of that without optimization, the power outputs obtained by the proposed method is more closer to the varying AGC signals, especially in the periods of $0\le t<5$ and $10\le t<15$. Moreover, the PV power output obtained by the proposed method is much higher than that without optimization, in which the maximum increment is about 6 MW at the 5th minute.

FIGURE 11

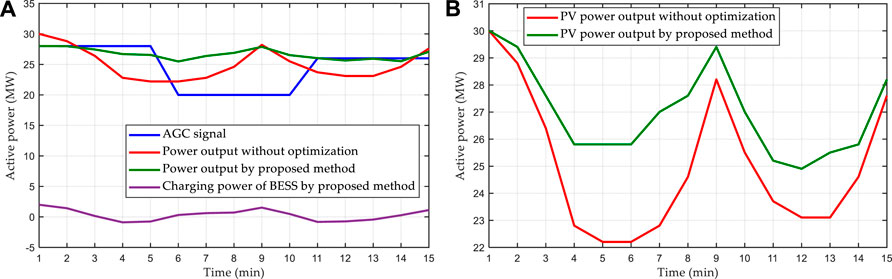
FIGURE 11. Optimal power outputs of the proposed method and that without optimization on the varying AGC signals.

Figure 12 gives the result comparison between proposed method and that without optimization on the varying AGC signals. It clearly shows that the proposed method can dramatically reduce the power deviations for both of two objective functions against to that without optimization. More specially, both of these two power deviations obtained by the proposed method are only about 46 and 69% of that without optimization.

FIGURE 12

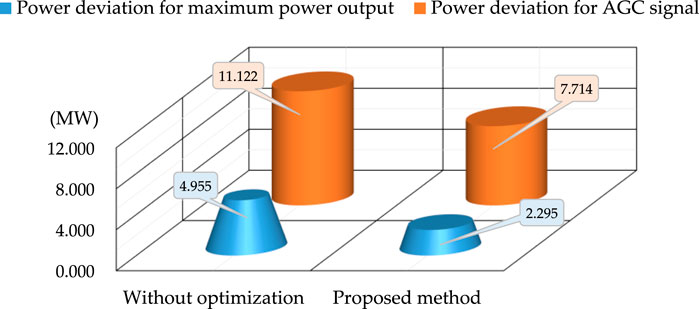
FIGURE 12. Result comparison between proposed method and that without optimization on the varying AGC signals.

Conclusion

In this paper, a novel bi-objective optimization method is proposed for optimal array reconfiguration of a PV power plant with a battery energy storage system, in which the main contributions can be summarized as follows:

1) The constructed OAR not only can achieve a maximum power output of PV power plant via the array reconfiguration under various irradiations, but also can effectively respond to the AGC signal via the power scheduling with BESS. As a result, the operation economy of the PV power plant and the operation safety of the connected power grid can be significantly improved.

2) The design of NSGA-II can efficiently find a high-quality Pareto front for OAR, thus the dispatchers of the PV power plant can select different high-quality optimal dispatch schemes to satisfy the current operating requirement from the Pareto front.

3) The design of VIKOR can objectively make a decision to select the best compromise solution from the obtained Pareto front, which can guarantee a fair preference on each objective function. Hence, the operation economy and safety can be improved simultaneously.

In future works, the control cost of PV array reconfiguration can be considered as an added objective function in OAR, thus the service life of the switching devices can be extended. As the number of objective functions, a more efficient multi-objective optimization algorithms will be more suitable to obtain a high-quality Pareto front for OAR.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

TH contributed to the conception of the study. TH and SL contributed significantly to analysis and manuscript preparation; YC and CL performed the data analyses and wrote the manuscript; SW helped perform the analysis with constructive discussions.

Funding

This work was jointly supported by Research on Regional Power Grid Frequency Regulation with Renewable Energy Participation (YNKJXM20191240), Research and Development Start-Up Foundation of Shantou University (NTF19001).

Conflict of Interest

TH, SL, and SW were employed by the company Yunnan Power Grid Co Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Babu, T. S., Ram, J. P., Miyatake, T. M., Blaabjerg, F., and Rajasekar, N. (2018). Particle Swarm Optimization Based Solar PV Array Reconfiguration of the Maximum Power Extraction under Partial Shading Conditions. IEEE Trans. Sustain. Energ. 9 (1), 74–85. doi:10.1109/tste.2017.2714905

CrossRef Full Text | Google Scholar

Babu, T. S., Yousri, D., and Balasubramanian, K. (2020). Photovoltaic Array Reconfiguration System for Maximizing the Harvested Power Using Population-Based Algorithms. IEEE Access 8, 2169–3536. doi:10.1109/access.2020.3000988

CrossRef Full Text | Google Scholar

Deb, K., Pratap, A., and Agarwal, S. (2002). A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 6 (2), 182–197. doi:10.1109/4235.996017

CrossRef Full Text | Google Scholar

Dhanalakshmi, B., and Rajasekar, N. (2018). A Novel Competence Square Based PV Array Reconfiguration Technique for Solar PV Maximum Power Extraction. Energ. Convers. Manag. 174, 897–912. doi:10.1016/j.enconman.2018.08.077

CrossRef Full Text | Google Scholar

Fathy, A. (2020). Butterfly Optimization Algorithm Based Methodology for Enhancing the Shaded Photovoltaic Array Extracted Power via Reconfiguration Process. Energ. Convers. Manag. 220, 113115. doi:10.1016/j.enconman.2020.113115

CrossRef Full Text | Google Scholar

Fathy, A. (2018). Recent Meta-Heuristic Grasshopper Optimization Algorithm for Optimal Reconfiguration of Partially Shaded PV Array. Sol. Energ. 171, 638–651. doi:10.1016/j.solener.2018.07.014

CrossRef Full Text | Google Scholar

Horoufiany, M., and Ghandehari, R. (2018). Optimization of the Sudoku Based Reconfiguration Technique for PV Arrays Power Enhancement under Mutual Shading Conditions. Sol. Energ. 159, 1037–1046. doi:10.1016/j.solener.2017.05.059

CrossRef Full Text | Google Scholar

Jin, X., Mu, Y., Wu, J., and Jia, H. (2017). Dynamic Economic Dispatch of a Hybrid Energy Microgrid Considering Building Based Virtual Energy Storage System. Appl. Energ. 194, 386–398. doi:10.1016/j.apenergy.2016.07.080

CrossRef Full Text | Google Scholar

Koad, R. B. A., Zobaa, A. F., and El-Shahat, A. (2017). A Novel MPPT Algorithm Based on Particle Swarm Optimization for Photovoltaic Systems. IEEE Trans. Sustain. Energ. 8 (2), 468–476. doi:10.1109/tste.2016.2606421

CrossRef Full Text | Google Scholar

Krishna, G. S., and Moger, T. (2019). Improved SuDoKu Reconfiguration Technique for Total-Cross-Tied PV Array to Enhance Maximum Power under Partial Shading Conditions. Renew. Sustain. Energ. Rev. 109, 333–348. doi:10.1016/j.rser.2019.04.037

Google Scholar

Lin, M., Chen, Z., Gou, X., and Xu, Z. (2021). Score Function Based on Concentration Degree for Probabilistic Linguistic Term Sets: An Application to TOPSIS and VIKOR. Inform. Sci. 551, 270–290. doi:10.1016/j.ins.2020.10.061

CrossRef Full Text | Google Scholar

Nasiruddin, I., Khatoon, S., Jalil, F., and Bansal, R. (2019). Shade Diffusion of Partial Shaded PV Array by Using Odd-Even Structure. Sol. Energ. 181, 519–529. doi:10.1016/j.solener.2019.01.076

CrossRef Full Text | Google Scholar

Pareek, S., and Dahiya, R. (2016). Enhanced Power Generation of Partial Shaded Photovoltaic Fields by Forecasting the Interconnection of Modules. Energy 95, 561–572. doi:10.1016/j.energy.2015.12.036

CrossRef Full Text | Google Scholar

Pillai, D. S., and Ram, J. P. (2018). Power and Mismatch Losses Mitigation by a Fixed Electrical Reconfiguration Technique for Partially Shaded Photovoltaic Arrays. Energy Convers. Manage. 172, 402–417. doi:10.1016/j.enconman.2018.07.016

CrossRef Full Text | Google Scholar

Potnuru, S. R., Pattabiraman, D., and Ganesan, S. I. (2015). Positioning of PV Panels for Reduction in Line Losses and Mismatch Losses in PV Array. Renew. Energ. 78, 264–275. doi:10.1016/j.renene.2014.12.055

CrossRef Full Text | Google Scholar

Rajan, N. A., Shrikant, K. D., Dhanalakshmi, B., and Natarajan, R. (2017). Solar PV Array Reconfiguration Using the Concept of Standard Deviation and Genetic Algorithm. Energ. Proced. 117, 1062–1069. doi:10.1016/j.egypro.2017.05.229

CrossRef Full Text | Google Scholar

Rajasekar, N., Kumar, N. K., and Venugopalan, R. (2013). Bacteril Foraging Algorithm Based Solar PV Parameter Estimation. Sol. Energ. 97, 255–265. doi:10.1016/j.solener.2013.08.019

CrossRef Full Text | Google Scholar

Rakesh, N., and Madhavaram, T. V. (2016). Performance Enhancement of Partially Shaded Solar PV Array Using Novel Shade Dispersion Technique. Front. Energ. 10, 227–239. doi:10.1007/s11708-016-0405-y

CrossRef Full Text | Google Scholar

Rani, B. I., Ilango, G. S., and Nagamani, C. (2013). Enhanced Power Generation from PV Array under Partial Shading Conditions by Shade Dispersion Using Su Do Ku Configuration. IEEE Trans. Sustain. Energ. 4, 594–601. doi:10.1109/tste.2012.2230033

CrossRef Full Text | Google Scholar

Rao, P. S., Ilango, G. S., and Nagamani, C. (2014). Maximum Power from PV Arrays Using a Fixed Configuration under Different Shading Conditions. IEEE J. Photovolt. 4 (2), 679–686. doi:10.1109/JPHOTOV.2014.2300239

Google Scholar

Sahu, B. K. (2015). A Study on Global Solar PV Energy Developments and Policies with Special Focus on the Top Ten Solar PV Power Producing Countries. Renew. Sustain. Energ. Rev. 43, 621–634. doi:10.1016/j.rser.2014.11.058

Google Scholar

Sahu, H. S., and Nayak, S. K. (2016). Extraction of Maximum Power from a PV Array under Nonuniform Irradiation Conditions. IEEE Trans. Electron. Devices 63 (12), 4825–4831. doi:10.1109/ted.2016.2616580

CrossRef Full Text | Google Scholar

Samikannu, S. M., Namani, R., and Subramaniam, S. K. (2016). Power Enhancement of Partially Shaded PV Arrays through Shade Dispersion Using Magic Square Configuration. J. Renew. Sust. Energ. 8, 063503. doi:10.1063/1.4972285

CrossRef Full Text | Google Scholar

Satpathy, P. R., and Sharma, R. (2019). Power and Mismatch Losses Mitigation by a Fixed Electrical Reconfiguration Technique for Partially Shaded Photovoltaic Arrays. Energ. Convers. Manag. 192, 52–70. doi:10.1016/j.enconman.2019.04.039

CrossRef Full Text | Google Scholar

Venkateswari, R., and Rajasekar, N. (2020). Power Enhancement of PV System via Physical Array Reconfiguration Based Lo Shu Technique. Energ. Convers. Manag. 215, 112885. doi:10.1016/j.enconman.2020.112885

CrossRef Full Text | Google Scholar

Winston, D. P., Kumaravel, S., and Kumar, B. P. (2020). Performance Improvement of Solar PV Array Topologies during Various Partial Shading Conditions. Sol. Energ. 196, 228–242. doi:10.1016/j.solener.2019.12.007

Google Scholar

Xi, L., Chen, J., Xu, Y., and Huang, Y. (2018). Smart Generation Control Based on Multi-Agent Reinforcement Learning with the Idea of the Time Tunnel. Energ. 153, 977–987. doi:10.1016/j.energy.2018.04.042

CrossRef Full Text | Google Scholar

Yadav, A. S., Pachauri, R. K., Chauhan, Y. K., Choudhury, S., and Singh, R. (2017). Performance Enhancement of Partially Shaded PV Array Using Novel Shade Dispersion Effect on Magic-Square Puzzle Configuration. Sol. Energ. 144, 780–797. doi:10.1016/j.solener.2017.01.011

CrossRef Full Text | Google Scholar

Yadav, K., and Kumar, B. (2020). Mitigation of Mismatch Power Losses of PV Array under Partial Shading Condition Using Novel Odd Even Configuration. Energ. Rep. 6, 427–437. doi:10.1016/j.egyr.2020.01.012

CrossRef Full Text | Google Scholar

Yousri, D., Allam, D., and Eteiba, M. B. (2020a). Optimal Photovoltaic Array Reconfiguration for Alleviating the Partial Shading Influence Based on a Modified Harris Hawks Optimizer. Energ. Convers. Manag. 206, 112470. doi:10.1016/j.enconman.2020.112470

CrossRef Full Text | Google Scholar

Yousri, D., Babu, T. S., Balasubramanian, K., and Osama, A. (2020d). Multi-Objective Grey Wolf Optimizer for Optimal Design of Switching Matrix for Shaded PV Array Dynamic Reconfiguration. IEEE Access 8, 159931–159946. doi:10.1109/access.2020.3018722

CrossRef Full Text | Google Scholar

Yousri, D., Babu, T. S., Beshr, E., and Eteiba, M. (2020b). A Robust Strategy Based on Marine Predators Algorithm for Large Scale Photovoltaic Array Reconfiguration to Mitigate the Partial Shading Effect on the Performance of PV System. IEEE Access 8, 112407–112426. doi:10.1109/access.2020.3000420

CrossRef Full Text | Google Scholar

Yousri, D., Babu, T. S., Mirjalili, S., and Natarajan, R. (2020c). A Novel Objective Function with Artificial Ecosystem-Based Optimization for Relieving the Mismatching Power Loss of Large-Scale Photovoltaic Array. Energ. Convers. Manage 225, 113385. doi:10.1016/j.enconman.2020.113385

CrossRef Full Text | Google Scholar

Zhang, X., Li, C., Li, Z., Yin, X., Yang, B., Gan, L., et al. (2021). Optimal Mileage-Based PV Array Reconfiguration Using Swarm Reinforcement Learning. Energ. Convers. Manage. 225, 113892. doi:10.1016/j.enconman.2021.113892

CrossRef Full Text | Google Scholar