Design and Evaluation of Fuzzy Adaptive Particle Swarm Optimization Based Maximum Power Point Tracking on Photovoltaic System Under Partial Shading Conditions

Artificial intelligence methods such as fuzzy logic and particle swarm optimization (PSO) have been applied to maximum power point tracking (MPPT) for solar panels. The P-V curve of a solar panel exhibits multiple peaks under partial shading condition (PSC) when all modules of a solar panel do not receive the same solar irradiation. Although conventional PSO has been shown to perform well under uniform insolation, it is often unable to find the global maximum power point under PSC. Fuzzy adaptive PSO controllers have been proposed for MPPT. However, the controller became computation-intensive in order to adjust the PSO parameters for each particle. In this paper, fuzzy adaptive PSO-based and conventional PSO-based MPPT are compared and evaluated in the aspect of design and performance. A simple fuzzy adaptive PSO controller for MPPT was designed to reach the global optimal point under PSC and uniform irradiation. The controller combines the advantages of both PSO and fuzzy control. The fuzzy controller dynamically adjusts the PSO parameter to improve the convergence speed and global search capability. Since tuning of the PSO parameter is designed to be common for all particles, it reduced the computation complexity. The fuzzy controller’s rule base is designed to obtain a fast transient response and stable steady state response. Design of the fuzzy adaptive PSO-based MPPT is verified with simulation results using a boost converter. The results are evaluated in comparison to the results using a conventional PSO controller under PSC. Simulation shows the fuzzy adaptive PSO-based MPPT is able to improve the global search process and increase the convergency speed. The comparison indicates the settling time using the fuzzy adaptive PSO-based MPPT is 14% faster under PSC on average and 30% faster under uniform irradiation than the settling time using the conventional PSO. Both the fuzzy adaptive and conventional PSO controllers have similar output power tracking accuracy.

1 Introduction

Solar power generation has seen rapid growth in the past decade (Madvar et al., 2018; Al-Dahidi et al., 2019; Guozden et al., 2020; Sohani et al., 2021). Solar power has the advantage of low maintenance, noiseless and environmentally friendly power generation. Improving photovoltaic (PV) efficiency is a key goal of research and helps make PV technology costs competitive with conventional sources of energy (Alizadeh et al., 2020; Maleki et al., 2020). A major challenge in the use of PV is posed by its nonlinear current–voltage (I–V) characteristics, which result in a unique maximum power point (MPP) on the power–voltage (P–V) curve. To improve efficiency, maximum power point tracking (MPPT) is needed along with power converters to ensure optimal utilization of solar power systems. The objective of MPPT is to extract the maximum amount of power under varying temperature and irradiation conditions. Several MPPT algorithms have been studied, including perturb and observe (P&O), incremental conductance, fractional open-circuit voltage, and fractional short-circuit current (Esram and Chapman, 2007). The solar panel model was linearized into a Thevenin equivalent circuit to design the MPPT (Nguyen et al., 2020). Artificial intelligence MPPT methods include fuzzy logic control and neural network. Fuzzy logic controllers do not need an accurate mathematical model, and are not sensitive to parameter changes (Khosravi et al., 2019; Khosravi et al., 2020). Fuzzy logic based MPPT has been shown to perform well under uniform insolation (Rezk et al., 2019). However, study of MPPT control methods has mainly focused on uniform insolation where only one maximum power point (MPP) exists in the power-voltage (P-V) curve.

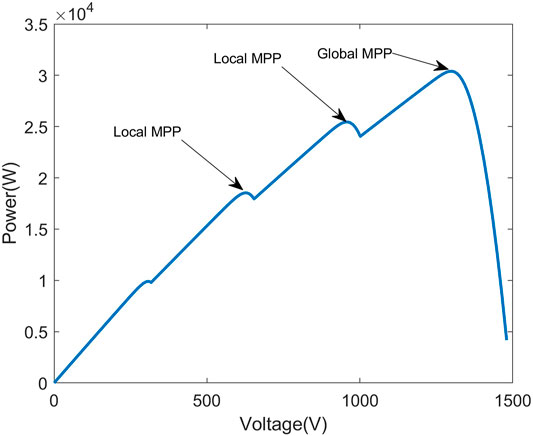
Partial shading condition (PSC) refers to conditions when all modules of a solar panel do not receive the same solar irradiation. PSCs are very common in solar power systems, especially in urban areas and in areas with trees and low moving clouds (Patel and Agarwal, 2008; Ghasemi et al., 2016). In PSC, multiple maximum power points (MPPs) are in the P-V curve. Conventional MPPT algorithms assume a single MPP and are unable to identify the global MPP among the local MPPs, thus they usually track local peaks. This can cause significant energy loss (Tey and Mekhilef, 2014). Therefore, it is necessary to develop new MPPT techniques to reliably track the global MPP under PSC (Chen et al., 2014).

Soft computing based algorithms were recently developed to obtain the global optimal solution under PSC. Biological optimization algorithms such as genetic algorithms (GA), gray wolf optimization, colony of flashing flies, artificial bee colony, and particle swarm optimization (PSO) have been applied to MPPT under PSC. Gray wolf optimization imitates the leadership hierarchy and hunting mechanism of gray wolves in nature. It was used to improve tracking efficiency and steady-state oscillations (Mohanty et al., 2016; AlShabi et al., 2021). Colony of flashing flies is inspired by the movement of fireflies. The tracking procedure consists of positioning the fireflies in the possible solution space, and based on the PV output power, the flies move to the promised regions (Sundareswaran et al., 2014). Artificial bee colony simulates the intelligent foraging behavior of a swarm of honeybees. The entire population is divided into three categories: employed bees, onlookers and scout bees. The cooperation and communication among the three groups lead to an optimal solution (Sundareswaran et al., 2015). Particle swarm optimization (PSO) is a population-based optimization technique inspired by the motion of bird flocks. It provides an effective metaheuristic approach that can be applied to optimization problems with several local optimal points (Al-Shabi et al., 2021). Compared to the other evolutionary algorithms, PSO method is simpler in structure, less computationally extensive and easier for experimental implementation. A number of conventional and modified PSO methods were reported for MPPT (Chen et al., 2010; Cheng et al., 2015; Renaudineau et al., 2015; Koad et al., 2017). PSO algorithm was used to tune the membership function of a fuzzy controller for MPPT to reduce the steady-state oscillation (Soufi et al., 2016; Priyadarshi et al., 2019). A deterministic PSO was introduced to improve the MPPT capability under PSC. Random numbers in the acceleration factor of conventional PSO were removed. The maximum change in velocity is restricted to a particular value based on P-V characteristics of PSC. It results in more consistent solution and simpler control structure. However, a previous study of the P-V characteristics under PSC is required (Ishaque and Salam, 2013). Conventional PSO was modified for MPPT, where the parameters were adjusted linearly to improve on accuracy (Liu et al., 2012). Tuning of PSO parameters in the literature were mostly linear. Since PSO is a nonlinear search process, linear tuning is not enough to achieve highly efficient algorithm, while nonlinear tuning can make the algorithm overly complicated (Merchaoui et al., 2020). In addition, advanced PSO control methods have not been fully investigated for PSC.

Presented in this paper is a fuzzy adaptive PSO-based MPPT. Motivation of the research is to combine the advantages of both PSO and fuzzy control to improve the speed of the MPPT controller, find a global optimal solution under both PSC and uniform irridiation, and keep the simple structure of PSO at the same time. Controllers based on fuzzy logic have been applied to a broad range of engineering problems, particularly those having nonlinear dynamics (Guo et al., 2009). Design of fuzzy controllers is based on expert knowledge about a plant instead of a precise mathematical model. The fuzzy controller dynamically adjusts the PSO parameter to improve the convergence speed. Simulation results show the controller is able to track the global MPP under PSC where multiple local MPP exist as well as under uniform irridiation Settling time using the proposed controller is 14% faster under PSC on average and 30% faster under uniform irradiation than the settling time using regular PSO controller.

The paper is organized as follows. Section 2 describes a conventional PSO controller. The proposed fuzzy adaptive PSO is presented in Section 3. Section 4 describes system configuration and simulation. Simulation results are reported and compared in Section 5. Finally, the conclusion and recommendations are made in the last section.

2 Conventional Particle Swarm Optimization

PSO is a stochastic population-based evolutionary algorithm search method modeled after the behavior of flocks of birds (Ishaque and Salam, 2013). PSO requires a swarm of particles. Each particle represents a possible solution. Initially A swarm of particles is randomly placed in the search space. The controller searches for the optimal solution with the particles’ velocity and position communicating with each other. Particles are moved around in a multi-dimensional space in search of the optimal solution. Each particle has its own personal best position, $P_{best}$. The next position $p^{k+1}$ depends on both $P_{best}$ and the global best position of the space, $G_{best}$. It is determined iteratively using 1, where the next position, $p^{k+1}$ represents the new duty cycle, d is the current duty cycle, and the velocity $v^{k+1}$, calculated by 1, represents the step size. Table 1 define the variables.

$p^{k+1}=d+v^{k+1}(1)$

$v^{k+1}=\omega v_j^k+c_1{r}_1\left(P_{best}-d\right)+c_2{r}_2\left(G_{best}-d\right)(2)$

TABLE 1

TABLE 1. Definition of variables.

In 2, ω stands for the inertia weight, and $c_1$ and $c_2$ are the cognitive and social parameters, respectively, that are responsible for acceleration. $r_1$ and $r_2$ are random variables that vary between 0 and 1. The acceleration coefficients $c_1$ and $c_2$ move each particle in the direction of $P_{best}$ and $G_{best}$. The inertial weight ω balances the global and local searches to reduce the number of iterations to obtain the global best solution.

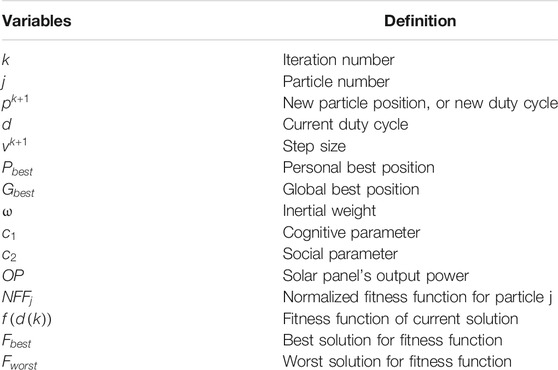
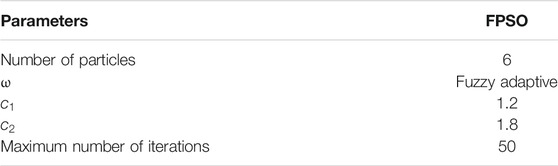
The flowchart of conventional PSO is presented in Figure 1. Inputs to the PSO controller are the voltage and current from the solar panel. 36 particles are placed in a 6$\times$6 matrix. Each position in the matrix represents a solution that includes the value of the duty cycle and output power. The initial values of particles were randomly chosen. Particles travel across the grid, calculating the power and duty cycle at each position. At the end of each iteration, the particles store the best solution. Individual best solutions are compared and the global best solution is updated. In the next iteration, the particles try to converge to the newly updated global best solution. When used for MPPT, the search process should satisfy the condition in 3 at each iteration, where $OP$ is the solar panel’s output power, j is the particle number, and k is the iteration number. The convergence criteria are met when velocities of all particles become smaller than a threshold, or when the maximum number of iterations is reached. The PSO algorithm will stop and output the obtained $G_{best}$ solution when the criteria are met. Therefore, the controller is able to identify the global MPP among the local MPPs through the global search process.

$O{P}_j^{k+1}>O{P}_j^k(3)$

FIGURE 1

FIGURE 1. Flowchart of conventional PSO.

3 Proposed Fuzzy Adaptive Particle Swarm Optimization Based MPPT

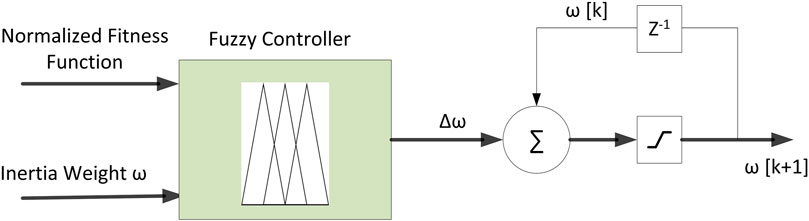
In 2, the inertial weight ω is a very important parameter. It is used to control the convergence behavior of PSO. An optimal value of ω is needed to find the MPP with as few iterations as possible. It balances the exploration and exploitation of the search process. During exploration, particles check different search areas to detect the region containing the optimal solution. After that, the particles concentrate on the best candidates to converge to the final solution. A higher value of ω promotes exploration, while a smaller value encourages an efficient exploitation process. In conventional PSO, ω is a constant. It results in a slow dynamic response for MPPT. To improve the performance, this paper used a fuzzy controller to vary the value of ω iteratively based on the fitness function and the inertial weight ω.

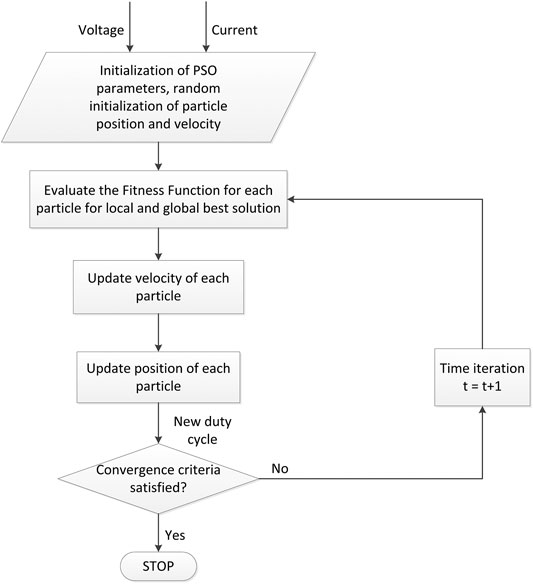
A fuzzy controller contains four main components: 1) the input membership functions that convert its inputs into information the inference mechanism can use to activate and apply rules, 2) the rule base that contains the expert’s linguistic description, 3) the interference mechanism that evaluates which control rules are relevant, and 4) the defuzzification interface that converts the result from the inference mechanism into the control output (Guo et al., 2009). The flowchart of the proposed fuzzy adaptive PSO based MPPT is shown in Figure 2.

FIGURE 2

FIGURE 2. Flowchart of the proposed fuzzy adaptive PSO controller.

The normalized fitness function is shown in 4, where $f\left(d\left(k\right)\right)$ is the current solution, $F_{best}$ is the best solution and $F_{worst}$ is the worst solution. The normalized fitness function quantifies the distance between the particle and global best position. When the normalized fitness function is large, it means the particle is far away from the MPP; therefore, the inertial weight ω should be increased to promote exploration. Conversely, when the normalized fitness function is small, it implies the particle is close to the MPP; therefore, a smaller value of ω is needed to enhance local search capability.

$NF{F}_j=\frac{f\left(d\left(k\right)\right)-F_{best}}{F_{worst}-F_{best}}(4)$

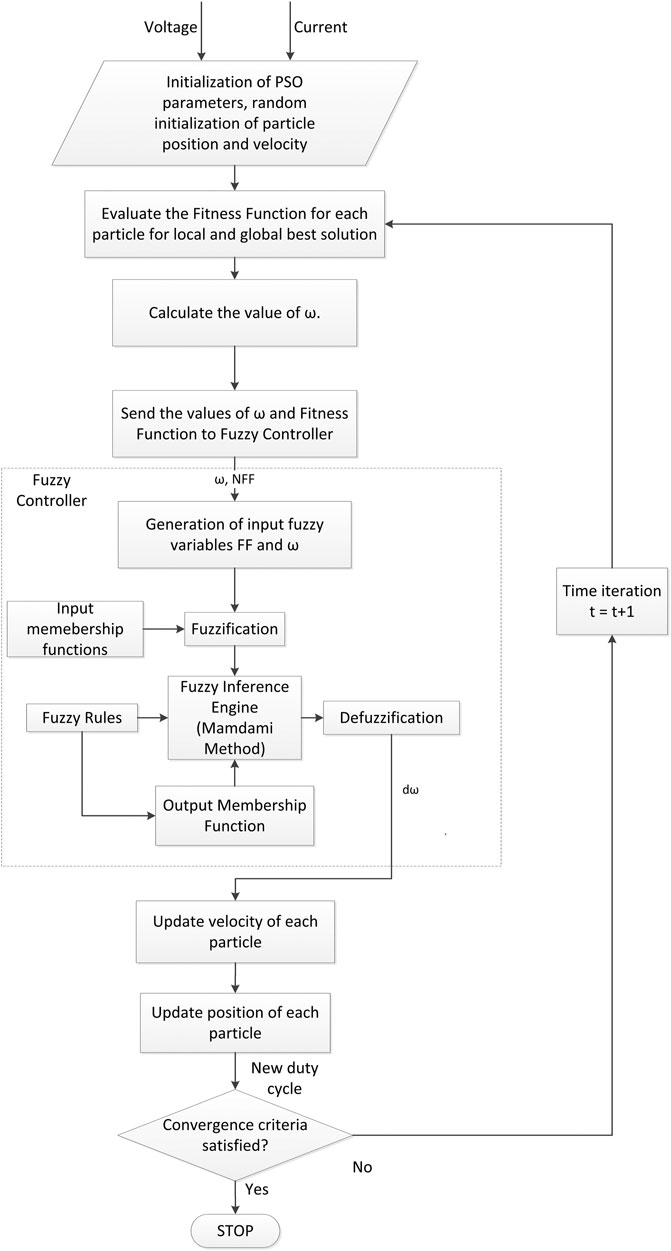
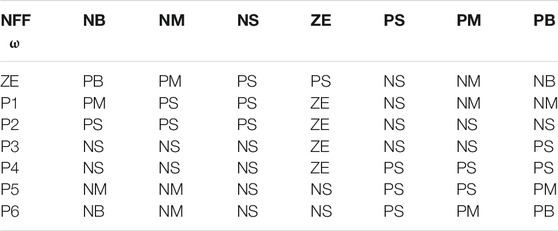
The normalized fitness function and the inertial weight ω are the inputs to the fuzzy controller. First, membership functions for the inputs and outputs are defined. Each universe of discourse is divided into fuzzy subsets. The membership functions are shown in Figure 3. There are seven fuzzy subsets in the fuzzy controller: $NB,NM,NS,Z,PS,PM,PB$, where N indicates negative, Z indicates zero, P represents positive, B indicates big, M indicates medium, and S indicates small. There are three fuzzy subsets for the positive and negative parts of the universe of discourse, respectively.

FIGURE 3

FIGURE 3. Membership functions of the fuzzy controller.

The rule base is derived from general knowledge of the PSO controller, and is tuned based on experimental results. There is a tradeoff between the size of the rule base and the performance of the controller. For the same universe of discourse, more membership functions results in finer control. The output of the fuzzy controller has less variations for small changes in either input, and a more accurate control is achieved. A 7$\times$7 rule base was designed, as shown in Table 2. The output of the fuzzy system is then added to the current ω to create the new and improved inertia weight shown in 5. A block diagram of the fuzzy controller is shown in Figure 4.

${\omega }^{k+1}={\omega }^k+\text{Δ}\omega (5)$

TABLE 2

TABLE 2. Fuzzy rules for given member functions.

FIGURE 4

FIGURE 4. Block diagram of fuzzy controller.

4 Simulation

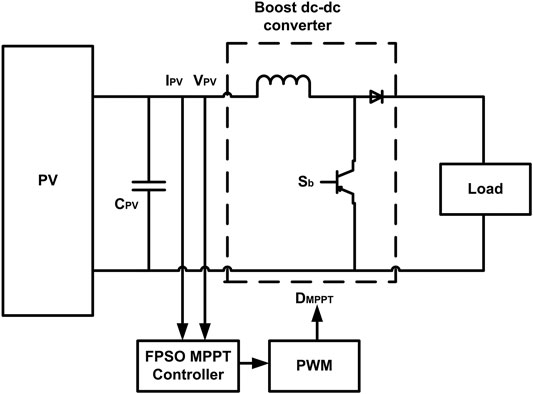
The system was simulated in Matlab/Simulink™. It includes four solar panels connected in series, a boost converter and the fuzzy adaptive PSO MPPT controller. Configuration of the system is shown in Figure 5. The solar panels and power converter were built using Simscape in Simulink. Simulink is a graphical programming environment for modeling, simulating and analyzing of dynamic systems, whereas Simscape is the physical modeling part in Simulink environment. The PSO controller is implemented using Matlab by writing a function. Rapid accelerator mode is used to increase the speed by generating an executable for the simulation. It only takes 3 s to run the simulation. Another option to implement artificial intelligence algorithms is Python language, an open source programming language. The advantage of using Matlab/Simulink™ is that it provides a productive computing environment for engineering systems in which physical components are conveniently available.

FIGURE 5

FIGURE 5. System Configuration.

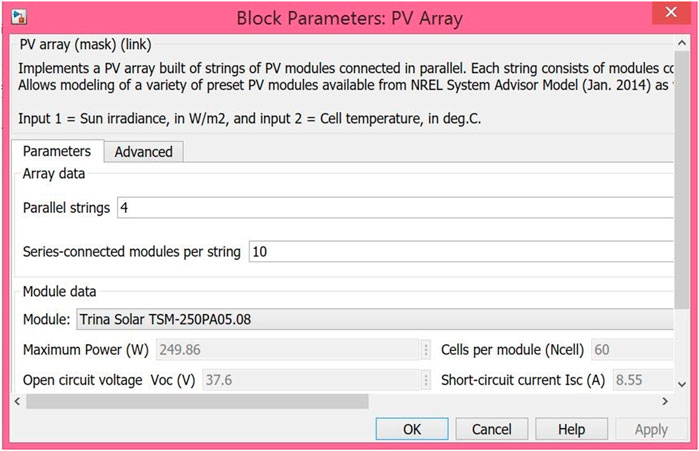
The PV array model in Simulink allows modeling of a variety of preset PV modules available from the National Renewable Energy Laboratory System Advisor Model as well as user-defined PV modules. PV module Trina Solar TSM-250PA05.08 was used for this simulation. The maximum output power is 249.86 W, with open circuit voltage Voc of 37.6 V, and short circuit current Isc of 8.55 A. The voltage at maximum power point V_mp is 31 V, and the current at maximum power point I_mp is 8.06 A. The PV array model has four parallel strings, and 10 series-connected modules per string. Figure 6 shows the parameter configurations of the PV array model in Simulink. Four PV arrays were then connected in series for the simulation.

FIGURE 6

FIGURE 6. Parameter Configuration of PV arrays.

The circuit parameters for the boost converter are V_in = 20 V, V_o = 12 V, L = 1.47 μH, C = 0.467 μF, and R = 53 $\text{Ω}$. The switching frequency is 50 kHz. Table 3 shows the parameters of the proposed fuzzy adaptive PSO-based MPPT controller.

TABLE 3

TABLE 3. Particle swarm optimization parameters.

5 Results

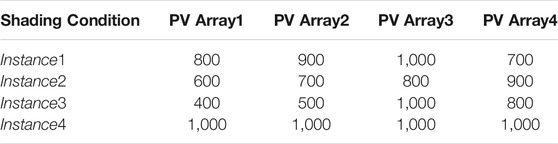
Simulation results of the fuzzy adaptive PSO MPPT and conventional PSO MPPT controllers are presented and compared in this section. Table 4 shows four operating conditions of irradiation levels for each of the four PV arrays connected in series. The first three instances are partial shading conditions, and the last one is uniform irradiation of 1000 W/$m^2$ without partial shading. For the first instance of partial shading, the P-V curve is shown in Figure 7, where the peak of the curve is the global maximum power point (MPP). There are a few local MPPs below the global MPP. Figure 8 compares the startup transient response using the proposed fuzzy adaptive PSO and the regular PSO MPPT controller. The settling time of the fuzzy adaptive PSO MPPT is 0.0983 s, while the settling time of the regular PSO is 0.1152 s.

TABLE 4

TABLE 4. Irridiance variations (W/$m^2$).

FIGURE 7

FIGURE 7. PV curve for irridiation 1.

FIGURE 8

FIGURE 8. Startup response of the fuzzy adaptive PSO and the convential PSO MPPT for irridiation 1.

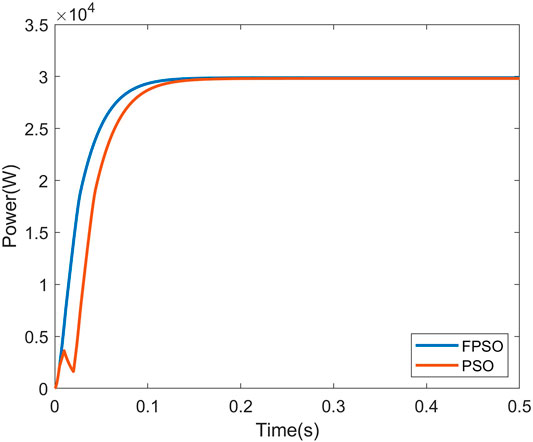
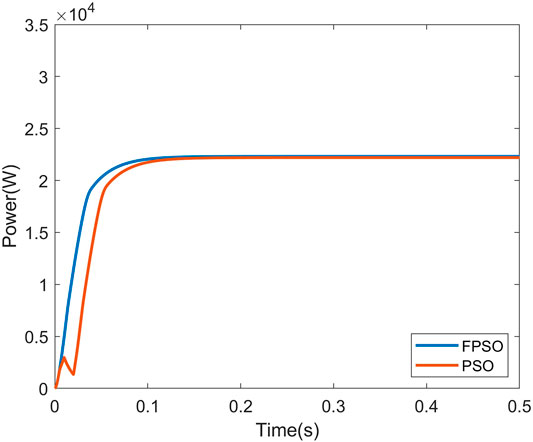
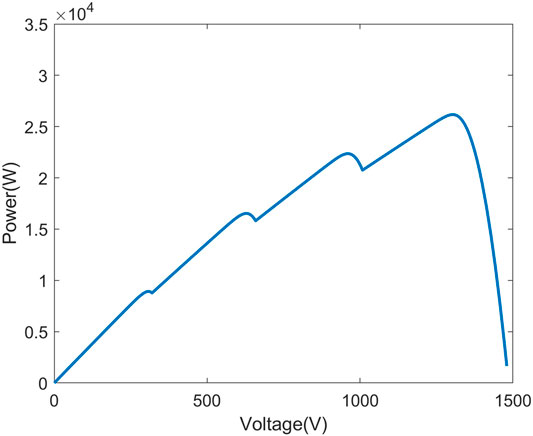
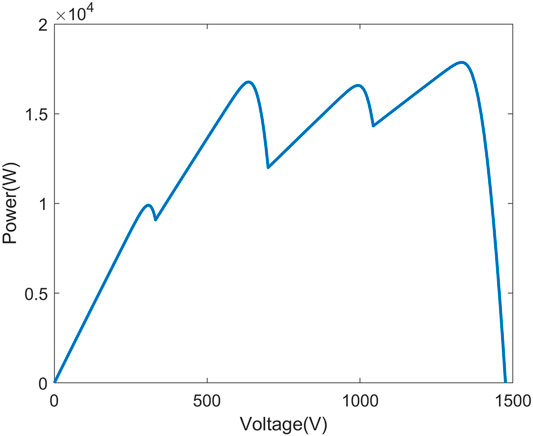
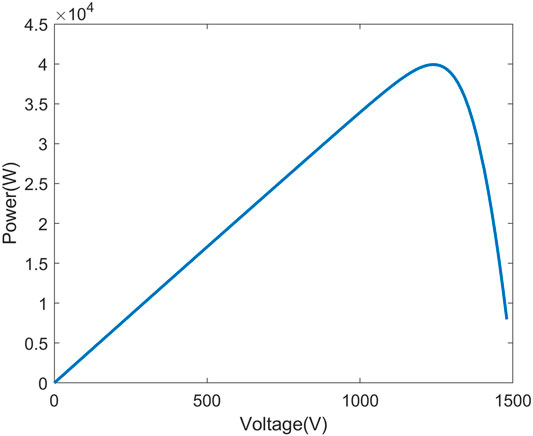
Figures 9–11 show the P-V curve for instances 2, 3, and 4, respectively. Figures 12–14 compare the startup response of the output power using fuzzy adaptive PSO and regular PSO controllers for irradiation levels of instances 2, 3, and 4, respectively. The results show that the fuzzy adaptive PSO controller is able to reach a steady state faster than the regular PSO controller. A comparison of the performance is quantified in Tables 5, 6. Table 5 shows that the settling time for the adaptive fuzzy PSO controller is faster than the regular PSO controller under all four irradiation conditions. Simulation results show that the controller is able to track the global MPP under PSC where multiple local MPP exist, as well as under uniform irradiation. The settling time using the proposed controller is 14% faster under PSC on average and 30% faster under uniform irradiation than the settling time using the regular PSO controller. Table 6 compares the output power and the maximum power point under the specific irradiation conditions. It shows both controllers were able to track the maximum power point under all four operating conditions.

FIGURE 9

FIGURE 9. Startup response of the fuzzy adaptive PSO and the convential PSO MPPT for irridiation 2.

FIGURE 10

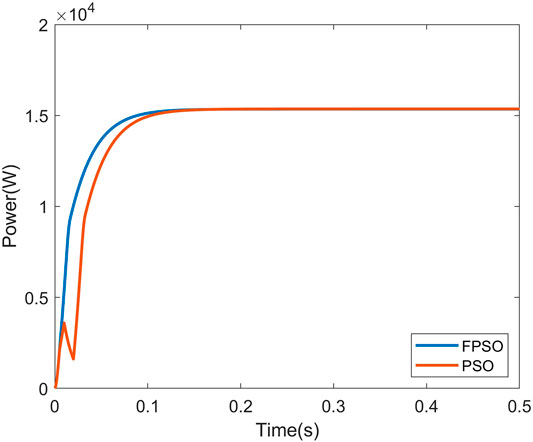
FIGURE 10. Startup response of the fuzzy adaptive PSO and the convential PSO MPPT for irridiation 3.

FIGURE 11

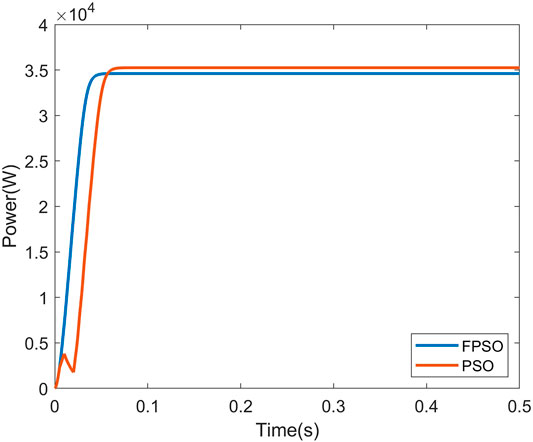
FIGURE 11. Startup response of the fuzzy adaptive PSO and the convential PSO MPPT for irridiation 4.

FIGURE 12

FIGURE 12. PV curve for irridiation 2.

FIGURE 13

FIGURE 13. PV curve for irridiation 3.

FIGURE 14

FIGURE 14. PV curve for irridiation 4.

TABLE 5

TABLE 5. Comparison of settling time for fuzzy adaptive PSO (FPSO) and conventional PSO.

TABLE 6

TABLE 6. Comparison of maximum power point (MPP), output power for fuzzy adaptive PSO (FPSO) and conventional PSO.

6 Conclusion

A fuzzy adaptive PSO-based MPPT was designed to track the maximum power point under partial shading conditions. The fuzzy controller was designed based on knowledge of the plant and computer simulations. The inertial weight was updated continuously by the fuzzy controller. Simulation results show that the fuzzy adaptive PSO-based MPPT was able to improve the global search process and increase the convergence speed. Compared to conventional PSO, the proposed controller achieved a faster response with accurate maximum power tracking. Future work can apply the proposed fuzzy adaptive PSO-based MPPT to isolated DC-DC converters such as flyback converters and current-fed dual active bridge converters for large scale grid-connected PV systems.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

LG and NA contributed to the conception and design of the study. Both authors performed the simulation, wrote the manuscript, contributed to manuscript revision, and approved the submitted version.

Funding

Partial support for this work was provided by the United States National Science Foundation’s Improving Undergraduate STEM Education (IUSE) program under Award No. DUE-1712146. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Al-Dahidi, S., Ayadi, O., Adeeb, J., and Louzazni, M. (2019). Assessment of Artificial Neural Networks Learning Algorithms and Training Datasets for Solar Photovoltaic Power Production Prediction. Front. Energ. Res. 7. doi:10.3389/fenrg.2019.00130

CrossRef Full Text | Google Scholar

Al-Shabi, M., Ghenai, C., Bettayeb, M., Faraz Ahmad, F., and El Haj Assad, M. (2021). Estimating PV Models Using Multi-Group Salp Swarm Algorithm. IJ-AI 10, 398–406. doi:10.11591/ijai.v10.i2.pp398-406

CrossRef Full Text | Google Scholar

Alizadeh, H., Alhuyi Nazari, M., Ghasempour, R., Shafii, M. B., and Akbarzadeh, A. (2020). Numerical Analysis of Photovoltaic Solar Panel Cooling by a Flat Plate Closed-Loop Pulsating Heat Pipe. Solar Energy 206, 455–463. doi:10.1016/j.solener.2020.05.058

CrossRef Full Text | Google Scholar

AlShabi, M., Ghenai, C., Bettayeb, M., Ahmad, F. F., and El Haj Assad, M. (2021). Multi-Group Grey Wolf Optimizer (MG-GWO) for Estimating Photovoltaic Solar Cell Model. J. Therm. Anal. Calorim. 144, 1655–1670. doi:10.1007/s10973-020-09895-2

CrossRef Full Text | Google Scholar

Chen, K., Tian, S., Cheng, Y., and Bai, L. (2014). An Improved MPPT Controller for Photovoltaic System under Partial Shading Condition. IEEE Trans. Sustain. Energ. 5, 978–985. doi:10.1109/tste.2014.2315653

CrossRef Full Text | Google Scholar

Chen, L. R., Chih-Hui Tsai, C. H., Yuan-Li Lin, Y. L., and Yen-Shin Lai, Y. S. (2010). A Biological Swarm Chasing Algorithm for Tracking the Pv Maximum Power point. IEEE Trans. Energ. Convers. 25, 484–493. doi:10.1109/tec.2009.2038067

CrossRef Full Text | Google Scholar

Cheng, P.-C., Peng, B.-R., Liu, Y.-H., Cheng, Y.-S., and Huang, J.-W. (2015). Optimization of A Fuzzy-Logic-Control-Based MPPT Algorithm Using the Particle Swarm Optimization Technique. Energies 8, 5338–5360. doi:10.3390/en8065338

CrossRef Full Text | Google Scholar

Esram, T., and Chapman, P. L. (2007). Comparison of Photovoltaic Array Maximum Power Point Tracking Techniques. IEEE Trans. Energ. Convers. 22, 439–449. doi:10.1109/tec.2006.874230

CrossRef Full Text | Google Scholar

Ghasemi, M. A., Foroushani, H. M., and Parniani, M. (2016). Partial Shading Detection and Smooth Maximum Power Point Tracking of PV Arrays under PSC. IEEE Trans. Power Electron. 31, 6281–6292. doi:10.1109/tpel.2015.2504515

CrossRef Full Text | Google Scholar

Guozden, T., Carbajal, J. P., Bianchi, E., and Solarte, A. (2020). Optimized Balance between Electricity Load and Wind-Solar Energy Production. Front. Energ. Res. 8, 16. doi:10.3389/fenrg.2020.00016

CrossRef Full Text | Google Scholar

Guo, L., Hung, J. Y., and Nelms, R. M. (2009). Evaluation of DSP-Based PID and Fuzzy Controllers for DC-DC Converters. IEEE Trans. Ind. Electron. 56, 2237–2248. doi:10.1109/tie.2009.2016955

CrossRef Full Text | Google Scholar

Ishaque, K., and Salam, Z. (2013). A Deterministic Particle Swarm Optimizationmaximum Power Point Tracker for Photovoltaicsystem under Partial Shading Condition. IEEE Trans. Ind. Electronics 60, 3195–3206. doi:10.1109/TIE.2012.2200223

Google Scholar

Khosravi, A., Malekan, M., Pabon, J. J. G., Zhao, X., and Assad, M. E. H. (2020). Design Parameter Modelling of Solar Power Tower System Using Adaptive Neuro-Fuzzy Inference System Optimized with a Combination of Genetic Algorithm and Teaching Learning-Based Optimization Algorithm. J. Clean. Prod. 244, 118904. doi:10.1016/j.jclepro.2019.118904

CrossRef Full Text | Google Scholar

Khosravi, A., Syri, S., Zhao, X., and Assad, M. E. H. (2019). An Artificial Intelligence Approach for Thermodynamic Modeling of Geothermal Based-Organic Rankine Cycle Equipped with Solar System. Geothermics 80, 138–154. doi:10.1016/j.geothermics.2019.03.003

CrossRef Full Text | Google Scholar

Koad, R. B. A., Zobaa, A. F., and El-Shahat, A. (2017). A Novel MPPT Algorithm Based on Particle Swarm Optimization for Photovoltaic Systems. IEEE Trans. Sustain. Energ. 8, 468–476. doi:10.1109/tste.2016.2606421

CrossRef Full Text | Google Scholar

Kok Soon Tey, K. S., and Mekhilef, S. (2014). Modified Incremental Conductance Algorithm for Photovoltaic System under Partial Shading Conditions and Load Variation. IEEE Trans. Ind. Electron. 61, 5384–5392. doi:10.1109/tie.2014.2304921

CrossRef Full Text | Google Scholar

Liu, Y. H., Huang, S. C., Huang, J. W., and Liang, W. C. (2012). A Particle Swarm Optimization-Based Maximum Power Point Tracking Algorithm for PV Systems Operating under Partially Shaded Conditions. IEEE Trans. Energ. Convers. 27, 1027–1035. doi:10.1109/tec.2012.2219533

CrossRef Full Text | Google Scholar

Maleki, A., Haghighi, A., El Haj Assad, M., Mahariq, I., and Alhuyi Nazari, M. (2020). A Review on the Approaches Employed for Cooling PV Cells. Solar Energy 209, 170–185. doi:10.1016/j.solener.2020.08.083

CrossRef Full Text | Google Scholar

Merchaoui, M., Hamouda, M., Sakly, A., and Mimouni, M. F. (2020). Fuzzy Logic Adaptive Particle Swarm Optimisation Based MPPT Controller for Photovoltaic Systems. IET Renew. Power Generation 14, 2933–2945. doi:10.1049/iet-rpg.2019.1207

CrossRef Full Text | Google Scholar

Madvar, D., Alhuyi Nazari, M., Tabe Arjmand, J., Aslani, A., Ghasempour, R., and Ahmadi, M. H. (2018). Analysis of Stakeholder Roles and the Challenges of Solar Energy Utilization in Iran. Int. J. Low-Carbon Tech. 13, 438–451. doi:10.1093/ijlct/cty044

CrossRef Full Text | Google Scholar

Mohanty, S., Subudhi, B., and Ray, P. K. (2016). A New MPPT Design Using Grey Wolf Optimization Technique for Photovoltaic System under Partial Shading Conditions. IEEE Trans. Sustain. Energ. 7, 181–188. doi:10.1109/tste.2015.2482120

CrossRef Full Text | Google Scholar

Nguyen, B. N., Nguyen, V. T., Duong, M. Q., Le, K. H., Nguyen, H. H., and Doan, A. T. (2020). Propose a MPPT Algorithm Based on Thevenin Equivalent Circuit for Improving Photovoltaic System Operation. Frontier Energ. Res. 8. doi:10.3389/fenrg.2020.00014

CrossRef Full Text | Google Scholar

Patel, H., and Agarwal, V. (2008). Maximum Power Point Tracking Scheme for PV Systems Operating under Partially Shaded Conditions. IEEE Trans. Ind. Electron. 55, 1689–1698. doi:10.1109/tie.2008.917118

CrossRef Full Text | Google Scholar

Priyadarshi, N., Padmanaban, S., Kiran Maroti, P., and Sharma, A. (2019). An Extensive Practical Investigation of Fpso-Based Mppt for Grid Integrated Pv System under Variable Operating Conditions with Anti-islanding protection. IEEE Syst. J. 13, 1861–1871. doi:10.1109/jsyst.2018.2817584

CrossRef Full Text | Google Scholar

Renaudineau, H., Donatantonio, F., Fontchastagner, J., Petrone, G., Spagnuolo, G., Martin, J.-P., et al. (2015). A PSO-Based Global MPPT Technique for Distributed PV Power Generation. IEEE Trans. Ind. Electron. 62, 1047–1058. doi:10.1109/tie.2014.2336600

CrossRef Full Text | Google Scholar

Rezk, H., Aly, M., Al-Dhaifallah, M., and Shoyama, M. (2019). Design and Hardware Implementation of New Adaptive Fuzzy Logic-Based MPPT Control Method for Photovoltaic Applications. IEEE Access 7, 106427–106438. doi:10.1109/access.2019.2932694

CrossRef Full Text | Google Scholar

Sohani, A., Hoseinzadeh, S., Samiezadeh, S., and Verhaert, I. (2021). Machine Learning Prediction Approach for Dynamic Performance Modeling of an Enhanced Solar Still Desalination System. J. Therm. Anal. Calorim.. doi:10.1007/s10973-021-10744-z

Google Scholar

Soufi, Y., Bechouat, M., and Kahla, S. (2016). Fuzzy-PSO Controller Design for Maximum Powerpoint Tracking in Photovoltaic System. Int. J. Hydrogen Energ. 42, 8680–8688.

Google Scholar

Sundareswaran, K., Peddapati, S., and Palani, S. (2014). MPPT of PV Systems under Partial Shaded Conditions through a Colony of Flashing Fireflies. IEEE Trans. Energ. Convers. 29, 463–472. doi:10.1109/tec.2014.2298237

CrossRef Full Text | Google Scholar

Sundareswaran, K., Sankar, P., Nayak, P. S. R., Simon, S. P., and Palani, S. (2015). Enhanced Energy Output from a PV System under Partial Shaded Conditions through Artificial Bee Colony. IEEE Trans. Sustain. Energ. 6, 198–209. doi:10.1109/tste.2014.2363521

CrossRef Full Text | Google Scholar