H∞–Adaptive H∞ Algorithm-Based State of Charge Estimation Considering the Hysteresis Effect for Lithium Polymer Battery

Introduction

Nowadays, energy crisis and environmental pollution issue force the fast application of sustainable energy on electrical equipment. Owing to natural advantages, lithium-ion batteries (LIBs) have been widely adopted in energy storage areas (Saha et al., 2019; Wei et al., 2019; Zhang et al., 2019; Feng et al., 2020). With the continuous improvement of lithium-ion batteries in energy density, enhancing their safety is becoming increasingly urgent for electric vehicle development (Divakaran et al., 2021). As a core function of the system, the accurate predicted SoC is a vital guarantee for LIBs’ safety and reliability (Zhang et al., 2017; Zhou et al., 2019).

In the past, numerous efforts have been made to improve the estimation performance. Firstly, simple and direct methods are the ampere-hour integral method and the open circuit voltage (OCV)–SoC lookup table (Zhang et al., 2016; Hu et al., 2020). Due to the error induced by the sensor failure and the imprecise initial value, studies about the former method are relatively rare. Otherwise, the latter always requires electric equipment to rest for hours. This method is also limited in practice. Secondly, the data-driven method is another alternative for the estimation, which mainly includes support vector machine, neural network (Ephrem et al., 2018), and fuzzy logic (Hametner and Jakubek, 2013). These approaches have the advantage of modeling systems with strong nonlinear characteristics. However, their prediction accuracies highly depend on the quantity and quality of the datasets used to train the LIBs’ model (Bian et al., 2019). Thirdly, the electrochemical model (Feng et al., 2020) and the equivalent circuit model (ECM) can be classified as model-based methods for the estimation. The former can reflect LIBs’ intrinsic parameters including conductivity and diffusivity but is limited by the heavy computational burden caused by tremendous partial differential equations (Hannan et al., 2017). Besides, ECMs such as the first-order RC model (Zhang et al., 2015; Yang et al., 2018; Lai et al., 2020), the second-order RC model (Hu et al., 2012), and the third-order RC model (Hu et al., 2018) have been used in the past to simulate the electrical behavior of the batteries. Otherwise, there exist nonlinear characteristics inside the batteries due to the hysteresis effect of the OCV. Therefore, some researchers build the ECM with the hysteresis unit aiming to further improve the estimation accuracy. For instance, based on the first-order battery RC model with the hysteresis unit, Verbrugge and Tate (2004) iteratively computed the SoC using the least-squares regression algorithm. Dong et al. (2016) embedded the hysteresis voltage into the second-order RC battery model and used dual invariant-imbedding algorithm for battery model and SoC estimations. However, these research studies did not compare the ECM considering the hysteresis effect with the ECM without considering that in terms of the estimation accuracy. On the other hand, the robust estimation algorithms for different ambient temperatures based on the ECM considering the hysteresis effect have rarely been reported in the literature.

Obtaining ECM’s parameters is the basis of computing the SoC. For this purpose, many algorithms have been employed to estimate these parameters, such as the least square, the particle swarm optimization, the genetic algorithm, the recursive least square, the extended Kalman filter, the H∞ filter, and the particle filter. A set of constant parameters can be obtained by the former three methods. Xiong et al., 2018, illustrated that parameters jitter largely when LIBs work at low ambient temperatures. Zhang et al., 2017, showed that both environmental temperature and battery aging can result in apparent changes in LIBs’ parameters. Therefore, the latter four methods are designed to identify these parameters in real-time and thus can reflect their variations.

After capturing the battery’s parameters, the space-state equation of the battery model should be solved. To this end, various algorithms such as the extended Kalman filter (Zhang et al., 2012), the unscented Kalman filter (He et al., 2016), and the particle filter (Chen et al., 2019) have been employed. However, for the aforementioned estimation algorithms, the process and the measurement of noise covariance matrices are set to be constant, which may not adapt various current loading conditions. Therefore, the adaptive technique was applied to the above filterings (Li et al., 2019; Li et al., 2020).

In this paper, the robust H∞ and the adaptive H∞ (AH∞) filterings were combined for the battery model and SoC estimations. To minimize the computational complexity of the SoC estimation approach, the hysteresis unit was integrated into the first-order RC battery model. Also, the H∞– AH∞ algorithm was developed under a dual-time frame to further drop the computational burden. Then, the battery model considering the hysteresis effect is compared with the model without considering that in terms of the estimation performance. Finally, the proposed estimation algorithm is evaluated against the dual H∞ filterings.

The rest of this paper is organized as follows. Section “Battery Experiment” details the battery experiments involved in this paper. The dual-time frame H∞–AH∞-based battery model parameters and SoC simultaneous estimation algorithm are deduced in the “Battery Model and Estimation Algorithms” section. Then, the employed battery model and the proposed approach are evaluated in the “Experimental Verification and Discussion” section. Finally, conclusions are drawn in the “Conclusion” section.

Battery Experiment

To evaluate the proposed approach in this work, corresponding battery testings were designed in this section. The battery test platform is introduced first. Then, relevant battery testings around this research are detailed.

A battery test platform as shown in our previous research (Feng et al., 2021) was utilized, including a YKYTEC battery test machine with 16 independent charging and discharging channels, a thermal chamber to regulate the operation temperature, and a computer with YKYTEC software.

The polymer battery cell in which the cathode material and anode material are LiNiMnCoO₂ and graphite, respectively, was tested on the platform. The basic parameters of the cell are given in Table 1.

TABLE 1

TABLE 1. Basic parameters of the tested battery cell.

The battery cell was tested by the characteristic test procedure at 20°C, 10°C, and 0°C. For the characteristic test, the available capacity testing was loaded on the cell to calibrate the actual capacity, followed by the incremental OCV testing (Yang et al., 2019) to acquire the OCV–SoC dataset. Then, a hybrid pulse current profile was loaded on the cell to test the responding terminal voltage. Referring to the research in the study by Ye et al., 2017, we defined the pulse current profile. As shown in Figure 1, the pulse current profile consisted of many cycles. In each cycle, the cell was first discharged using a current with 1C for 5 min, followed by a rest period for 5 min, followed by a charging process by the current with 0.1C for 5 min.

FIGURE 1

FIGURE 1. The dynamic pulse current profile.

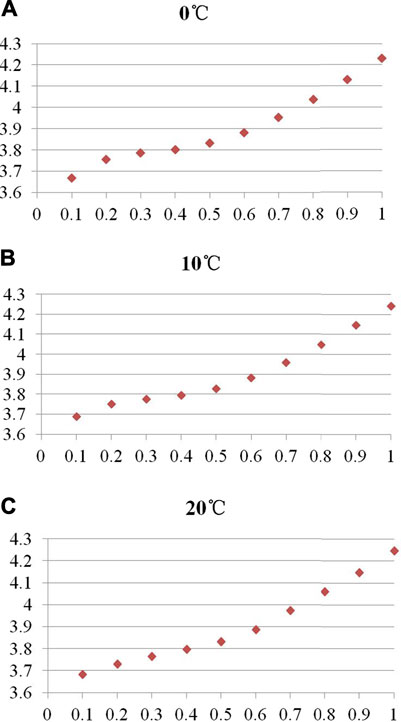
As a commonly used OCV calibrating method, the incremental OCV testing was carried out to obtain the OCV models in this work. Firstly, the cell was charged to 100% SoC with a current of 0.5C under the constant current and constant voltage (CCCV) mode (the charge cutoff current was 0.05C), and the cell was rested for 2 h when the charging process was finished. Secondly, the cell was discharged in every 10% SoC interval until the terminal voltage drops to the discharge cutoff voltage, and the cell was also rested for 2 h after every discharge interval was completed. During the discharge process, the current was set to 0.5C, and the corresponding SoC and terminal voltage were recorded at the end of every rest period. Thirdly, the cell was charged by the same routine as the discharge process. The CCCV mode is applied to the last charging SoC interval to fully charge the cell. Then, an averaging process of the charging and discharging OCV-SoC datasets (see Figures 2A–C) and a fitting process according to the six-order polynomial function were successively conducted to establish the traditional OCV model.

FIGURE 2

FIGURE 2. OCV–SoC dataset tested at three ambient temperatures. (A) 0°C; (B) 10°C; (C) 20°C.

Battery Model and the Estimation Algorithms

Battery Model

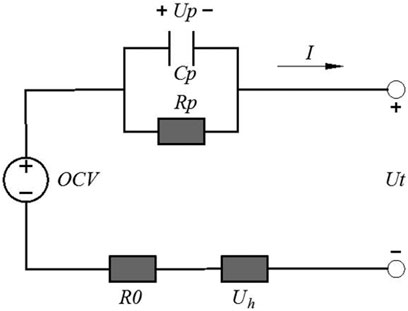
The first-order RC model with the hysteresis voltage as shown in Figure 3 is employed to simulate the nonlinear characteristics of the battery here. It consists of a voltage source OCV, an ohmic resistance R0, a polarization resistance Rp, a polarization capacitance Cp, and a hysteresis voltage U_h. Ut is the terminal voltage, and Up represents the polarization voltage. I represents the battery charging/discharging current.

FIGURE 3

FIGURE 3. The first-order RC model with the hysteresis voltage.

The electric characteristic of the battery model can be expressed as shown in Eq. 1.

$\{\begin{array}{l}\{\begin{array}{l}U{p}_k=\lambda U{p}_{k-1}+\left(1-\lambda \right)R{p}_k{I}_k\\ \lambda =\exp \left(\frac{-\Delta t}{R{p}_{k}C{p}_k}\right)\end{array},\\ \{\begin{array}{l}{V}_{h,k}=\lambda 1V_{h,k-1}+\left(1-\lambda 1\right)\mathrm{sgn}\left(I_k\right)\\ \lambda 1=\exp \left[-\left|{\gamma }_{k-1}{i}_{k-1}\Delta t\right|\right]\end{array}\\ U{t}_k=OC{V}_k-{\delta }_k{V}_{h,k}-I_k{R}_k-U{p}_k,\end{array},(1)$

where $\Delta t$ denotes the sampling time and equals one second; k is the microdiscrete-time index; and ${\gamma }_{k-1}$and ${\delta }_k$are hysteresis coefficients.

Battery Parameters Estimation Based on H∞

We assume that the space-state equation for parameters estimation is as shown in Eq. 2.

$\{\begin{array}{l}{X}_l=f\left(X_{l-1},u_{l-1}\right)+W_{l-1}\approx \frac{\partial X_l}{\partial X_{l-1}}{X}_{l-1}+W_{l-1}^{\prime }=F_{l-1}{X}_{l-1}+W_{l-1}^{\prime }\\ y_l=h\left(X_l,u_l\right)+v_l\approx \frac{\partial y_l}{\partial X_l}{X}_l+v_l^{\prime }=H_k{X}_l+v_l^{\prime }\end{array},(2)$

where$X_l$ represents the system state variable; $u_l$and $y_l$ are input and output of the system, respectively; $W_l^{\prime }$ and $v_l^{\prime }$ are process and measurement noise of the system with covariance matrices Q and R, respectively; $F_{l-1}=\partial X_l/\partial X_{l-1}$ and $H_l=\partial y_l/\partial X_l$ are coefficient matrices; l = k/L is the macrodiscrete-time index; and the L is the time scale defined by users.

As described in Eq. 3, our objective is to obtain the target matrix$O_l$,

$O_l={\Phi }_l{X}_l,(3)$

where $O_l$ is a linear combination of the state $X_l$ and ${\Phi }_l$ is a user-defined matrix according to the target matrix$O_l$.

According to the game theory, we should minimize the value of $\left(o_l-{\widehat{o}}_l\right)$ to make the cost function, as shown in Eq. 4, as small as possible.

$C=\frac{{\displaystyle {\sum }_{l=0}^{N-1}\parallel o_l-{\widehat{o}}_l{\parallel }_{S_l}^2}}{\parallel X_0-{\widehat{X}}_l{\parallel }_{P_0^{-1}}^2+{\displaystyle {\sum }_{l=0}^{N-1}\left(\parallel W_l^{\prime }{\parallel }_{Q_l^{-1}}^2+\parallel v_l^{\prime }{\parallel }_{R_l^{-1}}^2\right)}},(4)$

where $S_l$,$P_0$,$Q_l$, and $R_l$ are all user-defined symmetric positive matrices according to the specific problem.

To minimize the cost function, we should define a value of the performance boundary to make$C<1/\zeta$, and $\zeta$is defined by users.

For the first-order RC model, we define the state vector$X_l$as shown in Eq. 5.

$\{\begin{array}{l}{X}_l={(R{0}_l,R{p}_l,C{p}_l,OC{V}_l,{\delta }_l,{\gamma }_l,U{p}_l)}^T\\ R{0}_l=R{0}_{l-1},R{p}_l=R{p}_{l-1},C{p}_l=C{p}_{l-1}\\ {\delta }_l={\delta }_{l-1},{\gamma }_l={\gamma }_{l-1},OC{V}_l=OC{V}_{l-1}\end{array}.(5)$

Suppose that, IR_n →IR_m is a function from n-dimensional Euclidean space to m-dimensional Euclidean space. And, the function consists of a series of children functions as shown in Eq. 6.

$\left(\begin{array}{l}{y}_1(x_1,\cdot \cdot \cdot ,x_n)\\ \begin{array}{cccc}& ⋮& & \end{array}\\ y_m(x_1,\cdot \cdot \cdot ,x_n)\end{array}\right).(6)$

We can get the Jacobian matrix as shown in Eq. 7.

$\left(\begin{array}{lll}\frac{\partial y_1}{\partial x_1}\hfill & \cdots \hfill & \frac{\partial y_1}{\partial x_n}\hfill \\ ⋮\hfill & \ddots \hfill & ⋮\hfill \\ \frac{\partial y_m}{\partial x_1}\hfill & \cdots \hfill & \frac{\partial y_m}{\partial x_n}\hfill \end{array}\right).(7)$

Substituting Eqs. 1, 5, and 7 into Eq. 2, we get Eqs. 8 and 9.

$F_{l-1}=\left(\begin{array}{l}\mathrm{1,0,0,0,0,0,0}\\ \mathrm{0,1,0,0,0,0,0}\\ \mathrm{0,0,1,0,0,0,0}\\ \mathrm{0,0,0,1,0,0,0}\\ \mathrm{0,0,0,0,1,0,0}\\ \mathrm{0,0,0,0,0,1,0}\\ 0,\frac{\left(U{p}_{l-1}-R{p}_{l-1}{I}_{l-1}\right)\lambda \Delta t}{C{p}_{l-1}R{p}_{l-1}^2-I_{l-1}},\frac{\left(U{p}_{l-1}-R{p}_{l-1}{I}_{l-1}\right)\lambda \Delta t}{R{p}_{l-1}C{p}_{l-1}^2},\mathrm{0,0,0},\lambda \end{array}\right),(8)$

$H_l=\frac{\partial y_l}{\partial X_l}=\left(-I_l,\mathrm{0,0,1},-V_{h,k},0,-1\right).(9)$

In addition, to identify $R{0}_l$,$C{p}_l$,$R{p}_l$,${\delta }_l$, and ${\gamma }_l$, we define ${\Phi }_l$ as shown in Eq. 10.

${\Phi }_l=\left(\begin{array}{l}\mathrm{1,0,0,0,0,0,0}\\ \mathrm{0,1,0,0,0,0,0}\\ \mathrm{0,0,1,0,0,0,0}\\ \mathrm{0,0,0,0,0,0,0}\\ \mathrm{0,0,0,0,0,1,0}\\ \mathrm{0,0,0,0,0,0,0}\end{array}\right).(10)$

Battery SoC Estimation Based on AH∞

We assume that the space-state equation for SoC estimation is as shown in Eq. 11.

$\{\begin{array}{l}{X}_{a,k}=f\left(X_{a,k-1},u_{a,k-1}\right)+W_{a,k-1}\approx \frac{\partial X_{a,k}}{\partial X_{a,k-1}}{X}_{a,k-1}+W_{a,k-1}^{\prime }=A_{a,k-1}{X}_{a,k-1}+C_{a,k-1}{u}_{a,k-1}+W_{a,k-1}^{\prime }\\ y_{a,k}=h\left(X_{a,k},u_{a,k}\right)+v_{a,k}\approx \frac{\partial y_{a,k}}{\partial X_{a,k}}{X}_{a,k}+v_{a,k}^{\prime }=B_{a,k}{X}_{a,k}+v_{a,k}^{\prime }\\ O_{a,k}={\Phi }_{a,k}{X}_{a,k}\end{array},(11)$

where $X_{a,k}$ represents the system state variable; $u_{a,k-1}$and $y_{a,k}$ are input and output of the system, respectively; $W_{a,k-1}^{\prime }$ and $v_{a,k}^{\prime }$ are process and measurement noise of the system with covariance matrices $Q_a$and$R_a$, respectively; $A_{a,k-1},C_{a,k-1},$ and $B_{a,k}$ are coefficient matrices；$O_{a,k}$is a linear combination of the state$X_{a,k}$; ${\Phi }_{a,k}$ is a user-defined matrix according to the target matrix $O_{a,k}$.

SoC can be defined as shown in Eq. 12.

$So{C}_k=So{C}_{k-1}-\frac{{\eta }_C{I}_{k-1}\Delta t}{Ca},(12)$

where Ca denotes the current maximum available capacity of the battery and ${\eta }_C$represents the Ah efficiency.

Take dynamic electrical characteristics in Eq. 1 into consideration and define Eq. 13.

$X_{a,k}={\left(U{p}_k,V_{h,k},So{C}_k\right)}^T.(13)$

Parameters in Eq. 11 can be expressed as shown in Eq. 14.

$A_{a,k-1}=\left(\begin{array}{l}\lambda ,\mathrm{0,0}\\ 0,\lambda \mathrm{1,0}\\ \mathrm{0,0,1}\end{array}\right),C_{a,k-1}=\left(\begin{array}{l}(1-\lambda )R{p}_k{I}_k\\ (1-\lambda 1)\mathrm{sgn}\left(I_{k-1}\right)\\ \frac{-{\eta }_C{I}_{k-1}\Delta t}{Ca}\end{array}\right),B_{a,k}=\left(-1,-{\delta }_k,\frac{\partial \left(OC{V}_k\right)}{\partial \left(So{C}_k\right)}\right),(14)$

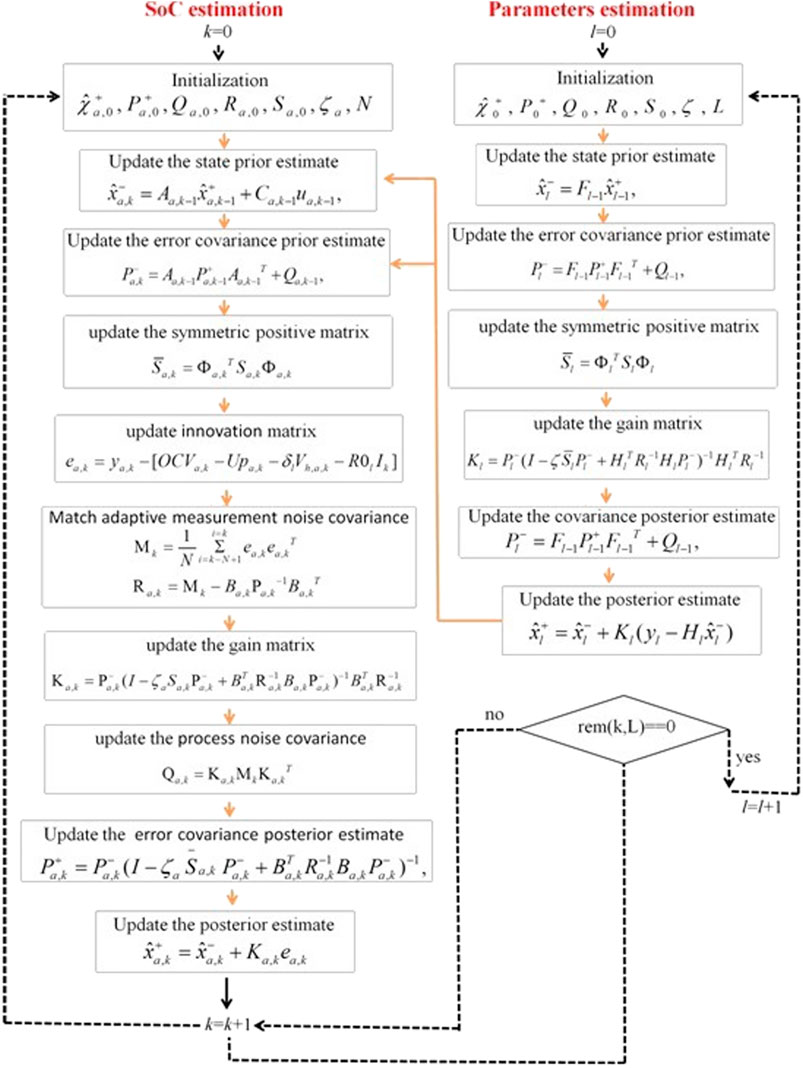
H∞–AH∞-Based Dual-Time Frame Parameters and SoC Coprediction Procedure

We have derived$X_l$, $F_{l-1}$, $H_l$, ${\Phi }_l$, $X_{a,k}$,$A_{a,k-1}$, $C_{a,k-1}$, and $B_{a,k}$. Then, we substitute these parameters into the multitime frame parameter and SoC coprediction procedure as follows, and thus, the battery parameter and SoC can be solved.

For k = 0,

Step 1: parameter and state initialization

(1) Set the state initial value

${\widehat{x}}_{a,0}^{+}=E\left(x_{a,0}\right),P_{a,0}^{+}=E\left[(x_{a,0}-{\widehat{x}}_{a,0}^{+}){(x_{a,0}-{\widehat{x}}_{a,0}^{+})}^T\right],Q_{a,0},R_{a,0},S_{a,0},{\zeta }_a,N,$

where ${\zeta }_a$is defined by users to determine the performance boundary for SoC computation and N means the time interval used to compute the measurement noise covariance R_a,k as shown in Eq. 20.

(2) Set the parameter initial value

${\widehat{x}}_0^{+}=E\left(x_0\right),P_0^{+}=E\left[(x_0-{\widehat{x}}_0^{+}){(x_0-{\widehat{x}}_0^{+})}^T\right],Q_0,R_0,S_0,\zeta ,L,$

where L is the constant defined by users to determine the time interval for parameters updation.

End

For k = 1, 2,….,∞,

Step 2: state estimate

1) Update the state prior estimate value ${\widehat{x}}_{a,k}^{-}$

${\widehat{x}}_{a,k}^{-}=A_{a,k-1}{\widehat{x}}_{a,k-1}^{+}+C_{a,k-1}{u}_{a,k-1}.(15)$

2) Update the error covariance prior estimate value $P_{a,k}^{-}$

$P_{a,k}^{-}=A_{a,k-1}{P}_{a,k-1}^{+}{A}_{a,k-1}^T+Q_{a,k-1}.(16)$

3) Update the symmetric positive matrix ${\overline{S}}_{a,k}$

${\overline{S}}_{a,k}={\Phi }_{a,k}^T{S}_{a,k}{\Phi }_{a,k}.(17)$

4) Update innovation matrix

$e_{a,k}=y_{a,k}-\left[OC{V}_{a,k}-U{p}_{a,k}-{\delta }_l{V}_{h,a,k}-R{0}_l{I}_k\right].(18)$

5) Match adaptive measurement noise covariance R_a,k

${\mathrm{M}}_k=\frac{1}{N}\underset{i=k-N+1}{\overset{i=k}{\Sigma }}{e}_{a,k}{e}_{a,k}^T,(19)$

${\mathrm{R}}_{a,k}={\mathrm{M}}_k-B_{a,k}{\mathrm{P}}_{a,k}^{-1}{B}_{a,k}^T.(20)$

6) Update Kalman gain matrix ${\mathrm{K}}_{a,k}$

${\mathrm{K}}_{a,k}={\mathrm{P}}_{a,k}^{-}{\left(I-{\zeta }_a{S}_{a,k}{\mathrm{P}}_{a,k}^{-}+B_{a,k}^T{\mathrm{R}}_{a,k}^{-1}{B}_{a,k}{\mathrm{P}}_{a,k}^{-}\right)}^{-1}{B}_{a,k}^T{\mathrm{R}}_{a,k}^{-1}.(21)$

7) Update process noise covariance estimation ${\mathrm{Q}}_{a,k}$

${\mathrm{Q}}_{a,k}={\mathrm{K}}_{a,k}{\mathrm{M}}_k{\mathrm{K}}_{a,k}^T.(22)$

8) Update the state posterior estimate value ${\widehat{x}}_{a,k}^{+}$

${\widehat{x}}_{a,k}^{+}={\widehat{x}}_{a,k}^{-}+K_{a,k}{e}_{a,k}.(23)$

9) Update the error covariance posterior estimate value $P_{a,k}^{+}$

$P_{a,k}^{+}=P_{a,k}^{-}{(I-{\zeta }_a{\stackrel{-}{S}}_{a,k}{P}_{a,k}^{-}+B_{a,k}^T{R}_{a,k}^{-1}{B}_{a,k}{P}_{a,k}^{-})}^{-1},(24)$

k = k+1;

End

If rem (k,L) = = 1,

Step 3: parameter estimate, for l = l+1,

1) Time update

1) Update the state prior estimate value ${\widehat{x}}_l^{-}$

${\widehat{x}}_l^{-}=F_{l-1}{\widehat{x}}_{l-1}^{+}.(25)$

2) Update the error covariance prior estimate value $P_l^{-}$

$P_l^{-}=F_{l-1}{P}_{l-1}^{+}{F}_{l-1}^T+Q_{l-1}.(26)$

3) Update the symmetric positive matrix ${\overline{S}}_l$

${\overline{S}}_l={\Phi }_l^T{S}_l{\Phi }_l.(27)$

2) Measurement update

1) Update the gain matrix $K_l$

$K_l=P_l^{-}{\left(I-\zeta {\overline{S}}_l{P}_l^{-}+H_l^T{R}_l^{-1}{H}_l{P}_l^{-}\right)}^{-1}{H}_l^T{R}_l^{-1}.(28)$

2) Update the state posterior estimate value ${\widehat{x}}_l^{+}$

${\widehat{x}}_l^{+}={\widehat{x}}_l^{-}+K_l\left(y_l-H_l{\widehat{x}}_l^{-}\right).(29)$

3) Update the error covariance posterior estimate value $P_l^{-}$

$P_l^{-}=F_{l-1}{P}_{l-1}^{+}{F}_{l-1}^T+Q_{l-1}.(30)$

End

The flowchart of the combined H∞–adaptive H∞ algorithm is shown in Figure 4.

FIGURE 4

FIGURE 4. The flowchart of the H∞–adaptive H∞ Algorithm.

Experimental Verification and Discussion

Parameter Estimation Results

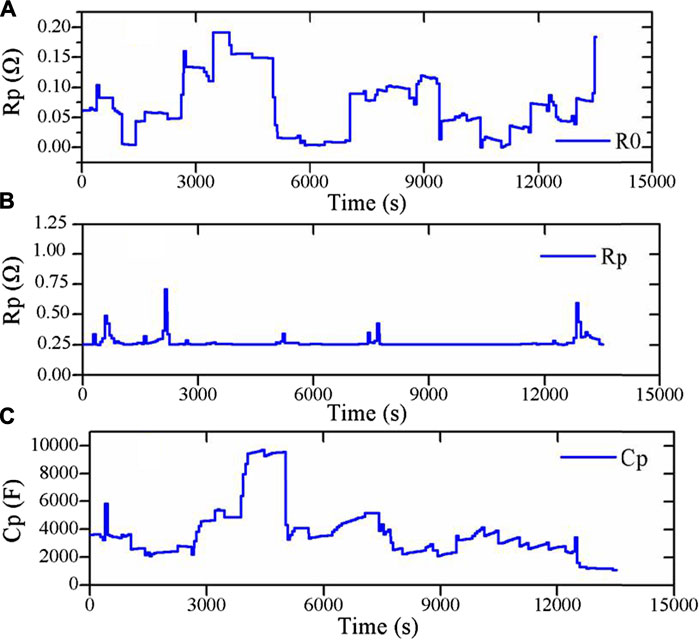
Figure 5 shows parameter estimation results based on the H∞ method for the cell tested at 0°C. Figures 5A–C show the estimated ohmic resistance R0, polarization resistance Rp, and polarization capacitance Cp, respectively. Figure 5A compares the measured Ut with the estimated one. We can observe that the former is very close to the latter. Figure 6 plots the comparison of the measured and the estimated terminal voltage. As shown in Figure 6B, the maximum estimate error occurs at the ending phase of the discharge process, and the maximum absolute error (MAXE) is about 10mV, which illustrates the accuracy of adequate battery parameter estimation.

FIGURE 5

FIGURE 5. Results of parameter identification. (A) R0; (B) Rp; (C) Cp.

FIGURE 6

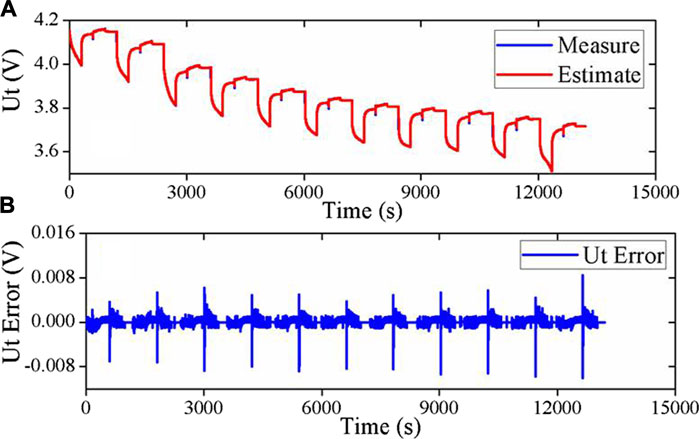
FIGURE 6. Estimated terminal voltage and error. (A) Comparison of the estimated Ut and measured one; (B)Ut error.

Evaluation of the Employed Battery Model

In this section, the effectiveness of the employed battery model in this paper is compared with the model without the hysteresis voltage in terms of the SoC estimation accuracy at three temperatures. For all the cases below, the initial SoCs are set to 80% away from the true value. For the convenience of statements in the later text, we define the employed battery model in this paper and the first-order RC battery model as model 1 and model 2, respectively.

Since the ambient temperature has a direct impact on the battery performance (Divakaran et al., 2020), the pulse current profiles were tested at 20°C, 10°C, and 0°C to verify the robustness of the battery model with the hysteresis unit against different temperatures. Figure 7 shows the estimation results of model 1 and model 2 at three temperatures. Figures 7A,B describe the estimated SoCs and estimation errors at 20°C, respectively. It can be observed that model 1 can acquire more accurate SoC than model 2. The MAXE of the SoC estimation by model 2 is 5.70%, while that by model 1 is only 4.60%. As a result, model 1 can further reduce the prediction error by 19.3% compared with model 2. Besides, the SoC can converge to the true value quickly within 30 s, which shows the fast convergence ability of the derived copredict algorithm.

FIGURE 7

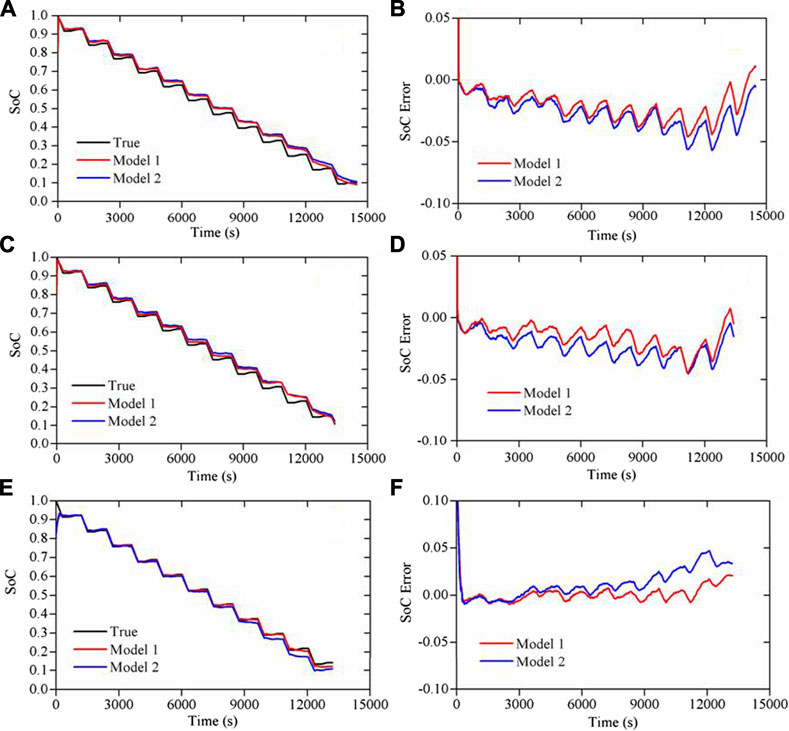
FIGURE 7. Comparison results at three temperatures. (A) Estimated SoCs at 20°C; (B) estimation errors at 20°C; (C) estimated SoCs at 10°C; (D) estimation errors at 10°C; (E) estimated SoCs at 0°C; (F) estimation errors at 0°C.

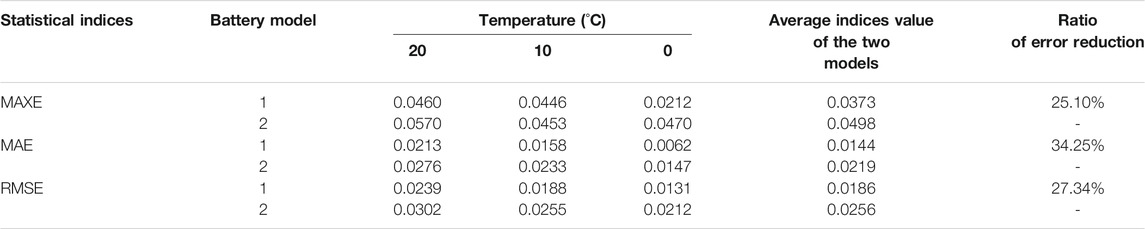
In addition to the MAXE, the mean absolute error (MAE) and the root mean square error (RMSE) are also used to verify the effectiveness of the employed battery model as shown in Table 2. It can be found that model 1 outperforms model 2 for all the two statistical indices at three battery testing temperatures.

TABLE 2

TABLE 2. Estimate errors and analysis.

Similarly, Figures 7C,D compare the two models from the aspect of the estimated SoC and the estimation error at 10°C, respectively. We can see that the estimated SoC by model 1 is closer to the true value than that by model 2 in the global SoC interval. The MAXE of estimation by model 2 and model 1 are 4.53 and 4.46%, respectively. Although the improvement is not notable as for the MAXE, both the MAE and the RMSE can be further dropped by model 1 as shown in Table 2. Especially for the MAE, the index can be reduced by about 32.2%. Besides, the convergence time can be controlled within 60 s.

Figures 7E,F show the estimated SoC and the corresponding estimation error of the two battery models at 0°C, respectively. Like cases above, the advantage of model 1 can also be found. The MAXE of estimation based on model 2 represents 4.70%, while model 1 can further drop the index to 2.12%. As a result, the MAXE can be reduced by about 55%. Compared with cases at 20°C and 10°C, it can be found that the accuracy improvement is more pronounced in this case. It illustrates the excellent prediction performance of the improved model for the cell tested at a low temperature of 0°C. Besides, the estimated SoC by model 1 can exhibit a shorter convergence time (i.e., 265 s), while the SoC based on model 2 converges to the true value when the time reaches about 300 s. Also, it can be found that model 1 can further reduce the estimation error in terms of both the MAE and the RMSE compared with model 2 for all the three battery testing temperatures as shown in Table 2. It illustrates that the battery model considering the hysteresis effect can not only drop the estimation error but also shorten the convergence period at the low-temperature environment.

On average, the MAXE, the MAE, and the RMSE can be reduced by about 25, 34, and 27% by the employed battery model in this paper, respectively, as shown in Table 2. Therefore, the conclusion can be drawn that the first-order RC battery model considering the hysteresis effect can further reduce the estimation error and simultaneously drop the convergence period compared with the model without considering that effect.

Evaluation of the Proposed Estimation Method

To evaluate the proposed dual-time frame H∞–AH∞ (DTF H∞–AH∞)-based SoC estimation algorithm, comparisons with the dual-time frame dual H∞ (DTFDH∞) method are conducted. The initial SoCs are all set to 80% away from the true values.

Figure 8 shows the comparison results of the above two estimation approaches. Overall, compared with the online estimation algorithm based on the proposed DTF H∞–AH∞, the estimation error curves based on the DTFDH∞ method cause larger fluctuations at all three temperatures.

FIGURE 8

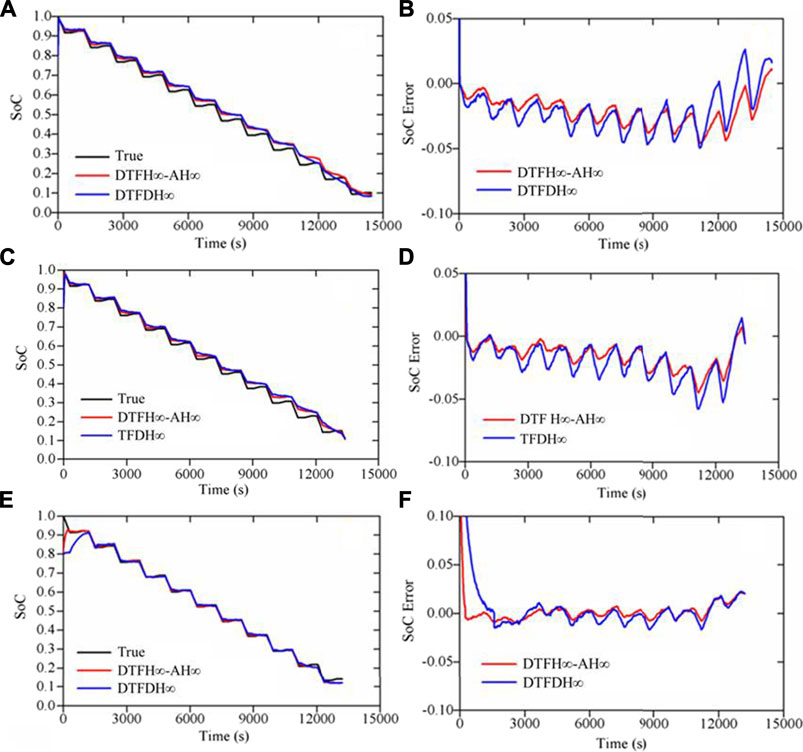
FIGURE 8. Comparison results for the cell tested at three temperatures. (A) Estimated SoCs at 20°C; (B) estimation errors at 20°C; (C) estimated SoCs at 10°C; (D) estimation errors at 10°C; (E) estimated SoCs at 0°C; (F) estimation errors at 0°C.

Figures 8A,B represent the estimated SoC and the estimation error at 20°C, respectively. It can be found that the MAXE of the DTF H∞–AH∞ method (i.e., 4.60%) is less than that of the DTFDH∞ method (i.e., 4.97%). Also, we can see that the convergence period of the latter (35 s) is enlarged compared with the former (30 s).

Figures 8C,D describe the estimated SoC and the estimation error at 0°C, respectively. The advantage of the DTF H∞–AH∞ method against the DTFDH∞ method can be clearly observed. The MAXE of the former and the latter are 2.12 and 2.25%, respectively. Besides, compared with the convergence period of the latter (85 s), that of the former drops to 60 s.

Figures 8E,F plot the estimation result and the error at 0°C, respectively. It can be noted that the DTF H∞–AH∞ method performs better than the other method in terms of both the estimation accuracy and the convergence speed. The MAXE of the former and latter methods are 2.12 and 2.25%, respectively, and the convergence time of the above two methods is 265 and 1600 s, respectively.

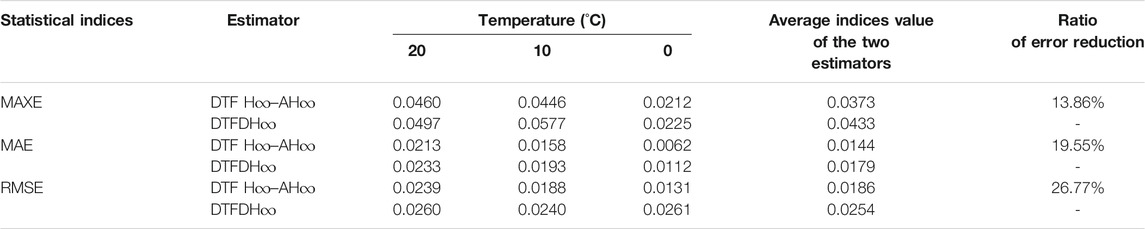
From Table 3, it can be found that the MAXE, the MAE, and the RMSE of estimation can be reduced by about 13, 19, and 26% on average by the DTF H∞–AH∞-based SoC estimation method, respectively. Accordingly, it demonstrates the effectiveness of the developed DTF H∞–AH∞ against the DTFDH∞ method in all the three temperatures stated above.

TABLE 3

TABLE 3. Estimate errors and analysis.

Conclusion

Accurate SoC estimation is the guarantee for safe and reliable running of the LIBs. The first-order RC battery model with hysteresis voltage is employed to simulate the electric characteristics of the lithium polymer battery, based on which a dual-time frame estimation algorithm based on the H∞ and the AH∞ filterings is used to simultaneously estimate the battery model parameters and the SoC.

The effectiveness of the employed battery model is compared with the traditional first-order RC battery model from the aspect of estimation accuracy at both the room temperature (20°C) and the low temperatures (10°C and 0°C). Finally, the proposed DTF H∞–AH∞-based estimation approach is evaluated against the DTFDH∞ method under the above battery testing conditions.

The results reveal that the battery model with the hysteresis voltage can outperform the model without that in terms of SoC estimation, and simultaneously, the MAXE, the MAE, and the RMSE of estimation can be reduced. Also, the employed battery model can shorten the estimation convergence period. In addition, the proposed DTF H∞–AH∞-based estimation algorithm has proved to be superior to the DTFDH∞-based method in terms of all the three statistical indices stated above, and the proposed estimation method can also further reduce the convergence time on the basis of the DTFDH∞ method. Ultimately, the estimation performance can be enhanced, thanks to the excellent performance of the DTF H∞–AH∞ estimation method, based on the employed battery model.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the National Natural Science Foundation of China (Grant no. 51775042).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

SoC, State of charge; LIBs, Lithium-ion batteries; OCV, Open circuit voltage; EMC, Equivalent circuit model; AH∞, Adaptive H∞; CCCV, Constant current constant voltage; MAXE, Maximum absolute error; MAE, Mean absolute error; RMSE, Root mean square error; DTF H∞–AH∞, Dual-time frame H∞–AH∞; DTFD, H∞ dual-time frame dual H∞; R0, Ohmic resistance; Rp, Polarization resistance; Cp, Polarization capacitance; Ut, Terminal voltage; Up, Polarization voltage; ${\gamma }_{k-1},{\delta }_k$, Hysteresis coefficients; ${\zeta }_a$, Coefficient for the performance boundary of SoC estimation; N, Constant for R_a,k determination; L, Time interval for updation of parameters.

References

Bian, C., He, H., Yang, S., and Huang, T. (2020). State-of-charge Sequence Estimation of Lithium-Ion Battery Based on Bidirectional Long Short-Term Memory Encoder-Decoder Architecture. J. Power Sourc. 449, 227558. doi:10.1016/j.jpowsour.2019.227558

CrossRef Full Text | Google Scholar

Chemali, E., Kollmeyer, P. J., Preindl, M., and Emadi, A. (2018). State-of-charge Estimation of Li-Ion Batteries Using Deep Neural Networks: A Machine Learning Approach. J. Power Sourc. 400, 242–255. doi:10.1016/j.jpowsour.2018.06.104

CrossRef Full Text | Google Scholar

Chen, Z., Sun, H., Dong, G., Wei, J., and Wu, J. (2019). Particle Filter-Based State-Of-Charge Estimation and Remaining-Dischargeable-Time Prediction Method for Lithium-Ion Batteries. J. Power Sourc. 414, 158–166. doi:10.1016/j.jpowsour.2019.01.012

CrossRef Full Text | Google Scholar

Divakaran, A. M., Hamilton, D., Manjunatha, K. N., and Minakshi, M. (2020). Design, Development and Thermal Analysis of Reusable Li-Ion Battery Module for Future Mobile and Stationary Applications. Energies 13, 1477. doi:10.3390/en13061477

CrossRef Full Text | Google Scholar

Divakaran, A. M., Minakshi, M., Bahri, P. A., Paul, S., Kumari, P., Divakaran, A. M., et al. (2021). Rational Design on Materials for Developing Next Generation Lithium-Ion Secondary Battery. Prog. Solid State. Chem. 62, 100298. doi:10.1016/j.progsolidstchem.2020.100298

CrossRef Full Text | Google Scholar

Dong, G., Wei, J., Zhang, C., and Chen, Z. (2016). Online State of Charge Estimation and Open Circuit Voltage Hysteresis Modeling of LiFePO4 Battery Using Invariant Imbedding Method. Appl. Energ. 162, 163–171. doi:10.1016/j.apenergy.2015.10.092

CrossRef Full Text | Google Scholar

Feng, F., Teng, S., Liu, K., Xie, J., Xie, Y., Liu, B., et al. (2020). Co-estimation of Lithium-Ion Battery State of Charge and State of Temperature Based on a Hybrid electrochemical-thermal-neural-network Model. J. Power Sourc. 455, 227935. doi:10.1016/j.jpowsour.2020.227935

CrossRef Full Text | Google Scholar

Feng, H., Wang, Z., and Zhang, F. (2021). A Comprehensive Evaluation of the Influence of Major Hysteresis on State of Charge Prediction of LiNiMnCoO2 Battery. Front. Energ. Res. 9, 666092. doi:10.3389/fenrg.2021.666092

CrossRef Full Text | Google Scholar

Hametner, C., and Jakubek, S. (2013). State of Charge Estimation for Lithium Ion Cells: Design of Experiments, Nonlinear Identification and Fuzzy Observer Design. J. Power Sourc. 238, 413–421. doi:10.1016/j.jpowsour.2013.04.040

CrossRef Full Text | Google Scholar

Hannan, M. A., Lipu, M. S. H., Hussain, A., and Mohamed, A. (2017). A Review of Lithium-Ion Battery State of Charge Estimation and Management System in Electric Vehicle Applications: Challenges and Recommendations. Renew. Sustain. Energ. Rev. 78, 834–854. doi:10.1016/j.rser.2017.05.001

CrossRef Full Text | Google Scholar

He, H., Xiong, R., and Peng, J. (2016). Real-time Estimation of Battery State-Of-Charge with Unscented Kalman Filter and RTOS μCOS-II Platform. Appl. Energ. 162, 1410–1418. doi:10.1016/j.apenergy.2015.01.120

CrossRef Full Text | Google Scholar

Hu, L., Hu, X., Che, Y., Feng, F., Lin, X., and Zhang, Z. (2020). Reliable State of Charge Estimation of Battery Packs Using Fuzzy Adaptive Federated Filtering. Appl. Energ. 262, 114569. doi:10.1016/j.apenergy.2020.114569

CrossRef Full Text | Google Scholar

Hu, M., Li, Y., Li, S., Fu, C., Qin, D., and Li, Z. (2018). Lithium-ion Battery Modeling and Parameter Identification Based on Fractional Theory. Energy 165, 153–163. doi:10.1016/j.energy.2018.09.101

CrossRef Full Text | Google Scholar

Hu, X., Li, S., and Peng, H. (2012). A Comparative Study of Equivalent Circuit Models for Li-Ion Batteries. J. Power Sourc. 198, 359–367. doi:10.1016/j.jpowsour.2011.10.013

CrossRef Full Text | Google Scholar

Lai, X., Wang, S., Ma, S., Xie, J., and Zheng, Y. (2020). Parameter Sensitivity Analysis and Simplification of Equivalent Circuit Model for the State of Charge of Lithium-Ion Batteries. Electrochim. Acta 330, 135239. doi:10.1016/j.electacta.2019.135239

CrossRef Full Text | Google Scholar

Li, W., Fan, Y., Ringbeck, F., Jöst, D., Han, X., Ouyang, M., et al. (2020). Electrochemical Model-Based State Estimation for Lithium-Ion Batteries with Adaptive Unscented Kalman Filter. J. Power Sourc. 476, 228534. doi:10.1016/j.jpowsour.2020.228534

CrossRef Full Text | Google Scholar

Li, X., Wang, Z., and Zhang, L. (2019). Co-estimation of Capacity and State-Of-Charge for Lithium-Ion Batteries in Electric Vehicles. Energy 174, 33–44. doi:10.1016/j.energy.2019.02.147

CrossRef Full Text | Google Scholar

Saha, P., Dey, S., and Khanra, M. (2019). Accurate Estimation of State-Of-Charge of Supercapacitor under Uncertain Leakage and Open Circuit Voltage Map. J. Power Sourc. 434, 226696. doi:10.1016/j.jpowsour.2019.226696

CrossRef Full Text | Google Scholar

Verbrugge, M., and Tate, E. (2004). Adaptive State of Charge Algorithm for Nickel Metal Hydride Batteries Including Hysteresis Phenomena. J. Power Sourc. 126, 236–249. doi:10.1016/j.jpowsour.2003.08.042

CrossRef Full Text | Google Scholar

Wei, Z., Zhao, J., Xiong, R., Dong, G., Pou, J., and Tseng, K. J. (2019). Online Estimation of Power Capacity with Noise Effect Attenuation for Lithium-Ion Battery. IEEE Trans. Ind. Electron. 66, 5724–5735. doi:10.1109/TIE.2018.2878122

CrossRef Full Text | Google Scholar

Xiong, R., Zhang, Y., He, H., Zhou, X., and Pecht, M. G. (2018). A Double-Scale, Particle-Filtering, Energy State Prediction Algorithm for Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 65, 1526–1538. doi:10.1109/TIE.2017.2733475

CrossRef Full Text | Google Scholar

Yang, D., Wang, Y., Pan, R., Chen, R., and Chen, Z. (2018). State-of-health Estimation for the Lithium-Ion Battery Based on Support Vector Regression. Appl. Energ. 227, 273–283. doi:10.1016/j.apenergy.2017.08.096

CrossRef Full Text | Google Scholar

Yang, J., Huang, W., Xia, B., and Mi, C. (2019). The Improved Open-Circuit Voltage Characterization Test Using Active Polarization Voltage Reduction Method. Appl. Energ. 237, 682–694. doi:10.1016/j.apenergy.2019.01.060

CrossRef Full Text | Google Scholar

Ye, M., Guo, H., and Cao, B. (2017). A Model-Based Adaptive State of Charge Estimator for a Lithium-Ion Battery Using an Improved Adaptive Particle Filter. Appl. Energ. 190, 740–748. doi:10.1016/j.apenergy.2016.12.133

CrossRef Full Text | Google Scholar

Zhang, C., Jiang, J., Gao, Y., Zhang, W., Liu, Q., and Hu, X. (2017). Charging Optimization in Lithium-Ion Batteries Based on Temperature Rise and Charge Time. Appl. Energ. 194, 569–577. doi:10.1016/j.apenergy.2016.10.059

CrossRef Full Text | Google Scholar

Zhang, C., Jiang, J., Zhang, L., Liu, S., Wang, L., and Loh, P. (2016). A Generalized SOC-OCV Model for Lithium-Ion Batteries and the SOC Estimation for LNMCO Battery. Energies 9, 900. doi:10.3390/en9110900

CrossRef Full Text | Google Scholar

Zhang, C., Jiang, J., Zhang, W., and Sharkh, S. M. (2012). Estimation of State of Charge of Lithium-Ion Batteries Used in HEV Using Robust Extended Kalman Filtering. Energies 5, 1098–1115. doi:10.3390/en5041098

CrossRef Full Text | Google Scholar

Zhang, C., Wang, L. Y., Li, X., Chen, W., Yin, G. G., and Jiang, J. (2015). Robust and Adaptive Estimation of State of Charge for Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 62, 4948–4957. doi:10.1109/TIE.2015.2403796

CrossRef Full Text | Google Scholar

Zhang, C., Wang, Y., Gao, Y., Wang, F., Mu, B., and Zhang, W. (2019). Accelerated Fading Recognition for Lithium-Ion Batteries with Nickel-Cobalt-Manganese Cathode Using Quantile Regression Method. Appl. Energ. 256, 113841. doi:10.1016/j.apenergy.2019.113841

CrossRef Full Text | Google Scholar

Zhou, Z., Duan, B., Kang, Y., Cui, N., Shang, Y., and Zhang, C. (2019). A Low-Complexity State of Charge Estimation Method for Series-Connected Lithium-Ion Battery Pack Used in Electric Vehicles. J. Power Sourc. 441, 226972. doi:10.1016/j.jpowsour.2019.226972

CrossRef Full Text | Google Scholar