Optimum Layout of Multiple Tree-type Boreholes in Low-Permeability Coal Seams to Improve Methane Drainage Performance

Extracting coal mine methane (CMM) is important for underground mining safety. The tree-type borehole drainage (TTBD) technique can effectively remove methane from coal seams. Determining a suitable drilling pattern for multiple tree-type boreholes will promote the efficient application of this technique in coal mines. Aimed at solving the problem that the optimum methane extraction layout for multiple tree-type boreholes is unclear, this study first constructed a full-coupled thermo-hydro-mechanical model to simulate methane flow in coal. This model and data from a coal mine were used to investigate the effect of multiple tree-type borehole layouts, tree-type borehole spacing, different Langmuir volume and different Langmuir pressure constants, and initial coal permeabilities on CMM drainage. The results show that the different tree-type borehole layouts result in significant differences in drainage and that the use of a rhombic sub-borehole layout can reduce the methane pre-drainage time by up to 44.4%. As the tree-type borehole spacing increases, the total time required for pre-drainage increases as a power function. As the Langmuir pressure constant, the fracture permeability, or the matrix permeability increases, the effective drainage zone expands. The effective drainage zone also expands when the Langmuir volume constant decreases but all these changes are accompanied by a shortening of the drainage completion time. These results can provide a reliable basis for optimizing tree-type borehole drilling layouts.

Introduction

Over the past few centuries, coal has been one of the world’s primary fossil fuel energy sources (Gyamfi et al., 2021; Li et al., 2021; Tsaa et al., 2021). Although many countries are currently reducing their coal consumption to decrease carbon dioxide emissions (Karacan and Warwick 2019; Adedoyin et al., 2020; Ge et al., 2020; Magazzino et al., 2020; Udi et al., 2020), coal still accounted for 27.2% of total global energy consumption in 2020 (BP 2021). During the formation of coal from plant debris, large volumes of methane are produced and sequestered, mainly by sorption. Coal mine methane (CMM) that is ejected from worked coal seams or other gas-bearing lithologies is a safety hazard in underground mines but this gas is also a form of relatively clean energy (Yang 2009; Ranathunga et al., 2014; Kędzior and Dreger 2019; Kholod et al., 2020). Draining CMM prior to and during coal mining can control the methane and allow this energy to be used, a tactic that suits China’s energy security strategy. Coal’s generally low permeability is the main factor that limits methane drainage from coal seams. In China, the permeabilities of most coal seams range only from 0.001∼0.0001 mD; this means that methane drainage is difficult and time consuming. The lead time for gas drainage through conventional boreholes commonly exceeds 2 years. As the mines opened to exploit coal resources become deeper, the coal’s permeability at the production face decreases and CMM pre-drainage becomes even more difficult (Xie 2019; Zhao Z. et al., 2020; Zhou et al., 2020). Under these conditions, the conventional method of drilling numerous closely spaced boreholes becomes unsatisfactorily (Gao et al., 2015; Lin et al., 2015). Because coal seam destressing to increase the coal’s permeability is beneficial for faster methane desorption and diffusion (Mordecai and Morris 1974; Palmer and Mansoori 1996; Zhu et al., 2013; Wang et al., 2016), borehole stimulation techniques for producing stress-relief zones are commonly employed in Chinese coal mines.

Techniques for stress reduction including hydraulic flushing, hydraulic slotting, hydraulic fracturing, and pre-splitting blasting have been developed. Because the cavities and slots produced by these techniques have small dimensions and it is difficult to ensure that the fractures in the stress-relief zones and the natural cleats in the coal are connected, the effect of a drainage zone produced by a cavity or slot is in many cases somewhat limited (Ge et al., 2014; Lin et al., 2015; Jiang et al., 2018). Hydraulic fracturing and pre-splitting blasting are stress relief methods that use high fluid pressures. The loading and unloading during and after blasting or fracturing shake the coal seam and relieve stress on local portions of the seam, however, these stress-relief zones are much smaller than those of cavities or slots. Hydraulic fracturing and pre-splitting blasting can achieve considerable stimulation in coal seams, but the creation of enhanced permeability area is easily influenced by the principle stress difference (Chen et al., 2017; Chi et al., 2018; Cheng et al., 2018; Huang et al., 2019) and thus CMM drainage is restricted. To better connect conventional boreholes to coal cleats and to create a large stress relief zone around a conventional borehole, a new method, tree-type borehole drainage (TTBD), was introduced by Lu et al. (2015) and Lu et al. (2019) (Figure 1). This method has been developed and tested in low-permeability coal seams (Xiao et al., 2018; Zhang et al., 2020). The TTBD method uses high-pressure waterjets generated by a self-propelled radially build multi-layer deep and long sub-boreholes in an existing cross-measure borehole. After employing TTBD, the conductivity pathways for CMM drainage are greatly increased (Ge et al., 2021; Xiao et al., 2021). Previous studies (Zhang et al., 2020; Zhang et al., 2021) focused mainly on analyzing the permeability enhancement and methane drainage capability of a single tree-type borehole. These studies showed that a single tree-type broehloe can deliver the desired levels of methane drainage from low-permeability coal seams. Because the TTBD method can effectively stimulate methane drainage from conventional boreholes and multiple boreholes are commonly needed to extract methane from the coal seams in underground coal mines, it is important to determine the optimum layouts for tree-type boreholes to guide future CMM drainage programs.

FIGURE 1

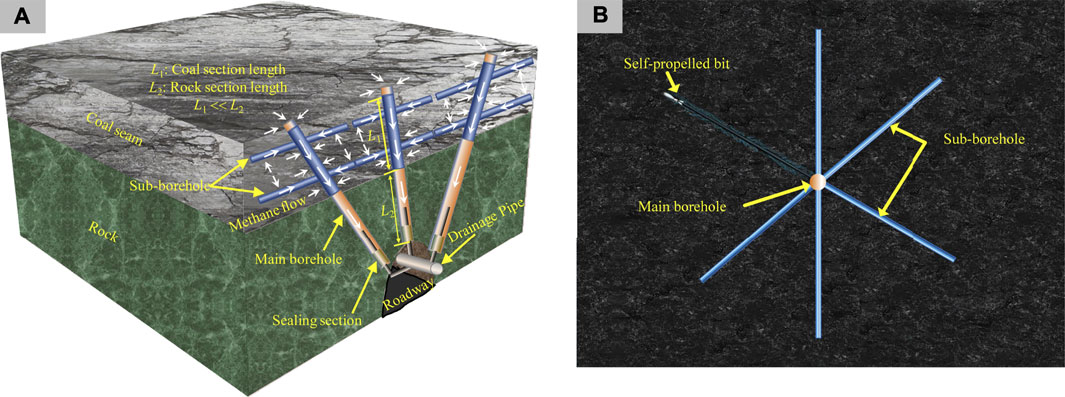
FIGURE 1. Illustrations showing tree-type borehole drainage technique. (A) Block diagram; (B) Plan view of a single boreole.

Experienced researchers have investigated both conventional borehole and stimulated l borehole layouts for enhancing underground CMM drainage. Using a thermo-hydro-mechanical (THM) coupled model, Gao et al. (2016) investigated the interactions between multiple borehole to optimize designs for multi-borehole layouts. Zhang et al. (2017) proposed a method for in-seam borehole hydraulic flushing and designed a methane drainage scheme taking the fact that multiple boreholes may interact with each other during gas extraction into account. Using numerical simulations, Liu et al. (2017) used the pressure decrease coefficient to quantitatively assess methane drainage from conventional drainage borehole layouts to determine which patterns delivered the best underground methane extraction. To determine the most judicious spacing for conventional drainage boreholes, Zhao et al. (2018) investigated the effect of gas seepage between adjacent boreholes on methane drainage. Considering the anisotropy of coal seams, Lin et al. (2019) discussed the optimal layout for conventional boreholes after analyzing gas flow fields. For the geological conditions relevant for a multi-seam mining mine, Szott et al. (2018) simulated drainage results for hydraulically slotting and hydraulically fracturing multiple boreholes. Zhang et al. (2019) investigated interactions among multiple boreholes and the effective drainage zone for different borehole layouts through physical simulation experiments in the laboratory. Si et al. (2019), to determine the best spacing for conventional boreholes for CMM drainage, introduced a transfer coefficient for methane exchange between fractures and coal matrix. Depending on a stress-dependent permeability relationship, Cheng et al. (2020) analyzed designs for conventional methane drainage borehole layouts in a protected coal seam.

Many investigators have carried out studies on the most appropriate layout of multiple boreholes in coal seams and these studies have helped to improve the methane recovery. However, the multiple tree-type borehole layout is completely different from the layouts proposed for conventional methane drainage boreholes and from the layouts for boreholes using other stress-relief methods due to these sub-boreholes. The excavation of sub-boreholes affects the permeability of the coal seam locally but they also establish gas flow paths in the nearby coal cleats and coal matrix. As a result, existing research cannot guide the large-scale application of TTBD program and the optimum tree-type borehole layout needed to conduct TTBD in underground coal mines is still unclear. To solve this problem, a full-coupled THM model correlating methane flow within coal fractures and matrix has been developed and is described in this paper. The THM model is integrated with geological data from a low-permeability coal seam to study the optimum layout for multiple tree-type boreholes in this type of seam. Finally, the effects of some important parameters on CMM drainage performance are examined. These results are significant because they provide scientific guidelines for optimizing the design of TTBD systems for engineering purposes.

Mathematical Equations for the Thermo-Hydro-Mechanical Model

The THM model correlating coal matrix and fracture methane flow is defined using the following assumptions. 1) Coal is a dual-poroelastic continuum composed of matrix and fractures. 2) Coal seams are saturated with methane and the methane absorption/adsorption by the matrix is governed by the Langmuir adsorption model. 3) Methane migration in fractures is by laminar flow and obeys Darcy’s law. Methane’s viscosity is constant. 4) Coal’s sorption-induced strain follows a Langmuir sorption relationship with the methane’s adsorbed pressure.

Governing Equation for Coal Deformation

Taking the thermal expansion/contraction and sorption-induced swelling/shrinkage of the coal matrix into consideration, the component of the total strain tensor for a non-isothermal dual-porosity coal can be represented by (Wu et al., 2010; Liu et al., 2011; Ge et al., 2019) Eq. 1:

${\epsilon }_{ij}=\frac{1}{2G}{\sigma }_{ij}-\left(\frac{1}{6G}-\frac{1}{9K}\right){\sigma }_{kk}{\delta }_{ij}+\frac{\alpha p_m{\delta }_{ij}+\beta p_f{\delta }_{ij}+K\left({\alpha }_{T}T{\delta }_{ij}+{\epsilon }_s{\delta }_{ij}\right)}{3K}(1)$

Where $G=D/2\left(1+\upsilon \right)$; $D={\left[1/E+1/a{K}_n\right]}^{-1}K=D/3\left(1-2\upsilon \right)$; $\alpha =1-K/K_s;\beta =1-K/a\cdot K_n$; δ_ij = 1 (i = j) or δ_ij = 0 (i≠j) is the Kronecker tensor; G is the shear modulus of coal [MPa]; K is the bulk modulus of coal [MPa]; α and β are the Biot coefficients [-] for fracture and coal matrix, respectively; p_f and p_m are methane pressure [MPa] in the fracture and the coal matrix, respectively; α_T is the coefficient of thermal expansion [1/K]; T is the reservoir temperature [K]; ${\epsilon }_s$ is matrix deformation induced by adsorption/desorption, [Note: this variable could be represented by the typical Langmuir-type equation ${\epsilon }_s={\epsilon }_L{p}_m/\left(p_m+p_L\right)$]; ${\epsilon }_L$is the Langmuir strain constant for the matrix [-]; $p_L$ the Langmuir pressure constant [MPa]; E is the elastic modulus of coal [MPa]; υ is the Poisson’s ratio [-]; K_s is the bulk modulus of coal grains [MPa]; K_n is the normal stiffness of fracture [MPa/m].

According to continuum mechanics theory, the stress equilibrium equation and the strain–displacement relationships for coal deformation can be calculated from Eq. 2: (Zhao Y. et al., 2020):

$\{\begin{array}{l}{\sigma }_{ij,j}+f_i=0\\ {\epsilon }_{ij}=\frac{1}{2}\left(u_{i,j}+u_{j,i}\right)\end{array}(2)$

where $f_i$ is the body force component and $u_i$ is the displacement component.

By substituting Eq. 1 into Eq. 2, the Navier-type equation that governs coal deformation, Eq. 3, is obtained:

$G{u}_{i,jj}+\frac{G}{1-2\nu }{u}_{j,ii}-\alpha p_{m,i}-\beta p_{f,i}-K{\alpha }_T{T}_{,i}-K{\epsilon }_L\frac{P_L}{{\left(p_m+P_L\right)}^2}{p}_{m,i}+f_i=0(3)$

Governing Equation for Methane Flow in Coal Seams

Methane migration in a coal seam during drainage obeys the law of mass conservation the equation for which can be expressed as (Zhang et al., 2008):

$\frac{\partial m}{\partial t}+\nabla \cdot \left({\rho }_g{q}_g\right)=Q_S(4)$

where t is the time of methane flow [s]; ${\rho }_g$ is the methane density [kg/m³]; q_g is the seepage velocity vector [m/s]; Q_S is the methane flow rate from its source [kg/(m³∙s)]; m is the total methane mass including both free gaseous methane and adsorbed methane [kg/m³]. Assuming that methane sorption only occurs in the matrix material, the methane stored in the matrix and fracture can be written as (Wu et al., 2010; Zhang et al., 2021):

$\{\begin{array}{l}{m}_m=\frac{{\varphi }_m{p}_m{\rho }_{gm}}{p_a}+{\rho }_{gm}{\rho }_c\frac{V_L{p}_m}{p_m+P_L}\left(1-A-W\right)\\ m_f={\varphi }_f{\rho }_{gf}\end{array}(5)$

Where m_m and m_f are the methane mass [kg/m³] in the coal matrix and fractures, respectively; ${\varphi }_m$ is the porosity of the matrix system [-]; ${\varphi }_f$is the porosity of the cleat system [-]; ${\rho }_c$ is the coal density [kg/m³];V_L is the Langmuir pressure constant [m³/kg]; A is coal ash [%]; W is the water content in the coal [%]; $p_a$ is standard atmospheric pressure [MPa]; ${\rho }_{gm}$ and ${\rho }_{gf}$ are the methane density in the coal matrix and fractures, respectively. These densities can be expressed by Eq. 6:

$\{\begin{array}{l}{\rho }_{gm}=\frac{M_g}{RT}{p}_m\\ {\rho }_{gf}=\frac{M_g}{RT}{p}_f\end{array}(6)$

where M_g is the molecular mass of CH₄ [kg/mol], and R is the universal gas constant [J/(mol•K)].

Taking into consideration the equations for fluid exchange between matrix and fractures (Lim and Aziz 1995) and with reference to previous research results (Ge et al., 2019), the governing equations for methane flow in the matrix–fracture system could be calculated from Eq. 7:

$\{\begin{array}{l}\frac{\partial m_m}{\partial t}+\nabla \left(-\frac{k_m}{\mu }{\rho }_{gm}\nabla p_m\right)=-\frac{{\rho }_{gm}{k}_m\psi }{\mu }\left(p_m-p_f\right)\\ {\varphi }_f\frac{\partial {\rho }_{gf}}{\partial t}+{\rho }_{gf}\frac{\partial {\varphi }_f}{\partial t}+\nabla \left(-\frac{k_f}{\mu }{\rho }_{gf}\nabla p_f\right)=\frac{{\rho }_{gm}{k}_m\psi }{\mu }\left(p_m-p_f\right)\end{array}(7)$

Where k_m is the matrix permeability [m²]; k_f is the fracture permeability [m²]; μ is the dynamic viscosity of methane [Pas]; $\psi =4\left(1/a_x^2+1/a_y^2\right)$ is the shape factor [1/m²]; $a_x$ and $a_y$ are the matrix spacing in the x- and y-directions [m].

Governing Equation of Heat Transfer in Coal Seams

Coal seams contain fluid and solid phases whose thermodynamic parameters are completely different. Any pre-existing geothermal equilibrium in a coal seam is disrupted during CMM extraction. By applying the law of energy conversation, the heat transfer in a dual-porosity coal seam under non-isothermal conditions has been described in the literature (Zhou et al., 1998; Zhu et al., 2011; Ge et al., 2019) and can be expressed by Eq. 8:

$\begin{array}{l}{\left(pC\right)}_M\frac{\partial T}{\partial t}+T{K}_g{\alpha }_g\left(\nabla \left(-\frac{k_m}{\mu }\nabla p_m\right)+\nabla \left(-\frac{k_f}{\mu }\nabla p_f\right)\right)+TK{\alpha }_T\frac{\partial {\epsilon }_v}{\partial t}={\lambda }_m{\nabla }^{2}T\\ +\frac{{\rho }_{gm}{k}_m{C}_g}{\mu }\nabla p_m\nabla T+\frac{{\rho }_{gf}{k}_f{C}_g}{\mu }\nabla p_f\nabla T\end{array}(8)$

Where ${\left(pC\right)}_M={\varphi }_m\left({\rho }_{gm}{C}_g\right)+{\varphi }_f\left({\rho }_{gf}{C}_g\right)+\left(1-{\varphi }_m-{\varphi }_f\right)\left({\rho }_c{C}_s\right)$ is the effective heat capacity of methane-bearing coal; ${\lambda }_M=\left({\varphi }_m+{\varphi }_f\right){\lambda }_g+\left(1-{\varphi }_m-{\varphi }_f\right){\lambda }_s$ is the heat conductivity coefficient for methane-bearing coal [J/(m∙s∙K)]; λ_s is the heat conductivity coefficient for the coal’s skeleton [J/(m∙s∙K)]; λ_g is the heat conductivity coefficient for methane [J/(m∙s∙K)]; C_g and C_s are the specific heat capacity [J/(kg∙K)] of the methane and the coal skeleton, respectively; K_g is the bulk modulus of methane [MPa], and ${\alpha }_g=1/T$ is the thermal expansion coefficient of methane [1/K].

Governing Equation for Coal Seam Porosity and Permeability

Coal is a fractured rock with permeability arising from both pores in the coal matrix and fractures that cut through the coal (Zhang et al., 2018; Cheng et al., 2021; Du et al., 2021; Lv et al., 2021). Since the impact of thermal changes effects on the coal’s permeability cannot be ignored (Perera et al., 2012; Li et al., 2020), we extended the matrix porosity and permeability model proposed by Zhang et al. (2008) to encompass the effect of the temperature on permeability. Using this extended model, the dynamic evolution of matrix porosity and permeability evolution during temperature changes can be calculated from the following Eq. 9:

$\{\begin{array}{l}{\varphi }_m=\frac{1}{1+S}\left[\left(1+S_0\right){\varphi }_{m0}+\alpha \left(S-S_0\right)\right]\\ k_m=k_{m0}{\left(\frac{1}{1+S}\left[\left(1+S_0\right)+\frac{\alpha }{{\varphi }_{m0}}\left(S-S_0\right)\right]\right)}^3\end{array}(9)$

where $S={\epsilon }_v+p_m/K_s-{\epsilon }_s-{\alpha }_{T}T$; $S_0={\epsilon }_{v0}-p_{m0}/K_s-{\epsilon }_L{p}_{m0}/p_{m0}+P_L-{\alpha }_T{T}_0$; k_m0 is the initial coal matrix permeability at the initial methane pressure p_m0 and matrix porosity ϕ_m0.

Expanding on the results of the previous research (Liu et al., 2010), the governing equation for the coal’s fracture permeability, an equation that incorporates sorption-induced swelling/shrinkage, thermal expansion, and effective stress, can be written as:

$\frac{k_{fi}}{k_{f0}}={\left[1+\frac{2\left(1-R_m\right)}{{\varphi }_{f0}}\left(\Delta {\epsilon }_j-\frac{1}{3}{\alpha }_T\Delta T-\frac{1}{3}\Delta {\epsilon }_s\right)\right]}^3,i\ne j(10)$

Where R_m= E/E_S is the reduction ratio of the elastic modulus [-]; ϕ_f0 and k_f0 are the initial fracture porosity and initial fracture permeability, respectively.

THM Model Coupling Relationships and Calculation Method

Equations 3, 7–10 constitute the THM coupling model used to simulate methane transport in a coal seam during CMM drainage. Figure 2 depicts the interactions and relationships simulated by the THM model. When CMM suction drainage begins using negative pressure, the free methane and heat in the fractures around the boreholes will rush out first. After that, the methane in the matrix will gradually be drained. The coal will be deformed by the change in effective stress and temperature and the coal matrix and fracture permeabilities, and thus methane flow will respond to these changes. The THM model governing equations are interdependent and interrelated, as shown in Figure 2. For this study, the whole set of coupled equations were solved discretely with the aid of Comsol Multiphysics (COMSOL Inc., Burlington, MA, United States), a finite element solver.

FIGURE 2

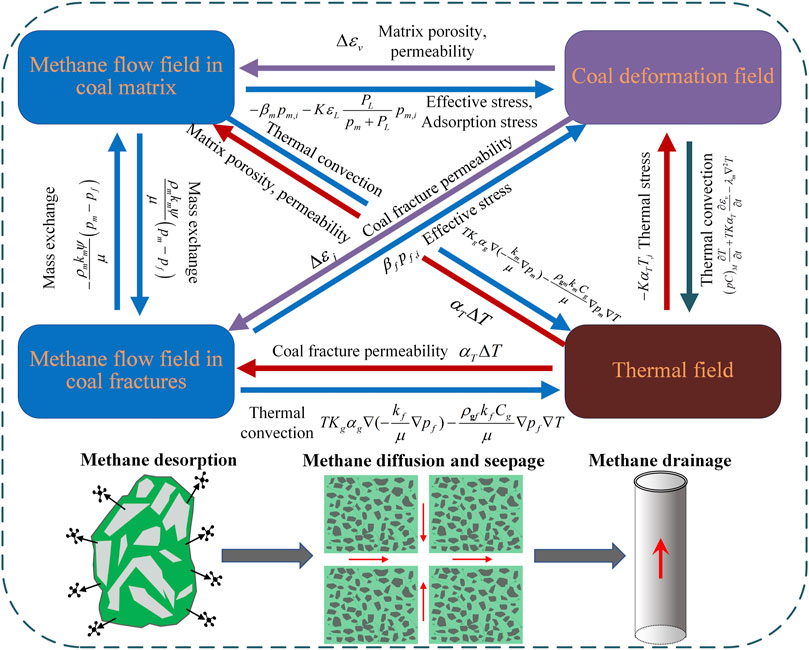
FIGURE 2. Diagram illustrating the interactons and cross-coupling relationships simulated by the THM coal seam gas drainage model.

Geometric Configurations for Tree-type Sub-boreholes

To select the optimum layout for multiple tree-type CMM drainage boreholes, the methane drainage efficiency of several possible tree-type sub-borehole configurations were compared. Figure 3 shows possible sub-borehole configurations for simulated methane drainage from nine tree-type boreholes. This study modeled four sub-boreholes from each main borehole. The sub-borehole configurations are a square layout, a rhombic layout, a parallel-mixed layout and a cross-mixed layout. The numerical models for the borehole layouts in Figure 3 were 50 by 50 m. The main tree-type boreholes were spaced 6 m apart and each main tree-type borehole had four 3 m long sub-boreholes. The main boreholes and the sub-boreholes were 94 and 25 mm in diameter, respectively. The boundary conditions for the models shown in Figure 3 were defined in accordance with the stresses on the Ji_15-17 seams in the Shoushan mine in Henan province, China. To reduce the number of main pre-drainage boreholes required in the Ji_15-17 seams and improve methane drainage, the Shoushan mine implemented a full field test of the TTBD method in one of its floor-level methane drainage roadways. The details of the geology of the Ji_15-17 seams are introduced in a previous study (Zhang et al., 2021). In the models constructed for the present study, the maximum horizontal stress, 19.5 MPa, was imposed on the models’ upper surfaces and the minimum horizontal stress, 12.5 MPa, was imposed on their right sides. The other sides were defined as roller boundaries. The coal was initially saturated with methane at a pressure of 1.38 MPa. A constant methane pressure of 116 mm Hg (∼15.5 kPa) was applied to all the tree-type boreholes; no flow conditions were applied to the other boundaries. The initial reservoir temperature was set to 323 K and the tree-type borehole walls were defined as temperature boundaries with a temperature of 293 K. The numerical models’ input parameters are given in Table 1 (Zhu et al., 2011; Xia et al., 2014; Li et al., 2016; Zheng et al., 2016; Zhang et al., 2021).

FIGURE 3

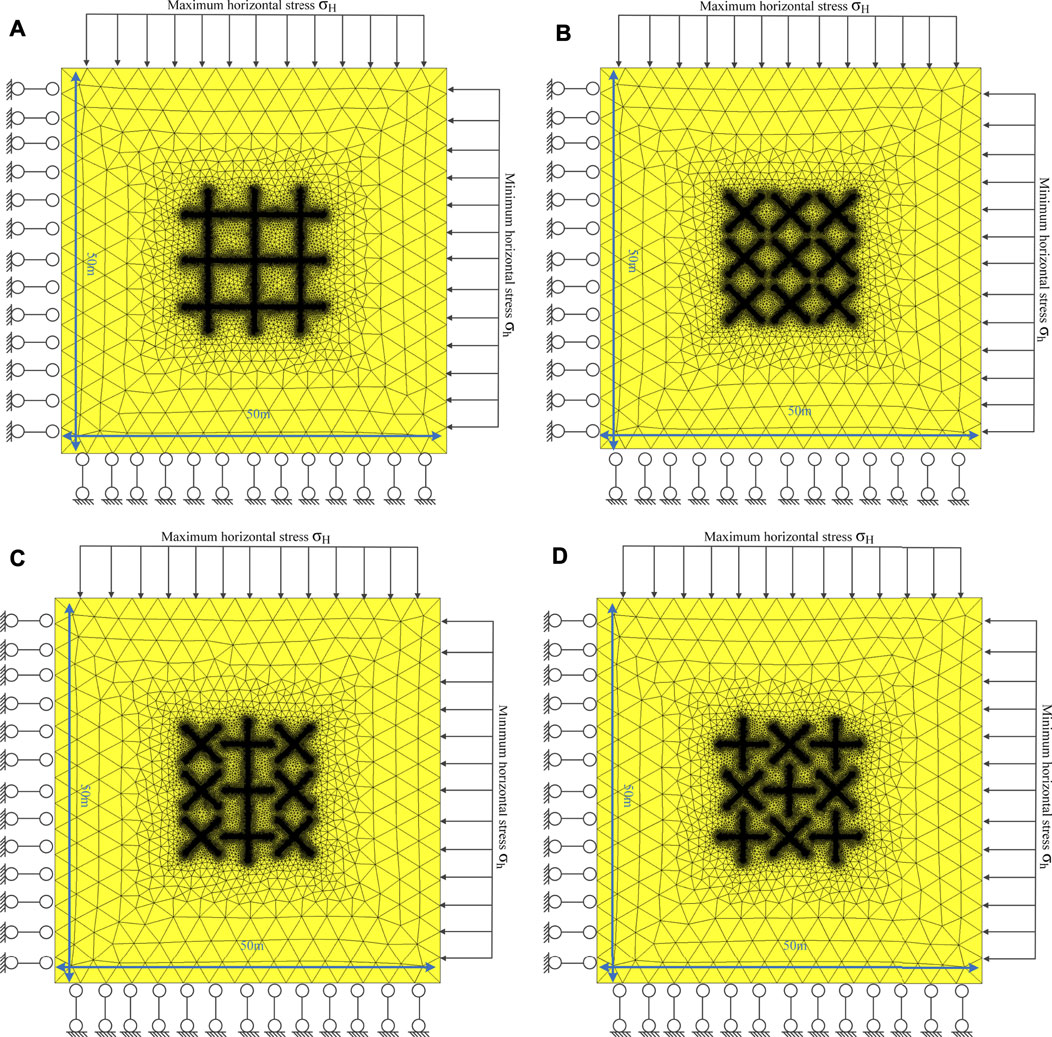
FIGURE 3. Diagram showing four possible tree-type sub-borehole configurations when four sub-boreholes are drilled from each main borehole. (A) Square layout; (B) Rhombic layout; (C) Parallel mixed layout; (D) Cross mixed layout.

TABLE 1

TABLE 1. Input parameters used in the numerical models.

Numerical Results and Discussion

During methane pre-drainage, the most important parameter for evaluating drainage effect produced by multiple boreholes in a coal seam is the effective drainage zone where the methane pressure is less than 0.74 MPa (Gao et al., 2016; Zhang et al., 2019). The pre-drainage time required to reduce the methane pressure in a coal seam to below 0.74 MPa is called as the completion time. In this section, the effective drainage zone produced by multiple tree-type boreholes and the corresponding drainage completion times are first analyzed with different sub-borehole configurations. The simulation results are compared with field data from tree-type borehole methane drainage program in the Shoushan mine to check the accuracy of the mathematical models. Then using the rhombic sub-borehole layout, the main tree-type borehole spacing, Langmuir volume constant, Langmuir pressure constant, coal fracture permeability, and coal matrix permeability are changed to study the effects of changes in these parameters on drainage performance.

Drainage From Multiple Tree-type Boreholes With Different Sub-borehole Configurations and Model Validation

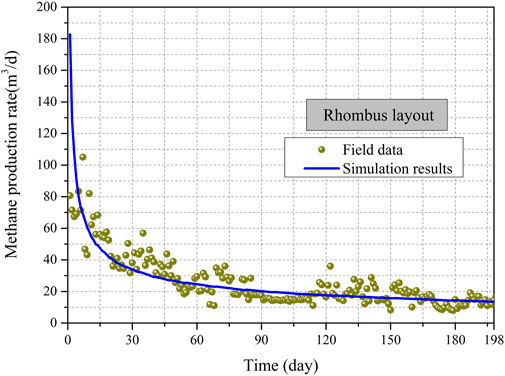
Figure 4 shows methane pressure in a coal seam at different times during modeled CMM drainage for different tree-type sub-borehole configurations. The letters S, R, P, and C designate the square, rhombic, parallel mixed and cross mixed sub-borehole layouts, respectively, and the “xxd” labels show the number of days since gas extraction was initiated. For example, the diagram labeled “R215d” shows methane pressure for a rhombic sub-borehole layout after 215 days of drainage. From Figure 4, it can be seen that methane pressure near the tree-type boreholes gradually decreases and the drainage zone expands as the gas extraction time increases. When the drainage time is less than the completion time, there are zones between tree-type sub-boreholes where the methane has not yet been drained (the red zones in Figure 5). As the drainage time lengthens, the methane pressure in these zones will gradually decrease and eventually it will fall below 0.74 MPa. When this occurs, CMM extraction has been completed. For different sub-borehole configurations, although the number of sub-boreholes is the same, the times required to complete extraction differ. The times required to drain a zone completely can differ by up to 44.4%. The differences in completion times can be clearly observed from Figures 4, 6. It is worth noting that if the drainage completion time is used as the only assessment criterion for drainage effectiveness, the rhombic tree-type borehole layout is better than the square, parallel mixed, and cross mixed layouts. These model results suggest that optimizing the tree-type sub-borehole layout can improve drainage performance. To check the accuracy of the THM model results, multiple tree-type boreholes with rhombic sub-borehole layouts were used to drain CMM from the Ji_15–17 seams in the Shoushan mine. After 198 days of gas extraction, the methane pressure between tree-type boreholes dropped to less than 0.74 MPa. The relative error in our simulated drainage completion time is 8.72%. Figure 7 shows field production data for methane extraction from the rhombic-configured tree-type boreholes in the Shoushan mine and simulated methane production results from the rhombic THM model. It can be seen that the simulated results and the field methane data match very well. These results show that the THM model is valid and it can be used to simulate tree-type borehole methane drainage accurately. The model can also be used to determine the most appropriate tree-type sub-borehole layout.

FIGURE 4

FIGURE 4. Methane pressures in a mode coal seam at different times during coal mine methane drainage by multiple tree-type boreholes with different sub-borehole configurations.

FIGURE 5

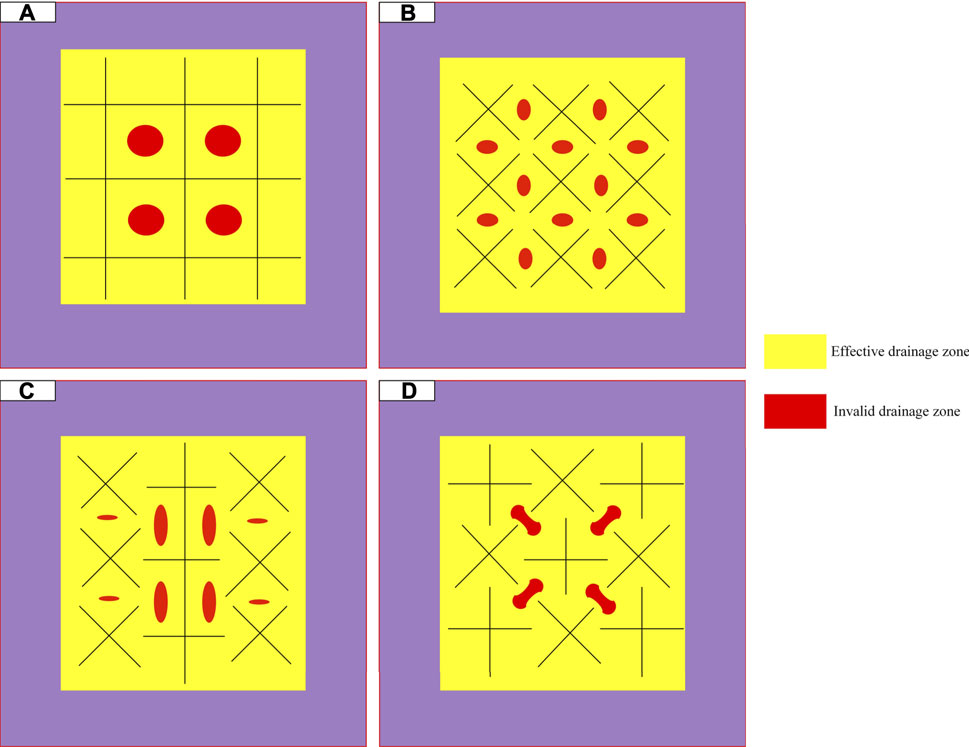
FIGURE 5. Sketches showing tree-type sub-boreholes during coal mine methane drainage. Zones where the methane has not yet been drained are shown in red. The sub-borehole layouts shown are: (A) Square layout; (B) Rhombic layout; (C) Parallel mixed layout; (D) Cross mixed layout.

FIGURE 6

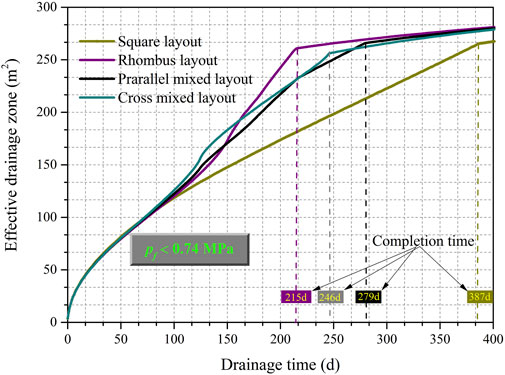
FIGURE 6. Graph showing effective drainage zone areas vs. drainage time for the four sub-borehole configurations shown in Figures 4, 5.

FIGURE 7

FIGURE 7. Methane production rates vs. drainage time.

Effect of Tree-type Borehole Spacing on the Drainage Performance

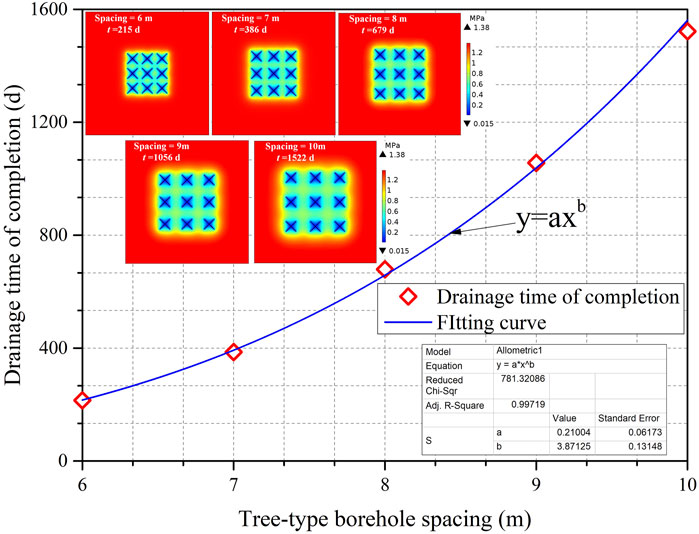
The design and optimization of tree-type borehole spacing for methane pre-drainage from coal reservoirs is an important issue that needs to be resolved. Drilling many closely spaced boreholes from an underground roadway into a coal seam is expensive and requires long construction times. A practical spacing would minimize the number boreholes while still achieving excellent methane drainage effect. Figure 8 displays the sizes of the effective drainage zones around multiple tree-type boreholes at different spacings for extraction times from zero to 2,000 days. The gas extraction completion times for each borehole spacing are also shown. From Figure 8, it is apparent that the size of the effective drainage zone for any borehole spacing first rises dramatically as the drainage time increases but then the zone size increases much more slowly after the pre-drainage completion time is reached. In a certain period in the early drainage stages, the shorter the tree-type borehole spacing, the larger the drainage zone. However, at longer drainage times, this relationship is reversed. The reason for this reversal is that the methane in the coal between closely spaced boreholes can be rapidly drained due to the strong interactions between the boreholes but with the passage of drainage time, drainage zone growth rates are restricted by the tree-type borehole spacing and the coal’s low permeability. To explore the relationship between tree-type borehole spacing and drainage efficiency, tree-type borehole spacings are shown plotted against drainage completion times in Figure 9. The figure shows that the time required to complete drainage differs considerably for different tree-type borehole spacings; the tree-type borehole spacing is related to the pre-drainage completion time by a power law. When the distance between the tree-type boreholes is increased from 6 to 10 m, the required drainage time increases from 215 to 1,522 days, an increase of more than six times. Thus, an appropriate distance between tree-type boreholes should be determined to obtain the most efficient CMM extractions possible. Doing so will improve the efficiency of mining operations.

FIGURE 8

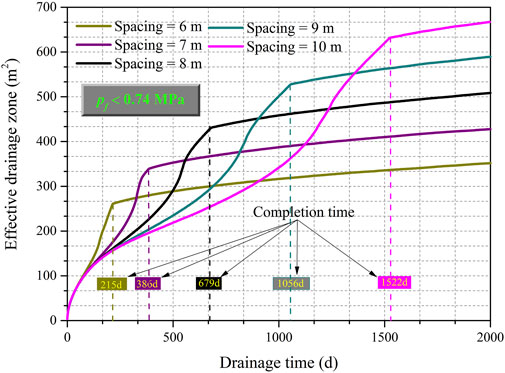
FIGURE 8. Effective drainage zone sizes around tree-type boreholes at different spacings for 0–2000 d gas extraction. Completion times (methane pressure <0.74 MPa) for each borehole spacing are also shown.

FIGURE 9

FIGURE 9. Drainage completion time vs tree-type borehole spacing.

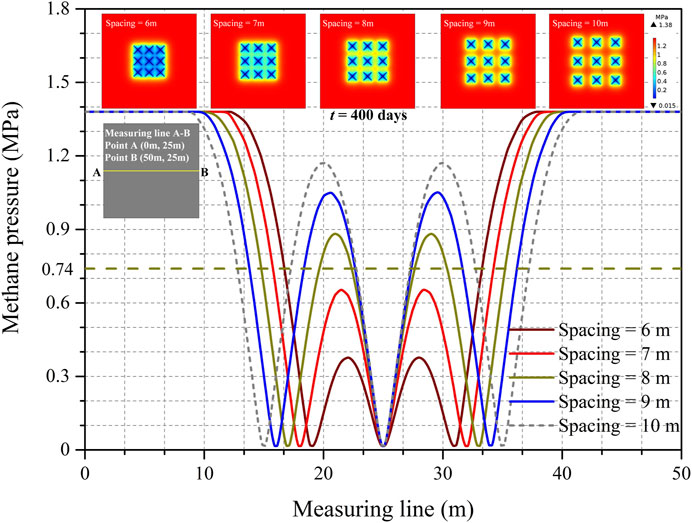
Actually, to promote pre-drainage construction when a coal face is not being worked and to eliminate the risk of coal and gas outbursts, coal mining companies will have to allocate sufficient lead time to allow for adequate methane drainage. The lead time is usually longer than the drainage completion time. How borehole spacing is designed is significantly important because the required lead time at the Shoushan mine is approximately 400 days. The distribution of methane pressure on the measuring line from point A (0, 25 m) to point B (50, 25 m) after 400 days of extraction is discussed. As shown on Figure 10, the larger the tree-type borehole spacing, the higher methane pressure in the coal seam. For the tree-type borehole spacing of 6 or 7 m, the methane pressure between the tree-type boreholes has been successfully reduced to below 0.74 MPa after 400 days of drainage. Thus, taking the drainage effect and the lead time allowed into account, a diamond-shaped sub-borehole layout in tree-type boreholes spaced 7 m apart could be recommended for extracting the CMM from Ji_15–17 coal seams in the Shoushan coal mine. These THM model simulation results can provide reliable support for optimizing the layout of tree-type boreholes to improve the efficiency of methane drainage programs in the field.

FIGURE 10

FIGURE 10. Methane pressure along measuring line (A)–(B).

Effect of Adsorption Characteristics on Drainage Performance

Figure 11 gives the influence of different Langmuir volume constants, V_L, on methane drainage performance of tree-type boreholes. After draining for the similar amount of time, the effective drainage zone areas decrease as the Langmuir volume constant increases (Figure 11A). Meanwhile, it can be found in Figure 11 that coal with different Langmuir volume constants reach drainage completion after different periods of time. The greater the Langmuir volume constant, the more time is needed to complete CMM extraction. The relationship between drainage completion time and the Langmuir volume constant is linear (Figure 11B). As the Langmuir volume constant is changed from 0.01 to 0.05 m³/kg, the time required for pre-drainage completion increases by a factor of approximately 3.9. The reason is that a higher Langmuir volume constant indicates that more methane is adsorbed and stored in the coal and this means there is more methane to be extracted.

FIGURE 11

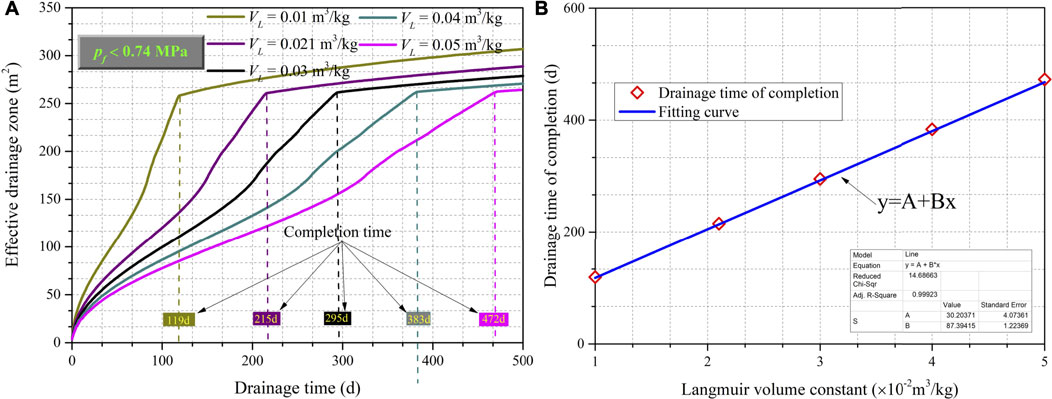
FIGURE 11. Effect of changes in the Langmuir volume constant (V_L) on drainage performance. (A) Effective drainage zone areas vs drainage time in days for five different V_L’s (B) Drainage completion time vs. Langmuir volume constants.

The Langmuir pressure constant P_L, is another parameter used to characterize adsorption. It is the pore pressure corresponding to one-half of the Langmuir volume (V_L/2). A graph showing how different P_L’s change effective drainage zone sizes and drainage completion times is shown as Figure 12. For the same drainage time, as the Langmuir pressure constant increases, the effective drainage zones expand (Figure 12A), but the final drainage completion times show a downward trend (Figure 12B). The reduction in the drainage time–P_L relationship follows a power law (Figure 12B). The time required for pre-drainage is reduced by 30.4 and 41.1% when the Langmuir pressure constant increases from 0.5 to 1.729 and 2.5 MPa, respectively. This occurs because the higher Langmuir pressure constants increase the gas desorption rate during drainage to some extent and this shortens the time required for pre-drainage. To summarize, the drainage performance of multiple boreholes is affected by the adsorption factors, therefore, it is fairly important that simulations consider the adsorption and that the coal’s adsorption parameters be measured accurately.

FIGURE 12

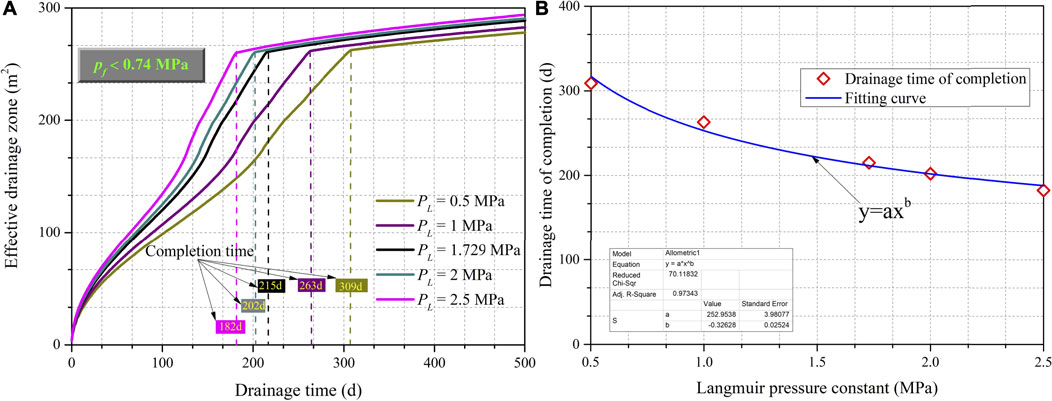
FIGURE 12. Effect of changes in the Langmuir pressure constant (P_L) on drainage performance. (A) Effective drainage zone areas vs drainage time in days for five different P_L’s (B) Drainage completion time vs. Langmuir pressure constants.

Effect of Initial Fracture and Matrix Permeability on Drainage Performance

Figure 13 displays the changes in the drainage performance for different initial fracture permeabilities, k_f0’s. As show in the figure, for the same amount of drainage time, an increase of the fracture permeability leads, as expected, to a larger effective drainage zone and the time required to complete the entire pre-drainage process decreases. The drainage completion times fall rapidly as k_f0 increases in the lower ranges of the initial fracture permeability considered whereas the drainage times decrease much more slowly in the higher initial fracture permeability ranges. The time required for pre-drainage is reduced by 92.2 and 58.8% when the initial fracture permeability is changed from 2 × 10⁻¹⁸ m² to 4 × 10⁻¹⁷ m² and from 4 × 10⁻¹⁷ m² to 1 × 10⁻¹⁶ m², respectively. A power function has been fitted to the drainage completion time–initial fracture permeability data (Figure 13B). Compared with fracture permeability, the effect of matrix permeability on the time required for pre-drainage is relatively minor. As Figure 14A shows, higher matrix permeabilities, k_m0’s, make the effective drainage zone for any given drainage time slightly larger. This results in a slow and linear downward trend in drainage completion times on the drainage completion time–initial matrix permeability plot (Figure 14B). The time needed to complete methane extraction decreases from 226 d for a matrix permeability of 2 × 10⁻¹⁸ m² to only 142 d for a matrix permeability of 1 × 10⁻¹⁷ m². Drainage performance is less sensitive to changes in matrix permeability than to changes in fracture permeability. The reason for this difference is that the fractures are the dominant pathways for methane migration. Indirectly, this also demonstrates that the TTBD method for enhancing fracture permeability through stress relief and the addition of sub-boreholes to connect the main boreholes to the fractures in the seams should be effective for CMM drainage.

FIGURE 13

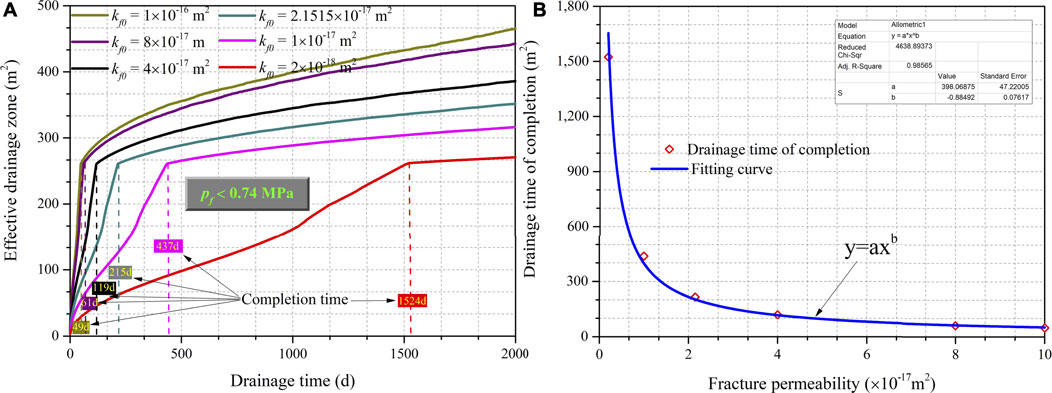
FIGURE 13. Effect of changes in the coal’s fracture permeability, k_f0, on drainage performance. (A) Effective drainage zone areas vs. drainage time in days. (B) Drainage completion time vs. initial fracture permeabilities.

FIGURE 14

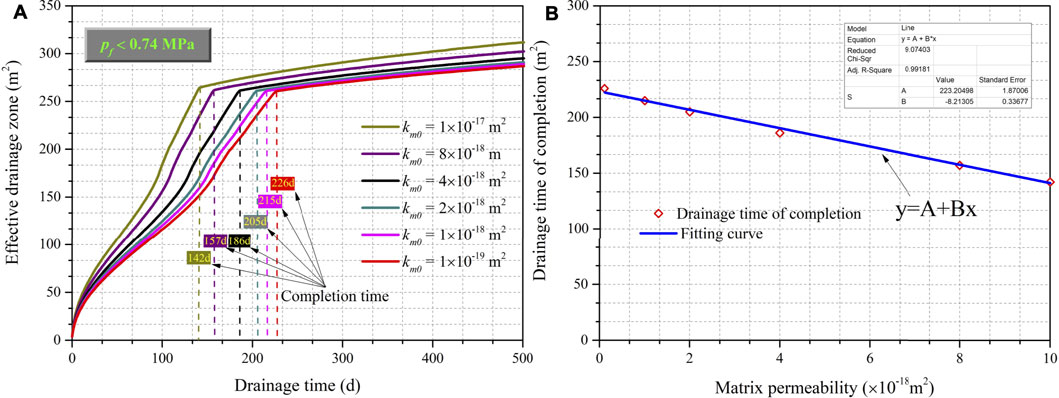
FIGURE 14. Effect of matrix permeability on the drainage performance. (A) Effective drainage zone versus vs. drainage time in days. (B) Drainage completion time vs. matrix permeabilities.

Conclusion

The tree-type borehole drainage (TTBD) technique is a completely new method for controlling methane in underground coal mines. This technique shows considerably promise for reducing the number of traditional cross-measure boreholes needed for methane control programs in floor drainage roadways and it reduces the time required to complete methane extraction. For this study, a full-coupled thermo-hydro-mechanical model for simulating methane drainage was developed and used to analyze the methane draining efficiency of different multiple tree-type borehole layouts. The extent to which different tree-type borehole spacings, different Langmuir volume and Langmuir pressure constants, and different fracture and matrix permeabilities influence methane drainage performance was investigated. On the basis of our numerical model simulation results, the following conclusions were drawn:

(1) When the same number of tree-type boreholes are drilled into the same coal seam, different tree-type borehole layouts and different sub-borehole configurations lead to differences in drainage efficiency. Methane extractions factors like the size of effective drainage zones, the presence of incompletely evacuated drainage zones and drainage completion times can all change. Optimizing the layout of the tree-type boreholes can improve methane drainage performance. Comparing the times required for methane pre-drainage shows that, the rhombic tree-type sub-borehole layouts is more suitable than square, parallel mixed or cross mixed layouts for methane extraction from the Ji_15–17 seams in the Shoushan mine.

(2) For all tree-type borehole spacings investigated, once gas extraction has begun, the effective drainage zone first expands sharply but after reaching the drainage completion time, the zone only increases slowly. As the size of tree-type borehole spacing increases, the size of the effective drainage zone decreases in the early stages of drainage, but this relationship reverses during the later stages. As a direct consequence, there is a positive power-law relationship between the tree-type borehole spacing and the drainage completion time. Considering drainage performance and the lead time allowed for adequate methane drainage in the Shoushan mine, the rhombic tree-type borehole layout with boreholes spaced 7 m apart is recommended for methane extraction from the Ji_15–17 coal seams.

(3) Differences in adsorption are capable of substantially affecting the drainage performance of tree-type boreholes, and a numerical model cannot underestimate the importance of adsorption. In our model, for the same amount of drainage time, increasing the Langmuir volume constant shrinks the size of the effective drainage zone but increases the time needed to complete extraction. However, as the Langmuir pressure constant increases, the effective drainage zone expands and the drainage completion time decreases. In addition, increasing the matrix and fracture permeabilities increases the size of the effective drainage zone and reduces the time required to complete pre-drainage although the effects of these two permeabilities on gas extraction are not of the same degree. The drainage performance of tree-type boreholes is much more sensitive to changes in fracture permeability than it is to changes in matrix permeability.

When CMM is drained from coal seams by multiple tree-type boreholes, the rhombic tree-type borehole layout can be adopted and the borehole spacing can be determined by combining the geologic data of coal mines with the simulation method introduced in this paper. The above findings lay the foundation for the application of TTBD to efficiently extract CMM from low-permeability coal seams.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

LZ: Methodology, Software, Writing-original draft. QQ: Conceptualization, Writing-review and editing, Language. KD: Validation experiment, Data collection, Supervision. SZ: Visualization, Validation experiment. YL: Editing, Investigation.

Funding

This work was jointly supported by the China Postdoctoral Science Foundation (Grant Nos. 2021M691390 and 2020M680490) and the National Key R and D Plan Key Special Funding Project (Grant No.2018YFC0807900).

Conflict of Interest

Authors LZ, QQ, and YL were employed by Emergency Science Research Academy, China Coal Research Institute, China Coal Technology and Engineering Group Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adebayo, T. S., Awosusi, A. A., Bekun, F. V., and Altuntaş, M. (2021). Coal Energy Consumption Beat Renewable Energy Consumption in South Africa: Developing Policy Framework for Sustainable Development. Renew. Energ. 175, 1012–1024. doi:10.1016/j.renene.2021.05.032

CrossRef Full Text | Google Scholar

Adedoyin, F. F., Gumede, M. I., Bekun, F. V., Etokakpan, M. U., and Balsalobre-Lorente, D. (2020). Modelling Coal Rent, Economic Growth and CO2 Emissions: Does Regulatory Quality Matter in BRICS Economies?. Sci. Total Environ. 710, 136284. doi:10.1016/j.scitotenv.2019.136284

PubMed Abstract | CrossRef Full Text | Google Scholar

BP (2021). Statistical Review of World Energy. Available at: https://www.bp.com/content/dam/bp/business-sites/en/global/corporate/pdfs/energy-economics/statistical-review/bp-stats-review-2021-full-report.pdf?utm_source=BP_Global_GroupCommunications_UK_external&utm_medium=email&utm_campaign=11599394_Statistical%20Review%202020%20-%20on%20the%20day%20reminder&dm_i=1PGC%2C6WM5E%2COV0LQ4%2CRQW75%2C1 (Accessed August 1, 2021).

Google Scholar

Chen, X., Xue, S., and Yuan, L. (2017). Coal Seam Drainage Enhancement Using Borehole Presplitting Basting Technology - A Case Study in Huainan. Int. J. Mining Sci. Technol. 27 (5), 771–775. doi:10.1016/j.ijmst.2017.07.015

CrossRef Full Text | Google Scholar

Cheng, Y., Lu, Y., Ge, Z., Cheng, L., Zheng, J., and Zhang, W. (2018). Experimental Study on Crack Propagation Control and Mechanism Analysis of Directional Hydraulic Fracturing. Fuel 218, 316–324. doi:10.1016/j.fuel.2018.01.034

CrossRef Full Text | Google Scholar

Cheng, Y., Zhang, X., Lu, Z., Pan, Z. j., Zeng, M., Du, X., et al. (2021). The Effect of Subcritical and Supercritical CO2 on the Pore Structure of Bituminous Coals. J. Nat. Gas Sci. Eng. 94 (10), 104132. doi:10.1016/j.jngse.2021.104132

CrossRef Full Text | Google Scholar

Cheng, Z., Pan, H., Zou, Q., Li, Z., Chen, L., Cao, J., et al. (2020). Gas Flow Characteristics and Optimization of Gas Drainage Borehole Layout in Protective Coal Seam Mining: A Case Study from the Shaqu Coal Mine, Shanxi Province, China. Nat. Resour. Res. 30 (2), 1481–1493. doi:10.1007/s11053-020-09775-4

CrossRef Full Text | Google Scholar

Chi, A., Xiao, X. L., Zhang, J., Dan, J., and Wen, J. T. (2018). Experimental Investigation of Propagation Mechanisms and Fracture Morphology for Coalbed Methane Reservoirs. Pet. Sci. 15 (4), 815–829. doi:10.1007/s12182-018-0252-z

CrossRef Full Text | Google Scholar

Du, X., Pang, D., Cheng, Y., Zhao, Y., Hou, Z., Liu, Z., et al. (2021). Adsorption of CH4, N2, CO2, and Their Mixture on Montmorillonite with Implications for Enhanced Hydrocarbon Extraction by Gas Injection. Appl. Clay Sci. 210, 106160. doi:10.1016/j.clay.2021.106160

CrossRef Full Text | Google Scholar

Gao, F., Xue, Y., Gao, Y., Zhang, Z., Teng, T., and Liang, X. (2016). Fully Coupled Thermo-Hydro-Mechanical Model for Extraction of Coal Seam Gas with Slotted Boreholes. J. Nat. Gas Sci. Eng. 31, 226–235. doi:10.1016/j.jngse.2016.03.002

CrossRef Full Text | Google Scholar

Gao, Y., Lin, B., Yang, W., Li, Z., Pang, Y., and Li, H. (2015). Drilling Large Diameter Cross-Measure Boreholes to Improve Gas Drainage in Highly Gassy Soft Coal Seams. J. Nat. Gas Sci. Eng. 26, 193–204. doi:10.1016/j.jngse.2015.05.035

CrossRef Full Text | Google Scholar

Ge, Z., Cao, S., Lu, Y., and Gao, F. (2021). Fracture Mechanism and Damage Characteristics of Coal Subjected to a Water Jet under Different Triaxial Stress Conditions. J. Pet. Sci. Eng. (In Press). doi:10.1016/j.petrol.2021.109157

CrossRef Full Text | Google Scholar

Ge, Z., Deng, K., Zhang, L., and Zuo, S. (2020). Development Potential Evaluation of CO 2 ‐ECBM in Abandoned Coal Mines. Greenhouse Gas Sci. Technol. 10 (3), 643–658. doi:10.1002/ghg.1986

CrossRef Full Text | Google Scholar

Ge, Z., Mei, X., Jia, Y., Lu, Y., and Xia, B. (2014). Influence Radius of Slotted Borehole Drainage by High Pressure Water Jet. J. Ming Saf. Eng. 31 (4), 657–664. doi:10.13545/j.issn1673-3363.2014.04.02

Google Scholar

Ge, Z., Zhang, L., Sun, J., and Hu, J. (2019). Fully Coupled Multi-Scale Model for Gas Extraction from Coal Seam Stimulated by Directional Hydraulic Fracturing. Appl. Sci. 9 (21), 4720. doi:10.3390/App9214720

CrossRef Full Text | Google Scholar

Gyamfi, B. A., Adedoyin, F. F., Bein, M. A., Bekun, F. V., and Agozie, D. Q. (2021). The Anthropogenic Consequences of Energy Consumption in E7 Economies: Juxtaposing Roles of Renewable, Coal, Nuclear, Oil and Gas Energy: Evidence from Panel Quantile Method. J. Clean. Prod. 295, 126373. doi:10.1016/j.jclepro.2021.126373

CrossRef Full Text | Google Scholar

Huang, C. G., Zhang, Y. B., He, J. F., Luo, Y., and Sun, Z. G. (2019). Permeability Improvements of an Outburst‐prone Coal Seam by Means of Presplitting and Blasting with Multiple Deep Boreholes. Energy Sci Eng 7 (5), 2223–2236. doi:10.1002/ese3.426

CrossRef Full Text | Google Scholar

Jiang, J., Yang, W., Cheng, Y., Lv, B., Zhang, K., and Zhao, K. (2018). Application of Hydraulic Flushing in Coal Seams to Reduce Hazardous Outbursts in the Mengjin Mine, China. Environ. Eng. Geosci. 24 (4), 425–440. doi:10.2113/Eeg-2110

CrossRef Full Text | Google Scholar

Karacan, C. Ö., and Warwick, P. D. (2019). Assessment of Coal Mine Methane (CMM) and Abandoned Mine Methane (AMM) Resource Potential of Longwall Mine Panels: Example from Northern Appalachian Basin, USA. Int. J. Coal Geology. 208, 37–53. doi:10.1016/j.coal.2019.04.005

CrossRef Full Text | Google Scholar

Kędzior, S., and Dreger, M. (2019). Methane Occurrence, Emissions and Hazards in the Upper Silesian Coal Basin, Poland. Int. J. Coal Geology. 211, 103226. doi:10.1016/j.coal.2019.103226

CrossRef Full Text | Google Scholar

Kholod, N., Evans, M., Pilcher, R. C., Roshchanka, V., Ruiz, F., Coté, M., et al. (2020). Global Methane Emissions from Coal Mining to Continue Growing Even with Declining Coal Production. J. Clean. Prod. 256, 120489. doi:10.1016/j.jclepro.2020.120489

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, B., Ren, C., Wang, Z., Li, J., Yang, K., and Xu, J. (2020). Experimental Study on Damage and the Permeability Evolution Process of Methane-Containing Coal under Different Temperature Conditions. J. Pet. Sci. Eng. 184, 106509. doi:10.1016/j.petrol.2019.106509

CrossRef Full Text | Google Scholar

Li, S., Fan, C., Han, J., Luo, M., Yang, Z., and Bi, H. (2016). A Fully Coupled Thermal-Hydraulic-Mechanical Model with Two-Phase Flow for Coalbed Methane Extraction. J. Nat. Gas Sci. Eng. 33, 324–336. doi:10.1016/j.jngse.2016.05.032

CrossRef Full Text | Google Scholar

Li, X., Chen, S., Wang, E., and Li, Z. (2021). Rockburst Mechanism in Coal Rock with Structural Surface and the Microseismic (MS) and Electromagnetic Radiation (EMR) Response. Eng. Fail. Anal. 124 (3), 105396. doi:10.1016/j.engfailanal.2021.105396

CrossRef Full Text | Google Scholar

Lim, K. T., and Aziz, K. (1995). Matrix-Fracture Transfer Shape Factors for Dual-Porosity Simulators. J. Pet. Sci. Eng. 13 (3-4), 169–178. doi:10.1016/0920-4105(95)00010-f

CrossRef Full Text | Google Scholar

Lin, B., Song, H., Zhao, Y., Liu, T., Kong, J., and Huang, Z. (2019). Significance of Gas Flow in Anisotropic Coal Seams to Underground Gas Drainage. J. Pet. Sci. Eng. 180, 808–819. doi:10.1016/j.petrol.2019.06.023

CrossRef Full Text | Google Scholar

Lin, B., Yan, F., Zhu, C., Zhou, Y., Zou, Q., Guo, C., et al. (2015). Cross-Borehole Hydraulic Slotting Technique for Preventing and Controlling Coal and Gas Outbursts during Coal Roadway Excavation. J. Nat. Gas Sci. Eng. 26, 518–525. doi:10.1016/j.jngse.2015.06.035

CrossRef Full Text | Google Scholar

Liu, J., Chen, Z., Elsworth, D., Miao, X., and Mao, X. (2010). Linking Gas-Sorption Induced Changes in Coal Permeability to Directional Strains through a Modulus Reduction Ratio. Int. J. Coal Geology. 83 (1), 21–30. doi:10.1016/j.coal.2010.04.006

CrossRef Full Text | Google Scholar

Liu, J., Chen, Z., Elsworth, D., Qu, H., and Chen, D. (2011). Interactions of Multiple Processes During CBM Extraction: A Critical Review. Int. J. Coal Geology. 87 (3-4), 175–189. doi:10.1016/j.coal.2011.06.004

CrossRef Full Text | Google Scholar

Liu, Z., Cheng, Y., Jiang, J., Li, W., and Jin, K. (2017). Interactions Between Coal Seam Gas Drainage Boreholes and the Impact of Such on Borehole Patterns. J. Nat. Gas Sci. Eng. 38, 597–607. doi:10.1016/j.jngse.2017.01.015

CrossRef Full Text | Google Scholar

Lu, Y., Xiao, S., Ge, Z., Zhou, Z., Ling, Y., and Wang, L. (2019). Experimental Study on Rock-Breaking Performance of Water Jets Generated by Self-Rotatory Bit and Rock Failure Mechanism. Powder Technol. 346, 203–216. doi:10.1016/j.powtec.2019.01.078

CrossRef Full Text | Google Scholar

Lu, Y., Zhou, Z., Ge, Z., Zhang, X., and Li, Q. (2015). Research on and Design of a Self-Propelled Nozzle for the Tree-Type Drilling Technique in Underground Coal Mines. Energies 8 (12), 14260–14271. doi:10.3390/en81212426

CrossRef Full Text | Google Scholar

Lv, A., Cheng, L., Aghighi, M. A., Masoumi, H., and Roshan, H. (2021). A Novel Workflow Based on Physics-Informed Machine Learning to Determine the Permeability Profile of Fractured Coal Seams Using Downhole Geophysical Logs. Mar. Pet. Geology. 131 (2), 105171. doi:10.1016/j.marpetgeo.2021.105171

CrossRef Full Text | Google Scholar

Magazzino, C., Bekun, F. V., Etokakpan, M. U., and Uzuner, G. (2020). Modeling the Dynamic Nexus Among Coal Consumption, Pollutant Emissions and Real Income: Empirical Evidence from South Africa. Environ. Sci. Pollut. Res. 27 (8), 8772–8782. doi:10.1007/s11356-019-07345-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Mordecai, M., and Morris, L. H. (1974). The Effect of Stress on the Flow of Gas through Coal Measure Strata. Int. J. Rock Mech. Mining Sci. Geomechanics Abstr. 11 (10), 2000. doi:10.1016/0148-9062(74)91151-6

CrossRef Full Text | Google Scholar

Palmer, I., and Mansoori, J. (1996). How Permeability Depends on Stress and Pore Pressure in Coalbeds: A New Model. Spe Reservoir Eval. Eng. 1 (6), 539–544. doi:10.2118/36737-ms

CrossRef Full Text | Google Scholar

Perera, M. S. A., Ranjith, P. G., Choi, S. K., and Airey, D. (2012). Investigation of Temperature Effect on Permeability of Naturally Fractured Black Coal for Carbon Dioxide Movement: An Experimental and Numerical Study. Fuel 94, 596–605. doi:10.1016/j.fuel.2011.10.026

CrossRef Full Text | Google Scholar

Ranathunga, A. S., Perera, M. S. A., and Ranjith, P. G. (2014). Deep Coal Seams as a Greener Energy Source: A Review. J. Geophys. Eng. 11 (6), 063001. doi:10.1088/1742-2132/11/6/063001

CrossRef Full Text | Google Scholar

Si, L., Li, Z., Yang, Y., and Gao, R. (2019). The Stage Evolution Characteristics of Gas Transport During Mine Gas Extraction: Its Application in Borehole Layout for Improving Gas Production. Fuel 241, 164–175. doi:10.1016/j.fuel.2018.12.038

CrossRef Full Text | Google Scholar

Szott, W., Słota-Valim, M., Gołąbek, A., Sowiżdżał, K., and Łętkowski, P. (2018). Numerical Studies of Improved Methane Drainage Technologies by Stimulating Coal Seams in Multi-Seam Mining Layouts. Int. J. Rock Mech. Mining Sci. 108, 157–168. doi:10.1016/j.ijrmms.2018.06.011

CrossRef Full Text | Google Scholar

Udi, J., Bekun, F. V., and Adedoyin, F. F. (2020). Modeling the Nexus Between Coal Consumption, FDI Inflow and Economic Expansion: Does Industrialization Matter in South Africa?. Environ. Sci. Pollut. Res. 27 (10), 10553–10564. doi:10.1007/s11356-020-07691-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, C., Liu, J., Feng, J., Wei, M., Wang, C., and Jiang, Y. (2016). Effects of Gas Diffusion from Fractures to Coal Matrix on the Evolution of Coal Strains: Experimental Observations. Int. J. Coal Geology. 162, 74–84. doi:10.1016/j.coal.2016.05.012

CrossRef Full Text | Google Scholar

Wu, Y., Liu, J., Elsworth, D., Chen, Z., Connell, L., and Pan, Z. (2010). Dual Poroelastic Response of a Coal Seam to CO2 Injection. Int. J. Greenhouse Gas Control. 4 (4), 668–678. doi:10.1016/j.ijggc.2010.02.004

CrossRef Full Text | Google Scholar

Xia, T., Zhou, F., Liu, J., Hu, S., and Liu, Y. (2014). A Fully Coupled Coal Deformation and Compositional Flow Model for the Control of the Pre-Mining Coal Seam Gas Extraction. Int. J. Rock Mech. Mining Sci. 72, 138–148. doi:10.1016/j.ijrmms.2014.08.012

CrossRef Full Text | Google Scholar

Xiao, S., Ge, Z., Lu, Y., Zhou, Z., Li, Q., and Wang, L. (2018). Investigation on Coal Fragmentation by High-Velocity Water Jet in Drilling: Size Distributions and Fractal Characteristics. Appl. Sci. 8, 1988. doi:10.3390/app8101988

CrossRef Full Text | Google Scholar

Xiao, S., Ren, Q., Guan, R., Liu, J., Wang, H., Cheng, Y., et al. (2021). Theoretical and Experimental Investigation on Fracture Response of Coal Impacted by High-Velocity Water Jet. Energ. Rep. 7 (5), 3210–3224. doi:10.1016/j.egyr.2021.05.029

CrossRef Full Text | Google Scholar

Xie, H. P. (2019). Research Review of the State Key Research Development Program of China:Deep Rock Mechanics and Mining Theory. J. China Coal Soc. 44 (05), 1283–1305. doi:10.13225/j.cnki.jccs.2019.6038

CrossRef Full Text | Google Scholar

Yang, M. (2009). Climate Change and Energy Policies, Coal and Coalmine Methane in China. Energy Policy 37 (8), 2858–2869. doi:10.1016/j.enpol.2009.02.048

CrossRef Full Text | Google Scholar

Zhang, C., Xu, J., Peng, S., Li, Q., and Yan, F. (2019). Experimental Study of Drainage Radius Considering Borehole Interaction Based on 3D Monitoring of Gas Pressure in Coal. Fuel 239, 955–963. doi:10.1016/j.fuel.2018.11.092

CrossRef Full Text | Google Scholar

Zhang, G., Ranjith, P. G., Perera, M. S. A., Haque, A., Choi, X., and Sampath, K. S. M. (2018). Characterization of Coal Porosity and Permeability Evolution by Demineralisation Using Image Processing Techniques: A Micro-Computed Tomography Study. J. Nat. Gas Sci. Eng. 56, 384–396. doi:10.1016/j.jngse.2018.06.020

CrossRef Full Text | Google Scholar

Zhang, H., Cheng, Y., Liu, Q., Yuan, L., Dong, J., Wang, L., et al. (2017). A Novel In-Seam Borehole Hydraulic flushing Gas Extraction Technology in the Heading Face: Enhanced Permeability Mechanism, Gas Flow Characteristics, and Application. J. Nat. Gas Sci. Eng. 46, 498–514. doi:10.1016/j.jngse.2017.08.022

CrossRef Full Text | Google Scholar

Zhang, H., Liu, J., and Elsworth, D. (2008). How Sorption-Induced Matrix Deformation Affects Gas Flow in Coal Seams: A New FE Model. Int. J. Rock Mech. Mining Sci. 45 (8), 1226–1236. doi:10.1016/j.ijrmms.2007.11.007

CrossRef Full Text | Google Scholar

Zhang, L., Ge, Z., Lu, Y., Zhou, Z., Xiao, S., and Zuo, S. (2021). Permeability Enhancement and Methane Drainage Capacity of Tree-Type Boreholes to Stimulate Low-Permeability Coal Seams. Arab J. Sci. Eng. 46 (1), 573–586. doi:10.1007/s13369-020-04961-1

CrossRef Full Text | Google Scholar

Zhang, L., Ge, Z., Lu, Y., Zhou, Z., Xiao, S., and Deng, K. (2020). Tree-Type Boreholes in Coal Mines for Enhancing Permeability and Methane Drainage: Theory and an Industrial-Scale Field Trial. Nat. Resour. Res. 29 (5), 3197–3213. doi:10.1007/s11053-020-09654-y

CrossRef Full Text | Google Scholar

Zhao, D., Liu, J., and Pan, J.-T. (2018). Study on Gas Seepage from Coal Seams in the Distance Between Boreholes for Gas Extraction. J. Loss Prev. Process Industries 54, 266–272. doi:10.1016/j.jlp.2018.04.013

CrossRef Full Text | Google Scholar

Zhao, Y., Lin, B., and Liu, T. (2020a). Thermo-Hydro-Mechanical Couplings Controlling Gas Migration in Heterogeneous and Elastically-Deformed Coal. Comput. Geotechnics 123, 103570. doi:10.1016/j.compgeo.2020.103570

CrossRef Full Text | Google Scholar

Zhao, Z., Sui, F., and Yan, J. (2020b). Prediction of Methane Content of Deep Coal Seams in the Sunan Mining Area in Anhui Province, China. Ijogct 23 (3), 351–364. doi:10.1504/Ijogct.2020.105778

CrossRef Full Text | Google Scholar

Zheng, C., Chen, Z., Kizil, M., Aminossadati, S., Zou, Q., and Gao, P. (2016). Characterisation of Mechanics and Flow fields Around In-Seam Methane Gas Drainage Borehole for Preventing Ventilation Air Leakage: A Case Study. Int. J. Coal Geology. 162, 123–138. doi:10.1016/j.coal.2016.06.008

CrossRef Full Text | Google Scholar

Zhou, H. W., Wang, X. Y., Zhang, L., Zhong, J. C., Wang, Z. H., and Rong, T. L. (2020). Permeability Evolution of Deep Coal Samples Subjected to Energy-Based Damage Variable. J. Nat. Gas Sci. Eng. 73, 103070. doi:10.1016/J.Jngse.2019.103070

CrossRef Full Text | Google Scholar

Zhou, Y., Rajapakse, R. K. N. D., and Graham, J. (1998). Coupled Heat-Moisture-Air Transfer in Deformable Unsaturated media. J. Eng. Mech. 124 (10), 1090–1099. doi:10.1061/(asce)0733-9399(1998)124:10(1090)

CrossRef Full Text | Google Scholar

Zhu, W. C., Wei, C. H., Li, S., Wei, J., and Zhang, M. S. (2013). Numerical Modeling on Destress Blasting in Coal Seam for Enhancing Gas Drainage. Int. J. Rock Mech. Mining Sci. 59, 179–190. doi:10.1016/j.ijrmms.2012.11.004

CrossRef Full Text | Google Scholar

Zhu, W. C., Wei, C. H., Liu, J., Qu, H. Y., and Elsworth, D. (2011). A Model of Coal-Gas Interaction under Variable Temperatures. Int. J. Coal Geology. 86 (2-3), 213–221. doi:10.1016/j.coal.2011.01.011

CrossRef Full Text | Google Scholar