- 1James Watt School of Engineering, The University of Glasgow, Glasgow, United Kingdom
- 2School of Engineering, The University of Edinburgh, Edinburgh, United Kingdom
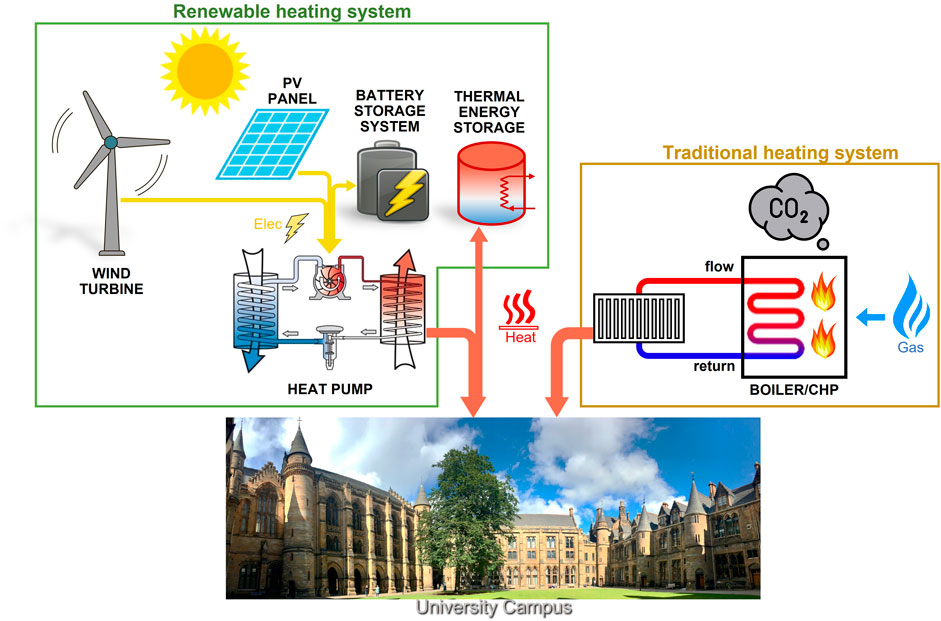
As the use of fossil fuels has led to global climate change due to global warming, most countries are aiming to reduce greenhouse gas emissions through the application of renewable energies. Due to the distributed and seasonal heating demand, the decarbonisation of heating is more challenging, especially for countries that are cold in winters. Electrically powered heat pumps are considered as an attractive solution for decarbonising heating sector. Since grid-powered heat pumps may significantly increase the power demand of the grid, this paper considers using local renewable energy to provide power for heat pumps, which is known as the grid independent renewable heating system including photovoltaic, wind turbine, battery storage system and thermal energy storage. This paper investigates a complete renewable heating system (RHS) framework and sizing the components to decarbonise building heating. The relationship between the reduction of gas consumption and the requirement of battery storage system (BSS) under the corresponding installation capacity of renewable components is analysed with their technical requirements. Then, according to different investment plans, this paper uses the particle swarm optimisation algorithm for optimal sizing of each component in the RHS to find a solution to minimise CO2 emissions. The results verify that the RHS with optimal sizing can minimise CO2 emissions and reduce the operational cost of natural gas. This work provides a feasible solution of how to invest the RHS to replace the existing heating system based on gas boilers and CHPs.
Introduction
In recent decades, the rapid consumption of fossil fuels has greatly reduced global resource reserves and has led to global climate abnormalities (Ekren and Ekren, 2008; Luna-Rubio et al., 2012; Eltamaly et al., 2016). In order to reduce the risk of climate change caused by global warming, it is very important to reduce energy consumption and greenhouse gas (GHG) emissions (Ndwali et al., 2020; Rinaldi et al., 2021). As part of the European Green Agreement, the European Union (EU) has set a goal to reduce its GHG emissions by 55% by 2030 and become the world’s first fully climate-neutral continent by 2050 (Maleki et al., 2016; Yue et al., 2020). Therefore, the EU has supported many energy projects in the past few years to enhance the role of renewable energy in the European energy plan (European Commission, 2016). To achieve these challenging goals, the energy structure of most countries needs to undergo major changes to reduce dependence on fossil fuels and the associated GHG emissions (da Silva Lima et al., 2021). Increased use of renewable energy sources will make important contributions, such as wind energy, solar energy, hydropower, tides, waves, geothermal energy, environmental thermal energy, biofuels and municipal waste (Edenhofer et al., 2011). Due to the non-dispatchable nature of many renewables, energy storage is also required. In recent years, the integrated energy network (IEN) has developed rapidly in terms of energy efficiency improvement, carbon dioxide emission reduction, and renewable energy integration.
In countries with cold winters, heating accounts for a large part of energy consumption and is usually heavily dependent on the burning of fossil fuels such as natural gas and coal (Liang et al., 2018). The current energy demand in the building sector, such as space heating and domestic hot water, accounts for 40% of the total energy demand in the EU (Tulus et al., 2016). Nearly half of the total energy consumption in the United Kingdom is used for heating, and this proportion is even higher in Scotland (Renaldi et al., 2017). While it is crucial to decarbonise heating, it is challenging due to the distributed demand and large seasonal variations. In 2017, the GHG emission of United Kingdom equals to 460 million tons of
Heat pumps (HPs) are considered to be the key technology for decarbonization in the heating industry (Kim et al., 2014; Al-Tameemi et al., 2019). The HP uses a small amount of work energy to convert a low-grade heat source into a higher-grade heat source. The technical details of HP will not be discussed in this article since a lot of literature has previously discussed it (Cengel and Boles, 2007; Ozgener and Hepbasli, 2007; Trillat-Berdal et al., 2007; Self et al., 2013; Casasso and Sethi, 2014; Arat and Arslan, 2017; Grassi, 2017). If the heat source is outside air, the system is called an air source heat pump. If the heat source is underground soil or groundwater, it is called a geothermal heat pump. Geothermal heat pump is one of the fastest growing renewable energy sources in the world (Li et al., 2021). In the long-term, electrifying heating based on HPs is an attractive solution for the decarbonized heating sector. However, this will significantly increase the peak power demand in winter and will bring further challenges to the national grid in terms of creating additional power generation capacity and balancing power generation and demand. In addition, if electric power is generated from fossil fuels, the decarbonization effect will not be fully realized. Therefore, this paper considers using local renewable energy, which is grid-independent, to power the heat pump for building heating and reduce the usage of traditional gas boiler for decarbonisation.
The development of IEN is to integrate electricity, heat and gas systems into an integrated power distribution network. However, the further integration of heating and power networks has also expanded the opportunities for demand-side management to integrate more variable renewable energy generation into the energy system. Due to the rapid growth, the renewable power generation has been extensively studied in the past decades (O'Shaughnessy et al., 2018; Liu et al., 2017). In particular, solar energy and wind energy are used as sources to supply power to the grid (Dragicevic et al., 2014; Jamal et al., 2019; Khezri et al., 2020). However, the main disadvantage of most renewable energy sources is their intermittent nature, as they fluctuate on a daily, weekly, and seasonal basis. In order to filter these changes, battery energy storage systems have been widely accepted as one of the potential solutions to shift the electrical load from peak hours to off-peak hours (Yang et al., 2018a; Wali et al., 2021). The idea of combining power generation cycle and HP cycle has been extensively studied, such as solar collector - HP (Trillat-Berdal et al., 2007), PV—HP (Kavian et al., 2020), HP—thermal energy storage (TES) (Renaldi et al., 2017), organic Rankine cycle (ORC) - HP water heaters (Liang et al., 2018). However, due to the large differences in local weather conditions, occupancy, energy prices, government subsidies and building types, this optimisation must be done for each component (Renaldi et al., 2017). When different energy vectors are intertwined in future smart energy systems, optimal sizing of each component is especially important. In the research on the optimal sizing of renewable energy systems, many papers have considered WT, PV, ESS, and fuel cells (Yang et al., 2020; Yang et al., 2021). However, the previous published papers only considered the perspective of electrical power use, and do not consider both heat demand and electricity generation together as well as the impact of heating demand that increases the electrical energy use under the trend of electrified heating in the future. In addition, most of the literature considers sizing from the aspect of technical requirements and does not incorporate future technology and price trends. Therefore, within the author’s knowledge, the past research has not done feasibility analysis and optimisation for different power generation, thermal systems and the investment allocation of each system.
This paper proposes a complete renewable heating system (RHS) framework, including PV, WT, BSS, HP, and TES, and provides a path to the decarbonisation with yearly investment decisions. In the context of British tariffs and government incentives, the size of each component in the system is optimised according to the annual investment cost (AIC) limit. Since there are many components in the RHS system that need to be optimised at the same time, the particle swarm optimisation (PSO) algorithm is selected for optimal sizing of the RHS. The optimisation goal is to obtain the least
Renewable Heating System Modelling
Traditional heating systems use combined heat and power (CHP) and gas boilers to consume gas to generate heat for space heating of buildings. The use of gas can cause a large amount of
Wind Turbine
The role of wind turbines (WT) is to convert wind energy, an environmentally friendly energy source, into a form of electrical energy. It is one of the most promising renewable energy sources and its global installed capacity is increasing year by year (Ren et al., 2021). According to the direction of their rotation axis, WTs can be classified into horizontal axis wind turbines (HAWT) and vertical axis wind turbines (VAWT). HAWT extracts wind energy on the horizontal axis and the blades rotate due to the lift provided by the aerodynamic force from wind. Because of it has higher efficiency than VAWT, the HAWT is more popular in research. However, HAWT needs to always point to the wind direction to work effectively. For unpredictable wind directions, the HAWT needs additional mechanisms to ensure that the blades are always facing the wind direction. The VAWT has its blades perpendicular to the ground and rotating around the vertical axis. VAWT can receive wind power from any direction. Compared with HAWT, VAWT has several advantages, including no need to face to the wind flow, the ability of generating electricity at low wind speed, no need for additional control on yaw and pitch, less maintenance costs, and less noise (Eriksson et al., 2008; Johari et al., 2018). However, VAWT has much lower efficiency at high wind speeds than HAWT, its dynamic stability is relatively poor due to its light weight, and it is vulnerable to backtracking wind. For the above reasons, VAWT is often installed in slow and turbulent wind environments, such as roof top, for low-power generation (Bhutta et al., 2012), while HAWT is often used for high-power generation in isolated and remote areas, such as on-shore or off-shore wind farms (Johari et al., 2018). In recent years, some researchers have combined the two types of WT together to improve its operational capabilities (Govind, 2017).
Although HAWT and VAWT have lots of difference in structure, control strategy and power efficiency, the methods they use to capture power from wind energy are the same, and thus can be expressed by the same equation. The available power output of a WT is proportional to the cube of the wind speed. If the wind speed is too low, the output power of the WT can be ignored. When the wind speed increases, the output power of the WT increases rapidly. Therefore, in order to ensure the normal operation of a WT, three threshold wind speeds usually need to be considered, including the cut-in speed, the rated speed and the cut-out speed (Ren et al., 2016). When the wind speed is lower than the cut-in speed, the WT stops to avoid unnecessary mechanical wear and energy consumption; when the wind speed is higher than the cut-in speed and lower than the rated speed, the WT controls its rotating speed to track the maximum power point referring to the current wind speed; when the wind speed is higher than the rated speed and lower than the cut-out speed, the WT adjusts its pitch angle to limit the captured wind power not to exceed the limit of the generator; when the wind speed exceeds the cut-out speed, the WT shuts down to protect the rotor and the generator from the damage of strong wind.
The power output of WT captured from wind is presented as
where
When designing a renewable energy system, it is necessary to determine the suitable capacity of the WT according to the rated power of the WT and the local wind resources. During the operation, it is necessary to consider whether the current wind speed has reached the cut-in speed, rated speed and cut-out speed, and calculate the power that the WT can generate according to the wind speed.
Solar Photovoltaic
Solar energy is another well-known clean energy. Since most parts of the world have sufficient solar irradiance, solar power generation technology has attracted a large number of researchers. Photovoltaic (PV) is a device that uses the photoelectric effect to directly and conveniently convert solar energy into electricity (Liu et al., 2017). In recent years, with the development of PV technology and the rapid decline of PV costs, large-scale grid-connected solar PV power stations have been built all over the world (Mandal et al., 2012).
However, PV systems are highly dependent on solar radiation and weather characteristics. Due to the variability of solar radiation and ambient temperature, the power output of the PV system is uncertain and random (Mandal et al., 2012). The uncertainty is from the alternation of day and night, effect of seasonal changes, and random cloud movement (Jamal et al., 2017; Jamal et al., 2019). Compared with the distributed PV system, the power output of the relatively concentrated and single format PV power generation system in a small area can change very quickly. An isolated community can be completely or partially obscured by fast-moving clouds in the span of a few seconds to a few minutes (Schmidt et al., 2017). The movement of the cloud will affect the performance of the PV system, so prediction must be made to avoid undesirable technical problems and cost losses (Jamal et al., 2019). Predicting the power output of a PV system is a challenging task.
For a photovoltaic array composed of PV panels, the maximum power output can be expressed as (Tao et al., 2010)
where
The power output of PV system mainly depends on the amount of solar radiation and the operating temperature of the installation location. In addition, as the equipment ages, the photoelectric conversion efficiency and power conversion efficiency will gradually decrease. But their changes in the system life cycle are very small, so they can be ignored. Therefore, as long as the solar radiation and panel temperature are known, the power output of the PV system can be predicted.
Battery Storage System
As the main renewable energy sources, solar and wind energy are intermittent and fluctuating weather resources. One of the possible solutions is to use a hybrid renewable energy system to integrate various renewable energy sources in the best combination (Yang et al., 2018a). A good example is the complementarity of solar and wind energy (Prasad et al., 2017). However, this approach still has large uncertainties. If the distributed resources cannot provide sufficient flexibility in power generation, network operators will have to limit the penetration rate of renewable energy to a certain level, which will adversely affect the use of renewable energy systems (Jamal et al., 2019). For example, the power generation of the PV system usually exceeds the residential electricity load during the day but cannot meet the demand in the late afternoon and evening when the residential load tends to increase (O'Shaughnessy et al., 2018). Therefore, in order to highly integrate variable wind and solar energy and reduce the impact of weather changes on renewable power generation, energy storage systems have been widely accepted as one of the potential solutions (e Silva and Hendrick, 2017; Babacan et al., 2017; Zhang et al., 2018; Ren et al., 2020). The main function of energy storage system is to compensate the imbalance between power generation and demand, transfer energy from periods of high power generation to periods of low power generation, so that the system can maintain full functionality under various operating conditions (Dragicevic et al., 2014).
ESS includes a variety of technologies, such as pumped water storage, compressed air energy storage, hydrogen storage, flywheels, supercapacitors, and batteries (da Silva Lima et al., 2021). The batteries have higher energy density than supercapacitors, higher charging rate than pumped water storage and less power loss than flywheels. Therefore, the battery storage system (BSS) is the most suitable storage system to store the electricity energy for such localised small-scale applications due to its advantage of higher charging rate, higher energy density and shorter response time. The response time of BSS is between milliseconds and seconds, while that of PHS and CAES are from a few seconds to minutes (Castillo and Gayme, 2014). Due to their durability, low maintenance and low social environmental impact, it is expected that the development and use of BSS will increase significantly in the next decades (da Silva Lima et al., 2021). Among batteries, the most used are lithium-ion batteries (LIB) and vanadium redox flow batteries (VRB). The advantages of LIB are its high energy density, high efficiency, long lifecycle, and more environment friendly characteristics. However, due to these advantages of LIB, they are also widely used in a variety of other applications, including small electronic products and electric vehicles. VRB is a good substitute for LIB because of its safety, long service life, better scalability and high recyclability (da Silva Lima et al., 2021). However, the disadvantage of VRB is its low energy density (Castillo and Gayme, 2014). Therefore, a VRB requires more floor space than a LIB at the same capacity.
In the charging and discharging behaviour of a battery, the state of charge (SOC) is often used to reflect the ratio of the battery’s remaining capacity to its rated capacity (Yang et al., 2018b). To protect battery lifecycle, it is necessary to limit the SOC within a certain range. During battery charging, the SOC can be given as (Zhang et al., 2018)
and during battery discharging, the SOC can be given as
where
Heat Pump
Heat pumps are a group of energy systems that can extract heat energy from lower temperature sources such as ambient air, soil, water in lakes and rivers, and then upgrade and deliver it at a higher temperature for heating applications (Watzlaf and Ackman, 2006). If the heat source is outside air, the system is called an air source heat pump (ASHP). If the heat source is the ground, soil or groundwater, it is called a geothermal heat pump (GHP). GHP is one of the fastest growing renewable energy sources in the world (Arat and Arslan, 2017). Compared with traditional heating fuels, such as natural gas, heating oil and propane, the effectiveness of operational cost of GHPs is directly related to the cost of electricity that drives the HP (Self et al., 2013). But the installation costs of GHPs can be an order of magnitude higher compared to a gas boiler.
Heat energy delivered by the HP normally exceeds its electricity consumption. Coefficient of performance (COP) defined as the ratio of heat output to input power is used to describe the energy performance of heat pumps (Casasso and Sethi, 2014). The COP of heat pumps can reach 3–5 or more depending on temperature conditions (Renaldi et al., 2017), which means the heat pump can provide 3–5 kW of heat by consuming 1 kW of electricity. Furthermore, the smaller temperature difference between the heat source and the radiator, the greater the COP of the HP system. In cold weather, the COP of an ASHP is usually about 2 or lower. Therefore, GHP have higher efficiency than ASHP because the underground temperature is closer to the required indoor conditions than the outdoor air temperature in winter and the GHP usually use water which reduces the size of the evaporator heat exchanger due to the higher energy density compared to air. However, as GHP requires higher installation costs and larger spaces, ASHP is more suitable for heating smaller spaces.
In HP applications, its COP can be affected by different variables, such as external temperature, water supply temperature, inlet water temperature and load factor. Simplifications can be made to reduce this complexity. The COP can be calculated as (Ozgener and Hepbasli, 2007):
where
The rate of heat transfer from the condenser is obtained as
In this study, the air source heat pump is considered. For simplification, the COP of the HP is modelled as a function of temperature lift, or the temperature lift is known as the difference between the supply water temperature
where
Thermal Energy Storage
The outdoor temperature changes between summer and winter during the year can produce huge changes of heat demand (Xu et al., 2018). In this case, a lot of heat will be wasted in the summer when the heating demand is minimal, and there will be insufficient heat in the winter. In addition, the mismatch between energy demand and supply is often observed. Among several storage technologies, thermal energy storage (TES) seems to be one of the most promising technologies that can compensate for the intermittent heat generation of new energy sources. The advantages of using TES in energy systems include improved overall efficiency, better reliability, bring better economy, reduced investment, and operating costs, and less pollution and
In recent decades, the TES technology has been widely studied. Considering the required storage time, the TES system can be divided into short-term storage and long-term storage. The short-term storage TES has a charging and discharging cycle of hours to several days, which is called diurnal thermal energy storage. The long-term storage TES can store heat for several months and is called seasonal TES (Dahash et al., 2019; Renaldi and Friedrich, 2019; Maximov et al., 2021). The principle of seasonal TES is to store heat energy through heating equipment in summer, and then discharge it for space heating in winter (Kubiński and Szabłowski, 2020). The use of TES can significantly increase the flexibility and self-consumption of renewable energy for end users (Waser et al., 2018). Therefore, this concept makes a significant contribution to the efficient use of renewable energy in district heating systems and the decarbonization of the building sector.
The most traditional TES design is provided in the form of a water tank. When there is excess thermal energy on the supply side, these tanks are charged (heated up), and when the demand for thermal energy exceeds the supply, these tanks are discharged (Abdelsalam et al., 2020). In the thermal system, the charging and discharging process of the storage tank can be carried out by direct heat exchange. The energy stored in the TES at time
where
Among the performance indicators used to evaluate TES, the most common is TES efficiency, which is the ratio of the total heat energy recovered from the heat accumulator at the discharge temperature to the total heat input at the charging temperature as (Dahash et al., 2019)
Optimal Sizing of Renewable Heating System
Optimisation Problem
The purpose of this study is to find the most effective investment plan to reduce
where
In this paper, the RHS uses the electricity from local renewable energy. Thus, it is assumed that electricity power generation has no
This equation only considers the
And
where
In practice, the output of power generator and heating equipment cannot exceed its rated value, and the energy stored by storage equipment cannot exceed its specified capacity. In addition, the annual installed capacity cannot be negative, which means that the total capacity of each component cannot be lower than the previous year. The constraints of all types of components are given as
In addition to the above technical constraints, another constraint is the financial budget. In this study, it is assumed that the investment plan has an Annual Investment Cost (AIC) limit. The investment cost in each year can be used to increase the capacity of any component, but the total cost cannot exceed AIC as
where
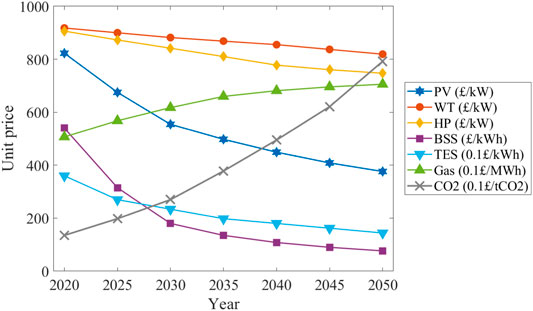
The forecasted component unit price in future years is obtained based on different financial assumptions in recently published papers (Keiner et al., 2019; Yue et al., 2020; Rinaldi et al., 2021). In this study, the financial forecast for the unit cost of components for 2020–2050 is in British pounds, as shown in Figure 2. The prediction shows that the unit prices of PV, WT, HP, BSS, and TES will continue to fall in the next few decades, while the unit price of natural gas and CO2 will increase rapidly in the coming decades.
Optimisation Approach
From the literature in the past decades, there are four main optimisation approaches that are commonly used, including the direct search, calculus-based optimisation, genetic algorithm (GA), and particle swarm optimisation (PSO). Direct search is a straightforward optimisation method that does not consider time delay and derivatives. Thus, the direct search method can be applied in optimising many nonlinear functions that have less dependence on its derivatives (Kolda et al., 2003). The most commonly used Calculus-based Optimisation method is to set the gradient of the objective function to zero (Kheiri, 2018). Another calculus-based optimisation method is Newton’s method, which is similar to the Steepest Descent Method that uses an iterative process from an initial guessed starting point to finally converge to the optimum point. The GA is a population-based algorithm to search for the global-optimum solution. The iterative process of GA will converge to better solutions based on the breeding of the parents with higher performance (Elbeltagi et al., 2005; Kheiri, 2018). However, the GA has shortages that it requires a large amount of non-optimal data as the requirement of global search (Kheiri, 2018). The PSO is a population-based metaheuristic algorithm that attempts to find the global optimal solution of the optimisation problem by simulating the social gathering behaviour of animals (Eberhart and Kennedy, 1995; Kheiri, 2018). This paper chooses the PSO method to find the optimal sizing of RHS due to its strength in finding the global optimal solution and easy to implement.
PSO method uses a large number of the swarm to search the optimum point globally and share the information among all swarm for the next search step. In the PSO algorithm, each feasible solution is called a particle, which is specified by a vector containing problem variables (Maleki et al., 2016). Particles can remember their previous optimal position and share it with others (Shi, 2001). The motion of each particle is composed of two randomly weighted influences and an initial random velocity (Shi, 2001). The PSO algorithm simulates the sociality of particle, combines the best position of the entire swarm and the trend of its own movement, effectively avoids the particles and swarm falling into the local optimal solutions (Baniasadi et al., 2020).
In the PSO algorithm, the state of each particle is represented by its position
where
Simulation of Renewable Heating System
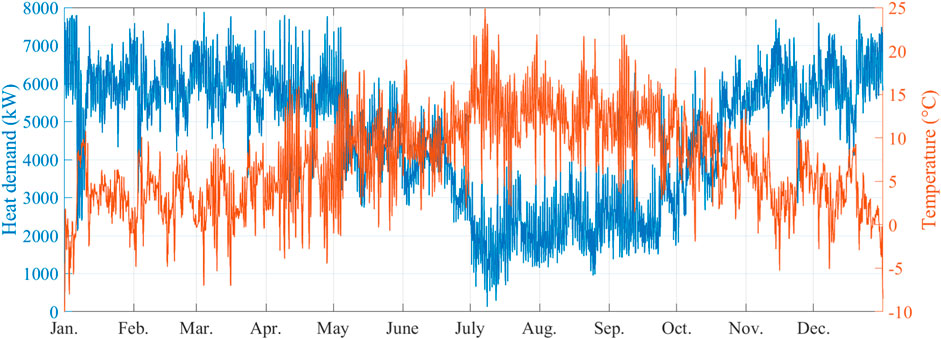
Heat demand is the most important input parameter for any heating system optimisation. It is essential to obtain good performance of the real system. A heat demand model needs to be established to predict the required heat through weather conditions such as ambient temperature. Modelling and simulation of energy systems are usually implemented using engineering models or data-driven models. The simulation test uses energy data from the Glasgow University campus as a case study. In our previous study, both the engineering modelling approach (Chen et al., 2019) and data-driven approach (Chen et al., 2020) have been used to predict the heat demand of campus buildings. The heat demand of the campus and the corresponding ambient temperature data are shown in Figure 3.
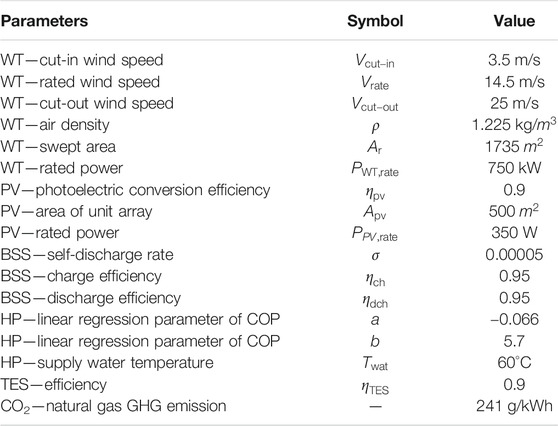
The hourly temperature obtained from the nearest weather station shows that the local annual temperature fluctuates between −10°C and 25°C. The heat demand data is recorded at the University Energy Centre, given as a blue line, varying from 0 kW to 8000 kW. From the data, the temperature is lower in winter and higher in summer, while the heat demand is the opposite. The parameters of each component in the RHS are given in Table 1.
Heat Pump Powered by Local Renewable Resources
In the previous simulation case, it can be found that the use of HP will bring additional power load to the grid. This shows that although the use of HP can greatly reduce
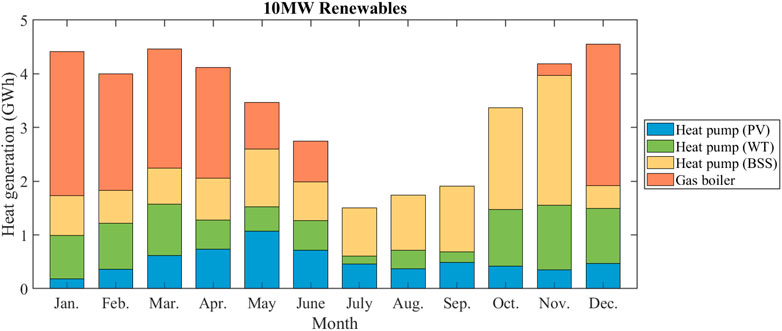
Figure 4 shows an example of monthly heat production when renewable generation capacity is 10 MW, where the rated power of PV and WT are both 5 MW. Since this case aims to consider the role of the BSS rather than its actual size, the capacity of the BSS is assumed to be large enough to store all unused energy from renewable energy sources. The blue part, the green part, and the yellow part in the bar chart represent the heat generated by the HP driven by power from PV, WT, and BSS, respectively. It can be seen from the results that, due to the large changes in the illumination time and the angle of solar radiation in high latitude areas such as Scotland, PV power generation is higher in summer and lower in winter. WT has the opposite trend as it will produce more power in winter and less power in summer. From the results of each month, the heat demand of the building in July, August, and September is less, so the heat demand can be fully supplied by HP. In addition, due to the low heat demand, the unconsumed power generated by renewable resources is stored in the BSS. Therefore, in October and November, most of the electricity is provided by the BSS that has stored electricity in the past few months. From December to April, the heat demand is high, but the power from renewable energy and BSS are low, so a large amount of heat is provided by gas boilers for building heating.
It can be seen from the above results that the natural gas consumption of gas boilers is related to the installed capacity of renewable energy. Therefore, the relationship between natural gas consumption and renewable energy installed capacity is shown in Figure 5A. Without the use of BSS, the gas consumption decreases slowly as the installed capacity of PV or WT increases, as shown by the dashed lines. Under the same installed capacity, WT-driven HP performs better than PV-driven HP in reduction of gas consumption. The reason is that WT’s power generation is large in winter and small in summer, which is more in line with building heat demand. However, PV power generation has a small amount of power generation in winter, so the power generation of PV in winter is not enough to support HP consumption. However, after using BSS with installed capacity in Figure 5B, the time distribution of renewable resources has less impact, and the total power generation is more important. As the installed capacity of renewable energy increases, the consumption of natural gas decreases faster since unconsumed electricity is stored in the BSS and used to assist the renewable energy generation. With the same installed capacity, PV can generate more electricity than WT, and thus results in less gas consumption. In this case, HP driven by PV can reduce gas consumption faster than HP driven by WT. However, due to the time mismatch between heat demand and PV power generation, the BSS capacity required for PV is much higher than that of WT. The required capacity of BSS corresponding to different renewable energy installation capacity is shown in Figure 5B. When the PV installed capacity reaches 15 MW, the gas consumption can be reduced to zero. The corresponding required BSS is nearly 5 GWh, which is a very high capacity, while the same installation capacity of WT requires the BSS for just 1 GWh, which is still a massive capacity. Therefore, this result only considers the technical requirements and does not consider the financial feasibility.
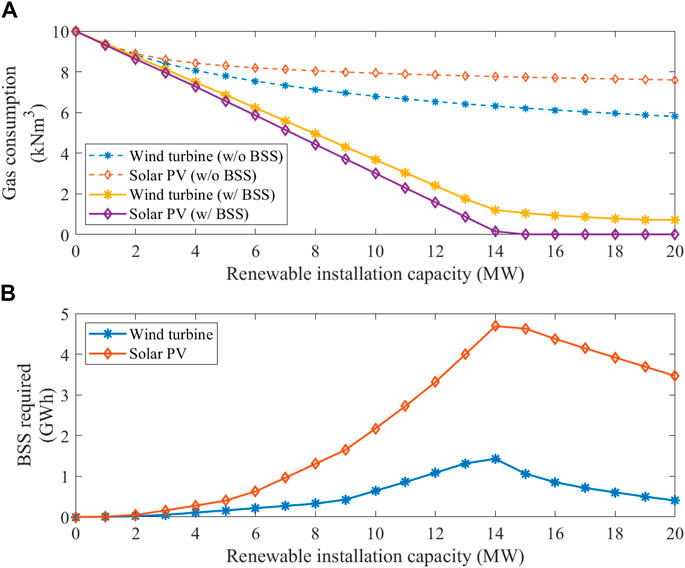
FIGURE 5. Boiler gas consumption and required ESS capacity according to the installation capacity of renewable energy.
The results in Figure 5 are for cases with only a single renewable generation technology, i.e., either PV or WT but not at the same time. The result shows that PV driven HP is better in terms of total power generation but requires more BSS for energy storage. For this reason, another method is to install PV and WT at the same time to combine their advantages. The gas consumption and the required BSS corresponding to the PV and WT at different rated powers are shown in the 2D surfaces of Figures 6A,B. When the rated power of PV and WT is greater than 7 MW, only 2.5 GWh of BSS can reduce natural gas consumption to zero, which is only half the installed capacity of PV alone.
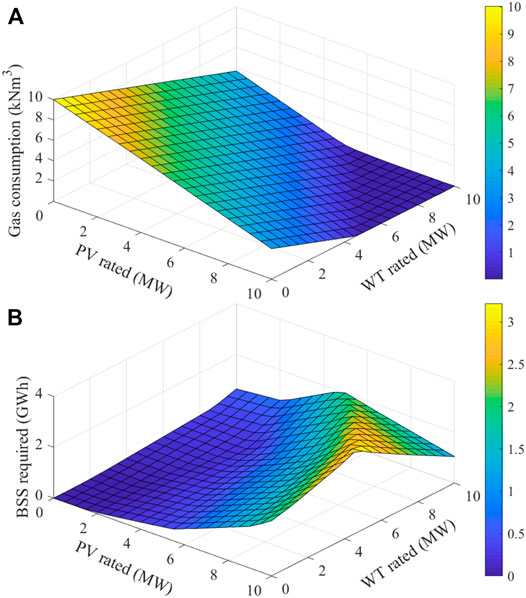
FIGURE 6. Boiler gas consumption and required BSS capacity according to the rated power of PV and WT.
Optimal Sizing Considering
The previous case only considered the technical requirements for the selection of components in RHS. This section considers the financial cost in reducing
The optimisation result is shown in Figure 7, which shows the annual investment capacity of each component in the RHS based on different investment budgets. For example, if the university plans to spend 100,000 pounds per year, as shown by the blue line, the optimal capacity of PV, WT, HP, BSS, and TES for investment according to the optimisation results are given in Figures 7A–E. Using the optimal scheme, the least
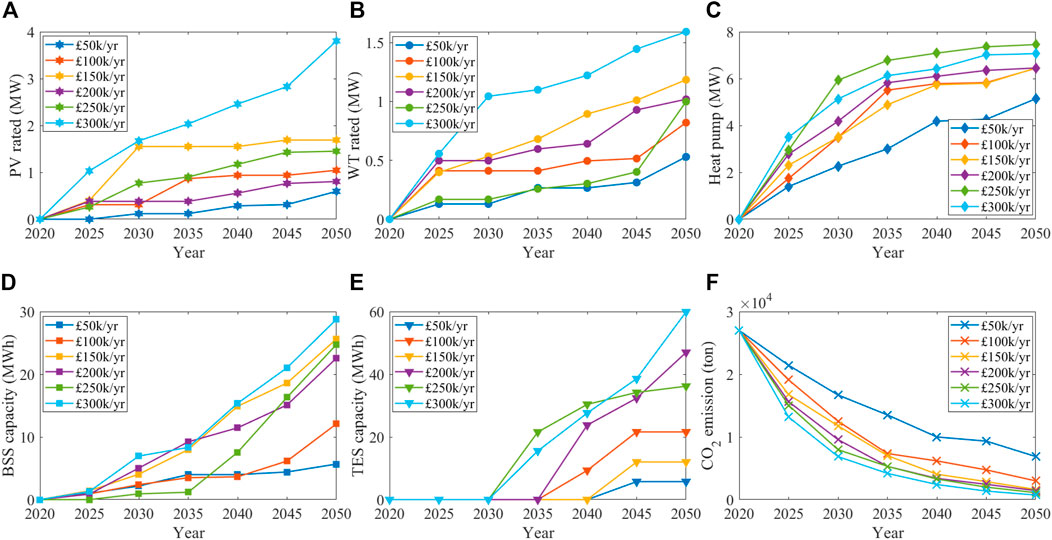
FIGURE 7. Optimisation result of installing renewable energy, heat pump and BSS, and the reduction of
Compared with different AIC, the more investment, the less
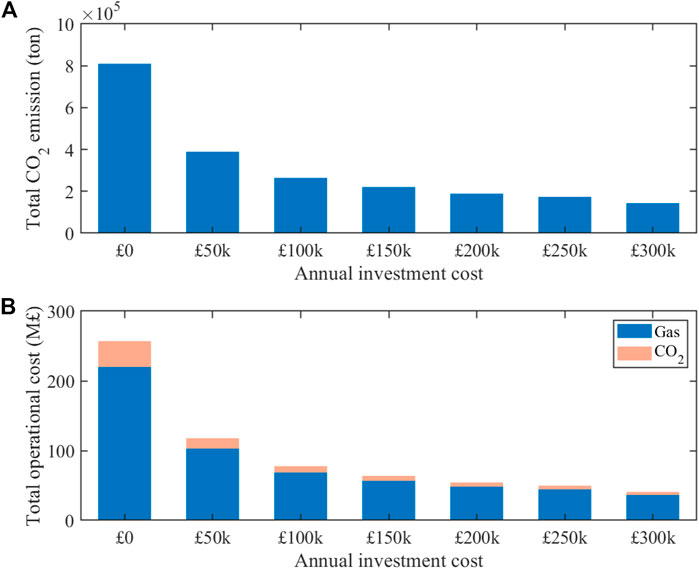
FIGURE 8. Total CO2 emission and total operational cost versus different annual investment cost until 2050.
The estimated
In addition to the total
Conclusion
This paper proposed a complete RHS framework, considering PV, WT, BSS, HP, and TES. In the RHS, it is analysed the reduction of gas consumption and the required BSS under the corresponding installed capacity of renewable components from their technical requirements. Meanwhile, in the context of British tariffs and government incentives, the size of each component in the system is optimised through the PSO algorithm according to different AICs. The results verify that the optimal size of RHS provided by this approach can minimise
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
SC, DF, and ZY contributed to conception and design of the study. SC performed the modelling and analysis and wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
The research presented in this article was undertaken as part of a project joint founded by Energy Technology Partnership (ETP), SP Distribution PLC (Scottish Power), grant number 146.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors would like to thank Gillian Brown for providing valuable information on the campus energy consumption.
References
Abdelsalam, M. Y., Teamah, H. M., Lightstone, M. F., and Cotton, J. S. (2020). Hybrid thermal Energy Storage with Phase Change Materials for Solar Domestic Hot Water Applications: Direct versus Indirect Heat Exchange Systems. Renew. Energ. 147, 77–88. doi:10.1016/j.renene.2019.08.121
Al-Tameemi, M. R. J., Liang, Y., and Yu, Z. (2019). Design Strategies and Control Methods for a Thermally Driven Heat Pump System Based on Combined Cycles. Front. Energ. Res. 7, 131. doi:10.3389/fenrg.2019.00131
Arat, H., and Arslan, O. (2017). Optimization of District Heating System Aided by Geothermal Heat Pump: A Novel Multistage with Multilevel ANN Modelling. Appl. Therm. Eng. 111, 608–623. doi:10.1016/j.applthermaleng.2016.09.150
Babacan, O., Ratnam, E. L., Disfani, V. R., and Kleissl, J. (2017). Distributed Energy Storage System Scheduling Considering Tariff Structure, Energy Arbitrage and Solar PV Penetration. Appl. Energ. 205, 1384–1393. doi:10.1016/j.apenergy.2017.08.025
Baniasadi, A., Habibi, D., Al-Saedi, W., Masoum, M. A. S., Das, C. K., and Mousavi, N. (2020). Optimal Sizing Design and Operation of Electrical and thermal Energy Storage Systems in Smart Buildings. J. Energ. Storage 28, 101186. doi:10.1016/j.est.2019.101186
Bhutta, M. M. A., Hayat, N., Farooq, A. U., Ali, Z., Jamil, R., and Hussain, Z. (2012). Vertical axis Wind Turbine–A Review of Various Configurations and Design Techniques. Renew. Sustain. Energ. Rev. 16 (4), 1926–1939. doi:10.1016/j.rser.2011.12.004
Casasso, A., and Sethi, R. (2014). Efficiency of Closed Loop Geothermal Heat Pumps: A Sensitivity Analysis. Renew. Energ. 62, 737–746. doi:10.1016/j.renene.2013.08.019
Castillo, A., and Gayme, D. F. (2014). Grid-scale Energy Storage Applications in Renewable Energy Integration: A Survey. Energ. Convers. Manag. 87, 885–894. doi:10.1016/j.enconman.2014.07.063
Cengel, Y. A., and Boles, M. A. (2007). Thermodynamics: An Engineering Approach 6th Editon (SI Units). New York: The McGraw-Hill Companies, Inc.
Chen, S., Friedrich, D., Yu, Z., and Yu, J. (2019). District Heating Network Demand Prediction Using a Physics-Based Energy Model with a Bayesian Approach for Parameter Calibration. Energies 12 (18), 3408. doi:10.3390/en12183408
Chen, S., Ren, Y., Friedrich, D., Yu, Z., and Yu, J. (2020). Sensitivity Analysis to Reduce Duplicated Features in ANN Training for District Heat Demand Prediction. Energy and AI 2, 100028. doi:10.1016/j.egyai.2020.100028
da Silva Lima, L., Quartier, M., Buchmayr, A., Sanjuan-Delmás, D., Laget, H., Corbisier, D., et al. (2021). Life Cycle Assessment of Lithium-Ion Batteries and Vanadium Redox Flow Batteries-Based Renewable Energy Storage Systems. Sustain. Energ. Tech. Assess. 46, 101286. doi:10.1016/j.seta.2021.101286
Dahash, A., Ochs, F., Janetti, M. B., and Streicher, W. (2019). Advances in Seasonal thermal Energy Storage for Solar District Heating Applications: A Critical Review on Large-Scale Hot-Water Tank and Pit thermal Energy Storage Systems. Appl. Energ. 239, 296–315. doi:10.1016/j.apenergy.2019.01.189
Dragicevic, T., Pandzic, H., Skrlec, D., Kuzle, I., Guerrero, J. M., and Kirschen, D. S. (2014). Capacity Optimization of Renewable Energy Sources and Battery Storage in an Autonomous Telecommunication Facility. IEEE Trans. Sustain. Energ. 5 (4), 1367–1378. doi:10.1109/tste.2014.2316480
Duncan, D., and Haydon, D. (2019). A Dear, Green Place”: Towards A Climate Change Strategy and Action Plan for the University of Glasgow. Available at: https://www.gla.ac.uk/myglasgow/sustainability/climatechangestrategy/ (Accessed November 2019).
e Silva, G. d. O., and Hendrick, P. (2017). Photovoltaic Self-Sufficiency of Belgian Households Using Lithium-Ion Batteries, and its Impact on the Grid. Appl. Energ. 195, 786–799. doi:10.1016/j.apenergy.2017.03.112
Eberhart, R., and Kennedy, J. (1995). “A New Optimizer Using Particle Swarm Theory,” in MHS'95. Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 Oct 1995 (IEEE).
Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Seyboth, K., Matschoss, P., Kadner, S., et al. (2011). Renewable Energy Sources and Climate Change Mitigation: Special Report of the Intergovernmental Panel on Climate Change. Cambridge University Press.
Ekren, O., and Ekren, B. Y. (2008). Size Optimization of a PV/wind Hybrid Energy Conversion System with Battery Storage Using Response Surface Methodology. Appl. Energ. 85 (11), 1086–1101. doi:10.1016/j.apenergy.2008.02.016
Elbeltagi, E., Hegazy, T., and Grierson, D. (2005). Comparison Among Five Evolutionary-Based Optimization Algorithms. Adv. Eng. Inform. 19 (1), 43–53. doi:10.1016/j.aei.2005.01.004
Eltamaly, A. M., Mohamed, M. A., and Alolah, A. I. (2016). A Novel Smart Grid Theory for Optimal Sizing of Hybrid Renewable Energy Systems. Sol. Energ. 124, 26–38. doi:10.1016/j.solener.2015.11.016
Eriksson, S., Bernhoff, H., and Leijon, M. (2008). Evaluation of Different Turbine Concepts for Wind Power. Renew. Sustain. Energ. Rev. 12 (5), 1419–1434. doi:10.1016/j.rser.2006.05.017
European Commission (2016). An EU Strategy on Heating and Cooling. Brussels, Belgium: European Commission, 51.
Govind, B. (2017). Increasing the Operational Capability of a Horizontal axis Wind Turbine by its Integration with a Vertical axis Wind Turbine. Appl. Energ. 199, 479–494. doi:10.1016/j.apenergy.2017.04.070
Jamal, T., Carter, C., Schmidt, T., Shafiullah, G. M., Calais, M., and Urmee, T. (2019). An Energy Flow Simulation Tool for Incorporating Short-Term PV Forecasting in a Diesel-PV-Battery Off-Grid Power Supply System. Appl. Energ. 254, 113718. doi:10.1016/j.apenergy.2019.113718
Jamal, T., Urmee, T., Calais, M., Shafiullah, G., and Carter, C. (2017). Technical Challenges of PV Deployment into Remote Australian Electricity Networks: A Review. Renew. Sustain. Energ. Rev. 77, 1309–1325. doi:10.1016/j.rser.2017.02.080
Johari, M., Jalil, M., and Shariff, M. F. M. (2018). Comparison of Horizontal axis Wind Turbine (HAWT) and Vertical axis Wind Turbine (VAWT). Int. J. Eng. Techn. 7 (4), 74–80. doi:10.14419/ijet.v7i4.13.21333
Kavian, S., Aghanajafi, C., Jafari Mosleh, H., Nazari, A., and Nazari, A. (2020). Exergy, Economic and Environmental Evaluation of an Optimized Hybrid Photovoltaic-Geothermal Heat Pump System. Appl. Energ. 276, 115469. doi:10.1016/j.apenergy.2020.115469
Keiner, D., Ram, M., Barbosa, L. D. S. N. S., Bogdanov, D., and Breyer, C. (2019). Cost Optimal Self-Consumption of PV Prosumers with Stationary Batteries, Heat Pumps, thermal Energy Storage and Electric Vehicles across the World up to 2050. Sol. Energ. 185, 406–423. doi:10.1016/j.solener.2019.04.081
Kheiri, F. (2018). A Review on Optimization Methods Applied in Energy-Efficient Building Geometry and Envelope Design. Renew. Sustain. Energ. Rev. 92, 897–920. doi:10.1016/j.rser.2018.04.080
Khezri, R., Mahmoudi, A., and Haque, M. H. (2020). Optimal Capacity of Solar PV and Battery Storage for Australian Grid-Connected Households. IEEE Trans. Ind. Applicat. 56 (5), 5319–5329. doi:10.1109/tia.2020.2998668
Kim, Y. W., Ramousse, J., Fraisse, G., Dalicieux, P., and Baranek, P. (2014). Optimal Sizing of a Thermoelectric Heat Pump (THP) for Heating Energy-Efficient Buildings. Energy Build. 70, 106–116. doi:10.1016/j.enbuild.2013.11.021
Kolda, T. G., Lewis, R. M., and Torczon, V. (2003). Optimization by Direct Search: New Perspectives on Some Classical and Modern Methods. SIAM Rev. 45 (3), 385–482. doi:10.1137/s003614450242889
Kubiński, K., and Szabłowski, Ł. (2020). Dynamic Model of Solar Heating Plant with Seasonal thermal Energy Storage. Renew. Energ. 145, 2025–2033. doi:10.1016/j.renene.2019.07.120
Li, H., Rane, S., and Yu, Z. (2021). Investigation of the Performance and Flow Characteristics of Two-phase Reaction Turbines in Total Flow Geothermal Systems. Renew. Energ. 175, 345–372. doi:10.1016/j.renene.2021.05.022
Liang, Y., Al-Tameemi, M., and Yu, Z. (2018). Investigation of a Gas-Fuelled Water Heater Based on Combined Power and Heat Pump Cycles. Appl. Energ. 212, 1476–1488. doi:10.1016/j.apenergy.2017.12.117
Liu, D., Xu, Y., Wei, Q., and Liu, X. (2017). Residential Energy Scheduling for Variable Weather Solar Energy Based on Adaptive Dynamic Programming. IEEE/CAA J. Autom. Sin. 5 (1), 36–46. doi:10.1109/jas.2017.7510739
Luna-Rubio, R., Trejo-Perea, M., Vargas-Vázquez, D., and Ríos-Moreno, G. J. (2012). Optimal Sizing of Renewable Hybrids Energy Systems: A Review of Methodologies. Sol. Energ. 86 (4), 1077–1088. doi:10.1016/j.solener.2011.10.016
Maleki, A., Khajeh, M. G., and Ameri, M. (2016). Optimal Sizing of a Grid Independent Hybrid Renewable Energy System Incorporating Resource Uncertainty, and Load Uncertainty. Int. J. Electr. Power Energ. Syst. 83, 514–524. doi:10.1016/j.ijepes.2016.04.008
Mandal, P., Madhira, S. T. S., haque, A. U., Meng, J., and Pineda, R. L. (2012). Forecasting Power Output of Solar Photovoltaic System Using Wavelet Transform and Artificial Intelligence Techniques. Proced. Comp. Sci. 12, 332–337. doi:10.1016/j.procs.2012.09.080
Maximov, S. A., Mehmood, S., and Friedrich, D. (2021). Multi-objective Optimisation of a Solar District Heating Network with Seasonal Storage for Conditions in Cities of Southern Chile. Sustain. Cities Soc. 73, 103087. doi:10.1016/j.scs.2021.103087
Mekontso, C., Abubakar, A., Madugu, S., Ibrahim, O., and Adediran, Y. A. (2019). Review of Optimization Techniques for Sizing Renewable Energy Systems. ComEngApp 8 (1), 13–30. doi:10.18495/comengapp.v8i1.285
Millar, M.-A., Yu, Z., Burnside, N., Jones, G., and Elrick, B. (2021). Identification of Key Performance Indicators and Complimentary Load Profiles for 5th Generation District Energy Networks. Appl. Energ. 291, 116672. doi:10.1016/j.apenergy.2021.116672
Ndwali, K., Njiri, J. G., and Wanjiru, E. M. (2020). Multi-objective Optimal Sizing of Grid Connected Photovoltaic Batteryless System Minimizing the Total Life Cycle Cost and the Grid Energy. Renew. Energ. 148, 1256–1265. doi:10.1016/j.renene.2019.10.065
O'Shaughnessy, E., Cutler, D., Ardani, K., and Margolis, R. (2018). Solar Plus: Optimization of Distributed Solar PV through Battery Storage and Dispatchable Load in Residential Buildings. Appl. Energ. 213, 11–21. doi:10.1016/j.apenergy.2017.12.118
Ozgener, O., and Hepbasli, A. (2007). Modeling and Performance Evaluation of Ground Source (Geothermal) Heat Pump Systems. Energy Build. 39 (1), 66–75. doi:10.1016/j.enbuild.2006.04.019
Prasad, A. A., Taylor, R. A., and Kay, M. (2017). Assessment of Solar and Wind Resource Synergy in Australia. Appl. Energ. 190, 354–367. doi:10.1016/j.apenergy.2016.12.135
Ren, Y., Li, L., Brindley, J., and Jiang, L. (2016). Nonlinear PI Control for Variable Pitch Wind Turbine. Control. Eng. Pract. 50, 84–94. doi:10.1016/j.conengprac.2016.02.004
Ren, Y., Rind, S. J., and Jiang, L. (2020). A Coordinated Control Strategy for Battery/supercapacitor Hybrid Energy Storage System to Eliminate Unbalanced Voltage in a Standalone AC Microgrid. J. Intell. Manufacturing Spec. Equipment 1, 3. doi:10.1108/JIMSE-08-2020-0007
Ren, Z., Verma, A. S., Li, Y., Teuwen, J. J. E., and Jiang, Z. (2021). Offshore Wind Turbine Operations and Maintenance: A State-Of-The-Art Review. Renew. Sustain. Energ. Rev. 144, 110886. doi:10.1016/j.rser.2021.110886
Renaldi, R., and Friedrich, D. (2019). Techno-economic Analysis of a Solar District Heating System with Seasonal thermal Storage in the UK. Appl. Energ. 236, 388–400. doi:10.1016/j.apenergy.2018.11.030
Renaldi, R., Kiprakis, A., and Friedrich, D. (2017). An Optimisation Framework for thermal Energy Storage Integration in a Residential Heat Pump Heating System. Appl. Energ. 186, 520–529. doi:10.1016/j.apenergy.2016.02.067
Rinaldi, A., Soini, M. C., Streicher, K., Patel, M. K., and Parra, D. (2021). Decarbonising Heat with Optimal PV and Storage Investments: A Detailed Sector Coupling Modelling Framework with Flexible Heat Pump Operation. Appl. Energ. 282, 116110. doi:10.1016/j.apenergy.2020.116110
Sarbu, I., and Sebarchievici, C. (2018). A Comprehensive Review of thermal Energy Storage. Sustainability 10 (1), 191. doi:10.3390/su10010191
Schmidt, T., Calais, M., Roy, E., Burton, A., Heinemann, D., Kilper, T., et al. (2017). Short-term Solar Forecasting Based on Sky Images to Enable Higher PV Generation in Remote Electricity Networks. Renew. Energ. Environ. Sustain. 2, 23. doi:10.1051/rees/2017028
Self, S. J., Reddy, B. V., and Rosen, M. A. (2013). Geothermal Heat Pump Systems: Status Review and Comparison with Other Heating Options. Appl. Energ. 101, 341–348. doi:10.1016/j.apenergy.2012.01.048
Shi, Y. (2001). “Particle Swarm Optimization: Developments, Applications and Resources,” in Proceedings of the 2001 congress on evolutionary computation (IEEE). IEEE Cat. No. 01TH8546.
Tao, C., Shanxu, D., and Changsong, C. (2010). “Forecasting Power Output for Grid-Connected Photovoltaic Power System without Using Solar Radiation Measurement,” in The 2nd International Symposium on Power Electronics for Distributed Generation Systems (IEEE). doi:10.1109/pedg.2010.5545754
Trillat-Berdal, V., Souyri, B., and Achard, G. (2007). Coupling of Geothermal Heat Pumps with thermal Solar Collectors. Appl. Therm. Eng. 27 (10), 1750–1755. doi:10.1016/j.applthermaleng.2006.07.022
Tulus, V., Boer, D., Cabeza, L. F., Jiménez, L., and Guillén-Gosálbez, G. (2016). Enhanced thermal Energy Supply via central Solar Heating Plants with Seasonal Storage: A Multi-Objective Optimization Approach. Appl. Energ. 181, 549–561. doi:10.1016/j.apenergy.2016.08.037
Vanlint, K. (2018). 2017 UK Greenhouse Gas Emissions, Provisional Figures. London: UK Department for Business, Energy and Industrial Strategy.
Wali, S. B., Hannan, M. A., Reza, M. S., Ker, P. J., Begum, R. A., Rahman, M. S. A., et al. (2021). Battery Storage Systems Integrated Renewable Energy Sources: A Biblio Metric Analysis towards Future Directions. J. Energ. Storage 35, 102296. doi:10.1016/j.est.2021.102296
Waser, R., Ghani, F., Maranda, S., O'Donovan, T. S., Schuetz, P., Zaglio, M., et al. (2018). Fast and Experimentally Validated Model of a Latent thermal Energy Storage Device for System Level Simulations. Appl. Energ. 231, 116–126. doi:10.1016/j.apenergy.2018.09.061
Watzlaf, G. R., and Ackman, T. E. (2006). Underground Mine Water for Heating and Cooling Using Geothermal Heat Pump Systems. Mine Water Environ. 25 (1), 1–14. doi:10.1007/s10230-006-0103-9
Xu, L., Torrens, J. I., Guo, F., Yang, X., and Hensen, J. L. M. (2018). Application of Large Underground Seasonal thermal Energy Storage in District Heating System: A Model-Based Energy Performance Assessment of a Pilot System in Chifeng, China. Appl. Therm. Eng. 137, 319–328. doi:10.1016/j.applthermaleng.2018.03.047
Yang, B., Wang, J., Chen, Y., Li, D., Zeng, C., Chen, Y., et al. (2020). Optimal Sizing and Placement of Energy Storage System in Power Grids: a State-Of-The-Art One-Stop Handbook. J. Energ. Storage 32, 101814. doi:10.1016/j.est.2020.101814
Yang, B., Yu, L., Chen, Y., Ye, H., Shao, R., Shu, H., et al. (2021). Modelling, Applications, and Evaluations of Optimal Sizing and Placement of Distributed Generations: A Critical State‐of‐the‐art Survey. Int. J. Energ. Res. 45 (3), 3615–3642. doi:10.1002/er.6104
Yang, J., Liu, J., Fang, Z., and Liu, W. (2018). Electricity Scheduling Strategy for home Energy Management System with Renewable Energy and Battery Storage: a Case Study. IET Renew. Power Gener. 12 (6), 639–648. doi:10.1049/iet-rpg.2017.0330
Yang, Y., Bremner, S., Menictas, C., and Kay, M. (2018). Battery Energy Storage System Size Determination in Renewable Energy Systems: A Review. Renew. Sustain. Energ. Rev. 91, 109–125. doi:10.1016/j.rser.2018.03.047
Yue, X., Patankar, N., Decarolis, J., Chiodi, A., Rogan, F., Deane, J. P., et al. (2020). Least Cost Energy System Pathways towards 100% Renewable Energy in Ireland by 2050. Energy (Oxf) 207, 118264. doi:10.1016/j.energy.2020.118264
Keywords: building heating decarbonisation, particle swarm optimisation, annual investment cost, renewable heating system, integrated energy network
Citation: Chen S, Friedrich D and Yu Z (2021) Optimal Sizing of a Grid Independent Renewable Heating System for Building Decarbonisation. Front. Energy Res. 9:746268. doi: 10.3389/fenrg.2021.746268
Received: 23 July 2021; Accepted: 03 August 2021;
Published: 17 August 2021.
Edited by:
Bo Yang, Kunming University of Science and Technology, ChinaReviewed by:
Xuehan Zhang, Korea University, South KoreaYixuan Chen, The University of Hong Kong, Hong Kong, SAR China
Copyright © 2021 Chen, Friedrich and Yu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhibin Yu, emhpYmluLnl1QGdsYXNnb3cuYWMudWs=
 Si Chen
Si Chen Daniel Friedrich
Daniel Friedrich Zhibin Yu
Zhibin Yu