Feedback Linearization Control Design for Battery/SMES Hybrid Energy Storage Systems Used in Distribution Network

A battery/superconducting magnetic energy storage (SMES) hybrid energy storage system (BSM-HESS) is designed for a power system. Meanwhile, a nonlinear feedback control (FLC) is adopted to achieve smooth and fast-tracking performance, and a rule-based strategy (RBS) is applied for power demand allocation. FLC can effectively compensate for the system’s nonlinearity to obtain the global consistent control performance; thus, it can properly solve the nonlinearity and modeling uncertainty of BSM-HESS. The effectiveness and advantages of FLC are evaluated via three cases, namely, heavy load condition, light load condition, and robustness with uncertain BSM-HESS parameters. Simulation results show that compared with proportional–integral–derivative (PID) control, FLC can achieve the best dynamic performance under various working conditions, which is beneficial for the system to quickly restore stable operation after large disturbance. In addition, the control cost of FLC is lower than that of PID control under both heavy load and light load conditions.

Introduction

In recent years, withlarge-scale and widespread integration of renewable energy into the power system, energy storage systems (ESSs) have become a hot research topic (Yang et al., 2015; Zhang et al., 2016; Bakeer et al., 2021). The energy storage system used in the power system refers to the device that can store a certain amount of electric energy and can quickly convey or absorb active and reactive power when abnormal events occur to the power system (Xi et al., 2016; ASV et al., 2020). In a transmission system, energy storage equipment is mostly installed on the transmission side of the line to improve the stability of system and rapid response speed (Zhang et al., 2015; Bakeer et al., 2021). In the distribution system, the energy storage device is usually equipped on the load side to protect the important load and balance frequency fluctuation (Nayak et al., 2021).

Electric energy storage has many forms that can mainly be divided into two types: energy storage and power storage (Chaibi et al., 2019; Li et al., 2019). Energy storage represented by leadacid battery, lithium battery, and sodiumsulfur battery has high energy density and long energy storage time but the low power density and short cycle life (Luo et al., 2015; Ruan et al., 2019). Power-type energy storage represented by a super capacitor, flywheel energy storage, and superconducting magnetic energy storage (SMES) has the advantages of high power density, fast response speed, and long cycle life but with deficiencies of low energy density and high self-discharge rate (Adhikari and Li, 2014; Akyurek and Rosing, 2016; Zhang et al., 2021).

It is difficult for a single energy storage technology to have all the aforementioned advantages at the same time to meet the requirements of different application modes (Lalouni et al., 2009; Khalid and Savkin, 2010; Worthmann et al., 2015). However, based on technical complementarity of volumetric energy storage and power-type energy storage, hybrid energy storage can be used to meet the technical requirements of various levels. At present, battery/SMES hybrid energy storage systems (BSM-HESSs) that can effectively improve the stability and reliability of the system have received worldwide research interests (Dali et al., 2010; Malysz et al., 2014; Melo et al., 2019). As the core of the control system, the design of the control strategy plays the most critical role that has both important theoretical and practical significance.

BSM-HESS can effectively improve system stability, the performance of which is closely related to the selected control mode (Bazargan et al., 2018; Serir et al., 2016; Teymour et al., 2014). At present, research on control schemes is mostly focused on proportional–integral–derivative (PID) control (Brenna et al., 2016). However, this method needs to establish an accurate mathematical system model and often focuses on the design of a certain operation point. When the operation point of system changes, the performance will be dramatically affected, and the robustness is poor (Hussain et al., 2017). In order to remedy the existing deficiencies, a large number of academic advanced nonlinear control theories are developed. Magdy et al. (2018) have proposed a coordination of load frequency control (LFC) and SMES technology using a new optimal PID controller–based moth swarm algorithm in the Egyptian power system while considering high wind power penetration. Besides, a new adaptive control strategy based on the particle swarm optimization algorithm is proposed for the optimization of control strategy for a hybrid electric vehicle energy storage system (Ye et al., 2020). Meanwhile, Lin and Lei (2017) have developed a hierarchical control strategy for a hybrid energy storage system. However, the aforementioned studies all have the characteristics of a complex structure, low implementation feasibility, and weak adaptability; thus, their control design needs to be further improved.

Over the last decade, research on the feedback linearization–based nonlinear control theory has achieved great progress, which can successfully transform nonlinear systems into linear systems through state feedback in coordinate transformation domain. Direct feedback linearization is a representative feedback linearization method based on input and output descriptions of the system, which has been utilized to solve many control problems of nonlinear systems. Therefore, a feedback linearization control (FLC) for BSM-HESS is proposed in this article, to realize an efficient and smooth tracking.

The remaining of this article is organized as follows: Battery/SMES Hybrid Energy Storage Systems Modeling introduces the BSM-HESS model. In FLC Design for BSM-HESS, FLC design is described. Case studies are carried out in Case Studies section, along with simulation results analysis. At last, Conclusion summarizes the main contributions of the study.

Battery/SMES Hybrid Energy Storage Systems Modeling

Distributed generation (DG) owns the merits of easy installation, pollution-free, and low costs. As a backup power source of the power system (Huang et al., 2021; Sai et al., 2021), it can ensure the stability and reliability of user’s electricity consumption. Although distributed energy has many advantages, there are still many shortcomings; for instance, the control mode of DG is very complex, and the access cost is high (Bizon, 2018; Shi et al., 2018). In addition, since DG is an uncontrollable source, it is imperative to solve the limitations and isolation problems of DG to reduce the influence of DG on large power grid (Murty and Kumar, 2021). In general, DG is a micro-generation unit that can realize energy conversion and independent control. Compared to a distribution network, DG can be regarded as a controlled unit, such that the difficulty of configuring the capacity of DG can be greatly reduced. Microgrids are vulnerable to internal distributed power supply and load fluctuations due to capacity and scale limitations, and ESS provides solutions for these problems. At present, it is difficult for a single energy storage device to simultaneously achieve multiple functions such as power quality improvement and microgrid stability control, so different energy storage devices need to be coupled together for use (Ali et al., 2010; Kasilingam and Pasupuleti, 2015; Olujobi, 2020).

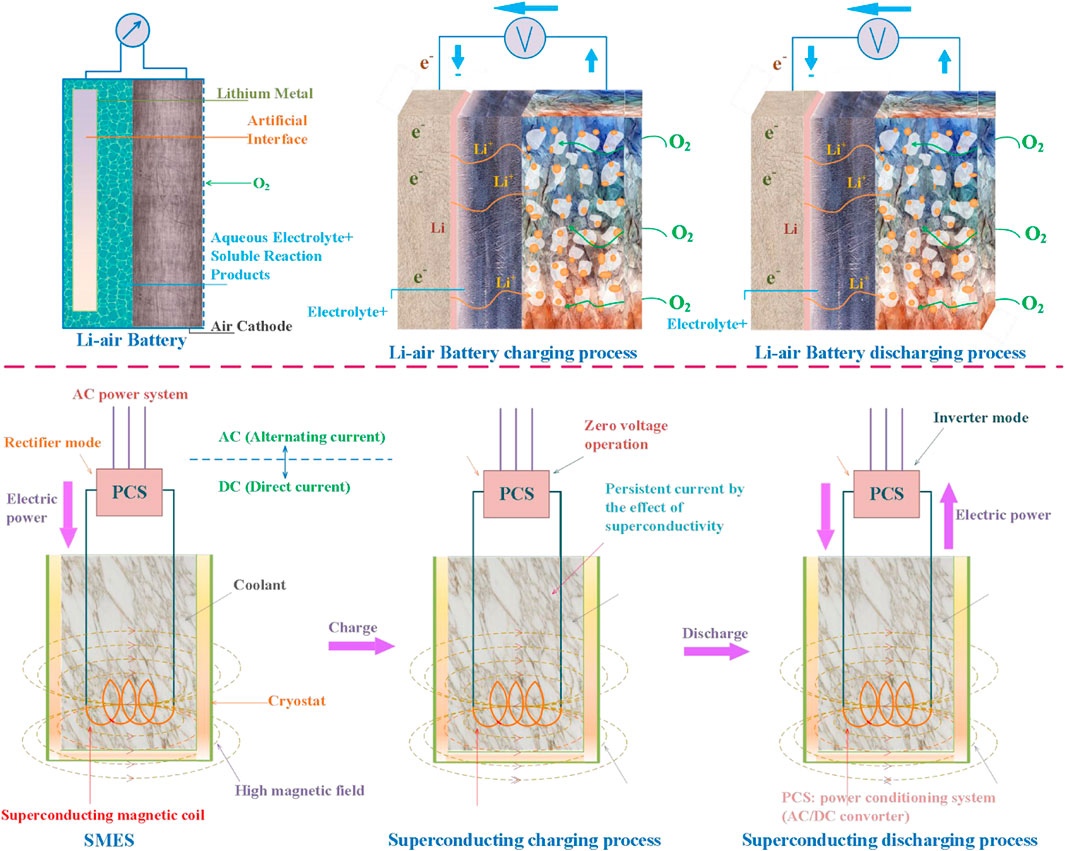
The combination of battery and SMES takes both the instantaneous power supply advantages of SMES and the long-term power supply capacity of battery into account, which specifies the excellent power supply characteristic of BSM-HESS. Besides, BSM-HESS has another advantage compatible with both, such as high energy density and high power density, which surpasses the effect of either (Jae Woong Shim et al., 2013; Kouchachvili et al., 2018). The charging and discharging models of key components of BSM-HESS, that is, battery and SMES, are presented in Figure 1.

FIGURE 1

FIGURE 1. Structure, charging, and discharging process of battery and SMES.

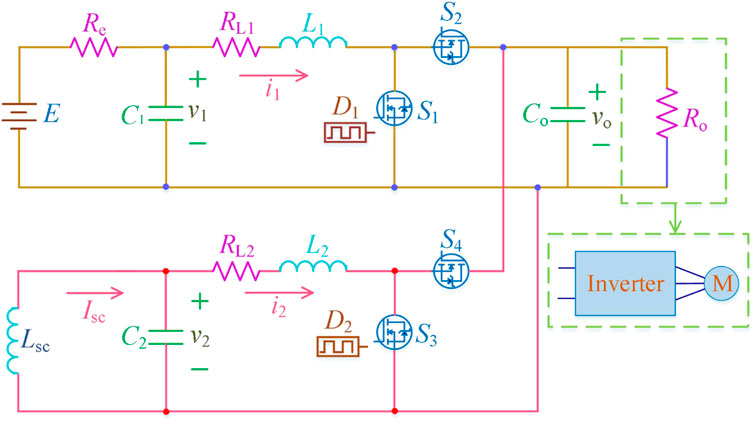
BSM-HESS generally includes SMES and battery that supply to the common load through a bidirectional buckboost converter with the same structure (Song et al., 2017), respectively. More specifically, the load is typically modeled as motors with an inverter that is equivalent to variable resistance in this model (Montoya et al., 2018). The configuration of BSM-HESS adopted in this study is shown in Figure 2. The mathematical equation corresponding to the configuration of BSM-HESS can be described as follows [ (Sai et al., 2021), 42]:

$\left[\begin{array}{c}{\dot{v}}_1\\ {\dot{v}}_2\\ {\dot{\dot{i}}}_1\\ {\dot{\dot{i}}}_2\\ {\dot{v}}_o\end{array}\right]=\left[\begin{array}{c}-\frac{v_1}{R_e{C}_1}-\frac{i_1}{C_1}+\frac{E}{R_e{C}_1}\\ \frac{I_{sc}-i_2}{C_2}\\ \frac{v_1-v_o}{L_1}-\left(\frac{R_{L1}+R_{\mathrm{o}\mathrm{n}2}}{L_1}\right)i_1\\ \frac{v_2}{L_2}+\left(\frac{R_{\mathrm{o}\mathrm{n}4}-R_{\mathrm{o}\mathrm{n}3}}{L_2}{D}_2-\frac{R_{L2}+R_{\mathrm{o}\mathrm{n}4}}{L_2}\right)i_2+(D_2-1)\frac{v_o}{L_2}\\ \left(1-D_1\right)\frac{i_1}{C_o}-\frac{v_o}{R{C}_o}+\frac{i_2}{C_o}\end{array}\right]+\left[\begin{array}{c}\begin{array}{cc}0& 0\end{array}\\ \begin{array}{cc}0& 0\end{array}\\ \begin{array}{cc}\frac{R_{\mathrm{o}\mathrm{n}2}-R_{\mathrm{o}\mathrm{n}1}}{L_1}{i}_1+\frac{v_o}{L_1}& 0\end{array}\\ \begin{array}{cc}0& 0\end{array}\\ \begin{array}{cc}0& -\frac{i_2}{C_o}\end{array}\end{array}\right]\left[\begin{array}{c}{D}_1\\ D_2\end{array}\right],(1)$

where duty cycles D₁ and D₂ are restricted in a subset of (0, 1) for the purpose of ensuring operation safety and efficiency. The meanings of other symbols can be referred to Nomenclature.

FIGURE 2

FIGURE 2. Configuration and equivalent circuit of BSM-HESS.

FLC Design for BSM-HESS

Rule-Based Strategy

The rule-based strategy (RBS), also called logical threshold control strategies, is widely used in engineering practice due to their simplicity and practicality. Heuristic rules or fuzzy logic rules are used to determine the control variable output according to preset conditions. It mainly includes state machine control, threshold control, and power tracking control to ensure the main components work in the most efficient area.

The load power P_demand is the prerequisite of the determination of a qualified EMS, where the power distribution between SMES and battery is optimized. The application constraints of BSM-HESS based on RBS are as follows:

(a) State of charge (SOC) of SMES:

$\frac{i_{sc}}{i_{sc\_\max }}\ge \frac{1}{2},(2)$

where $i_{sc}$ and $i_{\mathrm{sc\_max}}$ denote the current value and maximum allowable current value of the SMES, respectively. When the constraint is not satisfied, SMES will be charged by the battery with a constant power P_ch.

(b) SOC of battery:

$0.2\le \frac{Q_c}{Q_I}\le 0.9,(3)$

where $Q_{\text{c}}$ and $Q_{\text{I}}$ are the total charge of the battery and the remaining charge of the battery, respectively.

(c) Constraints of P_demand:

When P_demand ≥ 0 is satisfied, the constraints are as follows:

$\{\begin{array}{c}{P}_{\mathrm{demand}}=P_{\mathrm{demand}},P_{\mathrm{SMES}}=0\left(P_{\mathrm{demand}}\le P_{\min }\right)\\ P_{\min }=P_{\mathrm{battery}},P_{\mathrm{SMES}}=P_{\mathrm{demand}}-P_{\min }\left(P_{\mathrm{demand}}>P_{\min }\right)\end{array}.(4)$

The power threshold $P_{\text{min}}$ is set to ensure that once the power demand $P_{\text{demand}}$ is lower than the threshold, SMES will not supply power to the load.

When P_demand < 0 is satisfied, the regenerative energy is absorbed by SMES before the battery is fully charged, and the charging cycle is shortened, thus prolonging the battery life.

Feedback Linearization Control Theory

Feedback linearization is a typical approach in the nonlinear control theory. The idea is to transform a nonlinear system dynamic into an equivalent (fully or partly) linear one through a change of state variables and a suitable nonlinear control input, so that linear control techniques can be then applied to the nonlinear system.

Here, a standard affine multiple-input multiple-output system is considered in a neighborhood around an operation point $x_{\text{o}}$ of the form

$\{\begin{array}{c}\dot{x}=f\left(x\right)+g\left(x\right)u\\ y=h\left(x\right),\end{array}(5)$

where $x\in R^n$ is the state vector, $u\in R^m$ is the control input vector, $y\in R^m$ is the output vector, $f\left(x\right)\in R^n$, $g\left(x\right)\in R^{n\times m}$, and $h\left(x\right)\in R^m$ are smooth. The inputoutput linearization of a multiple input multiple output system is obtained via differentiating the output $y_i$ of the system until the input $u_j$ appears, assuming that $r_i$ is the smallest integer such that at least one of the inputs explicitly appears in $y_i^{\left(r_i\right)}$

$y_i^{\left(r_i\right)}=L_f^{r_i}{h}_i{\sum }_{j=1}^m{L}_{g_j}{L}_f^{r_i-1}{h}_i{u}_j,(6)$

where $y_i^{\left(r_i\right)}$ denotes the ith-order derivative of $y_i$, if $L_{g_j}{L}_f^{r_i-1}{h}_i\left(x\right)\ne 0$ for at least one j. For at least one $y_i$ gives

$\begin{array}{c}\left[\begin{array}{c}{y}_1^{\left(r_1\right)}\\ ⋮\\ y_m^{\left(r_m\right)}\end{array}\right]=\left[\begin{array}{c}{L}_f^{r_1}{h}_1\\ ⋮\\ L_f^{r_m}{h}_m\end{array}\right]+B\left(x\right)\left[\begin{array}{c}{u}_1\\ ⋮\\ u_m\end{array}\right]\end{array}.(7)$

$B\left(x\right)=\left[\begin{array}{ccc}{L}_{g_1}{L}_f^{r_1-1}{h}_1& \cdots & L_{g_m}{L}_f^{r_1-1}{h}_1\\ ⋮& ⋮& ⋮\\ L_{g_1}{L}_f^{r_m-1}{h}_m& \cdots & L_{g_m}{L}_f^{r_m-1}{h}_m\end{array}\right].(8)$

Here, $B\left(x\right)$ is the $n\times m$ control gain matrix, if $B\left(x\right)$ is invertible, the physical control law of the multiple input multiple output nonlinear system can be derived as follows:

$\begin{array}{c}\left(u\right)=B{\left(x\right)}^{-1}\left\{\left[\begin{array}{c}-L_f^{r_1}{h}_1\\ ⋮\\ -L_f^{r_m}{h}_m\end{array}\right]+\left[\begin{array}{c}{v}_1\\ ⋮\\ v_m\end{array}\right]\right\}\\ \left(v_i\right)=-{\sum }_{j=1}^{r_i-1}{\alpha }_j{y}_i^{\left(j\right)}\end{array},(9)$

where $v_i$ is the new input of the system and ${\alpha }_j$ is the linear control gain.

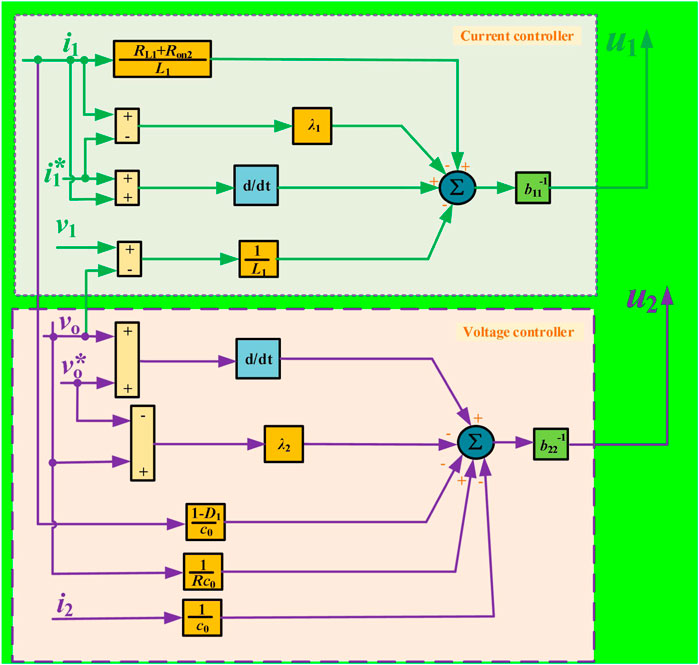
Underlying Controller Design

For BSM-HESS (1), the state vector can be defined as $x={\left(x_1,x_2,x_3,x_4,x_5\right)}^{\text{T}}={\left(v_1,v_2,i_1,i_2,v_{\text{o}}\right)}^{\text{T}}$, output $y={\left(y_1,y_2\right)}^{\text{T}}={\left(i_1,v_{\text{o}}\right)}^{\text{T}}$, control input $u={\left(u_1,u_2\right)}^{\text{T}}={\left(D_1,D_2\right)}^{\text{T}}$, and tracking error e = [e₁, e₂]^T = [$i_1$-$i_1^{\ast }$,$v_{\text{o}}$-$v_{\text{o}}^{\ast }$]^T. Then, the tracking error e is differentiated until the control input u explicitly appeared as follows:

$\{\begin{array}{c}{\dot{e}}_1=\frac{v_1}{L_1}+\left(\frac{R_{\mathrm{o}\mathrm{n}2}-R_{\mathrm{o}\mathrm{n}1}}{L_1}{D}_1-\frac{R_{L1}+R_{\mathrm{o}\mathrm{n}2}}{L_1}\right)i_1+(D_1-1)\frac{v_o}{L_1}-{\dot{\dot{i}}}_1^{\ast }\\ {\dot{e}}_2=\left(1-D_1\right)\frac{i_1}{C_o}+\left(1-D_2\right)\frac{i_2}{C_o}-\frac{v_o}{R{C}_o}-{\dot{v}}_o^{\ast }\end{array}.(10)$

In addition, system 2) can be represented in the concise matrix form as follows:

$\left[\begin{array}{c}{\dot{y}}_1\\ {\dot{y}}_2\end{array}\right]=\left[\begin{array}{c}{g}_1\left(x\right)\\ g_2\left(x\right)\end{array}\right]+B\left(x\right)\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right]-\left[\begin{array}{c}{\dot{\dot{i}}}_1^{\ast }\\ {\dot{v}}_o^{\ast }\end{array}\right],(11)$

where

$g_1\left(x\right)=\frac{v_1-v_{\text{o}}}{L_1}-\left(\frac{R_{\text{L}1}+R_{\text{on}2}}{L_1}\right)i_1(12)$

$g_2\left(x\right)=\left(1-D_1\right)\frac{i_1}{C_o}-\frac{v_o}{R{C}_o}+\frac{i_2}{C_o},(13)$

with

$B\left(x\right)=\left[\begin{array}{cc}{b}_{11}& 0\\ 0& b_{22}\end{array}\right]=\left[\begin{array}{cc}\frac{R_{\text{on}2}-R_{\text{on}1}}{L_1}{i}_1+\frac{v_{\text{o}}}{L_1}& 0\\ 0& -\frac{i_2}{C_{\text{o}}}\end{array}\right].(14)$

To ensure the aforementioned inputoutput linearization to be valid, the control gain matrix B(x) must be nonsingular among the whole operation range, that is,

$\det \left[B\left(x\right)\right]=- \frac{i_2[(R_{\mathrm{on}2}-R_{\mathrm{on}1})i_1+v_o]}{C_0{L}_1}\ne 0.(15)$

Since SMES current $i_2$ is always different from zero, for example, a value of zero means that SMES stops operating; thus, the controllability of SMES is lost. Meanwhile, DC bus voltage $v_{\text{o}}\ne (R_{\text{on}1}-R_{\text{on}2})i_1$ is always valid among the whole operation range. Therefore, the aforementioned condition is always valid.

The final FLC strategy is designed as follows:

$\left[\begin{array}{c}{u}_1\\ u_2\end{array}\right]=B^{-1}\left[\begin{array}{c}{\dot{y}}_1-\frac{v_1-v_o}{L_1}+\left(\frac{R_{L1}+R_{\mathrm{o}\mathrm{n}2}}{L_1}\right)i_1+{\dot{\dot{i}}}_1^{\ast }-{\lambda }_1{e}_1\\ {\dot{y}}_2-\left(1-D_1\right)\frac{i_1}{C_o}+\frac{v_o}{R{C}_o}-\frac{i_2}{C_o}+{\dot{v}}_o^{\ast }-{\lambda }_2{e}_2\end{array}\right],(16)$

where ${\lambda }_1$ and ${\lambda }_2$ are the control gains. In addition, the overall FLC structure of BSM-HESS is given in Figure 3.

FIGURE 3

FIGURE 3. Overall FLC structure for BSM-HESS.

Case Studies

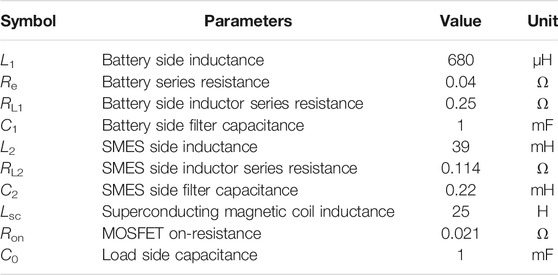
The parameters of BSM-HESS and controller are shown in Table 1 and Table 2, respectively. The initial SOC of the battery is set to 90%, the minimum voltage of the battery is 36 V, the maximum voltage is 144 V, and battery pack contains 48 LiFePO₄ cells that are connected in series. The rated current of SMES is 100A. In addition, in RBS, P_min = 2 kW and P_ch = 100 W. Case studies are carried out by Matlab/Simulink 2019b. Besides, the sampling rate was set to 10^–4 s, and ode23 was selected as the solver.

TABLE 1

TABLE 1. BSM-HESS parameters.

TABLE 2

TABLE 2. Controller parameters.

Heavy Load Condition

Based on the BSM-HESS model, the continuous step change of power demand of the power system under various conditions is studied to validate the specific tracking performance under heavy load conditions. In practical engineering application, heavy load condition usually occurs when the power system is connected with a large load. Here, the regenerative braking is carried out under the condition of corresponding negative load power, while the DC bus voltage reference is maintained at 160 V. The detailed system responses are shown in Figure 4, which shows that FLC can smoothly track the change of power demand and stably maintain the DC bus voltage. Compared with PID control, FLC has the smallest tracking error and the highest tracking speed. It is worth noting that such smooth tracking ability is very crucial for economic and reliable power system operation and can considerably prolong the battery service life.

FIGURE 4

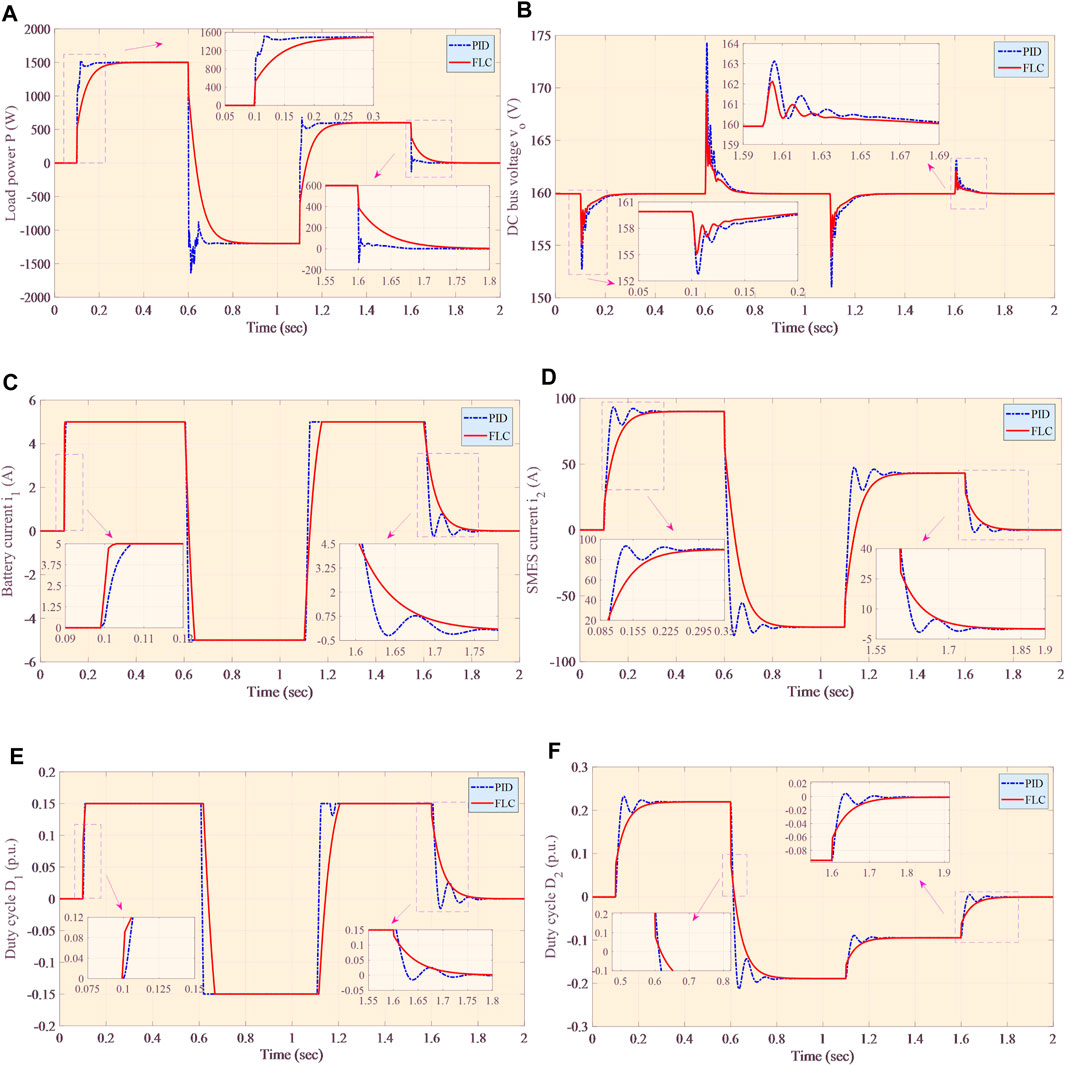
FIGURE 4. BSM-HESS responses under heavy load conditions. (A) Load power P, (B) DC bus voltage v_o, (C) battery current i₁, (D) SMES current i₂, (E) duty cycle D₁, and (F) duty cycle D₂.

Light Load Condition

The aim of this case is to study the control performance of FLC when the power system is connected with a small load. At this time, another power demand step change is used to compare the tracking performance between FLC and PID control. The corresponding responses are shown in Figure 5. It can be found that FLC achieves better tracking performance in terms of tracking speed and tracking error than PID control. In addition, FLC has smoother regulation of power P, while PID control oscillates severely. Similarly, for DC bus voltage, FLC has a small overshoot and can restore the disturbed power system in a short period of time, while PID control requires much more time for disturbed power system restoration with larger overshoot. Therefore, FLC can effectively decrease the charge and discharge frequency of the hybrid energy storage system, to reduce the wear and tear of the hybrid energy storage system.

FIGURE 5

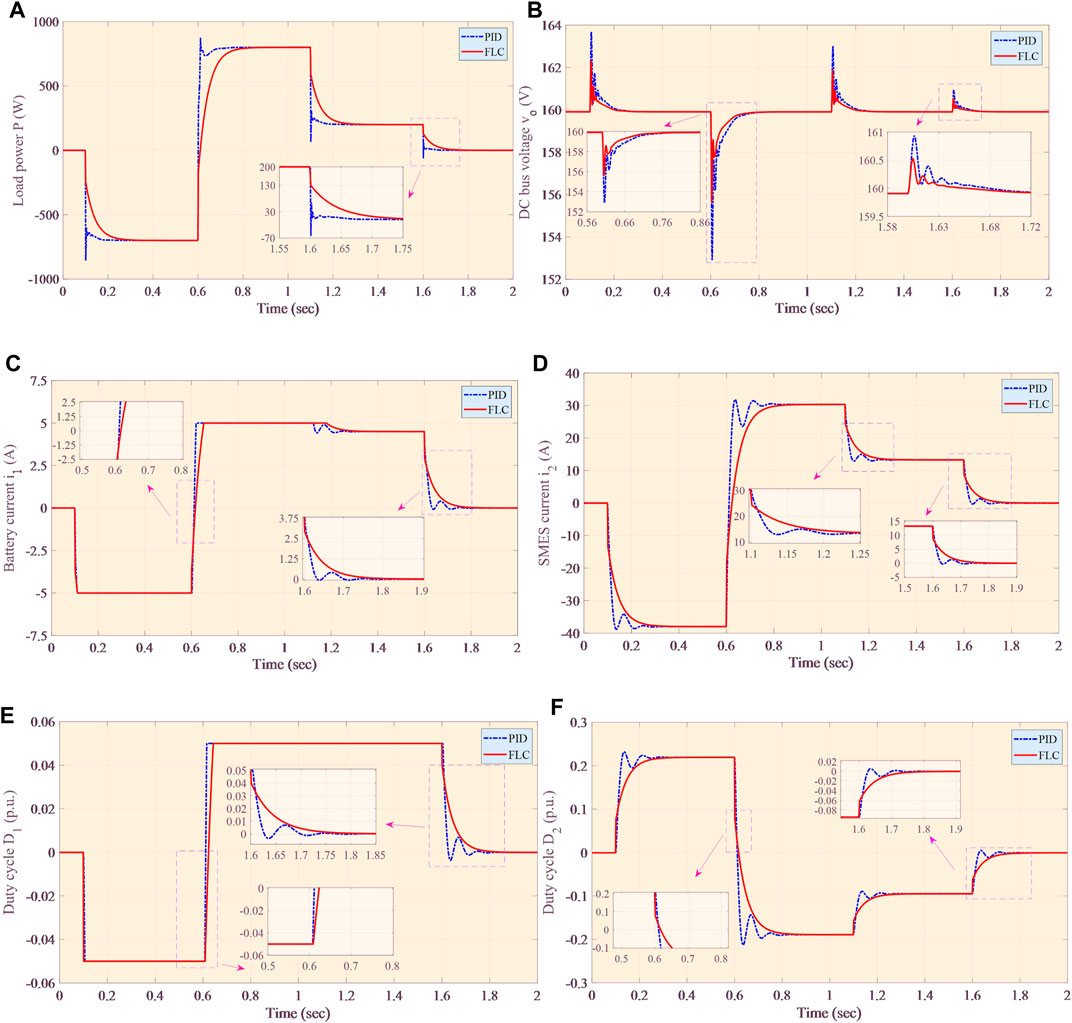
FIGURE 5. BSM-HESS responses under light load conditions. (A) Load power P, (B) DC bus voltage v_o, (C) battery current i₁, (D) SMES current i₂, (E) duty cycle D₁, and (F) duty cycle D₂.

Robustness With Uncertain BSM-HESS Parameters

This section is to study the robustness of FLC under the uncertainty of BSM-HESS parameters. Particularly, a series of plant–model mismatches of battery/SMES series resistances R_L1 and R_L2, as well as inductances L₁ and L₂ with ±20% variation around their rated value are applied. Then, a 25% load drop occurs and lasts for 100 ms, during which the absolute peak value of active power |P| is recorded, as shown in Figure 6. Note that the changes of PID control and FLC under the uncertainty of series resistance are 11.31 and 31.86%, respectively.

FIGURE 6

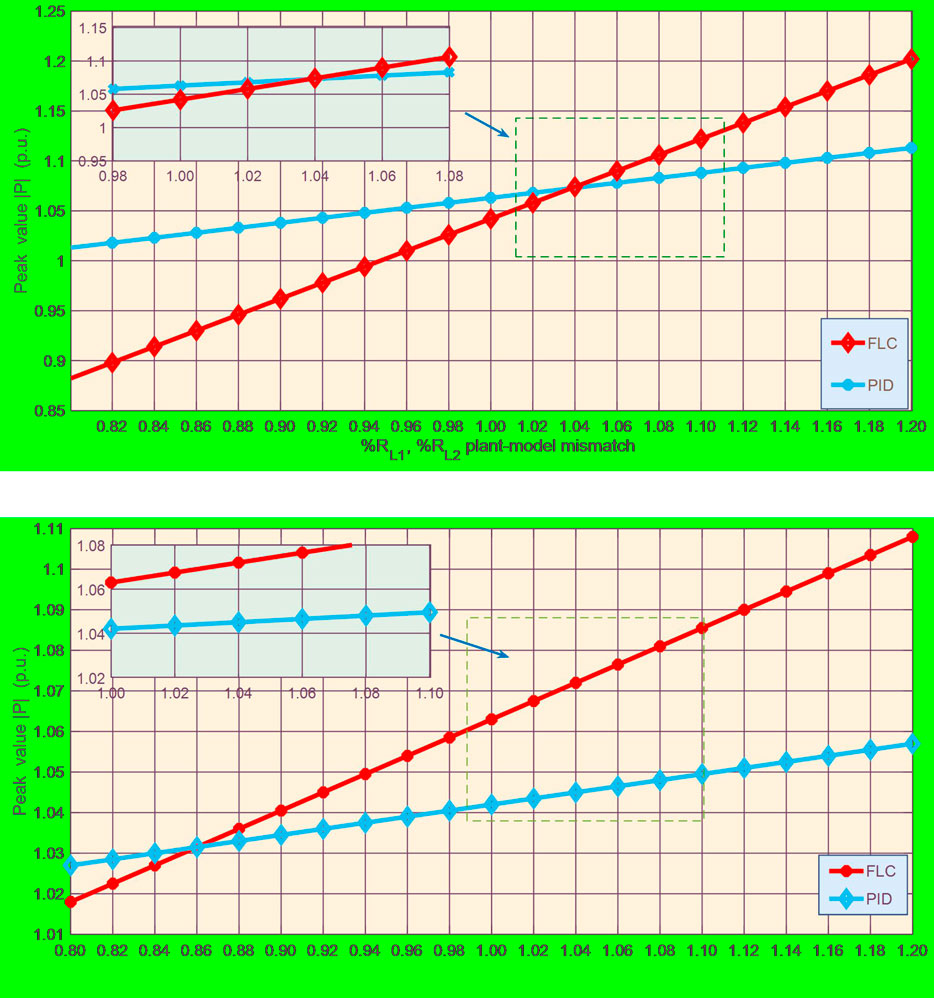
FIGURE 6. Absolute peak value of active power |P| obtained under a 25% load drop lasting 100 ms with 20% variation of the battery/SMES series resistances R_L1 and R_L2 as well as inductances L₁ and L₂.

Conclusion

In this study, an FLC is designed to realize an efficient and smooth power tracking for BSM-HESS, and its contributions are summarized as follows:

1. FLC can fully compensate the nonlinearity of the system to achieve a globally consistent control performance; thus, the transient performance can be considerably improved;

2. FLC requires an accurate BSM-HESS system model; thus, it lacks robustness against parameter uncertainties compared to PID control;

3. The effectiveness and superiority of FLC are comprehensively verified and compared with PID control based on three case studies. Simulation results show that FLC outperforms PID control in terms of overshoot and tracking rate.

In the future, the effectiveness of FCL will be further validated by a hardware-in-the-loop (HIL) experiment based on the dSpace platform to meet the practical needs of engineering application.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

CT: conceptualization, writing—original draft preparation, and investigation. YH: writing, reviewing and editing, supervision, and conceptualization.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adhikari, S., and Li, F. (2014). Coordinated V-F and P-Q Control of Solar Photovoltaic Generators with MPPT and Battery Storage in Microgrids. IEEE Trans. Smart Grid 5 (3), 1270–1281. doi:10.1109/tsg.2014.2301157

CrossRef Full Text | Google Scholar

Akyurek, A. S., and Rosing, T. S. (2016). Optimal Distributed Nonlinear Battery Control. IEEE J. Emerging Selected Top. Power Electronics 5 (3), 1045–1054.

Google Scholar

Ali, M. H., Wu, B., and Dougal, R. A. (2010). An Overview of SMES Applications in Power and Energy Systems. IEEE Trans. Sustain. Energ. 1 (1), 38–47. doi:10.1109/tste.2010.2044901

CrossRef Full Text | Google Scholar

Asv, V. L., Manyala, R. R., and Mangipudi, S. K. (2020). Design of a Robust PID-PSS for an Uncertain Power System with Simplified Stability Conditions. Prot. Control. Mod. Power Syst. 5 (1), 1–16. doi:10.1186/s41601-020-00165-9

CrossRef Full Text | Google Scholar

Bakeer, A., Salama, H. S., and Vokony, I. (2021). Integration of PV System with SMES Based on Model Predictive Control for Utility Grid Reliability Improvement. Prot. Control. Mod. Power Syst. 6 (1), 1–13. doi:10.1186/s41601-021-00191-1

CrossRef Full Text | Google Scholar

Bazargan, D., Bahrani, B., and Filizadeh, S. (2018). Reduced Capacitance Battery Storage DC-link Voltage Regulation and Dynamic Improvement Using a Feedforward Control Strategy. IEEE Trans. Energ. Convers. 33 (4), 1659–1668. doi:10.1109/tec.2018.2837627

CrossRef Full Text | Google Scholar

Bizon, N. (2018). Effective Mitigation of the Load Pulses by Controlling the Battery/SMES Hybrid Energy Storage System. Appl. Energ. 229, 459–473. doi:10.1016/j.apenergy.2018.08.013

CrossRef Full Text | Google Scholar

Brenna, M., Foiadelli, F., Longo, M., and Zaninelli, D. (2016). Energy Storage Control for Dispatching Photovoltaic Power. IEEE Trans. Smart Grid 9 (4), 2419–2428.

Google Scholar

Chaibi, Y., Allouhi, A., Salhi, M., and El-jouni, A. (2019). Annual Performance Analysis of Different Maximum Power point Tracking Techniques Used in Photovoltaic Systems. Prot. Control. Mod. Power Syst. 4 (4), 171–180. doi:10.1186/s41601-019-0129-1

CrossRef Full Text | Google Scholar

Dali, M., Belhadj, J., and Roboam, X. (2010). Hybrid Solar-Wind System with Battery Storage Operating in Grid-Connected and Standalone Mode: Control and Energy Management - Experimental Investigation. Energy 35 (6), 2587–2595. doi:10.1016/j.energy.2010.03.005

CrossRef Full Text | Google Scholar

Huang, K., Li, Y., Zhang, X., Liu, L., Zhu, Y., and Meng, X. (2021). Research on Power Control Strategy of Household-Level Electric Power Router Based on Hybrid Energy Storage Droop Control. Prot. Control. Mod. Power Syst. 6 (1), 1–13. doi:10.1186/s41601-021-00190-2

CrossRef Full Text | Google Scholar

Hussain, I., Ranjan, S., Das, D. C., and Sinha, N. (2017). Performance Analysis of Flower Pollination Algorithm Optimized PID Controller for Wind-PV-SMES-BESS-Diesel Autonomous Hybrid Power System. Int. J. Renew. Energ. Res. 7 (2), 643–651.

Google Scholar

Jae Woong Shim, J. W., Youngho Cho, Y., Seog-Joo Kim, S. J., Sang Won Min, S. W., and Kyeon Hur, K. (2013). Synergistic Control of SMES and Battery Energy Storage for Enabling Dispatchability of Renewable Energy Sources. IEEE Trans. Appl. Supercond. 23 (3), 5701205. doi:10.1109/tasc.2013.2241385

CrossRef Full Text | Google Scholar

Kasilingam, G., and Pasupuleti, J. (2015). Coordination of PSS and PID Controller for Power System Stability Enhancement - Overview. Indian J. Sci. Technology 8 (2), 142–151. doi:10.17485/ijst/2015/v8i2/58441

CrossRef Full Text | Google Scholar

Khalid, M., and Savkin, A. V. (2010). A Model Predictive Control Approach to the Problem of Wind Power Smoothing with Controlled Battery Storage. Renew. Energ. 35 (7), 1520–1526. doi:10.1016/j.renene.2009.11.030

CrossRef Full Text | Google Scholar

Kouchachvili, L., Yaïci, W., and Entchev, E. (2018). Hybrid Battery/supercapacitor Energy Storage System for the Electric Vehicles. J. Power Sourc. 374, 237–248. doi:10.1016/j.jpowsour.2017.11.040

CrossRef Full Text | Google Scholar

Lalouni, S., Rekioua, D., Rekioua, T., and Matagne, E. (2009). Fuzzy Logic Control of Stand-Alone Photovoltaic System with Battery Storage. J. Power Sourc. 193 (2), 899–907. doi:10.1016/j.jpowsour.2009.04.016

CrossRef Full Text | Google Scholar

Li, G. D., Li, G. Y., and Zhou, M. (2019). Model and Application of Renewable Energy Accommodation Capacity Calculation Considering Utilization Level of Interprovincial Tie-Line. Prot. Control. Mod. Power Syst. 4 (4), 1–12. doi:10.1186/s41601-019-0115-7

CrossRef Full Text | Google Scholar

Lin, X., and Lei, Y. (2017). Coordinated Control Strategies for SMES-Battery Hybrid Energy Storage Systems. IEEE Access 5, 23452–23465. doi:10.1109/access.2017.2761889

CrossRef Full Text | Google Scholar

Luo, X., Wang, J., Dooner, M., and Clarke, J. (2015). Overview of Current Development in Electrical Energy Storage Technologies and the Application Potential in Power System Operation. Appl. Energ. 137, 511–536. doi:10.1016/j.apenergy.2014.09.081

CrossRef Full Text | Google Scholar

Magdy, G., Mohamed, E. A., Shabib, G., Elbaset, A. A., and Mitani, Y. (2018). SMES Based a New PID Controller for Frequency Stability of a Real Hybrid Power System Considering High Wind Power Penetration. IET Renew. Power Generation 12 (11), 1304–1313. doi:10.1049/iet-rpg.2018.5096

CrossRef Full Text | Google Scholar

Malysz, P., Sirouspour, S., and Emadi, A. (2014). An Optimal Energy Storage Control Strategy for Grid-Connected Microgrids. IEEE Trans. Smart Grid 5 (4), 1785–1796. doi:10.1109/tsg.2014.2302396

CrossRef Full Text | Google Scholar

Melo, S. P., Brand, U., Vogt, T., Telle, J. S., Schuldt, F., and Maydell, K. v. (2019). Primary Frequency Control provided by Hybrid Battery Storage and Power-To-Heat System. Appl. Energ. 233-234, 220–231. doi:10.1016/j.apenergy.2018.09.177

CrossRef Full Text | Google Scholar

Montoya, O. D., Garcés, A., and Espinosa-Pérez, G. (2018). A Generalized Passivity-Based Control Approach for Power Compensation in Distribution Systems Using Electrical Energy Storage Systems. J. Energ. Storage 16, 259–268. doi:10.1016/j.est.2018.01.018

CrossRef Full Text | Google Scholar

Murty, V. V. S. N., and Kumar, A. (2021). Multi-objective Energy Management in Microgrids with Hybrid Energy Sources and Battery Energy Storage Systems. Prot. Control. Mod. Power Syst. 5 (1), 1–20. doi:10.1186/s41601-019-0147-z

CrossRef Full Text | Google Scholar

Nayak, P. C., Prusty, R. C., and Panda, S. (2021). Grasshopper Optimization Algorithm Optimized Multistage Controller for Automatic Generation Control of a Power System with FACTS Devices. Prot. Control. Mod. Power Syst. 6 (1), 1–15. doi:10.1186/s41601-021-00187-x

CrossRef Full Text | Google Scholar

Olujobi, O. J. (2020). The Legal Sustainability of Energy Substitution in Nigeria’s Electric Power Sector: Renewable Energy as Alternative. Prot. Control. Mod. Power Syst. 5 (1), 1–12. doi:10.1186/s41601-020-00179-3

CrossRef Full Text | Google Scholar

Ruan, J., Song, Q., and Yang, W. (2019). The Application of Hybrid Energy Storage System with Electrified Continuously Variable Transmission in Battery Electric Vehicle. Energy 183, 315–330. doi:10.1016/j.energy.2019.06.095

CrossRef Full Text | Google Scholar

Sai, L., Cheng, Z., Haomin, G., Qingxin, S., Tiancheng, T. E., Schomer, I., et al. (2021). Operational Optimization of a Building-Level Integrated Energy System Considering Additional Potential Benefits of Energy Storage. Prot. Control. Mod. Power Syst. 6 (1), 55–64. doi:10.1186/s41601-021-00184-0

CrossRef Full Text | Google Scholar

Serir, C., Rekioua, D., Mezzai, N., and Bacha, S. (2016). Supervisor Control and Optimization of Multi-Sources Pumping System with Battery Storage. Int. J. Hydrogen Energ. 41 (45), 20974–20986. doi:10.1016/j.ijhydene.2016.05.096

CrossRef Full Text | Google Scholar

Shi, Y., Xu, B., Tan, Y., Kirschen, D., and Zhang, B. (2018). Optimal Battery Control under Cycle Aging Mechanisms in Pay for Performance Settings. IEEE Trans. Automatic Control. 64 (6), 2324–2339. doi:10.1109/TAC.2018.2867507

CrossRef Full Text | Google Scholar

Song, Z., Hou, J., Hofmann, H., Li, J., and Ouyang, M. (2017). Sliding-mode and Lyapunov Function-Based Control for Battery/supercapacitor Hybrid Energy Storage System Used in Electric Vehicles. Energy 122, 601–612. doi:10.1016/j.energy.2017.01.098

CrossRef Full Text | Google Scholar

Teymour, H. R., Sutanto, D., Muttaqi, K. M., and Ciufo, P. (2014). Solar PV and Battery Storage Integration Using a New Configuration of a Three-Level NPC Inverter with Advanced Control Strategy. IEEE Trans. Energ. Convers. 29 (2), 354–365. doi:10.1109/tec.2014.2309698

CrossRef Full Text | Google Scholar

Worthmann, K., Kellett, C. M., Braun, P., Grüne, L., and Weller, S. R. (2015). Distributed and Decentralized Control of Residential Energy Systems Incorporating Battery Storage. IEEE Trans. Smart Grid 6 (4), 1914–1923. doi:10.1109/tsg.2015.2392081

CrossRef Full Text | Google Scholar

Xi, L., Yu, T., Yang, B., Zhang, X., and Qiu, X. (2016). A Wolf Pack Hunting Strategy Based Virtual Tribes Control for Automatic Generation Control of Smart Grid. Appl. Energ. 178, 198–211. doi:10.1016/j.apenergy.2016.06.041

CrossRef Full Text | Google Scholar

Yang, B., Jiang, L., Yao, W., and Wu, Q. H. (2015). Perturbation Estimation Based Coordinated Adaptive Passive Control for Multimachine Power Systems. Control. Eng. Pract. 44, 172–192. doi:10.1016/j.conengprac.2015.07.012

CrossRef Full Text | Google Scholar

Ye, K., Li, P., and Li, H. (2020). Optimization of Hybrid Energy Storage System Control Strategy for Pure Electric Vehicle Based on Typical Driving Cycle. Math. Probl. Eng. 2020 (9), 1–12. doi:10.1155/2020/1365195

CrossRef Full Text | Google Scholar

Zhang, X., Tan, T., Zhou, B., Yu, T., Yang, B., and Huang, X. (2021). Adaptive Distributed Auction-Based Algorithm for Optimal Mileage Based AGC Dispatch with High Participation of Renewable Energy. Int. J. Electr. Power Energ. Syst. 124, 106371. doi:10.1016/j.ijepes.2020.106371

CrossRef Full Text | Google Scholar

Zhang, X., Yu, T., Yang, B., and Li, L. (2016). Virtual Generation Tribe Based Robust Collaborative Consensus Algorithm for Dynamic Generation Command Dispatch Optimization of Smart Grid. Energy 101, 34–51. doi:10.1016/j.energy.2016.02.009

CrossRef Full Text | Google Scholar

Zhang, X., Yu, T., Yang, B., Zheng, L., and Huang, L. (2015). Approximate Ideal Multi-Objective Solution Q(λ) Learning for Optimal Carbon-Energy Combined-Flow in Multi-Energy Power Systems. Energ. Convers. Management 106, 543–556. doi:10.1016/j.enconman.2015.09.049

CrossRef Full Text | Google Scholar

Nomenclature

Variables

v₁, v₂, v_o voltages corresponding to C₁, C₂, and C_o

i₁, i₂ currents flowing through L₁ and L₂

E open-circuit voltage of battery

I_sc SMES current

Abbreviations

BSM-HESS battery/SMES hybrid energy storage system

SMES superconducting magnetic energy storage

RBS rule-based strategy

PID proportional–integral-derivative

FLC feedback linearization control

BSM-HESS parameters

C₁, C₂, C_o filter capacitances of battery side, SMES side, and load

L_SC inductance of superconducting magnetic coil

L₁, L₂ inductances of battery side and SMES side

R_e inner series resistances of battery

R_L1, R_L2 series resistances of battery side and SMES side

R_on1, R_on2, R_on3, R_on4 MOSFET on-resistances for S₁, S₂, S₃, and S₄

R_o equivalent load

D₁, D₂ duty cycle for the on-state of S₁ and S₃

FLC parameters

${\mathit{\lambda }}_1, {\mathit{\lambda }}_2$ control gains