- 1Center of Research Excellence in Renewable Energy and Power Systems, King Abdulaziz University, Jeddah, Saudi Arabia
- 2Department of Electrical and Computer Engineering, King Abdulaziz University, Jeddah, Saudi Arabia
- 3Department of Electrical Engineering, University of Hafr Al Batin, Hafr Al Batin, Saudi Arabia
A key factor in the performance of PV panels is the tilt angle, adjustable via various tracking systems. Fixed tilt angle PV panels miss out on most of the solar radiation each day whereas continuous tracking systems are not always cost-efficient, rather impractical in some cases. Therefore, adjusting the tilt angle using a limited number of periods per year can be a good, compromised solution. In this paper, a new approach is proposed to maximize the impact of solar radiation on PV panels by adjusting their tilt angles. Based on a limited number of periods or intervals per year, the optimal duration (number of days) of each period or interval along with the optimum tilt angle corresponding to each interval are determined by solving two interlinked optimization problems. These two problems are solved using the Most Valuable Player Algorithm (MVPA) combined with the Particle Swarm Optimization (PSO) algorithm. The case study for Yanbu, a western coastal city of Saudi Arabia has been investigated. The obtained results show that the enhanced solar power generation can be achieved by using optimal intervals and optimum tilt angle and provide a suitable benchmark for similar techniques to be used in the future to solve the problem of tilt angle adjustment for maximizing PV panels output.
Introduction
The world is leaning towards the use of renewable energy sources to fulfill the ever-increasing demand for electrical power. Among the green energy sources, solar energy is the most popular choice, due to its widely abundant and environment-friendly nature (Awasthi et al., 2020; Dey and Subudhi, 2020). Therefore, the countries around the globe are working to increase the amount of solar energy generation. Due to high solar radiation potential, Saudi Arabia has achieved significant advancement in exploiting the solar energy in recent past. Moreover, Saudi Arabia’s government has set a target to support around 5% of the national demand with solar energy (Alyahya and Irfan, 2016; G Khalil, 2021).
Optimization of various solar parameters is considered indispensable in the process of solar energy exploitation. One of these parameters is the global solar radiation and the appropriate selection of it may result in increased efficiency of solar system technologies like solar PV panels and solar collectors. The amount of incident radiation depends upon the orientation and tilt angle of the panel and collectors (El-Sebaii et al., 2010; Demain et al., 2013; Mawloud et al., 2020). The general practice is to install these facing the equator so that the orientation is towards South and North, in the northern and southern hemispheres, respectively. However, it is needed to find out the optimal tilt angle of the solar panel as it changes with the movement of the Sun, daily, weekly, and yearly. The optimization of the tilt angle is an effective approach to find the specific angle of the solar panel that ensures the maximum solar radiation of a location, for a particular period (Hafez et al., 2017). A solar tracker can be used to accomplish the task. However, using such a mechanical tool with separate energy support requirements is not suitable, practically and economically. Therefore, finding the optimal tilt angle for different time intervals of the year and orient the solar panels manually is a practical and energy-efficient solution to this problem. Factors like cloudiness (Armstrong and Hurley, 2010), flatness of the collector plate (Kern and Harris, 1975), location and clearness index (Elsayed, 1989), radioactive transfer properties (Smith et al., 2016) etc. are needed to be considered in the tilt angle calculation process since they affect the optimization of tilt angle and intervals directly.
• A healthy number of technical and academic works of literature are found on the topic of tilt angle optimization. The case studies are noted from different countries of the world. European solar radiation data is used to estimate the optimal tilt angle in (Calabrò, 2013). Research on Basrah city of Iraq concluded that the hectic daily adjustment of tilt angle can generate equal energy when compared to the yearly adjustment of 8 times (Hamad, n.d.). The article (Khahro et al., 2015) summarized that the energy can be saved up to 8% by adjusting the tilt angles monthly, instead of the yearly adjustment, where the experiment has been conducted in Sindh, Pakistan. Another tilt angle analysis was conducted in Spain (Navntoft et al., 2012) with the data of summer and winter seasons for four consecutive years. A similar study in Germany (Beringer et al., 2011) presented the variation of tilt angles in different months of a year. An empirical method-based approach was used on a dataset of Abu Dhabi, to study the effect of solar panel tilt angles (Jafarkazemi and Saadabadi, 2013) and suggested to adjust the tilt angles at least twice a year. Chang (Chang, 2010) presented the optimal results for seven cities of Taiwan whereas article (Nfaoui and El-Hami, 2020) discusses the case study of Morocco. Similar studies have been conducted on the cities of Saudi Arabia, too. Benghanem worked with the case study of Madinah city in (Benghanem, 2011). Dhahran, a city of the eastern province was presented in (Ramli and Bouchekara, 2018) whereas Tarek et al. analyzed the solar radiation data of some selected cities including Riyadh, Jeddah, Abha, and Al-Jouf (Kaddoura et al., 2016). Researchers gathered all such references in a review article (Yadav and Chandel, 2013) and documented a well-structured comparative analysis on the subject matter. In a recent study, various transposition models of PV tilted surface was investigated to increase the estimation accuracy of the global solar radiation in Palestine. It is found that the analysis of the measured data based on annual and monthly period could be represented by the transposition models (Nassar et al., 2020). Real time data acquisition system has been used to determine the optimal tilt angle in (Sharma et al., 2020).
• Although there are some complex and expensive instrumentations used in the measurement and parameterization of solar data, some direct and inexpensive methods based on prediction and diagnoses are also possible. One of such methods of determining the solar radiation is the prediction by artificial intelligence techniques. Nonlinear time-varying PSO (Chang, 2010), slope and orientation-based optimization (Despotovic and Nedic, 2015), Bee algorithm (Sarailoo et al., 2018), mathematical method (Tang and Wu, 2004), empirical corrections (El-Sebaii et al., 2010), vortex search algorithm (Ramli and Bouchekara, 2018) are documented in the literature as the searching tools of optimal tilt angle of the solar panel.
All the above-mentioned articles optimized the tilt angle of the solar panel only, considering that the panel will be equipped with the tracking system. However, a more practical solution is to find the optimal number of time intervals in a year to adjust the angles manually. This approach will save the cost of maintaining the tracking system and therefore, will be more suitable to be used in the domestic loads. A little has been reported in this field and the researchers have proposed a different number of yearly intervals to change the tilt angle. Reference (Saraf and Hamad, 1988) suggested that the number of intervals should be eight for Iraq whereas (Skeiker, 2009) proposed it to be 12 for Syria, in order to ensure the maximum utilization of solar radiation. With the data of nine different locations of the United States, (Akhlaghi et al., 2017; Sarailoo et al., 2018) comes with the conclusion that the solar output of daily intervals can almost be achieved by taking four intervals in a year. However, in most of the tilt angle optimization studies, methodology of the year division is not described that ensures the maximum solar radiation.
The purpose of this research is to simultaneously optimize the tilt angle of the solar panel and the number of days per period or interval of panel adjustment. It will analyze and predict solar radiation and tilt angle using the Most Valuable Player algorithm (MVPA), combined with the Particle Swarm Optimization (PSO) algorithm. MVPA was first proposed in 2017 (Bouchekara, 2020) as a novel algorithm with some excellent features of searching the global solution. However, as a new approach, it has not been implemented in the field of power and energy. On the other hand, PSO is one of the mostly used heuristic approaches in the field of power systems and energy conversions (Alrashidi et al., 2010; Zhou et al., 2016). The area of the investigation is Yanbu, a port city on the Red Sea coast of western region in Saudi Arabia.
The reminder of this paper is structured as follows. In Solar Radiation Model, the solar radiation model is described. In Proposed Approach the proposed approach is explained and detailed. The simulation results are discussed in Application and Results. Finally, the most important conclusions are drawn in Conclusions.
Solar Radiation Model
PV module’s output power is a function of solar radiation density and the angle between the Sun and the module itself (Ramli et al., 2015). Thus, the power obtained when solar radiation is normal to the PV surface would be different from the case when solar radiation falls with an angle onto the surface.
The total radiation
where:
The reflected radiation
where:
The direct beam radiation
where: Id is the diffuse radiation and Rb is the ratio between the tilted beam and horizontal beam radiation given by:
where θ is the incident angle at noon and its cosine is given by:
and θz, the zenith angle at solar noon, and its cosine is defined as:
where γ represents surface azimuth,
The declination angle is given as:
where: d represents a day in the year. It is to be noted that (284 + d) and (d-81) are mathematically equivalent, for a non-leap-year.
Finally, the diffuse radiation on a tilted surface
where Rd is the ratio between tilted diffuse and horizontal diffuse radiation and can be found by (Nfaoui and El-Hami, 2018):
Thus Eq. 1 becomes
According to Eq. 10, the direct and diffuse components of global radiation are needed for estimating global solar radiation on tilted surfaces.
Proposed Approach
Models Definition
It is obvious that the ideal adjustment interval of the tilt angle is 1 day; however, this is impractical. To solve this problem, the tilt angle is adjusted in a limited number of times per year (i.e., a certain Number of Periods (NP) or intervals per year). Here, two models can be defined and applied.
In the first model, NP is specified. Then the number of days per period is calculated by dividing the total number of days in a year (365) over NP. Therefore, the number of days is same for all periods (more accurately it is almost the same since 365 can sometimes be not a multiple of NP). For instance, if NP = 3, we will have three periods of 122, 122, and 121 days to adjust the tilt angle. It is assumed in this paper that the year starts on the 1st of January and ends on the 31st of December. Having said that, this partition is not mandatory, i.e., the studied period can be extended to more than 1 year. Generally, the starting and ending days can be predefined by the user or the engineer in charge of the investigation. This first model is the mostly used one in the literature to optimize the tilt angle of a solar panel.
In the second model, the Number of Days per each Period (
In this paper, a novel approach based on the second model is proposed for adjusting the tilt angle. The developed algorithm can run both methodologies to draw comparisons and ascertain the superiority of one method over the other one. Based on a given NP, the proposed approach can solve two interlinked optimization problems simultaneously. The objective of the first problem is to determine the
Optimization Problem Formulation
For both models, the treated problem in this paper can be formulated as follows:
where:
The aim of the optimization process treated in this paper is to maximize the total radiation. Therefore, the objective function is defined by:
The vector of design variables depends on the model chosen. For model = 1:
For model = 2:
where:
The constraints imposed on the problem are:
In other words, the sum of the number of days for all periods must be equal to the number of days per year (i.e., 365 days).
Optimization Algorithms
In the proposed approach two algorithms are interlinked to solve the formulated problem based on the model chosen which are the MVPA and the PSO.
The MVPA is a new optimization algorithm developed in (Bouchekara, 2020). Like other population-based algorithms it starts by defining a population of players in each region (i.e., the search space) then these players will evolve during games and practices to improve their skills through individual and collective competitions phases. Such process will analogically improve the quality of the solutions to the optimization problem in hand. The MVPA has been used in many studies with successful and efficient results like in (Liu et al., 2018; Alatas, 2019; Korashy et al., 2019; Ouili et al., 2019; Ramli and Bouchekara, 2019; Ramli and Bouchekara, 2020; Srilakshmi et al., 2020). Therefore, it has been selected for this study.
The second algorithm selected in this paper is the PSO. This algorithm with the Genetic Algorithm (GA) is the most well-known and widely used optimization metaheuristic algorithm. Using simple displacement rules a population of particles evolve to better locations (in the search space) and consequently the solutions converge toward the global minimum.
Implementation of the Proposed Approach
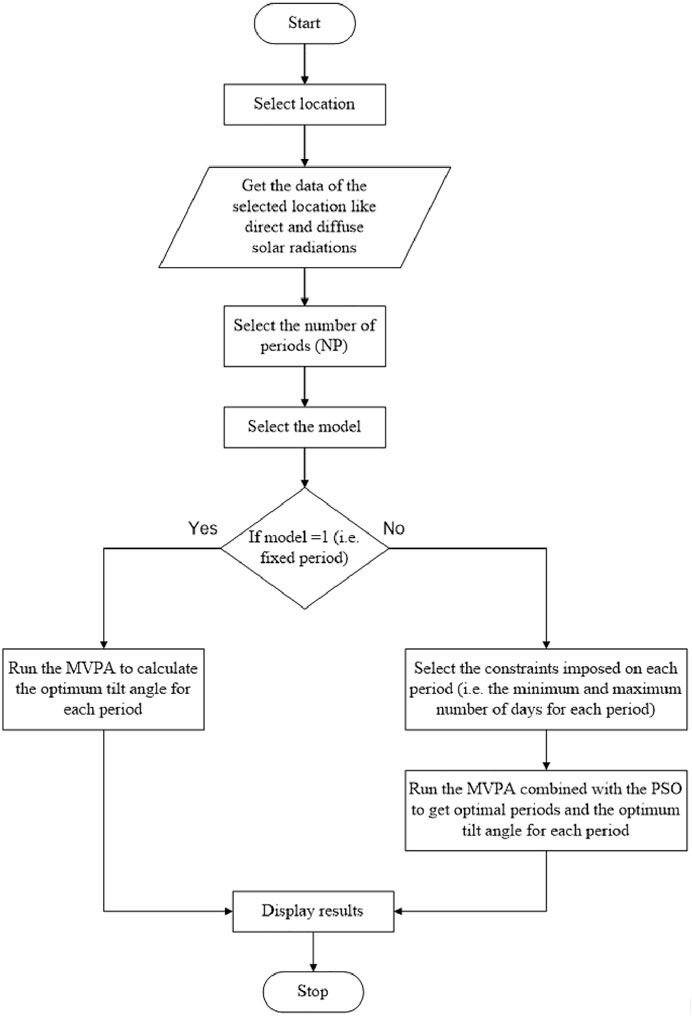
The flowchart of the proposed approach is given in Figure 1. A MATLAB-based program has been developed to implement this approach. This approach starts with a given location where the investigation is aimed to take place. Once the location is specified, the data of the selected location such as direct and diffuse solar radiations (needed for Eq. 10) is obtained (i.e., measured). Then two important parameters are defined: the number of periods or intervals (i.e., NP) and the model number (i.e., model 1 or model 2). If the first model of fixed period is chosen, the MVPA will run to calculate the optimum tilt angle for each period. For this model, the
Application and Results
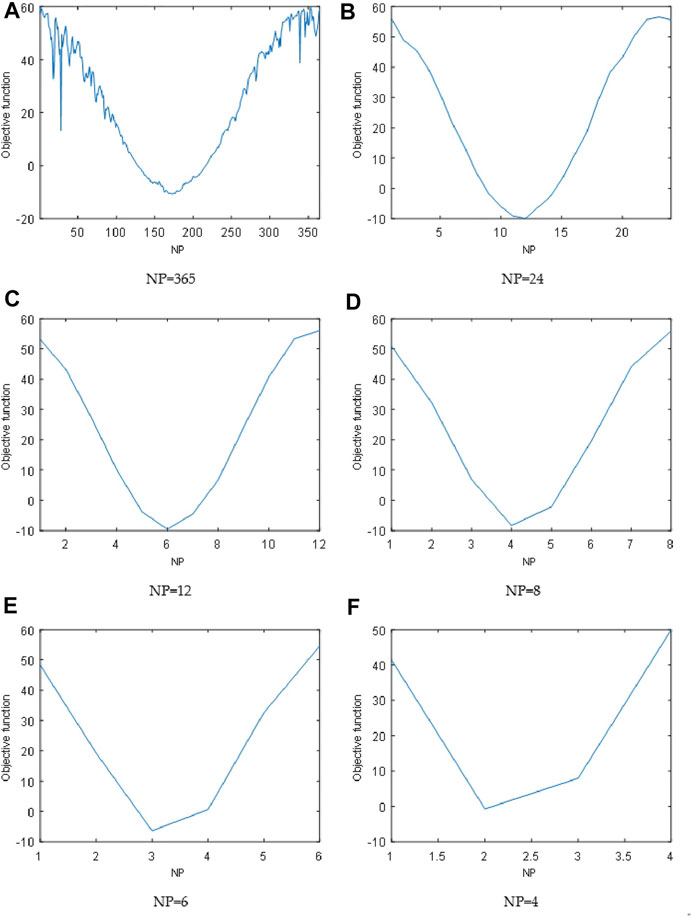
The proposed approach has been applied to estimate the optimum tilt angle for the city of Yanbu in Saudi Arabia. Six different NPs, NP = {365, 24, 12, 8, 6, 4}, are tested. The optimal angles found using model 1 for all the tested NPs are sketched in Figure 2. In Figure 2A, the optimum angle is obtained for NP = 365 (daily adjustment of the tilt angle). It varies between −10.72° corresponding to day number 173 and 59.88° corresponding to day number 353. In Figure 2B, the optimum angle is obtained for NP = 24. It varies between −10.20° corresponding to period number 12 and 56.58° corresponding to period number 1. In Figure 2C, the optimum angle is obtained for NP = 12. It varies between −9.41° corresponding to period number 6 and 56.15° corresponding to period number 12. In Figure 2D, the optimum angle is obtained for NP = 8. It varies between −7.94° corresponding to period number 4 and 55.64° corresponding to period number 8. In Figure 2E, the optimum angle is obtained for NP = 6. It varies between −5.75° corresponding to period number 3 and 54.27° corresponding to period number 6. In Figure 2F, the optimum angle is obtained for four periods. It varies between −0.78° corresponding to period number 2 and 49.43° corresponding to period number 4.
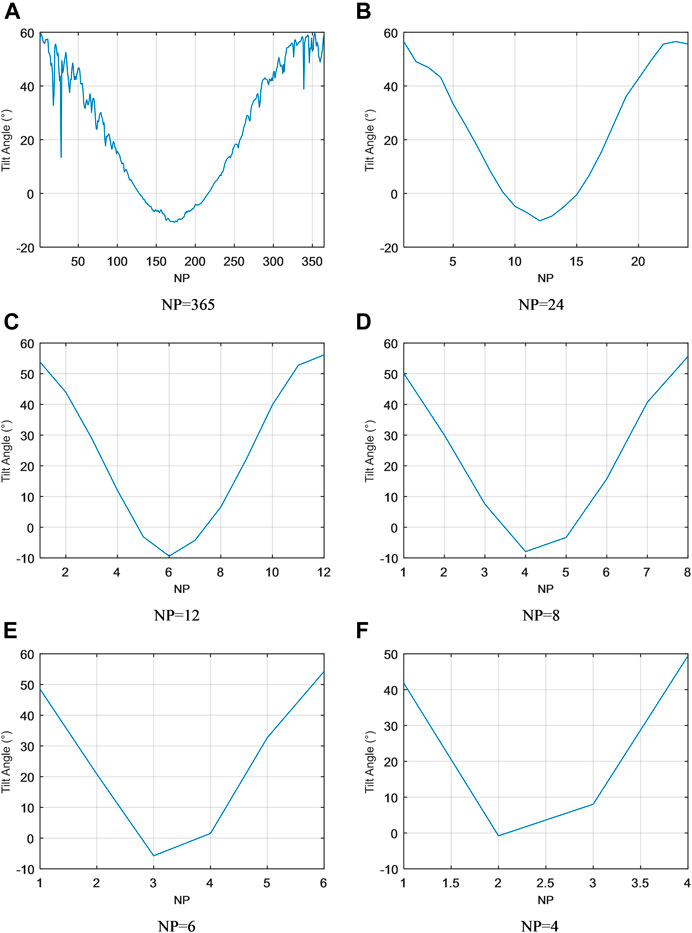
The optimal angles found using model 2 for all the tested NPs are illustrated in Figure 3. The same analysis presented for fixed periods or intervals can also be made on the results shown on this Figure 3.
The total radiations on a horizontal surface and the one on the optimum tilt angle found using model 2 are sketched in Figure 4. It can be seen from this figure that the proposed approach is much better than the one with fixed panels in the horizontal position in terms of receiving effective solar radiation.
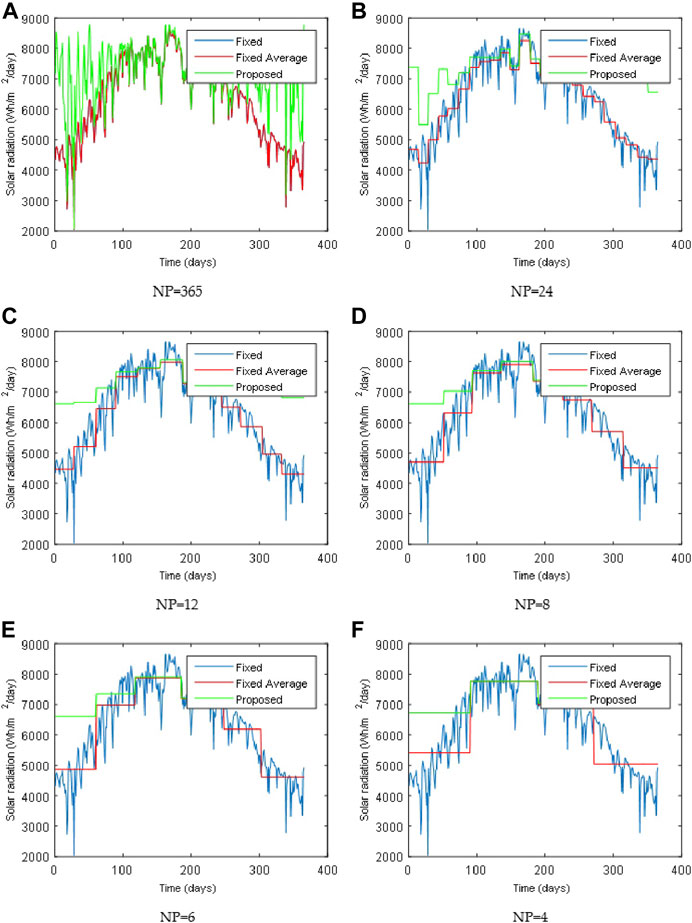
FIGURE 4. Comparison between the total radiations on a horizontal surface and an optimally tilted surface for different NPs.
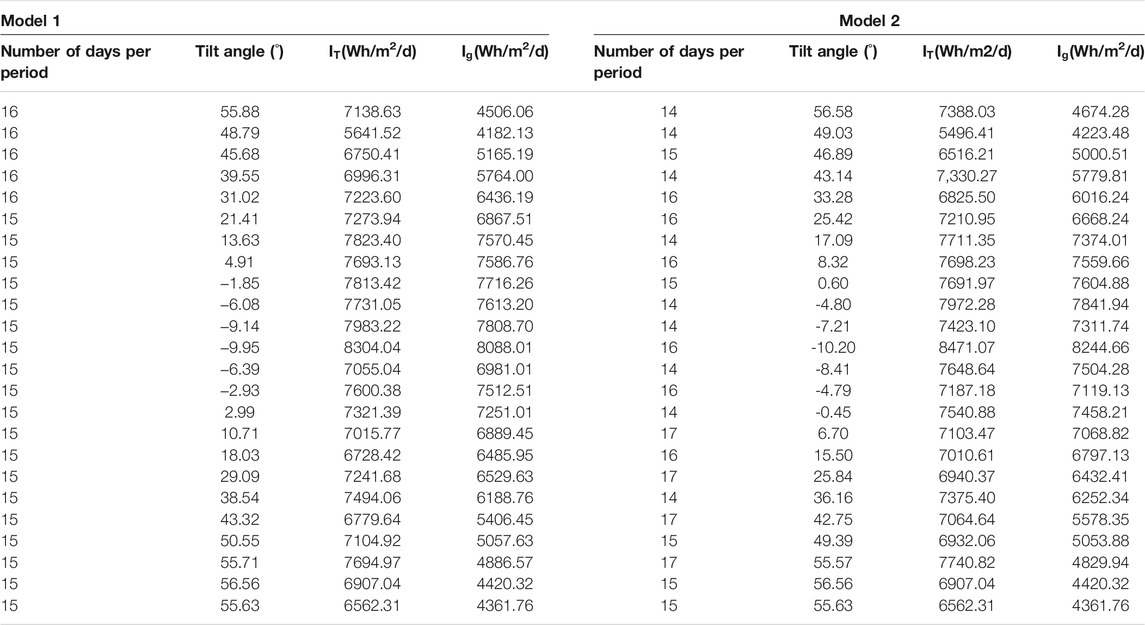
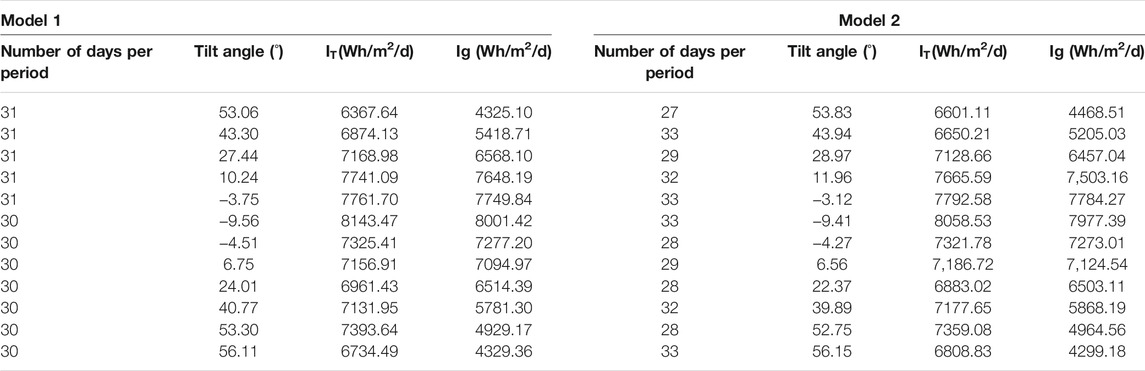
The optimal results found when NP = 24 are tabulated in Table 1. The first four columns correspond to model 1 while the remaining four columns correspond to model 2. In the first column of this table the number of days per period is given, in the second column the optimum tilt angle found is given, whereas, in the third and fourth column IT and Id are given, respectively. The same results are given for model 1 in the same order starting from column five to column 8. Some comments can be made from this table. For model 1, the number of days per period is either 15 or 16, as explained before. However, for model 2 the number of days per period can be 14, 15, 16, or 17.
For model 2, the total radiation received per day on the adjusted surface is 7239.58 Wh/m2/d, which is slightly higher than the one obtained using model 1 (7238.15 Wh/m2/d). Both quantities are notably higher than the radiation to be received by a fixed horizontal surface i.e., 6320.41 Wh/m2/d.
Accumulating the radiations over a year to see the advantage of model 2 over model 1, it is noted that the total radiation received per year on the adjusted surface using model 2 is 2642447.88 Wh/m2, which is higher than the yearly accumulated radiation obtained using model 1 i.e., 2641924.86 Wh/m2. It is pertinent that the radiation that could have been received by a fixed horizontal surface would be the least. In this case, its amount is 2306951.15 Wh/m2.
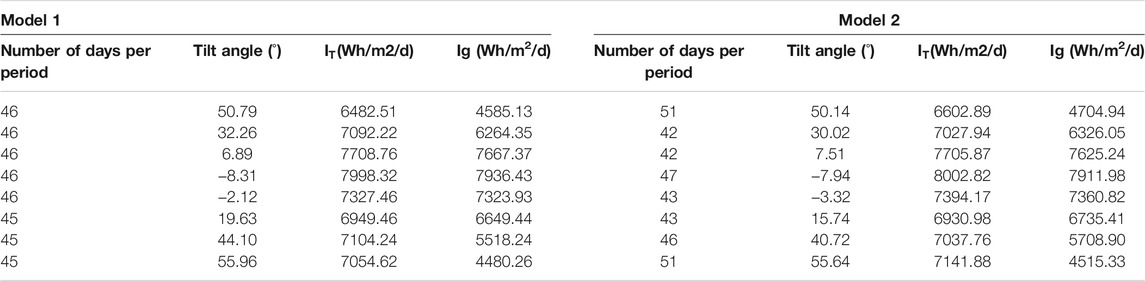
The optimal results found when NP = 12 are tabulated in Table 2. Similar observations can be made from this table. For model 1, the number of days per period is either 30 or 31 (since the number of days per period is fixed). However, for model 2 the number of days per period can be either 27, 28, 29, 32, or 33. Here also, the radiation received by model 2 is higher than that of using model 1. The yearly accumulation of solar radiation for model 2 is 2639382.81 Wh/m2, whereas, for model 1, this quantity amounts to 2638738.91 Wh/m2. Since the radiation received by a fixed horizontal surface does not depend upon NP, it would remain the same 2306951.15 Wh/m2 for all cases discussed here. The comparison of yearly radiation among different NPs is provided in Table 6.
Similarly, for NP = 8, the optimal results are tabulated in Table 3. Here again, model 1 would restrict the number of days per period to 45 and 46, whereas model 2 would allow a flexible number of days per period, allowing it to be either 42, 43, 46, 47, or 51. Using model 1, annual radiation received is found to be 2633900.88 Wh/m2. For model 2, this quantity is found to be 2635653.91 Wh/m2 which is 1753.03 Wh/m2 greater than that of model 1.
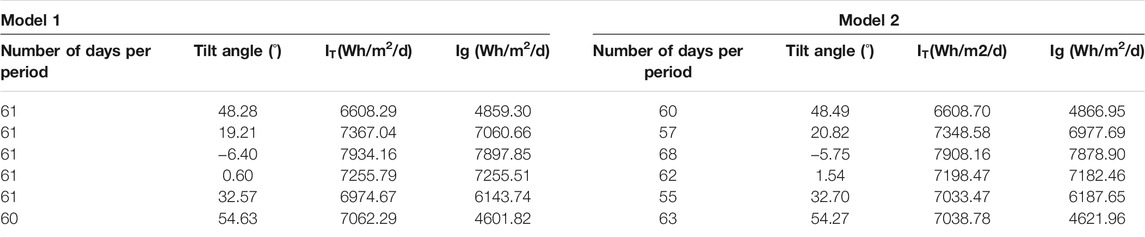
For NP = 6, the optimal results are tabulated in Table 4. In congruence with previous cases, model 1 allows days per period to be either 60 or 61, whereas, days per period in model 2 can be either 55, 57, 60, 62, 63, or 68. Likewise, the annual radiation received by model 2 is higher than that of model 1 by 1460.02 Wh/m2 — 2628274.55 Wh/m2 (model 1) subtracted from 2629734.57 Wh/m2 (model 2).
Finally, at NP = 4, the obtained optimal results are tabulated in Table 5. In continuation with the previous discussion, model 1 gives two options for days per period i.e., 45 or 46. For model 2, the number of days per period could take either 82, 90, 94, or 99. For model 2, the received annual radiation is 2614158.12 Wh/m2 which is 2167.38 Wh/m2 greater than that of model 1 (2611990.74 Wh/m2).
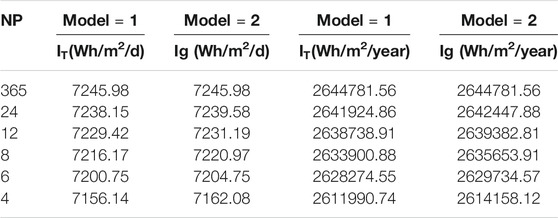
Based on the results of Table 6 it can be concluded that, when NP = 24, NP = 12, NP = 8, NP = 6, and NP = 4 the Ig increases by around 523, 644, 1753, 1,460, and 2,167 Wh/m2/year, respectively, if compared with the horizontal surface’s solar radiation. However, 6423.12 Wh/m2/d of solar radiation can be achieved by the panel if the required adjustments are made in daily basis. It is worth to mention that Ig and IT presented in this table are calculating by getting the average daily values by dividing the yearly values by 365 i.e., the number of days per year.
Conclusion
In this paper, two models of ascertaining PV panels tilt angles have been presented. Their results are compared with one another and with the base case of the fixed horizontal PV panel. The PV panel with the tendency to change its tilt angle every single day would capture maximum radiation but is economically infeasible. This fact has been used as a vantage point to figure out the number of days in one complete year after which the tilt angle can be manually changed. The geographical data of Saudi Arabian western coastal city, Yanbu, has been used to quantify the proposed hypothesis and associated benefits. An approach based on MVPA and PSO has been developed with two separate stipulations; named as models. In the first model, a year must be divided into periods comprising of a fixed number of days, whereas the second model is flexible with assigning the number of days to each period and thus provides an opportunity to receive maximum solar radiation at a certain tilt angle. Analysis of results reveals that with an increased number of adjustments in a year, better proficiency is achieved. Between the first and second models, the later one outperforms the former one for being more adaptive to the receiving radiations. For example, for NP = 4, using model 1 the tilt angles are 41.34°, −0.73°,7.93°, and 49.98° while using model 2 the optimal tilt angels found are 41.83°, −0.78°, 8.04°, and 49.43° which has improved the
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
HB and MR conceived the conceptualization and methodology. HB and MS conducted the normal analysis and writing. AM and MR conducted the data curation and visualization. MR, MS, and AM conducted the review and editing. MR managed funding acquisition. MR managed project administration All authors have agreed to the submitted version of the article.
Funding
This research work was funded by Institutional Fund Projects under grant no. (IFPRC-190-135-2020). Therefore, authors gratefully acknowledge technical and financial support from the Ministry of Education and King Abdulaziz University, Jeddah, Saudi Arabia.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Akhlaghi, S., Sangrody, H., Sarailoo, M., and Rezaeiahari, M. (2017). Efficient Operation of Residential Solar Panels with Determination of the Optimal Tilt Angle and Optimal Intervals Based on Forecasting Model. IET Renew. Power Generation 11, 1261–1267. doi:10.1049/iet-rpg.2016.1033
Alatas, B. (2019). Sports Inspired Computational Intelligence Algorithms for Global Optimization. Artif. Intell. Rev. 52, 1579–1627. doi:10.1007/s10462-017-9587-x
Alrashidi, M. R., Alhajri, M. F., Al-Othman, A. K., and El-Naggar, K. M. (2010). “Particle Swarm Optimization and its Applications in Power Systems,” in Computational Intelligence in Power Engineering. Studies in Computational Intelligence. Editors B. K. Panigrahi, A. Abraham, and S. Das (Berlin, Heidelberg: Springer), 302, 295–324. doi:10.1007/978-3-642-14013-6_10
Alyahya, S., and Irfan, M. A. (2016). The Techno-Economic Potential of Saudi Arabia׳s Solar Industry. Renew. Sustain. Energ. Rev. 55, 697–702. doi:10.1016/j.rser.2015.11.017
Armstrong, S., and Hurley, W. G. (2010). A New Methodology to Optimise Solar Energy Extraction under Cloudy Conditions. Renew. Energ. 35 (4), 780–787. doi:10.1016/j.renene.2009.10.018
Awasthi, A., Shukla, A. K., Murali Manohar, S. R., Dondariya, C., Shukla, K. N., Porwal, D., et al. (2020). Review on Sun Tracking Technology in Solar PV System. Energ. Rep. 6, 392–405. doi:10.1016/j.egyr.2020.02.004
Benghanem, M. (2011). Optimization of Tilt Angle for Solar Panel: Case Study for Madinah, Saudi Arabia. Appl. Energ. 88 (4), 1427–1433. doi:10.1016/j.apenergy.2010.10.001
Beringer, S., Schilke, H., Lohse, I., and Seckmeyer, G. (2011). Case Study Showing that the Tilt Angle of Photovoltaic Plants Is Nearly Irrelevant. Solar Energy 85 (3), 470–476. doi:10.1016/j.solener.2010.12.014
Bouchekara, H. R. E. H. (2020). Most Valuable Player Algorithm: a Novel Optimization Algorithm Inspired from Sport. Oper. Res. Int. J. 20, 139–195. doi:10.1007/s12351-017-0320-y
Calabrò, E. (2013). An Algorithm to Determine the Optimum Tilt Angle of a Solar Panel from Global Horizontal Solar Radiation. J. Renew. Energ. 2013, 1–12. doi:10.1155/2013/307547
Chang, Y.-P. (2010). Optimal the Tilt Angles for Photovoltaic Modules in Taiwan. Int. J. Electr. Power Energ. Syst. 32, 956–964. doi:10.1016/j.ijepes.2010.02.010
Demain, C., Journée, M., and Bertrand, C. (2013). Evaluation of Different Models to Estimate the Global Solar Radiation on Inclined Surfaces. Renew. Energ. 50, 710–721. doi:10.1016/j.renene.2012.07.031
Despotovic, M., and Nedic, V. (2015). Comparison of Optimum Tilt Angles of Solar Collectors Determined at Yearly, Seasonal and Monthly Levels. Energ. Convers. Manage. 97, 121–131. doi:10.1016/j.enconman.2015.03.054
Dey, D., and Subudhi, B. (2020). Design, Simulation and Economic Evaluation of 90 kW Grid Connected Photovoltaic System. Energ. Rep. 6, 1778–1787. doi:10.1016/j.egyr.2020.04.027
El-Sebaii, A. A., Al-Hazmi, F. S., Al-Ghamdi, A. A., and Yaghmour, S. J. (2010). Global, Direct and Diffuse Solar Radiation on Horizontal and Tilted Surfaces in Jeddah, Saudi Arabia. Appl. Energ. 87, 568–576. doi:10.1016/j.apenergy.2009.06.032
Elsayed, M. M. (1989). Optimum Orientation of Absorber Plates. Solar Energy 42, 89–102. doi:10.1016/0038-092X(89)90136-9
Hafez, A. Z., Soliman, A., El-Metwally, K. A., and Ismail, I. M. (2017). Tilt and Azimuth Angles in Solar Energy Applications - A Review. Renew. Sustain. Energ. Rev. 77 (C), 147–168. doi:10.1016/j.rser.2017.03.131
Jafarkazemi, F., and Saadabadi, S. A. (2013). Optimum Tilt Angle and Orientation of Solar Surfaces in Abu Dhabi, UAE. Renew. Energ. 56, 44–49. doi:10.1016/j.renene.2012.10.036
Kaddoura, T. O., Ramli, M. A. M., and Al-Turki, Y. A. (2016). On the Estimation of the Optimum Tilt Angle of PV Panel in Saudi Arabia. Renew. Sustain. Energ. Rev. 65, 626–634. doi:10.1016/j.rser.2016.07.032
Kern, J., and Harris, I. (1975). On the Optimum Tilt of a Solar Collector. Solar Energy 17, 97–102. doi:10.1016/0038-092X(75)90064-X
Khahro, S. F., Tabbassum, K., Talpur, S., Alvi, M. B., Liao, X., and Dong, L. (2015). Evaluation of Solar Energy Resources by Establishing Empirical Models for Diffuse Solar Radiation on Tilted Surface and Analysis for Optimum Tilt Angle for a Prospective Location in Southern Region of Sindh, Pakistan. Int. J. Electr. Power Energ. Syst. 64, 1073–1080. doi:10.1016/j.ijepes.2014.09.001
Khalil, A. G. A. (2021). Seeking Sustainable Development: Prospects for Saudi Arabia’s Transition from Oil to Renewable Energy. Glob. J. Res. Eng.
Korashy, A., Kamel, S., Youssef, A. R., and Jurado, F. (2019). “Most Valuable Player Algorithm for Solving Direction Overcurrent Relays Coordination Problem,” in Proceedings of the International Conference on Innovative Trends in Computer Engineering, ITCE 2019 (New York, NY, USA: Institute of Electrical and Electronics Engineers Inc.), 466–471. doi:10.1109/itce.2019.8646537
Liu, X., Luo, Q., Wang, D., Abdel-Baset, M., and Jiang, S. (2018). “An Improved Most Valuable Player Algorithm with Twice Training Mechanism,” in Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) (Berlin/Heidelberg, Germany, Volume 10954 LNCS: Springer-Verlag), 854–865. doi:10.1007/978-3-319-95930-6_85
Nassar, Y. F., Hafez, A. A., and Alsadi, S. Y. (2020). Multi-Factorial Comparison for 24 Distinct Transposition Models for Inclined Surface Solar Irradiance Computation in the State of Palestine: A Case Study. Front. Energ. Res. 7, 163. doi:10.3389/fenrg.2019.00163
Navntoft, L. C., Fernandez-Ibañez, P., and Garreta, F. (2012). UV Solar Radiation on a Tilted and Horizontal Plane: Analysis and Comparison of 4years of Measurements. Solar Energy 86, 307–318. doi:10.1016/j.solener.2011.10.004
Nfaoui, M., and El-Hami, K. (2018). Extracting the Maximum Energy from Solar Panels. Energ. Rep. 4, 536–545. doi:10.1016/j.egyr.2018.05.002
Nfaoui, M., and El-Hami, K. (2020). Optimal Tilt Angle and Orientation for Solar Photovoltaic Arrays: Case of Settat City in Morocco. Int. J. Ambient Energ. 41 (2), 214–223. doi:10.1080/01430750.2018.1451375
Ouili, M., Mehasni, R., Feliachi, M., Allag, H., Bouchekara, H. R. E. H., Berthiau, G., et al. (2019). Coupling of 3D Analytical Calculation and PSO for the Identification of Magnet Parameters Used in Magnetic Separation. Appl. Comput. Electromagn. Soc. J. 37.2019
Ramli, M. A. M., Bouchekara, H. R. E. H., and Alghamdi, A. S. (2019). Efficient Energy Management in a Microgrid with Intermittent Renewable Energy and Storage Sources. Sustainability 11, 3839. doi:10.3390/su11143839
Ramli, M. A. M., and Bouchekara, H. R. E. H. (2018). Estimation of Solar Radiation on PV Panel Surface with Optimum Tilt Angle Using Vortex Search Algorithm. IET Renew. Power Generation 12, 1138–1145. doi:10.1049/iet-rpg.2017.0830
Ramli, M. A. M., and Bouchekara, H. R. E. H. (2020). Wind Farm Layout Optimization Considering Obstacles Using a Binary Most Valuable Player Algorithm. IEEE Access 8, 131553–131564. doi:10.1109/ACCESS.2020.3009046
Ramli, M. A. M., Twaha, S., and Al-Turki, Y. A. (2015). Investigating the Performance of Support Vector Machine and Artificial Neural Networks in Predicting Solar Radiation on a Tilted Surface: Saudi Arabia Case Study. Energ. Convers. Manage. 105, 442–452. doi:10.1016/j.enconman.2015.07.083
Saraf, G. R., and Hamad, F. A. W. (1988). Optimum Tilt Angle for a Flat Plate Solar Collector. Energ. Convers. Manage. 28 (2), 185–191. doi:10.1016/0196-8904(88)90044-1
Sarailoo, M., Akhlaghi, S., Rezaeiahari, M., and Sangrody, H. (2017). “Residential Solar Panel Performance Improvement Based on Optimal Intervals and Optimal Tilt Angle,” in IEEE Power and Energy Society General Meeting (IEEE Computer Society), 1–5. doi:10.1109/PESGM.2017.8274587
Sharma, M. K., Kumar, D., Dhundhara, S., Gaur, D., and Verma, Y. P. (2020). Optimal Tilt Angle Determination for PV Panels Using Real Time Data Acquisition. Glob. Challenges 4 (8), 1900109–1900112. doi:10.1002/gch2.201900109
Shukla, K. N., Rangnekar, S., and Sudhakar, K. (2015). Comparative Study of Isotropic and Anisotropic Sky Models to Estimate Solar Radiation Incident on Tilted Surface: A Case Study for Bhopal, India. Energ. Rep. 1, 96–103. doi:10.1016/j.egyr.2015.03.003
Skeiker, K. (2009). Optimum Tilt Angle and Orientation for Solar Collectors in Syria. Energ. Convers. Manage. 50, 2439–2448. doi:10.1016/j.enconman.2009.05.031
Smith, C. J., Forster, P. M., and Crook, R. (2016). An All-Sky Radiative Transfer Method to Predict Optimal Tilt and Azimuth Angle of a Solar Collector. Solar Energy 123, 88–101. doi:10.1016/j.solener.2015.11.013
Srilakshmi, K., Ravi Babu, P., and Aravindhababu, P. (2020). An Enhanced Most Valuable Player Algorithm Based Optimal Power Flow Using Broyden's Method. Sustainable Energ. Tech. Assessments 42, 100801. doi:10.1016/j.seta.2020.100801
Tang, R., and Wu, T. (2004). Optimal Tilt-Angles for Solar Collectors Used in China. Appl. Energ. 79, 239–248. doi:10.1016/j.apenergy.2004.01.003
Yadav, A. K., and Chandel, S. S. (2013). Tilt Angle Optimization to Maximize Incident Solar Radiation: A Review. Renew. Sustain. Energ. Rev. 23, 503–513. doi:10.1016/j.rser.2013.02.027
Keywords: optimal intervals, optimum tilt angle, solar panel, solar radiation, most valuable player algorithm, particle swarm optimization
Citation: Ramli MAM, Bouchekara HREH, Shahriar MS, Milyani AH and Rawa M (2021) Maximization of Solar Radiation on PV Panels With Optimal Intervals and Tilt Angle: Case Study of Yanbu, Saudi Arabia. Front. Energy Res. 9:753998. doi: 10.3389/fenrg.2021.753998
Received: 05 August 2021; Accepted: 30 September 2021;
Published: 19 October 2021.
Edited by:
Ravishankar Sathyamurthy, KPR Institute of Engineering and Technology, IndiaReviewed by:
Ayong Hiendro, Tanjungpura University, IndonesiaMuthu Manokar A, B. S. Abdur Rahman Crescent Institute Of Science And Technology, India
Copyright © 2021 Ramli, Bouchekara, Shahriar, Milyani and Rawa. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Makbul A. M. Ramli, bXJhbWxpQGthdS5lZHUuc2E=
 Makbul A. M. Ramli
Makbul A. M. Ramli Houssem R. E. H. Bouchekara
Houssem R. E. H. Bouchekara Mohammad S. Shahriar3
Mohammad S. Shahriar3 Ahmad H. Milyani
Ahmad H. Milyani