Robust Optimal Dispatching of Wind Fire Energy Storage System Based on Equilibrium Optimization Algorithm

The uncertainty of wind resources is one of the main reasons for wind abandonment. Considering the uncertainty of wind power prediction, a robust optimal dispatching model is proposed for the wind fire energy storage system with advanced adiabatic compressed air energy storage (AA-CAES) technology. Herein, the operation constraints of the power plant and constraints of the reserved capacity are defined according to the operation characteristics of AA-CAES. Based on the limited scenario method, a solution framework is proposed to achieve the optimal robustness and economical operation of the system, which provides a new way for the application of the intelligent algorithm in the robust optimal dispatching. Specifically, a novel equilibrium optimization algorithm is employed to solve the optimal dispatching problem, which has good global search performance. The proposed solution is validated through simulations based on the IEEE-39 node system. The simulation results verify the effectiveness of the proposed dispatching model and the intelligent solver.

Introduction

Facing the challenge of global warming and energy crisis, wind power generation has been rapidly developed in recent years (Song et al., 2021b). In 2018, a significant growth of 51.3 GW was reached for the global installed capacity (Yang et al., 2021). However, due to the intermittence and uncertainty of wind power, its large-scale grid connection has brought a great challenge to the reliability of power system. Taking China as an example, the average wind abandonment rate in China was 4% in 2019. With the gradual increase of total installed capacity, the problem of wind abandonment has been increasingly prominent (Song et al., 2021a). In order to reduce the wind abandonment rate, the application of multiple energy complementary system and energy storage system has been widely concerned (Chen et al., 2022).

The application of energy storage system is one of the common methods to reduce the wind abandonment rate of wind farm. As a typical energy storage technology, conventional compressed air energy storage (C-CAES) has been widely used in integrated energy system. It was proved that the utilization of C-CAES can increase the flexibility of comprehensive energy system and improve economic benefits (Sedighizadeh et al., 2019). However, the application of C-CAES in the power system is limited, due to its high construction cost, low conversion efficiency and dependence on specific geographical conditions. As an improved energy storage mode of conventional one, advanced adiabatic compressed air energy storage (AA-CAES) can store compression heat and has the advantages of high efficiency, long service life, low cost, and fast response.

At present, AA-CAES has been applied into the integrated energy system dispatching. The energy system dispatching model based on AA-CAES was studied, and its value was analyzed in monopoly power market, energy market and reserve market (Ding et al., 2019). Based on the heating and power supply characteristics of AA-CAES, it was proposed an optimal dispatching model of zero carbon emission microgrid integrated with AA-CAES (Rui et al., 2016). This series of research verified the effectiveness of AA-CAES system in the integrated energy system, and provided potential dispatching schemes for the integrated energy system with AA-CAES. However, the existing researches only model the combination between the AA-CAES and the traditional energy. Moreover, the uncertainty of reserved capacity and renewable energy is seldom considered.

Generally, the optimal dispatching model of the power system usually presents the characteristics of nonlinearity, high dimension, strong coupling and multi constraints. Most optimal dispatching problems are solved for the whole time series. When using intelligent algorithms, there are problems such as high dimension and difficulty in meeting constraints. Based on these problems, an optimization framework suitable for the utilization of intelligent algorithms is proposed, which has better solution results and shorter solution time. Specifically, to solve the formulated optimal dispatching problem, it is employed a novel equilibrium optimization (EO) algorithm (Faramarzi et al., 2020), which has unique advantages in exploration, exploitation, and local minimum avoidance when solving high-dimensional, nonlinear and multi constraint problems.

Combining AA-CAES with renewable energy, a robust optimal scheduling model is established for the wind fire energy storage system, in which the limited scenario method is used to represent the uncertainty of wind power prediction. In order to solve the dispatching scheme corresponding to minimizing the comprehensive cost in the extreme scenario, an effective framework based on the intelligent algorithm solution is proposed. The novel EO algorithm is used to solve the dispatching scheme corresponding to the minimal comprehensive cost under different prediction error bounds. Finally, the effectiveness of the dispatching model and solution framework is verified under the improved IEEE-39 node.

The remainder of this paper is organized as follows. In section Robust Optimal Dispatching of Wind Fire Storage System, the robust optimal dispatching model of the wind fire storage system is established, and a solution framework based on the intelligent algorithm solution is proposed. Experimental validation and result analysis are shown in section Experimental Validation and Result Analysis. Finally, section Conclusion concludes the paper.

Robust Optimal Dispatching of Wind Fire Storage System

The limited scenario can represent all error scenarios in the uncertainty set. The robust optimal dispatching model can meet the dispatching of all scenarios only by meeting all limited scenarios. In this section, the limited scenario method is used to establish the robust optimal dispatching model of wind fire energy storage system, and the objective function and related constraints are presented.

Robust Optimal Dispatching Modelling

The limited scenario method is used to quantify the uncertainty of wind power prediction, and the established uncertainty set of wind power prediction is as follows:

$\left(1-\beta \right)P_{Wp,i}^t\le P_{Wp,i}^t\le \left(1+\beta \right)P_{Wp,i}^t(1)$

where $P_{Wp,i}^t$ is the predicted power generation of wind farm $i$ at time $t$, and $\beta$ is the scaling factor of wind power prediction error limit, which determines the performance of the system.

The integrated energy system studied in this paper includes wind power, thermal power and AA-CAES. Among them, the mechanism model includes operation constraints and reserved capacity constraints. The cost models of these three types of power stations can be expressed in three parts: energy cost, environmental cost and standby market cost. As a part of the comprehensive cost, the production cost of the integrated energy system can be expressed as:

$C_O=C_F+C_W+C_{CAES}+C_E+\left(C_{Lup}+C_{Ldown}\right)(2)$

where $C_F$, $C_W$ , $C_{CAES}$ are the power purchase cost of thermal power, wind power and AA-CAES, respectively. $C_E$ is environmental cost, and $C_{Lup}$ and $C_{Ldown}$ are the positive and negative standby market cost, respectively.

The power purchase cost, environmental cost and power purchase cost of thermal power, wind power and AA-CAES power stations are as follows:

$C_F={\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^{N_G}{p}_{f,i}{P}_{F,i}^t}}(3)$

$C_W={\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^{N_W}{p}_{w,i}{P}_{W,i}^t}}(4)$

$C_{CAES}={\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^{N_C}{p}_{c,g,i}{P}_{CAES,i}^t}}(5)$

$C_E={\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^{N_G}\left({\lambda }_s{\alpha }_i^s{P}_{F,i}^t\Delta t+{\lambda }_c{\alpha }_i^c{P}_{F,i}^t\Delta t\right)}}(6)$

$C_{Lup}={\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^{N_C}{p}_{caes,i,Lup}{P}_{CAES,i,Lup}^t}}+{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^{N_G}{p}_{f,i,Lup}{P}_{F,i,Lup}^t}}(7)$

$C_{Ldown}={\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^{N_C}{p}_{caes,i,Down}{P}_{CAES,i,Down}^t}}+{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^{N_G}{p}_{f,i,Down}{P}_{F,i,Down}^t}}(8)$

where $p_{f,i}$, $p_{w,i}$ and $p_{c,g,i}$ are the unit power purchase cost of wind power, thermal power and AA-CAES, respectively; $p_{c,c,i}$ is the unit cost required to buy electricity under the compression state of the power station. $p_{caes,i,Lup}$, $p_{caes,i,Down}$, $p_{f,i,Lup}$ and $p_{f,i,Down}$ are the unit power purchase cost of wind power and AA-CAES in positive and negative standby Market, respectively; ${\lambda }_s$ and ${\lambda }_c$ are the cost factor of gas emission of $S{O}_2$ and $C{O}_2$ respectively; $P_{F,i}^t$, $P_{W,i}^t$ and $P_{CAES,i}^t$ are the output of the corresponding unit at time $t$, respectively; $P_{F,i,Lup}^t$ and $P_{F,i,Ldown}^t$ are the positive and negative standby capacity provided by thermal power unit $i$ at time $t$, respectively. $N_G$, $N_W$ and $N_C$ are the number of thermal power units, wind power units and AA-CAES units, respectively; $T$ is the dispatching period which is set as 24 in this study.

In order to ensure the effectiveness and accuracy of the established dispatching model, some power system operation constraints need to be considered, including standby constraints, unit climbing constraints, wind power output constraints and wind power prediction uncertainty set constraints. The system operation constraints are set as follows:

• System power balance constraints and positive and negative reserved capacity constraints:

${\displaystyle \sum _{i=1}^{N_G}{P}_{F,i}^t}+{\displaystyle \sum _{i=1}^{N_W}{P}_{W,i}^t}+{\displaystyle \sum _{i=1}^{N_C}{P}_{CAES,i}^t}=P_{Load}^t(9)$

${\displaystyle \sum _{i=1}^{N_G}{P}_{F,i,Lup}^t}+{\displaystyle \sum _{i=1}^{N_C}{P}_{CAES,i,Lup}^t}\ge R_{Lup,min}^t(10)$

${\displaystyle \sum _{i=1}^{N_G}{P}_{F,i,Ldown}^t}+{\displaystyle \sum _{i=1}^{N_C}{P}_{CAES,i,Ldown}^t}\ge R_{Ldown,min}^t(11)$

• Thermal power unit output upper and lower limit constraints, positive and negative reserved capacity climbing constraints, start and stop constraints:

$P_{F,i}^t+P_{F,i,Lup}^t\le P_{F,i,\max }(12)$

$P_{F,i,min}\le P_{F,i}^t-P_{F,i,Ldown}^t(13)$

$0\le P_{F,i,Lup}^t\le r_{F,i,Lup}(14)$

$0\le P_{F,i,Ldown}^t\le r_{F,i,Ldown}(15)$

• Wind power output constraints and wind power prediction uncertainty set constraints:

$0\le P_{W,i}^t\le P_{Wp,i}^t(16)$

$\left(1-\beta \right)P_{Wp,i}^t\le P_{Wp,i}^t\le \left(1+\beta \right)P_{Wp,i}^t(17)$

where $P_{Load}^t$ is the load value at time $t$, $R_{Lup,min}^t$ and $R_{Ldown,min}^t$ are the minimum positive and negative reserved capacity required at time $t$, respectively. $r_{F,i,Lup}$ and $r_{F,i,Ldown}$ are the up and down climbing speed of thermal power unit $i$, respectively.

Baes on the established robust optimal dispatching model, the risk cost and comprehensive cost can be calculated. Risk cost includes the wind abandonment cost and load shedding cost. In this study, it is assumed that the probability distribution of wind power prediction is a normal distribution with the predicted value as the mean. Therefore, combined with the wind power probability distribution curve, the expected value of the wind power prediction range that fails to be absorbed by the dispatching plan can be obtained, which is the expected value of the abandoned wind power of the dispatching plan in this period. Meanwhile, the cost of wind abandonment also considers the fuel cost and environmental cost of thermal power. The expression of abandoned wind cost is as follows:

$C_{W,ab}={\displaystyle \sum _{t=1}^T\left(a_i{Q}_{W,abandon,t}^2+b_i{Q}_{W,abandon,t}+c_i+{\lambda }_s{\alpha }_i^s{Q}_{W,abandon,t}+{\lambda }_c{\alpha }_i^c{Q}_{W,abandon,t}\right)}(18)$

where $Q_{W,abandon,t}$ is the expected value of abandoned wind power corresponding to time $t$, and $a_i$, $b_i$, $c_i$ are the three fuel cost factors.

Meanwhile, the expected value is calculated by integrating the minimum wind power range that the system can dispatch, and then the expected value of abandoned wind power in the dispatching plan in this period can be obtained. Therefore, the load shedding cost can be expressed as:

$C_{W,cut}={\displaystyle \sum _{t=1}^T{p}_{cut,t}{Q}_{W,cut,t}}(19)$

where $p_{cut,t}$ is the unit cost required to cut off the load at time $t$, and $Q_{W,cut,t}$ is the expected value of cut-off load power at time $t$.

Combined with the abandoned wind cost, load shedding cost and production cost, the comprehensive cost can be finally obtained as follows:

$C_{Total}=C_O+C_{W,ab}+C_{W,cut}(20)$

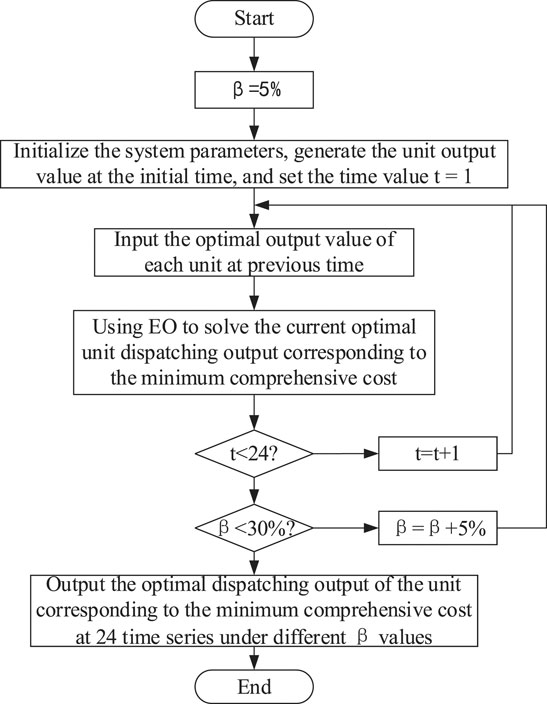
Solution Framework for Solving the Established Dispatching Model

According to the definition of wind power prediction uncertainty set by the limited scenario method, the scaling factor $\beta$ of the wind power prediction distribution will determine the system performance. The value of scaling factor $\beta$ depends on the user’s estimation of the degree of uncertainty of prediction. In this study, the effective range of scaling factor $\beta$ is set to be 5–30%. Based on the established robust optimal dispatching model, the robust optimization problem is formulated, and the final objective function is presented in a robust format as follows:

$\begin{array}{l}\min C_{Total}\left(P_w,P_F,P_{CAES},P_{F,Lup},P_{F,Ldown},P_{CAES,Lup},P_{CAES,Ldown},\beta \right)\\ s.t.\{\begin{array}{l}Eq.\left(9\right)-\left(17\right)\\ P_{F,min}^t\le P_F^t\le P_{F,max}^t\\ -P_{CAES,max}\le P_{CAES}\le P_{CAES,max}\\ P_{CAES,Lup,min}\le P_{CAES,Lup}\le P_{CAES,Lup,max}\\ P_{CAES,Ldown,min}\le P_{CAES,Ldown}\le P_{CAES,Ldown,max}\end{array}\\ \forall \beta \in \left[-30\%,30\%\right]\end{array}(\mathrm{21a})$

where $P_{F,min}^t$, $P_{F,max}^t$ are the minimum and maximum output of thermal power; $P_{CAES,max}$ is the maximum output of AA-CAES; $P_{CAES,Lup,min}$, $P_{CAES,Lup,max}$ are the minimum and maximum positive standby output of AA-CAES; $P_{CAES,Ldown,min}$, $P_{CAES,Ldown,max}$ are the minimum and maximum negative standby output of AA-CAES.

In order to solve the minimum comprehensive cost corresponding to the worst scenario under different $\beta$ value ranges, an effective solution framework is proposed as show in Figure 1. The specific procedure is carried out as follows:

FIGURE 1

FIGURE 1. The solution framework for solving the robust optimal dispatching model.

Initialization

Firstly, initialize $\beta =5\%$, set the current time value $t=1$, and set input parameters such as unit dispatching output boundary value, cost coefficient and electricity price. Set the initial unit output value as the lower limit of the processing range.

External circulation

Use EO algorithm to solve the optimal scheduling scheme corresponding to the minimum comprehensive cost in the next 24 times when $\beta =5\%$. When $\beta <30\%$, then $\beta =\beta +5\%$, and continue to use EO algorithm to solve the model at all 24 times under the updated $\beta$ condition. When $\beta >30\%$, the cycle ends and all the $\beta$ and its corresponding production cost, risk cost, minimum comprehensive cost and dispatching output are collected.

Internal circulation

First, input the initialized unit output value as the optimal output value at the previous time. Then, use EO algorithm to solve the dispatching model at present time moment, and get the corresponding production cost, risk cost and minimum comprehensive cost. When $t<24$, $t=t+1$ and the optimal dispatching output at the current time is used as the system input at the next time. In this way, the optimal dispatching output scheme corresponding to the minimum comprehensive cost under 24 time series at a determined $\beta$ value is obtained.

The Solver Based on the Equilibrium Optimization Algorithm

According to the established objective function and the relevant constraints, the optimal dispatching model can be transformed into an optimization problem. In order to ensure the solution speed and accuracy, EO algorithm is presented to solve this optimization problem. EO algorithm is inspired by control volume mass balance models used to estimate both dynamic and equilibrium state. Considering the high-dimensional and multi constraint characteristics of this optimization problem, the intelligent algorithm solver proposed in this paper solves a single-step time series and takes the optimal scheduling output at the current time as the input of the next time, which can effectively reduce the solution time while ensuring the solution accuracy. The solver based on EO algorithm is structurally divided into the following parts:

Initialization

Input the optimal dispatching output at the previous time and the system parameters. Determine the user defined parameters, number of design variables and their boundary conditions. Initialize the weight constant coefficient $a_1$ and $a_2$ of the global search and the generation probability $GP$.Based on system constraints and boundary constraints, generate $N$ random points, which are $D$ dimensional.

Individual concentration update

Step 1: When the current iteration number $Iter$ is less than the maximum iteration number, sort the individual concentration according to the fitness function, and put the four individuals with the highest concentration into the equilibrium pool as the optimal candidate solution. Then, save the best point of the previous time and compare it with the current best point. If the best point of the previous time is better than the current best point, the best point of the previous time will replace the current best point.

Step 2: Randomly select a candidate point in the equilibrium pool as $\overrightarrow{C_{eq}}$. Generate random vectors $\overrightarrow{\lambda }$ and $\overrightarrow{r}$. Update the parameter $t$ and $\overrightarrow{F}$ as Eq. 21a, Eq. 21b and Eq. 22. Based on the updated parameters, update the Individual concentration $\overrightarrow{C}$ as Eq. 23. If the updated Individual concentration $\overrightarrow{C}$ cannot meet the system constraints and boundary constraints, repeat step 2 to regenerate the individual concentration until the constraints are met.

$\mathbf{t}={\left(1-\frac{\mathit{I}\mathit{t}\mathit{e}\mathit{r}}{\mathit{M}\mathit{a}\mathit{x}\_\mathit{i}\mathit{t}\mathit{e}\mathit{r}}\right)}^{\left({\mathit{a}}_2\frac{\mathit{I}\mathit{t}\mathit{e}\mathit{r}}{\mathit{M}\mathit{a}\mathit{x}\_\mathit{i}\mathit{t}\mathit{e}\mathit{r}}\right)}(\mathrm{21b})$

where $Iter$ is the current number of iterations, and $Max\_iter$ is the maximum number of iterations.

$\overrightarrow{F}=a_{1}sign\left(\overrightarrow{r}-0.5\right)\left[e^{-\overrightarrow{\lambda }t}-1\right](22)$

where $\overrightarrow{\lambda }$ and $\overrightarrow{r}$ are random vectors, and $a_1$ is weight constant coefficient.

$\overrightarrow{C}=\overrightarrow{C_{eq}}+\left(\overrightarrow{C}-\overrightarrow{C_{eq}}\right)\overrightarrow{F}+\frac{\overrightarrow{G}}{\overrightarrow{\lambda }V}\left(1-\overrightarrow{F}\right)(23)$

where $\overrightarrow{C}$ is the individual concentration, $V$ is the unit set as 1, and $\overrightarrow{G}$ is the generation rate.

Full time series solution

The optimal dispatching output at time $t$ is taken as the system input at time $t+1$. On this basis, the optimal dispatching at time $t+1$ is solved. In this way, the optimal scheduling output, production cost, risk cost and the corresponding minimum comprehensive cost at each time in the whole time series are obtained. The minimum comprehensive cost under the whole time series is calculated and output as the optimal dispatching scheme of the whole time series under the corresponding $\beta$ value.

Experimental Validation and Result Analysis

In order to prove the effectiveness of the established robust optimal dispatching model and the proposed solution framework, the improved IEEE-39 node based on a real power grid case is used. The cost changes of the system under different $\beta$ values are compared. For the optimization problem, EO algorithm is compared with the traditional Grey Wolf Optimizer (GWO) algorithm.

Numerical Example Description

Referring to a regional power grid system in China, the IEEE-39 node system is appropriately modified. Its structure diagram is shown in Figure 2A. The wind farms 1 and 2 are connected to the system from nodes 1 and 2, respectively. AA-CAES power station and wind farm 3 are connected to the system from node 29. The predicted power generation curve and load curve of the wind farm are shown in Figure 2B, the minimum load is 800 MW, and the maximum load is 1600 MW.

FIGURE 2

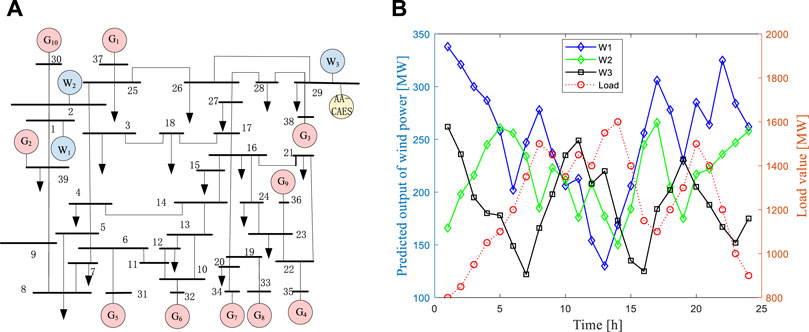
FIGURE 2. Example node system diagram and wind farm output prediction and load curve: (A) node system diagram; (B) wind farm output prediction and load curve.

Result Analysis

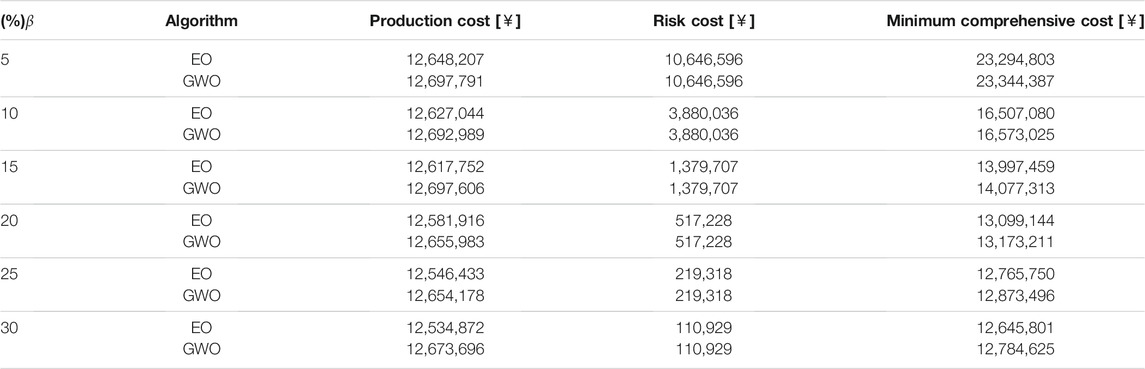
The production cost, risk cost and minimum comprehensive cost of the whole system under different $\beta$ values are shown in Table 1. It can be seen that with the increase of $\beta$ value, the minimum comprehensive cost and corresponding production cost of the system tend to decrease. When the $\beta$ value is 5, 10, 15, 20, 25 and 30%, the minimum comprehensive cost solved by EO algorithm is 23,294,803¥, 16,507,080¥, 13,997,459¥, 13,099,144¥, 12,765,750¥, and 12,645,801¥, respectively. The results show that increasing the uncertainty range can provide an effective way to further reduce the comprehensive cost. When more scenarios are considered, the minimum comprehensive cost decreases with the increase of $\beta$ value. Meanwhile, with the increase of uncertainty range, the space for comprehensive cost reduction decreases. On the other hand, with the increase of the uncertainty range, the risk cost decreases. At the same time, the production cost and minimum comprehensive cost obtained by EO algorithm under different $\beta$ values are smaller than GWO, indicating that EO has better global search performance in solving this optimization problem.

TABLE 1

TABLE 1. The production cost, risk cost and minimum comprehensive cost under different $\beta$ values.

When $\beta =5\%$, the dispatching plan and reserved capacity purchase plan of each power station are shown in Figure 3. As can be seen from Figures 3A–C, the capacity of thermal power units No. 1 and No. 2 is 350 MW, which undertakes the main output of thermal power in the dispatching process because of their large capacity and low production cost coefficient. When the load demand reaches the maximum, the output of No. 1 and No. 2 is 344 and 330 MW respectively. Meanwhile, considering the system requirement, the wind turbine output reaches the limit scenario boundary value, which is 95% of the predicted output. For No. 8, No. 9 and No. 10 thermal power units with small capacity of 50 MW, due to small capacity, high cost and lack of competitive advantage, the output is significantly lower than that of other units. AA-CAES undertakes most of the standby capacity due to its low cost and fast response, and its maximum standby capacity is 100 MW. Meanwhile, the output of AA-CAES is low at the peak of wind power output. For example, the output of AA-CAES in time 17 is only 9 MW. It is indicated that AA-CAES has the potential to promote wind power consumption. The minimum comprehensive cost at each time under the optimal scheduling scheme is shown in Figure 3D. Among the 24 dispatching times, the minimum comprehensive cost value solved by EO is less than GWO in 17 times. The change trend of minimum comprehensive cost is the same as that of load, which shows that the scheduling scheme tracks the load change well. Meanwhile, the minimum comprehensive cost obtained by EO is lower than GWO at most time, indicating that EO has better search accuracy and local optimal avoidance ability than GWO in solving the optimization problem. Combined with Figures 3A–C, it can be explained that the solution framework based on intelligent algorithm can determine an effective unit output scheduling scheme according to load changes, and EO algorithm can effectively solve this optimization problem and has better search ability than GWO.

FIGURE 3

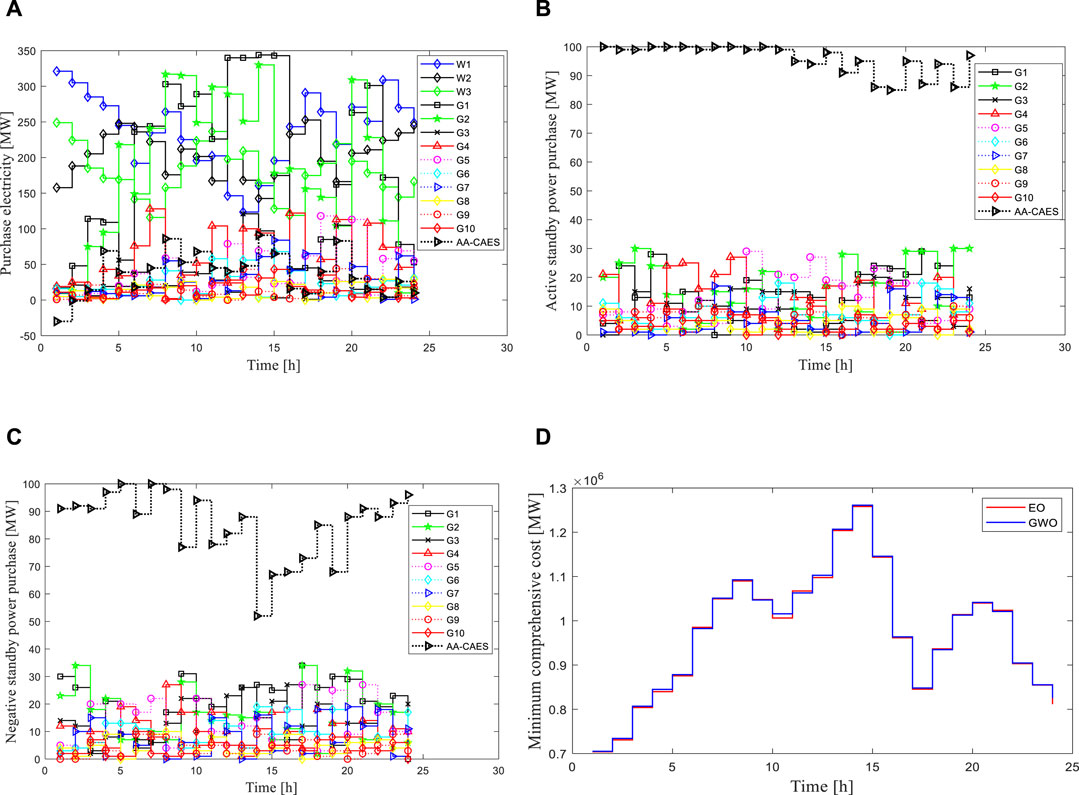
FIGURE 3. Optimal scheduling scheme and corresponding minimum comprehensive cost: (A) Unit output; (B) Unit active standby; (C) Unit negative standby; (D) Minimum comprehensive cost at all times.

Conclusion

This study has presented an effective intelligent algorithm solution framework for solving the established robust optimal dispatching model of wind fire energy storage which considering the application of AA-CAES and the uncertainty of wind power prediction. The simulation results show that the production cost and comprehensive cost can be further reduced by considering the uncertainty of wind power prediction. Meanwhile, the application of AA-CAES can increase the system flexibility and provide guarantee for system standby. On the other side, the equilibrium optimization algorithm shows better robustness and higher search accuracy than GWO in solving this optimization problem. In the future work, other uncertainties such as operation and maintenance uncertainty and energy storage location uncertainty will be further considered.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

XC: Ideas; Development of methodology; Writing- Original draft preparation. LH: Methodology; Creation of models, Writing- Reviewing and Editing. XZ: Verification, Conceptualization, Supervision. SH: Validation, Data curation, Conceptualization, Supervision. ZS: Programming, revise grammar and correct expression. ZW: Programming, software development. TC: Specifically performing the experiments. SD: Conducting a research and investigation process.

Funding

This work was supported in part by the Plan for Major Provincial Science & Technology Project of Anhui Province under Grant 202003a05020019, and in part by the Comprehensive Research Facility for Fusion Technology under Grant 2018-000052-73-01-001228.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, X., Huang, L., Liu, J., Song, D., and Yang, S. (2022). Peak Shaving Benefit Assessment Considering the Joint Operation of Nuclear and Battery Energy Storage Power Stations: Hainan Case Study. Energy 239, 121897. doi:10.1016/j.energy.2021.121897

CrossRef Full Text | Google Scholar

Ding, J., Xu, Y., Chen, H., Sun, W., Hu, S., and Sun, S. (2019). Value and Economic Estimation Model for Grid-Scale Energy Storage in Monopoly Power Markets. Appl. Energ. 240, 986–1002. doi:10.1016/j.apenergy.2019.02.063

CrossRef Full Text | Google Scholar

Faramarzi, A., Heidarinejad, M., Stephens, B., and Mirjalili, S. (2020). Equilibrium Optimizer: A Novel Optimization Algorithm. Knowledge-Based Syst. 191, 105190. doi:10.1016/j.knosys.2019.105190

CrossRef Full Text | Google Scholar

Rui, L., Laijun, C., Tiejiang, Y., and Chunlai, L. (2016). Optimal Dispatch of Zero-Carbon-Emission Micro Energy Internet Integrated with Non-Supplementary Fired Compressed Air Energy Storage System. J. Mod. Power Syst. Clean Energ. 4 (04), 566–580. doi:10.1007/s40565-016-0241-4

CrossRef Full Text | Google Scholar

Sedighizadeh, M., Esmaili, M., and Mousavi-Taghiabadi, S. M. (2019). Optimal Joint Energy and reserve Scheduling Considering Frequency Dynamics, Compressed Air Energy Storage, and Wind Turbines in an Electrical Power System. J. Energ. Storage 23, 220–233. doi:10.1016/j.est.2019.03.019

CrossRef Full Text | Google Scholar

Song, D., Zheng, S., Yang, S., Yang, J., Dong, M., Su, M., et al. (2021a). Annual Energy Production Estimation for Variable-Speed Wind Turbine at High-Altitude Site. J. Mod. Power Syst. Clean. Energ. 9 (3), 684–687. doi:10.35833/MPCE.2019.000240

CrossRef Full Text | Google Scholar

Song, D., Chang, Q., Zheng, S., Yang, S., Yang, J., and Joo, Y. (2021b). Adaptive Model Predictive Control for Yaw System of Variable-Speed Wind Turbines. J. Mod. Power Syst. Clean Energy 9 (1), 219–224. doi:10.35833/MPCE.2019.000467

CrossRef Full Text | Google Scholar

Yang, J., Fang, L., Song, D., Su, M., Yang, X., Huang, L., et al. (2021). Review of Control Strategy of Large Horizontal‐axis Wind Turbines Yaw System. Wind Energy 24 (2), 97–115. doi:10.1002/we.2564

CrossRef Full Text | Google Scholar