Incipient Chiller Fault Diagnosis Using an Optimized Least Squares Support Vector Machine With Gravitational Search Algorithm

Introduction

Centrifugal chillers are one of the most widely used heating, ventilation and air conditioning (HVAC) systems in large-scale buildings for maintaining a desired indoor thermal environment. Nearly half of the energy utilized in commercial buildings is used to maintain indoor thermal comfort (Enteria and Mizutani, 2011). Water chillers are more beneficial in large-scale buildings than direct expansion (DX) type A/C systems in terms of a larger operational range, higher system efficiency, and better part-load characteristic. Almost five million water chillers were in use in China at the end of 2017 (IEA, 2019), and space air conditioning (A/C) accounted for nearly 9.2% of total building energy consumption in 2016 (IEA, 2018). Unexpected chiller failures, on the other hand, might occur after a lengthy period of system operation. Chiller failures are one of the most common problems in building automation systems, lowering system reliability and reducing energy efficiency. Chiller failures are said to account for 42% of service resources and 26% of repair expenses (Comstock et al., 1999). As a result, it is critical to detect and diagnose chiller abnormalities as soon as possible for energy saving of buildings.

Generally, the fault detection and diagnosis (FDD) techniques may be classified into three groups, namely, quantitative model-based methods, qualitative model-based methods and process history based methods (Katipamula and Brambley, 2005a; Katipamula and Brambley, 2005b). Compared to the first two methods where a priori knowledge of process is assumed, only historical data are required for formulating the FDD model, and thus it has gained a wider application. The process history-based methods include gray-box models and black-box models. The first one uses first principles to establish the empirical model where its parameters (such as coefficients in the model) are identified from historical data, such as the state observer based (Shin et al., 2014) and the Kalman filter based (Sun et al., 2017) models. With the growing complexity of building energy systems, black-box model-based methodologies, also called data-driven approaches, have been viewed as a potential way to building performance simulation (Fan et al., 2021), system optimization (Xu et al., 2021b), as well as FDD of HVAC systems which include vapor compression refrigeration systems (Han et al., 2010), variable refrigerant flow (VRF) systems (Guo et al., 2017; Guo et al., 2018), air handling units (AHUs) (Li and Wen, 2014; Lee et al., 2019), building ventilating fan (Xu et al., 2021a) and water chillers (Zhao et al., 2013; Li et al., 2016; Wang et al., 2018). In comparison to the fault detection technique which aims to identify the fault-free operation from all other possible abnormal operations and can be simply treated as a special one-class classification problem, fault diagnosis, as a multiclass classification technique, is more complicated.

Incipient faults in systems always occur slowly and are usually unnoticed in their early stages. If diagnostic tools or proper monitoring systems ignore them, they could not be detectable until their effects become severe and cause catastrophic damages to systems (Safaeipour et al., 2021). A lower fault level will give a smaller impact on the system operation, making it harder to identify the incipient defects. Over the years, while a number of data-driven approaches have been successfully applied for fault diagnosis in chillers (Han et al., 2011; Yan et al., 2014; Huang et al., 2018; Wang et al., 2018; Xia et al., 2021a), timely identifying the faults at their incipient stages is still a significant challenge. For example, the diagnosis accuracies for the incipient faults of refrigerant over charging and lubricant over charging were only 48 and 54.3%, respectively, in a recently reported study (Huang et al., 2018). Therefore, more effects should be done to the enhanced fault diagnosis performance of the incipient chiller faults.

As a robust intelligence classifier, support vector machine (SVM) firstly maps the training data into a high-dimensional space via introducing a nonlinear feature function and then tries to maximize the separating margin of two different classes in the feature space at the same time minimizing training errors using conventional optimization methods (Chang and Lin, 2011). SVM can effectively overcome the problem of over-fitting and has a relatively high generalization capability. Therefore, it has been widely applied for fault diagnosis of HVAC systems. Liang and Du (2007) developed a multi-layer SVM classifier to identify the faults in a single zone HVAC system. Three different types of fault were successfully identified with an acceptable correct rate using a four-layer SVM classifier. Han et al. (2011) proposed an “one against one” multi-class SVM based chiller fault diagnosis method with its kernel parameters being tuned by genetic algorithm optimizer. Results showed that a significant improvement in fault diagnosis performance was achieved for the faults of refrigerant leak and refrigerant overcharge. Yan et al. (2014) studied a hybrid FDD method for water chillers, which incorporated auto-regressive model with exogenous variables and SVM. The FDD performance was compared to that in the case of using the multilayer perceptron neural network classifier, demonstrating the superiority of the proposed method in terms of higher prediction accuracy and lower false alarm rates. Sun et al. (2016) proposed a hybrid approach for identifying refrigerant charge faults in a multi-split air conditioning system. For filtering out the measuring noise, the proposed fault diagnosis method combined the SVM with wavelet de-noising.

However, as the solution of SVM can be regarded as solving a quadratic programming (QP) problem with inequality constraints, the increase of training samples will increase the computational complexity dramatically, resulting in difficult SVM training. Thus, Suykens and Vandewalle (1999) proposed a variation type of conventional SVM, named as least squares SVM (LS-SVM), which converts inequality constraints in SVM into equality constraints by minimizing squared error rather than non-negative error in objective function. As a result, the training of LS-SVM model can be expressed as in terms of solving a linear system instead of a quadratic programming problem, and thus reducing the computational complexity significantly. LS-SVM has gained wide applications in pattern recognition (Yu and Cheng, 2006), system modelling (Borin et al., 2006), time series prediction (Yu et al., 2009; Zhang et al., 2013) and fault diagnosis (Li et al., 2019; Zhao et al., 2020). In terms of the HVAC field, Gao et al. (2016) proposed a novel nonlinear autoregressive with exogenous (NARX) model for the cooling dehumidifier FDD based on LS-SVM. The parameters in NARX model were identified using LS-SVM algorithm, and further adopted for recognizing the faults of condenser fouling and compressor refrigerant insufficient. Han et al. (2019) developed a LS-SVM based fault diagnostic model for chiller FDD. Results showed that a higher fault diagnosis accuracy and a lower running time could be achieved as compared to the conventional SVM classifier. As a matter of fact, parameter optimization in LS-SVM classifier is of great significance for its learning performance and generalization capability. In this study reported by Han et al. (2019), a deterministic optimization algorithm, called grid search with 5-fold cross-validation, was performed to optimize the hyperparameters in LS-SVM classifier. However, grid search requires an exhaustive search over the parameter space, leading to an intensive computational complexity (Zhang et al., 2013). As compared to the deterministic approaches, the heuristic ones present a higher probability of obtaining a global solution, and thus have been employed for parameter optimization in formulating the fault diagnostic model. For example, Zhang et al. (2015) applied barebones particle swarm optimization and differential evolution method to search the optimal parameter combination in SVM based fault diagnostic system for rolling element bearings. An improved particle swarm optimization was introduced by Wang et al. (2019) for tuning the parameters in SVM classifier for fault diagnosis of nuclear power plants. Results showed that the optimization of critical parameters with PSO acquired more accurate and faster SVM classification than the conventional cross-validation approach. Recently, a novel heuristic search algorithm, called the gravitational search algorithm (GSA) (Rashedi et al., 2009), has been proposed and merged as a promising optimizer. GSA is motivated by gravitational law and the laws of motion, and has a flexible and well-balanced mechanism that enhances exploration and exploitation capabilities. It was previously reported that, compared with genetic algorithm and particle swarm optimization, the best regression accuracy and generalization capacity could be achieved when using GSA to optimize the parameters in LS-SVM (Zhang et al., 2013). Therefore, in this reported study, an GSA optimized LS-SVM method is proposed to develop the diagnostic model of incipient chiller fault.

On the other hand, in order to reduce the modelling complexity and computational cost, data decomposition is generally required before performing the multi-class classification. In view of the FDD methods used for HVAC systems, principal component analysis (PCA) is one of the most extensively adopted algorithms (Du et al., 2007; Chen and Lan, 2009; Zhao et al., 2013; Li et al., 2016; Wang et al., 2018; Yu et al., 2020). PCA is a linear data decomposition approach that preserves as much of the original data’s second order statistics as possible. Therefore, as a typical nonlinear process, it may not be suitable for reducing the data dimensionality of water chillers. Another data decomposition method, called kernel PCA (KPCA), has been merged as a promising technique for tackling the nonlinear problem (Lee et al., 2004; Wong et al., 2014). KPCA first projects the input space onto a high-dimensional feature space via a nonlinear mapping. Through introducing a positive semidefinite (psd) kernel function, which computes inner products in the kernel feature space, the kernel matrix thus could be constructed. Then, the principal components could be obtained by performing the eigen-decomposition of the kernel matrix. KPCA is more advantageous than the linear PCA in feature extraction and multi-class classification in a nonlinear system. However, no studies may be identified to apply KPCA based data decomposition method for chiller FDD.

To the best of the authors knowledge, while a number of relevant investigations on developing SVM classifiers for fault diagnosis of HVAC systems (Liang and Du, 2007; Chang and Lin, 2011; Han et al., 2011; Yan et al., 2014), identifying the chiller incipient chiller faults using KPCA-LSSVM method is not reported in the literature. Consequently, this paper reports the development of an GSA-optimized incipient fault diagnostic system for water chillers combining the LSSVM with KPCA. The paper is organized as follows. Firstly, the basics of KPCA, LSSVM classifier and GSA are introduced in Methods and Principles. Then the structure of the proposed fault diagnostic system is detailed in Proposed Fault Diagnostic System for Water Chillers. Experimental Data Descriptions gives a brief introduction of the experimental system from ASHRAE RP-1043. The validation results are presented in Validation of the Proposed Fault Diagnosis Method. Finally, the main contributions of the current study are summarized.

Methods and Principles

Kernel Principal Component Analysis

In KPCA, assuming a m dimensional observed data matrix, X∈R^m, its mapping onto a high-dimensional feature space, F, could be presented as Φ: R^m→F. In this regard, the covariance matrix in the high-dimensional feature space, F, can be evaluated as

${\mathbf{C}}^F=\frac{1}{N}{\displaystyle \sum _{k=1}^N\mathbf{\Phi }\left({\mathbf{x}}_k\right)\mathbf{\Phi }{\left({\mathbf{x}}_k\right)}^T}(1)$

where Φ(x_k) is the kth sample in the feature space with zero-mean and unit-variance, N the sample size. Then, a Gram kernel matrix, K, could be determined as

${\mathbf{K}}_{ij}=\langle \mathbf{\Phi }\left({\mathbf{x}}_i\right),\mathbf{\Phi }\left({\mathbf{x}}_j\right)\rangle =\mathbf{K}\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)(2)$

Through introducing a kernel function, this inner product can be obtained. In this paper, one of the most widely used kernel function, called Gaussian kernel, is adopted,

$\mathbf{K}\left(\mathbf{x},\mathit{y}\right)=\exp \left(-\frac{{\Vert \mathbf{x}-\mathbf{y}\Vert }^2}{2{\sigma }^2}\right)(3)$

where σ is the constant kernel parameter. The kernel matrix should be centralized as

$\tilde{\mathbf{K}}=\mathbf{K}-{\mathbf{I}}_{\mathbf{N}}\mathbf{K}-\mathbf{K}{\mathbf{I}}_{\mathbf{N}}+{\mathbf{I}}_{\mathbf{N}}\mathbf{K}{\mathbf{I}}_{\mathbf{N}}(4)$

Eigen-decomposing the kernel matrix, $\tilde{\mathbf{K}}$, yields

$\mathit{\lambda }\mathbf{\alpha }=\frac{1}{N}\tilde{\mathbf{K}}\mathbf{\alpha }(5)$

where, α = [α₁, α₂, …, α_N]^T is the orthonormal eigenvectors corresponding to the eigenvalues, λ₁≥λ₂≥…≥λ_N. Consequently, the score vector of the kth observation could be obtained via mapping Φ(x) onto the eigenvector v_k in F, namely,

$t_k=\langle {\mathbf{v}}_{\mathbf{k}},\mathbf{\Phi }\left(\mathbf{x}\right)\rangle ={\displaystyle \sum _{i=1}^N{\mathbf{\alpha }}_i^k\langle \mathbf{\Phi }\left({\mathbf{x}}_i\right),\mathbf{\Phi }\left(\mathbf{x}\right)\rangle }\text{,}k=\mathrm{1,2},\mathrm{...},d(6)$

where d is the number of PCs constructing the dominant space, which could be determined using the method of cumulative percent variance (CPV).

Least Squares Support Vector Machine

In LSSVM, assuming a training data set ${\left\{\left({\mathbf{x}}_i,y_i\right)\right\}}_{i=1}^N$, where N is the training data size, x_i∈R^m, is the input vector corresponding to its output, y_i, its classification problem could be mathematically expressed as an optimization problem as follows (Suykens and Vandewalle, 1999),

$\{\begin{array}{c}\min J\left(\mathbf{\omega },\mathbf{e}\right)=\frac{1}{2}{\mathbf{\omega }}^T\mathbf{\omega }+\frac{1}{2}\gamma {\displaystyle \sum _{i=1}^N{e}_i^2},\gamma >0\\ \text{s}\text{.t}\text{.}{y}_i\left[{\mathbf{\omega }}^T\phi \left({\mathbf{x}}_{\mathbf{i}}\right)+b\right]=1-e_i,i=1,\dots ,N\end{array}(7)$

where ω∈Z is the weight vector, b∈R is the bias. Z is the high-dimensional space projected by the nonlinear function φ(x) from the original space R. γ is the regularization parameter used for balancing the model complexity and prediction accuracy. e_i is the error between the actual output and the predicted one, demonstrating the deviation degree of the data from the idea condition of the classification model.

Through introducing the Lagrange multipliers, α_i, the objective function described in Eq. 7 can be rewritten as its Lagrangian form,

$L\left(\mathbf{\omega },b,\mathbf{e},\mathbf{\alpha }\right)=\frac{1}{2}{\mathbf{\omega }}^T\mathbf{\omega }+\frac{1}{2}\gamma {\displaystyle \sum _{i=1}^N{e}_i^2}-{\displaystyle \sum _{i=1}^N{\alpha }_i}\left\{y_i\left[{\mathbf{\omega }}^T\phi \left({\mathbf{x}}_i\right)+b\right]-1+e_i\right\}(8)$

Based on the Karush–Kuhn–Tucker conditions, taking the partial derivatives of Eq. 8 with respect to ω, b, e and α, respectively, yields

$\frac{\partial L}{\partial \mathbf{\omega }}=0\to \mathbf{\omega }={\displaystyle \sum _{i=1}^N{\alpha }_i}{y}_i\phi \left({\mathbf{x}}_i\right)(9)$

$\frac{\partial L}{\partial b}=0\to {\displaystyle \sum _{i=1}^N{\alpha }_i}{y}_i=0(10)$

$\frac{\partial L}{\partial e_i}=0\to {\alpha }_i=y{e}_i(11)$

$\frac{\partial L}{\partial {\alpha }_i}=0\to y_i\left[{\mathbf{\omega }}^T\phi \left({\mathbf{x}}_i\right)+b\right]-1+e_i=0(12)$

Eqs 9–12 can be rewritten as a linear equation set in a matrix form via eliminating e_i and ω,

$\left[\begin{array}{cc}0& {\mathbf{E}}^T\\ \mathbf{E}& \mathbf{\Omega }+\mathbf{E}{\gamma }^{-1}\end{array}\right]\left[\begin{array}{l}b\\ \mathbf{\alpha }\end{array}\right]=\left[\begin{array}{l}0\\ \mathbf{y}\end{array}\right](13)$

where E = [1,1, … , 1]^T, an N-dimension vector; $\mathbf{\alpha }={\left[{\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n\right]}^T$, the support-value vector; $\mathbf{y}={\left[y_1,y_2,\cdots ,y_n\right]}^T$, the output vector. Ω is an N×N symmetric matrix, and its elements, ${\Omega }_{ij}$, can be evaluated through introducing a kernel function K (∙),

${\Omega }_{ij}==\phi {\left({\mathbf{x}}_i\right)}^T\phi \left({\mathbf{x}}_j\right)=K\left({\mathbf{x}}_i,{\mathbf{x}}_j\right),i,j=1,\dots ,N(14)$

Consequently, via solving Eq. 13, α and b can be obtained, and the decision function for classification can be given by

$y\left(\mathbf{x}\right)=sign\left[{\displaystyle \sum _{i=1}^N{\alpha }_i{y}_{i}K\left(\mathbf{x},{\mathbf{x}}_i\right)+b}\right](15)$

As indicated by Eq. 15, the kernel function directly influences the output of the decision function, and thus the classification performance of LSSVM. In the current study, radial basis function (RBF), one of the most effective kernel functions in LSSVM (Lu et al., 2016; Han et al., 2019), was employed. Therefore, the width parameter, σ, in RBF, together with the regularization parameter, γ, should be tuned when developing the LSSVM based fault diagnostic system.

Gravitational Search Algorithm

Inspired by the Newtonian laws of gravity and motion, GSA was initially proposed by Rashedi et al. (2009). In GSA, all the agents can be regarded as objects with masses. All these objects were attracted by each other due to the gravity force, which will consequently cause a global movement of all objects towards those with heavier masses. The movements of the objects with heavy masses, namely, the good solutions, are slower than lighter ones, which guarantees the exploitation step of the algorithm.

In this optimizer, there are four specifications in each agent, namely, position, inertial mass, active gravitational mass, and passive gravitational mass. The position of the agent refers to a solution to the problem. Assuming a system with N agents, the position of the ith agent can be defined as

$X_i=\left(x_i^1,\dots ,x_i^d,\dots ,x_i^n\right),i=\mathrm{1,2},\dots ,N(16)$

where $x_i^d$ is the position of the ith agent in the dth dimension.

The force acting on the ith agent from the jth one as a given time, t, can be evaluated as

$F_{ij}^d\left(t\right)=G\left(t\right)\frac{M_{pi}\left(t\right)\times M_{aj}\left(t\right)}{R_{ij}\left(t\right)+\epsilon }\left(x_j^d\left(t\right)-x_i^d\left(t\right)\right)(17)$

where M_aj is the active gravitational mass corresponding to agent j, M_pi is the passive gravitational mass corresponding to agent i, ε is a small constant, and R_ij(t) is the Euclidian distance. G(t) is gravitational constant at time t, which is set to G₀ at the beginning and then exponentially decreased toward zero over time.

The total force that acts on the ith agent in a dimension d is defined as

$F_i^d\left(t\right)={\displaystyle \sum _{j=1,j\ne i}^{N}ran{d}_j}{F}_{ij}^d\left(t\right)(18)$

where rand_j is a random number ranging from 0 to 1.

Therefore, the acceleration of the ith agent at time t in the dth dimension can be evaluated as follows

$a_i^d\left(t\right)=\frac{F_i^d\left(t\right)}{M_{ii}\left(t\right)}(19)$

where M_ij is the inertial mass corresponding to agent i.

The position the ith agent in the dth dimension at the next time step can be updated based on the position at the current time step and the velocity, which is expressed as

$v_i^d\left(t+1\right)=ran{d}_i\times v_i^d\left(t\right)+a_i^d\left(t\right)(\mathrm{19a})$

$x_i^d\left(t+1\right)=x_i^d\left(t\right)+v_i^d\left(t+1\right)(20)$

where r and_i is also a uniform random number ranging from 0 to 1.

After computing the fitness of the ith agent at the current time step, fit_i(t), the gravitational and inertial masses for the ith agent could be updated as

$M_{ai}=M_{pi}=M_{ii}=M_i,i=\mathrm{1,2},\dots ,N(21)$

$m_i\left(t\right)=\frac{fi{t}_i\left(t\right)-worst\left(t\right)}{best\left(t\right)-worst\left(t\right)}(22)$

$M_i\left(t\right)=\frac{m_i\left(t\right)}{{\displaystyle \sum _{j=1}^N{M}_j\left(t\right)}}(23)$

where the best and worst fitness values are respectively defined as

$best\left(t\right)=\underset{j\in \left\{1,\dots ,N\right\}}{\max }fi{t}_j\left(t\right)(24)$

$worst\left(t\right)=\underset{j\in \left\{1,\dots ,N\right\}}{\min }fi{t}_j\left(t\right)(25)$

Based on Eqs 17–25, the best agent corresponding to the maximum value of fitness function can be determined.

Proposed Fault Diagnostic System for Water Chillers

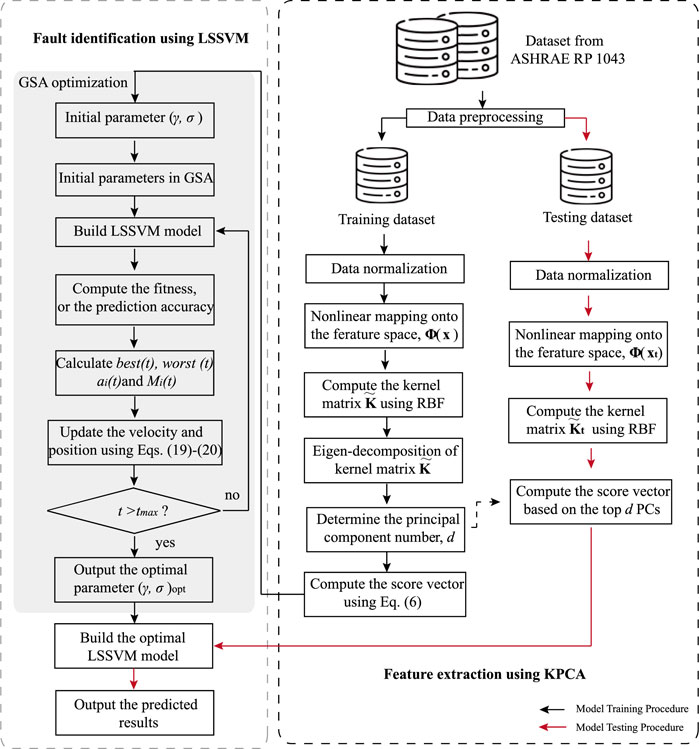
The structure of the proposed fault diagnostic system for centrifugal chillers is schematically shown in Figure 1. As seen, the fault diagnostic system includes two parts, namely, the feature extraction part and the fault identification part. The feature extraction in the proposed fault diagnostic system was performed using KPCA, while the fault identification was based on LSSVM classifier. It was previously shown that “one-against-one” logic was more suitable for the practical use of LSSVM (Chih-Wei and Chih-Jen, 2002). Hence, it was adopted to solve the multi-class classification problem in the current study. In both feature extraction and fault identification parts, there are two procedures, one for training the fault diagnostic model and the other for testing. These two procedures are detailed as follows, respectively.

FIGURE 1

FIGURE 1. Structure of the proposed fault diagnostic system.

In the model training process, the fault data from ASHARE RP-1043 were collected and then normalized. Secondly, the normalized data were mapped onto a feature space, Φ(x), which was nonlinearly related to the input space. Thirdly, using the RBF, the kernel matrix, $\tilde{\mathbf{K}}$, was evaluated, and thus it could be eigen-decomposed to compute the corresponding eigenvalues and eigenvectors. At the fourth step, through sorting the eigenvalues, the CPV for the top s PCs could be calculated, and the number of PC, d, determined based on a preset CPV limit. Finally, the score matrix for each observation could be obtained.

Next, in the fault identification part of model training process, GSA was adopted to optimize the kernel width parameter, σ, and the regularization parameter, γ, in LSSVM model. Firstly, these two parameters, (γ, σ), together with the parameters in GSA, namely, agent number, N, and the maximum time step, t_max, were initialized. Then, based on the data after being decomposed by KPCA, the LSSVM model for fault identification could be established. Thirdly, the fitness, namely, the fault diagnosis accuracy, was obtained, and thus the corresponding, best(t), worst(t), a_i(t) and M_i(t). Fourthly, the position of the agent, or the parameter required to be optimized, could be updated. This procedure was not stopped until the iteration time step, t, reached its maximum value. Finally, the optimal pair of parameters, (γ, σ)_opt was determined and the optimal LSSVM model established.

On the other hand, based on the proposed fault diagnostic model trained, the operating faults can be recognized. Given a testing dataset, x_t, through nonlinear mapping onto a feature space, Φ(x_t), its kernel matrix, ${\tilde{\mathbf{K}}}_{\mathrm{t}}$, could be evaluated. Then, the score matrix on the dominant subspace constructed by the top d PCs was obtained, and thus the original dataset, x_t, was compressed to a low-dimensional dataset, x_t’. Finally, the compressed dataset was input to the optimal LSSVM model, and the different types of fault could be identified.

Experimental Data Descriptions

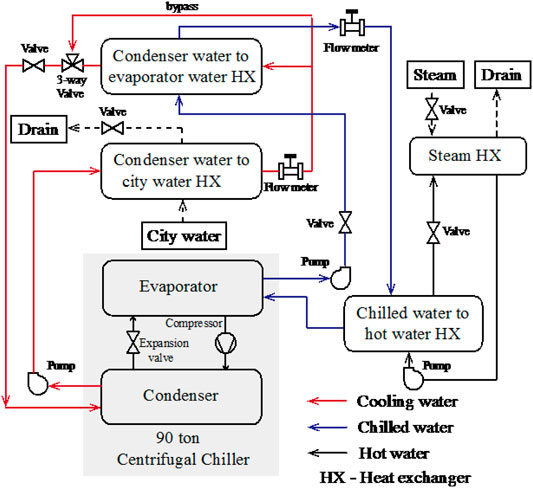
In order to validate the proposed fault diagnosis method, the operating data of a water-cooled chiller reported in the ASHRAE Research Project 1043 (RP-1043) (Comstock et al., 1999) were utilized. The experimental facility is schematically shown in Figure 2. A shell-and-tube evaporator and condenser were installed in the 90-ton centrifugal water chiller. There were five flow paths in the experimental system, namely, the chilled water circuit, the cooling water circuit, the hot water circuit, the city water supply and the steam water supply. Detailed descriptions of the experimental facility can be found in the report ASHRAE RP 1043 (Comstock et al., 1999).

FIGURE 2

FIGURE 2. Schematic diagram of the experimental centrifugal chiller reported in ASHRAE RP1043.

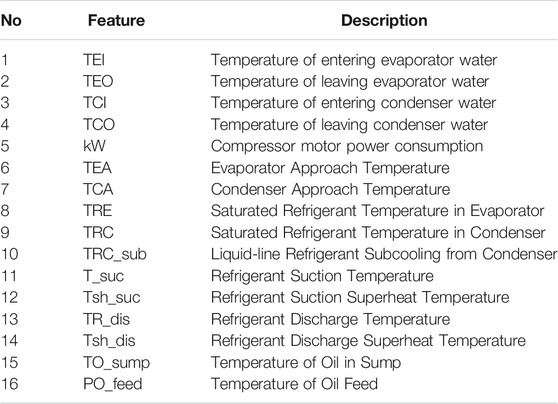
The experimental system was fully instrumented with highly-precise sensors. 48 operating parameters were directly measured and then used for evaluating the other 16 operating parameters, and thus totally 64 variables were recorded. Seven types of faults listed in Table 1 were manually imposed for generating their corresponding fault samples.

TABLE 1

TABLE 1. Fault types and their corresponding generation methods.

It should be pointed out that for the seven typical faults, each has four different severity levels, denoted by the symbols SL1 to SL4, corresponding to the least severe fault to the most severe one. Generally, in chiller routine operation, if a certain kind of fault occurs, its severity level gradually grows with time. Timely identifying the incipient fault is beneficial for reducing equipment downtime, energy waste, and maintenance expense. Hence, incipient fault identification is of vital significance to prevent serious performance deterioration and ensure an optimal system operation. A lower degree of fault severity level will have a lesser influence on the system operation, which makes it more difficult to identify the incipient faults than the serious ones (Yan et al., 2014; Huang et al., 2018). Therefore, in the current research, the seven typical faults at their least severity level, totally, seven categories, were considered to examine the proposed fault diagnosis method.

Validation of the Proposed Fault Diagnosis Method

Before developing the proposed fault diagnostic model, the sample data were required to be pre-processed to filter out the outliers and transient data between two steady states present. A geometrically weighted variance based filter was adopted to remove these measuring noises, which was the same as that developed in the previous studies (Xia et al., 2021b). Three key operating variables, namely, chilled water supply temperature, inlet water temperatures of the evaporator and condenser, were selected as the indicators of steady-state. Consequently, measuring noises were able to be removed if the related data went beyond the slop threshold predefined. The slop threshold and time window length were 0.2°C and 80s, respectively. Furthermore, the filtered data were also normalized in the data pre-processor for guaranteeing all the variables having even contributions.

Within the pre-processed dataset, 560 experimental samples were randomly selected and further separated into two parts; 420 samples (75% of the total samples) for training the fault diagnostic model, while the remaining 140 samples (25% of the total samples) for testing.

Feature Extraction

Before performing the feature extraction, the key features representing the inherent characteristics of chillers should be selected. In the current study, 16 variables were selected as the fault indicative features, which was the same as that used in a previous study (Zhao et al., 2013). The descriptions of these 16 indicative features are listed in Table 2.

TABLE 2

TABLE 2. Descriptions of the selected features.

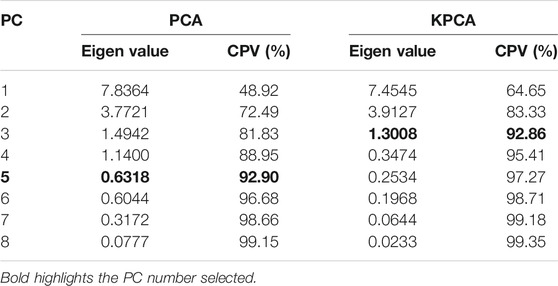
For reducing the modelling complexity and computational cost, KPCA based data decomposition was firstly performed to realize the feature extraction. In order to illustrate the performance of nonlinear data transformation using KPCA, conventional PCA was also employed. The CPVs for the top 8 PCs using PCA and KPCA are shown in Table 3. The limits of CPV for both PCA and KPCA were all predefined at 90%. As seen, the CPV for the first 5 PCs could reach at 92.9% based on PCA. Therefore, these top 5 PCs, corresponding to the eigenvalues of 7.8364, 3.7721, 1.4942, 1.1400, and 0.6318, were selected to construct the dominant subspace. On the other hand, when using KPCA for data decomposition, the CPV for the first 3 PCs was able to reach at 92.86%. Hence, the input 16 features were able to be compressed to these 3 uncorrelated comprehensive features. This superiority was due to the fact that according to Cover’s theorem, the nonlinear data structure in the input space is more likely to be linear after high-dimensional nonlinear mapping. Therefore, fewer PCs were required when performing the data decomposition in a high-dimensional feature space which was nonlinearly related to the input space.

TABLE 3

TABLE 3. Data decomposition results based on PCA and KPCA.

Fault Diagnosis Results

LSSVM Method Based on Grid Search With Cross Validation

As mentioned in Introduction, grid search with cross validation is predominantly used for parameter tuning in LSSVM. In this regard, the proposed KPCA based LSSVM (KPCA-LSSVM) fault diagnosis method with its parameters optimized by grid search with 10-fold cross validation was performed as the basis for comparison. In addition, the fault diagnostic models using single SVM, single LSSVM and LSSVM with PCA data decomposition (PCA-LSSVM) based on the same parameter tuning method were also developed for demonstrating the performance of the proposed KPCA-LSSVM method. The tuning results of (γ, σ) for SVM, LSSVM, PCA-LSSVM and KPCA-LSSVM classifiers were (32.056, 0.641), (2.158, 2.258), (1.138, 1.066) and (1.419, 1.886), respectively.

The fault diagnosis results as expressed in terms of the confusion matrixes are shown in Figure 3. As seen, for two of the most common faults, i.e., RefLeaf (fault code 3) and ConFoul (fault code 6), all four classifiers shared similar results with the reported fault diagnosis accuracy of over 85%. All the fault samples of ConFoul (fault code 6) could be correctly identified when using SVM classifier, while all that of RefLeaf (fault code 3) could be successfully recognized when using KPCA-LSSVM classifier. However, a closer look at the results of SVM classifier illustrated that only 20% fault samples of ReduEF (fault code 2) and RefOver (fault code 4) could be identified, and the overall fault diagnosis accuracy was about 73.57%. When using LSSVM, the fault diagnosis accuracies for these two types of fault could be significantly improved to 82.4 and 54.6%, respectively, and the overall fault diagnosis accuracy was reported at 83.57%. When performing the PCA based data decomposition before using LSSVM for multi-class classification, as shown in Figure 3C, the fault diagnosis accuracy for the fault of RefOver was further improved to 69.6%. While the overall performance of PCA-LSSVM was reported at about 85% which was not significantly improved as compared to that of LSSVM, its training time was much less than the single LSSVM classifier. The best performance among these four classifiers was achieved using KPCA-LSSVM method. As seen in Figure 3D, 100% fault samples for the faults of RefLeak (fault code 3), ExcsOil (fault code 5) and NonCon (fault code 7) could be correctively diagnosed. While the fault diagnosis accuracy for the fault of ReduEF was only 61.9% smaller than that of LSSVM and PCA-LSSVM methods, the overall accuracy was reported at about 89.29% larger than the other three classifiers.

FIGURE 3

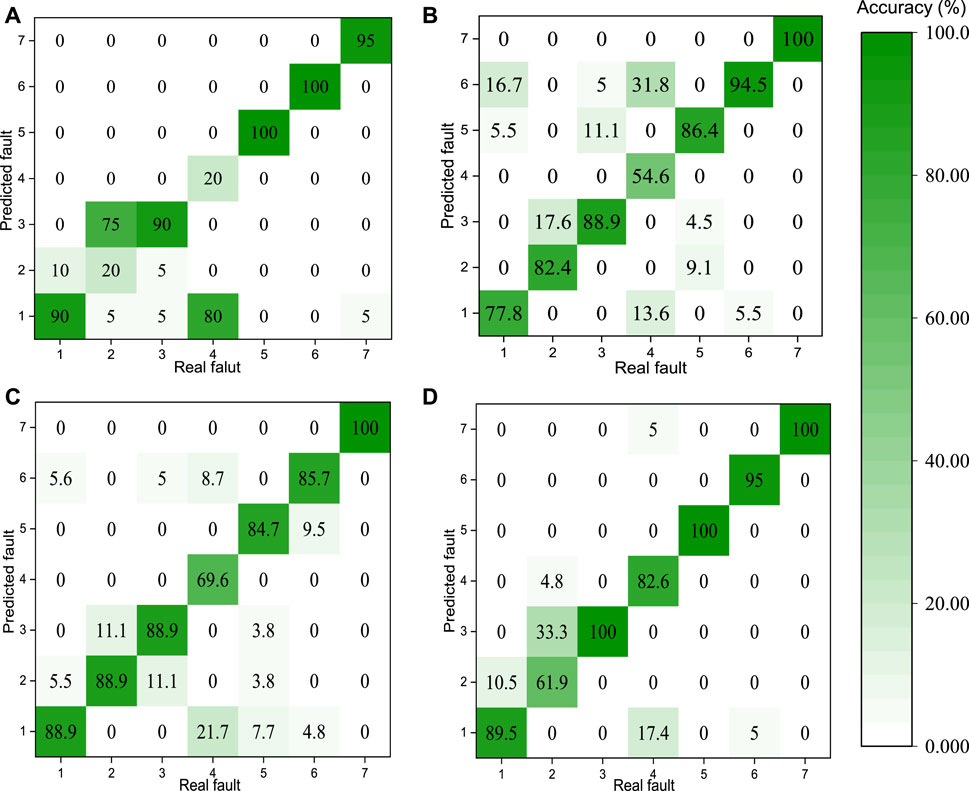
FIGURE 3. Fault diagnosis results for different methods: (A) SVM; (B) LSSVM; (C) PCA-LSSVM; (D) KPCA-LSSVM.

LSSVM Method Optimized by GSA

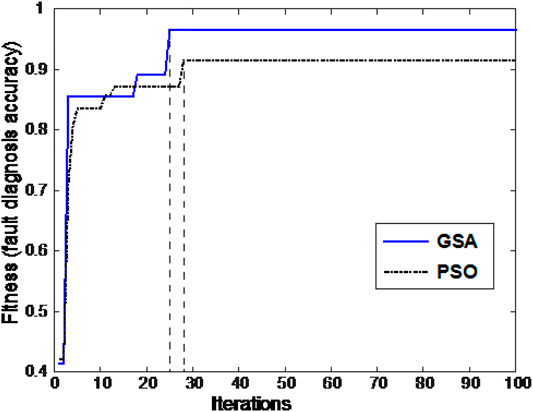
As mentioned in Introduction, parameter optimization in LS-SVM classifier is of great significance for its learning performance and the generalization capability. The results reported in LSSVM Method Based on Grid Search With Cross Validation were obtained based the conventional deterministic approach, namely, grid search with cross validation. In this Section, the fault diagnosis results based on KPCA-LSSVM method optimized by GSA (KPCA-LSSVM-GSA) are reported. In addition, another heuristic approach, called particle swarm optimization (PSO) algorithm, was also adopted to tune the parameters in LSSVM. In GSA, the agent number, N, was set at 30 and the maximum iteration time step was predefined at 100. The parameter tuning process as expressed in terms of the variation in fitness value with the increase of iteration step is shown in Figure 4. The fitness referred to the fault diagnosis accuracy when training the diagnostic model. As seen, the best fitness value of 91.6% was achieved at 28th iteration using PSO, while the value of 96.6% at 26th iteration was achieved using GSA. Their corresponding pairs of the regularization parameter, γ, and the kernel bandwidth, σ, were (1.634, 2.308) and (1.414, 1.047), respectively. Therefore, GSA was more advantageous than PSO when tuning the parameters in LSSVM, as expressed in terms of a higher fitness value and a shorter convergence time.

FIGURE 4

FIGURE 4. Parameter tuning results for GSA and PSO.

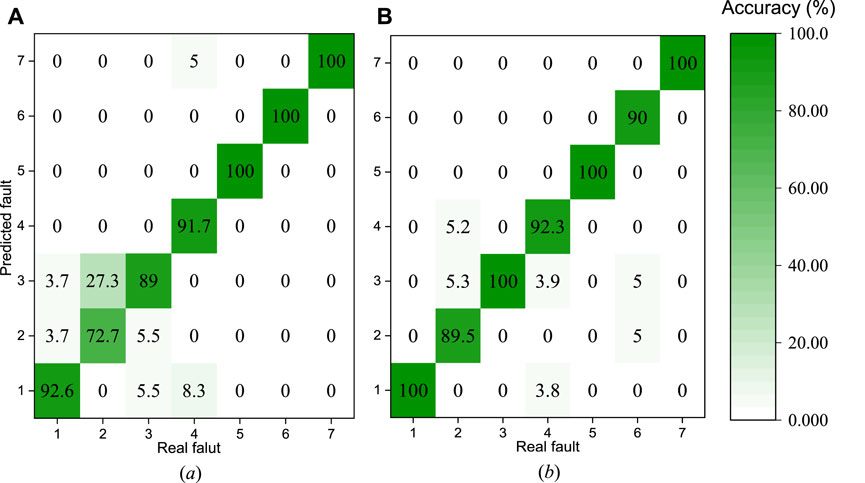
Figure 5 displays the fault diagnosis results based on the proposed KPCA-LSSVM method optimized by PSO and GSA. As seen, all the fault samples for the faults of ExcsOil (fault code 5) and NonCon (fault code 7) were able to be correctively diagnosed using both methods. When using the proposed KPCA-LSSVM-GSA method, the fault diagnosis accuracies for the remaining five types of fault, except for the fault of ConFoul (fault code 6), were larger than that in the case of using the KPCA-LSSVM-PSO method. While the fault diagnosis accuracy for the fault of ConFoul (fault code 6) was reported at 90%, it was acceptable in practical application. With respect to the KPCA-LSSVM-GSA method, its fault diagnosis accuracies for the fault of ReduCF (fault code 1), ReduEF (fault code 2), RefLeak (fault code 3) and RefOver (fault code 4) were 100, 89.5, 100, and 92.3%, respectively. For the KPCA-LSSVM-PSO method, the corresponding diagnosis accuracies were 92.6, 72.7, 89 and 91.7%, respectively. In short, the overall fault diagnosis accuracies of KPCA-LSSVM-PSO and KPCA-LSSVM-GSA methods were 91.42 and 95.7%, respectively, larger than that of KPCA-LSSVM method tuned by grid search with cross validation. These results indicated that the heuristic optimization methods were more suitable to tune the parameters in LSSVM as compared to the deterministic optimization method. Moreover, the fault diagnosis performance for KPCA-LSSVM-GSA method was better than the KPCA-LSSVM-PSO as expressed in terms of a higher overall fault diagnosis accuracy. This was because, as indicated in Figure 4, a better model training performance could be achieved using the GSA, and thus a higher fault diagnosis accuracy could be obtained using the GSA optimized parameters in LSSVM fault diagnostic model.

FIGURE 5

FIGURE 5. Fault diagnosis results for the proposed methods optimized by: (A) PSO, (B) GSA.

Discussions

The fault diagnosis results aforementioned demonstrating the proposed KPCA-LSSVM-GSA method shared the best fault diagnosis performance among these mentioned methods. The improvement in fault diagnosis performance owes to the following aspects. Firstly, as compared to the conventional PCA method, in water chillers whose operating process exhibits high nonlinearities, KPCA is more suitable for feature extraction. In addition, via converting inequality constraints in SVM into equality constraints by minimizing squared error rather than non-negative error in objective function, LSSVM classifier is more advantageous to tackle with the problems arising from the large amount of training samples. Finally, the fault diagnosis results indicated that GSA was an effective tool to tune the parameters in LSSVM. This was partially due to the fact that the heuristic optimizers generally present a higher probability of obtaining a global solution than the deterministic ones.

Moreover, as mentioned in Feature Extraction, the commonly used 16 variables were selected as the indicative features for validating the proposed FDD method. It is well acknowledged that feature selection significantly influences the FDD performance, and with the change of FDD methods, the corresponding indicative features selected may be varied. For example, instead of 16, 8 variables were selected when performing SVDD based method for fault detection (Li et al., 2016). Wang et al. (2018) selected 9 variables as input features, while Huang et al. (2018) used 10 variables for associative classifier based fault diagnostic model development. In this regard, more efforts will be done to examine the proposed method with different input features. Furthermore, it should be pointed out that the FDD results of the proposed method were based on the experimental data form ASHRAE RP-1043 reported in 1999. While lots of improvements have been made in water chillers to enhance the operational performance, the basic working process in water chillers is still unchanged, and thus the general results obtained and the related analysis should remain valid. It is our belief that the proposed fault diagnosis method is capable to be extended to other water chillers.

Conclusion

This article reports on the development of an effective way of diagnosing chiller failure using KPCA based LSSVM classifier with its parameters being optimized by GSA. The proposed fault diagnostic model was validated using the experimental data generated from ASHRAE RP-1043, and further compared with that in the case of using a single SVM classifier, single LSSVM classifier, PCA based LSSVM classifier, grid search algorithm tuned KPCA–LSSVM classifier and PSO tuned KPCA–LSSVM classifier. Results indicated that the best possible fault diagnosis performance could be accomplished with the proposed GSA tuned KPCA-LSSVM classifier. The main contributions are concluded as follows:

• Considering the nonlinearities exhibited in water chillers, KPCA is more suitable for feature extraction in comparison to the conventional PCA method. The overall fault diagnosis accuracy could be improved by about 5% using KPCA-LSSVM classifier as compared to the PCA-LSSVM classifier.

• In LSSVM classifier, its regularization parameter, γ, and kernel bandwidth, σ, play an essential role on the fault diagnosis performance. GSA is a promising tool to optimize the parameters in LSSVM classifier with a higher fault diagnosis accuracy and a shorter convergence time as compared to the PSO.

• 95.7% overall fault diagnosis accuracy could be achieved using the GSA optimized KPCA-LSSVM fault diagnosis method. In terms of the faults of ReduCF, RefLeak, ExcsOil and NonCon, 100% of fault samples were able to be correctively identified. The proposed fault diagnosis method is a promising candidate for realizing chiller fault diagnosis and can be implemented for monitoring the practical chiller operation.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

YX and QD contributed to conception and design of the study. JZ organized the database. YX wrote the first draft of the manuscript. AJ revised the manuscript. QD and AJ supervised this research. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This research was supported by the Natural Science Foundation of Zhejiang Province (Project Nos LQ19E060007 and LY20F030010). The financial supports for the Fundamental Research Funds for the Provincial Universities of Zhejiang (No. GK209907299001-309) are also gratefully acknowledged.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Borin, A., Ferrão, M. F., Mello, C., Maretto, D. A., and Poppi, R. J. (2006). Least-squares Support Vector Machines and Near Infrared Spectroscopy for Quantification of Common Adulterants in Powdered Milk. Analytica Chim. Acta 579, 25–32. doi:10.1016/j.aca.2006.07.008

CrossRef Full Text | Google Scholar

Chang, C.-C., and Lin, C.-J. (2011). Libsvm. ACM Trans. Intell. Syst. Technol. 2 (3), 1–27. doi:10.1145/1961189.1961199

CrossRef Full Text | Google Scholar

Chen, Y., and Lan, L. (2009). A Fault Detection Technique for Air-Source Heat Pump Water Chiller/heaters. Energy and Buildings 41, 881–887. doi:10.1016/j.enbuild.2009.03.007

CrossRef Full Text | Google Scholar

Chih-Wei Hsu, H., and Chih-Jen Lin, L. (2002). A Comparison of Methods for Multiclass Support Vector Machines. IEEE Trans. Neural Netw. 13, 415–425. doi:10.1109/72.991427

PubMed Abstract | CrossRef Full Text | Google Scholar

Comstock, M. C., Braun, J. E., and Bernhard, R. (1999). Development of Analysis Tools for the Evaluation of Fault Detection and Diagnostics in Chillers. West Lafayette, Indiana: Purdue University.

Google Scholar

Du, Z., Jin, X., and Wu, L. (2007). Fault Detection and Diagnosis Based on Improved PCA with JAA Method in VAV Systems. Building Environ. 42, 3221–3232. doi:10.1016/j.buildenv.2006.08.011

CrossRef Full Text | Google Scholar

Enteria, N., and Mizutani, K. (2011). The Role of the Thermally Activated Desiccant Cooling Technologies in the Issue of Energy and Environment. Renew. Sustain. Energ. Rev. 15, 2095–2122. doi:10.1016/j.rser.2011.01.013

CrossRef Full Text | Google Scholar

Fan, C., Yan, D., Xiao, F., Li, A., An, J., and Kang, X. (2021). Advanced Data Analytics for Enhancing Building Performances: From Data-Driven to Big Data-Driven Approaches. Build. Simul. 14, 3–24. doi:10.1007/s12273-020-0723-1

CrossRef Full Text | Google Scholar

Gao, Y., Liu, S., Li, F., and Liu, Z. (2016). Fault Detection and Diagnosis Method for Cooling Dehumidifier Based on LS-SVM NARX Model. Int. J. Refrigeration 61, 69–81. doi:10.1016/j.ijrefrig.2015.08.020

CrossRef Full Text | Google Scholar

Guo, Y., Li, G., Chen, H., Wang, J., Guo, M., Sun, S., et al. (2017). Optimized Neural Network-Based Fault Diagnosis Strategy for VRF System in Heating Mode Using Data Mining. Appl. Therm. Eng. 125, 1402–1413. doi:10.1016/j.applthermaleng.2017.07.065

CrossRef Full Text | Google Scholar

Guo, Y., Tan, Z., Chen, H., Li, G., Wang, J., Huang, R., et al. (2018). Deep Learning-Based Fault Diagnosis of Variable Refrigerant Flow Air-Conditioning System for Building Energy Saving. Appl. Energ. 225, 732–745. doi:10.1016/j.apenergy.2018.05.075

CrossRef Full Text | Google Scholar

Han, H., Cao, Z., Gu, B., and Ren, N. (2010). PCA-SVM-Based Automated Fault Detection and Diagnosis (AFDD) for Vapor-Compression Refrigeration Systems. Hvac&r Res. 16, 295–313. doi:10.1080/10789669.2010.10390906

CrossRef Full Text | Google Scholar

Han, H., Cui, X., Fan, Y., and Qing, H. (2019). Least Squares Support Vector Machine (LS-SVM)-based Chiller Fault Diagnosis Using Fault Indicative Features. Appl. Therm. Eng. 154, 540–547. doi:10.1016/j.applthermaleng.2019.03.111

CrossRef Full Text | Google Scholar

Han, H., Gu, B., Kang, J., and Li, Z. R. (2011). Study on a Hybrid SVM Model for Chiller FDD Applications. Appl. Therm. Eng. 31, 582–592. doi:10.1016/j.applthermaleng.2010.10.021

CrossRef Full Text | Google Scholar

Huang, R., Liu, J., Chen, H., Li, Z., Liu, J., Li, G., et al. (2018). An Effective Fault Diagnosis Method for Centrifugal Chillers Using Associative Classification. Appl. Therm. Eng. 136, 633–642. doi:10.1016/j.applthermaleng.2018.03.041

CrossRef Full Text | Google Scholar

IEA (2018). The Future of Cooling. Paris, France: International Energy Agency.

Google Scholar

IEA (2019). The Future of Cooling in China. Paris, France: International Energy Agency.

Google Scholar

Katipamula, S., and Brambley, M. (2005a). Review Article: Methods for Fault Detection, Diagnostics, and Prognostics for Building Systems-A Review, Part I. Hvac&r Res. 11, 3–25. doi:10.1080/10789669.2005.10391123

CrossRef Full Text | Google Scholar

Katipamula, S., and Brambley, M. (2005b). Review Article: Methods for Fault Detection, Diagnostics, and Prognostics for Building Systems-A Review, Part II. Hvac&r Res. 11, 169–187. doi:10.1080/10789669.2005.10391133

CrossRef Full Text | Google Scholar

Lee, J.-M., Yoo, C., Choi, S. W., Vanrolleghem, P. A., and Lee, I.-B. (2004). Nonlinear Process Monitoring Using Kernel Principal Component Analysis. Chem. Eng. Sci. 59, 223–234. doi:10.1016/j.ces.2003.09.012

CrossRef Full Text | Google Scholar

Lee, K.-P., Wu, B.-H., and Peng, S.-L. (2019). Deep-learning-based Fault Detection and Diagnosis of Air-Handling Units. Building Environ. 157, 24–33. doi:10.1016/j.buildenv.2019.04.029

CrossRef Full Text | Google Scholar

Li, G., Hu, Y., Chen, H., Shen, L., Li, H., Hu, M., et al. (2016). An Improved Fault Detection Method for Incipient Centrifugal Chiller Faults Using the PCA-R-SVDD Algorithm. Energy and Buildings 116, 104–113. doi:10.1016/j.enbuild.2015.12.045

CrossRef Full Text | Google Scholar

Li, S., and Wen, J. (2014). A Model-Based Fault Detection and Diagnostic Methodology Based on PCA Method and Wavelet Transform. Energy and Buildings 68, 63–71. doi:10.1016/j.enbuild.2013.08.044

CrossRef Full Text | Google Scholar

Li, X., Yang, Y., Pan, H., Cheng, J., and Cheng, J. (2019). A Novel Deep Stacking Least Squares Support Vector Machine for Rolling Bearing Fault Diagnosis. Comput. Industry 110, 36–47. doi:10.1016/j.compind.2019.05.005

CrossRef Full Text | Google Scholar

Liang, J., and Du, R. (2007). Model-based Fault Detection and Diagnosis of HVAC Systems Using Support Vector Machine Method. Int. J. Refrigeration 30, 1104–1114. doi:10.1016/j.ijrefrig.2006.12.012

CrossRef Full Text | Google Scholar

Lu, C., Chen, J., Hong, R., Feng, Y., and Li, Y. (2016). Degradation Trend Estimation of Slewing Bearing Based on LSSVM Model. Mech. Syst. Signal Process. 76-77, 353–366. doi:10.1016/j.ymssp.2016.02.031

CrossRef Full Text | Google Scholar

Rashedi, E., Nezamabadi-pour, H., and Saryazdi, S. (2009). GSA: A Gravitational Search Algorithm. Inf. Sci. 179, 2232–2248. doi:10.1016/j.ins.2009.03.004

CrossRef Full Text | Google Scholar

Safaeipour, H., Forouzanfar, M., and Casavola, A. (2021). A Survey and Classification of Incipient Fault Diagnosis Approaches. J. Process Control. 97, 1–16. doi:10.1016/j.jprocont.2020.11.005

CrossRef Full Text | Google Scholar

Shin, Y., Karng, S. W., and Kim, S. Y. (2014). Indoor Unit Fault Detector for a Multi-Split VRF System in Heating Mode. Int. J. Refrigeration 40, 152–160. doi:10.1016/j.ijrefrig.2013.11.009

CrossRef Full Text | Google Scholar

Sun, K., Li, G., Chen, H., Liu, J., Li, J., and Hu, W. (2016). A Novel Efficient SVM-Based Fault Diagnosis Method for Multi-Split Air Conditioning System's Refrigerant Charge Fault Amount. Appl. Therm. Eng. 108, 989–998. doi:10.1016/j.applthermaleng.2016.07.109

CrossRef Full Text | Google Scholar

Sun, L., Wu, J., Jia, H., and Liu, X. (2017). Research on Fault Detection Method for Heat Pump Air Conditioning System under Cold Weather. Chin. J. Chem. Eng. 25, 1812–1819. doi:10.1016/j.cjche.2017.06.009

CrossRef Full Text | Google Scholar

Suykens, J. A. K., and Vandewalle, J. (1999). Least Squares Support Vector Machine Classifiers. Neural Process. Lett. 9, 293–300. doi:10.1023/a:1018628609742

CrossRef Full Text | Google Scholar

Wang, H., Peng, M.-J., Wesley Hines, J., Zheng, G.-y., Liu, Y.-k., and Upadhyaya, B. R. (2019). A Hybrid Fault Diagnosis Methodology with Support Vector Machine and Improved Particle Swarm Optimization for Nuclear Power Plants. ISA Trans. 95, 358–371. doi:10.1016/j.isatra.2019.05.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z., Wang, L., Liang, K., and Tan, Y. (2018). Enhanced Chiller Fault Detection Using Bayesian Network and Principal Component Analysis. Appl. Therm. Eng. 141, 898–905. doi:10.1016/j.applthermaleng.2018.06.037

CrossRef Full Text | Google Scholar

Wong, P. K., Yang, Z., Vong, C. M., and Zhong, J. (2014). Real-time Fault Diagnosis for Gas Turbine Generator Systems Using Extreme Learning Machine. Neurocomputing 128, 249–257. doi:10.1016/j.neucom.2013.03.059

CrossRef Full Text | Google Scholar

Xia, Y., Ding, Q., Jing, N., Tang, Y., Jiang, A., and Jiangzhou, S. (2021a). An Enhanced Fault Detection Method for Centrifugal Chillers Using Kernel Density Estimation Based Kernel Entropy Component Analysis. Int. J. Refrigeration 129, 290–300. doi:10.1016/j.ijrefrig.2021.04.019

CrossRef Full Text | Google Scholar

Xia, Y., Ding, Q., Li, Z., and Jiang, A. (2021b). Fault Detection for Centrifugal Chillers Using a Kernel Entropy Component Analysis (KECA) Method. Build. Simul. 14, 53–61. doi:10.1007/s12273-019-0598-1

CrossRef Full Text | Google Scholar

Xu, Y., Chen, N., Shen, X., Xu, L., Pan, Z., and Pan, F. (2021a). Proposal and Experimental Case Study on Building Ventilating Fan Fault Diagnosis Based on Cuckoo Search Algorithm Optimized Extreme Learning Machine. Sustainable Energ. Tech. Assessments 45, 100975. doi:10.1016/j.seta.2020.100975

CrossRef Full Text | Google Scholar

Xu, Y., Mao, C., Huang, Y., Shen, X., Xu, X., and Chen, G. (2021b). Performance Evaluation and Multi-Objective Optimization of a Low-Temperature CO₂ Heat Pump Water Heater Based on Artificial Neural Network and New Economic Analysis. Energy 216, 119232. doi:10.1016/j.energy.2020.119232

CrossRef Full Text | Google Scholar

Yan, K., Shen, W., Mulumba, T., and Afshari, A. (2014). ARX Model Based Fault Detection and Diagnosis for Chillers Using Support Vector Machines. Energy and Buildings 81, 287–295. doi:10.1016/j.enbuild.2014.05.049

CrossRef Full Text | Google Scholar

Yu, K., and Cheng, Y. (2006). Discriminating the Genuineness of Chinese Medicines Using Least Squares Support Vector Machines. Chin. J. Anal. Chem. 34, 561–564. doi:10.1016/s1872-2040(06)60029-7

CrossRef Full Text | Google Scholar

Yu, L., Chen, H., Wang, S., and Lai, K. K. (2009). Evolving Least Squares Support Vector Machines for Stock Market Trend Mining. IEEE Trans. Evol. Computat. 13, 87–102. doi:10.1109/tevc.2008.928176

CrossRef Full Text | Google Scholar

Yu, X., Wu, J., and Gao, Y. (2020). Research on Refrigerant Leakage Identification for Heat Pump System Based on PCA-SVM Models. CIESC J. 71, 3151–3164. doi:10.11949/0438-1157.20191139

CrossRef Full Text | Google Scholar

Zhang, W., Niu, P., Li, G., and Li, P. (2013). Forecasting of Turbine Heat Rate with Online Least Squares Support Vector Machine Based on Gravitational Search Algorithm. Knowledge-Based Syst. 39, 34–44. doi:10.1016/j.knosys.2012.10.004

CrossRef Full Text | Google Scholar

Zhang, X., Qiu, D., and Chen, F. (2015). Support Vector Machine with Parameter Optimization by a Novel Hybrid Method and its Application to Fault Diagnosis. Neurocomputing 149, 641–651. doi:10.1016/j.neucom.2014.08.010

CrossRef Full Text | Google Scholar

Zhao, Y.-P., Wang, J.-J., Li, X.-Y., Peng, G.-J., and Yang, Z. (2020). Extended Least Squares Support Vector Machine with Applications to Fault Diagnosis of Aircraft Engine. ISA Trans. 97, 189–201. doi:10.1016/j.isatra.2019.08.036

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Y., Wang, S., and Xiao, F. (2013). Pattern Recognition-Based Chillers Fault Detection Method Using Support Vector Data Description (SVDD). Appl. Energ. 112, 1041–1048. doi:10.1016/j.apenergy.2012.12.043

CrossRef Full Text | Google Scholar

Glossary

σ kernel parameter

λ regularization parameter

b bias

e predicted error

α lagrange multiplier

y output

a acceleration in GSA

v velocity in GSA

x the position in GSA

F force in GSA

M_a active gravitational mass in GSA

M_p passive gravitational mass in GSA

M_i inertial mass in GSA

R euclidian distance in GSA

K(⋅) kernel function

Φ(⋅), φ(⋅) mapping function

x input vector

y output vector

ω weight vector

α orthonormal eigenvectors

C covariance matrix

K kernel matrix

A/C air conditioning

AHU air handling unit

CPV cumulative percent variance

DX direct expansion

FDD fault detection and diagnosis

GSA gravitational search algorithm

HVAC heating, ventilation and air conditioning

KPCA kernel principal component analysis

LSSVM least squares support vector machine

PC principal component

PCA principal component analysis

PSO particle swarm optimization

SVM support vector machine

VRF variable refrigerant flow