- State Key Laboratory of Reliability and Intelligence of Electrical Equipment, Hebei University of Technology, Tianjin, China
The increasing penetration of distributed energy resources and flexible electrical loads makes hybrid AC/DC distribution networks become a crucial trend for future modern distribution networks. To increase the flexibility and energy efficiency of hybrid AC/DC distribution networks, a decentralized and multi-objective coordinated optimization method by considering different control means is proposed. The salient feature of this method is that it comprehensively and properly models the full variety of possible control means (i.e., active/reactive power of distributed generation, on load tap changers, flexible distribution switch, voltage source converter). The abundant means are utilized to optimize operational cost, voltage deviation and network losses simultaneously. Then, a fully decentralized optimization method based on alternating direction multiplier method (ADMM) is proposed. The hybrid AC/DC distribution networks are divided into several sub-networks. Flexible interconnected electronic devices are utilized to transfer energy between different sub-networks to achieve the efficient and flexible utilization of controllable resources in hybrid AC/DC distribution networks. Finally, the proposed coordinated optimization method is tested on a modified dual IEEE 33-node network to demonstrate its effectiveness and advantages, and the performance of the centralized method and our proposed method is compared.
Introduction
In recent years, distributed energy resources, especially photovoltaic (PV) systems and distributed energy storage systems, and flexible electrical loads, such as electric vehicles, are continuously connected to distribution networks (Eajal et al., 2016; Liu et al., 2018). The physical form of distribution networks is experiencing a fast transition (Zhang et al., 2018; Jiang, 2021). Hybrid AC/DC distribution networks with the high-efficiency consumption and high-proportion access of new energy have become a crucial trend for future modern distribution networks. Moreover, the continuous development of power electronic technology brings flexible controllable electronic devices into distribution networks, such as inverter-based distributed generator, static var generator (SVG), flexible interconnection device, et al. (Ampofo and Myrzik, 2021; Cao et al., 2021). Compared to traditional controllers, controllable electronic devices with fast response, low operational cost and flexible control mode bring effective technical support the operation of distribution networks (Zhao et al., 2018; Qiao and Ma, 2020; Zhao et al., 2021). To utilize all the controllable devices to provide the ancillary service for operation optimization, it is necessary to study a new coordinated operation method for hybrid AC/DC distribution system considering multiple control means.
Extensive studies address the coordinated optimization problem in hybrid AC/DC distribution networks, which can be divided into three categories: centralized scheme (Capitanescu et al., 2014; Chamana and Chowdhury, 2018; Chen et al., 2019), distributed scheme (Wang et al., 2018a; Chai et al., 2018; Kouveliotis-Lysikatos et al., 2019), and decentralized scheme (Calderaro et al., 2014; Antoniadou-Plytaria et al., 2017; Xu and Wu, 2020). In centralized scheme, the control center needs to collect all the measurement data (i.e., the state of all nodes) to make a decision. In (Capitanescu et al., 2014), based on a centralized control, a comprehensive coordinated voltage management approach utilizing remotely controlled switches, on-load tap changers (OLTCs) and shunt capacitor banks while maximizing distributed generation’s (DG) active power outputs is proposed. With the scale of distribution networks becoming larger, centralized control cannot meet control requirements due to the heavy communication burden and poor scalability. However, in distributed control, there is not a single central controller, but instead there are multiple controllers. Each controller has its own specific object. All controllers coordinate together to reach a collective decision, which only requires exchange of information among neighboring controllers (e.g., through wireless or power line communications), and each local controller calculates its fair contribution to meet the system request. Zeraati et al. (2019) adopts a distributed voltages control strategy composed of two consistent algorithms, which effectively utilizes plug-in electric vehicles and PV. In (Robbins et al., 2013), a two-stage architecture for voltage control is proposed to manage DG’s reactive power, and the distributed control coordinates the power distribution among the nodes of the distribution networks to achieve voltage regulation. Moreover, a state between centralized and distributed control is called decentralized control. A typical example of decentralized control is the network partitioning into regions. Each region is optimized internally and exchanges only the key data of coupled lines and nodes with adjacent regions to complete the control strategy of the whole distribution networks. In (Wang et al., 2018b), a decentralized voltage control method based on a multi-agent system (MAS) with built-in incentives for various participants in distribution networks is proposed, and peer agents calculate voltage sensitivities via local and adjacent measurements in a fully decentralized approach. In (Wang et al., 2018c), a decentralized optimization control method based on sensitivity analysis and decentralized power regulation is proposed to allowing DGs to provide auxiliary services of voltage regulation. Considering the scale and flexibility of future distribution networks, decentralized and distributed architectures are feasible ways to relieve the burden of computation and communication, and to improve speed of control systems. Furthermore, with the number of independent system operators (ISOs) increasing in the future electricity market, decentralized schemes can deal with the competition among ISOs validly in a peer-to-peer frame. Thus, decentralized control is the promising way of operation optimization problems in future hybrid AC/DC distribution networks.
Most previous studies generally address the coordinated optimization problems of hybrid AC/DC distribution networks by considering only a subset among the available control means (Liu et al., 2012; Liu et al., 2019). In (Kim et al., 2015), shunt capacitors, OLTCs and DG’s reactive power are dispatched hourly for reducing network losses and improving voltage quality of distribution feeders. In (Zhang et al., 2018), a coordinated real-time voltage regulation method for hybrid AC/DC medium distribution networks is proposed to make full use of converter-based controllable devices, such as DGs, energy storage systems, and the voltage source converters (VSCs). Moreover, flexible distribution switch (FDS) as a novel power electronic device with high controllability can accurately regulate the active and reactive power flow of the connected feeders, making distribution network gradually transform from passive network to flexible distribution network. As a flexible and controllable medium, FDS has a huge impact on the optimization of voltage and power coordination in distribution networks (Wang et al., 2017; Zhang et al., 2019). In (Ji et al., 2017), a feeder load optimization model based on multi-terminal FDS is established to alleviate feeder load imbalance and reduce network losses of distribution networks. Cao et al. (2016) optimizes FDS with network reconfiguration to achieve optimal operation of the distribution network. However, few optimization methods consider FDS together with other control means in hybrid AC/DC distribution networks. FDS and VSC can achieve flexible energy transmission between AC/AC network and AC/DC network, realizing real-time, fast, sensitive and smooth power control. Based on their coordination and optimization methods, they will effectively realize the economic operation of AC and DC distribution networks and greatly improve distribution network flexibility and reliability.
In this paper, to target the above research gaps, a decentralized multi-objective coordinated optimization method in hybrid AC/DC flexible distribution networks is proposed. The method optimizes operational cost, voltage deviation and network losses simultaneously in a decentralized architecture, considering multiple control means including FDS, VSC, PV, etc. The major contributions of the paper are as follows: 1) The salient contribution of the proposed method is that it comprehensively and properly models the full variety of possible control means (i.e., PVs, SVG, OLTC, FDS, VSC) in hybrid AD/DC distribution networks. Various traditional and modern control means are utilized simultaneously, increasing asset utilization, economy and flexibility of distribution networks. 2) A decentralized coordinated optimization is proposed to pursue the safe, economic and flexible operation of hybrid AC/DC distribution networks. Compared with traditional centralized optimization, the proposed method releases the communication and computation burden, and increase the speed of control systems.
The reminder of this paper is organized as follows: Multi-Objective Optimization Model for Hybrid AC/DC Flexible Distribution Networks section presents the multi-objective optimization model in hybrid AC/DC flexible distribution networks; A Decentralized Coordinated Optimization Method Based on ADMM section develops a decentralized operation method considering the energy transfer between different districts; Case studies are presented in Case Studies section, while Conclusion section concludes this paper.
Multi-Objective Optimization Model for Hybrid AC/DC Flexible Distribution Networks
The operation optimization model proposed in this paper take into account the safety and economy of the distribution network operation. By combining network losses, nodal voltage deviation and regulation cost in the cost form, the multi-objective problem is transformed into a single-objective problem through a normalization function. The objective function is described as:
where F is the objective function value;
Network losses
Voltage deviation
Operational cost
Furthermore, the operation optimization model established in this paper needs to satisfy the constraints of power flow, VSC, FDS, OLTC, and PV, as well as constraints of secure operation. The constraints can be described as follows:
Power Flow Constraints
The hybrid AC/DC distribution network adopts the DistFlow model. AC and DC power flow constraints are formulated as Eqs 6–11 respectively.
where,
VSC Constraints
Considering active losses of VSC, the VSC branch constraints and capacity constraints are:
where
FDS Constraints
The power flow of FDS multi-terminal can be controlled flexibly based on the back-to-back VSC configuration of FDS. The FDS constraints are:
where
OLTC Constraints
The OLTC transformer ratio can be expressed as
where
PV Constraints
The PV should satisfy the power and capacity constraints. In this paper, the power factor of the PV model in the AC region is constant. The PV constraints are
where
Secure Operation Constraints
where,
A Decentralized Coordinated Optimization Method Based on ADMM
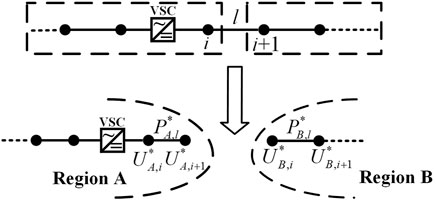
In this paper, the hybrid AC/DC distribution network is divided into sub-regions. Each region exchanges boundary information with adjacent regions based on ADMM algorithm and optimizes its own power flow based on the second-order cone planning (SOCP). The sub-regions can be further divided according to the actual operational requirements. Generally, in the hybrid AC/DC distribution networks, the branch with VSC is a typical coupling branch. For example, as shown in Figure 1, the coupling branch l between two regions are copied into two sub-regions. The constraints of each sub-region need to satisfy the boundary coupling conditions, as shown in Equations 21, 22.
where
After partition, the global optimization is transformed into multiple sub-region internal optimization. Based on ADMM, each region exchanges the boundary information, updates the global and pairwise variables, adjusts penalty factors according to the calculated primal residuals and dual residuals. The augmented Lagrangian method is used to establish the sub-region optimization model. The coupling equation constraint between regions is equivalent to the linear coupling equation constraint in the ADMM algorithm. The augmented Lagrangian function as shown in Eq. 23.
where
Each region calculates the corresponding primal residuals and dual residuals based on the boundary data of its own and adjacent regions, and then transmits the calculation results to adjacent regions via distributed communication lines to complete the interconnection of information between regions. The calculation formula of the primal residuals and the dual residual is
where n represents sub-region n.
In ADMM, an inappropriate penalty factor will affect the algorithm convergence. Therefore, to improve the performance of ADMM, an automatic adjustment of the penalty factor is used to make the penalty factor more adaptive to the solution of the iterative calculation and to reduce the effect of the initial penalty factor
where
The update iterations are continuously performed between regions until the maximum value of the primal residual and the dual residual is less than the convergence accuracy
where
The optimization problem of hybrid AC/DC distribution networks is a non-convex problem, which needs to convert into a convex problem based on second-order cone relaxation. The auxiliary variable is introduced to replace the squared term in the original equations, as shown in Equation 29.
The quadratic term in the objective function is replaced in order to linearize it. Since an absolute value term is contained in Equation 3, the auxiliary variable
The conical transformation of the power flow constraint conditions of Equations 5–7 is as follows
Using the second-order cone relaxation treatment Eq. 33, we have
The corresponding relaxation treatment in the DC region is the same as above.
For the circle constraints in Equations 14, 17, polygonal constraints can be used instead, using a description of the positive octagonal constraint as shown in Equation 35, and the same for the FDS constraints.
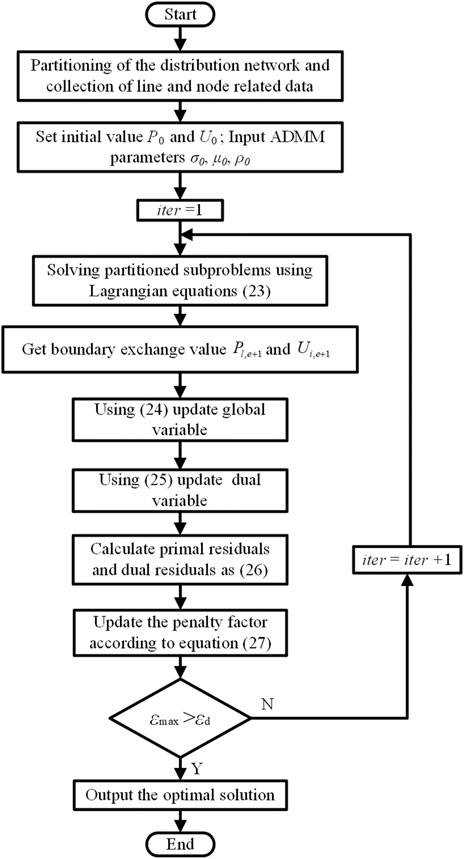
Taking the update iteration between regions A and B as an example, the flow chart of the proposed decentralized optimization method is shown in Figure 2.
Case Studies
Test System Parameters
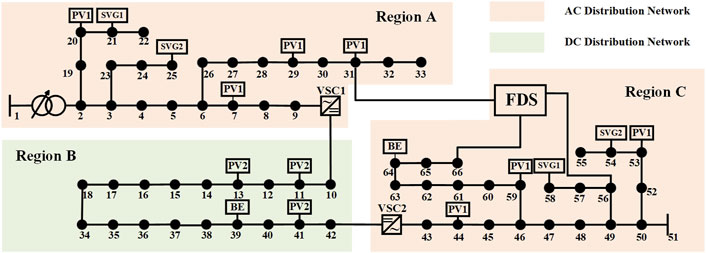
Case studies are carried out at a modified dual IEEE 33-bus hybrid AC/DC distribution network, as shown in Figure 3. The simulation has 66 nodes, VSC1 with constant voltage control is installed at Node 9–10, and VSC2 with PQ control is installed at Node 42–43. There is a three-terminal FDS in our system, with Terminal 1 at Node 31, Terminal 2 at Node 56 and Terminal 3 at Node 66. The hybrid AC/DC distribution network is divided into three regions. The node set of Region A is {1, 2, 3, ……,9, 19, 20, 21, ......33}, the node set of Region B is {10, 11, ......,18, 34, 35......42}, The node set of Region C is {43, 44, ……,66}. The AC reference voltage is 12.66 kV and DC reference voltage is ±10 kV. Node 1 and Node 51 are the slack nodes of region A and region C respectively. OLTC is installed on between Node1 and Node 2, with tap 1 ± 2*1.5%. The safe range of node voltage is [0.95–1.05] p.u., and the optimal voltage range is [0.985–1.015] p.u.. When the nodal voltage exceeds the safe range, the control system starts. The parameters of VSC and FDS, and SVG are shown in Table 1. In the ADMM, the initial values of σ0 and μ0 are set to 0, and the penalty factor ρ0 and the convergence accuracy ε0 are respectively 0.2 and 10–3. The weight coefficients
Simulation Analysis
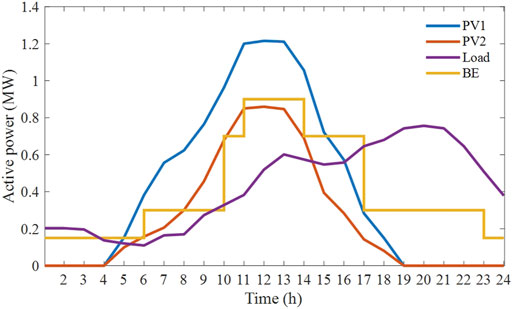
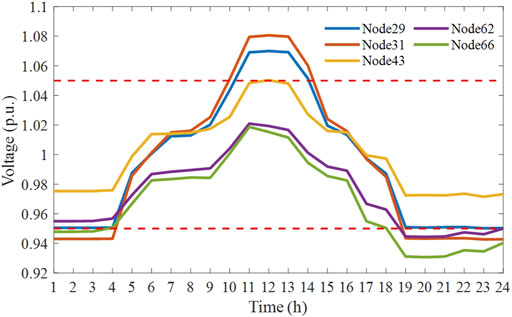
A 24 h simulation has been carried out here. Figure 5 shows the voltage profiles of five representational Nodes (Node 29, 31, 43, 62 and 66) without control. It shows that the voltage excursions occur during 10:00–14:00 and 18:00–4:00 respectively. In order to verify the performance of the proposed decentralized optimization method in our paper, simulations are carried out in five different cases at t = 12:00 and t = 20:00, when the voltage exceeds the upper and lower limit respectively. The five cases are set as follows:
Case 1: No control measures have been taken;
Case 2: Control means include VSCs and PV curtailment.
Case 3: Control means include VSCs, PV curtailment and FDS.
Case 4: Control means include VSCs, PV curtailment, FDS and OLTC.
Case 5: Based on Case 3, change the parameters of VSC1 into the active power limits ±2.5 MW, the reactive power limits ±1.5 Mvar and the capacity 2.5 MVA.
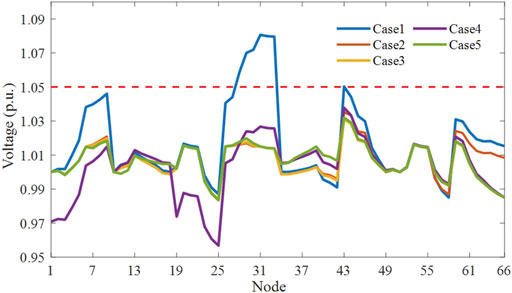
Taking t = 12:00 as an example to analyze voltage profiles exceeding the upper limits, the voltage profiles of the above five cases at t = 12:00 are shown in Figure 6. It can be seen that all the cases can solve the voltage excursions effectively. VSC capacity and FDS can affect the optimization performance. As shown in Figure 6, Compared the results of Case 3 and Case 5, it can be found that the nodal voltage of AC nodes are almost the same but the nodal voltage of major DC nodes (Node 34-Node 42) in Case 5 is higher than that in Case 3. This is because Case 5 with high-capacity VSC1 increases the active power transmitted between Region A and Region B, reduces the PV curtailment in Region B and then raises the voltage profile in Region B. Furthermore, the PV curtailment in Case 2–5 is 1.85, 1.41, 0.02, and 0.97 MW respectively. Compared with Case 2 and Case 3, the PV curtailment in Region A without FDS is 1.47 MW, and PV curtailment with FDS is reduced by 0.44 MW. It shows that FDS can transfer energy between sub-regions flexibly and increase energy efficiency in hybrid AC/DC flexible distribution networks.
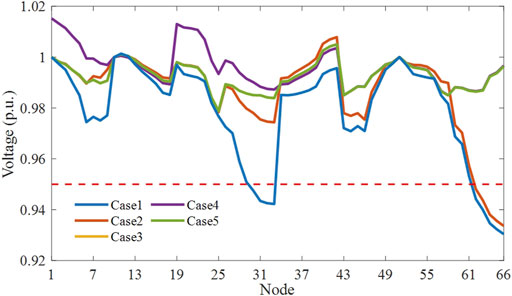
Taking t = 20:00 as an example to analyze voltage profiles exceeding the lower limits, the voltage profiles of the different cases are shown in Figure 7. As shown in Figure 7, there are still some nodes (Node 61–Node 66) with voltage excursions in Case 2, because both the slack node in Region C and the VSC with Constant voltage control are far from these nodes. The voltage profiles in Region B and Region C restrict more active power transfer into these nodes.
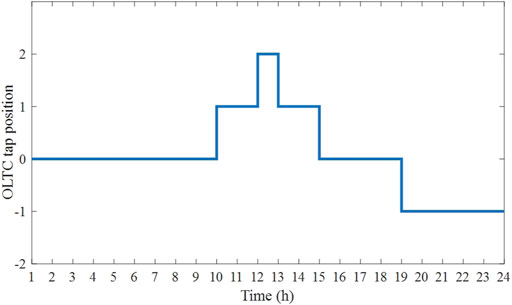
The 24-h simulation is carried out for Case 4 and OLTC tap position is obtained as shown in Figure 8. It can be found that OLTC adjusts the tap position upward during 10:00–14:00, and adjusts the tap position downward during 20:00–24:00. OLTC can regulate the voltage profile of the whole Region A. Comparing with Case 3 and Case 4 at 12:00, it can be seen that Case 3 cuts PVs to ensure voltage profile in a reasonable range. However, the OLTC in Case 4 adjusts the voltage profile to a lower lever so that the PV curtailment is reduced, avoiding the waste of renewable resources. Similarly, comparing with Case 3 and Case 4 at 20:00, OLTC lifts the voltage profile to decrease active power losses and further reduce the operational cost.
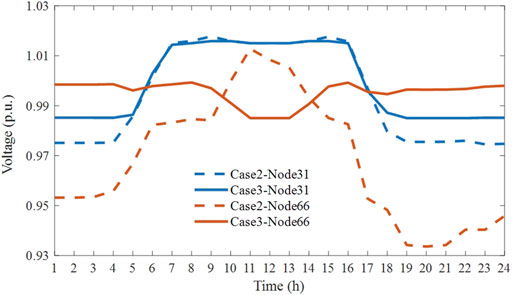
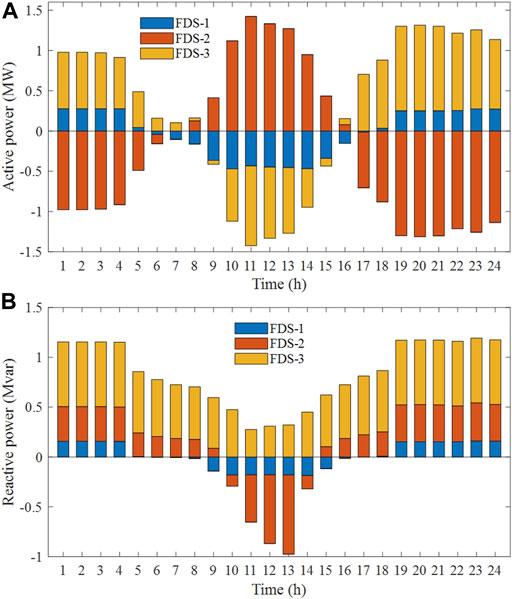
To further prove FDS’s influence of optimization performance, Figure 9 shows the voltage optimization of Node 31 and Node 66 in Case 2 and Case 3. It can be concluded that voltage of Node 31 is optimized within the voltage optimization range [0.985–1.015] by FDS. Moreover, the FDS improves the voltage profile at Node 66 obviously, especially controlling voltage from 0.9336 p.u. to 0.9964 p.u at 20:00. In order to explore the real-time regulation role of the FDS and to analyze the mechanism of its role in coordinating power flow, the active and reactive power output of the FDS in Case 3 is shown in Figure 10. The positive value of the active output means that FDS sends out active power. On the contrary, the active power is absorbed. The same applies to the reactive power. During the night, in order to maintain voltage stability, FDS Terminal 1 and 3 need to inject an amount of active power into the grid, and Terminal 2 absorbs active power. During the period of 9:00–16:00, Terminal 1 and 3 start to absorb active power to reduce PV curtailment. The FDS reactive power output depends on the system voltage and power demand. The FDS can produce or absorb reactive power, which is equivalent to a reactive power compensation device. With FDS, the total power output of the SVG in the grid all day is reduced by 42.7% compared to the original. In this way, control system may reduce the installment number of SVG to save the investment.
Comparison of Centralized and Decentralized Methods
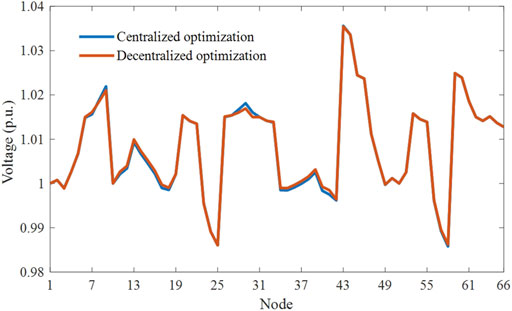
To compare the optimization results in our proposed decentralized method and traditional centralized methods, voltage profiles in Case 2 at 11:00 of different methods are shown in Figure 11. It is obvious that the voltage profiles of the decentralized and centralized methods are almost the same. The maximum error appears at Node 29, where the centralized result is 1.0181 p.u. and decentralized result is 1.0169 p.u., with the error 0.12%, verifying the accuracy of the proposed method in this paper. Furthermore, as shown in Table 2, the network losses, voltage deviation and PV curtailment of different sub-regions are listed. The error of these three parts in the hybrid AC/DC distribution networks are1.7, 3.7 and 0.6%, respectively. Therefore, the small errors demonstrate the effectiveness of the proposed decentralized method.
Compared with the centralized method, the decentralized method reduces the communication and calculation burden. For the modified dual IEEE 33-node distribution network in our paper, with topology and line parameters known, the centralized method needs to collect all the measurement data of the whole distribution network. The required data includes 187 parameters totally. In contrast, the decentralized control in this paper divides the hybrid AC/DC distribution network into three regions with its own control system. The three control systems measure data independently, with 72 parameters of Region A, 36 parameters of Region B and 72 parameters of Region C, respectively. Moreover, the adjacent regions exchange 4 parameters of the contact line with each other. In addition, the centralized method needs to solve an optimization problem with 34 optimization variables. In the proposed decentralized method, the number of optimization variables in Region C which has the most controllable resources, is 17. Moreover, the three control systems solve its own optimization problem in parallel. Accordingly, the proposed decentralized method reduces the communication and calculation burden obviously.
Conclusion
In this paper, a decentralized multi-objective coordinated optimization method in hybrid AC/DC flexible distribution networks is proposed. To optimize operational cost, voltage deviation and network losses simultaneously, a multi-objective coordinated optimization model is proposed by considering different control means. The performance and efficiency of the proposed model is illustrated using numerous cases, which shows that:
1) The proposed multi-objective coordinated optimization comprehensively and properly models the full variety of possible control means, including PV, FDS, VSC, SVG, and OLTC. Traditional and modern electronic means with different characteristics are considered simultaneously by optimizing operational cost of the whole hybrid AC/DC distribution networks. The coordination of different control resources can increase the asset utilization and decreases the investment of hybrid AC/DC distribution networks;
2) Flexible interconnection devices like VSC and FDS are utilized in the proposed method, which can transfer energy between different regions flexibly. With VSCs and FDS, the PV curtailment is decreased by 23.8%. The reactive power regulation ability of flexible interconnection devices reduces the demand of SVG by 42.7%, decreasing the SVG investment. Therefore, flexible interconnection devices can increase the efficiency and flexibility of hybrid AC/DC distribution networks;
3) A decentralized optimization based on ADMM is applied to divide the distribution network into several sub-regions, and each sub-region optimizes itself by exchanging information with adjacent sub-regions. The decentralized method obtains almost the same strategies with the traditional centralized method, but only requires 39% of communication and calculation amount in the centralized method.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Author Contributions
XW contributed toward supervision, conceptualization, and writing—review and editing. LG contributed toward methodology, software, data curation, and writing—original draft. DL contributed toward writing—review and editing.
Funding
This work was supported by the Natural Science Foundation of Hebei Province (Grant: E2019202146 and E2021202053), China Postdoctoral Science Foundation (Grant: 2019M660966 and 2021T140174) and the Hebei Education Department Foundation (Grant: BJ2020036).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ampofo, D. O., and Myrzik, J. M. A. (2021). Autonomous Adaptive Q(U) Control for Distributed Generation in Weak Medium‐voltage Distribution Grids. IET Energ. Syst. Integration 3 (2), 158–171. doi:10.1049/esi2.12010
Antoniadou-Plytaria, K. E., Kouveliotis-Lysikatos, I. N., Georgilakis, P. S., and Hatziargyriou, N. D. (2017). Distributed and Decentralized Voltage Control of Smart Distribution Networks: Models, Methods, and Future Research. IEEE Trans. Smart Grid 8 (6), 2999–3008. doi:10.1109/TSG.2017.2679238
Calderaro, V., Conio, G., Galdi, V., Massa, G., and Piccolo, A. (2014). Optimal Decentralized Voltage Control for Distribution Systems with Inverter-Based Distributed Generators. IEEE Trans. Power Syst. 29 (1), 230–241. doi:10.1109/TPWRS.2013.2280276
Cao, W., Wu, J., Jenkins, N., Wang, C., and Green, T. (2016). Benefits Analysis of Soft Open Points for Electrical Distribution Network Operation. Appl. Energ. 165, 36–47. doi:10.1016/j.apenergy.2015.12.022
Cao, J., Dong, C., Yu, X., Wang, R., Xiao, Q., and Jia, H. (2021). Modelling and Stability Assessment of the MMC‐HVDC Energy Interconnected System with the Cyber Delay of Communication Network. IET Energ. Syst. Integration 3 (1), 86–98. doi:10.1049/esi2.12006
Capitanescu, F., Bilibin, I., and Romero Ramos, E. (2014). A Comprehensive Centralized Approach for Voltage Constraints Management in Active Distribution Grid. IEEE Trans. Power Syst. 29 (2), 933–942. doi:10.1109/TPWRS.2013.2287897
Chai, Y., Guo, L., Wang, C., Zhao, Z., Du, X., and Pan, J. (2018). Network Partition and Voltage Coordination Control for Distribution Networks with High Penetration of Distributed PV Units. IEEE Trans. Power Syst. 33 (3), 3396–3407. doi:10.1109/TPWRS.2018.2813400
Chamana, M., and Chowdhury, B. H. (2018). Optimal Voltage Regulation of Distribution Networks with Cascaded Voltage Regulators in the Presence of High PV Penetration. IEEE Trans. Sustain. Energ. 9 (3), 1427–1436. doi:10.1109/TSTE.2017.2788869
Chen, L., Deng, Z., and Xu, X. (2019). Two-stage Dynamic Reactive Power Dispatch Strategy in Distribution Network Considering the Reactive Power Regulation of Distributed Generations. IEEE Trans. Power Syst. 34 (2), 1021–1032. doi:10.1109/TPWRS.2018.2875032
Eajal, A. A., Shaaban, M. F., Ponnambalam, K., and El-Saadany, E. F. (2016). Stochastic Centralized Dispatch Scheme for AC/DC Hybrid Smart Distribution Systems. IEEE Trans. Sustain. Energ. 7 (3), 1046–1059. doi:10.1109/TSTE.2016.2516530
Ji, H., Wang, C., Li, P., Zhao, J., Song, G., Ding, F., et al. (2017). An Enhanced SOCP-Based Method for Feeder Load Balancing Using the Multi-Terminal Soft Open point in Active Distribution Networks. Appl. Energ. 208, 986–995. doi:10.1016/j.apenergy.2017.09.051
Jiang, T. (2021). Guest Editorial: Artificial Intelligence and Data Analytics for Smart Grids with High Penetrations of Renewables. IET Energ. Syst. Integration 3 (3), 223–226. doi:10.1049/esi2.12040
Kim, Y. J., Kirtley, J. L., and Norford, L. K. (2015). Reactive Power Ancillary Service of Synchronous DGs in Coordination with Voltage Control Devices. IEEE Trans. Smart Grid 8 (2), 1. doi:10.1109/TSG.2015.2472967
Kouveliotis-Lysikatos, I. N., Koukoula, D. I., and Hatziargyriou, N. D. (2019). A Double-Layered Fully Distributed Voltage Control Method for Active Distribution Networks. IEEE Trans. Smart Grid 10 (2), 1465–1476. doi:10.1109/TSG.2017.2768239
Liu, X., Aichhorn, A., Liu, L., and Li, H. (2012). Coordinated Control of Distributed Energy Storage System with Tap Changer Transformers for Voltage Rise Mitigation under High Photovoltaic Penetration. IEEE Trans. Smart Grid 3 (2), 897–906. doi:10.1109/TSG.2011.2177501
Liu, Y., Guo, L., and Wang, C. (2018). A Robust Operation-Based Scheduling Optimization for Smart Distribution Networks with Multi-Microgrids. Appl. Energ. 228, 130–140. doi:10.1016/j.apenergy.2018.04.087
Liu, Y., Guo, L., Lu, C., Chai, Y., Gao, S., and Xu, B. (2019). A Fully Distributed Voltage Optimization Method for Distribution Networks Considering Integer Constraints of Step Voltage Regulators. IEEE Access 7, 60055–60066. doi:10.1109/ACCESS.2019.2912004
Qiao, F., and Ma, J. (2020). Voltage/var Control for Hybrid Distribution Networks Using Decomposition-Based Multiobjective Evolutionary Algorithm. IEEE Access 8, 12015–12025. doi:10.1109/ACCESS.2020.2965965
Robbins, B. A., Hadjicostis, C. N., and Dominguez-Garcia, A. D. (2013). A Two-Stage Distributed Architecture for Voltage Control in Power Distribution Systems. IEEE Trans. Power Syst. 28 (2), 1470–1482. doi:10.1109/TPWRS.2012.2211385
Wang, C., Song, G., Li, P., Ji, H., Zhao, J., and Wu, J. (2017). Optimal Siting and Sizing of Soft Open Points in Active Electrical Distribution Networks. Appl. Energ. 189, 301–309. doi:10.1016/j.apenergy.2016.12.075
Wang, X., Wang, C., Xu, T., Meng, H., Li, P., and Yu, L. (2018). Distributed Voltage Control for Active Distribution Networks Based on Distribution Phasor Measurement Units. Appl. Energ. 229, 804–813. doi:10.1016/j.apenergy.2018.08.042
Wang, X., Wang, C., Xu, T., Guo, L., Fan, S., and Wei, Z. (2018). Decentralised Voltage Control with Built‐in Incentives for Participants in Distribution Networks. IET Gener. Transm. Distrib. 12 (3), 790–797. doi:10.1049/iet-gtd.2017.0487
Wang, L., Bai, F., Yan, R., and Saha, T. K. (2018). Real-time Coordinated Voltage Control of PV Inverters and Energy Storage for Weak Networks with High PV Penetration. IEEE Trans. Power Syst. 33 (3), 3383–3395. doi:10.1109/TPWRS.2018.2789897
Xu, T., and Wu, W. (2020). Accelerated ADMM-Based Fully Distributed Inverter-Based Volt/Var Control Strategy for Active Distribution Networks. IEEE Trans. Ind. Inf. 16 (12), 7532–7543. doi:10.1109/TII.2020.2966713
Zeraati, M., Hamedani Golshan, M. E., and Guerrero, J. M. (2019). A Consensus-Based Cooperative Control of PEV Battery and PV Active Power Curtailment for Voltage Regulation in Distribution Networks. IEEE Trans. Smart Grid 10 (1), 670–680. doi:10.1109/TSG.2017.2749623
Zhang, L., Chen, Y., Shen, C., Tang, W., and Liang, J. (2018). Coordinated Voltage Regulation of Hybrid AC/DC Medium Voltage Distribution Networks. J. Mod. Power Syst. Clean. Energ. 6 (3), 463–472. doi:10.1007/s40565-017-0324-x
Zhang, G., Wang, Y., Peng, B., Lu, Y., Qiu, P., Xu, F., et al. (2019). Multi-objective Operation Optimization of Active Distribution Network Based on Three-Terminal Flexible Multi-State Switch. J. Renew. Sustain. Energ. 11 (2), 025501. doi:10.1063/1.5053614
Zhao, B., Qiu, H., Qin, R., Zhang, X., Gu, W., and Wang, C. (2018). Robust Optimal Dispatch of AC/DC Hybrid Microgrids Considering Generation and Load Uncertainties and Energy Storage Loss. IEEE Trans. Power Syst. 33 (6), 5945–5957. doi:10.1109/TPWRS.2018.2835464
Keywords: hybrid AC/DC distribution networks, multi-objective coordinated optimization, decentralized control, flexible electronic devices, alternating direction multiplier method
Citation: Wang X, Gu L and Liang D (2021) Decentralized and Multi-Objective Coordinated Optimization of Hybrid AC/DC Flexible Distribution Networks. Front. Energy Res. 9:762423. doi: 10.3389/fenrg.2021.762423
Received: 21 August 2021; Accepted: 28 September 2021;
Published: 19 October 2021.
Edited by:
Yue Zhou, Cardiff University, United KingdomReviewed by:
Wei Zhou, Dalian University of Technology, ChinaWei Gan, Cardiff University, United Kingdom
Copyright © 2021 Wang, Gu and Liang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dong Liang, bGlhbmdkb25nQGhlYnV0LmVkdS5jbg==
 Xiaoxue Wang
Xiaoxue Wang Liting Gu
Liting Gu Dong Liang
Dong Liang