Numerical Investigation of Pool Boiling Under Ocean Condition with Lattice Boltzmann Simulation. Part Ⅱ: Rolling Condition

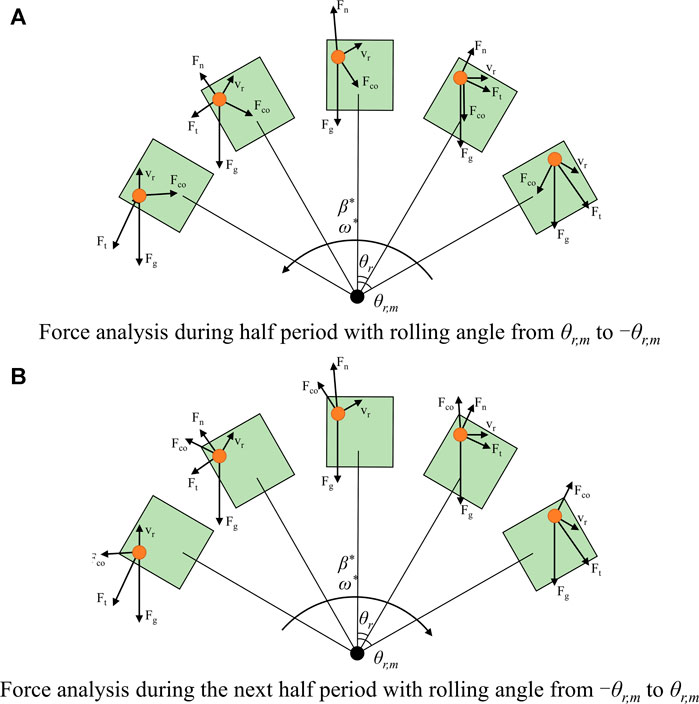
Rolling motion caused by ocean condition will induce more complicated inertial forces with their force directions changing all the time, which results more complex bubble behaviors and unique heat transfer characteristics. In this work, pool boiling under rolling condition is numerically simulated using multiple relaxation time phase change lattice Boltzmann method (LBM). Pool boiling patterns, boiling curve of time-averaged heat flux, transient heat flux and rolling effects on different pool boiling regions are investigated. The results show that pool boiling curve of time-averaged heat flux between rolling condition and static condition are not obvious until close to critical heat flux, and 9.3% higher CHF is achieved under rolling condition while worse heat transfer is discovered at film boiling. Moreover, distinct fluctuation of transient heat flux of pool boiling under rolling condition is found for all boiling regimes, and its variation pattern along with the rolling motion and bubble behavior is investigated. Furthermore, tangential inertial force caused by rolling motion has positive influence on heat transfer of pool boiling, while the centrifugal force has negative influence on heat transfer, since it is opposite to the gravity and hence decreases the buoyancy force. Besides, larger rolling amplitude and smaller rolling period will induce larger additional inertial forces, and thus make greater influences on the bubbles’ behavior and pool boiling heat transfer.

Introduction

Exploitation and utilization of ocean resources have been one of most promising directions of clean energy development, and investigations of marine power applications using steam-water power cycle with phase change (boiling and condensation) have received more and more attentions (Yan, 2017; Wang et al., 2019; Tian et al., 2020). As have been stated in Part Ⅰ of this paper series (Zou et al., 2021), marine power applications will suffer additional inertial forces caused by the ocean condition and exhibit different thermal–hydraulic characteristics, which are lack of enough understanding. Among the six-freedom marine motions (Wang et al., 2019), rolling is a fundamental rotational motion and is one of the most typical ocean conditions. Unlike heaving motion in Part Ⅰ of this paper series (Zou et al., 2021), the additional inertial forces caused by rolling motion are more complicated, since there are three kinds of induced inertial forces and they change their force directions all the time. It is representative and important to investigate the effects of rolling motion on the unique thermal-hydraulic characteristics inside marine applications.

As it has been summarized in Part Ⅰ of this paper series (Zou et al., 2021), literature about thermal-hydraulic characteristics of marine applications under ocean conditions have been concentrated on flow circulation and flow boiling (Tian et al., 2020), which have been adopted in marine reactors (O'Rourke, 2010). On the other hand, studies of pool boiling heat transfer under heaving motion is rather lacking, which is also important in pool boiling marine power plants, such as steam generator, sea water evaporator, blow off evaporator, thermal deaerator, etc (Yu, 2020). And the investigations about CHF (critical heat flux), HTC (heat transfer coefficient), bubble behaviors of flow boiling under heaving motion can be importantly referred. Most studies have shown that rolling motion could decrease CHF, with very few results of CHF enhancement. Pang and Gao (Pang et al., 1997) studied the rolling effects on CHF of flow boiling in an annular channel, and concluded that CHF was minished due to flow rate fluctuations. (Liu et al., 2012; Liu et al., 2018) proposed a theoretical model based on dry-out mechanism to predict the CHF of flow boiling under marine motions, and concluded that the CHF reduction was resulted from pulsating flow under rolling condition. On the contrary, Hwang et al. (Hwang et al., 2012) found both CHF enhancement at bubbly flow region and CHF deterioration at annular flow region under different rolling motions.

As for HTC of boiling under marine condition, most researchers have discovered that the transient HTC fluctuated dramatically during the motion period, and the rolling effects on time-averaged HTC is not confirmed. (Xiao et al., 2013) experimentally investigated flow boiling inside rectangular narrow channel, and showed that HTC and wall temperature taken periodic fluctuations under rolling motion. (Chen et al., 2016; Chen et al., 2017) stated that the fluctuation amplitude of HTC increased with the enlargement of rolling angle and rolling period, and the time-averaged HTC was close to that in the steady state. (Yuan et al., 2019) found that boiling curve of both pulsating flow and steady flow were almost overlapped, and the time-averaged HTC was little affected. However, (Ren et al., 2018) presented that the time-averaged HTC of flow boiling was enhanced by 31.33–115.43%, and the enhancement intensity increased with the aggrandizement of rolling angle and the decrease of rolling period.

Both CHF and HTC have been influenced by the bubble behaviors, such as bubble nucleation, bubble growth, departure, sliding, distribution and movement, which have investigated a lot in flow boiling. (Qin and Gao, 2008) theoretically analyzed the forces acting on the bubbles in flow boiling, and showed that rolling motion greatly altered the position of bubble departure and hence influenced the heat transfer performance. (Wei et al., 2011) numerically demonstrated that bubbles’ quick sliding and detachment were resulted from the fluctuation of mass flow rate caused by rolling motion. (Xie et al., 2014) found that bubble departure diameter fluctuated in a certain range during a rolling period. (Li et al., 2014; Li et al., 2015a) found the bubbles’ maximum diameter, lifetime, nucleation frequency and sliding velocity of flow boiling increased with increase of rolling angle, and the mean diameter of bubbles decreased compared to the static condition. In contrast, (Yuan et al., 2019) observed that bubble size under pulsating flow were much larger.

As elaborated above, in order to know the thermal-hydraulic characteristics of marine nuclear reactors, flow boiling under rolling condition has been deeply studied. However, few works have been done about the effects of rolling condition on pool boiling, which has also been widely applied to many boiling heat exchangers (Yu, 2020), such as steam generator, sea water evaporator, blow off evaporator, thermal deaerator, etc. Recently, (Tanjung and Jo, 2020; Tanjung et al., 2021) conducted experimental studies of pool boiling with rectangular flat heater under rolling condition. They found that vapor behaviors and CHF were opposite between the heated surface placed above and below the rolling axis. However, heat transfer performance of nucleation boiling such as HTC is absent.

Lattice Boltzmann method (LBM) has received extensive attention and has been developed to simulate multiphase flow (Huang et al., 2019; Huang et al., 2021) and phase change heat transfer (boiling, evaporation, condensation, etc.) (Cheng et al., 2014; Li et al., 2016), which could investigated CHF, HTC and bubble behaviors of pool boiling effectively. As reviewed in part Ⅰ of this paper series, pseudo-potential model has been most extensively applied among multiphase LBM, and a temperature field equation considering the source term of phase change was introduced. Different kinds of equations of state (EOS) for real gases have been incorporated, and spontaneous phase change such as bubble nucleation, bubble growth, bubble departure, et al. could be driven. With the help of this effective simulation method, the whole boiling curve including natural convection, nucleate boiling, CHF and film boiling was investigated (Li et al., 2015b; Gong and Cheng, 2015).

In this work, pseudo-potential LBM is adopted to study pool boiling under rolling motion. In Inertial forces under rolling condition, we discuss briefly the inertial forces under rolling condition. Then, pool boiling patterns, boiling curve and variance of transient heat flux under rolling condition are shown, and the influence of rolling motion on bubble behaviors, flow field and temperature field at different boiling regions are analyzed in Results and discussion. Besides, the conclusions drawn in this work are presented in Concluding remarks.

Inertial Forces Under Rolling Condition

Under rolling condition as shown in Figure 1, extra accelerations can be figured out with the change of θ_r. Assume that θ_r has sine relationship with time

$\begin{array}{l}{\theta }_r={\theta }_{r,m}sin\left(2\pi \frac{t}{t_p}\right)\\ {\omega }^{\ast }=\frac{d{\theta }_r}{dt}={\theta }_{r,m}\frac{2\pi }{t_p}\cos \left(2\pi \frac{t}{t_p}\right)\\ {\beta }^{\ast }=\frac{d{\omega }^{\ast }}{dt}=-{\theta }_{r.m}{\left(\frac{2\pi }{t_p}\right)}^{2}sin\left(2\pi \frac{t}{t_p}\right)\end{array}(1)$

where θ_r,m is the maximum rolling angle, t_p is rolling period, ω^* is the angular velocity, and β^* is the angular acceleration. In the simulation, rotating coordinate system is chosen, and the force direction is opposite to the acceleration. Inertial forces caused by rolling condition include tangential inertial force F_t, centripetal force F_n and Coriolis force F_co can be expressed as the volume force as

$\begin{array}{l}{\mathit{F}}_{\mathit{t}}=-\rho \left({\mathit{\beta }}^{\ast }\times \mathit{r}\right)\\ {\mathit{F}}_{\mathit{n}}=-\rho \left({\mathit{\omega }}^{\ast }\times \left({\mathit{\omega }}^{\ast }\times \mathit{r}\right)\right)\\ {\mathit{F}}_{\mathit{c}\mathit{o}}=-2\rho \left({\mathit{\omega }}^{\ast }\times {\mathit{v}}_{\mathit{r}}\right)\end{array}(2)$

where ρ is the density of fluid, r is the displacement of the fluid particle pointed from rolling axis, and v_r is the velocity of fluid particle relative to the rolling system. The inertial forces have also been shown in Figure 1.

FIGURE 1

FIGURE 1. Schematic diagram of rolling condition and additional inertial forces.

Results and Discussion

In this paper, pseudo-potential phase change LBM will be adopted to simulate pool boiling heat transfer under rolling motion. Since the LBM phase change model and the simulation parameters have been given in Part I of this paper series, we will not repeat its presentation here. In this section, heat transfer characteristics of pool boiling under rolling condition is given. Firstly, pool boiling patterns at different regimes and comparison of boiling curves under static or rolling condition is shown. Then, the fluctuation of transient heat flux during rolling period is presented. At last, the influences of rolling motion on pool boiling at different boiling regions are revealed.

Pool Boiling Patterns and Boiling Curve Under Rolling Condition

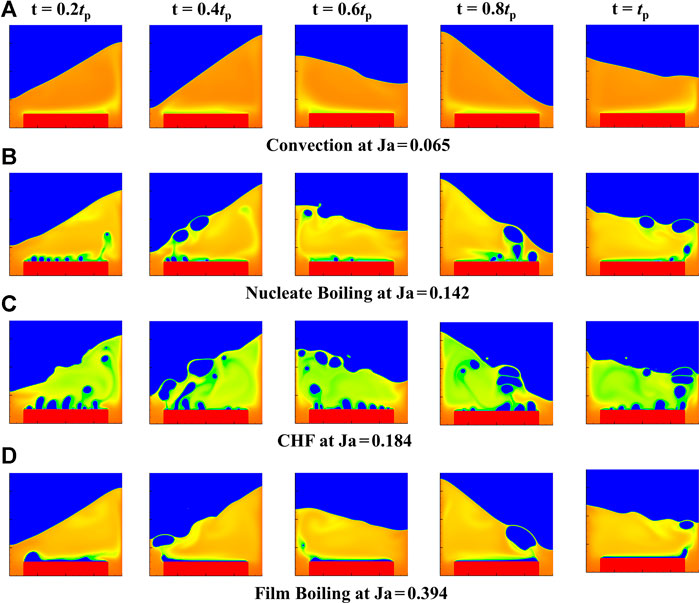
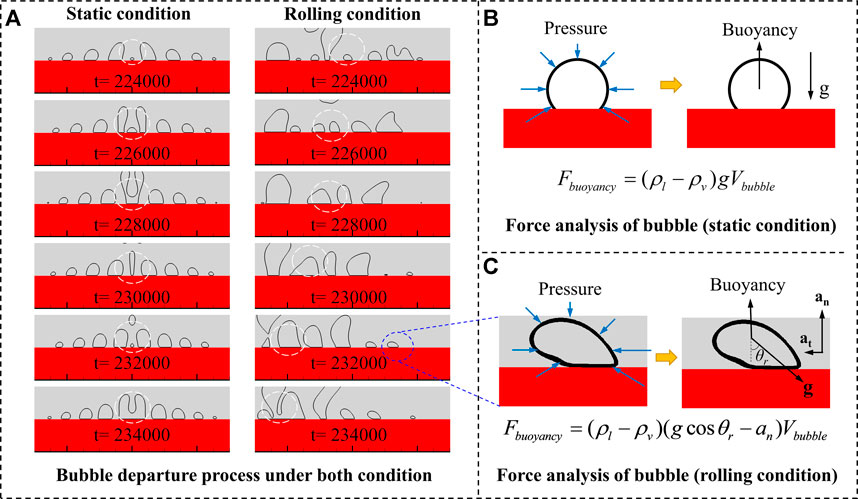
After verification of the model with empirical equations under static condition in Part I, pool boiling under rolling condition is simulated in this section with maximum rolling angle θ_r,m = 30^o and rolling period t_p = 100000δ_t, and the ratio of additional accelerations with gravity acceleration is: a_n/g = 0.06, a_t/g = 0.11. Figure 2 shows bubbles’ unique behaviors during one rolling period (t_p = 3 × 10⁵δ_t to 4 × 10⁵δ_t) at various pool boiling stages under rolling condition. Each column in Figure 2 has the same moment, and the time interval between neighboring column is 0.2t_p = 2 × 10⁴δ_t. The corresponding fluid field in detailed is showed in the table below: At convection regime (Ja = 0.065), no bubble nucleation occurs on the heater at low heat flux, and the liquid level swings during the rolling period. At higher wall superheat (Ja = 0.142), it comes to nucleate boiling regime, where the bubbles go through the process of nucleation, growth, sliding, coalescence, departure and swinging rising. The obvious non-uniform distribution of bubbles on the wall surface is resulted from bubbles’ nucleation and sliding. The bubbles burst after they rise laterally and periodically to the liquid level under rolling conditions. Then, CHF is obtained at Ja = 0.184, where the surface is partially occupied by small vapor films and local dry-out occurs. The bubbles tend to slide to the heater side with maximum rolling angle and depart from there. When the superheat still grows up to Ja = 0.394, the boiling pattern changes to film boiling where vapor film covers the whole heater surface and restrains the supplement of liquid. Then the vapor column forms and swings under the rolling condition, and big bubbles depart from the heater side at maximum rolling angle.

FIGURE 2

FIGURE 2. Various regions of pool boiling during one period under rolling condition.

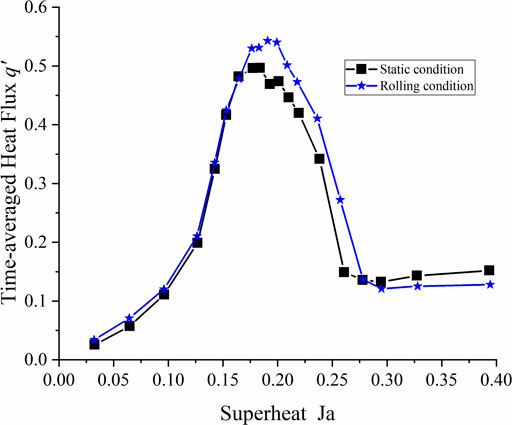
The comparison of boiling curve with time-averaged heat flux computed with time t from 40000δ_t to 140000δ_t corresponding to one rolling periods between rolling and static conditions is presented in Figure 3, it is shown that the rolling effects slightly increase the average heat transfer at convection and nucleate boiling regimes, and lead to 9.3% higher CHF. Furthermore, the rolling effects continue to strengthen heat flux in transition region. When it comes to film boiling, the heat flux under rolling condition will reduce and be lower than that at static condition. The rolling effects on the whole boiling curve under different boiling regimes will be analyzed as followed.

FIGURE 3

FIGURE 3. Boiling curve of pool boiling under static and rolling conditions.

Transient Heat Flux During the Rolling Period at Different Pool Boiling Regions

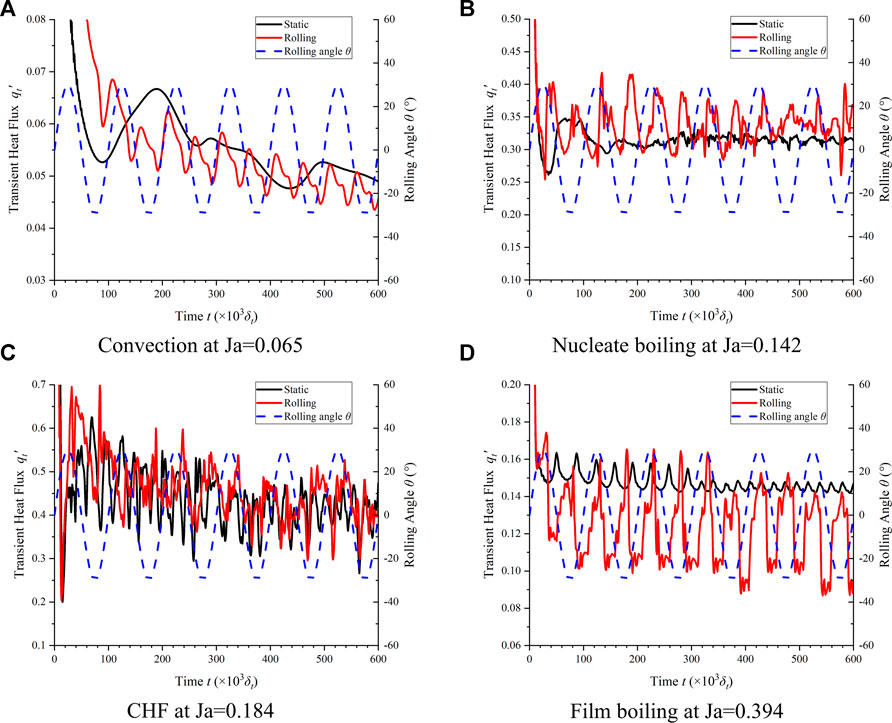
Transient heat flux varied with time under static and rolling conditions has been made a contrast in Figure 4, and the corresponding rolling angle is also plotted with blue dashed line. The transient heat flux $q_t\prime$ is computed as

$q_t^{\prime }=\frac{q_t}{q_{bo}}=\frac{1}{q_{bo}{L}_x}{\displaystyle {\int }_{L_x}-k_s{\left(\frac{\partial T}{\partial y}\right)}_{y=0}}dx(3)$

FIGURE 4

FIGURE 4. Transient heat flux during the rolling period at different pool boiling regions.

It is shown in Figure 4A that the transient heat flux at convection region decreases in the beginning, and rises to a stable status under static condition, which is in agreement with the results in the literature (Li et al., 2015b; Gong and Cheng, 2017; Zhou et al., 2019). On the contrary, the transient heat flux under rolling condition is higher at first and fluctuates slightly during the rolling period. Since no bubble nucleation exists in the convection regime and the value of heat flux is low, the rolling effects on heat transfer of single liquid phase are small.

As the superheat degree increases, it comes to nucleate boiling region and the transient heat flux is presented in Figure 4B. It is shown that distinct fluctuation of transient heat flux appears under both static and rolling conditions. Especially for pool boiling under rolling condition, high intensity and ordered oscillation of transient heat flux is observed during the rolling period, which is derived from the dynamic evolution of bubbles’ unique behaviors of nucleation, growth, sliding, coalescence and departure. It should be noted that the oscillation period of transient heat flux at nucleate boiling (Ja = 0.142) is almost 0.5t_p. This result can be explained from the periodic inertial force imposed on the bubbles as presented in Figure 1, which shows that centrifugal force F_n, tangential force F_t and Coriolis force F_co have not change unless the rolling system pass through the middle position. In other words, the variation period of additional inertial force exerted on the bubbles is almost half of rolling period, and it leads to the high intensity and ordered oscillation of transient heat flux. Besides, the transient heat flux under rolling condition has higher peek value and lower minimum value than that under static condition, which results in a close time-averaged heat flux.

More intense fluctuation of transient heat flux at CHF is given in Figure 4C. Different from nucleate boiling under rolling condition, similar random oscillations of transient heat flux appear for both static and rolling conditions, which can be attributed to the vigorous bubble behaviors at CHF. Moreover, the transient heat flux of pool boiling under rolling condition is higher than that under static condition during most part of rolling period, and it leads to the higher average heat flux at CHF region.

Relatively periodic variation of transient heat flux at film boiling under both static and rolling conditions is presented in Figure 4D. A stable vapor film forms at film boiling regime and the bubbles periodically depart from the vapor columns, which causes the regular variation of transient heat flux. It should be noted that the transient heat flux under rolling condition is always lower than that under static condition.

Influence of Rolling Effects on Convection Region

At convection heat transfer region, the rolling effects make the heat transfer change from natural convection to forced convection, which can be clearly seen from the temperature field and boundary layer in Figure 5. The tangential inertial force will drive the liquid moving parallelly on the surface as shown in Figure 5A, leading to a thinner boundary layer. And it can be explained from the temperature profile upon the heater surface as presented in Figure 5B, which indicates that temperature gradient (T_w—T)/Δy near the heater surface under rolling condition is larger, with Δy = y - y_heater representing the distance from heater surface. Moreover, the thinner boundary layer caused by tangential inertial force under rolling condition will result in better thermal performance.

FIGURE 5

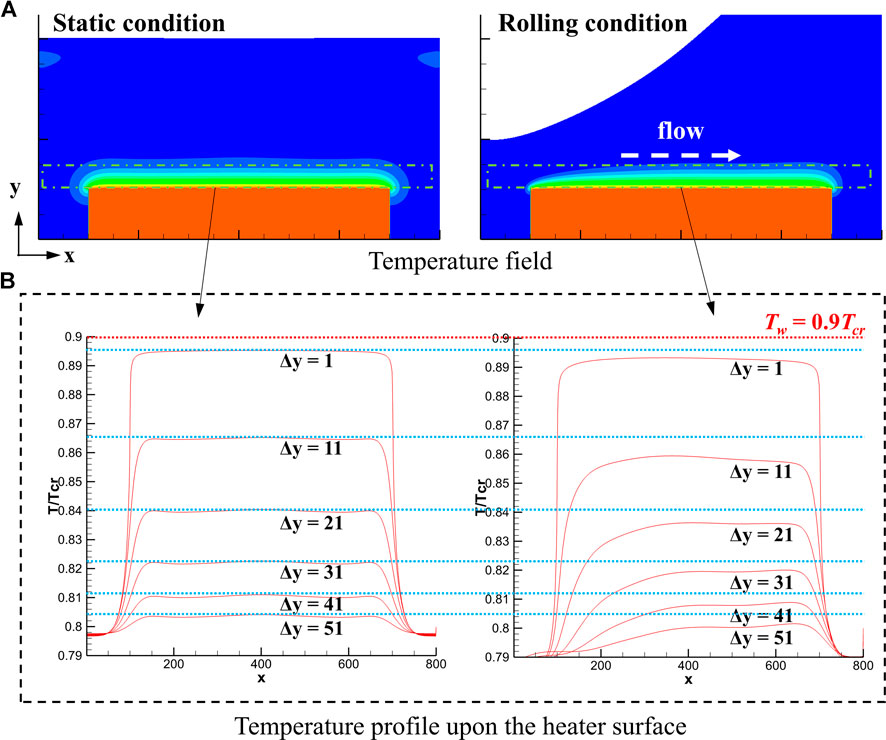
FIGURE 5. Analysis of heat transfer at convection region under both static and rolling conditions: (A) temperature field, (B) temperature profile upon the heater with Δy = y - y_heater representing the distance from heater surface.

On the contrary, the centrifugal force F_n is opposite to the gravity as seen in Figure 1, and hence the convection circulation between fluid upside and downside is weakened. It is shown in Figure 6A that convection circulation under static condition goes well and some vortexes have been formed. In contrast, much hot liquid flows upward and little cold liquid has been replenished to the wall under rolling condition. Moreover, we can also see the comparison of convection circulation between rolling condition and static condition from the isotherm diagram in Figure 6B. The isotherm lines always form cycles under static condition. On the other hand, for rolling condition, parallel liquid flows on the heater surface leads to overall thinner superheated layer at the beginning of 0.2t_p. Then, the flow field leans to one side at 0.6t_p and 0.8t_p without full convection cycle. After that, parallel flows account for the majority at t_p and it results in a thinner boundary layer again. To sum up, the tangential inertial force F_t has positive influence on the heat transfer, while the centrifugal force F_n makes negative effects under rolling condition, and heat transfer of convection region in this work will be slightly enhanced by rolling motion.

FIGURE 6

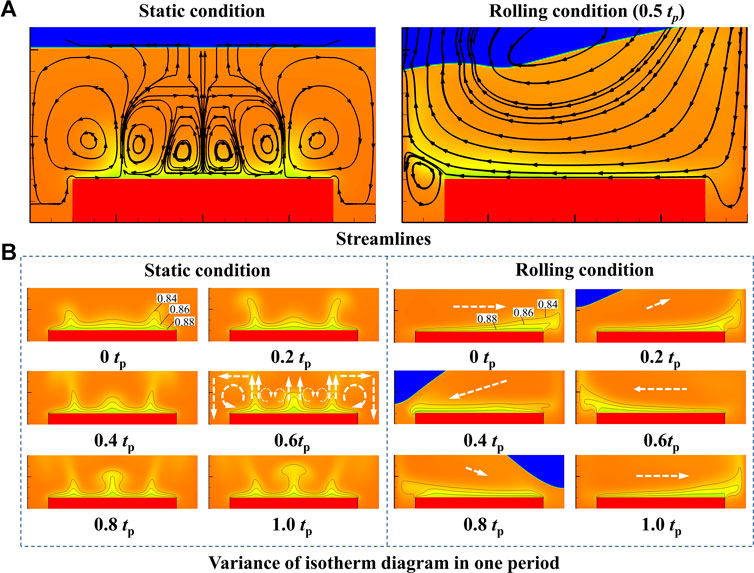
FIGURE 6. Analysis of convection circulation under both static and rolling conditions: (A) streamlines of the flow field; (B) variance of isotherm diagram in one period.

Influence of Rolling Effects on Nucleate Boiling

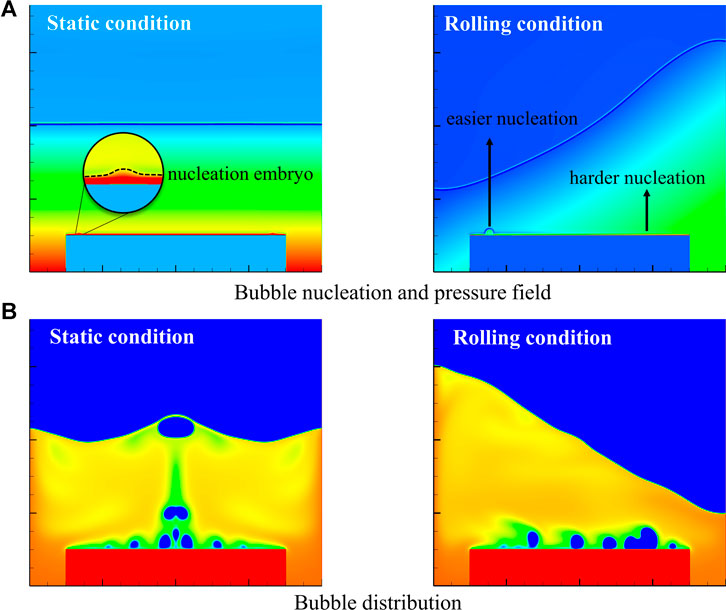
The difference of time-averaged heat flux between static condition and rolling condition is small at nucleate boiling, which is similar to the result in flow boiling and will be analyzed from the aspects of bubble behaviors, heat transfer near the triple-line and bubble departure. For bubble nucleation under rolling condition, the superheated liquid flows parallelly on the surface, leading to a non-uniform pressure field as shown in Figure 7A. Since bubble nucleation requires the force balance as indicated by Laplace law (p_in - p_out = σ/r), and thus nonuniformity of pressure filed gives rise to easier bubble nucleation at one side with lower external pressure and harder nucleation on the other side of the heater surface. Moreover, bubbles slide under the pressure gradient on the heater surface. Both non-uniform bubble nucleation and bubble sliding under rolling condition result in the asymmetrical bubble distribution as presented in Figure 7B. In contrast, bubble nucleation and distribution under static condition have been very uniform. Although the bubble behaviors exhibit huge difference between rolling condition and static condition, the bubble numbers make little difference as shown in Figure 7B, which means that the intensity of boiling process is similar and hence the time-averaged heat flux of both conditions is close to each other.

FIGURE 7

FIGURE 7. Bubble nucleation and distribution under both static and rolling conditions.

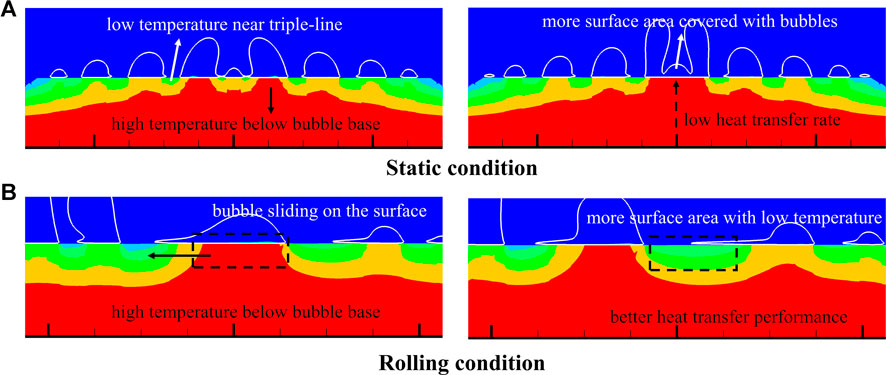
On the other hand, evaporation close to the triple-line is important for heat transfer of nucleate boiling. As shown in Figure 8, the surface below bubble base has higher temperature than surface position wetted with liquid because of the low conductivity of vapor, and the triple-line area is distinguished with lower temperature resulted from violent evaporation there. The tangential inertial force caused by rolling motion drives bubbles to slide on the surface, which enhances the evaporation near triple-line and increases the surface area with low temperature. And these results indicate that tangential inertial force imposed on the bubbles according to rolling motion has positive influence on heat transfer of nucleate boiling.

FIGURE 8

FIGURE 8. Temperature field inside the heater surface during bubble growth or sliding.

Besides, bubble departure has been deeply influenced by the directional variance of gravity and additional centrifugal force under rolling condition. Normally, buoyancy of a single bubble comes from the integral pressure under gravitational field as shown in Figure 9. Since the gravity is not parallel with the normal direction of heater surface any more under rolling condition, the buoyancy of bubble decreases. Moreover, the additional centrifugal force is at the same direction with bubble departure, which will also reduce the buoyancy. To sum up, the directional variance of gravity and additional centrifugal force has negative influence on heat transfer of nucleate boiling under rolling condition.

FIGURE 9

FIGURE 9. Bubble departure process and the force analysis under static and rolling conditions.

Influence of Rolling Effects on CHF

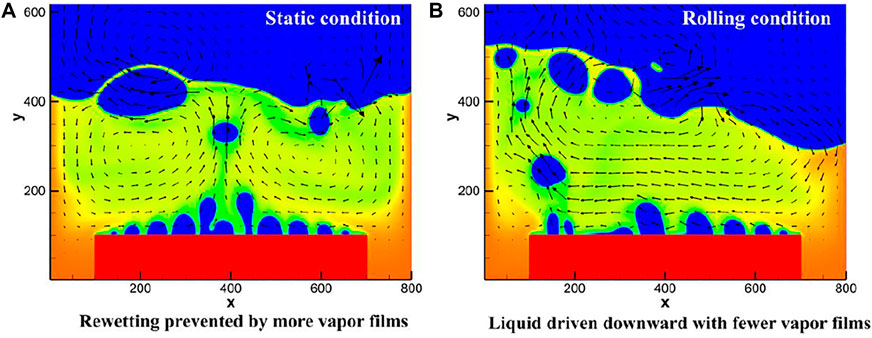
CHF is greatly influenced by the vapor film on the surface, and large-scale vapor film will prevent surface rewetting and decrease CHF. It can be seen from Figure 10 with velocity vector diagram, that the surface rewetting is enhanced under rolling condition, since the liquid is driven downward to the heater with fewer small vapor film. In contrast, the bubbles on the heater surface under static condition is dense and form more vapor films, which prevent the rewetting of heater.

FIGURE 10

FIGURE 10. Velocity vector diagram of pool boiling at CHF under static and rolling conditions.

Influence of Rolling Effects on Film Boiling

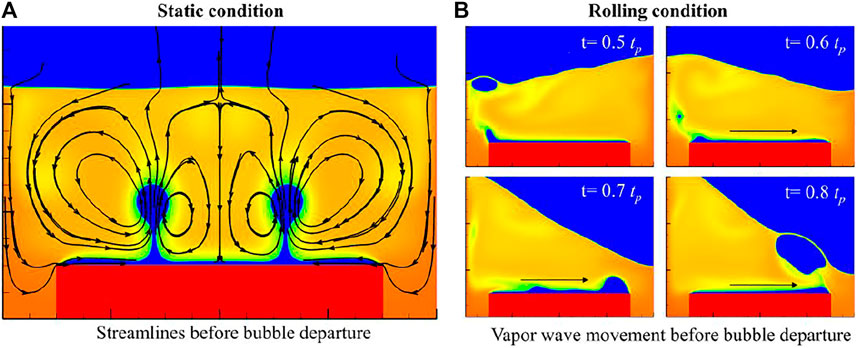
The influence of rolling effects on film boiling is shown in Figure 11. As discussed in 3.4, the buoyancy of bubble at departure decreases, leading to lower bubble departure frequency for film boiling under rolling condition. Besides, flow filed with sufficient circulation in the bulk liquid is favorable to bubble departure under static condition as demonstrated by the streamlines in Figure 11A. The eddy grows and exists for a long term, which helps the bubble depart from surface regularly, and there exists two departure bubbles. On the contrary, the long-existed eddy will be destroyed with rolling motion. The vapor wave moves from one side of the heater to the other side, and only one bubble departs from the surface (as seen in Figure 11B). The departure mode under rolling condition might delay a bubble’ leaving, as shown in Figure 11B, a small bubble on the left has to move to the other side for departure. In brief, lower bubbles’ departure frequency caused by decreasing buoyancy and fewer numbers of departure bubbles result in thicker vapor film and heat transfer deterioration in film boiling under rolling condition.

FIGURE 11

FIGURE 11. Analysis of bubble departure at film boiling under static and rolling conditions.

Influence of Rolling Parameters on Heat Flux

Figure 12 presents the influence of rolling parameters on transient heat flux with different rolling amplitudes and rolling periods. It can be seen from Eq. 1 and 2 that larger rolling amplitude and smaller rolling period will induce larger additional inertial forces, and thus make greater influences on the bubbles’ behavior and pool boiling heat transfer. Compare the fluctuation range of transient heat flux between Figure 12A and Figure 12B, it is found that smaller rolling period results in larger fluctuation of transient heat flux. And the oscillation of heat flux in smaller rolling amplitude is very low as seen in Figure 12C. Besides, we find that the time-averaged heat flux is a bit higher than static condition for cases in Figures 12A,B, while it’s a little lower for Figure 12C. As discussed in Influence of rolling effects on convection region, the rolling motion will force the fluid to flow along heater surface while destroy the natural convection circulation, so the convection heat transfer is strengthened with forced flow and weakened with disappearance of natural convection eddy. That’s to say, the overall heat transfer performance is related to rolling parameters.

FIGURE 12

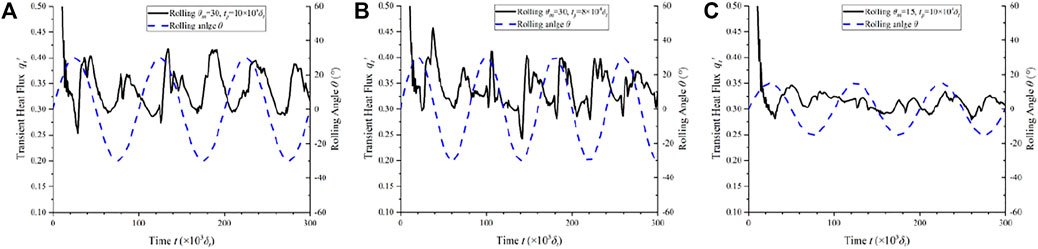
FIGURE 12. Transient heat flux with different rolling parameters at nucleate boiling regime, Ja = 0.142. (A) Maximum rolling angle θ_r,m = 30°, rolling period t_p = 10 × 10⁴δ_t. (B) θ_r,m = 30°, t_p = 8 × 10⁴δ_t. (C) θ_r,m = 15°, t_p = 10 × 10⁴δ_t.

Concluding Remarks

In this work, heat transfer characteristics of pool boiling under rolling condition is analyzed, and the results have been made comparison with that under static condition. Moreover, rolling effects on bubble behaviors and heat transfer at different pool boiling regions are studied. The following conclusions can be drawn from this paper:

1) Bubble behaviors under rolling condition is totally different from that under static condition, which goes through the process of nucleation, growth, sliding, coalescence, departure and swinging rising. And, boiling curves of time-averaged heat flux of static and rolling conditions are similar before CHF. Moreover, 9.3% higher CHF is achieved under rolling condition while worse heat transfer occurs at film boiling in this work.

2) Fluctuation of transient heat flux of pool boiling under rolling condition was found for all boiling regimes, especially at regions of nucleate boiling, transition boiling and film boiling. The oscillation period of transient heat flux at nucleate boiling (Ja = 0.143) is almost 0.5t_p in this work. Moreover, the fluctuation of transient heat flux is random and intense at transition boiling, while it is periodic and ordered at film boiling.

3) Better heat transfer is achieved under rolling condition at CHF, which is resulted from the enhanced rewetting with liquid driven downward to the heater with fewer vapor film. And heat transfer deterioration in film boiling under rolling condition is according to lower bubbles’ departure frequency caused by buoyancy’s decreasing and fewer numbers of departure bubbles.

4) Tangential inertial force caused by rolling motion has positive influence on heat transfer of pool boiling, since it drives the liquid to flow parallelly on the surface leading to a thinner boundary layer at convection, and it propels bubble to slide on the surface resulting in enhancement of evaporation at the triple-line. While the centrifugal force has negative influence on heat transfer, since it is opposite to the gravity and hence decreases the buoyancy force. And larger rolling amplitude and smaller rolling period will induce larger additional inertial forces, and thus make greater influences on the bubbles’ behavior and pool boiling heat transfer.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

QZ: Methodology, Formal analysis, Writing—Original Draft. XL: Conceptualization, Writing—review&editing, Supervision, Funding acquisition. YH: Formal analysis, Investigation. YC: Validation, Investigation. Pengkui Li: Validation.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

This work was supported by National Natural Science Foundation of China through Grant No. 51806155.

References

Chen, C., Gao, P.-Z., Tan, S.-C., and Yu, Z.-T. (2016). Boiling Heat Transfer Characteristics of Pulsating Flow in Rectangular Channel under Rolling Motion. Exp. Therm. Fluid Sci. 70, 246–254. doi:10.1016/j.expthermflusci.2015.09.013

CrossRef Full Text | Google Scholar

Chen, C., Wu, W., Li, L.-C., Liu, D.-M., Liu, J.-J., and Lan, S. (2017). Heat Transfer Characteristics of Oscillating Flow in a Narrow Channel under Rolling Motion. Ann. Nucl. Energ. 110, 668–678. doi:10.1016/j.anucene.2017.07.019

CrossRef Full Text | Google Scholar

Cheng, P., Quan, X., Gong, S., Liu, X., and Yang, L. (2014). Recent Analytical and Numerical Studies on Phase-Change Heat Transfer. Adv. Heat Transfer 64, 187–248. doi:10.1016/bs.aiht.2014.08.004

CrossRef Full Text | Google Scholar

Gong, S., and Cheng, P. (2017). Direct Numerical Simulations of Pool Boiling Curves Including Heater's thermal Responses and the Effect of Vapor Phase's thermal Conductivity. Int. Commun. Heat Mass Transfer 87, 61–71. doi:10.1016/j.icheatmasstransfer.2017.06.023

CrossRef Full Text | Google Scholar

Gong, S., and Cheng, P. (2015). Lattice Boltzmann Simulations for Surface Wettability Effects in Saturated Pool Boiling Heat Transfer. Int. J. Heat Mass Transfer 85, 635–646. doi:10.1016/j.ijheatmasstransfer.2015.02.008

CrossRef Full Text | Google Scholar

Huang, R., Wu, H., and Adams, N. A. (2019). Lattice Boltzmann Model with Self-Tuning Equation of State for Multiphase Flows. Phys. Rev. E 99 (2), 023303. doi:10.1103/PhysRevE.99.023303

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, R., Wu, H., and Adams, N. A. (2021). Mesoscopic Lattice Boltzmann Modeling of the Liquid-Vapor Phase Transition. Phys. Rev. Lett. 126 (24), 244501. doi:10.1103/physrevlett.126.244501

PubMed Abstract | CrossRef Full Text | Google Scholar

Hwang, J.-S., Lee, Y.-G., and Park, G.-C. (2012). Characteristics of Critical Heat Flux under Rolling Condition for Flow Boiling in Vertical Tube. Nucl. Eng. Des. 252, 153–162. doi:10.1016/j.nucengdes.2012.06.032

CrossRef Full Text | Google Scholar

Li, Q., Kang, Q. J., Francois, M. M., He, Y. L., and Luo, K. H. (2015). Lattice Boltzmann Modeling of Boiling Heat Transfer: the Boiling Curve and the Effects of Wettability. Int. J. Heat Mass Transfer 85, 787–796. doi:10.1016/j.ijheatmasstransfer.2015.01.136

CrossRef Full Text | Google Scholar

Li, Q., Luo, K. H., Kang, Q. J., He, Y. L., Chen, Q., and Liu, Q. (2016). Lattice Boltzmann Methods for Multiphase Flow and Phase-Change Heat Transfer. Prog. Energ. Combust. Sci. 52, 62–105. doi:10.1016/j.pecs.2015.10.001

CrossRef Full Text | Google Scholar

Li, S., Tan, S., Gao, P., and Xu, C. (2014). Experimental Research of Bubble Number Density and Bubble Size in Narrow Rectangular Channel under Rolling Motion. Nucl. Eng. Des. 268, 41–50. doi:10.1016/j.nucengdes.2013.11.084

CrossRef Full Text | Google Scholar

Li, S., Tan, S., Xu, C., and Gao, P. (2015). Visualization Study of Bubble Behavior in a Subcooled Flow Boiling Channel under Rolling Motion. Ann. Nucl. Energ. 76, 390–400. doi:10.1016/j.anucene.2014.10.004

CrossRef Full Text | Google Scholar

Liu, D., Tian, W., Xi, M., Chen, R., Qiu, S., and Su, G. H. (2018). Study on Safety Boundary of Flow Instability and CHF for Parallel Channels in Motion. Nucl. Eng. Des. 335, 219–230. doi:10.1016/j.nucengdes.2018.05.024

CrossRef Full Text | Google Scholar

Liu, W. X., Tian, W. X., Wu, Y. W., Su, G. H., Qiu, S. Z., Yan, X., et al. (2012). An Improved Mechanistic Critical Heat Flux Model and its Application to Motion Conditions. Prog. Nucl. Energ. 61, 88–101. doi:10.1016/j.pnucene.2012.07.002

CrossRef Full Text | Google Scholar

O'Rourke, R. (2010). Navy Nuclear-Powered Surface Ships: Background, Issues, and Options for Congress. Congressional Research Service, United States of America.

Google Scholar

Pang, F., Gao, P., and Wang, Z. (1997). Experimental Investigation on Effect of Rolling upon Critical Heat Flux (CHF) for Water at Atmospheric Pressure. Chin. J. Nucl. Sci. Eng. 17 (4), 367–371.

Google Scholar

Qin, S., and Gao, P. (2008). Effect of Rolling Motion on Forces Acting on Bubbles in Sub-cooled Boiling Flow. Nucl. Power Eng. 29 (2), 20–23.

Google Scholar

Ren, Y., Cai, W., and Jiang, Y. (2018). Numerical Study on Shell-Side Flow and Heat Transfer of Spiral-Wound Heat Exchanger under Sloshing Working Conditions. Appl. Therm. Eng. 134, 287–297. doi:10.1016/j.applthermaleng.2018.01.119

CrossRef Full Text | Google Scholar

Tanjung, E. F., and Jo, D. (2020). Visualization Study on Pool Boiling Critical Heat Flux under Rolling Motion. Int. J. Heat Mass Transfer 153, 119620. doi:10.1016/j.ijheatmasstransfer.2020.119620

CrossRef Full Text | Google Scholar

Tanjung, E. F., Kim, B. J., and Jo, D. (2021). Effects on Pool Boiling Critical Heat Flux (CHF) with Different Direction and Magnitude of Additional Accelerations Due to Rolling. Ann. Nucl. Energ. 154, 108095. doi:10.1016/j.anucene.2020.108095

CrossRef Full Text | Google Scholar

Tian, Z., Gu, B., Zhang, Y., and Gao, W. (2020). Flow Boiling Heat Transfer under marine Motions: A Comprehensive Review. Ann. Nucl. Energ. 143, 107455. doi:10.1016/j.anucene.2020.107455

CrossRef Full Text | Google Scholar

Wang, S., Yang, B., Zhou, Z., and Long, J. (2019). Review on thermal-hydraulic Characteristics of Nuclear Reactors under Ocean Conditions. Nucl. Sci. Eng. 193 (1-2), 14–32. doi:10.1080/00295639.2018.1512791

CrossRef Full Text | Google Scholar

Wei, J.-h., Pan, L.-m., Chen, D.-q., Zhang, H., Xu, J.-j., and Huang, Y.-p. (2011). Numerical Simulation of Bubble Behaviors in Subcooled Flow Boiling under Swing Motion. Nucl. Eng. Des. 241 (8), 2898–2908. doi:10.1016/j.nucengdes.2011.05.008

CrossRef Full Text | Google Scholar

Xiao, Y., Sun, L., and Gao, P. (2013). Study of the Boiling Heat Exchange Characteristics of a Flow in a Narrow Channel under the Rolling Condition. J. Eng. Therm. Energ. Power 28 (6), 585.

Google Scholar

Xie, T., Chen, B., Yan, X., Xu, J., Huang, Y., and Xiao, Z. (2014). Model Development and Analysis on Bubble Departure Diameter in Narrow Rectangular Channel under Rolling Motion. At. Energ. Sci. Techn. 48 (5), 801–805. doi:10.7538/yzk.2014.48.05.0801

CrossRef Full Text | Google Scholar

Yan, B. H. (2017). Review of the Nuclear Reactor thermal Hydraulic Research in Ocean Motions. Nucl. Eng. Des. 313, 370–385. doi:10.1016/j.nucengdes.2016.12.041

CrossRef Full Text | Google Scholar

Yu, J. (2020). Marine Nuclear Power Technology. Shanghai: Shanghai Jiao Tong University Press. doi:10.1007/978-981-15-2894-1

CrossRef Full Text | Google Scholar

Yuan, B., Zhang, Y., Liu, L., and Wei, J. (2019). Experimental Research on Subcooled Flow Boiling Heat Transfer Performance and Associated Bubble Characteristics under Pulsating Flow. Appl. Therm. Eng. 157, 113721. doi:10.1016/j.applthermaleng.2019.113721

CrossRef Full Text | Google Scholar

Zhou, P., Liu, Z., Liu, W., and Duan, X. (2019). LBM Simulates the Effect of Sole Nucleate Site Geometry on Pool Boiling. Appl. Therm. Eng. 160, 114027. doi:10.1016/j.applthermaleng.2019.114027

CrossRef Full Text | Google Scholar

Zou, Q., Liu, L., Hu, Y., Chang, Y., and Yang, R. (2021). Lattice Boltzmann Simulation of Pool Boiling under Ocean Condition. Part I: Heaving Condition. Front Ener Res. doi:10.3389/fenrg.2021.771758 Submitted for Publication.

CrossRef Full Text | Google Scholar

Nomenclature

F_t tangential inertial force

F_n centripetal force

F_co Coriolis force

g gravity

Ja Jacob number, dimensionless superheat

p pressure (Pa)

q heat flux (W/m²)

q’ dimensionless heat flux

q_bo reference boiling heat flux

r Radius of bubble position vector of fluid particle pointed from rotation axis

t time

t_p rolling period

T temperature(K)

T_cr critical temperature (K)

T_w wall temperature (K)

v_r actual fluid velocity vector

a_n centripetal acceleration

a_t tangential inertial acceleration

K_s thermal conductivity of solid

L_x length of heater

Greek symbol

ρ density (kg m⁻³)

ω^* angular velocity

β^* angular acceleration

θ_r rolling angle

θ_r,m maximum rolling angle