- Science and Technology on Reactor System Design Technology Laboratory, Nuclear Power Institute of China, Chengdu, China
Because of the double-heterogeneity (DH), dispersed particle-type systems cannot be described by traditional neutronic programs, and the volumetric homogenization method (VHM) will bring reactivity calculation deviation because of ignoring the spatial self-shielding effect of the particles. In this article, the relationship between the reactivity calculation deviation and the optical length of dispersed particle-type fuel and different types of burnable poisons is analyzed. Also then, it was proposed that the influencing factors of reactivity calculation deviation can be integrated to a physical quantity named theoretically modified optical length containing the influencing factors mentioned earlier. In addition, the DH physical boundary has forward that, when the theoretically modified optical length is larger than 10−4, reactivity calculation deviation of volumetric homogenization method will be larger than 100 pcm, and the DH of the dispersed particle-type systems should be considered.
Introduction
Particle-dispersed fuel can contain fission products under high temperature and deep burnup conditions and block the release of fission gas and fission fragments out of the fuel pellets. Because of its accident resistance and inherent safety, it has been widely used in fully ceramic microencapsulated (FCM) fuel (Cole and Maldonado, 2013; Xiang et al., 2014) of pressurized water reactors and the tristructural isotropic (TRISO) particle fuel of high-temperature gas-cooled reactors (Zhai et al., 2004; Zhang et al., 2021).
Particle-dispersed burnable poisons can increase the surface compatibility between the dispersed particles and the matrix by adding a coating layer on the surface of the particles and can improve the flexibility of the use of burnable poison. At the same time, because of the space self-shielding effect of the burnable poison particles, its burn speed is relatively slower than when a burnable poison is uniformed dispersed. So, the appropriate particle-dispersed burnable poison can be selected by selecting the type and particle size of the burnable poison to improve the flexibility of reactivity control (van Dam, 2000a; van Dam, 2000b; Kloosterman, 2003; Talamo, 2006).
Particle-dispersed fuels and burnable poisons have gradually attracted attention and applications due to the excellent characteristics mentioned earlier, but they have double-heterogeneity (DH), which cannot be described by traditional neutronic calculation programs (Sanchez and Pomraning, 1991; Hébert, 1993; Kim et al., 2005; Zhang et al., 2017a; Zhang et al., 2017b). The so-called DH refers to the heterogeneity of the core, cladding, and moderator on the macroscopic level and the heterogeneity of the dispersed particles and the matrix on the microscopic level. The traditional neutronic calculation program can only describe the macroscopic heterogeneity, and the simplest processing method for the DH is the Volumetric Homogenization Method (VHM), that is, the dispersed particles and the matrix are homogenized according to the volume weight, and then, the traditional neutronic calculation program can be used to model and calculate. In the world, a variety of types of DH processing methods have been proposed, e.g., the Sanchez–Pomraning method (Hébert, 1993; Sanchez and Pomraning, 1991) implemented in Dragon and Apollo, the reactivity equivalent-physical transformation method (Lei and Dong, 2020; Li et al., 2018) for treating the FCM (Kurt, 2012) fuel in advanced pressurized water reactor, and the equivalent homogenization method (She et al., 2017) implemented in VSOP (Teuchert et al., 1994) and PANGU (She et al., 2018; She et al., 2021) for treating the TRISO type fuel in high-temperature gas-cooled reactors.
Because the dispersed particles have a spatial self-shielding effect, the materials inside the particles cannot reflect the neutron absorption effect, and the direct use of the VHM will bring a certain degree of reactivity calculation deviation. It is necessary to study the size and influencing factors of the reactivity calculation deviation of the VHM and finally give the DH physical boundary of the dispersed particle system and point out when the VHM can be used for directly processing and when the DH of the system must be considered.
Calculation Object
The Monte Carlo program RMC (Wang et al., 2013) developed by Tsinghua University is used to model the random distribution of dispersed particles. A schematic diagram of the random distribution of dispersed particles in the matrix is shown in Figure 1.
To analyze the spatial self-shielding effect of dispersed particles, a fuel cell is structured as the calculation model, and the main parameters of the fuel cell are shown in Table 1.
First, the fuel particles with different enrichments, volume fractions, and particle radii are dispersed in the zirconium matrix, and the calculation deviation of the VHM of the dispersed fuel is analyzed. Then, the burnable poison particles of different burnable poison types, particle sizes, and volume fractions are dispersed in the fuel matrix with different enrichments, and the calculation deviation of the VHM of the particle-dispersed burnable poisons is analyzed. The detailed calculation parameters are shown in Table 2.
It should be noted that the calculation deviation of VHM in this paper is the reactivity calculation deviation between the grain model and the VHM model of RMC, and the calculation deviation caused by different programs can be ignored. The grain model is performed by the dispersion particle calculation function in RMC, which can simulate the random distribution of dispersed particles. Also, the variance of the results obtained by RMC remains within 0.0003, which is equivalent to 30 pcm, to maintain the accuracy of the calculation results.
Calculation Deviation Analysis of Volumetric Homogenization Method
Particle-Dispersed Fuel
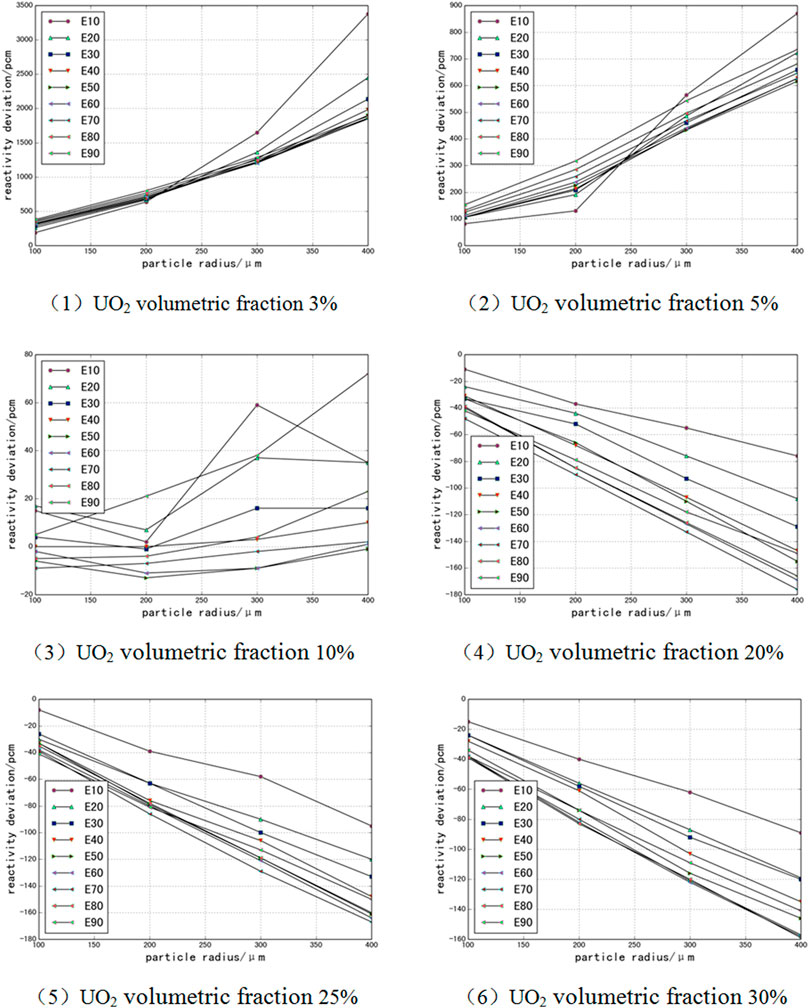
To analyze the reactivity calculation deviation of VHM on particle-dispersed fuel, in this section, the calculation cases cover three influencing factors, which is the fuel volumetric fraction in the range of 3–30%, the fuel enrichment in the range of 10–90%, and the particle radius in the range of 100–400 μm. Although 3–10% of the fuel volumetric fraction is difficult to encounter in engineering, here is a regular study for considering extreme cases. The main calculation results are shown in Figure 2, in which E10–E90 indicates that the enrichment degree is 10–90%. Each figure shows the reactivity calculation deviation curve with particle size between the VHM and particle model of the Monte Carlo program under different fuel volumetric fractions and different fuel enrichment.
It can be seen from Figure 2 that when the fuel volumetric fraction is 3 or 5%, if the dispersed particle radius is 100 μm, the calculation deviation of VHM will be greater than 100 pcm. Also, when the fuel volumetric fraction is 10%, even if the dispersed particle radius reaches 400 μm, the calculation deviation of the VHM is still less than 100 pcm. In addition, when the fuel volumetric fraction continues to increase to 20–30%, if the fuel enrichment is 90% and the radius of the dispersed particles is greater than 200 μm, the calculation deviation of VHM will be greater than 100 pcm.
If the radius of the dispersed particles is less than 100 μm and the fuel volumetric fraction is 10–30%, the calculation deviation of VHM will be less than 100 pcm, and there is no need to consider the DH. Also, if the radius of the dispersed particles is 250 μm, which is the typical size of the TRISO particle core, the fuel enrichment is higher than 20%, the calculation deviation of VHM will be greater than 100 pcm, and DH needs to be considered.
For dispersed UO2 particles, the calculation deviation of VHM decreases with the increase of the volumetric fraction of the dispersed particles, and the calculation deviation is the smallest at approximately 10% of the volumetric fraction. Also, the calculation deviations of VHM will increase with the increase of the size of the dispersed particles and the fuel enrichment.
The volumetric fraction of the dispersed fuel particles affects the probability that the neutrons flying out of the fuel particles will encounter the fuel particles again in the matrix, which may affect the self-shielding effect. As the calculation deviation of the VHM does not change significantly in the range of 10–30%, the in-depth analysis of the influencing factors of the volumetric fraction will not be done here.
Particle-Dispersed Burnable Poison
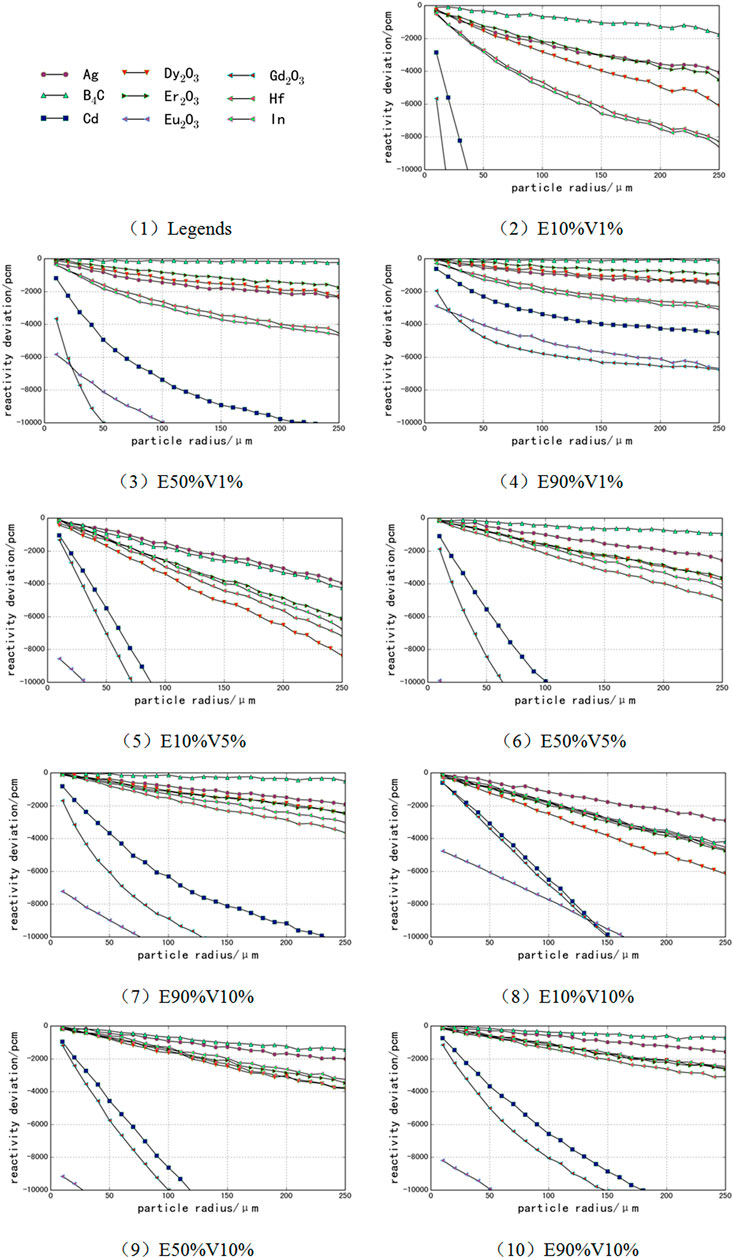
To comprehensively analyze the size of the DH of the cells containing different particle-dispersed burnable poison materials, in this section, the calculation deviations of different types of burnable poison particle systems will be compared, and the factors of different matrix fuel enrichment and poison particle volumetric fraction will be considered. Also, then, the calculation deviation of VHM with the particle radius will be analyzed. The main results are shown in Figure 3, in which “E90%V1%” indicates that the matrix fuel enrichment is 90%, and the volumetric fraction of burnable poison is 1%.
From the calculation results in Figure 3, it can be seen that the self-shielding effect of the dispersed particles of different burnable poison materials is different due to the different absorption cross-sections. The horizontally comparing results of different burnable poison materials show that when the fuel enrichment is 90% and the dispersed burnable poison volumetric fraction is as small as 1%, the DH of the system is the smallest. To ensure that the calculation deviation of the VHM is still less than 100 pcm, the radius of the dispersed B4C, Er2O3, Dy2O3, and Ag particles needs to be less than 20 μm. Therefore, in most cases of burnable poison particles, the calculation deviation of the VHM is relatively large, and its DH should be considered.
For different burnable poison materials, under the same particle size, particle volumetric fraction, and matrix fuel enrichment, the reactivity calculation deviation of the VHM is directly related to the absorption cross-section of the burnable poison. The larger the absorption cross-section, the stronger the self-shielding effect of the particles and the DH of the system, and the larger the deviation of the reactivity calculation of the VHM.
Relation Between Volumetric Homogenization Method Deviation and Optical Length
Relation Between Self-Shielding of Single Particle and Optical Length
From the analysis of the self-shielding effect of the particle-dispersed fuel and burnable poisons, it can be seen that the calculation deviation of the reactivity of VHM is related to many factors. To obtain the judgment condition of whether the DH system can be processed by VHM, the material cross-section and particle size of the dispersed particles should be considered comprehensively to the optical length to judge whether the system needs to consider DH (Pogosbekyan and Han, 2007):
The formula
The physical meaning of Eq. 1 is that when the material cross-section of the particle and the matrix differs to a certain degree, it will cause the flux difference between the materials. Also, when the particle size increases to a certain degree, the internal flux gradient inside the particle will also be caused by the space self-shielding effect. In addition, when the flux difference is greater than a certain level (10% is generally considered), the calculation deviation of VHM will not be negligible, and so, the general optical length limit of Eq. 1 is 0.1. When the inequality relationship in Eq. 1 holds, the DH effects of the system need to be considered.
Relation Between Self-Shielding of System and Optical Length
The calculation formula discussed earlier of the optical length only considers the effect between the matrix and a single particle and does not consider the influence of the mutual shielding effect between the particles on the cross-section, especially the resonance interference effect between the particles. After analysis, Eq. 1 can be revised as Eq. 2:
The formula
The theoretically modified optical length takes into account the volumetric fraction of dispersed particles and the enrichment of matrix fuel. For a specific cell, the larger the volumetric fraction of dispersed particles, the stronger the mutual shielding effect between particles, and so, the larger the theoretically modified optical length. For resonant nuclides, when the volumetric fraction of dispersed particles is large, the resonance interference effect between particles needs to be considered. Numerical fitting results show that the theoretically modified optical length is proportional to the square root of the volumetric fraction of dispersed particles for particles containing resonant nuclides, and the theoretically modified optical length is proportional to the volumetric fraction of dispersed particles for particles without resonant nuclides. Also, the theoretically modified optical length has an inverse relationship with the fuel enrichment of the matrix.
For a fuel cell, when the volumetric fraction of particles and the fuel enrichment of the matrix are determined, a very small particle size, such as the radius of 10 μm, can be used to calculate the material cross-section of the dispersed particles without self-shielding. Also, the cross-section of the matrix is less affected by the size of the dispersed particles and can be taken directly from the cross-section of the matrix when the particle size is 10 μm. At this time, the value on the left side of the Eq. 2 is related to the size of the dispersed particles. When the size of the dispersed particles is greater than a certain value, the theoretically modified optical length calculated according to the Eq. 2 is greater than the limit 10−4, the calculation deviation of VHM will be greater than 100 pcm, and the DH of the system needs to be considered.
Numerical Results
For the DH system of dispersed particles and burnable poisons described in this article, the relationship between the reactivity calculation deviation of VHM and the optical length or the theoretically modified optical length at different fuel enrichment and the fixed volumetric fraction of dispersed particles is shown in Figure 4, Also, then, the relationship between the reactivity calculation deviation of VHM and the optical length or the theoretically modified optical length under a different volumetric fraction of dispersed particles and the fixed matrix fuel enrichment is shown in Figure 5. Finally, the relationship between the calculation deviation of VHM and the theoretically modified optical length changes with the matrix fuel enrichment and the volumetric fraction of the dispersed particle is shown in Figure 6.
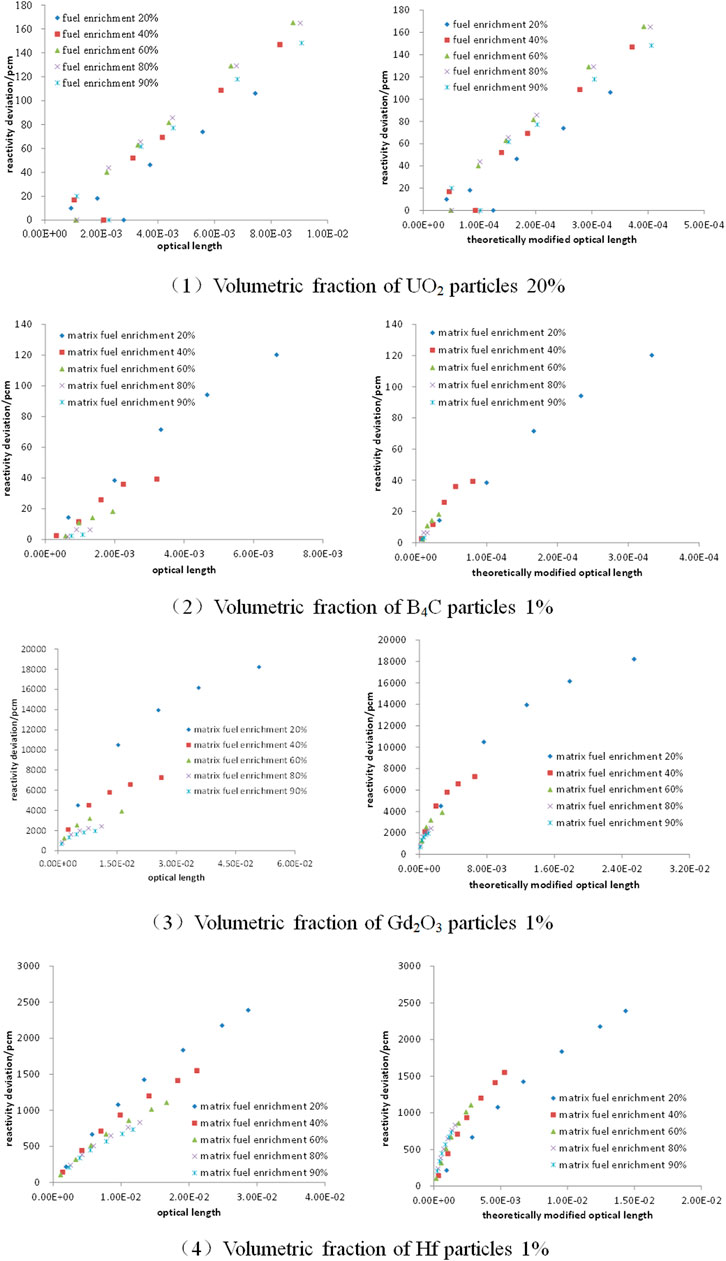
FIGURE 4. Relationship between reactivity deviation and optical length or theoretically modified optical length under different fuel enrichment of matrix.
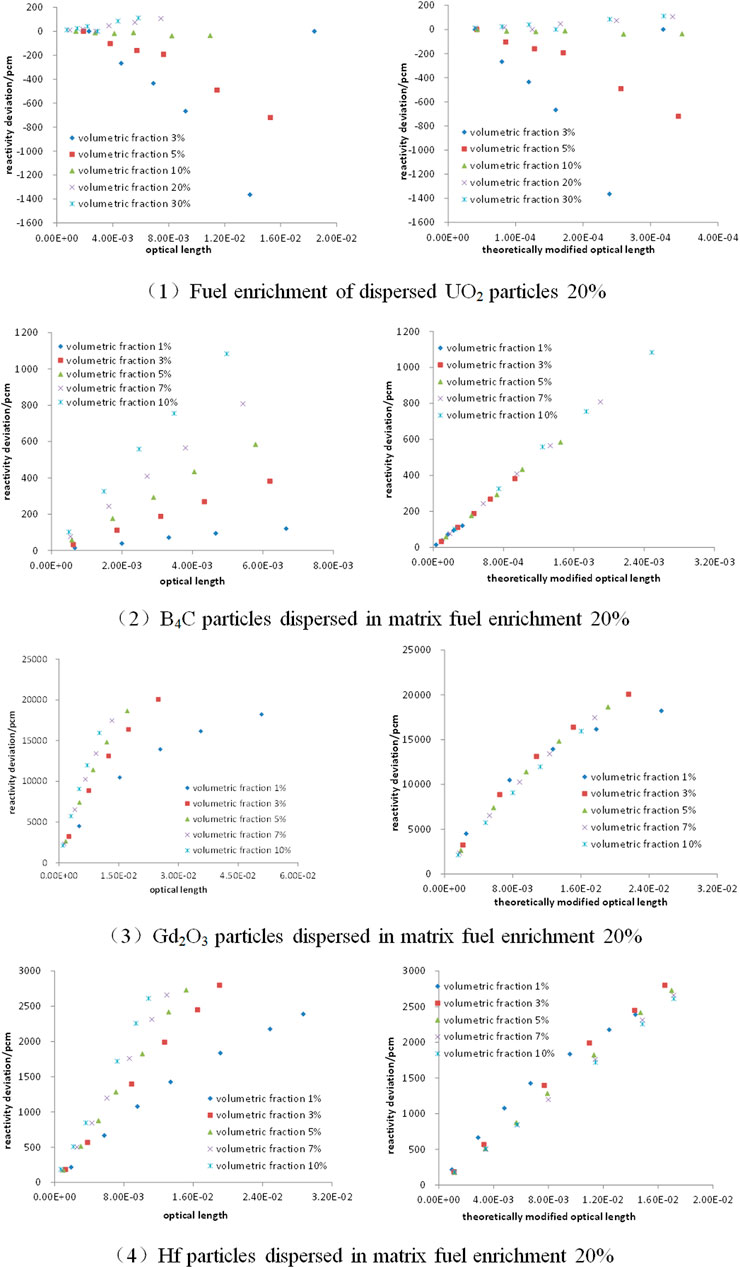
FIGURE 5. Relationship between reactivity deviation and optical length or theoretically modified optical length under different volumetric fraction of particles.
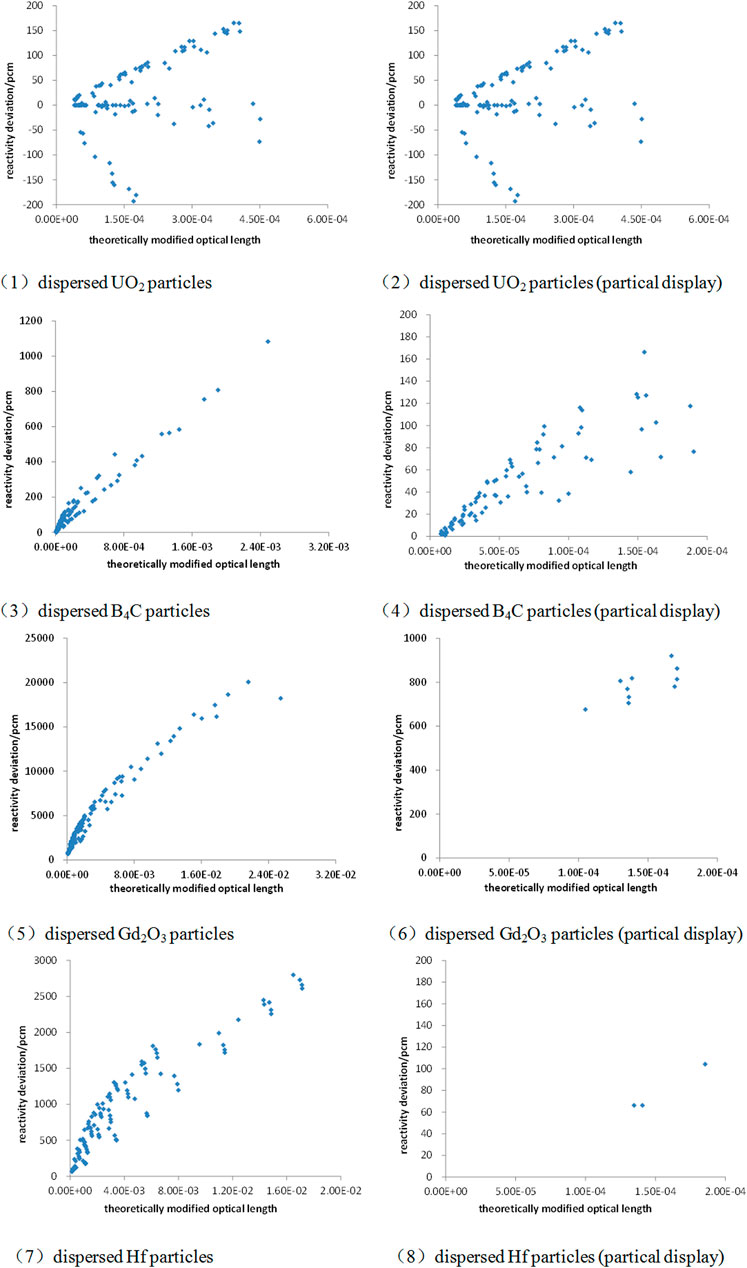
FIGURE 6. Relationship between reactivity deviation and optical length or theoretically modified optical length.
It can be seen from Figure 4 that after fixing the volumetric fraction of the dispersed particles, while changing the size of the dispersed particles, the reactivity calculation deviation of VHM and the theoretically modified optical length are almost linear at different enrichment of UO2 fuel particles or fuel matrix. The larger the theoretically modified optical length, the larger the calculation deviation of VHM. The use of theoretically modified optical length can reflect the law of different matrix enrichment better than optical length.
It can be seen from Figure 5 that after fixing the fuel enrichment, while changing the volumetric fraction of the dispersed fuel particles or burnable poisons, and changing the dispersed particle size at the same time, the reactivity calculation deviation of VHM and the theoretically modified optical length is also almost linear, except for the case where the fuel phase volume is less than 10%. The larger the theoretically modified optical length, the greater the reactivity calculation deviation of VHM. Because the fuel volumetric fraction of less than 10% rarely occurs, we will not analyze it in detail here. The use of theoretically modified optical length can reflect the law of different volumetric fractions of particles better than optical length.
It can be seen from Figure 6 that the relationship between the reactivity calculation deviation of VHM and the theoretically modified optical length are almost linear when the influence factors of fuel enrichment, particle phase volume, and particle size change. The greater the theoretically modified optical length, the larger the calculation deviation of VHM. When the theoretically modified optical length is 10−4, the cell reactivity calculation deviation of VHM is about 100 pcm.
Conclusion
In this paper, by analyzing the reactivity calculation deviation of VHM on particle-dispersed fuel and burnable poisons and its influencing factors, the type of dispersed particles, the type of matrix, the particle size, and other factors are integrated into the optical length, and further research is carried out to integrate the enrichment of fuel matrix and particles, the volumetric fraction of the dispersed particles, and the size of dispersed particles are into the physical quantity of the theoretically modified optical length, and the judgment methods of the particle-dispersed fuel and burnable poisons are integrated into a calculation formula, and the intuitive physical boundary of whether the DH system needs to be considered is given. For particle-dispersed fuel and burnable poison systems in FCM fuel loaded in pressurized water reactor, if the theoretically modified optical length is greater than 10−4, the reactivity calculation deviation of VHM will be greater than 100 pcm, and a DH calculation program needs to be used to consider the DH of the dispersed particles and the matrix in the system.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors without undue reservation.
Author Contributions
LL: conceptualization, methodology, and software. CX: conceptualization. YD: conceptualization. WL: conceptualization. LM: visualization and investigation. CL: visualization and investigation. LX: visualization and investigation. ZH: visualization and investigation. LS: visualization and investigation. TX: funding acquisition and supervision. ZN: funding acquisition and supervision.
Funding
This work is supported by the National Natural Science Foundation of China (approved no: 1170051016).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Cole, G., and Maldonado, I. (2013). A Neutronic Investigation of the Use of Fully Ceramic Microencapsulated Fuel for Pu/Np Burning in PWRs [J]. Fuel Cycle Management. doi:10.13182/NT13-75
Hébert, A. (1993). A Collision Probability Analysis of the Double-Heterogeneity Problem. Nucl. Sci. Eng. 115 (2), 177–184. doi:10.13182/nse115-177
Kim, Y., Kim, K., and Noh, J. (2005). Reactivity-Equivalent Physical Transformation for Homogenization of Double-Heterogeneous Fuels [C]. Busan, Korea: Transactions of Korean Nuclear Society Autumn Meeting.
Kloosterman, J. L. (2003). Application of Boron and Gadolinium Burnable Poison Particles in UO2 and PUO2 Fuels in HTRs. Ann. Nucl. Energ. 30, 1807–1819. doi:10.1016/s0306-4549(03)00134-8
Kurt, A. T. (2012). Microencapsulated Fuel Technology for Commercial Light Water and Advanced Reactor Application. Journals Nucl. Mater. 427, 209–224. doi:10.1016/j.jnucmat.2012.05.021
Lei, L., and Dong, Y. (2020). A Novel Reactivity-Equivalent Physical Transformation Method for Homogenization of Double-Heterogeneous Systems. Ann. Nucl. Energ. 142, 107396. doi:10.1080/00295639.2016.1272363
Li, J., She, D., and Shi, L. (2018). An Improved Reactivity-Equivalent Physical Transformation for Treating FCM Fuel with Burnable Poisons. Ann. Nucl. Energ. 121 (11), 577–581. doi:10.1016/j.anucene.2018.08.024
Pogosbekyan, L., and Han, G. (2007). Implementation of the Sanchez-Pomraning Double Heterogeneity Treatment Method in DeCART, Reactor Physics Laboratory.Seoul: Seoul National University.
Sanchez, R., and Pomraning, G. C. (1991). A Statistical Analysis of the Double Heterogeneity Problem. Ann. Nucl. Energ. 18 (7), 371–395. doi:10.1016/0306-4549(91)90073-7
She, D., Guo, J., and Liu, Z. (2018). PANGU Code for Pebble-Bed HTGR Reactor Physics and Fuel Cycle Simulations[J]. Ann. Nucl. Energ. 126, 48–58. doi:10.1016/j.anucene.2018.11.005
She, D., Xia, B., and Guo, J. (2021). Prediction Calculations for the First Criticality of the HTR-PM Using the PANGU Code[J]. Nucl. Sci. Tech. 32 (9), 1–7. doi:10.1007/s41365-021-00936-5
She, D., Liu, Z., and Shi, L. (2017). An Equivalent Homogenization Method for Treating the Stochastic media. Nucl. Sci. Eng. 185, 351–360. doi:10.1080/00295639.2016.1272363
Talamo, A. (2006). Effects of the Burnable Poison Heterogeneity on the Long Term Control of Excess of Reactivity. Ann. Nucl. Energ. 33, 794–803. doi:10.1016/j.anucene.2006.04.009
Teuchert, E., Haas, K. A., Rütten, H. J., Brockmann, H., Gerwin, H., Ohlig, U., et al. (1994). V.S.O.P. (94) Computer Code System for Reactor Physics and Fuel Cycle Simulation. Jülich, Germany: Forschungszentrum Jülich
van Dam, H. (2000a). Long-Term Control of Excess Reactivity by Burnable Particles. Ann. Nucl. Energ. 27, 733–743. doi:10.1016/s0306-4549(00)82014-9
van Dam, H. (2000b). Long-Term Control of Excess Reactivity by Burnable Poison in Reflector Regions. Ann. Nucl. Energ. 27, 63–69. doi:10.1016/s0306-4549(00)82005-8
Wang, K., Li, Z. G., and She, D. (2013). RMC-A Monte Carlo Code for Reactor Physics analysisJoint International Conference on Supercomputing in Nuclear Applications and Monte Carlo. Paris: France.
Xiang, Dai., Cao, X., Yu, S., and Zhu, C. (2014). Conceptual Core Design of an Innovative Small PWR Utilizing Fully Ceramic Microencapsulated Fuel. J. Prog. Nucl. Energ. 75, 63–71. doi:10.1016/j.pnucene.2014.04.010
Zhai, T., Kadak, A. C., and No, H. C. (2004). LOCA and Air Ingress Accident Analysis of a Pebble Bed Reactor, MIT Center for Advanced Nuclear Energy Systems [J]. MIT-ANP-TR-102.
Zhang, T., Yin, H., Li, X., She, D., Pan, Q., He, D., et al. (2021). Studies on calculation models of ASTRA critical facility benchmark using OpenMC. Ann. Nucl. Energy 158, 108291. doi:10.1016/j.anucene.2021.108291
Zhang, T., Wang, Y., Lewis, E. E., Smith, M. A., Yang, W. S., and Wu, H. (2017a). A Three-Dimensional Variational Nodal Method for Pin-resolved Neutron Transport Analysis of Pressurized Water Reactors. Nucl. Sci. Eng. 188 (2), 160–174. doi:10.1080/00295639.2017.1350002
Keywords: dispersed particle-type systems, double-heterogeneity, physical boundary, volumetric homogenization method, reactivity calculation deviation, optical length, corrected optical length
Citation: Lei L, Xiaoming C, Dong Y, Lianjie W, Mancang L, Liang C, Xiaoli L, Hongbo Z, Sinan L, Xiao T and Nan Z (2022) Theoretically Modified Optical Length Research on the Physical Boundary of the Double-Heterogeneous System. Front. Energy Res. 9:773067. doi: 10.3389/fenrg.2021.773067
Received: 09 September 2021; Accepted: 28 December 2021;
Published: 09 February 2022.
Edited by:
Tengfei Zhang, Shanghai Jiao Tong University, ChinaReviewed by:
Tiejun Zu, Xi’an Jiaotong University, ChinaZhitao Xu, North China University of Water Resources and Electric Power, China
Copyright © 2022 Lei, Xiaoming, Dong, Lianjie, Mancang, Liang, Xiaoli, Hongbo, Sinan, Xiao and Nan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chai Xiaoming, Y2hhaXhtQDE2My5jb20=
 Lou Lei
Lou Lei Chai Xiaoming*
Chai Xiaoming*