- 1Innovation Institute for Sustainable Maritime Architecture Research and Technology, Qingdao University of Technology, Qingdao, China
- 2Faculty of Environmental Engineering, The University of Kitakyushu, Kitakyushu, Japan
- 3School of Mechanical and Energy Engineering, Tongji University, Shanghai, China
- 4Energy and Environment Engineering Institute, Shanghai University of Electric Power, Shanghai, China
At present, countries all around the world have implemented energy-saving and emission reduction measures to achieve carbon neutralization. The combined cooling, heating, and power (CCHP) system is a high-efficiency energy system that can promote energy-saving and decrease carbon emissions. The choices of installed capacity and operation strategies impacts the economy, energy-saving, and environmental protection of combined cooling, heating, and power systems. The aim of this study was to determine the potential and comprehensive benefits of combined cooling, heating, and power systems based on the comprehensive performance assessment. In this study, a comprehensive performance index (CPI) method was presented to optimize the configurations and operation strategies of combined cooling, heating, and power systems in a Japan eco-campus, based on historically monitored data. According to the influencing factors of the combined cooling, heating, and power system in comprehensive performance index evaluation, the adaptability and development potential of economy, energy saving, and CO2 emission reduction were evaluated to consider future renovation of energy systems. In this study, we adopted a seasonal time-of-use (STOU) electricity price to evaluate the economic performance of combined cooling, heating, and power systems and compared them to the time-of-use (TOU) electricity price. The results indicated that the seasonal time-of-use electricity price was more economic in regions that had high cooling demand in summer. By comparing the CO2 emission coefficient of electricity in different regions in Japan, we could estimate that more than 40% of the cleaner energy ratio was positive. The results obtained can provide suggestions for the future development of combined cooling, heating, and power systems.
Introduction
Owing to the continuous growth in the world’s energy demand, the problems of energy consumption, greenhouse gas emission, and environmental pollution have become increasingly prominent (Jing et al., 2018). Combined cooling, heating, and power (CCHP) system has been recognized as an efficient and economic method to realize the integration of power generation, cooling, and heating through the cascade utilization of energy; notably, the comprehensive energy utilization efficiency of the system can reach 85% (Papadimitriou et al., 2020). There are various types of equipment in CCHP systems, and there is a coupling relationship between the equipment (Wu and Wang 2006). The equipment installed capacity and operation strategy have a significant impact on the economic and environmental benefits and energy efficiency of the systems. The configuration of equipment is crucial in such cases. Unreasonable configuration of equipment types and excessive capacity can lead to the waste of investment and low utilization efficiency of systems, whereas undersized capacity cannot meet the demand of the building in the area load demand, which may lead to an increase (rather than decrease) in energy consumption. At present, the economic benefits of CCHP systems are greatly reduced due to the mismatch of installed capacity (Lin et al., 2020). Therefore, to improve the performance of CCHP systems, the capacity and operation optimization of CCHP systems has become an important research direction.
Numerous studies have been conducted on the optimization of CCHP systems. Wang et al. (Wang et al., 2010a) optimized the capacity of power generation unit (PGU) selected in the design period and the fixed ratio of electric cooling to cool demand used in operation period. Ren et al. (Ren and Gao 2010) optimized the configuration and technology combination alternatives by minimizing the total energy cost. Furthermore, Ren et al. (Ren et al., 2021) optimized the hybrid CCHP systems for three buildings (hotel, office, and market) under different operation strategies. Kim et al. (Kim et al., 2019) selected the capacity of PGUs, value of thermal storage system, cooling/heating capacity ratio supplied by electrically driven systems, and maximum heat power from the storage system as the decision variables to optimized the CCHP system.
Notably, different optimization algorithms were applied to CCHP systems. Wang et al. (Wang et al., 2010b) employed particle swarm optimization algorithm (PSOA) to optimize the capacity of PGUs and heat storage tank, on-off coefficient of PGU, and ratio of electric cooling to cooling load. Sanaye et al. (Sanaye and Khakpaay 2014) optimized the capacity of gas engine, backup boiler, energy storage tank, electrical and absorption chiller by combining an optimization algorithm with the maximum rectangle method. Kong et al. (Kong et al., 2009) adopted a non-linear-programming (NLP) cost-minimization optimization model to determine the operation strategies for the CCHP system. Bischi et al. (Bischi et al., 2014) employed mixed integer nonlinear programming (MINLP) to determine an operating schedule. Cao et al. (Cao et al., 2020) used owl search algorithm (OSA) to increase the efficiency of the CCHP system, in comparison with the separation production system. Ghersi et al. (Ghersi et al., 2021) adopted genetic algorithm (GA) to optimize the capacity of the CCHP system.
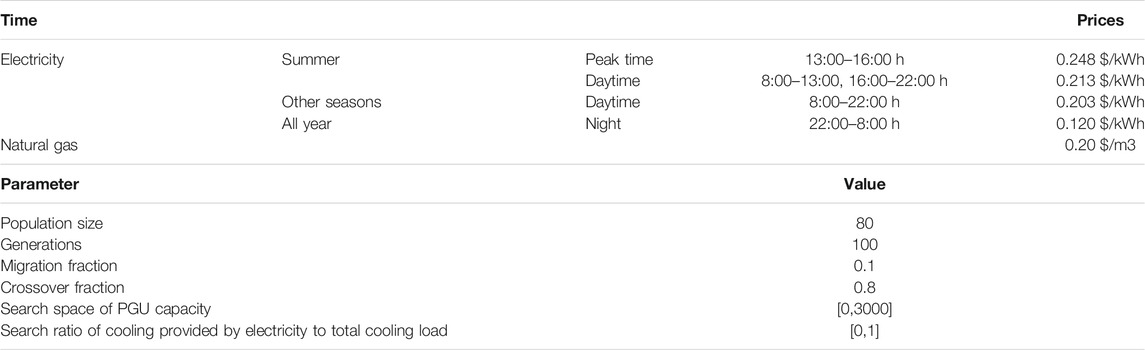
Conventional optimization is based on economy, and the most important parameter affecting economy is electricity price. Different electricity price mechanisms have different effects on the investment cost, operating cost, and energy saving of the CCHP system. Generally, to simplify calculations, most researchers used a fixed electricity price mechanism (Li et al., 2020; Soltani et al., 2020). Some researchers used time-of-use (TOU) electricity price to improve CCHP system utilization efficiency and reduce investment and operating costs (Wu et al., 2014). However, only a few studies have been conducted on the STOU electricity price mechanism. Seasonal price refers to an electricity price mechanism that reflects the cost of power supply in different seasons. The main purpose is to suppress the excessively rapid growth of electricity load during peak seasons to reduce investment and operating costs. However, only a few studies have been conducted on the combination of peak-valley and seasonal electricity price mechanisms.
Sensitivity analysis determines the change of decision evaluation criteria by changing one or more uncertainties. Yan et al. (Yan et al., 2016) and Zheng et al. (Zheng et al., 2018) analyzed the sensitivity of electricity price and natural gas price and explained the changes in important criteria at different prices. Zhang et al. (Zhang et al., 2020) analyzed the performance of the CCHP system and deduced that it can be improved by changing the electricity price, natural gas price, investment subsidy, and carbon tax. Delgado et al. (Delgado et al., 2017) analyzed the sensitivity of interest rate, heat export, and energy price escalation rates to address the behavior of the results due to changes in the economic context.
In addition to economic performance, the influencing factors of CCHP systems are also very important for energy saving and emission reduction (Wei et al., 2016). Therefore, it is essential to evaluate the comprehensive performance assessment of CCHP systems. Tamjidi et al. (Farahbakhsh and Chahartaghi 2020) assessed the payback period and profitably index of a novel integrated CCHP system from energy and economic perspectives. Li et al. (Li et al., 2019) presented a CCHP and ground source heat pump (GSHP) coupling system equipped with a heat exchanger and used life cycle cost saving rate and primary energy consumption saving ratio compared with separated generation system. Additionally, Wang et al. (Wang et al., 2011) used a comprehensive evaluation index to optimize the PGU capacity and the ratio of electric cooling to the cooling load.
As mentioned above, although many studies have focused on CCHP system optimization, there is still a lack of knowledge about the comprehensive performance analysis of the system to improve its development potential. The purpose of this study is to consider the comprehensive performance assessment of energy conservation and environmental protection and discuss the impact of different electricity price mechanisms on the development of CCHP system. In this study, the GA method was used to optimize the capacity of PGU and operation strategies for CCHP systems. Then, the economy, energy saving, and CO2 emission reduction of the CCHP system were analyzed. Finally, we conducted the sensitivity analysis of energy price and CO2 emission reduction. This study is organized as follows: Methods section introduces the energy flow of the CCHP and separated production (SP) systems and puts forth the evaluation index of CCHP systems and genetic algorithm (GA) optimization method used in our study. Case Study section introduces a case study and the corresponding parameters of a CCHP system. Section 4 analyzes the operation strategies, comprehensive performance, and sensitivity analysis of energy price and CO2 emission reduction potential of CCHP systems. The conclusions are provided in Section 5.
Methods
Energy Flow of CCHP and SP Systems
Firstly, the model of CCHP systems and SP systems were established and the decision variables were proposed. Then a single objective comprehensive evaluation system was established for assessing cost saving, energy saving, and CO2 emission reduction. Finally, the GA was used to optimize the CCHP and SP systems.
The energy flow of CCHP systems and SP systems was introduced, which was then, used to calculate the power generation, energy consumption, and capacity of a power generation unit (PGU) and auxiliary equipment to obtain the optimal result of these systems.
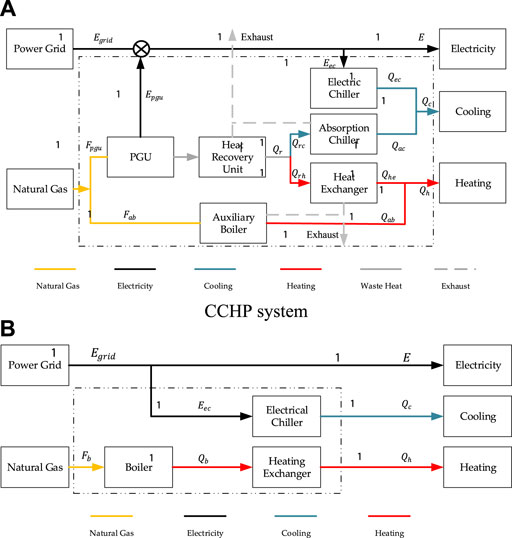
The CCHP system used in our study was driven by PGU, as shown in Figure 1A. Natural gas was supplied to PGU to produce electricity. Considering the optimal economy for users, the power generated by PGU is supplied directly to users. If generated power cannot meet the electricity demand, the shortage of power can be purchased from the power grid. The exhaust heat from PGU was recovered by the heat recovery unit, and then the steam generated by the heat recovery unit is used as a heat source to heat the heat exchanger to meet the heat demand of users. When the recovered heat could not meet the heating demand, sufficient heat was provided by the auxiliary boiler. The cooling demand was provided by a heat recovery unit through an absorption chiller, and the insufficient cooling was supplied by the electric chiller.
As shown in Figure 1B, the electricity demand of SP systems was supplied by the power grid, cooling demand was supplied by the electric chiller, and the heating demand was supplied by a gas boiler.
The balance of the electricity demand of CCHP systems is expressed as follows:
where
The fuel energy consumption of the PGU,
where
The waste heat generation of PGU,
where
The waste heat from the PGU was used to cover the cooling and heating demand and can be expressed as follows:
where
where
The cooling demand generated by the electric chiller,
Where
The fuel energy consumption of the auxiliary boiler,
where
The total fuel energy consumption of the CCHP systems,
The total electricity purchased from the grid of SP systems,
The total fuel energy consumption of the SP systems,
where
Decision Variables
Power Generation Unit Capacity
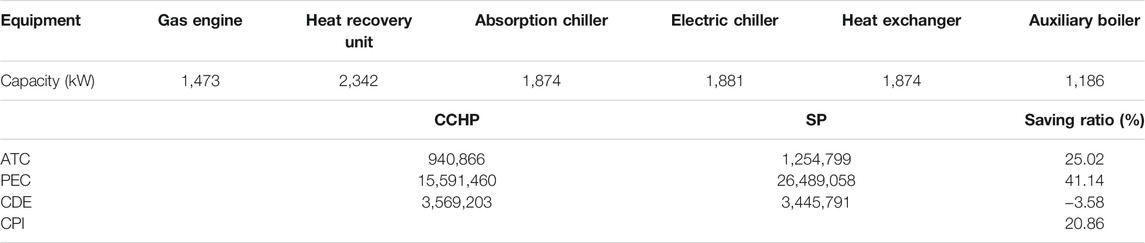
PGU capacity has a significant effect on the economic, energy-saving, and environmental performance of CCHP systems. When the capacity of the PGU is established, the capacity of heat recovery unit is determined using the maximum recovery heat of PGU. The absorption chiller uses the recovery heat of PGU to meet cooling demands, and therefore, the capacity of the system changes according to PGU. The capacity of other equipment was calculated using the cooling and heating loads.
Ratio of Cooling Load Provided by Electricity to Total Cooling Load
The total cooling load of the building was provided by the absorption chiller and the electric chiller. When the recovery heat generated by the PGU was sufficient to meet the cooling demand, the electric chiller stopped operating. Otherwise, the electric chiller needed to be operated to supplement the insufficient cooling demand. Considering the change of cooling demand at each moment, the optimized ratio of cooling load provided by the electricity to total cooling load ratio was not a fixed value, owing to the innumerable changes in the cooling demand. Therefore, it was necessary to optimize the ratio of cooling load provided by the electricity to total cooling load ratio.
Evaluation Index
Annual Total Cost Reduction
The annual investment cost (AIC) is the total investment cost of all equipment of CCHP systems, $/year, and can be expressed as:
where
The annual maintenance cost (AMC) was calculated using the following equation:
where
The annual operating cost (AOC) is the total cost of the gas consumption and electricity purchase in a year, $, and was calculated using the following equation (due to the labour cost accounts for a small proportion of the total operating cost, it can be neglected):
where
The annual total cost (ATC) is the sum of the above three costs and can be calculated using the following equation:
The cost-saving ratio (CSR) is the annual total cost-saving ratio of the CCHP systems compared with SP systems:
Primary Energy Consumption
Primary energy consumption (PEC) refers to the consumption of total fuels to meet the demand for electricity and thermal demands (kWh) and can be calculated using the following equation:
where
Primary energy saving ratio (PESR) was defined to assess the energy consumption of CCHP systems in comparison with SP systems, using the following equation:
Carbon Dioxide Emission Reduction
The impact of CCHP systems on the environment mainly comes from carbon dioxide emission (CDE); it can be determined using the emission conversion factors as follows:
where
Furthermore, the carbon dioxide emission reduction (CDER) was calculated using the following equation:
Payback Period
The static investment payback period refers to the time required to recover the entire investment amount without considering the value of time. The static payback period (PB) of the system was calculated using the following equation:
where
Objective Function
The weight coefficient method was used to weight sum each evaluation index for obtaining the final optimization results in this study. The comprehensive performance index (CPI) was considered as the objective function of the model and the maximum value; it was defined using the following equation:
where
Optimization
GA was designed and proposed according to the evolution law of organisms in nature. It is a method to search for the optimal solution by simulating the natural evolution process. GA can be used for global optimization because it can extend the search space to the whole problem (Wen et al., 2020).
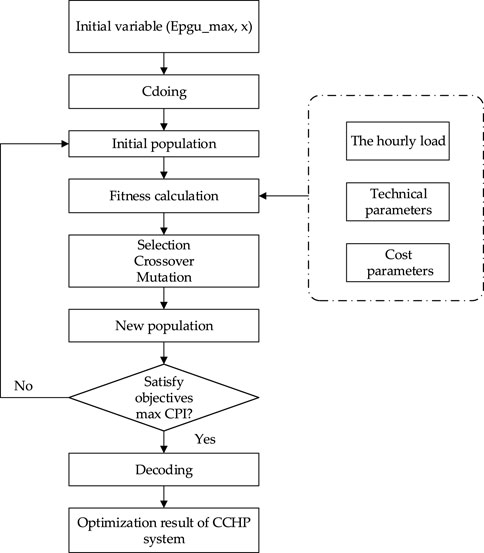
Notably, the optimization procedure of the CCHP systems is shown in Figure 2. It can be summarized as follows:
1. The initial population was created randomly.
2. Each individual of the population was coded into a binary number.
3. Due to the objective value being greater than 0, the opposite number of objective values was used as the input of fitness function. Then, the fitness of each individual was evaluated. If the objective function was optimal, the optimal individual was output. Otherwise, we proceeded on to the next step.
4. The individuals with high fitness values were selected, because the higher the fitness value, the more likely an individual is to be chosen for crossover.
5. Then, new individuals were created through reproduction, crossover, and mutation.
6. A new population with new individuals was created. When the max comprehensive performance index (CPI) was satisfied, the optimization was concluded. If not, the optimization process was restarted from Step 3.
In this study, the GA method was implemented using MATLAB software. The GA function of MATLAB was used to solve the objective function. It should be pointed out that a negative sign must be added to revise the default minimum value of the result in MATLAB to the maximum value, because a maximum value is required as the result of the simulation.
Introduction of Case Studies
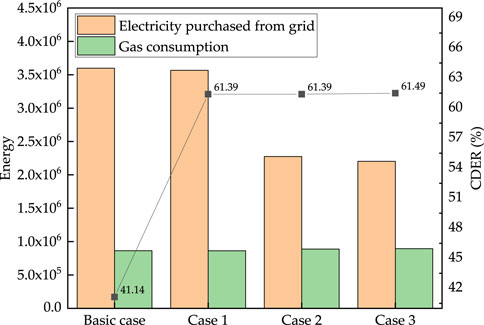
In this study, we compared different cases for energy saving analysis. The power generation efficiency of the gas engine and the coefficient of performance (COP) of the electric chiller affected the energy saving of the CCHP system. Three cases were considered for comparison with the basic case, and the measurements are shown in Table 1. In Case 1, the power generation efficiency and thermal efficiency of the gas engine remained unchanged, and the COP of the electric chiller increased to 4. In Case 2, the COP of the electric chiller remained unchanged, and the power generation efficiency of the gas engine is increased to 0.45; to ensure that the comprehensive energy utilization rate remained unchanged, the thermal efficiency of the gas engine was reduced to 0.327. In Case 3, the power generation efficiency of the gas engine increased to 0.45, thermal efficiency reduced to 0.327, and the COP of the electric chiller increased to 4.
Case Study
Introduction of Case and Energy Demands
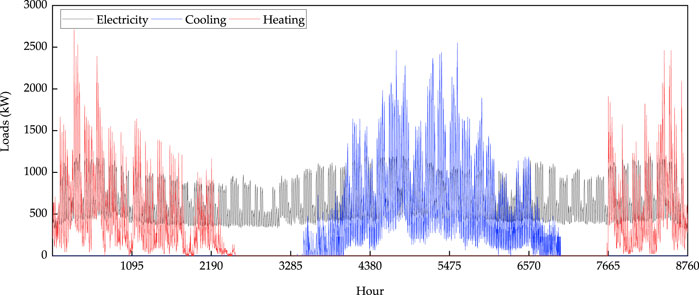
In this study, we chose the eco-campus of the Kitakyushu Science and Research Park (KSRP) in Japan as an example (Ren et al., 2010). KSRP is located in Kitakyushu, a world-renowned environmental symbiosis city, and is a scientific research core for environmentally friendly construction in Kitakyushu. The total area of KSRP is approximately 335 ha. The eco-campus has been using CCHP system since 2001 to provide electricity, cooling, and heating demand for the energy center, collaboration center, conference center, library, gym, teaching building and experiment building, technology development and exchange center. The buildings in the area are prefabricated buildings of 4-floor and below, and the fence structure has reached the standard of high-level energy-saving buildings. The area has received the A-class certification from CASBEE-block/region of Japan. The CCHP system can satisfy the larger electricity, cooling, and heating demand of the eco-campus, and effectively reduce the energy cost. The hourly electricity, cooling, and heating demands were obtained through the energy center of the KSRP (Figure 3).
Generally, there are two operation strategies of the CCHP system: following the electrical load and following the thermal load. When the system follows the electrical load, the excess heat will be generated. If there is no storage heat device, the excess heat will not be fully utilized and lead to the low utilization efficiency of energy. When the system follows the thermal load, it gives priority to meet the cooling and heating load of the building. If generated power cannot meet the electricity demand, the shortage of power can be purchased from the power grid, which makes full use of waste heat resources and makes the system more efficient of the energy utilization. The eco-campus energy demand is mainly electricity, heating and cooling. The demand for heating and cooling are significantly greater than the demand for electricity, and there is no heat storage device designed in the system. Therefore, in order to avoid more energy cost due to larger heating and cooling load and inefficient energy utilization, this study adopts following the thermal load (FTL).
Setting of Parameters
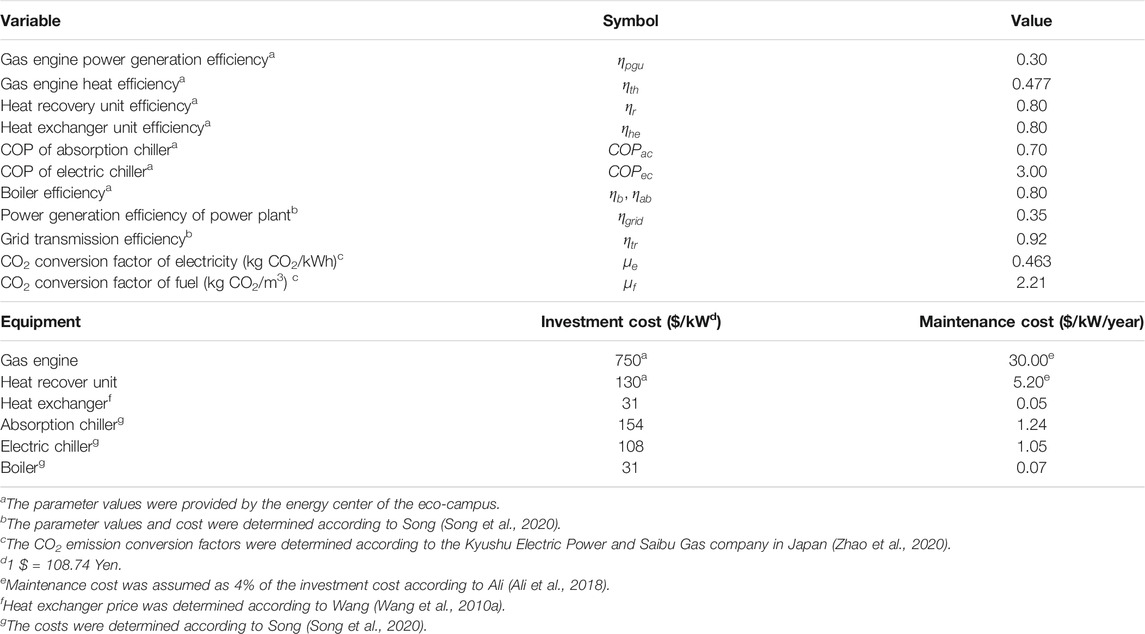
According to the investigation and based on the information provided by the energy center of the eco-campus and related studies, the technical parameters and investment cost and maintenance cost of the main equipment of the system are shown in Table 2. To reduce the operation cost, we adopted the STOU electricity price mechanism. The prices of electricity and gas and GA parameters are shown in Table 3.
Results and Discussion
Results of Optimization
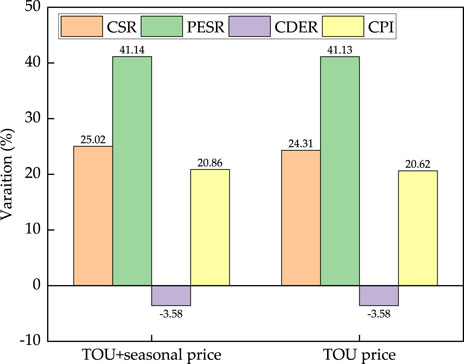
The equipment capacity of the CCHP system obtained after optimization is shown in Table 4. It can be seen that the cost-saving ratio was 25.02%, primary energy saving ratio was 41.14%, CO2 emission reduction ratio was −3.58%, and CPI was 20.86%. Because the CO2 emission coefficient of gas is 2.21 kg CO2/m3 and electricity is 0.463 kg CO2/kWh, the gas engine was only used for power generation; notably, more CO2 was generated when the recovered heat was not used. Therefore, in our study, the CO2 emission of CCHP system was higher than that of separated production (SP) system.
Figure 4A shows the hourly electricity generated from the gas engine and purchased from the grid. The yellow line in Figure 4A indicates the electricity purchased from the grid, and the lower part indicates the excess electricity generated by the gas engine. Notably, the excess electricity was generated by the gas engine in winter or summer, when the cooling and heating demands were high (and the electricity price was high). Because the system following the thermal load, the system prioritized meeting the cooling and heating demands, which increased the gas engine power generation (higher than the electricity demand). During the transition seasons, there was no demand for cooling and heating, and the gas engine power generation only needed to meet the electricity demand; in this case, the required electricity was purchased from the grid.
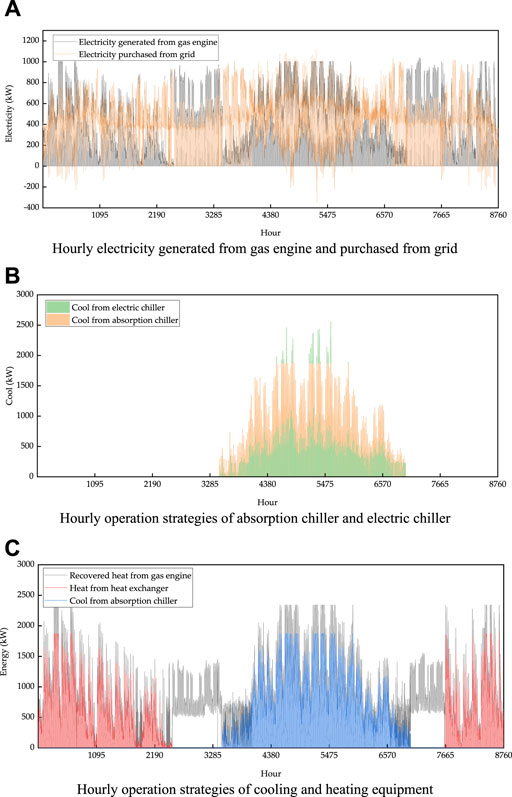
FIGURE 4. Hourly operation strategies of the CCHP system: (A) Hourly electricity generated from gas engine and purchased from grid, (B) Hourly operation strategies of absorption chiller and electric chiller, (C) Hourly operation strategies of cooling and heating equipment.
Figure 4B shows the hourly operation strategies of the absorption chiller and electric chiller. The electric chiller provided cooling mainly during the period of valley electricity prices and low cooling demands. The absorption chiller provided cooling during the day when electricity prices were high, and the electric chiller covered the unmet cooling demand during peak electricity prices.
Figure 4C shows the hourly operation strategies of the cooling and heating equipment. The gray line in Figure 4C represents the recovered heat generated by the gas engine. Due to the high demand for cooling and heating in winter and summer, the recovered heat could be fully utilized. However, during the transition season, there was no demand for cooling and heating, but large electricity demand; therefore, a gas engine was required to generate electricity to meet the electricity demand, and the recovered heat at this time was wasted.
Figures 5A,B shows the optimal strategies of the typical days in summer and winter. It can be seen that the gas engine runs from 8:00 to 21:00 and stops from 22:00 to 7:00. During the valley electricity price period in summer, all the cooling demand is provided by the electric chiller. During the day that the cooling demand is provided by the absorption chiller, and the insufficient cooling demand during the peak electricity price period is supplemented by the electric chiller. During the valley price period in winter, all the heating demand is provided by the auxiliary boiler. The heating demand is provided by the heat exchanger during the day, and the insufficient heat is supplemented by the auxiliary boiler. Because the gas engine stops during the valley electricity price period, the electricity at this time is all purchased from the grid to meet the electricity demand. The electricity supply of the gas engine during the day is determined by the demand for cooling and heating, and the unmet electricity demand is fulfilled by the grid. Figures 5C,D shows the economic comparison between the CCHP system and the SP system for typical days in summer and winter. It can be seen that the CCHP system has more economic advantages than the separate production system no matter in summer or winter. However, the energy cost of the CCHP system is higher than the separate production system during the period when the CCHP system is stop running, due to the heating and cooling demand during the valley electricity price period is provided by auxiliary equipment, which results in higher energy costs. In summer, CCHP systems save 53.47% of energy costs compared to separate production systems, and 51.20% of energy costs in winter. Therefore, using CCHP systems under this operation strategy has more economic potential than the separate production system.
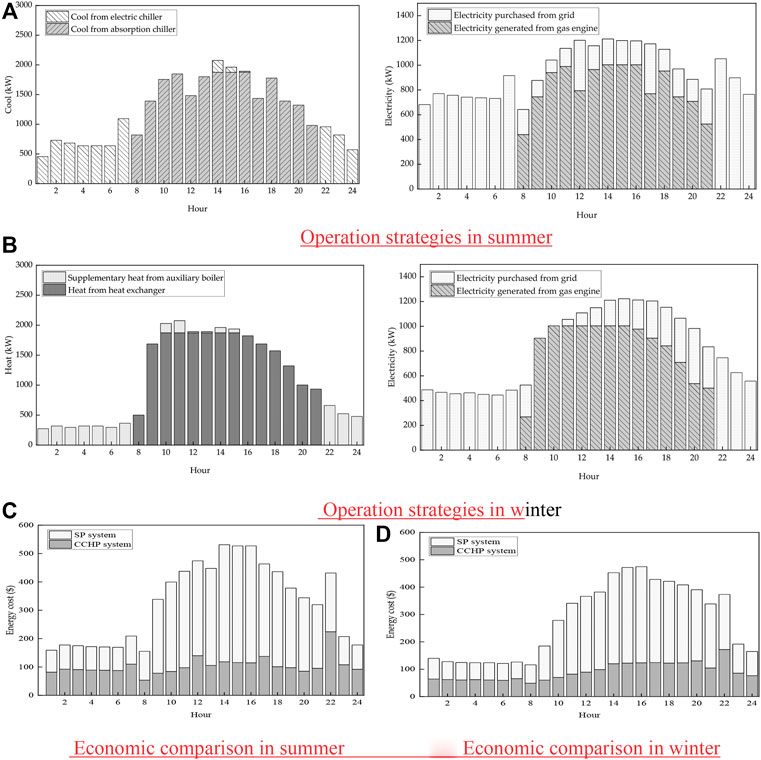
FIGURE 5. Optimal strategies and economic comparison between the CCHP system and the SP system for typical days in summer and winter: (A) Operation strategies in summer, (B) Operation strategies in winter, (C) Economic comparison in summer, (D) Economic comparison in winter.
Comprehensive Performance Analysis
Cost Saving Analysis
In Japan, there are many electricity pricing mechanisms. In this section, we have compared the seasonal time-of-use (STOU) and time-of-use (TOU) prices (Figure 6). We observed that the Primary energy saving ratio (PESR) and carbon dioxide emission reduction (CDER) were basically unaffected by the changes in the electricity price. The electric chiller needed to be operated to meet the largest cooling demand from 13:00 h to 16:00 h in summer, and peak electricity appeared in the period because of the STOU electricity mechanism. To save the operating cost during the peak period of electricity consumption, the gas engine was shut down during the valley price period, and all the cooling load was provided by the electric chiller. The gas engine was started during the day to meet the cooling demand as much as possible. In this way, the cooling load supplemented by the electric chiller was reduced, and the operation cost during the peak electricity price period in summer was saved in a large section. When the TOU price was adopted, the cost-saving ratio of the CCHP system was 24.31%. When the STOU was considered, the cost-saving ratio of the CCHP system was 25.02%. Thus, the TOU price has advantages for the economy of the CCHP system, but for the regions having large cooling demands in summer, it was more economic to adopt the STOU pricing mechanism.
Energy Saving Analysis
Figure 7 shows the energy consumption of the CCHP system in different cases. All cases had better energy-saving performance than the basic case; Case 3 was the ideal case and could save energy by 61.49%. Notably, the electricity purchase in Case 1 was significantly higher than that in Case 2, and the natural gas consumption of Case 2 was higher than that of Case 1, while the CDER remained the same. This is because Case 2 improved the power generation efficiency of the gas engine and increased the power generation of the gas engine, while the reduction of the thermal efficiency reduced the recovery heat generated by the gas engine and required more natural gas consumption to meet the heating demand in winter. Thus, improvement in the COP of the electric chiller and the power generation efficiency of the gas engine can save energy consumption.
CO2 Emission Reduction Analysis
The CO2 emission reduction performance in this study was negative. However, in Japan, the CO2 emission coefficient of electricity is different in each region. The reason for the different CO2 emission coefficients of electricity is that the proportion of renewable energy and nuclear power, which do not emit carbon dioxide, is different. Table 5, shows the CO2 emission coefficient of electricity in different regions, and the results are shown in Figure 8. In our study, the CDER of Hokkaido, Tohoku, Kinki, and Chugoku were positive, while those of other regions were negative. This shows that the CCHP system is more suitable in regions where the CO2 emission coefficient of electricity is greater than 0.5 and the CDER is positive. And we convert the CO2 emission coefficient of electricity into the clean energy ratio, accounting for 40%.
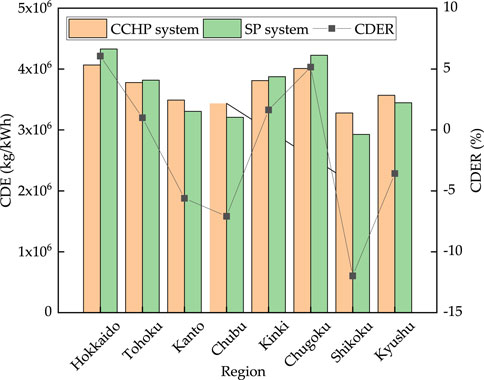
FIGURE 8. Carbon dioxide emission and Carbon dioxide emission reduction in different regions of Japan.
Sensitivity Analysis
Influence of Energy Price on the Economic Performance of CCHP System
The electricity price affects the operating cost of the CCHP system, and the operating costs account for a large proportion of the total system costs. Consider the electricity price in Table 3 as the basic price, and decrease or increase 0–50% of that to analyze the impact of electricity price on the CCHP system’s economic performance. Figure 9A shows the change in the payback period and the total cost-saving ratio of the CCHP system, with different electricity prices, when the gas price remained unchanged. With the increase in electricity price, the payback period showed a downward trend, while the cost-saving ratio showed an upward trend. When the electricity price dropped by 50%, the payback period of the CCHP system was 12.6 years, and the total cost-saving ratio (CSR) of that was 4.11%. However, when the electricity price increased by 50%, the payback period of the CCHP system was about 3.6 years, and the total CSR of that was 32.98%. This indicates that a drop in the electricity price can decrease the economic performance of the CCHP system. This is because all electricity consumption of the SP system was purchased from the grid, while the CCHP system could generate electricity by the gas engine; the electricity deficit was fulfilled by the grid, which greatly reduced the amount of electricity purchased.
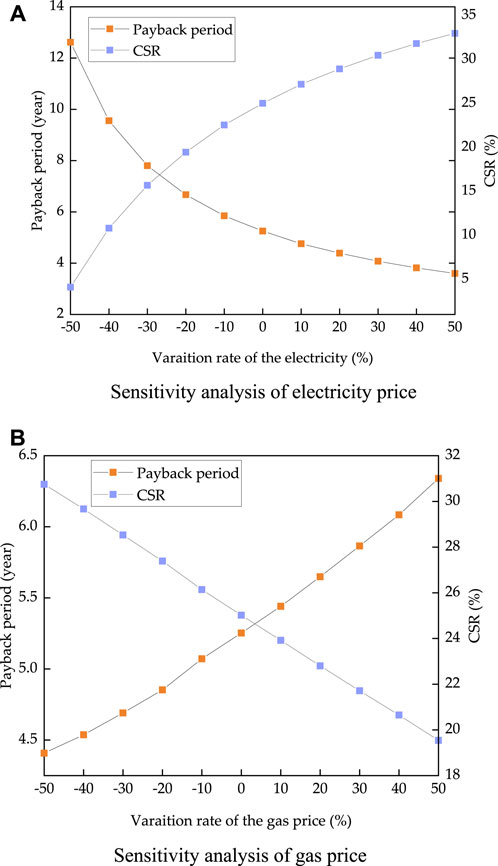
FIGURE 9. Sensitivity analysis of energy price: (A) Sensitivity analysis of electricity price, (B) Sensitivity analysis of gas price.
The natural gas price also affects the economic performance of the CCHO systems. The impact of gas price on the economic performance of the CCHP system is shown in Figure 9B. Contrary to the electricity price, the payback period of the CCHP system showed an increasing trend with increasing gas price, whereas the total CSR showed a downward trend. When the gas price dropped by 50%, the payback period was 4.4 years, and the total CSR was 30.75%. When the gas price increased by 50%, the payback period was 6.3 years, and the total CSR was 19.54%. The natural gas consumption of the CCHP system was greater than that of the SP system because natural gas was required by the CCHP system for power generation and boiler operation. Therefore, the increase in gas price can lead to a decrease in the economic performance of the CCHP system.
Influence of CO2 Emission Coefficients on the Economic Performance of CCHP System
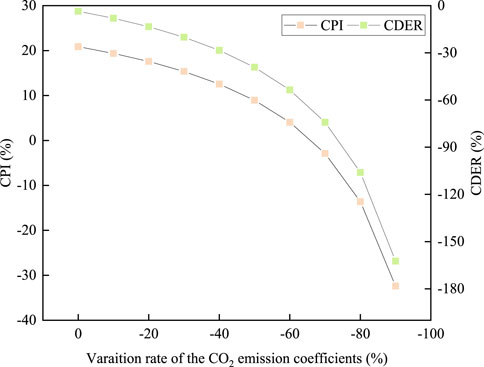
The CO2 emission coefficient of electricity affected the CO2 saving potential of CCHP systems. The CO2 emission coefficient in this study was calculated for the Kyushu region; the CDER was negative for the CCHP system, while the comprehensive performance index was positive. Figure 10 shows the effect of CO2 emission coefficient decreasing from 0 to 90%. Notably, the overall development direction of the power system in Japan is towards low-carbon development. When the CO2 emission coefficient of electricity in the Kyushu region was reduced to 67%, the impact of the economic and energy-saving index was offset, and the comprehensive performance index was below 0, which was not suitable for the CCHP system.
Through the sensitivity analysis of energy price and CO2 emission coefficient of electricity, it can be concluded that when the parameters change greatly, the comprehensive performance of CCHP systems will be significantly affected.
In this part, firstly, the optimization results are analyzed. Then the development potential of CCHP system is analyzed from three factors: cost saving, energy saving and carbon saving. Finally, the sensitivity analysis of energy price and carbon emission coefficient provides suggestions for the promotion of cogeneration system.
Conclusion
In this study, we optimized and evaluated the comprehensive performance of the CCHP system for an eco-campus in Japan. The genetic algorithm (GA) method was used to determine the capacity of each piece of equipment and the operation strategies of the CCHP system. A comprehensive performance index was proposed to evaluate the economy, energy-saving, and CO2 emission reduction potential of the CCHP system. Then, sensitivity analysis was conducted for determining the impacts of electricity and natural gas prices and CO2 emission on the performance of the CCHP system. The main conclusions of our study are as follows:
1. The economic performance of the CCHP system was better than that of the SP system and the total cost of the system could be reduced by 25.02%. The electricity and natural gas prices were selected as the factors that affect the economic performance of the CCHP system. With the increase of electricity price, the economic performance of the CCHP system improved; however, in the case of natural gas price, the opposite effect occurred. With the increase of natural gas prices, the economic performance of the system decreased. When the electricity price changed, the change range of the system payback period was from 3.6 to 12.6, while in the case of when the natural gas price changed, the change range of the payback period was from 4.4 to 6.3. This shows that changes in the electricity price can affect the economic performance of the CCHP system more than changes in the natural gas price. By comparing the economy of seasonal TOU price and TOU price, we found that it is more economical to use seasonal TOU price in areas that have an excessive cooling demand in summer.
2. By comparing the COP of the electric chiller and the power generation efficiency of the gas engine, we found that the improvement of the COP of the electric chiller and the power generation efficiency of the gas engine can greatly save the energy consumption of the CCHP system. When the efficiencies of these two parameters were improved at the same time, energy-saving was optimal.
3. After optimization, the result of CDER was negative because there was a wide variation in the CO2 emission coefficients of electricity and gas. However, the CO2 emission coefficients of electricity in different regions were different. By comparing the CO2 emission coefficients of electricity in different regions, we could conclude that the regions having a clean energy ratio higher than 40% were more suitable for the promotion of the CCHP system.
Overall, this study optimized and evaluated the CCHP system of a specific building to promote its comprehensive performance. And the influence of different electricity price mechanisms on the development of the CCHP system was analyzed. Our results can provide a reference for eco-campus to establish a CCHP system to improve the comprehensive performance. The comprehensive performance assessment method used in this study put forward suggestions on the adaptability and development potential of CCHP systems in the future.
This study mainly improved the performance by optimized the installed capacity and operation strategies of the CCHP system. However, the failure during equipment operation also seriously affects the development of CCHP system. Therefore, a more detailed optimization analysis of CCHP system should be carried out in combination with equipment maintenance in the future work Agency for Natural Resources and Energy, 2021.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
ZL, WG, and FQ contributed to the design of the study. ZL and LZ collated and analyzed the data. ZL and FQ have analyzed the data of the manuscript. ZL wrote the first draft of the manuscript. WG, FQ, LZ, and SK wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Agency for Natural Resources and Energy (2021). Available at: https://www.enecho.meti.go.jp/.
Ali, H., Eldrup, N. H., Normann, F., Andersson, V., Skagestad, R., Mathisen, A., et al. (2018). Cost Estimation of Heat Recovery Networks for Utilization of Industrial Excess Heat for Carbon Dioxide Absorption. Int. J. Greenhouse Gas Control. 74 (May), 219–228. doi:10.1016/j.ijggc.2018.05.003
Bischi, A., Taccari, L., Martelli, E., Amaldi, E., Manzolini, G., Silva, P., et al. (2014). A Detailed MILP Optimization Model for Combined Cooling, Heat and Power System Operation Planning. Energy. 74 (C), 12–26. doi:10.1016/j.energy.2014.02.042
Cao, Y., Wang, Q., Wang, Z., Jermsittiparsert, K., and Shafiee, M. (2020). A New Optimized Configuration for Capacity and Operation Improvement of CCHP System Based on Developed Owl Search Algorithm. Energ. Rep. 6, 315–324. doi:10.1016/j.egyr.2020.01.010
Delgado, B. M., Cao, S., Hasan, A., and Sirén, K. (2017). Multiobjective Optimization for Lifecycle Cost, Carbon Dioxide Emissions and Exergy of Residential Heat and Electricity Prosumers. Energ. Convers. Manage. 154 (April), 455–469. doi:10.1016/j.enconman.2017.11.037
Farahbakhsh, M. T., and Chahartaghi, M. (2020). Performance Analysis and Economic Assessment of a Combined Cooling Heating and Power (CCHP) System in Wastewater Treatment Plants (WWTPs). Energ. Convers. Manage. 224 (August). doi:10.1016/j.enconman.2020.113351
Ghersi, D. E., Amoura, M., Loubar, K., Desideri, U., and Tazerout, M. (2021). Multi-Objective Optimization of CCHP System with Hybrid Chiller Under New Electric Load Following Operation Strategy. Energy. 219, 119574. doi:10.1016/j.energy.2020.119574
Jing, R., Zhu, X., Zhu, Z., Wang, W., Meng, C., Shah, N., et al. (2018). A Multi-Objective Optimization and Multi-Criteria Evaluation Integrated Framework for Distributed Energy System Optimal Planning. Energ. Convers. Manage. 166 (April), 445–462. doi:10.1016/j.enconman.2018.04.054
Kim, J., Jung, Y., and Lee, H. (2019). Optimization of Dynamic Poly-Generation System and Evaluation of System Performance in Building Application. Energ. Convers. Manage. 201 (July), 112128. doi:10.1016/j.enconman.2019.112128
Kong, X. Q., Wang, R. Z., Li, Y., and Huang, X. H. (2009). Optimal Operation of a Micro-Combined Cooling, Heating and Power System Driven by a Gas Engine. Energ. Convers. Manage. 50 (3), 530–538. doi:10.1016/j.enconman.2008.10.020
Li, B., Hu, P., Zhu, N., Lei, F., and Xing, L. (2019). Performance Analysis and Optimization of a CCHP-GSHP Coupling System Based on Quantum Genetic Algorithm. Sustain. Cities Soc. 46 (December 2018), 101408. doi:10.1016/j.scs.2018.12.036
Li, Y., Tian, R., Wei, M., Xu, F., Zheng, S., Song, P., et al. (2020). An Improved Operation Strategy for CCHP System Based on High-Speed Railways Station Case Study. Energ. Convers. Manage. 216 (May), 112936. doi:10.1016/j.enconman.2020.112936
Lin, H., Yang, C., and Xu, X. (2020). A New Optimization Model of CCHP System Based on Genetic Algorithm. Sustain. Cities Soc. 52 (March 2019), 101811. doi:10.1016/j.scs.2019.101811
Papadimitriou, A., Vassiliou, V., Tataraki, K., Giannini, E., and Maroulis, Z. (2020). Economic Assessment of Cogeneration Systems in Operation. Energies. 13 (9), 2206. doi:10.3390/en13092206
Ren, F., Wei, Z., and Zhai, X. (2021). Multi-Objective Optimization and Evaluation of Hybrid CCHP Systems for Different Building Types. Energy. 215, 119096. doi:10.1016/j.energy.2020.119096
Ren, H., and Gao, W. (2010). A MILP Model for Integrated Plan and Evaluation of Distributed Energy Systems. Appl. Energ. 87 (3), 1001–1014. doi:10.1016/j.apenergy.2009.09.023
Ren, H., Zhou, W., Nakagami, K. i., Gao, W., and Wu, Q. (2010). Multi-Objective Optimization for the Operation of Distributed Energy Systems Considering Economic and Environmental Aspects. Appl. Energ. 87 (12), 3642–3651. doi:10.1016/j.apenergy.2010.06.013
Sanaye, S., and Khakpaay, N. (2014). Simultaneous Use of MRM (Maximum Rectangle Method) and Optimization Methods in Determining Nominal Capacity of Gas Engines in CCHP (Combined Cooling, Heating and Power) Systems. Energy. 72, 145–158. doi:10.1016/j.energy.2014.05.018
Soltani, M., Chahartaghi, M., Majid Hashemian, S., and Faghih Shojaei, A. (2020). Technical and Economic Evaluations of Combined Cooling, Heating and Power (CCHP) System With Gas Engine in Commercial Cold Storages. Energ. Convers. Manage. 214 (May), 112877. doi:10.1016/j.enconman.2020.112877
Song, Z., Liu, T., Liu, Y., Jiang, X., and Lin, Q. (2020). Study on the Optimization and Sensitivity Analysis of CCHP Systems for Industrial Park Facilities. Int. J. Electr. Power Energ. Syst. 120 (February), 105984. doi:10.1016/j.ijepes.2020.105984
Wang, J.-J., Jing, Y.-Y., and Zhang, C.-F. (2010a). Optimization of Capacity and Operation for CCHP System by Genetic Algorithm. Appl. Energ. 87 (4), 1325–1335. doi:10.1016/j.apenergy.2009.08.005
Wang, J., Zhai, Z., Jing, Y., and Zhang, C. (2010b). Particle Swarm Optimization for Redundant Building Cooling Heating and Power System. Appl. Energ. 87 (12), 3668–3679. doi:10.1016/j.apenergy.2010.06.021
Wang, J., Zhai, Z., Jing, Y., Zhang, X., and Zhang, C. (2011). Sensitivity Analysis of Optimal Model on Building Cooling Heating and Power System. Appl. Energ. 88 (12), 5143–5152. doi:10.1016/j.apenergy.2011.07.015
Wei, D., Chen, A., Sun, B., and Zhang, C. (2016). Multi-Objective Optimal Operation and Energy Coupling Analysis of Combined Cooling and Heating System. Energy. 98, 296–307. doi:10.1016/j.energy.2016.01.027
Wen, Q., Liu, G., Wu, W., and Liao, S. (2020). Genetic Algorithm-Based Operation Strategy Optimization and Multi-Criteria Evaluation of Distributed Energy System for Commercial Buildings. Energ. Convers. Manage. 226 (August), 113529. doi:10.1016/j.enconman.2020.113529
Wu, D. W., and Wang, R. Z. (2006). Combined Cooling, Heating and Power: A Review. Prog. Energ. Combustion Sci. 32 (5–6), 459–495. doi:10.1016/j.pecs.2006.02.001
Wu, Q., Ren, H., Gao, W., and Ren, J. (2014). Multi-Criteria Assessment of Combined Cooling, Heating and Power Systems Located in Different Regions in Japan. Appl. Therm. Eng. 73 (1), 660–670. doi:10.1016/j.applthermaleng.2014.08.020
Yan, B., Xue, S., Li, Y., Duan, J., and Zeng, M. (2016). Gas-Fired Combined Cooling, Heating and Power (CCHP) in Beijing: A Techno-Economic Analysis. Renew. Sustain. Energ. Rev. 63, 118–131. doi:10.1016/j.rser.2016.05.036
Zhang, L., Gao, W., Yang, Y., and Qian, F. (2020). Impacts of Investment Cost, Energy Prices and Carbon Tax on Promoting the Combined Cooling, Heating and Power (CCHP) System of an Amusement Park Resort in Shanghai. Energies. 13 (6), 4252. doi:10.3390/en13164252
Zhao, X., Gao, W., Qian, F., Li, Y., Ushifusa, Y., Yang, Z., et al. (2020). Economic Performance of Multi-Energy Supply System in a Zero-Carbon House. Energy and Buildings. 226, 110363. doi:10.1016/j.enbuild.2020.110363
Zheng, X., Wu, G., Qiu, Y., Zhan, X., Shah, N., Li, N., et al. (2018). A MINLP Multi-Objective Optimization Model for Operational Planning of a Case Study CCHP System in Urban China. Appl. Energ. 210, 1126–1140. doi:10.1016/j.apenergy.2017.06.038
Nomenclature
AIC annual investment cost ($/year)
AMC annual maintenance cost ($/year)
AOC annual operating cost ($/kWh)
ATC annual total cost ($/year)
C cost ($)
CCHP combined cooling heating and power
CDE carbon dioxide emission
CDER
COP coefficient of performance
CO2 carbon dioxide
CPI comprehensive performance index
CSR cost-saving ratio
E electricity demand (kWh)
F fuel consumption (m3)
FTL following the thermal load
GA genetic algorithm
I investment cost ($)
KSRP Kitakyushu science and research park
M maintenance cost ($)
N capacity of the equipment (kWh)
PEC primary energy consumption
PESR primary energy consumption ratio
PGU power generation unit
Q heat (kWh)
SP separated production
STOU seasonal time-of-use
TOU time-of-use
Greek letter
Subscript
Keywords: optimization model, comprehensive performance index (CPI), seasonal time-of-use (STOU) electricity price, sensitivity analysis, combined cooling, heating, power (CCHP) system
Citation: Liu Z, Gao W, Qian F, Zhang L and Kuroki S (2021) Potential Analysis and Optimization of Combined Cooling, Heating, and Power (CCHP) Systems for Eco-Campus Design Based on Comprehensive Performance Assessment. Front. Energy Res. 9:781634. doi: 10.3389/fenrg.2021.781634
Received: 23 September 2021; Accepted: 20 October 2021;
Published: 04 November 2021.
Edited by:
Antonio Rosato, University of Campania Luigi Vanvitelli, ItalyReviewed by:
Francesca Ceglia, University of Sannio, ItalyMaurizio Sasso, University of Sannio, Italy
Copyright © 2021 Liu, Gao, Qian, Zhang and Kuroki. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Weijun Gao, Z2Fvd2VpanVuQG1lLmNvbQ==
 Zhonghui Liu
Zhonghui Liu Weijun Gao
Weijun Gao Fanyue Qian
Fanyue Qian Liting Zhang4
Liting Zhang4