A deep reinforcement learning-based bidding strategy for participants in a peer-to-peer energy trading scenario

An efficient energy trading strategy is proven to have a vital role in reducing participants’ payment in the energy trading process of the power grid, which can greatly improve the operation efficiency of the power grid and the willingness of participants to take part in the energy trading. Nevertheless, with the increasing number of participants taking part in the energy trading, the stability and efficiency of the energy trading system are exposed to an extreme challenge. To address this issue, an actor-critic-based bidding strategy for energy trading participants is proposed in this paper. Specifically, we model the bidding strategy with sequential decision-making characteristics as a Markov decision process, which treats three elements, namely, total supply, total demand, and participants’ individual supply or demand, as the state and regards bidding price and volume as the action. In order to address the problem that the existing value-based reinforcement learning bidding strategy cannot be applied to the continuous action space environment, we propose an actor–critic architecture, which endows the actor the ability of learning the action execution and utilizes the critic to evaluate the long-term rewards conditioned by the current state–action pairs. Simulation results in energy trading scenarios with different numbers of participants indicate that the proposed method will obtain a higher cumulative reward than the traditional greedy method.

1 Introduction

As a typical cyber-physical system, the smart grid is gradually becoming a research hotspot due to its safe, economical, efficient, and environmentally friendly benefits (Gao et al., 2012). However, in the traditional retail energy market of smart grid, most buyers and sellers that have local electricity shortage and surplus could only choose to trade with the main grid utility company while suffering from some price gap (Chen and Su, 2019). The key to designing the next-generation retail electricity market is to grant trading participants the freedom to independently choose trading partners. The peer-to-peer business system is being pursued by the current research community, which fully considers the consumers’ willingness to choose the transaction partner and endows all customers an equal opportunity to individually and actively participate in the trading market (Cui et al., 2020; Anoh et al., 2020).

The double-auction mechanism is a key component to improving the energy trading efficiency of the power grid, which can determine the trading price and volume for multiple participants in the energy trading market (Vytelingum et al., 2008). Recently, the research efforts of double-auction mechanism can be divided into two ways: one is designing a novel energy auction framework (An et al., 2018; Ma et al., 2014), another is determining the optimal bidding strategy through optimization methods to reduce the payment and improve the satisfaction of energy trading participants (PankiRaj et al., 2019; Ramachandran et al., 2011). For the energy auction framework design, Xu et al. (2021) proposed a Vickrey–Clarke–Groves (VCG)-based double-auction to maximize the social welfare of the energy trading market. For the optimization of bidding strategy, Singh et al. (2022) presented a bidding model of the virtual power plant units participating in the carbon-integrated day-ahead energy trading market.

Although the double-auction mechanism in the energy trading market has been widely investigated, the abovementioned research efforts are often challenged by the dynamic and uncertain environment (e.g., buyer’s demand and seller’s supply), and the resulting traditional optimization methods, which need to obtain precise variable information, are hard to be deployed to optimize the bidding strategy of energy trading participants. Motivated by the advantages of the reinforcement learning (RL) method, which can search for the optimal strategy of decision-making problems without obtaining the precise environment dynamics (Mnih et al., 2015; Lillicrap et al., 2015; Galindo-Serrano and Giupponi, 2010), RL-based methods have been widely utilized to solve the optimization problem of energy trading participants’ bidding strategies (Xu et al., 2019; Wang et al., 2017; Wang et al., 2019). For instance, Wang et al. (2019) formulated the continuous double-auction mechanism as a Markov decision process (MDP) and then proposed a learning architecture based on Q-learning to reflect personalized bidding preferences.

Although the existing literature studies prove the effectiveness of the reinforcement learning algorithm in the double-auction mechanism field, there are still several problems that need to be addressed: 1) the existing RL-based trading approaches discretized the system states (e.g., the Q-learning-based bidding strategy in Wang et al. (2019)), which totally ignores the continuously changing characteristics of the power grid. 2) The abovementioned research efforts only use the state information at the current time step to determine the optimal bidding strategy (e.g., the DDPG-based electric vehicle charging strategy in Tao et al. (2022)), ignoring the relationship among states at multiple time steps.

In order to address the limitations mentioned earlier, in this study, we first designed a double-auction mechanism to determine the trading price and trading volume for energy trading participants. Then, we propose an actor–critic-based bidding algorithm to maximize the cumulative reward of participants in the energy trading market. The proposed method utilizes an actor network to generate continuous action and integrates the recurrent neural network to process the sequential state information of the power grid. Finally, we perform the simulations to illustrate the effectiveness of the proposed method, and the simulation results prove that the proposed method will obtain a higher cumulative reward than the traditional greedy method in energy trading scenarios with different numbers of participants.

Part of this work was published in Zhang and Yang (2020). Differently, in order to address the problem that the DQN-based approach in the conference version cannot explore the continuous action space, we utilize an actor–critic architecture to endow the actor the ability of generating the continuous action. In addition, we have added an additional component, namely, the main grid, to the system model and the MDP model, which makes the system model closer to reality. Finally, we perform the expanded simulations to illustrate the effectiveness of the proposed method compared with the existing scheme in energy trading scenarios with different numbers of participants. The remainder of this paper is arranged as follows: In Section 2, we briefly review the literature studies that are related to this paper. In Section 3, we present the system model and the designed double-auction mechanism. In Section 4, we model the bidding strategies of the buyer and seller as MDP. In Section 5, we present the actor–critic-based bidding strategy in detail. In Section 6, we perform simulations and present the results. Finally, in Section 7, we conclude this study.

2 Related work

The research on bidding strategies for energy trading can be divided into two categories: traditional modal-based optimization approaches (Fooladivanda et al., 2018; Herranz et al., 2012; Fang et al., 2016; Dou et al., 2020; Wu et al., 2016) and intelligent learning methods (Kim et al., 2016; Wang et al., 2019; Zhou et al., 2017; Xu et al., 2019). The former obtains the optimal bidding strategy of energy trading participants by constructing and solving mathematical optimization models.

Existing literature studies of traditional modal-based approaches are mostly concentrated on the bidding optimization problem (Fooladivanda et al., 2018; Wu et al., 2016; Fang et al., 2016), in which the optimal bidding functions were developed for the individual demand. In Fang et al. (2016), authors proposed a bi-level optimization model for the strategic bidding problem of load serving entities (LSEs), with the objective of maximizing the LSE’s revenue and minimizing the generation cost. In the work of Wu et al. (2016), optimal bidding strategies for the electric vehicle were formulated as the mathematical programming model with equilibrium constraints and a game theory approach was utilized to analyze the competition among the electric vehicles. Herranz et al. (2012) designed a genetic algorithm to optimize the parameters that define the best bidding strategy for an energy retailer who supplies energy. However, most of the aforementioned algorithms require us to iteratively solve the optimization models, which are time-consuming and impractical for practical applications.

Applying reinforcement learning algorithms to address the optimal bidding problem of energy trading fields has become a research hotspot. The fundamental reason behind this prosperity is that RL methods can obtain the optimal strategy through trial and error without requiring the exact environment model. For instance, Wang et al. (2019) formulated the sequential energy bidding problem as a Markov decision process (MDP) and utilized the classic Q-learning method to reflect personalized bidding preferences. Liu et al. (2021) used the multi-agent deep deterministic policy gradient (MADDPG) algorithm to address the non-cooperative and cooperative energy trading games between power companies. Tao et al. (2022) utilized the deep deterministic policy gradient (DDPG) method to generate the bidding price and bidding volume for an electric vehicle aggregator, which reduced the reliance of algorithm performance on the stochastic model. Zhu et al. (2022) proposed an online reinforcement learning algorithm to obtain the optimal bidding policy of distributed micro-grids and the optimal dispatching model of the distribution system operator.

3 System model and the double-auction mechanism

In this section, we first introduce the basic principle of deep reinforcement learning. Then, we will present the energy trading model used in this study and the double-auction mechanism for determining the valid price and allocations of trading.

3.1 Deep reinforcement learning

Recently, the reinforcement learning (RL) technique (Mnih et al., 2015) has been proven to be effective in addressing the sequential optimization problem through the interaction between the agent and environment. The fundamental operation process of deep reinforcement learning is described as follows: at each time step t, the agent first takes an action a_t conditioned on the state of the environment s_t and the policy π, denoted as a_t = π(s_t). Then, the environment will respond with a reward r_t to the agent and step into the next state s_t. It is to be noted that the purpose of the agent is to optimize the policy π that can maximize the cumulative reward, denoted as follows:

$R_t=\sum _{i=t}^T{\gamma }^{\left(i-t\right)}{r}_i,(1)$

where T is the stopping time step of the agent and γ stands for the discount factor. In order to estimate the cumulative reward, the RL-based method will estimate the Q value conditioned on the state s_t and action a_t, denoted as $Q(s_t,a_t)=\mathbb{E}[R_t|s_t,a_t]$ (RS and AG, 1998).

As a typical RL approach, the Q-learning method (RS and AG, 1998) utilizes a table to store and update the Q value of each state-action pair. The policy of the agent is to select the action that can maximize the Q value in the look-up table, which can be expressed as follows:

$a_t=\arg \underset{a}{\max }Q\left(s_t,a\right).(2)$

The deep Q-learning (DQL) method (Fang et al., 2016), which utilizes the deep neural network (DNN) parameterized by θ to store and update the Q value, greatly addresses the dimensional explosion challenge raised when the state is continuous and high-dimensional. The parameters of the deep Q network are updated through the back-propagation of the loss function described in the following:

$L_{\theta }={\left(Q_{\mathit{tar}}-Q\left(s_t,a_t\right)\right)}^2,(3)$

where Q_tar is the target Q value, denoted as

$Q_{\mathit{tar}}=r_t+\gamma \underset{a^{\prime }}{\max }Q\left(s_{t+1},a\prime \right).(4)$

3.2 Energy trading market

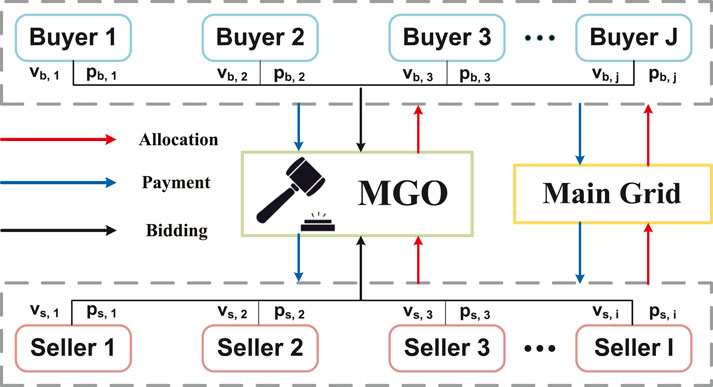
The energy trading market, which is illustrated in Figure 1 includes four categories of participants: the micro-grid operators (MGO), the main grid, buyers, and sellers Li et al. (2020). The micro-grids equipped with energy generation equipment (e.g., photovoltaics and diesel generators) that have surplus energy for sale are considered sellers, and the micro-grids with insufficient energy act as buyers. The MGO acts as the auctioneer that regulates the energy trading among buyers and sellers. The MGO first collects the demand and supply from buyers and sellers; then, it determines the payment and allocation rules to guarantee the supply–demand balance. It should be noted that the energy is transacted based on a double-auction mechanism through peer-to-peer (P2P) technologies Wang et al. (2014). When the trading participant cannot purchase/sell satisfactory energy volume in the P2P market, it could trade with the main grid through peer-to-grid (P2G) technologies (Chen and Su, 2019) at an unfavorable price.

FIGURE 1

FIGURE 1. Market structure.

3.3 Double-auction mechanism

In this study, a typical double-auction mechanism is utilized to determine the trading price and trading volume of micro-grids in the P2P market. We denote B and S as the sets of buyers and sellers, respectively. (v_b,i, p_b,i) is the bidding information of buyer i, in which v_b,i denotes the volume of energy that buyer i is willing to obtain and p_b,i represents the bidding price that buyer i is willing to pay for an unit of energy. Similarly, (v_s,j, p_s,j) represents the bidding information of seller j that is willing to accept. Valid price $p_t^v$ is a boundary value that determines whether a participant will win the bid at time t. Based on the aforementioned definitions, we present the operation process of the double-auction mechanism as follows:

1. Each buyer from set B and each seller from set S report their respective demand and supply to the MGO.

2. The MGO collects the demand and supply from buyers and sellers and declares the total demand and total supply to all participants.

3. Each buyer submits the (v_b,i, p_b,i), and each seller submits the (v_s,j, p_s,j) to the MGO.

4. The MGO announces the valid prices $p_{b,t}^v$ and $p_{s,t}^v$ for micro-grids in the energy trading market. It should be noted that $p_{b,t}^v$ is the valid price of the buyer, and any buyer that has the bidding price higher than $p_{b,t}^v$ can win the bid. $p_{s,t}^v$ is the valid price of the seller, and any seller that has the bidding price lower than $p_{s,t}^v$ can win the bid.

5. The MGO determines the allocation rule for winning participants. The allocation rule is derived based on the following two cases of comparing the total bidding volume of winning buyers and the total bidding volume of winning sellers:

Case A: $\sum _{i\in B_t^w}{v}_{b,i}\le \sum _{j\in S_t^w}{v}_{s,j}$:

$\begin{array}{cc}\hfill V\left(b,i\right)& =v_{b,i},\hfill \\ \hfill V\left(s,j\right)& =v_{s,j}-\frac{\mathrm{\Delta }}{|S_t|}.\hfill \end{array}(5)$

Case B: $\sum _{j\in S_t}{v}_{s,j}\le \sum _{i\in B_t}{v}_{b,i}$:

$\begin{array}{cc}\hfill V\left(b,i\right)& =v_{b,i}-\frac{\mathrm{\Delta }}{|B_t|},\hfill \\ \hfill V\left(s,j\right)& =v_{s,j},\hfill \end{array}(6)$

where $B_t^w$ and $S_t^w$ represent the winning set of buyer and seller, respectively. |B_t| represents the number of winning buyers at the time step t and |S_t| represents the number of winning seller and buyer sets at the time step t. V (⋅, ⋅) is the actual energy trading volume of a participant. $\mathrm{\Delta }=|\sum _{i\in B_t^w}{v}_{b,i}-\sum _{j\in S_t^w}{v}_{s,j}|$ represents the absolute value of the difference between the total demand of winning buyers and the total supply of winning sellers.

The valid price effectively ensures the truthfulness of the auction process (detailed proof is presented in our previous paper (Li et al., 2020)). In this paper, we only present the overall process of calculating the valid price.

1. Sort the bidding price of the winning buyer i ∈ B_t in descending order and sort the bidding price of the winning seller j ∈ S_t in ascending order, as follows:

$\begin{array}{cc}\hfill p_{b,1}& >p_{b,2}>\dots >p_{b,n}\hfill \\ \hfill p_{s,1}& <p_{s,2}<\dots <p_{s,m}.\hfill \end{array}(7)$

2. The valid price determination is derived based on the following four cases:

Case A: p_s,1 ≤ p_b,1: this case means that the minimum bidding price of sellers is smaller than or equal to the maximum bidding price of buyers. In this case, the transaction is denied; both buyers and sellers need to purchase/sell energy with the main grid to meet the needs of their transaction.

Case B: p_s,m ≤ p_b,n: this case means that the maximum bidding price of sellers is smaller than or equal to the minimum bidding price of sellers.

$\begin{array}{cc}\hfill p_b^v& =p_{b,n}\hfill \\ \hfill p_s^v& =p_{s,m}.\hfill \end{array}(8)$

Case C: p_b,l ≥ p_s,k ≥ p_b,l+1 and $\sum _1^{k-1}{v}_{s,j}\le \sum _1^l{v}_{b,i}\le \sum _1^k{v}_{s,j}$: this case means that the bidding price of the seller k is within the bidding price of the buyer l and l + 1. In addition, the sum of energy demand from buyer 1 to l is within the sum of energy supply from seller 1 to k − 1 and the sum of energy supply from seller 1 to k.

$\begin{array}{c}\hfill p_b^v=p_{b,l}\\ \hfill p_s^v=p_{s,k}.\end{array}(9)$

Case D: p_s,k+1 ≥ p_b,l ≥ p_s,k and $\sum _1^{l-1}{v}_{b,i}\le \sum _1^k{v}_{s,j}\le \sum _1^l{v}_{b,i}$: this case means that the bidding price of the buyer l is within the bidding price of the seller k and k + 1. In addition, the sum of energy supply from seller 1 to k is within the sum of energy demand from buyer 1 to l − 1 and the sum of energy demand from buyer 1 to l.

$\begin{array}{c}\hfill p_b^v=p_{b,l}\\ \hfill p_s^v=p_{s,k}.\end{array}(10)$

4 MDP model of the bidding strategy

We use a finite Markov decision process (MDP) model with discrete time steps to formulate the bidding behaviors of energy trading participants (including buyers and sellers). Specifically, we use t ∈ T to illustrate the discrete time step for the trading process. Buyers and sellers participating in energy trading are regarded as agents whose objectives are to pay the least cost and get the most profit, respectively. According to the characteristic of the MDP model, the state s_t at the current time step t is only related to the state s_t−1 and action a_t−1 at the previous time step t − 1. The MDP model consists of four elements (S, A, ζ and R), and the detailed descriptions are summarized as follows:

S is the state space of the MDP model, and s_t ∈ S denotes the environment state at time step t. $s_i^b$ and $s_j^s$ denote the states of the buyer i and seller j, respectively. Specifically, the state of the buyer i at the time step t is defined as follows:

$s_{t,i}^b=\left[D,P,d_i\right],(11)$

where D is the total demand of buyers, P is the total supply of sellers, and d_i is the buyer i’s own demand. It should be noted that D and P reflect the demand and supply relationship in the energy trading market, which greatly impacts the bidding strategies of energy trading participants. Specifically, when the total supply exceeds the total demand in the energy trading market, buyers are more willing to purchase the energy at a lower energy price. When the total demand exceeds the total supply, buyers will raise the bidding price in order to win the bid. Similarly, we define the state of the seller j at time t as follows:

$s_{t,j}^s=\left[P,D,e_j\right],(12)$

where e_j is the seller j’s own produce.

a_t ∈ A represents the action of the trading participants at time slot t, where A is the action space containing the available actions of the agent. In our trading scheme, we define the bidding action as a two-dimensional tuple.

$a_t=\left[p_t,v_t\right],(13)$

where p_t is the bidding price for a unit of energy and v_t is the bidding volume. In order to make the bidding prices more realistic, we impose the following restrictions on the bidding prices of both buyers and sellers:

$\begin{array}{c}\hfill p_{\mathit{main}}^s+\nu \le p_t^b\le p_{\mathit{main}}^b,\\ \hfill p_{\mathit{main}}^s\le p_t^s\le p_{\mathit{main}}^b-\nu ,\end{array}(14)$

where ν ≪ 1 is a small coefficient to restrict the bidding prices of energy trading participants. For buyers, on one hand, the bidding prices should be greater than the sellers’ price of directly selling the energy to the main grid to ensure the bid can be accepted. On the other hand, the bidding prices should be less than or equal to the buyers’ price of directly buying energy from the main grid to ensure the utilities obtained by the buyers participating in the P2P energy trading market are greater than directly trading with the main grid. Similarly, for sellers, the bidding prices should be lower than the buyers’ price of directly buying energy from the main grid and greater than or equal to the sellers’ price of directly selling the energy to the main grid. The abovementioned restrictions greatly encourage buyers and sellers to participate in the P2P trading market and grant trading participants the freedom to independently choose trading partners.

Due to the limitation of energy transmission, we assume that the bidding volume at time step t cannot exceed its maximum.

$v_t\le v_t^{\max },(15)$

where $v_t^{\max }$ is the maximum transmission volume at time t. In order to simplify the trading model, we assume $v_t^{\max }$ as a fixed value during the entire trading process.

ζ_t is the transition function, which represents the state transition probability from the state s_t at time step t to the state s_t+1 at time step t + 1 conditioned on the action a_t.

r_t is the immediate reward obtained by an agent at time step t. For the buyer i, the reward consists of two ingredients: profits in the P2P trading market and losses in trading with the main grid.

$r_{i,t}^b=\left(p_{i,t}^b-p_t^{v,b}\right)*V\left(i,t\right)-\left(p_{\mathit{main}}^b-p_{i,t}^b\right)*\left(v_{i,t}^b-V\left(i,t\right)\right),(16)$

where V (i, t) represents the actual trading volume of buyer i in the P2P trading market. The first term of the equation utilizes the difference between the actual trading price and the bidding price to represent buyers’ profits in the P2P trading market. Also, the second term illustrates the buyers’ loss in trading with the main grid by the difference between the main grid price and the bidding price.

Similarly, we define the immediate reward of the seller j as follows:

$r_{i,t}^s=\left(p_t^{v,s}-p_{j,t}^s\right)*V\left(j,t\right)-\left(p_{\mathit{main}}^s-p_{j,t}^s\right)*\left(v_{j,t}^s-V\left(j,t\right)\right).(17)$

5 DRL-based bidding strategy

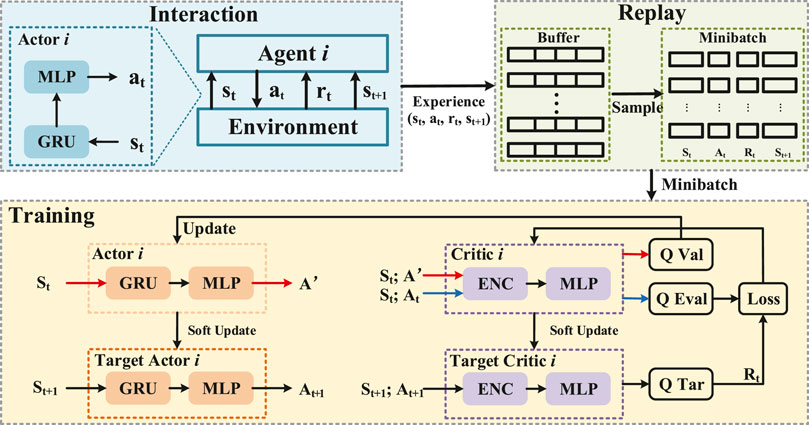
It should be noted that in the considered P2P energy trading market, it is hard for both buyers and sellers to determine their optimal bidding strategy through typical optimization methods (e.g., robust optimization), due to the difficulty of constructing the optimization model and the dynamic environment characteristics. In recent years, deep reinforcement learning has been deemed an effective method to obtain optimal strategies through trial and error without modeling the exact environment. Thus, we propose a DRL-based approach to search for the optimal bidding strategy for energy trading participants. The structure of the proposed DRL-based bidding scheme is illustrated in Figure 2. Specifically, the trading participants are regarded as the agents that repeatedly interact with the environment and continuously update the bidding strategies by environmental rewards. Before presenting the proposed algorithm, the neural network architecture is first introduced.

FIGURE 2

FIGURE 2. Deep reinforcement learning structure.

5.1 Deep neural network architecture

Traditional value-based DRL methods, such as DQN (Mnih et al., 2015), utilize the deep neural network to output the probability of executing each action. However, this kind of algorithm is impractical to be applied in the continuous action space environment due to the fine discretization of the action space leads to high computational overhead. To address that issue, we use the actor–critic-based paradigm, including the actor network π(s) to execute the action conditioned on the state and the critic network Q (s, a) to estimate the Q value conditioned on the state and action.

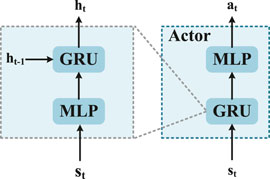
Specifically, the actor network π_η(s), which is parameterized by η, is a non-linear mapping from the partial state s_i of each agent to its individual action a_i. The structure of the actor network is presented in Figure 3. In order to endow the agent the ability of selecting the action condition on its entire state-action history, the actor network is built as the multi-layer perceptron (MLP) prefixed by a gate recurrent unit (GRU) network (Chung et al., 2014). GRU is a type of recurrent neural network (RNN), which has better performance in processing sequential data than RNN and long short-term memory (LSTM) (Gers et al., 1999). The GRU applies a gate structure, which calculates the hidden state information h_t, to memorize the sequential state information. It is to be noted that the input of the GRU at time step t − 1 contains the state s_i and the previous hidden state h_t−1. Thus, the output of GRU h_t contains information about the previous state, which is then transmitted to the MLP of the actor network for action selection.

$a_{i,t}={\pi }_{\eta }\left(s_{i,t},h_{i,t-1}\right).(18)$

FIGURE 3

FIGURE 3. Structure of the actor network.

The critic network Q_ϕ(s, a), which is parameterized by ϕ, estimates the value function with a non-linear mapping function from state s_i and action a_i of each agent to its value function Q_i, which is an approximate estimate of the cumulative reward R for a given state s_i by taking action a_i.

$Q_i=Q_{\varphi }\left(s_i,a_i\right)\approx \mathbb{E}\left[R|s_i,a_i\right].(19)$

It should be noted that for the structure of the critic network, we first utilize an embedding network to extract the characteristics of the input information and then use the MLP to output the value function.

5.2 Procedure of the proposed algorithm

5.2.1 Interaction and replay

In the reinforcement scheme, agents learn their optimal bidding strategy from continuously interacting with the environment and observing the environment reward. At a specific time step t, the agent first observes the total supply, total demand, and individual demand/supply from the environment to obtain the state value s(t) as described in Section 4. Then, each agent selects the bidding policy as an action a(t) = {p_t, q_t} based on the output of the actor network. For exploration, we apply the ϵ − greedy strategy to select an agent’s action (RS and AG, 1998), that is, randomly selecting an action with the probability 1 − ϵ or taking an action that corresponds to the output of an actor network conditioned on the current state with the probability ϵ.

$a_t=\left\{\begin{array}{ccc}\hfill & \text{Random}\left[a_{i,t}\in A\right]\hfill & \hfill \text{with\hspace{0.17em}probability}1-ϵ,\\ \hfill & a_{i,t}={\pi }_{\eta }\left(s_{i,t},h_{i,t-1}\right)\hfill & \hfill \text{with\hspace{0.17em}probability}ϵ.\end{array}\right.(20)$

It is worth mentioning that we set ϵ to 0 at the beginning of training in order to endow the agent the ability to explore the entire action space, while as the training progresses, the agent will gradually obtain information about the environment. Thus, we let ϵ increase a small value every training step. Next, MGO will calculate the valid price and determine energy allocation rules for each trading participant. Finally, the environment steps into the next state s (t + 1) based on the new total demand, total supply, and individual demand/supply after the transaction and generates a reward r(t) for each agent at the same time, reflecting the immediate evaluation of the action a(t) at the state s(t).

After the interaction, an experience consists of state s(t), action a(t), reward r(t), and next step state s (t + 1) will be stored in the replay buffer. Agents will utilize the experience [s(t), a_t, r(t) and s (t + 1)] in the replay buffer to train the policy.

5.2.2 Network training

In the training process, we use four deep neural networks to learn the bidding strategy of each trading participant, namely, the actor network π_η, target actor network π_η′, critic network Q_ϕ, and target critic network Q_ϕ′ as shown in Figure 2. At the beginning, we randomly initialize the hidden state of GRU, the parameters of the actor network η, and the critic network ϕ. The target parameters η′ and ϕ′ are copied from the main parameters η and ϕ every C time step in order to stabilize the training process (Lillicrap et al., 2015).

After the replay buffer has collected enough experience [s(t), a_t, r(t), s (t + 1)], we first sample the mini-batch from the replay buffer as a collection of N experiences $[S_{(}t\left.\right),A_t,R(t),S(t+1)]$. Then, we utilize S_t and A_t as the input of the critic network to obtain the evaluation of the value function.

$Q_{\text{eval}}=Q_{\varphi }\left(s_t,s_t\right).(21)$

After that, we use the target actor network to acquire the suggested action a_t+1 conditioned on the next state s_t+1.

$a_{t+1}={\pi }_{{\eta }^{\prime }}\left(s_{t+1},h_{t+1}\right).(22)$

Next, the suggested action a_t+1 and the next state s_t+1 are input into the target critic network. In this way, we can get the target value function by adding immediate rewards r_t to the output of the target critic network.

$Q_{\text{tar}}=r_t+\gamma Q_{{\varphi }^{\prime }}\left(s_{t+1},a_{t+1}\right),(23)$

in which γ is the discount factor for adjusting the balance of the future reward and the reward at the current time step. Based on the two abovementioned value functions, the loss function of the critic network is defined as the mean square error (MSE) of the evaluation value function and the target value function.

$L_{\varphi }=\sum _{i=1}^N{\left(Q_{\mathit{tar}}-Q_{\mathit{eval}}\right)}^2.(24)$

Finally, the parameters of the critic network ϕ are trained end-to-end by the back-propagation of the gradients of the critic network’s loss function.

$\varphi =\varphi -{\alpha }_1{\nabla }_{\varphi }{L}_{\varphi },(25)$

where α₁ is the learning rate of the critic network.

Furthermore, the actor network’s parameters η are updated by the gradient of the action’s performance conditioned on the state s_t; thus, we first obtain the action by the actor network.

$a^{\prime }={\pi }_{\eta }\left(s_t,h_t\right).(26)$

Then, the evaluation of the current action a′ can be derived from the critic network.

$q=Q_{\varphi }\left(s_t,a^{\prime }\right).(27)$

Finally, the gradient of updating the actor network is given by

${\nabla }_{\eta }{J}_{\eta }=\sum _{i=1}^N{\nabla }_{\eta }{\pi }_{\eta }\left(s_t,h_t\right){\nabla }_{a^{\prime }}Q.(28)$

Similarly, the parameters of the actor network η are trained by the back-propagation of the gradients with the actor network’s learning rate α₂.

$\eta =\eta -{\alpha }_2{\nabla }_{\eta }{J}_{\eta }.(29)$

The pseudocode of the training process is outlined in Algorithm 1, where the parameters of four neural networks are updated by the back-propagation of the gradient of the loss function and action evaluation. An optimal bidding strategy can be obtained by continuously updating the neural network parameters until convergence.

Algorithm 1. Training process for the DRL-based energy bidding strategy.

5.2.3 Testing

In order to evaluate the effectiveness of the proposed algorithm, we utilize the trained actor network π_η to verify the performance of the energy bidding strategies. Specifically, the testing process lasts for E₂ epoches. For each episode, at each time slot t, all the trading agents interact with the environment to obtain the current state s_t. Then, each agent regards the state s_t as the input of each actor network to obtain the bidding action. It is to be noted that in the testing phase, the action selection policy is slightly different from that in the training phase. Particularly, we ignore the random policy (ϵ policy) in the agents’ action selection phase and directly utilize the output of the actor network as the chosen action a_t = π_η(s_t) (greedy policy). Next, the MGO will determine the collection of the winner, the valid price, and the energy allocation rules for the trading participants. Finally, the environment responds to the agent with a reward r_t and steps into the next state s_t+1. We summarize the pseudocode of bidding strategy evaluation in Algorithm 2, where it can be seen that each agent uses its trained actor network to provide an automatic energy bid.

Algorithm 2. Testing process for the DRL-based energy bidding strategy.

6 Simulations

In this section, we conduct several experiments to prove the effectiveness of the proposed energy bidding strategies. The simulation settings are first presented. Then, we show the evaluation results of the proposed algorithm compared with the greedy method. Finally, the impacts of important algorithmic parameters on the bidding performance are evaluated.

6.1 Simulation setup

6.1.1 Parameters of the energy trading model

In order to perform the simulation of the energy trading behavior, we make the following assumptions about the trading model: the number of buyers is equal to the number of sellers and is initially set to 10. The training epoch E₁ is set to 10,000, and we assume each epoch contains 24 trading steps. In order to make the trading model realistic, we adopted a peak-valley pricing method for the main grid. The peak period lasts from 10 a.m. to 10 p.m., and the rest is the valley period. The price at which buyers directly purchase energy from the main grid $p_{\mathit{main}}^b$ and the price at which sellers directly sell energy to the main grid $p_{\mathit{main}}^s$ obey restricted normal distributions. Specifically, $p_{\mathit{main}}^b$ is sampled from $\mathcal{N}(0.45,1^2)$ with a limitation in range [0.4, 0.5] during valley periods and is sampled from $\mathcal{N}(0.55,1^2)$ with a boundary [0.5, 0.6] during peak periods. Similarly, we sample $p_{\mathit{main}}^s$ from $\mathcal{N}(0.35,1^2)$ within the interval [0.3, 0.4] during valley periods and sample from $\mathcal{N}(0.45,1^2)$ within the interval [0.4, 0.5] during peak periods. According to the actual energy dispatch data (An et al., 2018), we sample each buyer’s total demand and each seller’s total supply in one epoch from $\mathcal{N}(900,1^2)$ with the limit of [600, 1,200]. Moreover, we set the maximum transmission volume q^max to 5 and the balancing coefficient α to 0.1.

6.1.2 Parameters of the RL algorithm

The architecture of all GRU networks has a 64-dimensional hidden state with a fully connected network layer suffixed and prefixed. Exploration is performed in the training phase by the ϵ − greedy method. ϵ is set to 0.95 initially and decreases by 1e − 4 per training step, with the minimum ϵ set to 0.05. We set γ to 0.99. The volume of the replay buffer is set to 5e3, and the volume of the mini-batch is set to 32. The target networks are updated after every 10 training epoches. In addition, we apply the Adam optimizer to update the critic and actor networks, with the learning rates α₁ and α₂ set to 1e − 3 and 1e − 4, respectively. We freeze the training to test the performance every 200 training epoches, and each testing process contains 20 epoches. It should be noted that there is no need to explore in the testing phase, and thus, we set ϵ to 0 during testing.

6.2 Evaluation results

6.2.1 Effectiveness of the proposed method

In order to prove the effectiveness of the proposed method, we compare the agents’ cumulative reward obtained by the proposed method with that obtained by the greedy method in the energy trading scenario where the number of both buyers and sellers are 10 (Wang et al., 2017). It should be noted that the greedy method is a learning-based method that draws on the idea of robust optimization. At each time step t, each agent only cares about obtaining the maximum reward at the current time step, ignoring the future reward. Simulation results are provided in Figure 4, in which red lines represent the average cumulative reward obtained by the greedy method and blue lines represent the average cumulative reward obtained by the proposed method. In addition, in order to eliminate the influence of randomness on experimental results, we perform each simulation five times with different random seeds and show the deviation of the algorithm by the shaded area in Figure 4.

FIGURE 4

FIGURE 4. Average cumulative reward of (A) buyers and (B) sellers with the number of both buyers and sellers set as 10.

We first fix sellers’ bidding strategies as the greedy method and compare the optimization effect of the proposed algorithm on the bidding strategies of buyers with that of the greedy method. From Figure 4A, we can obviously see that buyers’ cumulative reward obtained by the proposed method is higher than that obtained by the greedy method. Specifically, buyers’ obtained cumulative reward of the proposed method reaches about −1.91, which is higher than that of the greedy method by about 68.3%. Then, we fix buyers’ bidding strategies as the greedy method and compare the optimization effect of the proposed algorithm on the bidding strategies of sellers with that of the greedy method. From Figure 4B, we can clearly see that sellers’ cumulative reward obtained by the proposed method is higher than that obtained by the greedy method. Specifically, sellers’ cumulative reward of the proposed method reaches to −2.38, which is higher than that of the greedy method by about 55.8%. Simulation results show that the proposed method is effective in optimizing the bidding strategies of both buyers and sellers in the energy trading scenarios.

6.2.2 Robustness of the proposed method

In order to prove the robustness of the proposed method, we verify the effectiveness of the proposed method in energy trading scenarios with different numbers of participants. We compare the performance of the proposed method and the greedy method as the number of energy trading participants is set to 5, 10, 15, and 20. Simulation results are presented in Figures 5–7, in which the solid lines represent the average cumulative reward of different algorithms and the shaded region shows the deviation of the algorithm for five runs under different random seeds. In order to intuitively show the results, we summarize the average cumulative rewards of the last ten training episodes in Table 1.

FIGURE 5

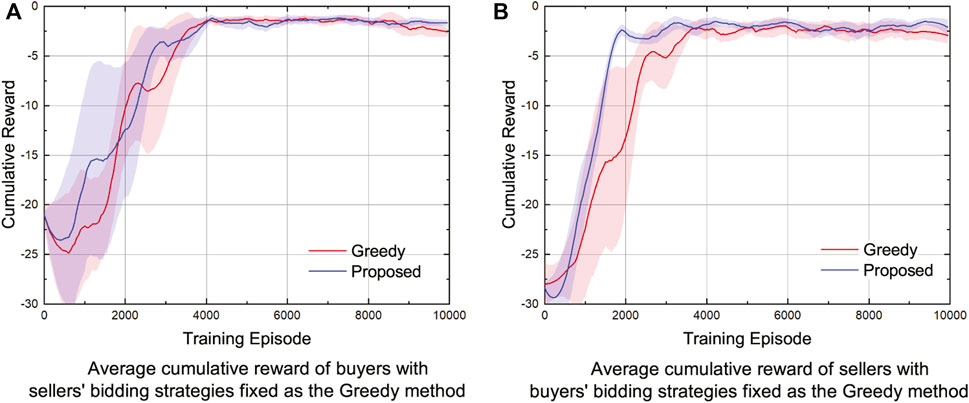
FIGURE 5. Average cumulative reward of (A) buyers and (B) sellers with the number of both buyers and sellers set as 5.

FIGURE 6

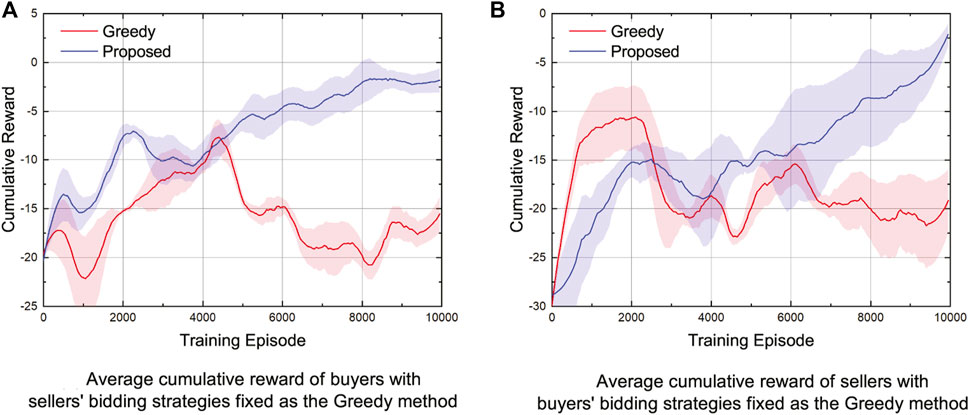
FIGURE 6. Average cumulative reward of (A) buyers and (B) sellers with the number of both buyers and sellers set as 15.

FIGURE 7

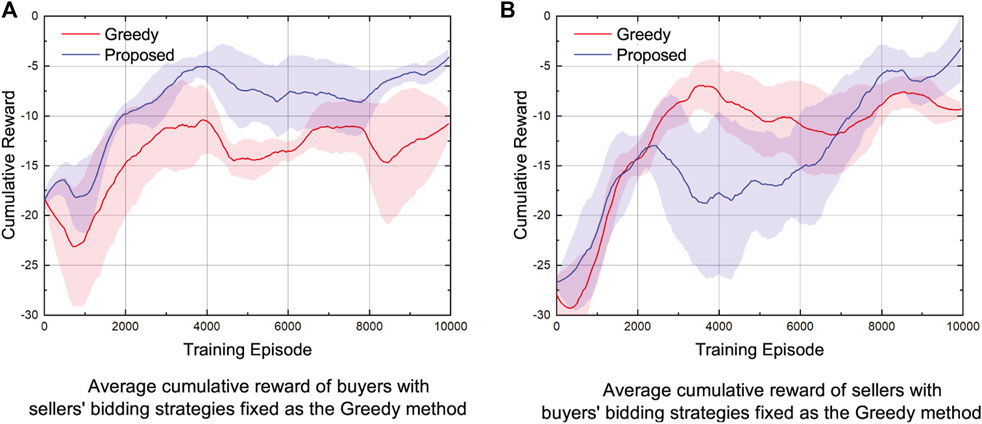
FIGURE 7. Average cumulative reward of (A) buyers and (B) sellers with the number of both buyers and sellers set as 20.

TABLE 1

TABLE 1. Average cumulative reward obtained by agents of different algorithms in the energy trading scenarios with a different number of participants.

From Table 1, we can clearly see that the cumulative reward obtained by the proposed method is higher than that obtained by the greedy method in all energy trading scenarios tested in this section. In particular, when sellers’ bidding strategies are fixed to the greedy method, the buyers’ obtained cumulative reward of the proposed method converges to about −1.67 in the energy trading scenario with five participants, which is higher than that of the greedy method by about 31.0%. In the energy trading scenario with 15 participants, buyers’ obtained cumulative reward of the proposed method reaches about −2.01, which is higher than that of the greedy method by 87.9%. Furthermore, buyers’ cumulative reward of the proposed method is higher than that of the greedy method by about 57.0% in the energy trading scenario with 20 participants. When buyers’ bidding strategies are fixed as the greedy method, sellers’ obtained cumulative rewards of the proposed method are higher than the obtained cumulative rewards of the greedy method by 34.8%, 80.8%, and 52.7% in the energy trading scenario with the number of participants being 5, 15, and 20, respectively. Simulation results in this section prove that the proposed method is robust given the number of participants in the energy trading scenarios.

We also perform the comparison between the proposed RL-based trading method and the random trading method to verify their effectiveness. Simulation results are provided in Table 1. From Table 1, we can clearly see that the proposed RL-based trading method can obtain a higher cumulative reward than the random trading method. Specifically, buyers’ obtained cumulative rewards of the proposed method are higher than the obtained cumulative reward of the random method by 92.7%, 91.3%, 91.7%, and 76.8% in the energy trading scenario with the number of participants being 5, 10, 15, and 20, respectively. In addition, sellers’ obtained cumulative rewards of the proposed method are higher than the obtained cumulative reward of the random method by 93.6%, 91.1%, 86.7%, and 83.1% in the energy trading scenario with the number of participants being 5, 10, 15, and 20, respectively.

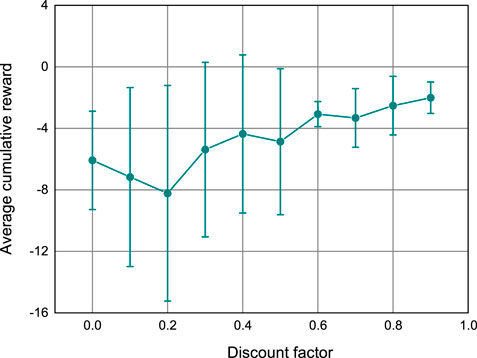
6.2.3 Impact of the discount factor

Finally, we investigated the performance of the proposed algorithm at different values of the discount factor in the energy trading scenario with a total of ten buyers and sellers. Fixing sellers’ bidding strategies as the greedy method, buyers’ average cumulative rewards of the proposed method with different discount factors are illustrated in Figure 8. Each γ in the set [0, 0.1, … , 0.9] is tested five times with different random seeds. The symbols and error bars show the mean and standard deviation over five runs, respectively. From Figure 8, we can see that as the value of γ increases, the cumulative reward obtained by the proposed method will also increase. The main reason behind the simulation results is that higher γ means more attention is paid to future rewards according to (1); as a consequence, the algorithm will obtain higher cumulative rewards.

FIGURE 8

FIGURE 8. Average cumulative reward obtained by agents under different discount factors.

7 Conclusion

In this paper, a deep reinforcement learning-based bidding strategy is proposed for buyers and sellers in the peer-to-peer energy trading market, in which the bidding strategy with sequential decision-making characteristics is modeled as a Markov decision process. In order to address the problem that existing RL-based trading approaches need to discretize the action space, we propose an actor–critic-based paradigm that utilizes the actor network to generate the continuous bidding price and bidding volume for buyers and sellers. In addition, we integrate the recurrent neural network into the actor network to process the sequential state information of the power grid. We verify the effectiveness of the proposed method in the peer-to-peer energy trading scenario. Simulation results show that the cumulative rewards of the proposed method are higher than those of the traditional greedy method in the energy trading scenario with a different number of participants.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

FZ: conceptualization, methodology, software, and writing. QY (corresponding author): investigation and supervision. DL: data curation and visualization.

Funding

This work was supported in part by the National Natural Science Foundation of China under Grant 61973247, 61673315 and 62173268, in part by the Key Program of the National Natural Science Foundation of China under Grant 61833015, in part by the Fundamental Research Funds for the Central Universities under Grant xzy022021050, in part by the National Postdoctoral Innovative Talents Support Program of China under Grant BX20200272.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

An, D., Yang, Q., Yu, W., Yang, X., Fu, X., and Zhao, W. (2018). Soda: Strategy-proof online double auction scheme for multimicrogrids bidding. IEEE Trans. Syst. Man. Cybern. Syst. 48, 1177–1190. doi:10.1109/TSMC.2017.2651072

CrossRef Full Text | Google Scholar

Anoh, K., Maharjan, S., Ikpehai, A., Zhang, Y., and Adebisi, B. (2020). Energy peer-to-peer trading in virtual microgrids in smart grids: A game-theoretic approach. IEEE Trans. Smart Grid 11, 1264–1275. doi:10.1109/TSG.2019.2934830

CrossRef Full Text | Google Scholar

Chen, T., and Su, W. (2019). Indirect customer-to-customer energy trading with reinforcement learning. IEEE Trans. Smart Grid 10, 4338–4348. doi:10.1109/tsg.2018.2857449

CrossRef Full Text | Google Scholar

Chung, J., Gulcehre, C., Cho, K., and Bengio, Y. (2014). Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv preprint arXiv:1412.3555.

Google Scholar

Cui, S., Wang, Y.-W., Shi, Y., and Xiao, J.-W. (2020). An efficient peer-to-peer energy-sharing framework for numerous community prosumers. IEEE Trans. Ind. Inf. 16, 7402–7412. doi:10.1109/tii.2019.2960802

CrossRef Full Text | Google Scholar

Dou, X., Wang, J., Hu, Q., and Li, Y. (2020). Bi-level bidding and multi-energy retail packages for integrated energy service providers considering multi-energy demand elasticity. CSEE J. Power Energy Syst., 1–14. doi:10.17775/CSEEJPES.2020.03010

CrossRef Full Text | Google Scholar

Fang, X., Hu, Q., Li, F., Wang, B., and Li, Y. (2016). Coupon-based demand response considering wind power uncertainty: A strategic bidding model for load serving entities. IEEE Trans. Power Syst. 31, 1025–1037. doi:10.1109/tpwrs.2015.2431271

CrossRef Full Text | Google Scholar

Fooladivanda, D., Xu, H., Domínguez-García, A. D., and Bose, S. (2018). Offer strategies for wholesale energy and regulation markets. IEEE Trans. Power Syst. 33, 7305–7308. doi:10.1109/tpwrs.2018.2868131

CrossRef Full Text | Google Scholar

Galindo-Serrano, A., and Giupponi, L. (2010). Distributed q-learning for aggregated interference control in cognitive radio networks. IEEE Trans. Veh. Technol. 59, 1823–1834. doi:10.1109/tvt.2010.2043124

CrossRef Full Text | Google Scholar

Gao, J., Xiao, Y., Liu, J., Liang, W., and Chen, C. L. (2012). A survey of communication/networking in smart grids. Future gener. Comput. Syst. 28, 391–404. doi:10.1016/j.future.2011.04.014

CrossRef Full Text | Google Scholar

Gers, F., Schmidhuber, J., and Cummins, F. (1999). Learning to forget: Continual prediction with lstm. Ninth Int. Conf. Artif. Neural Netw. ICANNConf. Publ. No. 470) 992, 850–8552.

CrossRef Full Text | Google Scholar

Herranz, R., Munoz San Roque, A., Villar, J., and Campos, F. A. (2012). Optimal demand-side bidding strategies in electricity spot markets. IEEE Trans. Power Syst. 27, 1204–1213. doi:10.1109/tpwrs.2012.2185960

CrossRef Full Text | Google Scholar

Kim, B.-G., Zhang, Y., van der Schaar, M., and Lee, J.-W. (2016). Dynamic pricing and energy consumption scheduling with reinforcement learning. IEEE Trans. Smart Grid 7, 2187–2198. doi:10.1109/tsg.2015.2495145

CrossRef Full Text | Google Scholar

Li, D., Yang, Q., Yu, W., An, D., Zhang, Y., and Zhao, W. (2020). Towards differential privacy-based online double auction for smart grid. IEEE Trans. Inf. Forensic. Secur. 15, 971–986. doi:10.1109/tifs.2019.2932911

CrossRef Full Text | Google Scholar

Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T., Tassa, Y., et al. (2015). Continuous control with deep reinforcement learning. arXiv preprint arXiv:1509.02971.

Google Scholar

Liu, D., Gao, Y., Wang, W., and Dong, Z. (2021). Research on bidding strategy of thermal power companies in electricity market based on multi-agent deep deterministic policy gradient. IEEE Access 9, 81750–81764. doi:10.1109/ACCESS.2021.3086002

CrossRef Full Text | Google Scholar

Ma, J., Deng, J., Song, L., and Han, Z. (2014). Incentive mechanism for demand side management in smart grid using auction. IEEE Trans. Smart Grid 5, 1379–1388. doi:10.1109/tsg.2014.2302915

CrossRef Full Text | Google Scholar

Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., et al. (2015). Human-level control through deep reinforcement learning. Nature 518, 529–533. doi:10.1038/nature14236

PubMed Abstract | CrossRef Full Text | Google Scholar

PankiRaj, J. S., Yassine, A., and Choudhury, S. (2019). An auction mechanism for profit maximization of peer-to-peer energy trading in smart grids. Procedia Comput. Sci. 151, 361–368. doi:10.1016/j.procs.2019.04.050

CrossRef Full Text | Google Scholar

Ramachandran, B., Srivastava, S. K., Edrington, C. S., and Cartes, D. A. (2011). An intelligent auction scheme for smart grid market using a hybrid immune algorithm. IEEE Trans. Ind. Electron. 58, 4603–4612. doi:10.1109/tie.2010.2102319

CrossRef Full Text | Google Scholar

Rs, S., and Ag, B. (1998). Reinforcement learning: An introduction, 1. Massachusetts, United States: MIT Press.

Google Scholar

Singh, K. N., Das, N., Maurya, M., Goswami, A. K., and Chudhury, N. B. D. (2022). “An intelligent bidding strategy based on social welfare of virtual power plant considering carbon trading,” in Proceedings of the IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy (PESGRE), Trivandrum, India, 2-5 Jan. 2022, 1–5. doi:10.1109/PESGRE52268.2022.9715918

CrossRef Full Text | Google Scholar

Tao, Y., Qiu, J., and Lai, S. (2022). Deep reinforcement learning based bidding strategy for evas in local energy market considering information asymmetry. IEEE Trans. Ind. Inf. 18, 3831–3842. doi:10.1109/TII.2021.3116275

CrossRef Full Text | Google Scholar

Vytelingum, P., Cliff, D., and Jennings, N. (2008). Strategic bidding in continuous double auctions. Artif. Intell. 172, 1700–1729. doi:10.1016/j.artint.2008.06.001

CrossRef Full Text | Google Scholar

Wang, H., Huang, T., Liao, X., Abu-Rub, H., and Chen, G. (2017). Reinforcement learning for constrained energy trading games with incomplete information. IEEE Trans. Cybern. 47, 3404–3416. doi:10.1109/TCYB.2016.2539300

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, N., Xu, W., Shao, W., and Xu, Z. (2019). A q-cube framework of reinforcement learning algorithm for continuous double auction among microgrids. Energies 12 (5), 2891–2917. doi:10.3390/en12152891

CrossRef Full Text | Google Scholar

Wang, Y., Saad, W., Han, Z., Poor, H. V., and Başar, T. (2014). A game-theoretic approach to energy trading in the smart grid. IEEE Trans. Smart Grid 5, 1439–1450. doi:10.1109/tsg.2013.2284664

CrossRef Full Text | Google Scholar

Wu, H., Shahidehpour, M., Alabdulwahab, A., and Abusorrah, A. (2016). A game theoretic approach to risk-based optimal bidding strategies for electric vehicle aggregators in electricity markets with variable wind energy resources. IEEE Trans. Sustain. Energy 7, 374–385. doi:10.1109/tste.2015.2498200

CrossRef Full Text | Google Scholar

Xu, H., Sun, H., Nikovski, D., Kitamura, S., Mori, K., and Hashimoto, H. (2019). Deep reinforcement learning for joint bidding and pricing of load serving entity. IEEE Trans. Smart Grid 10, 6366–6375. doi:10.1109/tsg.2019.2903756

CrossRef Full Text | Google Scholar

Xu, S., Zhao, Y., Li, Y., Cui, K., Cui, S., and Huang, C. (2021). “Truthful double-auction mechanisms for peer-to-peer energy trading in a local market,” in Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 23-25 Dec. 2021, 2458–2463. doi:10.1109/iSPEC53008.2021.9735918

CrossRef Full Text | Google Scholar

Zhang, F., and Yang, Q. (2020). “Energy trading in smart grid: A deep reinforcement learning-based approach,” in Proceedings of the 2020 Chinese Control And Decision Conference, Kunming, China, 22-24 Aug. 2020 (Piscataway, NY: IEEE), 3677–3682. doi:10.1109/CCDC49329.2020.9164350

CrossRef Full Text | Google Scholar

Zhou, J., Wang, K., Mao, W., Wang, Y., and Huang, P. (2017). “Smart bidding strategy of the demand-side loads based on the reinforcement learning,” in Proceedings of the IEEE Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 22-24 Oct. 2021, 1–5.

CrossRef Full Text | Google Scholar

Zhu, Z., Chan, K. W., Xia, S., and Bu, S. (2022). Optimal bi-level bidding and dispatching strategy between active distribution network and virtual alliances using distributed robust multi-agent deep reinforcement learning. IEEE Trans. Smart Grid 13, 2833–2843. doi:10.1109/TSG.2022.3164080

CrossRef Full Text | Google Scholar