Robust hybrid estimator for the state of charge of a lithium-ion battery

The use of batteries for diverse energy storage applications is increasing, primarily because of their high energy density, and lithium-ion batteries (LiBs) are of particular significance in this regard. However, designing estimators that are robust to compute the state of charge (SOC) of these batteries in the presence of disturbance signals arising from different battery types remains a challenge. Hence, this paper presents a hybrid estimator that combines the extended Kalman filter (EKF) and sliding mode observer (SMO) via a switching function and tracking closed loop to achieve the qualities of noise cancellation and disturbance rejection. Hybridization was carried out in such a way that the inactive observer tracks the output of the used observer, simultaneously feeding back a zero-sum signal to the input gain of the used observer. The results obtained show that noise filtering is preserved at a convergence time of .01 s. Also, the state of charge estimation interval improves greatly from a range of [1, .93] and [.94, .84] obtained from the extended Kalman filter and sliding mode observer, respectively, to a range of [1, 0], in spite of the added disturbance signals from a lithium–nickel (INR 18650) battery type.

1 Introduction

So far, lithium-ion batteries (LiBs) have been increasingly used in energy repository systems, power backups, and electronics (Orovwode et al., 2021) due to their inherent properties of dense energy, lower self-discharge, and prolonged cycle life (Guangzhong et al., 2016), more than conventional lead–acid batteries. LiBs constitute an essential energy repository system (Adeyemi et al., 2022) used in electrical vehicles and smart grids, hence the need for a battery management system (BMS). The BMS plays a significant role in monitoring the battery states, which include the state of charge (SOC) for the purpose of ensuring efficient and safe operation (ShichunYang et al., 2021; Zhang et al., 2017).

The SOC indicates the available battery capacity relative to the maximum capacity and lies in the range of 100 to 0 per cent. A typical challenge is that there is no known measuring instrument to determine the SOC. Thus, there is a continuous quest for developing state observers that can accurately estimate the SOC based on models that capture the internal dynamics of the LiB. One of the most popular models used in the SOC estimation task is the equivalent circuit model (ECM) composed of components such as resistors, capacitors, voltage sources, and, in some cases, hysteresis elements (Yujie et al., 2020). The attractiveness of the ECM is based on the less mathematical complexity in developing it and its fewer tuning parameters unlike the electrochemical models, which contain complex partial differential equations (Simin et al., 2017) and a significant number of tuning parameters.

SOC estimation methods are based on open-loop, model-free, and closed-loop techniques. The coulomb counting (CC) and open-circuit voltage (OCV) methods are examples of open-loop techniques. The former makes use of the current integration technique for SOC estimation, but it is prone to inaccuracies due to the initial current measurement error, which accumulates (Liu et al., 2021) and, in addition, requires the initial SOC to be known. The OCV method uses a non-linear fitting function to map the relationship between the SOC and OCV in order to set up a look-up table from which the SOC of the battery at any step time is obtained (Xu et al., 2020). In real time, carrying out OCV experiments usually requires a large amount of time for electrolytes in the battery to become uniformly distributed before the battery terminal voltage can be accurately measured (Peng et al., 2017). Model-free techniques include artificial neural networks (ANNs) (Samuel et al., 2021) and fuzzy logic (FL), which are developed as a black box, and by studying the trained dataset (Surajudeen et al., 2021) such as the terminal voltage, temperature, charge–discharge current, and cycle, the look-up table function that describes the relationship between the SOC and battery parameters can be determined (Liu et al., 2021). A major drawback is that the estimation accuracy of these models is dependent on the size of the trained data and quality of the dataset (Ng et al., 2009).

Closed-loop SOC estimation techniques include the Kalman filter (KF), particle filter (PF), unscented particle filter (UPF), and sliding mode observer (SMO). The superior advantage they have over other methods is the ability of handling real-time disturbance and uncertainties of the battery system by correction in the feedback non-open-loop structure, leading to high accuracies in SOC estimation (Yidan, 2020). The PF and UPF produce good estimate results when used in non-linear systems, but they are restricted to non-Gaussian noise distribution. However, the KF is best used for uncertainties represented as Gaussian distributions, but its shortcoming is that its accuracy decreases when applied to non-linear systems, i.e., it generates accurate estimates for linear processes only. To this end, various extensions of the Kalman filter, namely, the extended Kalman filter (EKF), dual extended Kalman Filter (DEKF), and dual Kalman Filter (DKF), have been developed to further improve the SOC accuracy for non-linear systems affected with Gaussian noise distribution. The SMO is seen as a paradigm shift from the traditional Luenberger observers and Urtink observers, in which they do not require the system to be observable before the sliding motion can be implemented. In traditional observers, the error between the plant and model output, decreases to zero in infinite time. However, SMOs guarantee the error is exactly zero, and the model state is exactly that of the plant, beginning from the instant the sliding motion takes place. They also offer high robustness to measurement uncertainties and disturbances (Bouchareb et al., 2020). A major drawback in these observers is that the sliding motion is majorly composed of chattering caused by the high switching gain present in the SMO feedback loop.

Over the years, several works have been carried out by researchers in estimating the battery SOC. The KF was implemented by Guangzhong et al. (2016) for onboard SOC applications. The performance results under experiment conditions, namely, the dynamic current, direct power, and discharge capability tests, showed estimation errors of about 4 percent. The method is limited to linear system applications, and the complexity of the algorithm also limits its practical implementation. Benedikt et al. (2021) proposed an EKF with a hysteresis-coupled battery model for multiple cell SOC determination. The method showed a 300 percent decrease in maximum error and high stability from an EKF with no hysteresis present in its battery model. The shortfall was that the EKF parameters were highly sensitive on the variations of the process noise, which had effect on its accuracy and convergence. To solve this problem, an improved EKF (IEKF) was proposed in Shichun et al. (2021) by developing noise filtering and adaptation methods as augments to an existing EKF. The results showed an under temperature disturbance and dynamic stress conditions (DSCs); the maximum errors were three percent and one per cent, respectively. However, the SOC response due to complex coupling effects of the battery was not considered.

By Wenhui et al. (2019), the SOC estimation for power LiB using a fuzzy logic sliding mode observer (FLSMO) was proposed. The work improved the performance of SMOs through the use of the fuzzy logic control (Atayero et al., 2012). The discharging test results showed that the FLSMO algorithm had a higher SOC estimation accuracy, with a considerable convergence rate. Compared with the sliding mode observer and extended Kalman filter, the FLSMO algorithm shows better performance regarding the robustness against the measurement noise and parameter disturbance. Sassi et al. (2018) carried out a comparison of the KF and SMO and noted the competitive nature of both methods with regards to the precision but concluded on the superiority of the SMO over KF in terms of handling parameter changes to uncertainties in the battery model.

To obtain desired qualities associated with two or more SOC estimation strategies, hybridization is required. The unique difference between a hybrid state estimator and existing state estimators is that it offers an approach for combining the strength of noise filtration, a characteristic of the EKF, and robustness, an attribute of SMO, in predicting the SOC of batteries, thus producing a better adaptive system to the uncertainties that arise from the environment and measurement instruments. In addition, the hybrid system consists of a well-posed dynamic system and draws both discrete time and continuous time behaviors of EKF and SMO state estimation algorithms to improve the accuracy of individual methods.

One of the challenges present in the SOC estimation subject is the problem of designing accurate state observers that can be adaptive to disturbances influencing the signal characteristics of lithium-ion batteries. A state observer designed for one battery type loses its estimation reliability when subjected to a different battery type due to variation of chemistry. In fact, the model sees the new input signals as a form of disturbance, and hence, the question that arises is how one can redesign the system to become insensitive to alien data in a way it maintains precise parameter predictions. This paper aims to address this issue by proposing the design and implementation of a hybrid estimator combining EKF and SMO state estimation strategies to improve the performance accuracy of the EKF and the robustness quality of both estimators in the face of complex LiB parameter disturbances due to the change of the battery type.

Beginning with this introductory section, the organization of this paper starts with data collection description in Section 2. The equivalent circuit model of the batteries derived in the discrete state space is presented in Section 3. The battery model parameter identification technique is discussed in Section 4. In Sections 5 and 6, developments of EKF and SMO state estimators are presented, respectively. Section 7 explains the hybridization procedure, while Section 8 presents the results and evaluation of estimators. The conclusion of this paper is given in Section 9.

2 Data collection

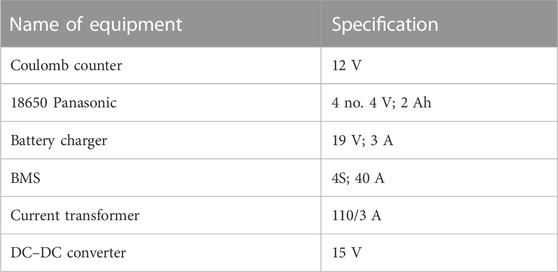
A charge and discharge experiment was carried out on 4 No. 4-V and 2-Ah Panasonic’s lithium-ion batteries connected in a series at room temperature. The materials used and the experimental setup are shown in Table 1 and Figure 1, respectively. The charge experiment was made possible through the DC–DC converter passing the charging current at the 1 C rate to flow into the batteries. The current transformer (CT) rated 3-A measures the current and passes the signal to the 12-V digital Coulomb counter for the measurement of the capacity, voltage, and current information on the batteries. The BMS helps regulate the batteries from overcharging and discharging and monitors the maximum cut-off voltage of 4 V and minimum cut-off voltage of 2.7 V for each cell set by the manufacturer. The cut-off voltage set was required to protect the batteries from overcharging and discharging by disconnecting the load from the batteries whenever the limits were reached. This is crucial in ensuring the batteries maintain maximum capacity, increased life, and are not damaged in an excessive charge or discharge process. For the discharge readings, a 3.8-V, 2.35-Ah mobile device was used as the load connected across the batteries in parallel and to the Coulomb counter for the measurement readings to be displayed. The current and voltage profiles for the discharge and charge experiment are shown in Figures 2A–D, respectively. The positive and negative values of the current profile in Figures 2A, C show the batteries were charged and discharged, respectively.

TABLE 1

TABLE 1. Experiment material specifications.

FIGURE 1

FIGURE 1. Experimental setup.

FIGURE 2

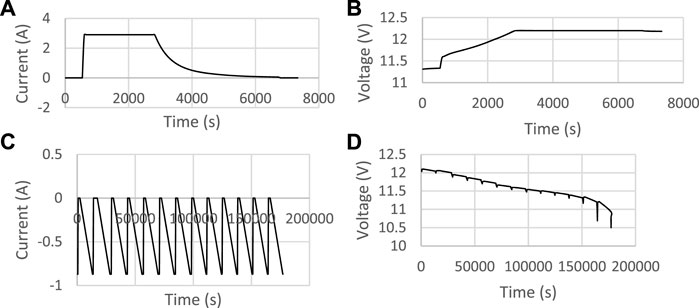
FIGURE 2. (A) Primary data charge current plot. (B) Primary data charge voltage plot. (C) Primary data discharge current plot. (D) Primary data discharge voltage plot.

TThe step-by-step procedures used in carrying out the experiment are outlined as follows:

Step 1. Connection of the batteries in a series.

Step 2. Connection of the battery terminals to the BMS.

Step 3. Connection of the BMS output to the CT.

Step 4. CT connected to the coulomb counter.

Step 5. The negative terminal of the CT passed to the negative terminal of the BMS, and positive terminal of the CT passed through the CT to the positive terminal of the BMS.

Step 6. The DC–DC converter is connected to the power pack.

Step 7. The converter voltage output is adjusted to 12 V.

Step 8. The converter is connected to the CT and BMS.

Step 9. The measurement reading is taken at the display interface of the coulomb counter.

3 Battery modeling

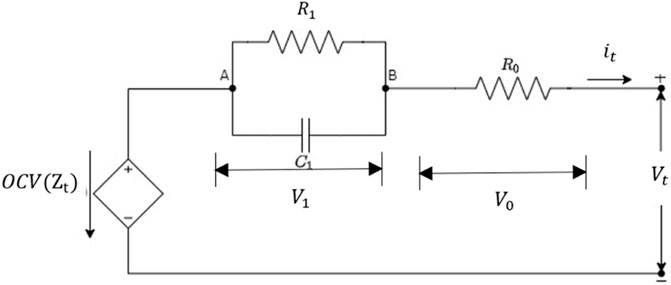
The choice of the model in representing the LiB internal states is the equivalent circuit model (ECM) due to its merits of simplicity, few parameters, and faster implementation in carrying out the SOC estimation. To carry out battery modeling with a reasonable level of accuracy and with less parameters, a first-order ECM choice is required. As shown in Figure 3, the first-order ECM can be regarded as an RC (resistor and capacitor) model. It consists of an open-circuit voltage (OCV), two internal resistors, and a single capacitor. The internal resistance, R₀, is responsible for the drop and rise of the measurement voltage profile, while the R₁C₁ term describes the transient behavior of the measurement voltage response.

FIGURE 3

FIGURE 3. First-order ECM model.

At node A, applying Kirchhoff’s current law (KCL), we obtain the following:

${\mathrm{i}}_{\mathrm{t}}={\mathrm{i}}_{{\mathrm{R}}_1+}{\mathrm{i}}_{{\mathrm{C}}_1}=\frac{{\mathrm{V}}_1}{{\mathrm{R}}_1}+{\mathrm{C}}_1{\dot{\mathrm{V}}}_1.(1)$

Making the derivative of ${\mathrm{V}}_1$ the subject of the formula, we obtain the following:

${\dot{\mathrm{V}}}_1=-\frac{{\mathrm{V}}_1}{{\mathrm{R}}_1{\mathrm{C}}_1}+\frac{1}{{\mathrm{C}}_1}{\mathrm{i}}_{\mathrm{t}}.(2)$

Taking Kirchhoff’s voltage law (KVL) across the full loop results, we obtain

${\mathrm{V}}_{\mathrm{t}}=\mathrm{O}\mathrm{C}\mathrm{V}\left({\mathrm{Z}}_{\mathrm{t}}\right)-{\mathrm{V}}_0-{\mathrm{V}}_1=\mathrm{O}\mathrm{C}\mathrm{V}-{\mathrm{R}}_0{\mathrm{i}}_{\mathrm{t}}-{\mathrm{V}}_1.(3)$

The SOC equation is given as follows:

${\mathrm{Z}}_{\mathrm{t}}={\mathrm{Z}}_0-\frac{{\mathrm{\eta }}_{\mathrm{k}}}{{\mathrm{Q}}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{t}}}{{\displaystyle \int }}_0^{\mathrm{t}}\mathrm{i}\mathrm{d}\mathrm{t},(4)$

where ${\mathrm{Z}}_{\mathrm{t}}$ refers to the state of charge at time $\mathrm{t}$, ${\mathrm{Z}}_0$, the initial state of charge (=100%), ${\mathrm{Q}}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{t}}$, the maximum battery capacity, ${\mathrm{\eta }}_{\mathrm{k}}$, the Coulombic efficiency, OCV, the open circuit voltage, and $\mathrm{i}$, the input current.

The following sign convention was used for the current:

$\mathrm{s}\mathrm{g}\mathrm{n}\left({\mathrm{i}}_{\mathrm{t}}\right)=\left\{\begin{array}{l}+,\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{h}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{g},\\ -,\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{c}\mathrm{h}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{g}.\end{array}\right.(5)$

The coulombic efficiency describes the efficiency of a charging process due to the number of electrons transferred into the cell. It can be estimated from the OCV charge and discharge curves (Benedikt et al., 2021), which is expressed as follows:

${\mathrm{\eta }}_{\mathrm{k}}=\left\{\begin{array}{l}1,{\mathrm{i}}_{\mathrm{k}}>0\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{h}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{g},\\ {\mathrm{\eta }}^{*},{\mathrm{i}}_{\mathrm{k}}<0\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{c}\mathrm{h}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{g}.\end{array}\right.(6)$

The next step is to discretize Eqs 2–4 using the sample time $\mathrm{k}+1$ as the present value and $\mathrm{k}$ as the previous value. To discretize Eq. 2, the difference ratio is approximated as follows:

${\dot{\mathrm{V}}}_1\cong \frac{{\mathrm{V}}_{1,\mathrm{k}+1}-{\mathrm{V}}_{1,\mathrm{k}}}{\mathrm{\delta }\mathrm{t}}=-\frac{{\mathrm{V}}_{1,\mathrm{k}}}{{\mathrm{R}}_1{\mathrm{C}}_1}+\frac{1}{{\mathrm{C}}_1}{\mathrm{i}}_{\mathrm{k}},(7)$

so that

${\mathrm{V}}_{1,\mathrm{k}+1}={\mathrm{V}}_{1,\mathrm{k}}\left(1-\frac{\mathrm{\delta }\mathrm{t}}{{\mathrm{R}}_1{\mathrm{C}}_1}\right)+\frac{\mathrm{\delta }\mathrm{t}}{{\mathrm{C}}_1}{\mathrm{i}}_{\mathrm{k}}.(8)$

The discretization of Eqs 3, 4 is straightforward. Therefore, the battery model is represented in the state space form as follows:

$\left[\begin{array}{c}{\mathrm{V}}_{1,\mathrm{k}+1}\\ {\mathrm{Z}}_{\mathrm{k}+1}\end{array}\right]=\left[\begin{array}{cc}1-\frac{\mathrm{\delta }\mathrm{t}}{{\mathrm{\tau }}_1}& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}{\mathrm{V}}_{1,\mathrm{k}}\\ {\mathrm{Z}}_{\mathrm{k}}\end{array}\right]+\left[\begin{array}{c}\frac{\mathrm{\delta }\mathrm{t}}{{\mathrm{C}}_1}\\ -\frac{\eta \mathrm{\delta }\mathrm{t}}{\mathrm{Q}}\end{array}\right]\left[{\mathrm{i}}_{\mathrm{k}}\right](9){\mathrm{V}}_{\mathrm{k}}=\mathrm{O}\mathrm{C}\mathrm{V}\left({\mathrm{Z}}_{\mathrm{k}}\right)-{\mathrm{R}}_0{\mathrm{i}}_{\mathrm{k}}-{\mathrm{V}}_{1,\mathrm{k}},$

where ${\mathrm{Z}}_{\mathrm{k}}$ is the state of charge, $\mathrm{O}\mathrm{C}\mathrm{V}$ is the open circuit voltage of the battery at no load, $\mathrm{Q}$ is the battery-rated capacity, and ${\mathrm{R}}_0$ is the battery ohmic resistance. The product ${\mathrm{R}}_1{\mathrm{C}}_1$ represents the polarization time constant ${\mathrm{\tau }}_1$; ${\mathrm{V}}_{1,\mathrm{k}}$ represents the current state of voltage across the capacitor ${\mathrm{C}}_1$ and resistor ${\mathrm{R}}_1$. The model’s output ${\mathrm{V}}_{\mathrm{k}}$ represents the terminal or observed voltage, and the input is the measured current ${\mathrm{i}}_{\mathrm{k}}$; ${\mathrm{\eta }}_{\mathrm{k}}$ represents the battery coulombic efficiency assumed as 1 in this paper.

4 Model parameter identification

A global pattern search algorithm (GPSA) available in the Simulink parameter optimization toolbox is used for the offline battery parameter identification to obtain the optimum values of the internal parameters, $\left\{\mathrm{O}\mathrm{C}\mathrm{V},{\mathrm{R}}_0,{\mathrm{\tau }}_1\right\}$. The algorithm generates these parameters by searching sets of points called the mesh around a current point determined to have had the least objective function, ${\displaystyle \sum }_{\mathrm{k}}^{\mathrm{n}}\left({{\mathrm{V}}_{\mathrm{t}}-\widehat{\mathrm{V}}}_{\mathrm{t}}\right)$ value. The step-by-step implementation is presented as follows:

Step 1. The number of independent $\mathrm{N}$ variables for the objective function is set.

Step 2. The initial point ${\mathrm{v}}_0$ is set along with upper and lower boundaries of model parameters.

Step 3. Pattern vectors are generated depending on $\mathrm{N}$. By default, for a $2\mathrm{N}$ maximal base, where $\mathrm{N}=2$ for the pattern vector, ${\mathrm{v}}_{\mathrm{i}}$ is represented as follows:

${\mathrm{v}}_1=\left[\begin{array}{cc}1& 0\end{array}\right];{\mathrm{v}}_2=\left[\begin{array}{cc}0& 1\end{array}\right];{\mathrm{v}}_3=\left[\begin{array}{cc}-1& 0\end{array}\right];{\mathrm{v}}_4=\left[\begin{array}{cc}0& -1\end{array}\right].(10)$

Step 4. The current mesh size ${∆}^{\mathrm{m}}$ is set.

Step 5. The mesh is computed as follows:

$\mathrm{m}={\mathrm{v}}_0+{∆}^{\mathrm{m}}\bullet {\mathrm{v}}_{\mathrm{i}}.(11)$

Step 6. The process of polling is initiated, following the direction produced by the pattern vector that generates a mesh point.

4.1 Parameter initialization

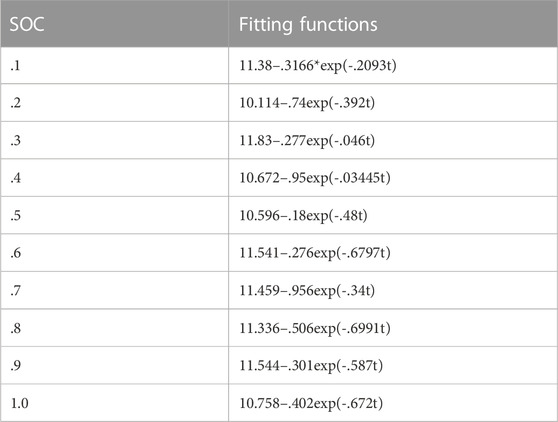
Proper parameter initialization of the battery model is essential for obtaining an accurate fitting relationship between the measured and estimated voltage input. Hence, the voltage discharge curve is partitioned into 10 pulses corresponding to an SOC value in the range [.1, 1.0] with a step value of .1. To compute the initial parameters (OCV, ${\mathrm{R}}_0$; ${\mathrm{R}}_1$), a mathematical comparison between the fitting functions in Table 2 described by the transient pulses and the transient terminal voltage in Eq. 12a, 12b, 12c is carried out as follows:

${\mathrm{V}}_{\mathrm{L}}=\mathrm{O}\mathrm{C}\mathrm{V}-{\mathrm{R}}_0{\mathrm{I}}_{\mathrm{t}}-{\mathrm{R}}_1{\mathrm{I}}_{\mathrm{t}}{\mathrm{e}}^{\frac{-\mathrm{t}}{{\tau }_1}}(\mathrm{12a})$

TABLE 2

TABLE 2. First order ECM parameters.

The transient terminal voltage ${\mathrm{V}}_{\mathrm{L}}$ describes the dynamic exponential behavior of the battery terminal voltage profile shown in Figure 2D after each rise and drop in the pulse and is derived from the transient solution of Eq. 2 by first recalling from basic principles; the general solution of a first-order non-homogenous linear differential Eq. 2 is given as follows:

${\mathrm{V}}_1={\mathrm{e}}^{\frac{-\mathrm{t}}{{\tau }_1}}\left[\int \frac{{\mathrm{i}}_{\mathrm{t}}}{{\mathrm{c}}_1}{\bullet \mathrm{e}}^{\frac{-\mathrm{t}}{{\tau }_1}}\bullet \mathrm{d}\mathrm{t}+\mathrm{k}\right](\mathrm{12b})$

Carrying out the integration in Eq. 12b and applying the initial condition, ${\mathrm{V}}_1\left(0\right)=0$. This implies $\mathrm{k}=-{\mathrm{R}}_1{\mathrm{i}}_{\mathrm{t}}$ so that

${\mathrm{V}}_1={\mathrm{R}}_1{\mathrm{i}}_{\mathrm{t}}-{\mathrm{R}}_1{\mathrm{i}}_{\mathrm{t}}{\mathrm{e}}^{\frac{-\mathrm{t}}{{\tau }_1}}(\mathrm{12c})$

Taking the transient portion of Eq. 12c, i.e., the term with the exponential function for the discharge case and then substituting it in Eq. 3, the transient terminal voltage equation ${\mathrm{V}}_{\mathrm{t}}$ = ${\mathrm{V}}_{\mathrm{L}}$ in Eq. 12a is obtained.

5 The extended Kalman filter algorithm

The non-linear dynamic state representation of the battery is expressed as follows:

${\mathrm{x}}_{\mathrm{k}+1}=\mathrm{f}\left({\mathrm{x}}_{\mathrm{k}},{\mathrm{u}}_{\mathrm{k}}\right)+{\mathrm{w}}_{\mathrm{k}}{\mathrm{y}}_{\mathrm{k}}=\mathrm{g}\left({\mathrm{x}}_{\mathrm{k}},{\mathrm{u}}_{\mathrm{k}}\right)+{\mathrm{v}}_{\mathrm{k}}(13)$

where $\mathrm{f}\left({\mathrm{x}}_{\mathrm{k}},{\mathrm{u}}_{\mathrm{k}}\right)$ represents the process of non-linear dynamics and $\mathrm{g}\left({\mathrm{x}}_{\mathrm{k}},{\mathrm{u}}_{\mathrm{k}}\right)$ represents the measurement of non-linear dynamics. The matrices, ${\mathrm{w}}_{\mathrm{k}}$ and ${\mathrm{v}}_{\mathrm{k}},$ represent the noise present in the process and measurement part of the system, respectively (Rui et al., 2017). A step-by-step implementation of the first-order EKF algorithm is given as follows using a hat (^∧) notation to identify the state estimates:

Step 1. Setting the internal state ${\mathrm{x}}_{\mathrm{k}+1}\left[0\right]=\left[\begin{array}{c}1\\ 0\end{array}\right]$ and system state error ${\mathrm{P}}_{\mathrm{k}+1}\left[0\right]={\left[0\right]}_{2\times 2}.$

Step 2. Calculating the priori estimates

${\widehat{\mathrm{x}}}_{\mathrm{k}+1|\mathrm{k}}={\mathrm{A}}_{\mathrm{k}}{\widehat{\mathrm{x}}}_{\mathrm{k}|\mathrm{k}}+{\mathrm{B}}_{\mathrm{k}}{\mathrm{u}}_{\mathrm{k}}{\mathrm{P}}_{\mathrm{k}+1}={\mathrm{A}}_{\mathrm{k}}{\mathrm{P}}_{\mathrm{k}|\mathrm{k}}{{\mathrm{A}}_{\mathrm{k}}}^{\mathrm{T}}+{\mathrm{Q}}_{\mathrm{k}}.(14)$

Step 3. Linearizing the system model (Awelewa et al. 2013) about ${\mathrm{x}}_{\mathrm{k}+1|\mathrm{k}}$ such that

${\mathrm{A}}_{\mathrm{k}}={\left(\frac{\partial \mathrm{f}\left({\mathrm{x}}_{\mathrm{k}},{\mathrm{u}}_{\mathrm{k}}\right)}{\partial {\mathrm{x}}_{\mathrm{k}}}\right)}_{{\mathrm{x}}_{\mathrm{k}+1|\mathrm{k}},{\mathrm{u}}_{\mathrm{k}}}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(1,{\mathrm{e}}^{\frac{-∆\mathrm{t}}{{\mathrm{\tau }}_1}}\right);{\mathrm{B}}_{\mathrm{k}}=\left(\begin{array}{c}{-\mathrm{\eta }}_{\mathrm{k}}\frac{∆\mathrm{t}}{{\mathrm{Q}}_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{t}}}\\ {\mathrm{R}}_1\left(1-{\mathrm{e}}^{\frac{-∆\mathrm{t}}{{\mathrm{\tau }}_1}}\right)\end{array}\right),(15)$

${\mathrm{C}}_{\mathrm{k}}={\left(\frac{\partial \mathrm{g}\left({\mathrm{x}}_{\mathrm{k}},{\mathrm{u}}_{\mathrm{k}}\right)}{\partial {\mathrm{x}}_{\mathrm{k}}}\right)}_{{\mathrm{x}}_{\mathrm{k}+1|\mathrm{k}},{\mathrm{u}}_{\mathrm{k}}}=\left[\frac{\partial {\mathrm{V}}_0}{\partial {\mathrm{Z}}_{\mathrm{k}}},-1\right].(16)$

The Jacobean matrices ${\mathrm{A}}_{\mathrm{k}}$, ${\mathrm{B}}_{\mathrm{k}}$, and ${\mathrm{C}}_{\mathrm{k}}$ were derived from the first-order Taylor series approximation (Awelewa et al., 2021) of (13); ${\mathrm{V}}_0$ is the OCV; ${\mathrm{Z}}_{\mathrm{k}}$ is the SOC, and the state vector is ${\mathrm{x}}_{\mathrm{k}}=\left[\begin{array}{c}{\mathrm{Z}}_{\mathrm{k}}\\ {\mathrm{V}}_{1,\mathrm{k}}\end{array}\right].$

Step 4. Calculating the Kalman gain ${\mathrm{K}}_{\mathrm{k}+1}$

${\mathrm{K}}_{\mathrm{k}+1}={{\mathrm{P}}_{\mathrm{k}+1|\mathrm{k}}{\mathrm{C}}^{\mathrm{T}}\left(\mathrm{C}{\mathrm{P}}_{\mathrm{k}+1|\mathrm{k}}{\mathrm{C}}^{\mathrm{T}}+{\mathrm{R}}_{\mathrm{k}+1}\right)}^{-1}.(17)$

Step 5. Calculating the a posteriori (Mohammed, 2013) estimates

${\widehat{\mathrm{x}}}_{\mathrm{k}+1│\mathrm{k}+1}={\widehat{\mathrm{x}}}_{\mathrm{k}+1│\mathrm{k}}+{\mathrm{K}}_{\mathrm{k}+1}\left({\mathrm{y}}_{\mathrm{k}}-{\widehat{\mathrm{y}}}_{\mathrm{k}}\right).(18)$

Step 6. Calculating the system state error

${\mathrm{P}}_{\mathrm{k}+1|\mathrm{k}+1}=\left(1-{\mathrm{K}}_{\mathrm{k}+1}{\mathrm{C}}_{\mathrm{k}+1}\right){\mathrm{P}}_{\mathrm{k}+1|\mathrm{k}}.(19)$

6 The sliding mode observer

From the first-order ECM in Figure 3, the equations representing the state dynamics of the LiB is deduced as follows:

${\mathrm{V}}_{\mathrm{t}}={\mathrm{V}}_{\mathrm{o}\mathrm{c}}\left(\mathrm{S}\mathrm{O}\mathrm{C}\right)-{\mathrm{R}}_0{\mathrm{I}}_{\mathrm{b}}-{\mathrm{V}}_1,(\mathrm{20a})$

${\dot{\mathrm{V}}}_1=\left(\frac{-1}{{\mathrm{R}}_1{\mathrm{C}}_1}\right){\mathrm{V}}_1+\left(\frac{1}{{\mathrm{C}}_1}\right){\mathrm{I}}_{\mathrm{b}},(\mathrm{20b})$

$\dot{\mathrm{S}\mathrm{O}\mathrm{C}}=\frac{-{\mathrm{I}}_{\mathrm{b}}}{{\mathrm{C}}_{\mathrm{b}}},(\mathrm{20c})$

where ${\mathrm{V}}_{\mathrm{o}\mathrm{c}}$ is the open-circuit voltage (OCV); ${\mathrm{I}}_{\mathrm{b}}$ is the battery current; ${\mathrm{V}}_1$ is the voltage across the RC pair; ${\mathrm{C}}_{\mathrm{b}}$ is the nominal battery capacity. The SOC derivative equation in Eq. 20c is deduced from the relationship ${\mathrm{S}\mathrm{O}\mathrm{C}}_{\mathrm{t}}={\mathrm{S}\mathrm{O}\mathrm{C}}_0-\frac{1}{{\mathrm{C}}_{\mathrm{b}}}\int \mathrm{i}\mathrm{d}\mathrm{t}$, which represents the current integration SOC technique.

From the terminal voltage equation, ${\mathrm{V}}_{\mathrm{t}}$ in Eq. 20a, we get the following equation:

${-\mathrm{I}}_{\mathrm{b}}=\frac{{\mathrm{V}}_{\mathrm{t}}-{\mathrm{V}}_{\mathrm{o}\mathrm{c}}+{\mathrm{V}}_1}{{\mathrm{R}}_0}.(21)$

Substituting Eq. 21 into Eq. 20c results in the following equation:

$\dot{\mathrm{S}\mathrm{O}\mathrm{C}}=\left(\frac{1}{{\mathrm{R}}_0{\mathrm{C}}_{\mathrm{b}}}\right)\left({\mathrm{V}}_{\mathrm{t}}-{\mathrm{V}}_{\mathrm{o}\mathrm{c}}+{\mathrm{V}}_1\right).(22)$

Differentiating ${\mathrm{V}}_{\mathrm{t}}$ in Eq. 20a gives the following equation:

${\dot{\mathrm{V}}}_{\mathrm{t}}=\frac{\mathrm{d}{\mathrm{V}}_{\mathrm{o}\mathrm{c}}}{\mathrm{d}\mathrm{S}\mathrm{O}\mathrm{C}}\bullet \frac{\mathrm{d}\mathrm{S}\mathrm{O}\mathrm{C}}{\mathrm{d}\mathrm{t}}-\frac{\mathrm{d}{\mathrm{V}}_1}{\mathrm{d}\mathrm{t}}.(23)$

Since $\frac{\mathrm{d}{\mathrm{V}}_{\mathrm{o}\mathrm{c}}}{\mathrm{d}\mathrm{S}\mathrm{O}\mathrm{C}}\approx 0$, substituting Eq. 20b gives the following:

${\dot{\mathrm{V}}}_{\mathrm{t}}=-{\dot{\mathrm{V}}}_1=\frac{{\mathrm{V}}_1}{{\mathrm{R}}_1{\mathrm{C}}_1}+\frac{{\mathrm{I}}_{\mathrm{b}}}{{\mathrm{C}}_{\mathrm{b}}}.(24)$

Making ${\mathrm{V}}_1$ the subject in Eq. 20a and substituting it in Eq. 24, we get the following expression:

${\dot{\mathrm{V}}}_{\mathrm{t}}=\frac{-1}{{\mathrm{R}}_1{\mathrm{C}}_1}{\mathrm{V}}_{\mathrm{t}}+\frac{1}{{\mathrm{R}}_1{\mathrm{C}}_1}{\mathrm{V}}_{\mathrm{o}\mathrm{c}}-\left(\frac{{\mathrm{R}}_0}{{\mathrm{R}}_1{\mathrm{C}}_1}+\frac{1}{{\mathrm{C}}_1}\right){\mathrm{I}}_{\mathrm{b}}.(25)$

Combining ${\dot{\mathrm{V}}}_{\mathrm{t}}$, ${\dot{\mathrm{V}}}_1$, and $\dot{\mathrm{S}\mathrm{O}\mathrm{C}}$ equations, the state dynamics of the battery becomes the following:

${\dot{\mathrm{V}}}_{\mathrm{t}}=\frac{-1}{{\mathrm{R}}_1{\mathrm{C}}_1}{\mathrm{V}}_{\mathrm{t}}+\frac{1}{{\mathrm{R}}_1{\mathrm{C}}_1}{\mathrm{V}}_{\mathrm{o}\mathrm{c}}-\left(\frac{{\mathrm{R}}_0}{{\mathrm{R}}_1{\mathrm{C}}_1}+\frac{1}{{\mathrm{C}}_1}\right){\mathrm{I}}_{\mathrm{b}}+∆{\mathrm{f}}_1{\dot{\mathrm{V}}}_1=\left(\frac{-1}{{\mathrm{R}}_1{\mathrm{C}}_1}\right){\mathrm{V}}_1+\left(\frac{1}{{\mathrm{C}}_1}\right){\mathrm{I}}_{\mathrm{b}}+∆{\mathrm{f}}_2,(26)$

$\dot{\mathrm{S}\mathrm{O}\mathrm{C}}=\left(\frac{1}{{\mathrm{R}}_0{\mathrm{C}}_{\mathrm{b}}}\right)\left({\mathrm{V}}_{\mathrm{t}}-{\mathrm{V}}_{\mathrm{o}\mathrm{c}}+{\mathrm{V}}_1\right)+∆{\mathrm{f}}_3,$

where $∆{\mathrm{f}}_1$, $∆{\mathrm{f}}_2,$ and $∆{\mathrm{f}}_3$ represent non-linear disturbances (uncertainties) added to the real system in Eq. 24, satisfying the Lipschitz boundary criterion ${‖∆\mathrm{f}\left(x\right)-∆\mathrm{f}\left(\widehat{x}\right)‖}_2\le \gamma {‖x-\widehat{x}‖}_2$. Here, $1\le \gamma$. The SMO equations are then proposed as follows:

${\dot{\widehat{\mathrm{V}}}}_{\mathrm{t}}=\frac{-1}{{\mathrm{R}}_1{\mathrm{C}}_1}{\widehat{\mathrm{V}}}_{\mathrm{t}}+\frac{1}{{\mathrm{R}}_1{\mathrm{C}}_1}{\widehat{\mathrm{V}}}_{\mathrm{o}\mathrm{c}}-\left(\frac{{\mathrm{R}}_0}{{\mathrm{R}}_1{\mathrm{C}}_1}+\frac{1}{{\mathrm{C}}_1}\right){\mathrm{I}}_{\mathrm{b}}+{\lambda }_1\mathrm{s}\mathrm{g}\mathrm{n}\left({\mathrm{e}}_{{\mathrm{V}}_{\mathrm{t}}}\right),$

${\dot{\widehat{\mathrm{V}}}}_1=\frac{-1}{{\mathrm{R}}_1{\mathrm{C}}_1}{\widehat{\mathrm{V}}}_1+\left(\frac{1}{{\mathrm{C}}_1}\right){\mathrm{I}}_{\mathrm{b}}+{\lambda }_2\mathrm{s}\mathrm{g}\mathrm{n}\left({\mathrm{e}}_{{\mathrm{V}}_{\mathrm{o}\mathrm{c}}}\right),(27)$

$\dot{\widehat{\mathrm{S}\mathrm{O}\mathrm{C}}}=\left(\frac{1}{{\mathrm{R}}_0{\mathrm{C}}_{\mathrm{b}}}\right)\left({\widehat{\mathrm{V}}}_{\mathrm{t}}-{\widehat{\mathrm{V}}}_{\mathrm{o}\mathrm{c}}+{\widehat{\mathrm{V}}}_1\right)+{\lambda }_3\mathrm{s}\mathrm{g}\mathrm{n}\left({\mathrm{e}}_{{\mathrm{V}}_{{\mathrm{R}}_1{\mathrm{C}}_1}}\right).$

Subtracting Eq. 27 from Eq. 26 gives the following error dynamics:

${\dot{\mathrm{e}}}_{{\mathrm{V}}_{\mathrm{t}}}=\frac{-1}{\mathrm{R}\mathrm{C}}{\mathrm{e}}_{{\mathrm{V}}_{\mathrm{t}}}+\frac{1}{\mathrm{R}\mathrm{C}}{\mathrm{e}}_{{\mathrm{V}}_{\mathrm{o}\mathrm{c}}}+∆{\mathrm{f}}_1-{\lambda }_1\mathrm{s}\mathrm{g}\mathrm{n}\left({\mathrm{e}}_{{\mathrm{V}}_{\mathrm{t}}}\right),(\mathrm{28a})$

${\dot{\mathrm{e}}}_{{\mathrm{V}}_1}=\left(\frac{-1}{{\mathrm{R}}_1{\mathrm{C}}_1}\right){\mathrm{e}}_{{\mathrm{V}}_1}+∆{\mathrm{f}}_2-{\lambda }_2\mathrm{s}\mathrm{g}\mathrm{n}\left({\mathrm{e}}_{{\mathrm{V}}_{\mathrm{o}\mathrm{c}}}\right),(\mathrm{28b})$

${\dot{\mathrm{e}}}_{\mathrm{S}\mathrm{O}\mathrm{C}}=\left(\frac{1}{{\mathrm{R}}_0{\mathrm{C}}_{\mathrm{b}}}\right)\left({\mathrm{e}}_{{\mathrm{V}}_{\mathrm{t}}}+{\mathrm{e}}_{{\mathrm{V}}_{\mathrm{o}\mathrm{c}}}+{\mathrm{e}}_{{\mathrm{V}}_1}\right)+∆{\mathrm{f}}_3-{\lambda }_3\mathrm{s}\mathrm{g}\mathrm{n}\left({\mathrm{e}}_{{\mathrm{V}}_1}\right),(\mathrm{28c})$

where the switching signal $\mathrm{s}\mathrm{g}\mathrm{n}\left(\mathrm{e}\right)=\left\{\begin{array}{c}+1,\mathrm{e}>0\\ -1,\mathrm{e}<0\end{array}\right.$ and state errors are defined as follows:

${\mathrm{e}}_{{\mathrm{V}}_{\mathrm{t}}}={\mathrm{V}}_{\mathrm{t}}-{\widehat{\mathrm{V}}}_{\mathrm{t}};{\mathrm{e}}_{{\mathrm{V}}_1}={\mathrm{V}}_1-{\widehat{\mathrm{V}}}_1;{\mathrm{e}}_{{\mathrm{V}}_{\mathrm{O}\mathrm{C}}}={\mathrm{V}}_{\mathrm{O}\mathrm{C}}-{\widehat{\mathrm{V}}}_{\mathrm{O}\mathrm{C}}=\mathrm{k}\left(\mathrm{S}\mathrm{O}\mathrm{C}-\widehat{\mathrm{S}\mathrm{O}\mathrm{C}}\right)=\mathrm{k}{\mathrm{e}}_{\mathrm{S}\mathrm{O}\mathrm{C}}.(29)$

To achieve stability (quadratic) of the terminal voltage error (${\mathrm{e}}_{{\mathrm{V}}_{\mathrm{t}}}$), the following Lyapunov function is chosen for a symmetric error:

${\mathrm{V}}_{\mathrm{v}\mathrm{t}}=\frac{1}{2}{{\mathrm{e}}_{{\mathrm{V}}_{\mathrm{t}}}}^2={{\mathrm{e}}_{{\mathrm{V}}_{\mathrm{t}}}}^{\mathrm{T}}\frac{1}{2}{\mathrm{e}}_{{\mathrm{V}}_{\mathrm{t}}}.(30)$

To achieve an ideal sliding motion, i.e., (${\mathrm{e}}_{{\mathrm{V}}_{\mathrm{t}}}=0$), then ${\dot{\mathrm{V}}}_{\mathrm{v}\mathrm{t}}<0$.

The sliding surface ${\mathrm{S}}_0=\left\{\left({\mathrm{e}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e}},{\mathrm{e}}_{{\mathrm{V}}_{\mathrm{t}}}\right):{\mathrm{e}}_{{\mathrm{V}}_{\mathrm{t}}}=0\right\}.$

Differentiating Eq. 30 gives the following:

${\dot{\mathrm{V}}}_{\mathrm{v}\mathrm{t}}={\mathrm{e}}_{{\mathrm{V}}_{\mathrm{t}}}\times {\dot{\mathrm{e}}}_{{\mathrm{V}}_{\mathrm{t}}}.(31)$

For the Lyapunov stability condition to be satisfied $\lambda \gg ∆\mathrm{f}$ so that ${\dot{\mathrm{V}}}_{\mathrm{v}\mathrm{t}}<0,$ which implies ${\dot{\mathrm{e}}}_{{\mathrm{V}}_{\mathrm{t}}}={\mathrm{e}}_{{\mathrm{V}}_{\mathrm{t}}}=0.$

By replacing ${\dot{\mathrm{e}}}_{{\mathrm{V}}_{\mathrm{t}}}={\mathrm{e}}_{{\mathrm{V}}_{\mathrm{t}}}=0$ in Eq. 28a and recalling ${\mathrm{e}}_{{\mathrm{V}}_{\mathrm{o}\mathrm{c}}}=\mathrm{k}{\mathrm{e}}_{\mathrm{S}\mathrm{O}\mathrm{C}}$, the equivalent injection signal is deduced as follows:

${\mathrm{e}}_{\mathrm{S}\mathrm{O}\mathrm{C}}=\frac{{\lambda }_1}{\mathrm{k}{\mathrm{b}}_1}\mathrm{s}\mathrm{g}\mathrm{n}\left({\mathrm{e}}_{{\mathrm{V}}_{\mathrm{t}}}\right).(32)$

Similarly, by replacing ${\dot{\mathrm{e}}}_{\mathrm{S}\mathrm{O}\mathrm{C}}={\mathrm{e}}_{\mathrm{S}\mathrm{O}\mathrm{C}}=0$ and ${\mathrm{e}}_{{\mathrm{V}}_{\mathrm{t}}}=0$ in Eq. 28c and substituting them in Eq. 32, we obtain the following equation:

${\mathrm{e}}_{{\mathrm{V}}_1}=\frac{{\lambda }_2}{{\mathrm{b}}_2}\mathrm{s}\mathrm{g}\mathrm{n}\left(\frac{{\lambda }_1}{\mathrm{k}{\mathrm{b}}_1}\right)\mathrm{s}\mathrm{g}\mathrm{n}\left({\mathrm{e}}_{{\mathrm{V}}_{\mathrm{t}}}\right).(33)$

The state vector $\left[\begin{array}{c}\mathrm{S}\mathrm{O}\mathrm{C}\\ {\mathrm{V}}_1\end{array}\right]$ can then be obtained by substituting the aforementioned injection signals into the error dynamics equations.

7 Hybridized estimator

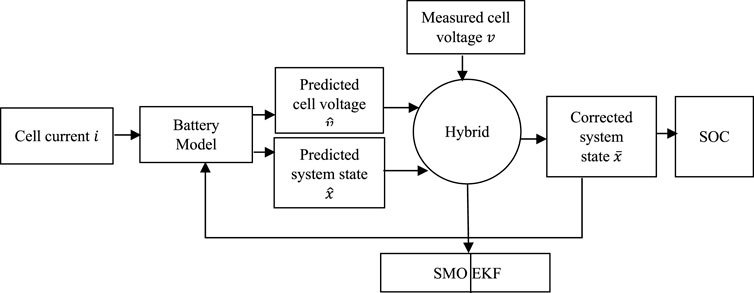
Among the estimators developed, this work observes certain intervals, in which the first-order EKF has poor performance. This means that there are regions where there is the presence of a mismatch between the EKF and Ah (referred to as the real SOC), typically at the SOC error bound [−.05, .05] and [−.1, .1]. In addition, the SMO has a slow convergence time when subjected to complex disturbances. To solve these problems, a hybrid EKF−SMO observer is designed, as shown in the block diagram of Figure 4 such that the inactive observer tracks the output of the used observer, simultaneously feeding back a zero-sum signal to the input gain of the used observer. The following steps are carried out in achieving the hybrid estimation:

FIGURE 4

FIGURE 4. Block diagram of the hybrid SOC estimator.

Step 1. Determination of intervals for switching to take place

Step 2. Connection of the current input source to both observers

Step 3. Back feeding the error obtained from the outputs of the two observers via a gain to the input of the currently used observer.

Step 4. Finally, tuning the observer gain to improve the response of hybridization.In brevity, switching is performed as follows:

${\mathrm{H}}_{\mathrm{s}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{c}\mathrm{h}}=\left\{\begin{array}{l}\mathrm{S}\mathrm{M}\mathrm{O}\left(\mathrm{S}\mathrm{O}\mathrm{C}\right),-0.05\le \mathrm{S}\mathrm{O}\mathrm{C}\le 0.05\mathrm{a}\mathrm{n}\mathrm{d}-0.1\le \mathrm{S}\mathrm{O}\mathrm{C}\le 0.1,\\ \mathrm{E}\mathrm{K}\mathrm{F}\left(\mathrm{S}\mathrm{O}\mathrm{C}\right),\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}.\end{array}\right.(34)$

8 Results and discussion

The performance of the first-order ECM based on discharge measurement data obtained from the experiment is presented in this section, followed by the response analysis of individual estimators and the robust hybrid estimator designed.

8.1 Parameter estimation performance

The optimum parameters (OCV, R₀, R₁, and ${\tau }_1$) of the battery model are shown in Table 3 from the GPSA results. With these parameter values, the model response is simulated via the discharge data voltage and current input obtained from the experiment to derive the model states (V₁ and Z_t) and output terminal voltage (V_t) of the batteries, as shown in Figure 5. This was carried out in order to validate the model developed and further visualize the real SOC, which will be used as a benchmark to test the performance of the EKF and SMO. The voltage plots in Figure 6 represent the measurement from the experiment and the estimation from the model parameter identification. Evidently, the extremely close fit verifies the accuracy of the model developed in this work, which is dependent on good parameter initialization discussed in Section 4.1.

TABLE 3

TABLE 3. Optimized parameter values for the first-order ECM.

FIGURE 5

FIGURE 5. Model response of the first-order ECM.

FIGURE 6

FIGURE 6. Measured vs. the estimated voltage response of the first-order ECM.

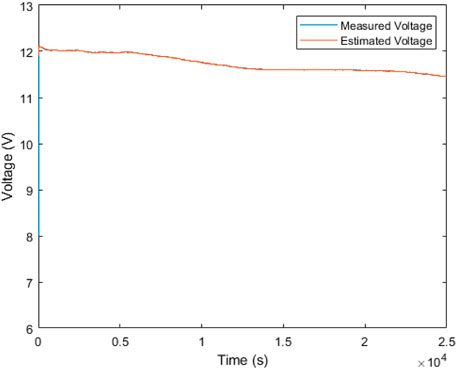
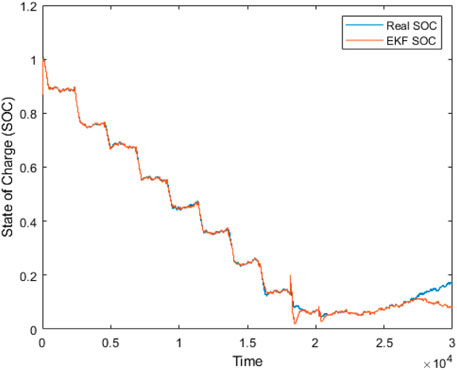
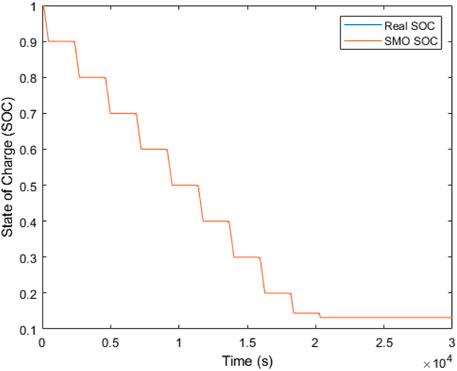
8.2 Validation of the EKF and SMO estimator

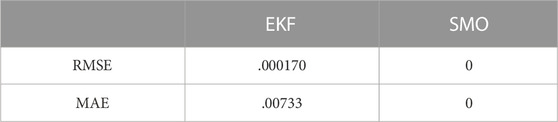
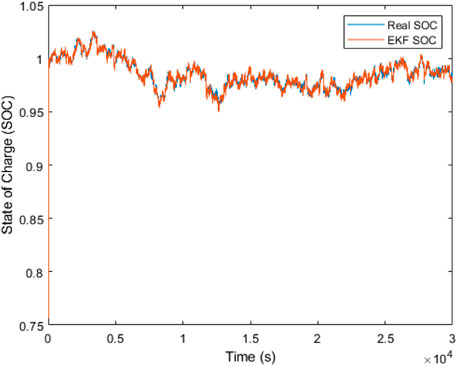
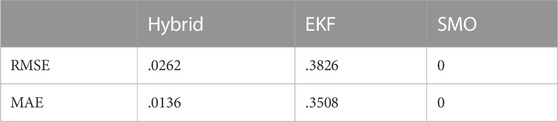
The response of the first-order EKF and SMO is shown in Figures 7, 8 respectively, with the root mean square error (RMSE) and maximum absolute error (MAE) values presented in Table 4. The benchmark used is the coulomb counting technique to compare the performance of both estimators. From the plots, it is evident that the SMO converges faster with a higher SOC estimation accuracy than the EKF. The SMO drove the error between the real and estimated SOC to zero, as shown by its RMSE and MAE values in Table 4. Both estimators show high quality in filtering the random white noise that is added to the input current and voltage measurement. However, it is observed beginning from t = 2.6 × 10⁴ that the EKF diverges from the ideal value in contrast to the SMO, which maintains a high matching behavior. The RMSE and MAE metrics of the EKF are approximately zero in Table 4 due to the large time range of matching between the real and estimated SOC, overwhelmingly exceeding the short time range of the mismatch, as shown in Figure 7.

FIGURE 7

FIGURE 7. Extended Kalman filter response.

FIGURE 8

FIGURE 8. Sliding mode observer response.

TABLE 4

TABLE 4. Estimator performance metrics.

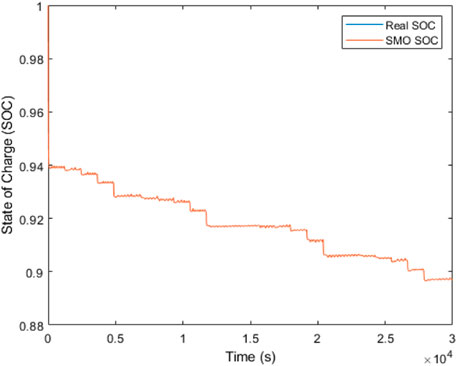
To test for robustness of the estimators designed, the current and voltage measurement inputs of the Panasonic 18650 batteries are interchanged with that of a 5 A h, 4V, lithium−nickel rechargeable (INR 18650) battery to see how far the stability behavior could be met in the face of complex disturbances. Figures 9, 10 show the performance of the EKF and SMO subjected to the disturbance. As seen, the SMO diverges from the initial SOC of 100% to begin at an initial SOC of 94% and later maintains an estimation of about 90% SOC. The EKF, on the other hand, maintains a sustained estimation in the SOC range of [1, .93]. This shows that the EKF experienced the greatest impact on its behavior compared to the SMO due to the complex disturbance. However, the filtering properties of both estimators are still preserved during the course of estimation.

FIGURE 9

FIGURE 9. Response of the SMO under INR 18650.

FIGURE 10

FIGURE 10. Response of the EKF under INR 18650.

8.3 Hybrid estimator performance

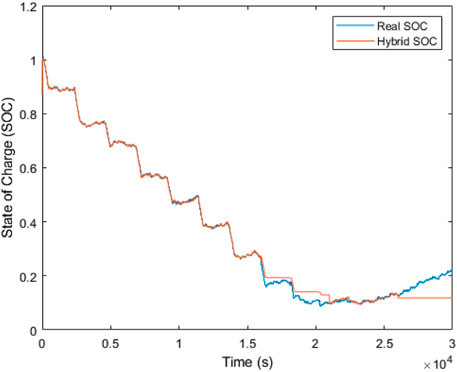
The hybrid estimator performance is shown in Figures 11, 12 for noise and with no noise additions to measurement inputs, respectively. The hybrid estimation goal in this work is to improve the response of the EKF and provide improved robustness to complex disturbances originating from other battery types. As Table 5 reveals, the improvement goal is met as the hybrid performance is seen to have two (2) decimal places of accuracy compared to the EKF estimation having an accuracy of a single decimal place. Furthermore, the hybrid estimation shows that the convergence starts at the initial SOC of 100% with an impressive error bound of 12.9%. It is observed that starting at time $t=2.5\times {10}^4$, the hybrid estimator is seen not following the real SOC in Figure 11 due to the non-adaptive filtering addition. However, upon removing the noise, as shown in Figure 12, the hybrid estimator is seen to draw closer to the real SOC from that time onwards.

FIGURE 11

FIGURE 11. Hybrid estimator performance under noisy measurements.

FIGURE 12

FIGURE 12. Hybrid estimator performance without the noise.

TABLE 5

TABLE 5. Performance metrics of the hybrid estimation performance.

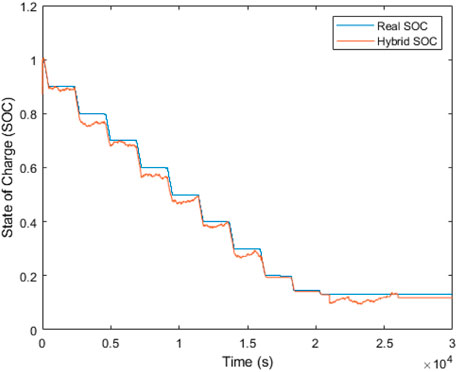
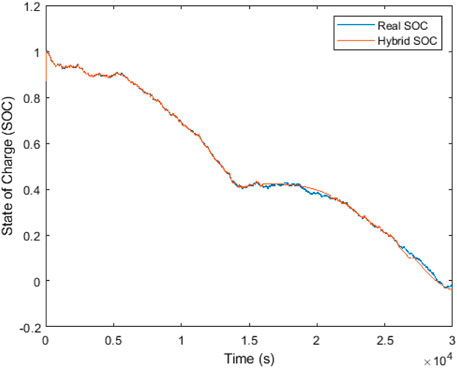
The hybrid estimator has also shown the ability to adjust its response to the measurement data on the INR 18650 used as the replica complex disturbance in Figure 13. It can be seen that unlike the EKF and SMO individual poor stability for parameter changes influenced by the chemistry of INR 18650, the hybrid estimator is observed to closely match the real SOC with the starting convergency time at nearly the initial time period, thereby supporting the merit of combining both estimators. Another observation from the result of hybridization is that the SOC estimation range has impressively improved from a range of [1, .93] to an estimation range of [1, 0], in spite of the disturbance addition. Varying the tracking gain of the SMO could increase the accuracy further but reduce the SOC estimation range. The hybrid improvement can be explained due to the role the tuning parameters of the EKF have in ensuring faster convergency and noise cancellation, and the role the SMO gains have in ensuring robustness.

FIGURE 13

FIGURE 13. Hybrid estimator performance under INR 18650.

9 Conclusion

This paper has demonstrated the use of a first-order equivalent circuit model in the implementation via the simulation of the extended Kalman filter (EKF) and sliding mode observer (SMO) for estimating the SOC of multi-cell LiB batteries under discharge measurement data. The response of the individual estimators and their hybridized form has been shown. Following the existing works carried out for the SOC estimation being reviewed, the hybrid method having an MAE value of 1.36 percent is seen to outperform both the onboard SOC estimation technique in Guangzhong et al. (2016) and the improved EKF technique developed in Shichun et al. (2021), having both MAE values of 4 percent and 3 percent, respectively. However, Benedikt et al. (2021) proposed that the work had an accuracy difference of roughly one-quarter compared to that of the hybrid MAE performance. This is because of the addition of a hysteresis element, which accounted for a more accurate battery model than that used in this paper. The traditional method such as the curve fitting-based SOC estimation has shown divergent characteristics (Yujie et al., 2020), especially during the starting phase due to the difficulty in deducing the parameters of suitable fitting functions describing the battery terminal voltage profile, making model identification parameters less accurate in the consequent outputting poor estimation results. Furthermore, the hybrid technique performance is not affected by a variation of the initial state estimates, a challenge commonly used for SOC estimation techniques including the coulomb counting integration method (Ng et al., 2009) we still face.

It is true that various hybrid estimation strategies have been developed in the literature such as by Alfi et al. (2014), where the radial bias neural network was used to obtain the output equation (linearized battery terminal voltage) so as to form a full state equation with the SOC variable in combination with the extended ${\mathrm{H}}_{\infty }$ filter, which was used for estimating the SOC. A contrast between the proposed model developed in this paper and similar hybrid works is that this work combines discrete and continuous form representations of the model equations for the EKF and SMO, respectively, in order to improve accuracy. Furthermore, in comparison to the work introduced by Alfi et al. (2014), the accuracy of the estimation carried out in this paper does not depend on large discharge data required for neural network training since the algorithms used here are procedure-based. The estimation accuracy in this work showed that the RMSE using the hybrid neural technique performed better with a negligible error difference of .12 percent. However, matching accuracy between both methods can be achieved by proper tuning of the EKF gain in contrast to the hybrid neural technique, which depends on the trial and error method for selecting a number of hidden neurons and learning rates. With a convergence time of about 1 s, the proposed method surpasses the 4 min time it took for the extended ${\mathrm{H}}_{\infty }$ filter to approach the real SOC, giving the former a significant advantage. These faster convergence characteristics can be attributed to accurate modeling of the battery in its non-linear form, as opposed to linearization carried out using the radial bias function.

In summary, the hybridized estimator shows an impressive SOC estimation range, convergence rate, and high matching results via the results discussed; these are the properties traditional SOC estimation methods lack. This demonstrates the quality of the hybrid technique in estimating multi-cell lithium-ion batteries and offers more research opportunities in designing estimators that are adaptive to complex disturbances arising from other battery types.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

All authors have contributed in designing an estimator that is robust and accurately sufficient to determine the state of charge (SOC) of LiBs in the presence of disturbance signals arising from other battery types.

Acknowledgments

The authors deeply recognize the assistance given by Covenant University in all aspects of this research, especially the payment of the publication charges.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adeyemi, K. T., Misra, S., Orovwode, H., and Adoghe, A. J. E. (2022). Modeling the Next Decade of Energy Sustainability: A Case of a Developing Country. Energies 15 (14), 5083.

Google Scholar

Alfi, A., Charkhgard, M., and Haddad Zarif, M. (2014). Hybrid state of charge estimation for lithium-ion batteries: Design and implementation. IET Power Electron. 7 (11), 2758–2764. doi:10.1049/iet-pel.2013.0746

CrossRef Full Text | Google Scholar

Atayero, A. A., Luka, M. K., and Alatishe, A. A. (2012). Neural-encoded fuzzy models for load balancing in 3GPP LTE. Int. J. Appl. Inf. Syst. 4. doi:10.5120/ijais12-450628

CrossRef Full Text | Google Scholar

Awelewa, A. A., Samuel, I. A., Ademola, A., and Iyiola, S. O. (2013). An undergraduate control tutorial on root locus-based magnetic levitation system stabilization. Int. J. Eng. Comput. Sci. 13 (1), 14–22.

Google Scholar

Awelewa, A., Omiloli, K., Olajube, A., and Samuel, I. (2021). “Design and optimization of an intelligent fuzzy logic controller for a nonlinear dynamic system,” in Proceedings of the 2021 International Conference on Decision Aid Sciences and Application (DASA), Sakheer, Bahrain, December, 2021, 687–694.

CrossRef Full Text | Google Scholar

Bouchareb, H., Saqli, K., M’sirdi, N. K., Bentaie, M. O., and Naamane, A. (2020). “Sliding mode observer design for battery state of charge estimation,” in Proceedings of the 2020 5th International Conference on Renewable Energies for Developing Countries (REDEC), Marrakech, Morocco, June, 2020, 1–5.

CrossRef Full Text | Google Scholar

Dong, Guangzhong, Wei, Jingwen, and Chen, Zonghai (2016). Kalman filter for onboard state of charge estimation and peak power capability analysis of lithium-ion batteries. J. Power Sources 328, 615–626. doi:10.1016/j.jpowsour.2016.08.065

CrossRef Full Text | Google Scholar

Mohammed, Farag. (2013). Lithium-ion batteries: Modelling and state of charge estimation. PhD thesis (Toronto, ON, Canada: University of Toronto).

Ng, K. S., Moo, C. S., Chen, Y. P., and Hsieh, Y. C. (2009). Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. Appl. energy 86 (9), 1506–1511. doi:10.1016/j.apenergy.2008.11.021

CrossRef Full Text | Google Scholar

Orovwode, H. E., Matthew, S., Amuta, E., Agbetuyi, F. A., and Odun-Ayo, I. (2021). Carbon footprint evaluation and environmental sustainability improvement through capacity optimization. International Journal of Energy Economics and Policy 11 (3), 454–459.

CrossRef Full Text | Google Scholar

Peng, S., Chen, C., Shi, H., and Yao, Z. (2017a). State of charge estimation of battery energy storage systems based on adaptive unscented Kalman filter with a noise statistics estimator. Ieee Access 5, 13202–13212. doi:10.1109/access.2017.2725301

CrossRef Full Text | Google Scholar

Peng, Simin, Chen, Chong, Shi, Hongbing, and Yao, Zhilei (2017b). State of charge estimation of battery energy storage systems based on adaptive unscented kalman filter with a noise statistics estimator. IEEE Access 5, 13202–13212. doi:10.1109/access.2017.2725301

CrossRef Full Text | Google Scholar

Rzepka, Benedikt, Simon, Bischof, and Blank, Thomas (2021). Implementing an extended kalman filter for soc estimation of a li-ion battery with hysteresis” A step-by-step guide. Energies 14 (13), 3733. doi:10.3390/en14133733

CrossRef Full Text | Google Scholar

Samuel, I., Soyemi, A., Awelewa, A., and Adekitan, A. (2021). Artificial neural network based load flow analysis for power system networks. IAENG Int. J. Comput. Sci. 48 (4).

Google Scholar

Sassi, H. B., Errahimi, F., and Najia, E. S. (2020). State of charge estimation by multi-innovation unscented Kalman filter for vehicular applications. J. Energy Storage 32, 101978. doi:10.1016/j.est.2020.101978

CrossRef Full Text | Google Scholar

Shichun, Y., Zhou, S., Hua, Y., Zhou, X., Liu, X., Pan, Y., et al. (2021). A parameter adaptive method for state of charge estimation of lithium-ion batteries with an improved extended Kalman filter. Sci. Rep. 11 (1), 1–15.

PubMed Abstract | Google Scholar

Surajudeen-Bakinde, N., Faruk, N., Oloyede, A., Abdulkarim, A., Olawoyin, L., Popoola, S., et al. (2021). Effect of membership functions and data size on the performance of ANFIS-based model for predicting path losses in the VHF and UHF bands. J. Eng. Res. 10, 203–226. doi:10.36909/jer.10457

CrossRef Full Text | Google Scholar

Wang, Yujie, Tian, Jiaqiang, Sun, Zhendong, Wang, Li, Xu, Ruilong, Li, Mince, et al. (2020). A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 131, 110015. doi:10.1016/j.rser.2020.110015

CrossRef Full Text | Google Scholar

Xiong, R., Cao, J., Yu, Q., He, H., and Sun, F. (2017). Critical review on the battery state of charge estimation methods for electric vehicles. Ieee Access 6, 1832–1843. doi:10.1109/access.2017.2780258

CrossRef Full Text | Google Scholar

Xu, Y., Hu, M., Zhou, A., Li, Y., Li, S., Fu, C., et al. (2020a). State of charge estimation for lithium-ion batteries based on adaptive dual Kalman filter. Appl. Math. Model. 77, 1255–1272. doi:10.1016/j.apm.2019.09.011

CrossRef Full Text | Google Scholar

Xu, Yidan, Hu, Minghui, Zhou, Anjian, Li, Yunxiao, Li, Shuxian, Fu, Chunyun, et al. (2020b). State of charge estimation for lithium-ion batteries based on adaptive dual kalman filter. Appl. Math. Model. 77, 1255–1272. doi:10.1016/j.apm.2019.09.011

CrossRef Full Text | Google Scholar

Yang, Shichun, Zhou, Sida, Yang, Hua, Zhou, Xinan, Liu, Xinhua, Pan, Yuwei, et al. (2021). A parameter adaptive method for state of charge estimation of lithium-ion batteries with an improved extended kalman filter. Sci. Rep. 11 (1), 5805–5815. doi:10.1038/s41598-021-84729-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, Wenhui, Xia, Bizhong, Wang, Wei, Lai, Yongzhi, Wang, Mingwang, and Wang, Huawen (2019). State of charge estimation for power lithium-ion battery using a fuzzy logic sliding mode observer. Energies 12 (13), 2491. doi:10.3390/en12132491

CrossRef Full Text | Google Scholar

Zheng, Liu, Yuan, Qiu, Yang, Chunshan, Ji, Jianbo, and Zhao, Zhenhua (2021). A state of charge estimation method for lithium-ion battery using pid compensator-based adaptive extended kalman filter. Complexity 2021. doi:10.1155/2021/6665509

CrossRef Full Text | Google Scholar