- School of Electrical Engineering, Vellore Institute of Technology, Vellore, India
Recently, wind power from renewable energy power generation has been extended quickly to another level. To the grid, most renewable generators synchronize through the power electronic converters controlled flexibly. The high-level wind power penetration into the power generation system affects the dynamic performance of the power system and presents substantial uncertainties in system operation. This study mainly focuses on reviewing the various types of stability analyses in high-level wind penetration of power generation systems. It describes several challenges and simulation analyses related to stability issues. A comparative analysis has also been carried out for the various types of stability related to different research studies. The data show that transient stability has been significantly focused on in most of the studies.
1 Introduction
Renewable energy resources increasingly penetrate modern power systems because of energy shortage crisis and environmental pressure. Recently, wind power integration projects have been launched in various countries. Wind power integration on a large scale presents substantial economic and environmental benefits to the society. The system exhibits several challenges in maintaining stability due to its stochastic nature and highly intermittent state. The power system stability can be affected after the integration of wind power into the utility grid due to several aspects, such as the replacement of the synchronous generator can reduce the effective inertia of the system. Due to the power electronics converter, the system alters its characteristics dynamically. The synchronous generator dispatch changes fast through the transmission network, power flow direction, and magnitude fluctuation (Xu et al., 2018). This proposed study reviews several types of stability issues of wind power integration in power systems and uncertainties present in the generation of wind power and satisfies the requirement of transient stability with several practices aimed at optimizing the system’s operating state.
The doubly fed induction generator (DFIG) model analyzed the stability in wind power systems. The DFIG consists of an induction generator with a mechanically driven rotor through a gearbox by a wind turbine and a rotor side convertor (RSC). It is electrically excited through the grid and exhibits a power electronic-based interface. The complex control system is responsible for efficient wind energy conversion to power electricity for proper electrical and mechanical dynamics regulation. The small-signal stability region (SSSR) concept extends to the robust small-signal stability region (RSSSR), wherein the system maintains the stability even during perturbations that occur due to renewable energy power generation’s volatile nodal injections and uncertainties (Pan et al., 2018).
Wind generators must provide ancillary services for systems with high-level wind penetration. As wind generation facilities increase worldwide, transmission system operators (TSOs) have changed grid code criteria. Under particular grid regulations, wind farms must provide inertial support, frequency regulation, and damping control. Synchronous generators typically deliver these services. However, due to the time-varying nature of such resources and the inherent modeling uncertainties that come along with their large-scale integration, this presents a formidable challenge. As a result, a sufficiently deterministic model of wind-dominated power systems is difficult to ensure. In the study by Husham et al. (2022), a Koopman-based model predictive controller (KMPC) was proposed to suppress the oscillations due to wind speed variations with climatic conditions and improve the control methodology for active and reactive power injections to the respective converters. Rahman et al. (2022) discussed clustering algorithms for large-scale wind power farms to access power system stability. Clustering algorithms are used to determine a probabilistic group of clusters representing equivalent wind farms and would hold true for most wind conditions throughout the year. The four aggregated wind farm models are subjected to small disturbances, frequency, and voltage stability analyses, also these wind farm models are analyzed considering a single unit for a better understanding.
A crucial sub-synchronous resonance (SSR) event in October 2009, persuaded by fixed series compensation, occurred in a wind farm with DFIG in Texas, United States. The SSR effect could not reflect critical factors like wind speed distribution, wind farms’ spatial distribution, wind turbine generators’ diversity, and network topology (Liu et al., 2018a). The developing VSC-MTDC grid shows some technological benefits concerning economics, modularity, and controllability focused on managing the frequency stability of traditional onshore AC grids (Wen et al., 2018). This study analyzes the robustness in the stability analysis of the wind power penetrated power system through stochastic optimization, which is risk-based, and estimates wind uncertainty. Furthermore, using devices such as ESS will reduce the required energy storage services (ESS) size by reactive power capabilities and wind farms. If the preferred voltage stability margin (VSM) increases, then the required ESS also increases as was shown by Jalali and Aldeen (2019).
The main contribution of this study involves
• reviewing the various research studies related to wind-penetrated power generation systems in terms of various types of stability,
• observing and studying the different techniques involved in improving the various types of stability issues and comparing them, and
• pictorially representing the analysis here in this review.
1.1 Article organization
This article is organized as follows: Section 2 describes the review of the stability analysis and the issues in wind-penetrated power generation systems. Various types of stability, namely, transient stability, dynamic stability, voltage stability, parametric stability, frequency stability, and other types of stability in power systems, are explained briefly, followed by a comparative analysis discussed in Section 3. The evaluation of the stability analysis is elaborated further. Finally, this article concludes in Section 4.
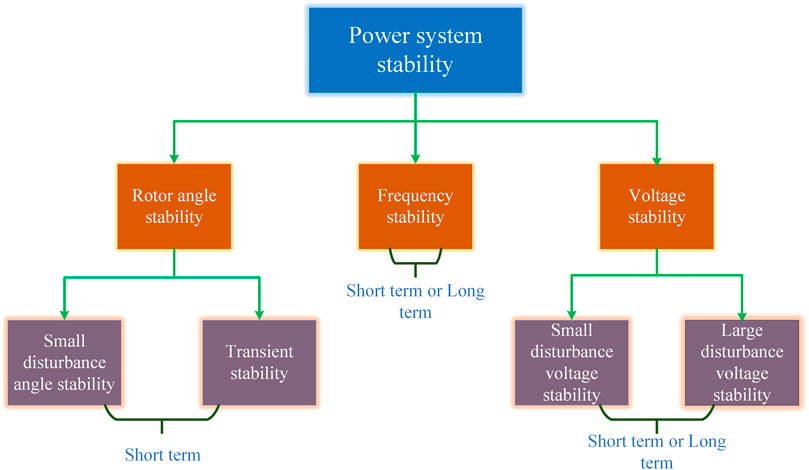
2 Types of stability in wind-penetrated power systems
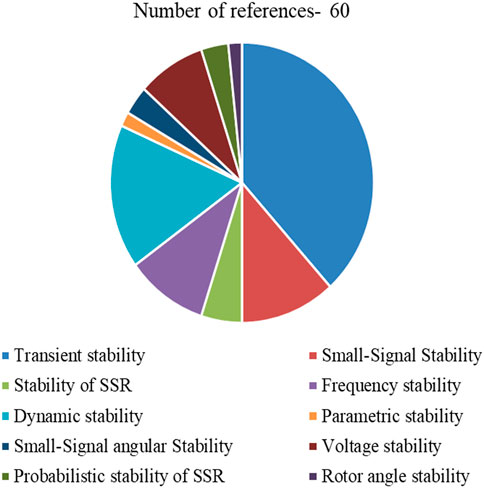
Various types of stabilities, namely, transient stability, dynamic stability, voltage stability, parametric stability, frequency stability, and other such types of stability in power systems, are explained briefly in Figure 1.
2.1 Transient stability
Transient stability is “the ability of the system to remain in synchronism when subjected to large disturbances.” Large disturbances can cause a variety of issues, such as faults, switching loads, and tripping. In most cases, the effects of these disturbances can lead to a large deviation of the generator rotor angles. It affects system synchronism to maintain stability.
Xu et al. (2018) developed a robust dispatch approach for the power system’s operation state optimization while sustaining transient stability with stochastic wind power generation and high variability. As an increased optimal power flow framework, the system is designed with differential-algebraic equations and uncertain variables. Based on the trajectory sensitivity analysis and one-machine infinite-equivalence of bus, the approximately equivalent algebraic equations are obtained by conversion using stability constraints. A small number of strategically represented chosen testing states are due to the uncertainty in wind power generation. This problem was solved iteratively by dividing the actual model into master problems and a sequence of slave issues based on the developed decomposition-based computation approach. This proposed method of dispatch focuses on a single period, i.e., 1 h. If we are to consider the dispatch of a multi-period, then the wind farm power output’s temporal dependency should be well designed.
Wang et al. (2018a) focused on the multi-machine power system’s stability improvement, combined with a hybrid wind-photovoltaic (PV) farm on a large scale using a supercapacitor (SC)-based energy storage unit. A wind turbine generator (WTG) of 300 MW simulated the hybrid and wind PV farm characteristics. The proposed SC connected with a proportional integral derivative supplementary damping controller (PID-SDC) and rendered efficient the damping characteristics that enhanced the transient performance of the proposed system subjected to a fault in three phases and short-circuited.
Ma et al. (2018a) explored the doubly fed induction generator (DFIG) current source–based model to analyze stability in wind power systems. Wind generator manufacturers developed this model, and generic models have simplified it. Moreover, it uses the current source–based model. Based on limited accurate measurements and chosen simulation scenarios, the proposed model was validated. The drawback was that the validity had not undergone any theoretical and systematic analysis of the current source model, and it may be considered unsuitable for application in real engineering. Hence, this study presents the current source model conditions for the analysis of stability in power systems. Furthermore, it investigates the model under asymmetrical and symmetrical fault conditions. This present source-based DFIG model has been practiced for validation in North China’s real wind farms.
Hui et al. (2019) proposed a robust feedback control method on the basis of linear parameter varying (LPV) for interconnected systems’ transient stability. This proposed method used mechanical power and DC channel power control in an interconnected system for the transient stability enhancement of the wind farm interconnected system. As a variable parameter linear model, the transient process has been designed mainly focusing on the interconnected system’s robust nonlinear characteristics and the transient process’s wind power uncertainty output. Four equal-value grids evaluated the proposed method in an interconnected system on a digital simulation platform through AC and DC lines. The proposed method exhibits better transient ability control impacts and response characteristics for wind power interconnected systems. Due to severe grid faults by loss of synchronization, wind farm tripping occurs.
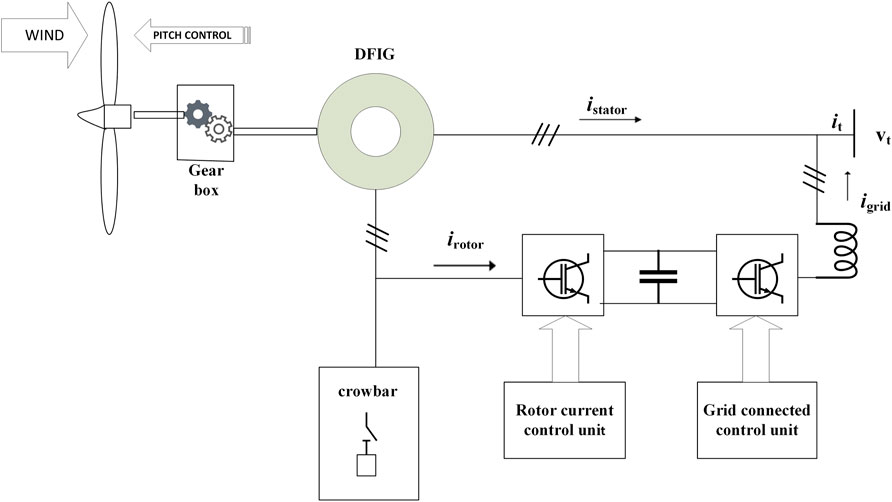
During severe faults in a grid, the system requires dynamic properties with special requirements for maintaining the wind farm synchronization with the power grid. The grid synchronization by Ma et al. (2018b) is explained as autonomous nonlinear differential equation motion with particular initial states. However, synchronization stability occurs due to deprived system dynamic properties and unsuitable initial states. The proposed method satisfies the requirements by adjusting the wind farm’s active and reactive output current during severe faults in a grid. The proposed method was executed and analyzed on DFIG- and PMSG-based wind farms. Figure 2 shows the schematic diagram of transient stability control of the DFIG.
In the study by Yu et al. (2018), power system control considers the post-contingency–based online identification of transient stability as significant since it enables the grid operator to decide and synchronize correction control actions during system failure. Machine learning methods used with synchrophasor measurements were used for evaluating transient stability and received more attention in protection and control systems. Based on a long short-term memory (LSTM) network, this proposed study developed the transient ability assessment system. This self-adaptive scenario balanced the accuracy and response time after the assessment and subsidized better accuracy. This proposed system exhibited a fast-training process and lesser difficulty. The proposed assessment system’s transient stability efficacy has been validated further in this study. The study by Ortega and Milano (2018) offers an in-depth stochastic analysis of the ESS impact on the transmission grid’s transient stability. This stated impact was verified by considering the mixed effects of network topologies, fault-clearing times, and various ESS technologies. In addition, the synchronous machines, storage devices, and the fault’s relative position were also considered. The stochastic time-domain simulations have also been considered for the all-island, Irish transmission system, 1479-bus model, resulting in nonintuitive endings.
Tang et al. (2018) developed a phase/magnitude dynamical model with unnatural consideration of timescale controller on rotor speed control for the theoretical evaluation of transient stability of DFIG-based wind turbines. This current model describes the unfair active power and active or reactive power output relationships. The synchronous generator and DFIG-based internal voltage vector show similarity but differ in the transient phase. The DFIG-based wind turbine system’s transient stability is analyzed in case of new instability, recognizing the variation from the synchronization generator system.
Datta et al. (2019) examined the battery energy storage system (BESS) performance and static compensator (STATCOM) in improvising the tremendous power system frequency stability and transient voltage, the additional capacity of power export enhancing among two interconnected power systems. A multi-machine power system proposes a BESS controlled by PI lead and lead-lag to give concurrent frequency regulation and voltage among the defined battery charge range and the system performance evaluated by the Finnish transmission grid. The proposed method compares with conventional methods based on several permanent and temporary fault conditions rendered by the Australian electricity market grid requirements. BESS results from improvements like power export show a 44% increase, while failure cases are seen in STATCOM. Moreover, the BESS lead-lag establishes better performance than PI lead–controlled BESS under the permanent and temporary faults in divergent events.
In DFIG, the low-voltage ride through the LVRT requirements changes the DFIG running state and brings about the system’s transient stability secondary impact. The DFIG output power mixes with the system’s mechanical power. This study minimizes the mathematical relationship and analyzes the superconducting magnetic energy storage (SMES) relationship, improving transient stability and access location (Jiang and Zhang, 2019). Dynamic characteristics of wind farms connected with the grid improved and obtained more extraordinary transient stability performance.
In the study by Pico and Johnson (2019), the transmission defects due to recent the California wildfires stimulated utility-scale disconnection conversion in PV plants. The investigations described that the PLL and DC side dynamics caused tripping commands that are typically un-modeled in a classical stability analysis. Because of these authors introduce a positive-sequence model for photovoltaic power plants that is derived on the fundamental principles of physics and controls to predict during the faults. For addressing the disadvantage, a sequence of PV plant models was derived from physical principles. The three-phase converter scale shows that the framework comprises closed-loop controllers, DC side dynamics, and PLL.
The principal purpose of the study by Eshkaftaki et al. (2020) was to improve the SG’s dynamic and transient performance using wind turbines with local DFIGs. The DFIG block is controlled by a designed transient controller (TC) and uses a modified generator in a motor regime operation mode. Furthermore, the electromagnetic torque band damping controller (ETBDC) consisting of two damping controllers is recommended to enhance the SG’s dynamic stability. There are three types of feedback: DFIG electromagnetic torque, SG speed modified torque, and SG electromagnetic torque in every damping controller. The genetic algorithm adjusts these controlled parameters. By comparing the transient indexes system, namely, SG accelerating energy, with and without using TC of DFIG inertia energy in two area network and critical clearing time (CCT), the TC performance is evaluated. Moreover, the dynamic performance indexes of the system like settling time, SG’s damping torque, eigenvalue, and overshoot have been related with and without using the two dynamic controllers. Moreover, these observe the proposed controller’s effectiveness in the study.
Liu et al. (2016) proposed a new strategy that was a coordinated “switching power system stabilizer” (SPSS) to enhance the multi-machine power system stability. Simulations consist of 4 generators, 11-bus power systems, and IEEE 68-bus with 16 generator power systems in which SPSS assesses the damping ability in aspects of enhancements in transient stability. Renedo et al. (2016) analyzed an active power control strategy for a multi-terminal VSC-HVDC system that enhances the transient stability of AC/DC hybrid grids—the weighted-average frequency observed by the MTDC system’s VSCs (WA-F). When compared to a strategy based on local frequency (LF), the study by Yousefian et al. (2017) mainly focused on an energy-based wide-area control on integrated power grids with wind. They proposed an algorithm of a nonlinear optimal control with “reinforcement learning (RL) and neural networks (NNs),” which, in using “approximate dynamic programming (ADP),” improves the wind-integrated power grid closed-loop performance. We observed that the suggested RL-based WAC enhanced system responses in simulations using the modified IEEE 68-bus system.
2.2 Small-signal stability
The small-signal stability in a power system is “the ability of the system to remain in synchronism when subjected to small disturbances.” If power system oscillations are suppressed during the disturbances, the system’s stability can be maintained over a long period.
Pan et al. (2018) addressed the small-signal stability region (SSSR) concept extension to the robust small-signal stability region” (RSSSR). The structured perturbation theory was first employed for the nodal injection perturbations in state-space formulations. This study considers the locations and intensity of the perturbations; RSSR in parameter subspace definition influences the structured singular value theory and stability radius theory. The “small-signal stability” of the power system’s systematic analysis enables region-wise perturbations. Furthermore, the system maintains stability even during renewable generation’s volatile nodal injections and uncertainty during perturbations. For the RSSSR boundaries, it constructs a linear closed-form approximation by the hyperplane approximation technique. Moreover, to make and learn from the RSSR boundary predictions, machine learning (ML) approaches have been employed.
The ML approaches' learning ability speeds up the computation on boundary significantly and simplifies the robust stability analysis of vast and complex power systems. Sadamoto et al. (2018) addressed the wind power integration concerned with the various growth of stability and power system dynamics retrofit control terms a new control design. Using retrofit controller, the rotor voltages of the induction generators that were doubly fed controlled for tie line power flow oscillations suppressing initiated by the wind farm’s inside disturbance. The major drawback considered was that closed-loop system stability has not been assured theoretically. The requirement of an exact wind farm model is necessary, and in future, the problem can be resolved by designing the controller using robust control theory. Huang et al. (2020) carried out a novel investigation where online detection of wind farm generalized short-circuit ratio (gSCR) was studied using current and voltage data from PMUs, which enables convenient online stability monitoring of wind farms. Ma et al. (2017a) found that on virtual inertia control, DFIG impacts the “power system small-signal stability” by considering the “phase-locked loop” (PLL). For a DFIG interconnected with conventional synchronous generators, it considers PLL and virtual inertia. The system’s dynamic characteristics vary due to the DFIG participating in electromechanical oscillations controlled by varying the PI values in PLL and virtual inertia.
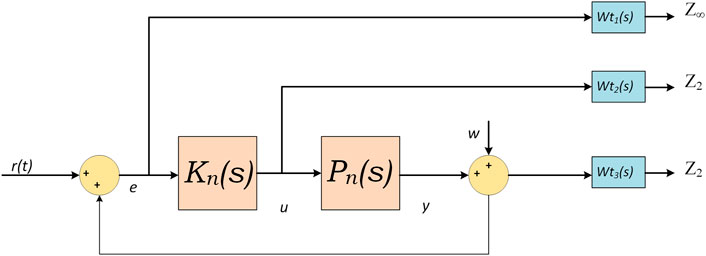
In the study by Ma et al. (2017b), the robust stochastic “small-signal stability” of the DFIG was integrated into a power system with virtual inertia, as mentioned earlier, and the methodology used was the sensitivity analysis method, which determined the connection between the state matrix variables and stochastic parameters using analytic function relationships. The stochastic power system stability issue turns into a solution for the problem of feasibility. Wen et al. (2017) proposed power electronics–based distributed power system stability analysis using “active front end (AFE) converters,” “voltage source inverters (VSIs),” and “grid-tied inverters (GTIs)” to process power flow as an analysis of AC stability and DQ frame impedance parameters. Liu et al. (2020a) investigated grid-integrated DFIG wind farms’ PLL parameters and power grid strength that impacts small-signal stability issues. They focused on finding the PLL oscillation mechanism and its influencing factors and developed a damping solution to that oscillation mode. To abate the PLL oscillations, they designed a different robust damping controller H2/H∞ for DFIG, which reduces the oscillations and improves small-signal stability. The structure of the robust damping controller is shown in Figure 3, where “r(t)” is the input signal of the controller and “e” is the error signal. “Kn(s)” and “Pn(s)” are controller gains; “Wt1(s), Wt2(s), and Wt3(s)” are weighting functions, and “Z∞” is the output channel associated with H∞ performance. “Z2” is the output channel associated with H2 performance.
2.3 Stability of sub-synchronous resonance
“Subsynchronous resonance is a phenomenon in which one or more of the resonant frequencies of the turbine generator shaft in thermal power units coincides through the generator with a natural resonant frequency of the electrical system with a long radial transmission network with series capacitors.”
In series, the compensated systems with several wind farms have detected the sub-synchronous resonance (SSR) issue elaborated by Liu et al. (2018a). The single-machine infinite bus system design has been simplified and used for further evaluation. It does not reflect the SSR effect, which is not from critical factors like wind speed distribution. This article, based on SSS, proposes a wind farm’s spatial distribution, wind turbine generators diversity, network topology, and an INM-impedance network model.
Moreover, with lumped independence, the INM was combined. The SSR stability was quantified by new stability criteria, which analyzed the features of impedance frequency. Even for wind power systems on a large scale, this proposed system has analyzed the SSR issue. For DFIG-based wind turbines interconnected with compensated transmission systems series, Karunanayake et al. (2020) specified the nonlinear sliding mode control SMC based on the mitigation method as a sub-synchronous resonance (SSR). This proposed method controls the rotor side converter by assuring the reactive power, and the decoupled torque of DFIG control ability sustains to mitigate SSR. For validations, on the model of DFIG wind turbines, the proposed method is executed on the Real Time Digital Simulator (RTDS) platform. At damping SSR, the controller shows positivity obtained from the results tested on different wind speeds and compensation levels.
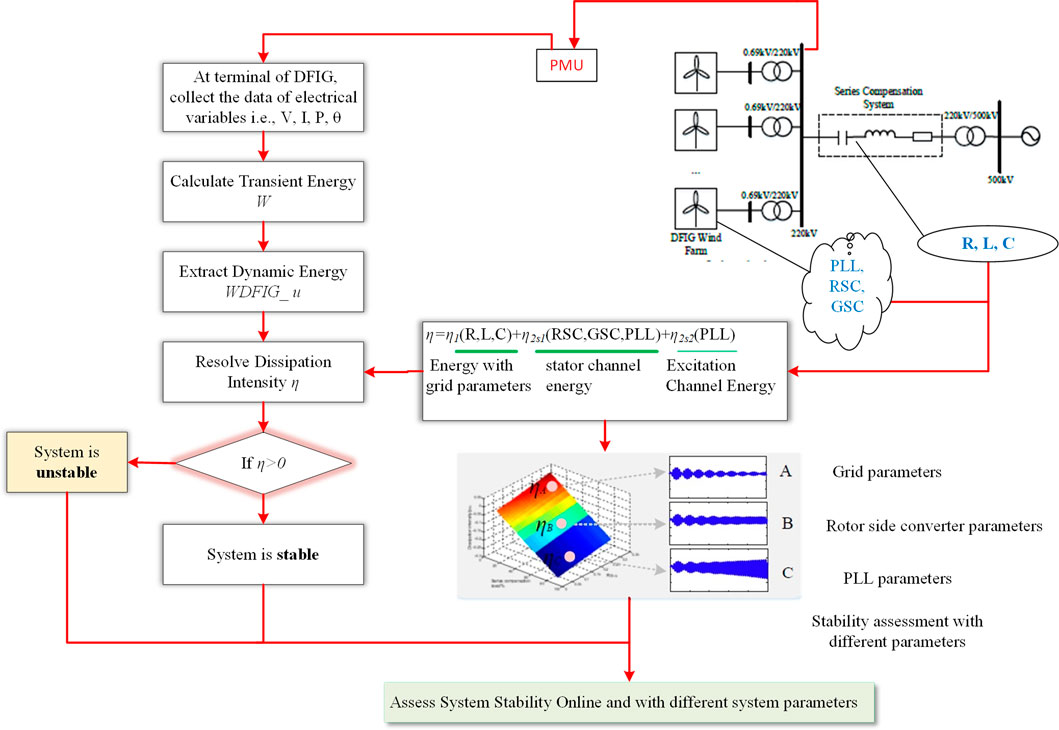
Ma et al. (2020) concentrated on sub-synchronous oscillations of DFIG stability estimations based on energy dissipation intensity analysis. According to the Lyapunov stability theory, the model of DFIG consists of an internal control and external network. Here, the proposed assessment method is represented in a logical diagram as shown in Figure 4. In this first step, collecting all the data of electrical variables at DFIG terminals with the help of phasor measurement units compares with steady-state values. Next, at the DFIG, variations of transient energy are estimated and the oscillation frequency and DFIG transient energy variation are obtained. Then, the dissipation intensity η can be calculated. The system’s stability can be judged by the value of η; when η > 0, the system is stable, and a larger value of η indicates higher stability. Also, when η = 0, the system is marginally stable, while η < 0 is negative stability and SSR oscillations diverge.
2.4 Probabilistic stability of sub-synchronous resonance
“In power system stability analysis, the system performance is based on a predefined scenario and ignores uncertainties in the system states and parameters. In modern power systems, consider all the uncertainties in the probabilistic approach to get accurate results.” The probabilistic approaches are highly appropriate for random and uncertain system analysis, which are the essential features of future power systems.
Chen et al. (2018) focused on assessing the probabilistic stability of SSR by using the piecewise probabilistic collocation method (PPCM), which concerns random wind speed. Because of the switching among various operational modes of the DFIG, the PPCM tackles the inherent nonlinearity. The lesser computational difficulty and damping accuracy in the probability density function (PDF) is achieved using the proposed PPCM. Various existing methods are available to describe the probabilistic distribution of wind speed: Rayleigh, Weibull, and Lognormal distribution methods. Among these methods, Weibull distribution ideally suits wind speed as a frequency histogram. The Weibull probabilistic model has also been designed in this study with two-year statistical wind speed data. Compared with the Monte Carlo method, consistency is obtained from using this proposed method. The SSR events field data in real-world wind farms offer effectiveness validation of the current model.
In their research work, Bian et al. (2016) carried out “power system stabilizers” (PSS) and “static VAR compensator” (SVC) damping controller coordination and optimizing these parameters to improve the “probabilistic small-signal stability” of the wind farm integrated power system. This novel algorithm is known as the “modified fruit fly optimization algorithm” (MFOA). With this, to coordinate and optimize the parameters, the probabilistic eigenvalue method was used. The proposed method improved the “parabolic small-signal stability” of DFIG-based wind firms integrated with synchronous generators.
2.5 Frequency stability
Frequency stability means “the ability of a power system to maintain steady frequency following a severe disturbance between generation and load.” Frequency stability depends on the ability to restore equilibrium between load and system generation. It can also lead to sustained frequency swings that can cause the generating system or load tripping.
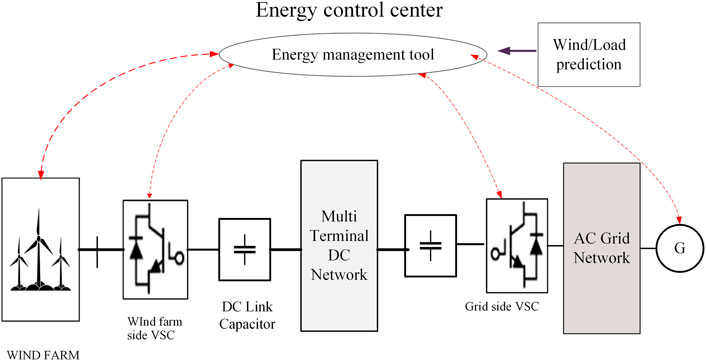
In the study by Wen et al. (2018), the onshore AC grid and offshore multiterminal DC grid–based voltage source convertor VSC-MTDC operation were examined to improve the system’s frequency stability by the unit commitment (UC) framework. Furthermore, it recognized three standard types of outages like wind farm side VSC loss, synchronous unit loss, and grid side VSC loss, which correspond to frequency dynamic constraints. Based on these, it integrated the AC/VSC MTDC system from the proposed frequency dynamics. Moreover, it effectively stabilized two grids among the GVSCs and WVSCs and examined the coordinated control approach. In Figure 5, the configuration of the AC/VSC-based MTDC system is shown. Here, the MTDC network is connected to offshore wind farms through the wind farm side voltage source converters (WVSC) and DC link capacitor. Similarly, the onshore AC grid is connected to the offshore VSC-MTDC grid through grid side voltage source converters (GVSC) and submarine HVDC cables. All the converters communicate with the energy management tool and track the voltages and power with local frequency control to detect any disturbance.
Renewable energy penetration has increased into the latest power systems, getting new oscillatory stability focused on this. Zhan et al. (2019) developed the analysis of the frequency-domain modal technique. It evaluated the dominant component’s participation, and several oscillatory modes were concerned. The oscillatory modes by loop impedance matrix or matrix of nodal admittance determinant’s zeroes located were worked out by the target system represented with impedance model network. The oscillation mode’s origin, respective components, and oscillation path were understood by the loop or nodal participation factors, component sensitivity, and branch observability derivation. The above-stated experiment was performed on a practical wind power system and a primary passive circuit that practices real sub-synchronous resonance. In addition, its effectiveness was evaluated by using electromagnetic transient simulations and theoretical results. This study evaluated the massive power systems with high penetration renewables.
Han et al. (2022) discussed the frequency oscillation problem, and a novel discrete-time domain modal analysis, proposing to reduce the sub-synchronous oscillations of RES connected to the power system. In this method, first, in the discrete-time domain, the frequency and damping ratio were calculated, and the system stability was evaluated from the calculated eigenvalues in discrete-time. Furthermore, the origin location, contributive components, and propagation paths of the oscillatory mode were determined by calculating the participation factors, component participation, branch current/node voltage observability matrix, and distribution coefficient for all modes based on matrix decomposition and node equations of the system-level model.
A supplementary optimal frequency controller was designed for variable speed wind turbines to be integrated into the power system to improve system stability in a study by Toulabi et al. (2018). The proposed controller regulates the frequency variations in wind farms, and the controller design parameters are designed using genetic algorithms.
Yang et al. (2022) described the power compensation control for a weak grid-connected DFIG wind farm. The synchronization of the wind farm to the weak grid during severe grid faults was studied to improve the frequency stability. The analysis was performed in a simulation and verified with experimental results.
In the study by Li et al. (2021), a SMES-based damping controller was designed to reduce low-frequency oscillations for enhancing the power system’s frequency stability. A finite Markov decision process that utilizes a deep reinforcement learning (DRL)–based agent was used to achieve the best possible results in terms of parameter optimization.
2.6 Dynamic stability
“Dynamic stability is the ability of a power system to return to a steady state of operation after significant disturbances (short circuit, the shutdown of any element of the power system, etc.).”
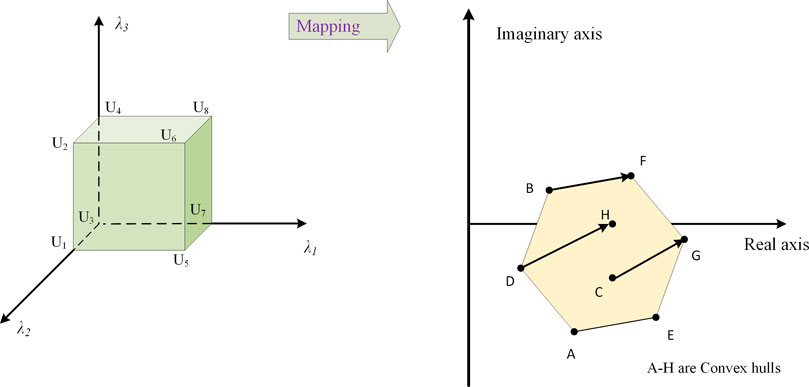
Shi et al. (2019) investigated the wind power penetrated power system’s robust stability analysis. The power system analysis can be imposed on the (D-stability) issue by focusing on the constraint of the damping ratio. The most familiar mapping theorem
Li et al. (2019) concentrated on real-world wind farms where the weak grid’s interconnection observed 4 and 30 Hz oscillations. The delivery of wind power is limited by these stability problems. This study proposes that the overall system stability improvises the mechanism-based feedback control approaches appropriate for voltage source converters that were vector based and engaged in type-3 and type-4 wind testbeds. The weak grid stability problem has to be demonstrated by the simplified linear model, and the reason was the power delivery coupling and voltage of the point of common coupling (PCC). The PCC voltage reduces when the power delivery increases, and hence the weak grid leads to instability. The feedback control approaches modulate DC-link voltage and power order through PCC voltage as input or the d-axis current. Finally, we see the efficient capability of stability improvement and wind power delivery further enhanced.
When a harmonic grid with parallel compensation joins the DFIG system, the harmonics and high-frequency resonance (HFR) exhibiting the frequency range may show intersections. Nian and Pang (2019) revealed that the coupling between the harmonics suppression control and HFR damping control provided by the harmonics suppressor and HFR damping led to an unstable situation of the DFIG system. Extra detection time of frequency of HFR results in HFR damping performance deterioration. Moreover, it achieves the harmonic current suppression and HFR damping control to further enhance DFIG system power quality associated with parallel compensation of the harmonic grid.
The IEEE 118-bus system uses a 12-bus system to evaluate the performance and effectiveness of the current study. Xiong et al. (2019) presented an optimal virtual inertia planning approach for power system stability improvement with renewable resources of large volumes penetrated by the DFIGs. The critical frequency drops are also exhibited in this study, and the DFIG stability are analyzed first. It calculates the local virtual inertia function form by the stability margin defined by the DFIG’s two predefined operation curves. Then, the planning strategy of virtual inertia is proposed, and the non-convex optimization issue is followed from the homogeneity of the stability margin. It uses the Lyapunov function to resolve these issues. The general stability was promoted, and the coherency level of the system stability margin improved, resulting in the proposed method. In the study by Liu et al. (2020b), with increased wind power penetration, the stability problems of the poor AC grid connection and DFIG-based wind turbines during low voltage could not be neglected. The exploration of the instability process of the DFIG system during the process of weak grid fault and a model based on the small-signal state are specified in this article. The article’s outcome depicted that the work was impacted by the rotor current control loop, phase-locked loop (PLL), and terminal voltage during dominant factor processing.
The system impact factor evaluated comprehensively indicated that the controller bandwidth in the expected condition does not apply to the fault because of the interaction between the grid and controller. It follows the optimized proportion that could be improved significantly. Experiments and simulations have evaluated the efficiency of the suggested system. The permanent magnet synchronous generator depends on wind turbines, and the virtual synchronous machine (VSM) was proposed by Muftau et al. (2020), and all operating modes allow continuous operation and guarantee maximum power point tracking in grid connected operations. In islanded operations, the power generation follows a load. During faults, the lower voltage ride-through capability exists. The optimal performance obtained by VSM stability in all operating models examines large and small perturbations. The linearized state-space model and participator factor analysis perform the VSM’s small-signal stability analysis using participator factor analysis and derived dominant mode controller effects. The VSM’s nonlinear model, dynamic performance, and transient stability analyzed. The VSM’s design guidelines and operational limits were recognized. Li et al. (2016) focused on multiple time delays of delay-dependent stability control for the power system. They designed a multiple time-delayed power system model consisting of PSS with time delays. Two H∞ controls develop schemes for time-varying multiple delayed systems by considering the “Lyapunov stability theory” and “linear matrix inequality” (LMI) method. The New England 10-machine, 39-bus system and a 2-area 4-machine power system were employed to demonstrate the effectiveness of the proposed methods.
Wang et al. (2017) proposed a novel framework consisting of “stochastic differential equations” (SDE) to ease the “long-term stability” analysis with spasmodic wind power generations. This framework considers discrete dynamics, playing a significant role in the “long-term stability” analysis. They developed a “deterministic hybrid model (DHM)” for the “stochastic hybrid model (SHM).” The computing burden of the uncertainty of wind power was reduced, which improves the dynamic stability under mild conditions.
2.7 Parametric stability
The parametric analysis was used to enhance the system stability in wind-penetrated power systems. In parametric analysis, more uncertain parameters were considered to enhance the power system stability.
In wind power assimilated power systems, Shi et al. (2018) focused on the analysis of parametric stability, and for that, they developed the rational fractional representation technique. It improves accuracy when using rational fractional parameters in a fitted parametric state matrix instead of conventional polynomials. For robust stability analysis, the generalized linear fractional transformation was used for standard linear
2.8 Voltage stability
Voltage stability means “the ability of a system to maintain steady-state voltages at all the system buses when subjected to a disturbance. If the disturbance is large, then it is called large-disturbance voltage stability.”
Jalali and Aldeen (2019) considered the energy storage devices (ESS), optimal placement, and sizing in wind-intensive power distributed generation. The expected voltage stability margin (VSM) should attain and require ESS size minimization. This study also focuses on reducing the reactive power import and reactive power loss from a network upstream through stochastic optimization, which is risk based and estimates the wind uncertainty. Furthermore, the ESS size required is reduced by additional means such as ESS devices’ reactive power capabilities and wind farms. If the preferred VSM increased, then the required ESS also increased asshown in the results. Yet, this kind of increase shortens using active network management (ANM) tools and voltage stability constraints, which are risk based. The traditional VAR compensation devices have become old and show minor changes for short-term voltage stability of high requirement satisfaction in power systems penetrated with high-level wind power. Hence, Liu et al. (2018b) proposed the STATCOMs technique for optimal dynamic VAR devices and also the power system upgraded with penetration of higher wind power and more excellent retirement of equipment. Three objectives have to be minimized, namely, proximity to steady-state index voltage collapse, retirement costs and upgrades, and unaccepted performance of the transient voltage index by the multi-objective optimization technique. Indefinite dynamic load models and several contingencies are considered in the real-world operating situation simulation. Through wind farm abilities, it designs low- and high-voltage rides. The New England 39-bus system of testing evaluates the proposed method.
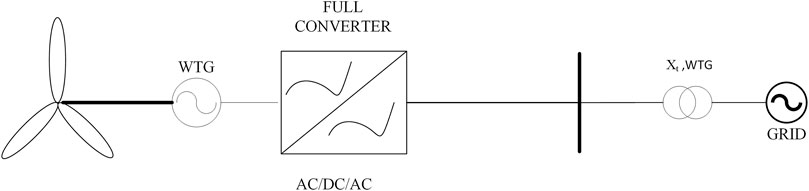
Kawabe et al. (2017) specified the photovoltaic (PV) system’s novel dynamic voltage support capability to improve the short-term voltage stability of the power system. The proposed DVS capability injects both active and reactive power in an organized manner. Souxes et al. (2020) focused on enhancing the power system stability issues under unfavorable network conditions with necessary support from wind farm power electronic converters. Protection schemes proposed for a weak transmission and network are integrated into wind farms to enhance long-term voltage stability during reactive emergency support. The schematic diagram of the full converter-based wind turbine is shown in Figure 7.
Milano (2016) proposed power and current injections for voltage and angle stability analysis, the comparison made with two formulations of both current and voltage injections on a dynamic 1479-bus model.
2.9 Small-signal angular stability
Small-signal angular stability means “the ability of synchronous machines of an interconnected power system to remain in synchronism after being subjected to a disturbance.”
Du et al. (2019) evaluated the power system’s small-signal angular stability affected by the virtual synchronous generator (VSG). Based on these two subsystems of the interconnected model the small signal angular stability evaluated. The other subsystem was the rest of the power system (ROPS). Based on these two subsystems of the interconnected model, and evaluated. When the VSG subsystem oscillation mode was in nearness to ROPS subsystem's electromechanical oscillation mode, the damping torque analysis applied indicated to VSG’s strong dynamic interactions for the small-signal angular stability decrease in the power system. Both subsystems’ modal proximity evaluates after setting the VSG parameters and avoids VSG due to the harmful effect of small-signal angular stability’s decrease in the power system. However, the modal proximity is avoided by this proposed article which assists in VSG design parameters. For wind power generation, finally, it offers two example power systems with several VSGs and transmission. Ma et al. (2017c) elaborated the angle stability analysis with multiple operating conditions by considering cascading failures of the power system. Based on the flow transfer theory, the power system divides into various operating conditions. The discrete Markov model establishes to analyze the angle stability.
2.10 Rotor angle stability
Rotor angle stability means “the ability of the system to remain in synchronism when subjected to a disturbance.” The rotor angle depends on the balance between a generator’s electromagnetic and mechanical torque to maintain stability.
To ensure grid security, Zhang et al. (2020) demonstrated that the frequency stability of the current dynamic analysis showed insufficiency because the virtual inertia control had impacted the first swing’s rotor angle stability. The novel virtual inertia control approach investigated in this study for wind turbines enhances the rotor angle stability of the first swing in the interconnected power grid. Here, the virtual inertia’s virtual energy in wind turbines was investigated and evaluated. The conversion of the transient energy system is grouped on the forward and backward directions of the swings of the rotor angle, and their virtual energies effect the two coherent generator groups. High wind penetration with 35% in a two-area interconnected power system has been provided in this study. Furthermore, it is comprised of two DFIG-based wind farms and simulated four traditional power plants. By regulating variable inertias and minimizing the rotor angle difference among coherent generator groups, wind turbines of virtual inertia support with more reliability resulted.
2.11 Stability issues in microgrids
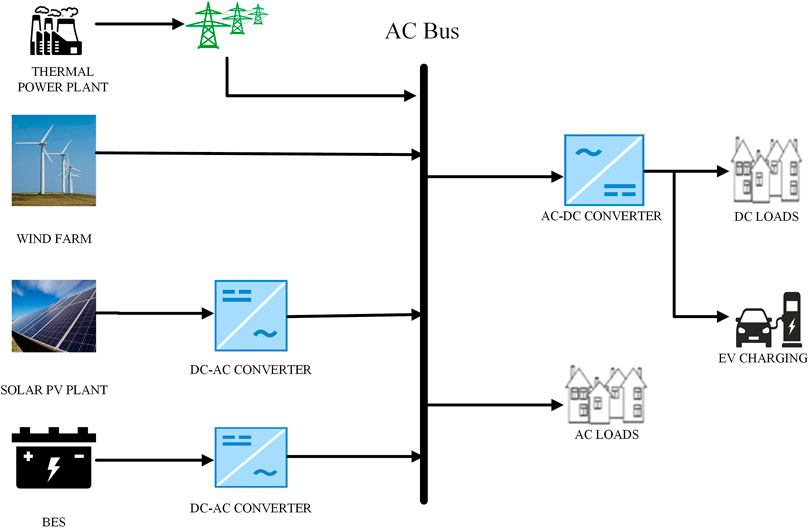
Majumder (2013) described different stability aspects in microgrids and discussed various methods in improving power system stability in DC microgrids. As illustrated in Figure 8, a microgrid can be represented by various micro sources and loads.
The research study by Bhosale and Agarwal (2019) used a fuzzy logic-based novel scheme for power flow control from a ultracapacitor in a battery. To regulate the DC bus voltage firmly, a fuzzy logic controller determines the UC convertor current reference. Low bandwidth controllers were developed to enhance current drawing quality from the battery. The fuzzy controller is simple to develop and does not require the understanding of the mathematical model of the system. Low complexity is assured during execution since it is a controller of single input and single output. Wind-up problems are not visible and faster controller is seen. Compared with the traditional frequency-based control approach, the proposed method shows better performance.
Wang et al. (2018b) described the stability analysis of a microgrid system consisting of a “seashore wave farm” (SWF), an “offshore wind farm” (OWF), and an “offshore tidal farm” (OTF) fed to the onshore power grid through a high-voltage DC (HVDC) link. They proposed VSC-based HVDC link with a PID damping controller, which evaluates a systematic approach by frequency domain analysis based on nonlinear simulations during severe three-phase faults at the power grid side. Puchalapalli et al. (2020) proposed a hybrid energy generation-based microgrid. It designs a bidirectional buck-boost DC-DC converter to improve the microgrid’s stability in various wind and solar weather conditions.
Xia et al. (2022) discussed the large signal stability of the AC microgrid, which is a single energy storage–based AC microgrid, with the nonlinear reduced order model designed to determine system stability during large disturbances.
Krismanto et al. (2021) studied the stability issues in grid-connected microgrids during uncertain conditions in RES. In order to confirm and characterize the modal interaction, three analytical methods were proposed: eigen-trajectories, the cross-participation factor, and the modal interaction index (MII). Monte Carlo (MC) simulation was proposed to determine the eigenvalues of the system and determine the small-signal stability of the system.
Mohamed et al. (2022) explored frequency stability enhancement in an interconnected microgrid. This article uses a fractional order load frequency controller with superconducting magnetic energy storage (SMES) virtual inertia system to assess and improve digital frequency relay coordination. Optimized fractional order controller based on slime mould optimization algorithm improves the coordination method (SMA). In the study by Zhang et al. (2021), voltage-based segment control was used to enhance the transient stability of the DC microgrid. When the DC voltage deviation is within the tolerant range, the VBS control allows SMES to function in the energy storage mode. When the voltage is outside the normal range because of transient power fluctuations, the SMES will carry out transient power regulation.
Hence, the above stated references have been reviewed based on types of stability, and the results of all the analyses are validated using the simulation method, namely, MATLAB/SIMULINK.
3 Comparison analysis
The following section describes the type of stability related to wind power in the power system, comparatively analyzed further and briefly tabulated below in Table 1.
Figure 9 depicts the type of stability used in every referenced article and states that transient stability is analyzed primarily in most research studies for other types of stability.
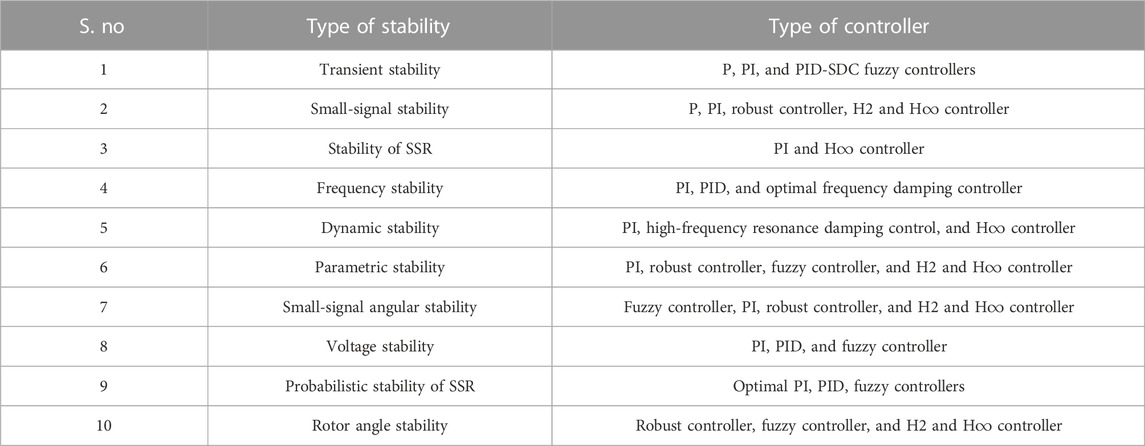
Table 2 represents the different controllers used to improve the various types of stability.
4 Conclusion
This article gives a concise summary of power system stability issues in large-scale wind-integrated power systems. The increasing wind power penetration has shown several challenges toward the stability types in power system generation due to uncertainty of wind speed. The system dynamic depicts variations in the performance of wind turbines that was also seen in this proposed study. This proposed review focused mainly on the types of stability toward the penetration in wind power generation systems. In most research works, a comparative analysis of sustainability has shown that transient stability has been substantially analyzed and compared with other types of stability like parametric stability, dynamic stability, frequency stability, and others. In recent years, many researchers have focused their studies on stability issues of renewable energy sources–based microgrids. It is the new trend in investigating the stability problems of microgrids. In the future, several other types of stability and analyses of the respective simulations and of their results should be studied in depth.
Author contributions
VY: conceptualization, methodology, software, formal analysis, writing—original draft, and data curation. BS: conceptualization, methodology, validation, investigation, resources, writing—review and editing, visualization, supervision, and project administration.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, editors, and reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bhosale, R., and Agarwal, V. (2019). Fuzzy logic control of the ultracapacitor interface for enhanced transient response and voltage stability of a dc microgrid. IEEE Trans. Ind. Appl. 55 (1), 712–720. doi:10.1109/TIA.2018.2870349
Bian, X. Y., Geng, Y., Lo, K. L., Fu, Y., and Zhou, Q. B. (2016). Coordination of PSSs and SVC damping controller to improve probabilistic small-signal stability of power system with wind farm integration. IEEE Trans. Power Syst. 31 (3), 2371–2382. doi:10.1109/TPWRS.2015.2458980
Chen, W., Xie, X., Wang, D., Liu, H., and Liu, H. (2018). Probabilistic stability analysis of subsynchronous resonance for series-compensated DFIG-based wind farms. IEEE Trans. Sustain. Energy 9 (1), 400–409. doi:10.1109/TSTE.2017.2737599
Datta, U., Kalam, A., and Shi, J. (2019). Battery energy storage system to stabilize transient voltage and frequency and enhance power export capability. IEEE Trans. Power Syst. 34 (3), 1845–1857. doi:10.1109/TPWRS.2018.2879608
Du, W., Fu, Q., and Wang, H. F. (2019). Power system small-signal angular stability affected by virtual synchronous generators. IEEE Trans. Power Syst. 34 (4), 3209–3219. doi:10.1109/TPWRS.2019.2896149
Eshkaftaki, A. A., Rabiee, A., Kargar, A., and Boroujeni, S. T. (2020). An applicable method to improve transient and dynamic performance of power system equipped with DFIG-based wind turbines. IEEE Trans. Power Syst. 35 (3), 2351–2361. doi:10.1109/TPWRS.2019.2954497
Han, Y., Sun, H., Huang, B., and Qin, S. (2022). Discrete-time domain modal analysis of oscillatory stability of renewables integrated power systems. IEEE Trans. Power Deliv. 37 (5), 4248–4260. doi:10.1109/TPWRD.2022.3148187
Huang, L., Xin, H., Li, Z., Ju, P., Yuan, H., and Wang, G. (2020). Identification of generalized short-circuit ratio for on-line stability monitoring of wind farms. IEEE Trans. Power Syst. 35 (4), 3282–3285. doi:10.1109/TPWRS.2020.2975413
Hui, Q., Yang, J., Yang, X., Chen, Z., Li, Y., and Teng, Y. (2019). A robust control strategy to improve transient stability for AC-DC interconnected power system with wind farms. CSEE J. Power Energy Syst. 5, 259. doi:10.17775/CSEEJPES.2019.00250
Husham, A., Kamwa, I., Abido, M. A., and Supreme, H. (2022). Decentralized stability enhancement of DFIG-based wind farms in large power systems: Koopman theoretic approach. IEEE Access 10, 27684–27697. doi:10.1109/ACCESS.2022.3157747
Jalali, A., and Aldeen, M. (2019). Risk-based stochastic allocation of ESS to ensure voltage stability margin for distribution systems. IEEE Trans. Power Syst. 34 (2), 1264–1277. doi:10.1109/TPWRS.2018.2873774
Jiang, H., and Zhang, C. (2019). A method of boosting transient stability of wind farm connected power system using S magnetic energy storage unit. IEEE Trans. Appl. Supercond. 29 (2), 1–5. doi:10.1109/TASC.2019.2892291
Karunanayake, C., Ravishankar, J., and Dong, Z. Y. (2020). Nonlinear SSR damping controller for DFIG based wind generators interfaced to series compensated transmission systems. IEEE Trans. Power Syst. 35 (2), 1156–1165. doi:10.1109/TPWRS.2019.2938230
Kawabe, K., Ota, Y., Yokoyama, A., and Tanaka, K. (2017). Novel dynamic voltage support capability of photovoltaic systems for improvement of short-term voltage stability in power systems. IEEE Trans. Power Syst. 32 (3), 1796–1804. doi:10.1109/TPWRS.2016.2592970
Krismanto, A. U., Mithulananthan, N., Setiadi, H., Setyawan, E. Y., and Abdillah, M. (2021). Impacts of grid-tied microgrid on stability and interaction of power systems considering RE uncertainties. Sustain. Energy, Grids Netw. 28, 100537. doi:10.1016/j.segan.2021.100537
Li, J., Chen, Z., Cai, D., Zhen, W., and Huang, Q. (2016). Delay-dependent stability control for power system with multiple time-delays. IEEE Trans. Power Syst. 31 (3), 2316–2326. doi:10.1109/TPWRS.2015.2456037
Li, T., Hu, W., Zhang, B., Zhang, G., Zhang, Z., and Chen, Z. (2021). SMES damping controller design and real-time parameters tuning for low-frequency oscillation. IEEE Trans. Appl. Supercond. 31 (8), 1–4. doi:10.1109/TASC.2021.3099759
Li, Y., Fan, L., and Miao, Z. (2019). Stability control for wind in weak grids. IEEE Trans. Sustain. Energy 10 (4), 2094–2103. doi:10.1109/TSTE.2018.2878745
Liu, H., Xie, X., Gao, X., Liu, H., and Li, Y. (2018). Stability analysis of SSR in multiple wind farms connected to series-compensated systems using impedance network model. IEEE Trans. Power Syst. 33 (3), 3118–3128. doi:10.1109/TPWRS.2017.2764159
Liu, J., Xu, Y., Dong, Z. Y., and Wong, K. P. (2018). Retirement-driven dynamic VAR planning for voltage stability enhancement of power systems with high-level wind power. IEEE Trans. Power Syst. 33 (2), 2282–2291. doi:10.1109/TPWRS.2017.2732441
Liu, J., Yao, W., Wen, J., Fang, J., Jiang, L., He, H., et al. (2020). Impact of power grid strength and PLL parameters on stability of grid-connected DFIG wind farm. IEEE Trans. Sustain. Energy 11 (1), 545–557. doi:10.1109/TSTE.2019.2897596
Liu, R., Yao, J., Wang, X., Sun, P., Pei, J., and Hu, J. (2020). Dynamic stability analysis and improved LVRT Schemes of DFIG-Based wind turbines during a symmetrical fault in a weak grid. IEEE Trans. Power Electron. 35 (1), 303–318. doi:10.1109/TPEL.2019.2911346
Liu, Y., Wu, Q. H., Kang, H., and Zhou, X. (2016). Switching power system stabilizer and its coordination for enhancement of multi-machine power system stability. CSEE Power Energy Syst. 2 (2), 98–106. doi:10.17775/CSEEJPES.2016.00027
Ma, J., Qiu, Y., Li, Y., Zhang, W., Song, Z., and Thorp, J. S. (2017). Research on the impact of DFIG virtual inertia control on power system small-signal stability considering the phase-locked loop. IEEE Trans. Power Syst. 32 (3), 2094–2105. doi:10.1109/TPWRS.2016.2594781
Ma, J., Shen, Y., and Phadke, A. G. (2020). Stability assessment of DFIG subsynchronous oscillation based on energy dissipation intensity analysis. IEEE Trans. Power Electron. 35 (8), 8074–8087. doi:10.1109/TPEL.2019.2962217
Ma, J., Song, Z., Zhang, Y., Zhao, Y., and Thorp, J. S. (2017). Robust stochastic stability analysis method of DFIG integration on power system considering virtual inertia control. IEEE Trans. Power Syst. 32 (5), 4069–4079. doi:10.1109/TPWRS.2017.2657650
Ma, J., Wang, S., Qiu, Y., Li, Y., Wang, Z., and Thorp, J. S. (2017). Angle stability analysis of power system with multiple operating conditions considering cascading failure. IEEE Trans. Power Syst. 32 (2), 1–882. doi:10.1109/TPWRS.2016.2566672
Ma, J., Zhao, D., Yao, L., Qian, M., Yamashita, K., and Zhu, L. (2018). Analysis on application of a current-source based DFIG wind generator model. CSEE J. Power Energy Syst. 4 (3), 352–361. doi:10.17775/CSEEJPES.2018.00060
Ma, S. K., Geng, H., Liu, L., Yang, G., and Pal, B. C. (2018). Grid-synchronization stability improvement of large scale wind farm during severe grid fault. IEEE Trans. Power Syst. 33 (1), 216–226. doi:10.1109/TPWRS.2017.2700050
Majumder, R. (2013). Some aspects of stability in microgrids. IEEE Trans. Power Syst. 28 (3), 3243–3252. doi:10.1109/TPWRS.2012.2234146
Milano, F. (2016). On current and power injection models for angle and voltage stability analysis of power systems. IEEE Trans. Power Syst. 31 (3), 2503–2504. doi:10.1109/TPWRS.2015.2449765
Mohamed, E. A., Aly, M., Elmelegi, A., Ahmed, E. M., Watanabe, M., and Said, S. M. (2022). Enhancement the frequency stability and protection of interconnected microgrid systems using advanced hybrid fractional order controller. IEEE Access 10, 111936–111961. doi:10.1109/ACCESS.2022.3216212
Muftau, B., Fazeli, M., and Egwebe, A. (2020). Stability analysis of a PMSG based virtual synchronous machine. Electr. Power Syst. Res. 180, 106170. doi:10.1016/J.EPSR.2019.106170
Nian, H., and Pang, B. (2019). Stability and power quality enhancement strategy for DFIG system connected to harmonic grid with parallel compensation. IEEE Trans. Energy Convers. 34 (2), 1010–1022. doi:10.1109/TEC.2018.2866619
Ortega, Á., and Milano, F. (2018). Stochastic transient stability analysis of transmission systems with inclusion of energy storage devices. IEEE Trans. Power Syst. 33 (1), 1077–1079. doi:10.1109/TPWRS.2017.2742400
Pan, Y., Liu, F., Chen, L., Wang, J., Qiu, F., Shen, C., et al. (2018). Towards the robust small-signal stability region of power systems under perturbations such as uncertain and volatile wind generation. IEEE Trans. Power Syst. 33 (2), 1790–1799. doi:10.1109/TPWRS.2017.2714759
Pico, H. N. V., and Johnson, B. B. (2019). Transient stability assessment of multi-machine multi-converter power systems. IEEE Trans. Power Syst. 34 (5), 3504–3514. doi:10.1109/TPWRS.2019.2898182
Puchalapalli, S., Tiwari, S. K., Singh, B., and Goel, P. K. (2020). A microgrid based on wind-driven DFIG, DG, and solar PV array for optimal fuel consumption. IEEE Trans. Ind. Appl. 56 (5), 4689–4699. doi:10.1109/TIA.2020.2999563
Rahman, M. T., Hasan, K. N., and Sokolowski, P. (2022). Evaluation of wind farm aggregation using probabilistic clustering algorithms for power system stability assessment. Sustain. Energy, Grids Netw. 30, 100678. doi:10.1016/j.segan.2022.100678
Renedo, J., Garcia-Cerrada, A., and Rouco, L. (2016). Active power control strategies for transient stability enhancement of AC/DC grids with VSC-HVDC multi-terminal systems. IEEE Trans. Power Syst. 31 (6), 4595–4604. doi:10.1109/TPWRS.2016.2517215
Sadamoto, T., Chakrabortty, A., Ishizaki, T., and Imura, J. I. (2018). Retrofit control of wind-integrated power systems. IEEE Trans. Power Syst. 33 (3), 2804–2815. doi:10.1109/TPWRS.2017.2750411
Shi, P., Jiang, C., Gan, D., Xin, H., Jia, L., Gao, X., et al. (2019). New value set approach for robust stability of power systems with wind power penetration. IEEE Trans. Sustain. Energy 10 (2), 811–821. doi:10.1109/TSTE.2018.2848703
Shi, P., Zhou, J., Gan, D., and Wang, Z. (2018). A rational fractional representation method for wind power integrated power system parametric stability analysis. IEEE Trans. Power Syst. 33 (6), 7122–7131. doi:10.1109/TPWRS.2018.2849400
Souxes, T., Parasidis, A., and Vournas, C. D. (2020). Stabilizing controls for wind generators participating in transmission V/Q support. IEEE Trans. Power Syst. 35 (5), 3627–3635. doi:10.1109/TPWRS.2020.2974956
Tang, W., Hu, J., Chang, Y., and Liu, F. (2018). Modeling of DFIG-based wind turbine for power system transient response analysis in rotor speed control timescale. IEEE Trans. Power Syst. 33 (6), 6795–6805. doi:10.1109/TPWRS.2018.2827402
Toulabi, M., Bahrami, S., and Ranjbar, A. M. (2018). Optimal supplementary frequency controller design using the wind farm frequency model and controller parameters stability region. ISA Trans. 74, 175–184. doi:10.1016/j.isatra.2018.01.011
Wang, L., Lin, C. Y., Wu, H. Y., and Prokhorov, A. V. (2018). Stability analysis of a microgrid system with a hybrid offshore wind and ocean energy farm fed to a power grid through an HVDC link. IEEE Trans. Ind. Appl. 54 (3), 2012–2022. doi:10.1109/TIA.2017.2787126
Wang, L., Vo, Q. S., and Prokhorov, A. V. (2018). Stability improvement of a multimachine power system connected with a large-scale hybrid wind-photovoltaic farm using a supercapacitor. IEEE Trans. Ind. Appl. 54 (1), 50–60. doi:10.1109/TIA.2017.2751004
Wang, X., Wang, T., Chiang, H. D., Wang, J., and Liu, H. (2017). A framework for dynamic stability analysis of power systems with volatile wind power. IEEE J. Emerg. Sel. Top. Circuits Syst. 7 (3), 422–431. doi:10.1109/JETCAS.2017.2657627
Wen, B., Burgos, R., Boroyevich, D., Mattavelli, P., and Shen, Z. (2017). AC stability analysis and <italic>dq</italic> frame impedance specifications in power-electronics-based distributed power systems. IEEE J. Emerg. Sel. Top. Power Electron. 5 (4), 1455–1465. doi:10.1109/JESTPE.2017.2728640
Wen, Y., Zhan, J., Chung, C. Y., and Li, W. (2018). Frequency stability enhancement of integrated AC/VSC-MTDC systems with massive infeed of offshore wind generation. IEEE Trans. Power Syst. 33 (5), 5135–5146. doi:10.1109/TPWRS.2018.2792906
Xia, Y., Lv, Z., Wei, W., and He, H. (2022). Large-signal stability analysis and control for small-scale AC microgrids with single storage. IEEE J. Emerg. Sel. Top. Power Electron. 10 (4), 4809–4820. doi:10.1109/JESTPE.2021.3135892
Xiong, L., Li, P., Wu, F. W., and Wang, J. (2019). Stability enhancement of power systems with high DFIG-wind turbine penetration via virtual inertia planning. IEEE Trans. Power Syst. 34 (2), 1352–1361. doi:10.1109/TPWRS.2018.2869925
Xu, Y., Yin, M., Dong, Z. Y., Zhang, R., Hill, D. J., and Zhang, Y. (2018). Robust dispatch of high wind power-penetrated power systems against transient instability. IEEE Trans. Power Syst. 33 (1), 174–186. doi:10.1109/TPWRS.2017.2699678
Yang, Y., Zhu, D., Zou, X., Chi, Y., and Kang, Y. (2022). Power compensation control for DFIG-based wind turbines to enhance synchronization stability during severe grid faults. IEEE Trans. Power Electron. 37 (9), 10139–10143. doi:10.1109/TPEL.2022.3168883
Yousefian, R., Bhattarai, R., and Kamalasadan, S. (2017). Transient stability enhancement of power grid with integrated wide area control of wind farms and synchronous generators. IEEE Trans. Power Syst. 32 (6), 4818–4831. doi:10.1109/TPWRS.2017.2676138
Yu, J. J. Q., Hill, D. J., Lam, A. Y. S., Gu, J., and Li, V. O. K. (2018). Intelligent time-adaptive transient stability assessment system. IEEE Trans. Power Syst. 33 (1), 1049–1058. doi:10.1109/TPWRS.2017.2707501
Zhan, Y., Xie, X., Liu, H., Liu, H., and Li, Y. (2019). Frequency-domain modal analysis of the oscillatory stability of power systems with high-penetration renewables. IEEE Trans. Sustain. Energy 10 (3), 1534–1543. doi:10.1109/TSTE.2019.2900348
Zhang, T. L., Zhou, Q., Mu, S., Li, H., Li, Y. J., and Wang, J. (2021). Voltage-based segmented control of superconducting magnetic energy storage for transient power fluctuation suppression in Island DC microgrid. IEEE Trans. Appl. Supercond. 31 (8), 1–5. doi:10.1109/TASC.2021.3101760
Keywords: stability analysis, wind turbine, power generation system, microgrid, transient stability
Citation: Yadav VV and Saravanan B (2022) Technical advances and stability analysis in wind-penetrated power generation systems—A review. Front. Energy Res. 10:1091512. doi: 10.3389/fenrg.2022.1091512
Received: 07 November 2022; Accepted: 02 December 2022;
Published: 19 December 2022.
Edited by:
Sarat Kumar Sahoo, Parala Maharaja Engineering College (P.M.E.C), IndiaReviewed by:
Saroj Padhan, Parala Maharaja Engineering College (P.M.E.C), IndiaRabindra Kumar Sahu, Veer Surendra Sai University of Technology, India
Copyright © 2022 Yadav and Saravanan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: B. Saravanan, YnNhcmF2YW5hbkB2aXQuYWMuaW4=
 V. Vishnuvardhan Yadav
V. Vishnuvardhan Yadav B. Saravanan
B. Saravanan