- 1Institute of Modern Physics, Chinese Academy of Sciences, Lanzhou, China
- 2School of Nuclear Science and Technology, University of Chinese Academy of Sciences, Beijing, China
- 3School of Nuclear Science and Technology, Lanzhou University, Lanzhou, China
In the simple gradient diffusion hypothesis, the turbulent Prandtl number (
1 Introduction
Liquid metals are widely considered coolants with good thermal-hydraulic characteristics for many energy systems, such as fast reactors and subcritical reactors (Gu and su, 2021; Wang et al., 2021). However, liquid metals’ low molecular Prandtl number
It is difficult, dangerous, and costly to experiment with liquid metals (Schroer et al., 2012; Ejenstam and Szakálos, 2015), while the computational fluid dynamics (CFD) method is more commonly applied to investigate the thermal-hydraulic properties of these liquids. However, in CFD, the computing cost required by the direct numerical simulation (DNS) method and the large eddy simulations (LES) method is too high to rely on this technique for a quick and economic calculation of heat transfer in complex geometries (Kawamura et al., 1999), while the Reynolds Averaged Navier–Stokes (RANS) method can be promoted. The velocity boundary layer and the temperature layer of traditional fluid (Pr ≈ 1) are generally considered to be similar in the RANS framework. In this way, one can obtain a constant turbulent Prandtl number
In the SGDH framework, Cheng (Cheng and Tak, 2006) derived a
Another popular model in the SGDH work, called the four-equation k-ε-kθ-εθ turbulent heat transfer model, is introduced into turbulent and thermal time-scales for the simulation of the explicit first-order turbulent heat diffusivity. The literature (Nagano and Kim, 1988; Abe et al., 1995; Nagano and Shimada. 1996) has contributed extensively to near-wall model closure and thermal turbulence effect for a four-equation model. In recent years, Manservisi (Manservisi and Menghini, 2014a) improved the four-equation k-ε-kθ-εθ model proposed by Abe and Nagano. The model predicted the heat transfer process of the plane, circular tube, triangular rod bundles, and quadrilateral rod bundles for
However, the application codes of an isotropic four-equation model in complex geometries are still lacking for liquid metals, and its reliability needs to be further verified and evaluated. So, in the present work, the four-equation model in an isotropic dissipation rate
2 Mathematical Model
2.1 Isotropic Four-Equation Turbulence Model
The incompressible RANS equations with no gravity and constant physical properties for the calculation of velocity, pressure, and temperature fields are considered as follows:
where
The turbulent viscosity
Due to low Pr fluids’ physical properties, there are great differences between the momentum and heat. A constant Prt ≈ 0.85–0.9 cannot give acceptable results for liquid metals. It is possible to consider
where
Both the turbulent Reynolds number
where
2.2 Turbulent Viscosity and Turbulent Thermal Diffusivity
Some dynamic and thermal time-scales should be applied to calculate the turbulent viscosity
where
and
where
and
The above model has been proved to be effective in producing correct turbulence behavior of liquid metal, which draws into the mixing time-scale
2.3 Wall Boundary Conditions for Turbulence Models
Appropriate boundary conditions should be applied to solve the four-equation turbulent models without the available wall functions. By using series expansions as shown in Table 2, the near-wall behaviors of dynamical and thermal turbulence variables
According to the definitions of Eqs 7, 8, when
2.4 Modified Navier–Stokes Equations for Periodic Boundary Conditions
For a fully developed turbulent field, the pressure gradient term in Eq. 2 is divided into the mean of the pressure gradient
For a fully developed temperature field, temperature T is written as follows:
where
3 Numerical Results and Analysis
3.1 Numerical Solver of the Isotropic Four-Equation Model
For the modified RANS system and the isotropic four-equation
where Q stands for
3.2 Numerical Verification of the Plane
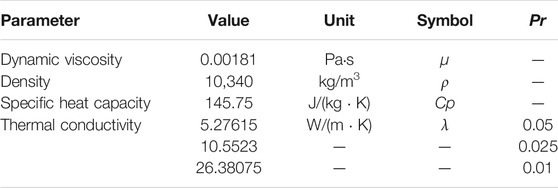
The full development process of different Pr fluids in a constant heat flow heated plane was studied using DNS (Kawamura et al., 1998; Kawamura et al., 1999; Tiselj and Cizelj, 2012). This study compares the DNS data with Pr = 0.01 ∼ 0.05. The plane geometry and mesh parameters are consistent with those in the literature (Su et al., 2021; Su and Gu, 2021). Here, the three-dimensional parallel plane with a flow length of 6.4 h, a spanwise width of 3.2 h, and a plane height of 2 h were selected as the calculation domain, where h is the half-height of the plane, 30.25 mm. The wall heat flux is set as qw = 360 kW/m2. Finally, 80, 50, and 100 nodes are divided into three directions, respectively: Flow direction, span direction, and height. Due to the symmetry of the plane, half of the plane is taken as the calculation domain, and the structured grid is used. The grid height of the first boundary layer is set to 3 × 10−6 m to meet the requirements of the low Reynolds number turbulence model,
3.2.1 Velocity Field Verification
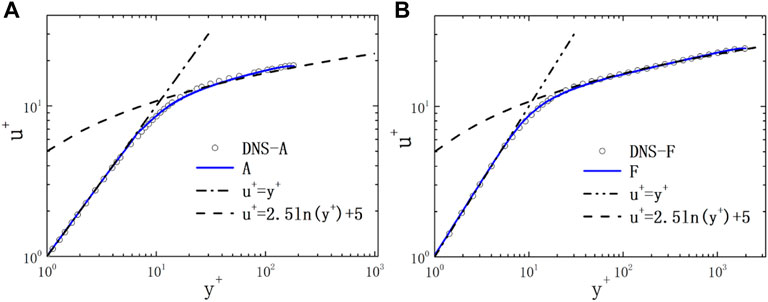
The dimensionless velocity
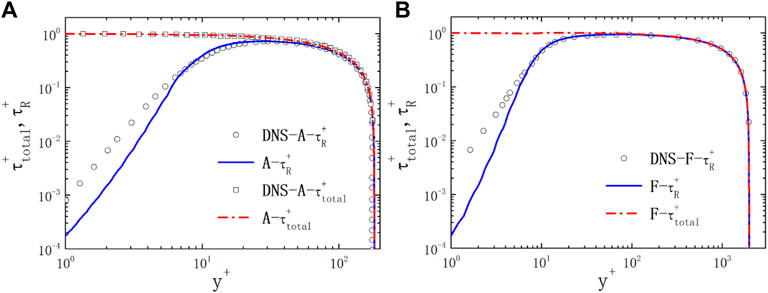
The distribution of dimensionless Reynolds stress
3.2.2 Temperature Field Verification
1) Pr = 0.01
The dimensionless temperature
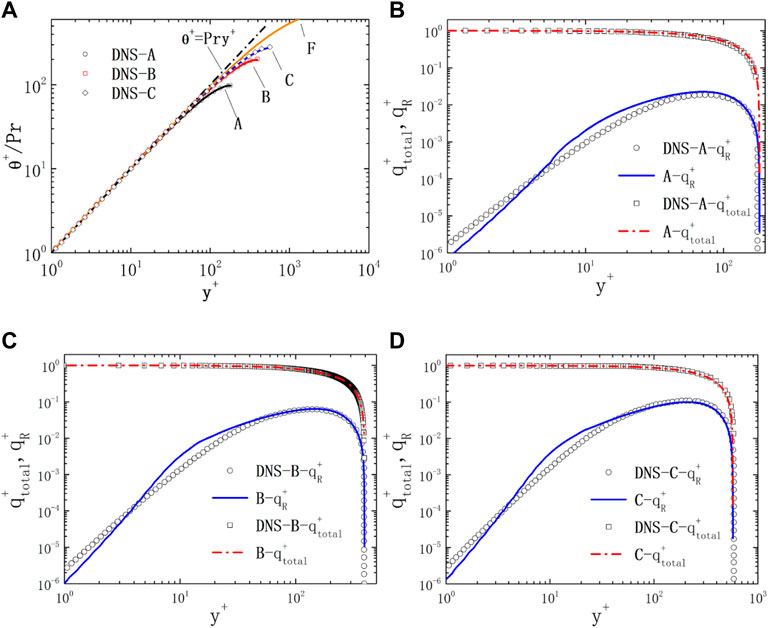
FIGURE 3. Non-dimensional temperature and heat flux of the plane for Pr = 0.01. (A) temperature; (B) heat flux of case A; (C) heat flux of case B; (D) heat flux of case C.
The distribution of dimensionless Reynolds heat flux
2) Pr = 0.025
The distribution of θ+/Pr of the
3) Pr=0.05
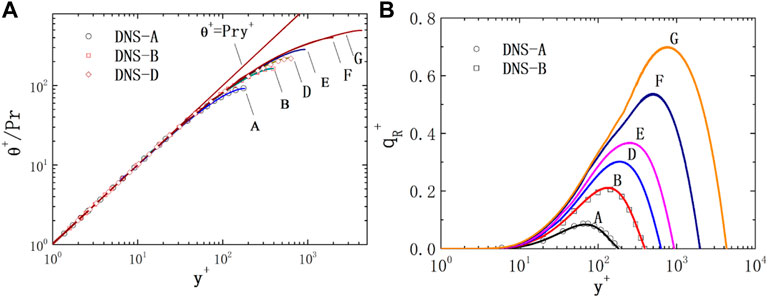
FIGURE 4. Non-dimensional temperature and heat flux of the plane for Pr = 0.025. (A) temperature; (B) heat flux.
As shown in Figure 5A, the dimensionless temperature θ+ of case A of Pr = 0.05 fluid is in good agreement with the DNS results. At the same Reynolds number, with the decrease in Pr, the molecular thermal conductivity increases and the average θ+ decreases. As shown in Figure 5B, the dimensionless Reynolds heat flux of case A of Pr = 0.05 fluid is in good agreement with the DNS results.
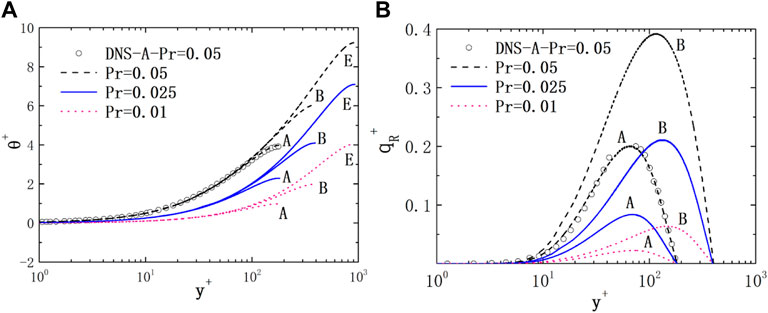
FIGURE 5. Non-dimensional temperature and heat flux of the plane for different Pr fluids. (A) temperature; (B) heat flux.
3.3 Numerical Analysis of the Square Bundle
To further analyze the applicability of the current isotropic four-equation model in complex geometries, the flow and heat of liquid metal with a Prandtl value of 0.01 in the quadrilateral infinite rod bundle were studied. Figure 6 shows the schematic diagram of the computational domain and local hexahedral mesh of the quadrilateral infinite rod bundle. Lines ab, bo, oc, and arc ca are the local distributions to be analyzed next. The flow parameters are reported in Table 4. The surfaces of rods in contact with the fluids are heated by uniform wall fluxes
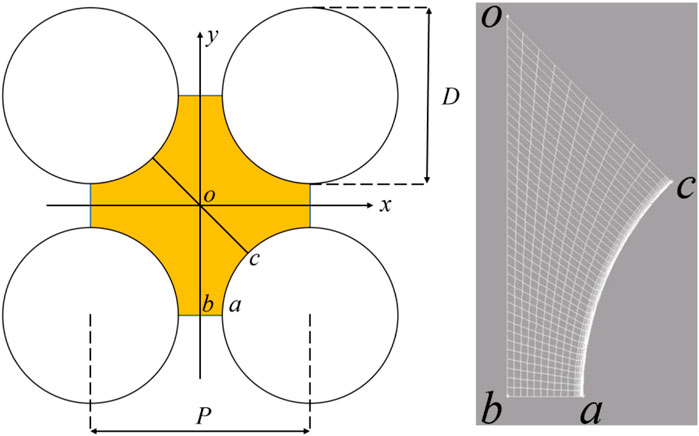
FIGURE 6. Schematic diagram of the quadrilateral infinite rod bundle. (A) flow area; (B) local mesh.
3.3.1 Heat Transfer Evaluation and Analysis
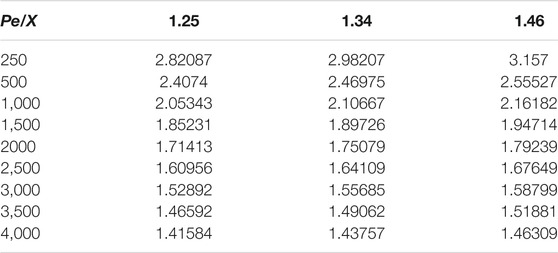
In Table 5, a few important heat transfer correlations of Nusselt number
where
First, the simulations for
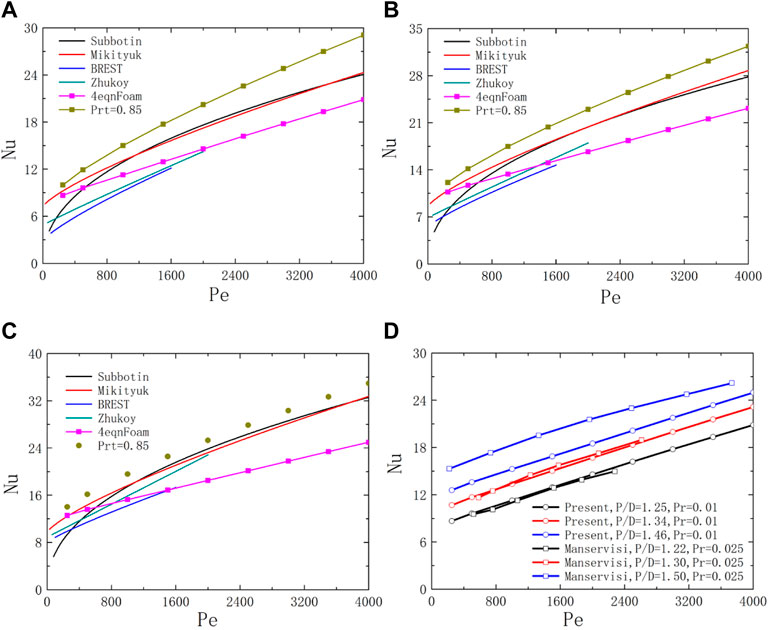
FIGURE 7. Schematic diagram of Nusselt number for the square bundle. (A) X = 1.25; (B) X = 1.34; (C) X = 1.46; (D) X = 1.22–1.5.
In Figures 7A–C, the prediction Nu of the isotropic
As shown in Figure 7D, the numerical slope in the Nu(Pe) line obtained using the
This present work focuses on the comparison of the effects of two turbulent thermal diffusion models (the
3.3.2 Turbulent Thermal Fields
1) Coolant and wall temperature
Figure 8 shows the dimensionless temperature
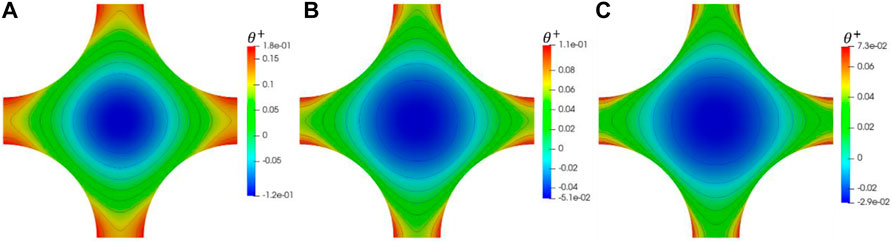
FIGURE 8. Schematic diagram of dimensionless temperature on a slice for square lattice X = 1.25. (A) Pe = 250; (B) Pe = 2000; (C) Pe = 4000.
Figure 6 has annotated the line ab, line bo, line oc, and arc ca, where points b and c represent the center of the gap and the channel, respectively. The dimensionless temperature field with Pe = 2000 is selected for analysis. In Figure 9A, with the decrease in P/D, the gap width decreases, and the overall dimensionless temperature distribution
2) Fluctuation and isotropic dissipation
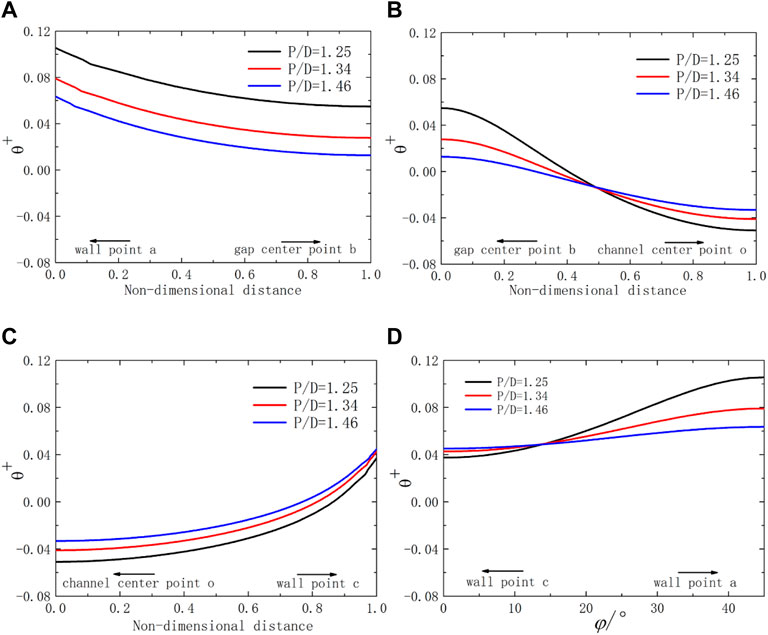
FIGURE 9. Schematic diagram of dimensionless temperature over lines for the square lattice at Pe = 2000 with different P/D ratios. (A) line ab; (B) line bo; (C) line oc; (D) arc ca.
The distribution and shape of
3) Turbulence and molecular thermal diffusivity
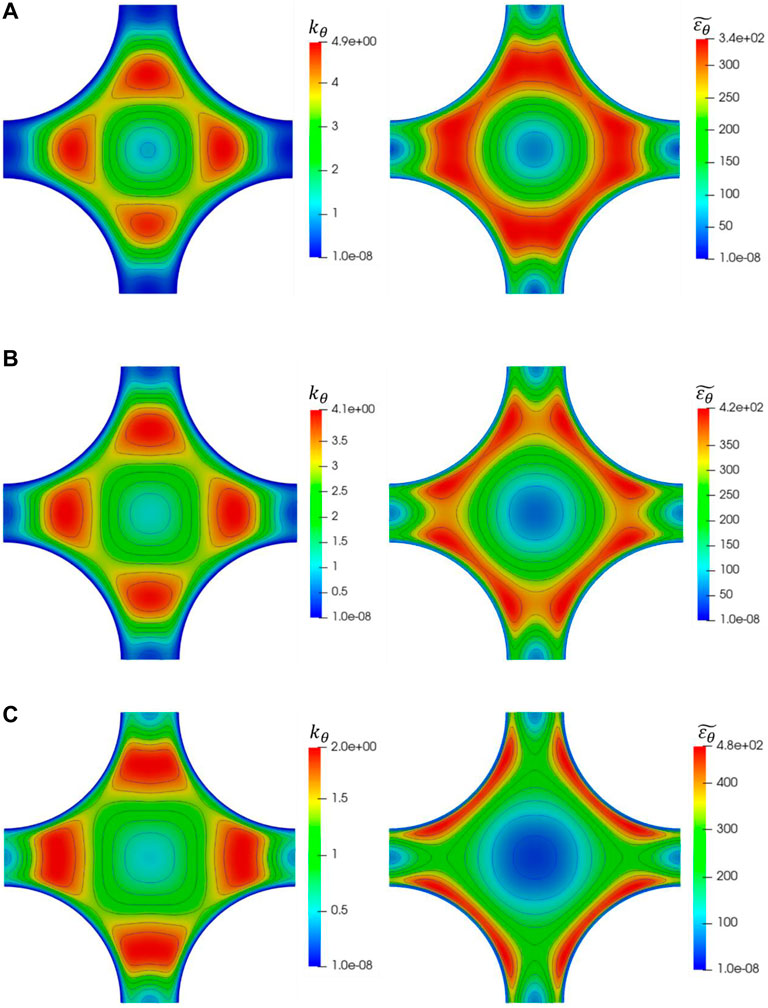
FIGURE 10. Schematic diagram of average temperature fluctuaion (left) and its isotropic dissipation (right) on a slice for square lattice X = 1.25. (A) Pe = 1000; (B) Pe = 2000; (C) Pe = 4000.
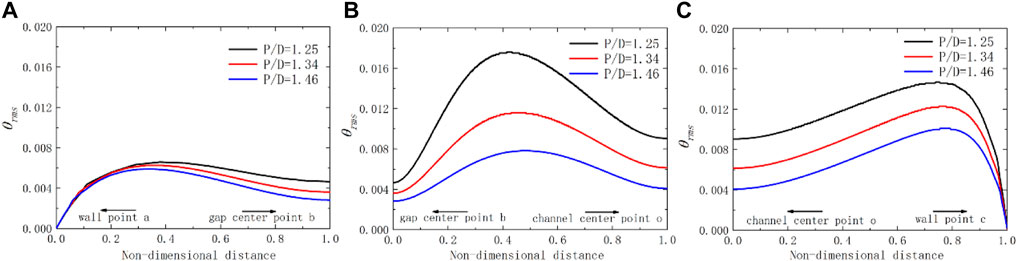
FIGURE 11. Schematic diagram of dimensionless temperature fluctuation over lines for the square lattice at Pe = 2000 with different P/D ratios. (A) line ab; (B) line bo; (C) line oc.
Figure 12 shows the proportional relationship of turbulent to molecular thermal diffusivity, that is, dimensionless thermal diffusivity
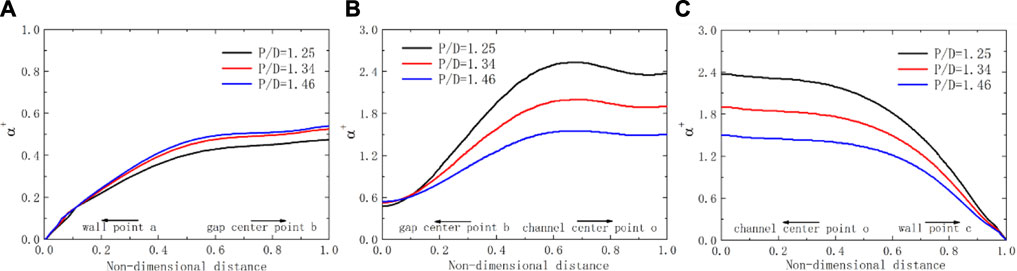
FIGURE 12. Schematic diagram of dimensionless thermal diffusivity over lines for the square lattice at Pe = 2000 with different P/D ratios. (A) line ab; (B) line bo; (C) line oc.
Thus, the specific value of turbulent to molecular thermal diffusivity represents the ratio of Reynolds to molecular heat flux. Reynolds heat flux is mainly caused by thermal diffusion caused by turbulent flow, while molecular heat conduction generates molecular heat flux. In Figure 12, in the area closest to the wall point a or c,
4) Turbulent Prandtl number
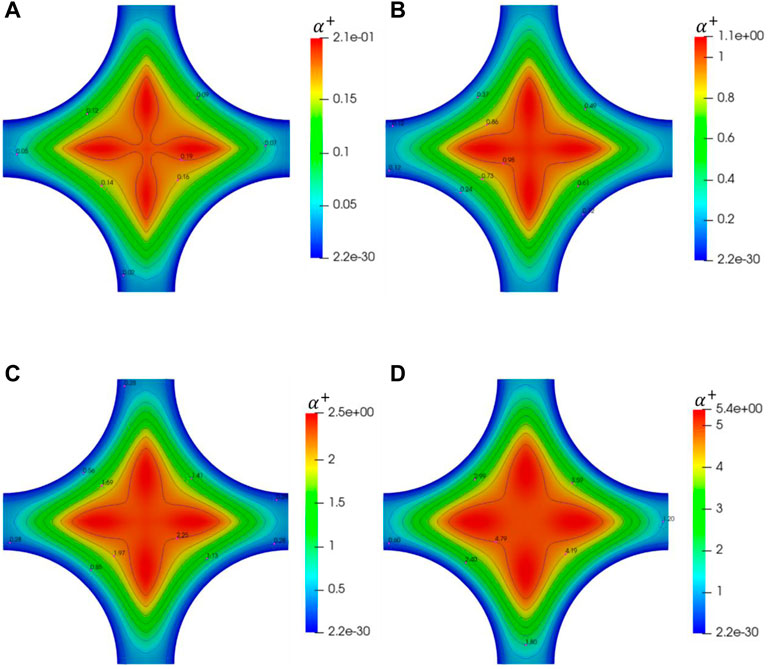
FIGURE 13. Schematic diagram of dimensionless thermal diffusivity on a slice for square lattice X = 1.25. (A) Pe = 250; (B) Pe = 1000; (C) Pe = 2000; (D) Pe = 4000.
In Figure 14, the Prt with the change of P/D is shown over the lines ab, bo, and oc for the square bundle with X = 1.25 at Pe =2000. The Prt is not constant and linear. It is larger than the general value of 0.85 for liquid metal. The Prt distribution on the line bo is to be smoother than that of lines ab and co. The value of Prt decreases over line ab when the value of P/D increases, while it increases over lines bo and oc. This phenomenon echoes the changing trend of dimensionless thermal diffusivity. In Figure 15, the turbulent Prandtl number on a slice for Pe = 1,000, 2000, and 4,000 for the square bundle is shown. When
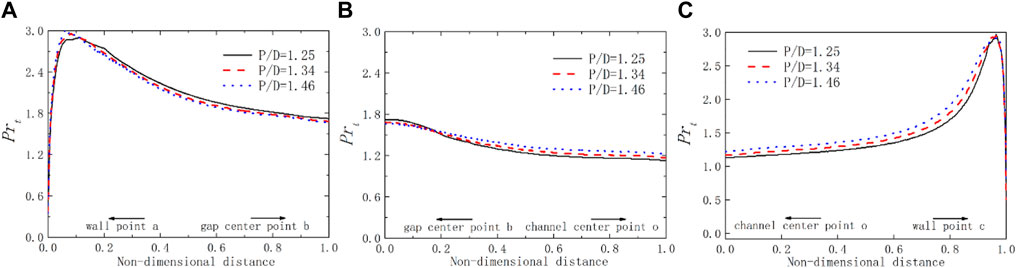
FIGURE 14. Schematic diagram of turbulent Prandtl number over lines for the square lattice at Pe = 2000 with different P/D ratios. (A) line ab; (B) line bo; (C) line oc.
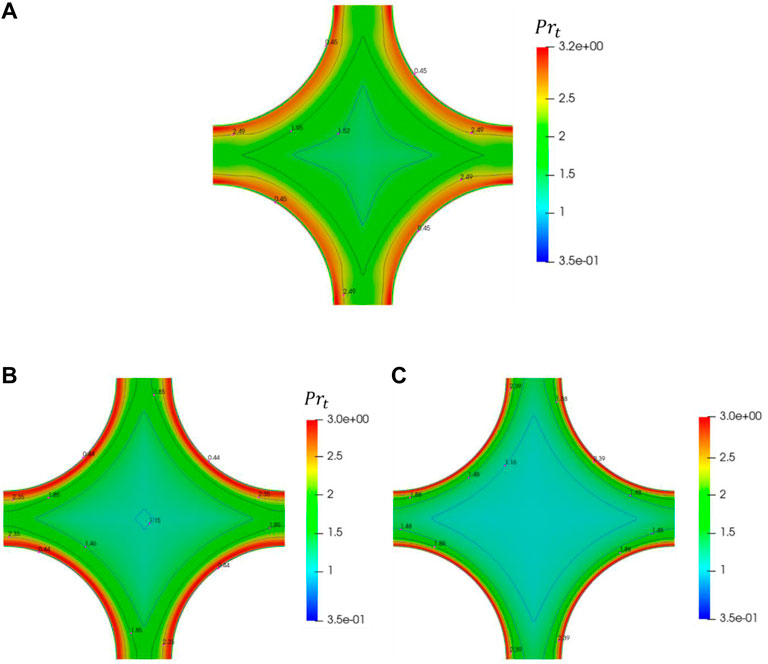
FIGURE 15. Schematic diagram of turbulent Prandtl number on a slice for square lattice X = 1.25. (A) Pe = 1000; (B) Pe = 2000; (C) Pe = 4000.
The average turbulent Prandtl number
Table 6 summarizes the calculation results of average turbulent Prandtl number
5) Performance analysis of the present four-equation model
When the same turbulence
4 Conclusion
The present work studied an isotropic four-equation model for low Pr number that uses simple Dirichlet wall boundaries. First, the turbulent heat transfer process of Pr = 0.01 ∼ 0.05 fluid in the uniformly heated plane is numerically studied on the open-source program OpenFOAM. Then the flow and heat of the isotropic four-equation of the quadrilateral infinite rod bundle region are evaluated and analyzed with low Prandtl number Pr = 0.01. In the SGDH framework, the Prt = 0.85 model and the isotropic four-equation model are compared with available experimental correlations in the range of Pe = 250–4,000 and P/D = 1.25–1.46. The numerical results show that.
1) The full development velocity, temperature, Reynolds stress, and Reynolds heat flow of Pr = 0.01 ∼ 0.05 fluid in-plane predicted using the isotropic four-equation model are in good agreement with the DNS results.
2) The Nu of the isotropic four-equation model lies between the experimental relationship, more conservative and similar to the Zhukov and BREST correlations for square rod bundles, while the Prt = 0.85 model gives too high a Nusselt number prediction to predict the integra heat properly. The slope of Nu predicted by the present isotropic four-equation model is similar to Manservisi’s model.
3) More detailed heat exchange phenomena and local temperature distribution are obtained using the four-equation model. At the same P/D, the average turbulent Prandtl number decreases with the increase in Pe, while at the same Pe, it increases when the value of P/D increases.
The isotropic four-equation model can provide more references for calculating the thermal-hydraulic phenomena of liquid metals. But its wider applicability needs further verification.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
XS: concept, research, writing, editing, code, and data processing. XL: modification, concept, research, and code. XW: research, modification, and code. YL: concept, editing, and research. QC: editing and research. QS: editing and research. XS: editing and research. GL: funding, project management, concept, and research.
Funding
This work was supported by the Research on key technology and safety verification of primary circuit, Grant No. 2020YFB1902104, and the Experimental study on thermal-hydraulics of fuel rod bundle, Grant No. Y828020XZ0.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abe, K., Kondoh, T., and Nagano, Y. (1995). A New Turbulence Model for Predicting Fluid Flow and Heat Transfer in Separating and Reattaching Flows-II. Thermal Field Calculations. Int. J. Heat Mass Transfer 38 (8), 1467–1481. doi:10.1016/0017-9310(94)00252-q
Adamov, E. O. (2001). Naturally Safe Lead-Cooled Fast Reactor for LargeScale Nuclear Power. Moscow: Dollezhal RDIPE.
Cerroni, D., Da Vià, R., Manservisi, S., Menghini, F., Pozzetti, G., and Scardovelli, R. (2015). Numerical Validation of Aκ-ω-Κθ-Ωθheat Transfer Turbulence Model for Heavy Liquid Metals. J. Phys. Conf. Ser. 655 (1), 012046. doi:10.1088/1742-6596/655/1/012046
Cheng, X., and Tak, N.-i. (2006). Investigation on Turbulent Heat Transfer to lead-bismuth Eutectic Flows in Circular Tubes for Nuclear Applications. Nucl. Eng. Des. 236 (4), 385–393. doi:10.1016/j.nucengdes.2005.09.006
Chierici, A., Chirco, L., Da Vià, R., and Manservisi, S. (2019). Numerical Simulation of a Turbulent Lead Bismuth Eutectic Flow inside a 19 Pin Nuclear Reactor Bundle with a Four Logarithmic Parameter Turbulence Model. J. Phys. Conf. Ser. 1224, 012030. doi:10.1088/1742-6596/1224/1/012030
Choi, S. K., and Kim, S. O. (2007). Treatment of Turbulent Heat Fluxes with the Elliptic-Blending Second-Moment Closure for Turbulent Natural Convection Flows. Int. J. Heat Mass Transfer 51 (9-10), 2377–2388. doi:10.1016/j.ijheatmasstransfer.2007.08.012
Da Vià, R., Giovacchini, V., and Manservisi, S. (2020). A Logarithmic Turbulent Heat Transfer Model in Applications with Liquid Metals for Pr = 0.01-0.025. Appl. Sci. 10 (12), 4337. doi:10.3390/app10124337
Da Vià, R., and Manservisi, S. (2019). Numerical Simulation of Forced and Mixed Convection Turbulent Liquid Sodium Flow over a Vertical Backward Facing Step with a Four Parameter Turbulence Model. Int. J. Heat Mass Transfer 135, 591–603. doi:10.1016/j.ijheatmasstransfer.2019.01.129
Da Vià, R., Manservisi, S., and Menghini, F. (2016). A K-Ω-Kθ-Ωθ Four Parameter Logarithmic Turbulence Model for Liquid Metals. Int. J. Heat Mass Transfer 101 (10), 1030–1041. doi:10.1016/j.ijheatmasstransfer.2016.05.084
Deng, B., Wu, W., and Xi, S. (2001). A Near-wall Two-Equation Heat Transfer Model for wall Turbulent Flows. Int. J. Heat Mass Transfer 44 (4), 691–698. doi:10.1016/s0017-9310(00)00131-9
Duponcheel, M., Bricteux, L., Manconi, M., Winckelmans, G., and Bartosiewicz, Y. (2014). Assessment of RANS and Improved Near-wall Modeling for Forced Convection at Low Prandtl Numbers Based on LES up to Reτ=2000. Int. J. Heat Mass Transfer 75, 470–482. doi:10.1016/j.ijheatmasstransfer.2014.03.080
Ejenstam, J., and Szakálos, P. (2015). Long Term Corrosion Resistance of Alumina Forming Austenitic Stainless Steels in Liquid lead. J. Nucl. Mater. 461, 164–170. doi:10.1016/j.jnucmat.2015.03.011
Ge, Z., Liu, J., Zhao, P., Nie, X., and Ye, M. (2017). Investigation on the Applicability of Turbulent-Prandtl-Number Models in Bare Rod Bundles for Heavy Liquid Metals. Nucl. Eng. Des. 314, 198–206. doi:10.1016/j.nucengdes.2017.01.032
Groetzbach, G. (2013). Challenges in Low-Prandtl Number Heat Transfer Simulation and Modelling. Nucl. Eng. Des. 264, 41–55. doi:10.1016/j.nucengdes.2012.09.039
Gu, L., and Su, X. (2021). Latest Research Progress for LBE Coolant Reactor of China Initiative Accelerator Driven System Project. Front. Energ. 15, 810–831. doi:10.1007/s11708-021-0760-1
Kawamura, H., Abe, H., and Matsuo, Y. (1999). DNS of Turbulent Heat Transfer in Channel Flow with Respect to Reynolds and Prandtl Number Effects. Int. J. Heat Fluid Flow 20 (3), 196–207. doi:10.1016/s0142-727x(99)00014-4
Kawamura, H., Ohsaka, K., Abe, H., and Yamamoto, K. (1998). DNS of Turbulent Heat Transfer in Channel Flow with Low to Medium-High Prandtl Number Fluid. Int. J. Heat Fluid Flow 19 (5), 482–491. doi:10.1016/s0142-727x(98)10026-7
Kays, W. M. (1994). Turbulent Prandtl Number-Where Are We? Asme Trans. J. Heat Transfer 116 (2), 284–295. doi:10.1115/1.2911398
Lai, Y. G., and So, R. M. C. (1990). Near-wall Modeling of Turbulent Heat Fluxes. Int. J. Heat Mass Transfer 33 (7), 1429–1440. doi:10.1016/0017-9310(90)90040-2
Manservisi, S., and Menghini, F. (2014a). A CFD Four Parameter Heat Transfer Turbulence Model for Engineering Applications in Heavy Liquid Metals. Int. J. Heat Mass Transfer 69 (2), 312–326. doi:10.1016/j.ijheatmasstransfer.2013.10.017
Manservisi, S., and Menghini, F. (2015). CFD Simulations in Heavy Liquid Metal Flows for Square Lattice Bare Rod Bundle Geometries with a Four Parameter Heat Transfer Turbulence Model. Nucl. Eng. Des. 295 (12), 251–260. doi:10.1016/j.nucengdes.2015.10.006
Manservisi, S., and Menghini, F. (2014b). Triangular Rod Bundle Simulations of a CFD κ-ϵ-κ-ϵ Heat Transfer Turbulence Model for Heavy Liquid Metals. Nucl. Eng. Des. 273, 251–270. doi:10.1016/j.nucengdes.2014.03.022
Mikityuk, K. (2009). Heat Transfer to Liquid Metal: Review of Data and Correlations for Tube Bundles. Nucl. Eng. Des. 239 (4), 680–687. doi:10.1016/j.nucengdes.2008.12.014
Moukalled, F., Mangani, L., and Darwish, M. (2016). The Finite Volume Method in Computational Fluid Dynamics. Berlin: Springer International Publishing.
Nagano, Y., Hattori, H., and Abe, K. (1997). Modeling the Turbulent Heat and Momentum Transfer in Flows under Different thermal Conditions. Fluid Dyn. Res. 20 (1-6), 127–142. doi:10.1016/s0169-5983(96)00049-4
Nagano, Y., and Kim, C. (1988). A Two-Equation Model for Heat Transport in Wall Turbulent Shear Flows. J. Heat Transfer 110 (3), 583–589. doi:10.1115/1.3250532
Nagano, Y., and Shimada, M. (1996). Development of a Two‐equation Heat Transfer Model Based on Direct Simulations of Turbulent Flows with Different Prandtl Numbers. Phys. Fluids 8 (12), 3379–3402. doi:10.1063/1.869124
Reynolds, A. J. (1975). The Prediction of Turbulent Prandtl and Schmidt Numbers. Int. J. Heat Mass Transfer 18 (9), 1055–1069. doi:10.1016/0017-9310(75)90223-9
Schroer, C., Wedemeyer, O., Skrypnik, A., Novotny, J., and Konys, J. (2012). Corrosion Kinetics of Steel T91 in Flowing Oxygen-Containing lead–bismuth Eutectic at 450 °C. J. Nucl. Mater. 431 (1-3), 105–112. doi:10.1016/j.jnucmat.2011.11.014
Shams, A., De Santis, A., and Roelofs, F. (2019). An Overview of the AHFM-NRG Formulations for the Accurate Prediction of Turbulent Flow and Heat Transfer in Low-Prandtl Number Flows. Nucl. Eng. Des. 355, 110342. doi:10.1016/j.nucengdes.2019.110342
Shikazono, N., and Kasagi, N. (1996). Second-moment Closure for Turbulent Scalar Transport at Various Prandtl Numbers. Int. J. Heat Mass Transfer 39 (14), 2977–2987. doi:10.1016/0017-9310(95)00339-8
Su, X. K., and Gu, L. (2021). Numerical Study on Turbulent Heat Transfer of LBE in an Annulus Based on A Four-Equation Model. Chinese Beijing: Atomic Energy Science and technology. Avaialbe at: http://kns.cnki.net/kcms/detail/11.2044.TL.20210720.181. doi:10.13832/j.jnpe.2021.S1.0026
Su, X. K., Gu, L., Peng, T. J., Jiatai, L., Xianwen, L., and Guan, W. (2021). Research on a Four-Equation Model Based on OpenFOAM. Nucl. Power Eng. 42 (S1), 26–32. (in chinese).
Subbotin, V. I., Ushakov, P. A., and Kirillov, P. L. (1965). “Heat Transfer in Elements of Reactors with a Liquid Metal Coolant,” in Proceedings of the 3rd International Conference on Peaceful Use of Nuclear Energy, Geneva, 192–200.
Tiselj, I., and Cizelj, L. (2012). DNS of Turbulent Channel Flow with Conjugate Heat Transfer at Prandtl Number 0.01. Nucl. Eng. Des. 253 (1), 153–160. doi:10.1016/j.nucengdes.2012.08.008
Wang, G., Gu, L., and Yun, D. (2021). Preliminary Multi-Physics Performance Analysis and Design Evaluation of UO2 Fuel for LBE-Cooled Subcritical Reactor of China Initiative Accelerator Driven System. Front. Energ. Res. doi:10.3389/FENRG.202110.3389/fenrg.2021.732801
Weller, H. G., Tabor, G., Jasak, H., and Fureby, C. (1998). A Tensorial Approach to Computational Continuum Mechanics Using Object-Oriented Techniques. Comput. Phys. 12 (6), 620–631. doi:10.1063/1.168744
You, B. H., Jeong, Y. H., and Addad, Y. (2019). Assessment of Advanced RANS Models Ability to Predict a Turbulent Swept Liquid Metal Flow over a Wire in a Channel. Nucl. Eng. Des. 353 (Nov), 1102061–11020614. doi:10.1016/j.nucengdes.2019.110206
Youssef, M. S. (2006). A Two-Equation Heat Transfer Model for wall Turbulent Shear Flows. J. Eng. Sci. 34 (6), 1877–1903. doi:10.21608/jesaun.2006.111184
Keywords: low Pr fluid, four-equation, OpenFOAM, heat transfer, liquid metal
Citation: Su X, Li X, Wang X, Liu Y, Chen Q, Shi Q, Sheng X and Gu L (2022) Development and Assessment of an Isotropic Four-Equation Model for Heat Transfer of Low Prandtl Number Fluids. Front. Energy Res. 10:816560. doi: 10.3389/fenrg.2022.816560
Received: 16 November 2021; Accepted: 14 January 2022;
Published: 08 February 2022.
Edited by:
Wei Ding, Helmholtz Association of German Research Centres (HZ), GermanyReviewed by:
Yacine Addad, Khalifa University, United Arab EmiratesLuteng Zhang, Chongqing University, China
Copyright © 2022 Su, Li, Wang, Liu, Chen, Shi, Sheng and Gu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Long Gu, Z3Vsb25nQGltcGNhcy5hYy5jbg==
 Xingkang Su
Xingkang Su Xianwen Li1,2
Xianwen Li1,2 Long Gu
Long Gu