A Stable Condition and Adaptive Diffusion Coefficients for the Coarse-Mesh Finite Difference Method

1 Introduction

The convergence rate (Kuzmin, 2010) of the source iteration (SI) (Adams and Larsen, 2002; Li et al., 2015b) is often low when solving the reactor neutron transport problem. Many acceleration methods (Adams and Larsen, 2002; Willert et al., 2014) have been developed to accelerate the iteration process, such as the extrapolation methods, the Krylov subspace methods, and the high-order/low-order (HOLO) methods which are usually found to be the most efficient (Kuzmin, 2010; Willert et al., 2014). Here, the HOLO methods refer to a series of acceleration methods with the same internal logic that employs proper coupling between high-order discretization and low-order discretization to obtain high-order accuracy and high convergence rate, such as the multigrid method (Wesseling, 1995), the partitioned-matrix (PM) method (Li et al., 2015b), the diffusion synthetic acceleration (DSA) method (Alcouffe, 1977), the coarse-mesh finite difference (CMFD) method (Smith, 2002), and so on (Adams and Larsen, 2002; Zhang, et al., 2018). Among them, the CMFD method and other similar methods which employ the neutron diffusion approximation for the low-order discretization are widely used in solving the reactor neutron transport problem (Smith, 2002; Lee et al., 2014; Zhang et al., 2019; Xu et al., 2020; Hao et al., 2021; Chan and Xiao, 2021; Zhao et al., 2022; Zhou et al., 2022) in recent years. However, the traditional CMFD method tends to fail due to iterative divergence for reactors with optically thick regions.

By reducing the coarse mesh size of the diffusion problem, increasing the number of transport sweeps, and adding over relaxation factors (Li et al., 2015a; Jarrett et al., 2016), the stability (Kuzmin, 2010) of CMFD can be improved to a certain extent. Compared with the traditional CMFD method, the pCMFD method and its variants (Yuk and Cho, 2017; Zhang et al., 2019) have improved stability by using partial neutron currents to calculate the coupling factors between high-order discretization and low-order discretization. The artificially diffusive CMFD (adCMFD) (Jarrett et al., 2016) and the optimally diffusive CMFD (odCMFD) (Zhu et al., 2016) can also improve the stability of the traditional CMFD method by improving the diffusion coefficients. The lpCMFD (Wang and Xiao, 2018; Wang and Zhu, 2021) method improves the stability of CMFD by flux prolongation. Some analyses of the variants of CMFD are available (Zhu, et al., 2017; Wang and Zhu, 2021). The IFDF (Xu, et al., 2020; Xu, et al., 2022) method adopts a coupling scheme different from the CMFD method and adaptively adjusts the diffusion coefficients during the iterative process, which was found to have better stability than the CMFD and adCMFD.

A stability principle, sign preservation rule (Tao, 2001) also known as the positive coefficients rule (Patankar, 1980), is required to obtain a stable discrete scheme in the field of numerical heat transfer. Its connotation is that the positive disturbance introduced at any grid should have a positive impact on other grids, which is physically reasonable. Considering the CMFD method, we found that the traditional CMFD equation could not physically reflect the response relationship between neutron currents and neutron fluxes, which was believed to be at least one main reason that causes the divergence of the iterative acceleration process.

In this paper, the condition for diffusion coefficients at the mesh surface is derived to keep the positive correlation between the neutron current and the negative values of the flux gradient by observing the sign preservation rule, the adaptive diffusion coefficient equation for the CMFD method is proposed, and the traditional CMFD method is revised as the rCMFD method. The theoretical derivation is presented in Section 2, the numerical results of different acceleration methods for three fast reactor problems obtained by modifying the hexagonal pitches of a small fast reactor benchmark problem are presented in Section 3, and the discussion and conclusion of this work are presented in Section 4.

2 Theoretical Derivation

2.1 Source Iteration

For high-order discretization, the discrete orders of spatial and angular dimensions of the neutron transport equation are high enough to give high accuracy. Taking the S_N method based on hexagonal-Z meshes as an example, the k-eigenvalue problem can be written as

$\mathit{L}\mathit{\psi }=\mathit{S}\mathit{\varphi }+\frac{\mathbf{1}}{\mathit{k}}\mathit{F}\mathit{\varphi },(1)$

where $L$ is the neutron leakage matrix, $\psi$ is the angular flux vector of every energy group, every spatial moment, and every discrete angle, $S$ is the neutron scattering matrix, $\varphi$ is the scalar flux vector, $k$ is the eigenvalue, and $F$ is the neutron fission matrix. The scalar flux vector could be calculated by the angular flux vector with

$\mathit{\varphi }=\mathit{T}\mathit{\psi },(2)$

where $T$ is a matrix to calculate the scalar flux vector $\varphi$ with the angular flux vector $\psi$. Eqs 1, 2 constitute the k-eigenvalue equations with high-order discretization, which could be solved by the classical power iteration also known as fission SI for the reactor problem:

${\mathit{\psi }}^{\left(\mathit{n}\right)}=\frac{\mathbf{1}}{{\mathit{k}}^{\left(\mathit{n}-\mathbf{1}\right)}}{\left(\mathit{L}-\mathit{S}\mathit{T}\right)}^{-\mathbf{1}}\mathit{F}{\mathit{\varphi }}^{\left(\mathit{n}-\mathbf{1}\right)},(3)$

${\mathit{\varphi }}^{\left(\mathit{n}\right)}=\mathit{T}{\mathit{\psi }}^{\left(\mathit{n}\right)},(4)$

$k^{\left(n\right)}=k^{\left(n-1\right)}\frac{\langle \mathit{F}{\varphi }^{\left(n\right)}\rangle }{\langle \mathit{F}{\varphi }^{\left(n-1\right)}\rangle },(5)$

where the superscript (n) or (n-1) is the iteration index and the symbol $\langle \rangle$ means integration over the phase space with the energy, angular, and spatial dimensions. The dimension of the matrix $\left(L-ST\right)$ is usually very large, and its inverse is usually not conducted by direct matrix operation but achieved by transport sweeps of every mesh, angle, and energy group for the S_N method.

2.2 Traditional Coarse-Mesh Finite Difference Method

The stability of source iteration is good, but the convergence rate is usually low especially for large reactor problems. The CMFD acceleration method is commonly used in the solution of the S_N k-eigenvalue problem. In the process of source iteration, the k-eigenvalue problem of transport corrected finite difference diffusion equation (low-order discretization) is solved to correct the high-order iterative variables.

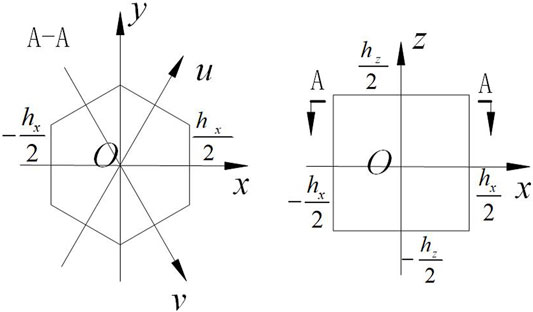
For a hexagonal-Z mesh as illustrated in Figure 1, the low-order neutron balance equation for every group to be solved can be written as

${\displaystyle {\sum }_{d=v,x,u,z}\left(J_{K_d+1/2}-J_{K_d-1/2}\right)}{A}_{K_d}+{\Sigma }_{r,K}{\varphi }_K{V}_K=Q_K{V}_K,(6)$

where $d$ is the dimension index with the possible values of v, x, u, z as illustrated in Figure 1, $J_{K_d\pm 1/2}$ is the normal neutron current at the mesh surface indexed by $K_d\pm 1/2$, $A_{K_d}$ is the surface area of mesh K along dimension d, ${\Sigma }_{r,K}$ is the removal cross section of mesh K, ${\varphi }_K$ is the scalar neutron flux of mesh K, $V_K$ is the volume of mesh K, and $Q_K$ is the neutron source of mesh K including the fission source and scattering source from other groups.

FIGURE 1

FIGURE 1. Illustration of a hexagonal-Z mesh.

For the CMFD method, the neutron currents and neutron fluxes in Eq. 6 are related by the transport corrected Fick’s law. For an inner mesh surface,

$J_{K_d+1/2}=-\frac{D_{K_d+1/2}}{h_{K_d+1/2}}\left({\varphi }_{K_d+1}-{\varphi }_K\right)-\frac{r_{K_d+1/2}}{h_{K_d+1/2}}\left({\varphi }_{K_d+1}+{\varphi }_K\right),(7)$

where

$D_{K_d+1/2}=\frac{2D_K{D}_{K_d+1}{h}_{K_d+1/2}}{h_{K_d}{D}_{K_d+1}+h_{K_d+1}{D}_K},(8)$

$r_{K_d+1/2}=-\frac{h_{K_d+1/2}{J}_{K_d+1/2}^{SN}+D_{K_d+1/2}\left({\varphi }_{K_d+1}^{SN}-{\varphi }_K^{SN}\right)}{{\varphi }_{K_d+1}^{SN}+{\varphi }_K^{SN}},(9)$

$h_{K_d+1/2}=\frac{1}{2}\left(h_{K_d}+h_{K_d+1}\right),(10)$

where $D_{K_d+1/2}$ is the common diffusion coefficient at the mesh surface, $r_{K_d+1/2}$ is the transport correction factor, h is the mesh size, and the superscript SN means the value is from the high-order transport calculation. For the boundary cases, take the mesh surface in the positive coordinate direction of mesh K as an example:

$J_{K_d+1/2}=\frac{D_{K_d+1/2}}{h_{K_d+1/2}}{\varphi }_K-\frac{r_{K_d+1/2}}{h_{K_d+1/2}}{\varphi }_K,(11)$

where

$D_{K_d+1/2}=\frac{2D_K{\alpha }_{K_d+1/2}{h}_{K_d}}{{\alpha }_{K_d+1/2}{h}_{K_d}+2D_K},(12)$

$r_{K_d+1/2}=-\frac{h_{K_d+1/2}{J}_{K_d+1/2}^{SN}-D_{K_d+1/2}{\varphi }_K^{SN}}{{\varphi }_K^{SN}},(13)$

in which ${\alpha }_{K_d+1/2}$ is the boundary parameter and equals 0 for the reflective boundary condition and 0.5 for the vacuum boundary condition.

Eqs 6–13 and the boundary equations for other cases constitute the coarse-mesh finite difference equations and can be solved with a linear solver for every group. Then, the low-order k-eigenvalue problem could be solved by source iteration or other more efficient algorithms. Details of the solution algorithm for the linear system with low-order discretization are not to be introduced here for simplicity. Finally, the iterative variables including k and scalar fluxes from high-order discretization are to be corrected:

$k=k^{DIF},(14)$

${\varphi }_{i,K}={\varphi }_{i,K}^{SN}\frac{{\varphi }_K^{DIF}}{{\varphi }_{0,K}^{SN}},i\ge 0,(15)$

where the superscript DIF means the value is the solution of the diffusion problem and the subscript $i$ is the expansion order of the spatial moment for the nodal S_N method.

2.3 A Stable Condition and Adaptive Diffusion Coefficients

The convergence rate of the CMFD method is usually high. However, the stability of the CMFD method is a problem for the transport problem with optically thick regions. Let us check the CMFD equations from the stability rule in the field of numerical heat transfer. For an inner mesh surface, the traditional Fick’s law without transport correction can be written as follows:

$J_{K_d+1/2}{h}_{K_d+1/2}=-{\varphi }_{K_d+1}{D}_{K_d+1/2}+{\varphi }_K{D}_{K_d+1/2}.(16)$

It is seen that the mesh-surface diffusion coefficient $D_{K_d+1/2}$ is always positive from Eq. 8, which means that $J_{K_d+1/2}$ will always decrease when ${\varphi }_{K_d+1}$ increases and always increase when ${\varphi }_K$ increases. This phenomenon obeys the physical law of diffusion and should be established in the transport corrected cases. Let us check the case of CMFD by rewriting Eq. 7 for inner mesh surfaces as follows:

$J_{K_d+1/2}{h}_{K_d+1/2}=-{\varphi }_{K_d+1}\left(D_{K_d+1/2}+r_{K_d+1/2}\right)+{\varphi }_K\left(D_{K_d+1/2}-r_{K_d+1/2}\right).(17)$

From Eqs 8, 9 it is seen that the coefficient $\left(D_{K_d+1/2}+r_{K_d+1/2}\right)$ of ${\varphi }_{K_d+1}$ and the coefficient $\left(D_{K_d+1/2}-r_{K_d+1/2}\right)$ of ${\varphi }_K$ are not guaranteed to be always positive, which means that the physical law of diffusion could not be guaranteed. So, the following conditions are required:

$D_{K_d+1/2}+r_{K_d+1/2}>0,(18)$

and

$D_{K_d+1/2}-r_{K_d+1/2}>0.(19)$

After substituting Eq. 9 into Eqs 18, 19, the condition becomes

$D_{K_d+1/2}>\frac{h_{K_d+1/2}}{2}\max \left(-\frac{J_{K_d+1/2}^{SN}}{{\varphi }_{K_d+1}^{SN}},\frac{J_{K_d+1/2}^{SN}}{{\varphi }_K^{SN}}\right).(20)$

Then, let us check Eq. 11 for the boundary cases; the following condition is obtained with similar derivation to the case of inner mesh surfaces:

$J_{K_d+1/2}^{SN}>0.(21)$

This condition is always met for the vacuum boundary condition. For the reflective boundary condition, nothing is required to meet the diffusion law since $J_{K_d+1/2}\equiv 0$. If the boundary surface is in the negative coordinate direction of mesh K, the response condition between the mesh-surface current and the mesh flux is also always met. All in all, only the condition of Eq. 20 of the inner mesh surface is necessary.

An interesting thing was found that Eq. 20 was very similar to the stability equation of the IFDF method (Xu et al., 2020; Xu et al., 2022) which had been found to be more stable than the traditional CMFD method and the adCMFD method for a large fast reactor core. For one-dimensional (1D) meshes, the stability condition of the IFDF method is

$D_K>\frac{h_K}{2}\max \left(-\frac{J_{K_d-1/2}^{SN}}{{\varphi }_K^{SN}},\frac{J_{K_d+1/2}^{SN}}{{\varphi }_K^{SN}}\right).(22)$

The difference is in the subscripts, and the condition for the diffusion coefficient at the mesh surface becomes the condition for the diffusion coefficient in the mesh.

In order to guarantee the condition in Eq. 20, Eq. (8) is modified to the following equation of adaptive diffusion coefficient:

$D_{K_d+1/2}=\max \left[\frac{2D_K{D}_{K_d+1}{h}_{K_d+1/2}}{h_{K_d}{D}_{K_d+1}+h_{K_d+1}{D}_K},\frac{c{h}_{K_d+1/2}}{2}\max \left(-\frac{J_{K_d+1/2}^{SN}}{{\varphi }_{K_d+1}^{SN}},\frac{J_{K_d+1/2}^{SN}}{{\varphi }_K^{SN}}\right)\right],(23)$

where c is an additional damping parameter which should be larger than 1. With c larger than 1, Eq. 23 gives a conservative condition to satisfy Eq. 20, and a larger value of c tends to increase the stability but decrease the convergence rate from our numerical tests. A value of 5 is recommended for c referring to the IFDF method and will be employed in the numerical tests of next section. When Eq. 20 is met, the traditional mesh-surface diffusion coefficient in Eq. 8 is employed to guarantee diagonal dominance of the low-order linear system, which will improve the solution speed of the low-order linear system; when Eq. 20 is not met, Eq. 23 will adaptively abandon Eq. 8 and employ a more conservative mesh-surface diffusion coefficient equation in Eq. 23 to meet the stable condition of Eq. 20.

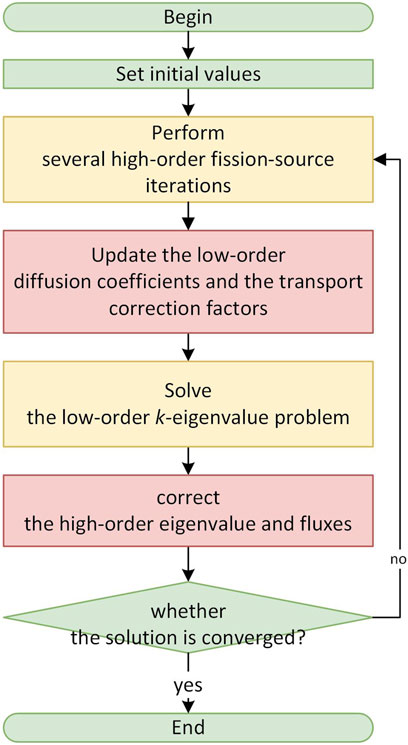
Employing Eq. 23, the traditional CMFD method is improved to the revised CMFD (rCMFD) method. Few changes are needed to modify a CMFD acceleration process to an rCMFD acceleration process. What we should do is to replace Eq. 8 with Eq. 23 and update the mesh-surface diffusion coefficients before solving the low-order k-eigenvalue problem. The process of the rCMFD method is illustrated in Figure 2.

FIGURE 2

FIGURE 2. Flowchart of the rCMFD acceleration method.

3 Numerical Results

3.1 Description of the Tests

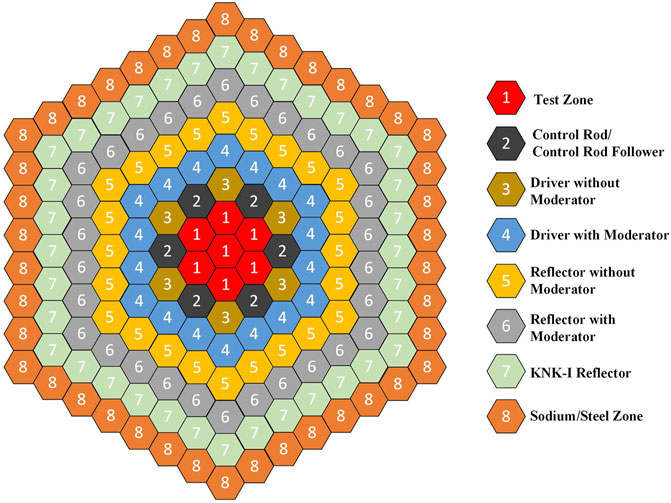
Three fast reactor core problems were employed to test the methods. The first one (core 1) is a small fast reactor benchmark problem with hexagonal assemblies (Takeda and Ikeda, 1991). The hexagonal pitches are 12.9904 cm, and the total height of the model is 190 cm. Four-group cross sections are provided by the benchmark for different regions of the core. The case of half-inserted control rods is employed. The radial layout of the core is presented in Figure 3. The second one (core 2) and the third one (core 3) are obtained by changing the hexagonal pitches of core 1 to 50 and 100 cm, respectively, which may be not very rational for reactor design but helpful to test the convergence of numerical methods for problems with optically thick meshes.

FIGURE 3

FIGURE 3. Radial layout of the small fast reactor core.

The three problems have been calculated by the DNTH (Wang et al., 2020) solver in the NECP-SARAX (Zheng et al., 2018) code system with different methods including pure fission-source iteration (SI), fission-source iteration with CMFD acceleration (SI-CMFD), fission-source iteration with adCMFD ($\eta =1/4$) acceleration (SI-adCMFD), fission-source iteration with odCMFD acceleration (SI-odCMFD), fission-source iteration with IFDF acceleration (SI-IFDF), and fission-source iteration with rCMFD acceleration (SI-rCMFD). The NECP-SARAX code system is a code system developed at Xi’an Jiaotong University for the neutronics analysis of advanced fast-spectrum reactors or facilities. The DNTH solver is an S_N nodal transport solver in NECP-SARAX for hexagonal-Z meshes with the capacity of large-scale parallel computing.

For all the cases, S₄ Legendre–Chebyshev angular quadrature was used; the number of hexagonal-Z meshes was $169\times 33$; the nodal interior variables were expanded with second-order polynomials; the nodal surface variables were expanded with first-order polynomials; the fission-source iteration criterion of high-order discretization was $1\times {10}^{-5}$; the scattering-source iteration criterion of high-order discretization was $5\times {10}^{-6}$; an iteration limit of 5 was employed for the inner scattering-source iteration; the fission-source iteration criterion of low-order discretization was $2.5\times {10}^{-6}$; one low-order linear system was solved before four high-order fission-source iterations were performed. All the calculations were performed on 2.0 GHz AMD Ryzen PRO 2500U w CPU core.

3.2 Results for Different Cases

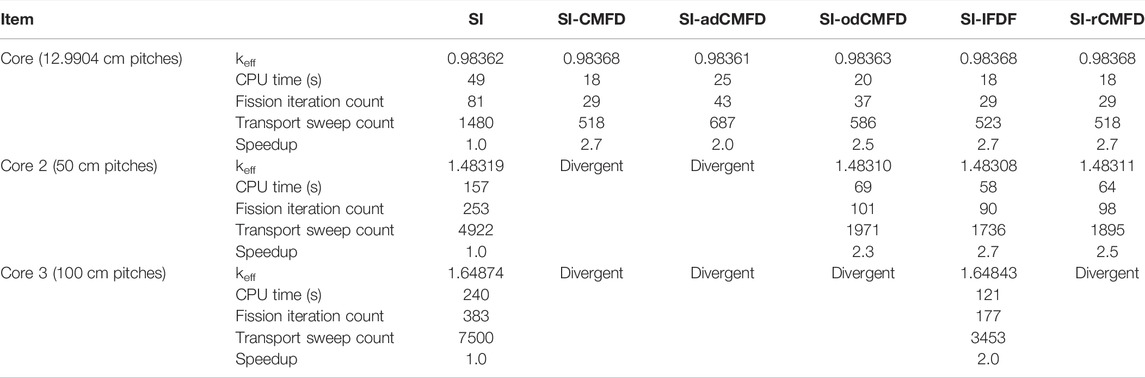
The results for the three reactor cores are presented in Table 1. In the table, one transport sweep means one update of all the mesh angular fluxes within one group, which is the main part of the time-consuming calculations, and the speedups are obtained by comparing the CPU time of every method with that of the SI scheme.

TABLE 1

TABLE 1. Numerical results of the tests for different methods.

As shown in Table 1, for core 1, the radial hexagonal pitches were 12.9904 cm, and every method could give a convergent result; there were some deviations between the k_eff of different methods, which was caused by the different convergence degrees of the inner scattering-source iteration; the speedup of SI-rCMFD was 2.7, which was higher than those of adCMFD and odCMFD and close to those of SI-CMFD and SI-IFDF. For core 2, the radial hexagonal pitches were 50 cm, SI-CMFD and SI-adCMFD failed to converge, while SI, SI-odCMFD, SI-IFDF, and SI-rCMFD proposed in this work still could give convergent results; the speedup of SI-rCMFD for core 2 was 2.5, which was a bit lower than 2.7 of SI-IFDF but higher than 2.3 of odCMFD. For core 3, the radial hexagonal pitches were 100 cm, SI-rCMFD also failed to converge, and only SI and SI-IFDF could give convergent results.

4 Discussion and Conclusion

After numerical tests of three fast reactor problems with different radial hexagonal pitches from 12.9904 to 100 cm by different acceleration methods, the advantages and limitations of the proposed rCMFD method were clarified. It was seen that the adaptive diffusion coefficients of this work were helpful to improve the stability of the traditional CMFD method without obvious loss of the convergence rate, and the improvement was even higher than those of the adCMFD method and the odCMFD method which had been found to be more stable than the traditional CMFD method. However, the rCMFD method failed for the third core with radial hexagonal pitches of 100 cm, while the IFDF method still could give a convergent result with a speedup of 2.0, which indicated that the rCMFD was still not unconditionally stable and the stable region was narrower than that of the IFDF method although the adaptive diffusion coefficient equations were similar for the rCMFD and IFDF. The inferiority of the rCMFD method compared with the IFDF method may be due to the fact that Fick’s law correction formula of the IFDF method is derived from the interface discontinuity relationship with clear physical significance, but Fick’s law correction formula of rCMFD is based on a heuristic hypothesis as the traditional CMFD method.

It is concluded that the stable condition derived in this work is necessary for the CMFD stability but perhaps not sufficient for unconditional stability, and the adaptive diffusion coefficients can effectively improve the stability of the traditional CMFD method without obvious loss of the convergence rate. Further research on spectral radius analysis of the rCMFD method and comparison between different methods is expected, which may enlighten sufficient stable conditions or higher improvements of the CMFD method.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, and further inquiries can be directed to the corresponding author.

Author Contributions

ZX performed the methods and presented the results. HW supervised the work. YZ and QZ were advisers.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer TZ is currently organizing a research topic with the author QZ.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

This study was inspired by Professor Wenquan Tao’s lecture on numerical heat transfer at Xi’an Jiaotong University. And we are very grateful to the reviewers for their helpful suggestions on this article.

References

Adams, M. L., and Larsen, E. W. (2002). Fast Iterative Methods for Discrete-Ordinates Particle Transport Calculations. Prog. Nucl. energy 40 (1), 3–159. doi:10.1016/S0149-1970(01)00023-3

CrossRef Full Text | Google Scholar

Alcouffe, R. E. (1977). Diffusion Synthetic Acceleration Methods for the Diamond-Differenced Discrete-Ordinates Equations. Nucl. Sci. Eng. 64 (2), 344–355. doi:10.13182/NSE77-1

CrossRef Full Text | Google Scholar

Chan, Y., and Xiao, S. (2021). Numerical Stability Analysis of Lp-CMFD Acceleration for the Discrete Ordinates Neutron Transport Calculation Discretized with Discontinuous Galerkin Finite Element Method. Ann. Nucl. Energy 153, 108036. doi:10.1016/j.anucene.2020.108036

CrossRef Full Text | Google Scholar

Hao, C., Liu, L., Kang, L., and Xu, Y. (2021). An Efficient Hybrid Multi-Level CMFD in Space and Energy for Accelerating the High-Fidelity Neutron Transport Calculation. Ann. Nucl. Energy 161, 108446. doi:10.1016/j.anucene.2021.108446

CrossRef Full Text | Google Scholar

Jarrett, M., Kochunas, B., Zhu, A., and Downar, T. (2016). Analysis of Stabilization Techniques for CMFD Acceleration of Neutron Transport Problems. Nucl. Sci. Eng. 184 (2), 208–227. doi:10.13182/NSE16-51

CrossRef Full Text | Google Scholar

Kuzmin, D. (2010). A Guide to Numerical Methods for Transport Equations. Erlangen, Germany: Friedrich–Alexander University Erlangen–Nürnberg.

Google Scholar

Lee, M. J., Joo, H. G., Lee, D., and Smith, K. (2014). Coarse Mesh Finite Difference Formulation for Accelerated Monte Carlo Eigenvalue Calculation. Ann. Nucl. Energy 65, 101–113. doi:10.1016/j.anucene.2013.10.025

CrossRef Full Text | Google Scholar

Li, L. L., Smith, K. S., and Forget, B. (2015a). Techniques for Stabilizing Coarse-Mesh Finite Difference (CMFD) in Methods of Characteristics (MOC). Nashville, TN: ANS M&C2015.

Google Scholar

Li, Y., Wang, Y., Liang, B., and Shen, W. (2015b). Partitioned-matrix Acceleration to the Fission-Source Iteration of the Variational Nodal Method. Prog. Nucl. Energy 85, 640–647. doi:10.1016/j.pnucene.2015.08.001

CrossRef Full Text | Google Scholar

Patankar, S. V. (1980). Numerical Heat Transfer and Fluid Flow. Boca Raton, FL: CRC Press.

Google Scholar

Smith, K. S. (2002). Full-core, 2-D, LWR Core Calculations with CASMO-4E. Seoul, Korea: PHYSOR 2002.

Google Scholar

Takeda, T., and Ikeda, H. (1991). 3-D Neutron Transport Benchmarks. J. Nucl. Sci. Technol. 28 (7), 656–669. doi:10.1080/18811248.1991.9731408

CrossRef Full Text | Google Scholar

Tao, W. (2001). Numerical Heat Transfer. Xi'an, China: Xi'an Jiaotong University Publishing Company.

Google Scholar

Wang, D., and Xiao, S. (2018). A Linear Prolongation Approach to Stabilizing CMFD. Nucl. Sci. Eng. 190 (1), 45–55. doi:10.1080/00295639.2017.1417347

CrossRef Full Text | Google Scholar

Wang, D., and Zhu, Z. (2021). A Revisit to CMFD Schemes: Fourier Analysis and Enhancement. Energies 14 (2), 424. doi:10.3390/en14020424

CrossRef Full Text | Google Scholar

Wang, Y., Xu, Z., Zheng, Y., and Wu, H. (2020). A New Hexagonal-Z Nodal SN Method in SARAX Code System. Ann. Nucl. Energy 144, 107546. doi:10.1016/j.anucene.2020.107546

CrossRef Full Text | Google Scholar

Wesseling, P. (1995). Introduction to Multigrid Methods (No. NASA-CR-195045). Hampton, VA: NASA Langley Research Center.

Google Scholar

Willert, J., Park, H., and Knoll, D. A. (2014). A Comparison of Acceleration Methods for Solving the Neutron Transport K -eigenvalue Problem. J. Comput. Phys. 274, 681–694. doi:10.1016/j.jcp.2014.06.044

CrossRef Full Text | Google Scholar

Xu, Z., Zheng, Y., Wang, Y., and Wu, H. (2020). IFDF Acceleration Method with Adaptive Diffusion Coefficients for SN Nodal Calculation in SARAX Code System. Ann. Nucl. Energy 136, 107056. doi:10.1016/j.anucene.2019.107056

CrossRef Full Text | Google Scholar

Xu, Z., Zheng, Y., and Wu, H. (2022). An IFDF Accelerated Parallel Nodal SN Method for XYZ Geometry in SARAX Code System. Ann. Nucl. Energy 166, 108710. doi:10.1016/j.anucene.2021.108710

CrossRef Full Text | Google Scholar

Yuk, S., and Cho, N. Z. (2017). Two-level Convergence Speedup Schemes for P-CMFD Acceleration in Neutron Transport Calculation. Nucl. Sci. Eng. 188 (1), 1–14. doi:10.1080/00295639.2017.1332891

CrossRef Full Text | Google Scholar

Zhang, G., Hsieh, A., Yang, W. S., and Jung, Y. S. (2019). Consistent pCMFD Acceleration Schemes of the Three-Dimensional Transport Code PROTEUS-MOC. Nucl. Sci. Eng. 193, 828–853. doi:10.1080/00295639.2018.1560854

CrossRef Full Text | Google Scholar

Zhang, T., Wu, H., Cao, L., and Li, Y. (2018). Acceleration of 3D Pin-By-Pin Calculations Based on the Heterogeneous Variational Nodal Method. Ann. Nucl. Energy 114, 165–174. doi:10.1016/j.anucene.2017.12.012

CrossRef Full Text | Google Scholar

Zhao, W., Chai, X., Zhang, B., Liu, J., Peng, X., Li, T., et al. (2022). A Nodal Method Based on CMFD for Pin-By-Pin SP3 Calculation. Ann. Nucl. Energy 167, 108849. doi:10.1016/j.anucene.2021.108849

CrossRef Full Text | Google Scholar

Zheng, Y., Du, X., Xu, Z., Zhou, S., Liu, Y., Wan, C., et al. (2018). SARAX: A New Code for Fast Reactor Analysis Part I: Methods. Nucl. Eng. Des. 340, 421–430. doi:10.1016/j.nucengdes.2018.10.008

CrossRef Full Text | Google Scholar

Zhou, X., Liu, Z., Cao, L., and Wu, H. (2022). Convergence Analysis for the CMFD Accelerated 2D/1D Neutron Transport Calculation Method Based on Fourier Analysis. Ann. Nucl. Energy 170, 108982. doi:10.1016/j.anucene.2022.108982

CrossRef Full Text | Google Scholar

Zhu, A., Jarrett, M., Xu, Y., Kochunas, B., Larsen, E., and Downar, T. (2016). An Optimally Diffusive Coarse Mesh Finite Difference Method to Accelerate Neutron Transport Calculations. Ann. Nucl. Energy 95, 116–124. doi:10.1016/j.anucene.2016.05.004

CrossRef Full Text | Google Scholar

Zhu, A., Kochunas, B., Xu, Y., Jarrett, M., Larsen, E., and Downar, T. (2017). Theoretical Convergence Rate Lower Bounds for Variants of Coarse Mesh Finite Difference to Accelerate Neutron Transport Calculations. Nucl. Sci. Eng. 186 (3), 224–238. doi:10.1080/00295639.2017.1293408

CrossRef Full Text | Google Scholar