- Shenzhen Polytechnic, Shenzhen, China
Emergency voltage control provides a real-time online response to maintain the long-term voltage stability of a power system. Searching for an optimal emergency control solution is a hard combinatorial optimization problem because of the highly dynamic and nonlinear characteristics of power systems with discrete control variables. Additionally, real-time response is required. A new mode-matching–based adaptive voltage control is proposed in this article to achieve a fast response by exploring local voltage profile modes and the technique of similarity ranking. First, some typical emergencies are studied in advance, and their control knowledge is collected for preparation. The set of local voltage profile modes and their corresponding optimal control solutions are stored as knowledge for each emergency. Second, fast online control is realized and the control solution is configured according to a similarity ranking among local voltage profile modes. Furthermore, a learning process is applied to accumulate knowledge in case of unprepared situations. Thus, improved control performances in the future are ensured. This article depends on a new concept of local voltage profile mode with which knowledge preparation, emergency identification, configuration of control, and knowledge accumulation work together to perform an effective response. Simulations of the IEEE 39-bus system verify the outcomes of this voltage control scheme.
Introduction
Modern power systems have become more complex with the interconnection of grids and the employment of new devices and techniques. Voltage stability depends on the ability of the combined generation and transmission systems to provide the power requested by loads (Hatziargyriou et al., 2020).
Toward low-carbon and economic operation of power systems, various renewable power generations, such as wind and PVs, have been integrated in a distributed manner (Guo et al., 2019; Li et al., 2020; Magnusson et al., 2020; Zhang et al., 2021). Voltage stability has been greatly challenged by the increasing penetration of distributed generation and intermittent renewable power sources. Researchers have paid close attention to voltage control to mitigate or avoid voltage instabilities (Yorino et al., 2015; Liu et al., 2017).
The common mechanism of long-term voltage instability is the progressive drop of bus voltages and even collapse after emergencies. An emergency control is the last safety enforcement measure to mitigate voltage instability, where control devices typically involve tap changers, switching capacitors, and load shedding. The research scope of this study is an emergency voltage control that concerns the optimization of coordinating various control devices.
Performing real-time optimization is difficult as power systems are extremely complex and dynamic. There are unpredictable uncertainties with operational point variations, structural changes, and even element failures. An adaptation is therefore necessary and adopted with voltage control that an adjustment mechanism is always applied to follow the changes or uncertainties of the controlled system.
Different from model-based adaptive control, data-driven adaptation techniques have attracted much attention (Zhang and Liu, 2008; Bu et al., 2017; Bu et al., 2018; Cai et al., 2020; Huang et al., 2020; Li et al., 2021). When the system models are complicated with exceedingly high order or high nonlinearity, a data-driven control can provide sufficiently good solutions in a reasonable time, based on a large amount of system data without involving the accurate system models. The consensus control of multi-agent systems is proposed to realize model-free adaptive control schemes (Bu et al., 2017; Bu et al., 2018). At the same time, many research efforts on model-free adaptive control techniques have been applied to achieve power system control. Intelligent learning control methods have been adopted to reveal the implicit features of system dynamics and find out the relationship between emergencies and controls (Huang et al., 2020; Li et al., 2021).
Applying data-driven adaptive schemes that are dependent on knowledge gathering, learning, and updating is possible with the development of computing and storing techniques. In terms of voltage control, knowledge may be gathered and accumulated explicitly by expert systems or fuzzy logic systems (Zhang and Liu, 2008) and implicitly by modern heuristic techniques and artificial neural networks. The principal component analysis is used to extract features, and then a map between the control solutions and system dynamics is established by a neural network (Cai et al., 2020).
With the increasing of system scales, there is a conflict between detecting and transferring full system information and a fast response speed. In this article, a new mode-matching–based adaptive voltage control (MMAVC) is proposed such that a fast online response is reached by means of local voltage profile modes (LVPM) and similarity ranking. In contrast to full system voltage profiles (Zhang and Liu, 2008; Cai et al., 2020), the LVPM only concerns local bus voltages for each control device. The aim is to present an algorithm that has reduced computation and is a good candidate for larger systems.
First, a part of the system knowledge is gathered and prepared off-line for typical emergencies with long-term global search. System knowledge is stored as LVPM of a set of emergencies and the corresponding optimal control solutions. LVPM are defined as the emergency mode and the associated controller mode which are used for emergency identification and control action identification, respectively. Second, according to the similarity between a saved emergency mode of LVPM to the current situation, the control action of each control device is reconfigured to form a new control solution and applied online with real-time response. A distance function is defined to measure the similarity between emergencies.
Besides, the stored knowledge is accumulated and updated online with a learning process such that the operational point variations and structural changes can be adaptively followed. For new cases, while no similar mode can be found, an online optimal search is used to obtain knowledge and is saved for future applications. With the process of preparation, configuration, and accumulation of knowledge, an efficient emergency voltage control is realized with a fast and gradually improved response.
As a data-driven–based adaptive control scheme, we have suggested an approach which shares the same control aim of an emergency control, but explores two main differences with present techniques:
1) The detection and perception of a voltage emergency are associated with control devices and their local voltage profiles. The monitored and concerned systems are thus narrowed down to a limited area. At the same time, a distributed control by which only local information is involved can be further developed based on this research.
2) In the previously mentioned data-driven–based works, researchers preferred to map controls and system states with machine learning techniques, thus the acquired knowledge is implicitly stored and hard to be adjusted. The technique of similarity ranking used in this study is an explicit exploration of knowledge that the distance between two faults is evaluated by a comparison between bus voltage profiles. The accumulation, adjustment, and updating of the knowledge base are thus performed in a much clear and easy way that no more training processes are required.
The rest of this article is organized as follows: the optimal coordinated voltage control (OCVC) is described in the Optimal Coordinated Voltage Control section. The section Mode-Matching Adaptive Voltage Control gives details of our MMAVC. A case study of the IEEE 39-bus power system tested is reported in the Simulation Results section. The conclusion is drawn in the Conclusion section.
Optimal Coordinated Voltage Control
Voltage stability refers to the ability of a power system to keep the voltage profiles of all buses within acceptable ranges after an emergency (Hatziargyriou et al., 2020). Thus, a set of optimal arrangements of voltage control devices with sequencing, timing, and tuning values for maintaining system voltage stability need to be provided by a coordinated voltage control scheme.
System Models and Simulation
A power system is an interconnected complex network. For voltage stability, the power system models can be expressed in the following hybrid differential–algebraic (DA) form (Hatziargyriou et al., 2020):
where
In terms of voltage control, the discrete control variables are used to represent control devices, such as tap changers, switching capacitors, and load shedding, which can be adjusted at discrete times. The optimal program is used to achieve the appropriate scheduling and subsequent operation of these discrete control devices. As a result, the system output represented by
Time-domain simulation is the main method to study the effectiveness of voltage controls, including dynamics. For long-term voltage instability, the quasi-steady-state (QSS) approximation is sufficient to capture the essential behavior of the system by neglecting the derivative terms in the generator mechanical and flux equations (Van Cutsem et al., 2006). In this article, the QSS simulation is performed to capture the dynamic process after an emergency, and the aggregate exponential recovery load model proposed by Hill (1993) is employed.
Model Predictive Control–Based Optimal Coordinated Voltage Control
Power systems are dynamic in the sense that the operational points and even the structure of the system may vary from time to time. An optimal control at one time instant might not be optimal at another time instant and is thus insufficient to follow the dynamic changes. In order to tackle these kinds of issues, model predictive control (MPC) (Larsson et al., 2002) is proposed, which is an advanced control scheme that has been widely applied in the process control of complex industrial systems.
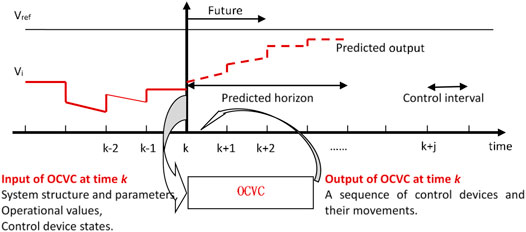
The possible output is predicted after selecting the input from candidate control solutions depending on the current model and states of the dynamic system. After comparing the predicted outputs of a set of candidate control solutions, the optimal solution that meets the objectives is applied to the system for the incoming control interval. Then, the predictive control window is moved to the next control interval, and all the system models and states are reevaluated (Figure 1).
For the study of voltage stability, the control target of the MPC is to keep the bus voltages at an expected level. The objective function can be defined as:
where
We consider a step at time k after an emergency event. With the objective of Eq. 2, the calculation steps of the MPC-based optimal coordinated voltage control are as follows:
Step a. Gathering input signals: the system information at time k is obtained as the input signal, including system parameters, operational values, and control device states.
Step b. Searching for optimal solution: the candidate control solutions, each of which contains a set of movements of a group of control devices, are generated. The predicted output of each candidate solution is simulated according to the system status, models, and input parameters with QSS approximate technique. Then, the control performance of the candidate control solutions is compared with their objective values
Step c. Applying control: the solution with the smallest value of
Step d. Waiting for the new incoming control interval and repeat from Step a.An emergency voltage control should meet all the search constraints and provide fast and effective controls within one control interval. A new adaptive control is proposed in this study, which continuously improves its control performance by accumulating the system knowledge from both off-line preparation and online learning.
Mode-Matching Adaptive Voltage Control
As knowledge plays a key role in the data-driven adaptive voltage control, a new way of defining system knowledge in terms of modes is proposed. An adjustment mechanism works in adaptive control to provide adaptations that meet the uncertainties of a system. Thus, the technique of LVPM and the adjustment mechanism, which is realized by a learning scheme, are applied for real-time control and knowledge accumulation.
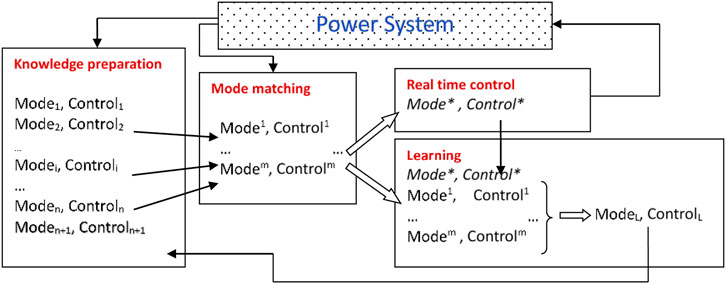
There are four basic functional parts of an MMAVC (Figure 2):
1) Knowledge preparation (off-line): a preparation for online control is applied to obtain a part of the knowledge. Some typical emergencies are triggered in the power system. An optimal control solution is searched and saved with its identification, i.e., a set of local voltage profile mode.
2) Mode matching (online): when voltage instability is detected in the power system, the LVPM are compared with the saved modes in the knowledge base. All the LVPM in the database are sequenced and ranked according to their closeness to the current mode.
3) Real-time control (online): a control solution is configured by combining the control actions from the controls of high-ranking modes. This step can be quickly realized and thus provides an instantaneous control to the system.
4) Learning for knowledge accumulation (online): a learning scheme is applied by an online optimal search to provide the adaptation to new situations and system dynamics. It is a global search guided by controls of high-ranking saved modes. After this learning search, the obtained optimal control is saved with its LVPM. Thus, the stored knowledge is updated and is gradually accumulated.
The details are presented in the following subsections for each of the four functional parts and the definition of LVPM.
Knowledge Preparation
An off-line long-term search is applied to search for optimal solutions for MPC-based coordinated voltage control. Modern heuristic algorithms have been proved to be easily applied for combinatorial optimization problems. We use the genetic algorithms (GA) for advantages of visiting wide areas in the solution space.
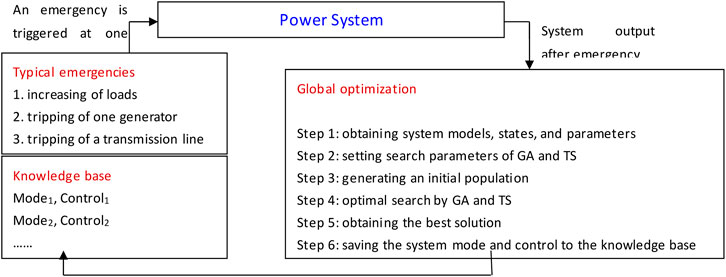
Long-term voltage instability is always triggered by outage of transmission and/or generation equipment after fault clearing when the load dynamics attempts to restore power consumption beyond the maximum power transfer limit (Hatziargyriou et al., 2020). Thus, an abnormal increase of loads and failure of generators or transmission lines are collectively regarded as typical emergencies. The control knowledge of these types of emergencies is optimally searched and stored as the basic preparation for online control.
Each of the typical emergencies is triggered in a studied power system (Figure 3). The system models, states, and parameters after an emergency are the inputs for the optimizer. A global long-term search by GA is applied. The optimal solution searched is saved with its LVPM after the emergency. A trade-off happens between online performance and off-line calculation burdens. More off-line preparations are preferred to obtain good start-up control performance.
Standard GA is a well-developed technique. An integer encoding where all the control devices are involved is used for GA optimal search (Table 1). If there are r, s, and t on-load tap changers (OLTCs), capacitors, and load shedding, respectively, their movement steps of control are stored in integer numbers to form a chromosome. For OLTCs, the values of STEPLTCi can be –1, 0, and 1. The movement steps for capacitors and load shedding can be an integer from −Smax to Smax, where Smax is the maximum possible movement steps of a control device.
After a search, the details concerning an emergency, specifically the LVPM and an optimal control solution, are obtained and can be formatted as off-line knowledge.
Local Voltage Profile Mode
With increasing system scales, it is time-consuming and even impossible to monitor and gather excessive system information. An emergency representation by which only the local voltage deviations to each control device are involved is studied to alleviate these issues.
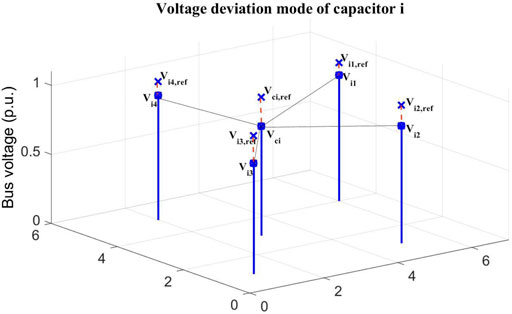
The LVPM are defined by the voltage deviation of the neighborhood of control devices. A neighborhood includes buses that are geographically closed to the device. Without losing generality, a neighborhood is defined by buses that are directly connected to a control device in this study.
As in Table 2, a transformer is connected between two buses while the neighborhood has all the connected buses for capacitors and loads as they are located on one bus. The number of buses connected to the capacitors and loads is from k = 2 to k = 6 in most practical cases.
The value of voltage deviation is calculated by subtracting the bus voltage from its reference value.
where
The neighborhood can be extended to include more buses that cover a wide area of a power system. A trade-off happens between the covered area of a neighborhood and calculation complexities. More system voltage information can be involved by extending the neighborhood. However, the complexity of the storing structure, saving and extracting schemes, and online exploring strategies increases accordingly.
The LVPM surrounding a control device are referred to as the controller mode, which presents a shape of voltage changes among a set of connected buses of the device. Each column of Table 2 is a controller mode. Figure 4 shows four buses that are directly connected to bus i, where capacitor i is located. Before the emergency, the bus voltages are the references for mode calculation. Vci,ref and Vi1,ref to Vi4,ref are all the reference values of bus i and buses i1 to i4, respectively. Once an emergency occurs, a voltage deviation occurs and the differences between the current values to the reference values are marked in red dashed lines. These five deviation values are stored in the knowledge base as the controller mode of capacitor i.
A set of controller modes form an emergency mode and map to a voltage instability emergency. The emergency mode contains a set of controller modes of all control devices in a power system. It will be used to match and rank close emergencies, configure an online control solution, and provide guidance to the online learning process.
For each emergency studied off-line, the LVPM, i.e., emergency mode i, together with the optimal control solution acquired via search, control i, are the knowledge stored for online applications.
Mode Matching and Ranking
Mode matching compares two emergency modes and discovers similar controller mode pieces. A sequence of emergency modes and control solutions is thus ranked according to their similarities to the current situation.
Immediately after an emergency is detected and the bus voltages deviate from their original values, the LVPM can be obtained and compared with the stored knowledge. Mode matching aims to obtain the similarities between two situations and discover a sequence of emergency modes according to their distance from the current situation.
Considering the limited experiences saved in the knowledge base and the huge number of possible voltage profiles after emergencies, two emergency modes that are the same may not always exist. A voltage control should be active enough to ensure system stability while avoiding excessive action. A normalization is applied where the real number values of voltage deviation are transformed into integer values. A tolerance threshold is also suggested to ignore small turbulence and avoid excessive activation.
The setup of tolerance threshold and normalization can be chosen according to the control preferences of operators, or by referring to the learning outcomes of voltage instability criteria. If the voltage deviation is within the tolerance threshold, no matter whether it is higher or lower than its original value, the normalized value of voltage deviation is 0. If the deviation of a bus voltage is greater than the threshold, then it is normalized into integral values in [−Vint, Vint].
The values of Vint show a set of voltage ranges that reflect the confidence of knowledge preparation. At the initial stage when MMAVC is applied online, a normalization scheme with smaller ranges, e.g., Vint = 2 or Vint = 3, can be adopted because insufficient knowledge is available and the opportunity of using these saved experiences should not be missed. A simple normalization may set Vint = 1 (Table 3). After online running, further knowledge can be acquired. The normalization ranges should be expanded with a larger value of Vint by which a more accurate comparison can be reached.
We assume that there are n saved emergency modes, h control devices in the system, and kj buses connected to the control device j, j = 1, …, h. When an emergency occurs online, the emergency mode is normalized as:
where the emergency mode and controller mode are represented by a capital letter,
The set of saved emergency modes is normalized as:
where
A comparison between the current situation,
where
It is a summary of voltage deviations for all connected buses,
If
The one with the least value of
After mode matching and ranking, the stored knowledge is sequenced according to their similarity to the current situation, and the same pieces of controller mode are identified in each saved emergency mode.
Real-Time Online Control
According to the ranks and the identified similar controller modes, an online control solution can be configured by combining the control pieces of the saved control solutions. It begins from the saved emergency mode which has
If the control solution is not fully developed, then the next emergency mode and its control solution are considered. The control pieces are only used to fill in the blank places for the unresolved parts. As an example (Table 4), a total of five saved emergency modes are ranked according to their values
Due to the incompleteness of the emergency mode M1, the saved emergency mode M2 is then considered. Three controller modes, i.e., C6, C7, and C8, are identified similarly to the current situation. Only C7 and C8 of M2 are used because C6 is already occupied by the control piece from M1. Next, the control action of C4 and C10 are adopted by the new control solution. None of the control actions of M4 participate in this new control solution because C1 and C10 of the new control solution have already been fulfilled. Finally, if full control cannot be reached, e.g., in this case, the place of C9 does not obtain values from any of the ranked emergency modes, then the control action of this place is left blank with its original value.
The following steps constitute the process of configuring a control solution:
Step 1. Setting initial parameters: Nrank = 1 and a blank control solution,
Step 2. Obtaining knowledge: the set of LVPM and their control solutions are obtained from the knowledge base.
Step 3. Ranking emergency modes: the comparison index,
Step 4. Identifying similar control modes: the similar control mode, which has
Step 5. Obtaining control action: the emergency mode with ranking = Nrank, and its control solution is selected. The control actions of the identified similar controller modes are adopted and saved into the corresponding places of
Step 6. Moving to next emergency mode: Nrank = Nrank + 1.
Step 7. Checking stopping criteria: if there are places in
Step 8. Obtaining full solution: if
Step 9. Applying control solution: the newly obtained control solution
Learning-Based Adaptation
To meet the dynamics of power systems, the stored knowledge should be accumulated and updated online. A learning scheme is adopted to provide the adaptation. After the control system is applied to provide online services, the learning process is triggered to acquire new knowledge and adjust knowledge from past experiences. Learning is applied when no identical emergency mode is found in the knowledge base. It allows more feasible solutions to be visited in an expanded area of solution space.
When an emergency happens, the LVPM, i.e., the ongoing emergency mode, are initially compared with emergency modes saved in the knowledge base. If no matching emergency mode, i.e.,
The learning search is realized by the population-based modern heuristic optimization algorithms. The standard GA is utilized for knowledge preparation. Unlike random offline long-term search, the learning search depends on past experiences and attempts to obtain an improved knowledge base.
For GA optimal search, half of the population of the initial generation is obtained from the control solutions stored in the knowledge base. The percentage of the acquired knowledge usage is flexible and can be adjusted according to the confidence of knowledge. When more emergencies are studied and saved in the database, the use of acquired experiences increases accordingly.
The selection and employment of saved emergency modes are based on their ranks. The roulette wheel selection is used to pick up individuals of the initial population. More initial individuals are generated by the control solutions of the emergency mode with lower values of
Based on this initial generation, an optimal search by standard GA is applied. After one run of optimal search, the obtained optimal solution is saved into the knowledge based on the form of LVPM and an optimal control solution. As the learning search is only adopted for knowledge accumulation and runs a background operation, it can be a long-term search to reach a preferred result.
Generally, the novelty of the MMAVC lies in the improved searching, storage, and online exploring efficiency. First, the monitored area of the LVPM is narrowed down to controller buses and their neighboring buses for online real-time control. Second, each snapshot of an emergency is contributed to the knowledge base in terms of the LVPM that the mode matching and ranking can be applied directly to and does not require any further training processes.
Simulation Results
The proposed MMAVC is demonstrated via an emergency voltage control in the New England 39-bus power system (Figure 5) (Ma et al., 2008). A total of 12 OLTCs and 19 load shedding are used. There are 17 capacitors arranged for each bus with load shedding except two generator buses. The OLTCs can be adjusted every 30 s and can move one step from the original position.
In practice, OLTCs and switching capacitors can be controlled such that the interval between two consecutive actions must be longer than the execution time. Load shedding is activated only when the required constraint cannot be satisfied by using any combination of the regular control devices.
The off-line knowledge preparation of an emergency is presented in the Knowledge Preparation section. The online real-time control of an unprepared emergency is described in the Online Control With Mode Matching section. For unprepared situations, online learning is activated, and the process of knowledge learning is demonstrated in the Learning for Knowledge Accumulation and Updating section.
Knowledge Preparation
For knowledge preparation, typical emergencies of abnormal increase of loads or failure of connected devices are considered. A total of four kinds of emergencies are gathered: 1) tripping of a generator; 2) tripping of a transmission line; 3) variation of a load; and 4) simultaneous variations of all loads.
A total of 9 generators, 46 transmission lines, and 19 loads comprise this system. The emergency of variation of one load is represented by a scaling parameter of 0.5 and 1.5 to simulate either decreasing or increasing loads, respectively. The simultaneous variations of all loads are set by multiplying the parameters of the loads ranging from 0.6 to 1.1 in a step size of 0.1. Tripping of Generator 31 is excluded because bus 31 is the swing bus for QSS simulation. The transmission lines with OLTCs are not involved because they are control devices waiting to be optimized. As a result, a total of 86 emergencies can be readily studied with an off-line long-term search.
Following the calculation steps in Figure 3, each emergency is activated in the IEEE 39-bus system. After 30 s of operation, one emergency is triggered. A detection time of 30 s is applied; an emergency control is started from 60 s. All the control devices are arranged with the same active time of 30 s. Thus, the possible activation times of the control devices are 60, 90, 120 s, and so on.
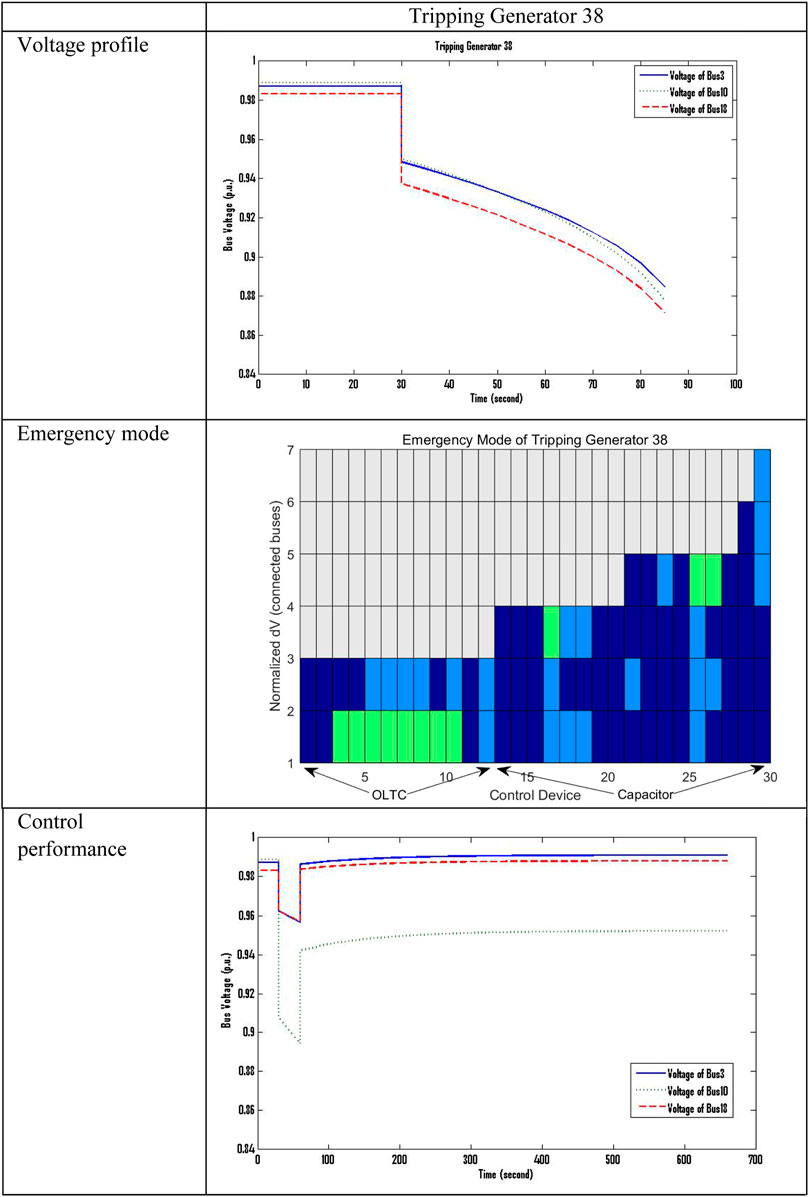
One emergency of tripping a generator is presented for demonstration in Figure 6. After the emergency of Tripping Generator 38 happens at 30 s, a blackout occurred for about 90 s.
The emergency mode is normalized into integers in the range of [−2, 2], whereas the threshold is set as 0.01 p.u. Each emergency mode is presented as a color map. Dark blue, blue, green, yellow and red corespond to integer values of −2 to 2, respectively. The horizontal axes indicate the number of control devices, including OLTCs and capacitors. For a proof of concept presentation, the controller modes of load shedding are not listed as they are not triggered in this case.
An emergency mode is a snapshot of the voltage deviation profile of an emergency. With the increasing system scales, the involved control devices are sparse and not evenly distributed in the system. In most cases, load shedding is not involved in optimal searched control solutions. Instead of full system models and operation states, the captured emergency mode is in a reduced representation by which a limited area of the system is considered.
A long-term search by GA is applied for 10 times of running with a population size of 200 and the maximum generation of 200. For each emergency, the searching time is approximately 160 min by using MATLAB and an Intel 3.4-GHz processor for simulation. The control performances are as presented in Figure 6. Both the searched control solution and its LVPM are saved in a long-term knowledge base.
Online Control With Mode Matching
After an off-line knowledge preparation, the MMAVC is applied online for emergency voltage control. When a prepared situation happens, a saved emergency mode is then identified and its corresponding control is adopted and applied to the system with no delay. If it is not a prepared emergency, mode matching, ranking, and configuration of control need to be applied.
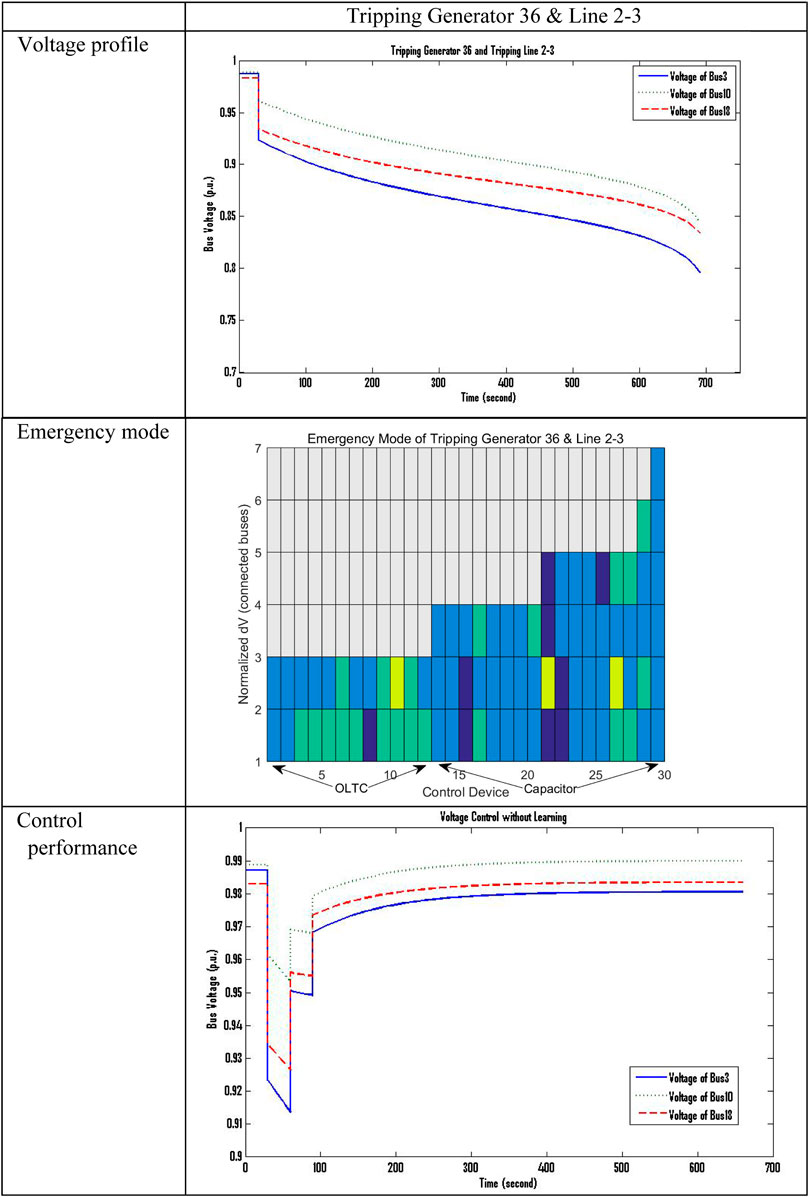
An emergency of simultaneously tripping two elements is used to demonstrate an unexpected situation. The testing scenario of an unexpected emergency is Tripping Generator 36 and Tripping Line 2, 3 together at 30 s. Voltage deviations are triggered, and a collapse occurs at approximately 700 s (Figure 7). The emergency mode after normalization is shown in a colormap.
The processes of mode matching and ranking are applied according to the predicted system output. For the first control interval, three saved emergency modes contribute to constructing the new emergency mode. These emergencies are Tripping of Lines 2, 3, Tripping of Lines 19–16, and Tripping of Lines 22–21, respectively, which share 16, 16, and 9 same controller modes and have ranks of 1, 2, and 10 among all control devices. In this case, the emergency modes which are ranked from 3 to 9 are not adopted because the same controller modes are covered by the top two ranked emergency modes. Accordingly, a set of control pieces are identified and form a new control solution.
In this example, the control solution is simply composed of three saved controller modes. For voltage instability, an emergency is always triggered by a lack or imbalance of reactive power. To adjust the reactive power, a voltage control shows a localized characteristic. For knowledge preparation, possible emergencies within a wide area of the system had been studied. Thus, a geographically close emergency can always be obtained.
After 30 s of detection, the emergency controls are generated and applied at the time instants 60 and 90 s. The knowledge-based control requires two control intervals for voltage recovery. It has a faster system response within only 1 s.
Learning for Knowledge Accumulation and Updating
After an unexpected emergency is detected, a learning process is triggered simultaneously. The initial population for a learning search is partly generated from saved knowledge. A population of 100 and a maximum generation of 100 are used in this case. It takes 4 min for each run of search.
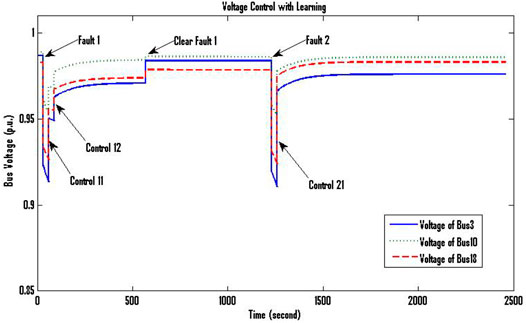
The testing scenario of learning control is designed in a way that an unexpected emergency of Tripping Generator 36 and Lines 2, 3 simultaneously happens twice at the time instants 30 and 1,230 s, respectively (Figure 8). The emergency at the time instant 30 s is cleared at 570 s.
When the first emergency happens, i.e., Fault 1, the control solution is configured through mode matching and ranking within saved knowledge. It takes two intervals of control, Control 11, and Control 12, to recover system voltages. A learning process is completed before the second emergency happens, i.e., Fault 2. When the same emergency happens again at the 1,230 s, the control performance is improved that only one control interval is performed. The bus voltages are recovered in the first control interval by Control 21.
After an emergency happens the LVPM and newly searched control solution is saved directly to improve the knowledge base. There are no more training efforts needed. In this example case, a piece of knowledge can be explored and applied shortly after its first occurrence. This feature of MMAVC achieves the advantage of accumulating knowledge quickly.
Conclusion
A novel adaptive voltage control scheme for the power system, namely mode-matching–based adaptive voltage control (MMAVC) is proposed in this article. Emergencies are identified in terms of their local voltage profile, named as emergency mode and controller mode. First, some possible emergencies are studied off-line with long-term global search. Their emergency modes and optimal control solutions are stored for knowledge preparation. Second, an online control solution is formed by mode matching, ranking, and similarity measurement that provides fast control with good system performance. Furthermore, a learning search is used for knowledge accumulation and updating. The experiments show that the control performance can be gradually improved, which is demonstrated in the response to the control.
This MMAVC has the following features and may inspire future research:
1) The knowledge used in this study involves LVPM which only concerns local voltage profiles surrounding control devices and the searched optimal control solution. The stored knowledge base can be easily updated with newly tested cases, and no further training is required.
2) A novel mode-matching scheme was developed for instant control. It provides adaptations meeting structural changes and operating point variations.
3) An off-line long-term search scheme was used for control knowledge preparation, while an online control performance is improved gradually with the learning scheme.
4) An interesting direction of this study for the future may lie in the sensitivity of the covered area of LVPM, the seriousness of uncertainties, and even the arrangement and distribution of control devices. Starting from this point, it also warrants further study for a distributed voltage control scheme.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.
Author Contributions
HM contributed to the main conception and analysis frame of this study. GW gave constructive discussion, contributed to the analysis, and made the conclusions. XG and ZZ performed the simulation and part of the analysis. YD contributed to the manuscript preparation.
Funding
This work is jointly supported by the Natural Science Foundation of Guangdong Province (2020A1515010461), and the Department of Education of Guangdong Province (6020210013K).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bu, X., Hou, Z., and Zhang, H. (2018). Data-Driven Multiagent Systems Consensus Tracking Using Model Free Adaptive Control. IEEE Trans. Neural Netw. Learn. Syst. 29 (5), 1514–1524. doi:10.1109/tnnls.2017.2673020
Bu, X., Yu, Q., Hou, Z., and Qian, W. (2017). Model Free Adaptive Iterative Learning Consensus Tracking Control for a Class of Nonlinear Multiagent Systems. IEEE Trans. Syst. Man, Cybernetics: Syst. 49 (4), 677–686. doi:10.1109/TSMC.2017.2734799
Cai, H., Ma, H., and Hill, D. J. (2020). A Data-Based Learning and Control Method for Long-Term Voltage Stability. IEEE Trans. Power Syst. 35 (4), 3203–3212. doi:10.1109/tpwrs.2020.2967434
Guo, Y., Gao, H., and Wu, Q. (2019). Distributed Cooperative Voltage Control of Wind Farms Based on Consensus Protocol. Int. J. Electr. Power Energy Syst. 104, 593–602. doi:10.1016/j.ijepes.2018.07.030
Hatziargyriou, H., Milanovic, J. V., Rahmann, C., Ajjarapu, V., Canizares, C., Erlich, I., et al. (2020). Definition and Classification of Power System Stability – Revisited & Extended. IEEE Trans. Power Syst. 36 (4), 3271–3281. doi:10.1109/TPWRS.2020.3041774
Hill, D. J. (1993). Nonlinear Dynamic Load Models with Recovery for Voltage Stability Studies. IEEE Trans. Power Syst. 8 (1), 166–176. doi:10.1109/59.221270
Huang, Q., Huang, R., Hao, W., Tan, J., Fan, R., and Huang, Z. (2020). Adaptive Power System Emergency Control Using Deep Reinforcement Learning. IEEE Trans. Smart Grid 11 (2), 1171–1182. doi:10.1109/tsg.2019.2933191
Larsson, M., Hill, D. J., and Olsson, G. (2002). Emergency Voltage Control Using Search and Predictive Control. Int. J. Electr. Power Energy Syst. 24 (2), 121–130. doi:10.1016/s0142-0615(01)00017-5
Li, Y., Gao, D. W., Gao, W., Zhang, H., and Zhou, J. (2020). Double-Mode Energy Management for Multi-Energy System via Distributed Dynamic Event-Triggered Newton-Raphson Algorithm. IEEE Trans. Smart Grid 11 (6), 5339–5356. doi:10.1109/tsg.2020.3005179
Li, Y., Gao, W., Yan, W., Huang, S., Wang, R., Gevorgian, V., et al. (2021). Data-Driven Optimal Control Strategy for Virtual Synchronous Generator via Deep Reinforcement Learning Approach. J. Mod. Power Syst. Clean Energy 9 (4), 919–929. doi:10.35833/mpce.2020.000267
Liu, Z., Clark, A., Lee, P., Bushnell, L., Kirschen, D., and Poovendran, R. (2017). Submodular Optimization for Voltage Control. IEEE Trans. Power Syst. 33 (1), 502–513. doi:10.1109/TPWRS.2017.2691320
Ma, H. M., Ng, K. T., and Man, K. F. (2008). Multiobjective Coordinated Power Voltage Control Using Jumping Genes Paradigm. IEEE Trans. Ind. Electronics 55 (No.11), 4075–4084. doi:10.1109/tie.2008.928107
Magnusson, S., Qu, G., and Li, N. (2020). Distributed Optimal Voltage Control with Asynchronous and Delayed Communication. IEEE Trans. Smart Grid 11 (No.4), 3469–3482. doi:10.1109/TSG.2020.2970768
Van Cutsem, T., Grenier, M.-E., and Lefebvre, D. (2006). Combined Detailed and Quasi Steady-State Time Simulations for Large-Disturbance Analysis. Int. J. Electr. Power Energy Syst. 28 (9), 634–642. doi:10.1016/j.ijepes.2006.03.005
Yorino, N., Zoka, Y., Watanabe, M., and Kurushima, T. (2015). An Optimal Autonomous Decentralized Control Method for Voltage Control Devices by Using a Multi-Agent System. IEEE Trans. Power Syst. 30 (5), 2225–2233. doi:10.1109/tpwrs.2014.2364193
Zhang, K., Zhou, B., Or, S. W., Li, C., Chung, C. Y., and Voropai, N. I. (2021). Optimal Coordinated Control of Multi-Renewable-To-Hydrogen Production System for Hydrogen Fueling Stations. IEEE Trans. Ind. Applicat. 58 (2), 2728–2739. doi:10.1109/TIA.2021.3093841
Keywords: emergency voltage control, learning control, local voltage profile mode, similarity ranking, adaptive control
Citation: Ma H, Wang G, Gao X, Zou Z and Dong Y (2022) An Adaptive Voltage Control Using Local Voltage Profile Mode and Similarity Ranking. Front. Energy Res. 10:865151. doi: 10.3389/fenrg.2022.865151
Received: 29 January 2022; Accepted: 14 March 2022;
Published: 19 May 2022.
Edited by:
Bin Zhou, Hunan University, ChinaReviewed by:
Zhiyuan Tang, Sichuan University, ChinaYushuai Li, University of Oslo, Norway
Liang Liang, Harbin Institute of Technology, Shenzhen, China
Copyright © 2022 Ma, Wang, Gao, Zou and Dong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Haomin Ma, bWFoYW9taW5Ac3pwdC5lZHUuY24=
 Haomin Ma
Haomin Ma Genping Wang
Genping Wang Xiang Gao
Xiang Gao Zhouyiao Zou
Zhouyiao Zou Yanfei Dong
Yanfei Dong