Multi-Objective Optimization of Multi-Energy Flow Coupling System With Carbon Emission Target Oriented

In this paper, aiming to achieve the target of carbon emission orientation, a multi-objective optimization model of the multi-energy flow coupling system is proposed, in which all the environmental protection, system economy, and energy efficiency are comprehensively considered as the addressed objectives. To solve the developed model, by combining the analytic hierarchy process (AHP) and the improved entropy weight method, a so-called AHP-improved entropy weight method is proposed and utilized for weighting the considered objectives, and the model is transformed into a single objective optimization problem, namely, the collaborative optimization model. Then, to expedite the process, a simplified primal dual interior point method is proposed to solve the model. Finally, the results of a case study indicate that the proposed multi-objective collaborative optimization can obtain the optimal solution of the system. In addition, the convergence and global optimization ability of the simplified primal dual interior point method show better characteristics when solving the proposed model.

1 Introduction

Energy is the basis and important guarantee for human survival. There are many problems in traditional energy systems, such as independent energy supply, low cascade utilization level, energy waste, and environmental pollution (Zhou et al., 2013; Fan et al., 2021; Hu et al., 2022). The multi-energy flow coupling system (MEFCS) is an energy system form that integrates public cold, heat, electricity, and gas. Its purpose is to integrate multiple energy sources, such as electric energy, natural gas, and thermal energy in a certain area, so as to realize collaborative optimal operation, collaborative management, and complementary mutual assistance among various forms of energy subsystems (Zhao et al., 2018; Klyapovskiy et al., 2019). In addition, under the background of “double carbon”, the transformation of clean and low-carbon energy is an inevitable trend of global energy development.

Traditional energy systems are planned and operated independently, and only a single situation needs to be considered in their optimal scheduling. However, for a multi-energy flow coupling system, the correlation among energy subsystems should be considered in planning and operation (Sirvent et al., 2017). In Liu et al. (2019), considering the multi-timescale characteristics, an electrical and thermal energy sharing model of interconnected microgrids with combined heating and power (CHP) and photovoltaic systems was built, in which CHP could operate in a hybrid mode by selecting the operating point flexibly. In Wang et al. (2019), a multi-objective bi-level optimization model considering the total cost and carbon dioxide emission was built, while the energy efficiency of multi-energy flow coupling system was ignored. In Barati et al. (2015) and Clegg and Mancarella (2016), under the condition of meeting the basic needs of power, gas, and heat loads, the coordinated planning of multi-energy flow coupling system was considered, in order to reduce the construction cost of transmission lines, gas pipelines, and power plants as much as possible. In Koltsaklis and Knápek (2021), the authors presented an optimization framework for the optimal scheduling of a multi-energy microgrid, where a number of aggregated end-users were considered. In Nicolosi et al. (2021), a novel mixed integer linear programming optimization algorithm has been developed to compute the optimal management of a micro-energy grid, where the total cost, the NOx, and the CO₂ emissions of the system were taken into consideration. To meet the safety constraints, in Wang D. et al. (2018), an optimal coordination control strategy (OCCS) for a hybrid energy storage system was developed considering the state-space equation to describe the OCCS, the constraints of the OCCS, and the objective function to express the optimal coordination control performance. In Sun et al. (2020), the authors considered the day ahead optimal scheduling problem of electricity gas interconnected systems, where the two-way energy flow was taken as a non-convex nonlinear mixed integer linear programming problem, and a second-order cone programming (SOCP) method has been proposed. In Luo et al. (2018) and Zhang et al. (2021), the uncertainty caused by renewable energy and multi-energy load was considered, and the robust optimization and stochastic optimization methods were adopted to deal with it respectively, so as to ensure that the system can still maintain stable operation under the worst conditions. In Ghosh and Kamalasadan (2017), a grid-connected two mass DFIG and a grid-supportive single mass squirrel cage induction generator-based flywheel energy storage system model have been considered for controller design and proof-of-concept exploration. In Wang L. et al. (2021), the flexible resources (FRs) on both the energy supply and load sides were introduced into the optimal dispatch of the integrated electricity-heat energy system (IEHES) and further modeled to alleviate the renewable fluctuations, and the solution for FRs participating in IEHES dispatch was given, with goals of maximizing the renewable penetration ratio and lowering operation costs. It can be seen that most of the existing results consider optimization of the economic objectives of the multi-energy flow coupling system, where the index is relatively single, and less consideration is paid on the carbon emission level in the operation of the system. At the same time, the operation strategy is the lack of comprehensive comparison and verification.

In solving the MEFCS collaborative optimization model, when considering multiple optimization objectives including carbon emission, investment and operation cost, and energy utilization, the traditional single objective optimization algorithm may be difficult to ensure that the solution result is the optimal solution of the original problem. In Wang W. et al. (2021), the load characteristics and various constraints of the integrated community energy system were considered, and the operating model with the goal of minimizing operating costs was optimized. In Ma et al. (2018), the energy consumption cost and environmental cost of the multi-energy flow coupling system were considered comprehensively, the optimal scheduling model of multi-energy flow coupling system was proposed, and the optimal scheduling model was transformed into a mixed integer linear programming problem. In Xiao et al. (2018), the method of the probability scenario had been used to model the uncertainties of the distributed renewable energies (DREs) and loads, which could better characterize the impact of uncertainty on the planning and design of the MEFCS. In Yang et al. (2018), a two-stage robust generation scheduling model was proposed for the dynamic safety constraints of the natural gas pipeline network and the uncertainty of wind power, and a new solution method was developed to avoid the nonlinearity of gas flow constraints. In Wu et al. (2021), the multi-objective optimization model was transformed into a single objective optimization model through the multi-objective programming hierarchical solution method, and the primal dual interior point method was used to solve the model. Based on the fast particle swarm optimization algorithm, in Qu et al. (2021), a dual-decomposition-based distributed algorithm was designed to address the problem that the data and information of the EHs during the operation were confidential and should be kept by each owner, where the optimal consensus problem was used for the dual problem to update the multipliers, in Li et al. (2020), the proposed MEFCS planning model, formulated as a two-stage MILP problem, was solved by the Benders decomposition (BD) method to determine the optimal capacity of each component in MEFCS planning.

To be pointed out that, the research on the optimization of multi-energy flow coupling system at home and abroad mainly focuses on the simplification of the optimization model. However, on the one hand, it will lead to the reduction of solution accuracy, at the same time, because the models are more and more complex, which are difficult to be simplified. Therefore, the heuristic algorithm has become an important way to deal with optimization problems. However, the traditional heuristic algorithm has the problems of poor convergence and easy to fall into local optimization, and how to find a simplified and better algorithm is another motivation of this paper. Based on the above discussions, in this paper, the environmental protection goal is taken as the leading factor, the economic and energy efficiency goals are comprehensively considered, the multi-objective collaborative optimization model is developed for the multi-energy flow coupling system, which can be transformed into a single objective optimization model through the linear combination of the analytic hierarchy process and the improved entropy weight method, and then the model can be solved by using the simplified primal dual interior point method. The results avoid falling into local optimization and accelerate convergence. Case studies verify the effectiveness of the proposed algorithm.

2 Modeling of Multi-Energy Flow Coupling System

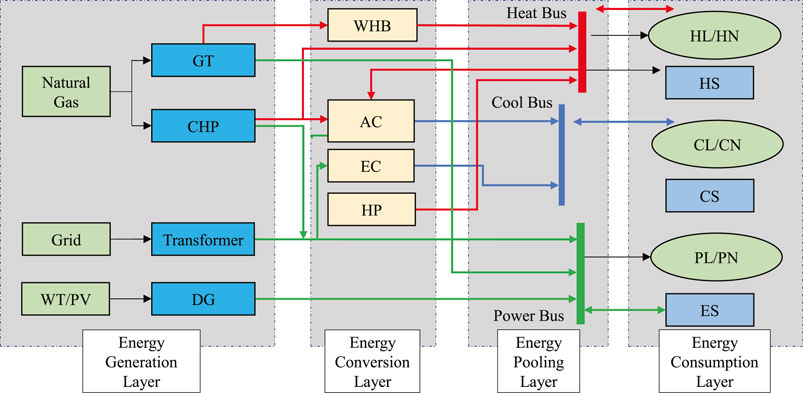
A typical multi-energy flow coupling system structure is shown in Figure 1, which is internally connected through the power grid, thermal pipe network, and cooling transmission network. The equipment involved distribution power source includes a wind turbine (WT) and photovoltaic (PV). Cogeneration includes CHP, a gas turbine (GT), a waste heat boiler (WHB), a ground source heat pump (HP), an electric refrigerator (ER), an absorption refrigerator (AR), and other energy conversion equipment, as well as electric energy storage (EES), heat energy storage (HES), and other energy storage equipment.

FIGURE 1

FIGURE 1. Typical structure of the multi-energy flow coupling system.

2.1 Modeling of Distributed Generations

2.1.1 Wind Turbine

$P_t^{\text{WT}}=\frac{1}{2}{\eta }_{\text{w}}\text{π}{r}^2\rho v_t^3,(1)$

where $P_t^{\text{WT}}$ indicates the wind turbine generation power (kW) in time period t, ${\eta }_{\text{w}}$ is the wind energy utilization efficiency of the wind turbine, $r$ represents the blade radius (m), $\rho$ represents the air density (${\text{kg/m}}^3$), and $v_t$ is the air velocity ($\text{m/s}$) in time period t.

2.1.2 Photovoltaic

$\{\begin{array}{l}{P}_t^{\text{PV}}=\frac{P_{\text{test}}{L}_t^{\text{ac}}\left[1+K\left({\theta }_t^{\text{s}}-{\theta }_t^{\text{r}}\right)\right]}{L_{\text{test}}},\\ {\theta }_t^{\text{s}}={\theta }_t^{\text{out}}+30R_t,\end{array}(2)$

where $P_t^{\text{PV}}$ refers to the output power (kW) of photovoltaic equipment during the period t, $P_{\text{test}}$ represents the test power (kW) under standard conditions t, $L_t^{\text{ac}}$ refers to the light intensity (${\text{W/m}}^2$) in the period t, $L_{\text{test}}$ is the test light intensity (${\text{W/m}}^2$) under standard conditions, K is the power temperature coefficient, which is taken as −0.0047; ${\theta }_t^{\text{s}}$, ${\theta }_t^{\text{r}}$, and ${\theta }_t^{\text{out}}$ represent the solar panel temperature, reference temperature, and external ambient temperature ($°\text{C}$), respectively; normally the reference temperature is taken as 25 $°\text{C}$; and $R_t$ expresses the solar radiation intensity (${\text{kW/m}}^2$) in time period t.

2.2 Modeling of Energy Conversion Unit

2.2.1 Cogeneration Unit

The cogeneration unit generates electric energy and heat energy at the same time by consuming natural gas. Its operation mode can be expressed as

$\{\begin{array}{l}{P}_t^{\text{CHP}}={\eta }^{\text{P,CHP}}{G}_t^{\text{CHP}},\\ H_t^{\text{CHP}}={\eta }^{\text{H,CHP}}{G}_t^{\text{CHP}},\end{array}(3)$

where $P_t^{\text{CHP}}$, $H_t^{\text{CHP}}$, and $G_t^{\text{CHP}}$ are the electric power, thermal power, and gas power consumed by the internal cogeneration unit in scheduling period t, respectively, and ${\eta }^{\text{P,CHP}}$ and ${\eta }^{\text{H,CHP}}$ are the power generation efficiency and heating efficiency of cogeneration units, respectively.

2.2.2 Gas Turbine and Waste Heat Boiler

The gas turbine generates electric energy by consuming natural gas, and part of the discharged flue gas can be transformed into available calorific value through a waste heat boiler. Their working characteristics can be expressed as

$\{\begin{array}{l}{P}_t^{\text{GT}}=\frac{{\eta }_{\text{GT}}{L}_{\text{gas}}{V}_t^{\text{gas}}}{t},\\ H_t^{\text{GT}}=P_t^{\text{GT}}\frac{\left(1-{\eta }_{\text{GT}}-{\eta }_{\text{l}}\right)}{{\eta }_{\text{GT}}},\\ H_t^{\text{WHB}}={\eta }_{\text{WHB}}{H}_t^{\text{GT}},\end{array}(4)$

where $P_t^{\text{GT}}$ and $H_t^{\text{GT}}$ indicate the gas turbine generation power and flue gas waste heat power during the period t, respectively; $L_{\text{gas}}$ represents the low calorific value of natural gas, which is set as 9.78 ${\text{kWh/m}}^3$ in this paper; $V_t^{\text{gas}}$ expresses the natural gas consumption during the period t; t is the scheduling period; ${\eta }_{\text{GT}}$ and ${\eta }_{\text{l}}$ represent the power generation efficiency and loss rate of gas turbine, respectively; ${\eta }_{\text{WHB}}$ is the recovery efficiency of the waste heat boiler; and $H_t^{\text{WHB}}$ is the heat recovery power of the waste heat boiler in time period.

2.2.3 Ground Source Heat Pump

The heat pump is a high-efficiency and energy-saving equipment in the multi-energy flow coupling system. It can convert low-grade heat energy into high-grade heat energy by consuming electric energy. Its operation mode is given by

$H_t^{\text{HP}}={\eta }_{\text{HP}}{P}_t^{\text{HP}},(5)$

where $H_t^{\text{HP}}$ and $P_t^{\text{HP}}$ represent the heat energy generated and electric energy consumed of the ground source heat pump during the period t, respectively; and ${\eta }_{\text{HP}}$ is the conversion efficiency of the heat pump.

2.2.4 Electric Chiller and Absorption Chiller

The electric chiller generates cold power by consuming electric power during operation, and the absorption chiller generates cold power by absorbing thermal power. Its mathematical model is as follows:

$\{\begin{array}{l}{C}_t^{\text{EC}}={\eta }_{\text{EC}}{P}_t^{\text{EC}},\\ {\eta }_{\text{AC}}=\frac{{\eta }_0^{\text{AC}}{\beta }_{\text{AC}}}{a_{\text{AC}}{\left({\beta }_{\text{AC}}\right)}^2+b_{\text{AC}}{\beta }_{\text{AC}}+c_{\text{AC}}},\\ C_t^{\text{AC}}={\eta }_{\text{AC}}{H}_t^{\text{AC}},\end{array}(6)$

where $C_t^{\text{EC}}$ and $C_t^{\text{AC}}$ represent the cool power generated in time period t of the electric chiller and absorption chiller, respectively; ${\eta }_{\text{EC}}$ and ${\eta }_{\text{AC}}$ represent the conversion efficiency of the electric chiller and absorption chiller, respectively; $P_t^{\text{EC}}$ indicates the electric energy consumed of the electric chiller during the period t; $H_t^{\text{AC}}$ represents the heat energy consumed of the absorption chiller during the period t; ${\eta }_0^{\text{AC}}$ is the rated conversion efficiency of the absorption chiller; $a_{\text{AC}}$, $b_{\text{AC}}$, and $c_{\text{AC}}$ are the refrigeration coefficient of the absorption chiller, respectively; and ${\beta }_{\text{AC}}$ is the load rate when the absorption chiller is working.

2.3 Modeling of Energy Storage Equipment

$E_{i,t}=E_{i,t-1}\left(1-{\sigma }_i\right)+P_{i,t}^{\text{c}}{\eta }_i^{\text{c}}-P_{i,t}^{\text{d}}/{\eta }_i^{\text{d}},(7)$

where $E_{i,t}$ represents the energy storage of energy storage equipment i in time period t, $P_{i,t}^{\text{c}}$ and $P_{i,t}^{\text{d}}$ are the charging power and discharging power of energy storage equipment i in time period t, ${\eta }_i^{\text{c}}$ and ${\eta }_i^{\text{d}}$ represent the charging efficiency and discharging efficiency of energy storage equipment i, and ${\sigma }_i$ is the consumption rate of energy storage equipment i.

3 Modeling of Multi-Objective Collaborative Optimization

In the multi-objective collaborative optimization of MEFCS considering carbon emissions, the optimization objectives considered in this paper include the environmental protection objective, economic objective, and energy efficiency objective.

3.1 Each Optimization Objective Function

3.1.1 Environmental Protection Objective

Aiming at minimizing the ${\text{CO}}_2$ emission of MEFCS in 1 day, the optimization model can be established as follows:

$\min F_1={\sum }_{t=1}^{24}\left[{\alpha }_{\text{gas}}\cdot \left(P_t^{\text{GT}}+G_t^{\text{CHP}}\right)+{\alpha }_{\text{grid}}\cdot \left(P_t^{\text{HP}}+P_t^{\text{EC}}\right)\right],(8)$

where ${\alpha }_{\text{gas}}$ and ${\alpha }_{\text{grid}}$ represent the ${\text{CO}}_2$ emission coefficient corresponding to the combustion of natural gas and the consumption of electric energy; in this paper, they are taken as 184 g/kWh and 877 g/kWh, respectively.

3.1.2 Economic Objective

In order to minimize the operation cost of MEFCS in 1 day, the optimization model can be formulated as

$\{\begin{array}{l}\min F_2={\sum }_{t=1}^{24}\left(c_{\text{grid}}{P}_t^{\text{grid}}+c_{\text{gas}}{G}_t^{\text{gas}}\right)+{\sum }_{i=1}^N{c}_i^{\text{ma}}{P}_i,\\ P_t^{\text{grid}}=P_t^{\text{HP}}+P_t^{\text{EC}},\\ G_t^{\text{gas}}=P_t^{\text{GT}}+G_t^{\text{CHP}},\end{array}(9)$

where $c_{\text{grid}}$ and $c_{\text{gas}}$ are the cost coefficients corresponding to the electric energy and natural gas consumed by the system, respectively; $c_i^{\text{ma}}$ is the maintenance cost of equipment i; $P_i$ is the rated capacity of equipment i; and N represents the total amount of equipment.

3.1.3 Energy Efficiency Objective

Primary energy utilization is defined as the ratio of MEFCS load to MEFCS primary energy input in a day. Aiming at the maximum utilization of primary energy, the optimization model can be formulated as

$\{\begin{array}{l}\max F_3=\frac{W_{PL}+W_{HL}+W_{CL}}{{\sum }_{t=1}^{24}\left(\frac{P_t^{\text{grid}}}{1-\zeta }+G_t^{\text{gas}}\right)},\\ W_{PL}={\sum }_{t=1}^{24}{P}_t^{\text{L}},\\ W_{HL}={\sum }_{t=1}^{24}{H}_t^{\text{L}},\\ W_{CL}={\sum }_{t=1}^{24}{C}_t^{\text{L}},\end{array}(10)$

where $W_{PL}$, $W_{HL}$, and $W_{CL}$ represent the total load of the system in a day, respectively, and $\zeta$ represents the network loss rate of transmission line, which is usually chosen as 5%.

3.2 Constraint Condition

3.2.1 Energy Balance Constraints

1) Power balance constraint

$\begin{array}{l}{P}_t^{\text{grid}}+P_t^{\text{CHP}}+P_t^{\text{GT}}+P_t^{\text{WT}}+P_t^{\text{PV}}+P_t^{\text{ES,d}}\\ =P_t^{\text{L}}+P_t^{\text{HP}}+P_t^{\text{ES,c}}+P_t^{\text{EC}}.\end{array}(11)$

2) Heat energy balance constraint

$\begin{array}{l}{H}_t^{\text{CHP}}+H_t^{\text{HP}}+H_t^{\text{WHB}}+H_t^{\text{HS,d}}\\ =H_t^{\text{L}}+H_t^{\text{HS,c}}+H_t^{\text{AC}}.\end{array}(12)$

3) Cool energy balance constraint

$C_t^{\text{EC}}+C_t^{\text{AC}}=C_t^{\text{L}}.(13)$

3.2.2 Upper and Lower Limits of Equipment Output

$\text{0}\le O_{i,t}\le P_i,(14)$

where $O_{i,t}$ represents the output power of equipment i in period t.

3.2.3 Energy Storage Constraints

$\{\begin{array}{l}{P}_{i,t}^{\text{c}}\le \upsilon {\overline{P}}_i^{\text{c}},\\ P_{i,t}^{\text{d}}\le \left(1-\upsilon \right){\overline{P}}_i^{\text{d}},\\ \upsilon \in \left\{\mathrm{0,1}\right\},\\ E_{i,1}=E_{i,24},\\ \underset{¯}{{\mu }_i}{P}_i\le E_{i,t}\le {\overline{\mu }}_i{P}_i,\end{array}(15)$

where ${\overline{P}}_i^{\text{c}}$ and ${\overline{P}}_i^{\text{d}}$ represent the upper limit of charging and discharging power of energy storage equipment i, respectively; $\upsilon$ represents 0–1 variable; $E_{i,t}$ is the energy storage of equipment i in period t; and ${\overline{\mu }}_i$ and $\underset{¯}{{\mu }_i}$ represent the upper and lower limits of the charging and discharging state of the energy storage equipment i, respectively.

3.3 Collaborative Optimization Objective

The developed optimization model is a multi-objective optimization problem. First, the optimal solution of each objective is obtained through single objective optimization, and then the optimization results of each objective are standardized, so the multi-objective optimization is transformed into single objective optimization with the help of the linear weighting method. Finally, the single objective optimization algorithm can be solved.

3.3.1 Normalization and Standardization

As the environmental protection goal and economic goal belong to very small goals, that is, the smaller the final result, the better, while the energy efficiency goal belongs to maximum goals, the larger the final result, the better. Therefore, before establishing the collaborative optimization objectives, each single objective should be normalized and standardized, which can be expressed as follows:

$S_1\left(F_i\right)=\{\begin{array}{l}1,F_i\le F_{i,\min },\\ \frac{F_{i,\max }-F_i}{F_{i,\max }-F_{i,\min }},\\ 0,F_i>F_{i,\max },\end{array}{F}_{i,\min }<F_i\le F_{i,\max },(16)$

$S_2\left(F_i\right)=\{\begin{array}{l}0,F_i\le F_{i,\min },\\ \frac{F_i-F_{i,\min }}{F_{i,\max }-F_{i,\min }},\\ 1,F_i>F_{i,\max },\end{array}{F}_{i,\min }<F_i\le F_{i,\max },(17)$

where $S_1$ and $S_2$ represent the membership function of very small target and maximum target, respectively, $F_i$ is the ith objective function, and $F_{i,\min }$ and $F_{i,\max }$ are the minimum and maximum of the ith objective function, respectively.

3.3.2 Index Weighting

Generally, the methods of weighting indicators can be divided into subjective method, objective method, and the combination of subjective and objective methods. The subjective weighting method is simple to operate and does not need the support of original data, but the subjectivity of weighting results is often too large. The objective weighting method can show the relationship between indicators well, but it has high requirements for the original data. Therefore, in this paper, a new combination method based on the analytic hierarchy process (AHP) and the improved entropy weight method is adopted.

The analytic hierarchy process first judges the relative importance of each index through decision-making experts and scores each index with an integer between 1 and 9, and then the judgment matrix is obtained,

$\mathrm{A}=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right],(18)$

where n denotes the number of indicators. A is a positive reciprocal matrix, which satisfies $a_{ij}=1/a_{ji}$.

To be noted that, due to the environmental protection goal is taken as the leading factor in this paper, when forming the judgment matrix, the score of the environmental protection index is relatively high so that the final weight is relatively maximum.

Then check the consistency of the judgment matrix,

$\{\begin{array}{l}CR=\frac{CI}{RI},\\ CI=\frac{{\lambda }_{\max }-n}{n-1},\end{array}(19)$

where $CR$ represents the consistency proportion. If $CR<0.1$, the consistency verification passes, otherwise the judgment matrix needs to be modified. $CI$ and $RI$ represent the consistency index and average random consistency index, respectively. ${\lambda }_{\max }$ is the maximum eigenvalue of judgment matrix A.

When the judgment matrix A passes the consistency check, the eigenvector corresponding to its maximum eigenvalue ${\lambda }_{\max }$ is obtained and normalized, that is, the weight vector is obtained by the analytic hierarchy process,

${\text{ω}}^1={\left[{\omega }_1^1,{\omega }_2^1,\cdots ,{\omega }_n^1\right]}^{\text{T}}.(20)$

The entropy weight method reflects the amount of information contained in each index through the entropy value of each index. Generally speaking, the smaller the entropy value, the greater the amount of index information and the greater the weight should be set. Since the standard entropy weight method is mainly applied to multiple schemes, the entropy weight method can be improved by

$\{\begin{array}{l}{p}_i=\frac{1+S_i}{\left(1+S_{i,\min }\right)+\left(1+S_i\right)+\left(1+S_{i,\max }\right)},\\ H_i=\frac{p_{i,\min }\ln p_{i,\min }+p_i\ln p_i+p_{i,\max }\ln p_{i,\max }}{\ln 3},\end{array}(21)$

where $p_i$ represents the characteristic specific gravity of the ith target, $H_i$ is the entropy of the ith target, and $S_i$ is the membership function of the ith objective.

To be noted that, this improvement is mainly to adapt to the optimization model. The objective functions have been processed and converted into the form of membership function. Therefore, in order to adapt to this form, the index value is replaced by membership $S_i$. Because this is not an evaluation problem, there are no multiple schemes to be evaluated. Therefore, the possible maximum and minimum values of each membership degree are substituted into the formula to reduce the individual deviation. In this way, there are three evaluation schemes in terms of quantity, that is, $m=3$. Therefore, the above formula is obtained.

According to the calculation results of entropy value of each index, the weight of each index can be obtained by

${\omega }_i^2=\frac{1-H_i}{n-{\sum }_{i=1}^n{H}_i}.(22)$

Therefore, the weight vector is obtained by the improved entropy weight method,

${\mathbf{\omega }}^2={\left[{\omega }_1^2,{\omega }_2^2,\cdots ,{\omega }_n^2\right]}^{\text{T}}.(23)$

In order to obtain the combined weight of AHP and improved entropy weight method, the coupling vector is taken as follows:

$\left[{\theta }^1,{\theta }^2\right]=\left[{\theta }_1^1,{\theta }_2^1,\cdots ,{\theta }_n^1,{\theta }_1^2,{\theta }_2^2,\cdots ,{\theta }_n^2\right],(24)$

where ${\theta }_i^1$ and ${\theta }_i^2$ represent the coupling weight of index I for weight coefficients ${\omega }_i^1$ and ${\omega }_i^2$, respectively, which can be expressed as

$\{\begin{array}{l}{\theta }_i^1=\frac{{\omega }_i^1}{{\omega }_i^1+{\omega }_i^2},\\ {\theta }_i^2=\frac{{\omega }_i^2}{{\omega }_i^1+{\omega }_i^2}.\end{array}(25)$

Therefore, the weight after coupling is

${\omega }_i^{\ast }={\theta }_i^1{\omega }_i^1+{\theta }_i^2{\omega }_i^2.(26)$

Normalize it, one has

${\omega }_i=\frac{{\theta }_i^1{\omega }_i^1+{\theta }_i^2{\omega }_i^2}{{\displaystyle {\sum }_{i=1}^n\left({\theta }_i^1{\omega }_i^1+{\theta }_i^2{\omega }_i^2\right)}}.(27)$

Then, the combined weight of the AHP improved entropy weight method can be finally expressed as

$\omega ={\left[{\omega }_1,{\omega }_2,\cdots ,{\omega }_n\right]}^{\text{T}}.(28)$

3.3.3 Collaborative Optimization Objective

After obtaining the index weight, combined with the standardized objective function in the above sections, we can obtain the comprehensive satisfaction goal, that is, the collaborative optimization objective is given as

$\max F={\omega }_1{S}_1\left(F_1\right)+{\omega }_2{S}_1\left(F_2\right)+{\omega }_3{S}_2\left(F_3\right).(29)$

4 Optimization Algorithm

Based on the above analysis, it can be found that the multi-objective collaborative optimization of the multi-energy flow coupling system considered in this paper is a complex nonlinear programming problem. In order to make the solution speed and convergence meet the requirements of practical problems, the simplified primal dual interior point algorithm is used in this paper. For the sake of brevity, first, the optimization model described above is transformed into the following general form:

$\{\begin{array}{l}\max F\left(\mathit{x}\right),\\ \text{s}\text{.t}\text{. }\mathit{h}\left(\mathit{x}\right)=0,\\ {\mathit{g}}_{\min }\le \mathit{g}\left(\mathit{x}\right)\le {\mathit{g}}_{\max },\end{array}(30)$

where $\mathrm{x}$ is the state variable, including the output power, external power purchase, gas purchase, etc., of each equipment, $\mathit{h}\left(\mathit{x}\right)$ is the equality constraint, including the power balance constraint of the system, the energy balance constraint at the beginning and end of the scheduling cycle of energy storage equipment, etc.; $\mathit{g}\left(\mathit{x}\right)$ is the inequality constraint, including the upper and lower limits of equipment output, energy storage charge and discharge constraints, etc.; and ${\mathit{g}}_{\max }$ and ${\mathit{g}}_{\min }$ represent the upper and lower bounds of the inequality, respectively.

When dealing with this optimization model with the traditional interior point algorithm, relaxation variables $\mathrm{u}={[u_1,\cdots ,u_r]}^{\text{T}}$ and $l={[l_1,\cdots ,l_r]}^{\text{T}}$ are introduced first, where r represents the number of inequality constraints; thus, the original inequality constraints are transformed into the equality constraints. The resulting optimization model is formulated as

$\{\begin{array}{l}\min -F\left(x\right),\\ \text{s}\text{.t}\text{. }h\left(x\right)=0,\\ g\left(x\right)+u=g_{\max },\\ gx-l=g_{\min },\\ u>\mathrm{0},l>\mathrm{0}\mathrm{.}\end{array}(31)$

At the same time, the size of relaxation variables $u$ and $l$ should be restricted to ensure that the objective function $F\left(x\right)$ is always far away from the solution boundary so that it can be solved in the feasible domain as follows:

$\{\begin{array}{l}\min -F\left(x\right)-\mu {\displaystyle \sum _{i=1}^r\log \left(l_i\right)}-\mu {\displaystyle \sum _{i=1}^r\log \left(u_i\right)},\\ \text{s}\text{.t}\text{. }h\left(x\right)=0,\\ g\left(x\right)+u=g_{\max },\\ g\left(x\right)-l=g_{\min },\end{array}(32)$

where $\mu$ represents the introduced disturbance factor.

At this point, the inequality constraints contained in the optimization model described in this paper have all been converted into the equality constraints, and the Lagrange function for this optimization problem can be expressed as

$\begin{array}{l}L=-F\left(x\right)-y^{T}h\left(x\right)\\ -z^T\left[g\left(x\right)-l-g_{\min }\right]\\ -w^T\left[g\left(x\right)+u-g_{\max }\right]\\ -\mu {\displaystyle \sum _{i=1}^r\log \left(l_i\right)}-\mu {\displaystyle \sum _{i=1}^r\log \left(u_i\right)},\end{array}(33)$

where $y$, $z$, and $w$ all represent the Lagrange operators, also known as the dual variables. By deriving this Lagrange function, the optimal solution to this optimization problem can be obtained.

In this paper, by simplifying the original dual interior point algorithm, the simplified original dual interior point method can be utilized to solve the optimization model, and the simplified process is to rewrite the inequality constraint to

$\{\begin{array}{l}\widehat{\mathit{g}}\left(\mathit{x}\right)\le {\widehat{\mathit{g}}}_{\max },\\ \widehat{\mathit{g}}\left(\mathit{x}\right)={\left[\mathit{g}\left(\mathit{x}\right),-\mathit{g}\left(\mathit{x}\right)\right]}^{\text{T}},\\ {\widehat{\mathit{g}}}_{\max }={\left[{\mathit{g}}_{\max },-{\mathit{g}}_{\max }\right]}^{\text{T}},\end{array}(34)$

where $\widehat{\mathit{g}}\left(\mathit{x}\right)$ and ${\widehat{\mathit{g}}}_{\max }$ represent the generalized inequality constraints and generalized upper bounds, respectively.

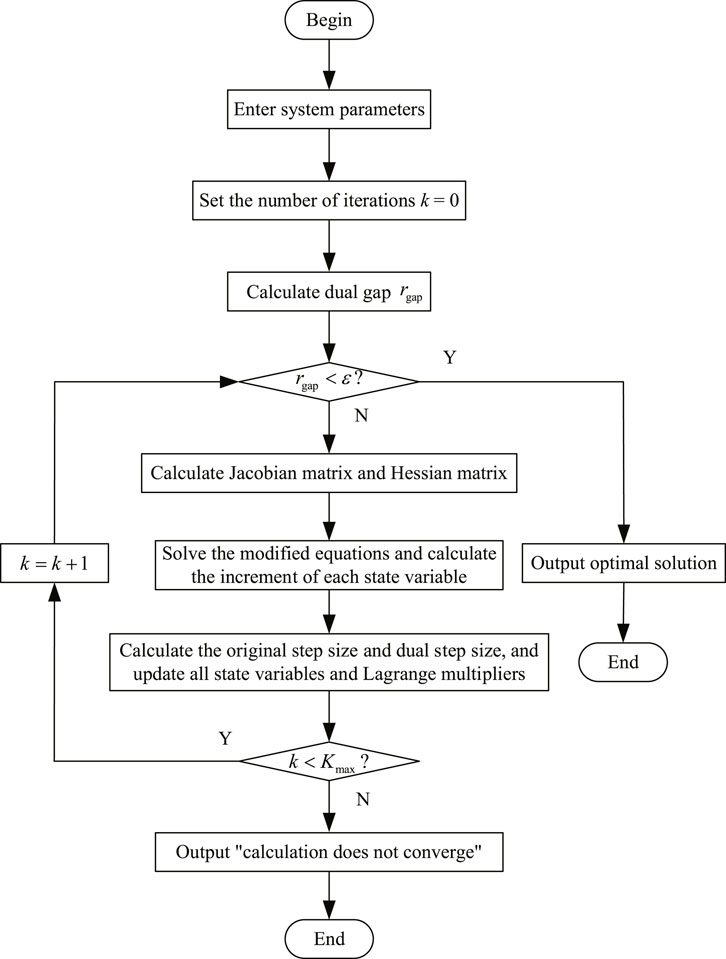
It can be found from the traditional interior point algorithm that in the process of dealing with inequality constraints, the upper and lower bounds of inequality constraints need to be relaxed, and then converted into equality constraints, respectively. At the same time, Lagrange operators are also introduced for equality constraints converted from upper-bound inequality constraints and lower-bound inequality constraints, respectively, which introduce more variables in the Lagrange function. This simplification algorithm greatly reduces the relaxation variables and corresponding Lagrange operators introduced in the optimization model, improves the convergence speed of the algorithm while guaranteeing the calculation accuracy, and reduces the amount of programming to a certain extent. The rest of the algorithm is handled similarly to the traditional algorithm, which are not discussed here. For ease of understanding, the multi-objective collaborative optimization calculation flow of the multi-energy flow coupling system based on the simplified primal dual interior point algorithm is shown in Figure 2, where $r_{\text{gap}}$ is the dual gap, $\epsilon$ represents the convergence accuracy, which is taken as 10–6 in this paper, and $K_{\max }$ represents the maximum number of iterations, normally is set as 300.

FIGURE 2

FIGURE 2. Calculation flow of multi-objective collaborative optimization.

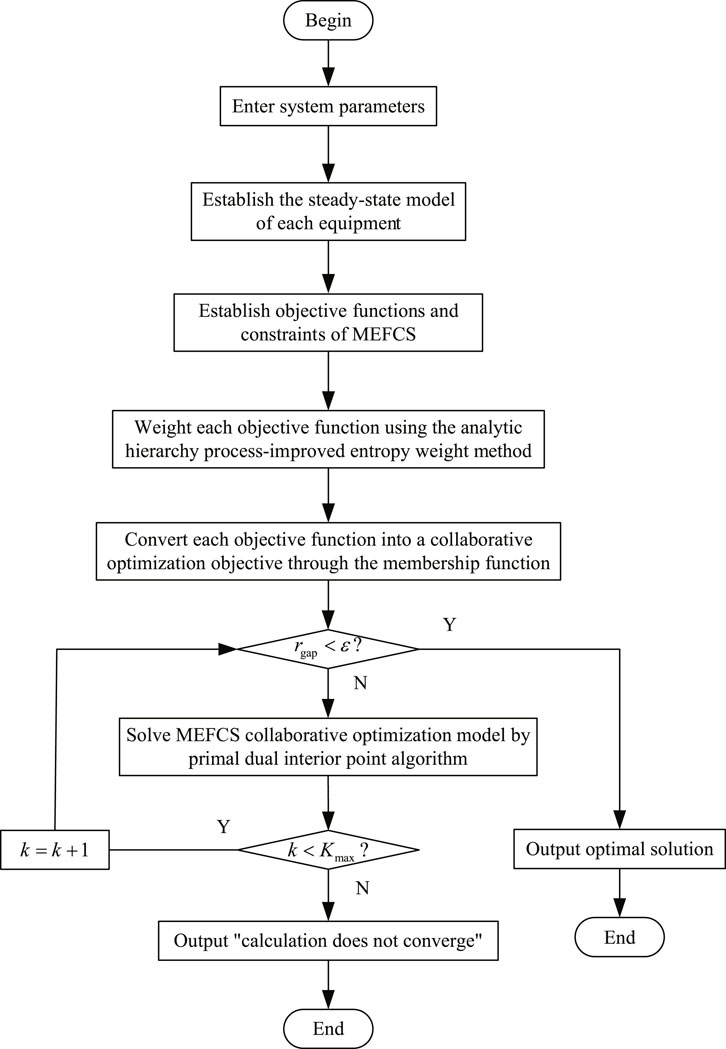
Based on the above analysis, the collaborative optimization of MEFCS dominated by the carbon emission targets in this paper can be summarized as the following steps:

Step 1. Enter parameter information of the multi-energy flow coupling system, such as system load, rated capacity of each unit, equipment parameters, and time-of-use electricity price.

Step 2. Establish the steady-state operation model of each equipment, as shown in Eqs 1–7.

Step 3. Establish the objective functions and constraints of the MEFCS, as shown in Eqs 8–15.

Step 4. Weight each objective function using the analytic hierarchy process-improved entropy weight method, as shown in Eqs 18–28.

Step 5. Convert each objective function into a collaborative optimization objective through the membership function and the obtained weight information, as shown in Eqs 16, 17, 29.

Step 6. Solve the MEFCS collaborative optimization model by the primal dual interior point algorithm until the optimal solution is obtained or the algorithm does not converge.

The above steps can be clearly represented by the flowchart shown in Figure 3.

FIGURE 3

FIGURE 3. Flowchart of the collaborative optimization of MEFCS.

5 Case Study

5.1 Case Description

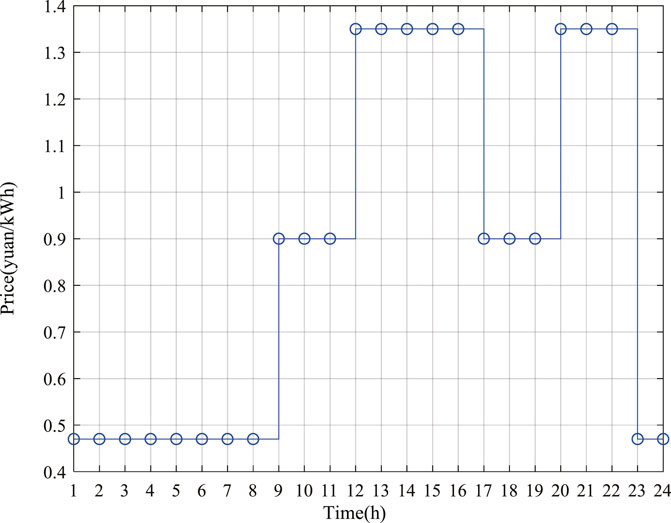
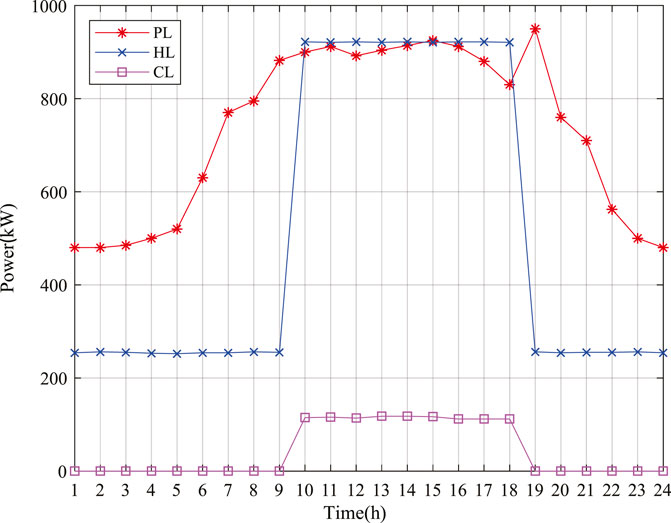
In this paper, the typical multi-energy flow coupling system shown in Figure 1 is selected as an example. The capacity of each equipment is as follows: one photovoltaic generator unit with a rated output of 700 kW and one wind turbine generator unit with a rated output of 500 kW, one cogeneration unit with a rated output of 3 MW, one gas turbine with a rated output of 2 MW, one waste heat boiler with a rated output of 1 MW, four heat pumps with a rated output of 500 kW, four electric refrigerators and four absorption refrigerators with a rated output of 200 kW, and four batteries and heat storage equipment with a rated capacity of 500 kwh. Other economic and technical parameters of the equipment can be found in Wang Y. et al. (2018) and Huang et al. (2019). The time of use electricity price information of the multi-energy flow coupling system is shown in Figure 4, and the price of natural gas is 2.71 yuan/m³ (Shen et al., 2020). The load data of the system are shown in Figure 5.

FIGURE 4

FIGURE 4. Power purchase price of MEFCS.

FIGURE 5

FIGURE 5. Load of MEFCS

5.2 Results Analysis

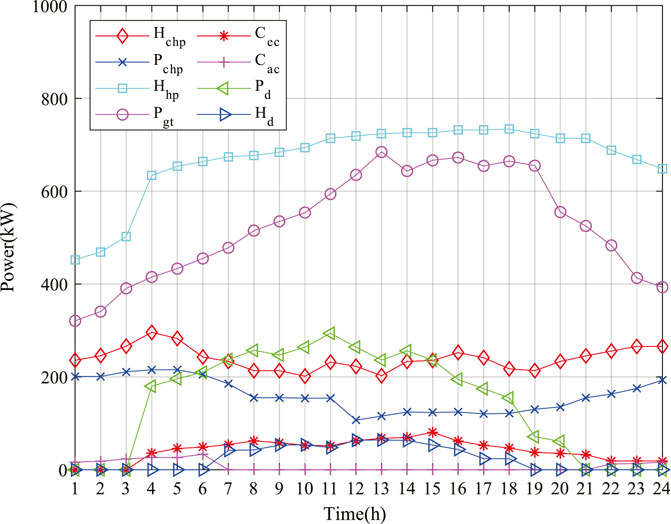
The output curve of each equipment is shown in Figure 6. It can be seen that the supply of electric energy and heat energy of the system is mainly guaranteed by a gas turbine and heat pump, but only the output of each equipment is not enough to meet the load demand during the peak load period of the system. At this time, the system needs to purchase electricity from the external power grid to jointly supply energy to the load. In addition, it can be seen from the figure that the discharge time of the power storage equipment is 03:00–21:00, and the heat release time of the heat storage equipment is 06:00–19:00. In other periods, that energy storage equipment is in the charged states.

FIGURE 6

FIGURE 6. Output of each equipment of MEFCS.

While using the multi-objective collaborative optimization model proposed in this paper to solve the multi-energy flow coupling system, three separate objectives are solved respectively. After finding the individual optimization of each objective, its state variables are substituted into the other two objectives to obtain the respective results of the three objectives in this case. The comparison between the operation results of each scheme and the operation results of multi-objective collaborative optimization is shown in Table 1. It can be found from Table 1 that the CO2 emission under multi-objective collaborative optimization increases by 3.8% compared with that under single objective F1 optimization, the system operation cost increases by 6.1% compared with that under single objective F2 optimization, and the primary energy utilization rate decreases by 7.2% compared with that under single objective F3 optimization. Although each objective under multi-objective collaborative optimization is not the optimal solution, the contradiction and conflict between each single objective are balanced in the optimization process. On the premise of taking the minimum carbon emission of the system as the leading objective, the comprehensive satisfaction of the system is significantly higher than the solution results of each single objective, and a relatively satisfactory optimal scheduling scheme is given.

TABLE 1

TABLE 1. Comparison between multi-objective collaborative optimization and single-objective optimization.

In order to further compare the differences between the multi-objective collaborative optimization proposed in this paper and the traditional single objective optimization, the optimization results of each single objective and the multi-objective collaborative optimization results are analyzed period by period, as shown in Figure 7. In the figure, $F_{123-1}$, $F_{123-2}$, and $F_{123-3}$ represent the environmental protection objective, economic objective, and energy efficiency objective under collaborative optimization, while $F_{11}$, $F_{22}$, and $F_{33}$ represent the environmental protection objective, economic objective, and energy efficiency objective under single objective optimization. Figure 7A shows the carbon emissions in each period of the two optimization methods. It can be seen from the figure that the two carbon emission curves cross each other. Except that the carbon emissions during collaborative optimization in 17:00–21:00 are significantly higher than those in single objective optimization, they are very close in other times. It shows that when taking the minimum carbon emission as the leading objective, the effect of collaborative optimization is not different from the single objective optimization with the minimum carbon emission, and the working state of each equipment is also relatively stable. Figure 7B shows the cost curves of the two optimization methods. During 3:00–12:00, the cost of multi-objective collaborative optimization is about 100 yuan/h higher than that of single objective optimization, and the two curves almost coincide after 12:00. It can be seen from Table 1 that the comprehensive satisfaction of multi-objective collaborative optimization is obviously higher than that of single objective optimization. On this basis, it ensures that the operation cost of the system is not too high, and it is almost the same as that of single objective optimization in most periods, indicating that the result of multi-objective collaborative optimization is ideal. Figure 7C shows the comparison of energy efficiency of the two methods in each period. Although the operation energy efficiency of multi-objective optimization in each period is not as good as that of single objective energy efficiency optimization, the overall operation result is relatively stable, indicating that each equipment can achieve stable energy supply and continuous output during the operation of the system, and the working state is not easy to fluctuate violently.

FIGURE 7

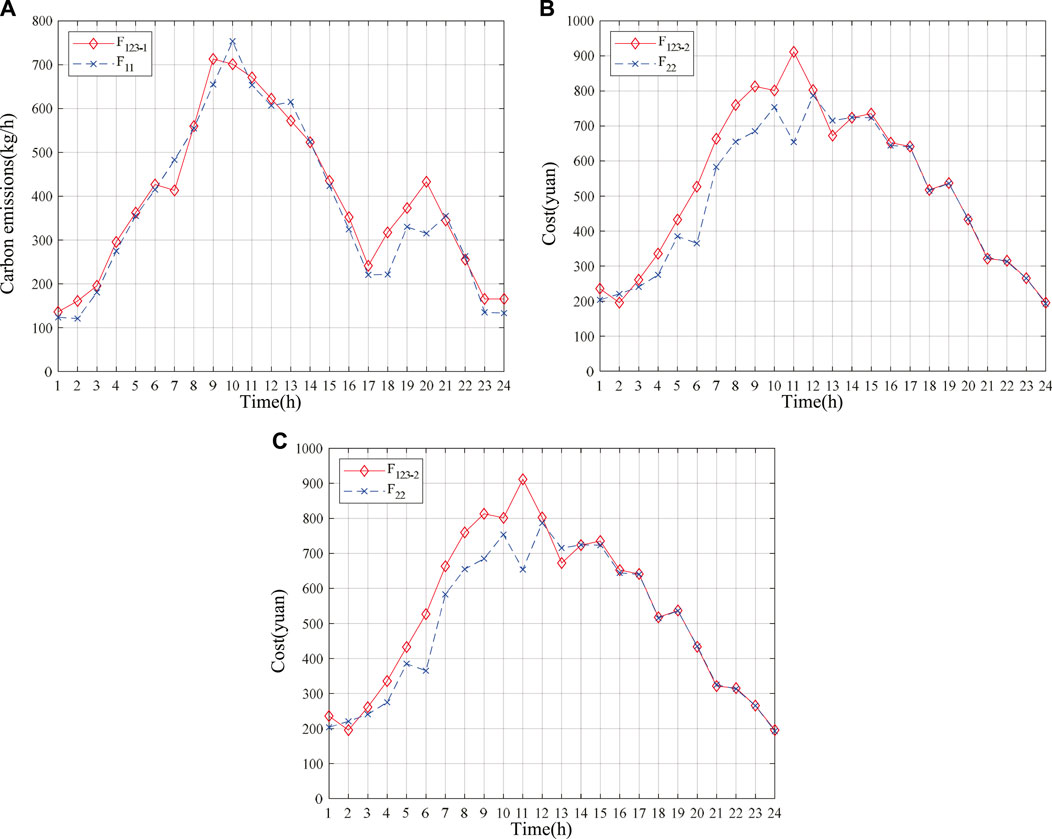
FIGURE 7. Period by period analysis of single objective and multi-objective optimization results. (A) Comparison of environmental protection objectives by period. (B) Period by period comparison of economic objectives. (C) Period by period comparison of energy efficiency objectives.

In order to highlight the effectiveness of the simplified primal dual interior point method proposed in this paper, the particle swarm optimization (PSO) algorithm is selected to compare with the algorithm proposed in this paper. The solution process curves of the simplified primal dual interior point method and particle swarm optimization algorithm for the system comprehensive satisfaction objective are shown in Figures 8A,B, respectively. They tend to converge at the 25th and 65th iterations, respectively. It can be seen that the convergence of the simplified primal dual interior point method is better than that of the particle swarm optimization algorithm. In addition, from the solution results of the two algorithms, it can be seen that the simplified primal dual interior point method finally converges near 0.9685, while the particle swarm optimization algorithm finally converges only near 0.8352, which still has a certain deviation from the global optimal solution. Therefore, the global optimization ability of the simplified primal dual interior point method proposed in this paper is also stronger than that of the particle swarm optimization algorithm.

FIGURE 8

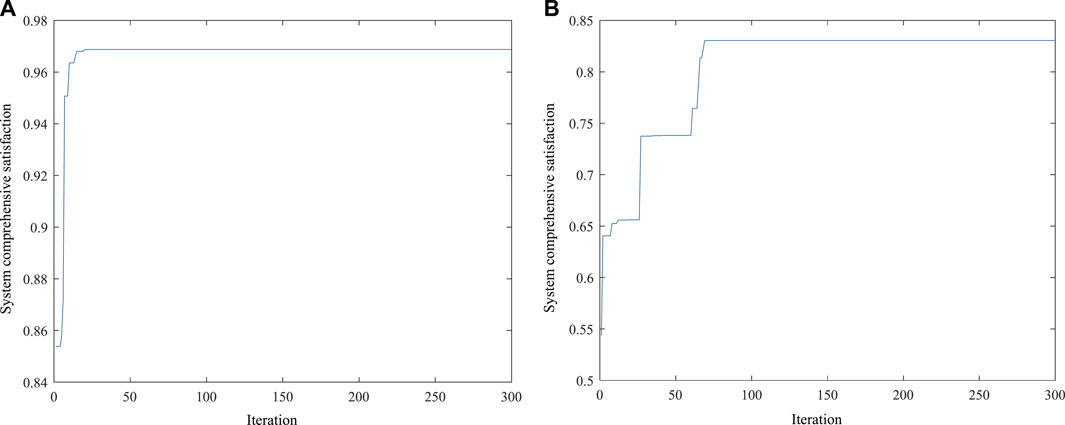
FIGURE 8. Solving process of the comprehensive satisfaction objective for MEFCS. (A) Simplified primal dual interior point method. (B) Particle swarm optimization algorithm.

6 Conclusion

In this paper, the multi-objective collaborative optimization model of MEFCS has been developed considering each of the environmental protection, system economy, and energy efficiency as the objectives of this study, in which the carbon emission orientation goal could be achieved. Moreover, the simplified primal dual interior point method has been used to solve the constructed model. According to the obtained results, the following findings have been concluded: 1) The contradiction and conflict between the three objectives (CO2 emission, system operation cost, and primary energy utilization rate) were relatively balanced under the proposed collaborative optimization operation, which have clearly demonstrated that the satisfaction of collaborative optimization operation considering multiple objectives could be higher than that considering a single objective of the system. 2) Each equipment of the system could achieve stable energy supply as well as continuous output throughout the whole operation process, whereas the working state was difficult to fluctuate sorely. 3) At the same time, the operator could adjust the weight of the three objectives through his own will, so as to get the best operation results that meet his requirements. 4) In addition, the simulation results have illustrated that the simplified primal dual interior point method being adopted in this paper has better convergence and global optimization ability in multi-objective collaborative optimization. However, more investigations are needed regarding the sensitivity analysis on the critical parameters of the multi-energy flow coupling system, which will be considered in our future research work.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

XZ: Methodology, software, writing—original draft, data curation. YY: Conceptualization of this study, supervision, review and editing. HW: Review and editing.

Funding

This work was supported by the National Natural Science Foundation of China (No. 51477041).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Barati, F., Seifi, H., Sepasian, M. S., Nateghi, A., Shafie-khah, M., and Catalao, J. P. S. (2015). Multi-period Integrated Framework of Generation, Transmission, and Natural Gas Grid Expansion Planning for Large-Scale Systems. IEEE Trans. Power Syst. 30 (5), 2527–2537. doi:10.1109/TPWRS.2014.2365705

CrossRef Full Text | Google Scholar

Clegg, S., and Mancarella, P. (2016). Integrated Electrical and Gas Network Flexibility Assessment in Low-Carbon Multi-Energy Systems. IEEE Trans. Sustain. Energ. 7 (2), 718–731. doi:10.1109/TSTE.2015.2497329

CrossRef Full Text | Google Scholar

Fan, D., Dou, X., Xu, Y., Wu, C., Xue, G., and Shao, Y. (2021). A Dynamic Multi-Stage Planning Method for Integrated Energy Systems Considering Development Stages. Front. Energ. Res. 9, 723702. doi:10.3389/fenrg.2021.723702

CrossRef Full Text | Google Scholar

Ghosh, S., and Kamalasadan, S. (2017). An Energy Function-Based Optimal Control Strategy for Output Stabilization of Integrated DFIG-Flywheel Energy Storage System. IEEE Trans. Smart Grid. 8 (4), 1922–1931. doi:10.1109/TSG.2015.2510866

CrossRef Full Text | Google Scholar

Hu, Q., Liang, Y., Ding, H., Quan, X., Wang, Q., and Bai, L. (2022). Topological Partition Based Multi-Energy Flow Calculation Method for Complex Integrated Energy Systems. Energy. 244, 123152. doi:10.1016/j.energy.2022.123152

CrossRef Full Text | Google Scholar

Huang, W., Zhang, N., Yang, J., Wang, Y., and Kang, C. (2019). Optimal Configuration Planning of Multi-Energy Systems Considering Distributed Renewable Energy. IEEE Trans. Smart Grid. 10 (2), 1452–1464. doi:10.1109/TSG.2017.2767860

CrossRef Full Text | Google Scholar

Klyapovskiy, S., You, S., Cai, H., and Bindner, H. W. (2019). Integrated Planning of a Large-Scale Heat Pump in View of Heat and Power Networks. IEEE Trans. Ind. Applicat. 55 (1), 5–15. doi:10.1109/TIA.2018.2864114

CrossRef Full Text | Google Scholar

Koltsaklis, N. E., and Knápek, J. (2021). Optimal Scheduling of a Multi-Energy Microgrid. Chem. Eng. Trans. 88, 901–906. doi:10.3303/CET2188150

CrossRef Full Text | Google Scholar

Li, C., Yang, H., Shahidehpour, M., Xu, Z., Zhou, B., Cao, Y., et al. (2020). Optimal Planning of Islanded Integrated Energy System with Solar-Biogas Energy Supply. IEEE Trans. Sustain. Energ. 11 (4), 2437–2448. doi:10.1109/TSTE.2019.2958562

CrossRef Full Text | Google Scholar

Liu, N., Wang, J., and Wang, L. (2019). Hybrid Energy Sharing for Multiple Microgrids in an Integrated Heat-Electricity Energy System. IEEE Trans. Sustain. Energ. 10 (3), 1139–1151. doi:10.1109/TSTE.2018.2861986

CrossRef Full Text | Google Scholar

Luo, Z., Gu, W., Wu, Z., Wang, Z., and Tang, Y. (2018). A Robust Optimization Method for Energy Management of CCHP Microgrid. J. Mod. Power Syst. Clean. Energ. 6 (1), 132–144. doi:10.1007/s40565-017-0290-3

CrossRef Full Text | Google Scholar

Ma, T., Wu, J., Hao, L., Lee, W.-J., Yan, H., and Li, D. (2018). The Optimal Structure Planning and Energy Management Strategies of Smart Multi Energy Systems. Energy. 160, 122–141. doi:10.1016/j.energy.2018.06.198

CrossRef Full Text | Google Scholar

Nicolosi, F. F., Alberizzi, J. C., Caligiuri, C., and Renzi, M. (2021). Unit Commitment Optimization of a Micro-grid with a MILP Algorithm: Role of the Emissions, Bio-Fuels and Power Generation Technology. Energ. Rep. 7, 8639–8651. doi:10.1016/j.egyr.2021.04.020

CrossRef Full Text | Google Scholar

Qu, M., Ding, T., Jia, W., Zhu, S., Yang, Y., and Blaabjerg, F. (2021). Distributed Optimal Control of Energy Hubs for Micro-integrated Energy Systems. IEEE Trans. Syst. Man. Cybern, Syst. 51 (4), 2145–2158. doi:10.1109/TSMC.2020.3012113

CrossRef Full Text | Google Scholar

Shen, F., Zhao, L., Du, W., Zhong, W., and Qian, F. (2020). Large-scale Industrial Energy Systems Optimization under Uncertainty: A Data-Driven Robust Optimization Approach. Appl. Energ. 259, 114199. doi:10.1016/j.apenergy.2019.114199

CrossRef Full Text | Google Scholar

Sirvent, M., Kanelakis, N., Geissler, B., and Biskas, P. (2017). Linearized Model for Optimization of Coupled Electricity and Natural Gas Systems. J. Mod. Power Syst. Clean. Energ. 5 (3), 364–374. doi:10.1007/s40565-017-0275-2

CrossRef Full Text | Google Scholar

Sun, Y., Zhang, B., Ge, L., Sidrov, D., Wang, J., and Xu, Z. (2020). Day-ahead Optimization Schedule for Gas-Electric Integrated Energy System Based on Second-Order Cone Programming. Csee Jpes. 6 (1), 142–151. doi:10.17775/CSEEJPES.2019.00860

CrossRef Full Text | Google Scholar

Wang, D., Zhi, Y., Zhi, Y., Yu, B., Chen, Z., An, Q., et al. (2018). Optimal Coordination Control Strategy of Hybrid Energy Storage Systems for Tie-Line Smoothing Services in Integrated Community Energy Systems. Csee Jpes. 4 (4), 408–416. doi:10.17775/CSEEJPES.2017.01050

CrossRef Full Text | Google Scholar

Wang, Y., Zhang, N., Zhuo, Z., Kang, C., and Kirschen, D. (2018). Mixed-integer Linear Programming-Based Optimal Configuration Planning for Energy Hub: Starting from Scratch. Appl. Energ. 210, 1141–1150. doi:10.1016/j.apenergy.2017.08.114

CrossRef Full Text | Google Scholar

Wang, L., Hou, C., Ye, B., Wang, X., Yin, C., and Cong, H. (2021). Optimal Operation Analysis of Integrated Community Energy System Considering the Uncertainty of Demand Response. IEEE Trans. Power Syst. 36 (4), 3681–3691. doi:10.1109/TPWRS.2021.3051720

CrossRef Full Text | Google Scholar

Wang, W., Huang, S., Zhang, G., Liu, J., and Chen, Z. (2021). Optimal Operation of an Integrated Electricity-Heat Energy System Considering Flexible Resources Dispatch for Renewable Integration. J. Mod. Power Syst. Cle. 9 (4), 699–710. doi:10.35833/MPCE.2020.000917

CrossRef Full Text | Google Scholar

Wang, Y., Li, R., Dong, H., Ma, Y., Yang, J., Zhang, F., et al. (2019). Capacity Planning and Optimization of Business Park-Level Integrated Energy System Based on Investment Constraints. Energy. 189, 116345. doi:10.1016/j.energy.2019.116345

CrossRef Full Text | Google Scholar

Wu, J., Li, B., Chen, J., Ding, Y., Lou, Q., Xing, X., et al. (2021). Multi-objective Optimal Scheduling of Offshore Micro Integrated Energy System Considering Natural Gas Emission. Int. J. Electr. Power Energ. Syst. 125, 106535. doi:10.1016/j.ijepes.2020.106535

CrossRef Full Text | Google Scholar

Xiao, H., Pei, W., Pei, W., Dong, Z., and Kong, L. (2018). Bi-level Planning for Integrated Energy Systems Incorporating Demand Response and Energy Storage under Uncertain Environments Using Novel Metamodel. Csee Jpes. 4 (2), 155–167. doi:10.17775/CSEEJPES.2017.01260

CrossRef Full Text | Google Scholar

Yang, J., Zhang, N., Kang, C., and Xia, Q. (2018). Effect of Natural Gas Flow Dynamics in Robust Generation Scheduling under Wind Uncertainty. IEEE Trans. Power Syst. 33 (2), 2087–2097. doi:10.1109/TPWRS.2017.2733222

CrossRef Full Text | Google Scholar

Zhang, S., Gu, W., Yao, S., Lu, S., Zhou, S., and Wu, Z. (2021). Partitional Decoupling Method for Fast Calculation of Energy Flow in a Large-Scale Heat and Electricity Integrated Energy System. IEEE Trans. Sustain. Energ. 12 (1), 501–513. doi:10.1109/TSTE.2020.3008189

CrossRef Full Text | Google Scholar

Zhao, B., Conejo, A. J., and Sioshansi, R. (2018). Coordinated Expansion Planning of Natural Gas and Electric Power Systems. IEEE Trans. Power Syst. 33 (3), 3064–3075. doi:10.1109/TPWRS.2017.2759198

CrossRef Full Text | Google Scholar

Zhou, Z., Liu, P., Li, Z., and Ni, W. (2013). An Engineering Approach to the Optimal Design of Distributed Energy Systems in China. Appl. Therm. Eng. 53 (2), 387–396. doi:10.1016/j.applthermaleng.2012.01.067

CrossRef Full Text | Google Scholar

Glossary

Acronyms

AHP Analytic hierarchy process

AR Absorption refrigerator

BD Benders decomposition

CHP Combined heating and power

DRE Distributed renewable energy

EES Electric energy storage

ER Electric refrigerator

FRs Flexible resources

GT Gas turbine

HP Heat pump

HES Heat energy storage

IEHES Integrated electricity-heat energy system

MEFCS Multi-energy flow coupling system

OCCS Optimal coordination control strategy

PV Photovoltaic

SOCP Second-order cone programming

WHB Waste heat boiler

WT Wind turbine

Parameters

${\eta }_{\text{w}}$ Wind energy utilization efficiency

$r$ Blade radius

$\rho$ Air density

$P_{\text{test}}$ Test power under standard conditions

$L_{\text{test}}$ Test light intensity under standard conditions

K Power temperature coefficient

${\eta }^{\text{P,CHP}}$ Power generation efficiency

${\eta }^{\text{H,CHP}}$ Heating efficiency of cogeneration units

$L_{\text{gas}}$ Low calorific value of natural gas

${\eta }_{\text{GT}}$ Power generation efficiency

${\eta }_{\text{l}}$ Loss rate of gas turbine

${\eta }_{\text{WHB}}$ Recovery efficiency of waste heat boiler

${\eta }_{\text{HP}}$ Conversion efficiency of the heat pump

${\eta }_{\text{EC}}$ ${\eta }_{\text{AC}}$ Conversion efficiency of electric chiller and absorption chiller

${\eta }_0^{\text{AC}}$ Conversion efficiency of absorption chiller

$a_{\text{AC}}$ $b_{\text{AC}}$ $c_{\text{AC}}$ Refrigeration coefficients of absorption chiller

${\beta }_{\text{AC}}$ Load rate

${\alpha }_{\text{gas}}$ ${\alpha }_{\text{grid}}$ CO₂ emission coefficient corresponding to the combustion of natural gas and the consumption of electric energy

$c_{\text{grid}}$ $c_{\text{gas}}$ Cost coefficients corresponding to the electric energy and natural gas consumed by the system

N Total amount of equipment

$W_{PL}$ $W_{HL}$ $W_{CL}$ Total load of the system in a day

$\zeta$ Network loss rate of transmission line

$CR$ Consistency proportion

$CI$ Consistency index

$RI$ Average random consistency index

Variables

$P_t^{\text{WT}}$ Wind turbine generation power in period t

$v_t$ Air velocity in period t

$P_t^{\text{PV}}$ Output power of photovoltaic equipment in period t

$L_t^{\text{ac}}$ Light intensity in period t

${\theta }_t^{\text{s}}$ Solar panel temperature in period t

${\theta }_t^{\text{r}}$ Reference temperature in period t

${\theta }_t^{\text{out}}$ External ambient temperature in period t

$R_t$ Solar radiation intensity in period t

$P_t^{\text{CHP}}$ Electric power consumed by internal cogeneration unit in period t

$H_t^{\text{CHP}}$ Thermal power consumed by the internal cogeneration unit in period t

$G_t^{\text{CHP}}$ Gas power consumed by the internal cogeneration unit in period t

$P_t^{\text{GT}}$ Gas turbine generation power in period t

$H_t^{\text{GT}}$ Flue gas waste heat power in period t

$V_t^{\text{gas}}$ Natural gas consumption during in period t

$H_t^{\text{WHB}}$ Heat recovery power of the waste heat boiler in period t

$H_t^{\text{HP}}$ Heat energy generated of the ground source heat pump in period t

$P_t^{\text{HP}}$ Electric energy consumed of the ground source heat pump in period t

$C_t^{\text{EC}}$ Cool power generated of EC in period t

$C_t^{\text{AC}}$ Cool power generated of AC in period t

$P_t^{\text{EC}}$ Electric energy consumed of the electric chiller in period t

$H_t^{\text{AC}}$ Heat energy consumed of the absorption chiller in period t

$E_{i,t}$ Energy storage of energy storage equipment i in period t Energy storage of equipment i in period t

$P_{i,t}^{\text{c}}$ $P_{i,t}^{\text{d}}$ Charging power and discharging power of energy storage equipment i in period t

$O_{i,t}$ Output power of equipment i in period t

${\overline{P}}_i^{\text{c}}$ ${\overline{P}}_i^{\text{d}}$ Upper limit of the charging and discharging power of energy storage equipment i

$E_{i,t}$ Energy storage of energy storage equipment i in period t Energy storage of equipment i in period t

${\sigma }_i$ Consumption rate of energy storage equipment i

$c_i^{\text{ma}}$ Maintenance cost of equipment i

$P_i$ Rated capacity of equipment i

${\overline{\mu }}_i$ $\underset{¯}{{\mu }_i}$ Upper and lower limits of the charging and discharging state of the energy storage equipment i

$S_1$ $S_2$ Membership function of a very small target and maximum target

$F_i$ ith objective function

$F_{i,\min }$ $F_{i,\max }$ Minimum and maximum of the ith objective function

${\eta }_i^{\text{c}}$ ${\eta }_i^{\text{d}}$ Charging efficiency and discharging efficiency of energy storage equipment i

${\lambda }_{\max }$ Maximum eigenvalue

$p_i$ Characteristic specific gravity of the ith target

$H_i$ Entropy of the ith target

$S_i$ Membership function of the ith objective

$x$ State variable

$\mathit{h}\left(x\right)$ Equality constraint

$g\left(x\right)$ Inequality constraint

$g_{\max }$ ${\mathit{g}}_{\min }$ Upper and lower bounds of inequality

$\widehat{g}\left(x\right)$ Generalized inequality constraints

${\widehat{g}}_{\max }$ Generalized upper bounds